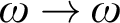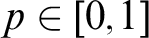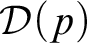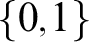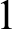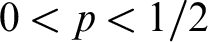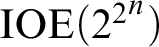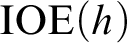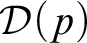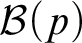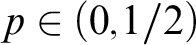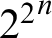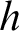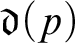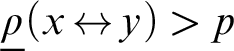1. Introduction
It is of fundamental interest in computability theory to determine the inherent computational complexity of an object, such as an infinite bit sequence, or more generally a function f on the natural numbers. To determine this complexity, one can place the object within classes of objects that all have a similar complexity. Among such classes, we will focus on highness properties. They specify a sense in which the object in question is computationally powerful.
The
$\Gamma $
-value of an infinite bit sequence A, introduced by Andrews et al. [Reference Andrews, Cai, Diamondstone, Jockusch and Lempp1], is a real in between
$0$
and
$1$
that in a sense measures how well all oracle sets in its Turing degree can be approximated by computable sequences. For each
$p\in (0,1]$
, “
$\Gamma (A)<p$
” is a highness property of A. The values
$0, 1/2$
and
$1$
occur [Reference Andrews, Cai, Diamondstone, Jockusch and Lempp1, Reference Hirschfeldt, Jockusch, McNicholl and Schupp11]. Further,
$\Gamma (A)> 1/2 {\,\Leftrightarrow\,} \Gamma (A) =1 {\,\Leftrightarrow\,} A$
is computable [Reference Hirschfeldt, Jockusch, McNicholl and Schupp11]. Andrews et al. asked whether the
$\Gamma $
-value can be strictly between
$0$
and
$1/2$
. The precise definition of
$\Gamma (A)$
will be given shortly in Section 1.1.
Monin [Reference Monin19] answered their question in the negative, and also characterized the degrees with
$\Gamma $
-value
$< 1/2$
. He built on some initial work of the present authors [Reference Monin and Nies17] involving functions that agree with each computable function infinitely often.
Our goal is to provide a systematic approach to the topic, relying on an analogy between highness properties of oracles and cardinal characteristics in set theory. In particular we apply methods analogous to the ones in [Reference Monin19] to cardinal characteristics.
Cardinal characteristics measure how far the set theoretic universe deviates from satisfying the continuum hypothesis. They are natural cardinals greater that
$\aleph _{0}$
and at most
$2^{\aleph _{0}}$
. We provide two examples. For functions
$f, g \colon {\omega } \to {\omega }$
, we say that g dominates f if
$g(n) \ge f(n)$
for sufficiently large n. The unbounding number
${\mathfrak {b}}$
is the least size of a collection of functions f such that no single function dominates the entire collection. The domination number
${\mathfrak {d}}$
is the least size of a collection of functions so that each function is dominated by a function in the collection. Clearly
${\mathfrak {b}} \le {\mathfrak {d}}$
; in appropriate models of set theory the inequality can be made strict, and one can ensure that
${\mathfrak {d}}< 2^{\aleph _{0}}$
. For an introduction to the topic see e.g. Blass [Reference Blass, Foreman and Kanamori3]. A general reference on cardinal characteristics is the book [Reference Bartoszyński and Judah2].
The analogy between cardinal characteristics and highness properties of oracles in computability theory was first noticed and studied by Rupprecht [Reference Rupprecht22, Reference Rupprecht23]. For instance, he observed that the analog of
${\mathfrak {b}}$
is the usual highness
$A^{\prime } \ge _{T} {\emptyset }^{\prime \prime }$
of an oracle A, and the analog of
${\mathfrak {d}}$
is being of hyperimmune degree. Elaborating on Rupprecht’s work, Brooke-Taylor et al. [Reference Brendle, Brooke-Taylor, Ng and Nies4] investigated the analogy via a notation system that makes it possible to automatically transfer many highness properties of oracles into cardinal characteristics, and vice versa.
The rest of the introduction will provide more detail on the notions mentioned above, and describe the main results.
1.1. Defining the
$\Gamma $
-value of a sequence
We recall how to define the
$\Gamma $
-value of an infinite bit sequence (often simply termed “sequence”); this definition will only depend on its Turing degree. For a sequence Z, also viewed as a subset of
${\omega }$
, the lower density is defined by
$$ \begin{align*} \underline \rho (Z) = \liminf\nolimits_{n} \frac{|Z \cap [0, n)|}{n}. \end{align*} $$
For sequences
$X,Y$
one denotes by
$X{\,\Leftrightarrow\,} Y$
the sequence Z such that
$Z(n) = 1$
iff
$ X(n) = Y(n)$
. To measure how closely a sequence A can be approximated by a computable sequence X, Hirschfeldt et al. [Reference Hirschfeldt, Jockusch, McNicholl and Schupp11] defined
$$ \begin{align*} \gamma(A)= {\mathop{\mathrm{sup}}} \{ \underline \rho(A\leftrightarrow X)\colon \, X \, \textrm{is computable}\}. \end{align*} $$
Clearly this depends on the particular sequence A, rather than its Turing complexity. Andrews et al. [Reference Andrews, Cai, Diamondstone, Jockusch and Lempp1] were the first to study the infimum of the
$\gamma $
-values over all Y in the Turing degree of A:
$$ \begin{align*} \Gamma(A) = \inf \{ \gamma(Y) \colon \, Y \equiv_{T} A \}. \end{align*} $$
Nies [Reference Nies, Day, Fellows, Greenberg, Khoussainov, Melnikov and Rosamond21, Section 7] contains some background on the
$\Gamma $
-value; in particular, that
$1- \Gamma (A)$
can be seen as a Hausdorff pseudodistance between
$\{Y \colon \, Y {\leq _{\text {T}}} A\}$
and the computable sets with respect to the Besicovitch distance
$\overline \rho (U \triangle V)$
between bit sequences
$U,V$
(where
$\overline \rho $
is the upper density). Thus, a large value
$\Gamma (A)$
literally means that A is “close to computable”.
1.2. Duality
Cardinal characteristics often come in pairs of dual cardinals. This duality stems from the way the characteristics are defined based on relations between suitable spaces. For instance, the unbounding number
${\mathfrak {b}}$
is the dual of the domination number
${\mathfrak {d}}$
. The detail will be given in Definition 4.1.
Brendle and Nies in [Reference Nies6, Section 7], starting from the work in [Reference Hirschfeldt, Jockusch, McNicholl and Schupp11, 1], considered for
$p \in [0,1/2]$
highness properties
${\mathcal {D}}(p)$
such that
$$ \begin{align} \Gamma(A)< p \Rightarrow A \in {\mathcal{D}}(p) \Rightarrow \Gamma(A)\le p. \end{align} $$
They defined
${\mathcal {D}}(p)$
to be the set of oracles A that compute a bit sequence Y such that
$\underline \rho ( Y {\,\Leftrightarrow\,} X) \le p$
for each computable sequence X. They then applied the framework of Rupprecht [Reference Rupprecht22], in the notation of Brooke-Taylor et al. [Reference Brendle, Brooke-Taylor, Ng and Nies4]. This led to cardinal characteristics
${\mathfrak {d}}(p)$
, the least size of a set G of bit sequences so that for each bit sequence x there is a bit sequence y in G such that
$\underline \rho (x {\,\Leftrightarrow\,} y)>p$
. Dualising this both in computability and in set theory, they introduced for each
$0\le p < 1/2$
the highness property
${\mathcal {B}}(p)$
, the class of oracles A that compute a bit sequence Y such that for each computable sequence X, we have
$\underline \rho (X {\,\Leftrightarrow\,} Y)> p$
, and the analogous cardinal characteristic
${\mathfrak {b}}(p)$
, the least size of a set F of bit sequences so that for each bit sequence y, there is a bit sequence x in F such that
$\underline \rho (x {\,\Leftrightarrow\,} y) \le p$
.
1.3. Coincidences
Extending Monin’s methods [Reference Monin and Nies17], we will show that all the highness properties
${\mathcal {D}}(p)$
coincide for
$0< p < 1/2$
, and similarly for the highness properties
${\mathcal {B}}(p)$
. Since
$\Gamma (A)< p \Rightarrow A \in {\mathcal {D}}(p)$
, we reobtain Monin’s result that
$\Gamma (A) < 1/2$
implies
$\Gamma (A) = 0$
. Via analogous methods within set theory, we show that
$\text {ZFC}$
proves the coincidence of all the
${\mathfrak {d}}(p)$
, and of all the
${\mathfrak {b}}(p)$
, for
$0< p < 1/2$
.
In Subsection 1.6 we will describe the coincidences in computability in more detail. We first need to discuss some more concepts.
1.4. Medvedev and Muchnik reducibility
A nonempty subset
${\mathcal {B}}$
of Baire space is called a mass problem. A function
$f \in {\mathcal {B}}$
is called a solution to the problem. The easiest problem in this sense is the set of all functions.
In this paper we will phrase our highness properties in the language of mass problems (rather than upward closed sets of Turing degrees as in [Reference Brendle, Brooke-Taylor, Ng and Nies4]), and compare them via Medvedev and Muchnik reducibility. The advantage of this approach is that we can keep track of potential uniformities when we give reductions showing that one property is at least as computationally powerful as another.
Let
${\mathcal {B}}$
and
$ {\mathcal {C}}$
be mass problems. The reducibilities provide two variants of saying that any solution to
${\mathcal {C}}$
yields a solution to
${\mathcal {B}}$
. The first, also called strong reducibility, is the uniform version: one writes
${\mathcal {B}} \le _{S} {\mathcal {C}}$
(and says that
$ {\mathcal {B}}$
is Medvedev reducible to
${\mathcal {C}}$
) if there is a Turing functional
$\Gamma $
with domain containing
${\mathcal {C}}$
such that
${\forall } g \in {\mathcal {C}} [ \Gamma ^{g} \in {\mathcal {B}}]$
. Note that
${\mathcal {B}} \supseteq {\mathcal {C}}$
implies
${\mathcal {B}} \le _{S} {\mathcal {C}}$
via the identity functional. One writes
${\mathcal {B}} \le _{W} {\mathcal {C}}$
(and says that
$ {\mathcal {B}}$
is weakly, or Muchnik reducible to
${\mathcal {C}}$
) if
${\forall } g \in {\mathcal {C}}\ {\exists } f \in {\mathcal {B}} [ f \le _{T} g]$
. Muchnik degrees correspond to end segments in the Turing degrees via sending
${\mathcal {C}}$
to the collection of oracles computing a member of
${\mathcal {C}}$
. In this way, viewing highness properties as mass problems and comparing them via Muchnik reducibility
$\le _{W}$
, is equivalent to viewing them as end segments in the Turing degrees and comparing them via reverse inclusion.
1.5. A pair of dual mass problems for functions
One can determine the computational complexity of an object by comparing it to computable objects of the same type. This idea was used to introduce the density-related mass problems
${\mathcal {D}}(p)$
and
${\mathcal {B}}(p)$
. We will apply it to introduce two further mass problems of importance in this paper. We say that a function f is
$\text {IOE}$
if
${\exists }^{\infty } n \, [f(n) = r(n) ]$
for each computable function r. We say that f is
$\text {AED}$
if
$\forall ^{\infty } n \, [f(n) \neq r(n) ]$
for each computable function r. (
$\text {IOE}$
stands for “infinitely often equal”, while
$\text {AED}$
stands for “almost everywhere different”.)
The study of the class
$\text {AED}$
can be traced back to Jockusch [Reference Jockusch, Fenstad, Frolov and Hilpinen12, Theorem 7]. He actually considered a stronger property of a function f he denoted by SDNR:
${\forall }^{\infty } n \, [f(n) \neq r(n) ]$
for each partial computable function r. Kjos-Hanssen et al. [Reference Kjos-Hanssen, Merkle and Stephan15, Theorem 5.1
$(1)\to (2)$
] showed that each nonhigh
$\text {AED}$
function is SDNR.
The class
$\text {IOE}$
was introduced much later. Kurtz [Reference Kurtz16] showed that the mass problem of weakly 1-generic sets is Muchnik equivalent to the functions not dominated by a computable function (the corresponding end segment consists of the hyperimmune Turing degrees). Using this fact, it is not hard to show that
$\text {IOE}$
is also Muchnik equivalent to the class of functions not dominated by a computable function.
An order function h is a nondecreasing, unbounded computable function. In computability theory, one often uses order functions as bounds to parameterize known classes of measuring computational complexity. For instance,
$\text {DNC}(h)$
is the class of diagonally noncomputable functions
$f<h$
. For another example, an oracle A is h-traceable if each A-partial computable function has a c.e. trace of size bounded by h (see e.g. [Reference Nies20, Chapter 8]).
We focus on versions of the classes
$\text {IOE}$
and
$\text {AED}$
parameterized by an order function h. By
$\text {IOE}(h)$
we denote the mass problem of functions f such
${\exists }^{\infty } n \, [f(n) = r(n) ]$
for each computable function
$r< h$
. Dually,
$\text {AED}(h)$
is the mass problem of functions
$f< h$
such that
$\forall ^{\infty } n \, [f(n) \neq r(n) ]$
for each computable function r.
Note that
$g\le h$
implies
$\text {IOE}(g) \supseteq \text {IOE}(h)$
and
$\text {AED}(g) \subseteq \text {AED}(h)$
. One can now ask the following: For an order function h that grows sufficiently much faster than an order function g, do we obtain
$\text {IOE}(g) <_{W} \text {IOE}(h)$
and
$\text {AED}(g)>_{W} \text {AED}(h)$
?
For the operator
$\text {IOE}$
, separations for some rather special cases of functions
$g,h$
were obtained in [Reference Monin and Nies17]. We answer the full question for IOE in the affirmative. Theorem 5.3, which is joint work with Joseph S. Miller that will be included here, roughly speaking states that h needs to be growing faster than
$2^{g(2^{n\cdot n})}$
for a separation.
For the operator
$\text {AED}$
, the answer was known already. Recent work of Khan and Miller [Reference Khan and Miller14] provides a hierarchy for the mass problems of low
$\text {DNR}(h)$
functions. Khan and Nies [Reference Nies8, Section 2] turned these mass problems into mass problems
$\text {AED}(\widetilde h)$
for
$\widetilde h$
close to h, preserving weak reducibility.
The characteristics
${\mathfrak {b}}(\neq ^{*}, h)$
are analogous to the mass problems
$\text {AED}(h)$
; detail will be given in Section 4. Kamo and Osuga [Reference Kamo and Osuga13] have proved that it is consistent with ZFC to have distinct cardinal characteristics
${\mathfrak {b}}(\neq ^{*}\!, h)$
depending on the growth of the function h. A similar result is unknown at present for the dual characteristics
${\mathfrak {d}}(\neq ^{*}\!, h)$
.
1.6. Density
With the reducibilities discussed in Section 1.4 in mind, the above mentioned highness properties related to
$\Gamma $
, introduced by Brendle and Nies in [Reference Nies6, Section 7], will now be considered as mass problems. They consist of
$\{0,1\}$
-valued functions on
${\omega }$
, i.e., infinite bit sequences. Let p be a real with
$0 \le p< 1$
.
${\mathcal {D}}(p)$
is the set of bit sequences y such that
$\underline \rho (x {\,\Leftrightarrow\,} y) \le p$
for each computable set x. Note that this resembles the definition of
$\text {IOE}$
.
${\mathcal {B}}(p)$
is the set of bit sequences y such that
$\underline \rho (x {\,\Leftrightarrow\,} y)> p$
for each computable set x. This resembles the definition of
$\text {AED}$
.
Clearly
$0 \le p<q < 1$
implies
${\mathcal {D}}(p) \subseteq {\mathcal {D}}(q)$
and
${\mathcal {B}}(p) \supseteq {\mathcal {B}}(q)$
. Our first result, Theorem 3.5, shows that there actually is no proper hierarchy in the Muchnik degrees when the parameter is positive. It also provides a characterization by a combinatorial class, relying on agreement of functions with computable functions, rather than on density:
$$ \begin{align*} {\mathcal{D}}(p)\equiv_{W} \textrm{IOE}(2^{(2^{n})} ) \textrm{ and } {\mathcal{B}}(p)\equiv_{S} \textrm{ AED }(2^{(2^{n})}) \end{align*} $$
for arbitrary
$p\in (0,1/2)$
. The corresponding result for cardinal characteristics is Theorem 4.5 below. The outer exponential function in the bound simply stems from the fact that we view function values as encoded by binary numbers, which correspond to blocks in the bit sequences: if a bound h has the form
$2^{\widehat {h}}$
for an order function
$\widehat {h}$
, then a function
$f < h$
naturally corresponds to a bit sequence which is the concatenation of blocks of length
$\widehat {h}(i)$
for
$i \in {\omega }$
.
As part of the proof of Theorem 3.5, we show in a lemma that the parameterized classes
$\text {IOE}(h)$
and
$\text {AED}(h)$
don’t depend too sensitively on the bound h: if
$g(n) = h(2n)$
then
$\text {IOE}(g) \equiv _{W} \text {IOE}(h)$
and
$\text {AED}(g) \equiv _{S} \text {AED}(h)$
. Since the first equivalence we obtain is merely Muchnik, in Theorem 3.5 we also only have Muchnik in its first equivalence. Note that by the lemma, in the above, we can replace
$\text {IOE}(2^{(2^{n})})$
by
$\text {IOE}(2^{(2^{n\cdot r})})$
for any
$r>0$
.
We remark that after the first version of this paper was posted on arXiv in December 2017 [Reference Monin and Nies18], as part of a large study, Greenberg et al. [Reference Greenberg, Kuyper and Turetsky9] sketched their own version of our coincidence results for highness classes and for cardinal characteristics. Based on the work of Rupprecht, they introduced a systematic machinery that also applies to reductions. It now suffices to state a single abstract theorem [Reference Greenberg, Kuyper and Turetsky9, Theorem 6.15], which implies all four coincidences.
We think that each approach has its advantages. Ours is more direct and requires the reader to assimilate less general theory before proceeding to the result; it also deals in a concrete way with the nonuniformities in the computability case, for instance in Lemma 3.1. Their approach is general, and hence superior to ours towards understanding the reason for the persistent analogies between set theory and computability, and the dualities within each area. Also, once the general machinery is available, it saves work in proving particular coincidences.
2. Defining mass problems based on relations
Towards proving our main theorems, we will need a general formalism to define mass problems based on relations, similar to [Reference Brendle, Brooke-Taylor, Ng and Nies4]. We consider “spaces”
$X,Y$
, which will be effectively closed subsets of Baire space. Let the variable x range over X, and let y range over Y. Let
$R \subseteq X \times Y$
be a relation, and let
$S = \{ \langle y,x \rangle \in Y \times X \colon \neg x \mathbin{R} y\}$
.
Definition 2.1. We define the pair of dual mass problems
$$ \begin{align*} {\mathcal{B}}(R) &= \{ y\in Y \colon {\forall} x \textrm{ computable } [x\mathbin{R}y] \} \\ {\mathcal{D}}(R) = {\mathcal{B}}(S) &= \{ x \in X \colon {\forall} y \textrm{ computable } [\neg x\mathbin{R}y] \}. \end{align*} $$
To reobtain the mass problems discussed in the introduction, we consider the following two types of relation.
Definition 2.2. 1. Let
$h \colon \omega \to \omega - \{0,1\} $
. Define for
$ x \in {{\hspace{-0.0001pt}}}^{\omega }\omega $
and
$y \in \prod _{n} \{0, \ldots , h(n)-1\} \subseteq {{\hspace{-0.0001pt}}}^{\omega }\omega $
,
$$ \begin{align*} x \neq^{*}_{h} y \Leftrightarrow {\forall}^{\infty} n \, [ x(n) \neq y(n)]. \end{align*} $$
2. Recall that
$\underline \rho (z) = \liminf _{n} |z \cap n|/n$
for a bit sequence z. Let
$ 0 \le p < 1$
. Define, for
$x,y \in {{\hspace{-0.0001pt}}}^{\omega } 2$
$$ \begin{align*} x \bowtie_{p} y \Leftrightarrow \underline \rho (x \leftrightarrow y)>p, \end{align*} $$
where
$x {\,\Leftrightarrow\,} y$
is the set of n such that
$x(n) = y(n)$
.
For the convenience of the reader we summarise the specific mass problems determined by these relations.
Remark 2.3. Let h be a computable function. Let p be a real with
${0 \le p \le 1/2}$
.
is our notation for
${\mathcal {D}}(\neq ^{*}_{h})$
, the set of functions y such that for each computable function
$x < h$
, we have
${\exists }^{\infty } n \, x(n) = y(n)$
.
is our notation for
${\mathcal {B}}(\neq ^{*}_{h})$
, the set of functions
$y < h$
such that for each computable function x, we have
${\forall }^{\infty } n \, x(n) \neq y(n)$
.
is our short notation for
${\mathcal {D}}(\bowtie _{p})$
, the set of bit sequences y such that for each computable set x, we have
$\underline {\rho } (x {\,\Leftrightarrow\,} y) \leq p$
.
is our short notation for
${\mathcal{B}}(\bowtie _{p})$
, the set of bit sequences y such that for each computable set x, we have
$\underline {\rho } (x {\,\Leftrightarrow\,} y)> p$
.
3. Coincidences of Muchnik degrees
As mentioned, our goal is to show
$$ \begin{align*} \mathcal{D}(p) \equiv_{W} \textrm{IOE}(2^{(2^{n})}) \textrm{ and } \mathcal{B}(p) \equiv_{S} \textrm{ AED }(2^{(2^{n})}) \end{align*} $$
for arbitrary
$p\in (0,1/2)$
. We begin with some preliminary facts of independent interest. On occasion we denote a function
$\lambda n. f(n)$
simply by
$f(n)$
.
-
(i) Let h be nondecreasing and
$g(n) = h(2n)$
. We have
$\mathrm{IOE}(h) \equiv _{W}\mathrm{IOE}(g)$
and
$\mathrm{AED}(h) \equiv _{S} \mathrm{AED}(g)$
. -
(ii) For each
$a,b>1$
we have
$\mathrm{IOE}(2^{(a^{n})})\equiv _{W}\mathrm{IOE}(2^{(b^{n})})$
and
$\mathrm{AED}(2^{(a^{n})}) \equiv _{S} \mathrm{AED}(2^{(b^{n})})$
.
Note that the duality appears to be incomplete: for the statement involving the
$\mathrm{IOE}$
-type problems, we only obtain weak equivalence. We ignore at present whether strong equivalence holds.
Proof. (i) Trivially,
$h \le g$
simplies
$\mathrm{IOE}(h) \supseteq \mathrm{IOE}(g)$
and
$\mathrm{AED}(h) \subseteq \mathrm{AED}(g)$
. So it suffices to provide only one reduction in each case.
Let
$y < h$
be a function in
$\mathrm{IOE}(h)$
. Let
$\widehat {y}_{1} < h(2n)$
and
$\widehat {y}_{2} < h(2n+1)$
be defined by
$\widehat {y}_{1}(n) = y(2n)$
and
$\widehat {y}_{2}(n) = y(2n+1)$
. We claim that at least one function among
$\widehat {y}_{1}, \widehat {y}_{2}$
belongs to
$\mathrm{IOE}( g)$
. Suppose otherwise. Then there are computable functions
$x_{1},x_{2} < g$
which differ almost all the time from
$\widehat {y}_{1}$
and
$\widehat {y}_{2}$
, respectively. Since h is nondecreasing, the computable function x defined by
$x(2n) = x_{1}(n)$
and
$x(2n+1) = x_{2}(n)$
satisfies
$x < h$
. It is clear that x differs almost all the time from y, which contradicts
$y \in \mathrm{IOE}(h)$
.
Let
$y < g$
be a function in
$\mathrm{AED}( g)$
. Let
$\widehat {y}(2n+i) = y(n)$
for
$i \le 1$
, so that
$\widehat {y} < h$
. Given any computable function x, for almost every n we have
$x(2n) \neq y(n) $
and
$x(2n+1) \neq y(n)$
. Therefore
$ x(n) \neq \widehat {y}(n)$
for almost every n. Hence
$\widehat {y} \in \mathrm{AED}(h)$
.
(ii) is immediate from (i) by iteration, using that
$a^{2^{i}}>b$
and
$b^{2^{i}}>a$
for sufficiently large i.⊣
The following operators will be used for the rest of the section.
Definition 3.2. (The operators
$L_{h}$
and
$K_{h}$
)
Let h be a function of the form
$2^{\widehat {h}}$
with
$\widehat {h} \colon \, \omega \to \omega $
, and let
$X_{h}$
be the space of all h-bounded functions. For such a function we view
$x(n)$
either as a number, or as a binary string of length
$\widehat {h}(n)$
via the binary expansion with leading zeros allowed. We define
$L_{h}\colon X_{h} \to {{\hspace{-0.0001pt}}}^{\omega } 2$
by
$L_{h}(x) = \prod _{n} x(n) $
, i.e. the concatenation of these strings. We let
$K_{h} \colon {{\hspace{-0.0001pt}}}^{\omega } 2 \to X_{h}$
be the inverse of
$L_{h}$
.
Lemma 3.3. Let
$a \in \omega - \{0\}$
. We have
$$ \begin{align*} \mathrm{IOE}(2^{(a^{n})}) \ge_{S} {\mathcal{D}}(1/a) \mbox{ and }\mathrm{AED} (2^{(a^{n})}) \le_{S} {\mathcal{B}}(1/a). \end{align*} $$
Proof. Let
$I_{m}$
for
$m \ge 2$
be the
$(m-1)$
th consecutive interval of length
$a^{m}$
in
$\omega -\{0\}$
, i.e.
$$ \begin{align*} I_{m} = \left [\frac{a^{m}-1}{a-1} , \frac{a^{m+1} -1 } {a-1}\right). \end{align*} $$
Let
$h(m) = 2^{(a^{m})}$
. Let us first show that
$\mathrm{IOE}(2^{(a^{n})}) \ge _{S} {\mathcal {D}}(1/a)$
. Let
$y < 2^{(a^{n})}$
be a function in
$\mathrm{IOE}(2^{(a^{n})})$
and let
$\widehat {y} = L_{h}(y)$
. Given a computable set x, let
${x^{\prime }=K_{h}(1-x)}$
(where
$1-x$
is the complement of x). As
$x^{\prime }(m)=y(m)$
for infinitely many m, for infinitely many intervals m, all bits of x with location in
$I_{m}$
differ from all the bits of
$\widehat {y}$
in this location. It follows that
$\widehat {y} \in {\mathcal {D}}(1/a)$
.
Let us now show that
$\mathrm{AED}(2^{(a^{n})}) \le _{S} {\mathcal {B}}(1/a)$
. Let
$y \in {\mathcal {B}}(1/a)$
, and let
$\widehat {y} = K_{h}(y)$
. Given a computable function
$x < h$
, let
$x^{\prime } = 1- L_{h}(x)$
. Since
$\underline \rho ( x^{\prime } {\,\Leftrightarrow\,} y)> 1/a$
, for large enough n, there is
$k \in I_{n}$
such that
$x^{\prime }(k) = y(k)$
. Hence we cannot have
$x(n) = \widehat {y}(n)$
. Thus
$\widehat {y} \in \mathrm{AED}(2^{(a^{n})})$
.⊣
Remark 3.4. Let
$\widehat {h}$
be an order function such that
${\forall } a\, {\forall }^{\infty } m \, \widehat {h}(m) \ge a^{m}$
. An argument similar to the one in the foregoing proof shows that
$$ \begin{align*} \mathrm{IOE}(2^{\widehat{h}(m)}) \ge_{S} {\mathcal{D}}(0) \textrm{ and AED } (2^{\widehat{h}(m)}) \le_{S} {\mathcal{B}}(0). \end{align*} $$
In this case one chooses the mth interval of length
$\widehat {h} (m)$
.
Theorem 3.5. Fix any
$p\in (0,1/2)$
. We have
$$ \begin{align*} \mathcal{D}(p) \equiv_{W} \mathrm{IOE} ({2^{(2^{n})}}) \textrm{ and } \mathcal{B}(p)\equiv_{S} \mathrm{AED}({2^{(2^{n})}}). \end{align*} $$
The rest of the section is dedicated to the proof of Theorem 3.5. The two foregoing lemmas imply
$\mathcal {D}(p)\le _{W} \mathrm{IOE}({2^{(2^{n})}})$
and
$\mathcal {B}(p)\ge _{S} \mathrm{AED}({2^{(2^{n})}})$
. It remains to show the more difficult converse reductions
${\mathcal {D}}(p)\ge _{W} \mathrm{IOE} ({2^{(2^{n})}}) $
and
${\mathcal {B}}(p)\le _{S} \mathrm{AED}({2^{(2^{n})}})$
. Let us informally describe the proof of the first reduction, which is based on arguments in Monin’s proof [Reference Monin19] that
$\Gamma (A)< 1/2 \Leftrightarrow \Gamma (A) = 0$
for each
$A \subseteq \omega $
.
Given
$A \in {\mathcal {D}}(p)$
we want to find a function
$ f{\leq _{\text {T}}} A$
that agrees with each computable function
$g < 2^{(2^{n})}$
infinitely often. For an appropriate k let
$\widehat {h}(n) = \lfloor {2^{n/k}}\rfloor $
and
$h(n) =2^{\widehat {h}(n)}$
. We split the bits of A into consecutive intervals of length
$\widehat {h}(n)$
. The first step (Claim 3.8) makes the crucial transition from the density setting towards the setting of functions agreeing on certain arguments. We will show that for k large enough, the function
$f_{0}=K_{h}(A)< h$
has the property that for each computable function
$g< h$
, for infinitely many n,
$f_{0}(n)$
and
$ g(n) $
disagree on a fraction of fewer than p bits when viewed as binary strings of length
$\widehat {h}(n)$
.
In the second step (Claim 3.12) we use
$f_{0}$
to compute a special kind of approximation s to computable functions: for each n,
$s(n)$
is a set of L many values (where L is an appropriate constant) such that for every computable function
$g < h$
we have
$\exists ^{\infty } n\ g(n) \in s(n)$
. Such a function s will be called a slalom (another term in use is “trace”); we also say that s captures g. This important step uses a result from the theory of error-correcting codes, which determines the constant L.
In the third step (Claim 3.13), which is nonuniform, we replace s by a slalom
$s^{\prime }$
such that still
$s^{\prime }(n)$
has size at most L, but now all computable functions g with
$g(n) < 2^{(2^{Ln})}$
are captured infinitely often.
In a final, nonuniform step (Claim 3.14) we then compute from
$s^{\prime }$
a function f as required; for some i,
$f(n)$
is the ith block of length
$2^{n}$
of the ith element of
$s(n)$
.
We now provide the detailed argument. For this recall Definition 2.1.
Definition 3.6. For strings
$x,y$
of length r, the normalized Hamming distance is defined as the proportion of bits on which
$x,y$
disagree, that is,
$$ \begin{align*} d(x,y) = \frac 1 r |\{ i \colon x(n) (i) \neq y(n)(i) \}|. \end{align*} $$
Definition 3.7. Let h be a function of the form
$2^{\widehat {h}}$
with
$\widehat {h} \colon \, \omega \to \omega $
, and let
$X_{h}$
be the space of h-bounded functions. Let
$q \in (0, 1/2)$
. We define a relation on
$X_{h} \times X_{h}$
by:
$$ \begin{align*} x \neq^{*}_{\widehat{h},q} y \Leftrightarrow {\forall}^{\infty} n \, [ d(x(n), y(n)) \ge q] \end{align*} $$
namely for almost every n the strings
$x(n)$
and
$y(n)$
disagree on a proportion of at least q of the bits. We will usually write
${\langle}\!\neq ^{*}\!\!, \widehat {h},q {\rangle }$
for this relation.
Claim 3.8. Let
$q \in (0, 1/2)$
. For each
$c\in \omega $
such that
$\frac 2 c<q$
, there is
$k \in \omega $
such that
$$ \begin{align*} {\mathcal{D}}\bigg(q- \frac{2}{c}\bigg) &\ge_{S} {\mathcal{D}} {\langle}\! \neq^{*}\!\!, \lfloor {2^{n/k}}\rfloor, q{\rangle} \textrm{ and } \\ {\mathcal{B}}\bigg(q- \frac{2}{c}\bigg) &\le_{S} {\mathcal{B}} {\langle}\! \neq^{*}\!\!, \lfloor {2^{n/k}} \rfloor, q{\rangle}. \end{align*} $$
Proof. Let k be large enough so that
${\alpha } -1 < \frac {1}{2c}$
where
${\alpha } = {2^{1/k}}$
. Let
$\widehat {h}(n) = \lfloor {\alpha }^{n} \rfloor $
and
$h = {2^{\widehat {h}}}$
. Write
$H(n) = \sum _{r\le n} \widehat {h}(r)$
. By the usual formula for the geometric series,
$$ \begin{align*} \sum\limits_{r\le n} {\alpha}^{r} = \frac {{\alpha}^{n+1} -1} {{\alpha} -1} \le H(n)+ n+1 \end{align*} $$
and therefore
${\alpha }^{n+1} -1 \le \frac 1 {2c} (H(n)+n+1)$
. If n is sufficiently large so that
$H(n) \ge n+1 +2c$
, we now have
$$ \begin{align} \widehat{h}(n+1) \le \frac 1 c H(n). \end{align} $$
To prove the claim we also rely on the following.
Fact 3.9. Let
$x,y < h$
be functions such that
${\forall }^{\infty } n \, [d(x(n), y(n) ) \leq 1 - q]$
. Then
$\underline \rho (L_{h}(x) {\,\Leftrightarrow\,} L_{h}(y))> q- \frac 2c$
.
To see this, note that by hypothesis, for almost every n we have that
$L_{h}(y) {\! \upharpoonright _{H(n)}}$
agrees with
$L_{h}(x) {\! \upharpoonright _{H(n)}}$
on a fraction of at least q bits. For any n and any m with
$H(n) \leq m \leq {H(n+1)}$
, we have that
$L_{h}(y) {\! \upharpoonright _{m}}$
agrees with
$L_{h}(x) {\! \upharpoonright _{m}}$
on a fraction of at least
$\frac {H(n) q}{H(n) + \widehat {h}(n+1)}$
bits, which is by (2) a fraction of at least
$\frac {H(n) q}{H(n) + (1/c) H(n)}$
bits. It follows that for almost every m, we have that
$L_{h}(y) {\! \upharpoonright _{m}}$
agrees with
$L_{h}(x) {\! \upharpoonright _{m}}$
on a fraction of at least
$\frac {q}{1 + 1/c}> q - \frac 2c$
bits. This implies in particular that
$\underline \rho (L_{h}(x) {\,\Leftrightarrow\,} L_{h}(y))> q- \frac 2c$
. The fact is proved.
First we show that
${\mathcal {D}}(q- \frac 2c) \ge _{S} {\mathcal {D}} {\langle}\!\! \neq ^{*}, \lfloor {2^{n/k}} \rfloor , q{\rangle }$
. Let
$y \in {\mathcal {D}}(q- \frac 2c)$
. Let
$y^{\prime } = K_{h}(y)$
. By the fact above, there is no computable function
$x < h$
such that
${\forall }^{\infty } n \, [d(x(n), y^{\prime }(n) ) \leq 1 - q]$
, as otherwise we would have
$L_{h}(y^{\prime }) = y \notin {\mathcal {D}}(q- \frac 2c)$
which is a contradiction. Therefore, for every computable function
$x < h$
we have
$\exists ^{\infty } n \, [d(x(n), y^{\prime }(n) )> 1 - q]$
. Now let
$x < h$
be a computable function and let
$x^{\prime } = K_{h}(1 - L_{h}(x))$
. As
$x^{\prime } < h$
is computable we must have
$\exists ^{\infty } n \, [d(x^{\prime }(n), y^{\prime }(n) )> 1 - q]$
. But then we also have
$\exists ^{\infty } n \, [d(x(n), y^{\prime }(n) ) < q]$
. As this is true for any computable function
$x < h$
we then have
$y^{\prime } \in {\mathcal {D}} {\langle}\!\! \neq ^{*}, \lfloor {2^{n/k}} \rfloor , q{\rangle }$
.
Second, we show that
${\mathcal {B}}(q- 2/c) \le _{S} {\mathcal {B}} {\langle}\!\! \neq ^{*}, \lfloor {2^{n/k}} \rfloor , q{\rangle }$
.
Let
$y \in {\mathcal {B}} {\langle } \neq ^{*}, \lfloor {2^{n/k}} \rfloor , q{\rangle }$
. Thus,
$y< h$
and
${\forall }^{\infty } n \, [d(x(n), y(n) \ge q]$
for each computable function
$x < h$
. Let
$y^{\prime } = K_{h}(1 - L_{h}(y))$
. Then
$$ \begin{align*} {\forall}^{\infty} n \, [d(x(n), y^{\prime}(n) ) \le 1 - q] \end{align*} $$
for each computable function
$x < h$
. By the fact above, we then have that
$\underline \rho (L_{h}(x) {\,\Leftrightarrow\,} L_{h}(y^{\prime }))> q- 2/c$
for each computable function
$x < h$
. It follows that
$L_{h}(y^{\prime }) \in B(q- 2/c)$
.⊣3.8
For
$L \in \omega $
, an L-slalom (also called trace) is a function
$s\colon \, \omega \to \omega ^{[\le L]}$
, i.e. a function that maps natural numbers to sets of natural numbers with a size of at most L.
Definition 3.10. Fix a function
$u \colon \omega \to \omega $
and
$L \in \omega $
. Let X be the space of L-slaloms (or traces) s such that
$\max s(n) < u(n)$
for each n. Thus s maps natural numbers to sets of natural numbers of size at most L, represented by strong indices. Let Y be the set of functions such that
$y(n) < u (n)$
for each n. Define a relation on
$X \times Y$
by
$$ \begin{align*} s \not \ni^{*}_{u,L} y \Leftrightarrow {\forall}^{\infty} n [s(n) \not \ni y(n)]. \end{align*} $$
We will write
${\langle } \not \ni ^{*}, u ,L {\rangle } $
for this relation.
For what follows, we use the list decoding capacity theorem from the theory of error-correcting codes due to Elias [Reference Elias5]. Given
$q $
as above and
$L \in \omega $
, for each r there is a “fairly large” set C of strings of length r (the allowed code words) such that for each string, at most L strings in C have normalized Hamming distance less than q from
${\sigma }$
. Intuitively speaking, there is only a small set of strings that could be the error-corrected version of
${\sigma }$
.
Given a string
${\sigma }$
of length r, let
$B_{q}({\sigma })$
denote an open ball of radius q around
${\sigma }$
in the normalized Hamming distance, namely,
$$ \begin{align*} B_{q}({\sigma}) = \{ \tau \in {{\hspace{-0.0001pt}}}^{r} 2 \colon \, \sigma, \tau \textrm{ disagree on fewer than } qr \textrm{ bits} \}. \end{align*} $$
Theorem 3.11. (List decoding, Elias [Reference Elias5])
Let
$q\in (0,1/2)$
. There are
$\epsilon>0$
and
$L \in \omega $
such that for each r, there is a set C of
${2^{\lfloor \epsilon r \rfloor }}$
strings of length r as follows:
$$ \begin{align*} \forall {\sigma} \in {{\hspace{-0.0001pt}}}^{r} 2 \, \big[ | B_{q}({\sigma}) \cap C | \le L\big]. \end{align*} $$
The previous theorem allows us to show the following:
Claim 3.12. Given
$q < 1/2$
, let
$L, \epsilon $
be as in Theorem
3.11
. Fix a nondecreasing computable function
$\widehat {h}$
, and let
$u(n)= {2^{\lfloor \epsilon \widehat {h}(n) \rfloor }}$
. We have
$$ \begin{align*} {\mathcal{D}} {\langle}\!\! \neq^{*}\!\!, \widehat{h} , q{\rangle} \ge_{S} {\mathcal{D}} {\langle}\!\! \not \ni^{*}\!\!, u,L {\rangle} \textrm{ and } {\mathcal{B}} {\langle}\!\! \neq^{*}\!\!, \widehat{h} , q{\rangle} \leq_{S} {\mathcal{B}} {\langle}\!\! \not \ni^{*}\!\!, u,L {\rangle}. \end{align*} $$
Proof. Given a number r of the form
$\widehat {h}(n)$
, one can compute a set
$C= C_{r}$
as in Theorem 3.11. Since
$|C_{r}| = {2^{\lfloor \epsilon r \rfloor }}$
there is a uniformly computable sequence
$\langle \sigma ^{r}_{i}\rangle _{i< {2^{\lfloor \epsilon r \rfloor }}}$
listing
$C_{r}$
in increasing lexicographical order.
First we show that
${\mathcal {D}} {\langle}\!\! \neq ^{*}\!\!, \widehat {h} , q{\rangle } \ge _{S} {\mathcal {D}} {\langle}\!\! \not \ni ^{*}, u,L {\rangle }$
. Suppose that
$y \in {\mathcal {D}} {\langle}\!\! \neq ^{*}\!\!, \widehat {h} , q{\rangle }$
. Let s be the uniformly y-computable L-slalom such that
$$ \begin{align*} s(n) = \{i < u(n) \colon \, d({\sigma}^{\widehat{h}(n)}_{i}, y(n) ) < q\}. \end{align*} $$
Let now
$x < u$
be a computable function. Since
$d({\sigma }^{\widehat {h}(n)}_{x(n)}, y(n) ) < q$
for infinitely many n, for infinitely many n we have
$x(n) \in s(n)$
. It follows that
$s \in {{\mathcal {D}} {\langle}\! \not \ni ^{*}\!\!, u,L {\rangle }}$
, as required.
Second, we show that
${\mathcal {B}} {\langle}\!\! \not \ni ^{*}\!\!, u,L {\rangle } \geq _{S} {\mathcal {B}} {\langle}\!\! \neq ^{*}\!\!, \widehat {h} , q{\rangle }$
. Suppose that
$y \in {{\mathcal {B}} {\langle}\!\! \not \ni ^{*}\!\!, u,L {\rangle }}$
. Let
$h = 2^{\widehat {h}}$
, and let
$\widetilde y < h $
be the function given by
$\widetilde y(n)= {\sigma }^{\widehat {h}(n)}_{y(n)}$
. We show that
$\widetilde y \in {\mathcal {B}} {\langle}\!\! \neq ^{*}\!\!, \widehat {h} , q{\rangle }$
. Let
$x < h$
be a computable function. Let
$$ \begin{align*} s_{x}(n) = \{i < u(n) \colon \, d({\sigma}^{\widehat{h}(n)}_{i}, x(n) )< q\}. \end{align*} $$
Note that
$\langle s_{x}(n) \rangle _{n \in \omega }$
is an L-slalom because the listing
$\langle {\sigma ^{r}_{i}}\rangle _{i < 2^{\lfloor \epsilon r \rfloor }}$
has no repetitions. Since
$y \in {\mathcal {B}} \langle \not \ni ^{*}\!\!, u,L \rangle $
, for almost every n we have
$y(n) \not \in s_{x}(n)$
. Hence also for almost every n we have
$d(\widetilde y(n),x(n) \ge q$
, as required.⊣3.12
We next need an amplification tool in the context of slaloms. The proof is almost Lemma 3.1(i), so we omit it.
Claim 3.13. Let
$ L \in \omega $
, let the computable function u be nondecreasing and let
$w(n) = u(2n)$
. We have
$$ \begin{align*} {\mathcal{D}} {\langle}\!\! \not \ni^{*}\!\!, u,L {\rangle} \equiv_{W} {\mathcal{D}} {\langle}\!\! \not \ni^{*}\!\!, w,L {\rangle} \textrm{ and } {\mathcal{B}} {\langle}\!\! \not \ni^{*}\!\!,u, L {\rangle} \equiv_{S} {\mathcal{B}}{\langle}\!\! \not \ni^{*}\!\!,w,L{\rangle}. \end{align*} $$
Iterating the claim, starting with the function
$\widehat {h}(n) = \lfloor 2^{n/k}\rfloor $
with k as in Claim 3.8, we obtain that
${\mathcal {D}}\langle\!\! \not \ni ^{*}\!\!, 2^{\widehat {h}}, L\rangle \equiv _{W} {\mathcal {D}} \langle\!\! \not \ni ^{*}\!\!,{2^{(L 2^{n})}}, L\rangle $
and
${{\mathcal {B}}{\langle}\!\! \not \ni ^{*}\!\!, 2^{\widehat {h}}, L\rangle \equiv _{S} {\mathcal {B}} \langle\! \not \ni ^{*}\!\!,{2^{(L 2^{n})}}, L\rangle }$
. It remains to verify the following, which would work for any computable function
$\widehat {h}(n)$
in place of the
$2^{n}$
in the exponents.
$$ \begin{align*} \mathcal{D} \langle\not \ni^{*}\!\!,2^{(L 2^{n})}, L\rangle \geq_{W}\ \mathrm{IOE}(2^{(2^{n})}) \textrm{ and } {\mathcal{B}} {\langle}\! \not \ni^{*}\!\!,{2^{(L 2^{n})}}, L {\rangle} \leq_{S}\ \mathrm{AED}(2^{(2^{n})}). \end{align*} $$
Proof. Given n, we write a number
$k< 2^{(L 2^{n})}$
in binary with leading zeros if necessary, and so can view k as a binary string of length
$L {2^{n}}$
. We view such a string as consisting of L consecutive blocks of length
${2^{n}}$
.
First we show
${\mathcal {D}} \langle \not \ni ^{*}\!\!, 2^{(L 2^{n})}, L\rangle \geq _{W}\mathrm{IOE}(2^{(2^{n})})$
. Let
$s \in {\mathcal {D}} {\langle}\! \not \ni ^{*}\!\!, 2^{(L 2^{n})}, L \rangle $
. For every
$i < L$
, let
$y_{i}$
be the s-computable function such that
$y_{i}(n)$
is the ith block of the ith element of
$s(n)$
. Suppose for a contradiction that for every i we have a computable function
$x_{i} \leq 2^{(2^{n})}$
which differs on almost every argument from
$y_{i}$
. Let
$x \leq 2^{(L2^{n})}$
be the computable function defined by
$x(n)$
to be the concatenation of
$x_{i}(n)$
for each
$i \leq L$
. Then also for almost every n we have
$s(n) \not \ni x(n)$
, which is a contradiction. Therefore we must have that
$y_{i} \in \mathrm{IOE}({2^{(2^{n})}})$
for some
$i \leq L$
.
Second, we show
$\mathrm{AED}(2^{(2^{n})}) \geq _{S} {\mathcal {B}} {\langle}\!\! \not \ni ^{*}\!\!, {2^{(L 2^{n})}}, L\rangle $
. Let
$y \in \mathrm{AED}(2^{(2^{n})})$
. That is,
$y< 2^{(2^{n})}$
and
${\forall }^{\infty } n \, x(n) \neq y(n)$
for each computable function x. Let
$y^{\prime }$
be the function bounded by
$2^{(L2^{n})}$
such that for each n, each block of
$y^{\prime }(n)$
equals
$y(n)$
. Given a computable L-slalom s with
$\max s(n) < 2^{(L2^{n})}$
, for
$i< L$
let
$x_{i}$
be the computable function such that
$x_{i}(n) $
is the ith block of the ith element of
$s(n)$
(as before we may assume that each string in
$s(n)$
has length
$L2^{n}$
). For sufficiently large n, we have for all
$i < L$
that
$y(n) \neq x_{i}(n)$
. Hence
${\forall }^{\infty } n \, s(n) \not \ni y^{\prime }(n)$
and thus
$y^{\prime } \in {\mathcal {B}} {\langle}\! \not \ni ^{*}\!\!,{2^{(L2^{n})}}\rangle $
.⊣3.14
Using the results above, we can now finish the arguments that
${\mathcal {D}}(p) \geq _{W} \mathrm{IOE}({2^{(2^{n})}})$
and
$\mathrm{AED}(2^{(2^{n})}) \geq _{S} {\mathcal {B}}(p)$
.
Proof of Theorem 3.5, completed Pick c large enough such that
${q= p+\frac 2c} < 1/2$
. By Claim 3.8 there is k such that
$$ \begin{align*} {\mathcal{D}}(p) \geq_{S} {\mathcal{D}} {\langle}\!\! \neq^{*}\!\!, \lfloor {2^{n/k}} \rfloor, q{\rangle} \textrm{ and } {\mathcal{B}} {\langle}\!\! \neq^{*}\!\!, \lfloor {2^{n/k}} \rfloor, q{\rangle} \geq_{S} {\mathcal{B}}(p). \end{align*} $$
By Claim 3.12 there are
$L\in \omega $
and
$\epsilon>0$
such that where
$\widehat {h}(n) = \lfloor {2^{n/k}}\rfloor $
and
${u(n)= {2^{\lfloor \epsilon \widehat {h}(n) \rfloor }}}$
,
$$ \begin{align*} {\mathcal{D}} {\langle}\!\! \neq^{*}\!\!, \widehat{h} , q{\rangle} \ge_{S} {\mathcal{D}} {\langle}\!\! \not \ni^{*}\!\!, u,L {\rangle}\quad \textrm{and}\quad {\mathcal{B}} {\langle}\!\!\! \not \ni^{*}\!\!, u,L {\rangle} \geq_{S} {\mathcal{B}} {\langle}\! \neq^{*}\!\!, \widehat{h} , q{\rangle}. \end{align*} $$
Applying Claim 3.13 sufficiently often we have
$$ \begin{align*} {\mathcal{D}} {\langle}\!\! \not \ni^{*}\!\!, u,L {\rangle} \equiv_{W} {\mathcal{D}} {\langle}\!\! \not \ni^{*}\!\!, {2^{(L2^{n})}}, L {\rangle}\quad \textrm{and}\quad {\mathcal{B}} {\langle}\!\! \not \ni^{*}\!\!,u, L {\rangle} \equiv_{S} {\mathcal{B}}{\langle}\!\! \not \ni^{*}\!\!, {2^{(L2^{n})}}, L{\rangle}. \end{align*} $$
Finally
$$ \begin{align*} {\mathcal{D}} {\langle}\!\! \not \ni^{*}\!\!,{2^{(L 2^{n})}}, L {\rangle} \geq_{W}\mathrm{IOE}(2^{(2^{n})})\quad \textrm{and}\quad \mathrm{AED } (2^{(2^{n})}) \geq_{S} {\mathcal{B}} {\langle}\!\! \not \ni^{*}\!\!,2^{(L2^{n})}, L {\rangle}. \end{align*} $$
by Claim 3.14. Combining all this yields the theorem.⊣3.5
The
$\Delta $
-value of a Turing oracle
The
$\Gamma $
-value of a Turing oracle A was defined in Subsection 1.1 of the introduction. It is closely connected to the classes
${\mathcal {D}}(p)$
as in Equation 1 above. (Recall that we now view these classes as mass problems, so in Equation 1 we replace
$A \in {\mathcal {D}}(p)$
there by
${\exists } Y \le _{T} A \, [ Y \in {\mathcal {D}}(p)] $
.) Its dual was first considered by Merkle, Stephan and the second author [Reference Nies7, Part 3], and then in [Reference Nies, Day, Fellows, Greenberg, Khoussainov, Melnikov and Rosamond21, Section 7].
Definition 3.15. Let
$$ \begin{align*} \delta(A)&= \inf\{ \underline \rho(A\leftrightarrow X)\colon \, X \, \textrm{computable} \}\\ \Delta(A) & = \sup \{ \delta(Y) \colon \, Y \le_{T} A \}. \end{align*} $$
Intuitively,
$\Gamma (A)$
measures how well computable sets can approximate the sets that A computes, counting the asymptotically worst case (the infimum over all
$Y \le _{T} A$
). In contrast,
$\Delta (A)$
measures how well the sets that A computes can approximate the computable sets, counting the asymptotically best case (the supremum over all
$Y \le _{T} A$
). Clearly
$\Delta (A) \le 1/2$
for each A.
-
(i)
$\Gamma (A) < 1/2$
implies
$\Gamma (A) =0$
. -
(ii)
$\Delta (A)>0 $
implies
$\Delta (A) = 1/2$
.
Proof. By the definitions, for each
$p \in (0, 1/2)$
, we have
$$ \begin{align*} \Gamma(A)< p \Rightarrow {\exists} Y \le_{T} A \, [Y \in {\mathcal{D}}(p)] \Rightarrow \Gamma(A)\le p \end{align*} $$
and dually
$$ \begin{align*} \Delta(A)> p \Rightarrow {\exists} Y {\leq_{\textrm{T}}} A \, [Y \in {\mathcal{B}}(p)] \Rightarrow \Delta(A)\ge p. \end{align*} $$
Now apply Theorem 3.5.⊣
The
$\Delta $
-values
$0$
and
$1/2$
can be realized by the following two facts already mentioned in [Reference Nies7, Part 3].
Proposition 3.17. Let A compute a Schnorr random Y. Then
$\Delta (A) = 1/2$
.
Proof. If Y is Schnorr random, then
$\underline \rho (A \leftrightarrow X) = 1/2$
for every computable set A.⊣
Proposition 3.18. Suppose A is 2-generic. Then
$\Delta (A) = 0$
.
Proof.
A is neither high nor d.n.c., so A is not in
${\mathcal {B}}(\neq ^{*})$
as defined in [Reference Brendle, Brooke-Taylor, Ng and Nies4, Section 3.2]. Hence A does not compute a function in
$\mathrm{AED}$
, the mass problem from Subsection 1.5 where no computable bound is imposed on the function. In particular A is does not compute a function in
$\mathrm{AED}( {2^{(2^{n})}})$
, hence
$\Delta (A)=0$
by the second equivalence in Theorem 3.5.⊣
Corollary 3.16 shows that there is no interesting spectrum of values for either
$\Gamma $
or
$\Delta $
, somewhat defeating the original purpose of finely measuring the complexity of an oracle by comparing it to the computable sets. However, more interesting spectra might be obtained for reducibilities stronger than Turing. Harrison-Trainor [Reference Harrison-Trainor10] shows that for many-one reducibility, every value in
$[0,1/2]$
is assumed in the case of
$\Gamma $
. For
$\Delta $
this hasn’t been studied.
4. Analog of Theorem 3.5 for cardinal characteristics
As before let
$R \subseteq X \times Y$
be a relation between spaces
$X,Y$
; we also assume now that
$\forall x \; \exists y \; [x \mathbin{R} y]$
and
$\forall y \; \exists x \; \neg [x \mathbin{R} y]$
. Let
$S = \{ \langle y,x \rangle \in Y \times X \colon \neg x\mathbin{R} y\}$
.
Definition 4.1. One defines pairs of dual cardinal characteristics by
$$ \begin{align*} {\mathfrak{d}}(R) &= \min\{|G|:G\subseteq Y \land \, \forall x \in X \, \exists y \in G \, x\mathbin{R} y\} \\ {\mathfrak{b}}(R) = {\mathfrak{d}} (S) & = \min\{|F|:F\subseteq X \land \, \forall y\in Y \exists x \in F \, \neg x\mathbin{R} y\}.\end{align*} $$
Note that, in comparison to Definition 2.1, the defining properties are negated. For a discussion of this, see the beginning of Section 3 of Brendle et al. [Reference Brendle, Brooke-Taylor, Ng and Nies4].
We obtain the characteristics discussed in the introduction as
${\mathfrak {d}}(R)$
and
${\mathfrak {b}}(R)$
for the two types of relations R introduced in Def. 2.2. We summarise briefly:
For
$ x \in {{\hspace{-0.0001pt}}}^{\omega }\omega $
and
$y \in \Pi _{n} \{0, \ldots , h(n)-1\}$
, let
$x \neq ^{*}_{h} y {\,\Leftrightarrow\,} {\forall }^{\infty } n \, [ x(n) \neq y(n)]$
.
For
$ 0 \le p \le 1/2$
, for
$x,y \in {{\hspace{-0.0001pt}}}^{\omega } 2$
, let
$x \bowtie _{p} y \,\Leftrightarrow\, \underline \rho (x \,\Leftrightarrow\, y)>p$
.
Remark 4.2. It will be convenient for the reader to express the characteristics from Definition 4.1 for these relations in words, with some short notation.
is the least size of a set G of h-bounded functions so that for each function x there is a function y in G such that
${\forall }^{\infty } n [ x(n) \neq y(n)]$
. (Of course it suffices to require this for h-bounded x. The systematic notation is
${\mathfrak {d}}(\neq ^{*}_{h})$
.)
is the least size of a set F of functions such that for each h-bounded function y, there is a function x in F such that
${\exists }^{\infty } n \, x(n) = y(n)$
. (We can require that each function in F is h-bounded. The systematic notation is
${\mathfrak {b}}(\neq ^{*}_{h})$
.)
is short for
${\mathfrak {d}}(\bowtie _{p}) $
, the least size of a set G of bit sequences such that for each bit sequence x there is a bit sequence y in G so that
$\underline \rho (x {\,\Leftrightarrow\,} y)>p$
.
is short for
${\mathfrak {b}}(\bowtie _{p}) $
, the least size of a set F of bit sequences such that for each bit sequence y, there is a bit sequence x in F so that
$\underline \rho (x {\,\Leftrightarrow\,} y) \le p$
.
Our main goal is to show that
${\mathfrak {d}}(p)= {\mathfrak {d}}(\neq ^{*}\!\!, 2^{(2^{n})})$
and
${\mathfrak {b}}(p)= {\mathfrak {b}}(\neq ^{*}\!\!, 2^{(2^{n})})$
for each
$p\in (0,1/2)$
. Of course the proofs are similar to the ones in Section 3, except that the issue of uniformity disappears. See the above-mentioned Greenberg et al. [Reference Greenberg, Kuyper and Turetsky9, Theorem 6.15] for an exposition of the results deriving them from a common core. We begin with some preliminary facts of independent interest. The first lemma amplifies bounds without changing the cardinal characteristics.
-
(i) Let h be nondecreasing and
$g(n) = h(2n)$
. We have
${\mathfrak {d}}(\neq ^{*}\!\!,h) = {\mathfrak {d}}(\neq ^{*}\!\!,g)$
and
${\mathfrak {b}}(\neq ^{*}\!\!,h) = {\mathfrak {b}}(\neq ^{*}\!\!,g)$
. -
(ii) For each
$a,b>1$
we have
${\mathfrak {d}}(\neq ^{*}\!\!,2^{(a^{n})}) = {\mathfrak {d}}{(\neq ^{*}\!\!,2^{(b^{n})})}$
and
${\mathfrak {b}}(\neq ^{*}\!\!, 2^{(a^{n})}) = {\mathfrak {b}}{(\neq ^{*}\!\!,2^{(b^{n})})}$
.
Proof.
-
(i) Trivially,
$h \le g$
implies that
${\mathfrak {d}}(\neq ^{*}\!\!,h) \ge {\mathfrak {d}}(\neq ^{*}\!\!,g)$
and
${\mathfrak {b}}(\neq ^{*}\!\!,h) \le {\mathfrak {b}}(\neq ^{*}\!\!,g)$
. So it suffices to show two inequalities.
: Let G be a witness set for
${\mathfrak {d}}(\neq ^{*}\!\!,g)$
. Note that G is also a witness set for
${\mathfrak {d}}(\neq ^{*}\!\!,h(2n+1))$
. Let
$\widehat {G}= \{p_{0} \oplus p_{1}\colon \, p_{0}, p_{1} \in G \}$
, where
$(p_{0} \oplus p_{1})(2m+i) = p_{i}(m)$
for
$i= 0,1$
. Each function in
$\widehat {G}$
is bounded by h. Since G is infinite,
$|\widehat {G}| = |G|$
. Clearly
$\widehat {G}$
is a witness set for
${\mathfrak {d}}(\neq ^{*}\!\!,h)$
.
: Let F be a witness set for
${\mathfrak {b}}(\neq ^{*}\!\!,h)$
. Let
$\widehat {F}$
consist of the functions of the form
$ n \to p(2n)$
, or of the form
$n \to p(2n+1)$
, where
$p \in F$
. Then
$|\widehat {F}| = |F|$
, and each function in
$\widehat {F}$
is g bounded.Clearly,
$\widehat {F}$
is a witness set for
${\mathfrak {b}}(\neq ^{*}\!\!,g)$
: if q is g-bounded, then
$\widehat {q}$
is h bounded where
$\widehat {q}(2n+i) = q(n)$
for
$i=0,1$
. Let
$p\in F$
be such that
${\exists }^{\infty } k \, p(k) = \widehat {q}(k)$
. Let
$i \le 1 $
be such that infinitely many such k have parity i. Then the function
$n \to p(2n+i) $
, which is in
$\widehat {F}$
, is as required. -
(ii) is immediate from (i) by iteration.⊣
Lemma 4.4. Let
$a \in \omega - \{0\}$
. We have
${\mathfrak {d}}( \neq ^{*}\!\!,2^{(a^{n})}) \le {\mathfrak {d}}(1/a)$
and
${\mathfrak {b}}( \neq ^{*}\!\!,{2^{(a^{n})}}) \ge {\mathfrak {b}}(1/a)$
.
Proof. As in Section 3, for
$m \ge 2$
let
$I_{m}$
be the
$(m-1)$
th consecutive interval of length
$a^{m}$
in
$\omega -\{0\}$
. First let G be a witness set for
${\mathfrak {d}}(1/a)$
. Let
$h(n) = 2^{(a^{n})}$
. Recall the operators
$K_{h}$
and
$L_{h}$
from Definition 3.2. We show that
$\widehat G = \{ K_{h}(y) \colon \, y \in G \}$
is a witness set for
${\mathfrak {d}}( \neq ^{*}\!\!, 2^{(a^{n})})$
. Otherwise there is a sequence
$x\in {{\hspace{-0.0001pt}}}^{\omega } 2$
such that for each
$y \in \widehat G$
there are infinitely many m with
$x(m) = K_{h}(y)(m)$
. Let
$x^{\prime } =1-x$
, that is
$0$
s and
$1$
s are interchanged. Then for each
$y \in G$
, for infinitely many m,
$L_{h}(x^{\prime }) (i) \neq y(i)$
for each
$i \in I_{m}$
. If we let
$n = 1+ \max I_{m}$
, the proportion of
$i < n$
such that
$ L_{h}(x) (i) = y^{\prime }(i)$
is therefore at most
$(a^{m}-1) / (a^{m+1}-1)$
, which converges to
$1/a$
as
$m \to \infty $
. This contradicts the choice of G.
Now let F be a witness set for
${\mathfrak {b}}(\neq ^{*}\!\!, h)$
. Let
$\widehat {F} = \{ 1- L_{h}(x) \colon \, x \in F \}$
. For each
$y \in {{{\hspace{-0.0001pt}}}^{\omega } 2}$
there is
$x\in F$
such that
${\exists }^{\infty } n \, K_{h}(y)(n) = x(n)$
. This implies
$\underline \rho (y {\,\Leftrightarrow\,} x^{\prime }) \le 1/a $
where
$ x^{\prime } = 1- L_{h}(x) \in \widehat {F}$
. Hence
$\widehat {F}$
is a witness set for
${\mathfrak {b}}(1/a)$
.⊣
Theorem 4.5. Fix any
$p\in (0,1/2)$
. We have
$$ \begin{align*} {\mathfrak{d}}(p)= {\mathfrak{d}}(\neq^{*}\!\!, 2^{(2^{n})}) \textrm{ and } {\mathfrak{b}}(p)= {\mathfrak{b}}({\neq^{*}\!\!, 2^{(2^{n})}}). \end{align*} $$
Proof. By the two foregoing lemmas we have
$\mathfrak {d}(p) \ge \mathfrak {d}(\neq ^{*}\!\!, 2^{(2^{n})})$
and
${\mathfrak {b}}(p)\le {\mathfrak {b}}({\neq ^{*}\!\!, 2^{(2^{n})}})$
. It remains to show the converse inequalities:
${\mathfrak {d}}(p) \le {\mathfrak {d}}(\neq ^{*}\!\!, 2^{(2^{n})})$
and
${\mathfrak {b}}(p)\ge {\mathfrak {b}}(\neq ^{*}\!\!, 2^{(2^{n})})$
.
Recall from Definitions 3.6 and 3.7 that for strings
$x,y$
of length r,
$$ \begin{align*} d(x,y) = \frac 1 r |\{ i \colon x(n) (i) \neq y(n)(i) \}|. \end{align*} $$
If h is a function of the form
$2^{\widehat {h}}$
with
$\widehat {h} \colon \, \omega \to \omega $
,
$X=Y= X_{h}$
denotes the space of h-bounded functions. For
$q \in (0, 1/2)$
, we defined a relation on
$X \times Y$
by
$$ \begin{align*} x \neq^{*}_{\widehat{h},q} y \Leftrightarrow {\forall}^{\infty} n \, [ d(x(n), y(n)) \ge q]. \end{align*} $$
For ease of notation we continue to denote this relation by
${\langle}\! \neq ^{*}\!\!, \widehat {h}, q {\rangle }$
.
Claim 4.6. For each
$c\in \omega $
there is
$k \in \omega $
such that
$$ \begin{align*} {\mathfrak{d}}\bigg(q- \frac 2c\bigg) &\le {\mathfrak{d}} {\langle}\! \neq^{*}\!\!, \lfloor 2^{n/k} \rfloor, q{\rangle}, \textrm{ and } \\ {\mathfrak{b}}\bigg(q- \frac 2c\bigg) &\ge {\mathfrak{b}} {\langle}\! \neq^{*}\!\!, \lfloor 2^{n/k} \rfloor, q{\rangle}. \end{align*} $$
Proof. As in the proof of Claim 3.8, let
$k $
be large enough so that
$2^{1/k} -1 < \frac {1}{2c}$
. Let
$\widehat {h}(n) = \lfloor 2^{n/k}\rfloor $
and
$h = 2^{\widehat {h}}$
. Write
$H(n) = \sum _{r\le n} \widehat {h}(r)$
. We refer to the bits with position in
$[H(n), H(n+1)) $
as Block n. Recall from the proof of Claim 3.8 that for sufficiently large n
$$ \begin{align*} \widehat{h}(n+1) \le \frac{1}{c} H(n). \end{align*} $$
For the inequality involving
${\mathfrak {d}}$
, let G be a witness set for
${\mathfrak {d}} {\langle } \neq ^{*}, \widehat {h} , q{\rangle }$
. Thus, for each function
$x < h$
there is a function
$y \in G$
such that for almost all n,
$L_{h}(x), L_{h}(y)$
disagree on a proportion of q bits of Block n. Let z be the complement of
$L_{h}(y)$
. Given m, let n be such that
$H(n) \le m < H(n+1)$
. Since
$m- H(n) \le \frac {1}{c} H(n)$
, for large enough m,
$L_{h}(x) $
and z agree up to m on a proportion of at least
$q - 1.5/c$
bits. So the set of complements of the
$L_{h}(y)$
,
$y \in G$
, forms a witness set for
${\mathfrak {d}}(q- 2/c)$
as required.
For the inequality involving
${\mathfrak {b}}$
, let F be a witness set for
${\mathfrak {b}}(q-2/c)$
. Thus, for each
$y \in {{\hspace{-0.0001pt}}}^{\omega } 2$
there is
$x \in F$
such that
$\underline \rho (y {\,\Leftrightarrow\,} x) \le q-2/c$
. Let
$\widehat {F} = \{K_{h}(1 -x) \colon \, x \in F \}$
. We show that
$\widehat {F}$
is a witness set for
${\mathfrak {b}} {\langle}\! \neq ^{*}\!\!, \lfloor {2^{n/k}} \rfloor , q{\rangle }$
.
Give a function
$y < h$
, let
$y^{\prime } = L_{h}(y)$
. There is
$x \in F$
such that
$\underline {\rho } (y^{\prime } {\,\Leftrightarrow\,} x) \le q - 2/c$
, and hence
$\overline {\rho } (y^{\prime } {\,\Leftrightarrow\,} x^{\prime } ) \ge 1- q+ 2/c$
where
$x^{\prime } = 1 -x$
is the complement and
$\overline {\rho }$
denotes the upper density. Then there are infinitely many m such that the strings
$y^{\prime }{\! \upharpoonright _{m}}$
and
$x^{\prime }{\! \upharpoonright _{m}}$
agree on a proportion of
$> 1- q+1/c$
bits. Suppose that
$H(n) \le m < H(n+1)$
, then the contribution of disagreement of Block n is at most
$1/c$
. So there are infinitely many k so that in Block k,
$y^{\prime }$
and
$x^{\prime }$
agree on a proportion of more than
$1-q$
bits, and hence disagree on a proportion of fewer than q bits.⊣4.6
In the following recall Definition 3.10, and in particular that for
$L \in \omega $
and a function u, for any L-slalom s and function
$y < u$
,
$$ \begin{align*} s \not \ni^{*}_{u,L} y \Leftrightarrow {\forall}^{\infty} n [s(n) \not \ni y(n)]. \end{align*} $$
We also write
${\langle}\!\! \not \ni ^{*}\!\!, u ,L {\rangle } $
for this relation.
Claim 4.7. Given
$q < 1/2$
, let
$L, \epsilon $
be as in Theorem
3.11
. Fix a nondecreasing function
$\widehat {h}$
, and let
$u(n)= {2^{\lfloor \epsilon \widehat {h}(n) \rfloor }}$
. We have
$$ \begin{align*} {\mathfrak{d}} {\langle}\!\! \neq^{*}\!\!, \widehat{h} , q{\rangle} \le {\mathfrak{d}} {\langle}\!\! \not \ni^{*}\!\!, u,L {\rangle} \textrm{ and } {\mathfrak{b}} {\langle}\!\! \neq^{*}\!\!, \widehat{h} , q{\rangle} \ge {\mathfrak{b}} {\langle}\!\! \not \ni^{*}\!\!, u,L {\rangle}. \end{align*} $$
Proof. For the inequality involving
${\mathfrak {d}}$
, let G be a set of functions bounded by u such that
$|G| < {\mathfrak {d}} {\langle}\!\! \neq ^{*}\!\!, \widehat {h} , q{\rangle }$
. We show that G is not a witness set for the right hand side
${\mathfrak {d}} {\langle}\!\! \not \ni ^{*}\!\!, u,L {\rangle }$
.
For each r of the form
$\widehat {h}(n)$
choose a set
$C= C_{r}$
as in Theorem 3.11. Since
$|C_{r}| = {2^{\lfloor \epsilon r \rfloor }}$
we may choose a sequence
$\langle \sigma ^{r}_{i}\rangle _{i< {2^{\lfloor \epsilon r \rfloor }}}$
listing
$C_{r}$
without repetitions. For a function
$y < u$
let
$\widetilde y$
be the function given by
$\widetilde y(n)= {\sigma }^{\widehat {h}(n)}_{y(n)}$
. (Thus,
$\widetilde y(n)$
is a binary string of length
$\widehat {h}(n)$
.) Let
$\widetilde G = \{ \widetilde y \colon \, y \in G \}$
. Then
$|\widetilde G| \le |G| < {\mathfrak {d}} {\langle}\!\! \neq ^{*}\!\!, \widehat {h} , q{\rangle } $
. So there is a function x with
$x(n) \in {{\hspace{-0.0001pt}}}^{\widehat {h}(n)}2$
for each n such that for each
$\widetilde y \in \widetilde G$
we have
${\exists }^{\infty } n \, [d(x(n), \widetilde y(n)) < q]$
. Let s be the slalom given by
$$ \begin{align*} s(n) = \{ i \colon \, d (x(n), {\sigma}^{\widehat{h}(n)}_{i} )< q \}. \end{align*} $$
Note that by the choice of the
$C_{r}$
according to Theorem 3.11 and since the listing of
$C_{r}$
has no repetitions, s is an L-slalom. By definition,
$\max s(n) < u(n)$
. So, for each
$y \in G$
we have
${\exists }^{\infty } n \, [s(n) \ni y(n)]$
. Hence G is not a witness set for
${\mathfrak {d}} {\langle}\!\! \not \ni ^{*}\!\!, u,L {\rangle }$
.
For the inequality involving
${\mathfrak {b}}$
, suppose F is a witness set for
${\mathfrak {b}} {\langle}\!\! \neq ^{*}\!\!, \widehat {h} , q{\rangle }$
. That is, for each
$h= {2^{\widehat {h}}}$
-bounded function y, there is
$x\in F$
such that
$$ \begin{align*} {\exists}^{\infty} n \, [ d(x(n), y(n)) <q] \end{align*} $$
(as usual we view
$x(n), y(n)$
as binary strings of length
$\widehat {h}(n)$
). For
$x\in F$
let
$s_{x}$
be the L-slalom such that
$$ \begin{align*} s_{x}(n) = \{i < u(n) \colon \, d({\sigma}^{\widehat{h}(n)}_{i}, x(n) )< q\}. \end{align*} $$
Let
$\widehat F = \{s_{x} \colon \, x \in F\}$
. Given an u-bounded function y, let
$\widetilde y(n) = {\sigma }^{\widehat {h}(n)}_{y(n)}$
. There is
$x \in F$
such that
$d(x(n), \widetilde y(n)) < q$
for infinitely many n. This means that
$y(n) \in s_{x}(n)$
. Hence
$\widehat F$
is a witness set for
${\mathfrak {b}} {\langle}\!\! \not \ni ^{*}, u,L {\rangle }$
.⊣4.7
We next need an amplification tool in the context of slaloms. As before, the proof is like the one of Lemma 4.3(i), so we omit it.
Claim 4.8. Let
$ L \in \omega $
, let the function u be nondecreasing and let
$w(n) = u(2n)$
. We have
${\mathfrak {d}}({\langle}\!\! \not \ni ^{*}\!\!,u, L {\rangle } = {\mathfrak {d}}{\langle}\!\! \not \ni ^{*}\!\!,w,L{\rangle }$
and
${\mathfrak {b}}({\langle}\!\! \not \ni ^{*}\!\!,u, L {\rangle } = {\mathfrak {b}}{\langle}\!\! \not \ni ^{*}\!\!,w,L{\rangle }$
.
Iterating the claim, starting with the function
$\widehat {h}(n) = \lfloor {2^{n/k}}\rfloor $
with k as in Claim 4.6, we obtain that
${\mathfrak {d}} {\langle}\!\! \not \ni ^{*}\!\!,2^{\widehat {h}}, L {\rangle }= {\mathfrak {d}} {\langle}\!\! \not \ni ^{*}\!\!,{2^{(L 2^{n})}}, L {\rangle }$
, and similarly
${\mathfrak {b}} {\langle}\!\! \not \ni ^{*}\!\!,{2^{\widehat {h}}}, L {\rangle } = {\mathfrak {b}} {\langle}\!\! \not \ni ^{*}\!\!,{2^{(L 2^{n})}}, L {\rangle }$
. It remains to verify the following.
$$ \begin{align*} {\mathfrak{d}} {\langle}\!\! \not \ni^{*}\!\!,{2^{(L 2^{n})}}, L {\rangle} \le {\mathfrak{d}}(\neq^{*}\!\!, 2^{(2^{n})}) \textrm{ and } {\mathfrak{b}} {\langle}\!\! \not \ni^{*}\!\!,{2^{(L 2^{n})}}, L {\rangle} \ge {\mathfrak{b}}(\neq^{*}\!\!, 2^{(2^{n})}). \end{align*} $$
Proof. Given n, recall from Section 3 that we write a number
$k < 2^{(L2^{n})}$
in binary with leading zeros if necessary, and so can view k as a binary string of length
$L {2^{n}}$
.
For the inequality involving
${\mathfrak {d}}$
, let G be a witness set for
${\mathfrak {d}}(\neq ^{*}\!\!, 2^{(2^{n})})$
. For functions
$y_{1}, \ldots , y_{L}$
such that
$y_{i}(n) < 2^{(2^{n})}$
for each n, let
$(y_{1}, \ldots , y_{L})$
denote the function y with
$y(n) < {2^{(L 2^{n})}}$
for each n such that the ith block of
$y(n)$
equals
$y_{i}(n)$
for each i with
$1 \le i \le L$
. Let
$$ \begin{align*} \widehat{G} = \{ (y_{1}, \ldots, y_{n}) \colon \, y_{1}, \ldots, y_{L} \in G\}. \end{align*} $$
Since
$G $
is infinite we have
$|\widehat {G}| = |G|$
. We check that
$\widehat {G}$
is a witness set for the left hand side
${\mathfrak {d}} {\langle}\!\! \not \ni ^{*}\!\!,{2^{(L 2^{n})}}{\rangle }$
. Given an L-slalom s bounded by
${2^{(L {2^{n}})}}$
we may assume that
$s(n) $
has exactly L members, and they are binary strings of length
$L {2^{n}}$
. For
$i \le L$
let
$x_{i}(n) $
be the ith block of the ith string in
$s(n) $
, so that
$|x_{i}(n)| = {2^{n}}$
. Viewing the
$x_{i}$
as functions bounded by
$2^{(2^{n})}$
, we can choose
$y_{1}, \ldots , y_{L} \in G$
such that
${\forall }^{\infty } n \, x_{i}(n) \neq y_{i}(n)$
. Let
$y = (y_{1}, \ldots , y_{n}) \in \widehat {G}$
. Then
${\forall }^{\infty } n \, [s(n) \not \ni y(n)]$
, as required.
For the inequality involving
${\mathfrak {b}}$
, let F be a witness set for
${\mathfrak {b}} {\langle}\!\! \not \ni ^{*}\!\!,{2^{(L 2^{n})}}$
. That is, F is a set of L-slaloms s such that for each function y with
$y(n) < 2^{(L 2^{n})}$
, there is
$s\in F$
such that
$s(n) \ni y(n)$
for infinitely many n.
Let
$\widehat {F}$
be the set of functions
$s_{i}$
, for
$s\in F$
and
$i<L$
, such that
$s_{i}(n) $
is the ith block of the ith element of
$s(n)$
(as before we may assume that each string in
$s(n)$
has length
$L2^{n}$
). Now let y be a given function bounded by
$2^{(2^{n})}$
. Let
$y^{\prime }$
be the function bounded by
$2^{(L2^{n})}$
such that for each n, each block of
$y^{\prime }(n)$
equals
$y(n)$
. There is
$s\in F$
such that
$s(n) \ni y^{\prime }(n)$
for infinitely many n. There is
$i<L$
such that
$y^{\prime }(n)$
is the ith string in
$s(n)$
for infinitely many of these n, and hence
$y(n) = s_{i}(n)$
. Thus
$\widehat {F}$
is a witness set for
${\mathfrak {b}}(\neq ^{*}\!\!, {2^{(2^{n})}})$
.⊣4.9
We can now summarise the argument that
${\mathfrak {d}}(p) \le {\mathfrak {d}}(\neq ^{*}\!\!, 2^{(2^{n})})$
for
$p < 1/2$
. Pick c large enough such that
$q= p+2/c < 1/2$
. By Claim 4.6 there is k such that
${\mathfrak {d}}(p) \le {\mathfrak {d}} {\langle}\!\! \neq ^{*}\!\!, \lfloor {2^{n/k}} \rfloor , q{\rangle }$
. By Claim 4.7 there are L,
$\epsilon $
such that where
$\widehat {h}(n) = \lfloor {2^{n/k}} \rfloor $
, we have
${\mathfrak {d}} {\langle}\!\! \neq ^{*}\!\!, \widehat {h} , q{\rangle } \le {\mathfrak {d}} {\langle}\!\! \not \ni ^{*}\!\!, u,L {\rangle }$
, where
$u(n)= 2^{\lfloor \epsilon \widehat {h}(n)\rfloor }$
. Applying Claim 4.8 sufficiently many times we have
${\mathfrak {d}} {\langle}\!\! \not \ni ^{*}\!\!, u,L {\rangle } \le {\mathfrak {d}} {\langle}\!\! \not \ni ^{*}\!\!, 2^{(L 2^{n})}, L {\rangle }$
. Finally,
${\mathfrak {d}} {\langle}\!\! \not \ni ^{*}\!\!,2^{(L 2^{n})}, L {\rangle } {\le {\mathfrak {d}}(\neq ^{*}\!\!, 2^{(2^{n})})}$
by Claim 4.9.
The argument for
${\mathfrak {b}}(p)\ge {\mathfrak {b}}(\neq ^{*}\!\!, 2^{(2^{n})})$
,
$p < 1/2$
, is dual to the above.⊣
5. A proper hierarchy of problems
$\mathrm{IOE}(h)$
in the weak degrees
Recall that by
$\mathrm{IOE}(h)$
we denote the mass problem of functions f such that
${\exists }^{\infty } n \, [f(n) = r(n) ]$
for each computable function
$r< h$
. In this section we study how the Muchnik degree of
$\mathrm{IOE}(h)$
depends on the function h. In [Reference Monin and Nies17] the authors obtained the following two results:
Theorem 5.1. ([Reference Monin and Nies17], Theorem IV.1)
Let
$c \geq 2$
be any integer, which we view as a constant function.
$$ \begin{align*} \mathrm{IOE}(2) \equiv_{S} \mathrm{IOE}( c) \equiv_{S} \{ X \colon \, X \textrm{ is not computable} \}. \end{align*} $$
The difficult part of the theorem is to show that
$\mathrm{IOE}(2) \geq _{S} \mathrm{IOE} (c)$
for
$c> 2$
. This can be done using error-correcting codes.
Theorem 5.2. ([Reference Monin and Nies17], Section 4)
For any pair of order functions
$F < G$
such that
$\sum _{n} 1/F(n) = \infty $
and
$\sum _{n} 1/G(n) < \infty $
, we have
$\mathrm{IOE}(F) <_{W} \mathrm{IOE}(G)$
.
We now show that given any order function F, one can find a function
$G> F$
such that:
$$ \begin{align*} \mathrm{IOE}(F) <_{W} \mathrm{IOE}(G). \end{align*} $$
Given an order function F, we let
$w_{F}(n)$
be the number of possible combinations of n first values for functions
$f \leq F$
, that is,
$$ \begin{align*} w_{F}(n) = \Pi_{0 \leq i \leq n} F(i). \end{align*} $$
To improve the readability of expressions with iterated exponentiation, we will mostly write
$ \exp (x)$
for
$2^{x}$
.
Theorem 5.3. (with Joseph Miller)
Let
$F \in {{\hspace{-0.0001pt}}}^{\omega } \omega $
be an order function. Let
$G \in {{\hspace{-0.0001pt}}}^{\omega } \omega $
be an order function with
$G(n) \geq 2$
for every n and such that:
$$ \begin{align*} \forall k\ \forall^{\infty} n\ \exp(w_{F}(\exp(n \cdot k)) )< G(n). \end{align*} $$
There exists a function
$f \in \mathrm{IOE}(F)$
and such that
$g \notin \mathrm{IOE}(G)$
for every
$g \leq _{T} f$
.
For instance, if
$F(n) = n$
we can let
$G(n) = \exp \,\exp \,\exp (n^{2})$
.
The rest of the section is dedicated to the proof of Theorem 5.3. Let us first introduce some terminology.
Definition 5.4. By a tree we mean a set of strings closed under prefixes. Let
$H : \omega \rightarrow \omega $
. We denote by
${{\hspace{-0.0001pt}}}^{<\omega } H$
the tree consisting of the strings
${\sigma }$
such that
${\sigma }(i) < H(i)$
for each
$i < |\sigma |$
.
Let
$T \subseteq {{\hspace{-0.0001pt}}}^{<\omega } H$
be a tree. We say that T is H-full-branching if for every
$f < H$
we have
$f \in [T]$
. For a string
$\sigma \in {{\hspace{-0.0001pt}}}^{<\omega } \omega $
and
$n> |\sigma |$
, we say that T is
$H {\! \upharpoonright _{n}}$
-full-branching above
$\sigma $
if for every
$f < H$
with
$\sigma \prec f$
we have
$f {\! \upharpoonright _{n}}\ \in T$
.
Given a node
$\sigma $
of length m and a
$H {\! \upharpoonright _{{m+n}}}$
-full-branching tree T above
$\sigma $
, we sometimes say that n is the height of the full-branching part of T. We begin with one of those lemma whose statement is more complicated than the proof.
Lemma 5.5. Let
$H : \omega \rightarrow \omega $
. Let
$\sigma \in {{\hspace{-0.0001pt}}}^{<\omega } H$
with
$|\sigma | = m$
. Let
$n \in \omega $
and let
$T \subseteq {{\hspace{-0.0001pt}}}^{<\omega } H$
be a finite
$H {\! \upharpoonright _{m + 2n}}$
-full-branching tree above
$\sigma $
. Let
$\sigma _{0}, \dots , \sigma _{k}$
be all the leaves of T. Consider a partition
$C_{1},C_{2}$
of these leaves. Then one of the following holds:
-
(i) If we keep only the nodes compatible with some element of
$C_{1}$
and discard the rest, the remaining tree is
$H {\! \upharpoonright _{m + n}}$
-full-branching above
$\sigma $
. -
(ii) If we keep only the nodes compatible with some element of
$C_{2}$
and discard the rest, there exists a node
$\tau \succ \sigma $
of length
$m+n$
such that the remaining tree is
$H {\! \upharpoonright _{m + 2n}}$
-full-branching above
$\tau $
.
In particular, in both cases, the full-branching part of the remaining tree has height n.
Proof. Suppose (i) fails. Then there is a string
$\tau \succ \sigma $
,
$\tau \in T$
of length
$m+n$
such that all the extensions in T of length
$m+2n$
of
$\tau $
are leaves of T which are not in
$C_{1}$
. Then these leaves are in
$C_{2}$
. So (ii) holds.⊣
Given any functional
$\Phi $
, we will be able to compute an infinite tree
$T \subseteq {{\hspace{-0.0001pt}}}^{<\omega } F$
such that:
-
(1) For every path
$X \in [T]$
we have that
$\Phi (X) \notin \mathrm{IOE}(G)$
. -
(2) For every path
$X \in [T]$
, there are infinitely many m such that T is
$F {\! \upharpoonright _{m+1}}$
-full-branching above
$X {\! \upharpoonright _{m}}$
. -
(3) T has no dead ends.
Note that (3) ensures that the tree is computable in a strong sense: if a node
$\sigma $
is in T, then there exists an infinite path
$X \in [T]$
with
$X \succ \sigma $
. By combining (2) with (3) we actually know that the set of infinite paths extending
$\sigma $
is perfect. While (1) ensures that no path of T computes an element of
$\mathrm{IOE}(G)$
via
$\Phi $
, (2) ensures that the tree T still contains an element of
$\mathrm{IOE}(F)$
. Also, starting from the tree
${{\hspace{-0.0001pt}}}^{<\omega } F$
, one can compute a subtree T which satisfies (1) and (2) using Lemma 5.5.
In order to help the reader understand the full proof, we sketch here a construction to obtain, under the assumption that G grows sufficiently faster than F, a computable tree T that satisfies (1)–(3) given some functional
$\Phi $
. Of course this allows us to “defeat” only one functional
$\Phi $
. To defeat more than one functional
$\Phi $
we would need not only to obtain (2), but to obtain a computable tree for which we have infinitely many large full-branching blocks. In this case we can repeat the construction in the tree we end up with, so as to defeat yet another functional. This will be achieved by the upcoming Lemma 5.7, elaborating on the ideas already present in the construction we discuss now.
Sketch of a construction to obtain (1), (2), and (3)
We work here under the assumptions of Theorem 5.3. Note however that in the simpler case of defeating only one functional, the assumption on how fast G grows compared to F can be relaxed somewhat: we merely need that
$$ \begin{align*} \forall k\ \forall^{\infty} n\ \exp(k \cdot F(k + \exp(n))) < G(n). \end{align*} $$
In the following all strings will be chosen from the F-full-branching tree. We can suppose without loss of generality that given any
$\sigma $
and any n there exists an extension
$\tau $
of
$\sigma $
such that
$\Phi (\tau , n)$
is defined. Otherwise there is a string
$\sigma $
and some n such that
$\Phi (X, n)$
is undefined for every path X extending
$\sigma $
and the desired tree T is given by all the nodes compatible with
$\sigma $
.
The construction inductively defines finite trees
$T_{0} \subset T_{1} \subset \cdots $
together with integers
$n_{0} < n_{1} < \cdots $
such that:
-
(a) For every k, every leaf of
$T_{k}$
has a full-branching extensions in
$T_{k+1}$
. -
(b) For every k, every leaf
$\rho \in T_{k}$
and every
$t < n_{k}$
, every value
$\Phi (\rho , t)$
is defined. -
(c) For every k, every
$t \leq n_{k}$
one value smaller than G(t) is different from
$\Phi (\rho , t)$
for every leaf
$\rho \in T_{k}$
. -
(d) For every k we have
$\exp (c) < G(n_{k})$
where c is the number of leaves in
$T_{k}$
Note that unlike (a) (b) and (c), (d) does not achieve by itself anything we want, but it will be necessary at each step to continue the induction, in particular in order to show (c).
To begin the inductive definitions, let
$n_{0}$
be least such that
$$ \begin{align*} \exp(F(\exp(n_{0}))) < G(n_{0}). \end{align*} $$
Consider the
$F {\! \upharpoonright _{\exp (n_{0})}}$
-full-branching tree above the empty string. Let
$\sigma _{0}, \dots , \sigma _{c}$
be an enumeration of the leaves of this
$F {\! \upharpoonright _{\exp (n_{0})}}$
-full-branching tree. For each
$i \leq c$
, we look for an extension
$\tau _{i}$
of
$\sigma _{i}$
such that
$\Phi (\tau _{i}, t)$
is defined for every
$t \leq n_{0}$
. We can assume without loss of generality that every node
$\tau _{i}$
has the same length
$m_{0}$
(presumably much larger than
$n_{0}$
). We now partition the set of nodes
$\tau _{i}$
into those such that
$\Phi (\tau _{i}, 0) = 0$
and those such that
$\Phi (\tau _{i}, 0) \neq 0$
. By Lemma 5.5, we can either remove all nodes of length
$m_{0}$
forcing
$\Phi (0) = 0$
, or all nodes of length
$m_{0}$
forcing another value (and everything compatible with these nodes), in such a way that we have a node
$\sigma $
above which the tree consisting of the nodes we keep is
$F {\! \upharpoonright _{|{\sigma }| + \exp (n_{0}-1)}}$
-full branching. Note that
$\sigma $
can be either the root of the tree or a string of length
$\exp (n_{0}-1)$
.
We inductively continue the previous operation for each of the
$n_{0}$
first values of
$\Phi $
. At the end, we have a node
$\sigma $
above which there is a
$F {\! \upharpoonright _{|\sigma | + 1}}$
-full-branching tree, and such that given any
$t \leq n_{0}$
, the remaining nodes
$\tau _{i}$
of length
$m_{0}$
are altogether such that
$\Phi (\tau _{i}, t)=0$
or such that
$\Phi (\tau _{i}, t) \neq 0$
. Let
$T_{0}$
be the tree consisting of the remaining nodes
$\tau _{i}$
and everything below them. For every
$t \leq n_{0}$
, in the first case we define
$g(t) = 1$
and in the second
$g(t) = 0$
. Note that as
$\exp (F(\exp (n_{0}))) < G(n_{0})$
, then also we must have
$\exp (c) < G(n_{0})$
where c is the number of nodes of length
$m_{0}$
in
$T_{0}$
.
Suppose now by induction that we have a finite tree
$T_{k}$
with leaves
$\tau _{0}, \dots , \tau _{c} \in T_{k}$
each of length
$m_{k}$
, and a value
$n_{k}$
such that (a), (b), (c) and (d) are verified. In particular we have
$\exp (c) < G(n_{k})$
. Let
$n_{k+1}> n_{k}$
be the smallest such that
$$ \begin{align*} \exp(c \cdot F(m_{k} + \exp(n_{k+1}))) < G(n_{k+1}). \end{align*} $$
Let us show that for any a with
$0 \leq a \leq c$
, we can computably find a finite tree
$T^{a}$
whose nodes are all compatible with
$\tau _{a}$
and such that:
-
•
$T^{a}$
is
$F {\! \upharpoonright _{|\sigma | + 1}}$
-full branching above some
$\sigma \succ \tau _{a}$
. -
• Each leaf
$\rho $
of
$T^{a}$
is such that
$\Phi (\rho , t)$
is defined for
$n_{k} < t \leq n_{k+1}$
. -
• For every
$n_{k} < t \leq n_{k+1}$
, there is at least one value smaller than
$G(t)$
which is different from every value
$\Phi (\rho , t)$
for leaves
$\rho $
of
$T^{a}$
.
For any
$a \leq c$
we do the following: consider the finite
$F {\! \upharpoonright _{|\tau _{a}| + \exp (n_{k+1})}}$
-full branching tree above
$\tau _{a}$
. Let
$\sigma _{0}, \dots , \sigma _{k}$
be an enumeration of the leaves of this finite tree. For each of these nodes
$\sigma _{i}$
, look for an extension
$\tau _{i}^{\prime }$
such that
$\Phi (\tau _{i}^{\prime }, t)$
is defined for every
$n_{k} < t \leq n_{n+1}$
. Let
${T^{a}}^{\prime }$
be the finite tree consisting of these extensions
$\tau _{i}^{\prime }$
and everything below them.
We now partition the set of leaves of
${T^{a}}^{\prime }$
into two sets
$C_{1}$
and
$C_{2}$
such that the leaves
$\rho $
in
$C_{1}$
are these for which the ath bit of
$\Phi (\rho , n_{k}+1)$
is
$0$
and the leaves in
$C_{2}$
are these for which the ath bit of
$\Phi (\rho , n_{k}+1)$
is
$1$
. By the Lemma 5.5, we can either remove all nodes of
$C_{1}$
or all nodes of
$C_{2}$
(and everything compatible with these nodes), in such a way that we have a node
$\sigma \in {T^{a}}^{\prime }$
such that the tree consisting of the nodes we keep, is
$F{\! \upharpoonright _{|\sigma | + \exp (n_{k+1}-1)}}$
-full branching above
$\sigma $
.
We inductively continue the previous operation for each of the next values of
$\Phi $
up to
$n_{k+1}$
. At the end, we have a node
$\sigma \in {T^{a}}^{\prime }$
above which there is a
$F {\! \upharpoonright _{|\sigma | + 1}}$
-full-branching tree as follows: for each
$n_{k} < t \leq n_{k+1}$
, for all the remaining leaves
$\tau ^{\prime }$
of our
$F {\! \upharpoonright _{|\sigma | + 1}}$
-full-branching tree, the ath bit of
$\Phi (\tau ^{\prime }, t)$
is the same. We define the tree
$T^{a}$
to be this set of remaining leaves
$\tau ^{\prime }$
and everything below them.
Once every tree
$T^{a}$
has been defined, we define each value of
$g(t)$
for
$n_{k} < t \leq n_{k+1}$
, as follows: If the leaves
$\rho $
of
$T^{a}$
are such that the ath bit of
$\Phi (\rho , t)$
equals
$0$
, then the ath bit of
$g(n)$
is defined to be
$1$
, and vice-versa. Recall that we have
$\exp (c) < G(n_{k})$
. In particular any number coded on at most c bits is smaller than
$G(t)$
for any
$n_{k} < t \leq n_{k+1}$
. It follows that
$g(t) < G(t)$
for any
$n_{k} < t \leq n_{k+1}$
. Also we necessarily have that
$g(t)$
is different from every possible value
$\Phi (\rho , t)$
for every leaf
$\rho \in \bigcup _{a \leq c} T^{a}$
. Let
$T_{k+1} = \bigcup _{a \leq c} T^{a}$
. Note that by the choice of
$n_{k+1}$
we have that
$\exp (d) < G(n_{k+1})$
where d is the number of leaves in
$T_{k+1}$
.
By continuing the induction, we define a computable subtree
$T = \bigcup _{k} T_{k}$
of the F-full-branching tree as well as a computable function
$g < G$
, such that along any path of T, infinitely many nodes are full-branching, and such that for any
$f \in [T]$
we have that
$\Phi (f, n) \neq g(n)$
for any n.⊣
Suppose now that we want to defeat every functional. Let
$\Phi _{0}, \Phi _{1}, \Phi _{2}, \dots $
be a list of all functionals. The previous proof gives us a tree
$T_{0}$
which defeats
$\Phi _{0}$
. To defeat
$\Phi _{1}$
, we have to perform a similar construction, but starting now from the computable tree
$T_{0}$
in place of the F-full-branching tree
${{\hspace{-0.0001pt}}}^{<\omega } F$
. In this way we obtain a computable tree
$T_{1} \subseteq T_{0}$
which defeats both
$\Phi _{0}$
and
$\Phi _{1}$
. The main problem is that to use Lemma 5.5 we need to work in a tree that has large full-branching blocks (which is the case of
${{\hspace{-0.0001pt}}}^{<\omega } F$
). Also if
$T_{0}$
itself does not have large full-branching blocks, it is not necessarily possible to defeat
$\Phi _{1}$
starting from
$T_{0}$
in place of
${{\hspace{-0.0001pt}}}^{<\omega } F$
. To overcome this problem, it is not sufficient to merely ensure (2) for
$T_{0}$
: we actually need to ensure that for every path
$X \in T_{0}$
, there are infinitely many m such that
$T_{0}$
is
$F {\! \upharpoonright _{m+n_{m}}}$
-full-branching above
$X {\! \upharpoonright _{m}}$
for
$n_{m}$
sufficiently large. This leads to the following definition:
Definition 5.6. Let
$F,G \in {{\hspace{-0.0001pt}}}^{\omega } \omega $
be order functions. Let
$T \subseteq {{\hspace{-0.0001pt}}}^{<\omega } F$
be a finite tree. Let
$n_{1} < n_{2} < \dots < n_{k}$
. We say that T is G-fat for
$(n_{1}, n_{2}, \dots , n_{k})$
s if for every leaf
$\sigma \in T$
, there exists
$m_{1} < m_{2} < \dots < m_{k} < |\sigma |$
such that for every
$1 \leq t \leq k$
:
-
(1) The tree T is
$F {\! \upharpoonright _{m_{t} + \exp (n_{t} \cdot t)}}$
-full-branching above
$\sigma {\! \upharpoonright _{m_{t}}}$
. -
(2)
$\exp (w_{F}(m_{t} + \exp (n_{t} \cdot t))) < G(n_{t})$
.
We say that
$T\subseteq {{\hspace{-0.0001pt}}}^{<\omega } F$
is infinitely often G-fat if there exists an infinite sequence
$n_{1} < n_{2} < \cdots $
such that for every k, there exists m such that T restricted to its node of length m, is G-fat for
$(n_{1}, \dots , n_{k})$
.
The following lemma is the heart of the proof. It says that for any computable infinitely often G-fat tree T and any functional
$\Phi $
, there is a computable infinitely often G-fat tree
$T^{\prime } \subseteq T$
such that no path of
$T^{\prime }$
computes an element of
$\mathrm{IOE}(G)$
via
$\Phi $
.
Lemma 5.7. Let
$F \in {{\hspace{-0.0001pt}}}^{\omega } \omega $
be an order function. Let
$G \in {{\hspace{-0.0001pt}}}^{\omega } \omega $
be an order function such that
$G(n) \geq 2$
for every n. Let
$T \subseteq {{\hspace{-0.0001pt}}}^{<\omega } F$
be a computable infinitely often G-fat tree with no dead ends. Let
$\Phi $
be a functional. There exists a computable infinitely often G-fat tree
$T^{\prime } \subseteq T$
with no dead ends, and a computable function
$g < G$
such that for every path
$X \in [T^{\prime }]$
for which
$\Phi (X)$
is total, we have
$\Phi (X, n) \neq g(n)$
for every n.
Before giving the proof of the lemma, we show how to use it in order to obtain the proof of Theorem 5.3, using simple forcing machinery.
Proof of Theorem 5.3 Let
$F \in {{\hspace{-0.0001pt}}}^{\omega } \omega $
be an order function. Let
$G \in {{\hspace{-0.0001pt}}}^{\omega } \omega $
be an order function with
$G(n) \geq 2$
for every n and such that:
$$ \begin{align*} \forall k\ \forall^{\infty} n\ \exp(w_{F}(\exp(n \cdot k)) < G(n). \end{align*} $$
Let us show that there exists a function
$f \in \mathrm{IOE}(F)$
and such that
$g \notin \mathrm{IOE}(G)$
for every
$g \leq _{T} f$
. The proof is done by forcing, using Lemma 5.7. We first need to argue that under the above hypothesis, the tree
$T = {{\hspace{-0.0001pt}}}^{<\omega } F$
is infinitely often G-fat. In what follows, the notation
$T {\! \upharpoonright _{n}}$
refers to the finite tree consisting of the nodes of T of length smaller than or equal to n. Let
$n_{1}$
be the smallest such that
$\exp (w_{F}(\exp (n_{1}))) < G(n_{1})$
. The tree
$T {\! \upharpoonright _{\exp (n_{1})}}$
is
$F {\! \upharpoonright _{\exp (n_{1})}}$
-full-branching above the empty string and in particular the tree
$T {\! \upharpoonright _{\exp (n_{1})}}$
is G-fat for
$(n_{1})$
. Suppose now that we have defined
$n_{1} < \dots < n_{k}$
such that
$T {\! \upharpoonright _{\exp (n_{k})}}$
is G-fat for
$(n_{1}, \dots , n_{k})$
. Let
$n_{k+1}$
be the smallest such that
$$ \begin{align*} \begin{array}{ll} &\exp(n_{k}) + \exp(n_{k+1} \cdot (k+1))<\exp(n_{k+1} \cdot (k+2)) \\ \textrm{ and }&\exp(w_{F}(\exp(n_{k+1} \cdot (k+2))))<G(n_{k+1}). \end{array} \end{align*} $$
Then in particular we have
$$ \begin{align*} \exp(w_{F}(\exp(n_{k}) + \exp(n_{k+1} \cdot (k+1)))) < G(n_{k+1}). \end{align*} $$
It follows that the tree
$T {\! \upharpoonright _{\exp (n_{k+1})}}$
is G-fat for
$(n_{1}, \dots , n_{k}, n_{k+1})$
. Therefore the tree T is infinitely often G-fat for the infinite sequence
$\{n_{k}\}_{1 \leq k < \omega }$
.
So we start the forcing with the tree
$T = {{\hspace{-0.0001pt}}}^{<\omega } F$
. Let
${\mathcal P}$
be the set of forcing conditions consisting of all the computable infinitely often G-fat subtrees of T with no dead ends. For two forcing conditions
$P_{1},P_{2} \in {\mathcal P}$
, the partial order
$P_{2} \preceq P_{1}$
is defined by
$P_{2} \subseteq P_{1}$
. Let
$\Phi $
be a functional. By Lemma 5.7, the set of infinitely often G-fat trees
$P \in {\mathcal P}$
such that for every path X of
$[P]$
we have
$\Phi (X) \notin \mathrm{IOE}(G)$
, is dense in
${\mathcal P}$
.
We simply have to argue that for any computable function
$f < F$
, the set of infinitely often G-fat trees
$P \in {\mathcal P}$
such that every path X of
$[P]$
equals at least once to f, is dense in
${\mathcal P}$
. It is clear, because given a tree
$P \in {\mathcal P}$
, consider any node
$\tau \in P$
of length m such that P is
$F{\! \upharpoonright _{m+1}}$
-full-branching above
$\tau $
. Let
$\tau ^{\prime }$
equals
$\tau {\widehat {\phantom {\alpha }}} f(m+1)$
. Note that
$\tau ^{\prime } \in P$
. Now let
$P^{\prime }$
to be the nodes of P which are compatible with
$\tau ^{\prime }$
. It is clear that
$P^{\prime } \in {\mathcal P}$
and that
$P^{\prime } \preceq P$
. Thus the set of infinitely often G-fat trees
$P \in {\mathcal P}$
such that every path X of P equals at least once to f, is dense in
${\mathcal P}$
.
Consider now any sufficiently generic set of conditions
$\{P_{n}\}_{n \in \omega }$
with
$P_{1} \succ {P_{2} \succ \cdots}$
. We have that
$\bigcap _{n} P_{n}$
contains at least one infinite path X. Also this path necessarily equals at least once every computable function bounded by F, and thus equals infinitely often every computable function bounded by F. It follows that
$X \in \mathrm{IOE}(F)$
. Furthermore for any function
$\Phi $
we have that
$\Phi (X) \notin \mathrm{IOE}(G)$
. This shows the theorem.⊣
Proof of Lemma 5.7 Figure 1 illustrates a part of the proof. Suppose first that there exists a node
$\sigma \in T$
such that for every
$X \succ \sigma $
with
$X \in [T]$
, we have that
$\Phi (X)$
is partial. Then we define the computable tree
$T^{\prime }$
to be the nodes of T compatible with
$\sigma $
. It is clear that
$T^{\prime }$
is infinitely often G-fat. Also as
$\Phi (X)$
is partial for every
$X \in [T^{\prime }]$
this case of the lemma is verified.
Figure 1 Construction of
$T_{k+1}$
from
$T_{k}$
in Lemma 5.7. We have
$2^{c}~<~G(n_{k})$
and for every
$ n_{k} < t \leq n_{k+1}$
, the ath bit of
$ \Phi (\rho , t)$
is the same for every
$ \rho \in T_{a}^{k+1}$
.
So we can now suppose without loss of generality that for every node
$\sigma \in T$
and every n, there exists an extension
$\tau \succeq \sigma $
such that
$\Phi (\tau , n)$
is defined. From T we want to find
$T^{\prime } \subset T$
as in the lemma. This is done step-by-step. At each step k we find values
$n_{1} < \dots < n_{k}$
and a finite tree
$T_{k} \supseteq T_{k-1}$
such that
$T_{k}$
is G-fat for
$(n_{1} < n_{2} < \dots < n_{k})$
and such that for leaves
$\rho $
of
$T_{k}$
, the values
$\Phi (\rho , e)$
are all different from something smaller than
$G(e)$
for every
$e \leq n_{k}$
. However, we do not show right away that the values
$\Phi (\rho , e)$
are all different from something smaller than
$G(e)$
. We first show that we can make large group of leaves which all agree on a specific bit. The fact that we can use that to have the values
$\Phi (\rho , e)$
all different from something smaller than
$G(e)$
will be made clear later. Here is a claim which says how one step is done: building the tree
$T_{k}$
from the tree
$T_{k-1}$
.
Claim 5.8. Let
$T \subseteq {{\hspace{-0.0001pt}}}^{<\omega } F$
be a computable infinitely often G-fat tree. Let
$n_{1} < {n_{2} < \dots < n_{k-1}}$
. Suppose that a finite tree
$T_{k-1} \subseteq T$
is G-fat for
$(n_{1} < n_{2} < \dots < n_{k-1})$
. Let
$\sigma _{0}, \dots , \sigma _{c}$
be the leaves of
$T_{k-1}$
. Then there exists
$n_{k}$
such that above each node
$\sigma _{a}$
for
$0 \leq a \leq c$
, we can find an extension
$\tau _{a} \succeq \sigma _{a}$
of length
$m_{a}$
and a finite tree
$T^{a} \subseteq T$
whose nodes are all comparable with
$\tau _{a}$
and such that:
-
(1)
$T^{a}$
is
$F {\! \upharpoonright _{m_{a} + \exp (n_{k} \cdot k)}}$
-full-branching above
$\tau _{a}$
. -
(2) For every e with
$n_{k-1} < e \leq n_{k}$
and every leaf
$\rho \in T^{a}$
, the value
$\Phi (\rho , e)$
is defined. -
(3) For every e with
$n_{k-1} < e \leq n_{k}$
, there exists
$i \in \{0,1\}$
such that for every leaf
$\rho \in T^{a}$
, the ath bit of
$\Phi (\rho , e)$
equals i. -
(4)
$\exp (w_{F}(m_{a}+\exp (n_{k} \cdot k))) < G(n_{k})$
.
In particular, letting
$T_{k} = \bigcup _{a < c} T^{a}$
, we have that
$T_{k} \subseteq T$
is G-fat for
$(n_{1} < {n_{2} < \dots < n_{k}})$
.⊣
We first show how to use this claim in order to build the tree
$T^{\prime }$
and the computable function g of the lemma. At step
$1$
we apply the claim starting from the empty tree, with the empty string as the only leaf. The claim gives us some
$n_{1}> 0$
and a finite subtree
$T_{1} \subseteq T$
which is G-fat for
$(n_{1})$
and such that for every
$e \leq n_{1}$
, the first bit of
$\Phi (e, \rho )$
is the same for every leaf
$\rho $
of
$T_{1}$
. We define in the mean time the computable function
$g(e)$
for
$e \leq n_{1}$
so that its first bit is different from the one forced on leaves of
$T_{1}$
. Note that
$g(e) \in \{0,1\}$
and that as
$G(e) \geq 2$
we necessarily have
$g(e) < G(e)$
for
$e \leq n_{1}$
. We now deal with a crucial point for the rest of the induction, corresponding to the point (d), in the proof that defeats only one functional. As
$T_{1}$
is G-fat for
$(n_{1})$
, there exists a node
$\tau _{1} \in T_{1}$
of length
$m_{1}$
such that
$T_{1}$
is
$F {\! \upharpoonright _{m_{1} + \exp (n_{1})}}$
-full-branching above
$\tau _{1}$
and such that
$\exp (w_{F}(m_{1}+(\exp (n_{1})))) < G(n_{1})$
(using (4) of the claim). Let c be the number of leaves of
$T_{1}$
. Note that
$w_{F}(m_{1}+(\exp (n_{1}))$
is the number of nodes in the
$F{\! \upharpoonright _{m_{1}+\exp (n_{1})}}$
-full-branching tree above the empty string. As c is the number of nodes in the
$F{\! \upharpoonright _{m_{1}+\exp (n_{1})}}$
-full-branching tree above
$\tau _{1}$
, it follows that
$c \leq w_{F}(m_{1}+\exp (n_{1}))$
and then that
$\exp (c) < G(n_{1})$
. Just as in the proof that defeats only one functional, this will allow us to continue the induction and in particular to have values smaller than
$G(n_{1} + t)$
for which we can continue to define g.
Suppose now by induction that at step k we have a sequence
$n_{1} < \dots < n_{k}$
and a finite tree
$T_{k} \subseteq T$
which is G-fat for
$(n_{1}, \dots , n_{k})$
. Let
$\sigma _{0}, \dots , \sigma _{c}$
be the leaves of
$T_{k}$
and suppose also that c is such that
$\exp (c) < G(n_{k})$
. Let us define
$n_{k+1}> n_{k}$
and a finite tree
$T_{k+1} \subseteq T$
, G-fat for
$(n_{1}, \dots , n_{k}, n_{k+1})$
, and which extends
$T_{k}$
, together with values
$g(e)$
for
$n_{k} < e \leq n_{k+1}$
such that
$g(e) < G(e)$
and such that
$g(e)$
is different from
$\Phi (e, \rho )$
for every leaf
$\rho $
of
$T_{k+1}$
. Using the above claim, we find
$n_{k+1}> n_{k}$
and above each node
$\sigma _{a}$
for
$a \leq c$
we find an extension
$\tau _{a} \succeq \sigma _{a}$
of length
$m_{a}$
and a finite tree
$T_{k+1}^{a} \subseteq T$
such that
$T_{k+1}^{a}$
is
$F {\! \upharpoonright _{m_{a} + \exp (n_{k+1} \cdot (k+1))}}$
-full-branching above
$\tau _{a}$
. Also for every e with
$n_{k} < e \leq n_{k+1}$
, the ath bit of
$\Phi (e, \rho )$
is the same for every leaf
$\rho $
of
$T_{k+1}^{a}$
. We can use that to define the values of
$g(e)$
for
$n_{k} < e \leq n_{k+1}$
the following way: if the ath bit of
$\Phi (e, \rho )$
is
$0$
for every leaf
$\rho $
of
$T_{k+1}^{a}$
, then the ath bit of g is set to
$1$
, and vice-versa. This is here that we need to use the induction hypothesis
$\exp (c) < G(n_{k})$
. It implies in particular that
$\exp (c) < G(e)$
for
$n_{k} < e \leq n_{k+1}$
(as G is an order function). Also at most c bits of
$g(e)$
are set to something, which implies
$g(e) \leq \exp (c)$
and thus
$g(e) < G(e)$
.
Let now
$T_{k+1} = \bigcup _{a < c} T_{k+1}^{a}$
. It is clear that
$T_{k+1}$
is G-fat for
$(n_{0}, \dots , n_{k+1})$
. Let d be the number of leaves of
$T_{k+1}$
. All we need to show now to continue the induction is that
$\exp (d) < G(n_{k+1})$
. To see this, let
$b \leq c$
be such that
$m_{b} \geq m_{a}$
for
$a \leq c$
. We now have by (4) of the claim that
$\exp (w_{F}(m_{b}+\exp (n_{k+1} \cdot (k+1)))) < G(n_{k+1})$
. Also
$w_{F}(m_{b}+\exp (n_{k+1} \cdot (k+1)))$
is the number of nodes in the
$F {\! \upharpoonright _{m_{b} + \exp (n_{k+1} \cdot (k+1))}}$
-full-branching tree above the empty string. And by the choice of
$m_{b}$
, for every
$a \leq c$
we have that the tree
$T_{k+1}^{a}$
is included in the
$F {\! \upharpoonright _{m_{b} + (\exp (n_{k+1}\cdot (k+1))}}$
-full-branching tree above the empty string. It follows that for d the number of leaves in
$T_{k+1}$
, we must have
$d \leq w_{F}(m_{b}+\exp (n_{k+1}\cdot (k+1)))$
and thus that we must have
$\exp (d) < G(n_{k+1})$
.
The tree
$T^{\prime }$
is then defined to be
$\bigcup _{k} T_{k}$
. It is clear that by construction, the tree
$T^{\prime }$
is computable with no dead ends, infinitely often G-fat, and that for every path
$X \in [T^{\prime }]$
, we have
$\Phi (X, n) \neq g(n)$
for every e.
Let us now give the proof of the claim. Figure 2 illustrates a part of this proof. By hypothesis T is infinitely often G-fat. In particular, there exists
$n_{k}> n_{k-1}$
such that above every
$\sigma _{a}$
, we have
$m_{a}^{\prime } \in \omega $
and an extension
$\tau _{a}^{\prime } \succ \sigma _{a}$
of length
$m_{a}^{\prime }$
, such that T is
$F {\! \upharpoonright _{m_{a}^{\prime } + \exp (n_{k} \cdot (k+1))}}$
-full-branching above
$\tau _{a}^{\prime }$
with
$$ \begin{align*} \exp(w_{F}(m_{a}^{\prime}+\exp(n_{k} \cdot (k+1))) < G(n_{k}). \end{align*} $$
Figure 2 Construction of
$T^{a}$
in the claim of Lemma 5.7.
$T_{a}$
is the result of thinning the full-branching part above
$\tau _{a}^{\prime }$
into a full-branching part above an extension
$ \tau _{a} \succeq \tau _{a}^{\prime }$
.
Note that here, we truly mean
$\exp (n_{k} \cdot (k+1))$
and not
$\exp (n_{k} \cdot k)$
. Given
$\tau _{a}^{\prime }$
of length
$m_{a}^{\prime }$
, for each node of T of length
$m_{a}^{\prime } + \exp (n_{k} \cdot (k+1))$
extending
$\tau _{a}^{\prime }$
, we find an extension
$\rho \in T$
of this node such that the values
$\Phi (\rho , t)$
are defined for every t with
$n_{k-1} < t \leq n_{k}$
. We define the tree
${T^{a}}^{\prime }$
to be all these nodes
$\rho $
and their prefixes. We now inductively apply Lemma 5.5 to the tree
${T^{a}}^{\prime }$
, so that for every t with
$n_{k-1} < t \leq n_{k}$
, the ath bit of
$\Phi (t, \rho )$
is the same on every leaf
$\rho $
of
${T^{a}}^{\prime }$
. Let us explain the first step. Given
${T^{a}}^{\prime }$
, we partition its leaves into these for which the ath bit of
$\Phi (n_{k-1}+1, \rho )$
is
$0$
, and these for which the ath bit of
$\Phi (n_{k-1}+1, \rho )$
is
$1$
. We then thin the tree
${T^{a}}^{\prime }$
as described in Lemma 5.5, so that the height of the full-branching part of
${T^{a}}^{\prime }$
is halved, and the ath bit of
$\Phi (n_{k-1}+1, \rho )$
is the same for all the remaining leaves. We then inductively apply Lemma 5.5 on the successive resulting trees, to deal with the ath bit of all the values
$\Phi (t, \rho )$
for
$n_{k-1} < t \leq n_{k}$
. Let
$T^{a}$
be the tree resulting of the successive applications from Lemma 5.5.
It is clear by design that (2) and (3) of the claim are satisfied. Let us verify (1). Each time we applied Lemma 5.5, it halved the height of the full-branching part of
${T^{a}}^{\prime }$
. We applied Lemma 5.5 at most
$n_{k}$
times. Also
${T^{a}}^{\prime }$
is
$F {\! \upharpoonright _{m_{a}^{\prime } + \exp (n_{k} \cdot (k+1))}}$
-full-branching above
$\tau _{a}^{\prime }$
. This means in particular that its full-branching part has height
$\exp (n_{k} \cdot (k+1))$
. It follows that the full-branching part of
$T^{a}$
has height at least
$\exp (n_{k} \cdot (k+1)) \exp (-n_{k}) = \exp (n_{k} \cdot k)$
. Thus we have that
$T^{a}$
is
$F {\! \upharpoonright _{m_{a} + \exp (n_{k} \cdot k)}}$
-full branching above some node
$\tau _{a} \succeq \tau _{a}^{\prime }$
of length
$m_{a}$
. Thus also (1) is verified.
It remains to verify (4). Recall that
$n_{k}$
and (for every a) the strings
$\tau _{a}^{\prime }$
of length
$m_{a}^{\prime }$
were picked such that
$$ \begin{align*} \exp(w_{F}(m_{a}^{\prime}+(\exp(n_{k} \cdot (k+1)))) < G(n_{k}). \end{align*} $$
In order to verify (4), we now want to show for every a that:
$$ \begin{align*} \exp(w_{F}(m_{a}+(\exp(n_{k} \cdot k))) < G(n_{k}). \end{align*} $$
It suffices to show for every a that
$m_{a} + \exp (n_{k} \cdot k) \leq m_{a}^{\prime } + \exp (n_{k} \cdot (k+1))$
. Recall that
$m_{a}$
is the length of the string
$\tau _{a}$
extending
$\tau _{a}^{\prime }$
, resulting of the successive applications of Lemma 5.5 to the full-branching part of
${T^{a}}^{\prime }$
. In particular we have
$\tau _{a} \in {T^{a}}^{\prime }$
. Also the quantities
$\exp (n_{k} \cdot (k+1))$
and
$\exp (n_{k} \cdot k)$
are respectively the height of the full-branching part of
${T^{a}}^{\prime }$
and the height of the full-branching part of
$T^{a} \subseteq {T^{a}}^{\prime }$
. It easily follows that
$m_{a} + \exp (n_{k} \cdot k) \leq m_{a}^{\prime } + \exp (n_{k} \cdot (k+1))$
.
6. Some open questions
Theorem 3.5 implies that there are no
$\Gamma $
-values strictly between
$0$
and
$1/2$
. However, if
$\Gamma (X) < 1/2$
, the lemma does not provide a single set
$Y \leq _{T} X$
such that
$\Gamma (Y) = 0$
.
Question 6.1. Let X be a set such that
$\Gamma (X) = 0$
. Is there a set
$Y \leq _{T} X$
such that
$\gamma (Y) = 0$
? Equivalently, is
${\mathcal {D}}(0) \equiv _{W} {\mathcal {D}}(1/4)$
?
This question is actually connected to other questions regarding the hierarchy of mass problem
$\mathrm{IOE}(h)$
in the Muchnik degrees. We showed in Theorem 5.3 that this hierarchy is proper, but given f, the function
$g> f$
we provide such that
$\mathrm{IOE}(f) <_{W} \mathrm{IOE}(g)$
grows rather fast compared to f. We do not know for instance if given any f we have
$\mathrm{IOE}(f) <_{W} \mathrm{IOE}(\lambda n . f(n^{2}))$
. So we ask here the following question:
Question 6.2. Does there exist a computable function f with
$\forall a \in \omega \ \forall ^{\infty } n\ f(n)> 2^{(a^{n})}$
such that
$\mathrm{IOE}(2^{(2^{n})}) \equiv _{W} \mathrm{IOE}(f)$
?
A positive answer to this question would also provide a positive answer to Question 6.1. For, by Remark 3.4,
$ \mathrm{IOE}(f) \ge _{S} {\mathcal {D}}(0)$
, and we have
${\mathcal {D}}(0) \ge _{S} {\mathcal {D}}(1/4) \equiv _{W} \mathrm{IOE}(2^{(2^{n})})$
.
There is also a question regarding the sets X such that
$\Gamma (X) = 1/2$
.
Question 6.3. Let X be a set with
$\Gamma (X) = 1/2$
. Let
$Y \leq _{T} X$
. Is there a computable set A such that
$\underline \rho (Y {\,\Leftrightarrow\,} A) = 1/2$
?
Again, the proof of Theorem 3.5 does not help answering this question. All we have is an affirmative answer to the question for all the known examples of sets X with a
$\Gamma $
-value of
$1/2$
.
Finally we ask for an analog of Theorem 5.3 for cardinal characteristics.
Question 6.4. Given an order function F, is there a faster growing order function G such that
${\mathfrak {d}}(\neq ^{*}\!\!, G) < {\mathfrak {d}}(\neq ^{*}\!\!, F)$
is consistent with ZFC?
Acknowledgments
As mentioned, several of the questions studied here arose in work of Jörg Brendle and the second author that has been archived in [Reference Nies6, Section 7], where the cardinal characteristics relating to density were introduced. We thank Brendle for these very helpful discussions. We thank Joseph Miller for his contribution towards Section 5 in this paper. Nies was supported in part by the Marsden Fund of the Royal Society of New Zealand, UoA 13-184 and UoA 19-346. The work was completed while the authors visited the Institute for Mathematical Sciences at NUS during the 2017 programme “Aspects of Computation”.
