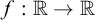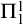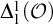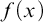1 Introduction
We revisit a notion from classic real analysis, namely Luzin’s property (N), from the perspective of computability theory. A function
$f : \mathbb {R} \to \mathbb {R}$
has Luzin’s (N), if the image of any (Lebesgue) null set under f has again measure
$0$
. This concept was studied extensively by Luzin in his thesis [13]. For functions with bounded variation, this notion is just equivalent to absolutely continuous functions—but already for general continuous functions, Luzin’s (N) is a somewhat intricate property. A formal result amounting to this was obtained by Holický, Ponomarev, Zajček and Zelený, showing that the set of functions with Luzin’s (N) is
$\Pi ^1_1$
-complete in the space of continuous functions [Reference Holický, Ponomarev, Zajíček and Zelený9].
From a computability-theoretic perspective, Luzin’s (N) is readily seen to be some kind of randomness reflection: By contraposition, it states that whenever
$f[A]$
has positive measure (i.e. contains a random point for a suitable notion of randomness), then A has positive measure, too (i.e. contains a random point). It thus seems plausible that for some suitable randomness notion, Luzin’s (N) for computable functions is equivalent to saying that whenever
$f(x)$
is random, then so is x. Our main finding (Theorem 16) is that this is indeed the case, and that
$\Pi ^1_1$
-randomness is such a suitable randomness notion. An indication that this is a nontrivial result is that our proof uses ingredients such as Friedman’s conjecture (turned into a theorem by Martin [Reference Friedman8, Reference Martin14, Reference Yu28]).
While the exploration of how randomness interacts with function application, and the general links to real analysis, has a long tradition (see e.g. the survey by Rute [Reference Rute21]), the concepts of randomness preservation (if x is random, so is
$f(x)$
) and no-randomness-from-nothing (if y is random, then there is some random
$x \in f^{-1}(y)$
) have received far more attention than randomness reflection. Our results not only fill this gap, but may shed a light on why randomness reflection has been less popular: As the most natural notion of randomness reflection turns out to be
$\Pi ^1_1$
-randomness reflection, we see that studying higher randomness is essential for this endeavour.
Our theorems and proofs generally refer to computability. However, we stress that since the results relativize, one can obtain immediate consequences in classic real analysis. An example of this is Corollary 17, which recovers a theorem by Banach. More such examples can be found in §8, where, by applying relativized computability method, we are able to prove some results in classical analysis. While we are not aware of such consequences that would advance the state of the art in real analysis, it is plausible that future use of our techniques could accomplish this.
Overview of our paper
In §2 we do not discuss randomness reflection at all, but rather prove a result in higher randomness of independent interest. Theorem 1 is of the form “if a somewhat random X is hyp-computed by a very random Y, then X is already very random.” It is the higher randomness analog of [Reference Miller and Yu15, Theorem 4.3] by Miller and the third author. This result is a core ingredient of our main theorem.
§3.1 contains the main theorem of our paper, the equivalence of Luzin’s (N) for computable functions with
$\Pi ^1_1$
-randomness reflection and with
$\Delta ^1_1({\mathcal {O}})$
-randomness reflection. We consider higher Kurtz randomness in §3.3, and show that for continuous functions
$f:\mathbb R\rightarrow \mathbb R$
, Luzin’s (N) is equivalent to the reflection of
${\mathcal {O}}$
-Kurtz randomness, and separate this from
$\Delta ^1_1$
-Kurtz randomness reflection. In §3.4 we discuss the open questions raised by our main theorem: Just because Luzin’s (N) is equivalent to reflection of several higher randomness notions does not mean that it cannot be also equivalent to randomness reflection for some “lower” notions. For Martin–Löf-randomness reflection and weak-2-randomness reflection, we provide a separation from Luzin’s (N) in §4.
In §5 and §6 we consider Luzin’s (N) for more restricted classes of functions, namely functions with bounded variation and strictly increasing functions. Here Luzin’s (N) turns out to be equivalent to weak-2-randomness reflection, but we can still separate it from several other randomness-reflection-notion. These investigations tie in to a project by Bienvenu and Merkle [Reference Bienvenu and Merkle2] regarding how two computable measures being mutually absolutely continuous (i.e. having the same null sets) relates to randomness notions for these measures coinciding.
In §7 we take a very generic look at the complexity of randomness reflection, and show that the
$\Pi ^1_1$
-hardness established for Luzin’s (N) in [Reference Holický, Ponomarev, Zajíček and Zelený9] applies to almost all other randomness reflection notions, too.
§8 contains a brief digression about functions where the image of null sets is small in some other sense (countable or meagre). We prove these classical analysis results via various classical and higher computability methods.
We then conclude in §9 with a discussion of how this line of investigation could be continued in the future.
2 Randomness and hyperarithmetic reductions
Throughout, we assume familiarity with the theory of algorithmic randomness and higher randomness in particular. A standard references for the former are [Reference Downey and Hirschfeldt6] and [Reference Nies17]. For the latter, readers may refer to [Reference Chong and Yu5]. We use standard computability-theoretic notation. The Lebesgue measure is denoted by
$\lambda $
.
Our goal in this section is to establish the following:
Theorem 1. Let Y be
$\Delta ^1_1(Z)$
-random and
$\Pi ^1_1$
-random, let X be
$\Delta ^1_1$
-random and let
$X \leq _h Y$
. Then X is
$\Delta ^1_1(Z)$
-random.
This is a higher-randomness counterpart to [Reference Miller and Yu15, Theorem 4.3], and the proof proceeds by adapting both the proof of [Reference Miller and Yu15, Theorem 4.3] and [Reference Miller and Yu15, Lemma 4.2]. We will use the theorem in the following form:
Corollary 2. Let
$Z \geq _h {\mathcal {O}}$
. If X is
$\Delta ^1_1$
-random, Y is
$\Delta ^1_1(Z)$
-random and
$X \leq _h Y$
, then X is
$\Delta ^1_1(Z)$
-random.
Lemma 3. Fix
$\alpha \in {\mathcal {O}}$
and
$e \in \mathbb {N}$
. If X is
$\Delta ^1_1$
-random, then:
$$\begin{align*}\exists c \ \forall n \ \lambda(\{Y \mid \varphi_e(Y^{(\alpha)}) \in [X_{\upharpoonright n}]\}) < 2^{-n+c}.\end{align*}$$
Proof Analogous to the proof of [Reference Miller and Yu15, Lemma 4.2]. Let
$\mathcal {H}_\sigma = \{Y \mid \varphi _e(Y^{(\alpha )}) \in [\sigma ]\}$
, and then let
$F_i = \{\sigma \mid \lambda (\mathcal {H}_\sigma )> 2^{-|\sigma | + i}\}$
. By construction, the
$\mathcal {H}_{\sigma }$
are uniformly
$\Delta ^0_{\alpha +1}$
(as subsets of
${\{0,1\}^{\mathbb {N}}}$
), and so the sets
$F_i$
are uniformly
$\Delta ^0_{\alpha +2}$
(as subsets of
$2^{<\omega }$
).
A counting argument shows that
$\lambda ([F_i]) < 2^{-i}$
: Pick a prefix free set
$D \subseteq F_i$
with
$[D] = [F_i]$
. Then:
$$\begin{align*}1 \geq \lambda\left(\bigcup_{\sigma \in D} \mathcal{H}_\sigma\right) = \sum_{\sigma \in D} \lambda(\mathcal{H}_\sigma) \geq \sum_{\sigma \in D} 2^{-|\sigma| + i} = 2^{i}\lambda([F_i]).\end{align*}$$
We see that
$([F_i])_{i \in \mathbb {N}}$
is a Martin–Löf test relative to
$\emptyset ^{\alpha +2}$
. Since X is
$\Delta ^1_1$
-random, there has to be some
$c \in \mathbb {N}$
with
$X \notin [F_c]$
. This in turn means that
$\forall n \in \mathbb {N} \ X_{\upharpoonright n} \notin F_c$
, which by definition of
$F_c$
is the desired claim.⊣
Fact 4 (Sacks [Reference Sacks22])
$\Delta ^1_1(Z)$
-randomness (defined by being contained in no
$\Delta ^1_1(Z)$
-null sets) is equivalent to being
$\hat {Z}$
-random for every
$\hat {Z} \in \Delta ^1_1(Z)$
.
Lemma 5. Fix
$\alpha \in {\mathcal {O}}$
and
$e \in \mathbb {N}$
. If
$X = \varphi _e(Y^{(\alpha )})$
, X is
$\Delta ^1_1$
-random and Y is
$\Delta ^1_1(Z)$
-random, then X is
$\Delta ^1_1(Z)$
-random.
Proof We follow the proof of [Reference Miller and Yu15, Theorem 4.3]. Let c be the constant guaranteed for X by Lemma 3. As in the proof of Lemma 3, let
$\mathcal {H}_\sigma = \{W \mid \varphi _e(W^{(\alpha )}) \in [\sigma ]\}$
. Let
$\mathcal {G}_\sigma = \mathcal {H}_\sigma $
if
$\lambda (\mathcal {H}_\sigma ) < 2^{-|\sigma | + c}$
and
$\mathcal {G}_\sigma = \emptyset $
else. Note that
$\mathcal {G}_\sigma $
is still uniformly
$\Delta ^1_1$
. The choice of c in particular guarantees that
$Y \in \mathcal {G}_{X_{\upharpoonright n}}$
for each
$n \in \mathbb {N}$
.
Let
$\cap _n U_n$
denote a Martin–Löf test relative to
$\hat Z$
for some
$\hat Z \in \Delta ^1_1(Z)$
. By Fact 4, it suffices to show that
$X\not \in \cap _n U_n$
. We set
$\mathcal {K}_i = \bigcup _{\sigma \in U_{c+i}} \mathcal {G}_\sigma $
, and
$\mathcal {K} = \bigcap _{i \in \mathbb {N}} \mathcal {K}_i$
. We find that
$\mathcal {K}$
is
$\Delta ^1_1(Z)$
. Moreover, we have that:
$$\begin{align*}\lambda(\mathcal{K}_i) \leq \sum_{\sigma \in U_{c+i}} \lambda(\mathcal{G}_\sigma) \leq \sum_{\sigma \in U_{c+i}} 2^{-|\sigma| + c} \leq 2^{-i}.\end{align*}$$
Hence, it follows that
$\lambda (\mathcal {K}) = 0$
, so for some i,
$Y \not \in \mathcal K_i$
. Then
$X \not \in U_{c+i}$
, because
$Y \in \mathcal G_\sigma $
for all
$\sigma \prec X$
.⊣
Fact 6 (Sacks [Reference Sacks22])
If Y is
$\Pi ^1_1$
-random, then
$\omega _1^{\mathrm {CK}} = \omega _1^{\mathrm {CK},Y}$
.
Proof of Theorem 1 Since Y is
$\Pi ^1_1$
-random, we know that
$X \leq _h Y$
implies the existence of some
$\alpha \in {\mathcal {O}}$
and
$e \in \mathbb {N}$
such that
$X = \varphi _e(Y^{(\alpha )})$
(rather than merely
$\alpha \in {\mathcal {O}}^Y$
). We can thus invoke Lemma 5 to conclude that X is
$\Delta ^1_1(Z)$
-random.⊣
As an aside, the requirement in Theorem 1 that Y be
$\Pi ^1_1$
-random might be unexpected at first—it has no clear counterpart in [Reference Miller and Yu15, Theorem 4.3]. The following example, which is not needed for anything else in the paper, shows that this assumption is necessary.
Example 7. There are
$\Delta ^1_1$
-random X and
$\Delta ^1_1(Z)$
-random Y with
$X \leq _h Y$
but X is not
$\Delta ^1_1(Z)$
-random. In fact, we shall chose
$X = Z$
, and make X even
$\Pi ^1_1$
-random.
Proof Let Y be a
$\Delta ^1_1$
-random satisfying
$Y \geq _h {\mathcal {O}}$
. The existence of such a Y was shown in [Reference Chong, Nies and Yu3]. Let X be Martin–Löf random relative to
$Y \oplus {\mathcal {O}}$
while satisfying
$X \leq _h Y$
. This choice ensures that X is
$\Pi ^1_1$
-random (so in particular
$\Delta ^1_1$
-random).
By van Lambalgen’s theorem relativized to
$\emptyset ^{(\alpha )}$
, if both X and Y are
$\Delta ^1_1$
-random, then for any
$\alpha < \omega _1^{\mathrm {CK}}$
it holds that X is
$Y \oplus \emptyset ^{(\alpha )}$
-random iff
$X \oplus Y$
is
$\emptyset ^{(\alpha )}$
-random iff Y is
$X \oplus \emptyset ^{(\alpha )}$
-random. Since by choice of X, we know that in particular X is
$Y \oplus \emptyset ^{(\alpha )}$
-random, we conclude that Y is
$X \oplus \emptyset ^{(\alpha )}$
-random.
From ([Reference Chong and Yu4, Corollary 4.3]) it follows that for
$\Pi ^1_1$
-random X and
$\beta < \omega _1^{\mathrm {CK}}$
it holds that
$X^{(\beta )} \leq _{\mathrm {T}} X \oplus \emptyset ^{(\beta )}$
. (The conclusion above surely does not require full
$\Pi ^1_1$
-randomness of X, but too much precision would take us afield.) Together with the above, this shows that Y is
$X^{(\alpha )}$
-random for every
$\alpha < \omega _1^{\mathrm {CK}}$
. Since X is
$\Pi ^1_1$
-random, by Fact 6 we have that
$\omega _1^{\mathrm {CK}} = \omega _1^{\mathrm {CK},X}$
, and thus that Y is Z-random for any
$Z \in \Delta ^1_1(X)$
. By Fact 4 this establishes Y to be
$\Delta ^1_1(X)$
-random. But trivially, X cannot be
$\Delta ^1_1(X)$
-random.⊣
3 Luzin’s (N) and randomness reflection
Definition 8. A function satisfies Luzin’s (N) iff the image of every null set is null.
Definition 9. For any randomness notion R and a function f, we say that f reflects R -randomness if
$f(x)$
is R-random implies x is R-random for all x in the domain of f.
3.1 Luzin’s (N) and higher Martin–Löf randomness reflection
By noting that the sets of points not Martin–Löf random relative to some oracle are canonical choices of null sets, we obtain the following:
Proposition 10. The following are equivalent for a computable function
${f : \mathbb {R} \to \mathbb {R}}$
:
-
1. f satisfies Luzin’s (N).
-
2.
$\forall p \in {\{0,1\}^{\mathbb {N}}} \ \exists q \in {\{0,1\}^{\mathbb {N}}} \ f(x) \in \mathrm {MLR}(q) \Rightarrow x \in \mathrm {MLR}(p).$
-
3.
$\forall p \in {\{0,1\}^{\mathbb {N}}} \ f(x) \in \Delta ^1_1\mathrm {-random}(p) \Rightarrow x \in \mathrm {MLR}(p).$
-
4.
$\forall p \in {\{0,1\}^{\mathbb {N}}} \ f(x) \in \Delta ^1_1\mathrm {-random}(p) \Rightarrow x \in \Delta ^1_1\mathrm {-random}(p).$
Proof
-
$1 \Leftrightarrow 2.$
Each null set is contained in a set of the form
$\mathrm {MLR}(q)^C$
for some oracle
$q \in {\{0,1\}^{\mathbb {N}}}$
. Luzin’s (N) is thus equivalent to saying that for any p there is a q with
$f[\mathrm {MLR}(p)^C] \subseteq \mathrm {MLR}(q)^C$
. Taking the contrapositive yields
$2$
.
-
$2 \Rightarrow 3.$
Any
$\Sigma ^1_1$
-null set is contained in a
$\Delta ^1_1$
-null set [Reference Sacks22]. The set
$\{f(x) \mid x \notin \mathrm {MLR}(p)\}$
is
$\Sigma ^1_1(p)$
, so if it is contained in any
$\mathrm {MLR}(q)^C$
, it is contained in a
$\Delta ^1_1(p)$
null set, and hence in
$(\Delta ^1_1\mathrm {-random}(p))^C$
.
-
$3 \Rightarrow 1.$
Trivial.
-
$3 \Rightarrow 4.$
Assume that
$4$
fails, i.e. that there is some
$p \in {\{0,1\}^{\mathbb {N}}}$
and some
$x \notin \Delta ^1_1\mathrm {-random}(p)$
with
$f(x) \in \Delta ^1_1\mathrm {-random}(p)$
. But if
$x \notin \Delta ^1_1\mathrm {-random}(p)$
, then there is some
$q \leq _h p$
with
$x \notin \mathrm {MLR}(q)$
, but
$f(x) \in \Delta ^1_1\mathrm {-random}(q) = \Delta ^1_1\mathrm {-random}(p)$
, hence
$3$
is violated, too.
-
$4 \Rightarrow 3.$
Trivial.⊣
Corollary 11. A computable function satisfying Luzin’s (N) reflects
$\Delta ^1_1$
-randomness relative to any oracle.
We can now ask whether reflecting
$\Delta ^1_1$
-randomness relative to some specific oracle already suffices.
Fact 12 ([Reference Martin14, Reference Yu28])
If A is an uncountable
$\Delta ^1_1(y)$
-class such that
$y\leq _h z$
for every
$z\in A$
, then there is some
$x \in A$
with
${\mathcal {O}}^y \leq _h x$
.
Fact 13 (Sacks [Reference Sacks22])
If
${\mathcal {O}} \leq _h x$
, then x is not
$\Delta ^1_1({\mathcal {O}})$
-random.
Corollary 14. If computable f reflects
$\Delta ^1_1({\mathcal {O}})$
-randomness, then for any
$\Delta ^1_1({\mathcal {O}})$
-random y we find that
$f^{-1}(y)$
is countable.
Proof Assume that y is
$\Delta ^1_1({\mathcal {O}})$
-random and
$f^{-1}(y)$
is uncountable. Then by Fact 12, there is some
$x \in f^{-1}(y)$
with
${\mathcal {O}} \leq _h x$
. By Fact 13, we find that x is not
$\Delta ^1_1({\mathcal {O}})$
-random, contradicting that f reflects
$\Delta ^1_1({\mathcal {O}})$
-randomness.⊣
Observation 15. The following are equivalent for computable
$f : \mathbb {R} \to \mathbb {R}$
:
-
1. For almost all y it holds that
$f^{-1}(\{y\})$
is countable. -
2. For every
$\Delta ^1_1$
-random y it holds that
$f^{-1}(\{y\})$
is countable.
Proof The implication
$2 \Rightarrow 1$
is trivial. For the other direction, note that
$$\begin{align*}\{y \mid f^{-1}(\{y\}) \ \mathrm{is uncountable}\}\end{align*}$$
is
$\Sigma ^1_1$
. This holds because for a
$ \Sigma ^1_1$
-set A, being uncountable is equivalent to containing an element which is not hyperarithmetic relative to A. Due to Kleene’s HYP-quantification theorem, an existential quantifier over nonhyperarithmetic elements is equivalent to an unrestricted existential quantifier. By assumption, it is a null set. Any
$\Sigma ^1_1$
-null set is contained in a
$\Delta ^1_1$
-null set, so it is then contained in a
$\Delta ^1_1$
-null set, and so cannot contain any
$\Delta ^1_1$
-randoms.⊣
Theorem 16. The following are equivalent for computable
$f : \mathbb {R} \to \mathbb {R}$
:
-
1. f satisfies Luzin’s (N).
-
2. f reflects
$\Delta ^1_1({\mathcal {O}})$
-randomness. -
3. f reflects
$\Delta ^1_1$
-randomness and for almost all y,
$f^{-1}(y)$
is countable. -
4. f reflects
$\Pi ^1_1$
-randomness.
Proof That
$1$
implies
$2$
follows from Proposition 10. To see that
$2$
implies
$1$
, we show that if f reflects
$\Delta ^1_1({\mathcal {O}})$
-randomness, then it reflects
$\Delta ^1_1(r)$
-randomness for all
$r \geq _T {\mathcal {O}}$
. This will be enough because if f reflects
$\Delta ^1_1(r)$
-randomness for all
$r \geq _T {\mathcal {O}}$
, then for any
$p \in \{0,1\}^{\mathbb N}$
, if
$f(x) \in \mathrm {MLR}({\mathcal {O}}^{p\oplus {\mathcal {O}}})$
, then
$f(x)$
is
$\Delta ^1_1(p\oplus {\mathcal {O}})$
-random, so x is
$\Delta ^1_1(p \oplus {\mathcal {O}})$
-random, so
$x \in \mathrm {MLR}(p)$
. Thus f satisfies condition 2 of Proposition 10.
So let y be
$\Delta ^1_1(r)$
-random for some
$r \geq _T {\mathcal {O}}$
. By Corollary 14,
$f^{-1}(y)$
is countable. So if
$x \in f^{-1}(y)$
, then
$x \leq _h y$
. Since f reflects
$\Delta ^1_1({\mathcal {O}})$
-randomness, we know that x is
$\Delta ^1_1$
-random. We can thus invoke Theorem 1 to conclude that x is
$\Delta ^1_1(r)$
-random, and have reached our goal. (Note that y is
$\Pi ^1_1$
-random because
$r\geq _T {\mathcal {O}}$
.)
To see that
$1$
implies
$3$
we use Proposition 10 and Corollary 14. The proof that
$3$
implies
$1$
proceeds analogously to the proof that
$2$
implies
$1$
, except that we conclude that
$f^{-1}(\{y\})$
is countable from Observation 15 rather than Corollary 14.
To see that
$3$
implies
$4$
, by Observation 15, in fact the inverse image of every
$\Delta ^1_1$
-random point is countable. In particular if y is
$\Pi ^1_1$
-random, then
$f^{-1}(y)$
is countable. We use the following characterization of
$\Pi ^1_1$
-randomness due to Stern: y is
$\Pi ^1_1$
-random if and only if y is
$\Delta ^1_1$
-random and
$\omega _1^y = \omega _1^{\mathrm {CK}}$
[Reference Stern26, Reference Stern27, Reference Chong, Nies and Yu3]. Recall also that
$\omega _1^y = \omega _1^{\mathrm {CK}}$
if and only if
$y \not \geq _h {\mathcal {O}}$
[Reference Sacks23, Corollary 7.7]. Let
$x \in f^{-1}(y)$
. By
$\Delta ^1_1$
-randomness reflection, x is
$\Delta ^1_1$
-random. Since
$f^{-1}(y)$
is countable,
$y \geq _h x$
. Thus
$x \not \geq _h {\mathcal {O}}$
. Therefore x is
$\Pi ^1_1$
-random.
The proof that
$4$
implies
$1$
is the same as how conditions
$2$
or
$3$
implied
$1$
. Letting y be
$\Delta ^1_1(r)$
-random, since
$r\geq _T {\mathcal {O}}$
then y is
$\Pi ^1_1$
-random. If
$f^{-1}(y)$
were uncountable, by Fact 12, it would contain some x with
$x \geq _h {\mathcal {O}}$
, contradicting
$\Pi ^1_1$
-randomness reflection.⊣
3.2 A note on the countability of fibers
We obtain as a corollary a reproof of a theorem by Banach [Reference Banach1], cf. [Reference Saks24, Chapter IX, Theorem 7.3]:
Corollary 17. If f is continuous and satisfies Luzin’s (N), then for almost all y we find that
$f^{-1}(y)$
is countable.
The following generalization to measurable functions was also known, but we give a new proof.
Corollary 18.
-
1. If f satisfies Luzin’s (N) and there are a continuous function g and a Borel set A so that f agrees with g on A, then for almost every real
$y \in f(A)$
we find that
$f^{-1}(y)\cap A$
is countable. -
2. If f satisfies Luzin’s (N) and is measurable, then for almost every real y we find that
$f^{-1}(y)$
is countable.
Proof 1. Fix a real x so that g is computable in x and A is
$\Delta ^1_1(x)$
. Assume that y is
$\Delta ^1_1({\mathcal {O}}^x)$
-random and
$f^{-1}(y)\cap A=g^{-1}(y)\cap A$
is uncountable. Since
$ A$
is
$\Delta ^1_1(x)$
, by Claim 12, then there is some
$z \in g^{-1}(y)\cap A=f^{-1}(y)\cap A $
with
${\mathcal {O}}^x \leq _h z\oplus x$
. By Fact 13, we find that z is not
$\Delta ^1_1({\mathcal {O}}^x)$
-random, contradicting that g reflects
$\Delta ^1_1({\mathcal {O}}^x)$
-randomness.
2. By Luzin’s theorem, there are a sequence Borel sets
$\{A_n\}_{n\in \omega }$
and continuous functions
$\{g_n\}_{n\in \omega }$
so that
$\mathbb {R}\setminus \bigcup _n A_n$
is null and f agrees with
$g_n$
over
$A_n$
for every n. As f has Luzin’s (N), also
$f[\mathbb {R}\setminus \bigcup _n A_n]$
is null, and thus can be ignored for our argument. For
$y \notin f[\mathbb {R}\setminus \bigcup _n A_n]$
, we find that
$f^{-1}(y) \subseteq \bigcup _{n \in \mathbb {N}} g_n^{-1}(y)$
. Since each set in the right-hand union is countable for almost all y by Corollary 17, the union itself is countable for almost all y, proving the claim.⊣
Note that the Borelness of the set A in the corollary above cannot be replaced by “arbitrary set,” as it is consistent with
$\mathrm {ZFC}$
that the corresponding statement is false. For example, assuming the continuums hypothesis (
$\mathrm {CH}$
) or the even weaker Martin’s axiom (
$\mathrm {MA}$
) suffices to construct a counterexample. We do not know whether the following proposition can be proved within
$\mathrm {ZFC}$
.
Proposition 19 (
$\mathrm {ZFC}+\mathrm {MA}$
)
There is a function
$f : {[0, 1]} \to {[0, 1]}$
having Luzin’s (N) and a set
$A \subseteq {[0, 1]}$
such that
$f|_{A}$
is a computable,
$f[A]$
is non-null, and for any
$y \in f[A]$
the set
$f^{-1}(\{y\}) \cap A$
is uncountable.
Proof We actually need only a weaker condition than
$\mathrm {MA}$
for our construction, namely the equality
$\operatorname {cof}(\mathcal {L}) = \operatorname {cov}(\mathcal {L}) = \operatorname {non}(\mathcal {L})$
in Cichoń’s diagram. Recall that
$\operatorname {cof}(\mathcal {L})$
is the least cardinality of a set R of null sets such that any null set is a subset of an element of R;
$\operatorname {cov}(\mathcal {L})$
is the least cardinal
$\alpha $
such that
${[0, 1]}$
is a union of
$\alpha $
-many null sets, and
$\operatorname {non}(\mathcal {L})$
is the least cardinal of a non-null set. It is a consequence of
$\mathrm {MA}$
that all these cardinals are
$2^{\aleph _0}$
. As they all are clearly uncountable and at most the continuum,
$\mathrm {CH}$
trivially implies the same. Let
$\kappa $
denote the value of these three invariants.
First, we observe that
$\kappa = \operatorname {cof}(\mathcal {L})$
means that there exists a family
$(z_\alpha )_{\alpha < \kappa }$
such that a set
$A \subseteq {\{0,1\}^{\mathbb {N}}}$
is null iff
$A \subseteq \mathrm {MLR}(z_\alpha )^C$
for some
$\alpha < \kappa $
. Next, we point out that
$\kappa = \operatorname {cov}(\mathcal {L})$
means that for any
$\alpha < \kappa $
and family
$(w_\beta )_{\beta < \alpha }$
there exists some u which is Martin–Löf random relative to all
$w_\beta $
.
We start with a family
$(z_\alpha )_{\alpha < \kappa }$
as above, and then choose
$(x_\alpha )_{\alpha < \kappa }$
such that each
$x_\alpha $
is Martin–Löf random relative to any
$z_\beta $
for
$\beta \leq \alpha $
. We then choose another sequence
$(y_\alpha )_{\alpha < \kappa }$
such that
$y_\alpha $
is Martin–Löf random relative to any
$x_\beta \oplus z_\gamma $
for
$\beta, \gamma \leq \alpha $
. We identify
${\{0,1\}^{\mathbb {N}}}$
with a positive measure subset of
${[0, 1]}$
(a fat Cantor set), and then define
$A = \{y_\beta \oplus x_\alpha \mid \alpha \leq \beta < \kappa \}$
, and
$f : {[0, 1]} \to {[0, 1]}$
as
$f(y_\beta \oplus x_\alpha ) = x_\alpha $
and
$f(w) = 0$
for
$w \notin A$
.
As
$f|_A$
is just the projection, it is clear that it is computable. To see that
$f[A]$
is non-null, note that if it were null, it would need to be contained in
$\mathrm {MLR}(z_\alpha )^C$
for some
$\alpha < \kappa $
. But
$x_\alpha \in f[A]$
is explicitly chosen to prevent this. For any
$x_\alpha \in f[A]$
, we find that
$f^{-1}(\{x_\alpha \}) \cap A = \{y_\beta \oplus x_\alpha \mid \alpha \leq \beta < \kappa \}$
has cardinality
$\kappa $
, and
$\kappa $
is uncountable.
It remains to argue that f has Luzin’s (N). As f is constant outside of A, we only need to consider null sets
$B \subseteq A$
. Again invoking van Lambalgen’s theorem, we see that any
$y_\beta \oplus x_\alpha $
is Martin–Löf random relative to
$z_\gamma $
whenever
$\gamma \leq \alpha \leq \beta $
. As such, each null
$B \subseteq A$
is contained in some
$\{y_\beta \oplus x_\alpha \mid \alpha \leq \beta < \gamma \}$
for
$\gamma < \kappa $
. It follows that
$f[B] \subseteq \{x_\alpha \mid \alpha < \gamma \}$
has cardinality strictly below
$\kappa $
, and hence is null due to
$\kappa = \operatorname {non}(\mathcal {L})$
.⊣
That all fibers are countable is just preservation of h-degrees:
Observation 20. For computable
$f : \mathbb {R} \to \mathbb {R}$
the following are equivalent:
-
1. f preserves h-degrees, i.e.
$\forall x \in {[0, 1]} \ x \equiv _h f(x)$
. -
2. For all
$y \in \mathbb {R}$
,
$f^{-1}(y)$
is countable.
3.3 Luzin’s (N) and higher Kurtz randomness reflection
In his thesis [Reference Luzin13], Luzin showed that if a continuous function
$f:\mathbb R \rightarrow \mathbb R$
fails to have property
$(N)$
, then in fact there is a compact witness to this failure. For the reader’s convenience, we give a proof of this fact below.
Proposition 21. Let
$f : \mathbb R \to \mathbb R$
be continuous and map some null set to a non-null set. Then there is a compact subset
$A \subseteq \mathbb R$
with
$\lambda (A) = 0$
and
$\lambda (f(A))> 0$
.
Proof Observe that a function
$f:\mathbb R\rightarrow \mathbb R$
satisfies Luzin’s (N) if and only if its restriction
$f\upharpoonright [a,b]$
satisfies Luzin’s (N) for every closed interval
$[a,b]$
. So without loss of generality, we assume that f fails Lusin’s (N) because
$\mu (A) = 0$
but
$\mu (f(A)) = d> 0$
for some
$A \subseteq [a,b]$
. As every null set is contained in a
$\mathbf {\Pi }^0_2$
-null set, without loss of generality we can assume
$A = \cap _n U_n$
for some decreasing sequence of open sets
$U_n$
. Each
$U_n$
is itself equal to an increasing union of closed sets. The idea is by picking big enough closed
$F_n \subseteq U_n$
, we can find a closed set
$\bigcap _{n \in \mathbb {N}} F_n \subseteq A$
whose image still has positive measure. How large to pick the
$F_n$
? Let
$F_0 \subseteq U_0$
be large enough that
$\mu (f(F_0\cap A))> d/2$
. In general, if we have found
$(F_i)_{i<n}$
such that
$\mu (f(\cap _{i<n} F_i \cap A))>d/2$
, then since
$A \subseteq U_n$
, we can find closed
$F_n \subseteq U_n$
large enough that
$\mu (f(\cap _{i<n} F_i \cap F_n \cap A))>d/2$
as well. Therefore for all n, we have
$\mu (f(\cap _{i<n} F_i))>d/2$
, and therefore
$\mu (\cap _n f(\cap _{i<n} F_i)) \geq d/2$
. Claim:
$\cap _n f(\cap _{i<n} F_i) = f(\cap _n F_n)$
. One direction is clear. In the other, suppose that
$y \in \cap _n f(\cap _{i<n} F_i)$
. Then
$\cap _{i<n} F_n \cap f^{-1}(y) \neq \emptyset $
for all n. By compactness,
$\cap _n F_n \cap f^{-1}(y) \neq \emptyset $
.⊣
As the image of as images of compact sets under continuous functions are uniformly compact, this shows that Luzin’s (N) implies the reflection of all kinds of Kurtz randomness. This is in contrast to the situation for Martin–Löf randomness, because the image of a
$\mathbf \Pi ^0_2$
set under a continuous f is not even
$\mathbf \Pi ^0_2$
in general, let alone with the same oracle.
Proposition 22. If
$f:\mathbb R \rightarrow \mathbb R$
satisfies Luzin’s (N), then f reflects Kurtz randomness relative to every oracle.
Proof Given oracle Z, suppose that x is not Z-Kurtz random because
$x \in F$
, where F is a Z-computable compact set of measure 0. Then
$f(F)$
is also a Z-computable compact set, which has measure 0 because f has Luzin’s (N). Therefore,
$f(x)$
is also not Z-Kurtz random.⊣
An immediate consequence is that any f with Luzin’s (N) also reflects
$\Delta ^1_1$
-Kurtz randomness relative to every oracle. In general, Kurtz randomness reflection for stronger oracles implies it for weaker ones.
Proposition 23. If a continuous function
$f:\mathbb R \rightarrow \mathbb R$
reflects Z-Kurtz randomness, then f reflects X-Kurtz randomness for every
$X \leq _T Z$
.
Proof Assume that f reflects Z-Kurtz randomness. Suppose x is not X-Kurtz random. Let P be an X-computable compact null set with
$x \in P$
. Then
$f(P)$
is an X-computable compact set, which is null because P is also Z-computable. Therefore,
$f(x)$
is not X-Kurtz random.⊣
Additionally, any witness to the failure of Luzin’s (N) also provides an oracle relative to which Kurtz randomness reflection fails.
Proposition 24. Suppose that
$f:\mathbb R \rightarrow \mathbb R$
and
$A \subseteq \mathbb R$
is a Z-computable compact null set with
$\lambda (f(A))>0$
. Then f does not reflect Z-Kurtz randomness.
Proof Since
$f(A)$
is also Z-computable and has positive measure, it must contain some Z-Kurtz random y. There is some
$x \in A$
with
$f(x) = y$
, but since A is a Z-computable compact null set, it cannot contain any Z-Kurtz randoms. Hence, f does not reflect Z-Kurtz randomness.⊣
We can thus characterize Luzin’s (N) in terms of Kurtz randomness reflection.
Theorem 25. The following are equivalent for computable
$f : \mathbb R \to \mathbb R$
:
-
1. f has Luzin’s (N).
-
2. For every
${\mathcal {O}}$
-computable compact set A with
$\lambda (A) = 0$
also
$\lambda (f(A)) = 0$
. -
3. f reflects
${\mathcal {O}}$
-Kurtz randomness.
Proof
-
$1 \Rightarrow 2.$
Trivial.
-
$2 \Rightarrow 1.$
We observe that given computable
$f : \mathbb R \to \mathbb R$
and number n, the set is a
$$\begin{align*}\{A \subseteq \mathbb [-n,n] \text{ compact } \mid \lambda(A) = 0 \wedge \lambda(f(A)) \geq 2^{-n}\}\end{align*}$$
$\Pi ^0_2$
-subset of the Polish space of compact subsets of
$[-n,n]$
. By Proposition 21, if f fails Luzin’s (N), this set is non-empty for some n. If it is non-empty, it must have an
${\mathcal {O}}$
-computable element by Kleene’s basis theorem.
-
$1 \Rightarrow 3.$
By Proposition 22.
-
$3 \Rightarrow 2.$
By Proposition 24.⊣
We also see that
$\Delta ^1_1$
-Kurtz randomness reflection does not suffice for a characterization.
Lemma 26. Reflecting
$\Delta ^1_1$
-Kurtz randomness is a
$\Sigma ^1_1$
-property of continuous functions of type
$f : \mathbb R \to \mathbb R$
.
Proof By Proposition 24, reflecting
$\Delta ^1_1$
-Kurtz randomness is equivalent to the statement that for any
$\Delta ^1_1$
compact set A with
$\lambda (A) = 0$
we have
$\lambda (f(A)) = 0$
. By Kleene’s HYP quantification theorem [Reference Kleene11, Reference Kleene12], a universal quantification over
$\Delta ^1_1$
can be replaced by an existential quantification over Baire space. That
$\lambda (A) = 0$
implies
$\lambda (f(A)) = 0$
is a
$\Delta ^0_3$
-statement for given f and A.⊣
Corollary 27. Reflecting
$\Delta ^1_1$
-Kurtz randomness is strictly weaker than Luzin’s (N).
Proof By Proposition 22, Luzin’s (N) implies
$\Delta ^1_1$
-Kurtz randomness reflection. By Lemma 26 reflecting
$\Delta ^1_1$
-Kurtz randomness is a
$\Sigma ^1_1$
-property. But it was shown in [Reference Holický, Ponomarev, Zajíček and Zelený9] that Luzin’s (N) is
$\Pi ^1_1$
-complete for continuous functions. Thus the two notions cannot coincide.⊣
3.4 Open questions
Theorems 16 and 25 tell us that
$\Delta ^1_1({\mathcal {O}})$
-randomness reflection and
${\mathcal {O}}$
-Kurtz randomness reflection each characterize Luzin’s (N) for computable functions. This does not rule out that other kinds of randomness reflection could also characterize Luzin’s (N). In the next section we shall see that none of MLR-reflection, W2R-reflection, or MLR
$(\emptyset ')$
-reflection imply Luzin’s (N) for arbitrary computable functions (Corollary 31). Because reflection asks for the same level of randomness on both sides, there are no completely trivial implications between the
$\mathbf \Pi ^0_2$
-type randomness reflection notions. Indeed, results in [Reference Bienvenu and Merkle2] suggest that the implication structure between
$\mathbf \Pi ^0_2$
-type randomness reflection notions may have little relation to the implication structure between notions of randomness. However, the most interesting open question seems to be:
Open Question 28. Can a computable function reflect
$\Delta ^1_1$
-randomness but fail Luzin’s (N)?
By Theorem 16 any such example would need to have a positive measure of fibers being uncountable, which is incompatible with most niceness conditions. We also do not know the answer to the above question if
$\Delta ^1_1$
-randomness is replaced with Martin–Löf randomness relative to
$\emptyset ^{(\alpha )}$
for any
$\alpha \geq 2$
.
Related questions concern basis theorems for failures of Luzin’s (N). We have already seen in Theorem 25 that any computable f which fails Luzin’s (N) must see that failure witnessed by a
$\mathcal O$
-computable compact set. The proof shows that such a set can also be chosen hyperarithemetically low, by applying Gandy basis theorem in place of the Kleene. On the other hand, Corollary 27 shows that a function which fails Luzin’s (N) need not have a hyperarithmetic compact witness. Indeed, one can obtain specific examples of this separation by feeding pseudo-well-orders into the
$\Pi ^1_1$
-completeness construction of [Reference Holický, Ponomarev, Zajíček and Zelený9]. Thus the results for compact witnesses are rather tight overall.
The situation for the minimum complexity of
$\mathbf \Pi ^0_2$
witnesses is less well understood. The proof of Corollary 31 shows that a computable function may fail Luzin’s (N) while still mapping all rapidly null
$\Pi ^0_2(\emptyset ')$
sets to null sets. That is, the set
$\mathrm {MLR}(\emptyset ')^C$
is mapped to a null set.
Open Question 29. Can a computable function map
$W3R^C$
to a null set but fail Luzin’s (N)? Equivalently, can a computable function map all null
$\Pi ^0_2(\emptyset ')$
sets to null sets while failing Luzin’s (N)?
We note that the functions produced by the
$\Pi ^1_1$
-completeness construction of [Reference Holický, Ponomarev, Zajíček and Zelený9] are of no help because the failure of Lusin’s (N), when it occurs, is witnessed by an effectively null
$\Pi ^0_2$
set.
4 Separating Luzin’s (N) from MLR-reflection
We present a construction of a computable function that violates Luzin’s (N), and yet is piecewise-linear in a neighborhood of every point that is not
$\mathrm {MLR}(\emptyset ')$
. Here, we say that f is piecewise-linear in a neighborhood of x, if there are rationals
$a < x < b$
such that
$f|_{[a,x]}$
and
$f|_{[x,b]}$
are linear functions. Computable piecewise-linear functions reflect essentially all kinds of randomness.
Theorem 30. For each
$\Pi ^0_1(\emptyset ')$
-set
$A \subseteq {[0, 1]}$
there is a computable function
$f : {[0, 1]} \to {[0, 1]}$
such that:
-
1. For every
$x \in {[0, 1]} \setminus A$
, f is piecewise-linear on a neighborhood of x. -
2. For every
$\varepsilon>0$
, there is a null
$\Pi ^0_1(\emptyset '')$
set
$B \subseteq A$
such that
$\lambda (f[B]) \geq \lambda (A) - \varepsilon $
.
Corollary 31. There is a computable function
$f : {[0, 1]} \to {[0, 1]}$
that reflects ML-randomness, weak-2-randomness and ML(
$\emptyset '$
)-randomness, yet does not have Luzin’s (N), nor reflects weak-3-randomness.
Proof Let A be the complement of the first component of a universal ML(
$\emptyset '$
)-test. Then
$\lambda (A)> \frac {1}{2}$
. We invoke Theorem 30 on A and
$\epsilon = \frac {1}{4}$
. The resulting function is the desired one: If
$x \in {[0, 1]}$
is not ML(
$\emptyset '$
)-random, then
$x \notin A$
, f is piecewise-linear on a neighborhood of x, and thus
$f(x)$
is not ML(
$\emptyset '$
)-random. As such, we conclude that whenever
$f(x)$
is ML(
$\emptyset '$
)-random, then so is x (same for the other notions).
Since we can choose the witness B as being
$\Pi ^0_1(\emptyset '')$
, it is also
$\Pi ^0_2(\emptyset ')$
, and thus contains only elements which are not weak-3-random. Since
$f[B]$
has positive measure, it contains a weak-3-random—hence f does not reflect weak-3-randomness.⊣
We remark that this is the strongest result possible for the strategy we are using. We are making sure that f reflects
$\mathrm {MLR}(\emptyset ')$
-randomness by making f piecewise-linear in a neighborhood of every non-
$\mathrm {MLR}(\emptyset ')$
point. However, the following proposition shows that the set of points where f can be this simple has a descriptive complexity of
$\Sigma ^0_1(\emptyset ')$
. But the weak-3-nonrandoms are not contained in any
$\Sigma ^0_1(\emptyset ')$
set except
${[0, 1]}$
.
Proposition 32. Let
$f : \mathbb {R} \to \mathbb {R}$
be computable. The set of points where f is locally piecewise-linear is
$\Sigma ^0_1(\emptyset ')$
.
Proof We consider the property
$\mathrm {2L}$
of a function f and an interval
$[a,b]$
that there is some
$x \in [a,b]$
such that both
$f|_{[a,x]}$
and
$f|_{[x,b]}$
are linear. We first claim that this is a
$\Pi ^0_1$
-property. To this, we observe that
$\mathrm {2L}$
is equivalent to:
$$ \begin{align} &\forall n \in \mathbb{N} \quad \exists i \leq n \quad \forall j \in \{0,\ldots,n-2\} \setminus \{i-1,i,i+1\} \nonumber\\ &\qquad f\left(a + \frac{j}{n}\right) - f\left(a + \frac{j+1}{n}\right) = f\left(a + \frac{j+1}{n}\right) - f\left(a + \frac{j+2}{n}\right) \end{align} $$
Next, we observe that f is locally piecewise-linear in x iff there is some rational interval
$(a,b) \ni x$
such that f has property
$\mathrm {2L}$
on
$[a,b]$
. Using
$\emptyset '$
, we can enumerate all these intervals.⊣
Generalizing this idea slightly, recall that a function is bi-Lipschitz, if both the function and its inverse are Lipschitz functions, i.e. if there exists some constant L such that
$d(f(x),f(y)) \leq Ld(x,y) \leq L^2d(f(x),f(y))$
for all
$x, y$
in the domain. Since computable locally bi-Lipschitz functions preserve and reflect all kinds of randomness, Another way for f to ensure a given notion of randomness reflection is by being locally bi-Lipschitz on the nonrandom points for that notion. However, we still get a
$\Sigma ^0_1(\emptyset ')$
-set of suitable points.
Proposition 33. Let
$f : \mathbb {R} \to \mathbb {R}$
be computable. The set of points where f is locally bi-Lipschitz is
$\Sigma ^0_1(\emptyset ')$
.
Proof The following is a co-c.e. property in
$a,b \in \mathbb {Q}$
and
$L \in \mathbb {N}$
and
$f \in \mathcal {C}(\mathbb {R},\mathbb {R})$
:
$$\begin{align*}\forall x,y \in [a,b] \quad d(x,y) \leq Ld(f(x),f(y)) \leq L^2d(x,y)\end{align*}$$
We obtain the set of points where f is locally bi-Lipschitz by taking the union of all
$(a,b)$
having the property above for some
$L \in \mathbb {N}$
– access to
$\emptyset '$
suffices to get such an enumeration.⊣
4.1 High-level proof sketch
Before diving into the details of the proof of Theorem 30 we give a high-level sketch of what is going on. Consider first the case where A is
$\Pi ^0_1$
. Then
$A = \cap _n A_n$
, where each
$A_n$
is a finite union of closed intervals and
$A_{n+1}\subseteq A_n$
. We iteratively define a sequence of piecewise linear functions
$f_0,f_1,\dots $
, where
$f_0:{[0, 1]} \rightarrow {[0, 1]}$
is the identity, and
$f_{n}$
is obtained from
$f_{n-1}$
by performing a “tripling” operation on those line segments of
$f_{n-1}$
which are contained in
$A_{n}$
. In order to “triple” a line segment, we replace it by a zig-zag of three line segments each of which has triple the slope of the original. (See Figure 1) We want to make the sequence
$(f_n)$
converge in the supremum norm, so before tripling we add invisible break points to
$f_{n-1}$
so that none of its linear pieces are more than
$2^{-n}$
tall. Letting f be the limit function, observe that if
$x \not \in A_n$
, then f coincides with
$f_n$
on a neighborhood of x, and thus f is linear on a neighborhood of x. On the other hand, A is then exactly the set of points where we tripled infinitely often.
Figure 1 Demonstrating the interactive construction of the function f in the proof of Theorem 30.
Next we describe how to find a closed set
$B\subseteq A$
such that
$\lambda (f(B)) \geq \lambda (A)$
. (The
$\varepsilon $
in the statement of the theorem exists in order to bring down the descriptive complexity of B, but we can ignore it for now.) We want
$B\subseteq A$
, so of course we throw out of B any interval that leaves A. Also, every time we perform a tripling, we choose two-thirds of the tripled interval to throw out of B. We do this so that the one-third which we keep has maximal measure of intersection with A. Observe that
$\lambda (B) = 0$
.
Here is why
$\lambda (f(B))\geq \lambda (A)$
. Let
$B_0 = [0,1]$
and let
$B_n$
denote the set of points that remain in B at the end of stage n. By induction,
$f_n \upharpoonright B_n$
is injective (except possibly at break points) and
$\lambda (f_n(B_n\cap A)) \geq \lambda (A)$
. The key to the induction is that by the choice of thirds, we always have
$3^n\lambda (B_n\cap A) \geq \lambda (A)$
, and since
$f_n$
has slope
$\pm 3^n$
on all of
$B_n$
and is essentially injective,
$\lambda (f_n(B_n \cap A)) = 3^n\lambda (B_n\cap A)$
. It now follows that
$\lambda (f_n(B_n)) \geq \lambda (A)$
for all n. Furthermore, since the continuous image of a compact set is uniformly compact, we cannot have
$\lambda (f(B)) < \lambda (A)$
, for this would have been witnessed already for some
$\lambda (f_n(B_n))$
. This completes the sketch for the case where A is
$\Pi ^0_1$
.
If A is
$\Pi ^0_1(\emptyset ')$
, we can do essentially the same construction, tripling on the stage-n approximation to
$A_n$
instead of
$A_n$
itself. Any interval which is going to leave A eventually leaves the approximations for good, so the key features of the above argument are maintained even as the structure of the triplings gets more complicated.
4.2 Proof of Theorem 30
The remainder of this section is devoted to the preparation for the proof of Theorem 30, and the proof itself.
Lemma 34. Given a
$\Pi ^0_1(\emptyset ')$
-set
$A \subseteq {[0, 1]}$
and some open
$U \supseteq A$
we can compute some open V with
$A \subseteq V \subseteq U$
such that
$d(V,U^C)> 0$
.
Proof Since
$U^C$
and A are disjoint closed sets, there is some
$N \in \mathbb {N}$
such that
$d(U^C,A)> 2^{-N}$
. If we actually had access to A, we could compute a suitable N. Since A is computable from
$\emptyset '$
, we can compute N with finitely many mindchanges. The monotonicity of correctness here means we can actually obtain suitable
$N \in \mathbb {N}_<$
. We now obtain V by enumerating an interval
$(a,b)$
into V once we have learned that U covers
$[a-2^{-N},b+2^{-N}]$
(which is semidecidable in
$U \in \mathcal {O}(\mathbb {R})$
and
$N \in \mathbb {N}_<$
).⊣
For an interval
$[a,b]$
, let
$T_0([a,b]) = [a, a + \frac {b-a}{3}]$
,
$T_1([a,b]) = [a + \frac {b-a}{3}, a + 2\frac {b-a}{3}]$
and
$T_2([a,b]) = [a + 2\frac {b-a}{3}, b]$
.
Lemma 35. Let A be a
$\Pi ^0_1(\emptyset ')$
set. Then there is a computable double-sequence
$(I^k_n)_{k,n \in \mathbb {N}}$
of closed intervals with the following properties:
-
1.
$A = \bigcap _{n \in \mathbb {N}} \bigcup _{k \in \mathbb {N}} I^k_n$
. -
2.
$I^k_n$
and
$I^\ell _n$
intersect in at most one point. -
3. For
$m < n$
, we find that
$\bigcup _{k \in \mathbb {N}} I^k_n$
has positive distance to the complement of
$\bigcup _{k \in \mathbb {N}} I^k_m$
. -
4.
$\forall k, n \in \mathbb {N} \quad |I^k_n| \geq |I^{k+1}_n|$
-
5. Fix
$n> 0$
. For each k there are
$\ell $
, i such that
$|I^k_{n}| < 3^{-2}|I^\ell _{n-1}|$
and
$I^k_n \subseteq T_i(I^\ell _{n-1})$
.
Proof Any
$\Pi ^0_1(\emptyset ')$
is in particular
$\Pi ^0_2$
, and thus has
$\Pi ^0_2$
-approximation
$A = \bigcap _{n \in \mathbb {N}} U_n$
. We invoke Lemma 34 inductively first on A and
$U_0$
to obtain
$V_0$
, then on A and
$U_1 \cap V_0$
to obtain
$V_1$
, and so on. This will ensure Condition (3). We can effectively write any open set
$V_n \subseteq {[0, 1]}$
as a union of closed intervals such that the pairwise intersections contain at most one point. To make Conditions (4) and (5) work it suffices to subdivide intervals sufficiently much.⊣
Definition 36. An interval J is well-located relative to
$(I^k_n)_{k,n \in \mathbb {N}}$
, if for all
$k, n$
one of the following hold:
-
1.
$|J \cap I^k_n| \leq 1$
-
2.
$J \supseteq I^k_n$
-
3.
$J \subseteq T_i(I^k_n)$
for some
$i \in \{0,1,2\}$
For well-located J, let its depth be the greatest n such that
$J \subseteq I^k_n$
for some k. We call two well-located intervals
$J_0, J_1$
peers, if whenever
$J_b \subsetneq I^k_n$
for both
$b \in \{0,1\}$
and some
$k, n$
, then there is one
$i \in \{0,1,2\}$
such that
$J_b \subseteq T_i(I^k_n)$
for both
$b \in \{0,1\}$
.
Note that our requirements for the
$(I^k_n)_{k,n \in \mathbb {N}}$
in Lemma 35 in particular ensure that each
$I^{k_0}_{n_0}$
is well-located relative to
$(I^k_n)_{n,k \in \mathbb {N}}$
.
Definition 37. We are given a double-sequence
$(I^k_n)_{k,n \in \mathbb {N}}$
for a set A as in Lemma 35 and
$\varepsilon> 0$
. Let
$N_n \in \mathbb {N}$
be chosen sufficiently large such that
$\lambda (\bigcup _{k> N_n} I_n^k) < 3^{-n}2^{-n-2}\varepsilon $
. Let
$b_{k,n} \in \{0,1,2\}$
be chosen such that
$\lambda (T_{b_{k,n}}(I^k_n) \cap A) + 3^{-n}2^{-n-3-k}\varepsilon \geq \lambda (T_{c}(I^k_n) \cap A)$
for all
$k, n \in \mathbb {N}$
and
$c \in \{0,1,2\}$
. Let
$\ell _{n,k}$
and
$i_{n,k}$
be the witnesses for Condition 5 in Lemma 35. We then inductively define
$\mathfrak {I}_0^\varepsilon = \{I_0^k \mid k \leq N_0\}$
and:
$$\begin{align*}\mathfrak{I}_n^\varepsilon = \{I_n^k \mid k \leq N_n \wedge I^{\ell_{n,k}}_{n-1} \in \mathfrak{I}_{n-1} \wedge b_{\ell_{n,k},(n-1)} = i_{n,k}\}\end{align*}$$
In words, the intervals in
$\mathfrak {I}_n^\varepsilon $
are those on the nth level which occur inside a particular third of their parent intervals on the
$n-1$
st level which has the maximal measure of its intersection with the set A. By construction, the intervals in
$\mathfrak {I}_n$
are pairwise peers.
Lemma 38. Starting with a
$\Pi ^0_1(\emptyset ')$
-set A, we can compute the sets
$\mathfrak {I}_n^\varepsilon $
relative to
$\emptyset ''$
.
Proof As the double-sequence
$(I^k_n)_{k,n \in \mathbb {N}}$
is computable, we can obtain the sufficiently large
$N_n$
by using
$\emptyset '$
. We have
$T_{c}(I^k_n) \cap A$
available to us as
$\Pi ^0_1(\emptyset ')$
-sets, so
$\emptyset ''$
lets us compute
$\lambda (T_{c}(I^k_n) \cap A) \in \mathbb {R}$
. Then getting the choices for the
$b_{k,n}$
right can be done computably. The witnesses
$\ell _{n,k}$
,
$i_{n,k}$
can also be found computably.⊣
Lemma 39.
$3^{-n} \geq \lambda (\bigcup \mathfrak {I}_n^\varepsilon ) \geq 3^{-n}(\lambda (A)-\varepsilon )$
Proof We prove both inequalities by induction. For the first, the base case is trivial. For the induction step, we note that
$(\bigcup \mathfrak {I}_{n+1}^\varepsilon ) \subseteq \bigcup _{I^k_n \in \mathfrak {I}_n^\varepsilon } T_{b_{k,n}}(I^k_n)$
, and that
$\lambda \left (\bigcup _{I^k_n \in \mathfrak {I}_n^\varepsilon } T_{b_{k,n}}(I^k_n) \right ) = \frac {1}{3} \lambda (\bigcup \mathfrak {I}_n^\varepsilon )$
.
For the second inequality, we prove a stronger claim, namely that
$\lambda (A \cap \bigcup \mathfrak {I}_n^\varepsilon ) \geq 3^{-n}(\lambda (A)-(1-2^{-n-1})\varepsilon )$
. The base case follows from
$\bigcup _{k \in \mathbb {N}} I_0^k \supseteq A$
together with the choice of
$N_0$
. We then observe that
$A \cap (\bigcup \mathfrak {I}_{n+1}^\varepsilon ) = A \cap \bigcup \{I^k_{n+1} \mid \exists I^\ell _n \in \mathfrak {I}_n^\varepsilon \ \exists i \in \{0,1,2\} \ \ I^k_{n+1} \subseteq T_i(I^\ell _n)\}$
. By definition of
$b_{\ell,n}$
in Definition 37, this also means that
$\lambda (A \cap (\bigcup \mathfrak {I}_{n+1}^\varepsilon )) + 3^{-n}2^{-n-2}\varepsilon \geq 3^{-1}\lambda (A \cap \bigcup \{I^k_{n+1} \mid \exists I^\ell _n \in \mathfrak {I}_n^\varepsilon \ \ I^k_{n+1} \subseteq T_{b_{\ell ,n}}(I^\ell _n)\})$
. The set on the right hand side differs from
$\bigcup \mathfrak {I}_n^\varepsilon $
only by the fact that in the latter, we restrict to
$\ell \leq N_n$
. By the induction hypothesis together with the guarantee that
$\lambda (\bigcup _{k> N_n} I_n^k) < 3^{-n}2^{-n-2}\varepsilon $
we get the desired claim.⊣
Lemma 40. For a sequence
$(I^k_n)_{k,n \in \mathbb {N}}$
as in Lemma 35 and
$x \notin A$
, it holds that there exists some
$a < x < b$
and some
$N \in \mathbb {N}$
such that
$I^k_n \cap (a,b) = \emptyset $
for every
$n> N$
.
Proof If
$x \notin A$
, then there is some N with
$x \notin \bigcup _{k \in \mathbb {N}} I^k_N$
. By Condition 3 of Lemma 35, we have that x has positive distance to
$\bigcup _{k \in \mathbb {N}} I^k_{N+1}$
, hence there exists an interval
$(a,b)$
around x disjoint from
$\bigcup _{k \in \mathbb {N}} I^k_{N+1}$
, and by monotonicity, also from
$\bigcup _{k \in \mathbb {N}} I^k_{n}$
for every
$n> N$
.⊣
Proof of Theorem 30
Preparation: We note that for each
$\Pi ^0_2$
-set A and each
$n \in \mathbb {N}$
, there is a
$\Pi ^0_1(\emptyset ')$
-set C with
$C \subseteq A$
and
$\lambda (C) \geq \lambda (A) - 2^{-n}$
. We can assume w.l.o.g. that A is already
$\Pi ^0_1(\emptyset ')$
. We then obtain a computable double-sequence
$(I^k_n)_{k,n \in \mathbb {N}}$
as in Lemma 35.
Construction: We obtain our function f as the limit of functions
$f_{N,K}$
for
$N,K \in \mathbb {N}$
.
$f_{0,0}$
is the identity on
${[0, 1]}$
. The construction of
$f_{N,K}$
takes into account only intervals
$I^k_n$
with
$n \leq N$
and
$|I^k_n|> 2^{-K}$
, of which there are only finitely many (and by monotonicity of the enumerations, we can be sure that we have found them all). We process intervals with smaller n first, and replace the linear growth f currently has on
$I^k_n$
by a triple as shown in Figure 1. Property 5 from Lemma 35 ensures that through the process, the function is linear on each interval
$I^k_n$
yet to be processed. We then define
$f_N := \lim _{K \to \infty } f_{N,K}$
and
$f := \lim _{N \to \infty } f_N$
.
That the first limit has a computable rate of convergence follows from the monotonicity of
$|I^k_n|$
in k. Since the size of the intervals shrinks sufficiently fast compared to the potential growth rates of
$f_N$
, we see that we also do have a computable rate of convergence of
$(f_N)_{N \in \mathbb {N}}$
.
Property 1: If
$x \notin A$
, we can invoke Lemma 40 to obtain a neighbourhood U of x that is disjoint from any
$I^k_n$
for
$n> N$
. But that ensures that
$f|_U$
is
$3^N$
-Lipschitz, and and by potentially restricting the interval further we can make f locally bi-Lipschitz.
Lemma 41.
-
1. Let J be well-located at depth N. Then
$f[J] = f_N[J]$
. -
2. Let J be well-located at depth n. Then
$\lambda (f[J]) = 3^n\lambda (J)$
. -
3. Let
$J_0, J_1$
be peer well-located intervals. Then
$|f[J_0] \cap f[J_1]| \leq 1$
.
Proof
-
1. First, we observe that for any
$M> N$
it holds that
$f_{M}[J] = f_N[J]$
, since all modifications based on intervals
$I^k_n$
with
$n> N$
will affect
$f|_J$
at most by locally replacing the shape of the graph with a different shape having the same range. It remains to argue that the identity of the image
$f_{M}[J]$
is preserved by limits. Since
${[0, 1]}$
is compact and Hausdorff, we find that
$\mathcal {A}({[0, 1]}) \cong \mathcal {K}({[0, 1]})$
, hence we can compute
$g[J] \in \mathcal {A}({[0, 1]})$
from g and
$A \in \mathcal {A}({[0, 1]})$
. We have access to
$g[A] \in \mathcal {V}({[0, 1]})$
given
$A \in \mathcal {V}({[0, 1]})$
anyway. Since
$\mathcal {A}({[0, 1]}) \wedge \mathcal {V}({[0, 1]})$
is Hausdorff [Reference Pauly19], this yields the claim. -
2. By (1.), it suffices to show
$\lambda (f_n[J]) = 3^n\lambda (J)$
instead. Now
$(f_n)|_J$
is just a linear function with slope
$3^n$
, which yields the claim. -
3. If
$J_0,J_1$
are peers and well-located, and
$J_0 \subseteq I^k_n$
but
$J_1 \nsubseteq I^k_n$
, then
$I^k_n$
and
$J_1$
are also peers. It thus suffices to prove the claim for the case where
$J_0 = I^{k_0}_{n+1}$
and
$J_1 = I^{k_1}_{n+1}$
. These are both contained in the same
$T_i(I^\ell _{n})$
, and
$(f_n)|_{T_i(I^\ell _{n})}$
is a linear function. Since
$|J_0 \cap J_1| \leq 1$
it follows that
$|f_n[J_0] \cap f_n[J_1]| \leq 1$
. By
$(1.)$
, this already yields the claim.⊣
Property 2: We obtain the desired set B as
$B = \bigcap _{n \in \mathbb {N}} \left (\bigcup \mathfrak {I}_n^\varepsilon \right )$
. Since each
$\mathfrak {I}^\varepsilon _n$
is a finite collection of closed intervals, B is indeed closed. Since the intersection is nested and
$\lambda (\bigcup \mathfrak {I}_n^\varepsilon ) \leq 3^{-n}$
by the first part of Lemma 39, we conclude that
$\lambda (B) = 0$
. Since the intervals in
$\mathfrak {I}_n^\varepsilon $
are well-located and pairwise peers, we know that
$\lambda (f([\bigcup \mathfrak {I}_n^\varepsilon ])) = 3^n\lambda (\bigcup \mathfrak {I}_n^\varepsilon )$
by Lemma 41 2&3. Invoking the second inequality from Lemma 39 then lets us conclude
$\lambda (f([\bigcup \mathfrak {I}_n^\varepsilon ])) \geq (\lambda (A)-\varepsilon )$
. Since this estimate holds for every stage of a nested intersection of compact sets, it follows that
$\lambda (f[B]) \geq \lambda (A)-\varepsilon $
as desired. That B is obtainable by an oracle of the claimed strength follows from Lemma 38.
5 Luzin’s (N), absolute continuity and bounded variation
We recall the definitions of absolute continuity and bounded variation:
Definition 42. A function
$f : {[0, 1]} \to \mathbb {R}$
is absolutely continuous, if for every
$\varepsilon>0$
and every
$x_0 < y_0 < x_1 < y_1 \cdots < x_k < y_k$
there is a
$\mathbb \delta>0$
such that:
$$\begin{align*}\Sigma_{i \leq k} |y_i - x_i| < \delta \quad \Rightarrow \quad \Sigma_{i \leq k} |f(y_i) - f(x_i)| < \varepsilon.\end{align*}$$
Definition 43. A function
$f : {[0, 1]} \to \mathbb {R}$
has bounded variation, if there is some bound
$M \in \mathbb {N}$
such that for any
$k \in \mathbb {N}$
and any
$x_0 < x_1 < \cdots < x_k$
it holds that
$$\begin{align*}\Sigma_{i < k} |f(x_{i+1}) - f(x_i)| < M\end{align*}$$
Being absolutely continuous implies having bounded variation. These notions are related to Luzin’s (N) by the following classical fact:
Fact 44 (see [Reference Saks24], Theorem VII.6.7)
A continuous function is absolutely continuous iff it has both bounded variation and Luzin’s (N).
We observe that being absolutely continuous is a
$\Pi ^0_3$
-property, and recall that Luzin’s (N) is
$\Pi ^1_1$
-complete [Reference Holický, Ponomarev, Zajíček and Zelený9]. As such, restricting our attention to functions of bounded variation should alter the situation significantly.
Proposition 45. If
$f : {[0, 1]} \to \mathbb {R}$
is computable and absolutely continuous, then f reflects weak-2-randomness.
Proof First, we consider how we can exploit connectedness of
$\mathbb {R}$
to say something about the images of open sets under computable functions. We are given open sets in the form
$U = \bigcup _{i \in \mathbb {N}} I_{i}$
, where each
$I_{i}$
is an open interval with rational endpoints. We can then compute
$\sup f(I_{i})$
and
$\inf f(I_{i})$
(as these are equal to
$\max f(\overline {I_{n,i}})$
and
$\min f(\overline {I_{n,i}})$
, and we can compute minima and maxima of continuous functions on compact sets). Let
$V = \bigcup _{i \in \mathbb {N}} (\inf f(I_{i}),\sup f(I_{i}))$
. We note that we can compute V from U, that
$V \subseteq f[U]$
, and that
$f[U] \setminus V$
can only contain computable points. In particular,
$\lambda (V) = \lambda (f[U])$
.
Now we assume that f additionally is absolutely continuous, and that we are dealing with a
$\Pi ^0_2$
-null set
$A = \bigcap _{n \in \mathbb {N}} U_n$
witnessing that some
$x \in A$
is not weak-2-random. We assume that
$U_{n+1} \subseteq U_n$
. As A is null, we know that
$\lim _{n \to \infty } \lambda (U_n) = 0$
. Since f is absolutely continuous, we also have
$\lim _{n \to \infty } f[U_n] = 0$
. Let
$V_n$
be obtained from
$U_n$
as in the first paragraph, and
$B = \bigcap _{n \in \mathbb {N}} V_n$
. It follows that
$\lambda (B) = 0$
, and moreover,
$f[A]$
is contained in B with the potential exception of some computable points. So we can conclude that
$f(x)$
is not weak-2-random, either because
$f(x)$
is computable, or because
$f(x) \in B$
.⊣
Note that if we had started with a Martin–Löf test in the argument above, we would have no guarantee of ending up with one, because the modulus of absolute continuity is not computable in general. Indeed, absolute continuity does not imply MLR reflection. See Corollary 53.
Lemma 46. If
$f:[0,1]\rightarrow \mathbb R$
is computable, has bounded variation, and reflects
$\emptyset '$
-Kurtz randomness, then f has property
$(N)$
.
Proof Suppose that f does not have
$(N)$
. Since f has bounded variation, it must fail absolute continuity. Let
$\varepsilon>0$
be such that for all
$\delta>0$
, there is a finite union of intervals
$A_\delta \subseteq [0,1]$
with
$\lambda (A_\delta )<\delta $
and
$\lambda (f(A_\delta ))>\varepsilon $
. Computably, given
$\delta $
we can find such
$A_\delta $
by searching. Let
$A = \cap _n U_n$
, where
$U_n = \cup _{m>n} A_{2^{-m}}$
. Then A is
$\Pi ^0_2$
, and
$\lambda (A) = 0$
, and
$\lambda (\cap _n f(U_n)) \geq \varepsilon $
. We claim that its subset
$f(A)$
also has
$\lambda (f(A)) \geq \varepsilon $
. Let
$\text {Var}_f:[0,1]\rightarrow \mathbb R$
denote the cumulative variation function of f, defined by setting
$\text {Var}_f(x)$
to be equal to the variation of f on
$[0,x]$
. Since f has bounded variation and
$U_{n+1}\subseteq U_n$
,
$\sum _n \text {Var}_f(U_{n}\setminus U_{n+1})$
is finite, so by choosing N large enough, we can make
$\sum _{n>N} \lambda (f(U_n\setminus U_{n+1}))$
as small as we like. Now observe that no matter how large N we choose,
$$\begin{align*}\left(\bigcap_n f(U_n) \setminus f(A)\right) \subseteq \bigcup_{n>N} f(U_n \setminus U_{n+1}).\end{align*}$$
This proves the claim. We have found a
$\Pi ^0_2$
set
$A=\cap _n U_n$
which witnesses the failure of
$(N)$
.
Observe that for any c.e. open set U,
$\lambda (f(U))$
is c.e.. Therefore, since f has bounded variation,
$\emptyset '$
can search around to find, for each n, a closed set
$F_n \subseteq U_n$
such that
$\lambda (f(U_n\setminus F_n)) < 2^{-n-2}\varepsilon $
. The existence of such a closed set is guaranteed by f having bounded variation.
Let
$F = \cap _n F_n$
. Then
$F \subseteq A$
and
$A \setminus F = \cup _n (A\setminus F_n)$
. So
$$\begin{align*}\lambda(f(A\setminus F)) \leq \sum_n \lambda(f(A \setminus F_n)) \leq \sum_n \lambda(f(U_n\setminus F_n)) \leq \sum_n 2^{-n-2}\varepsilon < \varepsilon.\end{align*}$$
The positive measure of
$f(F)$
then follows as
$$\begin{align*}\varepsilon \leq \lambda(f(A)) \leq \lambda(f(A\setminus F)) + \lambda(f(F)).\end{align*}$$
Therefore, F is an
$\emptyset '$
-computable closed set of measure zero whose image has positive measure. So f does not reflect
$\emptyset '$
-Kurtz randomness.⊣
Theorem 47. The following are equivalent for computable functions
$f : {[0, 1]} \to \mathbb {R}$
having bounded variation:
-
1. f has Luzin’s (N).
-
2. f reflects weak-2-randomness.
-
3. f reflects
$\emptyset '$
-Kurtz randomness. -
4. f reflects
$\Delta ^1_1({\mathcal {O}})$
-randomness. -
5. f reflects Z-Kurtz randomness for any
$Z \geq \emptyset '$
.
Proof The implication from
$1$
to
$2$
is given by Proposition 45. To see that
$2$
implies
$3$
, first observe that weak-2-randomness reflection implies that
$\lambda (f(A)) = 0$
for any null
$\Pi ^0_2$
set A, for if
$f(A)$
had positive measure then it would certainly contain weak-2-random elements. A
$\Pi ^0_1(\emptyset ')$
set is in particular
$\Pi ^0_2$
, so the image of any
$\emptyset '$
-Kurtz test has measure 0, and is thus also an
$\emptyset '$
-Kurtz test because the continuous image of a compact set is uniformly compact. The implication
$3 \Rightarrow 1$
is in Lemma 46.
Finally, the equivalence of 1 and 4 is just Theorem 16, the implication from 1 to 5 is Proposition 22, and the implication from 5 to 3 is Proposition 23.⊣
Corollary 48. If a computable function
$f : {[0, 1]} \to \mathbb {R}$
of bounded variation reflects ML-randomness, then it has Luzin’s (N).
The converse is false; see Corollary 53.
Proof The same argument works as for the implication
$2 \Rightarrow 3$
in Theorem 47.⊣
In this section we have stated all results for
$f:{[0, 1]} \rightarrow \mathbb R$
because this is a natural setting in which to consider functions of bounded variation. Of course, our pointwise results are equally true for any computable
$f:\mathbb R \rightarrow \mathbb R$
which is locally of bounded variation.
An often useful result about continuous functions of bounded variation is that they can be obtained as difference between two strictly increasing continuous functions. In light of our investigation of Luzin’s (N) for strictly increasing functions, one could wonder why we are not exploiting this property here. There are two obstacles: One the one hand, the computable counterpart of the decomposition result is false: There is a computable function of bounded variation, which cannot be written as the difference between any two strictly increasing computable functions [Reference Zheng and Rettinger29]. On the other hand, Luzin’s (N) is very badly behaved for sums. For example, for every continuous function f having Luzin’s (N) there exists another continuous function g having Luzin’s (N) such that
$f + g$
fails (N) [Reference Pokorný20].
6 The relationship to absolute continuity of measures
For increasing functions we see a connection to absolute continuity of measures. Recall that a measure
$\mu $
is absolutely continuous w.r.t. a measure
$\nu $
(in symbols
$\mu \ll \nu $
), if
$\nu (A) = 0$
implies that
$\mu (A) = 0$
. The notions are related through the following observations:
Observation 49. If continuous surjective
$f : {[0, 1]} \to {[0, 1]}$
is increasing, then the probability measure
$\mu $
defined as
$\mu (A) = \lambda (f(A))$
is nonatomic, and
$\mu \ll \lambda $
iff f has Luzin’s (N).
Observation 50. If
$\mu $
is a non-atomic measure on
${[0, 1]}$
, then its cumulative distribution function
$\operatorname {cdf}_\mu (x) :=\mu ([0,x])$
is a continuous increasing function which has Luzin’s (N) iff
$\mu \ll \lambda $
.
In [Reference Bienvenu and Merkle2], Bienvenu and Merkle have done an extensive survey of the conditions under which two computable measures
$\mu $
and
$\nu $
share the same randoms for a variety of notions of randomness (Kurtz, computable, Schnorr, MLR, and weak-2-random). Two trivial situations where
$\mu $
-randomness and
$\lambda $
-randomness fail to coincide is if
$\mu $
has an atom or if
$\mu (J)=0$
for some open interval J. When discussing the connections among Luzin’s (N), randomness reflection, and coincidence of randomness notions, we will restrict our attention to computable measures
$\mu $
which avoid these two degenerate situations. When
$\mu $
is atomless,
$\operatorname {cdf}_\mu $
is continuous and computable. To say
$\mu (J)>0$
for all open intervals J, it is equivalent to say that
$\operatorname {cdf}_\mu $
is strictly increasing. When the degenerate situations are avoided,
$\operatorname {cdf}_\mu $
is a computable homeomorphism of
${[0, 1]}$
, so
$\operatorname {cdf}^{\,-1}_\mu $
is also a computable homeomorphism. In this situation, randomness reflection for
$\operatorname {cdf}_\mu $
is exactly randomness preservation for
$\operatorname {cdf}^{\,-1}_\mu $
.
Proposition 51. Let
$\mu $
be a nonatomic computable probability measure on
${[0, 1]}$
with
$\operatorname {cdf}_\mu $
strictly increasing. Then x is
$\mu $
-MLR (
$\mu $
-Schnorr random,
$\mu $
-Kurtz random,
$\mu $
-
$\Delta ^1_1$
-random) iff
$\operatorname {cdf}_\mu (x)$
is Martin–Löf random (Schnorr random, Kurtz random,
$\Delta ^1_1$
-random) w.r.t. the Lebesgue measure.
Proof For any set A, we have
$\mu (A) = \lambda (\operatorname {cdf}_\mu (A))$
, and
$\operatorname {cdf}_\mu $
and
$\operatorname {cdf}_\mu ^{-1}$
are both computable homeomorphisms. We can thus move any relevant test from domain to codomain and vice versa.⊣
Therefore,
$\operatorname {cdf}_\mu $
reflects a given notion of randomness exactly when the
$\mu $
-randoms are contained in the
$\lambda $
-randoms for that notion of randomness. Similarly,
$\operatorname {cdf}_\mu ^{-1}$
reflects a given notion of randomness exactly when the
$\lambda $
-randoms are contained in the
$\mu $
-randoms.
Using our previous results, we obtain the following corollary. The equivalence of 1 and 4 was proved in [Reference Bienvenu and Merkle2, Proposition 58], but the others are new.
Corollary 52. The following are equivalent for a computable probability measure
$\mu $
.
-
1.
$\mu $
is mutually absolutely continuous with the Lebesgue measure. -
2.
$\operatorname {cdf}_\mu $
is a homeomorphism and both
$\operatorname {cdf}_\mu $
and
$\operatorname {cdf}_\mu ^{\,-1}$
have Luzin’s (N). -
3.
$\mu $
-
$\Delta ^1_1({\mathcal {O}})$
-randomness and
$\Delta ^1_1({\mathcal {O}})$
-randomness coincide. -
4.
$\mu $
-weak-2-randomness and weak-2-randomness coincide. -
5.
$\mu $
-Kurtz(
$\emptyset '$
)-randomness and Kurtz(
$\emptyset '$
)-randomness coincide.
Proof First observe that in all cases above,
$\operatorname {cdf}_\mu $
is a homeomorphism. That is because none of the cases is compatible with
$\mu $
having an atom or assigning measure 0 to an interval.
Then
$1 \iff 2$
follows from Observation 50 for the case of
$\operatorname {cdf}_\mu $
, and by similar reasoning for the case of
$\operatorname {cdf}_\mu ^{\,-1}$
.
Since
$\operatorname {cdf}_\mu $
and
$\operatorname {cdf}_\mu ^{\,-1}$
are computable functions of bounded variation, by Theorems 16 and 47, they have Luzin’s (N) if and only if they reflect each kind of randomness mentioned in
$3$
–
$6$
. So the implications
$2\iff 3, 2\iff 4,$
and
$2\iff 5$
now follow from Proposition 51.⊣
Bienvenu and Merkle also give some separations. In particular, they show as [Reference Bienvenu and Merkle2, Proposition 51 a)] that there exists a computable probability measure
$\mu $
which is mutually absolutely continuous with Lebesgue measure, but
$\mu $
-MLR does not coincide with
$\lambda $
-MLR,
$\mu $
-Schnorr random does not coincide with with
$\lambda $
-Schnorr random, and
$\mu $
-computably random does not coincide with
$\lambda $
-computably random. Essentially,
$\mu $
is obtained by thinning out the Lebesgue measure around Chaitin’s
$\Omega $
in a way that derandomizes
$\Omega $
without introducing new null sets.
Corollary 53. Luzin’s (N) does not imply any of Martin–Löf randomness reflection, Schnorr randomness reflection nor computable-randomness reflection; even for strictly increasing computable functions.
Proof If Luzin’s (N) were to imply reflection for any of these kinds of randomness, they could be included in the list in Corollary 52 by the same reasoning, but this would contradict Bienvenu and Merkle’s result above.⊣
We still need to discuss reflection of (unrelativized) Kurtz randomness. In [Reference Bienvenu and Merkle2, Proposition 56], Bienvenu and Merkle construct a non-atomic computable probability measure
$\mu $
such that
$\mu $
-Kurtz random and Kurtz random coincide, yet makes the Lebesgue measure not absolutely continuous relative to
$\mu $
. The construction is based on an involved characterization of
$2$
-randomness in terms of Kolmogorov complexity obtained by Nies, Stephan and Terwijn [Reference Nies, Stephan and Terwijn18]. We could already conclude that Kurtz randomness reflection does not imply Luzin’s (N) from this, but instead we will provide a direct, more elementary construction in the following. Our separation works “the other way around,” that is we obtain a probability measure
$\mu $
which is not absolutely continuous w.r.t. the Lebesgue measure. This shows that the Lebesgue measure has no extremal position for relative absolutely continuity inside the class of measures having the same Kurtz randoms. For comparison, a measure satisfies Steinhaus theorem iff it is absolutely continuous w.r.t. Lebesgue measure [Reference Yevgeny and Mospan16].
Theorem 54. There is an increasing surjective computable function
$f : {[0, 1]} \to {[0, 1]}$
which is not absolutely continuous, yet for any
$\Pi ^0_1$
set A with
$\lambda (A) = 0$
, it holds that
$\lambda (f(A)) = 0$
.
Corollary 55. There is a nonatomic probability measure
$\mu $
such that
$\mu $
-Kurtz random and Kurtz random coincide, yet
$\mu \not \ll \lambda $
.
Proof Let
$\hat \mu $
be the probability measure whose cumulative distribution function is f, equivalently
$\hat \mu (B) := \lambda (f(B))$
. Since f does not have Luzin’s (N), there is some set B with
$\lambda (B) = 0$
and
$\hat \mu (B)>0$
. Let
$\mu = \frac {1}{2}\hat \mu + \frac {1}{2}\lambda $
. Then using the same B, we see that
$\mu \not \ll \lambda $
. On the other hand, if A is a
$\Pi ^0_1$
set, then
$\lambda (A) = 0$
implies
$\hat \mu (A) = 0$
, and thus
$\lambda (A) = 0$
if and only if
$\mu (A) = 0$
.⊣
Corollary 56. For increasing computable functions
$f : {[0, 1]} \to {[0, 1]}$
, reflecting Kurtz randomness does not imply Luzin’s (N).
We prepare our construction. Suppose
$h:[0,1]\rightarrow [0,1]$
is a piecewise linear increasing function,
$B \subseteq [0,1]$
is a finite union of intervals with rational endpoints, and
$\delta>0$
. We define a new function
$$\begin{align*}\operatorname{Concentrate}(h,B,\delta):[0,1]\rightarrow [0,1]\end{align*}$$
which concentrates
$\lambda (B)$
-much measure onto a set of Lebesgue measure at most
$\delta $
, as follows.
Definition 57 (Definition of Concentrate)
Given
$h, B, \delta $
as above, write
$B = \cup _{k<n} I_k$
where
$I_k$
are almost disjoint intervals and
$h\upharpoonright h^{-1}(I_k)$
is linear (contained in a single piece of the piecewise function). Modify h on each interval
$h^{-1}(I_k)$
by substituting a piecewise linear function which alternates between a slope of 0 and a large positive slope. The modification is chosen in a canonical computable way to obtain the following outcomes. Below,
$\hat h$
denotes
$\operatorname {Concentrate}(h,B,\delta )$
.
-
1.
$h = \hat h$
outside of
$h^{-1}(B)$
. -
2. Letting F denote the union of the pieces of
$\hat h^{-1}(B)$
which have positive slope, we have
$\lambda (F)<\delta $
and
$f(F) = B$
, and -
3. For all x,
$|h(x) - \hat h(x)|<\delta $
.
Lemma 58. Suppose that
$(B_n)_{n \in \mathbb {N}}$
is a computable sequence of finite unions of intervals in
${[0, 1]}$
. Define a sequence of functions
$(f_n)_{n \in \mathbb {N}}$
inductively by setting
$f_0(x) = x$
and
$$\begin{align*}f_{n+1} = \operatorname{Concentrate}(f_n, B_n, 2^{-n}).\end{align*}$$
Then
$(f_n)_{n \in \mathbb {N}}$
converges uniformly to a computable increasing function f. Furthermore, if there is some
$\varepsilon>0$
such that
$\lambda (B_n)>\varepsilon $
for all n, then f fails Lusin’s (N).
Proof The uniform convergence to a computable f follows from the third property in the definition of
$\operatorname {Concentrate}$
, and f is increasing because each
$f_n$
is. Observe that
$\operatorname {Concentrate}$
never changes the value of h at a break point of h. Therefore, the second property in the definition of
$\operatorname {Concentrate}$
, which tells us that
$f_n(F) = B$
for some F with
$\lambda (F)<2^{-n}$
, implies that
$f(F) = B$
as well (here we also used the fact that f is continuous and increasing). It follows that f is not absolutely continuous, and thus fails Lusin’s (N).⊣
Proof of Theorem 54 We construct a computable sequence
$(B_n)_{n \in \mathbb {N}}$
such that
$\lambda (B_n)> 1/2$
for all n, and argue that the function f constructed as in Lemma 58 satisfies
$\lambda (f(P))=0$
whenever
$P \in \Pi ^0_1$
and
$\lambda (P)=0$
.
The strategy for a single
$\Pi ^0_1$
class
$P_e$
is as follows. Let
$C_{e,0}$
be some interval of length
$\varepsilon _e$
. Let
$B_s = [0,1]\setminus C_{e,s}$
. As long as
$f_s(P_{e,s})\cap C_{e,s}$
has measure at least
$\varepsilon _e/2$
, define
$C_{e,s+1} = C_{e,s}$
. If
$f(P_{e,s})\cap C_{e,s}$
has measure less than
$\varepsilon _e/2$
, define
$C_{e,s+1} = (f_s(P_{e,s}) \cap C_{e,s}) \cup C$
, where C is a new interval or finite union of intervals almost disjoint from
$\cup _{t\leq s} C_{e,t}$
. Choose C so that that
$C_{e,s+1}$
has measure
$\varepsilon _e$
, if possible; if this is not possible, choose C so that
$\cup _{t\leq s+1} C_{e,t} = [0,1]$
. In the latter case the measure of
$C_{e,s+1}$
may be less than
$\varepsilon _e$
and this is also fine. If we reach this degenerate situation, we also stop checking the measures and simply let
$C_{e,t} = C_{e,s+1}$
for all
$t>s$
.
We claim that if
$\lambda (P_e) = 0$
, then
$\lambda (f(P_e)) = 0$
. Suppose at some stage s we have that the measure of
$f_s(P_{e,s}) \cap C_{e,s}$
is greater than
$\varepsilon _e/2$
. If this continues for all
$t>s$
, then f and
$f_s$
coincide on the set
$J:= f^{-1}(C_{e,s})$
. It follows that f is piecewise linear on J, but
$f(P_e\cap J)$
has positive measure; this is impossible since
$P_e$
has measure 0. We conclude that nothing lasts forever; eventually we do reach a stage s where
$\cup _{t\leq s} C_{e,s} = [0,1]$
. Since
$C_{e,s}$
never changes again, f and
$f_s$
again coincide on
$J:= f^{-1}(C_{e,s})$
. Observe also that
$P_e \subseteq J$
. Since
$f_s$
is piecewise linear and
$\lambda (P_e) = 0$
, we also have
$\lambda (f_s(P_e)) = 0$
, and thus
$\lambda (f(P_e)) = 0$
.
The above strategy works purely with negative requirements, specifically freezing f on
$f_s^{-1}(C_{e,s})$
. If other requirements also freeze f on other places, it has no effect on the proof above. The only thing to consider when combining requirements is that we need to make sure
$\lambda (B_s)>1/2$
for all s, where we now define
$$\begin{align*}B_s = [0,1] \setminus \bigcup_{e<s} C_{e,s}.\end{align*}$$
Since we always have
$\lambda (C_{e,s}) \leq \varepsilon _e$
, we can keep the sets
$B_s$
large by choosing the values of
$\varepsilon _e$
to satisfy
$\sum _e \varepsilon _e < 1/2$
.⊣
7
$\Pi ^1_1$
-hardness of randomness reflection
If we do not restrict the domain of the functions to (locally) compact spaces, then essentially any form of randomness reflection is
$\Pi ^1_1$
-hard. We show a construction which yields a function having either null range, or is surjective when restricted to a specific null subset of its domain. In particular, our construction is independent of the randomness notions involved.
Theorem 59. Let
$K, L \subseteq {[0, 1]}^2$
be non-empty sets containing only Kurtz randoms. Then “whenever
$f(x) \in K$
, then already
$x \in L$
” is a
$\Pi ^1_1$
-hard property of continuous functions
$f : ({[0, 1]} \setminus \mathbb {Q}) \times {[0, 1]} \to {[0, 1]}^2$
.
Proof It is well-known that
${[0, 1]} \setminus \mathbb {Q}$
and
$\mathbb {N}^{\mathbb {N}}$
are homeomorphic, and even computably so. We identify the spaces in such a way that the Lebesgue measure induced on
$\mathbb {N}^{\mathbb {N}}$
satisfies
$\lambda (\{p \in \mathbb {N}^{\mathbb {N}} \mid \forall n \ p_{2n} = p_{2n+1}\}) = 0$
.
We construct a function
$f_T : \mathbb {N}^{\mathbb {N}} \times {[0, 1]} \to {[0, 1]}^2$
from a countably-branching tree T. First, we modify T to obtain
$\hat {T} = \{w_0w_0w_1w_1\ldots w_{n-1}w_{n-1}w_n \mid w \in T\} \cup \{w_0w_0w_1w_1\ldots w_{n-1}w_{n-1}w_nw_n \mid w \in T\}$
. Clearly, T is well-founded iff
$\hat {T}$
is, and
$[\hat {T}]$
contains no Kurz-randoms (so in particular,
$[\hat {T}] \times {[0, 1]} \cap L = \emptyset $
). For any
$p \in \mathbb {N}^{\mathbb {N}}$
, let
$|T,p| = n$
iff n is minimal such that
$p_{\upharpoonright n} \notin \hat {T}$
, and
$|T,p| = \infty $
if
$p \in [\hat {T}]$
.
Let
$s_\infty : {[0, 1]} \to {[0, 1]}^2$
be a computable space-filling curve, and let
$(s_n)_{n \in \mathbb {N}}$
be a computable fast Cauchy sequence converging to
$s_\infty $
such that any
$s_n({[0, 1]})$
is a finite union of line segments. We then define
$f_T(p,x) = s_{|T,p|}(x)$
. This construction is computable in T. We claim that
$f_T$
has our reflection property iff T is well-founded.
If T is well-founded, then the range of
$f_T$
is
$\bigcup _{n \in \mathbb {N}} s_n({[0, 1]})$
. Since any
$s_n({[0, 1]})$
is a null
$\Pi ^0_1$
-set, we see that
$f_T$
never takes any Kurtz random values (in particular, none in K), and thus vacuously, if
$f(x) \in K$
then
$x \in L$
. The argument in fact establishes that for arbitrary T, whenever
$p \notin \hat {T}$
then
$f_T(p,x)$
is not Kurtz random regardless of x.
Now assume that T is ill-founded and that
$y \in K$
. We find that
$f_T^{-1}(\{y\}) = [\hat {T}] \times s_\infty ^{-1}(\{y\})$
. Since
$\hat {T}$
is ill-founded and
$s_\infty $
is space-filling, this set is non-empty. But by construction of
$\hat {T}$
, it cannot contain any elements of L. Hence,
$f_T$
does not have our reflection property.⊣
8 A glimpse at related notions
As a slight digression, we have a look at related properties of functions, namely those where the image of null sets are required to belong to some other ideals of small sets, such as being countable or being meager. These properties were investigated by Sierpinski [Reference Sierpinski25] and Erdös [Reference Erdös7], amongst others. Our results are formulated in some generality, but as a consequence, we do see that we do not get any “regular” functions with these properties. In contrast, Erdös showed that under
$\mathrm {CH}$
there is a bijection
$f : \mathbb {R} \to \mathbb {R}$
mapping meager sets to null sets with
$f^{-1}$
mapping null sets to meager sets.
Theorem 60.
-
(1) If A is a non-null
$\mathbf {\Sigma }^1_1$
set and f is a continuous function mapping any null subset of A to a countable set, then the range of f restricted to A is countable. In particular, if A is an interval, then range of f restricted to A is a constant function. -
(2) Assume
$\mathrm {CH}$
, there is a function f mapping any null set to a countable set such that the range of f is
$\mathbb {R}$
, and
$f(A)$
is uncountable for any non-null set A but for every y,
$f^{-1}(y)$
is an uncountable Borel null set. -
(3) If A is a non-null set and f is a continuous function mapping any null subset of A to a meager set, then the range of f restricted to A is meager. In particular, if A is an interval, then range of f restricted to A is a constant function.
-
(4) If f is a measurable function and maps a null set to a meager set, then the range of f is meager. In particular, if f is continuous with the property, then f is constant.
-
(5) If f has the Baire property and maps a meager set to a null set, then the range of f is null. In particular, if f is continuous with the property, then f is constant.
Proof (1). Fix a real x so that f is computable in x and A is
$\Sigma ^1_1(x)$
. Now for any real
$z\in A$
, let g be a
$\Delta ^1_1( {\mathcal {O}}^{x\oplus z})$
-generic real. Then z cannot be Martin–Löf random relative to g and so there there must be a
$\Delta ^1_1(g)$
-null set G so that
$z\in G\cap A$
. By the assumption,
$f(G\cap A)$
is a
$\Sigma ^1_1(x\oplus g)$
-countable set and so every real in
$f(G\cap A)$
is hyperarithmetically below
$x\oplus g$
. In particular,
$f(z)\leq _h x\oplus g$
. Since f is computable in x, we also have that
$f(z)\leq _h x\oplus z$
. Then
$f(z)\leq _h x$
since g is
$\Delta ^1_1( {\mathcal {O}}^{x\oplus z})$
-generic real. By the arbitrarility of z, the range of f restricted to A is countable. So if A is an interval, then range of f restricted to A is a constant function.
(2). Fix an enumeration of nonempty
$G_{\delta }$
-null sets
$\{G_{\alpha }\}_{\alpha <\aleph _1}$
and all the reals
$\{y_{\alpha }\}_{\alpha <\aleph _1}$
. We define f and
$\{\beta _{\alpha }\}_{\alpha <\aleph _1}$
by induction on
$\alpha $
.
At stage
$0$
, define
$f(x)=y_0$
for any
$x\in G_0$
. Define
$\beta _0=0$
.
At stage
$\alpha <\aleph _1$
, let
$\beta _{\alpha }$
be the least ordinal
$\gamma $
so that
$G_{\gamma }\setminus \bigcup _{\alpha '<\alpha }(\bigcup _{\gamma '\leq \beta _{\alpha '} }G_{\gamma '})$
is uncountable. Define
$f(x)=y_{\alpha }$
for any
$x\in G_{\gamma }\setminus \bigcup _{\alpha '<\alpha }(\bigcup _{\gamma '\leq \beta _{\alpha '} }G_{\gamma '})$
.
Clearly the range of f is
$\mathbb {R}$
. Moreover, for any
$\alpha <\aleph _1$
,
$f^{-1}(y_{\alpha })=G_{\beta _{\alpha }}\setminus \bigcup _{\alpha '<\alpha }(\bigcup _{\gamma '\leq \beta _{\alpha '} }G_{\gamma '})$
is an uncountable Borel null set. Now for any null set A, there must be some
$\alpha <\aleph _1$
so that
$A\subseteq G_{\alpha }$
. By the construction,
$f(A)\subseteq f(G_{\alpha })\subseteq \{y_{\beta }\mid \beta \leq \alpha \}$
is a countable set.
(3). Fix a real x so that f is computable in x restricted to A. Fix a
$2$
-x-random real
$r\in A$
. Then
$f(r)\leq _T x\oplus r$
. But
$f(r)$
cannot be
$2$
-x-generic (see [Reference Nies, Stephan and Terwijn18]). So the range f restricted to
$A\cap \{r\mid r \mbox { is a }2-x\mbox {-random}\}$
is meager. But
$A\setminus \{r\mid r \mbox { is a }2-x\mbox {-random}\}$
is a null set. So, by the assumption on f, the range of f restricted to A is meager.
(4). Suppose that f is measurable function and maps a null set to a meager set. Without loss of generality, we may assume that the domain of f is
$[0,1]$
. Then there is a sequence closed sets
$\{F_n\}_{n\in \omega }$
so that
$[0,1]\setminus \bigcup _{n\in \omega }F_n$
is null and f restricted to
$F_n$
is continuous for every n. By (3), the range of f restricted to
$F_n$
is a meager set. So the range of f restricted to
$\bigcup _{n\in \omega } F_n$
is also a meager set. Note that
$[0,1]\setminus \bigcup _{n\in \omega }F_n$
is null. So the range of f is meager. In particular, if f is continuous with the property, then f is constant.
(5). This is dual to (4).⊣
9 Outlook
The most prominent avenue of future research seems to be the resolution of Question 28, asking for a separation (or equivalence proof) of
$\Delta ^1_1$
-randomness reflection and
$\Delta ^1_1({\mathcal {O}})$
-randomness reflection. There are a few further aspects that merit further investigation, though.
Topological properties
While we have not been systematic in exploring the impact of topological properties of the domain (and maybe codomain) of the functions we explore, we observe that our proofs differ in the requirements they put on the spaces involved. For example, the majority of the arguments presented in §3.1 and §3.2 are relying just on the theory of randomness, and are thus applicable to any space where randomness works as usual (see [Reference Hoyrup and Rojas10]). In §3.3, (local) compactness of the domain is a core ingredient in our arguments. In §5 we do use particular properties of the reals, in particular connectedness. Further investigation of how topological properties of spaces relate to how randomness reflection behaves for functions on them seems warranted.
Formalizing randomness reflection
With the exception of Theorem 59, we have only considered symmetric notions of randomness reflection: Whenever
$f(x)$
is random in some sense, we demand that x is random in the very same sense. While this seems natural, a downside is that we do not get trivial implications between different notions of
$\mathbf \Pi ^0_2$
-type randomness reflection. We could consider the full square of reflection notions,
$(K,L)$
-randomness reflection being that whenever
$f(x)$
is K-random, then x is L-random for randomness notions K,L. An extremal version also makes sense, where we just ask for when the image of all nonrandoms under f has positive measure. Whenever the latter property holds for some randomness notion L, then f cannot have
$(K,L)$
-randomness reflection for any randomness notion K at all. We typically prove nonrandomness reflection in this manner.
It seems too early to pass judgement on what precise formulations of randomness reflection will ultimately be the most fruitful.
Functions beyond measurability
So far, the most general class of functions we considered for Luzin’s (N) were the measurable functions. If we consider unrestricted functions in full generality, it is unsurprising that we quickly move beyond the confines of ZFC. For example, we are wondering whether Corollary 17 holds for all functions having Luzin’s (N)? An investigation into such questions is on its way by Yinhe Peng and the third author.
Acknowledgments
This project was begun while all three authors were in attendance at the Oberwolfach Seminar on Computability Theory in January 2018. The second and third authors collaborated on it while attending the IMS/NUS workshop Recursion Theory, Set Theory and Interactions in May–June 2019. The second author was also partially supported by the Cada R. and Susan Wynn Grove Early Career Professorship in Mathematics. The third author was partially supported by National Natural Science Fund of China, No. 11671196.
