Published online by Cambridge University Press: 04 September 2020
Given a regular cardinal 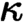 $\kappa $
such that
$\kappa $
such that 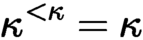 $\kappa ^{<\kappa }=\kappa $
(or any regular
$\kappa ^{<\kappa }=\kappa $
(or any regular 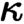 $\kappa $
if the Generalized Continuum Hypothesis holds), we study a class of toposes with enough points, the
$\kappa $
if the Generalized Continuum Hypothesis holds), we study a class of toposes with enough points, the 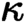 $\kappa $
-separable toposes. These are equivalent to sheaf toposes over a site with
$\kappa $
-separable toposes. These are equivalent to sheaf toposes over a site with 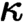 $\kappa $
-small limits that has at most
$\kappa $
-small limits that has at most 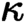 $\kappa $
many objects and morphisms, the (basis for the) topology being generated by at most
$\kappa $
many objects and morphisms, the (basis for the) topology being generated by at most 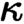 $\kappa $
many covering families, and that satisfy a further exactness property T. We prove that these toposes have enough
$\kappa $
many covering families, and that satisfy a further exactness property T. We prove that these toposes have enough 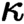 $\kappa $
-points, that is, points whose inverse image preserve all
$\kappa $
-points, that is, points whose inverse image preserve all 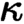 $\kappa $
-small limits. This generalizes the separable toposes of Makkai and Reyes, that are a particular case when
$\kappa $
-small limits. This generalizes the separable toposes of Makkai and Reyes, that are a particular case when 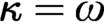 $\kappa =\omega $
, when property T is trivially satisfied. This result is essentially a completeness theorem for a certain infinitary logic that we call
$\kappa =\omega $
, when property T is trivially satisfied. This result is essentially a completeness theorem for a certain infinitary logic that we call 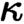 $\kappa $
-geometric, where conjunctions of less than
$\kappa $
-geometric, where conjunctions of less than 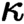 $\kappa $
formulas and existential quantification on less than
$\kappa $
formulas and existential quantification on less than  $\kappa $
many variables is allowed. We prove that
$\kappa $
many variables is allowed. We prove that  $\kappa $
-geometric theories have a
$\kappa $
-geometric theories have a  $\kappa $
-classifying topos having property T, the universal property being that models of the theory in a Grothendieck topos with property T correspond to
$\kappa $
-classifying topos having property T, the universal property being that models of the theory in a Grothendieck topos with property T correspond to 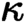 $\kappa $
-geometric morphisms (geometric morphisms the inverse image of which preserves all
$\kappa $
-geometric morphisms (geometric morphisms the inverse image of which preserves all 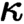 $\kappa $
-small limits) into that topos. Moreover, we prove that
$\kappa $
-small limits) into that topos. Moreover, we prove that  $\kappa $
-separable toposes occur as the
$\kappa $
-separable toposes occur as the 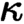 $\kappa $
-classifying toposes of
$\kappa $
-classifying toposes of 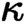 $\kappa $
-geometric theories of at most
$\kappa $
-geometric theories of at most  $\kappa $
many axioms in canonical form, and that every such
$\kappa $
many axioms in canonical form, and that every such 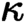 $\kappa $
-classifying topos is
$\kappa $
-classifying topos is  $\kappa $
-separable. Finally, we consider the case when
$\kappa $
-separable. Finally, we consider the case when  $\kappa $
is weakly compact and study the
$\kappa $
is weakly compact and study the  $\kappa $
-classifying topos of a
$\kappa $
-classifying topos of a 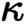 $\kappa $
-coherent theory (with at most
$\kappa $
-coherent theory (with at most 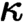 $\kappa $
many axioms), that is, a theory where only disjunction of less than
$\kappa $
many axioms), that is, a theory where only disjunction of less than 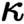 $\kappa $
formulas are allowed, obtaining a version of Deligne’s theorem for
$\kappa $
formulas are allowed, obtaining a version of Deligne’s theorem for 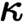 $\kappa $
-coherent toposes from which we can derive, among other things, Karp’s completeness theorem for infinitary classical logic.
$\kappa $
-coherent toposes from which we can derive, among other things, Karp’s completeness theorem for infinitary classical logic.