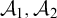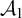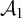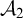1 Introduction
There are well-known results (see [Reference Ash and Knight1, Reference Ash and Knight2]) putting conditions on a pair of structures
$\mathcal {A}_1,\mathcal {A}_2$
such that for any
$\Pi ^0_{\alpha }$
set
$S\subseteq \omega $
, there is a uniformly computable sequence of structures
$(\mathcal {C}_n)_{n\in \omega }$
with
$$ \begin{align*}\mathcal{C}_n\cong \left\{\begin{array}{ll} \mathcal{A}_1, & \mbox{if } n\in S,\\ \mathcal{A}_2, & \mbox{if } n\notin S. \end{array}\right.\ \end{align*} $$
Here we consider a different question on pairs of structures.
Problem 1. For which pairs of structures
$\mathcal {A}_1,\mathcal {A}_2$
is there a uniform effective procedure that, given copies of both structures, unlabeled, always produces a copy of
$\mathcal {A}_1$
?
To state the problem precisely, we first say how to give copies of the two structures in a way that does not indicate which is which.
Definition 1 (unlabeled pair)
Let L be a language consisting of relation symbols
$R_j$
, and let
$\mathcal {A}_1,\mathcal {A}_2$
be two L-structures. The unlabeled pair
$\mathcal {A}_1|\mathcal {A}_2$
is the structure
$\mathcal {B} = (B,\sim ,(R_j^*)_j)$
such that
-
1.
$\sim $
is an equivalence relation on B with just two equivalence classes, -
2. for each j,
$R_j^*$
(a relation of the same arity as
$R_j$
) is the union of its restrictions to the two
$\sim $
-classes, and -
3. one of the two
$\sim $
-classes, with the restrictions of the relations
$R_j^*$
, forms an L-structure isomorphic to
$\mathcal {A}_1$
, while the other
$\sim $
-class, with the restrictions of the relations
$R_j^*$
, forms an L-structure isomorphic to
$\mathcal {A}_2$
.
Our languages are all computable. The formulas that we consider are all elementary first order unless we specifically say otherwise. Our structures all have universe a subset of
$\omega $
. We identify a structure
$\mathcal {A}$
with its atomic diagram
$D(\mathcal {A})$
, and we identify this, via Gödel numbering, with a subset of
$\omega $
, and then with the characteristic function of that set. To make our problem precise, we need one more definition—“Medvedev reducibility.” This is defined for arbitrary “problems,” where a problem is a subset of
$\omega ^{\omega }$
.
Definition 2 (Medvedev reducibility)
For
$P,Q\subseteq \omega ^{\omega }$
, we say that P is Medvedev reducible to Q, and we write
$P\leq _s Q$
, if there is a Turing operator that takes all elements of Q to elements of P.
The problems that concern us consist of the copies of a given structure.
Notation. We write
$\mathcal {A}\leq _s\mathcal {B}$
if there is a Turing operator that takes copies of
$\mathcal {B}$
to copies of
$\mathcal {A}$
.
Our problem is stated precisely as follows.
Problem 1. For which pairs of structures
$\mathcal {A}_1,\mathcal {A}_2$
do we have
$\mathcal {A}_1\leq _s\mathcal {A}_1|\mathcal {A}_2$
?
Kalimullin [Reference Kalimullin7] showed that there are structures
$\mathcal {A}$
and
$\mathcal {B}$
such that for some
$b\in \mathcal {B}$
,
$\mathcal {A}\leq _s(\mathcal {B},b)$
but
$\mathcal {A}\not \leq _s\mathcal {B}$
. Our problem is related to this. For a pair of structures
$\mathcal {A}_1,\mathcal {A}_2$
, if
$\mathcal {B} = \mathcal {A}_1|\mathcal {A}_2$
, then for any
$b\in \mathcal {B}$
, we have
$\mathcal {A}_1\leq _s(\mathcal {B},b)$
.
In Section 2, we give positive results saying that
$\mathcal {A}_1\leq _s\mathcal {A}_1|\mathcal {A}_2$
under any of the following general conditions.
-
1.
$\mathcal {A}_1$
has a computable copy, -
2. there is an existential sentence true in just one of
$\mathcal {A}_1,\mathcal {A}_2$
, and -
3.
$\mathcal {A}_1,\mathcal {A}_2$
satisfy the same existential sentences, but differ on some computable infinitary
$\Sigma _2$
sentence.
Items (2) and (3) might suggest that if
$\mathcal {A}_1,\mathcal {A}_2$
resemble each other a great deal, then
$\mathcal {A}_1\not \leq _s\mathcal {A}_1|\mathcal {A}_2$
. The orderings
$\omega _1^{CK}$
and
$\omega _1^{CK}(1+\eta )$
satisfy the same
$\Sigma _{\alpha }$
and
$\Pi _{\alpha }$
sentences of
$L_{\omega _1\omega }$
for all computable ordinals
$\alpha $
. However, in Section 3, we show that
$\omega _1^{CK}\leq _s\omega _1^{CK}|H$
. In Section 4, we describe the construction of a pair
$\mathcal {A}_1,\mathcal {A}_2$
such that
$\mathcal {A}_1\not \leq _s \mathcal {A}_1|\mathcal {A}_2$
. In Section 5, we prove some helpful preliminary results on Cohen forcing. In Section 6, we use these results to complete our proof that
$\mathcal {A}_1\not \leq _s \mathcal {A}_1|\mathcal {A}_2$
.
2 Positive results
Proposition 2.1. If
$\mathcal {A}_1$
has a computable copy, then for all
$\mathcal {A}_2$
,
$\mathcal {A}_1\leq _s \mathcal {A}_1|\mathcal {A}_2$
.
Proof. If
$\mathcal {A}_1$
has a computable copy, then for the Medvedev reduction, we ignore the input and just build a copy of
$\mathcal {A}_1$
.⊣
Proposition 2.2. If there is an existential sentence true in just one of
$\mathcal {A}_1,\mathcal {A}_2$
, then
$\mathcal {A}_1\leq _s\mathcal {A}_1|\mathcal {A}_2$
.
Proof. Suppose
$\mathcal {A}_1$
and
$\mathcal {A}_2$
differ on the existential sentence
$\varphi $
. Let
$\mathcal {B}$
be a copy of
$\mathcal {A}_1|\mathcal {A}_2$
, with structures
$\mathcal {B}_1,\mathcal {B}_2$
on the two
$\sim $
-classes. The Medvedev reduction watches for evidence that
$\varphi $
is true in one of the structures
$\mathcal {B}_i$
and then builds a copy of the appropriate structure.⊣
Proposition 2.3. Suppose
$\mathcal {A}_1,\mathcal {A}_2$
satisfy the same existential sentences but differ on some computable
$\Sigma _2$
sentence. Then
$\mathcal {A}_1\leq _s\mathcal {A}_1|\mathcal {A}_2$
.
Proof. Let
$\mathcal {B}$
be a copy of
$\mathcal {A}_1|\mathcal {A}_2$
, and let
$\mathcal {B}_1,\mathcal {B}_2$
be the structures on the two
$\sim $
-classes in
$\mathcal {B}$
. We build a copy
$\mathcal {C}$
of
$\mathcal {A}_1$
, with universe
$\omega $
—we think of
$\omega $
as a set of constants. Let
$(\alpha _k)_{k\in \omega }$
be a computable list of all atomic sentences in the language
$L\cup \omega $
. We proceed in stages. At stage s, we have a target structure,
$\mathcal {B}_1$
or
$\mathcal {B}_2$
, which we believe to be a copy of
$\mathcal {A}_1$
. We determine a finite part
$d_s$
of the diagram of
$\mathcal {C}$
and a finite partial isomorphism
$f_s$
from
$\mathcal {C}$
to the stage s target structure. We maintain the following conditions:
-
1.
$f_s$
is defined on all constants n that appear in the sentences of
$d_s$
and -
2.
$f_s$
maps the constants in its domain to distinct elements of the target structure, interpreting the constants, so as to make the sentences of
$d_s$
true.
First, we describe a procedure to determine the stage s target structure. Suppose
$\varphi $
is a computable
$\Sigma _2$
sentence true in just one of the structures
$\mathcal {A}_i$
. For simplicity, we suppose that
$\varphi $
is true in
$\mathcal {A}_1$
. We may suppose that
$\varphi $
has the form
$(\exists \bar {x})\psi (\bar {x})$
, where
$\psi (\bar {x})$
is computable
$\Pi _1$
. For each of the structures
$\mathcal {B}_i$
, we have a computable list of the tuples
$(\bar {b}^i_k)_{k\in \omega }$
in
$\mathcal {B}_i$
appropriate to substitute for
$\bar {x}$
. At stage
$0$
we arbitrarily let
$\mathcal {B}_1$
be the target structure, and we designate
$\bar {b}^1_0$
as the target tuple.
Given the stage s target structure
$\mathcal {B}_i$
and target tuple
$\bar {b}^i_k$
, we let the stage
$s+1$
target structure and tuple be the same until/unless we find evidence that
$\bar {b}^i_k$
fails to satisfy
$\psi (\bar {x})$
in
$\mathcal {B}_i$
. If we find such evidence, then we discard the target tuple (permanently) and take the other structure as our target and the first tuple in it not previously discarded as our target tuple. The computable
$\Pi _1$
formula
$\psi (\bar {x})$
is a c.e. conjunction of finitary universal formulas
$\psi _j(\bar {x}) = (\forall \bar {u}_j)\delta _j(\bar {u}_j,\bar {x})$
. At stage
$s+1$
, we check that
$\mathcal {B}_i\models \delta _j(\bar {d},\bar {b}^i_k)$
for the first s tuples
$\bar {d}$
appropriate for
$\bar {u}_j$
, and we discard
$\bar {b}^i_k$
if this is not the case. Note that the target structure and target tuple will eventually stabilize. The stable target structure will be the
$\mathcal {B}_i$
that is a copy of
$\mathcal {A}_1$
, and the stable target tuple will be the first tuple
$\bar {b}^i_k$
that satisfies all of
$\psi (\bar {x})$
.
Above, we assumed that the sentence
$\varphi $
is true in
$\mathcal {A}_1$
. Now, suppose that
$\varphi $
is true in
$\mathcal {A}_2$
, not
$\mathcal {A}_1$
. In this case, our target structure at every stage is the opposite of the one chosen above. At stage
$0$
, the target structure is
$\mathcal {B}_2$
. At later stages, the target structure is the opposite of the one in which we have a current target tuple that might plausibly witness satisfaction of the computable
$\Sigma _2$
sentence
$(\exists \bar {x})\psi (\bar {x})$
. Again the target structure and target tuple will stabilize. The stable target tuple will satisfy
$\psi (\bar {x})$
in one of the structures
$\mathcal {B}_i$
—the one isomorphic to
$\mathcal {A}_2$
. The stable target structure is the other
$\mathcal {B}_i$
—the one isomorphic to
$\mathcal {A}_1$
.
Having determined the target structure at stage s, we define
$f_s$
and
$d_s$
. We start with
$d_0 = \emptyset $
, and
$f_0 = \emptyset $
. At stage
$s+1$
, we let
$d_{s+1}$
be the result of adding one of the sentences
$\pm \alpha _s$
to
$d_s$
, and we define
$f_{s+1}$
so that it makes the sentences of
$d_{s+1}$
true in the stage
$s+1$
target structure. There are two cases.
Case 1. Suppose the stage
$s+1$
target structure is the same as that at stage s. Then
$f_{s+1}$
extends
$f_s$
. We include in the domain of
$f_{s+1}$
any constants that appear in
$\alpha _s$
, mapping those not in
$dom(f_s)$
to the first few elements of the target structure not in
$ran(f_s)$
. We let
$d_{s+1}$
be the result of adding to
$d_s$
one of
$\pm \alpha _s$
, chosen so that
$f_{s+1}$
makes the sentence true in the target structure.
Case 2. Suppose the stage
$s+1$
target structure differs from the stage s target structure. Say that the conjunction of
$d_s$
is
$\delta (\bar {d})$
, where
$\bar {d}$
is the tuple of constants mentioned. The existential sentence
$(\exists \bar {x})\delta (\bar {x})$
is true in the stage s target structure, so it is also true in the stage
$s+1$
target structure. Say that the stage
$s+1$
target structure is
$\mathcal {B}_i$
, and take f mapping
$\bar {d}\ 1-1$
to some tuple in
$\mathcal {B}_i$
so as to make
$\delta (\bar {d})$
true. Let
$f_{s+1}$
be an extension of f mapping any new constants that appear in
$\alpha _s$
to the first few elements of the target structure not in
$ran(f)$
. As in Case 1, we let
$d_{s+1}$
be the result of adding
$\pm \alpha _s$
to
$d_s$
so that
$f_{s+1}$
makes the sentence true in the target structure.
We let
$\mathcal {C}$
be the structure with atomic diagram
$\cup _s d_s$
. The target structure will eventually stabilize. Say that for all
$t\geq s$
, the target structure at stage t is
$\mathcal {B}_i$
. This is a copy of
$\mathcal {A}_1$
. The functions
$f_t$
for
$t\geq s$
form a chain, and the union
$F = \cup _{t\geq s}f_t$
is an isomorphism from
$\mathcal {C}$
onto
$\mathcal {B}_i$
. So,
$\mathcal {C}$
is a copy of
$\mathcal {A}_1$
, as required.⊣
For a structure
$\mathcal {A}$
, the jump is the structure
$\mathcal {A}'$
obtained by adding to
$\mathcal {A}$
the relations defined by computable
$\Sigma _1$
formulas. The important fact about the jump structure is that for
$n\geq 1$
, any relation defined in
$\mathcal {A}$
by a computable
$\Sigma _{n+1}$
formula is defined in
$\mathcal {A}'$
by a computable
$\Sigma _n$
formula. See [Reference Montalban12] for a discussion of jump structures.
Recall that a structure
$\mathcal {A}$
admits strong jump inversion if for any set X such that
$X'$
computes a copy of
$\mathcal {A}'$
, X computes a copy of
$\mathcal {A}$
(see [Reference Calvert, Frolov, Harizanov, Knight, McCoy, Soskova and Vatev3]).
Proposition 2.4. Suppose that
$\mathcal {A}_1$
and
$\mathcal {A}_2$
differ on a computable
$\Sigma _3$
sentence but satisfy the same
$\Sigma _2$
sentences. Suppose also that
$\mathcal {A}_1$
admits strong jump inversion. Then
$\mathcal {A}_1\leq _s\mathcal {A}_1|\mathcal {A}_2$
.
Proof. We have a uniform
$\Delta ^0_2$
procedure that, given a copy of
$\mathcal {A}_1|\mathcal {A}_2$
, produces a copy of
$\mathcal {A}_1'|\mathcal {A}_2'$
. The computable
$\Sigma _3$
sentence that distinguishes
$\mathcal {A}_1$
from
$\mathcal {A}_2$
translates into a computable
$\Sigma _2$
sentence that distinguishes
$\mathcal {A}_1'$
from
$\mathcal {A}_2'$
. Proposition 2.3 yields a copy of
$\mathcal {A}_1'$
, computable in
$D(\mathcal {B})'$
. Since
$\mathcal {A}_1$
admits strong jump inversion, we get a copy that is computable in
$D(\mathcal {B})$
.⊣
The result above applies to some familiar classes of structures. By a well-known result of Downey and Jockusch [Reference Downey and Jockusch5], Boolean algebras admit strong jump inversion. By a result of Marker and Miller [Reference Marker and Miller10], differentially closed fields of characteristic
$0$
admit strong jump inversion.
3 The orderings
$\omega _1^{CK}$
and
$H$
Recall that
$\omega _1^{CK}$
is the first non-computable ordinal. The Harrison ordering, denoted by H, is a computable ordering of type
$\omega _1^{CK}(1+\eta )$
, with no infinite hyperarithmetical decreasing sequence. These two orderings are similar—they satisfy the same
$\Sigma _{\alpha }$
sentences for all computable ordinals
$\alpha $
. Thus, the result below may seem surprising. We will give only a brief account of the proof, with some references for the background. The material from this section will not be used later.
Proposition 3.1.
$\omega _1^{CK}\leq _s\omega _1^{CK}|H$
.
Before proving this, we say something about products of finite sequences, and of trees (see [Reference Montalban12]).
Definition 3.
-
1. For finite sequences
$\sigma _1 = (m_1,\ldots ,m_k)$
and
$\sigma _2 = (n_1,\ldots ,n_k)$
, of the same length, the product is
$\sigma _1*\sigma _2 = (\langle m_1,n_1\rangle ,\ldots ,\langle m_s,n_s\rangle )$
. -
2. For trees
$T_1,T_2\subseteq \omega ^{<\omega }$
, the product tree is
$T_1*T_2$
, consisting of the sequences
$\sigma _1*\sigma _2$
, for
$\sigma _1\in T_1$
and
$\sigma _2\in T_2$
(
$\sigma _1$
and
$\sigma _2$
have the same length).
Remarks. The tree rank (foundation rank) of the node
$\sigma _1*\sigma _2$
in
$T_1*T_2$
is the minimum of the ranks of
$\sigma _1$
in
$T_1$
and
$\sigma _2$
in
$T_2$
. Then
$rk(T_1*T_2) = min\{rk(T_1),rk(T_2)\}$
.
We turn to the proof of Proposition 3.1, saying that
$\omega _1^{CK}\leq _s \omega _1^{CK}|H$
.
Proof. Given orderings
$\mathcal {B}_1,\mathcal {B}_2$
, one of type
$\omega _1^{CK}$
and the other of type
$\omega _1^{CK}(1+\eta )$
, we apply a uniform effective procedure to obtain trees
$T_1$
,
$T_2$
, where
$T_i$
is the set of finite decreasing sequences in
$\mathcal {B}_i$
. Applying a second uniform effective procedure, we obtain the product tree
$T_1*T_2$
. Since
$T_{\omega _1^{CK}}$
has no path,
$T_1*T_2$
has no path.
Claim 1.
$T_{\omega _1^{CK}}$
has rank
$\omega _1^{CK}$
. To see this, note that in
$T_{\omega _1^{CK}}$
, for each node
$\sigma $
at level
$1$
, the tree below
$\sigma $
consists of decreasing sequences of ordinals below some computable ordinal
$\alpha $
. For the tree
$T_{<\alpha }$
of sequences below
$\alpha $
, the rank is
$\alpha $
. These
$\alpha $
’s are the ranks of the nodes at level
$1$
in
$T_{\omega _1^{CK}}$
.
The tree
$T_H$
of decreasing sequences in the Harrison ordering is unranked—the fact that H is not well-ordered means that
$T_H$
has paths. Since
$T_{\omega _1^{CK}}$
has rank
$\omega _1^{CK}$
and
$T_H$
is unranked,
$T_1*T_2$
has rank
$\omega _1^{CK}$
. Applying a third uniform effective procedure, we form the Kleene–Brouwer ordering of the product tree. Recall that for a tree
$T\subseteq \omega ^{<\omega }$
, the Kleene–Brouwer ordering
$KB(T)$
is the ordering on T such that
$\sigma <_{KB(T)} \tau $
if either
$\sigma $
properly extends
$\tau $
or else there is some k such that
$\sigma ,\tau $
agree on the initial segment of length k, and
$\sigma (k) < \tau (k)$
. See [Reference Rogers13] for more on the Kleene–Brouwer ordering.
Claim 2. For each
$\alpha $
, let
$T_{<\alpha }$
be the tree of decreasing sequences below the ordinal
$\alpha $
. Then
$KB(T_{<\alpha })$
has type at most
$\omega ^{\alpha } + 1$
. For a node of rank
$0$
, the tree below has just the top node
$\emptyset $
, and the order type of the Kleene–Brouwer ordering is
$1$
. For a node of rank
$1$
, there may be infinitely many successors of rank
$0$
, ordered in type
$\omega $
, so the Kleene–Brouwer ordering has type at most
$\omega +1$
. For a node of rank
$\alpha +1$
, there may be infinitely many successors of rank
$\alpha $
, ordered in type
$\omega $
, so the ordering has type at most
$((\omega ^{\alpha } + 1)\cdot \omega )+1 = \omega ^{\alpha +1} + 1$
. For
$\alpha $
a limit ordinal, a node of rank
$\alpha $
may have successors of arbitrarily large ranks
$\beta _n < \alpha $
, and the ordering may have type
$(\sum _n \omega ^{\beta _n} + 1) + 1 = \omega ^{\alpha } + 1$
. For our product tree, of rank
$\omega _1^{CK}$
, the Kleene–Brouwer has type
$\omega _1^{CK} + 1$
. Applying one final uniform effective procedure, we remove the top node of the product tree, which is the last element in the Kleene–Brouwer ordering. The result is an ordering of type
$\omega _1^{CK}$
.⊣
4 Construction of example—an outline
We believe that for most pairs of structures
$\mathcal {A}_1,\mathcal {A}_2$
, there should not be a uniform Turing operator witnessing that
$\mathcal {A}_1\leq _s\mathcal {A}_1|\mathcal {A}_2$
. However, at present, we have one specially constructed example for which we can prove that
$\mathcal {A}_1\not \leq _s\mathcal {A}_1|\mathcal {A}_2$
, plus further examples obtained from this one by well-known coding tricks.
4.1 Outline
The construction of the example is somewhat delicate. Here is the outline.
-
1. Let X be a “sufficiently generic” subset of
$\omega $
. -
2. Split X into “even” and “odd” parts
$$ \begin{align*}\begin{array}{cc} X_1 = \{n:2n\in X\}, & X_2 = \{n:2n+1\in X\}. \end{array}\end{align*} $$
-
3. Let
$S_i$
be the family of sets Y such that
$X_i\Delta Y$
is finite. -
4. Let
$\mathcal {A}_i$
be a graph coding the family
$S_i$
.
We say more about the graphs that code the families of sets.
4.2 Graphs and enumerations
Definition 4 (Daisies)
For a set A, the daisy
$D_A$
is an undirected graph consisting of a center point with infinitely many cycles, which we call “petals.” The petals all share the center point but are otherwise disjoint. There is a petal of length
$$ \begin{align*} \left\{\begin{array}{@{}cc} 2n+3, & \text{for } n\in A,\\ 2n+4, & \text{for } n\notin A. \end{array}\right.\end{align*} $$
Definition 5 (Bunches of daisies)
For a family
$S\subseteq P(\omega )$
,
$G_S$
is the undirected graph with one connected component of form
$D_A$
for each
$A\in S$
—that is all.
Our structures
$\mathcal {A}_1$
and
$\mathcal {A}_2$
are bunches of daisies;
$\mathcal {A}_i = G_{S_i}$
, where
$S_i$
is the set of finite variants of
$X_i$
.
Definition 6. For a countable family
$S\subseteq P(\omega )$
, an enumeration is a relation
$R\subseteq \omega ^2$
such that the family of sets
$R_n = \{x:(n,x)\in R\}$
is equal to S.
The following is well-known, and easy to prove (see [Reference Ash and Knight1]).
Lemma 4.1. There are uniform Turing operators
$\Phi $
and
$\Psi $
such that for all countable families S,
-
1.
$\Phi $
takes each copy of
$G(S)$
to an enumeration of S and -
2.
$\Psi $
takes each enumeration of S to a copy of
$G(S)$
.
4.3 Two kinds of forcing
To prove that
$\mathcal {A}_1\not \leq _s\mathcal {A}_1|\mathcal {A}_2$
, we borrow ideas from Lachlan and Soare, who, in [Reference Lachlan and Soare8, Reference Lachlan and Soare9
], proved some results on enumerations of families of sets related to arithmetic. We say just a little about the results, leaving certain terms—Scott set, Turing ideal—undefined, since these things are not involved in our construction. Let
$\mathcal {A}$
be the family of arithmetical sets. The main result of [Reference Lachlan and Soare9] says that there is an enumeration E of a Scott set
$\mathcal {S}\supseteq \mathcal {A}$
such that E does not compute an enumeration of
$\mathcal {A}$
. In the proof, the Scott set S is the Turing ideal generated by the arithmetical sets and a Cohen generic X, and E is a generic enumeration of S. We use the same two kinds of forcing to produce the generic set X, and to produce generic enumerations of the families
$S_1,S_2$
, derived from X.
Each forcing language includes the language of arithmetic—the language of the structure
$\mathcal {N} = (\omega ,+, \cdot ,<, 0,S)$
. We use relation symbols for the operations
$+$
and
$\cdot $
, but S is denoted by an operation symbol, and
$0$
is a constant. Each natural number is named by a unique term. We write n as an abbreviation for the unique term
$S^{n}(0)$
that names the number n.
We have indicated how we will construct the structures
$\mathcal {A}_1,\mathcal {A}_2$
. In Section 5, we describe Cohen generics, and say how certain variants of a Cohen generic are themselves Cohen generic.
5 Cohen forcing
To produce the generic set X, we use Cohen forcing. The forcing conditions are elements of
$2^{<\omega }$
. As we said in the outline, we will split X into the even part
$X_1 = \{n:2n\in X\}$
, and the odd part
$X_2 = \{n:2n+1\in X\}$
. The family
$S_1$
consists of the sets that differ finitely from
$X_1$
and the family
$S_2$
consists of the sets that differ finitely from
$X_2$
.
Lemma 5.1. There are elementary first order formulas that, for all sets U, define in
$(\mathcal {N},U)$
the even and odd parts
$U_1,U_2$
.
Proof. We have
$x\in U_1$
iff
$(\exists y)2y\in U$
, and
$x\in U_2$
iff
$(\exists y)2y+1\in U$
.⊣
For a set U, let
$S(U)$
be the set of finite variants of U. These variants have the form
$(U\cup D_{n_1}) - D_{n_2}$
, where
$(D_n)_{n\in \omega }$
is the standard computable list of finite sets.
Definition 7. For a set U, the special enumeration of the set
$S(U)$
is the enumeration E such that for
$n = \langle n_1,n_2\rangle $
,
$E_n = (U\cup D_{n_1}) - D_{n_2}$
.
The following is clear from the definition.
Lemma 5.2. There is an elementary first order formula
$E(U,n,x)$
that, for all U, defines in
$(\mathcal {N},U)$
the special enumeration of
$S(U)$
.
Then the following is also clear.
Lemma 5.3. There are elementary first order formulas that, for all sets U, define in
$(\mathcal {N},U)$
the special enumerations P of
$S(U_1)$
and Q of
$S(U_2)$
.
Our forcing language is the elementary first order language of the structure
$(\mathcal {N},U)$
. The special enumerations
$P,Q$
of
$S(U_1),S(U_2)$
are defined in
$(\mathcal {N},U)$
. We define the forcing relation
$p\Vdash ^C\varphi $
, for
$p\in 2^{<\omega }$
and
$\varphi $
an elementary first order sentence in the forcing language.
Definition 8 (Forcing)
-
1. If
$\varphi $
is an atomic sentence in the language of
$\mathcal {N}$
, then
$p \Vdash ^C \varphi $
if
$\mathcal {N}\models \varphi $
, -
2.
$p\Vdash ^C U(m)$
if
$m\in dom(p)$
and
$p(m) = 1$
, -
3.
$p\Vdash ^C (\varphi \vee \psi )$
if
$p\Vdash ^C\varphi $
or
$p\Vdash ^C\psi $
, -
4.
$p\Vdash ^C (\varphi \ \&\ \psi )$
if
$p\Vdash ^C\varphi $
and
$p\Vdash ^C\psi $
, -
5.
$p\Vdash ^C\neg {\varphi }$
if there is no
$q\supseteq p$
such that
$q\Vdash ^C\varphi $
, and -
6.
$p\Vdash ^C(\exists x)\varphi (x)$
if
$p\Vdash ^C\varphi (n)$
for some n.
Note: We omit the clause for the universal quantifier, thinking of
$(\forall x)\varphi $
as an abbreviation for
$\neg {(\exists x)\neg {\varphi }}$
.
The usual forcing lemmas hold.
Definition 9 (Generic Sets)
A set
$U \subseteq \omega $
is generic if for each elementary first order sentence
$\varphi $
in the forcing language, there is some forcing condition
$p\subseteq \chi _U$
that decides
$\varphi $
; i.e., either
$p\Vdash ^C\varphi $
or
$p\Vdash ^C\neg {\varphi }$
.
5.1 Modifying a Cohen generic
We consider ways to modify a Cohen generic to produce further Cohen generics. These results are somewhat similar to results by Cohen in the context of finding models of set theory in which the axiom of choice does not hold. These results showed that a permutation fixing all but finitely many elements of a model preserves the forcing relation between forcing conditions and sentences after each is acted upon by that permutation [Reference Cohen4].
We have already mentioned the even and odd parts
$U_1,U_2$
of a generic U. In Lemma 5.1, we saw that
$U_1,U_2$
are definable in
$(\mathcal {N},U)$
. We mention two further kinds of modification that will be of special importance.
Definition 10 (Switch)
For a set
$U\subseteq \omega $
, the switch is
$$ \begin{align*} U^s = \{2n:2n+1\in U\}\cup\{2n+1:2n\in U\} \ {.} \end{align*} $$
Note that
$(U^s)_1 = U_2$
and
$(U^s)_2 = U_1$
.
The following is clear from the definition.
Lemma 5.4. There is an elementary first order formula that, for all U, defines
$U^s$
in
$(\mathcal {N},U)$
.
We will see that if U is generic, then so is
$U^s$
.
Definition 11 (Finite variant)
If X is generic, and
$p\in 2^{<\omega }$
, then
$X^p$
is the set Y such that
$$ \begin{align*}\chi_Y(x) = \left\{\begin{array}{@{}cc} p(x), & \mbox{ if } x\in dom(p),\\ \chi_X(x), & \mbox{if } x\notin dom(p). \end{array}\right.\end{align*} $$
Lemma 5.5. For each
$p\in 2^{<\omega }$
, there is an elementary first order formula that, for all U, defines
$U^p$
in
$(\mathcal {N},U)$
.
Proof. Suppose p has length n. Then we have the definition
$$ \begin{align*} \bigvee_{k < n,p(k) = 1} x = k \vee (x> n\ \&\ Ux){.} \\[-46pt]\end{align*} $$
⊣
We will see that if U is generic, then for all
$p\in 2^{<\omega }$
,
$U^p$
is also generic. Note that if U is generic and
$p\in 2^{<\omega }$
, we may form the swap
$U^s$
and then the finite variant
$U^{sp} = (U^s)^p$
. This will be generic.
We give a general result with conditions guaranteeing that a modification of a generic set is generic. Our modifications will be definable in terms of the original generic.
Definition 12. Let
$\varphi (U,x)$
be a formula in the language of arithmetic expanded by the unary predicate U. We write
$U^{\varphi }$
for the set
$\{n:(\mathcal {N},U)\models \varphi (n)\}$
.
For an elementary first order formula
$\psi = \psi (U,\bar {x})$
in the forcing language, the predicate U occurs in atomic sub-formulas of the form
$U\tau $
, where
$\tau $
is a term in the language of arithmetic. By our choice of language, each term is either a variable or the name for some natural number n. We have said that we may write n for the name.
Definition 13. We write
$\psi (U^{\varphi },\bar {x})$
for the result of replacing all atomic sub-formulas of
$\psi $
of form
$U\tau $
by
$\varphi (U,\tau )$
.
For a formula
$\varphi (U,x)$
, we define a function
$F^{\varphi }$
on forcing conditions that might determine a generic U.
Definition 14. Let
$\varphi = \varphi (U,x)$
be a formula in the forcing language, with just the free variable x. For
$p\in 2^{<\omega }$
, let
$F^{\varphi }(p)$
consist of the pairs
$(n,1)$
such that for all
$p'\supseteq p$
,
$p'\not \Vdash ^C\neg {\varphi (n)}$
and
$(n,0)$
such that for all
$p'\supseteq p$
,
$p'\not \Vdash ^C\varphi (n)$
.
From the definition, it is immediate that
$F^{\varphi }(p)$
is a partial function from
$\omega $
to
$2$
—the domain need not be a natural number. The following is clear.
Lemma 5.6. If
$p'\supseteq p$
, then
$F^{\varphi }(p')\supseteq F^{\varphi }(p)$
.
Here is the general result giving conditions on the formula
$\varphi $
sufficient to guarantee that if U is generic, then
$U^{\varphi }$
is also generic.
Theorem 5.7. Let
$\varphi = \varphi (U,x)$
be a formula in the forcing language, with just the free variable x. Suppose the following conditions are satisfied:
-
1. for all
$p\in 2^{<\omega }$
, the partial function
$F^{\varphi }(p)$
is finite and -
2. for each
$q\in 2^{<\omega }$
such that
$q\supseteq F^{\varphi }(p)$
, there is some
$p'\in 2^{<\omega }$
such that
$p'\supseteq p$
and
$F^{\varphi }(p')\supseteq q$
.
Then if U is generic,
$U^{\varphi }$
is also generic.
Remark. Condition (1) does not imply that
$F^{\varphi }(p)$
is a forcing condition—it may be defined on m and not on some
$k < m$
.
To prove Theorem 5.7, we first prove two lemmas.
Lemma 5.8. For all sentences
$\psi (U)$
in the forcing language, and all
$p\in 2^{<\omega }$
, the following are equivalent:
-
1.
$(\exists p'\supseteq p) p'\Vdash ^C\psi (U^{\varphi })$
and -
2.
$(\exists q\supseteq F^{\varphi }(p)) q\Vdash ^C \psi (U)$
.
Proof. We proceed by induction on the sentences
$\psi $
in the forcing language.
-
1. Suppose
$\psi = \psi (U^{\varphi })$
is an atomic sentence in the language of arithmetic. Then
$\psi (U) = \psi (U^{\varphi })$
. Any and all forcing conditions force
$\psi $
just in case it is true in
$\mathcal {N}$
. So, the statement holds for
$\psi $
. -
2. Suppose
$\psi $
is
$Un$
. We have
$U^{\varphi } n = \varphi (n)$
. Suppose
$(\exists p'\supseteq p)p'\Vdash ^C\varphi (n)$
. By Lemma 5.6,
$F^{\varphi }(p')\supseteq F^{\varphi }(p)$
. If
$p'\Vdash ^C\psi (U^{\varphi })$
, then
$F^{\varphi }(p')$
maps n to
$1$
, and any and all forcing conditions
$q\supseteq F^{\varphi }(p')$
must force
$Un$
. Suppose
$(\exists q\supseteq F^{\varphi }(p)) q\Vdash ^C Un$
. By assumption, there is some
$p'\supseteq p$
such that
$F^{\varphi }(p')\supseteq q$
. No extension of
$p'$
forces
$\neg {\varphi }(n)$
, so some
$p''\supseteq p'$
must force
$\varphi (n)$
, which is
$U^{\varphi }(n)$
. -
3. Consider
$(\psi _1\vee \psi _2)$
. If some
$p'\supseteq p$
forces
$(\psi _1\vee \psi _2)(U^{\varphi })$
, it forces one of the disjuncts
$\psi _i(U^{\varphi })$
. By HI, some
$q\supseteq F^{\varphi }(p)$
forces
$\psi _i(U)$
, so it forces
$(\psi _1\vee \psi _2)(U)$
. If some
$q\supseteq F^{\varphi }(p)$
forces
$(\psi _1\vee \psi _2)(U)$
, it forces one of the disjuncts
$\psi _i(U)$
. By HI, some
$p'\supseteq p$
forces
$\psi _i(U^{\varphi })$
, and then it forces
$(\psi _1(U^{\varphi })\vee \psi _2(U^{\varphi })) = (\psi _1\vee \psi _2)(U^{\varphi })$
. -
4. Consider
$(\psi _1\ \&\ \psi _2)$
. Suppose some
$p'\supseteq p$
forces
$(\psi _1\ \&\ \psi _2)(U^{\varphi })$
. Then
$p'$
forces both of the conjuncts
$\psi _i(U^{\varphi })$
. By HI, there exists
$q_1\supseteq F^{\varphi }(p)$
such that
$q_1$
forces
$\psi _1(U)$
. There exists
$p''\supseteq p'$
such that
$F^{\varphi }(p")\supseteq q_1$
. Then
$p"$
forces
$\psi _2(U^{\varphi })$
. By HI, there is some
$q_2\supseteq F^{\varphi }(p")$
such that
$q_2$
forces
$\psi _2(U)$
. Since
$q_2\supseteq q_1$
, it also forces
$\psi _1(U)$
, so it forces the conjunction. Now, suppose some
$q\supseteq F^{\varphi }(p)$
forces
$(\psi _1\ \&\ \psi _2)(U)$
. This q forces both conjuncts
$\psi _i(U)$
. Take
$p'\supseteq p$
such that
$F^{\varphi }(p')\supseteq q$
, and let
$q'\supseteq F^{\varphi }(p')$
. Then
$q'$
forces
$\psi _1(U)$
. By HI, there is some
$p''\supseteq p'$
such that
$p"$
forces
$\psi _1(U^{\varphi })$
. Take
$q''\supseteq F^{\varphi }(p")$
. Then
$q"$
forces
$\psi _2(U)$
, so by HI, there is some
$p"'\supseteq p"$
such that
$p"'$
forces
$\psi _2(U^{\varphi })$
. Since
$p"'\supseteq p"$
, it forces
$\psi _1(U^{\varphi })$
, so it forces the conjunction. -
5. Consider
$(\exists x)\psi (x)$
. Suppose
$p'\supseteq p$
forces
$((\exists x)\psi (x))(U^{\varphi })$
. Then
$p'$
forces
$(\psi (n))(U^{\varphi })$
for some n. By HI, there exists
$q\supseteq F^{\varphi }(p)$
forcing
$(\psi (n))(U)$
and therefore forcing
$((\exists x)\psi (x))(U)$
. Suppose
$q\supseteq F^{\varphi }(p)$
forces
$((\exists x)\psi (x))(U)$
. Then q forces
$\psi (n)(U)$
, for some n. By HI, there exists
$p'\supseteq p$
forcing
$\psi (n)(U^{\varphi })$
, and then
$p'$
forces
$((\exists x)\psi (x))(U^{\varphi })$
. -
6. Consider
$\neg {\psi }$
. Suppose
$(\exists p'\supseteq p) p'\Vdash ^C\neg {\psi (U^{\varphi })}$
. For
$q\supseteq F^{\varphi }(p')$
, our assumption gives
$p''\supseteq p'$
such that
$F^{\varphi }(p")\supseteq q$
. We cannot have q forcing
$\psi (U)$
, for then there would be
$p''\supseteq p'$
forcing
$\psi (U^{\varphi })$
. So, any
$q\supseteq F^{\varphi }(p')$
must force
$\neg {\psi (U^{\varphi })}$
. Now, suppose
$(\exists q\supseteq F^{\varphi }(p)$
such that
$q\Vdash ^C \neg {\psi }$
. Take
$p'\supseteq p$
such that
$F^{\varphi }(p')\supseteq q$
. No extension of
$p'$
can force
$\psi (U^{\varphi })$
, for then there would be
$q''\supseteq F^{\varphi }(p')$
forcing
$\psi (U)$
.⊣
Lemma 5.9. For all sentences
$\psi (U)$
in the forcing language and all p, if
$p\Vdash ^C\psi (U^{\varphi })$
, then for all forcing conditions
$q\supseteq F^{\varphi }(p)$
,
$q\Vdash ^C\psi (U)$
.
Proof. Again we proceed by induction on
$\psi $
-
1. If
$\psi $
is an atomic sentence in the language of arithmetic, then
$\psi (U) = \psi (U^{\varphi })$
, and all forcing conditions force
$\psi $
just in case it is true in
$\mathcal {N}$
. -
2. Let
$\psi $
have form
$Un$
. Then
$\psi (U^{\varphi }) = \varphi (U,n)$
. If
$p\Vdash ^C\varphi (U,n)$
, then
$F^{\varphi }(p)(n) = 1$
. For all forcing conditions
$q\supseteq F^{\varphi }(p)$
,
$q(n) = 1$
, so
$q\Vdash ^C Un$
. -
3. Consider
$(\psi _1\vee \psi _2)$
. If
$p\Vdash ^C(\psi _1\vee \psi _2)(U^{\varphi })$
, then p forces one of the disjuncts
$\psi _i(U^{\varphi })$
. By HI, all
$q\supseteq F^{\varphi }(p)$
force
$\psi _i(U)$
, so they force the disjunction. -
4. Consider
$(\psi _1\ \&\ \psi _2)$
. If
$p\Vdash ^C(\psi _1\ \&\ \psi _2)(U^{\varphi })$
, then p forces both conjuncts
$\psi _i(U^{\varphi })$
. By HI, any
$q\supseteq F^{\varphi }(p)$
must force both of the conjuncts
$\psi _i(U)$
, so it forces the conjunction. -
5. Consider
$(\exists x)\psi (x)$
. If
$p\Vdash ^C((\exists x)\psi )(U^{\varphi })$
, then p forces
$\psi (n)(U^{\varphi })$
, for some n. By HI, any
$q\supseteq F^{\varphi }(p)$
must force
$\psi (n)(U)$
, so it forces
$((\exists x)\psi )(U)$
. -
6. Suppose
$p\Vdash ^C\neg {\psi (U^{\varphi })}$
. Take
$q\supseteq F^{\varphi }(p)$
. By Lemma 5.8, since no extension of p forces
$\psi (U^{\varphi })$
, no extension of q forces
$\psi (U)$
. This means that q forces
$\neg {\psi (U)}$
.⊣
We are ready to complete the proof of Theorem 5.7. We assume that U is generic. To show that
$U^{\varphi }$
is also generic, we must show that for each sentence
$\psi (U)$
, there is some forcing condition
$q\subseteq \chi _{U^{\varphi }}$
such that q decides
$\psi (U)$
.
Proof of Theorem 5.7. Let
$\psi (U)$
be a sentence in the forcing language. Since U is generic, there is some
$p\subseteq \chi _U$
such that p decides the sentence
$\psi (U^{\varphi })$
. Without loss, suppose p forces
$\psi (U^{\varphi })$
. Now,
$F^{\varphi }(p)\subseteq \chi _{U^{\varphi }}$
. Moreover, there is a forcing condition q (with domain a natural number) such that
$F^{\varphi }(p)\subseteq q\subseteq \chi _{U^{\varphi }}$
. By Lemma 5.9, this q must force
$\psi (U)$
.⊣
We turn to the specific modifications that we need.
Corollary 5.10. If U is generic, then so are
$U_1,U_2$
.
Proof. We consider
$U_1$
. Let
$\varphi $
be the formula from Lemma 5.1 defining
$U_1$
in
$(\mathcal {N},U)$
. For each p,
$F^{\varphi }(p)$
consists of the pairs
$(n,i)$
such that
$2n\in dom(p)$
and
$p(2n) = i$
, for
$i = 0,1$
. This is a finite function. For
$q\supseteq F^{\varphi }(p)$
, of length n, let
$p'$
be an extension of p of length
$2n$
such that
$p'(2k) = q(k)$
, for all
$k < n$
. Then
$F^{\varphi }(p')\supseteq q$
. Applying Theorem 5.7, we get the fact that
$U_1$
is generic.⊣
Corollary 5.11. If U is generic, then
$U^s$
is also generic.
Proof. Let
$\varphi $
be the formula from Lemma 5.4, defining
$U^s$
in
$(\mathcal {N},U)$
. For each p,
$F^{\varphi }(p)$
consists of the pairs
$(2k,1)$
where
$p(2k+1) = 1$
,
$(2k+1,1)$
, where
$p(2k) = 1$
,
$(2k,0)$
, where
$p(2k+1) = 0$
, and
$(2k+1,0)$
, where
$p(2k+1) = 1$
. This is finite. Suppose
$q\supseteq F^{\varphi }(p)$
. We extend q if necessary so that the length is even. We then define
$p'\supseteq p$
, of the same length as q, so that if
$2m$
is an even element of
$dom(q)$
, then
$p'(2m+1) = q(2m)$
, and if
$2m+1$
is an odd element of
$dom(q)$
, then
$p'(2m) = q(2m+1)$
. Then
$F^{\varphi }(p')\supseteq q$
. Applying Theorem 5.7, we get the fact that
$U^s$
is generic.⊣
Corollary 5.12. If U is generic and
$r\in 2^{<\omega }$
, then
$U^r$
is generic.
Proof. Let
$\varphi $
be the formula from Lemma 5.5, defining
$U^r$
in
$(\mathcal {N},U)$
. For each p,
$F^{\varphi }(p)$
consists of the pairs
$(k,1)$
such that
$k\in dom(r)$
and
$r(k) = 1$
or
$k\in dom(p) - dom(r)$
and
$p(k) = 1$
, and the pairs
$(k,0)$
such that
$k\in dom(r)$
and
$r(k) = 0$
or
$k\in dom(p) - dom(r)$
and
$p(k) = 0$
. This is a finite function. For a forcing condition
$q\supseteq F^{\varphi }(p)$
, let
$p'\supseteq p$
be the function of the same length as q, such that for
$k\in dom(q) - dom(p)$
,
$p'(k) = q(k)$
. Then
$F^{\varphi }(p')\supseteq q$
. Applying Theorem 5.7, we get the fact that
$U^r$
is generic.⊣
6 Completing the example
In the previous section, we talked about Cohen forcing. We say a little about generic enumerations. Then we complete the proof that our example works.
6.1 Generic enumerations
For an arbitrary set
$U\subseteq \omega $
, we can form the even and odd parts
$U_1,U_2$
, and we get the families of sets
$S_1,S_2$
consisting of finite variants of
$U_1,U_2$
, respectively. We obtain special enumerations P of
$S_1$
and Q of
$S_2$
, defined in
$(\mathcal {N},U)$
by elementary first order formulas—these formulas are the same for all U. For convenience, we consider the “base” structure to be
$(\mathcal {N},U,P,Q)$
instead of
$(\mathcal {N},U)$
. We produce generic enumerations
$R_1,R_2$
of the families
$S_1,S_2$
. We obtain
$R_1,R_2$
from a generic pair of functions
$f,g\in \omega ^{\omega }$
. The set with
$R_1$
-index n is the one with P-index
$f(n)$
, and the set with
$R_2$
-index n is the one with Q-index
$g(n)$
. The forcing conditions are pairs
$(\sigma ,\tau )\in \omega ^{<\omega }\times \omega ^{<\omega }$
—representing possible initial segments of
$(f,g)$
. We define the relation
$(\sigma ,\tau )\Vdash ^E\varphi $
, for elementary first order sentences
$\varphi $
in the language of the structure
$(\mathcal {N},U,P,Q,R_1,R_2)$
. We use binary relation symbols for the enumerations
$P,Q,R_1,R_2$
.
Definition 15.
-
1. For an atomic sentence
$\varphi $
in the language of the base structure
$(\mathcal {N},U,P,Q)$
,
$(\sigma ,\tau )\Vdash ^E\varphi $
if
$(\mathcal {N},U,P,Q)\models \varphi $
, -
2. for
$\varphi $
of the form
$R_1(m,n)$
,
$(\sigma ,\tau )\Vdash ^E\alpha $
if
$m\in dom(\sigma )$
and for
$k = \sigma (m)$
,
$P(k,n)$
holds, -
3. for
$\varphi $
of form
$R_2(m,n)$
,
$(\sigma ,\tau )\Vdash ^E\varphi $
if
$m\in dom(\tau )$
and for
$k = \tau (m)$
,
$Q(k,n)$
holds, -
4.
$(\sigma ,\tau )\Vdash ^E(\varphi \vee \psi )$
if
$(\sigma ,\tau )\Vdash ^E\varphi $
or
$(\sigma ,\tau )\Vdash ^E\psi $
, -
5.
$(\sigma ,\tau )$
forces
$(\varphi \ \&\ \psi )$
if it forces both
$\varphi $
and
$\psi $
, -
6.
$(\sigma ,\tau )\Vdash ^E\neg {\varphi }$
if there do not exist
$(\sigma ',\tau ')\supseteq (\sigma ,\tau )$
such that
$(\sigma ',\tau ')\Vdash ^E\varphi $
, and -
7.
$(\sigma ,\tau )\Vdash ^E(\exists x)\varphi (x)$
if
$(\sigma ,\tau )\Vdash ^E\varphi (n)$
for some n.
For an arbitrary set
$U\subseteq \omega $
, let
$U_1,U_2$
be the even and odd parts, let
$S_1,S_2$
be the family of finite variants of
$U_1,U_2$
, respectively, and let
$P,S$
be the special enumerations of
$S_1,S_2$
.
Definition 16. A chain of forcing conditions
$(\sigma _n,\tau _n)_{n\in \omega }$
is a complete forcing sequence if for each elementary first order sentence
$\varphi $
in the forcing language, there is some n such that
$(\sigma _n,\tau _n)$
decides
$\varphi $
, for each m, there is some n such that
$n\in ran(\sigma _n)$
, and for each m, there is some n such that
$n\in ran(\tau _n)$
.
The usual forcing lemmas hold, so that complete forcing sequences exist. For a complete forcing sequence
$(\sigma _n,\tau _n)_{n\in \omega }$
, we get a pair of permutations of
$\omega \ f = \cup _n\sigma _n$
and
$g = \cup _n\sigma _n$
. The pair of permutations yields a pair of enumerations
$R_1$
of
$S_1$
and
$R_2$
of
$S_2$
, where the set with
$R_1$
-index n is the one with P-index
$f(n)$
and the set with
$R_2$
-index n is the one with Q-index
$g(n)$
.
Definition 17. For families
$S_1,S_2$
obtained from a set U as above, we say that
$R_1,R_2$
are a generic pair of enumerations of
$S_1,S_2$
if they are obtained from a complete forcing sequence—chosen to decide all sentences in the forcing language.
The lemma stated below says precisely how we can define forcing of statements about the generic enumerations in the language appropriate for describing the Cohen generic.
Recall that if U is an arbitrary subset of
$\omega $
, we have even and odd parts
$U_1$
,
$U_2$
, with families
$S_1$
and
$S_2$
consisting of the finite variants of
$U_1,U_2$
, respectively, and we have special enumerations P and Q, defined from U, in a uniform way. For any U, the forcing conditions for producing generic enumerations
$R_1,R_2$
of the families
$S_1,S_2$
are the same.
Lemma 6.1 (Definability of forcing)
For each formula
$\varphi (\bar {x})$
in the language of
$(\mathcal {N},U,P,Q,R_1,R_2)$
, there is a formula
$Force_{\varphi }(u,v,\bar {x})$
in the language of
$(\mathcal {N},U,P,Q)$
such that for all sets U, with resulting special enumerations
$P,Q$
, for all forcing conditions
$(\sigma ,\tau )$
(for producing generic enumerations) and all
$\bar {n}$
appropriate for
$\bar {x}$
,
$(\sigma ,\tau )\Vdash ^E \varphi (\bar {n})$
iff
$(\mathcal {N},X,P,Q)\models Force_{\varphi }(\sigma ,\tau ,\bar {n})$
.
Proof. First, in the language of arithmetic, we have a formula
$force(u,v)$
saying that the pair
$(u,v)$
is a forcing condition; i.e.,
$u,v$
are codes for finite partial
$1-1$
functions. We define the formulas
$Force_{\varphi }(u,v,\bar {x})$
by induction on formulas
$\varphi (\bar {x})$
.
-
1. For
$\varphi (\bar {x})$
an atomic formula in the language of
$(\mathcal {N},U,P,Q)$
,
$Force_{\varphi }(u,v,\bar {x})$
is the formula
$(force(u,v)\ \&\ \varphi (\bar {x}))$
, saying that
$(u,v)$
is a forcing condition and
$\varphi (\bar {x})$
holds, -
2. for
$\varphi $
of the form
$R_1(x,y)$
,
$Force_{\varphi }(u,v,x,y)$
is the conjunction of
$force(u,v)$
with the formula saying that
$x\in dom(u)$
and
$P(u(x),y)$
, -
3. for
$\varphi $
of form
$R_2(x,y)$
,
$Force_{\varphi }(u,v,x,y)$
is the conjunction of
$force(u,v)$
with the formula saying that
$x\in dom(v)$
and
$Q(v(x),y)$
, -
4.
$Force_{(\varphi \vee \psi )}(u,v,\bar {x}) = (Force_{\varphi }(u,v,\bar {x})\vee Force_{\psi }(u,v,\bar {x}))$
, -
5.
$Force_{(\varphi \ \&\ \psi )}(u,v,\bar {x}) = (Force_{\varphi }(u,v,\bar {x})\ \&\ Force_{\psi }(u,v,\bar {x}))$
, -
6.
$Force_{\neg {\varphi }}(u,v,\bar {x})$
says that for all
$u'\supseteq u$
and
$v'\supseteq v$
,
$\neg {Force_{\varphi }(u',v',\bar {x})}$
, and -
7. for
$\varphi (\bar {x}) = (\exists y)\psi (\bar {x},y)$
,
$Force_{\varphi }(u,v,\bar {x}) = (\exists y)Force_{\psi }(u,v,\bar {x},y)$
.⊣
6.1.1 Important sentences
$PCopy_e$
We identify
$R_1$
with a copy of
$\mathcal {A}_1$
, and
$R_2$
with a copy of
$\mathcal {A}_2$
. Effectively in these, we get
$\mathcal {B}\cong \mathcal {A}_1|\mathcal {A}_2$
, where in
$\mathcal {B}$
,
$0$
is in the equivalence class that is a copy of
$\mathcal {A}_1$
. For each oracle procedure
$\varphi _e$
, we let
$PCopy_e$
be the sentence saying that
$\varphi _e^{\mathcal {B}}$
is an enumeration E of the same family of sets as P. We identify E with a copy of the graph coding that family of sets. We may take
$PCopy_e$
to start with a universal quantifier.
6.2 Completing the proof
We are ready to combine the two kinds of forcing to show that our example has the desired properties.
Proposition 6.2. Let X be generic, and let
$\mathcal {A}_1,\mathcal {A}_2$
be as described. Then
$\mathcal {A}_1\not \leq _s\mathcal {A}_1|\mathcal {A}_2$
.
Proof. Suppose
$\mathcal {A}_1\leq _s\mathcal {A}_1|\mathcal {A}_2$
, witnessed by the Turing operator
$\Phi = \varphi _e$
. We expect a contradiction. For any generic pair of enumerations
$R_1,R_2$
of the families
$S_1,S_2$
obtained from the even and odd parts of X, we must have
$(\mathcal {N},X,P,Q,R_1,R_2)\models PCopy_e$
. Then
$(\emptyset ,\emptyset )\Vdash ^E PCopy_e$
. By definability of forcing,
$(\mathcal {N},X,P,Q)\models Force_{PCopy_e}(\emptyset ,\emptyset )$
. There must be some p, a forcing condition for producing the Cohen generic X, such that
$p\Vdash ^C Force_{PCopy_e}(\emptyset ,\emptyset )$
.
We consider the switch
$X^s$
, and then
$X^{sp}$
, where this is the extension of p that agrees with
$X^s$
on all
$k\notin dom(p)$
. By the results on variants of Cohen generics,
$X^s$
and
$X^{sp}$
are generic. Let
$X_1^*, X_2^*$
be the even and odd parts of
$X^{sp}$
. We can see that
$S(X_1^*) = S_2$
and
$S(X_2^*) = S_1$
. Let
$P^*,Q^*$
be the special enumerations of
$S_2,S_1$
defined in
$(\mathcal {N},X^{sp})$
. Let
$R_1^*,R_2^*$
be generic enumerations of
$S_2,S_1$
, obtained with the base structure
$(\mathcal {N},X^{sp},P^*,Q^*)$
. Then
$(\mathcal {N},X^{sp},P^*,Q^*,R_1^*,R_2^*)\models PCopy_e$
. But, let us think what this means. The pair
$(R_1^*,R_2^*)$
yields a copy
$\mathcal {B}^*$
of
$\mathcal {A}_1|\mathcal {A}_2$
, and
$\varphi _e^{\mathcal {B}^*}$
gives a copy of the graph coding the family enumerated by
$P^*$
—this is
$\mathcal {A}_2$
. We have the expected contradiction. This shows that
$\mathcal {A}_1\not \leq _s\mathcal {A}_1|\mathcal {A}_2$
.⊣
7 Conclusion
What we have constructed is a pair of graphs
$\mathcal {A}_1,\mathcal {A}_2$
such that
$\mathcal {A}_1\not \leq _s\mathcal {A}_1|\mathcal {A}_2$
. We can apply standard results to transform the graphs into groups or fields.
Proposition 7.1. Let
$K_1,K_2$
be two classes of structures, closed under isomorphism. Suppose we have uniform Turing operators
$\Phi $
and
$\Psi $
such that
$\Phi :K_1\rightarrow K_2$
, where for
$\mathcal {A}_1,\mathcal {A}_2\in K_1$
,
$\mathcal {A}_1\cong \mathcal {A}_2$
iff
$\Phi (\mathcal {A}_1)\cong \Phi (\mathcal {A}_2)$
, and for all
$\mathcal {A}\in K_1$
,
$\Psi $
takes copies of
$\Phi (\mathcal {A})$
to copies of
$\mathcal {A}$
. Then for
$\mathcal {A}_1,\mathcal {A}_2\in K$
,
$\Phi (\mathcal {A}_1)\leq _s\Phi (\mathcal {A}_1)|\Phi (\mathcal {A}_2)$
implies
$\mathcal {A}_1\leq _s\mathcal {A}_1|\mathcal {A}_2$
.
Proof. Let
$\mathcal {B}_1 = \Phi (\mathcal {A}_i)$
. Supposing that
$\mathcal {B}_1\leq _s\mathcal {B}_1|\mathcal {B}_2$
via
$\Theta $
, we show that
$\mathcal {A}_1\leq _s \mathcal {A}_1|\mathcal {A}_2$
. Given a copy of
$\mathcal {A}_1|\mathcal {A}_2$
, we apply
$\Phi $
to produce a copy of
$\mathcal {B}_1|\mathcal {B}_2$
. Next, we apply
$\Theta $
to produce a copy of
$\mathcal {B}_1$
. Finally, we apply
$\Psi $
to get a copy of
$\mathcal {A}_1$
.⊣
There are general results of Hirschfeldt et al. [Reference Hirschfeldt, Khoussainov, Shore and Slinko6] that yield operators
$\Phi $
and
$\Psi $
as in the Proposition. The results of Hirschfeldt et al. can be applied when
$K_1$
is the class of graphs and
$K_2$
is any of several familiar classes, including lattices, partial orders, commutative semigroups, rings, integral domains, and nilpotent groups. A result of Miller et al. [Reference Miller, Poonen, Schoutens and Shlapentokh11] lets us add to this list the class of fields.
So far, the examples we know with
$\mathcal {A}_1\not \leq _s\mathcal {A}_1|\mathcal {A}_2$
are all derived from a generic set. We have no general conditions that we can apply to already-existing structures
$\mathcal {A}_1,\mathcal {A}_2$
to show that
$\mathcal {A}_1\not \leq _s\mathcal {A}_1|\mathcal {A}_2$
.
Acknowledgments
Rachael Alvir and Julia F. Knight are grateful for support from NSF grant #DMS 1800692.
