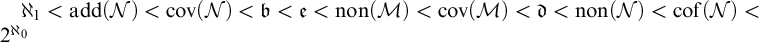1 Introduction
1.1 Background on Cichoń’s maximum and evasion number
Cardinal invariants of the continuum are cardinals characterizing some structure of the continuum. Well-known examples are the bounding number
$\mathfrak {b}$
and the dominating number
$\mathfrak {d}$
: For
$f,g\in {\omega }^\omega $
, let
$f\leq ^*g$
be defined by:
$ f(n)\leq g(n)$
for all but finitely many
$n<\omega $
. And we define
$\mathfrak {b}$
and
$\mathfrak {d}$
as follows:
-
•
. -
•
.
.
.Other examples are those related to an ideal on the reals Let X be a set and
$I\subseteq \mathcal {P}(X)$
be an ideal containing all singletons. We define the following four numbers on I:
-
•
$\operatorname {\mathrm {add}}(I):=\min \{|\mathcal {A}|:\mathcal {A}\subseteq I,~\bigcup \mathcal {A}\notin I\}$
. -
•
$\operatorname {\mathrm {cov}}(I):=\min \{|\mathcal {A}|:\mathcal {A}\subseteq I,~\bigcup \mathcal {A}=X\}$
. -
•
$\operatorname {\mathrm {non}}(I):=\min {\{}|A|:A\subseteq X,~A\notin I\}$
. -
•
$\operatorname {\mathrm {cof}}(I):=\min {\{}|\mathcal {A}|:\mathcal {A}\subseteq I~\forall B\in I~\exists A\in \mathcal {A}~B\subseteq A\}$
.
The set of all Lebesgue null sets
$\mathcal {N}$
and the set of all meager sets
$\mathcal {M}$
are ideals on
$X=\mathbb {R}$
, so we can define the
$2*4=8$
cardinal invariants.
The relationship of these
$2+8=10$
cardinal invariants is illustrated in Cichoń’s diagram (see Figure 1). It is said to be complete in the sense that we cannot prove any more inequalities between two cardinal invariants in the diagram, in other words, no other arrows can be added to the diagram. Moreover, it is known that the diagram can be “divided into two parts anywhere”. More precisely, any assignment of
$\aleph _1$
and
$\aleph _2$
to its numbers is consistent whenever it does not contradict the arrows and the two equations
$\operatorname {\mathrm {non}}(\mathcal {M})=\min \{\mathfrak {b},\operatorname {\mathrm {cov}}(\mathcal {M})\}$
and
$\operatorname {\mathrm {cof}}(\mathcal {M})=\max \{\mathfrak {d},\operatorname {\mathrm {non}}(\mathcal {M})\}$
(see [Reference Bartoszyński and Judah5, Chapter 7]).
Figure 1 Cichoń’s diagram. An arrow
$\mathfrak {x}\to \mathfrak {y}$
denotes that
$\mathfrak {x}\leq \mathfrak {y}$
holds. Also
$\operatorname {\mathrm {non}}(\mathcal {M})=\min \{\mathfrak {b},\operatorname {\mathrm {cov}}(\mathcal {M})\}$
and
$\operatorname {\mathrm {cof}}(\mathcal {M})=\max \{\mathfrak {d},\operatorname {\mathrm {non}}(\mathcal {M})\}$
hold.
Since the separations of Cichoń’s diagram with two values are well studied, we are naturally interested in the separation with more values and in this sense the ultimate question is the following
Question 1. Can we separate Cichoń’s diagram with as many values as possible? In other words, can we construct a model where all the cardinal invariants except for the two dependent numbers
$\operatorname {\mathrm {non}}(\mathcal {M})$
and
$\operatorname {\mathrm {cof}}(\mathcal {M})$
are pairwise different?
Such a model is called Cichoń’s maximum model. The question was positively solved by Goldstern, Kellner, and Shelah [Reference Goldstern, Kellner and Shelah19], assuming four strongly compact cardinals. They constructed a model whose separation order is as in Figure 2. Later, they and Mejía [Reference Goldstern, Kellner, Mejía and Shelah18] eliminated the large cardinal assumption and hence proved that Cichoń’s maximum is consistent with ZFC.
Figure 2 Cichoń’s maximum constructed in [Reference Goldstern, Kellner and Shelah19].
$\aleph _1<\theta _1<\cdots <\theta _8<\theta _{\mathfrak {c}}$
are regular cardinals.
$\operatorname {\mathrm {non}}(\mathcal {M})$
and
$\operatorname {\mathrm {cof}}(\mathcal {M})$
are omitted as dots “
$\cdot $
” since they have dependent values.
Consequently, the following natural question arises
Question 2. Can we add to Cichoń’s maximum other cardinal invariants with distinct values?
We can, as has been shown, e.g., in [Reference Goldstern, Kellner, Mejía and Shelah15] (where
$\mathfrak {m},\mathfrak {p}$
and
$\mathfrak {h}$
are added), or [Reference Goldstern, Kellner, Mejía and Shelah16] (where
$\mathfrak {s}$
and
$\mathfrak {r}$
are added).
In this paper, we focus on the evasion number
$\mathfrak {e}$
, which was first introduced by Blass [Reference Blass6].
Definition 1.1.
-
• A pair
$\pi =(D,\{\pi _n:n\in D\})$
is a predictor if
$D\in [{\omega }]^\omega $
and each
$\pi _n$
is a function
$\pi _n\colon \omega ^n\to \omega $
.
$\operatorname {\mathrm {Pred}}$
denotes the set of all predictors. -
•
$\pi \in \operatorname {\mathrm {Pred}}$
predicts
$f\in {\omega }^\omega $
if
$f(n)=\pi _n(f{\mathpunct {\upharpoonright }} n)$
for all but finitely many
$n\in D$
. f evades
$\pi $
if
$\pi $
does not predict f. -
• The prediction number
$\mathfrak {pr}$
and the evasion number
$\mathfrak {e}$
are defined as followsFootnote
1
:
The two numbers are embedded into Cichoń’s diagram as in Figure 3.
Figure 3 Cichoń’s diagram with evasion/prediction numbers.
1.2 Main Results
We proveFootnote 2 that they are instances answering Question 2. More concretely, we can add the prediction and evasion numbers to Cichoń’s maximum with distinct values as in Figure 4
Figure 4 Cichoń’s maximum with evasion/prediction numbers.
The construction of Cichoń’s maximum consists of two steps: the first one is to separate the left side of the diagram with additional properties and the second one is to separate the right side (point-symmetrically) using these properties. In [Reference Goldstern, Kellner and Shelah19], the large cardinal assumption was used in the second step to apply Boolean Ultrapowers. In [Reference Goldstern, Kellner, Mejía and Shelah18], they introduced the submodel method instead, which is a general technique to separate the right side without large cardinals.
Let us focus on the first step. The main work to separate the left side is to keep the bounding number
$\mathfrak {b}$
small through the forcing iteration, since the naive bookkeeping iteration to increase the cardinal invariants in the left side guarantees the smallness of the other numbers but not of
$\mathfrak {b}$
. To tackle the problem, in [Reference Goldstern, Kellner and Shelah19] they used the ultrafilter-limit method, which was first introduced by Goldstern, Mejía, and Shelah [Reference Goldstern, Mejía and Shelah20] to separate the left side of the diagram.
We introduce a new limit method called closed-ultrafilter-limit (Definition 3.2), which is a variant of ultrafilter-limit, and prove that it keeps
$\mathfrak {e}$
small
Theorem B (Main Lemma 3.26).
Closed-ultrafilter-limits keep
$\mathfrak {e}$
small.
We also prove that the two ultrafilter-limit methods can be mixed and obtain the separation model of Figure 4 (Theorem A, Theorem 4.11).
Moreover, we prove that we can control the values of the following variants of the evasion/prediction numbers
Definition 1.2.
-
(1) A predictor
$\pi $
bounding-predicts
$f\in {\omega }^\omega $
if
$f(n)\leq \pi (f{\mathpunct {\upharpoonright }} n)$
for all but finitely many
$n\in D$
.
${\mathfrak {pr}^*}$
and
${\mathfrak {e}^*}$
denote the prediction/evasion number respectively with respect to the bounding-prediction. -
(2) Let
$g\in \left (\omega +1\setminus 2\right )^\omega $
. ( “
$\setminus 2$
” is required to exclude trivial cases.) g-prediction is the prediction where the range of functions f is restricted to
$\prod _{n<\omega }g(n)$
and
$\mathfrak {pr}_g$
and
$\mathfrak {e}_g$
denote the prediction/evasion number respectively with respect to the g-prediction. Namely, Define:
The new numbers can be embedded into the diagram as in Figure 5. We obtain the following separation result
Figure 5 Cichoń’s diagram with the variants of evasion/prediction numbers.
Figure 6 Separation constellation of Theorem Theorem C.
1.3 Structure of the paper
In Section 2, we review the relational systems, the Tukey order and the general preservation theory of fsi (finite support iteration), such as goodness. In Section 3, we present the notion of ultrafilter-limit, which was first introduced in [Reference Goldstern, Mejía and Shelah20]. Also, we introduce the new notion closed-ultrafilter-limit and prove Theorem Theorem B, which is specific for this new limit notion. In Section 4, we present the application of Theorem Theorem B and prove the separation results Theorem Theorem A and Theorem Theorem C. Finally, we conclude the paper leaving some open questions presented in Section 5.
2 Relational systems and preservation theory
Definition 2.1.
-
•
$\mathbf {R}=\langle X,Y,\sqsubset \rangle $
is a relational system if X and Y are non-empty sets and
$\sqsubset \subseteq X\times Y$
. -
• We call an element of X a challenge, an element of Y a response, and “
$x\sqsubset y$
” “x is met by y”. -
•
$F\subseteq X$
is
$\mathbf {R}$
-unbounded if no response meets all challenges in F. -
•
$F\subseteq Y$
is
$\mathbf {R}$
-dominating if every challenge is met by some response in F. -
•
$\mathbf {R}$
is non-trivial if X is
$\mathbf {R}$
-unbounded and Y is
$\mathbf {R}$
-dominating. For non-trivial
$\mathbf {R}$
, define-
–
, and -
–
.
-
, and
.In this section, we assume
$\mathbf {R}$
is non-trivial.
Definition and Fact 2.2.
-
(1) For
, we get
$\mathfrak {b}(\mathbf {D})=\mathfrak {b}, \mathfrak {d}(\mathbf {D})=\mathfrak {d}$
. -
(2) Define
, where
$f\sqsubset ^{\mathrm {p}}\pi :\Leftrightarrow f$
is predicted by
$\pi $
. Also, define , where
$f\sqsubset ^{\mathrm {bp}}\pi :\Leftrightarrow f$
is bounding-predicted by
$\pi $
and where
$g\in (\omega +1\setminus 2)^\omega $
. We have
$\mathfrak {b}(\mathbf {PR})=\mathfrak {e}, \mathfrak {d}(\mathbf {PR})=\mathfrak {pr}$
,
$\mathfrak {b}(\mathbf {BPR})={\mathfrak {e}^*}, \mathfrak {d}(\mathbf {BPR})={\mathfrak {pr}^*}$
,
$\mathfrak {b}(\mathbf {PR}_g)=\mathfrak {e}_g, \mathfrak {d}(\mathbf {PR}_g)=\mathfrak {pr}_g$
. -
(3) For an ideal I on X, define two relational systems
and . We have
$\mathfrak {b}(\bar {I})=\operatorname {\mathrm {add}}(I),\mathfrak {d}(\bar {I})=\operatorname {\mathrm {cof}}(I)$
and
$\mathfrak {b}(C_I)=\operatorname {\mathrm {non}}(I),~\mathfrak {d}(C_I)=\operatorname {\mathrm {cov}}(I)$
. If I is an ideal, then we will write
$\mathbf {R}\preceq _T I$
to mean
$\mathbf {R}\preceq _T\bar {I}$
; and analogously for
$\succeq _T$
and
$\cong _T$
.
, we get 
, where 
, where 
where 
and 
. We have 
Definition 2.3.
$\mathbf {R}^\bot $
denotes the dual of
$\mathbf {R}=\langle X,Y,\sqsubset \rangle $
, i.e., 
where
$y\sqsubset ^\bot x:\Leftrightarrow \lnot (x\sqsubset y)$
.
Definition 2.4. For relational systems
$\mathbf {R}=\langle X,Y,\sqsubset \rangle , \mathbf {R}^{\prime }=\langle X^{\prime },Y^{\prime },\sqsubset ^{\prime }\rangle $
,
$(\Phi _-,\Phi _+):\mathbf {R}\rightarrow \mathbf {R}^\prime $
is a Tukey connection from
$\mathbf {R}$
into
$\mathbf {R}^{\prime }$
if
$\Phi _-:X\rightarrow X^{\prime }$
and
$\Phi _+:Y^{\prime }\rightarrow Y$
are functions such that:
$$ \begin{align*} \forall x\in X~\forall y^{\prime}\in Y^{\prime}~\Phi_-(x)\sqsubset^{\prime} y^{\prime}\Rightarrow x \sqsubset \Phi_{+} (y^{\prime}). \end{align*} $$
We write
$\mathbf {R}\preceq _T\mathbf {R}^{\prime }$
if there is a Tukey connection from
$\mathbf {R}$
into
$\mathbf {R}^{\prime }$
and call
$\preceq _T$
the Tukey order. Tukey equivalence
$\mathbf {R}\cong _T\mathbf {R}^{\prime }$
is defined as:
$\mathbf {R}\preceq _T\mathbf {R}^{\prime }$
and
$\mathbf {R}^{\prime }\preceq _T\mathbf {R}$
.
Fact 2.5.
-
(1)
$\mathbf {R}\preceq _T\mathbf {R}^{\prime }$
implies
$(\mathbf {R}^{\prime })^\bot \preceq _T\mathbf {R}^\bot $
. -
(2)
$\mathbf {R}\preceq _T\mathbf {R}^{\prime }$
implies
$\mathfrak {b}(\mathbf {R}^{\prime })\leq \mathfrak {b}(\mathbf {R})$
and
$\mathfrak {d}(\mathbf {R})\leq \mathfrak {d}(\mathbf {R}^{\prime })$
. -
(3)
$\mathfrak {b}(\mathbf {R}^\bot )=\mathfrak {d}(\mathbf {R})$
and
$\mathfrak {d}(\mathbf {R}^\bot )=\mathfrak {b}(\mathbf {R}^\bot )$
.
In the rest of this section, we fix an uncountable regular cardinal
$\theta $
and a set A of size
$\geq \theta $
.
$[A]^{<\theta }$
is an ideal on A, so
$C_{[A]^{<\theta }}$
is a relational system as in Definition and Fact 2.2(3) and
$\mathfrak {b}(C_{[A]^{<\theta }})=\theta $
and
$\mathfrak {d}(C_{[A]^{<\theta }})=|A|$
. For a relational system
$\mathbf {R}$
, we can calculate
$\mathfrak {b}(\mathbf {R})$
and
$\mathfrak {d}(\mathbf {R})$
from “outside” and “inside”, using this
$C_{[A]^{<\theta }}$
Corollary 2.6.
-
(outside) If
$\mathbf {R}\preceq _T C_{[A]^{<\theta }}$
, then
$\theta \leq \mathfrak {b}(\mathbf {R})$
and
$\mathfrak {d}(\mathbf {R})\leq |A|$
. -
(inside) If
$C_{[A]^{<\theta }}\preceq _T \mathbf {R}$
, then
$\mathfrak {b}(\mathbf {R})\leq \theta $
and
$|A|\leq \mathfrak {d}(\mathbf {R})$
.
Both “
$\mathbf {R}\preceq _T C_{[A]^{<\theta }}$
” and “
$C_{[A]^{<\theta }}\preceq _T \mathbf {R}$
” have the following characterizations
Fact 2.7. [Reference Cardona and Mejía10, Lemma 1.16] Assume
$|X|\geq \theta $
where
$\mathbf {R}=\langle X,Y,\sqsubset \rangle $
.
-
(1)
$\mathbf {R}\preceq _T C_{[X]^{<\theta }}$
iff
$\mathfrak {b}(\mathbf {R})\geq \theta $
. -
(2)
$C_{[A]^{<\theta }}\preceq _T\mathbf {R}$
iff there exists
$\langle x_a:a\in A\rangle $
such that every
$y\in Y$
meets only
$<\theta $
-many
$x_a$
.
To separate the right side by using submodels after having separated the left side, “
$\mathbf {R}\cong _T C_{[A]^{<\theta }}$
” does not work, but “
$\mathbf {R}\cong _T[A]^{<\theta }$
” does. The following fact gives a sufficient condition which implies
$C_{[A]^{<\theta }}\cong _T [A]^{<\theta }$
Fact 2.8. [Reference Cardona and Mejía10, Lemma 1.15] If
$|A|^{<\theta }=|A|$
, then
$C_{[A]^{<\theta }}\cong _T [A]^{<\theta }$
.
Fact 2.9. [Reference Cardona and Mejía10, Lemma 2.11] Every ccc poset forces
$[A]^{<\theta }\cong _T[A]^{<\theta }\cap V$
and
$C_{[A]^{<\theta }}\cong _T C_{[A]^{<\theta }}\cap V$
. Moreover,
$\mathfrak {x}([A]^{<\theta })=\mathfrak {x}^V([A]^{<\theta })$
where
$\mathfrak {x}$
represents “
$\operatorname {\mathrm {add}}$
”, “
$\operatorname {\mathrm {cov}}$
”, “
$\operatorname {\mathrm {non}}$
” or “
$\operatorname {\mathrm {cof}}$
”.
When performing a forcing iteration, the “outside” direction is easily satisfied by bookkeeping, while the other one, “inside” direction needs more discussion and actually it is usually the main work of separating cardinal invariants.
In the context of separating cardinal invariants of the continuum by finite support iteration (fsi) of ccc forcings, the notions of “Polish relational system” and “good” (introduced in [Reference Judah and Shelah21] and [Reference Brendle7]) work well.
Definition 2.10.
$\mathbf {R}=\langle X,Y,\sqsubset \rangle $
is a Polish relational system (Prs) if:
-
(1) X is a perfect Polish space.
-
(2) Y is analytic in a Polish space Z.
-
(3)
$\sqsubset =\bigcup _{n<\omega }\sqsubset _n$
where
$\langle \sqsubset _n:n<\omega \rangle $
is an (
$\subseteq $
-)increasing sequence of closed subsets of
$X\times Z$
such that for any
$n<\omega $
and any
$y\in Y$
,
$\{x\in X:x\sqsubset _n y\}$
is closed nowhere dense.
When dealing with a Prs, we interpret it depending on the model we are working in.
In the rest of this section,
$\mathbf {R}=\langle X,Y,\sqsubset \rangle $
denotes a Prs.
Definition 2.11. A poset
$\mathbb {P}$
is
$\theta $
-
$\mathbf {R}$
-good if for any
$\mathbb {P}$
-name
$\dot {y}$
for a member of Y, there is a non-empty set
$Y_0\subseteq Y$
of size
$<\theta $
such that for any
$x\in X$
, if x is not met by any
$y\in Y_0$
, then
$\mathbb {P}$
forces x is not met by
$\dot {y}$
. If
$\theta =\aleph _1$
, we say “
$\mathbf {R}$
-good” instead of “
$\aleph _1$
-
$\mathbf {R}$
-good”.
The following two facts show that goodness works well for the “inside” direction of fsi of ccc forcings
Fact 2.12. ([Reference Brendle, Cardona and Mejía4, Corollary 4.10], [Reference Judah and Shelah21]).
Any fsi of ccc
$\theta $
-
$\mathbf {R}$
-good posets is again
$\theta $
-
$\mathbf {R}$
-good.
Fact 2.13. ([Reference Brendle, Cardona and Mejía4, Theorem 4.11], [Reference Fuchino and Mejía14]).
Let
$\mathbb {P}$
be a fsi of non-trivial ccc
$\theta $
-
$\mathbf {R}$
-good posets of length
$\gamma \geq \theta $
. Then,
$\mathbb {P}$
forces
$C_{[\gamma ]^{<\theta }}\preceq _T\mathbf {R}$
.
An example of a good poset is a small one
Fact 2.14. ([Reference Bartoszyński and Judah5, Theorem 6.4.7], [Reference Mejía24, Lemma 4]).
Every poset of size
$<\theta $
is
$\theta $
-
$\mathbf {R}$
-good. In particular, Cohen forcing is
$\mathbf {R}$
-good.
To treat goodness, we have to characterize cardinal invariants using a Prs. While
$\mathbf {D},\mathbf {PR},\mathbf {BPR}$
and
$\mathbf {PR}_g$
are canonically Prs’s, the cardinal invariants on ideals need other characterizations
Example 2.15.
-
(1) For
$k<\omega $
, let
$\mathrm {id}^k\in {\omega }^\omega $
denote the function
$i\mapsto i^k$
for each
$i<\omega $
and let .Let
$\mathcal {S}=\mathcal {S}(\omega ,\mathcal {H})$
be the set of all functions
$\varphi \colon \omega \to [\omega ]^{<\omega }$
such that there is
$h\in \mathcal {H}$
with
$|\varphi (i)|\leq h(i)$
for all
$i<\omega $
. Let
$\mathbf {Lc}^*=\langle {\omega }^\omega ,\mathcal {S},\in ^*\rangle $
be the Prs where
$x\in ^*\varphi :\Leftrightarrow x(n)\in \varphi (n)$
for all but finitely many
$n<\omega $
.As a consequence of [Reference Bartoszynski1],
$\mathbf {Lc}^*\cong _T\mathcal {N}$
holds, so
$\mathfrak {b}(\mathbf {Lc}^*)=\operatorname {\mathrm {add}}(\mathcal {N})$
and
$\mathfrak {d}(\mathbf {Lc}^*)=\operatorname {\mathrm {cof}}(\mathcal {N})$
.Any
$\mu $
-centered poset is
$\mu ^+$
-
$\mathbf {Lc}^*$
-good [Reference Brendle7, Reference Judah and Shelah21].Any Boolean algebra with a strictly positive finitely additive measure is
$\mathbf {Lc}^*$
-good [Reference Kamburelis22]. In particular, so is any subalgebra of random forcing. -
(2) For each
$n<\omega $
, let (endowed with the discrete topology) where
$\mathbf {Lb}_2$
is the standard Lebesgue measure on
$2^\omega $
. Put with the product topology, which is a perfect Polish space. For
$x\in \Omega $
, let , a Borel null set in
$2^\omega $
. Define the Prs where
$x\sqsubset ^{\mathbf {Cn}}z:\Leftrightarrow z\notin N^*_x$
. Since
$\langle N^*_x:x\in \Omega \rangle $
is cofinal in
$\mathcal {N}(2^\omega )$
(the set of all null sets in
$2^\omega $
),
$\mathbf {Cn}\cong _T C_{\mathcal {N}}^\bot $
holds, so
$\mathfrak {b}(\mathbf {Cn})=\operatorname {\mathrm {cov}}(\mathcal {N})$
and
$\mathfrak {d}(\mathbf {Cn})=\operatorname {\mathrm {non}}(\mathcal {N})$
.Any
$\mu $
-centered poset is
$\mu ^+$
-
$\mathbf {Cn}$
-good [Reference Brendle7]. -
(3) Let
and define the Prs where
$x\in ^\bullet f:\Leftrightarrow |\{s\in {2^{<\omega }}:x\supseteq f(s)\}|<\omega $
. Note that
$\mathbf {Mg}\cong _T C_{\mathcal {M}}$
and hence
$\mathfrak {b}(\mathbf {Mg})=\operatorname {\mathrm {non}}(\mathcal {M})$
and
$\mathfrak {d}(\mathbf {Mg})=\operatorname {\mathrm {cov}}(\mathcal {M})$
.
.
(endowed with the discrete topology) where 
with the product topology, which is a perfect Polish space. For 
, a Borel null set in 
where 
and define the Prs 
where 
Summarizing the properties of the “inside” direction and the goodness, we obtain the following corollary, which will be actually applied to the iteration in Section 4
Corollary 2.16. Let
$\mathbb {P}$
be a fsi of ccc forcings of length
$\gamma \geq \theta $
.
-
(1) Assume that each iterand is either:
-
• of size
$<\theta $
, -
• a subalgebra of random forcing, or
-
•
$\sigma $
-centered.
Then,
$\mathbb {P}$
forces
$C_{[\gamma ]^{<\theta }}\preceq _T\mathbf {Lc}^*$
, in particular,
$\operatorname {\mathrm {add}}(\mathcal {N})\leq \theta $
. -
-
(2) Assume that each iterand is either:
-
• of size
$<\theta $
, or -
•
$\sigma $
-centered.
Then,
$\mathbb {P}$
forces
$C_{[\gamma ]^{<\theta }}\preceq _T\mathbf {Cn}$
, in particular,
$\operatorname {\mathrm {cov}}(\mathcal {N})\leq \theta $
. -
-
(3) Assume that each iterand is:
-
• of size
$<\theta $
.
Then,
$\mathbb {P}$
forces
$C_{[\gamma ]^{<\theta }}\preceq _T\mathbf {Mg}$
, in particular,
$\operatorname {\mathrm {non}}(\mathcal {M})\leq \theta $
. -
Remark 2.17. In [Reference Goldstern, Kellner and Shelah19], the “outside” direction is treated by introducing “
$\operatorname {\mathrm {COB}}$
” (short for cone of bounds). For a directed partially ordered set
$(S,\leq _S)$
,
$\operatorname {\mathrm {COB}}(\mathbf {R},\mathbb {P},S)$
stands for “there exists a sequence
$\langle \dot {y}_s:s\in S\rangle $
of
$\mathbb {P}$
-names of responses such that for every
$\mathbb {P}$
-name
$\dot {x}$
of a challenge, there exists
$s\in S$
such that for any
$t\geq _S s$
,
$\Vdash _{\mathbb {P}}\dot {x} \sqsubset \dot {y}_t$
”.
If
$\theta \leq \lambda $
and
$\mathbb {P}$
is ccc, then
$\operatorname {\mathrm {COB}}(\mathbf {R},\mathbb {P},[\lambda ]^{<\theta })$
is equivalent to
$\Vdash _{\mathbb {P}} \mathbf {R}\preceq _T[\lambda ]^{<\theta }\cap V\cong _T[\lambda ]^{<\theta }$
[Reference Cardona and Mejía10, Remark 2.13]. Moreover, if
$\lambda ^{<\theta }=\lambda $
, it is also equivalent to
$\Vdash _{\mathbb {P}} \mathbf {R}\preceq _T C_{[\lambda ]^{<\theta }\cap V}\cong _TC_{[\lambda ]^{<\theta }}$
by Fact 2.8.
Remark 2.18. In [Reference Goldstern, Kellner and Shelah19], the “inside” direction is treated by introducing “
$\operatorname {\mathrm {LCU}}$
” (short for linearly cofinally unbounded). For a limit ordinal
$\gamma $
,
$\operatorname {\mathrm {LCU}}(\mathbf {R},\mathbb {P},\gamma )$
stands for “there exists a sequence
$\langle \dot {x}_\alpha :\alpha <\gamma \rangle $
of
$\mathbb {P}$
-names of challenges such that for every
$\mathbb {P}$
-name
$\dot {y}$
of a response, there exists
$\alpha <\gamma $
such that for any
$\beta \geq \alpha $
,
$\Vdash _{\mathbb {P}}\lnot (\dot {x}_\beta \sqsubset \dot {y})$
”(hence
$\operatorname {\mathrm {LCU}}(\mathbf {R},\mathbb {P},\gamma )\Leftrightarrow \operatorname {\mathrm {COB}}(\mathbf {R}^\bot ,\mathbb {P},(\gamma ,\leq ))$
). If
$\gamma =\lambda $
is a regular cardinal of size
$\geq \theta $
and
$\mathbb {P}$
is ccc, then
$\operatorname {\mathrm {LCU}}(\mathbf {R},\mathbb {P},\gamma )$
is equivalent to
$\Vdash _{\mathbb {P}} C_{[\lambda ]^{<\theta }\cap V}\cong _TC_{[\lambda ]^{<\theta }}\preceq _T\mathbf {R}$
. Moreover, if
$\lambda ^{<\theta }=\lambda $
, it is also equivalent to
$\Vdash _{\mathbb {P}} [\lambda ]^{<\theta }\cap V\cong _T [\lambda ]^{<\theta }\preceq _T\mathbf {R}$
by Fact 2.8.
3 ultrafilter limit and closedness
3.1 General Theory
We basically follow the presentation of [Reference Cardona, Mejía and Uribe-Zapata12] to describe the general theory of (closed-)ultrafilter-limits. Also, the original ideas are already in [Reference Goldstern, Mejía and Shelah20].
Definition 3.1. ([Reference Mejía25, Section 5]).
Let
$\Gamma $
be a class for subsets of posets, i.e.,
$\Gamma \in \prod _{\mathbb {P}}\mathcal {P}(\mathcal {P}(\mathbb {P}))$
, a (class) function. (e.g., 
“centered” is an example of a class for subsets of poset and in this case
$\Gamma (\mathbb {P})$
denotes the set of all centered subsets of
$\mathbb {P}$
for each poset
$\mathbb {P}$
.)
-
• A poset
$\mathbb {P}$
is
$\mu $
-
$\Gamma $
-covered if
$\mathbb {P}$
is a union of
$\leq \mu $
-many subsets in
$\Gamma (\mathbb {P})$
. As usual, when
$\mu =\aleph _0$
, we use “
$\sigma $
-
$\Gamma $
-covered” instead of “
$\aleph _0$
-
$\Gamma $
-covered”. Moreover, we often just say “
$\mu $
-
$\Gamma $
” instead of “
$\mu $
-
$\Gamma $
-covered”. -
• Abusing notation, we write “
$\Gamma \subseteq \Gamma ^\prime $
” if
$\Gamma (\mathbb {P})\subseteq \Gamma ^\prime (\mathbb {P})$
holds for every poset
$\mathbb {P}$
.
In this paper, an “ultrafilter” means a non-principal ultrafilter.
Definition 3.2. Let D be an ultrafilter on
$\omega $
and
$\mathbb {P}$
be a poset.
-
(1)
$Q\subseteq \mathbb {P}$
is D-lim-linked (
$\in \Lambda ^{\mathrm {lim}}_D(\mathbb {P})$
) if there exist a function
$\lim ^D\colon Q^\omega \to \mathbb {P}$
and a
$\mathbb {P}$
-name
$\dot {D}^\prime $
of an ultrafilter extending D such that for any countable sequence
$\bar {q}=\langle q_m:m<\omega \rangle \in Q^\omega $
, (3.1)
$$ \begin{align} \textstyle{\lim^D\bar{q}} \Vdash \{m<\omega:q_m \in \dot{G}\}\in \dot{D}^\prime. \end{align} $$
Moreover, if
$\operatorname {\mathrm {ran}}(\lim ^D)\subseteq Q$
, we say Q is c-D-lim-linked (closed-D-lim-linked,
$\in \Lambda ^{\mathrm {lim}}_{\mathrm {c}D}(\mathbb {P})$
). -
(2) Q is (c-)uf-lim-linked (short for (closed-)ultrafilter-limit-linked) if Q is (c-)D-lim-linked for every ultrafilter D.
-
(3)
and .
and 
. We often say “
$\mathbb {P}$
has (c-)uf-limits” instead of “
$\mathbb {P}$
is
$\sigma $
-(c-)uf-lim-linked”.
Example 3.3. Singletons are c-uf-lim-linked and hence every poset
$\mathbb {P}$
is
$|\mathbb {P}|$
-c-uf-lim-linked.
To define “
$\langle (\mathbb {P}_\xi ,\dot {\mathbb {Q}}_\xi ):\xi <\gamma \rangle $
is a fsi of
$\mu $
-
$\Gamma $
-covered forcings (
$\mu ^+$
-
$\Gamma $
-iteration, below)” in a general way, we have the covering of each iterand
$\dot {\mathbb {Q}}_\xi $
witnessed by some complete subposet
$\mathbb {P}^-_\xi $
of
$\mathbb {P}_\xi $
, not necessarily by
$\mathbb {P}_\xi $
.
Definition 3.4.
-
• A
$\kappa $
-
$\Gamma $
-iteration is a fsi
$\langle (\mathbb {P}_\eta ,\dot {\mathbb {Q}}_\xi ):\eta \leq \gamma ,\xi <\gamma \rangle $
of ccc forcings, with witnesses
$\langle \mathbb {P}_\xi ^-:\xi <\gamma \rangle $
,
$\langle \theta _\xi :\xi <\gamma \rangle $
and
$\langle \dot {Q}_{\xi ,\zeta }:\zeta <\theta _\xi ,\xi <\gamma \rangle $
satisfying for all
$\xi <\gamma $
:-
(1)
$\mathbb {P}^-_\xi \lessdot \mathbb {P}_\xi $
. -
(2)
$\theta _\xi $
is a cardinal of size
$<\kappa $
. -
(3)
$\dot {\mathbb {Q}}_\xi $
and
$\langle \dot {Q}_{\xi ,\zeta }:\zeta <\theta _\xi \rangle $
are
$\mathbb {P}^-_\xi $
-names and
$\mathbb {P}^-_\xi $
forces that
$\bigcup _{\zeta <\theta _\xi }\dot {Q}_{\xi ,\zeta }=\dot {\mathbb {Q}}_\xi $
and
$\dot {Q}_{\xi ,\zeta }\in \Gamma (\dot {\mathbb {Q}}_\xi )$
for each
$\zeta <\theta _\xi $
.
-
-
•
$\xi <\gamma $
is a trivial stage if
$\Vdash _{\mathbb {P}^-_\xi }|\dot {Q}_{\xi ,\zeta }|=1$
for all
$\zeta <\theta _\xi $
.
$S^-$
is the set of all trivial stages and . -
• A guardrail for the iteration is a function
$h\in \prod _{\xi <\gamma }\theta _\xi $
. -
•
$H\subseteq \prod _{\xi <\gamma }\theta _\xi $
is complete if any countable partial function in
$\prod _{\xi <\gamma }\theta _\xi $
is extended to some (total) function in H. -
•
$\mathbb {P}^h_\eta $
is the set of conditions
$p\in \mathbb {P}_\eta $
following h, i.e., for each
$\xi \in \operatorname {\mathrm {dom}}(p)$
,
$p(\xi )$
is a
$\mathbb {P}^-_\xi $
-name and
$\Vdash _{\mathbb {P}^-_\xi }p(\xi )\in \dot {Q}_{\xi ,h(\xi )}$
.
.
The notion “p follows h” only depends on the values of h on
$\operatorname {\mathrm {dom}}(p)$
:
Fact 3.5. Let
$p\in \mathbb {P}^h_\eta $
and assume that a guardrail g satisfies
$g{\mathpunct {\upharpoonright }}\operatorname {\mathrm {dom}}(p)=h{\mathpunct {\upharpoonright }}\operatorname {\mathrm {dom}}(p)$
. Then,
$p\in \mathbb {P}^g_\eta $
.
If every finite partial guardrail can be extended to some
$h\in H$
, in particular if H is complete, then there are densely many conditions which follow some
$h\in H$
:
Lemma 3.6. If every finite partial guardrail can be extended to some
$h\in H$
, then
$\bigcup _{h\in H}\mathbb {P}^h_\eta $
is dense in
$\mathbb {P}_\eta $
for all
$\eta \leq \gamma $
.
Proof. Induction on
$\eta $
.
The following theorem and corollary give a sufficient cardinal arithmetic to have a complete set of guardrails of small size:
Theorem 3.7. ([Reference Engelking and Karłowicz13]).
Let
$\theta \leq \mu \leq \chi $
be infinite cardinals with
$\chi \leq 2^\mu $
. Then, there is
$F\subseteq {^{\chi }\mu }$
of size
$\leq \mu ^{<\theta }$
such that any partial function
$\chi \to \mu $
of size
$<\theta $
can be extended to some (total) function in F.
Corollary 3.8. Assume
$\aleph _1\leq \mu \leq |\gamma |\leq 2^\mu $
and
$\mu ^+=\kappa $
. Then, for any
$\langle \theta _\xi <\kappa :\xi <\gamma \rangle $
, there exists a complete set of guardrails of size
$\leq \mu ^{\aleph _0}$
which works for each
$\kappa $
-
$\Gamma $
-iteration of length
$\gamma $
using
$\langle \theta _\xi :\xi <\gamma \rangle $
.
In this section, let
$\Gamma _{\mathrm {uf}}$
represent
$\Lambda ^{\mathrm {lim}}_{\mathrm {uf}}$
or
$\Lambda ^{\mathrm {lim}}_{\mathrm {cuf}}$
.
Definition 3.9. A
$\kappa $
-
$\Gamma _{\mathrm {uf}}$
-iteration has
$\Gamma _{\mathrm {uf}}$
-limits on H if
-
(1)
$H\subseteq \prod _{\xi <\gamma }\theta _\xi $
is a set of guardrails. -
(2) For
$h\in H$
,
$\langle \dot {D}^h_\xi :\xi \leq \gamma \rangle $
is a sequence such that
$\dot {D}^h_\xi $
is a
$\mathbb {P}_\xi $
-name of a non-principal ultrafilter on
$\omega $
. -
(3) If
$\xi <\eta \leq \gamma $
, then
$\Vdash _{\mathbb {P}_\eta }\dot {D}^h_\xi \subseteq \dot {D}^h_\eta $
. -
(4) For
$ \xi \in S^+$
,
$\Vdash _{\mathbb {P}_\xi } (\dot {D}^h_\xi )^-\in V^{\mathbb {P}^-_\xi }$
where . -
(5) Whenever
$\langle \xi _m:m<\omega \rangle \subseteq \gamma $
and
$\bar {q}=\langle \dot {q}_m:m<\omega \rangle $
satisfying
$\Vdash _{\mathbb {P}^-_{\xi _m}}\dot {q}_m\in \dot {Q}_{\xi _m,h(\xi _m)}$
for each
$m<\omega $
:-
(a) If
$\langle \xi _m:m<\omega \rangle $
is constant with value
$\xi $
, then (3.2)
$$ \begin{align} \Vdash_{\mathbb{P}_\xi}\textstyle{\lim^{(\dot{D}^h_\xi)^-}}\bar{q}\Vdash_{\dot{\mathbb{Q}}_\xi}\{m<\omega:\dot{q}_m\in \dot{H}_\xi\} \in\dot{D}^h_{\xi+1}. \end{align} $$
(
$\dot {H}_\xi $
denotes the canonical name of
$\dot {\mathbb {Q}}_\xi $
-generic filter over
$V^{\mathbb {P}_\xi }$
.) -
(b) If
$\langle \xi _m:m<\omega \rangle $
is strictly increasing, then (3.3)
$$ \begin{align} \Vdash_{\mathbb{P}_\gamma}\{m<\omega:\dot{q}_m\in \dot{G}_\gamma\}\in\dot{D}^h_\gamma. \end{align} $$
-
.
Justification for (3.2) is as follows:
We have:
-
•
$(\dot {D}^h_\xi )^-$
is an ultrafilter in
$ V^{\mathbb {P}^-_\xi }$
by (4). -
•
$\Vdash _{\mathbb {P}^-_\xi }\dot {Q}_{\xi ,h(\xi )}\in \Lambda ^{\mathrm {lim}}_{\mathrm {uf}}(\dot {\mathbb {Q}}_\xi )$
by (3) in Definition 3.4. -
•
$\Vdash _{\mathbb {P}^-_\xi }\dot {q}_m\in \dot {Q}_{\xi ,h(\xi )}$
for all
$m<\omega $
.
Thus, we can consider “
$\lim ^{(\dot {D}^h_\xi )^-}\bar {q}$
” in
$V^{\mathbb {P}^-_\xi }$
and hence in
$V^{\mathbb {P}_\xi }$
. Moreover, abusing notation, we also use “
$\lim ^{(\dot {D}^h_\xi )^-}\bar {q}$
” for a trivial stage
$\xi \in S^-$
to denote the constant value of
$\bar {q}$
. Even though
$(\dot {D}^h_\xi )^-$
is not defined for
$\xi \in S^-$
,
$\lim ^{(\dot {D}^h_\xi )^-}\bar {q}$
works like an ultrafilter-limit since it trivially forces
$\{m<\omega :\dot {q}_m\in \dot {H}_\xi \}=\omega $
, and particularly (3.2) is satisfied as long as
$\dot {D}^h_{\xi +1}$
is an ultrafilter.
Justification for (3.3) is that in the standard way we identify
$\dot {q}_m$
with a condition p in
$\mathbb {P}_\gamma $
defined by 
and 
, so (3.3) is a valid statement.
It seems to be possible to extend the iteration at a successor step by the direct use of the definition of uf-lim-linkedness in Definition 3.2 (actually the purpose of the notion is to realize this successor step), but actually such a simple direct use does not work:
Recall that we are in a slightly complicated situation where there are two models,
$V^{\mathbb {P}_\gamma }$
and
$V^{\mathbb {P}^-_\gamma }$
, and two ultrafilters,
$\dot {D}^h_\gamma \in V^{\mathbb {P}_\gamma }$
and
$(\dot {D}^h_\gamma )^-\in V^{\mathbb {P}^-_\gamma }$
. Hence, the definition of uf-lim-linkedness in Definition 3.2 only helps to extend
$(\dot {D}^h_\gamma )^-$
, not
$\dot {D}^h_\gamma $
, since the statement “
$\dot {Q}_{\gamma ,\zeta }\in \Gamma (\dot {\mathbb {Q}}_\gamma )$
(for each
$\zeta <\theta _\gamma $
)” holds in
$ V^{\mathbb {P}^-_\gamma }$
, not in
$V^{\mathbb {P}_\gamma }$
.
Thus, we need the following lemma which helps to amalgamate ultrafilters:
Lemma 3.10. ([Reference Brendle, Cardona and Mejía3, Lemma 3.20]).
Let
$M\subseteq N$
be transitive models of set theory,
$\mathbb {P}\in M$
be a poset,
$D_0\in M,D_0^\prime \in N$
be ultrafilters and
$\dot {D}_1\in M^{\mathbb {P}}$
be a name of an ultrafilter. If
$D_0\subseteq D_0^\prime $
and
$\Vdash _{M,\mathbb {P}}D_0\subseteq \dot {D}_1$
, then there exists
$\dot {D}_1^\prime \in N^{\mathbb {P}}$
, a name of an ultrafilter such that
$\Vdash _{N,\mathbb {P}}D_0^\prime ,\dot {D}_1\subseteq \dot {D}_1^\prime $
. (Here, we write
$\Vdash _{M,\mathbb {P}}\varphi $
for
$M\vDash (\Vdash _{\mathbb {P}}\varphi )$
).
Proof. It is enough to show that
$\Vdash _{N,\mathbb {P}}\text {"}D_0^\prime \cup \dot {D}_1$
has SFIP”. (SFIP is short for Strong Finite Intersection Property and means “every finite subset has infinite intersection”.) We show that for any
$A\in D_0^\prime $
and any
$\Vdash _{M,\mathbb {P}}\dot {B}\in \dot {D}_1$
,
$\Vdash _{N,\mathbb {P}}A\cap \dot {B}\neq \emptyset $
. Let
$p\in \mathbb {P}$
be arbitrary and 
. Since
$p\Vdash _{M,\mathbb {P}}\dot {B}\subseteq B^\prime $
and
$\Vdash _{M,\mathbb {P}}D_0\subseteq \dot {D}_1$
, we obtain
$B^\prime \in D_0$
. Hence in N, we can find
$c\in A\cap B^\prime $
. Let
$q\leq p$
be a witness of
$c\in B^\prime $
. Note that an N-generic filter G is trivially M-generic as well, so
$q\Vdash _{M,\mathbb {P}}c\in \dot {B}$
implies
$q\Vdash _{N,\mathbb {P}}c\in \dot {B}$
. Thus,
$q\Vdash _{N,\mathbb {P}}c\in A\cap \dot {B}$
and since p is arbitrary, we have
$\Vdash _{N,\mathbb {P}}A\cap \dot {B}\neq \emptyset $
.
Lemma 3.11. Let
$\mathbb {P}_{\gamma +1}$
be a
$\kappa $
-
$\Gamma _{\mathrm {uf}}$
-iteration (of length
$\gamma +1$
) and suppose
$\mathbb {P}_\gamma =\mathbb {P}_{\gamma +1}{\mathpunct {\upharpoonright }}\gamma $
has
$\Gamma _{\mathrm {uf}}$
-limits on H. If
$\gamma \in S^-$
, or if
$\gamma \in S^+$
and:
$$ \begin{align} \Vdash_{\mathbb{P}_\gamma} (\dot{D}^h_\gamma)^-\in V^{\mathbb{P}^-_\gamma}\text{ for all }h\in H, \end{align} $$
then we can find
$\{\dot {D}^h_{\gamma +1}:h\in H\}$
witnessing that
$\mathbb {P}_{\gamma +1}$
has
$\Gamma _{\mathrm {uf}}$
-limits on H.
Proof. If
$\gamma \in S^-$
, any
$\dot {D}^h_{\gamma +1}$
extending
$\dot {D}^h_\gamma $
for
$h\in H$
satisfies (3.2) since every ultrafilter contains
$\omega $
. Thus, we may assume
$\gamma \in S^+$
. By Definition 3.2, for each
$h\in H$
we can find a
$\mathbb {P}^-_\gamma *\dot {\mathbb {Q}}_\gamma $
-name
$\dot {D}^\prime $
of an ultrafilter extending
$(\dot {D}^h_\gamma )^-$
such that for any
$\bar {q}=\langle \dot {q}_m:m<\omega \rangle $
satisfying
$\Vdash _{\mathbb {P}^-_\gamma }\dot {q}_m\in \dot {Q}_{\gamma ,h(\gamma )}$
for all
$m<\omega $
:
$$ \begin{align} \Vdash_{\mathbb{P}^-_\gamma}\textstyle{\lim^{(\dot{D}^h_\gamma)^-}}\bar{q}\Vdash_{\dot{Q}_\gamma}\{m<\omega:\dot{q}_m\in \dot{H}_\gamma\} \in\dot{D}^\prime. \end{align} $$
Since
$(\dot {D}^h_\gamma )^-$
is extended to
$\dot {D}^h_\gamma $
and
$\dot {D}^\prime $
, we can find a
$\mathbb {P}_\gamma *\dot {\mathbb {Q}}_\gamma =\mathbb {P}_{\gamma +1}$
-name
$\dot {D}^h_{\gamma +1}$
of an ultrafilter extending
$\dot {D}^h_\gamma $
and
$\dot {D}^\prime $
by Lemma 3.10. This
$\dot {D}^h_{\gamma +1}$
satisfies (3.2) and we are done.
We give a sufficient condition satisfying the assumption (3.4):
Lemma 3.12. Let
$\mathbb {P}$
be a ccc poset,
$\dot {D}$
a
$\mathbb {P}$
-name of a set of reals,
$\Theta $
a sufficiently large regular cardinal and
$N\preccurlyeq H_\Theta $
a
$\sigma $
-closed submodel containing
$\dot {D}$
, i.e.,
$N^\omega \cup \{\dot {D}\}\subseteq N$
. Then, 
is a complete subposet of
$\mathbb {P}$
and
$\Vdash _{\mathbb {P}}\dot {D}\cap V^{\mathbb {P}^-}\in V^{\mathbb {P}^-}$
.
Proof. Since
$\mathbb {P}$
is ccc and N is
$\sigma $
-closed, N contains all maximal antichains in
$\mathbb {P}^-$
and hence
$\mathbb {P}^-\lessdot \mathbb {P}$
by elementarity. Moreover, we may identify a (nice)
$\mathbb {P}^-$
-name of a real and a (nice)
$\mathbb {P}$
-name of a real in N. Define a
$\mathbb {P}^-$
-name
$\tau $
by
$(\sigma ,p)\in \tau :\Leftrightarrow \sigma $
is a nice
$\mathbb {P}^-$
-name of a real and
$p\in \mathbb {P}^-$
satisfies
$p\Vdash _{\mathbb {P}}\sigma \in \dot {D}$
. We obtain
$\Vdash _{\mathbb {P}}\tau =\dot {D}\cap V^{\mathbb {P}^-}$
and we are done.
Thus, if we are under the assumption of Lemma 3.11 without (3.4), and additionally if
$N\supseteq N^\omega \cup \{\dot {D}^h_\gamma :h\in H\}$
and
$\mathbb {P}^-_\gamma =\mathbb {P}_\gamma \cap N$
, then (3.4) is satisfied by Lemma 3.12.
For the limit step of the construction of the ultrafilters
$\dot {D}^h_\gamma $
, we use centeredness:
Lemma 3.13. Let
$\gamma $
be limit and
$\mathbb {P}_\gamma $
be a
$\kappa $
-
$\left (\Lambda (\mathrm {centered})\cap \Gamma _{\mathrm {uf}}\right ) $
-iteration. If
$\langle \dot {D}^h_\xi :\xi <\gamma , h\in H\rangle $
witnesses that for any
$\xi <\gamma $
,
$\mathbb {P}_\xi =\mathbb {P}_\gamma {\mathpunct {\upharpoonright }}\xi $
has
$\Gamma _{\mathrm {uf}}$
-limits on H, then we can find
$\langle \dot {D}^h_\gamma :h\in H\rangle $
such that
$\langle \dot {D}^h_\xi :\xi \leq \gamma , h\in H\rangle $
witnesses
$\mathbb {P}_\gamma $
has
$\Gamma _{\mathrm {uf}}$
-limits on H.
Proof. For
$\operatorname {\mathrm {cf}}(\gamma )>\omega $
there is nothing to do, so we assume
$\operatorname {\mathrm {cf}}(\gamma )=\omega $
. Let
$h\in H$
be arbitrary and S be the collection of
$\bar {q}=\langle \dot {q}_m:m<\omega \rangle $
such that for some increasing
$\langle \xi _m<\gamma :m<\omega \rangle $
,
$\Vdash _{\mathbb {P}^-_{\xi _m}}\dot {q}_m\in \dot {Q}_{\xi _m,h(\xi _m)}$
holds for each
$m<\omega $
(Note that
$\xi _m\to \gamma $
since
$\xi _m$
are increasing and
$\operatorname {\mathrm {cf}}(\gamma )=\omega $
). For
$\bar {q}\in S$
, let 
. We will show:
$$ \begin{align} \Vdash_{\mathbb{P}_\gamma}\text{"}\bigcup_{\xi<\gamma}\dot{D}^h_\xi\cup\{\dot{A}(\bar{q}):\bar{q}\in S\}\text{ has SFIP}\text{"}. \end{align} $$
If not, there exist
$p\in \mathbb {P}_\gamma $
,
$\xi <\gamma $
,
$\mathbb {P}_\xi $
-name
$\dot {A}$
of an element of
$\dot {D}^h_\xi $
,
$\{\bar {q}^i=\langle \dot {q}^i_m:m<\omega \rangle :i<n\}\in [S]^{<\omega }$
and increasing ordinals
$\langle \xi _m^i<\gamma :m<\omega \rangle $
for
$i<n$
such that
$\Vdash _{\mathbb {P}^-_{\xi ^i_m}}\dot {q}_m^i\in \dot {Q}_{\xi ^i_m,h(\xi ^i_m)}$
holds for
$m<\omega $
and
$i<n$
and the following holds:
$$ \begin{align} p\Vdash_{\mathbb{P}_\gamma}\dot{A}\cap \bigcap_{i<n} \dot{A}(\bar{q}^i)=\emptyset. \end{align} $$
We may assume that
$p\in \mathbb {P}_\xi $
. Since all
$\langle \xi ^i_m<\gamma :m<\omega \rangle $
are increasing and converge to
$\gamma $
, there is
$m_0<\omega $
such that
$\xi _m^i>\xi $
for any
$m>m_0$
and
$i<n$
. By Induction Hypothesis,
$p\Vdash _{\mathbb {P}_\xi }\text {"}\dot {D}^h_\xi $
is an ultrafilter” and hence we can pick
$q\leq _{\mathbb {P}_\xi } p$
and
$m>m_0$
such that
$q\Vdash _{\mathbb {P}_\xi }m\in \dot {A}$
. Let us reorder
$\{\xi _m^i:i<n\}=\{\xi ^0<\cdots <\xi ^{l-1}\}$
. Inducting on
$j<l$
, we construct
$q_j\in \mathbb {P}_{\xi _j}$
. Let 
and
$j<l$
and assume we have constructed
$q_{j-1}$
. Let 
. Since
$\mathbb {P}_{\xi ^j}$
forces that all
$\dot {q}^i_m$
for
$i\in I_j$
are in the same centered component
$\dot {Q}_{\xi ^j,h(\xi ^j)}$
, we can pick
$p_j\leq q_{j-1}$
in
$\mathbb {P}_{\xi ^j}$
and a
$\mathbb {P}_{\xi ^j}$
-name
$\dot {q}_j$
of a condition in
$\dot {\mathbb {Q}}_{\xi ^j}$
such that for each
$i\in I_j$
,
$p_j\Vdash _{\mathbb {P}_{\xi ^j}}\dot {q}_j\leq \dot {q}^i_m$
. Let 
. By construction, 
satisfies
$q^\prime \leq q\leq p$
and
$q^\prime {\mathpunct {\upharpoonright }}\xi _m^i\Vdash _{\mathbb {P}_{\xi _m}} q^\prime (\xi _m^i)\leq \dot {q}^i_m$
for all
$i<n$
, so in particular,
$q^\prime \Vdash _{\mathbb {P}_\gamma }m\in \dot {A}\cap \bigcap _{i<n} \dot {A}(\bar {q}^i)$
, which contradicts (3.7).
3.2 Uniform
$\Delta $
-system
From now on, we always assume
$\mathbb {P}_\gamma $
is a
$\kappa $
-
$\Gamma _{\mathrm {uf}}$
-iteration with
$\Gamma _{\mathrm {uf}}$
-limits on H. To define ultrafilter-limits for “refined” sequences of conditions in
$\mathbb {P}_\gamma $
, we introduce the notion of uniform
$\Delta $
-system, which is a more refined
$\Delta $
-system of conditions in
$\mathbb {P}^h_\gamma $
(see [Reference Uribe-Zapata27, Definition 4.3.19]):
Definition 3.14. Let
$\delta $
be an ordinal,
$h\in H$
and
$\bar {p}=\langle p_ m: m<\delta \rangle \in (\mathbb {P}_\gamma ^h)^\delta $
.
$\bar {p}$
is an h-uniform
$\Delta $
-system if:
-
(1)
$\{\operatorname {\mathrm {dom}}(p_ m): m<\delta \}$
forms a
$\Delta $
-system with some root
$\nabla $
. -
(2) All
$|\operatorname {\mathrm {dom}}(p_ m)|$
are the same
$n^\prime $
and
$\operatorname {\mathrm {dom}}(p_ m)=\{\alpha _{n, m}:n<n^\prime \}$
is the increasing enumeration. -
(3) There is
$r^\prime \subseteq n^\prime $
such that
$n\in r^\prime \Leftrightarrow \alpha _{n, m}\in \nabla $
for
$n<n^\prime $
. -
(4) For
$n\in n^\prime \setminus r^\prime $
,
$\langle \alpha _{n, m}: m<\delta \rangle $
is (strictly) increasing.
$\Delta $
-System Lemma for this uniform
$\Delta $
-system also holds:
Lemma 3.15. ([Reference Uribe-Zapata27, Theorem 4.3.20]).
Assume that
$\theta>|H|$
is regular and
$\{p_m:m<\theta \}\subseteq \bigcup _{h\in H}\mathbb {P}^h_\gamma $
. Then, there exist
$I\in [\theta ]^\theta $
and
$h\in H$
such that
$\{p_m:m\in I\}$
forms an h-uniform
$\Delta $
-system.
Proof. Almost direct from
$\Delta $
-System Lemma. (see e.g., [Reference Uribe-Zapata27, Theorem 4.3.20]).
Definition 3.16. Let
$\bar {p}=\langle p_m:m<\omega \rangle \in (\mathbb {P}^h_\gamma )^\omega $
be an h-uniform (countable)
$\Delta $
-system with root
$\nabla $
. We define the limit condition
$p^\infty =\lim ^h\bar {p}\in \mathbb {P}_\gamma $
as follows:
-
(1)
. -
(2) For
$\xi \in \nabla $
,
$\Vdash _{\mathbb {P}^-_\xi }p^\infty (\xi ):=\lim ^{(\dot {D}^h_\xi )^-}\langle p_m(\xi ):m<\omega \rangle $
.
.
The ultrafilter limit condition forces that ultrafilter many conditions are in the generic filter
Lemma 3.17.
$\lim ^h\bar {p}\Vdash _{\mathbb {P}_\gamma }\{m<\omega :p_m\in \dot {G}_\gamma \}\in \dot {D}^h_\gamma $
.
Proof. Induct on
$\gamma $
.
$\textit {Successor step.}$
Let
$\bar {p}=\langle (p_m,\dot {q}_m):m<\omega \rangle \in (\mathbb {P}^h_{\gamma +1})^\omega $
be an h-uniform
$\Delta $
-system with root
$\nabla $
. To avoid triviality, we may assume that
$\gamma \in \nabla $
. Also we may assume that
$\Vdash _{\mathbb {P}^-_\gamma }\dot {q}_m\in \dot {Q}_{\gamma ,h(\gamma )}$
for each
$m<\omega $
. Let 
and 
. By Induction Hypothesis, 
. By (3.2), 
Thus,
$\lim ^h\bar {p}=p^\infty *\dot {q}^\infty \Vdash _{\mathbb {P}_{\gamma +1}}\{m<\omega :(p_m,\dot {q}_m)\in \dot {G}_\gamma *\dot {H}_\gamma \}\supseteq \dot {A}\cap \dot {B}\in \dot {D}^h_{\gamma +1}$
.
$\textit {Limit step.}$
Let
$\gamma $
be limit and
$\bar {p}=\langle p_m:m<\omega \rangle \in (\mathbb {P}^h_\gamma )^\omega $
be an h uniform-
$\Delta $
-system. We use the same parameters as in Definition 3.14. Let 
and 
. Since
$\bar {p}{\mathpunct {\upharpoonright }}\xi $
is also an h-uniform
$\Delta $
-system with root
$\nabla $
, 
. By Induction Hypothesis, 
. Let 
. Since
$\langle \alpha _{n,m}:m<\omega \rangle $
is increasing for
$n\in \left [n^{\prime \prime },n^\prime \right )$
, by (3.3), 
for
$n\in \left [n^{\prime \prime },n^\prime \right )$
. Since
$\operatorname {\mathrm {dom}}(p_m)=\operatorname {\mathrm {dom}}(p{\mathpunct {\upharpoonright }}\xi )\cup \{\alpha _{n,m}:n\in \left [n^{\prime \prime },n^\prime \right )\}$
,
$p^\infty \Vdash _{\mathbb {P}_\gamma }\{m<\omega :p_m\in \dot {G}_\gamma \}=\dot {A}\cap \bigcap _{n\in \left [n^{\prime \prime },n^\prime \right )} \dot {B}_n\in \dot {D}^h_\gamma $
.
Corollary 3.18. Let
$\bar {p}=\langle p_m :m<\omega \rangle $
,
$h\in H$
and
$p^\infty =\lim ^h\bar {p}$
as above and let
$\varphi $
be a formula of the forcing language without parameter m. If all
$p_m$
force
$\varphi $
, then
$p^\infty $
also forces
$\varphi $
.
Proof. Let G be any generic filter containing
$p^\infty $
. By Lemma 3.17, in particular, there exists
$p_m\in G$
. Since
$p_m$
forces
$\varphi $
,
$V[G]\vDash \varphi $
and recall that G is arbitrary containing
$p^\infty $
.
The following lemma is specific for
$\Lambda ^{\mathrm {lim}}_{\mathrm {cuf}}$
and actually this is why we consider the notion of closedness
Lemma 3.19. Consider the case
$\Gamma _{\mathrm {uf}}=\Lambda ^{\mathrm {lim}}_{\mathrm {cuf}}$
. If
$\bar {p}\in (\mathbb {P}^h_\gamma )^\omega $
, then
$\lim ^h\bar {p}\in \mathbb {P}^h_\gamma $
.
3.3 Application to bounding-prediction
To control cardinal invariants using a
$\kappa $
-
$\Gamma _{\mathrm {uf}}$
-iteration
$\mathbb {P}_\gamma $
with
$\Gamma _{\mathrm {uf}}$
-limits, it is useful to iterate Cohen forcings in the first half of the iteration. For this purpose, we assume the following in this subsection
Assumption 3.20.
-
(1)
$\kappa <\lambda $
are uncountable regular cardinals and
$\gamma =\lambda +\lambda $
. -
(2)
$\mathbb {P}_\gamma $
is a
$\Gamma _{\mathrm {uf}}$
-iteration with
$\Gamma _{\mathrm {uf}}$
-limits on H (with the same parameters as in Definition 3.4 and 3.9). -
(3) H is complete and
$|H|<\kappa $
. -
(4) For
$\xi <\lambda $
,
$\Vdash _{\mathbb {P}^-_\xi }\dot {\mathbb {Q}}_\xi =\mathbb {C}$
, the Cohen forcing. Note that
$\mathbb {C}$
is
$\kappa $
-
$\Gamma _{\mathrm {uf}}$
-linked by Example 3.3.
As mentioned above, in [Reference Goldstern, Mejía and Shelah20] they introduced the notion of ultrafilter-limits to keep the bounding number
$\mathfrak {b}$
small through the iteration and separated the left side of Cichoń’s diagram. This is described as follows using the notions we have already defined above
Theorem 3.21. ([Reference Goldstern, Kellner and Shelah19, Lemma 1.31], [Reference Goldstern, Mejía and Shelah20, Main Lemma 4.6]).
Consider the case
$\Gamma _{\mathrm {uf}}=\Lambda ^{\mathrm {lim}}_{\mathrm {uf}}$
. Then,
$\mathbb {P}_\gamma $
forces
$C_{[\lambda ]^{<\kappa }}\preceq _T \mathbf {D}$
, in particular,
$\mathfrak {b}\leq \kappa $
.
Remark 3.22. Note that in Theorem 3.21 and Main Lemma 3.26 below, we do not require centeredness. The justification is that while we need centeredness when constructing a
$\kappa $
-
$\Gamma _{\mathrm {uf}}$
-iteration
$\mathbb {P}_\gamma $
with
$\Gamma _{\mathrm {uf}}$
-limits at limit steps (see Lemma 3.13), after having constructed the iteration we do not need centeredness anymore in the argument itself of controlling cardinal invariants. The reason why we state the theorem and the main lemma in the current way is related to Question 5.4 in Section 5, in order to clarify where the problem discussed in the question lies.
We shall carry out a similar argument for closed-ultrafilter-limits to keep
${\mathfrak {e}^*}$
small, using the lemmas in the previous subsection, which are specific for this new limit notion. First, we introduce some notation on the bounding-prediction.
Definition 3.23. For a predictor
$\pi =(A,\langle \pi _k:k\in A \rangle )\in \operatorname {\mathrm {Pred}}$
and
$f\in {\omega }^\omega $
, we write
$f\sqsubset ^{\mathrm {bp}}_n \pi $
if
$f(k)\leq \pi _k(f{\mathpunct {\upharpoonright }} k)$
for all
$k\geq n$
in A. Note that
$\sqsubset ^{\mathrm {bp}}=\bigcup _{n<\omega }\sqsubset ^{\mathrm {bp}}_n $
(see Definition and Fact 2.2) and we say n is a starting point of
$f\sqsubset ^{\mathrm {bp}}\pi $
if
$f\sqsubset ^{\mathrm {bp}}_n \pi $
holds (we do not require the minimality of such n).
By applying the general theory of (c-)uf-limit to bounding-prediction, we can exclude a possible prediction point and preserve the information of the initial segment of predicted reals
Lemma 3.24. Let
$\dot {\pi }=(\dot {A},\langle \dot {\pi }_k:k\in \dot {A}\rangle )$
be a
$\mathbb {P}_\gamma $
-name of a predictor,
$n^*\leq j<\omega $
,
$t\in \omega ^{j-1}$
and
$\bar {p}=\langle p_m:m<\omega \rangle $
be an h-uniform
$\Delta $
-system.
Assume that each
$p_m$
forces:
$$ \begin{align} \text{there is }c\in{\omega}^\omega\text{such that }c{\mathpunct{\upharpoonright}} j=t^\frown m\text{ and }c\sqsubset^{\mathrm{bp}}_{n^*}\dot{\pi}. \end{align} $$
Then,
$\lim ^h\bar {p}$
forces:
$$ \begin{align} j-1\notin\dot{A}\text{, and} \end{align} $$
$$ \begin{align} \text{there is }c\in{\omega}^\omega\text{ such that }c{\mathpunct{\upharpoonright}} (j-1)=t\text{ and }c\sqsubset^{\mathrm{bp}}_{n^*}\dot{\pi}. \end{align} $$
Proof. Let G be any generic filter containing 
and work in
$V[G]$
. By Lemma 3.17, 
. Let
$c_m\in {\omega }^\omega $
be a witness of (3.8) for each
$m\in M$
.
If
$j-1\in \dot {A}[G]$
, then
$c_m(j-1)=m\leq \dot {\pi }[G](c_m{\mathpunct {\upharpoonright }} (j-1))=\dot {\pi }[G](t)$
for each
$m\in M$
, which contradicts that
$M\in \dot {D}^h[G]$
is infinite and
$\dot {\pi }[G](t)$
is a natural number. Thus,
$j-1\notin \dot {A}[G]$
and since G is arbitrary containing
$p^\infty $
, we obtain (3.9). (3.10) is direct from Corollary 3.18.
Remark 3.25. This proof highlights the difference between bounding prediction and g-prediction for
$g\in (\omega \setminus 2)^\omega $
since in the case of g-prediction, we cannot consider such infinitely many
$p_m$
. Indeed, the forcing poset
$\mathbb {PR}_g$
(defined later) has closed-ultrafilter-limits and increases
$\mathfrak {e}_g$
and hence the limits actually do not keep
$\mathfrak {e}_g$
small.
Lemma 3.24 tells us one limit condition excludes one possible prediction point and preserves the information of shorter initial segments of predicted reals. Thus, the strategy to prove Main Lemma 3.26 below, which states that closed-ultrafilter-limits keep
${\mathfrak {e}^*}$
small, is as follows:
-
(1) Assume the negation of the conclusion towards contradiction.
-
(2) By a
$\Delta $
-system argument and arranging Cohen reals (as witnesses of c in Lemma 3.24), satisfy the assumption of Lemma 3.24. -
(3) Taking limits infinitely many times (guaranteed by Lemma 3.19) in some suitable order, exclude potential elements of
$\dot {A}$
“downwards” and ultimately obtain a condition for each j which excludes the points between
$n^*$
and j. -
(4) Finally, take the limit of the ultimate conditions and exclude points “upwards” (
$j\to \infty $
), i.e., almost all points, which contradicts that there are infinitely many prediction points.
Main Lemma 3.26. Consider the case
$\Gamma _{\mathrm {uf}}=\Lambda ^{\mathrm {lim}}_{\mathrm {cuf}}$
. Then,
$\mathbb {P}_\gamma $
forces
$C_{[\lambda ]^{<\kappa }}\preceq _T \mathbf {BPR}$
, in particular,
$\mathfrak {e}\leq {\mathfrak {e}^*}\leq \kappa $
.
Proof. Let 
be Cohen reals (as members of
${\omega }^\omega $
) added in the first
$\lambda $
stages. We shall show that
$\bar {c}$
witnesses Fact 2.7(2), an equivalent condition of
$C_{[\lambda ]^{<\kappa }}\preceq _T \mathbf {BPR}$
.
Assume towards contradiction that there exist a condition
$p\in \mathbb {P}_\gamma $
and a
$\mathbb {P}_\gamma $
-name of a predictor
$\dot {\pi }=(\dot {A},\langle \dot {\pi }_k:k\in \dot {A}\rangle )$
such that
$p\Vdash \dot {c}_\beta \sqsubset ^{\mathrm {bp}} \dot {\pi }\text { for } \kappa \text {-many }\dot {c}_\beta $
. In particular, for each
$i<\kappa $
we can pick
$p_i\leq p$
,
$\beta _i<\lambda $
and
$n_i<\omega $
such that
$\beta _i\geq i$
and
$ p_i\Vdash \dot {c}_{\beta _i}\sqsubset ^{\mathrm {bp}}_{n_i}\dot {\pi }$
. By extending and thinning, we may assume:
-
(1)
$\beta _i\in \operatorname {\mathrm {dom}}(p_i)$
. (By extending
$p_i$
.) -
(2) All
$ p_i$
follow a common guardrail
$h\in H$
. (
$|H|<\kappa $
.) -
(3)
$\{p_i:i<\kappa \}$
forms a uniform
$\Delta $
-system with root
$\nabla $
. (By Lemma 3.15.) -
(4)
$\beta _i\notin \nabla $
, hence all
$\beta _i$
are distinct. (Since
$\beta _i\geq i$
,
$\beta _i$
are eventually out of the finite set
$\nabla $
.) -
(5) All
$n_i$
are equal to
$ n^*$
. -
(6) All
$p_i(\beta _i)$
are the same Cohen condition
$s\in \omega ^{<\omega }$
. -
(7)
$|s|=n^*$
. (By extending s or increasing
$n^*$
.)
In particular, we have that:
$$ \begin{align} \text{For each }i<\kappa, p_i\text{ forces }\dot{c}_{\beta_i}{\mathpunct{\upharpoonright}} n^*=s\text{ and }\dot{c}_{\beta_i}\sqsubset^{\mathrm{bp}}_{n^*}\dot{\pi}. \end{align} $$
Pick the first
$\omega $
many
$p_i$
and fix some bijection
$i\colon \omega ^{<\omega }\to \omega $
. Fix any
$n<\omega $
. (For simplicity, we assume
$n\geq 3$
). For each
$\sigma \in \omega ^n$
, define
$q_\sigma \leq p_{i(\sigma )}$
by extending the
$\beta _{i(\sigma )}$
-th position
$q_\sigma (\beta _{i(\sigma )}):=s^\frown \sigma $
. By (3.11), we have:
$$ \begin{align} \text{For each }\sigma\in\omega^{<\omega}, q_\sigma\text{ forces }\dot{c}_{\beta_{i(\sigma)}}{\mathpunct{\upharpoonright}}(n^*+n)=s^\frown\sigma\text{ and }\dot{c}_{\beta_{i(\sigma)}}\sqsubset^{\mathrm{bp}}_{n^*}\dot{\pi}. \end{align} $$
Fix
$\tau \in \omega ^{n-1}$
and we consider the sequence 
. When defining
$q_\sigma $
we changed the
$\beta _{i(\sigma )}$
-th position which is out of
$\nabla $
, so
$\{q_{\tau ^\frown m}:m<\omega \}$
forms a uniform
$\Delta $
-system with root
$\nabla $
, following some new countable partial guardrail
$h^\prime $
. Since H is complete,
$h^\prime $
is extended to some
$h_\tau \in H$
. Note that
$$ \begin{align} h_\tau{\mathpunct{\upharpoonright}}\nabla=h^\prime{\mathpunct{\upharpoonright}}\nabla=h{\mathpunct{\upharpoonright}}\nabla. \end{align} $$
Let
$q^\infty _\tau :=\lim ^{h_\tau }\bar {q}_\tau $
.
By Lemma 3.19,
$q^\infty _\tau $
follows
$h_\tau $
and by Definition 3.16,
$\operatorname {\mathrm {dom}}(q^\infty _\tau )=\nabla $
. Thus, by (3.13) and Fact 3.5,
$q^\infty _\tau $
also follows h. By (3.12), each
$q_{\tau ^\frown m}$
forces that:
$$ \begin{align} \text{there exists }c\in{\omega}^\omega\text{ such that } c{\mathpunct{\upharpoonright}}(n^*+n)=s^\frown\tau^\frown m\text{ and }c\sqsubset^{\mathrm{bp}}_{n^*}\dot{\pi}. \end{align} $$
Thus, we are under the assumption of Lemma 3.24 and hence obtain:
$$ \begin{align} q^\infty_\tau\text{ forces } n^*+n-1\notin\dot{A}\text{ and }\varphi_\tau, \end{align} $$
where:
$$ \begin{align} \varphi_\tau:\equiv\text{"there exists }c\in{\omega}^\omega\text{ such that } c{\mathpunct{\upharpoonright}}(n^*+n-1)=s^\frown\tau\text{ and }c\sqsubset^{\mathrm{bp}}_{n^*}\dot{\pi}\text{".} \end{align} $$
Unfix
$\tau $
and fix
$\rho \in \omega ^{n-2}$
. We consider the sequence 
. Since all
$q^\infty _{\rho ^\frown m}$
follow h and have domain
$\nabla $
, they form a uniform
$\Delta $
-system with root
$\nabla $
and have a limit
$q^\infty _\rho :=\lim ^h\bar {q}_\rho $
. Similarly, we have that
$\operatorname {\mathrm {dom}}(q^\infty _\rho )=\nabla $
and
$q^\infty _\rho $
follows h. Note that each
$q^\infty _{\rho ^\frown m}$
forces
$n^*+n-1\notin \dot {A}$
and
$\varphi _{\rho ^\frown m}$
. Thus, we are under the assumption of Lemma 3.24 and hence obtain that
$q^\infty _\rho $
forces:
-
•
$n^*+n-1\notin \dot {A}$
. -
•
$n^*+n-2\notin \dot {A}$
. -
•
$\text {there exists }c\in {\omega }^\omega \text { such that }c{\mathpunct {\upharpoonright }}(n^*+n-2)=s^\frown \rho \text { and }c\sqsubset ^{\mathrm {bp}}_{n^*}\dot {\pi }$
.
(The first item is direct from Corollary 3.18.) Continuing this way, we ultimately obtain 
with the following properties:
-
•
$\operatorname {\mathrm {dom}}(q^n)=\nabla $
and
$q^n$
follows h (hence they form an h-uniform
$\Delta $
-system). -
•
$q^n$
forces
$ \left [n^*,n^*+n\right ) \cap \dot {A}=\emptyset $
.
Finally, unfix n and let
$q^\infty $
be the limit condition of the ultimate conditions
$q^\infty :=\lim ^h\langle q^n:n<\omega \rangle $
.
$q^\infty $
forces that for infinitely many
$n<\omega $
,
$\left [n^*,n^*+n\right ) \cap \dot {A}=\emptyset $
, which contradicts that
$\dot {A}$
is infinite.
Remark 3.27. The tricks of the proof are as follows:
-
• By quantifying over c, we succeeded to define
$\varphi _\tau $
without parameter m and apply Lemma 3.24. -
• By using the intervals
$\left [n^*,n^*+n\right )$
, we succeeded to capture the infinite set
$\dot {A}$
.
3.4 Forcing-free characterization and concrete forcing notions
We introduce a forcing-free characterization of “
$Q\subseteq \mathbb {P}$
is (c-)uf-lim-linked”:
Lemma 3.28. Let D be an ultrafilter on
$\omega $
,
$\mathbb {P}$
a poset,
$Q\subseteq \mathbb {P}$
,
$\lim ^D\colon Q^\omega \to \mathbb {P}$
. Then, the following are equivalent:
-
(1)
$\lim ^D$
witnesses Q is D-lim-linked. -
(2)
$\lim ^D$
satisfies
$(\star )_n$
below for all
$n<\omega $
$$ \begin{align*} (\star)_n:& \text{"Given }\bar{q}^j=\langle q_m^j:m<\omega\rangle\in Q^\omega\text{ for }j<n\text{ and }r\leq\textstyle{\lim^D}\bar{q}^j\text{ for all }j<n,\\ &\text{then }\{m<\omega:r \text{ and all }q_m^j \text{ for } j<n \text{ have a common extension}\}\in D\text{"}. \end{align*} $$
Proof.
$(1)\Rightarrow (2)$
: Let
$\dot {D}$
be the
$\mathbb {P}$
-name of an ultrafilter extending D as in Definition 3.2. Then, r forces:
Thus, we have
$B\in D$
since B is in the ground model.
$(2)\Rightarrow (1)$
: For
$\bar {q}=\langle q_m:m<\omega \rangle \in Q^\omega $
, let 
. We show
$\Vdash _{\mathbb {P}}\text {"} D\cup \{\dot {A}(\bar {q}):\bar {q}\in Q^\omega \cap V,~\lim ^D\bar {q}\in \dot {G}\}$
has SFIP”. If not, there exist
$r\in \mathbb {P}$
,
$A\in D$
,
$n<\omega $
and
$\bar {q}^j=\langle q_m^j:m<\omega \rangle \in Q^\omega $
satisfying
$r\Vdash \lim ^D\bar {q}^j\in \dot {G}$
for
$j<n$
, such that
$r\Vdash A\cap \bigcap _{j<n}\dot {A}(\bar {q}^j)=\emptyset $
. We may assume that
$r\leq \lim ^D\bar {q}^j$
for all
$j<n$
. By
$(\star )_n$
, we can find some
$m\in A$
and
$\tilde {r}\leq r$
extending all
$q^j_m$
. Thus,
$\tilde r\Vdash m\in A\cap \bigcap _{j<n}\dot {A}(\bar {q}^j)$
, which is a contradiction. Hence, we can take a name of an ultrafilter
$\dot {D}^\prime $
extending
$D\cup \{\dot {A}(\bar {q}):\bar {q}\in Q^\omega \cap V,~\lim ^D\bar {q}\in \dot {G}\}$
. Let
$\bar {q}=\langle q_m:m<\omega \rangle \in Q^\omega $
be arbitrary. Since
$\lim ^D\bar {q}\Vdash \lim ^D\bar {q}\in \dot {G}$
trivially holds,
$\lim ^D\bar {q}\Vdash \dot {A}(\bar {q})=\{m<\omega :q_m\in \dot {G}\}\in \dot {D}^\prime $
is obtained and we are done.
This characterization in Lemma 3.28 enables us to investigate whether a poset
$\mathbb {P}$
has ultrafilter-limits without considering forcings. Note that the closedness can be easily checked, since the conditions (1) and (2) in Lemma 3.28 share the same witness
$\lim ^D$
.
Using this characterization, we show that some concrete forcing notions have ultrafilter-limits.
Lemma 3.29. ([Reference Goldstern, Kellner and Shelah19]).
Eventually different forcing
$\mathbb {E}$
has ultrafilter-limits, where
$\mathbb {E}$
is defined as follows in this paper:
-
•
. -
•
$(s^\prime ,k^\prime ,\varphi ^\prime )\le (s,k,\varphi )$
if
$s^\prime \supseteq s$
,
$k^\prime \ge k$
,
$\varphi ^\prime (i) \supseteq \varphi (i)$
for all
$i<\omega $
and
$s^\prime (i)\notin \varphi (i)$
for all
$i\in \operatorname {\mathrm {dom}}(s^\prime \setminus s)$
.
.
Proof. For
$s\in \omega ^{<\omega }$
and
$k<\omega $
, let 
. We show 
is uf-lim-linked. Let D be any ultrafilter and define
$\lim ^D\colon Q^\omega \to Q$
,
$\bar {q}=\langle q_m=(s,k,\varphi _m):m<\omega \rangle \mapsto (s,k,\varphi ^\infty )$
as follows:
$$\begin{align*}j\in \varphi_\infty(i) \Leftrightarrow \{ m<\omega: j\in \varphi_m(i)\}\in D. \end{align*}$$
We check first
$(\star )_1$
and then
$(\star )_n$
for
$n\geq 2$
(
$(\star )_0$
trivially holds).
The case
$(\star )_1$
: Assume that
$\bar {q}=\langle q_m:m<\omega \rangle \in Q^\omega $
and
$r\leq \lim ^D\bar {q}$
. Let
$r=(s^\prime ,k^\prime ,\varphi ^\prime )$
and
$\lim ^D\bar {q}=(s,k,\varphi ^\infty )$
. Since
$r\leq \lim ^D\bar {q}$
,
$s^\prime (i)\notin \varphi _\infty (i)$
for all
$i\in \operatorname {\mathrm {dom}}(s^\prime \setminus s)$
. That is,
$\{m<\omega :s^\prime (i)\in \varphi _m(i)\}\notin D$
. Since D is an ultrafilter,
$A^i :=\{m: s^\prime (i)\notin \varphi _m(i)\}\in D$
for
$i\in \operatorname {\mathrm {dom}}(s^\prime \setminus s)$
. Let 
and for
$m\in A$
,
$s^\prime (i)\notin \varphi _m(i)$
for all
$i\in \operatorname {\mathrm {dom}}(s^\prime \setminus s)$
. Thus,
$q_m$
is compatible with r.
The case
$(\star )_n$
: Suppose that:
-
•
$n\geq 2$
and
$\bar {q}^j=\langle q_m^j:m<\omega \rangle \in Q^\omega $
for
$j<n$
, -
•
$r\leq \lim ^D\bar {q}^j$
for all
$j<n$
By
$(\star )_1$
, 
. Let
$m\in A$
and define
$r=(s^\prime ,k^\prime ,\varphi ^\prime )$
and
$q^j_m=(s,k,\varphi ^j_m)$
. Since
$s^\prime \supseteq s$
,
$k^\prime \ge k$
and r and
$q_m^j$
are compatible, the condition 
extends r and all
$q_m^j$
for
$j<n$
where 
for each
$i<\omega $
. Thus, A witnesses
$(\star )_n$
holds.
Corollary 3.30.
$\mathbb {E}$
is
$\sigma $
-
$\left ( \Lambda (\text {centered})\cap \Lambda ^{\mathrm {lim}}_{\mathrm {cuf}}\right ) $
-covered.
Proof.
Q in the previous proof is centered and the limit function
$\lim ^D$
is closed in Q.
The next example of a forcing notion with ultrafilter-limits is g-prediction forcing
$\mathbb {PR}_g$
, which generically adds a g-predictor and hence increases
$\mathfrak {e}_g$
, introduced in [Reference Brendle8]Footnote
3
.
Definition 3.31. Fix
$g\in \left (\omega +1\setminus 2\right )^\omega $
. g-prediction forcing
$\mathbb {PR}_g$
consists of tuples
$(d,\pi ,F)$
satisfying:
-
(1)
$d\in {2^{<\omega }}$
. -
(2)
$\pi =\langle \pi _n:n\in d^{-1}(\{1\})\rangle $
. -
(3) for each
$n\in d^{-1}(\{1\})$
,
$\pi _n$
is a finite partial function of
$\prod _{k<n}g(k)\to g(n)$
. -
(4)
$F\in [\prod _{n<\omega }g(n)]^{<\omega }$
-
(5) for each
$f,f^\prime \in F, f{\mathpunct {\upharpoonright }}|d|=f^\prime {\mathpunct {\upharpoonright }}|d|$
implies
$f=f^\prime $
.
$(d^\prime ,\pi ^\prime ,F^\prime )\leq (d,\pi ,F)$
if:
-
(i)
$d^\prime \supseteq d$
. -
(ii)
$\forall n\in d^{-1}(\{1\}), \pi _n^\prime \supseteq \pi _n$
. -
(iii)
$F^\prime \supseteq F$
. -
(iv) For all
$ n\in (d^\prime )^{-1}(\{1\})\setminus d^{-1}(\{1\})$
and
$f\in F$
, we have
$f{\mathpunct {\upharpoonright }} n\in \operatorname {\mathrm {dom}}(\pi ^\prime _n)$
and
$\pi ^\prime _n(f{\mathpunct {\upharpoonright }} n)=f(n)$
.
When
$g(n)=\omega $
for all
$n<\omega $
, we write
$\mathbb {PR}$
instead of
$\mathbb {PR}_g$
and just call it “prediction forcing”.
We introduce a useful notation
Definition 3.32. For
$N<\omega $
, let 
be the sequence of length N whose values are all
$0$
. Namely, 
.
Lemma 3.33. ([Reference Brendle and Shelah9]).
$\mathbb {PR}_g$
has ultrafilter-limits for any
$g\in \left (\omega +1\setminus 2\right )^\omega $
. If
$g\in \left (\omega \setminus 2\right )^\omega $
, then
$\mathbb {PR}_g$
has closed-ultrafilter-limits.
Proof. Fix
$k<\omega $
,
$d,\pi $
and
$f^*=\{f^*_l\in \omega ^{|d|}:l<k\}$
where each
$f^*_l$
is different. Let
$Q\subseteq \mathbb {PR}_g$
consist of every
$(d^\prime ,\pi ^\prime ,F^\prime )$
such that
$d^\prime =d, \pi ^\prime =\pi $
and
$F^\prime =\{f^\prime _l:l<k\})$
where
$f^\prime _l{\mathpunct {\upharpoonright }}|d|=f^*_l$
for all
$l<k$
. It is enough to show that Q is uf-lim-linked. Let D be any ultrafilter. For
$\bar {f}=\langle f^i\in {\omega }^\omega :i<\omega \rangle $
, if
$\bar {f}$
satisfies that for each
$n<\omega $
, there (uniquely) exists
$a_n<\omega $
such that
$\{i<\omega :f^i(n)=a_n\}\in D$
, we define
$\bar {f}^\infty \in {\omega }^\omega $
by
$ \bar {f}^\infty (n)=a_n$
for each
$n<\omega $
. Note that
${\bar {f}}^\infty $
is always defined if
$g\in \left (\omega \setminus 2\right )^\omega $
.
For
$\bar {q}=\langle q_m=(d,\pi ,\{f^m_l:l<k\})\in \mathbb {PR}:m<\omega \rangle \in Q^\omega $
, define
$\lim ^D\bar {q}$
as follows:
-
•
, . -
•
. -
• For
$l\in B$
, let
$n_l$
be the first
$n<\omega $
where no
$a<\omega $
satisfies:
$\{m<\omega :f^m_l(n)=a\}\in D$
(hence
$n_l\geq |d|$
). -
•
(if
$B=\emptyset $
, ). -
•
. -
•
.
, 
.
.
(if 
).
.
.To see
$\lim ^D\bar {q}$
is a condition, it is enough to show that any
$\bar {f}_l^\infty ,\bar {f}_{l^\prime }^\infty \in F^\infty $
with
$\bar {f}_l^\infty {\mathpunct {\upharpoonright }}|d^\infty |=\bar {f}_{l^\prime }^\infty {\mathpunct {\upharpoonright }}|d^\infty |$
satisfies
$\bar {f}_l^\infty =\bar {f}_{l^\prime }^\infty $
. Since
$f^*_l=\bar {f}_{l}^\infty {\mathpunct {\upharpoonright }}|d|=\bar {f}_{l^\prime }^\infty {\mathpunct {\upharpoonright }}|d|=f^*_{l^\prime }$
, we have
$l=l^\prime $
and hence
$\lim ^D\bar {q}$
is a valid condition.
Note that if
$g\in \left (\omega \setminus 2\right )^\omega $
, then
$A=k, B=\emptyset , n^\infty =|d|, d^\infty =d$
and hence
$\lim ^D\bar {q}\in Q$
(for any D).
So, it is enough to show that
$\lim ^D$
satisfies
$(\star )_n$
for
$n<\omega $
. We check first
$(\star )_n$
for
$n\geq 2$
assuming
$(\star )_1$
and then
$(\star )_1$
since the former is easier to show.
The case
$(\star )_n$
: Assuming
$(\star )_1$
, suppose that:
-
•
$n\geq 2$
and
$\bar {q}^j=\langle q_m^j:m<\omega \rangle \in Q^\omega $
for
$j<n$
, -
•
$r\leq \lim ^D\bar {q}^j$
for all
$j<n$
By
$(\star )_1$
, 
. Let
$m\in A$
and put
$r=(d^\prime ,\pi ^\prime ,F^\prime )$
and
$q^j_m=(d,\pi ,F^j_m)$
. Then, the condition 
extends r and all
$q_m^j$
for
$j<n$
where N is large enough to satisfy that any distinct functions in
$F^\prime \cup \bigcup _{i<n}F_i$
have different values before
$|d^\prime |+N$
(hence
$\tilde {r}$
is a condition and hereafter we use “N is large enough” in this sense).
The case
$(\star )_1$
: Assume that
$\bar {q}=\langle q_m:m<\omega \rangle \in Q^\omega $
and
$r\leq \lim ^D\bar {q}=(d^\infty ,\pi ,F^\infty )$
. Let 
and 
.
Fix
$l\in A$
and
$n\in \mathrm {New}$
. By the definition of
$\bar {f}_l^\infty $
, 
. Along with
$r\leq \lim ^D\bar {q}$
, for
$m\in X_0$
,
$\pi ^r_n(f^m_l{\mathpunct {\upharpoonright }} n)=\bar {f}_l^\infty (n)=f^m_l(n)$
.
Unfixing l and n, we have:
Fix
$l\in B$
and
$n\in \mathrm {New}$
. Let 
. Since
$l\in B$
, 
. Since
$n_l<n^\infty \leq n$
, for all
$m\in X_2, f^m_l{\mathpunct {\upharpoonright }} n\notin \operatorname {\mathrm {dom}}(\pi ^r_n)$
. Unfixing l and n, we have:
It is enough to show that for all
$m\in X_1\cap X_3$
,
$q_m$
and r are compatible. Fix such m and define (as a common extension of
$q_m$
and r) 
as follows:
-
•
. -
•
where N is large enough. -
• For all
$n\in (d^r)^{-1}(\{1\}), \pi ^\prime _n\supseteq \pi ^r_n$
and for all
$l\in B$
and
$n\in \mathrm {New}, \pi ^\prime _n(f^m_l{\mathpunct {\upharpoonright }} n)=f^m_l(n)$
(This can be done by (3.18)).
.
where N is large enough.
$q^\prime \leq r$
trivially holds since
$(d^\prime )^{-1}(\{1\})\setminus (d^r)^{-1}(\{1\})=\emptyset $
.
To see
$q^\prime \leq q_m$
, we have to show:
$$ \begin{align} \text{For all } l<k \text{ and } n\in(d^r)^{-1}(\{1\})\setminus (d)^{-1}(\{1\}), \pi^\prime_n(f^m_l{\mathpunct{\upharpoonright}} n)=f^m_l(n). \end{align} $$
If
$l\in A$
, (3.17) implies (3.19), while if
$l\in B$
, (3.19) holds by the definition of
$\pi ^\prime $
.
Corollary 3.34.
$\mathbb {PR}_g$
is
$\sigma $
-
$\left ( \Lambda (\text {centered})\cap \Lambda ^{\mathrm {lim}}_{\mathrm {uf}}\right ) $
-covered. Moreover, if
$g\in (\omega \setminus 2)^\omega $
,
$\mathbb {PR}_g$
is
$\sigma $
-
$\left ( \Lambda (\text {centered})\cap \Lambda ^{\mathrm {lim}}_{\mathrm {cuf}}\right )$
-covered.
Proof.
Q in the previous proof is centered since any finitely many conditions
$\{(d,\pi ,F_i)\in Q:i<n\}$
have a common extension 
where N is large enough.
4 Separation
4.1 Separation of the left side
We are ready to prove the main theorem, Cichoń’s maximum with evasion number. We roughly follow the flow of the original construction of Cichoń’s maximum in [Reference Goldstern, Kellner and Shelah19] and [Reference Goldstern, Kellner, Mejía and Shelah18], i.e., we first separate the left side of the diagram by performing a fsi and then the right side by submodel method introduced in [Reference Goldstern, Kellner, Mejía and Shelah18].
Definition 4.1.
-
•
, the Cohen forcing. -
•
and , the Amoeba forcing. -
•
and , the random forcing. -
•
and , the Hechler forcing. -
•
, and . -
•
and .
, the Cohen forcing.
and 
, the Amoeba forcing.
and 
, the random forcing.
and 
, the Hechler forcing.
, 
and 
.
and 
.Let 
and 
be the index sets.
Hence, 
is the poset which increases 
for each 
. Also note that
$\mathbf {R}_4^*\preceq _T\mathbf {R}_4$
.
Assumption 4.2.
-
(1)
$\lambda _1<\cdots <\lambda _6$
are regular uncountable cardinals. -
(2)
$\lambda _3=\mu _3^+$
and
$\lambda _4=\mu _4^+$
are successor cardinals and
$\mu _3$
is regular. -
(3)
implies for all . -
(4)
$\lambda _6^{<\lambda _5}=\lambda _6$
, hence for all .
implies 
for all 
.
for all 
.Lemma 4.3. Every ccc poset forces 
for any 
.
Thus, we often identify the four relational systems in Lemma 4.3 in this section.
To satisfy Assumption 3.20, we define the following
Definition 4.4. Put 
, 
, 
, the length of the iteration we shall perform. Fix some cofinal partition
$S_1\cup \cdots \cup S_5=\gamma \setminus S_0$
and for
$\xi <\gamma $
, let 
denote the unique 
such that 
.
We additionally assume the following cardinal arithmetic to obtain a complete set of guardrails
Assumption 4.5.
$\lambda _6\leq 2^{\mu _3}$
.
Lemma 4.6. There exist complete sets H and
$H^\prime $
of guardrails of length
$\gamma $
for
$\lambda _3$
-
$\Lambda ^{\mathrm {lim}}_{\mathrm {uf}}$
-iteration of size
$<\lambda _3$
and
$\lambda _4$
-
$\Lambda ^{\mathrm {lim}}_{\mathrm {cuf}}$
-iteration of size
$<\lambda _4$
, respectively.
Construction 4.7. We can construct a ccc finite support iteration 
of length
$\gamma $
satisfying the following items:
-
(1)
is a
$\lambda _3$
-
$\Lambda ^{\mathrm {lim}}_{\mathrm {uf}}$
-iteration and has
$\Lambda ^{\mathrm {lim}}_{\mathrm {uf}}$
-limits on H with the following witnesses:-
•
$\langle \mathbb {P}_\xi ^-:\xi <\gamma \rangle $
, the complete subposets witnessing
$\Lambda ^{\mathrm {lim}}_{\mathrm {uf}}$
-linkedness. -
•
$\bar {Q}=\langle \dot {Q}_{\xi ,\zeta }:\zeta <\theta _\xi ,\xi <\gamma \rangle $
, the
$\Lambda ^{\mathrm {lim}}_{\mathrm {uf}}$
-linked components. -
•
$\bar {D}=\langle \dot {D}^h_\xi :\xi \leq \gamma ,~h\in H \rangle $
, the ultrafilters. -
•
, the trivial stages and , the non trivial stages.
-
-
(2)
is also a
$\lambda _4$
-
$\Lambda ^{\mathrm {lim}}_{\mathrm {cuf}}$
-iteration and has
$\Lambda ^{\mathrm {lim}}_{\mathrm {cuf}}$
-limits on
$H^\prime $
with the following witnesses:-
•
$\langle \mathbb {P}_\xi ^-:\xi <\gamma \rangle $
, the (same as above) complete subposets witnessing
$\Lambda ^{\mathrm {lim}}_{\mathrm {cuf}}$
-linkedness. -
•
$\bar {R}=\langle \dot {R}_{\xi ,\zeta }:\zeta <\theta _\xi ,\xi <\gamma \rangle $
, the
$\Lambda ^{\mathrm {lim}}_{\mathrm {cuf}}$
-linked components. -
•
$\langle \dot {E}^{h^\prime }_\xi :\xi \leq \gamma ,~h^\prime \in H^\prime \rangle $
, the ultrafilters. -
•
, the trivial stages and , the non-trivial stages.
-
-
(3) For each
$\xi \in \gamma \setminus S_0$
,
$N_\xi \preccurlyeq H_\Theta $
is a submodel where
$\Theta $
is a sufficiently large regular cardinal satisfying:-
(a)
. -
(b)
$N_\xi $
is
$\sigma $
-closed, i.e.,
$(N_\xi )^\omega \subseteq N_\xi $
. -
(c) For any
,
$\eta <\gamma $
and set of (nice names of) reals A in
$V^{\mathbb {P}_\eta }$
of size , there is some (above
$\eta $
) such that
$A\subseteq N_\xi $
. -
(d) If
, then
$\{\dot {D}^h_\xi :h\in H \}\subseteq N_\xi $
. -
(e) If
, then
$\{\dot {D}^h_\xi :h\in H \},\{\dot {E}^{h^\prime }_\xi :h^\prime \in H^\prime \}\subseteq N_\xi $
.
-
-
(4) For
$\xi \in S_0$
, and for
$\xi \in \gamma \setminus S_0$
, (since
$\mathbb {P}_\xi $
is ccc and
$N_\xi $
is
$\sigma $
-closed,
$\mathbb {P}_\xi ^-\lessdot \mathbb {P}_\xi $
). -
(5) For each
$\xi <\gamma $
, .(Here,
does not denote a forcing poset in the ground model, but denotes the poset interpreted in the
$\mathbb {P}^-_\xi $
-extension. Also note that holds since there are at most -many reals in the
$\mathbb {P}^-_\xi $
-extension. Moreover, for
$\xi \in S_0$
,
$\dot {\mathbb {Q}}_\xi $
is always (forced to be) the same Cohen forcing
$\mathbb {C}$
.) -
(6)
$\bar {Q}$
and
$\bar {R}$
are determined in the canonical way: In the case of
$\bar {Q}$
, if , split
$\dot {\mathbb {Q}}_\xi $
into singletons and if , split the
$\sigma $
-
$\Lambda ^{\mathrm {lim}}_{\mathrm {uf}}$
-linked iterand
$\dot {\mathbb {Q}}_\xi $
into the
$\omega $
-many
$\Lambda ^{\mathrm {lim}}_{\mathrm {uf}}$
-linked components. In the case of
$\bar {R}$
, do it similarly.
is a 
, the trivial stages and 
, the non trivial stages.
is also a 
, the trivial stages and 
, the non-trivial stages.
.
, 
, there is some 
(above 
, then 
, then 
and for 
(since 
.
does not denote a forcing poset in the ground model, but denotes the poset interpreted in the 
holds since there are at most 
-many reals in the 
, split 
, split the 
We explain why the construction is possible:
Successor step. At stage
$\xi (\geq \lambda )$
, we can take some
$N_\xi $
satisfying Construction 4.7(3), by Assumption 4.2(3) for Construction 4.7(3)(3b) and by Assumption 4.2 (4) for Construction 4.7(3)(3c), the bookkeeping condition. By Lemma 3.11, Corollary 3.30 and Corollary 3.34, we obtain suitable
$\{\dot {D}^h_{\xi +1}:h\in H \}$
and
$\{\dot {E}^{h^\prime }_{\xi +1}:h^\prime \in H^\prime \}$
(including the case 
): E.g., consider the most complicated case 
. Since
$\xi \in S^+$
,
$(\dot {D}^h_\xi )^-=\dot {D}^h_\xi \cap V^{\mathbb {P}_\xi ^-}$
and
$\dot {D}^h_\xi \in N_\xi $
. Hence by Lemma 3.12,
$(\dot {D}^h_\xi )^-\in V^{\mathbb {P}^-_\xi }$
holds. Thus, the assumption (3.4) for
$\dot {D}^h_\xi $
is satisfied and since
$\xi \in T^-$
, Lemma 3.11 can be applied for both
$\dot {D}^h_\xi $
and
$\dot {E}^{h^\prime }_\xi $
. The other cases are similar and simpler: If 
, then
$\xi $
is trivial for both
$\bar {D}$
and
$\bar {E}$
. If 
, then
$\xi $
is non-trivial for both, but
$\{\dot {D}^h_\xi :h\in H \},\{\dot {E}^{h^\prime }_\xi :h^\prime \in H^\prime \}\subseteq N_\xi $
. Hence, Lemma 3.11 can be applied in any case.
Limit step. Direct from Lemma 3.13, Corollary 3.30, and Corollary 3.34.
Thus, we can perform the iteration construction.
Theorem 4.8.
forces for each 
, 
, in particular, 
and 
(the same things also hold for
$\mathbf {R}_4^*$
) (see Figure 7).
Figure 7 Constellation of 
and 
.
Proof. Fact 2.7 and Construction 4.7 (3)(3c) imply 
for all 
.
For 
and
$5$
, applying Corollary 2.16 with 
, we obtain 
.
For 
, Theorem 3.21 implies
$C_{[\lambda _6]^{<\lambda _3}}\preceq _T\mathbf {R}_3$
.
For 
, Main Lemma 3.26 implies
$C_{[\lambda _6]^{<\lambda _4}}\preceq _T\mathbf {R}_4^*\preceq _T\mathbf {R}_4$
.
4.2 Recovery of GCH
To apply the submodel method to separate the right side, we actually need some cardinal arithmetic (see [Reference Goldstern, Kellner, Mejía and Shelah18], [Reference Cardona and Mejía10]), which is satisfied (particularly) under GCH, but conflicts with Assumption 4.5, which we have used for the completeness of the sets H and
$H^\prime $
of guardrails. To avoid the conflict, we shall reconstruct the iteration under GCH. The idea is as follows: By considering some extension model where Assumption 4.5 is satisfied, we construct 
there. At the same time, we mimic the construction in the ground model and obtain an iteration 
(in the ground model), which actually forces the same separation. While the argument of recovering GCH is already described in [Reference Goldstern, Kellner and Shelah19], we give an explanation below for the sake of completenessFootnote
4
.
Assume GCH hereafter and Assumption 4.2.
Construction 4.9. We shall construct a fsi 
and submodels
$\langle N_\xi :\xi \in \gamma \setminus S_0\rangle $
such that 
for
$\xi \in S_0$
and for
$\xi \in \gamma \setminus S_0$
:
-
(1)
. -
(2)
$N_\xi $
is
$\sigma $
-closed. -
(3) For any
,
$\eta <\gamma $
and set of (nice names of) reals A in
$V^{\mathbb {P}_\eta }$
of size , there is some (above
$\eta $
) such that
$A\subseteq N_\xi $
. -
(4)
where .
.
, 
, there is some 
(above 
where 
. Let 
. Since
$\mu _3$
is regular,
$\mathbb {S}$
is
$<\mu _3$
-closed and since
$\mu _3^{<\mu _3}=\mu _3$
(by GCH), it is
$\mu _3^+$
-cc (by standard
$\Delta $
-system argument). Note that it forces
$2^{\mu _3}=\lambda _6$
and hence Assumption 4.5 is satisfied in the
$\mathbb {S}$
-extension (and so is Assumption 4.2). Hence, Construction 4.7 and Theorem 4.8 hold in the
$\mathbb {S}$
-extension, even if
$H_\Theta $
is replaced with 
(Since
$\Theta $
is sufficiently large, M contains all we shall require even in the
$\mathbb {S}$
-extention. Hereafter whenever considering Construction 4.7 in the
$\mathbb {S}$
-extension, we assume this replacement).
We explain why Construction 4.9 is possible. We inductively construct 
in the ground model and 
in the
$\mathbb {S}$
-extension simultaneously, both of which share the same
$\bar {N}=\langle N_\xi :\xi \in \gamma \setminus S_0\rangle $
. Note that since
$\mathbb {S}$
is
$<\mu _3$
-closed and
$\mu _3^+$
-cc, 
is cofinal in 
for all 
, (
$\mathbb {R}$
denotes the (same) set of all reals) and hence the bookkeeping conditions are the same. Assume that
$\xi \in \gamma \setminus S_0$
and we have constructed in the ground model
$\langle N_\eta :\eta \in \xi \setminus S_0\rangle $
and in the
$\mathbb {S}$
-extension all objects of 
with parameters
$\eta <\xi $
. If 
, since what we require for
$N_\xi $
are the same, we can pick some
$N_\xi $
which is suitable for both of the constructions. If 
, in the
$\mathbb {S}$
-extension
$N_\xi $
has to contain names of ultrafilters which are only in the extension. We first obtain an
$\mathbb {S}$
-name
$\dot {N}^0_\xi $
with the suitable properties in Construction 4.7(3). Since
$\Vdash _{\mathbb {S}} \dot {N}^0_\xi \subseteq M\subseteq V $
and
$\mathbb {S}$
is
$\mu _3^+$
-cc, we can obtain (in the ground model) a
$\sigma $
-closed submodel
$N^1_\xi \supseteq \dot {N}^0_\xi $
of size 
. Again getting into the
$\mathbb {S}$
-extension, we obtain a (
$\mathbb {S}$
-name of)
$\sigma $
-closed submodel
$\dot {N}^2_\xi \supseteq N_\xi ^1$
of size 
with the suitable properties in Construction 4.7(3). Again, in the ground model, we can obtain a
$\sigma $
-closed submodel
$N^3_\xi \supseteq \dot {N}^2_\xi $
of size 
. Continuing this way
$\omega _1$
-many times (At limit steps, take the union of all the previous (names of) submodels.), we ultimately obtain 
in the ground model, which satisfies the suitable properties in the
$\mathbb {S}$
-extension. In the extension, 
and 
are essentially the same since they share the same
$\bar {N}$
, which determines their structures.
We show that 
also forces the consequence of Theorem 4.8. By a bookkeeping argument, 
holds for each 
. For 
and
$5$
, we similarly obtain 
. For 
by Fact 2.7, it is enough to show that the first
$\lambda _6$
-many Cohen reals
$\langle \dot {c}_\beta :\beta <\lambda _6\rangle $
witness that every response
$\dot {y}$
meets only 
-many
$\dot {c}_\beta $
. Given such a 
-name
$\dot {y}$
, working in the
$\mathbb {S}$
-extension and interpreting
$\dot {y}$
as a 
-name, we obtain some 
such that for any
$\beta \in \lambda _6\setminus B$
,
$\dot {c}_\beta $
is not met by
$\dot {y}$
. Since
$\mathbb {S}$
is
$\mu _3^+$
-cc, we can find such B in the ground model. Now, for any
$\beta \in \lambda _6\setminus B$
, 
“
$\dot {c}_\beta $
is not met by
$\dot {y}$
” and by absoluteness, 
“
$\dot {c}_\beta $
is not met by
$\dot {y}$
” and we are done. Hence we obtain the following theorem
Theorem 4.10. Assume GCH and Assumption 4.2. Then, there exists a ccc poset 
which forces for each 
, 
, in particular, 
and 
(the same things also hold for
$\mathbf {R}_4^*$
).
4.3 Separation of the right side
Thanks to Theorem 4.10, we are now in the situation where we can apply the submodel method, which was introduced in [Reference Goldstern, Kellner, Mejía and Shelah18] and enables us to separate the right side of the diagram.
Theorem 4.11. Assume GCH and
$\aleph _1\leq \theta _1\leq \cdots \leq \theta _{10}$
are regular and
$\theta _{\mathfrak {c}}$
is an infinite cardinal such that
$\theta _{\mathfrak {c}}\geq \theta _{10}$
and
$\theta _{\mathfrak {c}}^{\aleph _0}=\theta _{\mathfrak {c}}$
. Then, there exists a ccc poset 
which forces 
and 
for each 
(the same things also hold for
$\mathbf {R}_4^*$
) and
$\mathfrak {c}=\theta _{\mathfrak {c}}$
(see Figure 8).
Figure 8 Constellation of 
.
Proof. See [Reference Goldstern, Kellner, Mejía and Shelah18].
4.4 Controlling
$\mathfrak {e}_{ubd}$
Toward the proof of Theorem Theorem C, where g-prediction (Definition 1.2) is treated in the separation, let us consider
$\mathfrak {e}_g$
for
$g\in (\omega \setminus 2)^\omega $
.
Definition 4.12.
for
$g\in (\omega \setminus 2)^\omega $
.
By Corollary 3.34, the poset
$\mathbb {PR}_g$
, which increases
$\mathfrak {e}_g$
, is
$\sigma $
-c-uf-lim-linked. Thus, performing an iteration where the
$\sigma $
-c-uf-lim-linked forcing
$\mathbb {E}$
is replaced with
$\mathbb {PR}_g$
and where g runs through all
$g\in (\omega \setminus 2)^\omega $
by bookkeeping, we obtain the following:
Theorem 4.13. (Corresponding to Theorem 4.10, the construction of ).
). Assume GCH and Assumption 4.2. Then, there exists a ccc poset 
which forces for each 
, 
, in particular, 
and 
(the same things also hold for
$\mathbf {R}_4^*$
and
$\mathbf {R}_5^g$
for
$g\in (\omega \setminus 2)^\omega $
).
Theorem 4.14. (Corresponding to Theorem 4.11, the construction of ).
). Assume GCH and
$\aleph _1\leq \theta _1\leq \cdots \leq \theta _{10}$
are regular and
$\theta _{\mathfrak {c}}$
is infinite cardinal such that
$\theta _{\mathfrak {c}}\geq \theta _{10}$
and
$\theta _{\mathfrak {c}}^{\aleph _0}=\theta _{\mathfrak {c}}$
. Then, there exists a ccc poset 
which forces 
and 
for each 
(the same things also hold for
$\mathbf {R}_4^*$
and
$\mathbf {R}_5^g$
for
$g\in (\omega \setminus 2)^\omega $
) and
$\mathfrak {c}=\theta _{\mathfrak {c}}$
(see Figure 9).
Figure 9 Constellation of
$\mathbb {P}^\prime _{\mathrm {fin}}$
.
5 Questions
Question 5.1. Are there other cardinal invariants which are not below
${\mathfrak {e}^*}$
and kept small through forcings with closed-ultrafilter-limits?
In the left side of Cichoń’s diagram, many cardinal invariants are either below
${\mathfrak {e}^*}$
or above
$\mathfrak {e}_{ubd}$
(hence closed-ultrafilter-limits do not keep them small) and a remaining candidate is
$\operatorname {\mathrm {cov}}(\mathcal {N})$
. However, not only it is unclear whether c-uf-limits keep it small, but also even if they did, it would be unclear whether there would be an application since most of the known forcings with c-uf-limits are either
$\sigma $
-centered or sub-random, which keep
$\operatorname {\mathrm {cov}}(\mathcal {N})$
small without resorting to c-uf-limits.
Question 5.2. Can the closedness argument in Main Lemma 3.26 be generalized to some fact such as “closed-Fr-Knaster posets preserve strongly
$\kappa $
-
$\mathbf {PR}^*$
-unbounded families from the ground model” described in [Reference Brendle, Cardona and Mejía3]?
The fact that ultrafilter limits keep
$\mathfrak {b}$
small (Theorem 3.21) is generalized to the fact “For regular uncountable
$\kappa $
,
$\kappa $
-Fr-Knaster posets preserve strongly
$\kappa $
-
$\mathbf {D}$
-unbounded families from the ground model” [Reference Brendle, Cardona and Mejía3, Theorem 3.12], where:
-
• Fr denotes the following linkedness notion: “
$Q\subseteq \mathbb {P}$
is Fr-linked if there is
$\lim \colon Q^\omega \to \mathbb {P}$
such that
$\lim \langle q_m\rangle _{m<\omega }\Vdash _{\mathbb {P}} |\{m<\omega :q_m\in \dot {G}\}|=\omega $
for any
$\langle q_m\rangle _{m<\omega }\in Q^\omega $
”, -
• a
$\kappa $
-Fr-Knaster poset is a poset such that any family of conditions of size
$\kappa $
has a Fr-linked subfamily of size
$\kappa $
, and -
• a strongly
$\kappa $
-
$\mathbf {D}$
-unbounded family is a family of size
$\geq \kappa $
such that any real can only dominate
$<\kappa $
-many reals in the family.
We are naturally interested in the possibility of this kind of generalization for closed-ultrafilter-limits. However, the proof of Main Lemma 3.26 basically depends on the freedom to arrange the initial segment of Cohen reals, and it seems to be hard to reflect the freedom to the reals in the ground model.
Question 5.3. In addition to Theorem 4.14 (Figure 9), can we separate
$\mathfrak {e}$
and
${\mathfrak {e}^*}$
(and the dual numbers
$\mathfrak {pr}$
and
${\mathfrak {pr}^*}$
)?
In fact, even the consistency of
$\max \{\mathfrak {e},\mathfrak {b}\}<{\mathfrak {e}^*}$
is not known (
$\mathfrak {e}<{\mathfrak {e}^*}$
and
$\mathfrak {b}<{\mathfrak {e}^*}$
are known to be consistent: Brendle [Reference Brendle8] proved the consistency of
$\mathfrak {e}<\mathfrak {b}(\leq {\mathfrak {e}^*})$
, while he and Shelah [Reference Brendle and Shelah9] proved that of
$\mathfrak {b}<\mathfrak {e}(\leq {\mathfrak {e}^*})$
. Also, the latter is obtained as a corollary of Theorem 4.11.). We can naively define a poset
$\mathbb {PR}^*$
which generically adds a bounding-predictor and hence increase
${\mathfrak {e}^*}$
, by changing the Definition 3.31 (iv) to “For all
$ n\in (d^\prime )^{-1}(\{1\})\setminus d^{-1}(\{1\})$
and
$f\in F$
, we have
$f{\mathpunct {\upharpoonright }} n\in \operatorname {\mathrm {dom}}(\pi ^\prime _n)$
and
$\pi ^\prime _n(f{\mathpunct {\upharpoonright }} n)=f(n)$
”. We can also show that
$\mathbb {PR}^*$
has ultrafilter-limits by a similar proof to that of Lemma 3.33 and hence it keeps
$\mathfrak {b}$
small. However, it is unclear whether it also keeps
$\mathfrak {e}$
small.
Question 5.4. Can we additionally separate
$\mathfrak {e}_{ubd}$
and
$\operatorname {\mathrm {non}}(\mathcal {M})$
(and the dual numbers
$\mathfrak {pr}_{ubd}$
and
$\operatorname {\mathrm {cov}}(\mathcal {M})$
)?
This question has a deep background.
After the first construction of Cichoń’s maximum in [Reference Goldstern, Kellner and Shelah19], Kellner, Shelah, and Tănasie [Reference Kellner, Shelah and Tănasie23] constructedFootnote
5
Cichoń’s maximum for another order illustrated in Figure 10, introducing the FAM-limit
Footnote
6
method, which focuses on (and actually is short for) finitely additive measures on
$\omega $
and keeps the bounding number
$\mathfrak {b}$
small as the ultrafilter-limit does.
Figure 10 Cichoń’s maximum constructed in [Reference Kellner, Shelah and Tănasie23]. Compared with the original one in [Reference Goldstern, Kellner and Shelah19] (Figure 2),
$\mathfrak {b}$
and
$\operatorname {\mathrm {cov}}(\mathcal {N})$
,
$\mathfrak {d}$
and
$\operatorname {\mathrm {non}}(\mathcal {N})$
are exchanged.
Later, Goldstern, Kellner, Mejía, and Shelah [Reference Goldstern, Kellner, Mejía and Shelah17] proved that the FAM-limit keeps the evasion number
$\mathfrak {e}$
small. Recently, Uribe-Zapata [Reference Uribe-Zapata27] formalized the theory of the FAM-limits and he, Cardona and Mejía generalized the result above as follows:
Theorem 5.5 [Reference Cardona, Mejía and Uribe-Zapata11].
FAM-limits keep
$\operatorname {\mathrm {non}}(\mathcal {E})$
small.
$\mathcal {E}$
denotes the
$\sigma $
-ideal generated by closed null sets and the four numbers related to the ideal
$\mathcal {E}$
have the relationship illustrated in Figure 11 (Bartoszynski and Shelah [Reference Bartoszynski and Shelah2, Theorem 3.1] proved
$\operatorname {\mathrm {add}}(\mathcal {E})=\operatorname {\mathrm {non}}(\mathcal {M})$
and
$\operatorname {\mathrm {cof}}(\mathcal {E})=\operatorname {\mathrm {cof}}(\mathcal {M})$
. The other new arrows are obtained by easy observations: e.g., a g-predictor predicts only
$F_\sigma $
null many reals and hence
$\mathfrak {e}_{ubd}\leq \operatorname {\mathrm {non}}(\mathcal {E})$
and
$\operatorname {\mathrm {cov}}(\mathcal {E})\leq \mathfrak {pr}_{ubd}$
hold). Hence, FAM-limits seem to work for Question 5.4 by keeping
$\operatorname {\mathrm {non}}(\mathcal {E})$
and
$\mathfrak {e}_{ubd}$
small.
Figure 11 Cichoń’s diagram and other cardinal invariants.
In [Reference Kellner, Shelah and Tănasie23], they also introduced the poset
$\widetilde {\mathbb {E}}$
instead of
$\mathbb {E}$
, which increases
$\operatorname {\mathrm {non}}(\mathcal {M})$
as
$\mathbb {E}$
does, but has FAM-limits, which
$\mathbb {E}$
does not have. (Cardona, Mejía, and Uribe-Zapata [Reference Cardona, Mejía and Uribe-Zapata11] proved that
$\mathbb {E}$
increases
$\operatorname {\mathrm {non}}(\mathcal {E})$
and hence does not have FAM-limits.) Thus, if
$\widetilde {\mathbb {E}}$
also had closed-ultrafilter-limits, by mixing all the three limit methods as in Theorem 4.11 and 4.14, it would seem to be possible to additionally separate
$\mathfrak {e}_{ubd}$
and
$\operatorname {\mathrm {non}}(\mathcal {M})$
by replacing
$\mathbb {E}$
with
$\widetilde {\mathbb {E}}$
through the iteration. In fact, Goldstern, Kellner, Mejía, and Shelah [Reference Goldstern, Kellner, Mejía and Shelah17] proved that
$\widetilde {\mathbb {E}}$
actually has (closed-)ultrafilter-limits.
However, recall that when constructing the names of ultrafilters at limit steps in the proof of Lemma 3.13, we resorted to the centeredness, which
$\widetilde {\mathbb {E}}$
does not have. We have no idea on how to overcome this problem without resorting to centerednessFootnote
7
.
Acknowledgments
The author thanks his supervisor Jörg Brendle for his invaluable comments and Diego A. Mejía for his helpful advice. The author is also grateful to the anonymous referee for his/her corrections and suggestions.
Funding
This work was supported by JST SPRING, Japan (Grant No. JPMJSP2148).
