Hostname: page-component-745bb68f8f-grxwn Total loading time: 0 Render date: 2025-02-11T18:43:20.881Z Has data issue: false hasContentIssue false
  • English
  • Français

Powers of the ideal of Lebesgue measure zero sets

Published online by Cambridge University Press:  12 March 2014

Maxim R. Burke
Maxim R. Burke*
Affiliation:
Department of Mathematics, University of California, Berkeley, California 94720
Get access Rights & Permissions [Opens in a new window]

Abstract

We investigate the cofinality of the partial order 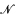κ of functions from a regular cardinal κ into the ideal 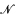of Lebesgue measure zero subsets of R. We show that when add (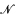) = κ and the covering lemma holds with respect to an inner model of GCH, then cf (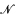κ) = max{cf(κκ), cf([cf(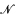)]κ)}. We also give an example to show that the covering assumption cannot be removed.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 56 , Issue 1 , March 1991 , pp. 103 - 107
Copyright
Copyright © Association for Symbolic Logic 1991

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[Baum]Baumgartner, J. E., Iterated forcing, Surveys in set theory (Mathias, A. R. D., editor), Cambridge University Press, Cambridge, 1983, pp. 1–59.Google Scholar
[Burke]Burke, M. R., Some applications of set theory to measure theory, Ph.D. thesis, University of Toronto, Toronto, 1988.Google Scholar
[Frem 1]Fremlin, D. H., On the additivity and cofinality of Radon measures, Mathematika, vol. 31 (1984), pp. 323–335.CrossRefGoogle Scholar
[Frem 2]Fremlin, D. H., Cichon's diagram, Séminaire d'Initiation à l'Analyse (Choquet, G.et al., editors), vol. 23, Université Pierre et Marie Curie, Paris, 1984, pp. 5.01–5.13.Google Scholar
[Frem 3]Fremlin, D. H., The partially ordered sets of measure theory and Tukey's ordering, preprint, 1988.Google Scholar
[Jech]Jech, T., Set theory, Academic Press, New York, 1973.Google Scholar
[Kun]Kunen, K., Random and Cohen reals, Handbook of set-theoretic topology (Kunen, K. and Vaughan, J. E., editors), North-Holland, Amsterdam, 1984, pp. 887–911.CrossRefGoogle Scholar
[Mag]Magidor, M., On the singular cardinals problem. I, Israel Journal of Mathematics, vol. 28 (1977), pp. 1–31.CrossRefGoogle Scholar