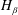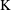1 Introduction
Laser-induced breakdown (LIB) has been studied in condensed media and mainly it has been applied to solid targets; LIB in liquids has gained less attention due to the lower sensitivity of the laser-induced breakdown spectroscopy (LIBS) technique and to technical difficulties in performing LIB in liquid. In spite of the classic troubles with LIBS analysis of liquids, an increasing number of publications have appeared where LIB has become an important phenomenon for scientific and technological interest. This is because LIB is a powerful technique for in situ elemental analysis, on-line monitoring and can be performed in various environments. For instance, LIB has the potential for cooling or wastewater monitoring in industry applications, thermoelectric applications (Wachter & Cremers Reference Wachter and Cremers1987; Samek et al. Reference Samek, Beddows, Kaiser, Kukhlevsky, Liska, Telle and Young2000; Fichet et al. Reference Fichet, Mauchien, Wagner and Moulin2001), for the examination of pollution in ground and drinking water (Moskvin, Moskvin & Ardashnikova Reference Moskvin, Moskvin and Ardashnikova2000) and for geological marine research (Fabre et al. Reference Fabre, Boiron, Dubessy, Cathelineau and Banks2002). The aqueous solutions are of the most interest for enhanced analysis of liquids because water is not only omnipresent in industrial, pharmaceuticals and environmental specimens but also is ubiquitous in biological samples (Cheung & Yeung Reference Cheung and Yeung1993; Ng, Ho & Cheung Reference Ng, Ho and Cheung1997). Furthermore, the most important application of this phenomenon is the medical one because most surgical techniques are based on optical breakdown and its associated phenomena. Accordingly, a significant investigation has been dedicated to understanding LIB in ocular media for both ocular damage and different surgery types of the eye (Aron-Rosa et al. Reference Aron-Rosa, Aron, Griesemann and Thyzel1980; Docchio, Sacchi & Marshall Reference Docchio, Sacchi and Marshall1986), i.e. laser safety and laser medicine. Most of this research has been carried out on saline solutions rather than real ocular solutions using visible and near infrared ultrashort laser pulses (Docchio et al. Reference Docchio, Sacchi and Marshall1986; Rockwell et al. Reference Rockwell, Cain, Noojin, Roach, Rogers, Mayo and Toth1993; Kennedy et al. Reference Kennedy, Boppart, Hammer, Rockwell, Noojin and Roach1995; Hammer et al. Reference Hammer, Thomas, Noojin, Rockwell, Kennedy and Roach1996).
For LIBS measurements of aqueous solutions, different configurations of the sample were investigated such as the formation of plasma on a liquid surface (Fichet et al. 1996; Arca et al.
Reference Arca, Ciucci, Palleschi, Rastelli and Tognoni1997; Berman & Wolf Reference Berman and Wolf1998), in bulk solutions (Cremers, Radziemski & Loree Reference Cremers, Radziemski and Loree1984; Kitamori et al.
Reference Kitamori, Matsui, Sakagami and Sawada1989; Knopp, Scherbaum & Kim Reference Knopp, Scherbaum and Kim1996; Koch et al.
Reference Koch, Garen, Müller and Neu2004), on droplets (Archontaki & Crouch Reference Archontaki and Crouch1988; Wen-Feng Hsieh Reference Wen-Feng1988; Poulain & Alexander Reference Poulain and Alexander1995) and in liquid jets (Ito, Ueki & Nakamura Reference Ito, Ueki and Nakamura1995; Nakamura et al.
Reference Nakamura, Ito, Sone, Hiraga and Kaneko1996; Sturgeon Reference Sturgeon1998; Lo & Cheung Reference Lo and Cheung2002; Rai, Yueh & Singh Reference Rai, Yueh and Singh2008). Producing a visible plasma and a system for on-line LIBS analysis requires the solution of problems associated with plasmas formed in liquid. On one hand, plasma formed on a liquid surface creates strong splashing and shock waves that are related to the vaporization of the liquids, creating aerosols beyond the surface. The first effect leads to opacity of collection optics and thus the optics needs to be frequently cleaned to eliminate material cast out and splashed from the liquid. The second effect disrupts the laser beam and the emitted light returned to spectrometers and for repetitive laser pulses it changes the liquid surface position with respect to laser focus and thus lowers the precision of spectral measurements. In addition, aerosols produced by laser–liquid interaction absorb the laser beam and partly hinder the laser from reaching the surface. Diverse geometrical configurations have been proposed to decrease splashing and ripple without any specific preparation of the liquid sample (Charfi & Harith Reference Charfi and Harith2002; Fichet et al. 2002). Plasmas formed in bulk solutions prevent splashing but exhibit another drawback where the plasma suffers from a short lifetime, of the order of 1
$\unicode[STIX]{x03BC}$
s or less in aqueous media (Cremers et al.
Reference Cremers, Radziemski and Loree1984; Kitamori et al.
Reference Kitamori, Matsui, Sakagami and Sawada1989) compared with 5–20
$\unicode[STIX]{x03BC}$
s at a liquid surface in ambient air (Samek et al.
Reference Samek, Beddows, Kaiser, Kukhlevsky, Liska, Telle and Young2000). The observed emission intensity is decreased due to the plasma temperature decreasing from fast plasma quenching (Wachter & Cremers Reference Wachter and Cremers1987; Hosoda et al.
Reference Hosoda, Aoshima, Itoh and Tsuchiya1999; Samek et al.
Reference Samek, Beddows, Kaiser, Kukhlevsky, Liska, Telle and Young2000), the spectral line broadening due to the Stark effect and moving breakdown that generates fluctuations in the distance between the plasma and the laser beam focus (Kitamori et al.
Reference Kitamori, Matsui, Sakagami and Sawada1989; Koch et al.
Reference Koch, Garen, Müller and Neu2004). As a final point, a turbid or coloured solution sample can produce significant matrix effects for LIBS in water (Wachter & Cremers Reference Wachter and Cremers1987). The main drawback of bulk water is that the plasma emission intensity is lower than the intensity of the plasma emission at the surface for reasons such as laser and plasma absorption by the liquid. Thus liquids have to be transparent at a carefully chosen laser wavelength and scattering on suspended particles (Bunkin & Lobeyev Reference Bunkin and Lobeyev1997) or radiation shielding by means of high density plasma (Hammer et al.
Reference Hammer, Jansen, Frenz, Noojin, Thomas, Noack, Vogel, Rockwell and Welch1997) and fast quenching in dense medium in the face of double-pulse laser techniques. In general, to surpass such problems several experimental LIBS configurations have been suggested for liquid surface (Cremers et al.
Reference Cremers, Radziemski and Loree1984; Arca et al.
Reference Arca, Ciucci, Palleschi, Rastelli and Tognoni1997), bulk liquid (Kitamori et al.
Reference Kitamori, Matsui, Sakagami and Sawada1989) and liquid jets (Nakamura et al.
Reference Nakamura, Ito, Sone, Hiraga and Kaneko1996). The phenomenon of the breakdown in a liquid illuminated by a focused laser pulse comprises a sequence beginning with the breakdown and rapidly expanding cavities, followed by shock-wave propagation, cavity deceleration and bubble collapse. The local breakdown or explosion takes place in the liquid with the deposition of the laser energy and the light accompanying the breakdown indicates a hot plasma formation. Consequently, shock waves are formed around the hot spot as the vapour cavity expands explosively with sound speed velocity in the liquid after the laser pulse (Felix & Ellis Reference Felix and Ellis1971). When a pulsed laser is focused into water, breakdown will take place when the laser field intensity in the focal volume exceeds the breakdown threshold, and this leads to the plasma formation. Such a plasma can be heated to a very high temperature of 6000–15 000
$\text{K}$
(Barnes & Rieckhoff Reference Barnes and Rieckhoff1968; Thomas et al.
Reference Thomas, Hammer, Noojin, Stolarski, Rockwell and Roach1996) and to pressures as high as 20–60 kbar (Vogel & Lauterborn Reference Vogel and Lauterborn1988; Vogel et al.
Reference Vogel, Busch, Jungnickel and Birngruber1994) by inverse Bremsstrahlung absorption where the laser radiation resides in a focal volume for some fraction of pulse duration after plasma formation. If the plasma is absorbed, reflected or scattered a reduction in the transmitted laser energy to the breakdown region occurs, a phenomenon known as plasma shielding. Such an effect is highly desirable during intraocular microsurgery within the eye. Plasma shielding may be reduced by increasing the transmission around the plasma edges due to beam aberration that can pass laser energy away from the optical axis (Evans & Morgan Reference Evans and Morgan1969; Kennedy, Hammer & Rockwell Reference Kennedy, Hammer and Rockwell1997). The high plasma temperature and pressure can result in thermal expansion of the plasma at supersonic velocities associated with acoustic signatures, shock-wave creation and cavitation bubble effects. This expansion process takes place during and after the passage of the laser pulse while another type of expansion during the passage of the laser pulse may be due to continued ionization (Kennedy et al.
Reference Kennedy, Hammer and Rockwell1997). For the nanosecond (ns) and picosecond (ps) regimes and at suprathreshold LIB, the plasma expands along the beam toward the laser leading to a new plasma formation away from the original breakdown site and this phenomenon is known as moving breakdown (Docchio et al.
Reference Docchio, Regondi, Capon and Mellerio1988; Hammer et al.
Reference Hammer, Jansen, Frenz, Noojin, Thomas, Noack, Vogel, Rockwell and Welch1997). There are three mechanisms that have been used to explain plasma expansion phenomena, which are (i) the laser-supported detonation wave model suitable for gasses, (ii) the ionization wave model and (iii) the moving breakdown model which has been used in an aqueous solution by Docchio et al. (Reference Docchio, Regondi, Capon and Mellerio1988). This model supposed that breakdown takes place individually at several sites for ns; therefore it occurs first at the focus and then spreads to threshold sites. Docchio et al. (Reference Docchio, Regondi, Capon and Mellerio1988) reported that the moving breakdown model is the principle theoretical tool utilized to explain plasma expansion for ns pulses in an aqueous solution LIB. He modified the model to include the spatial and temporal characteristics of Gaussian laser beams, plasma shielding and the starting time. A plasma produces a luminescent spectrum due to three sources: Bremsstrahlung from free electrons, electron–ion recombination emissions producing a broadband spectrum used as a LIB experimental indicator and then recombination at bound state transitions generating spectral lines of the medium. After the laser pulse has passed, the plasma starts to cool and decay by thermal conduction into the surrounding liquid and the energy losses due to the shock wave and spectral emission, i.e. Bremsstrahlung emission. However, plasma decay can be evaluated by monitoring plasma emission whose lifetime is shorter than the plasma decay time.
Even though the LIB applications in liquids are of considerable interest for in situ measurements (Kennedy et al. Reference Kennedy, Hammer and Rockwell1997; De Giacomo et al. Reference De Giacomo, Dell’Aglio, De Pascale and Capitelli2007; Lazic & Jovićević Reference Lazic and Jovićević2014) few investigations have been done attempting to characterize the plasmas produced by aqueous LIB using distilled water. Hammer et al. (Reference Hammer, Thomas, Noojin, Rockwell, Kennedy and Roach1996, Reference Hammer, Jansen, Frenz, Noojin, Thomas, Noack, Vogel, Rockwell and Welch1997) investigated the LIB mechanism in high purity water, saline and tap water. De Giacomo and his co-worker have studied the basic aspects of laser-induced breakdown in liquids using tap water and seawater as well as a metallic target submerged in water (De Giacomo et al. Reference De Giacomo, Dell’Aglio, Colao and Fantoni2004, Reference De Giacomo, Dell’Aglio, Colao, Fantoni and Lazic2005, Reference De Giacomo, Dell’Aglio, De Pascale and Capitelli2007). Angel et al. (Reference Angel, Bonvallet, Lawrence-Snyder, Pearman and Register2016) investigated the use of double-pulse LIBS underwater using seawater. Popov et al. (Reference Popov, Drozdova, Zaytsev, Biryukova, Zorov and Labutin2016) reported the salinity effect of different types of natural water, i.e. fresh and seawater as well as mineral water, on the plasma parameters to optimize the experimental conditions. To our knowledge there have been many studies on LIBS in distilled water.
Distilled water is a reasonable simulate of aqueous solutions for the vitreous humour of the eye corresponding to the latter’s LIB threshold. Thus, the motivation of the present work is to study plasma formation in bulk distilled water by using a double-pulse LIBS (DP-LIBS) experiment. This study aims to clarify the main aspects of bulk water LIB that must be considered for plasma analysis which include the temporal evolution of the plasma, the plasma temperature and electron density and emission lifetime.
2 Methodology
The experimental set-up used to generate a plasma in bulk water is presented in figure 1. It consists of two nanosecond Nd:YAG lasers, a
$10\times 10$
cm glass container equipped with a lens and a spectroscopic system. The two laser sources are operating at their fundamental wavelength (1064 nm). The first pulse is produced by a Specrta-Physics laser (INDI-50) whose maximum energy is 450 mJ, a pulse duration of 6 ns at full width at half maximum (FWHM), with a repetition rate up to 20 Hz. The second pulse is produced by a continuum laser (Surelite II) with a pulse duration of 10 ns at FWHM, repetition rate up to 10 Hz and maximum energy of 350 mJ. The two laser beams were aligned collinearly by using beam splitter (40/60 @1064 nm). The beams were focused into the bulk water sample (distilled water) by using a pair of plano-convex lenses of 5 cm focal length. The effective focal length is 2.5 cm in the air but in water it becomes 3.0 cm due to the larger refractive index in water. The two lasers have been synchronized using a digital pulse generator (Stanford Research, Model DG535) in order to control the inter-pulse delay between the two pulses. One of the two lenses is placed and sealed in a 2.5 cm hole on the side wall of the glass container. In front of the container, the other lens is placed at a distance of 2.5 cm from the embedded lens. This configuration has been used in order to avoid splashing, eliminating deposition of water droplets and stopping bubbles from previous sparks accumulating on the face ofthe lens (Kennedy et al.
Reference Kennedy, Hammer and Rockwell1997) and to avoid lens damage by total internal reflection of the laser beam from water back through the lens when a single 3 cm focal length lens was used.
Figure 1. Typical LIBS set-up, where B.S is beam splitter, L1, L2 plano-convex lenses
$f=5$
cm.
The plasma emission was collected using a pair of plano-convex lenses of 5 cm focal length working as a telescopic system in an orthogonal configuration to maximize the collected emission. The water column above the focal spot was approximately 1.7 cm. The plasma image (
$1:1$
) was focused on one end of quartz optical fibre with an aperture of 200
$\unicode[STIX]{x03BC}$
m, which was aligned with the plume centreline. Then it was directed by the other fibre end to the entry of the Echelle system coupled to an intensified imagining scientific charge-coupled device (ICCD) allowing simultaneous spectral analysis. Then a computer was used for data processing and storage. The used gateable ICCD camera is a Princeton, I MAX with high-resolution CCD sensor of
$1024\times 1024$
pixels with pixel size
$13\times 13~\unicode[STIX]{x03BC}$
m and imaging area
$13.3\times 13.3~\unicode[STIX]{x03BC}$
m. The Echelle spectrometer used is a PI-Echelle spectrometer (SE200PI-HO high order, high resolution, Princeton, USA) with a focal length: 20 cm, a numerical aperture (f-number):10, and constant spectral resolution
$\unicode[STIX]{x1D706}/N\unicode[STIX]{x1D706}=3100$
, where
$N\unicode[STIX]{x1D706}$
is the FWHM peak width and
$\unicode[STIX]{x1D706}$
is the wavelength over a wavelength range 190–1100 nm displayable in a single spectrum. The resolving power (
$\unicode[STIX]{x1D706}/N\unicode[STIX]{x1D706}$
) assumes a
$13\times 13~\unicode[STIX]{x03BC}$
m CCD with
$13\times 13~\unicode[STIX]{x03BC}$
m pixels. The Echelle grating is a diffraction grating which has a number of lines (1 mm) much less than a conventional spectrometer and to avoid overlapping of grating of different orders, a quartz prism is positioned in front of grating where various orders are scratched vertically in the focal plane of Echelle spectrometer. The second laser pulse trigger was connected to a pulse delay generator (Stanford delay generator DG535) for the synchronization of laser pulses and ICCD. Further, a fast photodiode (rise time 1 ns) and a fast oscilloscope (500 MHz) were used to ensure timing reliability of the inter-pulse delay which was set by the generator unit. The spectral response of the detection system and wavelength calibration has been performed by a reference mercury lamp. To decrease the spectral fluctuations, a run of 50 pairs of laser pulses was arranged for every single measurement at a repetition rate of 1 Hz. Low repetition was used to prevent splashing and accumulation of water droplets on the telescopic system. The analysis of the emission spectra was accomplished using Grams version 8.0 spectroscopic data analysis software (Galactic Industrial Salem, NH, USA) taking into account that the plasma emission signal was corrected by subtracting the dark signal of the detector using the software.
For DP-LIBS optimization studies, the plasma emission spectrum was recorded over a range of system parameters in order to optimize signal-to-noise ratio and spectra reproducibility. Such parameters were the inter-pulse delay between the two pulses (
$\unicode[STIX]{x0394}T$
), the laser energy of two pulses separately (
$E_{1}$
,
$E_{2}$
), and the number of laser shots as well as the detector parameters as gate delay compared to the second laser pulse (
$t_{d}$
) and gate width (
$t_{b}$
), which were controlled by computer. The key timing parameters are illustrated in figure 2 as used previously in the literature (Pichahchy, Cremers & Ferris Reference Pichahchy, Cremers and Ferris1997). Thus temporally resolved optical emission spectroscopy was utilized to examine the plasma evolution and the spectral line intensity and to evaluate plasma parameters such as the electron density and plasma temperature because the emission spectrum analysis was established on the evolution of the line intensity spectral distribution and broadening (Hammer et al.
Reference Hammer, Jansen, Frenz, Noojin, Thomas, Noack, Vogel, Rockwell and Welch1997). In the following section, the obtained experimental data will be discussed and explained in detail.
Figure 2. Details of timing scheme utilized for the experiments, where
$E_{1}$
is the first pulse,
$E_{2}$
is the second laser pulse,
$\unicode[STIX]{x0394}T$
is the inter-pulse delay,
$t_{d}$
is the gate delay and
$t_{b}$
is the gate width.
3 Results and discussion
Figure 3. Temporal evolution of plasma spectra at gate width 10
$\unicode[STIX]{x03BC}$
s as a function of (a) inter-pulse delay at gate delay 166 ns and (b) gate delay at inter-pulse delay 30
$\unicode[STIX]{x03BC}$
s.
3.1 Plasma emission spectra
When the laser pulse is focused into water, the laser dissociates liquid
$H_{2}O$
into hydrogen and oxygen, which are then ionized. Initially, single pulse laser induced breakdown spectroscopy (SP-LIBS) has been used for generating plasmas in water where the obtained spectrum is dominated by intense continuum emission attributable to free electron processes, that is Bremsstrahlung emission and electron–ion recombination, corresponding to high electron density and characterized by a short duration as a result of fast quenching by thermal conduction (De Giacomo et al.
Reference De Giacomo, Dell’Aglio, Colao and Fantoni2004). Therefore, the emission of ionized hydrogen and oxygen as the main elements of distilled water is difficult to detect and not significant in a water plasma. Due to this limited effect, and in order to obtain clear spectra more suitable for plasma diagnostics as well as improved signal and sensitivity, the DP-LIBS experiment is more effective for such purpose because it enhances the line emission intensity and reduces the continuum spectrum.
For DP-LIBS in water, the first pulse causes the bubble formation while the second pulse acts to excite the pre-formed plasma inside the bubble (Pichahchy et al. Reference Pichahchy, Cremers and Ferris1997; Tognoni et al. Reference Tognoni, Palleschi, Corsi and Cristoforetti2002; De Giacomo et al. Reference De Giacomo, Dell’Aglio, Colao and Fantoni2004, Reference De Giacomo, Dell’Aglio, De Pascale and Capitelli2007). The bubble is a gaseous environment formed by high temperature and pressure (Casavola et al. Reference Casavola, De Giacomo, Dell’Aglio, Taccogna, Colonna, De Pascale and Longo2005), and consequently reduces the plasma-quenching rate, which prompts an environment for plasma line emission similar to that attained with SP-LIBS in air. The emission spectra of a water plasma was examined over a range of experimental parameters by varying the inter-pulse delay between the two pulses and the acquisition gate delay after the termination of the second laser pulse to study their effects on the emission line intensity and the temporal behaviour of the plasma parameters. The analysis of the spectra shows that intense emission lines of hydrogen at 486.133 nm and 656.29 nm, as well as the triplet oxygen lines at 777 nm, characterize the emission spectra of the distilled water, as shown in figure 3(a,b). Such emission lines are considered good candidates for optimizing the experimental conditions and studying the effect of experimental parameters on plasma emission intensity and other parameters. These studies will be discussed explicitly in the following subsections taking into account that the line emission intensity is normalized to their maximum line emission intensity.
3.1.1 Inter-pulse delay effect
The emission from the water plasma in the present work is recorded by altering the inter-pulse delay by adjusting the triggering time of the second laser pulse with respect to the first pulse.
3.1.2 Inter-pulse delay effect
Previous DP-LIBS studies of aqueous solutions indicated enhancement at diverse delay time scales between the two laser pulses. The emission from the water plasma in the present work is recorded by altering the inter-pulse delay by adjusting the triggering time of the second laser pulse with respect to the first pulse.
The effect of the inter-pulse delay (
$\unicode[STIX]{x0394}T$
) is investigated over a range 15–70
$\unicode[STIX]{x03BC}$
s, and the emission intensity is recorded at gate delays of 166–200 ns and a gate width of 10
$\unicode[STIX]{x03BC}$
s, where the gate delay is varied with respect to the second laser pulse. To study the temporal performance of the spectral line intensities with inter-pulse delay, a relation between the line intensity and the inter-pulse delay for
$H_{\unicode[STIX]{x1D6FC}}$
at 656.27 nm,
$H_{\unicode[STIX]{x1D6FD}}$
at 486.133 nm and
$O(\text{I})$
at 777.29 nm were recorded. It is observed that the three spectral lines have the same behaviour with the inter-pulse delay, as illustrated in figure 4(a,b,c). From figure 4, it is obvious that the signal initially increases with an increasing inter-pulse delay and reaches its maximum value at
$\unicode[STIX]{x0394}T\approx 30~\unicode[STIX]{x03BC}$
s. Then the signal intensity begins to decrease at the inter-pulse delay between 35 and 60
$\unicode[STIX]{x03BC}$
s. The intensity rapidly decreased from 60 to 70
$\unicode[STIX]{x03BC}$
s, as shown by analysing the emission spectra in figure 3(a), and it is observed that the
$H_{\unicode[STIX]{x1D6FC}}$
line has its minimum intensity value while the
$H_{\unicode[STIX]{x1D6FD}}$
and
$O(\text{I})$
lines are barely detectable at
$\unicode[STIX]{x0394}T\approx 70~\unicode[STIX]{x03BC}$
s because the spectrum is dominated by intense continuum.
Figure 4. Temporal evolution of the emission intensity as a function of inter-pulse delay at different inter-pulse delays and fixed gate delay and fixed gate width of 10
$\unicode[STIX]{x03BC}$
s for (a)
$H_{\unicode[STIX]{x1D6FC}}$
at 656.27 nm, (b)
$H_{\unicode[STIX]{x1D6FD}}$
at 486.133 nm and (c)
$O(I)$
at 777.29 nm.
Figure 5. Temporal evolution of the emission intensity as a function of gate delay at different inter-pulse delays and a fixed gate width of 10
$\unicode[STIX]{x03BC}$
s for (a)
$H_{\unicode[STIX]{x1D6FC}}$
, (b)
$H_{\unicode[STIX]{x1D6FD}}$
and (c)
$O(I)$
.
The increase in the line intensity may be attributable to the efficient laser-induced bubble expansion corresponding to the separation in time between the first and the second laser pulses (De Giacomo et al.
Reference De Giacomo, Dell’Aglio, Colao and Fantoni2004). This inter-pulse delay leads to an increase in the spatial extent of the pre-formed plasma induced by the second laser pulse resulting in better atomization and a larger plasma volume, which results in a more intense and longer line emission (De Giacomo et al.
Reference De Giacomo, Dell’Aglio, Colao and Fantoni2004, Reference De Giacomo, Dell’Aglio, De Pascale and Capitelli2007; Pichahchy et al.
Reference Pichahchy, Cremers and Ferris1997). However, the emission intensity obtained by inter-pulse delay at 30
$\unicode[STIX]{x03BC}$
s is larger than that at 60
$\unicode[STIX]{x03BC}$
s although the bubble reaches its maximum expansion at the latter inter-pulse delay, which is due to the strong confinement effect of the bubble on the pre-formed plasma. The bubble induced by the first laser pulse is confined the pre-formed plasma inside a small volume with an environment similar to that in air conditions which is characterized by better thermalization (De Giacomo et al.
Reference De Giacomo, Dell’Aglio, Casavola, Colonna, De Pascale and Capitelli2006) resulting in intense emission lines. The rapid decrease in line emission over the inter-pulse delay of 60–70
$\unicode[STIX]{x03BC}$
s is due to bubble collapse and is attributed to residual bubbles formed due to the tension field around the focal region resulting in cavity bubble deceleration, which was induced by the first laser pulse (Felix & Ellis Reference Felix and Ellis1971). In addition, this experiment showed that the bubble lasts for at least 60
$\unicode[STIX]{x03BC}$
s before collapsing, which agrees with the published literature of laser-induced bubble lifetime in a bulk solution (Kennedy et al.
Reference Kennedy, Hammer and Rockwell1997).
3.1.3 Detection time window effect
The discrimination of analyte emission from the background emission with delay time using the detector gating has the largest effect of reducing the initial plasma continuum emission and maximizing the signal intensity. For the present work, the temporal evolution of the plasma emission as a function of gate delay with respect to the second laser pulse is recorded at different inter-pulse delay times and at a gate width of 10
$\unicode[STIX]{x03BC}$
s, as shown in figure 5, which illustrates the relationship among the line emission intensities and gate delay for the selected three lines. From figure 5(a,b,c), it is observed that the strongest line emission occurs at the start of acquisition and after the termination of the second pulse, where the emission intensity of the
$H_{\unicode[STIX]{x1D6FC}}$
,
$H_{\unicode[STIX]{x1D6FD}}$
and
$O(\text{I})$
lines have maximum values at gate delays of 166 and 170 ns. Then they begins to decrease slowly over the range 180 until 190 ns and are barely detectable at 200 ns. The lines begin to disappear at 220 ns and disappear completely at 240 ns. It is clearly noted that the emission signal of the hydrogen and oxygen lines decrease with increasing gate delay.
The decrease in line emission as a result of the increase in gate delay suggests that the plasma lifetime is of short duration in water even in the DP-LIBS mode. This result can be interpreted in terms of increasing the electron–ion recombination rate (De Giacomo et al. Reference De Giacomo, Dell’Aglio, Colao and Fantoni2004) and to the interaction between the expanding plasma and the neighbouring water via thermal conduction resulting in the efficacious heat redistribution between water molecules which causes the plasma to quickly cool down (Pichahchy et al. Reference Pichahchy, Cremers and Ferris1997; De Giacomo et al. Reference De Giacomo, Dell’Aglio, De Pascale and Capitelli2007). Therefore, it is noted that there is an optimum gate delay for the permanent inter-pulse delay to achieve the maximum emission line signal.
Moreover, to consider the consequent signal fluctuation, it is essential to adjust the gate width in order to provide a better resolution time. In the present work, the effect of gate width is investigated at optimum inter-pulse delay as well as a gate delay of 30 and 40
$\unicode[STIX]{x03BC}$
s and 166, 170, 180 ns. Figure 6(a,b) illustrates the relation between the gate width (
$t_{b}$
) and the emission intensity at the selected gate delays and inter-pulse delays. Such a relation shows that the intensity increases by increasing the gate width until 1
$\unicode[STIX]{x03BC}$
s, then it becomes saturated, i.e. increases with little variation, over the range 1–25
$\unicode[STIX]{x03BC}$
s. It was found from emission spectra, which have been collected at gate widths of 100 and 500 ns, that they are dominated by continuum emission and then the signal intensity is maximized by increasing the gate width to 1
$\unicode[STIX]{x03BC}$
s and a further increase in the gate width does not provide significant enhancement in the plasma emission. It was noted that the gate width should be selected to minimize the background signal as well as to allow for the collection of maximum plasma emission.
a
Figure 6. (a,b) Temporal evolution of the emission intensity from the selected lines as a function of gate width at an inter-pulse delay of 30
$\unicode[STIX]{x03BC}$
s and at a gate delay (a) 166 ns and (b) 180 ns. (c,d) Temporal evolution of the emission intensity from the selected lines as a function of gate width at a gate delay of 170 ns and at inter-pulse delay (c) 30
$\unicode[STIX]{x03BC}$
s and (d) 40
$\unicode[STIX]{x03BC}$
s.
Figure 7. (a) The emission intensity of
$H_{\unicode[STIX]{x1D6FC}}$
,
$H_{\unicode[STIX]{x1D6FD}}$
and
$O$
(I) as a function of the first laser pulse energy
$E_{1}$
at fixed second laser energy
$E_{2}=108$
mJ. (b) The emission intensity as a function of the second laser pulse energy
$E_{2}$
for
$H_{\unicode[STIX]{x1D6FC}}$
,
$H\unicode[STIX]{x1D6FD}$
and
$O(I)$
lines at fixed first laser energy
$E_{1}=80$
mJ.
3.1.4 Laser pulse energy effect
As the DP-LIBS experiment used two laser pulses, the energies of these two pulses need to be optimized to maximize the plasma emission intensity. Therefore, the disparity in the emission intensity of the hydrogen (486, 656 nm) and oxygen (777 nm) lines, as well as the signal enhancement for various laser energies of the first and the second laser pulse, are investigated. Meanwhile the benefits of the DP configuration were dominated by the first laser pulse, which generates the ambient conditions. In the present work it induces gaseous bubble formation and we focus on the energy effect of the first laser pulse on the emission intensity.
During the present experiment, the first laser pulse energy was increased up to 120 mJ while the second laser pulse was kept constant at 108 mJ. The emission spectrum intensity was recorded at 30
$\unicode[STIX]{x03BC}$
s inter-pulse delay, 170 ns gate delay and 1
$\unicode[STIX]{x03BC}$
s gate width. The obtained emission intensity of the three lines is plotted as a function of the first laser pulse energy and is given in figure 7(a). Investigating the effect of the first laser pulse energy, a growth of the emission intensities occurs between the lowest energy at
$E_{1}\approx 96$
mJ and the maximum energy at
$E_{1}\approx 120$
mJ. It is obvious that the line signal increases as the first laser pulse energy is increased but this is not a significant increase. Such an increase could be due to more efficient cavitation bubble formation resulting in an increase of the bubble size into which the plasma produced by the second laser pulse enlarges as well as increasing the emitting volume (Pichahchy et al.
Reference Pichahchy, Cremers and Ferris1997).
In addition, the effect of the second laser pulse energy on the plasma emission intensity has been investigated, where the energy of the second pulse varied from
$E_{2}\approx 85$
mJ to
$E_{2}\approx 124$
mJ, while
$E_{1}$
was kept fixed at 80 mJ. The emission intensity was recorded at the same temporal conditions as discussed in the previous paragraph. The relation between emission intensity and the second laser pulse energy is shown in figure 7(b). It is noted that the emission intensity decreases with a further increase in the second laser pulse energy but this also is not a significant decrease. Such a decrease could be due to plasma shielding that reduces the transmission of the laser energy into the focal volume (Cremers et al.
Reference Cremers, Radziemski and Loree1984; Berman & Wolf Reference Berman and Wolf1998). It is noted that the emission intensity is directly proportional to the first laser pulse; while it is inversely proportional with the second one at the experimental parameters of gate delay, gate width and inter-pulse delay mentioned above. However, this behaviour of both the first and second laser pulse energy also effect the combined energy causing breakdown and plasma formation provides interesting possibilities and requires further experimental investigation.
3.2 Plasma parameter determination
To entirely define the plasma characteristics and clear up the plasma dynamics, the temporal evolution of the plasma parameters in distilled water has been examined. The starting point to determine the plasma parameters is that all calculations are carried out with the instrumental background subtracted from the spectrum, and the line intensities for the spectral response of the system have been corrected. Then the obtained emission intensities normalize to the background emission. The spectroscopic data of emission lines utilized for this propose are listed in table 1 National Institute of Standards and Technology (NIST), which summarize the energy, the statistical weights of upper and lower levels and the transition probability. In the following subsections, the plasma electron density as well as plasma temperature calculation will be discussed.
Table 1. The spectroscopic data for the emission lines used for plasma parameter determination.
3.2.1 Plasma electron density
A more reliable and still simple method to evaluate the electron density with reasonable accuracy is the Stark broadening measurement of the atomic lines. The hydrogen lines
$H_{\unicode[STIX]{x1D6FD}}$
(486.133 nm) and
$H_{\unicode[STIX]{x1D6FC}}$
(656.27 nm) have been chosen for the electron density measurements in the present work.
Based on the theory of Stark broadening (Griem Reference Griem1964, Reference Griem1974) that takes into consideration quasi-static ions and the impact electron broadening effect, the expression for electron density in terms of hydrogen line width is given by:
$$\begin{eqnarray}N_{e}=C(N_{e},T)\unicode[STIX]{x0394}\unicode[STIX]{x1D706}^{3/2},\end{eqnarray}$$
where the parameter
$C$
(
$N_{e}$
,
$T$
) determines the relative contribution of electron collisions on the electrostatic field, which weakly depends on
$T$
and
$N_{e}$
and is tabulated by Griem (Reference Griem1974), where
$\unicode[STIX]{x0394}\unicode[STIX]{x1D706}$
is the true FWHM in Angstroms.
It was observed that the
$H_{\unicode[STIX]{x1D6FC}}$
line is a well-isolated line characterized by high signal to noise ratio and is observed after the termination of the second laser pulse. In addition, it is important to verify that the plasma is optically thin, which means there is no self-absorption because this phenomenon causes spectral line saturation and a distorted width leading to line broadening and derivation of the wrong plasma parameter values. Thus, the self-absorption coefficient (SA) of the
$H_{\unicode[STIX]{x1D6FC}}$
line from the intensity ratio of
$H_{\unicode[STIX]{x1D6FC}}$
and
$H_{\unicode[STIX]{x1D6FD}}$
has been taken into account when calculating the electron density of the plasma. The SA is easily calculated following the SA definition and solving of the equations by El Sherbini et al. (Reference El Sherbini, El Sherbini, Hegazy, Cristoforetti, Legnaioli, Palleschi, Pardini, Salvetti and Tognoni2005). According to this study, it can be assumed that there is a moderate self-absorption in the
$H_{\unicode[STIX]{x1D6FC}}$
line, which in turns out has little effect on the electron density value. As discussed in § 3.1, the plasma is confined inside the laser-induced bubble so the small variation of SA may be due to the confinement effect of these bubbles.
Figure 8. Electron density as a function of (a) gate delay at fixed inter-pulse delay,
$\unicode[STIX]{x0394}T$
of
$30~\unicode[STIX]{x03BC}$
s and (b) inter-pulse delay at fixed gate delay,
$t_{d}$
of 166 ns, both at fixed gate width of 10
$\unicode[STIX]{x03BC}$
s.
Figure 9. Temporal evolution of electron density as a function of inter-pulse delay at different gate delays and a fixed gate width of 10
$\unicode[STIX]{x03BC}$
s.
Figure 10. Temporal evolution of electron density as a function of gate delay at different inter-pulse delays and a fixed gate width of 10
$\unicode[STIX]{x03BC}$
s.
Figure 11. (a) Plasma temperature as a function of inter-pulse delay at different gate delays and a fixed gate width of
$10~\unicode[STIX]{x03BC}$
s. (b) Exponential decay fitting curve of temperature with inter-pulse delay at a fixed gate delay and gate widths of 170 ns and 10
$\unicode[STIX]{x03BC}$
s respectively.
Figure 12. (a) Plasma temperature as a function of gate delay at different inter-pulse delays and a fixed gate width of 10
$\unicode[STIX]{x03BC}$
s. (b) Exponential decay of fitting curve of plasma temperature with gate delay at fixed inter-pulse delay of 35
$\unicode[STIX]{x03BC}$
s and a gate width of 10
$\unicode[STIX]{x03BC}$
s.
Supporting this are the electron densities derived from the measured FWHM of the Stark broadening of the
$H_{\unicode[STIX]{x1D6FD}}$
and
$H_{\unicode[STIX]{x1D6FC}}$
lines which are compared. The obtained electron density values for both the
$H_{\unicode[STIX]{x1D6FD}}$
and
$H_{\unicode[STIX]{x1D6FC}}$
lines are plotted as a function of gate delay and inter-pulse delay at a gate width of 10
$\unicode[STIX]{x03BC}$
s and are shown in figure 8(a,b) which illustrates that there is a deviation between
$N_{e}$
values from the
$H_{\unicode[STIX]{x1D6FD}}$
and
$H_{\unicode[STIX]{x1D6FC}}$
lines. The
$N_{e}$
values varied between 1.55E
$+$
18 cm
$^{-3}$
to 4.89E
$+$
17 cm
$^{-3}$
at the measured FWHM of the
$H_{\unicode[STIX]{x1D6FC}}$
line, while it varied between 2.61E
$+$
17 cm
$^{-3}$
to 1.32E
$+$
17 cm
$^{-3}$
when using the
$H_{\unicode[STIX]{x1D6FD}}$
line over a range of experimental parameters. As mentioned in the literature (Kennedy et al.
Reference Kennedy, Hammer and Rockwell1997) this result may not come as a surprise, where the
$H_{\unicode[STIX]{x1D6FD}}$
line is useful as a density standard for the
$N_{e}$
value up to
${\approx}10\text{E}+17~\text{cm}^{-3}$
and above this value it is preferable to use the
$H_{\unicode[STIX]{x1D6FC}}$
line because the
$H_{\unicode[STIX]{x1D6FD}}$
line becomes too broad to be separated from the underlying continuum or from the
$H_{\unicode[STIX]{x1D6FE}}$
line (Kennedy et al.
Reference Kennedy, Hammer and Rockwell1997; Pichahchy et al.
Reference Pichahchy, Cremers and Ferris1997; Tognoni et al.
Reference Tognoni, Palleschi, Corsi and Cristoforetti2002; De Giacomo et al.
Reference De Giacomo, Dell’Aglio, Colao and Fantoni2004; Casavola et al.
Reference Casavola, De Giacomo, Dell’Aglio, Taccogna, Colonna, De Pascale and Longo2005; De Giacomo et al.
Reference De Giacomo, Dell’Aglio, De Pascale and Capitelli2007).
To study the inter-pulse delay effect (
$\unicode[STIX]{x0394}T$
) and the gate delay (
$t_{d}$
), a relation between the calculated
$N_{e}$
values, derived from the
$H_{\unicode[STIX]{x1D6FC}}$
, against
$\unicode[STIX]{x0394}T$
and
$t_{d}$
are plotted and shown in figure 9 and figure 10 respectively. Figure 9 shows the
$N_{e}$
value decreases when the inter-pulse delay increases, which is an inverse trend with the LIBS emission intensity at early times. Since the plasma electron density depends on the degree of ionization, the evaporation rate and the plasma expansion velocity the reduction of electron density with time may be attributed to the increase of the plasma expansion velocity as a result of bubble expansion, leading to a higher electron–ion recombination rate (De Giacomo et al.
Reference De Giacomo, Dell’Aglio, Colao and Fantoni2004, Reference De Giacomo, Dell’Aglio, De Pascale and Capitelli2007). In addition, increasing the inter-pulse delay results in reduction of the laser energy carried by each pulse due to scattering or mechanical effects associated with plasma formed in water, and consequently reduction of excited atoms and ions (Kennedy et al.
Reference Kennedy, Hammer and Rockwell1997; Pichahchy et al.
Reference Pichahchy, Cremers and Ferris1997).
Figure 10 shows the relation between the electron density and the gate delay, where the
$N_{e}$
values decrease with increasing gate delay for given inter-pulse delays. This b gate delay behaviour indicates that the plasma begins to decay. The decrease in
$N_{e}$
may be due to less energy being absorbed by the plasma after the second laser pulse termination which results in a decrease of
$N_{e}$
with increasing gate delay. The result also may be due to an increasing electron–ion recombination rate (De Giacomo et al.
Reference De Giacomo, Dell’Aglio, Colao and Fantoni2004) or electron diffusion from a high concentration region at higher electron density (Kennedy et al.
Reference Kennedy, Hammer and Rockwell1997). However, an important note is that the variation of
$N_{e}$
with gate delay is slow, which suggests the confinement effect of the bubble induced by the first laser pulse.
3.2.2 Plasma electron temperature
The plasma temperature can be determined from the relative line intensity of the same element. The measured intensity is used with the Boltzmann equation to estimate the plasma excitation temperature which should be equal to the electron kinetic temperature under local thermodynamic equilibrium (LTE). In the present work and in the framework of the LTE approximation, the plasma temperature has been evaluated using the Boltzmann line pair method for the same species with the same ionization stage as established by equation (3.2) (Griem Reference Griem1964, Reference Griem1974):
$$\begin{eqnarray}\frac{I_{1}}{I_{2}}=\frac{g_{1}}{g_{2}}\frac{A_{1}}{A_{2}}\frac{\unicode[STIX]{x1D706}_{2}}{\unicode[STIX]{x1D706}_{1}}\exp \left(\frac{-|E_{2}-E_{1}|}{KT_{e}}\right),\end{eqnarray}$$
where 1 and 2 denote discrete lines in the pair, i.e. two different transitions within the same species at the same stage of ionization. A good candidate line pair in the present work is the oxygen lines of
$O(I)$
at 645.598 nm and
$O(I)$
at 844.625 nm, which are relatively isolated non-resonant emission lines, and thus are considered appropriate for temperature measurements using the Boltzmann line pair method.
The obtained plasma temperature values at different gate delays are plotted as a function of inter-pulse delay at a fixed gate width of 10
$\unicode[STIX]{x03BC}$
s, as shown in figure 11(a). The exponential decay of plasma temperature with inter-pulse delay is given by figure 11(b). Figure 11 shows that the temperature decreases with increasing inter-pulse delay, e.g. it decreases from 16 828
$\text{K}$
at 25
$\unicode[STIX]{x03BC}$
s to 14 564
$\text{K}$
at 50
$\unicode[STIX]{x03BC}$
s at a gate delay of 170 ns and gate width of 10
$\unicode[STIX]{x03BC}$
s. The decrease of plasma temperature with the inter-pulse delay results from the plasma confinement effect which is caused by the bubble pressure, as discussed previously in § 3.1.1. The bubble expansion results in a lower pressure, which in turn causes longer expansion of the pre-formed plasma induced by the second laser pulse and thus the plasma temperature decreases.
Moreover, to study the temporal evolution of the plasma temperature with gate delay, plasma temperature values are plotted as a function of gate delay at different inter-pulse delay times and a fixed gate width of 10
$\unicode[STIX]{x03BC}$
s, as shown in figure 12(a). It is observed that by increasing the gate delay, the plasma temperature decreases exponentially with a slow variation, as given by figure 12(b), e.g. from 15 923 to 11 665
$\text{K}$
at an inter-pulse delay of 35
$\unicode[STIX]{x03BC}$
s and indicates the bubble confinement effect generated by the first laser pulse. The temperature decreases with increasing gate delay time which enhances the recombination rate (De Giacomo et al.
Reference De Giacomo, Dell’Aglio, Colao and Fantoni2004; El Sherbini et al.
Reference El Sherbini, El Sherbini, Hegazy, Cristoforetti, Legnaioli, Palleschi, Pardini, Salvetti and Tognoni2005) as discussed previously in § 3.1.2. In other words, after the laser pulse is terminated, the plasma initiates the cooling and decay process through allowing energy losses to the shock wave, spectral emission and thermal conduction into the surrounding water. When the plasma has cooled, it decays by means of electron–ion recombination. In the present work, the decrease in the plasma temperature can be related to increasing the cold plasma contribution due to bubble expansion as a result of increasing the inter-pulse delay as well as the gate delay times.
It is worth mentioning that for analytical plasmas, the condition of LTE is often cited as being vital for reliable quantification. Thermal equilibrium means that all processes in the plasma are collision dominated and the plasma can be described by a single temperature parameter, i.e.
$T_{e}=T_{i}$
. This is valid locally and for a particular time domain in the plasma evolution. Thus in the present work, the simple criterion of the McWhirter formula given by the following equation has been used for testing the existence of LTE (DeMichelis Reference DeMichelis1969). Substituting in (3.3) with the temperature values calculated from the Boltzmann equations, a value for the electron density
$N_{e}$
less than the electron density calculated from the Stark method is obtained, which means that the LTE condition is valid over a range of inter-pulse delays as well as gate delays for a gate width of 10
$\unicode[STIX]{x03BC}$
s.
$$\begin{eqnarray}N_{e}\geqslant 1.6\times 10^{12}T^{1/2}(\unicode[STIX]{x0394}E)^{3}\,\text{cm}^{-3},\end{eqnarray}$$
where
$\unicode[STIX]{x0394}E$
(ev) is the highest energy transition and
$T$
(
$\text{K}$
) is the plasma temperature.
4 Conclusion
In the present work, the temporal evolution of plasma emission induced by laser absorption in bulk water has been studied using the optical emission spectroscopy technique (OES) by applying dual pulses LIBS in a collinear configuration. The effects of experimental parameters such as inter-pulse delay, detection time window and laser pulse energy on the behaviour of the plasma emission and plasma parameters have been discussed. Strong dependence of the plasma emission intensity on the separation between the two lasers pulses was observed. Whereas, the strongest plasma emission intensity occurs for acquisitions beginning after the termination of the second laser pulse at short gate delays, and suggests that a plasma in water has a short lifetime even with the DP-LIBS technique. Further, it was found that the plasma emission intensity is directly proportional to the first laser pulse while it is inversely proportional to the second pulse at fixed experimental parameters. However, the effect of laser energy from both the first and second pulse requires further investigation.
In addition, the temporal evolution of the temperature and electron density of the plasma has been evaluated using OES, since they play an essential role in completely describing the plasma characteristics and clarifying different processes during the plasma lifetime such as dissociation, atomization, ionization and excitation. The behaviour of the plasma parameters was studied over a range of experimental parameters, and was in agreement with the temporal behaviour of the plasma emission and its correlation to the bubble dynamics.
The obtained results give insight into the LIB phenomenon and its dynamic properties in water that must be considered in ophthalmology. For example, the hot plasmas produced by LIB are used as a surgical tool to cut intraocular tissue. The simulation of LIB in the vitreous humour of the eye using distilled water helps to understand the interaction between the laser and the vitreous humour, which in turn leads to better performance of eye surgery.
