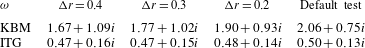1 Introduction
The ballooning mode (Connor, Hastie & Taylor Reference Connor, Hastie and Taylor1978) is an electromagnetic instability driven mainly by the pressure gradient, and is considered to be one of the most important instabilities in the high-confinement mode (H-mode) stage of tokamaks. The H-mode is important for tokamaks since it can improve the plasma confinement to make fusion more economically feasible. The ideal peeling-ballooning mode (Connor et al. Reference Connor, Hastie, Wilson and Miller1998) and kinetic ballooning mode (KBM) (Tang, Connor & Hastie Reference Tang, Connor and Hastie1980; Belli & Candy Reference Belli and Candy2010; Holod & Lin Reference Holod and Lin2013; Tang et al. Reference Tang, Xu, Ma, Bass, Holland and Candy2016) are invoked to predict the constraints of the H-mode pedestal (Snyder et al. Reference Snyder, Groebner, Hughes, Osborne, Beurskens, Leonard, Wilson and Xu2011). The linear and nonlinear physics of the peeling-ballooning mode have recently been studied intensively with fluid codes, such as the eigenvalue code ELITE (Wilson et al. Reference Wilson, Snyder, Huysmans and Miller2002) and initial value code BOUT++ (Dudson et al. Reference Dudson, Umansky, Xu, Snyder and Wilson2009). These studies have helped explain several important aspects (e.g. mode numbers) of H-mode experiments (cf. Liu et al. Reference Liu, Xu, Gao, Xia, Joseph, Meyer, Liu, Xu, Shao and Ding2014). However, the fluid model ignores many important kinetic effects, such as the wave–particle resonance and finite Larmor radius effect, which may play a critical role in the formation of the H-mode pedestal. A complete understanding of the electromagnetic instabilities in the tokamak edge is still in progress. Even after one decade of efforts, gyrokinetic electromagnetic simulation is still working on code–code verification due to its great challenge.
As an effort of code verification, the linear properties of the KBM have recently been compared amongst various gyrokinetic continuum codes, including GS2 (Bourdelle et al. Reference Bourdelle, Dorland, Garbet, Hammett, Kotschenreuther, Rewoldt and Synakowski2003; Joiner, Hirose & Dorland Reference Joiner, Hirose and Dorland2010) and GYRO (Belli & Candy Reference Belli and Candy2010; Moradi et al. Reference Moradi, Pusztai, Mollen and Fulop2012). The KBM is found to be sensitive to parallel magnetic fluctuation (Belli & Candy Reference Belli and Candy2010) and the treatment of the radial pressure gradient term in the drift velocity (Belli & Candy Reference Belli and Candy2010). The parallel magnetic fluctuation is not considered in this paper. Regarding the radial pressure gradient term, this effect may be particular to flux-tube continuum codes, as the pressure gradient-driven magnetic drift is automatically included in gyrokinetic particle simulations (Holod et al. Reference Holod, Zhang, Xiao and Lin2009). A newly published paper (Gorler et al. Reference Gorler, Tronko, Hornsby, Bottino, Kleiber, Norscini, Grandgirard, Jenko and Sonnendrucker2016) using the continuum code GENE shows that in order to obtain consistent linear growth rates, a radially global simulation model must be used. However, the details of the global equilibrium profile model used in this study were not specified. In this paper, we use gyrokinetic particle simulations to emphasize that, even in global simulations, the details of the equilibrium magnetic configuration are important for studies of the KBM. In contrast, they are not critical for electrostatic simulation, such as for the standard ion temperature gradient (ITG) mode or trapped electron mode (TEM). The stabilization effect of the Shafranov shift on the KBM is also demonstrated by our simulations. This suggests that, for the purpose of experimental validation, the realistic Shafranov shift is an indispensable component (Moradi et al. Reference Moradi, Pusztai, Voitsekhovitch, Garzotti, Bourdelle, Pueschel, Lupelli and Romanelli2014; Citrin et al. Reference Citrin, Garcia, Gorler, Jenko, Mantica, Told, Bourdelle, Hatch, Hogeweij and Johnson2015). In addition, the global radial profile of the plasma equilibrium is important for electromagnetic simulations such as for the KBM, while for electrostatic ITG/TEM simulation, the linear growth rate and frequency depend only on the peak value of the global gradients.
For electrostatic simulations of tokamak plasmas, the equilibrium magnetic geometry is critical for quantitative study of the nonlinear physics (Xiao & Catto Reference Xiao and Catto2006; Lapillonne et al.
Reference Lapillonne, Brunner, Dannert, Jolliet, Marinoni, Villard, Gorler, Jenko and Merz2009; Lin et al.
Reference Lin, Ethier, Hahm and Tang2012). GTC has recently implemented real tokamak geometry (Xiao et al.
Reference Xiao, Holod, Wang, Lin and Zhang2015) from EFIT (Lao et al.
Reference Lao, Greene, Wang, Helton and Zawadzki1985)/VMEC (Hirshman & Whitson Reference Hirshman and Whitson1983) for experimental validations (cf. Wang et al.
Reference Wang, Lin, Holod, Heidbrink, Tobias, Van Zeeland and Austin2013). It has been found that ignoring the difference in the poloidal angle between torus coordinates
$(r,\unicode[STIX]{x1D703}_{0},\unicode[STIX]{x1D701}_{0})$
and flux coordinates
$(r_{f},\unicode[STIX]{x1D703}_{f},\unicode[STIX]{x1D701}_{f})$
could lead to significant differences in the turbulent transport simulated by various gyrokinetic codes (Lin & Hahm Reference Lin and Hahm2004; Lapillonne et al.
Reference Lapillonne, Brunner, Dannert, Jolliet, Marinoni, Villard, Gorler, Jenko and Merz2009; Lin et al.
Reference Lin, Ethier, Hahm and Tang2012). For electromagnetic simulations of finite-
$\unicode[STIX]{x1D6FD}$
plasmas, the electromagnetic effect may dominate. The electromagnetic capability has been implemented in the global gyrokinetic simulation code GTC (Holod et al.
Reference Holod, Zhang, Xiao and Lin2009). The semi-analytical, global Shafranov equilibrium is implemented (Xie Reference Xie2014; Xie Reference Xie2015; Xiao et al.
Reference Xiao, Holod, Wang, Lin and Zhang2015) to second order in the GTC code to study the magnetic equilibrium effects for the electromagnetic KBM. It is found that a slight difference in the equilibrium can cause a large difference in the linear KBM frequency and growth rate. The local and global profiles also provide rather different linear frequencies and growth rates.
2 Equilibrium sensitivity
In this work, we consider a low-
$\unicode[STIX]{x1D6FD}$
model equilibrium with
$\unicode[STIX]{x1D6FD}\sim \unicode[STIX]{x1D716}^{2}$
, where
$\unicode[STIX]{x1D716}=r/R_{0}\ll 1$
is the inverse aspect ratio. Under the boundary condition given by a circular conducting wall, the equilibrium flux surfaces are concentric circles to lowest order. To second order, the flux surfaces are shifted circles, which can be defined in terms of the usual cylindrical coordinates
$(R,\unicode[STIX]{x1D719}_{c},Z)$
by the following equations:
$$\begin{eqnarray}\displaystyle & \displaystyle R=R_{0}+r_{s}\cos \unicode[STIX]{x1D703}_{s}-\unicode[STIX]{x1D6E5}(r_{s}), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D719}_{c}=-\unicode[STIX]{x1D701}_{s}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle Z=r_{s}\sin \unicode[STIX]{x1D703}_{s}, & \displaystyle\end{eqnarray}$$
$R_{0}$
is the major radius and the Shafranov shift
$\unicode[STIX]{x1D6E5}(0)=0$
. (Note: some authors use
$\unicode[STIX]{x1D6E5}|_{r_{s}=a}=0$
, where
$a$
is the minor radius. However, what really matters is the derivative of the Shafranov shift.) The relations between Boozer flux coordinates
$(r_{f},\unicode[STIX]{x1D703}_{f},\unicode[STIX]{x1D701}_{f})$
and geometry coordinates
$(r_{s},\unicode[STIX]{x1D703}_{s},\unicode[STIX]{x1D701}_{s})$
are
$r=r_{s}$
,
$\unicode[STIX]{x1D701}_{f}=\unicode[STIX]{x1D701}_{s}$
and
$\unicode[STIX]{x1D703}_{f}=\unicode[STIX]{x1D703}_{s}-(\unicode[STIX]{x1D716}+\unicode[STIX]{x1D6E5}^{\prime })\sin \unicode[STIX]{x1D703}_{s}$
(Meiss & Hazeltine Reference Meiss and Hazeltine1990). Here
$\unicode[STIX]{x1D6E5}^{\prime }$
is the radial derivative of the Shafranov shift
$\unicode[STIX]{x1D6E5}(r)=\int _{0}^{r}((q^{2}\,\text{d}r)/(r^{3}R_{0}))\int _{0}^{r}[r^{2}/q^{2}-2(R_{0}^{2}/B_{0}^{2})rp^{\prime }]r\,\text{d}r$
(White Reference White2001), where
$q$
is the safety factor,
$B_{0}$
is the on-axis magnetic field and
$p$
is the normalized pressure. In the gyrokinetic community, three types of so called
$s$
–
$\unicode[STIX]{x1D6FC}$
models (
$s=(r/q)\,\text{d}q/\text{d}r$
,
$\unicode[STIX]{x1D6FC}=-R_{0}q^{2}\unicode[STIX]{x1D6FD}^{\prime }$
, where
$\unicode[STIX]{x1D6FD}$
is the ratio between plasma and magnetic field pressures) are generally used, with Model-a: lowest-order approximation
$\unicode[STIX]{x1D703}=\unicode[STIX]{x1D703}_{s}$
, Model-b: first-order approximation without the Shafranov shift,
$\unicode[STIX]{x1D6E5}=0$
and
$\unicode[STIX]{x1D703}=\unicode[STIX]{x1D703}_{s}-\unicode[STIX]{x1D716}\sin \unicode[STIX]{x1D703}_{s}$
and Model-c:
$\unicode[STIX]{x1D6E5}\neq 0$
and
$\unicode[STIX]{x1D703}=\unicode[STIX]{x1D703}_{s}-(\unicode[STIX]{x1D716}+\unicode[STIX]{x1D6E5}^{\prime })\sin \unicode[STIX]{x1D703}_{s}$
. Model-a and Model-b differ in the definition of poloidal angle
$\unicode[STIX]{x1D703}$
. In Model-a, the poloidal angle
$\unicode[STIX]{x1D703}$
is simplified as the geometric poloidal angle. In Model-b, the poloidal angle is a flux coordinate and contains higher-order corrections in
$\unicode[STIX]{x1D716}$
.
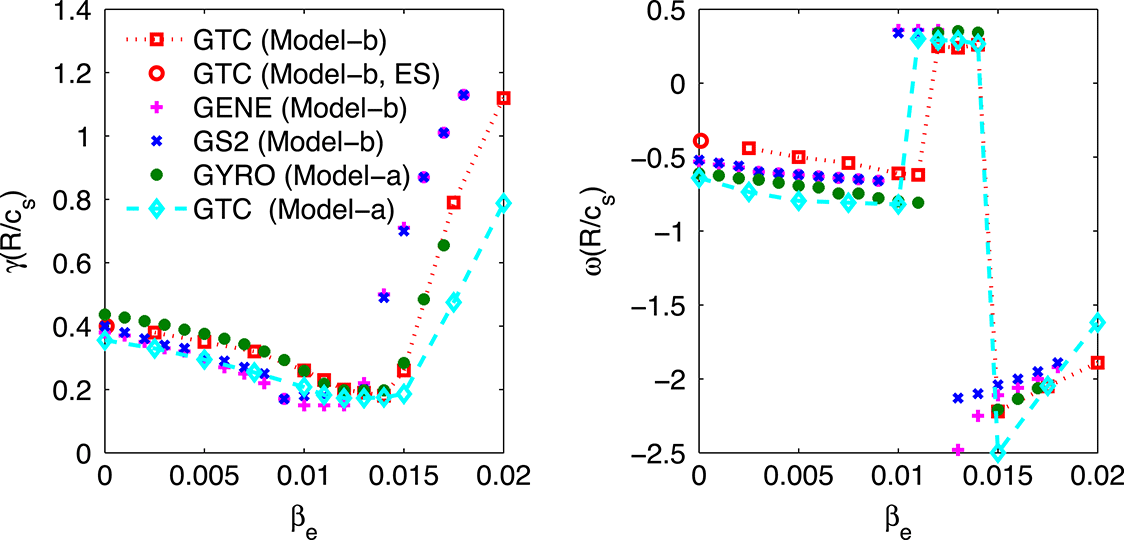
Figure 1. Scan over
$\unicode[STIX]{x1D6FD}_{e}$
comparing GTC with other gyrokinetic codes (GYRO, GENE and GS2) for different equilibrium field models. The transition from ITG to TEM and to KBM is clearly shown as
$\unicode[STIX]{x1D6FD}_{e}$
increases. The equilibrium implementations do not affect the ITG and TEM significantly, but do affect the KBM branch significantly. Data are partly taken from Candy (Reference Candy2005), Pueschel, Kammerer & Jenko (Reference Pueschel, Kammerer and Jenko2008), Belli & Candy (Reference Belli and Candy2010), Holod & Lin (Reference Holod and Lin2013). ES means electrostatic simulation.
Figure 1 shows the linear frequency and growth rate for a scan over
$\unicode[STIX]{x1D6FD}_{e}$
, comparing the GTC results with those from other gyrokinetic codes (GYRO, GENE and GS2). Here the Cyclone base case parameters (Dimits et al.
Reference Dimits, Bateman, Beer, Cohen, Dorland, Hammett, Kim, Kinsey, Kotschenreuther and Kritz2000) are employed, i.e.
$s=0.78$
,
$q=1.4$
,
$r/R_{0}=0.18$
,
$R_{0}/L_{T}=6.9$
,
$R_{0}/L_{n}=2.2$
and
$T_{i}=T_{e}$
, where
$L_{n}=-\text{d}\ln n/\text{d}r$
and
$L_{T}=-\text{d}\ln T/\text{d}r$
. Also,
$k_{\unicode[STIX]{x1D703}}\unicode[STIX]{x1D70C}_{i}=0.22$
, where
$k_{\unicode[STIX]{x1D703}}=nq/r$
and
$\unicode[STIX]{x1D70C}_{i}=\sqrt{T_{i}/m_{i}}/\unicode[STIX]{x1D6FA}_{ci}$
is the ion Larmor radius. In addition, the following parameters are used in the simulation:
$m_{i}/m_{e}=1837$
,
$R_{0}=83.5~\text{cm}$
,
$\unicode[STIX]{x1D70C}_{i}/a=125$
,
$B_{0}=2.0T$
,
$T_{e}=T_{i}=2.2~\text{keV}$
. We set-up different
$\unicode[STIX]{x1D6FD}_{e}$
parameters by varying the electron density
$n_{e}$
(Holod & Lin Reference Holod and Lin2013), e.g. for
$\unicode[STIX]{x1D6FD}_{e}=2.0\,\%$
,
$n_{e}=0.90\times 10^{14}~\text{cm}^{-3}$
. In figure 1, the data for GENE/GS2/GYRO are interpolated from the original data with
$k_{\unicode[STIX]{x1D703}}\unicode[STIX]{x1D70C}_{i}=0.20$
and 0.25 in Candy (Reference Candy2005), Pueschel et al. (Reference Pueschel, Kammerer and Jenko2008), Belli & Candy (Reference Belli and Candy2010). The transition from ITG (ion temperature gradient mode) to TEM (trapped electron mode) and to KBM is clearly shown as
$\unicode[STIX]{x1D6FD}_{e}$
increases. The GTC (Model-b) electromagnetic (Holod et al.
Reference Holod, Zhang, Xiao and Lin2009; Holod & Lin Reference Holod and Lin2013) simulation recovers the GTC (Model-b, ES) electrostatic (Lin & Hahm Reference Lin and Hahm2004) result as
$\unicode[STIX]{x1D6FD}_{e}\rightarrow 0$
. This shows that the GTC electromagnetic simulation converges to the electrostatic simulation in the low-
$\unicode[STIX]{x1D6FD}$
limit. In figure 1 the equilibrium implemented in GYRO is Model-a while that in GS2/GENE is Model-b by default. In the GTC code, both Model-a and Model-b are implemented. As can been seen in figure 1, while the equilibrium implementation does not largely affect the ITG, TEM and their transitions, it does significantly affect the linear growth rate of KBM. The GTC code gives a real frequency for the KBM branch similar to the other gyrokinetic codes, but gives a smaller growth rate. For example, for the case with
$\unicode[STIX]{x1D6FD}_{e}=1.75\,\%$
and Model-a,
$\unicode[STIX]{x1D6FE}^{GYRO}\simeq 1.5\unicode[STIX]{x1D6FE}^{GTC}$
. We note that this difference could come from the difference in the equilibrium profiles, as is shown in the latter part of this paper. That is, other gyrokinetic codes like GYRO use local flux-tube geometry, whereas the GTC code uses a global geometry. A linear electromagnetic gyrokinetic study has previously been carried out for the DIII-D H-mode pedestal (Wang et al.
Reference Wang, Xu, Candy, Groebner, Snyder, Chen, Parker, Wan, Lu and Dong2012), which shows that the frequency and growth rate can have a 50 % deviation among several gyrokinetic codes with local equilibrium settings. We also note that the gyrokinetic code GEM with flux-tube equilibrium shows good agreement with the aforementioned gyrokinetic codes such as GYRO for the ITG and TEM instabilities based on a different set of parameters (Chen et al.
Reference Chen, Parker, Wan and Bravenec2013).
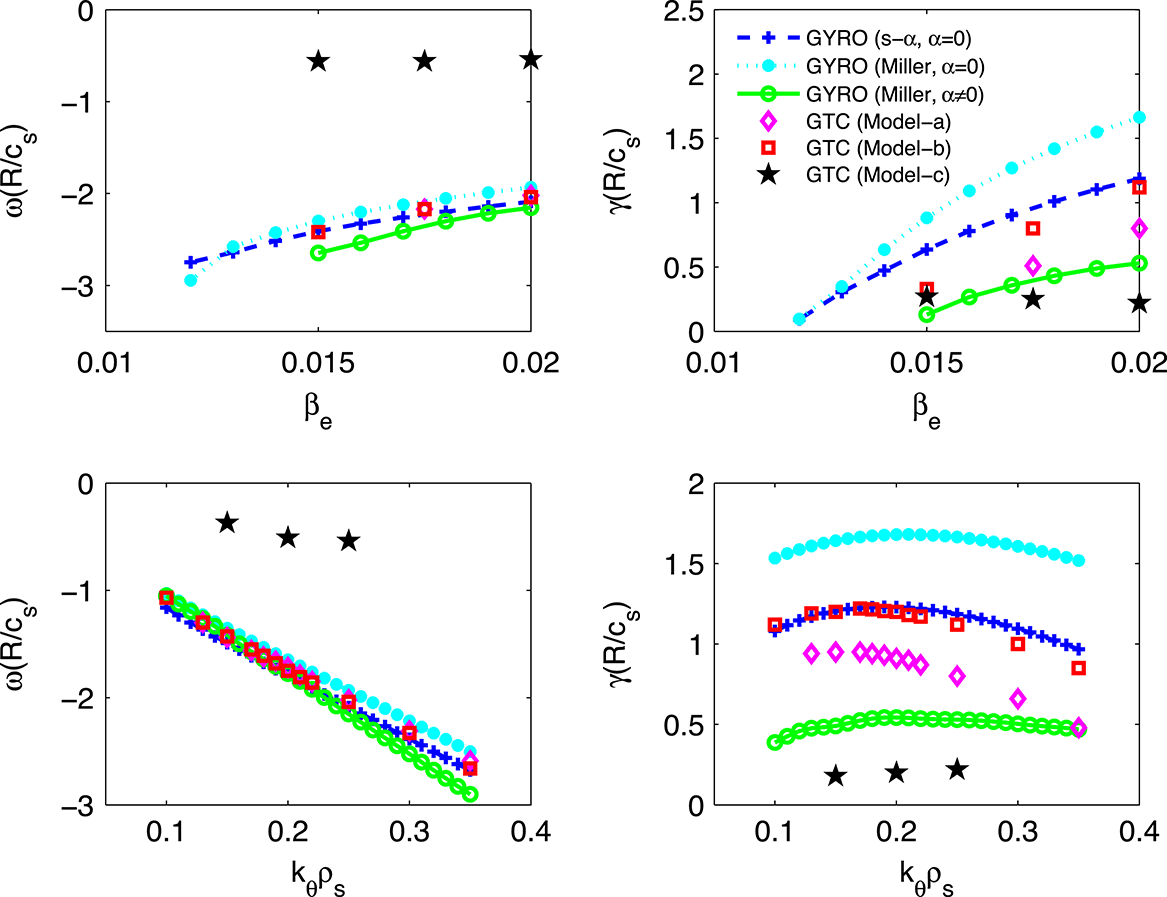
Figure 2. GTC versus GYRO for different equilibrium implementations. GYRO (
$s$
–
$\unicode[STIX]{x1D6FC}$
,
$\unicode[STIX]{x1D6FC}=0$
) is Model-a; GYRO (Miller,
$\unicode[STIX]{x1D6FC}=0$
) is Model-b; GYRO (Miller,
$\unicode[STIX]{x1D6FC}\neq 0$
) is Model-c.
To further quantify the effect of the equilibrium implementation, figure 2 shows a more detailed scan of
$\unicode[STIX]{x1D6FD}_{e}$
(with
$k_{\unicode[STIX]{x1D703}}\unicode[STIX]{x1D70C}_{i}=0.22$
) and
$k_{\unicode[STIX]{x1D703}}\unicode[STIX]{x1D70C}_{i}$
(with
$\unicode[STIX]{x1D6FD}_{e}=1.75\,\%$
) for the KBM branch. It is well known that Shafranov shift has a great effect on the stability of the KBM (Moradi et al.
Reference Moradi, Pusztai, Voitsekhovitch, Garzotti, Bourdelle, Pueschel, Lupelli and Romanelli2014; Citrin et al.
Reference Citrin, Garcia, Gorler, Jenko, Mantica, Told, Bourdelle, Hatch, Hogeweij and Johnson2015). Indeed, we find a large discrepancy in both the frequency and growth rate if the Shafranov shift is considered in the GTC simulation, as shown in figure 2. Both
$\unicode[STIX]{x1D714}$
and
$\unicode[STIX]{x1D6FE}$
become much smaller in magnitude when the Shafranov shift is included. It is observed that the electromagnetic perturbations still dominate the electrostatic perturbations, with
$A_{\Vert }/\unicode[STIX]{x1D719}\sim 3{-}6$
in ideal Alfvén wave units (i.e.
$A_{\Vert }/\unicode[STIX]{x1D719}=1$
for the ideal Alfvén eigenmode). This suggests that the mode is still an electromagnetic mode, such as a KBM. In addition, we have also compared the Shafranov shift effect on the ITG instability. In the GTC simulation, the differences in
$\unicode[STIX]{x1D714}$
and
$\unicode[STIX]{x1D6FE}$
between equilibriums with and without Shafranov shift are less than 5 % (Xie Reference Xie2014; Xie Reference Xie2015).
These findings suggest that an accurate global equilibrium, rather than a local equilibrium model, is crucial to validate experiments with gyrokinetic simulations. Another important factor for the gyrokinetic simulation is the density and temperature profiles and their associated gradients. To illustrate that the local profiles may not be suitable for validating experiments described by the KBM, we compare results from various equilibrium profiles using the GTC code. In figures 1 and 2, the following global profile (‘default test’) for GTC is used:
$q=0.82+1.1(\unicode[STIX]{x1D713}/\unicode[STIX]{x1D713}_{w})+1.0(\unicode[STIX]{x1D713}/\unicode[STIX]{x1D713}_{w})^{2}$
,
$n_{i}=n_{e}=1.0+0.205\{\tanh [(0.3-(\unicode[STIX]{x1D713}/\unicode[STIX]{x1D713}_{w}))/0.4]-1.0\}$
and
$T_{i}=T_{e}=1.0+0.415\{\tanh [(0.18-(\unicode[STIX]{x1D713}/\unicode[STIX]{x1D713}_{w}))/0.4]-1.0\}$
. Here
$\unicode[STIX]{x1D713}$
is the poloidal flux and
$\unicode[STIX]{x1D713}_{w}=\unicode[STIX]{x1D713}(r=a)=0.0375B_{0}R_{0}^{2}$
, which gives
$a/R_{0}=0.36$
. The local parameters at
$r=0.5a$
(which is the position where the density and temperature profiles peak) are the same as the Cyclone base case. To model the local equilibrium profile, we use the following gradients to calculate the density and temperature profiles:
$R_{0}/L_{n}=2.22\text{e}^{-[(r/a-0.5)/\unicode[STIX]{x0394}r]^{6}}$
and
$R_{0}/L_{T}=6.92\text{e}^{-[(r/a-0.5)/\unicode[STIX]{x0394}r]^{6}}$
, where
$\unicode[STIX]{x0394}r$
is the radial width of the local profile. The density and temperature profiles are reproduced to be consistent with these gradient profiles. Figure 3 shows the
$R_{0}/L_{n}$
used in GTC to model local equilibrium profiles, where the plateau gradient equals the peak value of the test gradient profile. In the electrostatic simulations for the ITG and TEM, the linear frequency and growth rate are not sensitive to
$\unicode[STIX]{x0394}r$
. Table 1 shows the electromagnetic simulation results for the ITG and KBM with different local profile widths
$\unicode[STIX]{x0394}r$
. We see that the frequency and growth rate for ITG change little for different equilibrium profile implementations. However, the frequency and growth rate for the KBM change by approximately 25 % for different equilibrium profile implementations. To ensure that this difference comes from the equilibrium, in the above simulations, the massless fluid model for electrons (Lin & Chen Reference Lin and Chen2001; Holod et al.
Reference Holod, Zhang, Xiao and Lin2009) (where the TEM is excluded) and Model-a equilibrium (to exclude the Shafranov shift) are used. The only difference between the ITG and KBM simulations is
$\unicode[STIX]{x1D6FD}_{e}$
, i.e.
$\unicode[STIX]{x1D6FD}_{e}^{ITG}=0.25\,\%$
and
$\unicode[STIX]{x1D6FD}_{e}^{KBM}=1.75\,\%$
respectively. The results confirm that the KBM is very sensitive to the equilibrium profiles. This sensitivity to the radial profile may be caused by the relatively larger radial extension of the KBM. To fully understand this issue, further analytic investigation is required. Overall, this suggests that an exact global equilibrium, such as from EFIT/VMEC, needs to be used in gyrokinetic simulations to verify codes and to validate experiments with the KBM as the dominant instability.
Figure 3. Various equilibrium profiles of
$R_{0}/L_{n}$
used in GTC.
3 Summary and discussion
We report that the linear physics of the KBM, in contrast to the ITG and TEM, is extremely sensitive to the equilibrium implementation in the gyrokinetic code. A second-order difference in the magnetic equilibrium can result in a factor of two or more difference in the real frequency and growth rate. This suggests that an accurate global equilibrium is required for validation of gyrokinetic simulations of the KBM.
Acknowledgements
H.S.X. would like to thank X. Q. Xu for useful discussions and J. Candy for information on the
$s$
–
$\unicode[STIX]{x1D6FC}$
model. The work is supported by the National Magnetic Confinement Fusion Energy Program under grant nos. 2015GB110000, 2013GB111000, China NSFC under grant no. 11575158, the Recruitment Program of Global Youth Experts, and US DOE SciDac GSEP centers.
