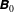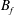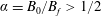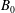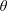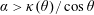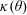1 Introduction
Collisionless plasmas can sustain shock waves with a front much smaller than the particle mean free path (Sagdeev & Kennel Reference Sagdeev and Kennel1991). These shocks, which are mediated by collective plasma effects rather than binary collisions, have been dubbed ‘collisionless shocks’. It is well known that the encounter of two collisional fluids generates two counter-propagating shock waves (Zel’dovich & Raizer Reference Zel’dovich and Raizer2002). Likewise, the encounter of two collisionless plasmas generate two counter-propagating collisionless shock waves (Forslund & Shonk Reference Forslund and Shonk1970; Silva et al. Reference Silva, Fonseca, Tonge, Dawson, Mori and Medvedev2003; Spitkovsky Reference Spitkovsky2008; Ryutov Reference Ryutov2018). In the collisional case, the shocks are launched when the two fluids make contact. In the collisionless case, the two plasmas start interpenetrating as the long mean free path prevents them from ‘bumping’ into each other. As a counter-streaming plasma system, the interpenetrating region quickly turns unstable. The instability grows, saturates and creates a localized turbulence which stops the incoming flow, initiating the density build-up in the overlapping region (Bret et al. Reference Bret, Stockem, Fiuza, Ruyer, Gremillet, Narayan and Silva2013, Reference Bret, Stockem, Narayan and Silva2014; Dieckmann & Bret Reference Dieckmann and Bret2017).
Various kind of instabilities do grow in the overlapping region (Bret, Gremillet & Dieckmann Reference Bret, Gremillet and Dieckmann2010). However, the fastest growing one takes the lead and eventually defines the ensuing turbulence. When the system is such that the filamentation, or Weibel, instability grows faster, magnetic filaments are generated (Medvedev & Loeb Reference Medvedev and Loeb1999; Wiersma & Achterberg Reference Wiersma and Achterberg2004; Lyubarsky & Eichler Reference Lyubarsky and Eichler2006; Kato Reference Kato2007; Lemoine et al. Reference Lemoine, Gremillet, Pelletier and Vanthieghem2019). In a pair plasmaFootnote 1, the conditions required for the Weibel instability to lead the linear phase have been studied in Bret (Reference Bret2016a) for a flow-aligned field, and in Bret & Dieckmann (Reference Bret and Dieckmann2017) for an oblique field. A mildly relativistic flow is required. Also, accounting for an oblique field supposes the Larmor radius of the particles is large compared to the dimensions of the system. Since the field modifies the hierarchy of unstable modes, it can prompt another mode than Weibel to lead the linear phase. In such cases, studies found so far that a shock still forms (Bret et al. Reference Bret, Pe’er, Sironi, Sa̧dowski and Narayan2017; Dieckmann & Bret Reference Dieckmann and Bret2017, Reference Dieckmann and Bret2018), mediated by the growth of the non-Weibel leading instability, like a two-stream for example.
Since the blocking of the flow entering the filaments is key for the shock formation, it is interesting to study under which conditions a test particle will be stopped in these magnetic filaments. Recently, a toy model of the process successfully reproduced the criteria for shock formation in the case of pair plasmas (Bret Reference Bret2015). When implemented accounting for a flow-aligned magnetic field (Bret Reference Bret2016b), the same kind of model could predict how too strong a field can deeply affect the shock formed (Bret et al. Reference Bret, Pe’er, Sironi, Sa̧dowski and Narayan2017; Bret & Narayan Reference Bret and Narayan2018). In view of the many settings involving oblique magnetic fields, we extend here the previous model to the case of an oblique field.
Figure 1. Set-up considered. We can consider 
$\unicode[STIX]{x1D711}=\unicode[STIX]{x03C0}/2$ since the direction of the flow, the field and the 
$\boldsymbol{k}$ of the fastest growing Weibel mode, are coplanar for the fastest growing Weibel modes (Bret Reference Bret2014; Novo, Bret & Sinha Reference Novo, Bret and Sinha2016).
The system considered is sketched in figure 1. The half-space 
$z\geqslant 0$ is filled with the magnetic filaments 
$\unicode[STIX]{x1D63D}_{f}=B_{f}\sin (kx)~\boldsymbol{e}_{y}$. In principle, we should consider any possible orientation for 
$\unicode[STIX]{x1D63D}_{0}$, thus having to consider the angles 
$\unicode[STIX]{x1D703}$ and 
$\unicode[STIX]{x1D711}$. Yet, previous works in a three-dimensional geometry found that the fastest growing Weibel modes are found with a wave vector coplanar with the field 
$\unicode[STIX]{x1D63D}_{0}$ and the direction of the flow (Bret Reference Bret2014; Novo et al. Reference Novo, Bret and Sinha2016). Here, the initial flow giving rise to Weibel is along 
$z$ and we set up the axis so that 
$\boldsymbol{k}$ is along 
$x$. We can therefore consider 
$\unicode[STIX]{x1D711}=\unicode[STIX]{x03C0}/2$ so that 
$\unicode[STIX]{x1D63D}_{0}=B_{0}(\sin \unicode[STIX]{x1D703},0,\cos \unicode[STIX]{x1D703})$.
A test particle is injected at 
$(x_{0},0,0)$ with velocity 
$\boldsymbol{v}_{0}=(0,0,v_{0})$ and Lorentz factor 
$\unicode[STIX]{x1D6FE}_{0}=(1-v_{0}^{2}/c^{2})^{-1/2}$, mimicking a particle of the flow entering the filamented overlapping region. Our goal is to determine under which conditions the particle streams through the magnetic filaments to 
$z=+\infty$, or is trapped inside. As explained in previous articles (Bret Reference Bret2015, Reference Bret2016b), in the present toy model, this dichotomy comes down to determining whether test particles stream through the filaments, or bounce back to the region 
$z<0$. The reason for this is that, in a more realistic setting, particles reaching the filaments and turning back will likely be trapped in the turbulent region between the upstream and the downstream. This problem is clearly related to that of the shock formation, since the density build-up leading to the shock requires the incoming flow to be trapped in the filaments.
2 Equations of motion
Since the Lorentz factor 
$\unicode[STIX]{x1D6FE}_{0}$ is a constant of the motion, the equation of motion for our test particle of mass 
$m$ and charge 
$q$ reads,
$$\begin{eqnarray}m\unicode[STIX]{x1D6FE}_{0}\ddot{\boldsymbol{x}}=q\frac{\dot{\boldsymbol{x}}}{c}\times (\unicode[STIX]{x1D63D}_{f}+\unicode[STIX]{x1D63D}_{0}).\end{eqnarray}$$ Explaining each component, we find for 
$z>0$,
$$\begin{eqnarray}\displaystyle & \displaystyle \ddot{x}=\frac{qB_{f}}{\unicode[STIX]{x1D6FE}_{0}mc}\left[\frac{B_{0}}{B_{f}}{\dot{y}}\cos \unicode[STIX]{x1D703}-{\dot{z}}\sin kx\right], & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \ddot{y} =\frac{qB_{f}}{\unicode[STIX]{x1D6FE}_{0}mc}\frac{B_{0}}{B_{f}}[{\dot{z}}\sin \unicode[STIX]{x1D703}-{\dot{x}}\cos \unicode[STIX]{x1D703}], & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \ddot{z}=\frac{qB_{f}}{\unicode[STIX]{x1D6FE}_{0}mc}\left[-\frac{B_{0}}{B_{f}}{\dot{y}}\sin \unicode[STIX]{x1D703}+{\dot{x}}\sin kx\right], & \displaystyle\end{eqnarray}$$ while 
$B_{f}=0$ for 
$z<0$. We can now define the following dimensionless variables,
$$\begin{eqnarray}\boldsymbol{X}=k\boldsymbol{x},\quad \unicode[STIX]{x1D6FC}=\frac{B_{0}}{B_{f}},\quad \unicode[STIX]{x1D70F}=t\unicode[STIX]{x1D714}_{B_{f}},\quad \text{with }\unicode[STIX]{x1D714}_{B_{f}}=\frac{qB_{f}}{\unicode[STIX]{x1D6FE}_{0}mc}.\end{eqnarray}$$With these variables, the system (2.2)–(2.4) reads,
$$\begin{eqnarray}\left.\begin{array}{@{}l@{}}\ddot{X}=-{\dot{Z}}{\mathcal{H}}(Z)\sin X+\unicode[STIX]{x1D6FC}{\dot{Y}}\cos \unicode[STIX]{x1D703},\\ \ddot{Y} =\unicode[STIX]{x1D6FC}({\dot{Z}}\sin \unicode[STIX]{x1D703}-{\dot{X}}\cos \unicode[STIX]{x1D703}),\\ \ddot{Z}={\dot{X}}{\mathcal{H}}(Z)\sin X-\unicode[STIX]{x1D6FC}{\dot{Y}}\sin \unicode[STIX]{x1D703},\end{array}\right\}\end{eqnarray}$$ where 
${\mathcal{H}}$ is the Heaviside step function 
${\mathcal{H}}(x)=0$ for 
$x<0$ and 
${\mathcal{H}}(x)=1$ for 
$x\geqslant 0$. The initial conditions are,
$$\begin{eqnarray}\left.\begin{array}{@{}l@{}}\boldsymbol{X}(\unicode[STIX]{x1D70F}=0)=(X_{0},0,0)\quad \text{with }X_{0}\equiv kx_{0},\\ \dot{\boldsymbol{X}}(\unicode[STIX]{x1D70F}=0)=(0,0,{\dot{Z}}_{0})\quad \text{with }{\dot{Z}}_{0}\equiv {\displaystyle \frac{kv_{0}}{\unicode[STIX]{x1D714}_{B_{f}}}}.\end{array}\right\}\end{eqnarray}$$3 Constants of the motion and chaotic behaviour
The total field in the region 
$z>0$ reads 
$\unicode[STIX]{x1D63D}=(B_{0}\sin \unicode[STIX]{x1D703},B_{f}\sin (kx),B_{0}\cos \unicode[STIX]{x1D703})$. It can be written as 
$\unicode[STIX]{x1D63D}=\unicode[STIX]{x1D735}\times \unicode[STIX]{x1D63C}$, with the vector potential in the Coulomb gauge,
$$\begin{eqnarray}\unicode[STIX]{x1D63C}=\left(\begin{array}{@{}c@{}}0\\ B_{0}x\cos \unicode[STIX]{x1D703}\\ B_{0}y\sin \unicode[STIX]{x1D703}+B_{f}{\displaystyle \frac{\cos (kx)}{k}}\end{array}\right).\end{eqnarray}$$The canonical momentum then reads (Jackson Reference Jackson1998),
$$\begin{eqnarray}\boldsymbol{P}=\boldsymbol{p}+\frac{q}{c}\unicode[STIX]{x1D63C}=\left(\begin{array}{@{}c@{}}p_{x}\\ p_{y}+{\displaystyle \frac{q}{c}}B_{0}x\cos \unicode[STIX]{x1D703}\\ p_{z}+{\displaystyle \frac{q}{c}}\left(B_{0}y\sin \unicode[STIX]{x1D703}+B_{f}{\displaystyle \frac{\cos (kx)}{k}}\right)\end{array}\right),\end{eqnarray}$$ where 
$\boldsymbol{p}=\unicode[STIX]{x1D6FE}_{0}m\boldsymbol{v}$. Since it does not explicitly depend on 
$z$, the 
$z$ component is a constant of the motion. It can equally be obtained by time integrating (2.4). Note that for 
$\unicode[STIX]{x1D703}=0$, the 
$y$ dependence vanishes so that the 
$y$ component of the canonical momentum is also a constant of the motion (Bret Reference Bret2016b).
We can derive another constant of the motion from (2.3). Time integrating it and remembering 
${\dot{y}}(t=0)=z(t=0)=0$, we find,
$$\begin{eqnarray}{\dot{y}}=\frac{qB_{0}}{\unicode[STIX]{x1D6FE}_{0}mc}[z\sin \unicode[STIX]{x1D703}-(x-x_{0})\cos \unicode[STIX]{x1D703}].\end{eqnarray}$$ Since 
$x_{0}$ is obviously a constant, we can express it in terms of the other variables and obtain an invariant, that is
$$\begin{eqnarray}\displaystyle x_{0} & = & \displaystyle x-z\tan \unicode[STIX]{x1D703}+\frac{c}{qB_{0}\cos \unicode[STIX]{x1D703}}\unicode[STIX]{x1D6FE}_{0}m{\dot{y}}\nonumber\\ \displaystyle & = & \displaystyle x-z\tan \unicode[STIX]{x1D703}+\frac{c}{qB_{0}\cos \unicode[STIX]{x1D703}}\left(P_{y}-\frac{q}{c}A_{y}\right).\end{eqnarray}$$Finally, the Hamiltonian,
$$\begin{eqnarray}{\mathcal{H}}=c\sqrt{c^{2}m^{2}+\left(\boldsymbol{P}-\frac{q}{c}\unicode[STIX]{x1D63C}\right)^{2}},\end{eqnarray}$$ is also a constant of the motion. Replacing 
$A_{y}$ in (3.4) by its expression from (3.1), we therefore have the following constants of the motion,
$$\begin{eqnarray}\displaystyle & \displaystyle {\mathcal{H}}\equiv C_{1}=c\sqrt{c^{2}m^{2}+\left(\boldsymbol{P}-\frac{q}{c}\unicode[STIX]{x1D63C}\right)^{2}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle C_{2}=P_{z}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle x_{0}\equiv C_{3}=\frac{c}{qB_{0}\cos \unicode[STIX]{x1D703}}P_{y}-z\tan \unicode[STIX]{x1D703}. & \displaystyle\end{eqnarray}$$ According to Liouville’s theorem on integrable systems, an 
$n$-dimensional Hamiltonian system is integrable if it has 
$n$ constants of motion 
$C_{j}(x_{i},P_{i},t)_{j\in [1\ldots n]}$ in involution (Chen & Palmadesso Reference Chen and Palmadesso1986; Ott Reference Ott2002; Lichtenberg & Lieberman Reference Lichtenberg and Lieberman2013), that is,
$$\begin{eqnarray}\{C_{j},C_{k}\}=\mathop{\sum }_{i=1}^{3}\left(\frac{\unicode[STIX]{x2202}C_{j}}{\unicode[STIX]{x2202}x_{i}}\frac{\unicode[STIX]{x2202}C_{k}}{\unicode[STIX]{x2202}P_{i}}-\frac{\unicode[STIX]{x2202}C_{k}}{\unicode[STIX]{x2202}x_{i}}\frac{\unicode[STIX]{x2202}C_{j}}{\unicode[STIX]{x2202}P_{i}}\right)=0,\quad \forall (j,k),\end{eqnarray}$$ where 
$\{f,g\}$ is the Poisson bracket of 
$f$ and 
$g$. It is easily checked that, 
$C_{2,3}$ being constants of the motion, 
$\{{\mathcal{H}},C_{2}\}=\{{\mathcal{H}},C_{3}\}=0$. However,
$$\begin{eqnarray}\{C_{2},C_{3}\}=-\text{tan}\,\unicode[STIX]{x1D703}.\end{eqnarray}$$ As a result, the system is integrable only for 
$\unicode[STIX]{x1D703}=0$ (Bret Reference Bret2016b). Otherwise, it is chaotic, as will be checked numerically in the following sections.
4 Reduction of the number of free parameters
The free parameters of the system (2.2)–(2.4) with initial conditions (2.7) are 
$(X_{0},{\dot{Z}}_{0},\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D703})$. In order to deal with a more tractable phase space parameter, we now reduce its dimension, accounting for the physical context of the problem.
Consider the magnetic filaments generated by the growth of the filamentation instability triggered by the counter-streaming of 2 cold (thermal spread 
$\unicode[STIX]{x0394}v\ll v$) symmetric pair plasmas. Both plasma shells have identical density 
$n$ in the laboratory frame, and initial velocities 
$\pm v\boldsymbol{e}_{z}$. We denote 
$\unicode[STIX]{x1D6FD}=v/c$. The Lorentz factor 
$\unicode[STIX]{x1D6FE}_{0}$ previously defined equally reads 
$\unicode[STIX]{x1D6FE}_{0}=(1-\unicode[STIX]{x1D6FD}^{2})^{-1/2}$ since the test particles entering the magnetic filaments belong to the same plasma shells.
The wave vector 
$\boldsymbol{k}$ defining the magnetic filaments is also the wave vector of the fastest growing filamentation modes. We can then set (Bret et al. Reference Bret, Stockem, Fiuza, Ruyer, Gremillet, Narayan and Silva2013),
$$\begin{eqnarray}k=\frac{\unicode[STIX]{x1D714}_{p}}{c\sqrt{\unicode[STIX]{x1D6FE}_{0}}},\end{eqnarray}$$ where 
$\unicode[STIX]{x1D714}_{p}^{2}=4\unicode[STIX]{x03C0}nq^{2}/m$, so that,
$$\begin{eqnarray}{\dot{Z}}_{0}=\frac{\unicode[STIX]{x1D6FD}}{\sqrt{\unicode[STIX]{x1D6FE}_{0}}}\frac{\unicode[STIX]{x1D714}_{p}}{\unicode[STIX]{x1D714}_{B_{f}}}=\frac{\unicode[STIX]{x1D6FD}}{\sqrt{\unicode[STIX]{x1D6FE}_{0}}}\frac{\unicode[STIX]{x1D714}_{B_{0}}}{\unicode[STIX]{x1D714}_{B_{f}}}\frac{\unicode[STIX]{x1D714}_{p}}{\unicode[STIX]{x1D714}_{B_{0}}}=\frac{\unicode[STIX]{x1D6FD}}{\sqrt{\unicode[STIX]{x1D6FE}_{0}}}\unicode[STIX]{x1D6FC}\frac{\unicode[STIX]{x1D714}_{p}}{\unicode[STIX]{x1D714}_{B_{0}}},\end{eqnarray}$$where,
$$\begin{eqnarray}\unicode[STIX]{x1D714}_{B_{0}}=\frac{qB_{0}}{\unicode[STIX]{x1D6FE}_{0}mc}.\end{eqnarray}$$ The peak field 
$B_{f}$ in the filaments can be estimated from the growth rate 
$\unicode[STIX]{x1D6FF}$ of the instability, considering 
$\unicode[STIX]{x1D714}_{B_{f}}\sim \unicode[STIX]{x1D6FF}$ (Davidson et al. Reference Davidson, Hammer, Haber and Wagner1972; Grassi et al. Reference Grassi, Grech, Amiranoff, Pegoraro, Macchi and Riconda2017). It turns out that, over the domain 
$\unicode[STIX]{x1D6FF}\gg \unicode[STIX]{x1D714}_{B_{0}}$, the growth rate 
$\unicode[STIX]{x1D6FF}$ depends weakly on 
$\unicode[STIX]{x1D703}$ and can be well approximated by (Stockem, Lerche & Schlickeiser Reference Stockem, Lerche and Schlickeiser2006; Bret Reference Bret2014),
$$\begin{eqnarray}\unicode[STIX]{x1D714}_{B_{f}}\sim \unicode[STIX]{x1D6FF}=\unicode[STIX]{x1D714}_{p}\sqrt{\frac{2\unicode[STIX]{x1D6FD}^{2}}{\unicode[STIX]{x1D6FE}_{0}}-\left(\frac{\unicode[STIX]{x1D714}_{B_{0}}}{\unicode[STIX]{x1D714}_{p}}\right)^{2}},\end{eqnarray}$$so that,
$$\begin{eqnarray}\unicode[STIX]{x1D714}_{B_{f}}=\frac{\unicode[STIX]{x1D714}_{B_{0}}}{\unicode[STIX]{x1D6FC}}=\unicode[STIX]{x1D714}_{p}\sqrt{\frac{2\unicode[STIX]{x1D6FD}^{2}}{\unicode[STIX]{x1D6FE}_{0}}-\left(\frac{\unicode[STIX]{x1D714}_{B_{0}}}{\unicode[STIX]{x1D714}_{p}}\right)^{2}}.\end{eqnarray}$$ This expression allows us to express 
$\unicode[STIX]{x1D714}_{B_{0}}/\unicode[STIX]{x1D714}_{p}$ as,
$$\begin{eqnarray}\frac{\unicode[STIX]{x1D714}_{B_{0}}}{\unicode[STIX]{x1D714}_{p}}=\sqrt{\frac{2}{\unicode[STIX]{x1D6FE}_{0}}}\frac{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}{\sqrt{1+\unicode[STIX]{x1D6FC}^{2}}},\end{eqnarray}$$so that (4.2) eventually reads,
$$\begin{eqnarray}{\dot{Z}}_{0}=\sqrt{\frac{1+\unicode[STIX]{x1D6FC}^{2}}{2}}.\end{eqnarray}$$ The parameters phase space is thus reduced to three dimensions, 
$(X_{0},\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D703})$.
5 Numerical exploration
It was previously found that, for 
$\unicode[STIX]{x1D703}=0$, all particles stream through the filaments, no matter their initial position and velocity, if 
$\unicode[STIX]{x1D6FC}>1/2$ (Bret Reference Bret2016b). Clearly, for 
$\unicode[STIX]{x1D703}=\unicode[STIX]{x03C0}/2$, no particle can stream to 
$z=+\infty$. As we shall see, the 
$\unicode[STIX]{x1D703}$-dependent threshold value of 
$\unicode[STIX]{x1D6FC}$ beyond which all particles go to 
$\infty$ is simply 
$\propto 1/\cos \unicode[STIX]{x1D703}$.
The system (2.6)–(2.7) is solved using the Mathematica ‘NDSolve’ function. The equations are invariant under the change 
$X\rightarrow X+2\unicode[STIX]{x03C0}$, so that we can restrict the investigation to 
$X_{0}\in [-\unicode[STIX]{x03C0},\unicode[STIX]{x03C0}]$. Unless 
$\unicode[STIX]{x1D703}=0$, there are no other trivial symmetries. In particular, the transformation 
$\unicode[STIX]{x1D703}\rightarrow -\unicode[STIX]{x1D703}$ does not leave the system invariant. We shall detail the case 
$\unicode[STIX]{x1D703}\in [0,\unicode[STIX]{x03C0}/2]$ and only give the results, which are very similar although not identical, for 
$\unicode[STIX]{x1D703}\in [-\unicode[STIX]{x03C0}/2,0]$.
Figure 2. Value of 
$Z(\unicode[STIX]{x1D70F}_{\text{max}})$ in terms of 
$X_{0}$ for 
$\unicode[STIX]{x1D70F}_{\text{max}}=10^{3}$ and two values of 
$\unicode[STIX]{x1D703}$.
The numerical exploration is conducted by solving the equations and looking for the value of 
$Z$ at a large time 
$\unicode[STIX]{x1D70F}=\unicode[STIX]{x1D70F}_{\text{max}}$. Figure 2 shows the value of 
$Z(\unicode[STIX]{x1D70F}_{\text{max}})$ in terms of 
$X_{0}\in [0,2\unicode[STIX]{x03C0}]$ for the specified values of 
$(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D703})$ and 
$\unicode[STIX]{x1D70F}_{\text{max}}=10^{3}$. Similar results have been obtained for larger values of 
$\unicode[STIX]{x1D70F}$ like 
$\unicode[STIX]{x1D70F}=10^{4}$, or even smaller ones, such as 
$\unicode[STIX]{x1D70F}=500$. For 
$\unicode[STIX]{x1D703}=\unicode[STIX]{x03C0}/4$, save a few exceptions for some values of 
$X_{0}$, all particles bounced back to the 
$z<0$ region. As explained in Bret (Reference Bret2015, Reference Bret2016b), this means that, in a more realistic setting, they would likely be trapped in the filaments.
Figure 3. Value of 
$Z(\unicode[STIX]{x1D70F}_{\text{max}})$ for 
$\unicode[STIX]{x1D703}=\unicode[STIX]{x03C0}/4$ and increasingly small 
$X_{0}$ intervals.
As evidenced by figure 2(a), the function 
$Z(\unicode[STIX]{x1D70F}_{\text{max}})$ is smooth for 
$\unicode[STIX]{x1D703}=0$. Yet, for 
$\unicode[STIX]{x1D703}=\unicode[STIX]{x03C0}/4$ (b), the result features regions where 
$Z(\unicode[STIX]{x1D70F}_{\text{max}})$ varies strongly with 
$X_{0}$. In order to identify chaos, figure 3 presents a series of successive zooms of figure 2(b), where the function 
$Z(\unicode[STIX]{x1D70F}_{\text{max}})$ is plotted over an increasingly small 
$X_{0}$ interval inside 
$X_{0}\in [\unicode[STIX]{x03C0}/4,\unicode[STIX]{x03C0}/2]$.
As expected from the analysis conducted in § 3, the system is chaotic. Note that chaotic trajectories in magnetic field lines have already been identified in the literature (Chen & Palmadesso Reference Chen and Palmadesso1986; Büchner & Zelenyi Reference Büchner and Zelenyi1989; Ram & Dasgupta Reference Ram and Dasgupta2010; Cambon et al. Reference Cambon, Leoncini, Vittot, Dumont and Garbet2014).
Figure 2 has been plotted by solving the system for 
$N+1$ particles shot from 
$X_{0}(j)=j2\unicode[STIX]{x03C0}/N$ with 
$j=0\ldots N$. We denote by 
$Z_{j}(\unicode[STIX]{x1D70F}_{\text{max}})$ the value of 
$Z$ reached by the 
$j$th particle at 
$\unicode[STIX]{x1D70F}=\unicode[STIX]{x1D70F}_{\text{max}}$. Then, we define the following function,
$$\begin{eqnarray}\unicode[STIX]{x1D719}(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D703})=\frac{1}{N+1}\mathop{\sum }_{j=0}^{N}{\mathcal{H}}[-Z_{j}(\unicode[STIX]{x1D70F}_{\text{max}})],\end{eqnarray}$$ where 
${\mathcal{H}}$ is again the Heaviside function.
Figure 4. Plot on the function 
$\unicode[STIX]{x1D719}$ defined by (5.1), in terms of 
$\unicode[STIX]{x1D6FC}$ and for 
$\unicode[STIX]{x1D703}=0$ and 
$\unicode[STIX]{x03C0}/5$.
The function 
$\unicode[STIX]{x1D719}$ represents therefore the fraction of particles that bounced back against the magnetic filaments. Figure 4(a) plots it in terms of 
$\unicode[STIX]{x1D6FC}$ for 
$\unicode[STIX]{x1D703}=0$. For 
$\unicode[STIX]{x1D6FC}=0$, that is 
$B_{0}=0$, approximately 40 % of the particles bounce back, i.e. are trapped in the filaments. As 
$\unicode[STIX]{x1D6FC}$ is increased, the field 
$\unicode[STIX]{x1D63D}_{0}$ guides the test particles more and more efficiently until 
$\unicode[STIX]{x1D6FC}\sim 0.5$, where all the particles stream through the filaments. In turn, figure 4(b) displays the case 
$\unicode[STIX]{x1D703}=\unicode[STIX]{x03C0}/5$. Being oblique, the field 
$\unicode[STIX]{x1D63D}_{0}$ is less efficient in guiding the particles through the filaments, and more efficient in trapping them inside. As a result, it takes a higher value of 
$B_{0}$, that is, 
$\unicode[STIX]{x1D6FC}=1.4$, to reach 
$\unicode[STIX]{x1D719}=0$.
Figure 5. (a) Numerical computation of 
$\unicode[STIX]{x1D6FC}_{c}(\unicode[STIX]{x1D703})$ (blue dots) compared to 
$1/\cos \unicode[STIX]{x1D703}$ (red line). (b) Values of the 
$\unicode[STIX]{x1D705}(\unicode[STIX]{x1D703})$ function entering the expression of 
$\unicode[STIX]{x1D6FC}_{c}$ in (5.3), in terms of 
$\unicode[STIX]{x1D703}$.
Similar numerical calculations have been conducted for various values of 
$\unicode[STIX]{x1D703}\in [0,\unicode[STIX]{x03C0}/2]$. We finally define 
$\unicode[STIX]{x1D6FC}_{c}(\unicode[STIX]{x1D703})$ as,
$$\begin{eqnarray}\unicode[STIX]{x1D719}(\unicode[STIX]{x1D6FC}_{c})=0.\end{eqnarray}$$ Here, 
$\unicode[STIX]{x1D6FC}_{c}(\unicode[STIX]{x1D703})$ is therefore the threshold value of 
$\unicode[STIX]{x1D6FC}$ beyond which all particles bounce back against the filamented region, i.e. 
$\unicode[STIX]{x1D719}(\unicode[STIX]{x1D6FC}\geqslant \unicode[STIX]{x1D6FC}_{c})=0$. It is plotted in figure 5 and can be well approximated by,
$$\begin{eqnarray}\unicode[STIX]{x1D6FC}_{c}=\unicode[STIX]{x1D705}(\unicode[STIX]{x1D703})\frac{1}{\cos \unicode[STIX]{x1D703}},\end{eqnarray}$$ where 
$\unicode[STIX]{x1D705}(\unicode[STIX]{x1D703})$ is of order unity (see figure 5b).
Figure 6. Same as figure 2(b), but for 
$\unicode[STIX]{x1D703}=-\unicode[STIX]{x03C0}/4$.
5.1 Case 
$\unicode[STIX]{x1D703}<0$
As already noticed, there is no invariance by the change 
$\unicode[STIX]{x1D703}\rightarrow -\unicode[STIX]{x1D703}$. Figure 6 plots the counterpart of figure 2(b), but for 
$\unicode[STIX]{x1D703}=-\unicode[STIX]{x03C0}/4$. Although quite similar, the results are not identical. The numerical analysis detailed above for 
$\unicode[STIX]{x1D703}\in [0,\unicode[STIX]{x03C0}/2]$ has been conducted for 
$\unicode[STIX]{x1D703}\in [-\unicode[STIX]{x03C0}/2,0]$. The function 
$\unicode[STIX]{x1D6FC}_{c}(\unicode[STIX]{x1D703}<0)$ again adjusts very well to the right-hand side of (5.3), with the values of 
$\unicode[STIX]{x1D705}(\unicode[STIX]{x1D703})$ plotted in figure 5(b).
6 Conclusion
A model previously developed to study test particle trapping in magnetic filaments has been extended to the case of an oblique external magnetic field. The result makes perfect physical sense: up to a constant 
$\unicode[STIX]{x1D705}$ of order unity, only the component of the field parallel to the filaments is relevant. The criterion obtained in Bret (Reference Bret2016b) for a flow-aligned field, namely that particles are trapped if 
$\unicode[STIX]{x1D6FC}>1/2$, now reads,
$$\begin{eqnarray}\unicode[STIX]{x1D6FC}>\frac{\unicode[STIX]{x1D705}(\unicode[STIX]{x1D703})}{\cos \unicode[STIX]{x1D703}},\end{eqnarray}$$ where 
$\unicode[STIX]{x1D705}(\unicode[STIX]{x1D703})$ is of order unity. As a consequence, a parallel field affects the shock more than an oblique one. Kinetic effects triggered by a parallel field can significantly modify the shock structure while a perpendicular field will rather ‘help’ the shock formation. This is in agreement with theoretical works which found a parallel field can divide by 2 the density jump expected from the Magnetohydrodynamic (MHD) Rankine–Hugoniot conditions (Bret et al. Reference Bret, Pe’er, Sironi, Sa̧dowski and Narayan2017; Bret & Narayan Reference Bret and Narayan2018), while the departure from MHD is less pronounced in the perpendicular case (Bret & Narayan Reference Bret and Narayan2019).
Acknowledgements
A.B. acknowledges support by grants ENE2016-75703-R from the Spanish Ministerio de Educación and SBPLY/17/180501/000264 from the Junta de Comunidades de Castilla-La Mancha. Thanks are due to I. Kourakis and D. Bénisti for enriching discussions.
