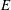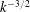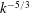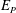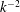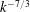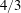1 Introduction
For a large variety of astrophysical and geophysical turbulent flows such as in the interstellar medium and stellar winds, the fluid can be conductive, thus creating a complex interplay between the magnetic and velocity fields. The dynamics of both fields can be significantly altered depending on the forcing mechanisms applied or not to the turbulent flow. A relevant framework to model such configurations is magnetohydrodynamics (MHD) turbulence, where the two fields are strongly coupled through the Lorentz force. The MHD framework has been considered multiple times to describe low frequency solar wind dynamics for instance (Galtier Reference Galtier2009; Boldyrev et al. Reference Boldyrev, Perez, Borovsky and Podesta2011).
In the last decades, multiple configurations have been studied, from isotropic MHD turbulence (IMHDT) (Pouquet, Frisch & Léorat Reference Pouquet, Frisch and Léorat1976; Müller & Biskamp Reference Müller and Biskamp2000; Müller & Grappin Reference Müller and Grappin2004; Carati et al.
Reference Carati, Debliquy, Knaepen, Teaca and Verma2006; Yoshimatsu Reference Yoshimatsu2012) to strong MHD where a mean magnetic field renders the flow highly anisotropic (Müller, Biskamp & Grappin Reference Müller, Biskamp and Grappin2003; Müller & Grappin Reference Müller and Grappin2005; Mason, Cattaneo & Boldyrev Reference Mason, Cattaneo and Boldyrev2008; Perez & Boldyrev Reference Perez and Boldyrev2009; Boldyrev et al.
Reference Boldyrev, Perez, Borovsky and Podesta2011; Perez et al.
Reference Perez, Mason, Boldyrev and Cattaneo2012), through weak MHD where the flow tends to be two-dimensional with a dynamics mainly governed by waves rather than inertial effects (Galtier, Pouquet & Mangeney Reference Galtier, Pouquet and Mangeney2005; Boldyrev & Perez Reference Boldyrev and Perez2009; Galtier Reference Galtier2009) and quasi-static MHD where only the equation for the velocity field is considered, with a ohmic term (Favier et al.
Reference Favier, Godeferd, Cambon, Delache and Bos2011). Obviously, the previous list is not exhaustive and several other frameworks exist: see Biskamp (Reference Biskamp2003), Galtier (Reference Galtier2016) for a review. It appears than even in the simplest case, namely IMHDT without kinetic and magnetic helicities or a mean magnetic field, two different inertial scalings are found for the spectrum
![]() $E(k,t)$
of the total energy: the
$E(k,t)$
of the total energy: the
![]() $k^{-3/2}$
scaling following the phenomenology by Iroshnikov (Reference Iroshnikov1964), Kraichnan (Reference Kraichnan1965), hereafter IK; and the hydrodynamic Kolmogorov (Reference Kolmogorov1941) phenomenology yielding a
$k^{-3/2}$
scaling following the phenomenology by Iroshnikov (Reference Iroshnikov1964), Kraichnan (Reference Kraichnan1965), hereafter IK; and the hydrodynamic Kolmogorov (Reference Kolmogorov1941) phenomenology yielding a
![]() $k^{-5/3}$
inertial scaling. This discrepancy is an illustration of the complexity of MHD turbulence, even in an apparently simple framework: it seems that in some of the direct numerical simulations (DNS) dealing with fully isotropic MHD, sometimes the Reynolds numbers is not large enough so that the
$k^{-5/3}$
inertial scaling. This discrepancy is an illustration of the complexity of MHD turbulence, even in an apparently simple framework: it seems that in some of the direct numerical simulations (DNS) dealing with fully isotropic MHD, sometimes the Reynolds numbers is not large enough so that the
![]() $k^{-3/2}$
and
$k^{-3/2}$
and
![]() $k^{-5/3}$
inertial scalings can be hardly distinguished.
$k^{-5/3}$
inertial scalings can be hardly distinguished.
A good way to get rid of the Reynolds number limitation could be to use spectral models, such as the eddy-damped quasi-normal Markovian (EDQNM) approximation (Orszag Reference Orszag1970). Using an earlier fundamental study (Kraichnan & Nagarajan Reference Kraichnan and Nagarajan1967), this closure was further extended from hydrodynamics turbulence to isotropic helical MHD by Pouquet et al. (Reference Pouquet, Frisch and Léorat1976): in the latter work, which also investigates the effect of kinetic helicity and magnetic helicity, the IK scaling
![]() $E\sim k^{-3/2}$
is obtained as a consequence of the modelling choice, along with the inverse cascade of magnetic helicity in
$E\sim k^{-3/2}$
is obtained as a consequence of the modelling choice, along with the inverse cascade of magnetic helicity in
![]() $k^{-2}$
, a feature which will not be addressed here.
$k^{-2}$
, a feature which will not be addressed here.
Note that both the Iroshnikov (Reference Iroshnikov1964) and Kraichnan (Reference Kraichnan1965) approaches yield the
![]() $k^{-3/2}$
inertial scaling, but it is worth recalling that they use very different arguments. For the former, a mean magnetic field
$k^{-3/2}$
inertial scaling, but it is worth recalling that they use very different arguments. For the former, a mean magnetic field
![]() $\boldsymbol{B}^{0}$
is considered, thus it is essentially an anisotropic configuration. Whereas for the latter, no external magnetic field is present, and it is considered that at each scale
$\boldsymbol{B}^{0}$
is considered, thus it is essentially an anisotropic configuration. Whereas for the latter, no external magnetic field is present, and it is considered that at each scale
![]() $\unicode[STIX]{x1D706}$
, the magnetic fluctuations of larger scales
$\unicode[STIX]{x1D706}$
, the magnetic fluctuations of larger scales
![]() $l\geqslant \unicode[STIX]{x1D706}$
can be seen as a local mean magnetic field. Both methods provide the inertial
$l\geqslant \unicode[STIX]{x1D706}$
can be seen as a local mean magnetic field. Both methods provide the inertial
![]() $k^{-3/2}$
scaling but are fundamentally different. Hence, the vision of Iroshnikov (Reference Iroshnikov1964) may be compatible with DNS results in which
$k^{-3/2}$
scaling but are fundamentally different. Hence, the vision of Iroshnikov (Reference Iroshnikov1964) may be compatible with DNS results in which
![]() $E\sim k_{\bot }^{-3/2}$
(Müller & Grappin Reference Müller and Grappin2005; Boldyrev Reference Boldyrev2006; Mason et al.
Reference Mason, Cattaneo and Boldyrev2008; Perez & Boldyrev Reference Perez and Boldyrev2009; Boldyrev et al.
Reference Boldyrev, Perez, Borovsky and Podesta2011; Perez et al.
Reference Perez, Mason, Boldyrev and Cattaneo2012), where
$E\sim k_{\bot }^{-3/2}$
(Müller & Grappin Reference Müller and Grappin2005; Boldyrev Reference Boldyrev2006; Mason et al.
Reference Mason, Cattaneo and Boldyrev2008; Perez & Boldyrev Reference Perez and Boldyrev2009; Boldyrev et al.
Reference Boldyrev, Perez, Borovsky and Podesta2011; Perez et al.
Reference Perez, Mason, Boldyrev and Cattaneo2012), where
![]() $k_{\bot }$
is the component of the wavevector
$k_{\bot }$
is the component of the wavevector
![]() $\boldsymbol{k}$
perpendicular to the imposed mean magnetic field. At variance with this
$\boldsymbol{k}$
perpendicular to the imposed mean magnetic field. At variance with this
![]() $k_{\bot }^{-3/2}$
scaling, Goldreich & Sridhar (Reference Goldreich and Sridhar1995) predicts
$k_{\bot }^{-3/2}$
scaling, Goldreich & Sridhar (Reference Goldreich and Sridhar1995) predicts
![]() $k_{\bot }^{-5/3}$
, and there are arguments and simulations in favour of this scaling too (Beresnyak Reference Beresnyak2011, Reference Beresnyak2014).
$k_{\bot }^{-5/3}$
, and there are arguments and simulations in favour of this scaling too (Beresnyak Reference Beresnyak2011, Reference Beresnyak2014).
Therefore, two questions arise from these considerations. What is the inertial scaling of
![]() $E$
in terms of
$E$
in terms of
![]() $k_{\bot }$
in a anisotropic configuration? And in terms of
$k_{\bot }$
in a anisotropic configuration? And in terms of
![]() $k$
in the isotropic case? Even if the former is of great interest nowadays, studying isotropic MHD remains important and relevant as indicated by Mininni & Pouquet (Reference Mininni and Pouquet2007), namely: ‘in the absence of
$k$
in the isotropic case? Even if the former is of great interest nowadays, studying isotropic MHD remains important and relevant as indicated by Mininni & Pouquet (Reference Mininni and Pouquet2007), namely: ‘in the absence of
![]() $\boldsymbol{B}^{0}$
and for isotropic initial conditions, one may assume that isotropy is still preserved in the large and intermediate scales’. In addition for IMHDT, it has been shown (i) in Lee et al. (Reference Lee, Brachet, Pouquet, Mininni and Rosenberg2010) that the inertial scaling of
$\boldsymbol{B}^{0}$
and for isotropic initial conditions, one may assume that isotropy is still preserved in the large and intermediate scales’. In addition for IMHDT, it has been shown (i) in Lee et al. (Reference Lee, Brachet, Pouquet, Mininni and Rosenberg2010) that the inertial scaling of
![]() $E$
strongly depends at short times on initial parameters; and (ii) in Alexakis (Reference Alexakis2013), with non-zero magnetic helicity, that with distinct helical forcing terms for the velocity and magnetic fields of various intensities, the resulting kinetic energy spectrum scales more like
$E$
strongly depends at short times on initial parameters; and (ii) in Alexakis (Reference Alexakis2013), with non-zero magnetic helicity, that with distinct helical forcing terms for the velocity and magnetic fields of various intensities, the resulting kinetic energy spectrum scales more like
![]() $k^{-3/2}$
and the magnetic energy spectrum more like
$k^{-3/2}$
and the magnetic energy spectrum more like
![]() $k^{-5/3}$
. These two examples further illustrate the complexity of IMHDT and that there are still open questions and mechanisms to be understood. This is why in the present work we study isotropic MHD with EDQNM, without mean magnetic field, to analyse different topics, such as the decay of the total energy, whose prediction is a fundamental question. The deep understanding of isotropic MHD is a necessary first step toward the modelling of strong MHD, where a three-dimensional EDQNM model in terms of
$k^{-5/3}$
. These two examples further illustrate the complexity of IMHDT and that there are still open questions and mechanisms to be understood. This is why in the present work we study isotropic MHD with EDQNM, without mean magnetic field, to analyse different topics, such as the decay of the total energy, whose prediction is a fundamental question. The deep understanding of isotropic MHD is a necessary first step toward the modelling of strong MHD, where a three-dimensional EDQNM model in terms of
![]() $\boldsymbol{k}$
should be analytically derived, analogously to what exists for rotation (Cambon & Jacquin Reference Cambon and Jacquin1989; Cambon, Mansour & Godeferd Reference Cambon, Mansour and Godeferd1997), and this will be reported elsewhere.
$\boldsymbol{k}$
should be analytically derived, analogously to what exists for rotation (Cambon & Jacquin Reference Cambon and Jacquin1989; Cambon, Mansour & Godeferd Reference Cambon, Mansour and Godeferd1997), and this will be reported elsewhere.
As mentioned above, the decay of the total energy
![]() $K$
deserves some attention. Indeed, its prediction remains quite controversial: several decay rates are proposed with no clear dependence on initial conditions, such as the infrared slope
$K$
deserves some attention. Indeed, its prediction remains quite controversial: several decay rates are proposed with no clear dependence on initial conditions, such as the infrared slope
![]() $\unicode[STIX]{x1D70E}$
of the spectrum at large scales
$\unicode[STIX]{x1D70E}$
of the spectrum at large scales
![]() $E(k\rightarrow 0)\sim k^{\unicode[STIX]{x1D70E}}$
, except the work of Galtier, Politano & Pouquet (Reference Galtier, Politano and Pouquet1997) which will be discussed in more detail later. Yet, the total energy
$E(k\rightarrow 0)\sim k^{\unicode[STIX]{x1D70E}}$
, except the work of Galtier, Politano & Pouquet (Reference Galtier, Politano and Pouquet1997) which will be discussed in more detail later. Yet, the total energy
![]() $K$
, defined as the sum of the kinetic energy
$K$
, defined as the sum of the kinetic energy
![]() $K_{V}$
and the magnetic energy
$K_{V}$
and the magnetic energy
![]() $K_{B}$
, is an inviscid invariant of MHD turbulence and as such deserves great theoretical interest. If one compares the number of papers dedicated to the decay of kinetic energy in hydrodynamics turbulence with the ones dedicated to the decay of total energy in MHD turbulence, the difference is striking. Using EDQNM, we aim at deriving a theoretical prediction for the decay of
$K_{B}$
, is an inviscid invariant of MHD turbulence and as such deserves great theoretical interest. If one compares the number of papers dedicated to the decay of kinetic energy in hydrodynamics turbulence with the ones dedicated to the decay of total energy in MHD turbulence, the difference is striking. Using EDQNM, we aim at deriving a theoretical prediction for the decay of
![]() $K$
at large Reynolds numbers, similarly to what was recently done for the helicity and the passive scalar variance in homogeneous isotropic turbulence (HIT) (Briard et al.
Reference Briard, Gomez, Sagaut and Memari2015; Briard & Gomez Reference Briard and Gomez2017).
$K$
at large Reynolds numbers, similarly to what was recently done for the helicity and the passive scalar variance in homogeneous isotropic turbulence (HIT) (Briard et al.
Reference Briard, Gomez, Sagaut and Memari2015; Briard & Gomez Reference Briard and Gomez2017).
Moreover, EDQNM permits to analyse in a simple way pressure spectra: in the framework of HIT and starting from the Poisson equation, it is possible to express the pressure spectrum as a function of the kinetic energy spectra (Lesieur, Ossia & Metais Reference Lesieur, Ossia and Metais1999; Meldi & Sagaut Reference Meldi and Sagaut2013b ). Here for MHD turbulence, there is an additional contribution of the magnetic field to the Poisson equation, coming from the Laplace force. Thus, it is proposed to study the respective contributions of the kinetic and magnetic fields to the total pressure spectrum.
In addition to magnetic helicity (not studied here) and total energy, MHD turbulence has a third inviscid invariant, namely cross-helicity, which is the scalar product of the fluctuating velocity and magnetic fields. The first analytical considerations about the spectral modelling of cross-helicity date back to Frisch et al. (Reference Frisch, Pouquet, Léorat and Mazure1975). Later, simplified EDQNM equations were used by Grappin et al. (Reference Grappin, Frisch, Léorat and Pouquet1982), Grappin, Pouquet & Léorat (Reference Grappin, Pouquet and Léorat1983) to investigate the influence of cross-helicity on the kinetic and magnetic energy spectra. The main hypothesis in these two references, on top of the EDQNM procedure, was to consider equipartition between kinetic and magnetic energies, by assuming the presence of a mean magnetic field with random orientation, so that the flow remained statistically isotropic instead of axisymmetric. Thus, it appears that high Reynolds numbers simulations of the full EDQNM equations for MHD with cross-helicity were not presented, even though the interest in the cross-helicity increased in the past years (Chandran Reference Chandran2008; Matthaeus et al. Reference Matthaeus, Pouquet, Mininni, Dmitruk and Breech2008; Beresnyak & Lazarian Reference Beresnyak and Lazarian2008; Perez & Boldyrev Reference Perez and Boldyrev2009; Boldyrev et al. Reference Boldyrev, Perez, Borovsky and Podesta2011). As said earlier, we choose to address isotropic MHD turbulence here, without a background mean magnetic field, to further understand the interactions between the cross-correlation and the kinetic and magnetic fields, and to better disentangle strong anisotropic effects from intrinsic properties of the velocity–magnetic correlation.
The manuscript is organized as follows. In § 2, the main equations of MHD are recalled, and the EDQNM formalism for the kinetic, magnetic and cross-helical fields is presented. Then, in § 3, balanced isotropic MHD is considered, with zero cross-correlation: first, inertial scalings of the kinetic, magnetic and residual spectra are addressed, along with some discussion about nonlinear transfers. Then, the decay of the total energy is investigated, and theoretical decay exponents are proposed and assessed numerically. Afterwards, in § 4, the emphasis is put on the modelling of the cross-helicity, its impact on spectral scalings and short-time dynamics; pressure spectra are also analysed. Section 5 is dedicated to statistics in physical space, with in particular the numerical assessment of the
![]() $4/3$
rd laws for total energy and cross-helicity. Conclusions and perspectives are gathered in the final section.
$4/3$
rd laws for total energy and cross-helicity. Conclusions and perspectives are gathered in the final section.
2 Spectral evolution equations for isotropic MHD turbulence
In this part, the evolution equations of the velocity and magnetic fields are presented with the spectral formalism: the emphasis is put on the second-order moments. To this end, the EDQNM approximation is used to close the nonlinear third-order correlations: some generality is kept in the derivations on purpose. Finally, in the framework of IMHDT turbulence, the final equations of the spherically averaged spectra are presented.
2.1 Spectral evolution equations of magnetohydrodynamics
The evolution equation of a conducting fluid of fluctuating velocity
![]() $u_{i}$
, submitted to the Laplace force (magnetic part of the Lorentz force), reads
$u_{i}$
, submitted to the Laplace force (magnetic part of the Lorentz force), reads
where
![]() $b_{i}$
is the fluctuating magnetic field,
$b_{i}$
is the fluctuating magnetic field,
![]() $\boldsymbol{B}^{0}$
a possible external mean magnetic field,
$\boldsymbol{B}^{0}$
a possible external mean magnetic field,
![]() $\unicode[STIX]{x1D708}$
the kinematic viscosity and
$\unicode[STIX]{x1D708}$
the kinematic viscosity and
![]() $p^{\ast }$
the total pressure. Both
$p^{\ast }$
the total pressure. Both
![]() $u_{i}$
and
$u_{i}$
and
![]() $b_{i}$
are solenoidal, i.e.
$b_{i}$
are solenoidal, i.e.
![]() $\text{div}(\boldsymbol{u})=\text{div}(\boldsymbol{b})=0$
. The equation of
$\text{div}(\boldsymbol{u})=\text{div}(\boldsymbol{b})=0$
. The equation of
![]() $b_{i}$
is obtained by combining the Maxwell–Faraday law, the Ohm law (without the Hall term) and the Maxwell–Ampère law, so that
$b_{i}$
is obtained by combining the Maxwell–Faraday law, the Ohm law (without the Hall term) and the Maxwell–Ampère law, so that
where
![]() $\unicode[STIX]{x1D702}$
is the magnetic diffusivity, or resistivity. We choose a unit magnetic Prandtl number, so that
$\unicode[STIX]{x1D702}$
is the magnetic diffusivity, or resistivity. We choose a unit magnetic Prandtl number, so that
![]() $\unicode[STIX]{x1D708}=\unicode[STIX]{x1D702}$
. When dropping
$\unicode[STIX]{x1D708}=\unicode[STIX]{x1D702}$
. When dropping
![]() $\boldsymbol{B}^{0}$
in the latter equation, one remarks that it is similar to the equation of vorticity
$\boldsymbol{B}^{0}$
in the latter equation, one remarks that it is similar to the equation of vorticity
![]() $\unicode[STIX]{x1D74E}$
, which is the so-called Batchelor analogy (Batchelor Reference Batchelor1950). Furthermore, it is worth noting that
$\unicode[STIX]{x1D74E}$
, which is the so-called Batchelor analogy (Batchelor Reference Batchelor1950). Furthermore, it is worth noting that
![]() $\boldsymbol{b}$
is a pseudo-vector like
$\boldsymbol{b}$
is a pseudo-vector like
![]() $\unicode[STIX]{x1D74E}$
, since it is defined as
$\unicode[STIX]{x1D74E}$
, since it is defined as
![]() $\unicode[STIX]{x1D735}\times \boldsymbol{a}$
, where the true vector
$\unicode[STIX]{x1D735}\times \boldsymbol{a}$
, where the true vector
![]() $\boldsymbol{a}$
is the magnetic potential (some considerations about the modelling of
$\boldsymbol{a}$
is the magnetic potential (some considerations about the modelling of
![]() $\boldsymbol{a}$
are proposed in appendix A.1).
$\boldsymbol{a}$
are proposed in appendix A.1).
The spectral counterpart of (2.1) and (2.2) are given by
where the Kraichnan operator is given by
![]() $2P_{imn}=k_{m}P_{in}+k_{n}P_{im}$
, with the projector
$2P_{imn}=k_{m}P_{in}+k_{n}P_{im}$
, with the projector
![]() $P_{ij}=\unicode[STIX]{x1D6FF}_{ij}-\unicode[STIX]{x1D6FC}_{i}\unicode[STIX]{x1D6FC}_{j}$
and
$P_{ij}=\unicode[STIX]{x1D6FF}_{ij}-\unicode[STIX]{x1D6FC}_{i}\unicode[STIX]{x1D6FC}_{j}$
and
![]() $\unicode[STIX]{x1D6FC}_{i}=k_{i}/k$
, and
$\unicode[STIX]{x1D6FC}_{i}=k_{i}/k$
, and
![]() $\hat{(\cdot )}$
denotes the Fourier transform. In homogeneous turbulence, the spectral second-order moments of interest, namely the Reynolds tensor
$\hat{(\cdot )}$
denotes the Fourier transform. In homogeneous turbulence, the spectral second-order moments of interest, namely the Reynolds tensor
![]() $\hat{\unicode[STIX]{x1D619}}_{ij}$
, the magnetic tensor
$\hat{\unicode[STIX]{x1D619}}_{ij}$
, the magnetic tensor
![]() $\hat{\unicode[STIX]{x1D609}}_{ij}$
, and the velocity–magnetic correlation
$\hat{\unicode[STIX]{x1D609}}_{ij}$
, and the velocity–magnetic correlation
![]() $\hat{\unicode[STIX]{x1D60F}}_{ij}^{c}$
, are defined as
$\hat{\unicode[STIX]{x1D60F}}_{ij}^{c}$
, are defined as
where
![]() $(\cdot )^{\ast }$
denotes the complex conjugate, and
$(\cdot )^{\ast }$
denotes the complex conjugate, and
![]() $\langle \cdot \rangle$
an ensemble average. Their evolution equations read
$\langle \cdot \rangle$
an ensemble average. Their evolution equations read
where the time dependence has been omitted for clarity. One can note from (2.10) that in the presence of a mean magnetic field
![]() $\boldsymbol{B}^{0}$
, kinetic helicity and magnetic helicity could produce the cross-correlation
$\boldsymbol{B}^{0}$
, kinetic helicity and magnetic helicity could produce the cross-correlation
![]() $\hat{\unicode[STIX]{x1D60F}}_{ij}^{c}$
. The nonlinear kinetic transfer
$\hat{\unicode[STIX]{x1D60F}}_{ij}^{c}$
. The nonlinear kinetic transfer
![]() $T_{ij}^{\text{V(hyd)}}$
, which is always present in hydrodynamics turbulence, is the same as in HIT, meaning
$T_{ij}^{\text{V(hyd)}}$
, which is always present in hydrodynamics turbulence, is the same as in HIT, meaning
where
![]() $\unicode[STIX]{x1D61A}_{ijn}^{uuu}$
is the spectral triple velocity correlation
$\unicode[STIX]{x1D61A}_{ijn}^{uuu}$
is the spectral triple velocity correlation
The nonlinear magnetic transfer
![]() $\unicode[STIX]{x1D61B}_{ij}^{\text{V(mag)}}$
represents the retro-action of the magnetic field on the velocity one through the Laplace force, and reads
$\unicode[STIX]{x1D61B}_{ij}^{\text{V(mag)}}$
represents the retro-action of the magnetic field on the velocity one through the Laplace force, and reads
where
![]() $\unicode[STIX]{x1D61A}_{ijn}^{ubb}$
is the spectral velocity–magnetic–magnetic correlation defined as
$\unicode[STIX]{x1D61A}_{ijn}^{ubb}$
is the spectral velocity–magnetic–magnetic correlation defined as
Then, for the magnetic equation, one has
Finally, for the cross-helicity, the nonlinear transfer involves two additional three-point correlations
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D61B}_{ij}^{c}(\boldsymbol{k},t) & = & \displaystyle k_{l}\int \left(\unicode[STIX]{x1D61A}_{lji}^{uub\ast }(\boldsymbol{p},\boldsymbol{k},t)-\unicode[STIX]{x1D61A}_{jli}^{uub\ast }(\boldsymbol{p},\boldsymbol{k},t)\right)\text{d}^{3}\boldsymbol{p}\nonumber\\ \displaystyle & & \displaystyle +\,P_{imn}(\boldsymbol{k})\int \left(\unicode[STIX]{x1D61A}_{njm}^{uub}(\boldsymbol{k},\boldsymbol{p},t)-\unicode[STIX]{x1D61A}_{njm}^{bbb}(\boldsymbol{k},\boldsymbol{p},t)\right)\text{d}^{3}\boldsymbol{p},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D61B}_{ij}^{c}(\boldsymbol{k},t) & = & \displaystyle k_{l}\int \left(\unicode[STIX]{x1D61A}_{lji}^{uub\ast }(\boldsymbol{p},\boldsymbol{k},t)-\unicode[STIX]{x1D61A}_{jli}^{uub\ast }(\boldsymbol{p},\boldsymbol{k},t)\right)\text{d}^{3}\boldsymbol{p}\nonumber\\ \displaystyle & & \displaystyle +\,P_{imn}(\boldsymbol{k})\int \left(\unicode[STIX]{x1D61A}_{njm}^{uub}(\boldsymbol{k},\boldsymbol{p},t)-\unicode[STIX]{x1D61A}_{njm}^{bbb}(\boldsymbol{k},\boldsymbol{p},t)\right)\text{d}^{3}\boldsymbol{p},\end{eqnarray}$$
with
More details about cross-helical nonlinear transfers are given later in § 4 for imbalanced MHD.
2.2 EDQNM procedure and eddy damping
In this part, the EDQNM procedure is briefly presented, and more details can be found in Sagaut & Cambon (Reference Sagaut and Cambon2008) for the non-conducting case. The first step is to express
![]() $\unicode[STIX]{x1D61B}_{ijn}^{\text{xxx}}$
, which is the nonlinear transfer in the equation for the triple correlation
$\unicode[STIX]{x1D61B}_{ijn}^{\text{xxx}}$
, which is the nonlinear transfer in the equation for the triple correlation
![]() $\unicode[STIX]{x1D61A}_{ijn}^{\text{xxx}}$
, as function of the previous second-order moments thanks to the quasi-normal approximation, where
$\unicode[STIX]{x1D61A}_{ijn}^{\text{xxx}}$
, as function of the previous second-order moments thanks to the quasi-normal approximation, where
![]() $x$
stands for either
$x$
stands for either
![]() $u$
or
$u$
or
![]() $b$
. Then, an eddy-damping term is used to model the departure of the statistics from normal laws. In hydrodynamics turbulence, this yields
$b$
. Then, an eddy-damping term is used to model the departure of the statistics from normal laws. In hydrodynamics turbulence, this yields
where
![]() $\unicode[STIX]{x1D61B}_{ijn}^{\text{QN,uuu}}$
is the quasi-normal expression of
$\unicode[STIX]{x1D61B}_{ijn}^{\text{QN,uuu}}$
is the quasi-normal expression of
![]() $\unicode[STIX]{x1D61B}_{ijn}^{\text{uuu}}$
, and
$\unicode[STIX]{x1D61B}_{ijn}^{\text{uuu}}$
, and
![]() $\unicode[STIX]{x1D707}_{1}$
is the classical eddy-damping term
$\unicode[STIX]{x1D707}_{1}$
is the classical eddy-damping term
with
![]() $E_{V}$
the kinetic energy spectrum. This procedure must be repeated in MHD for
$E_{V}$
the kinetic energy spectrum. This procedure must be repeated in MHD for
![]() $\unicode[STIX]{x1D61B}_{ijn}^{\text{QN,bbb}}$
,
$\unicode[STIX]{x1D61B}_{ijn}^{\text{QN,bbb}}$
,
![]() $\unicode[STIX]{x1D61B}_{ijn}^{\text{QN,uub}}$
and
$\unicode[STIX]{x1D61B}_{ijn}^{\text{QN,uub}}$
and
![]() $\unicode[STIX]{x1D61B}_{ijn}^{\text{QN,ubb}}$
. Using the definitions of the three-point correlations and the expressions of the nonlinear transfers (2.11)–(2.18) one gets after some algebra
$\unicode[STIX]{x1D61B}_{ijn}^{\text{QN,ubb}}$
. Using the definitions of the three-point correlations and the expressions of the nonlinear transfers (2.11)–(2.18) one gets after some algebra
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D61B}_{ijn}^{\text{QN,ubb}}(\boldsymbol{k},\boldsymbol{p}) & = & \displaystyle 2P_{jpq}(\boldsymbol{k})\left[\hat{\unicode[STIX]{x1D60F}}_{pi}^{c}(\boldsymbol{q})\hat{\unicode[STIX]{x1D60F}}_{qn}^{c}(\boldsymbol{p})-\hat{\unicode[STIX]{x1D609}}_{pi}(\boldsymbol{q})\hat{\unicode[STIX]{x1D609}}_{qn}(\boldsymbol{p})\right]\nonumber\\ \displaystyle & & \displaystyle +\,p_{l}\left[\hat{\unicode[STIX]{x1D619}}_{lj}(\boldsymbol{k})B_{ni}(\boldsymbol{q})+\hat{\unicode[STIX]{x1D60F}}_{li}^{c}(\boldsymbol{q})\hat{\unicode[STIX]{x1D60F}}_{jn}^{c}(-\boldsymbol{k})-\hat{\unicode[STIX]{x1D60F}}_{ni}^{c}(\boldsymbol{q})\hat{\unicode[STIX]{x1D60F}}_{jl}^{c}(-\boldsymbol{k})-\hat{\unicode[STIX]{x1D619}}_{nj}(\boldsymbol{k})B_{li}(\boldsymbol{q})\right]\nonumber\\ \displaystyle & & \displaystyle +\,q_{l}\left[\hat{\unicode[STIX]{x1D619}}_{lj}(\boldsymbol{k})B_{in}(\boldsymbol{p})+\hat{\unicode[STIX]{x1D60F}}_{ln}^{c}(\boldsymbol{p})\hat{\unicode[STIX]{x1D60F}}_{ji}^{c}(-\boldsymbol{k})-\hat{\unicode[STIX]{x1D60F}}_{in}^{c}(\boldsymbol{p})\hat{\unicode[STIX]{x1D60F}}_{jl}^{c}(-\boldsymbol{k})-\hat{\unicode[STIX]{x1D619}}_{ij}(\boldsymbol{k})B_{ln}(\boldsymbol{p})\right],\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D61B}_{ijn}^{\text{QN,ubb}}(\boldsymbol{k},\boldsymbol{p}) & = & \displaystyle 2P_{jpq}(\boldsymbol{k})\left[\hat{\unicode[STIX]{x1D60F}}_{pi}^{c}(\boldsymbol{q})\hat{\unicode[STIX]{x1D60F}}_{qn}^{c}(\boldsymbol{p})-\hat{\unicode[STIX]{x1D609}}_{pi}(\boldsymbol{q})\hat{\unicode[STIX]{x1D609}}_{qn}(\boldsymbol{p})\right]\nonumber\\ \displaystyle & & \displaystyle +\,p_{l}\left[\hat{\unicode[STIX]{x1D619}}_{lj}(\boldsymbol{k})B_{ni}(\boldsymbol{q})+\hat{\unicode[STIX]{x1D60F}}_{li}^{c}(\boldsymbol{q})\hat{\unicode[STIX]{x1D60F}}_{jn}^{c}(-\boldsymbol{k})-\hat{\unicode[STIX]{x1D60F}}_{ni}^{c}(\boldsymbol{q})\hat{\unicode[STIX]{x1D60F}}_{jl}^{c}(-\boldsymbol{k})-\hat{\unicode[STIX]{x1D619}}_{nj}(\boldsymbol{k})B_{li}(\boldsymbol{q})\right]\nonumber\\ \displaystyle & & \displaystyle +\,q_{l}\left[\hat{\unicode[STIX]{x1D619}}_{lj}(\boldsymbol{k})B_{in}(\boldsymbol{p})+\hat{\unicode[STIX]{x1D60F}}_{ln}^{c}(\boldsymbol{p})\hat{\unicode[STIX]{x1D60F}}_{ji}^{c}(-\boldsymbol{k})-\hat{\unicode[STIX]{x1D60F}}_{in}^{c}(\boldsymbol{p})\hat{\unicode[STIX]{x1D60F}}_{jl}^{c}(-\boldsymbol{k})-\hat{\unicode[STIX]{x1D619}}_{ij}(\boldsymbol{k})B_{ln}(\boldsymbol{p})\right],\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D61B}_{ijn}^{\text{QN,uub}}(\boldsymbol{k},\boldsymbol{p}) & = & \displaystyle 2P_{npq}(\boldsymbol{p})\left[\hat{\unicode[STIX]{x1D60F}}_{pj}^{c}(\boldsymbol{k})\hat{\unicode[STIX]{x1D619}}_{qi}(\boldsymbol{q})-\hat{\unicode[STIX]{x1D609}}_{pj}(\boldsymbol{k})\hat{\unicode[STIX]{x1D60F}}_{iq}^{c}(-\boldsymbol{q})\right]\nonumber\\ \displaystyle & & \displaystyle \!+\,2P_{ipq}(\boldsymbol{q})\left[\hat{\unicode[STIX]{x1D60F}}_{pj}^{c}(\boldsymbol{k})\hat{\unicode[STIX]{x1D619}}_{qn}(\boldsymbol{p})-\hat{\unicode[STIX]{x1D609}}_{pj}(\boldsymbol{k})\hat{\unicode[STIX]{x1D60F}}_{nq}^{c}(-\boldsymbol{p})\right]\nonumber\\ \displaystyle & & \displaystyle \!+\,k_{l}\left[\hat{\unicode[STIX]{x1D60F}}_{ij}^{c}(-\boldsymbol{q})\hat{\unicode[STIX]{x1D619}}_{ln}(\boldsymbol{p})+\hat{\unicode[STIX]{x1D60F}}_{nj}^{c}(-\boldsymbol{p})\hat{\unicode[STIX]{x1D619}}_{li}(\boldsymbol{q})-\hat{\unicode[STIX]{x1D60F}}_{nl}^{c}(-\boldsymbol{p})\hat{\unicode[STIX]{x1D619}}_{ji}(\boldsymbol{q})-\hat{\unicode[STIX]{x1D60F}}_{il}^{c}(-\boldsymbol{q})\hat{\unicode[STIX]{x1D619}}_{jn}(\boldsymbol{p})\right]\!,\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D61B}_{ijn}^{\text{QN,uub}}(\boldsymbol{k},\boldsymbol{p}) & = & \displaystyle 2P_{npq}(\boldsymbol{p})\left[\hat{\unicode[STIX]{x1D60F}}_{pj}^{c}(\boldsymbol{k})\hat{\unicode[STIX]{x1D619}}_{qi}(\boldsymbol{q})-\hat{\unicode[STIX]{x1D609}}_{pj}(\boldsymbol{k})\hat{\unicode[STIX]{x1D60F}}_{iq}^{c}(-\boldsymbol{q})\right]\nonumber\\ \displaystyle & & \displaystyle \!+\,2P_{ipq}(\boldsymbol{q})\left[\hat{\unicode[STIX]{x1D60F}}_{pj}^{c}(\boldsymbol{k})\hat{\unicode[STIX]{x1D619}}_{qn}(\boldsymbol{p})-\hat{\unicode[STIX]{x1D609}}_{pj}(\boldsymbol{k})\hat{\unicode[STIX]{x1D60F}}_{nq}^{c}(-\boldsymbol{p})\right]\nonumber\\ \displaystyle & & \displaystyle \!+\,k_{l}\left[\hat{\unicode[STIX]{x1D60F}}_{ij}^{c}(-\boldsymbol{q})\hat{\unicode[STIX]{x1D619}}_{ln}(\boldsymbol{p})+\hat{\unicode[STIX]{x1D60F}}_{nj}^{c}(-\boldsymbol{p})\hat{\unicode[STIX]{x1D619}}_{li}(\boldsymbol{q})-\hat{\unicode[STIX]{x1D60F}}_{nl}^{c}(-\boldsymbol{p})\hat{\unicode[STIX]{x1D619}}_{ji}(\boldsymbol{q})-\hat{\unicode[STIX]{x1D60F}}_{il}^{c}(-\boldsymbol{q})\hat{\unicode[STIX]{x1D619}}_{jn}(\boldsymbol{p})\right]\!,\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D61B}_{ijn}^{\text{QN,bbb}}(\boldsymbol{k},\boldsymbol{p}) & = & \displaystyle k_{l}\left[\hat{\unicode[STIX]{x1D60F}}_{li}^{c}(\boldsymbol{q})\hat{\unicode[STIX]{x1D609}}_{jn}(\boldsymbol{p})+\hat{\unicode[STIX]{x1D60F}}_{ln}^{c}(\boldsymbol{p})\hat{\unicode[STIX]{x1D609}}_{ji}(\boldsymbol{q})-\hat{\unicode[STIX]{x1D60F}}_{ji}^{c}(\boldsymbol{q})\hat{\unicode[STIX]{x1D609}}_{ln}(\boldsymbol{p})-\hat{\unicode[STIX]{x1D60F}}_{jn}^{c}(\boldsymbol{p})\hat{\unicode[STIX]{x1D609}}_{li}(\boldsymbol{q})\right]\nonumber\\ \displaystyle & & \displaystyle +\,p_{l}\left[\hat{\unicode[STIX]{x1D60F}}_{li}^{c}(\boldsymbol{q})\hat{\unicode[STIX]{x1D609}}_{nj}(\boldsymbol{k})+\hat{\unicode[STIX]{x1D609}}_{ni}(\boldsymbol{q})\hat{\unicode[STIX]{x1D60F}}_{lj}^{c}(\boldsymbol{k})-\hat{\unicode[STIX]{x1D60F}}_{ni}^{c}(\boldsymbol{q})\hat{\unicode[STIX]{x1D609}}_{lj}(\boldsymbol{k})-\hat{\unicode[STIX]{x1D60F}}_{nj}^{c}(\boldsymbol{k})\hat{\unicode[STIX]{x1D609}}_{li}(\boldsymbol{q})\right]\nonumber\\ \displaystyle & & \displaystyle +\,q_{l}\left[\hat{\unicode[STIX]{x1D60F}}_{ln}^{c}(\boldsymbol{p})\hat{\unicode[STIX]{x1D609}}_{ij}(\boldsymbol{k})+\hat{\unicode[STIX]{x1D609}}_{in}(\boldsymbol{p})\hat{\unicode[STIX]{x1D60F}}_{lj}^{c}(\boldsymbol{k})-\hat{\unicode[STIX]{x1D60F}}_{in}^{c}(\boldsymbol{p})\hat{\unicode[STIX]{x1D609}}_{lj}(\boldsymbol{k})-\hat{\unicode[STIX]{x1D60F}}_{ij}^{c}(\boldsymbol{k})\hat{\unicode[STIX]{x1D609}}_{ln}(\boldsymbol{p})\right].\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D61B}_{ijn}^{\text{QN,bbb}}(\boldsymbol{k},\boldsymbol{p}) & = & \displaystyle k_{l}\left[\hat{\unicode[STIX]{x1D60F}}_{li}^{c}(\boldsymbol{q})\hat{\unicode[STIX]{x1D609}}_{jn}(\boldsymbol{p})+\hat{\unicode[STIX]{x1D60F}}_{ln}^{c}(\boldsymbol{p})\hat{\unicode[STIX]{x1D609}}_{ji}(\boldsymbol{q})-\hat{\unicode[STIX]{x1D60F}}_{ji}^{c}(\boldsymbol{q})\hat{\unicode[STIX]{x1D609}}_{ln}(\boldsymbol{p})-\hat{\unicode[STIX]{x1D60F}}_{jn}^{c}(\boldsymbol{p})\hat{\unicode[STIX]{x1D609}}_{li}(\boldsymbol{q})\right]\nonumber\\ \displaystyle & & \displaystyle +\,p_{l}\left[\hat{\unicode[STIX]{x1D60F}}_{li}^{c}(\boldsymbol{q})\hat{\unicode[STIX]{x1D609}}_{nj}(\boldsymbol{k})+\hat{\unicode[STIX]{x1D609}}_{ni}(\boldsymbol{q})\hat{\unicode[STIX]{x1D60F}}_{lj}^{c}(\boldsymbol{k})-\hat{\unicode[STIX]{x1D60F}}_{ni}^{c}(\boldsymbol{q})\hat{\unicode[STIX]{x1D609}}_{lj}(\boldsymbol{k})-\hat{\unicode[STIX]{x1D60F}}_{nj}^{c}(\boldsymbol{k})\hat{\unicode[STIX]{x1D609}}_{li}(\boldsymbol{q})\right]\nonumber\\ \displaystyle & & \displaystyle +\,q_{l}\left[\hat{\unicode[STIX]{x1D60F}}_{ln}^{c}(\boldsymbol{p})\hat{\unicode[STIX]{x1D609}}_{ij}(\boldsymbol{k})+\hat{\unicode[STIX]{x1D609}}_{in}(\boldsymbol{p})\hat{\unicode[STIX]{x1D60F}}_{lj}^{c}(\boldsymbol{k})-\hat{\unicode[STIX]{x1D60F}}_{in}^{c}(\boldsymbol{p})\hat{\unicode[STIX]{x1D609}}_{lj}(\boldsymbol{k})-\hat{\unicode[STIX]{x1D60F}}_{ij}^{c}(\boldsymbol{k})\hat{\unicode[STIX]{x1D609}}_{ln}(\boldsymbol{p})\right].\end{eqnarray}$$
These expressions are the most general one can get: only homogeneity was assumed, not isotropy. They could be simplified by using classical
![]() $\boldsymbol{p}\leftrightarrow \boldsymbol{q}$
symmetry. Hereafter, isotropic MHD turbulence is considered, so that there is no mean magnetic field
$\boldsymbol{p}\leftrightarrow \boldsymbol{q}$
symmetry. Hereafter, isotropic MHD turbulence is considered, so that there is no mean magnetic field
![]() $\boldsymbol{B}^{0}$
. Firstly, in this framework with mirror symmetry invariance, also called isotropic balanced MHD, the cross-correlation
$\boldsymbol{B}^{0}$
. Firstly, in this framework with mirror symmetry invariance, also called isotropic balanced MHD, the cross-correlation
![]() $\hat{\unicode[STIX]{x1D60F}}_{ij}^{c}$
vanishes so that
$\hat{\unicode[STIX]{x1D60F}}_{ij}^{c}$
vanishes so that
![]() $\unicode[STIX]{x1D61B}_{imn}^{\text{QN,uub}}=\unicode[STIX]{x1D61B}_{imn}^{\text{QN,bbb}}=0$
, and only part of
$\unicode[STIX]{x1D61B}_{imn}^{\text{QN,uub}}=\unicode[STIX]{x1D61B}_{imn}^{\text{QN,bbb}}=0$
, and only part of
![]() $\unicode[STIX]{x1D61B}_{imn}^{\text{QN,ubb}}$
remains. The kinetic and magnetic helicities, contained in
$\unicode[STIX]{x1D61B}_{imn}^{\text{QN,ubb}}$
remains. The kinetic and magnetic helicities, contained in
![]() $\hat{\unicode[STIX]{x1D619}}_{ij}$
and
$\hat{\unicode[STIX]{x1D619}}_{ij}$
and
![]() $\hat{\unicode[STIX]{x1D609}}_{ij}$
and defined in the following section for generality purposes, are zero as well. Non-zero cross-helicity is considered in § 4.
$\hat{\unicode[STIX]{x1D609}}_{ij}$
and defined in the following section for generality purposes, are zero as well. Non-zero cross-helicity is considered in § 4.
Moreover, as intensively discussed in Pouquet et al. (Reference Pouquet, Frisch and Léorat1976), Baerenzung et al. (Reference Baerenzung, Politano, Ponty and Pouquet2008), an additional eddy-damping term
![]() $\unicode[STIX]{x1D707}_{A}$
should be added to
$\unicode[STIX]{x1D707}_{A}$
should be added to
![]() $\unicode[STIX]{x1D707}_{1}$
to take into account the propagation of Alfvén waves, where
$\unicode[STIX]{x1D707}_{1}$
to take into account the propagation of Alfvén waves, where
where
![]() $E_{B}$
is the magnetic energy spectrum. Furthermore
$E_{B}$
is the magnetic energy spectrum. Furthermore
![]() $E_{V}$
is replaced in (2.20) by the total energy spectrum
$E_{V}$
is replaced in (2.20) by the total energy spectrum
![]() $E=E_{V}+E_{B}$
, linked to the inviscid invariant total energy. The constant in
$E=E_{V}+E_{B}$
, linked to the inviscid invariant total energy. The constant in
![]() $\unicode[STIX]{x1D707}_{A}$
is chosen so that when
$\unicode[STIX]{x1D707}_{A}$
is chosen so that when
![]() $k\rightarrow \infty$
,
$k\rightarrow \infty$
,
![]() $\unicode[STIX]{x1D707}_{A}$
is the Alfvén time:
$\unicode[STIX]{x1D707}_{A}$
is the Alfvén time:
![]() $\unicode[STIX]{x1D707}_{A}^{-1}=(kb_{0})^{-1}=\unicode[STIX]{x1D70F}_{A}$
, where the magnetic energy in IMHDT reads
$\unicode[STIX]{x1D707}_{A}^{-1}=(kb_{0})^{-1}=\unicode[STIX]{x1D70F}_{A}$
, where the magnetic energy in IMHDT reads
![]() $3b_{0}^{2}/2$
.
$3b_{0}^{2}/2$
.
Combining the quasi-normal approximation, the eddy-damping terms and the classical Markovianization step to ensure realizability of the spectra in HIT (Orszag Reference Orszag1970; Lesieur Reference Lesieur2008; Sagaut & Cambon Reference Sagaut and Cambon2008), it is possible to express the triple correlations as function of the second-order moments for MHD, thus permitting to close the evolution equations (2.8)–(2.10)
where
![]() $\unicode[STIX]{x1D703}_{kpq}$
is the characteristic time of the third-order correlations, containing the eddy-damping terms, according to
$\unicode[STIX]{x1D703}_{kpq}$
is the characteristic time of the third-order correlations, containing the eddy-damping terms, according to
One can observe in figure 1(a) that
![]() $\unicode[STIX]{x1D707}_{A}>\unicode[STIX]{x1D707}_{1}$
in the entire inertial range, so that
$\unicode[STIX]{x1D707}_{A}>\unicode[STIX]{x1D707}_{1}$
in the entire inertial range, so that
![]() ${\unicode[STIX]{x1D707}_{A}}^{-1}$
becomes the smallest time scale of the problem. The inertial scaling of the total energy spectrum being determined by the smallest time scale through nonlinear transfers (Lee et al.
Reference Lee, Brachet, Pouquet, Mininni and Rosenberg2010), it follows that the choice of
${\unicode[STIX]{x1D707}_{A}}^{-1}$
becomes the smallest time scale of the problem. The inertial scaling of the total energy spectrum being determined by the smallest time scale through nonlinear transfers (Lee et al.
Reference Lee, Brachet, Pouquet, Mininni and Rosenberg2010), it follows that the choice of
![]() $\unicode[STIX]{x1D707}_{A}$
prescribes the inertial scaling of the total energy spectrum
$\unicode[STIX]{x1D707}_{A}$
prescribes the inertial scaling of the total energy spectrum
![]() $E$
: within this isotropic EDQNM modelling, this amounts to
$E$
: within this isotropic EDQNM modelling, this amounts to
![]() $E\sim k^{-3/2}$
as revealed in § 3. This is also true in the presence of cross-helicity, see later in § 4. Note that if one does not ensure
$E\sim k^{-3/2}$
as revealed in § 3. This is also true in the presence of cross-helicity, see later in § 4. Note that if one does not ensure
![]() $\unicode[STIX]{x1D707}_{A}>\unicode[STIX]{x1D707}_{1}$
, realizability is not guaranteed anymore, meaning that either
$\unicode[STIX]{x1D707}_{A}>\unicode[STIX]{x1D707}_{1}$
, realizability is not guaranteed anymore, meaning that either
![]() $E_{V}$
or
$E_{V}$
or
![]() $E_{B}$
can become negative. Consequently in what follows, we do not investigate whether one has
$E_{B}$
can become negative. Consequently in what follows, we do not investigate whether one has
![]() $E\sim k^{-3/2}$
or
$E\sim k^{-3/2}$
or
![]() $E\sim k^{-5/3}$
in IMHDT, but rather the asymptotic results one can obtain from a given inertial scaling.
$E\sim k^{-5/3}$
in IMHDT, but rather the asymptotic results one can obtain from a given inertial scaling.
Moreover, it appears in figure 1(a) that for sufficiently large
![]() $k$
, one has
$k$
, one has
![]() $\unicode[STIX]{x1D707}_{A}(k)\sim k$
, as expected (Pouquet et al.
Reference Pouquet, Frisch and Léorat1976). Indeed, as previously mentioned, when
$\unicode[STIX]{x1D707}_{A}(k)\sim k$
, as expected (Pouquet et al.
Reference Pouquet, Frisch and Léorat1976). Indeed, as previously mentioned, when
![]() $k\rightarrow \infty$
, one has
$k\rightarrow \infty$
, one has
![]() $\unicode[STIX]{x1D707}_{A}\simeq kb_{0}$
since
$\unicode[STIX]{x1D707}_{A}\simeq kb_{0}$
since
![]() $\int _{0}^{\infty }E_{B}\,\text{d}k=3b_{0}^{2}/2$
. This further illustrates that the Alfvén time
$\int _{0}^{\infty }E_{B}\,\text{d}k=3b_{0}^{2}/2$
. This further illustrates that the Alfvén time
![]() $\unicode[STIX]{x1D70F}_{A}=(kb_{0})^{-1}$
is the characteristic time of the inertial range. Also, in the inertial range, the classical eddy-damping part
$\unicode[STIX]{x1D70F}_{A}=(kb_{0})^{-1}$
is the characteristic time of the inertial range. Also, in the inertial range, the classical eddy-damping part
![]() $\unicode[STIX]{x1D707}_{1}$
evolves as
$\unicode[STIX]{x1D707}_{1}$
evolves as
![]() $k^{3/4}$
, which is consistent with previous arguments: from its definition (2.20), dimensional analysis yields
$k^{3/4}$
, which is consistent with previous arguments: from its definition (2.20), dimensional analysis yields
![]() $\unicode[STIX]{x1D707}_{1}\sim \sqrt{k^{3}E}=(\unicode[STIX]{x1D716}b_{0}k^{3})^{1/4}$
: this is different from HIT where
$\unicode[STIX]{x1D707}_{1}\sim \sqrt{k^{3}E}=(\unicode[STIX]{x1D716}b_{0}k^{3})^{1/4}$
: this is different from HIT where
![]() $\unicode[STIX]{x1D707}_{1}\sim \unicode[STIX]{x1D70F}_{V}^{-1}\sim (k^{2}\unicode[STIX]{x1D716}_{V})^{1/3}$
.
$\unicode[STIX]{x1D707}_{1}\sim \unicode[STIX]{x1D70F}_{V}^{-1}\sim (k^{2}\unicode[STIX]{x1D716}_{V})^{1/3}$
.

Figure 1. (a) Different contributions in the eddy-damping term
![]() $\unicode[STIX]{x1D707}_{k}$
, defined in (2.26), of the characteristic time
$\unicode[STIX]{x1D707}_{k}$
, defined in (2.26), of the characteristic time
![]() $\unicode[STIX]{x1D703}_{kpq}$
at
$\unicode[STIX]{x1D703}_{kpq}$
at
![]() $Re_{\unicode[STIX]{x1D706}}=6\times 10^{3}$
, along with the integral and dissipative wavenumbers
$Re_{\unicode[STIX]{x1D706}}=6\times 10^{3}$
, along with the integral and dissipative wavenumbers
![]() $k_{L}$
and
$k_{L}$
and
![]() $k_{\unicode[STIX]{x1D702}}^{\text{MHD}}$
, defined later on. (b) Total energy spectrum
$k_{\unicode[STIX]{x1D702}}^{\text{MHD}}$
, defined later on. (b) Total energy spectrum
![]() $E(k,t)$
, with initial condition (2.44) and
$E(k,t)$
, with initial condition (2.44) and
![]() $E_{V}(k,t=0)=0$
at
$E_{V}(k,t=0)=0$
at
![]() $Re_{\unicode[STIX]{x1D706}}=260$
, compared to spectra obtained in Lee et al. (Reference Lee, Brachet, Pouquet, Mininni and Rosenberg2010) with various initial conditions (I6, A6, C6).
$Re_{\unicode[STIX]{x1D706}}=260$
, compared to spectra obtained in Lee et al. (Reference Lee, Brachet, Pouquet, Mininni and Rosenberg2010) with various initial conditions (I6, A6, C6).
2.3 Spherically averaged equations for isotropic MHD
In isotropic MHD turbulence without a mean magnetic field, the solenoidal spectral tensors
![]() $\hat{\unicode[STIX]{x1D619}}_{ij}$
and
$\hat{\unicode[STIX]{x1D619}}_{ij}$
and
![]() $\hat{\unicode[STIX]{x1D609}}_{ij}$
are decomposed as
$\hat{\unicode[STIX]{x1D609}}_{ij}$
are decomposed as
where
![]() ${\mathcal{E}}^{V}$
and
${\mathcal{E}}^{V}$
and
![]() ${\mathcal{E}}^{B}$
are the kinetic and magnetic energy densities, and
${\mathcal{E}}^{B}$
are the kinetic and magnetic energy densities, and
![]() ${\mathcal{H}}^{V}$
and
${\mathcal{H}}^{V}$
and
![]() ${\mathcal{H}}^{B}$
are the kinetic and ‘super’ magnetic helicity densities, given by
${\mathcal{H}}^{B}$
are the kinetic and ‘super’ magnetic helicity densities, given by
The definitions are similar for
![]() ${\mathcal{E}}^{B}$
and
${\mathcal{E}}^{B}$
and
![]() ${\mathcal{H}}^{B}$
. At this point, it is of importance to precise that the magnetic helicity
${\mathcal{H}}^{B}$
. At this point, it is of importance to precise that the magnetic helicity
![]() $H_{M}$
, which is an inviscid invariant of the MHD equations, is linked to
$H_{M}$
, which is an inviscid invariant of the MHD equations, is linked to
![]() ${\mathcal{H}}^{B}$
through
${\mathcal{H}}^{B}$
through
with
![]() $\boldsymbol{j}$
the normalized current density. In the following developments, IMHDT is considered (with mirror symmetry) so that both
$\boldsymbol{j}$
the normalized current density. In the following developments, IMHDT is considered (with mirror symmetry) so that both
![]() ${\mathcal{H}}^{V}$
and
${\mathcal{H}}^{V}$
and
![]() ${\mathcal{H}}^{B}$
vanish. Then, the evolution equations of the energy densities
${\mathcal{H}}^{B}$
vanish. Then, the evolution equations of the energy densities
![]() ${\mathcal{E}}^{V}$
and
${\mathcal{E}}^{V}$
and
![]() ${\mathcal{E}}^{B}$
read
${\mathcal{E}}^{B}$
read
where the nonlinear transfers are given by
with
![]() $\Re$
denoting the real part. The final equations for isotropic MHD turbulence are obtained by spherically averaging the evolution equations (2.31)–(2.32) of
$\Re$
denoting the real part. The final equations for isotropic MHD turbulence are obtained by spherically averaging the evolution equations (2.31)–(2.32) of
![]() ${\mathcal{E}}^{V}$
and
${\mathcal{E}}^{V}$
and
![]() ${\mathcal{E}}^{B}$
: the kinetic energy and magnetic energy spectra are then defined as
${\mathcal{E}}^{B}$
: the kinetic energy and magnetic energy spectra are then defined as
where
![]() $S_{k}$
is a sphere of radius
$S_{k}$
is a sphere of radius
![]() $k$
. From the definitions of the kinetic and magnetic spectra and equations (2.31)–(2.32), one straightforwardly obtains
$k$
. From the definitions of the kinetic and magnetic spectra and equations (2.31)–(2.32), one straightforwardly obtains
The spherically averaged nonlinear kinetic hydrodynamic transfer is
 $$\begin{eqnarray}\displaystyle S^{\text{V(hyd)}}(k,t) & = & \displaystyle \int _{S_{k}}T_{{\mathcal{E}}}^{\text{V(hyd)}}(\boldsymbol{k},t)\,\text{d}^{2}\boldsymbol{k}\nonumber\\ \displaystyle & = & \displaystyle 16\unicode[STIX]{x03C0}^{2}\int _{\unicode[STIX]{x1D6E5}_{k}}\unicode[STIX]{x1D703}_{kpq}k^{2}p^{2}q(xy+z^{3}){\mathcal{E}}_{0}^{V^{\prime \prime }}({\mathcal{E}}_{0}^{V^{\prime }}-{\mathcal{E}}_{0}^{V})\,\text{d}p\,\text{d}q,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle S^{\text{V(hyd)}}(k,t) & = & \displaystyle \int _{S_{k}}T_{{\mathcal{E}}}^{\text{V(hyd)}}(\boldsymbol{k},t)\,\text{d}^{2}\boldsymbol{k}\nonumber\\ \displaystyle & = & \displaystyle 16\unicode[STIX]{x03C0}^{2}\int _{\unicode[STIX]{x1D6E5}_{k}}\unicode[STIX]{x1D703}_{kpq}k^{2}p^{2}q(xy+z^{3}){\mathcal{E}}_{0}^{V^{\prime \prime }}({\mathcal{E}}_{0}^{V^{\prime }}-{\mathcal{E}}_{0}^{V})\,\text{d}p\,\text{d}q,\end{eqnarray}$$
with
![]() $\unicode[STIX]{x1D6E5}_{k}$
the domain where
$\unicode[STIX]{x1D6E5}_{k}$
the domain where
![]() $k$
,
$k$
,
![]() $p$
and
$p$
and
![]() $q$
are the lengths of the sides of the triangle formed by the triad, and
$q$
are the lengths of the sides of the triangle formed by the triad, and
![]() $x$
,
$x$
,
![]() $y$
and
$y$
and
![]() $z$
are the cosines of the angles formed by
$z$
are the cosines of the angles formed by
![]() $\boldsymbol{p}$
and
$\boldsymbol{p}$
and
![]() $\boldsymbol{q}$
,
$\boldsymbol{q}$
,
![]() $\boldsymbol{q}$
and
$\boldsymbol{q}$
and
![]() $\boldsymbol{k}$
and
$\boldsymbol{k}$
and
![]() $\boldsymbol{k}$
and
$\boldsymbol{k}$
and
![]() $\boldsymbol{p}$
. The spherically averaged nonlinear kinetic MHD transfer reads
$\boldsymbol{p}$
. The spherically averaged nonlinear kinetic MHD transfer reads
 $$\begin{eqnarray}\displaystyle S^{\text{V(mag)}}(k,t) & = & \displaystyle \int _{S_{k}}T_{{\mathcal{E}}}^{\text{V(mag)}}(\boldsymbol{k},t)\,\text{d}^{2}\boldsymbol{k}\nonumber\\ \displaystyle & = & \displaystyle 16\unicode[STIX]{x03C0}^{2}\int _{\unicode[STIX]{x1D6E5}_{k}}\unicode[STIX]{x1D703}_{kpq}k^{2}p^{2}qz(1-y^{2}){\mathcal{E}}_{0}^{B^{\prime \prime }}({\mathcal{E}}_{0}^{B^{\prime }}-{\mathcal{E}}_{0}^{V})\,\text{d}p\,\text{d}q,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle S^{\text{V(mag)}}(k,t) & = & \displaystyle \int _{S_{k}}T_{{\mathcal{E}}}^{\text{V(mag)}}(\boldsymbol{k},t)\,\text{d}^{2}\boldsymbol{k}\nonumber\\ \displaystyle & = & \displaystyle 16\unicode[STIX]{x03C0}^{2}\int _{\unicode[STIX]{x1D6E5}_{k}}\unicode[STIX]{x1D703}_{kpq}k^{2}p^{2}qz(1-y^{2}){\mathcal{E}}_{0}^{B^{\prime \prime }}({\mathcal{E}}_{0}^{B^{\prime }}-{\mathcal{E}}_{0}^{V})\,\text{d}p\,\text{d}q,\end{eqnarray}$$
and the spherically averaged nonlinear magnetic transfer is
 $$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle S^{\text{B(mag)}}(k,t)=\int _{S_{k}}T_{{\mathcal{E}}}^{\text{B(mag)}}(\boldsymbol{k},t)\,\text{d}^{2}\boldsymbol{k}\nonumber\\ \displaystyle & & \displaystyle \displaystyle \quad =16\unicode[STIX]{x03C0}^{2}\int _{\unicode[STIX]{x1D6E5}_{k}}\unicode[STIX]{x1D703}_{kpq}k^{2}p^{2}q\left((xy+z){\mathcal{E}}_{0}^{V^{\prime \prime }}({\mathcal{E}}_{0}^{B^{\prime }}-{\mathcal{E}}_{0}^{B})+z(1-x^{2}){\mathcal{E}}_{0}^{B^{\prime \prime }}({\mathcal{E}}_{0}^{V^{\prime }}-{\mathcal{E}}_{0}^{B})\right)\text{d}p\,\text{d}q,\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle S^{\text{B(mag)}}(k,t)=\int _{S_{k}}T_{{\mathcal{E}}}^{\text{B(mag)}}(\boldsymbol{k},t)\,\text{d}^{2}\boldsymbol{k}\nonumber\\ \displaystyle & & \displaystyle \displaystyle \quad =16\unicode[STIX]{x03C0}^{2}\int _{\unicode[STIX]{x1D6E5}_{k}}\unicode[STIX]{x1D703}_{kpq}k^{2}p^{2}q\left((xy+z){\mathcal{E}}_{0}^{V^{\prime \prime }}({\mathcal{E}}_{0}^{B^{\prime }}-{\mathcal{E}}_{0}^{B})+z(1-x^{2}){\mathcal{E}}_{0}^{B^{\prime \prime }}({\mathcal{E}}_{0}^{V^{\prime }}-{\mathcal{E}}_{0}^{B})\right)\text{d}p\,\text{d}q,\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
where
![]() ${\mathcal{E}}_{0}^{V}=E_{V}(k)/(4\unicode[STIX]{x03C0}k^{2})$
,
${\mathcal{E}}_{0}^{V}=E_{V}(k)/(4\unicode[STIX]{x03C0}k^{2})$
,
![]() ${\mathcal{E}}_{0}^{V^{\prime }}=E_{V}(p)/(4\unicode[STIX]{x03C0}p^{2})$
,
${\mathcal{E}}_{0}^{V^{\prime }}=E_{V}(p)/(4\unicode[STIX]{x03C0}p^{2})$
,
![]() ${\mathcal{E}}_{0}^{V^{\prime \prime }}=E_{V}(q)/(4\unicode[STIX]{x03C0}q^{2})$
and similarly for the magnetic energy spectrum. About the nonlinear transfers:
${\mathcal{E}}_{0}^{V^{\prime \prime }}=E_{V}(q)/(4\unicode[STIX]{x03C0}q^{2})$
and similarly for the magnetic energy spectrum. About the nonlinear transfers:
![]() $S^{\text{V(hyd)}}$
is conservative, with zero integral over
$S^{\text{V(hyd)}}$
is conservative, with zero integral over
![]() $k$
, whereas only the sum
$k$
, whereas only the sum
![]() $S^{\text{V(mag)}}+S^{\text{B(mag)}}$
is conservative. The expressions of the two later transfer terms are in agreement with Kraichnan & Nagarajan (Reference Kraichnan and Nagarajan1967), Zhou, Schilling & Ghosh (Reference Zhou, Schilling and Ghosh2002), and there are typo errors in Pouquet et al. (Reference Pouquet, Frisch and Léorat1976), Müller & Grappin (Reference Müller and Grappin2004), Baerenzung et al. (Reference Baerenzung, Politano, Ponty and Pouquet2008). The typos in the reference paper Pouquet et al. (Reference Pouquet, Frisch and Léorat1976) were corrected in Léorat, Pouquet & Frisch (Reference Léorat, Pouquet and Frisch1981), precisely pages 441–442 therein.
$S^{\text{V(mag)}}+S^{\text{B(mag)}}$
is conservative. The expressions of the two later transfer terms are in agreement with Kraichnan & Nagarajan (Reference Kraichnan and Nagarajan1967), Zhou, Schilling & Ghosh (Reference Zhou, Schilling and Ghosh2002), and there are typo errors in Pouquet et al. (Reference Pouquet, Frisch and Léorat1976), Müller & Grappin (Reference Müller and Grappin2004), Baerenzung et al. (Reference Baerenzung, Politano, Ponty and Pouquet2008). The typos in the reference paper Pouquet et al. (Reference Pouquet, Frisch and Léorat1976) were corrected in Léorat, Pouquet & Frisch (Reference Léorat, Pouquet and Frisch1981), precisely pages 441–442 therein.
The kinetic energy and its dissipation rate are given by
The magnetic quantities are obtained by changing
![]() $()_{V}\rightarrow ()_{B}$
,
$()_{V}\rightarrow ()_{B}$
,
![]() $u_{i}\rightarrow b_{i}$
and
$u_{i}\rightarrow b_{i}$
and
![]() $\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D702}$
. Since only the total energy
$\unicode[STIX]{x1D708}\rightarrow \unicode[STIX]{x1D702}$
. Since only the total energy
![]() $K=K_{V}+K_{B}$
is an inviscid invariant of MHD, we define also the total energy dissipation rate as
$K=K_{V}+K_{B}$
is an inviscid invariant of MHD, we define also the total energy dissipation rate as
![]() $\unicode[STIX]{x1D716}=\unicode[STIX]{x1D716}_{V}+\unicode[STIX]{x1D716}_{B}$
, and the integral scale as
$\unicode[STIX]{x1D716}=\unicode[STIX]{x1D716}_{V}+\unicode[STIX]{x1D716}_{B}$
, and the integral scale as
Further information about the evolution equations of the total energy
![]() $K$
and total dissipation
$K$
and total dissipation
![]() $\unicode[STIX]{x1D716}$
can be found in appendix B.1.
$\unicode[STIX]{x1D716}$
can be found in appendix B.1.
2.4 Numerical set-up and initial conditions
The time evolution of the kinetic and magnetic spectra
![]() $E_{V}(k,t)$
and
$E_{V}(k,t)$
and
![]() $E_{B}(k,t)$
is obtained by solving two coupled integro-differential equations using a third-order Runge–Kutta scheme with implicit treatment of viscous terms. The wavenumber space is discretized using a logarithmic mesh
$E_{B}(k,t)$
is obtained by solving two coupled integro-differential equations using a third-order Runge–Kutta scheme with implicit treatment of viscous terms. The wavenumber space is discretized using a logarithmic mesh
![]() $k_{i+1}=rk_{i}$
for
$k_{i+1}=rk_{i}$
for
![]() $i=1,\ldots ,n$
, where
$i=1,\ldots ,n$
, where
![]() $n$
is the total number of modes and
$n$
is the total number of modes and
![]() $r=10^{1/f}$
,
$r=10^{1/f}$
,
![]() $f=15$
is the number of points per decade. This mesh spans from
$f=15$
is the number of points per decade. This mesh spans from
![]() $k_{\text{min}}=10^{-4}k_{L}$
to
$k_{\text{min}}=10^{-4}k_{L}$
to
![]() $k_{\text{max}}=10k_{\unicode[STIX]{x1D702}}$
, where
$k_{\text{max}}=10k_{\unicode[STIX]{x1D702}}$
, where
![]() $k_{L}=1/L$
is the integral wavenumber, and
$k_{L}=1/L$
is the integral wavenumber, and
![]() $k_{\unicode[STIX]{x1D702}}=(\unicode[STIX]{x1D716}/\unicode[STIX]{x1D708}^{3})^{1/4}$
is the Kolmogorov wavenumber. It will be shown hereafter that the relevant dissipation wavenumber
$k_{\unicode[STIX]{x1D702}}=(\unicode[STIX]{x1D716}/\unicode[STIX]{x1D708}^{3})^{1/4}$
is the Kolmogorov wavenumber. It will be shown hereafter that the relevant dissipation wavenumber
![]() $k_{\unicode[STIX]{x1D702}}^{\text{MHD}}$
for MHD is smaller than
$k_{\unicode[STIX]{x1D702}}^{\text{MHD}}$
for MHD is smaller than
![]() $k_{\unicode[STIX]{x1D702}}$
. The characteristic time used for normalization is the eddy turnover time
$k_{\unicode[STIX]{x1D702}}$
. The characteristic time used for normalization is the eddy turnover time
![]() $\unicode[STIX]{x1D70F}_{0}=K(0)/\unicode[STIX]{x1D716}(0)$
. The initial Reynolds number is varied between
$\unicode[STIX]{x1D70F}_{0}=K(0)/\unicode[STIX]{x1D716}(0)$
. The initial Reynolds number is varied between
![]() $5\times 10^{3}\leqslant Re_{\unicode[STIX]{x1D706}}(0)\leqslant 5\times 10^{4}$
depending on the cases considered.
$5\times 10^{3}\leqslant Re_{\unicode[STIX]{x1D706}}(0)\leqslant 5\times 10^{4}$
depending on the cases considered.
The following initial condition is chosen for the magnetic energy spectrum if not mentioned otherwise
with
![]() $C_{B}$
so that
$C_{B}$
so that
![]() $\int _{0}^{\infty }E_{B}(k,t=0)\,\text{d}k=1$
. The kinetic energy spectrum is initially either zero, or equal to
$\int _{0}^{\infty }E_{B}(k,t=0)\,\text{d}k=1$
. The kinetic energy spectrum is initially either zero, or equal to
![]() $E_{B}$
: the following results, and notably the inertial scalings and decay laws, are not modified asymptotically by choosing different initial relative intensities between the kinetic and magnetic fields. In both cases, the infrared slope
$E_{B}$
: the following results, and notably the inertial scalings and decay laws, are not modified asymptotically by choosing different initial relative intensities between the kinetic and magnetic fields. In both cases, the infrared slope
![]() $\unicode[STIX]{x1D70E}_{B}$
of the magnetic energy spectrum is the large scale initial condition (recall that in hydrodynamics turbulence, the infrared slopes
$\unicode[STIX]{x1D70E}_{B}$
of the magnetic energy spectrum is the large scale initial condition (recall that in hydrodynamics turbulence, the infrared slopes
![]() $\unicode[STIX]{x1D70E}_{V}=2$
and
$\unicode[STIX]{x1D70E}_{V}=2$
and
![]() $\unicode[STIX]{x1D70E}_{V}=4$
for the kinetic energy spectrum correspond respectively to Saffman and Batchelor turbulence). In agreement with classical arguments given in Lesieur & Ossia (Reference Lesieur and Ossia2000), Lesieur (Reference Lesieur2008), if initially zero,
$\unicode[STIX]{x1D70E}_{V}=4$
for the kinetic energy spectrum correspond respectively to Saffman and Batchelor turbulence). In agreement with classical arguments given in Lesieur & Ossia (Reference Lesieur and Ossia2000), Lesieur (Reference Lesieur2008), if initially zero,
![]() $E_{V}$
has an infrared slope
$E_{V}$
has an infrared slope
![]() $\unicode[STIX]{x1D70E}_{V}=4$
once created. If
$\unicode[STIX]{x1D70E}_{V}=4$
once created. If
![]() $E_{V}=E_{B}$
initially, then
$E_{V}=E_{B}$
initially, then
![]() $\unicode[STIX]{x1D70E}_{V}=\unicode[STIX]{x1D70E}_{B}$
. A particular attention has to be given to the time step. Indeed in MHD, one needs to take into account the characteristic propagation time of Alfvén waves
$\unicode[STIX]{x1D70E}_{V}=\unicode[STIX]{x1D70E}_{B}$
. A particular attention has to be given to the time step. Indeed in MHD, one needs to take into account the characteristic propagation time of Alfvén waves
![]() $\unicode[STIX]{x1D70F}_{A}\sim (kb_{0})^{-1}$
. This is essential and considerably reduces the time step. Consequently, even with EDQNM, the duration of the simulations can be rather long at large Reynolds numbers if one wants to capture several turnover times, but is still much less than with DNS.
$\unicode[STIX]{x1D70F}_{A}\sim (kb_{0})^{-1}$
. This is essential and considerably reduces the time step. Consequently, even with EDQNM, the duration of the simulations can be rather long at large Reynolds numbers if one wants to capture several turnover times, but is still much less than with DNS.
3 The decay of balanced isotropic MHD turbulence
In the following parts, balanced IMHDT is considered, meaning that the cross-helicity is zero:
![]() $\langle \boldsymbol{u}\boldsymbol{\cdot }\boldsymbol{b}\rangle =0$
. The imbalanced case is addressed in § 4. First, spectral scalings for the kinetic, magnetic and total energy spectra
$\langle \boldsymbol{u}\boldsymbol{\cdot }\boldsymbol{b}\rangle =0$
. The imbalanced case is addressed in § 4. First, spectral scalings for the kinetic, magnetic and total energy spectra
![]() $E_{V}(k,t)$
,
$E_{V}(k,t)$
,
![]() $E_{B}(k,t)$
and
$E_{B}(k,t)$
and
![]() $E(k,t)$
, are presented within the EDQNM modelling, and compared to spectra obtained in Lee et al. (Reference Lee, Brachet, Pouquet, Mininni and Rosenberg2010). The different characteristic time scales involved in the dynamics and the nonlinear transfers are studied as well. Finally, the decay of the total energy of the flow is analysed: theoretical predictions are derived and assessed numerically, which is the most important contribution of this work for balanced MHD. Note that the scaling of the residual energy spectrum is addressed in appendix A.2.
$E(k,t)$
, are presented within the EDQNM modelling, and compared to spectra obtained in Lee et al. (Reference Lee, Brachet, Pouquet, Mininni and Rosenberg2010). The different characteristic time scales involved in the dynamics and the nonlinear transfers are studied as well. Finally, the decay of the total energy of the flow is analysed: theoretical predictions are derived and assessed numerically, which is the most important contribution of this work for balanced MHD. Note that the scaling of the residual energy spectrum is addressed in appendix A.2.
3.1 Kinetic energy and magnetic spectra
 $E_{V}(k,t)$
and
$E_{V}(k,t)$
and
 $E_{B}(k,t)$
$E_{B}(k,t)$
The phenomenological arguments given by Kraichnan (Reference Kraichnan1965) to derive the
![]() $k^{-3/2}$
isotropic inertial scaling are first briefly recalled. Unlike HIT where the local time of the cascade is
$k^{-3/2}$
isotropic inertial scaling are first briefly recalled. Unlike HIT where the local time of the cascade is
![]() $\unicode[STIX]{x1D70F}_{V}=(k^{3}E_{V})^{-1/2}$
, the characteristic transfer time
$\unicode[STIX]{x1D70F}_{V}=(k^{3}E_{V})^{-1/2}$
, the characteristic transfer time
![]() $\unicode[STIX]{x1D70F}_{\text{tr}}$
of energy in MHD is longer. This MHD transfer time
$\unicode[STIX]{x1D70F}_{\text{tr}}$
of energy in MHD is longer. This MHD transfer time
![]() $\unicode[STIX]{x1D70F}_{\text{tr}}$
can be seen as the characteristic time of waves packet distortion, and is linked to the characteristic Alfvén time
$\unicode[STIX]{x1D70F}_{\text{tr}}$
can be seen as the characteristic time of waves packet distortion, and is linked to the characteristic Alfvén time
![]() $\unicode[STIX]{x1D70F}_{A}\sim (kb_{0})^{-1}$
which reflects the duration of interactions between two counter-propagating Alfvén waves. Indeed, in Kraichnan’s phenomenology, the transfer of energy at a scale
$\unicode[STIX]{x1D70F}_{A}\sim (kb_{0})^{-1}$
which reflects the duration of interactions between two counter-propagating Alfvén waves. Indeed, in Kraichnan’s phenomenology, the transfer of energy at a scale
![]() $l\sim k^{-1}$
results from the cumulative effects of multiple interactions and collisions between counter propagating Alfvén wave packets, which evolve along the magnetic field of scales larger than
$l\sim k^{-1}$
results from the cumulative effects of multiple interactions and collisions between counter propagating Alfvén wave packets, which evolve along the magnetic field of scales larger than
![]() $l$
. Consequently, the transfer time in MHD turbulence is
$l$
. Consequently, the transfer time in MHD turbulence is
![]() $\unicode[STIX]{x1D70F}_{\text{tr}}=\unicode[STIX]{x1D70F}_{V}^{2}/\unicode[STIX]{x1D70F}_{A}\sim lb_{0}/u^{2}$
(Pouquet Reference Pouquet1996; Gomez, Politano & Pouquet Reference Gomez, Politano and Pouquet1999; Galtier Reference Galtier2016), unlike HIT where
$\unicode[STIX]{x1D70F}_{\text{tr}}=\unicode[STIX]{x1D70F}_{V}^{2}/\unicode[STIX]{x1D70F}_{A}\sim lb_{0}/u^{2}$
(Pouquet Reference Pouquet1996; Gomez, Politano & Pouquet Reference Gomez, Politano and Pouquet1999; Galtier Reference Galtier2016), unlike HIT where
![]() $\unicode[STIX]{x1D70F}_{\text{tr}}=\unicode[STIX]{x1D70F}_{V}\sim l/u$
. From these considerations, one can express the total energy dissipation rate
$\unicode[STIX]{x1D70F}_{\text{tr}}=\unicode[STIX]{x1D70F}_{V}\sim l/u$
. From these considerations, one can express the total energy dissipation rate
![]() $\unicode[STIX]{x1D716}$
as the ratio of the local square velocity
$\unicode[STIX]{x1D716}$
as the ratio of the local square velocity
![]() $u^{2}\sim (kE)$
to the transfer time according to
$u^{2}\sim (kE)$
to the transfer time according to
so that one has in the inertial range
This scaling is referred to as the Iroshnikov–Kraichnan (IK) one, and this analysis also gives that
![]() $E_{V}$
and
$E_{V}$
and
![]() $E_{B}$
have a
$E_{B}$
have a
![]() $k^{-3/2}$
inertial scaling like
$k^{-3/2}$
inertial scaling like
![]() $E$
. The constant is found here to be of order
$E$
. The constant is found here to be of order
![]() $2\leqslant C_{\text{IK}}\leqslant 3$
for
$2\leqslant C_{\text{IK}}\leqslant 3$
for
![]() $10^{3}\leqslant Re_{\unicode[STIX]{x1D706}}\sim 10^{4}$
, which is higher than the Kolmogorov constant in HIT, and this feature is in agreement with Beresnyak (Reference Beresnyak2011).
$10^{3}\leqslant Re_{\unicode[STIX]{x1D706}}\sim 10^{4}$
, which is higher than the Kolmogorov constant in HIT, and this feature is in agreement with Beresnyak (Reference Beresnyak2011).
Within the isotropic EDQNM framework, the
![]() $k^{-3/2}$
scaling is a consequence of the choice of the additional eddy-damping term
$k^{-3/2}$
scaling is a consequence of the choice of the additional eddy-damping term
![]() $\unicode[STIX]{x1D707}_{A}$
defined in (2.24). This is illustrated in figure 2 for
$\unicode[STIX]{x1D707}_{A}$
defined in (2.24). This is illustrated in figure 2 for
![]() $\unicode[STIX]{x1D70E}_{B}=2$
. Note that the
$\unicode[STIX]{x1D70E}_{B}=2$
. Note that the
![]() $k^{-3/2}$
inertial scaling also holds for
$k^{-3/2}$
inertial scaling also holds for
![]() $E_{+}$
and
$E_{+}$
and
![]() $E_{-}$
associated with the Elsässer variables
$E_{-}$
associated with the Elsässer variables
![]() $\boldsymbol{z}^{\pm }=\boldsymbol{u}\pm \boldsymbol{b}$
. The kinetic energy spectrum, initially zero in figure 2, is created within the first turnover time by
$\boldsymbol{z}^{\pm }=\boldsymbol{u}\pm \boldsymbol{b}$
. The kinetic energy spectrum, initially zero in figure 2, is created within the first turnover time by
![]() $S^{\text{V(mag)}}$
, with an infrared slope
$S^{\text{V(mag)}}$
, with an infrared slope
![]() $\unicode[STIX]{x1D70E}_{V}=4$
, and consequently experiences a backscatter of energy (Lesieur & Ossia Reference Lesieur and Ossia2000). Whereas at large scales the magnetic spectrum scales with
$\unicode[STIX]{x1D70E}_{V}=4$
, and consequently experiences a backscatter of energy (Lesieur & Ossia Reference Lesieur and Ossia2000). Whereas at large scales the magnetic spectrum scales with
![]() $E_{B}\sim k^{2}$
. Two other cases (
$E_{B}\sim k^{2}$
. Two other cases (
![]() $\unicode[STIX]{x1D70E}_{B}=4$
with
$\unicode[STIX]{x1D70E}_{B}=4$
with
![]() $E_{V}=0$
;
$E_{V}=0$
;
![]() $\unicode[STIX]{x1D70E}_{B}=2$
with
$\unicode[STIX]{x1D70E}_{B}=2$
with
![]() $E_{V}=E_{B}$
) presented in appendix A.2 show that the
$E_{V}=E_{B}$
) presented in appendix A.2 show that the
![]() $k^{-3/2}$
inertial scaling is independent of initial conditions after a few turnover times. This notably implies that the inertial scaling does not depend on the kinetic to magnetic energy ratio
$k^{-3/2}$
inertial scaling is independent of initial conditions after a few turnover times. This notably implies that the inertial scaling does not depend on the kinetic to magnetic energy ratio
![]() $K_{V}/K_{B}$
, which only slightly varies with initial conditions (see later figure 11(d)).
$K_{V}/K_{B}$
, which only slightly varies with initial conditions (see later figure 11(d)).

Figure 2. Time evolution of the kinetic energy and magnetic energy spectra
![]() $E_{V}(k,t)$
and
$E_{V}(k,t)$
and
![]() $E_{B}(k,t)$
for
$E_{B}(k,t)$
for
![]() $\unicode[STIX]{x1D70E}_{B}=2$
, from
$\unicode[STIX]{x1D70E}_{B}=2$
, from
![]() $t=0$
to
$t=0$
to
![]() $t=10^{3}\unicode[STIX]{x1D70F}_{0}$
, with initially
$t=10^{3}\unicode[STIX]{x1D70F}_{0}$
, with initially
![]() $E_{V}=0$
. (a) Kinetic energy spectrum
$E_{V}=0$
. (a) Kinetic energy spectrum
![]() $E_{V}(k,t)$
. (b) Magnetic energy spectrum
$E_{V}(k,t)$
. (b) Magnetic energy spectrum
![]() $E_{B}(k,t)$
.
$E_{B}(k,t)$
.
This
![]() $k^{-3/2}$
scaling for
$k^{-3/2}$
scaling for
![]() $E_{V}$
and
$E_{V}$
and
![]() $E_{B}$
is in agreement with numerical simulations of IMHDT (Grappin et al.
Reference Grappin, Frisch, Léorat and Pouquet1982; Mininni & Pouquet Reference Mininni and Pouquet2007; Yoshimatsu Reference Yoshimatsu2012). However, still in the isotropic case, some studies report rather a Kolmogorov
$E_{B}$
is in agreement with numerical simulations of IMHDT (Grappin et al.
Reference Grappin, Frisch, Léorat and Pouquet1982; Mininni & Pouquet Reference Mininni and Pouquet2007; Yoshimatsu Reference Yoshimatsu2012). However, still in the isotropic case, some studies report rather a Kolmogorov
![]() $k^{-5/3}$
inertial scaling, at odds with the previous IK
$k^{-5/3}$
inertial scaling, at odds with the previous IK
![]() $k^{-3/2}$
inertial scaling (Müller & Biskamp Reference Müller and Biskamp2000; Müller & Grappin Reference Müller and Grappin2004, Reference Müller and Grappin2005; Alexakis, Mininni & Pouquet Reference Alexakis, Mininni and Pouquet2005). Finally, in some cases both scalings are possible (Haugen, Brandenburg & Dobler Reference Haugen, Brandenburg and Dobler2004; Lee et al.
Reference Lee, Brachet, Pouquet, Mininni and Rosenberg2010; Alexakis Reference Alexakis2013), depending on the Reynolds number, the possible forcing terms and initial parameters. The total energy spectrum
$k^{-3/2}$
inertial scaling (Müller & Biskamp Reference Müller and Biskamp2000; Müller & Grappin Reference Müller and Grappin2004, Reference Müller and Grappin2005; Alexakis, Mininni & Pouquet Reference Alexakis, Mininni and Pouquet2005). Finally, in some cases both scalings are possible (Haugen, Brandenburg & Dobler Reference Haugen, Brandenburg and Dobler2004; Lee et al.
Reference Lee, Brachet, Pouquet, Mininni and Rosenberg2010; Alexakis Reference Alexakis2013), depending on the Reynolds number, the possible forcing terms and initial parameters. The total energy spectrum
![]() $E(k,t)$
, obtained with EDQNM and the initial condition (2.44) with
$E(k,t)$
, obtained with EDQNM and the initial condition (2.44) with
![]() $E_{V}(k,t=0)=0$
, is presented in figure 1(b) at moderate Reynolds numbers, and compared to spectra obtained by Lee et al. (Reference Lee, Brachet, Pouquet, Mininni and Rosenberg2010) for different initial conditions. One can see that at
$E_{V}(k,t=0)=0$
, is presented in figure 1(b) at moderate Reynolds numbers, and compared to spectra obtained by Lee et al. (Reference Lee, Brachet, Pouquet, Mininni and Rosenberg2010) for different initial conditions. One can see that at
![]() $Re_{\unicode[STIX]{x1D706}}=260$
, the difference between the
$Re_{\unicode[STIX]{x1D706}}=260$
, the difference between the
![]() $k^{-5/3}$
and
$k^{-5/3}$
and
![]() $k^{-3/2}$
inertial scalings is quite subtle. Above all, our spectrum
$k^{-3/2}$
inertial scalings is quite subtle. Above all, our spectrum
![]() $E$
is consistently contained between the different DNS results, obtained after six turnover times, thus showing some quantitative good agreement between EDQNM and DNS.
$E$
is consistently contained between the different DNS results, obtained after six turnover times, thus showing some quantitative good agreement between EDQNM and DNS.
3.2 Spectral kinetic and magnetic nonlinear transfers
The emphasis is now put on the nonlinear transfers of kinetic and magnetic energies. It is firstly observed in figure 3(a) that all kinetic and magnetic spherically averaged nonlinear transfer terms bring energy from large to small scales, in agreement with Alexakis et al. (Reference Alexakis, Mininni and Pouquet2005). The fluxes, computed according to
![]() $\unicode[STIX]{x1D6F1}(k)=-\int _{0}^{k}S(p)\,\text{d}p$
, reveal several important features:
$\unicode[STIX]{x1D6F1}(k)=-\int _{0}^{k}S(p)\,\text{d}p$
, reveal several important features:
-
(i) The purely hydrodynamic isotropic kinetic flux
 $\unicode[STIX]{x1D6F1}^{\text{V(hyd)}}$
is conservative.
$\unicode[STIX]{x1D6F1}^{\text{V(hyd)}}$
is conservative. -
(ii) The magnetic part
 $\unicode[STIX]{x1D6F1}^{\text{V(mag)}}$
of the total kinetic flux
$\unicode[STIX]{x1D6F1}^{\text{V(mag)}}$
of the total kinetic flux
 $\unicode[STIX]{x1D6F1}^{\text{V}}=\unicode[STIX]{x1D6F1}^{\text{V(hyd)}}+\unicode[STIX]{x1D6F1}^{\text{V(mag)}}$
is not conservative, so that
$\unicode[STIX]{x1D6F1}^{\text{V}}=\unicode[STIX]{x1D6F1}^{\text{V(hyd)}}+\unicode[STIX]{x1D6F1}^{\text{V(mag)}}$
is not conservative, so that
 $\unicode[STIX]{x1D6F1}^{\text{V}}$
is not.
$\unicode[STIX]{x1D6F1}^{\text{V}}$
is not. -
(iii) The total magnetic flux
 $\unicode[STIX]{x1D6F1}^{\text{(mag)}}=\unicode[STIX]{x1D6F1}^{\text{B(mag)}}+\unicode[STIX]{x1D6F1}^{\text{V(mag)}}$
is conservative, in agreement with pioneering developments in Kraichnan & Nagarajan (Reference Kraichnan and Nagarajan1967).
$\unicode[STIX]{x1D6F1}^{\text{(mag)}}=\unicode[STIX]{x1D6F1}^{\text{B(mag)}}+\unicode[STIX]{x1D6F1}^{\text{V(mag)}}$
is conservative, in agreement with pioneering developments in Kraichnan & Nagarajan (Reference Kraichnan and Nagarajan1967). -
(iv) Finally, consistently with the total energy being an inviscid invariant, the total flux
 $\unicode[STIX]{x1D6F1}^{\text{V(tot)}}=\unicode[STIX]{x1D6F1}^{\text{V(hyd)}}+\unicode[STIX]{x1D6F1}^{\text{V(mag)}}+\unicode[STIX]{x1D6F1}^{\text{B(mag)}}$
is conservative.
$\unicode[STIX]{x1D6F1}^{\text{V(tot)}}=\unicode[STIX]{x1D6F1}^{\text{V(hyd)}}+\unicode[STIX]{x1D6F1}^{\text{V(mag)}}+\unicode[STIX]{x1D6F1}^{\text{B(mag)}}$
is conservative.
One can remark in figure 3(a) that the dissipative wavenumber displayed is not the Kolmogorov wavenumber
![]() $k_{\unicode[STIX]{x1D702}}=(\unicode[STIX]{x1D716}_{V}/\unicode[STIX]{x1D708}^{3})^{1/4}$
, but its equivalent for MHD turbulence, namely
$k_{\unicode[STIX]{x1D702}}=(\unicode[STIX]{x1D716}_{V}/\unicode[STIX]{x1D708}^{3})^{1/4}$
, but its equivalent for MHD turbulence, namely
![]() $k_{\unicode[STIX]{x1D702}}^{\text{MHD}}$
(Biskamp & Welter Reference Biskamp and Welter1989; Diamond & Biskamp Reference Diamond and Biskamp1990; Pouquet Reference Pouquet1996). This characteristic wavenumber is obtained by equating
$k_{\unicode[STIX]{x1D702}}^{\text{MHD}}$
(Biskamp & Welter Reference Biskamp and Welter1989; Diamond & Biskamp Reference Diamond and Biskamp1990; Pouquet Reference Pouquet1996). This characteristic wavenumber is obtained by equating
![]() $(\unicode[STIX]{x1D708}{k_{\unicode[STIX]{x1D702}}^{\text{MHD}}}^{2})^{-1}$
and
$(\unicode[STIX]{x1D708}{k_{\unicode[STIX]{x1D702}}^{\text{MHD}}}^{2})^{-1}$
and
![]() $\unicode[STIX]{x1D70F}_{\text{tr}}(k_{\unicode[STIX]{x1D702}}^{\text{MHD}})=\sqrt{b_{0}/\unicode[STIX]{x1D716}k_{\unicode[STIX]{x1D702}}^{\text{MHD}}}$
, so that
$\unicode[STIX]{x1D70F}_{\text{tr}}(k_{\unicode[STIX]{x1D702}}^{\text{MHD}})=\sqrt{b_{0}/\unicode[STIX]{x1D716}k_{\unicode[STIX]{x1D702}}^{\text{MHD}}}$
, so that
The fact that
![]() $k_{\unicode[STIX]{x1D702}}^{\text{MHD}}$
is more relevant than
$k_{\unicode[STIX]{x1D702}}^{\text{MHD}}$
is more relevant than
![]() $k_{\unicode[STIX]{x1D702}}$
in MHD turbulence is illustrated in figure 11 in appendix A.2.
$k_{\unicode[STIX]{x1D702}}$
in MHD turbulence is illustrated in figure 11 in appendix A.2.

Figure 3. Kinetic and magnetic normalized nonlinear transfers and fluxes, at
![]() $Re_{\unicode[STIX]{x1D706}}\simeq 10^{4}$
, for
$Re_{\unicode[STIX]{x1D706}}\simeq 10^{4}$
, for
![]() $\unicode[STIX]{x1D70E}_{B}=2$
, along with the integral and dissipative wavenumbers
$\unicode[STIX]{x1D70E}_{B}=2$
, along with the integral and dissipative wavenumbers
![]() $k_{L}$
, and
$k_{L}$
, and
![]() $k_{\unicode[STIX]{x1D702}}^{\text{MHD}}$
. (a) Kinetic
$k_{\unicode[STIX]{x1D702}}^{\text{MHD}}$
. (a) Kinetic
![]() $S^{\text{V(hyd)}}+S^{\text{V(mag)}}=S^{\text{V}}$
and magnetic
$S^{\text{V(hyd)}}+S^{\text{V(mag)}}=S^{\text{V}}$
and magnetic
![]() $S^{\text{(mag)}}=S^{\text{V(mag)}}+S^{\text{B(mag)}}$
nonlinear transfers. (b) Corresponding kinetic and magnetic fluxes.
$S^{\text{(mag)}}=S^{\text{V(mag)}}+S^{\text{B(mag)}}$
nonlinear transfers. (b) Corresponding kinetic and magnetic fluxes.
3.3 Decay of the total energy
 $K(t)$
$K(t)$
In this part, the decay of the total energy
![]() $K=K_{V}+K_{B}$
in isotropic MHD turbulence, which evolves according to
$K=K_{V}+K_{B}$
in isotropic MHD turbulence, which evolves according to
![]() $\text{d}K/\text{d}t=-\unicode[STIX]{x1D716}$
is addressed. One can define the algebraic time exponents
$\text{d}K/\text{d}t=-\unicode[STIX]{x1D716}$
is addressed. One can define the algebraic time exponents
![]() $\unicode[STIX]{x1D6FC}$
and
$\unicode[STIX]{x1D6FC}$
and
![]() $\unicode[STIX]{x1D6FC}_{L}$
as
$\unicode[STIX]{x1D6FC}_{L}$
as
![]() $K\sim t^{\unicode[STIX]{x1D6FC}}$
and
$K\sim t^{\unicode[STIX]{x1D6FC}}$
and
![]() $L\sim t^{\unicode[STIX]{x1D6FC}_{L}}$
, where
$L\sim t^{\unicode[STIX]{x1D6FC}_{L}}$
, where
![]() $L$
is the total integral scale, defined in (2.43). It is assumed for the developments hereafter that the kinetic and magnetic integral scales evolve similarly, which is assessed numerically. From figure 2 and the IK scaling (3.2), it was shown that in the inertial range, the total energy spectrum scales in
$L$
is the total integral scale, defined in (2.43). It is assumed for the developments hereafter that the kinetic and magnetic integral scales evolve similarly, which is assessed numerically. From figure 2 and the IK scaling (3.2), it was shown that in the inertial range, the total energy spectrum scales in
![]() $E=E_{V}+E_{B}\sim \sqrt{\unicode[STIX]{x1D716}b_{0}}k^{-3/2}$
. Secondly, at large scales, the infrared slope of
$E=E_{V}+E_{B}\sim \sqrt{\unicode[STIX]{x1D716}b_{0}}k^{-3/2}$
. Secondly, at large scales, the infrared slope of
![]() $E$
is the one of the most energetic (smallest infrared slope) spectrum: given the initial conditions (2.44) chosen here, one has
$E$
is the one of the most energetic (smallest infrared slope) spectrum: given the initial conditions (2.44) chosen here, one has
![]() $E\sim k^{\unicode[STIX]{x1D70E}-p}$
, with
$E\sim k^{\unicode[STIX]{x1D70E}-p}$
, with
![]() $\unicode[STIX]{x1D70E}=\unicode[STIX]{x1D70E}_{B}$
, and where
$\unicode[STIX]{x1D70E}=\unicode[STIX]{x1D70E}_{B}$
, and where
![]() $p$
is a backscatter parameter which accounts for strong inverse transfers in hydrodynamics Batchelor turbulence (Lesieur & Ossia Reference Lesieur and Ossia2000; Meldi & Sagaut Reference Meldi and Sagaut2013a
; Briard et al.
Reference Briard, Gomez, Sagaut and Memari2015).
$p$
is a backscatter parameter which accounts for strong inverse transfers in hydrodynamics Batchelor turbulence (Lesieur & Ossia Reference Lesieur and Ossia2000; Meldi & Sagaut Reference Meldi and Sagaut2013a
; Briard et al.
Reference Briard, Gomez, Sagaut and Memari2015).
The prediction of the decay of the total energy in MHD turbulence was addressed in several papers (Hossain et al. Reference Hossain, Gray, Pontius, Matthaeus and Oughton1995; Pouquet Reference Pouquet1996; Galtier et al. Reference Galtier, Politano and Pouquet1997, Reference Galtier, Zienicke, Politano and Pouquet1999; Kalelkar & Pandit Reference Kalelkar and Pandit2004; Banerjee & Jedamzik Reference Banerjee and Jedamzik2004). Since in Hossain et al. (Reference Hossain, Gray, Pontius, Matthaeus and Oughton1995) the infrared slopes of the spectra are not considered, we rather focus on the other references. Notably, in Galtier et al. (Reference Galtier, Politano and Pouquet1997), the predictions are, for the total energy and the integral scale,
These predictions were assessed in two-dimensional simulations in Galtier et al. (Reference Galtier, Politano and Pouquet1997) within the first 10 turnover times, and are further analysed in Galtier et al. (Reference Galtier, Zienicke, Politano and Pouquet1999). One of the conclusions of these theoretical decay exponents is that MHD turbulence decays more slowly than non-magnetic isotropic turbulence. This is nevertheless at odds with Banerjee & Jedamzik (Reference Banerjee and Jedamzik2004), where stronger decay rates for the kinetic and magnetic energies are obtained, closer to HIT predictions than (3.4).
However, two-dimensional turbulence might be more representative of strong MHD turbulence, where the cascade of energy occurs preferentially in the direction perpendicular to the mean magnetic field
![]() $\boldsymbol{B}^{0}$
, than isotropic MHD turbulence with no mean magnetic field. In this view, we propose new theoretical time exponents for the total energy and the integral scale in IMHDT. The method is similar to what is done in HIT (George Reference George1992), and extended to MHD in Pouquet (Reference Pouquet1996), Galtier et al. (Reference Galtier, Politano and Pouquet1997).
$\boldsymbol{B}^{0}$
, than isotropic MHD turbulence with no mean magnetic field. In this view, we propose new theoretical time exponents for the total energy and the integral scale in IMHDT. The method is similar to what is done in HIT (George Reference George1992), and extended to MHD in Pouquet (Reference Pouquet1996), Galtier et al. (Reference Galtier, Politano and Pouquet1997).
First, for a total energy spectrum scaling in
![]() $E\sim k^{\unicode[STIX]{x1D70E}-p}$
at large scales, the total energy evolves as
$E\sim k^{\unicode[STIX]{x1D70E}-p}$
at large scales, the total energy evolves as
![]() $K\sim L^{-(\unicode[STIX]{x1D70E}-p+1)}\sim t^{-\unicode[STIX]{x1D6FC}_{L}(\unicode[STIX]{x1D70E}-p+1)}$
, with
$K\sim L^{-(\unicode[STIX]{x1D70E}-p+1)}\sim t^{-\unicode[STIX]{x1D6FC}_{L}(\unicode[STIX]{x1D70E}-p+1)}$
, with
![]() $L\sim t^{\unicode[STIX]{x1D6FC}_{L}}$
. Since
$L\sim t^{\unicode[STIX]{x1D6FC}_{L}}$
. Since
![]() $K\sim t^{\unicode[STIX]{x1D6FC}}$
, one gets
$K\sim t^{\unicode[STIX]{x1D6FC}}$
, one gets
This relation, also verified in HIT, is given in Galtier et al. (Reference Galtier, Politano and Pouquet1997) without the backscatter parameter
![]() $p$
. The second step is to link the decay exponent
$p$
. The second step is to link the decay exponent
![]() $\unicode[STIX]{x1D6FC}-1$
of the total dissipation rate
$\unicode[STIX]{x1D6FC}-1$
of the total dissipation rate
![]() $\unicode[STIX]{x1D716}$
to the expression (3.5). In HIT, one uses
$\unicode[STIX]{x1D716}$
to the expression (3.5). In HIT, one uses
![]() $\unicode[STIX]{x1D716}_{V}\sim u^{3}/L_{V}$
(George Reference George1992). For MHD turbulence, (3.1) is used instead, with
$\unicode[STIX]{x1D716}_{V}\sim u^{3}/L_{V}$
(George Reference George1992). For MHD turbulence, (3.1) is used instead, with
![]() $\unicode[STIX]{x1D70F}_{\text{tr}}=Lb_{0}/u^{2}$
, so that
$\unicode[STIX]{x1D70F}_{\text{tr}}=Lb_{0}/u^{2}$
, so that
![]() $\unicode[STIX]{x1D716}\sim u^{4}/(Lb_{0})$
. From this point, our development differs from Galtier et al. (Reference Galtier, Politano and Pouquet1997): in the latter reference,
$\unicode[STIX]{x1D716}\sim u^{4}/(Lb_{0})$
. From this point, our development differs from Galtier et al. (Reference Galtier, Politano and Pouquet1997): in the latter reference,
![]() $b_{0}\sim B_{0}$
is independent of time and might reflect a background mean magnetic field. This gives
$b_{0}\sim B_{0}$
is independent of time and might reflect a background mean magnetic field. This gives
![]() $\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FC}_{L}-1$
so that (3.4) is recovered.
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FC}_{L}-1$
so that (3.4) is recovered.
On the contrary, we claim that in isotropic MHD turbulence without mean magnetic field,
![]() $b_{0}=\sqrt{2K_{B}/3}$
varies with time because the magnetic energies does. Furthermore, we assume that total, kinetic and magnetic energies, have the same asymptotic decay exponent
$b_{0}=\sqrt{2K_{B}/3}$
varies with time because the magnetic energies does. Furthermore, we assume that total, kinetic and magnetic energies, have the same asymptotic decay exponent
![]() $\unicode[STIX]{x1D6FC}$
, even if they have different intensities, so that
$\unicode[STIX]{x1D6FC}$
, even if they have different intensities, so that
![]() $b_{0}\sim t^{\unicode[STIX]{x1D6FC}/2}$
. This provides
$b_{0}\sim t^{\unicode[STIX]{x1D6FC}/2}$
. This provides
![]() $\unicode[STIX]{x1D6FC}_{L}=1+\unicode[STIX]{x1D6FC}/2$
. Combined with (3.5), this eventually yields our theoretical predictions for the decay of the total energy and integral scale in isotropic MHD turbulence
$\unicode[STIX]{x1D6FC}_{L}=1+\unicode[STIX]{x1D6FC}/2$
. Combined with (3.5), this eventually yields our theoretical predictions for the decay of the total energy and integral scale in isotropic MHD turbulence
The striking feature is that these predictions are identical to the predictions for kinetic energy in HIT (Meldi & Sagaut Reference Meldi and Sagaut2013a
; Briard et al.
Reference Briard, Gomez, Sagaut and Memari2015), despite the non-Kolmogorov scaling of both
![]() $E_{V}(k,t)$
and
$E_{V}(k,t)$
and
![]() $E_{B}(k,t)$
. Only the backscatter parameter
$E_{B}(k,t)$
. Only the backscatter parameter
![]() $p$
is changed for
$p$
is changed for
![]() $\unicode[STIX]{x1D70E}=4$
from
$\unicode[STIX]{x1D70E}=4$
from
![]() $p=0.55$
in HIT to
$p=0.55$
in HIT to
![]() $p=1/3$
in IMHDT, which is a rather small difference. These theoretical decay rates span from
$p=1/3$
in IMHDT, which is a rather small difference. These theoretical decay rates span from
![]() $-1$
for
$-1$
for
![]() $\unicode[STIX]{x1D70E}=1$
to
$\unicode[STIX]{x1D70E}=1$
to
![]() $-1.4$
for
$-1.4$
for
![]() $\unicode[STIX]{x1D70E}=4$
: these values are closer to the three-dimensional simulations of Banerjee & Jedamzik (Reference Banerjee and Jedamzik2004) than the two-dimensional ones of Galtier et al. (Reference Galtier, Politano and Pouquet1997). Note that our prediction (3.6) is in agreement with the self-similar analysis of Campanelli (Reference Campanelli2016).
$\unicode[STIX]{x1D70E}=4$
: these values are closer to the three-dimensional simulations of Banerjee & Jedamzik (Reference Banerjee and Jedamzik2004) than the two-dimensional ones of Galtier et al. (Reference Galtier, Politano and Pouquet1997). Note that our prediction (3.6) is in agreement with the self-similar analysis of Campanelli (Reference Campanelli2016).
These new predictions for
![]() $K$
and
$K$
and
![]() $L$
are successfully assessed numerically in figure 4 for
$L$
are successfully assessed numerically in figure 4 for
![]() $\unicode[STIX]{x1D70E}_{B}=2$
and
$\unicode[STIX]{x1D70E}_{B}=2$
and
![]() $\unicode[STIX]{x1D70E}_{B}=4$
. Supplementary simulations revealed that both the decay exponents of kinetic energy
$\unicode[STIX]{x1D70E}_{B}=4$
. Supplementary simulations revealed that both the decay exponents of kinetic energy
![]() $\unicode[STIX]{x1D6FC}_{V}$
and magnetic energy
$\unicode[STIX]{x1D6FC}_{V}$
and magnetic energy
![]() $\unicode[STIX]{x1D6FC}_{B}$
are in agreement with (3.6) for the different initial conditions investigated in appendix A.2: in particular, if
$\unicode[STIX]{x1D6FC}_{B}$
are in agreement with (3.6) for the different initial conditions investigated in appendix A.2: in particular, if
![]() $\unicode[STIX]{x1D70E}_{B}=\unicode[STIX]{x1D70E}=2$
and
$\unicode[STIX]{x1D70E}_{B}=\unicode[STIX]{x1D70E}=2$
and
![]() $\unicode[STIX]{x1D70E}_{V}=4$
, one has still
$\unicode[STIX]{x1D70E}_{V}=4$
, one has still
![]() $\unicode[STIX]{x1D6FC}_{V}=\unicode[STIX]{x1D6FC}_{B}=\unicode[STIX]{x1D6FC}$
since the large scale dynamics is driven by the magnetic field. Also, even though not presented here, we obtained that (i) the decay exponent
$\unicode[STIX]{x1D6FC}_{V}=\unicode[STIX]{x1D6FC}_{B}=\unicode[STIX]{x1D6FC}$
since the large scale dynamics is driven by the magnetic field. Also, even though not presented here, we obtained that (i) the decay exponent
![]() $\unicode[STIX]{x1D6FC}$
of the total energy follows the usual predictions for kinetic energy in HIT at low Reynolds numbers as well; (ii) in the saturated case where
$\unicode[STIX]{x1D6FC}$
of the total energy follows the usual predictions for kinetic energy in HIT at low Reynolds numbers as well; (ii) in the saturated case where
![]() $k_{\text{min}}/k_{L}(0)=1$
, one has
$k_{\text{min}}/k_{L}(0)=1$
, one has
![]() $K\sim t^{-2}$
, like kinetic energy in HIT (take
$K\sim t^{-2}$
, like kinetic energy in HIT (take
![]() $\unicode[STIX]{x1D70E}\rightarrow \infty$
in (3.6)); and (iii) the value of
$\unicode[STIX]{x1D70E}\rightarrow \infty$
in (3.6)); and (iii) the value of
![]() $\unicode[STIX]{x1D6FC}$
, for a given
$\unicode[STIX]{x1D6FC}$
, for a given
![]() $\unicode[STIX]{x1D70E}$
, is independent of the kinetic to magnetic energy ratio
$\unicode[STIX]{x1D70E}$
, is independent of the kinetic to magnetic energy ratio
![]() $K_{V}/K_{B}$
.
$K_{V}/K_{B}$
.

Figure 4. Time exponents
![]() $\unicode[STIX]{x1D6FC}$
and
$\unicode[STIX]{x1D6FC}$
and
![]() $\unicode[STIX]{x1D6FC}_{L}$
of the total energy
$\unicode[STIX]{x1D6FC}_{L}$
of the total energy
![]() $K$
and integral scale
$K$
and integral scale
![]() $L$
for
$L$
for
![]() $\unicode[STIX]{x1D70E}=2$
(black) and
$\unicode[STIX]{x1D70E}=2$
(black) and
![]() $\unicode[STIX]{x1D70E}=4$
(grey), with initial conditions (2.44). Lines represent the present simulations, and symbols the theoretical predictions (3.6); ◯ for
$\unicode[STIX]{x1D70E}=4$
(grey), with initial conditions (2.44). Lines represent the present simulations, and symbols the theoretical predictions (3.6); ◯ for
![]() $\unicode[STIX]{x1D6FC}$
and
$\unicode[STIX]{x1D6FC}$
and
![]() $\Box$
for
$\Box$
for
![]() $\unicode[STIX]{x1D6FC}_{L}$
. (a) Total energy (——); see appendix A.2 for the decay exponent
$\unicode[STIX]{x1D6FC}_{L}$
. (a) Total energy (——); see appendix A.2 for the decay exponent
![]() $\unicode[STIX]{x1D6FC}_{R}$
of residual energy (
$\unicode[STIX]{x1D6FC}_{R}$
of residual energy (
![]() $--$
). (b) Integral scale growth.
$--$
). (b) Integral scale growth.
Some additional features should be pointed out about (3.6): first, for
![]() $\unicode[STIX]{x1D70E}=1$
, one has
$\unicode[STIX]{x1D70E}=1$
, one has
![]() $K\sim t^{-1}$
, a decay rate discussed in Hossain et al. (Reference Hossain, Gray, Pontius, Matthaeus and Oughton1995), Galtier et al. (Reference Galtier, Politano and Pouquet1997), and which is in agreement with a different approach (Kalelkar & Pandit (Reference Kalelkar and Pandit2004), equation (11) therein, for
$K\sim t^{-1}$
, a decay rate discussed in Hossain et al. (Reference Hossain, Gray, Pontius, Matthaeus and Oughton1995), Galtier et al. (Reference Galtier, Politano and Pouquet1997), and which is in agreement with a different approach (Kalelkar & Pandit (Reference Kalelkar and Pandit2004), equation (11) therein, for
![]() $q=1$
,
$q=1$
,
![]() $E\sim k^{q}$
). Furthermore, these theoretical decay exponents are fully consistent with the IK scaling (3.2): indeed, the continuity of the total energy spectrum in
$E\sim k^{q}$
). Furthermore, these theoretical decay exponents are fully consistent with the IK scaling (3.2): indeed, the continuity of the total energy spectrum in
![]() $k_{L}=1/L$
gives
$k_{L}=1/L$
gives
from which (3.6) directly follows.
In this section, it has been shown that the total energy decays in isotropic MHD similarly to kinetic energy in HIT, with a slight difference due to inverse nonlinear transfers only when
![]() $\unicode[STIX]{x1D70E}=4$
. This prediction, assessed numerically, is an important finding of the present work, and strongly differs from the predictions by Galtier et al. (Reference Galtier, Politano and Pouquet1997), essentially because we insisted on the fact that
$\unicode[STIX]{x1D70E}=4$
. This prediction, assessed numerically, is an important finding of the present work, and strongly differs from the predictions by Galtier et al. (Reference Galtier, Politano and Pouquet1997), essentially because we insisted on the fact that
![]() $b_{0}$
varies with time, which is a reasonable statement in the absence of a mean magnetic field.
$b_{0}$
varies with time, which is a reasonable statement in the absence of a mean magnetic field.
4 Imbalanced isotropic MHD turbulence
In this section, the emphasis is put on the spectral modelling of the velocity–magnetic correlation
![]() $\hat{\unicode[STIX]{x1D60F}}_{ij}^{c}(\boldsymbol{k})=\langle \hat{u} _{i}^{\ast }(\boldsymbol{k})\hat{b}_{j}(\boldsymbol{k})\rangle$
, which corresponds to
$\hat{\unicode[STIX]{x1D60F}}_{ij}^{c}(\boldsymbol{k})=\langle \hat{u} _{i}^{\ast }(\boldsymbol{k})\hat{b}_{j}(\boldsymbol{k})\rangle$
, which corresponds to
![]() $\langle u_{i}(\boldsymbol{x})b_{j}(\boldsymbol{x}+\boldsymbol{r})\rangle$
in physical space, with
$\langle u_{i}(\boldsymbol{x})b_{j}(\boldsymbol{x}+\boldsymbol{r})\rangle$
in physical space, with
![]() $\boldsymbol{r}$
the separation vector. Some fundamental results about spectral modelling are firstly exposed, and then the nonlinear transfer terms associated with cross-helicity are computed within the EDQNM framework. Finally, numerical results of decaying MHD turbulence with an initial non-zero cross-helicity are presented, i.e. imbalanced isotropic MHD without a mean magnetic field, in order to identify the impact of the cross-correlation on the scalings of
$\boldsymbol{r}$
the separation vector. Some fundamental results about spectral modelling are firstly exposed, and then the nonlinear transfer terms associated with cross-helicity are computed within the EDQNM framework. Finally, numerical results of decaying MHD turbulence with an initial non-zero cross-helicity are presented, i.e. imbalanced isotropic MHD without a mean magnetic field, in order to identify the impact of the cross-correlation on the scalings of
![]() $E_{B}(k,t)$
and
$E_{B}(k,t)$
and
![]() $E_{V}(k,t)$
, and on the decay of
$E_{V}(k,t)$
, and on the decay of
![]() $K$
. Pressure spectra are addressed as well. It is worth mentioning that such a framework of non-zero cross-helicity without mean magnetic field was also briefly addressed in Wan et al. (Reference Wan, Oughton, Servidio and Matthaeus2012).
$K$
. Pressure spectra are addressed as well. It is worth mentioning that such a framework of non-zero cross-helicity without mean magnetic field was also briefly addressed in Wan et al. (Reference Wan, Oughton, Servidio and Matthaeus2012).
4.1 Modelling of the spectral cross-correlation
 $\hat{\unicode[STIX]{x1D60F}}_{ij}^{c}$
$\hat{\unicode[STIX]{x1D60F}}_{ij}^{c}$
Helical decompositions of the spectral fluctuating velocity and magnetic fields are firstly considered, i.e.
where
![]() $N_{i}$
are the helical modes (Cambon & Jacquin Reference Cambon and Jacquin1989) which verify
$N_{i}$
are the helical modes (Cambon & Jacquin Reference Cambon and Jacquin1989) which verify
![]() $k_{i}N_{i}=0$
,
$k_{i}N_{i}=0$
,
![]() $N_{i}N_{i}=0$
and
$N_{i}N_{i}=0$
and
![]() $N_{i}(-\boldsymbol{k})=N_{i}^{\ast }(\boldsymbol{k})$
. Because of Hermitian symmetry for
$N_{i}(-\boldsymbol{k})=N_{i}^{\ast }(\boldsymbol{k})$
. Because of Hermitian symmetry for
![]() $\hat{u} _{i}$
and
$\hat{u} _{i}$
and
![]() $\hat{b}_{i}$
, namely
$\hat{b}_{i}$
, namely
![]() $\hat{u} _{i}^{\ast }(\boldsymbol{k})=\hat{u} _{i}(-\boldsymbol{k})$
and
$\hat{u} _{i}^{\ast }(\boldsymbol{k})=\hat{u} _{i}(-\boldsymbol{k})$
and
![]() $\hat{b}_{i}^{\ast }(\boldsymbol{k})=\hat{b}_{i}(-\boldsymbol{k})$
, this property is verified as well for the
$\hat{b}_{i}^{\ast }(\boldsymbol{k})=\hat{b}_{i}(-\boldsymbol{k})$
, this property is verified as well for the
![]() $\pm$
components,
$\pm$
components,
![]() $u_{\pm }^{\ast }(\boldsymbol{k})=u_{\pm }(-\boldsymbol{k})$
and
$u_{\pm }^{\ast }(\boldsymbol{k})=u_{\pm }(-\boldsymbol{k})$
and
![]() $b_{\pm }^{\ast }(\boldsymbol{k})=b_{\pm }(-\boldsymbol{k})$
. Using these decompositions, it directly follows that
$b_{\pm }^{\ast }(\boldsymbol{k})=b_{\pm }(-\boldsymbol{k})$
. Using these decompositions, it directly follows that
where the time dependence has been omitted for clarity. The cross-helicity density
![]() ${\mathcal{H}}_{c}$
is half the trace of the spectral cross-correlation
${\mathcal{H}}_{c}$
is half the trace of the spectral cross-correlation
is real, and verifies
![]() ${\mathcal{H}}_{c}^{\ast }(\boldsymbol{k})={\mathcal{H}}_{c}(-\boldsymbol{k})$
. The cross-helicity
${\mathcal{H}}_{c}^{\ast }(\boldsymbol{k})={\mathcal{H}}_{c}(-\boldsymbol{k})$
. The cross-helicity
![]() $K_{c}$
is linked to the cross-helical spectrum
$K_{c}$
is linked to the cross-helical spectrum
![]() $H_{c}$
through
$H_{c}$
through
A non-zero cross-helicity breaks the mirror symmetry of the flow since
![]() $\boldsymbol{b}$
is a pseudo-vector, consistently with the decomposition of Frisch et al. (Reference Frisch, Pouquet, Léorat and Mazure1975). Nevertheless, it is possible to consider cross-helicity without magnetic helicity and kinetic helicity.
$\boldsymbol{b}$
is a pseudo-vector, consistently with the decomposition of Frisch et al. (Reference Frisch, Pouquet, Léorat and Mazure1975). Nevertheless, it is possible to consider cross-helicity without magnetic helicity and kinetic helicity.
The second right-hand side term of (4.2) can be non-zero in non-helical turbulence. This term
![]() $F^{\text{EM}}$
is linked to the cross-correlation through
$F^{\text{EM}}$
is linked to the cross-correlation through
The quantity
![]() $F^{\text{EM}}$
verifies
$F^{\text{EM}}$
verifies
![]() $F^{\text{EM *}}(\boldsymbol{k})=F^{\text{EM}}(-\boldsymbol{k})$
. It follows that
$F^{\text{EM *}}(\boldsymbol{k})=F^{\text{EM}}(-\boldsymbol{k})$
. It follows that
![]() $F^{\text{EM}}$
is linked to the electromotive force through
$F^{\text{EM}}$
is linked to the electromotive force through
However, the electromotive force is not considered here in the framework of isotropic MHD turbulence: indeed it would create a mean magnetic field, and thus break the isotropy of the flow, according to
The two last right-hand side terms of (4.2) might be non-zero in complex flows such as rotating or sheared MHD turbulence, and may be interpreted as a mixed kinetic-magnetic polarization. But they always vanish in isotropic MHD turbulence with or without helicity, so that they are discarded from this point. Consequently, the decomposition is similar to the one proposed in Frisch et al. (Reference Frisch, Pouquet, Léorat and Mazure1975), and one has
In what follows, the spherically averaged equation for the cross-helical spectrum is derived, along with its corresponding spherically averaged nonlinear transfer, and with the additional kinetic and magnetic transfer terms resulting from the presence of
![]() $H_{c}(k,t)$
.
$H_{c}(k,t)$
.
4.2 Equation for the cross-helical spectrum
 $H_{c}(k,t)$
$H_{c}(k,t)$
In this part, we derive the evolution equation of the cross-helical spectrum
![]() $H_{c}(k,t)$
in a manner analogous to what was done in § 2 for
$H_{c}(k,t)$
in a manner analogous to what was done in § 2 for
![]() $E_{V}(k,t)$
and
$E_{V}(k,t)$
and
![]() $E_{B}(k,t)$
. Starting from (2.10), and using the modelling of the cross-correlation studied previously, which amounts to
$E_{B}(k,t)$
. Starting from (2.10), and using the modelling of the cross-correlation studied previously, which amounts to
![]() $\hat{\unicode[STIX]{x1D60F}}_{ij}^{c}={\mathcal{H}}_{c}P_{ij}$
in IMHDT, yields
$\hat{\unicode[STIX]{x1D60F}}_{ij}^{c}={\mathcal{H}}_{c}P_{ij}$
in IMHDT, yields
Then, the EDQNM procedure is applied, and the quasi-normal expressions (2.22) and (2.23) are used to compute explicitly
![]() $\unicode[STIX]{x1D61B}_{ii}^{c}$
from (2.16). After classical algebra, this gives the final equation for the cross-helical spectrum
$\unicode[STIX]{x1D61B}_{ii}^{c}$
from (2.16). After classical algebra, this gives the final equation for the cross-helical spectrum
with
![]() $S^{c}$
the spherically averaged cross-helical nonlinear transfer
$S^{c}$
the spherically averaged cross-helical nonlinear transfer
 $$\begin{eqnarray}\displaystyle S^{c}(k,t) & = & \displaystyle \frac{1}{2}\int _{S_{k}}\unicode[STIX]{x1D61B}_{ii}^{c}(\boldsymbol{k},t)\text{d}^{2}\boldsymbol{k}\nonumber\\ \displaystyle & = & \displaystyle 8\unicode[STIX]{x03C0}^{2}\int _{\unicode[STIX]{x1D6E5}_{k}}\unicode[STIX]{x1D703}_{kpq}k^{2}pq\left[2k(y^{2}-z^{2}){\mathcal{H}}_{c}^{\prime \prime }({\mathcal{E}}_{0}^{V^{\prime }}+{\mathcal{E}}_{0}^{B^{\prime }})+p\left((xy+z^{3})({\mathcal{H}}_{c}^{\prime \prime }{\mathcal{E}}_{0}^{B}-{\mathcal{H}}_{c}{\mathcal{E}}_{0}^{V})\right.\right.\nonumber\\ \displaystyle & & \displaystyle +\,(xy+z)({\mathcal{H}}_{c}^{\prime \prime }{\mathcal{E}}_{0}^{V}-{\mathcal{H}}_{c}{\mathcal{E}}_{0}^{V^{\prime \prime }})+z(1-y^{2})({\mathcal{H}}_{c}^{\prime \prime }{\mathcal{E}}_{0}^{B}-{\mathcal{H}}_{c}{\mathcal{E}}_{0}^{B^{\prime \prime }})\nonumber\\ \displaystyle & & \displaystyle +\,\left.\left.z(1-x^{2})({\mathcal{H}}_{c}^{\prime \prime }{\mathcal{E}}_{0}^{V}-{\mathcal{H}}_{c}{\mathcal{E}}_{0}^{B^{\prime \prime }})\right)\right]\text{d}p\,\text{d}q,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle S^{c}(k,t) & = & \displaystyle \frac{1}{2}\int _{S_{k}}\unicode[STIX]{x1D61B}_{ii}^{c}(\boldsymbol{k},t)\text{d}^{2}\boldsymbol{k}\nonumber\\ \displaystyle & = & \displaystyle 8\unicode[STIX]{x03C0}^{2}\int _{\unicode[STIX]{x1D6E5}_{k}}\unicode[STIX]{x1D703}_{kpq}k^{2}pq\left[2k(y^{2}-z^{2}){\mathcal{H}}_{c}^{\prime \prime }({\mathcal{E}}_{0}^{V^{\prime }}+{\mathcal{E}}_{0}^{B^{\prime }})+p\left((xy+z^{3})({\mathcal{H}}_{c}^{\prime \prime }{\mathcal{E}}_{0}^{B}-{\mathcal{H}}_{c}{\mathcal{E}}_{0}^{V})\right.\right.\nonumber\\ \displaystyle & & \displaystyle +\,(xy+z)({\mathcal{H}}_{c}^{\prime \prime }{\mathcal{E}}_{0}^{V}-{\mathcal{H}}_{c}{\mathcal{E}}_{0}^{V^{\prime \prime }})+z(1-y^{2})({\mathcal{H}}_{c}^{\prime \prime }{\mathcal{E}}_{0}^{B}-{\mathcal{H}}_{c}{\mathcal{E}}_{0}^{B^{\prime \prime }})\nonumber\\ \displaystyle & & \displaystyle +\,\left.\left.z(1-x^{2})({\mathcal{H}}_{c}^{\prime \prime }{\mathcal{E}}_{0}^{V}-{\mathcal{H}}_{c}{\mathcal{E}}_{0}^{B^{\prime \prime }})\right)\right]\text{d}p\,\text{d}q,\end{eqnarray}$$
with
![]() ${\mathcal{H}}_{c}=H_{c}(k)/(4\unicode[STIX]{x03C0}k^{2})$
,
${\mathcal{H}}_{c}=H_{c}(k)/(4\unicode[STIX]{x03C0}k^{2})$
,
![]() ${\mathcal{H}}_{c}^{\prime }=H_{c}(p)/(4\unicode[STIX]{x03C0}p^{2})$
and
${\mathcal{H}}_{c}^{\prime }=H_{c}(p)/(4\unicode[STIX]{x03C0}p^{2})$
and
![]() ${\mathcal{H}}_{c}^{\prime \prime }=H_{c}(q)/(4\unicode[STIX]{x03C0}q^{2})$
. Since the cross-helicity
${\mathcal{H}}_{c}^{\prime \prime }=H_{c}(q)/(4\unicode[STIX]{x03C0}q^{2})$
. Since the cross-helicity
![]() $K_{c}(t)$
is an inviscid invariant of isotropic MHD turbulence, its nonlinear transfer
$K_{c}(t)$
is an inviscid invariant of isotropic MHD turbulence, its nonlinear transfer
![]() $S^{c}$
is conservative, in agreement with the evolution equation
$S^{c}$
is conservative, in agreement with the evolution equation
where
![]() $\unicode[STIX]{x1D716}_{c}$
is the cross-helicity dissipation rate. Furthermore, according to the quasi-normal expression (2.21), the cross-helical spectrum also impacts the magnetic nonlinear transfers
$\unicode[STIX]{x1D716}_{c}$
is the cross-helicity dissipation rate. Furthermore, according to the quasi-normal expression (2.21), the cross-helical spectrum also impacts the magnetic nonlinear transfers
![]() $S^{\text{V(mag)}}$
and
$S^{\text{V(mag)}}$
and
![]() $S^{\text{B(mag)}}$
. Here are the additional contributions created by a non-zero cross-helicity in the evolution equations of
$S^{\text{B(mag)}}$
. Here are the additional contributions created by a non-zero cross-helicity in the evolution equations of
![]() $E_{V}(k,t)$
and
$E_{V}(k,t)$
and
![]() $E_{B}(k,t)$
:
$E_{B}(k,t)$
:
Both
![]() $S^{\text{V(cross)}}$
and
$S^{\text{V(cross)}}$
and
![]() $S^{\text{B(cross)}}$
are not conservative separately, but the sum has zero integral over the whole wavenumber space. From now on, we write
$S^{\text{B(cross)}}$
are not conservative separately, but the sum has zero integral over the whole wavenumber space. From now on, we write
![]() $S^{\text{B}}=S^{\text{B(mag)}}+S^{\text{B(cross)}}$
and
$S^{\text{B}}=S^{\text{B(mag)}}+S^{\text{B(cross)}}$
and
![]() $S^{\text{V}}=S^{\text{V(hyd)}}+S^{\text{V(mag)}}+S^{\text{V(cross)}}$
. These explicit expressions for the three nonlinear transfers involving the cross-helical spectrum are new. The different contributions of the cross-helical, kinetic and magnetic spectra can be disentangled easily, and this does not prevent us from analysing afterwards
$S^{\text{V}}=S^{\text{V(hyd)}}+S^{\text{V(mag)}}+S^{\text{V(cross)}}$
. These explicit expressions for the three nonlinear transfers involving the cross-helical spectrum are new. The different contributions of the cross-helical, kinetic and magnetic spectra can be disentangled easily, and this does not prevent us from analysing afterwards
![]() $E_{+}$
and
$E_{+}$
and
![]() $E_{-}$
, linked to the Elsässer variables
$E_{-}$
, linked to the Elsässer variables
![]() $\boldsymbol{z}^{\pm }=\boldsymbol{u}\pm \boldsymbol{b}$
. On the contrary, in Grappin et al. (Reference Grappin, Frisch, Léorat and Pouquet1982, Reference Grappin, Pouquet and Léorat1983), the cross-helical transfer terms must be deduced from those associated with
$\boldsymbol{z}^{\pm }=\boldsymbol{u}\pm \boldsymbol{b}$
. On the contrary, in Grappin et al. (Reference Grappin, Frisch, Léorat and Pouquet1982, Reference Grappin, Pouquet and Léorat1983), the cross-helical transfer terms must be deduced from those associated with
![]() $E_{+}$
and
$E_{+}$
and
![]() $E_{-}$
, with
$E_{-}$
, with
![]() $H_{c}=(E_{+}-E_{-})/4$
.
$H_{c}=(E_{+}-E_{-})/4$
.
At each time and each wavenumber
![]() $k$
, the cross-helical spectrum must satisfy the realizability condition given in Frisch et al. (Reference Frisch, Pouquet, Léorat and Mazure1975), namely
$k$
, the cross-helical spectrum must satisfy the realizability condition given in Frisch et al. (Reference Frisch, Pouquet, Léorat and Mazure1975), namely
For the numerical simulations of isotropic imbalanced MHD, we choose
![]() $E_{V}(k,t=0)=E_{B}(k,t=0)$
given by (2.44), with an infrared slope
$E_{V}(k,t=0)=E_{B}(k,t=0)$
given by (2.44), with an infrared slope
![]() $\unicode[STIX]{x1D70E}=\unicode[STIX]{x1D70E}_{B}=\unicode[STIX]{x1D70E}_{V}$
which is either
$\unicode[STIX]{x1D70E}=\unicode[STIX]{x1D70E}_{B}=\unicode[STIX]{x1D70E}_{V}$
which is either
![]() $\unicode[STIX]{x1D70E}=2$
or
$\unicode[STIX]{x1D70E}=2$
or
![]() $\unicode[STIX]{x1D70E}=4$
. To ensure that (4.15) is always verified, we choose
$\unicode[STIX]{x1D70E}=4$
. To ensure that (4.15) is always verified, we choose
![]() $H_{c}(k,t=0)=\sqrt{E_{V}(k,t=0)E_{B}(k,t=0)}/c_{\text{cond}}$
with
$H_{c}(k,t=0)=\sqrt{E_{V}(k,t=0)E_{B}(k,t=0)}/c_{\text{cond}}$
with
![]() $c_{\text{cond}}=10$
: for smaller values of
$c_{\text{cond}}=10$
: for smaller values of
![]() $c_{\text{cond}}$
down to unity, the realizability condition can be violated at large scales after a few turnover times.
$c_{\text{cond}}$
down to unity, the realizability condition can be violated at large scales after a few turnover times.
It is worth noting that the complete spectral evolution equations of
![]() $E_{V}$
,
$E_{V}$
,
![]() $E_{B}$
and
$E_{B}$
and
![]() $H_{c}$
are entirely solved numerically unlike in Grappin et al. (Reference Grappin, Frisch, Léorat and Pouquet1982). In the latter reference, reduced equations are obtained with the assumption that equipartition between kinetic and magnetic energy is reached, by imposing a strong mean magnetic field with random orientation to remain statistically isotropic.
$H_{c}$
are entirely solved numerically unlike in Grappin et al. (Reference Grappin, Frisch, Léorat and Pouquet1982). In the latter reference, reduced equations are obtained with the assumption that equipartition between kinetic and magnetic energy is reached, by imposing a strong mean magnetic field with random orientation to remain statistically isotropic.
In what follows, four different features are addressed in imbalanced IMHDT: the nonlinear transfers, the decay of cross-helicity, the spectral scaling of the main spectra with notably the impact of moderate Reynolds numbers, and finally pressure spectra.
4.3 Spectral nonlinear transfers in imbalanced MHD
In this section, we investigate the nonlinear spectral transfers of kinetic energy, magnetic energy and cross-helicity, and their associated fluxes. It is recalled that both
![]() $K=K_{V}+K_{B}$
and
$K=K_{V}+K_{B}$
and
![]() $K_{c}$
are inviscid invariants of MHD turbulence. To visualize the imbalance of MHD turbulence due to a non-zero cross-correlation
$K_{c}$
are inviscid invariants of MHD turbulence. To visualize the imbalance of MHD turbulence due to a non-zero cross-correlation
![]() $\langle u_{i}b_{i}\rangle$
, it is convenient to work with the Elsässer spectra
$\langle u_{i}b_{i}\rangle$
, it is convenient to work with the Elsässer spectra
whose integrals over the whole wavenumber space, which we call the Elsässer energies
![]() $K_{\pm }$
, are inviscid invariants of MHD turbulence as well (in the balanced case, one has
$K_{\pm }$
, are inviscid invariants of MHD turbulence as well (in the balanced case, one has
![]() $E_{+}=E_{-}=E=E_{V}+E_{B}$
).
$E_{+}=E_{-}=E=E_{V}+E_{B}$
).
The different fluxes, normalized by the total dissipation rate
![]() $\unicode[STIX]{x1D716}$
, are first presented in figure 5(a). The Elsässer, cross-helical and total fluxes
$\unicode[STIX]{x1D716}$
, are first presented in figure 5(a). The Elsässer, cross-helical and total fluxes
![]() $\unicode[STIX]{x1D6F1}_{+}$
,
$\unicode[STIX]{x1D6F1}_{+}$
,
![]() $\unicode[STIX]{x1D6F1}_{-}$
,
$\unicode[STIX]{x1D6F1}_{-}$
,
![]() $\unicode[STIX]{x1D6F1}^{c}$
, and
$\unicode[STIX]{x1D6F1}^{c}$
, and
![]() $\unicode[STIX]{x1D6F1}^{\text{V}}+\unicode[STIX]{x1D6F1}^{\text{B}}$
, linked to the inviscid invariants
$\unicode[STIX]{x1D6F1}^{\text{V}}+\unicode[STIX]{x1D6F1}^{\text{B}}$
, linked to the inviscid invariants
![]() $K_{+}$
,
$K_{+}$
,
![]() $K_{-}$
,
$K_{-}$
,
![]() $K_{c}$
and
$K_{c}$
and
![]() $K$
, are consistently conservative. The + Elsässer flux in slightly more intense than the
$K$
, are consistently conservative. The + Elsässer flux in slightly more intense than the
![]() $-$
one. Moreover, the Elsässer and total fluxes are much stronger than the cross-helical one, which was multiplied by 10 for readability reasons. One can remark that around the integral wavenumber
$-$
one. Moreover, the Elsässer and total fluxes are much stronger than the cross-helical one, which was multiplied by 10 for readability reasons. One can remark that around the integral wavenumber
![]() $k_{L}$
, the cross-helical flux is negative, meaning that part of the cross-helicity is transferred towards large scales. This is not a transient effect, and remains rather subdominant since the main part of the cross-helical flux is positive and constant in the inertial range. This could also be a signature of inviscid invariants not positive–definite: indeed, a similar feature was observed for kinetic helicity in HIT (Briard & Gomez Reference Briard and Gomez2017).
$k_{L}$
, the cross-helical flux is negative, meaning that part of the cross-helicity is transferred towards large scales. This is not a transient effect, and remains rather subdominant since the main part of the cross-helical flux is positive and constant in the inertial range. This could also be a signature of inviscid invariants not positive–definite: indeed, a similar feature was observed for kinetic helicity in HIT (Briard & Gomez Reference Briard and Gomez2017).

Figure 5. Nonlinear transfers and fluxes, normalized by
![]() $\unicode[STIX]{x1D716}$
, at
$\unicode[STIX]{x1D716}$
, at
![]() $Re_{\unicode[STIX]{x1D706}}(t=30\unicode[STIX]{x1D70F}_{0})=4\times 10^{4}$
for
$Re_{\unicode[STIX]{x1D706}}(t=30\unicode[STIX]{x1D70F}_{0})=4\times 10^{4}$
for
![]() $\unicode[STIX]{x1D70E}=2$
, along with the integral and dissipative wavenumbers
$\unicode[STIX]{x1D70E}=2$
, along with the integral and dissipative wavenumbers
![]() $k_{L}$
and
$k_{L}$
and
![]() $k_{\unicode[STIX]{x1D702}}^{\text{MHD}}$
. For better readability, the cross-helical transfer and flux were multiplied by
$k_{\unicode[STIX]{x1D702}}^{\text{MHD}}$
. For better readability, the cross-helical transfer and flux were multiplied by
![]() $10$
. (a) Cross-helical flux
$10$
. (a) Cross-helical flux
![]() $\unicode[STIX]{x1D6F1}^{c}$
, Elsässer fluxes
$\unicode[STIX]{x1D6F1}^{c}$
, Elsässer fluxes
![]() $\unicode[STIX]{x1D6F1}_{+}$
and
$\unicode[STIX]{x1D6F1}_{+}$
and
![]() $\unicode[STIX]{x1D6F1}_{-}$
and total energy flux
$\unicode[STIX]{x1D6F1}_{-}$
and total energy flux
![]() $\unicode[STIX]{x1D6F1}^{\text{V}}+\unicode[STIX]{x1D6F1}^{\text{B}}$
. (b) Kinetic energy transfers (black):
$\unicode[STIX]{x1D6F1}^{\text{V}}+\unicode[STIX]{x1D6F1}^{\text{B}}$
. (b) Kinetic energy transfers (black):
![]() $S^{\text{V(hyd)}}$
,
$S^{\text{V(hyd)}}$
,
![]() $S^{\text{V(mag)}}$
and
$S^{\text{V(mag)}}$
and
![]() $S^{\text{V(cross)}}$
; Magnetic energy transfers (grey):
$S^{\text{V(cross)}}$
; Magnetic energy transfers (grey):
![]() $S^{\text{B(mag)}}$
, and
$S^{\text{B(mag)}}$
, and
![]() $S^{\text{B(cross)}}$
. (c) Total transfer
$S^{\text{B(cross)}}$
. (c) Total transfer
![]() $S^{\text{V}}+S^{\text{B}}$
(black) and cross-helical transfer
$S^{\text{V}}+S^{\text{B}}$
(black) and cross-helical transfer
![]() $S^{c}$
(grey); arrows indicate the direction of the transfers.
$S^{c}$
(grey); arrows indicate the direction of the transfers.
This is better illustrated in figure 5(b), where the five kinetic and magnetic nonlinear spherically averaged transfers are displayed, namely
![]() $S^{\text{V(hyd)}}$
,
$S^{\text{V(hyd)}}$
,
![]() $S^{\text{V(mag)}}$
,
$S^{\text{V(mag)}}$
,
![]() $S^{\text{V(cross)}}$
,
$S^{\text{V(cross)}}$
,
![]() $S^{\text{B(mag)}}$
and
$S^{\text{B(mag)}}$
and
![]() $S^{\text{B(cross)}}$
. These transfer terms can be decomposed into two groups: the ones already present in balanced MHD,
$S^{\text{B(cross)}}$
. These transfer terms can be decomposed into two groups: the ones already present in balanced MHD,
![]() $S^{\text{V(hyd)}}$
,
$S^{\text{V(hyd)}}$
,
![]() $S^{\text{V(mag)}}$
and
$S^{\text{V(mag)}}$
and
![]() $S^{\text{B(mag)}}$
, which are direct transfers from large to small scales. Whereas the terms arising from the presence of cross-helicity,
$S^{\text{B(mag)}}$
, which are direct transfers from large to small scales. Whereas the terms arising from the presence of cross-helicity,
![]() $S^{\text{V(cross)}}$
and
$S^{\text{V(cross)}}$
and
![]() $S^{\text{B(cross)}}$
, are inverse transfers stronger at large scales, and as intense as the others.
$S^{\text{B(cross)}}$
, are inverse transfers stronger at large scales, and as intense as the others.
Furthermore, in figure 5(c), the total and cross-helical nonlinear transfers
![]() $S^{\text{V}}+S^{\text{B}}$
and
$S^{\text{V}}+S^{\text{B}}$
and
![]() $S^{c}$
are presented. The transfer of total energy is much more intense than the one of cross-helicity: total energy is taken from a large range of scales and brought to smaller scales close to
$S^{c}$
are presented. The transfer of total energy is much more intense than the one of cross-helicity: total energy is taken from a large range of scales and brought to smaller scales close to
![]() $k_{\unicode[STIX]{x1D702}}^{\text{MHD}}$
. Whereas
$k_{\unicode[STIX]{x1D702}}^{\text{MHD}}$
. Whereas
![]() $S^{c}$
is much less intense and transfers cross-helicity in a more complex way: indeed, most of the cross-helicity is taken from a narrow band of large scales to a wide range of smaller scales. But in addition, large scales cross-helicity is also brought at scales bigger than
$S^{c}$
is much less intense and transfers cross-helicity in a more complex way: indeed, most of the cross-helicity is taken from a narrow band of large scales to a wide range of smaller scales. But in addition, large scales cross-helicity is also brought at scales bigger than
![]() $k_{L}^{-1}$
, illustrating some strong inverse transfer mechanisms. Moreover, one can observe that around
$k_{L}^{-1}$
, illustrating some strong inverse transfer mechanisms. Moreover, one can observe that around
![]() $k_{\unicode[STIX]{x1D702}}^{\text{MHD}}$
, cross-helicity is also slightly transferred to larger scales. These different directions of transfers are sketched with arrows in figure 5(c).
$k_{\unicode[STIX]{x1D702}}^{\text{MHD}}$
, cross-helicity is also slightly transferred to larger scales. These different directions of transfers are sketched with arrows in figure 5(c).
4.4 Decay of cross-helicity
The impact of a non-zero initial cross-helicity on the decay is illustrated in figure 6(a): it is shown that with a sufficient initial velocity–magnetic correlation, here for
![]() $H_{c}(k,t=0)=0.5\sqrt{E_{V}(k,t=0)E_{B}(k,t=0)}$
, the decay of the total energy
$H_{c}(k,t=0)=0.5\sqrt{E_{V}(k,t=0)E_{B}(k,t=0)}$
, the decay of the total energy
![]() $K$
is slightly delayed. If the amount of initial cross-helicity is too weak, there is no visible effect on
$K$
is slightly delayed. If the amount of initial cross-helicity is too weak, there is no visible effect on
![]() $K$
. Note that this kind of initial delay is analogous to what was observed in HIT with kinetic helicity (André & Lesieur Reference André and Lesieur1977; Briard & Gomez Reference Briard and Gomez2017). Furthermore, during the decay of
$K$
. Note that this kind of initial delay is analogous to what was observed in HIT with kinetic helicity (André & Lesieur Reference André and Lesieur1977; Briard & Gomez Reference Briard and Gomez2017). Furthermore, during the decay of
![]() $K_{V}$
,
$K_{V}$
,
![]() $K_{B}$
and
$K_{B}$
and
![]() $K_{c}$
, the normalized correlation
$K_{c}$
, the normalized correlation
![]() $\unicode[STIX]{x1D70C}_{c}=K_{c}/\sqrt{K_{V}K_{B}}$
, linked to the averaged cosine of the angle between
$\unicode[STIX]{x1D70C}_{c}=K_{c}/\sqrt{K_{V}K_{B}}$
, linked to the averaged cosine of the angle between
![]() $\boldsymbol{u}$
and
$\boldsymbol{u}$
and
![]() $\boldsymbol{b}$
, increases linearly time, from the initial value to unity, meaning toward alignment in the same direction of the velocity and magnetic fields.
$\boldsymbol{b}$
, increases linearly time, from the initial value to unity, meaning toward alignment in the same direction of the velocity and magnetic fields.
The asymptotic decay of cross-helicity is finally briefly discussed. As mentioned above, because of the slow increase of the normalized correlation
![]() $\unicode[STIX]{x1D70C}_{c}$
, the realizability condition (4.15) is eventually broken for large times. In other words, this means that long-time decay with several hundreds of turnover times, as in figure 4, cannot be easily performed. Note that this is not a limitation for DNS because in practice only a few turnover times are computed. We nevertheless propose some quantitative information about the decay exponent
$\unicode[STIX]{x1D70C}_{c}$
, the realizability condition (4.15) is eventually broken for large times. In other words, this means that long-time decay with several hundreds of turnover times, as in figure 4, cannot be easily performed. Note that this is not a limitation for DNS because in practice only a few turnover times are computed. We nevertheless propose some quantitative information about the decay exponent
![]() $\unicode[STIX]{x1D6FC}_{c}$
of cross-helicity, by choosing
$\unicode[STIX]{x1D6FC}_{c}$
of cross-helicity, by choosing
![]() $K_{c}(t=0)=10^{-2}$
, so that a few hundred turnover times occur with the realizability condition satisfied.
$K_{c}(t=0)=10^{-2}$
, so that a few hundred turnover times occur with the realizability condition satisfied.
Three conclusions can be drawn from figure 6(b): (i) the decay of cross-helicity is very slow compared to the decay of total energy; (ii) the decay exponent
![]() $\unicode[STIX]{x1D6FC}_{c}$
of
$\unicode[STIX]{x1D6FC}_{c}$
of
![]() $K_{c}$
seems to be independent of
$K_{c}$
seems to be independent of
![]() $\unicode[STIX]{x1D70E}$
, since one has
$\unicode[STIX]{x1D70E}$
, since one has
![]() $\unicode[STIX]{x1D6FC}_{c}\simeq -0.2$
for both
$\unicode[STIX]{x1D6FC}_{c}\simeq -0.2$
for both
![]() $\unicode[STIX]{x1D70E}=2$
and
$\unicode[STIX]{x1D70E}=2$
and
![]() $\unicode[STIX]{x1D70E}=4$
; and (iii) the presence of cross-helicity does not modify the decay exponent of the total energy, since the previous theoretical predictions (3.6) are recovered: see inset of figure 6(b) where
$\unicode[STIX]{x1D70E}=4$
; and (iii) the presence of cross-helicity does not modify the decay exponent of the total energy, since the previous theoretical predictions (3.6) are recovered: see inset of figure 6(b) where
![]() $\unicode[STIX]{x1D6FC}=-1.2$
for
$\unicode[STIX]{x1D6FC}=-1.2$
for
![]() $\unicode[STIX]{x1D70E}=2$
and
$\unicode[STIX]{x1D70E}=2$
and
![]() $\unicode[STIX]{x1D6FC}=-1.4$
for
$\unicode[STIX]{x1D6FC}=-1.4$
for
![]() $\unicode[STIX]{x1D70E}=4$
. It follows from these three features that the decay of cross-helicity in isotropic MHD is quite different from the decay of kinetic helicity in isotropic hydrodynamic turbulence (Briard & Gomez Reference Briard and Gomez2017).
$\unicode[STIX]{x1D70E}=4$
. It follows from these three features that the decay of cross-helicity in isotropic MHD is quite different from the decay of kinetic helicity in isotropic hydrodynamic turbulence (Briard & Gomez Reference Briard and Gomez2017).

Figure 6. Decay of total energy and cross-helicity. (a) Impact of initial cross-helicity
![]() $K_{c}(t=0)$
on the early decay of the total energy
$K_{c}(t=0)$
on the early decay of the total energy
![]() $K$
compared to the balanced case (in grey) for
$K$
compared to the balanced case (in grey) for
![]() $\unicode[STIX]{x1D70E}=2$
. (b) Long-time decay of cross-helicity with
$\unicode[STIX]{x1D70E}=2$
. (b) Long-time decay of cross-helicity with
![]() $K_{c}(t=0)=10^{-2}$
, for
$K_{c}(t=0)=10^{-2}$
, for
![]() $\unicode[STIX]{x1D70E}=2$
(black) and
$\unicode[STIX]{x1D70E}=2$
(black) and
![]() $\unicode[STIX]{x1D70E}=4$
(grey); the inset represents the decay of total energy during the same simulation.
$\unicode[STIX]{x1D70E}=4$
(grey); the inset represents the decay of total energy during the same simulation.
4.5 The inertial scaling of the cross-helical spectrum
 $H_{c}(k,t)$
$H_{c}(k,t)$
In this part, the emphasis is put on the inertial scaling of the cross-helical spectrum
![]() $H_{c}(k,t)$
. First, the total energy and cross-helical spectra
$H_{c}(k,t)$
. First, the total energy and cross-helical spectra
![]() $E(k,t)$
and
$E(k,t)$
and
![]() $H_{c}(k,t)$
are presented in figure 7(a) for
$H_{c}(k,t)$
are presented in figure 7(a) for
![]() $\unicode[STIX]{x1D70E}=2$
. The inertial scaling of
$\unicode[STIX]{x1D70E}=2$
. The inertial scaling of
![]() $E$
remains
$E$
remains
![]() $k^{-3/2}$
, similarly to the balanced case: even though not presented,
$k^{-3/2}$
, similarly to the balanced case: even though not presented,
![]() $E_{V}$
and
$E_{V}$
and
![]() $E_{B}$
still scale in
$E_{B}$
still scale in
![]() $k^{-3/2}$
despite the presence of cross-helicity. The effects of the cross-helicity are more visible on the Elsässer spectra which are discussed in the next section.
$k^{-3/2}$
despite the presence of cross-helicity. The effects of the cross-helicity are more visible on the Elsässer spectra which are discussed in the next section.
The cross-helical spectrum itself scales with a slope close to
![]() $k^{-5/3}$
, and is negative at small scales, similarly to what was obtained for the kinetic helicity in skew–isotropic turbulence (Briard & Gomez Reference Briard and Gomez2017). One could conclude from these observations, at least within the EDQNM framework, that spectra of quantities not positive–definite, such as
$k^{-5/3}$
, and is negative at small scales, similarly to what was obtained for the kinetic helicity in skew–isotropic turbulence (Briard & Gomez Reference Briard and Gomez2017). One could conclude from these observations, at least within the EDQNM framework, that spectra of quantities not positive–definite, such as
![]() $\langle \boldsymbol{u}\boldsymbol{\cdot }\unicode[STIX]{x1D74E}\rangle$
and
$\langle \boldsymbol{u}\boldsymbol{\cdot }\unicode[STIX]{x1D74E}\rangle$
and
![]() $\langle \boldsymbol{u}\boldsymbol{\cdot }\boldsymbol{b}\rangle$
, exhibit negative values at small scales, if
$\langle \boldsymbol{u}\boldsymbol{\cdot }\boldsymbol{b}\rangle$
, exhibit negative values at small scales, if
![]() $\langle \boldsymbol{u}\boldsymbol{\cdot }\unicode[STIX]{x1D74E}\rangle$
and
$\langle \boldsymbol{u}\boldsymbol{\cdot }\unicode[STIX]{x1D74E}\rangle$
and
![]() $\langle \boldsymbol{u}\boldsymbol{\cdot }\boldsymbol{b}\rangle$
are positive initially.
$\langle \boldsymbol{u}\boldsymbol{\cdot }\boldsymbol{b}\rangle$
are positive initially.

Figure 7. Cross-helical spectra for imbalanced MHD for
![]() $\unicode[STIX]{x1D70E}=2$
. (a) Total energy and cross-helical spectra
$\unicode[STIX]{x1D70E}=2$
. (a) Total energy and cross-helical spectra
![]() $E(k,t)$
and
$E(k,t)$
and
![]() $H_{c}(k,t)$
at
$H_{c}(k,t)$
at
![]() $Re_{\unicode[STIX]{x1D706}}(t=30\unicode[STIX]{x1D70F}_{0})=4\times 10^{4}$
along with the integral and dissipative wavenumbers
$Re_{\unicode[STIX]{x1D706}}(t=30\unicode[STIX]{x1D70F}_{0})=4\times 10^{4}$
along with the integral and dissipative wavenumbers
![]() $k_{L}$
and
$k_{L}$
and
![]() $k_{\unicode[STIX]{x1D702}}^{\text{MHD}}$
. (b) Spectral slope of
$k_{\unicode[STIX]{x1D702}}^{\text{MHD}}$
. (b) Spectral slope of
![]() $H_{c}$
, given by
$H_{c}$
, given by
![]() $\log H_{c}/\log k$
for different
$\log H_{c}/\log k$
for different
![]() $Re_{\unicode[STIX]{x1D706}}$
: the
$Re_{\unicode[STIX]{x1D706}}$
: the
![]() $-5/3$
and
$-5/3$
and
![]() $-2$
slopes are indicated in grey; Inset: focus on the inertial range.
$-2$
slopes are indicated in grey; Inset: focus on the inertial range.
The present
![]() $k^{-5/3}$
scaling is different from the
$k^{-5/3}$
scaling is different from the
![]() $k^{-2}$
one of Grappin et al. (Reference Grappin, Frisch, Léorat and Pouquet1982): there are at least two arguments to explain the difference, in favour of the present
$k^{-2}$
one of Grappin et al. (Reference Grappin, Frisch, Léorat and Pouquet1982): there are at least two arguments to explain the difference, in favour of the present
![]() $k^{-5/3}$
inertial range. Firstly, in Grappin et al. (Reference Grappin, Frisch, Léorat and Pouquet1982), as already explained, simplified EDQNM equations are solved numerically, with the assumption that there is a strong uniform magnetic field of random orientation that causes equipartition of kinetic and magnetic energies, i.e.
$k^{-5/3}$
inertial range. Firstly, in Grappin et al. (Reference Grappin, Frisch, Léorat and Pouquet1982), as already explained, simplified EDQNM equations are solved numerically, with the assumption that there is a strong uniform magnetic field of random orientation that causes equipartition of kinetic and magnetic energies, i.e.
![]() $E_{V}=E_{B}$
at all scales. The difference between the present
$E_{V}=E_{B}$
at all scales. The difference between the present
![]() $k^{-5/3}$
and
$k^{-5/3}$
and
![]() $k^{-2}$
scalings could thus result from this assumption, but this is rather difficult to quantify. The second argument is a strong Reynolds number effect. In Grappin et al. (Reference Grappin, Frisch, Léorat and Pouquet1982), the Reynolds number is lower than in our case, where
$k^{-2}$
scalings could thus result from this assumption, but this is rather difficult to quantify. The second argument is a strong Reynolds number effect. In Grappin et al. (Reference Grappin, Frisch, Léorat and Pouquet1982), the Reynolds number is lower than in our case, where
![]() $Re_{\unicode[STIX]{x1D706}}=4\times 10^{4}$
, corresponding to almost two additional decades in wavenumber space. To better illustrate this feature, the slope of
$Re_{\unicode[STIX]{x1D706}}=4\times 10^{4}$
, corresponding to almost two additional decades in wavenumber space. To better illustrate this feature, the slope of
![]() $H_{c}$
for different
$H_{c}$
for different
![]() $Re_{\unicode[STIX]{x1D706}}$
is presented in figure 7(b): there is a clear influence of the Reynolds number on the spectral slope of the cross-helical spectrum. Indeed, for moderate
$Re_{\unicode[STIX]{x1D706}}$
is presented in figure 7(b): there is a clear influence of the Reynolds number on the spectral slope of the cross-helical spectrum. Indeed, for moderate
![]() $Re_{\unicode[STIX]{x1D706}}\sim 250$
, the slope of
$Re_{\unicode[STIX]{x1D706}}\sim 250$
, the slope of
![]() $H_{c}$
is close to
$H_{c}$
is close to
![]() $k^{-2}$
, whereas very large Reynolds numbers are needed to obtain a steady result, close to
$k^{-2}$
, whereas very large Reynolds numbers are needed to obtain a steady result, close to
![]() $k^{-5/3}$
here. Nevertheless, the tendency of our results is in agreement with Grappin et al. (Reference Grappin, Frisch, Léorat and Pouquet1982) regarding the spectral slope of
$k^{-5/3}$
here. Nevertheless, the tendency of our results is in agreement with Grappin et al. (Reference Grappin, Frisch, Léorat and Pouquet1982) regarding the spectral slope of
![]() $H_{c}$
, in a sense that it is steeper than the one of
$H_{c}$
, in a sense that it is steeper than the one of
![]() $E$
.
$E$
.
Finally, one can remark that the
![]() $-5/3$
slope of the cross-helical spectrum is similar to the one of the kinetic helicity spectrum in HIT, framework in which kinetic helicity is an inviscid invariant, unlike in MHD. If we go further assuming the
$-5/3$
slope of the cross-helical spectrum is similar to the one of the kinetic helicity spectrum in HIT, framework in which kinetic helicity is an inviscid invariant, unlike in MHD. If we go further assuming the
![]() $k^{-5/3}$
dependence, dimensional analysis provides (i)
$k^{-5/3}$
dependence, dimensional analysis provides (i)
![]() $H_{c}(k)\sim \unicode[STIX]{x1D716}_{c}^{a}\unicode[STIX]{x1D716}^{b}k^{-5/3}$
with
$H_{c}(k)\sim \unicode[STIX]{x1D716}_{c}^{a}\unicode[STIX]{x1D716}^{b}k^{-5/3}$
with
![]() $a+b=2/3$
, and
$a+b=2/3$
, and
![]() $a\neq 0$
since spectra of inviscid invariants are expressed in general as function of their dissipation rate, and (ii) no dependence on
$a\neq 0$
since spectra of inviscid invariants are expressed in general as function of their dissipation rate, and (ii) no dependence on
![]() $b_{0}$
. The latter somehow means that the dynamics of
$b_{0}$
. The latter somehow means that the dynamics of
![]() $H_{c}$
becomes much less dependent on the Alfvèn time
$H_{c}$
becomes much less dependent on the Alfvèn time
![]() $\unicode[STIX]{x1D70F}_{A}=(kb_{0})^{-1}$
, which is consistent with the cross-helicity reducing initially the nonlinear transfers, as shown in figure 6(a). Compensating
$\unicode[STIX]{x1D70F}_{A}=(kb_{0})^{-1}$
, which is consistent with the cross-helicity reducing initially the nonlinear transfers, as shown in figure 6(a). Compensating
![]() $H_{c}$
with the different possibilities for
$H_{c}$
with the different possibilities for
![]() $a$
and
$a$
and
![]() $b$
indicates that a relevant scaling could be
$b$
indicates that a relevant scaling could be
which gives
![]() $C_{c}\simeq 3$
, similar to the value of
$C_{c}\simeq 3$
, similar to the value of
![]() $C_{\text{IK}}$
for
$C_{\text{IK}}$
for
![]() $E$
. Choosing a ‘linear’ dependency on
$E$
. Choosing a ‘linear’ dependency on
![]() $\unicode[STIX]{x1D716}_{c}$
(
$\unicode[STIX]{x1D716}_{c}$
(
![]() $a=1$
and
$a=1$
and
![]() $b=-1/3$
) yields a way too large constant compared to other usual constants (
$b=-1/3$
) yields a way too large constant compared to other usual constants (
![]() $C_{c}\geqslant 30$
): the fact that
$C_{c}\geqslant 30$
): the fact that
![]() $H_{c}$
should not depend linearly on
$H_{c}$
should not depend linearly on
![]() $\unicode[STIX]{x1D716}_{c}$
is consistent with some arguments proposed by Grappin et al. (Reference Grappin, Frisch, Léorat and Pouquet1982).
$\unicode[STIX]{x1D716}_{c}$
is consistent with some arguments proposed by Grappin et al. (Reference Grappin, Frisch, Léorat and Pouquet1982).
Now that the inertial scaling of
![]() $H_{c}$
has been addressed and the impact of moderate Reynolds numbers highlighted, the effects of cross-helicity on the Elsässer spectra and on the short-time dynamics are analysed.
$H_{c}$
has been addressed and the impact of moderate Reynolds numbers highlighted, the effects of cross-helicity on the Elsässer spectra and on the short-time dynamics are analysed.
4.6
 $E_{+}$
,
$E_{+}$
,
 $E_{-}$
and the short-time dynamics
$E_{-}$
and the short-time dynamics
It has been shown in figure 6(a) that a sufficient amount of initial cross-helicity
![]() $K_{c}(t=0)$
could slightly delay the initial decay of total energy
$K_{c}(t=0)$
could slightly delay the initial decay of total energy
![]() $K$
, a feature similar to what is obtained in HIT with initial kinetic helicity (André & Lesieur Reference André and Lesieur1977). Furthermore, it was revealed in the previous section that the presence of cross-helicity was not changing the inertial scaling of the kinetic, magnetic and total spectra
$K$
, a feature similar to what is obtained in HIT with initial kinetic helicity (André & Lesieur Reference André and Lesieur1977). Furthermore, it was revealed in the previous section that the presence of cross-helicity was not changing the inertial scaling of the kinetic, magnetic and total spectra
![]() $E_{V}$
,
$E_{V}$
,
![]() $E_{B}$
and
$E_{B}$
and
![]() $E=E_{V}+E_{B}$
. Therefore, it is proposed in this part to briefly illustrate the impact of cross-helicity on the inertial scalings of the Elsässer spectra
$E=E_{V}+E_{B}$
. Therefore, it is proposed in this part to briefly illustrate the impact of cross-helicity on the inertial scalings of the Elsässer spectra
![]() $E_{+}$
and
$E_{+}$
and
![]() $E_{-}$
defined in (4.16), and on the short-time dynamics as well.
$E_{-}$
defined in (4.16), and on the short-time dynamics as well.
One can observe in figure 8(a) that adding a greater amount of initial cross-helicity tends to increase the kinetic to magnetic energy ratio
![]() $K_{V}/K_{B}$
, along with the positive Elsässer energy
$K_{V}/K_{B}$
, along with the positive Elsässer energy
![]() $K_{+}$
, the latter being expected from the definition (4.16). Some justification are proposed hereafter to justify the increase of kinetic energy by adding cross-helicity in the flow. Regarding the asymptotic value of
$K_{+}$
, the latter being expected from the definition (4.16). Some justification are proposed hereafter to justify the increase of kinetic energy by adding cross-helicity in the flow. Regarding the asymptotic value of
![]() $K_{V}/K_{B}$
for the balanced case, it is worth noting that it is rather independent of the Reynolds number and only slightly depends on the initial conditions (see figure 11(d) in appendix A.2 for more details).
$K_{V}/K_{B}$
for the balanced case, it is worth noting that it is rather independent of the Reynolds number and only slightly depends on the initial conditions (see figure 11(d) in appendix A.2 for more details).

Figure 8. (a) Impact of the initial cross-helicity
![]() $K_{c}(t=0)$
on the short-time dynamics, for
$K_{c}(t=0)$
on the short-time dynamics, for
![]() $\unicode[STIX]{x1D70E}=2$
and
$\unicode[STIX]{x1D70E}=2$
and
![]() $E_{V}(k,t=0)=E_{B}(k,t=0)$
, on the ratios
$E_{V}(k,t=0)=E_{B}(k,t=0)$
, on the ratios
![]() $K_{V}/K_{B}$
(black) and
$K_{V}/K_{B}$
(black) and
![]() $K_{-}/K_{+}$
(grey). (b) Elsässer spectra
$K_{-}/K_{+}$
(grey). (b) Elsässer spectra
![]() $E_{+}$
and
$E_{+}$
and
![]() $E_{-}$
, for
$E_{-}$
, for
![]() $\unicode[STIX]{x1D70E}=2$
and
$\unicode[STIX]{x1D70E}=2$
and
![]() $Re_{\unicode[STIX]{x1D706}}(t=30\unicode[STIX]{x1D70F}_{0})=2\times 10^{3}$
, with initial condition
$Re_{\unicode[STIX]{x1D706}}(t=30\unicode[STIX]{x1D70F}_{0})=2\times 10^{3}$
, with initial condition
![]() $H_{c}(k,t=0)=0.1\sqrt{E_{V}(k,t=0)E_{B}(k,t=0)}$
; The inset gives the slope
$H_{c}(k,t=0)=0.1\sqrt{E_{V}(k,t=0)E_{B}(k,t=0)}$
; The inset gives the slope
![]() $\log E_{\pm }/\log k$
in the inertial range.
$\log E_{\pm }/\log k$
in the inertial range.
The Elsässer spectra
![]() $E_{+}$
and
$E_{+}$
and
![]() $E_{-}$
are presented in figure 8(b). Unlike for
$E_{-}$
are presented in figure 8(b). Unlike for
![]() $E_{V}$
,
$E_{V}$
,
![]() $E_{B}$
and
$E_{B}$
and
![]() $E$
, a slight departure is observed for their inertial scaling with respect to the IK prediction in
$E$
, a slight departure is observed for their inertial scaling with respect to the IK prediction in
![]() $k^{-3/2}$
: the spectral slope of
$k^{-3/2}$
: the spectral slope of
![]() $E_{+}$
is steeper, between
$E_{+}$
is steeper, between
![]() $k^{-1.55}$
and
$k^{-1.55}$
and
![]() $k^{-5/3}$
, whereas the opposite happens for
$k^{-5/3}$
, whereas the opposite happens for
![]() $E_{-}$
, where the slope is approximately between
$E_{-}$
, where the slope is approximately between
![]() $k^{-1.2}$
and
$k^{-1.2}$
and
![]() $k^{-4/3}$
. It is rather difficult to determine the exact scalings of
$k^{-4/3}$
. It is rather difficult to determine the exact scalings of
![]() $E_{+}$
and
$E_{+}$
and
![]() $E_{-}$
since the inertial slopes slightly vary with both
$E_{-}$
since the inertial slopes slightly vary with both
![]() $K_{c}(t=0)$
and the Reynolds number. Nevertheless, the finding that the slope of
$K_{c}(t=0)$
and the Reynolds number. Nevertheless, the finding that the slope of
![]() $E_{+}$
becomes steeper than
$E_{+}$
becomes steeper than
![]() $-3/2$
and the one of
$-3/2$
and the one of
![]() $E_{-}$
less steep is a robust feature, already obtained in Grappin et al. (Reference Grappin, Frisch, Léorat and Pouquet1982). In fact, even though equipartition is not assumed here unlike the latter reference, the inertial spectral slopes obtained for
$E_{-}$
less steep is a robust feature, already obtained in Grappin et al. (Reference Grappin, Frisch, Léorat and Pouquet1982). In fact, even though equipartition is not assumed here unlike the latter reference, the inertial spectral slopes obtained for
![]() $E_{+}\sim k^{-m_{+}}$
and
$E_{+}\sim k^{-m_{+}}$
and
![]() $E_{-}\sim k^{-m_{-}}$
are in agreement with the prediction of Grappin and coworkers, namely
$E_{-}\sim k^{-m_{-}}$
are in agreement with the prediction of Grappin and coworkers, namely
![]() $m_{+}+m_{-}\simeq 3$
.
$m_{+}+m_{-}\simeq 3$
.
Now, we wish to interpret physically the meaning of the departure of
![]() $E_{+}$
and
$E_{+}$
and
![]() $E_{-}$
from the IK
$E_{-}$
from the IK
![]() $k^{-3/2}$
scaling. It is clear from figure 8(b) that the Elsässer spectrum
$k^{-3/2}$
scaling. It is clear from figure 8(b) that the Elsässer spectrum
![]() $E_{+}$
is the most intense, consistently with the fluxes displayed earlier in figure 5(a). In terms of the Elsässer variables
$E_{+}$
is the most intense, consistently with the fluxes displayed earlier in figure 5(a). In terms of the Elsässer variables
![]() $\boldsymbol{z}^{\pm }=\boldsymbol{u}\pm \boldsymbol{b}$
, it means that adding some positive
$\boldsymbol{z}^{\pm }=\boldsymbol{u}\pm \boldsymbol{b}$
, it means that adding some positive
![]() $\langle \boldsymbol{u}\boldsymbol{\cdot }\boldsymbol{b}\rangle$
in the flow enhances the dynamics of
$\langle \boldsymbol{u}\boldsymbol{\cdot }\boldsymbol{b}\rangle$
in the flow enhances the dynamics of
![]() $\boldsymbol{z}^{+}$
, thus making
$\boldsymbol{z}^{+}$
, thus making
![]() $E_{-}$
less intense than
$E_{-}$
less intense than
![]() $E_{+}$
. Therefore,
$E_{+}$
. Therefore,
![]() $\boldsymbol{z}^{+}$
is transported by a subdominant field at large scales, leading to a Kolmogorov-like local transfer mechanism for
$\boldsymbol{z}^{+}$
is transported by a subdominant field at large scales, leading to a Kolmogorov-like local transfer mechanism for
![]() $E_{+}$
, with the characteristic time
$E_{+}$
, with the characteristic time
![]() $\unicode[STIX]{x1D70F}_{V}=(\unicode[STIX]{x1D716}k^{2})^{-1/3}$
like in HIT. This further justifies that the scaling of
$\unicode[STIX]{x1D70F}_{V}=(\unicode[STIX]{x1D716}k^{2})^{-1/3}$
like in HIT. This further justifies that the scaling of
![]() $E_{+}$
tends to
$E_{+}$
tends to
![]() $k^{-5/3}$
. On the contrary, since the transport of
$k^{-5/3}$
. On the contrary, since the transport of
![]() $\boldsymbol{z}^{-}$
is amplified, the ‘Alfvénization’ phenomenon is increased for
$\boldsymbol{z}^{-}$
is amplified, the ‘Alfvénization’ phenomenon is increased for
![]() $E_{-}$
and the nonlinear transfers are slowed down, thus explaining the slope less steep than
$E_{-}$
and the nonlinear transfers are slowed down, thus explaining the slope less steep than
![]() $-3/2$
, close to
$-3/2$
, close to
![]() $E_{-}\sim k^{-4/3}$
. Incidentally, the fact that the Kolmogorov-type dynamics is dominant (because
$E_{-}\sim k^{-4/3}$
. Incidentally, the fact that the Kolmogorov-type dynamics is dominant (because
![]() $E_{+}>E_{-}$
at the most energetic scales) is consistent with the growth of the kinetic to magnetic energy ratio in figure 8(a), and with the phenomenology of Dobrowolny, Mangeney & Veltri (Reference Dobrowolny, Mangeney and Veltri1980) as well, where
$E_{+}>E_{-}$
at the most energetic scales) is consistent with the growth of the kinetic to magnetic energy ratio in figure 8(a), and with the phenomenology of Dobrowolny, Mangeney & Veltri (Reference Dobrowolny, Mangeney and Veltri1980) as well, where
![]() $E_{+}$
should prevail if positive cross-correlation is initially dominant.
$E_{+}$
should prevail if positive cross-correlation is initially dominant.
Based on these observations, one could propose theoretical scalings for the Elsässer spectra in imbalanced IMHDT. Proceeding as in § 3.1, one would have
![]() $\unicode[STIX]{x1D716}_{+}=kE_{+}(k)/\unicode[STIX]{x1D70F}_{V}(k)$
so that
$\unicode[STIX]{x1D716}_{+}=kE_{+}(k)/\unicode[STIX]{x1D70F}_{V}(k)$
so that
![]() $E_{+}\sim \unicode[STIX]{x1D716}_{+}\unicode[STIX]{x1D716}^{-1/3}k^{-5/3}$
and
$E_{+}\sim \unicode[STIX]{x1D716}_{+}\unicode[STIX]{x1D716}^{-1/3}k^{-5/3}$
and
![]() $\unicode[STIX]{x1D716}_{-}=kE_{-}/\unicode[STIX]{x1D70F}_{\text{tr}}(k)$
with
$\unicode[STIX]{x1D716}_{-}=kE_{-}/\unicode[STIX]{x1D70F}_{\text{tr}}(k)$
with
![]() $\unicode[STIX]{x1D70F}_{\text{tr}}(k)=(k^{2}\unicode[STIX]{x1D716})^{-2/3}/(kb_{0})^{-1}$
so that
$\unicode[STIX]{x1D70F}_{\text{tr}}(k)=(k^{2}\unicode[STIX]{x1D716})^{-2/3}/(kb_{0})^{-1}$
so that
![]() $E_{-}\sim \unicode[STIX]{x1D716}_{-}b_{0}\unicode[STIX]{x1D716}^{-2/3}k^{-4/3}$
.
$E_{-}\sim \unicode[STIX]{x1D716}_{-}b_{0}\unicode[STIX]{x1D716}^{-2/3}k^{-4/3}$
.
The conclusion is that cross-helicity affects both the early dynamics of the decaying turbulent flow, and the inertial scalings of the Elsässer spectra as well, with different mechanisms at stake for
![]() $E_{+}$
and
$E_{+}$
and
![]() $E_{-}$
. If one injects instead negative correlation
$E_{-}$
. If one injects instead negative correlation
![]() $\langle \boldsymbol{u}\boldsymbol{\cdot }\boldsymbol{b}\rangle$
, the previous findings are still verified by changing the
$\langle \boldsymbol{u}\boldsymbol{\cdot }\boldsymbol{b}\rangle$
, the previous findings are still verified by changing the
![]() $()_{+}$
and
$()_{+}$
and
![]() $()_{-}$
quantities. The
$()_{-}$
quantities. The
![]() $k^{-5/3}$
and
$k^{-5/3}$
and
![]() $k^{-4/3}$
scalings for
$k^{-4/3}$
scalings for
![]() $E_{+}$
and
$E_{+}$
and
![]() $E_{-}$
respectively deserve more investigation, since two different effects are in competition: a larger Reynolds number which brings the slopes closer to
$E_{-}$
respectively deserve more investigation, since two different effects are in competition: a larger Reynolds number which brings the slopes closer to
![]() $k^{-3/2}$
, and a greater normalized cross-helicity
$k^{-3/2}$
, and a greater normalized cross-helicity
![]() $\unicode[STIX]{x1D70C}_{c}$
which on the contrary makes the slopes depart from
$\unicode[STIX]{x1D70C}_{c}$
which on the contrary makes the slopes depart from
![]() $k^{-3/2}$
.
$k^{-3/2}$
.
4.7 Pressure spectrum
 $E_{P}(k,t)$
$E_{P}(k,t)$
Now that the impact of cross-helicity on the kinetic energy, magnetic energy, and Elsässer spectra has been discussed, the emphasis is put here on pressure spectra. The evolution equation of the pressure fluctuations, the so-called Poisson equation, is obtained by taking the divergence of the velocity fluctuations equation (2.1)
The spectral two-point second-order pressure correlation is then defined as
where the spectral fluctuating pressure is given by
The spectral second-order pressure correlation reads, after some algebra,
The pressure spectrum, obtained by spherically averaging
![]() ${\mathcal{E}}_{P}$
, is then
${\mathcal{E}}_{P}$
, is then
 $$\begin{eqnarray}\displaystyle E_{P}(k,t) & = & \displaystyle \displaystyle \int _{S_{k}}{\mathcal{E}}_{P}(\boldsymbol{k},t)\,\text{d}^{2}\boldsymbol{k}=E_{P}^{\text{(hyd)}}(k,t)+E_{P}^{\text{(mag)}}(k,t)+E_{P}^{\text{(cross)}}(k,t)\nonumber\\ \displaystyle & = & \displaystyle \displaystyle 16\unicode[STIX]{x03C0}^{2}\int _{\unicode[STIX]{x1D6E5}_{k}}kpq(1-y^{2})(1-z^{2})({\mathcal{E}}_{0}^{V^{\prime }}{\mathcal{E}}_{0}^{V^{\prime \prime }}+{\mathcal{E}}_{0}^{B^{\prime }}{\mathcal{E}}_{0}^{B^{\prime \prime }})\,\text{d}p\,\text{d}q\nonumber\\ \displaystyle & & \displaystyle -\,\displaystyle 32\unicode[STIX]{x03C0}^{2}\int _{\unicode[STIX]{x1D6E5}_{k}}kpq(1-y^{2}-z^{2}+y^{2}z^{2}){\mathcal{H}}_{c}^{\prime }{\mathcal{H}}_{c}^{\prime \prime }\,\text{d}p\,\text{d}q,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle E_{P}(k,t) & = & \displaystyle \displaystyle \int _{S_{k}}{\mathcal{E}}_{P}(\boldsymbol{k},t)\,\text{d}^{2}\boldsymbol{k}=E_{P}^{\text{(hyd)}}(k,t)+E_{P}^{\text{(mag)}}(k,t)+E_{P}^{\text{(cross)}}(k,t)\nonumber\\ \displaystyle & = & \displaystyle \displaystyle 16\unicode[STIX]{x03C0}^{2}\int _{\unicode[STIX]{x1D6E5}_{k}}kpq(1-y^{2})(1-z^{2})({\mathcal{E}}_{0}^{V^{\prime }}{\mathcal{E}}_{0}^{V^{\prime \prime }}+{\mathcal{E}}_{0}^{B^{\prime }}{\mathcal{E}}_{0}^{B^{\prime \prime }})\,\text{d}p\,\text{d}q\nonumber\\ \displaystyle & & \displaystyle -\,\displaystyle 32\unicode[STIX]{x03C0}^{2}\int _{\unicode[STIX]{x1D6E5}_{k}}kpq(1-y^{2}-z^{2}+y^{2}z^{2}){\mathcal{H}}_{c}^{\prime }{\mathcal{H}}_{c}^{\prime \prime }\,\text{d}p\,\text{d}q,\end{eqnarray}$$
where
![]() $E_{P}^{\text{(hyd)}}$
is the classical pressure spectrum of HIT (Meldi & Sagaut Reference Meldi and Sagaut2013b
; Briard, Iyer & Gomez Reference Briard, Iyer and Gomez2017),
$E_{P}^{\text{(hyd)}}$
is the classical pressure spectrum of HIT (Meldi & Sagaut Reference Meldi and Sagaut2013b
; Briard, Iyer & Gomez Reference Briard, Iyer and Gomez2017),
![]() $E_{P}^{\text{(mag)}}$
is the additional contribution in MHD resulting from the Laplace force and
$E_{P}^{\text{(mag)}}$
is the additional contribution in MHD resulting from the Laplace force and
![]() $E_{P}^{\text{(cross)}}$
corresponds to the impact of cross-helicity. In the following simulations, the pressure spectrum is set to zero initially: it is always found that the infrared scaling is
$E_{P}^{\text{(cross)}}$
corresponds to the impact of cross-helicity. In the following simulations, the pressure spectrum is set to zero initially: it is always found that the infrared scaling is
![]() $k^{2}$
, as in HIT (Lesieur et al.
Reference Lesieur, Ossia and Metais1999).
$k^{2}$
, as in HIT (Lesieur et al.
Reference Lesieur, Ossia and Metais1999).
In balanced MHD (with
![]() $E_{P}^{\text{(cross)}}=0$
), it follows that the scaling of the pressure spectrum is different from its
$E_{P}^{\text{(cross)}}=0$
), it follows that the scaling of the pressure spectrum is different from its
![]() $k^{-7/3}$
inertial scaling in HIT: indeed, by dimensional analysis, one obtains
$k^{-7/3}$
inertial scaling in HIT: indeed, by dimensional analysis, one obtains
![]() $E_{P}\sim kE_{B}(k)^{2}\sim kE_{V}(k)^{2}$
, so that
$E_{P}\sim kE_{B}(k)^{2}\sim kE_{V}(k)^{2}$
, so that
This
![]() $k^{-2}$
inertial scaling is assessed in figure 9(a) for
$k^{-2}$
inertial scaling is assessed in figure 9(a) for
![]() $E_{P}^{\text{(mag)}}$
and
$E_{P}^{\text{(mag)}}$
and
![]() $E_{P}^{\text{(iso)}}$
, and thus for
$E_{P}^{\text{(iso)}}$
, and thus for
![]() $E_{P}$
as well. One can remark that at large scales,
$E_{P}$
as well. One can remark that at large scales,
![]() $E_{P}^{\text{(mag)}}$
is more intense than
$E_{P}^{\text{(mag)}}$
is more intense than
![]() $E_{P}^{\text{(hyd)}}$
: this is because of the initial conditions (2.44), where
$E_{P}^{\text{(hyd)}}$
: this is because of the initial conditions (2.44), where
![]() $E_{B}\sim k^{2}$
and
$E_{B}\sim k^{2}$
and
![]() $E_{V}\sim k^{4}$
at large scales. Note that the pressure variance, defined as
$E_{V}\sim k^{4}$
at large scales. Note that the pressure variance, defined as
![]() $K_{P}=\int _{0}^{\infty }E_{P}(k)\,\text{d}k$
, decays at a rate
$K_{P}=\int _{0}^{\infty }E_{P}(k)\,\text{d}k$
, decays at a rate
![]() $2\unicode[STIX]{x1D6FC}$
, with
$2\unicode[STIX]{x1D6FC}$
, with
![]() $K\sim t^{\unicode[STIX]{x1D6FC}}$
, for dimensional reasons since
$K\sim t^{\unicode[STIX]{x1D6FC}}$
, for dimensional reasons since
![]() $p^{2}\sim u^{4}$
, similarly to HIT (Meldi & Sagaut Reference Meldi and Sagaut2013b
).
$p^{2}\sim u^{4}$
, similarly to HIT (Meldi & Sagaut Reference Meldi and Sagaut2013b
).

Figure 9. Pressure spectra for balanced and imbalanced isotropic MHD, for
![]() $\unicode[STIX]{x1D70E}=2$
at
$\unicode[STIX]{x1D70E}=2$
at
![]() $Re_{\unicode[STIX]{x1D706}}=3\times 10^{3}$
, along with the integral and dissipative wavenumbers
$Re_{\unicode[STIX]{x1D706}}=3\times 10^{3}$
, along with the integral and dissipative wavenumbers
![]() $k_{L}$
and
$k_{L}$
and
![]() $k_{\unicode[STIX]{x1D702}}^{\text{MHD}}$
, with initial condition
$k_{\unicode[STIX]{x1D702}}^{\text{MHD}}$
, with initial condition
![]() $E_{B}(k,t=0)=E_{V}(k,t=0)$
. (a) Balanced case:
$E_{B}(k,t=0)=E_{V}(k,t=0)$
. (a) Balanced case:
![]() $E_{P}(k,t)$
with its isotropic and magnetic parts
$E_{P}(k,t)$
with its isotropic and magnetic parts
![]() $E_{P}^{\text{(hyd)}}(k,t)$
and
$E_{P}^{\text{(hyd)}}(k,t)$
and
![]() $E_{P}^{\text{(mag)}}(k,t)$
. (b) Imbalanced case:
$E_{P}^{\text{(mag)}}(k,t)$
. (b) Imbalanced case:
![]() $E_{P}^{\text{(hyd)}}(k,t)$
,
$E_{P}^{\text{(hyd)}}(k,t)$
,
![]() $E_{P}^{\text{(mag)}}(k,t)$
and
$E_{P}^{\text{(mag)}}(k,t)$
and
![]() $E_{P}^{\text{(cross)}}(k,t)$
.
$E_{P}^{\text{(cross)}}(k,t)$
.
For imbalanced MHD, if an inertial
![]() $k^{-5/3}$
scaling is assumed for the cross-helical spectrum, as shown previously in figure 7(a), it follows that
$k^{-5/3}$
scaling is assumed for the cross-helical spectrum, as shown previously in figure 7(a), it follows that
![]() $E_{P}^{\text{(cross)}}\sim kH_{c}(k)^{2}\sim k^{-7/3}$
: this scaling is recovered here in figure 9(b), and one can observe that
$E_{P}^{\text{(cross)}}\sim kH_{c}(k)^{2}\sim k^{-7/3}$
: this scaling is recovered here in figure 9(b), and one can observe that
![]() $E_{P}^{\text{(cross)}}$
is mainly negative, which is expected given its expression (4.22). Other possible effects of cross-helicity on the hydrodynamic and MHD parts are rather difficult to quantify, since the scaling of
$E_{P}^{\text{(cross)}}$
is mainly negative, which is expected given its expression (4.22). Other possible effects of cross-helicity on the hydrodynamic and MHD parts are rather difficult to quantify, since the scaling of
![]() $E_{P}^{\text{(mag)}}$
and
$E_{P}^{\text{(mag)}}$
and
![]() $E_{P}^{\text{(iso)}}$
remains like
$E_{P}^{\text{(iso)}}$
remains like
![]() $k^{-2}$
.
$k^{-2}$
.
5 Assessment of the
 $4/3$
rd laws for isotropic MHD
$4/3$
rd laws for isotropic MHD
In this part, we focus on statistics of homogeneous isotropic balanced and imbalanced MHD turbulence. The objective is to assess the two
![]() $4/3$
rd laws for the total energy and cross-helicity. Note that some calculations and simplifications are proposed in appendices B.1 and B.2 regarding the evolution equation of the total dissipation rate
$4/3$
rd laws for the total energy and cross-helicity. Note that some calculations and simplifications are proposed in appendices B.1 and B.2 regarding the evolution equation of the total dissipation rate
![]() $\unicode[STIX]{x1D716}$
.
$\unicode[STIX]{x1D716}$
.
We aim at assessing at large Reynolds numbers in both decaying balanced and imbalanced IMHDT the asymptotic
![]() $4/3$
rd laws for structure functions, derived in Politano & Pouquet (Reference Politano and Pouquet1998a
), namely
$4/3$
rd laws for structure functions, derived in Politano & Pouquet (Reference Politano and Pouquet1998a
), namely
where
![]() $r$
is the distance between two points located in
$r$
is the distance between two points located in
![]() $\boldsymbol{x}$
and
$\boldsymbol{x}$
and
![]() $\boldsymbol{x}^{\prime }=\boldsymbol{x}+\boldsymbol{r}$
, the subscript
$\boldsymbol{x}^{\prime }=\boldsymbol{x}+\boldsymbol{r}$
, the subscript
![]() $()_{L}$
refers to the component along
$()_{L}$
refers to the component along
![]() $\boldsymbol{r}$
, the prime
$\boldsymbol{r}$
, the prime
![]() $^{\prime }$
to quantities expressed in
$^{\prime }$
to quantities expressed in
![]() $\boldsymbol{x}^{\prime }$
and the increment is defined as
$\boldsymbol{x}^{\prime }$
and the increment is defined as
![]() $\unicode[STIX]{x1D6FF}u_{i}=u_{i}^{\prime }-u_{i}$
. The second scaling (5.2) is specific to imbalanced MHD, whereas the first one (5.1) is supposed to be verified in both imbalanced and balanced MHD. One can remark that the definition of
$\unicode[STIX]{x1D6FF}u_{i}=u_{i}^{\prime }-u_{i}$
. The second scaling (5.2) is specific to imbalanced MHD, whereas the first one (5.1) is supposed to be verified in both imbalanced and balanced MHD. One can remark that the definition of
![]() $D_{c}^{\text{(MHD)}}$
differs from Politano & Pouquet (Reference Politano and Pouquet1998a
): indeed, here cross-helicity is defined as
$D_{c}^{\text{(MHD)}}$
differs from Politano & Pouquet (Reference Politano and Pouquet1998a
): indeed, here cross-helicity is defined as
![]() $\langle u_{i}b_{i}\rangle /2$
and not
$\langle u_{i}b_{i}\rangle /2$
and not
![]() $\langle u_{i}b_{i}\rangle$
. The term
$\langle u_{i}b_{i}\rangle$
. The term
![]() $\langle \unicode[STIX]{x1D6FF}b_{L}\unicode[STIX]{x1D6FF}u_{i}\unicode[STIX]{x1D6FF}b_{i}\rangle$
is linked to the coupling between the equations for the velocity and magnetic fields, and is non-zero even without cross-helicity.
$\langle \unicode[STIX]{x1D6FF}b_{L}\unicode[STIX]{x1D6FF}u_{i}\unicode[STIX]{x1D6FF}b_{i}\rangle$
is linked to the coupling between the equations for the velocity and magnetic fields, and is non-zero even without cross-helicity.
In order to assess at large Reynolds numbers these two expressions, we need to derive formulae which allow us to compute
![]() $D^{\text{(MHD)}}$
and
$D^{\text{(MHD)}}$
and
![]() $D_{c}^{\text{(MHD)}}$
from the spectral nonlinear transfers. The evolution equations of the kinetic, magnetic and cross-helical structure functions
$D_{c}^{\text{(MHD)}}$
from the spectral nonlinear transfers. The evolution equations of the kinetic, magnetic and cross-helical structure functions
![]() $\langle \unicode[STIX]{x1D6FF}u_{i}\unicode[STIX]{x1D6FF}u_{i}\rangle$
,
$\langle \unicode[STIX]{x1D6FF}u_{i}\unicode[STIX]{x1D6FF}u_{i}\rangle$
,
![]() $\langle \unicode[STIX]{x1D6FF}b_{i}\unicode[STIX]{x1D6FF}b_{i}\rangle$
and
$\langle \unicode[STIX]{x1D6FF}b_{i}\unicode[STIX]{x1D6FF}b_{i}\rangle$
and
![]() $\langle \unicode[STIX]{x1D6FF}u_{i}\unicode[STIX]{x1D6FF}b_{i}\rangle$
read
$\langle \unicode[STIX]{x1D6FF}u_{i}\unicode[STIX]{x1D6FF}b_{i}\rangle$
read
For the latter equation (5.5), a unit magnetic Prandtl number (
![]() $\unicode[STIX]{x1D708}=\unicode[STIX]{x1D702}$
) was assumed for simplicity. Summing (5.3) and (5.4), and further neglecting the time derivative along with the viscous terms, negligible in the inertial range at large Reynolds numbers, one gets
$\unicode[STIX]{x1D708}=\unicode[STIX]{x1D702}$
) was assumed for simplicity. Summing (5.3) and (5.4), and further neglecting the time derivative along with the viscous terms, negligible in the inertial range at large Reynolds numbers, one gets
The final step consists into writing
![]() $\unicode[STIX]{x1D6FF}u_{j}=r_{j}\unicode[STIX]{x1D6FF}u_{L}/r$
, and using
$\unicode[STIX]{x1D6FF}u_{j}=r_{j}\unicode[STIX]{x1D6FF}u_{L}/r$
, and using
![]() $\unicode[STIX]{x2202}_{r_{j}}(r_{j}D^{\text{(MHD)}}/r)=\unicode[STIX]{x2202}_{r}(r^{2}D^{\text{(MHD)}})/r^{2}$
, so that integration yields (5.1). Proceeding similarly with (5.5) allows us to recover (5.2).
$\unicode[STIX]{x2202}_{r_{j}}(r_{j}D^{\text{(MHD)}}/r)=\unicode[STIX]{x2202}_{r}(r^{2}D^{\text{(MHD)}})/r^{2}$
, so that integration yields (5.1). Proceeding similarly with (5.5) allows us to recover (5.2).
To obtain a relation between spectral and physical quantities, additional equations are needed. We define the two-point kinetic, magnetic and cross-helical correlations in physical space
along with the scalar quantities
![]() $2R(r)=\langle u_{i}u_{i}^{\prime }\rangle$
,
$2R(r)=\langle u_{i}u_{i}^{\prime }\rangle$
,
![]() $2B(r)=\langle b_{i}b_{i}^{\prime }\rangle$
and
$2B(r)=\langle b_{i}b_{i}^{\prime }\rangle$
and
![]() $2H(r)=\langle u_{i}b_{i}^{\prime }\rangle$
, which are linked to the previous structure functions through
$2H(r)=\langle u_{i}b_{i}^{\prime }\rangle$
, which are linked to the previous structure functions through
![]() $\langle \unicode[STIX]{x1D6FF}u_{i}\unicode[STIX]{x1D6FF}u_{i}\rangle =4K_{V}-4R$
, and similarly for the magnetic field and the cross-helicity. The evolution equations of
$\langle \unicode[STIX]{x1D6FF}u_{i}\unicode[STIX]{x1D6FF}u_{i}\rangle =4K_{V}-4R$
, and similarly for the magnetic field and the cross-helicity. The evolution equations of
![]() $R$
,
$R$
,
![]() $B$
and
$B$
and
![]() $H$
thus read
$H$
thus read
which were notably obtained in Chandrasekhar (Reference Chandrasekhar1951). Summing the two first equations, and using the previous relations yields
 $$\begin{eqnarray}\displaystyle -4\unicode[STIX]{x1D716}-\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}\langle \unicode[STIX]{x1D6FF}u_{i}\unicode[STIX]{x1D6FF}u_{i}+\unicode[STIX]{x1D6FF}b_{i}\unicode[STIX]{x1D6FF}b_{i}\rangle & = & \displaystyle \frac{8}{r^{2}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}r}\left(r^{2}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}r}(\unicode[STIX]{x1D708}R+\unicode[STIX]{x1D702}B)\right)\nonumber\\ \displaystyle & & \displaystyle +\,4\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}r_{l}}\langle \underbrace{u_{i}u_{l}u_{i}^{\prime }-b_{i}b_{l}u_{i}^{\prime }}_{\text{(i)}}+\underbrace{u_{l}b_{i}b_{i}^{\prime }-u_{i}b_{l}b_{i}^{\prime }}_{\text{(ii)}}\rangle .\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle -4\unicode[STIX]{x1D716}-\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}\langle \unicode[STIX]{x1D6FF}u_{i}\unicode[STIX]{x1D6FF}u_{i}+\unicode[STIX]{x1D6FF}b_{i}\unicode[STIX]{x1D6FF}b_{i}\rangle & = & \displaystyle \frac{8}{r^{2}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}r}\left(r^{2}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}r}(\unicode[STIX]{x1D708}R+\unicode[STIX]{x1D702}B)\right)\nonumber\\ \displaystyle & & \displaystyle +\,4\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}r_{l}}\langle \underbrace{u_{i}u_{l}u_{i}^{\prime }-b_{i}b_{l}u_{i}^{\prime }}_{\text{(i)}}+\underbrace{u_{l}b_{i}b_{i}^{\prime }-u_{i}b_{l}b_{i}^{\prime }}_{\text{(ii)}}\rangle .\end{eqnarray}$$
Dropping the time derivative and viscous terms, and further identifying with (5.6) gives that
![]() $\unicode[STIX]{x2202}_{r}(r^{2}D^{\text{(MHD)}})=4r^{2}\unicode[STIX]{x2202}_{r_{l}}\langle (\text{i})+(\text{ii})\rangle$
. Proceeding similarly with the equation of
$\unicode[STIX]{x2202}_{r}(r^{2}D^{\text{(MHD)}})=4r^{2}\unicode[STIX]{x2202}_{r_{l}}\langle (\text{i})+(\text{ii})\rangle$
. Proceeding similarly with the equation of
![]() $H$
, and identifying with the equations of
$H$
, and identifying with the equations of
![]() $E_{V}+E_{B}$
and
$E_{V}+E_{B}$
and
![]() $H_{c}$
, finally yields
$H_{c}$
, finally yields
and these formulae are completely analogous to the ones used for kinetic and helical structure functions in isotropic turbulence (Briard & Gomez Reference Briard and Gomez2017). Some details about the
![]() $(\text{i})$
and
$(\text{i})$
and
![]() $(\text{ii})$
terms are given in appendix B.3, along with their link to the
$(\text{ii})$
terms are given in appendix B.3, along with their link to the
![]() $4/5$
th law for balanced isotropic MHD turbulence.
$4/5$
th law for balanced isotropic MHD turbulence.
The spectral-to-physical space formulae (5.12) and (5.13) are used to assess the
![]() $4/3$
rd laws of balanced and imbalanced MHD turbulence in figure 10(a,b). First, for the fully isotropic case in figure 10(a) at
$4/3$
rd laws of balanced and imbalanced MHD turbulence in figure 10(a,b). First, for the fully isotropic case in figure 10(a) at
![]() $Re_{\unicode[STIX]{x1D706}}=2\times 10^{4}$
, there is a satisfactory agreement for the compensated structure function with the expected value
$Re_{\unicode[STIX]{x1D706}}=2\times 10^{4}$
, there is a satisfactory agreement for the compensated structure function with the expected value
![]() $4/3$
, comparable to recent results in HIT (Briard & Gomez Reference Briard and Gomez2017). The difference is attributed to the non-stationarity since the turbulence is not forced in the present simulations. Secondly, for the case with cross-helicity in figure 10(b) at
$4/3$
, comparable to recent results in HIT (Briard & Gomez Reference Briard and Gomez2017). The difference is attributed to the non-stationarity since the turbulence is not forced in the present simulations. Secondly, for the case with cross-helicity in figure 10(b) at
![]() $Re_{\unicode[STIX]{x1D706}}=4\times 10^{4}$
, the agreement with the expected
$Re_{\unicode[STIX]{x1D706}}=4\times 10^{4}$
, the agreement with the expected
![]() $4/3$
is satisfactory as well. A noteworthy feature is that
$4/3$
is satisfactory as well. A noteworthy feature is that
![]() $-D_{c}^{\text{(MHD)}}/r\unicode[STIX]{x1D716}_{c}$
tends to
$-D_{c}^{\text{(MHD)}}/r\unicode[STIX]{x1D716}_{c}$
tends to
![]() $4/3$
at inertial scales slightly larger than the ones for which
$4/3$
at inertial scales slightly larger than the ones for which
![]() $-D^{\text{(MHD)}}/r\unicode[STIX]{x1D716}$
tends to
$-D^{\text{(MHD)}}/r\unicode[STIX]{x1D716}$
tends to
![]() $4/3$
. In addition, unlike the structure function of total energy, the cross-helical structure functions is negative at scales larger than the integral one
$4/3$
. In addition, unlike the structure function of total energy, the cross-helical structure functions is negative at scales larger than the integral one
![]() $L$
. For both the balanced and imbalanced cases, there is less than
$L$
. For both the balanced and imbalanced cases, there is less than
![]() $3\,\%$
departure from the theoretical prediction
$3\,\%$
departure from the theoretical prediction
![]() $4/3$
, derived for infinite Reynolds numbers and stationary turbulence.
$4/3$
, derived for infinite Reynolds numbers and stationary turbulence.

Figure 10. Compensated structure functions for balanced and imbalanced MHD turbulence for
![]() $\unicode[STIX]{x1D70E}=2$
, along with the integral and dissipative scales
$\unicode[STIX]{x1D70E}=2$
, along with the integral and dissipative scales
![]() $L$
and
$L$
and
![]() $\unicode[STIX]{x1D702}^{\text{MHD}}$
. (a)
$\unicode[STIX]{x1D702}^{\text{MHD}}$
. (a)
![]() $-D^{\text{MHD}}/(\unicode[STIX]{x1D716}r)$
at
$-D^{\text{MHD}}/(\unicode[STIX]{x1D716}r)$
at
![]() $Re_{\unicode[STIX]{x1D706}}=2\times 10^{4}$
. (b)
$Re_{\unicode[STIX]{x1D706}}=2\times 10^{4}$
. (b)
![]() $-D^{\text{MHD}}/(\unicode[STIX]{x1D716}r)$
and
$-D^{\text{MHD}}/(\unicode[STIX]{x1D716}r)$
and
![]() $-D_{c}^{\text{MHD}}/(\unicode[STIX]{x1D716}_{c}r)$
at
$-D_{c}^{\text{MHD}}/(\unicode[STIX]{x1D716}_{c}r)$
at
![]() $Re_{\unicode[STIX]{x1D706}}=4\times 10^{4}$
.
$Re_{\unicode[STIX]{x1D706}}=4\times 10^{4}$
.
The
![]() $4/3$
rd laws for total energy and cross-helicity were assessed numerically here in decaying isotropic MHD turbulence within
$4/3$
rd laws for total energy and cross-helicity were assessed numerically here in decaying isotropic MHD turbulence within
![]() $3\,\%$
. This slight departure from the expected
$3\,\%$
. This slight departure from the expected
![]() $4/3$
is due to the non-stationarity, and not to the inertial scalings of the spectra. Indeed, both the IK
$4/3$
is due to the non-stationarity, and not to the inertial scalings of the spectra. Indeed, both the IK
![]() $k^{-3/2}$
inertial scaling of the total energy spectrum and the Kolmogorov
$k^{-3/2}$
inertial scaling of the total energy spectrum and the Kolmogorov
![]() $k^{-5/3}$
inertial scaling of the cross-helical spectrum are compatible with the
$k^{-5/3}$
inertial scaling of the cross-helical spectrum are compatible with the
![]() $4/3$
rd scaling of the third-order structure functions.
$4/3$
rd scaling of the third-order structure functions.
6 Conclusion and perspectives
In this work, decaying isotropic MHD turbulence (IMHDT) was investigated numerically at large Reynolds numbers using EDQNM, without any background mean magnetic field, as done in the pioneering study of Pouquet et al. (Reference Pouquet, Frisch and Léorat1976). Within the EDQNM modelling, an eddy-damping term
![]() $\unicode[STIX]{x1D707}_{A}$
is added to take into account the interactions of Alfvén waves packets and ensure realizability. Consequently, since
$\unicode[STIX]{x1D707}_{A}$
is added to take into account the interactions of Alfvén waves packets and ensure realizability. Consequently, since
![]() ${\unicode[STIX]{x1D707}_{A}}^{-1}$
becomes the characteristic time of the inertial range, the total energy spectrum
${\unicode[STIX]{x1D707}_{A}}^{-1}$
becomes the characteristic time of the inertial range, the total energy spectrum
![]() $E(k,t)$
follows the
$E(k,t)$
follows the
![]() $k^{-3/2}$
Iroshnikov–Kraichnan (IK) scaling. Therefore, the objective of this work is not to analyse if the inertial scaling is
$k^{-3/2}$
Iroshnikov–Kraichnan (IK) scaling. Therefore, the objective of this work is not to analyse if the inertial scaling is
![]() $k^{-3/2}$
or
$k^{-3/2}$
or
![]() $k^{-5/3}$
since it is prescribed by the modelling, but rather to analyse the decay of total energy, and the impact of cross-helicity on the global dynamics. The overall purpose of this work was also to propose a solid basis for future works in anisotropic MHD turbulence, in order to further disentangle the complex interactions between the different fields at stake. The first part dealt with balanced MHD, in which cross-helicity is zero; in the second part, cross-helicity was initially injected in the flow at large scales; and in the last part, statistics were addressed in physical space.
$k^{-5/3}$
since it is prescribed by the modelling, but rather to analyse the decay of total energy, and the impact of cross-helicity on the global dynamics. The overall purpose of this work was also to propose a solid basis for future works in anisotropic MHD turbulence, in order to further disentangle the complex interactions between the different fields at stake. The first part dealt with balanced MHD, in which cross-helicity is zero; in the second part, cross-helicity was initially injected in the flow at large scales; and in the last part, statistics were addressed in physical space.
For balanced IMHDT, the total, kinetic and magnetic energy spectra verify the IK scaling, namely
![]() $E\sim E_{V}\sim E_{B}\sim k^{-3/2}$
: the different kinetic and magnetic nonlinear transfers exchange energy from large to small scales, and no significant inverse cascades mechanisms were found. The residual energy spectrum
$E\sim E_{V}\sim E_{B}\sim k^{-3/2}$
: the different kinetic and magnetic nonlinear transfers exchange energy from large to small scales, and no significant inverse cascades mechanisms were found. The residual energy spectrum
![]() $E_{R}$
was investigated in appendix A as well for various initial conditions. The main original contribution is the prediction of the long-time decay of the total energy
$E_{R}$
was investigated in appendix A as well for various initial conditions. The main original contribution is the prediction of the long-time decay of the total energy
![]() $K$
at large Reynolds numbers as a function of the large scale infrared slope
$K$
at large Reynolds numbers as a function of the large scale infrared slope
![]() $\unicode[STIX]{x1D70E}$
. A new theoretical time exponent
$\unicode[STIX]{x1D70E}$
. A new theoretical time exponent
![]() $\unicode[STIX]{x1D6FC}$
is derived, with
$\unicode[STIX]{x1D6FC}$
is derived, with
![]() $K\sim t^{\unicode[STIX]{x1D6FC}}$
, which is interestingly the same as the one of kinetic energy in HIT (Lesieur Reference Lesieur2008; Meldi & Sagaut Reference Meldi and Sagaut2013a
), and assessed numerically. It is worth noting that an inertial scaling in
$K\sim t^{\unicode[STIX]{x1D6FC}}$
, which is interestingly the same as the one of kinetic energy in HIT (Lesieur Reference Lesieur2008; Meldi & Sagaut Reference Meldi and Sagaut2013a
), and assessed numerically. It is worth noting that an inertial scaling in
![]() $k^{-3/2}$
is compatible with a decay rate of the total energy similar to the decay rate of kinetic energy in isotropic hydrodynamic turbulence, the framework in which the kinetic energy spectrum scales as
$k^{-3/2}$
is compatible with a decay rate of the total energy similar to the decay rate of kinetic energy in isotropic hydrodynamic turbulence, the framework in which the kinetic energy spectrum scales as
![]() $k^{-5/3}$
. Our prediction is at variance with Galtier et al. (Reference Galtier, Zienicke, Politano and Pouquet1999), where the root mean square of the magnetic energy
$k^{-5/3}$
. Our prediction is at variance with Galtier et al. (Reference Galtier, Zienicke, Politano and Pouquet1999), where the root mean square of the magnetic energy
![]() $b_{0}$
is assumed to be constant. Hence, we believe that the prediction of the latter reference should be more adapted to strong MHD with a mean magnetic field, when the turbulent transfers occur mainly in the plane perpendicular to
$b_{0}$
is assumed to be constant. Hence, we believe that the prediction of the latter reference should be more adapted to strong MHD with a mean magnetic field, when the turbulent transfers occur mainly in the plane perpendicular to
![]() $\boldsymbol{B}^{0}$
. This needs to be verified by three-dimensional DNS, a rather complex task since a great number of turnover times is required.
$\boldsymbol{B}^{0}$
. This needs to be verified by three-dimensional DNS, a rather complex task since a great number of turnover times is required.
In a second part, an initial non-zero cross-helicity
![]() $\langle \boldsymbol{u}\boldsymbol{\cdot }\boldsymbol{b}\rangle$
was injected at large scales to better understand what are the effects of the velocity–magnetic correlation on the spectral scalings and dynamics, still without a mean magnetic field to discard considerations about the anisotropy of the flow. We derived a complete spectral modelling for the cross-helicity, which reduces to the expression of Frisch et al. (Reference Frisch, Pouquet, Léorat and Mazure1975) for IMHDT. In particular, the velocity–magnetic correlation can contain effects from the electromotive force, and more subtle anisotropic features possibly present in rotating or shear MHD turbulence. Beyond these theoretical considerations, three effects of cross-helicity can be highlighted: (i) the initial reduction of nonlinear transfers, similarly to the effect of kinetic helicity in HIT (Briard & Gomez Reference Briard and Gomez2017); (ii) the increase of the kinetic to magnetic energy ratio with larger amount of positive initial
$\langle \boldsymbol{u}\boldsymbol{\cdot }\boldsymbol{b}\rangle$
was injected at large scales to better understand what are the effects of the velocity–magnetic correlation on the spectral scalings and dynamics, still without a mean magnetic field to discard considerations about the anisotropy of the flow. We derived a complete spectral modelling for the cross-helicity, which reduces to the expression of Frisch et al. (Reference Frisch, Pouquet, Léorat and Mazure1975) for IMHDT. In particular, the velocity–magnetic correlation can contain effects from the electromotive force, and more subtle anisotropic features possibly present in rotating or shear MHD turbulence. Beyond these theoretical considerations, three effects of cross-helicity can be highlighted: (i) the initial reduction of nonlinear transfers, similarly to the effect of kinetic helicity in HIT (Briard & Gomez Reference Briard and Gomez2017); (ii) the increase of the kinetic to magnetic energy ratio with larger amount of positive initial
![]() $\langle \boldsymbol{u}\boldsymbol{\cdot }\boldsymbol{b}\rangle$
; and (iii) the fact that
$\langle \boldsymbol{u}\boldsymbol{\cdot }\boldsymbol{b}\rangle$
; and (iii) the fact that
![]() $K_{c}$
decays much slowly than
$K_{c}$
decays much slowly than
![]() $K$
, with a decay exponent close to
$K$
, with a decay exponent close to
![]() $-0.2$
very likely independent of the large scale infrared slope
$-0.2$
very likely independent of the large scale infrared slope
![]() $\unicode[STIX]{x1D70E}$
.
$\unicode[STIX]{x1D70E}$
.
The important and original result of this section is that the cross-helical spectrum
![]() $H_{c}$
experiences a significant effect from moderate Reynolds numbers in the inertial range. Indeed, it scales as
$H_{c}$
experiences a significant effect from moderate Reynolds numbers in the inertial range. Indeed, it scales as
![]() $H_{c}\sim k^{-5/3}$
for large
$H_{c}\sim k^{-5/3}$
for large
![]() $Re_{\unicode[STIX]{x1D706}}$
only, whereas for lower
$Re_{\unicode[STIX]{x1D706}}$
only, whereas for lower
![]() $Re_{\unicode[STIX]{x1D706}}$
, a transient scaling close to
$Re_{\unicode[STIX]{x1D706}}$
, a transient scaling close to
![]() $k^{-2}$
is found. Consequently, moderate Reynolds numbers effects explain the difference between the present
$k^{-2}$
is found. Consequently, moderate Reynolds numbers effects explain the difference between the present
![]() $H_{c}\sim k^{-5/3}$
scaling and the
$H_{c}\sim k^{-5/3}$
scaling and the
![]() $H_{c}\sim k^{-2}$
proposed by Grappin et al. (Reference Grappin, Frisch, Léorat and Pouquet1982). Moreover, it was shown numerically that despite the presence of cross-helicity, the spectra
$H_{c}\sim k^{-2}$
proposed by Grappin et al. (Reference Grappin, Frisch, Léorat and Pouquet1982). Moreover, it was shown numerically that despite the presence of cross-helicity, the spectra
![]() $E$
,
$E$
,
![]() $E_{V}$
and
$E_{V}$
and
![]() $E_{B}$
still scale in
$E_{B}$
still scale in
![]() $k^{-3/2}$
in the present work. The net effect of the velocity–magnetic correlation can be observed through the Elsässer spectra
$k^{-3/2}$
in the present work. The net effect of the velocity–magnetic correlation can be observed through the Elsässer spectra
![]() $E_{+}$
and
$E_{+}$
and
![]() $E_{-}$
, which both depart from the
$E_{-}$
, which both depart from the
![]() $k^{-3/2}$
IK scaling. More precisely, it seems that with enough cross-helicity, the Elsässer spectra slowly approach
$k^{-3/2}$
IK scaling. More precisely, it seems that with enough cross-helicity, the Elsässer spectra slowly approach
![]() $E_{+}\sim k^{-5/3}$
and
$E_{+}\sim k^{-5/3}$
and
![]() $E_{-}\sim k^{-4/3}$
, because the dynamics of
$E_{-}\sim k^{-4/3}$
, because the dynamics of
![]() $E_{+}$
becomes Kolmogorov-like, with a characteristic time
$E_{+}$
becomes Kolmogorov-like, with a characteristic time
![]() $(k^{2}\unicode[STIX]{x1D716})^{-1/3}$
, whereas the ‘Alfvénization’ is enhanced for
$(k^{2}\unicode[STIX]{x1D716})^{-1/3}$
, whereas the ‘Alfvénization’ is enhanced for
![]() $E_{-}$
, thus slowing down even more the transfers. Some work still needs to be done to determine what should be the final scalings of the
$E_{-}$
, thus slowing down even more the transfers. Some work still needs to be done to determine what should be the final scalings of the
![]() $E_{\pm }$
spectra, since they depend on both the relative level of cross-helicity, which increases with time, and the Reynolds number. The important conclusion nevertheless remains that cross-helicity does not make the total, kinetic and magnetic energy spectra deviate from the
$E_{\pm }$
spectra, since they depend on both the relative level of cross-helicity, which increases with time, and the Reynolds number. The important conclusion nevertheless remains that cross-helicity does not make the total, kinetic and magnetic energy spectra deviate from the
![]() $k^{-3/2}$
scaling in the isotropic framework, only the Elsässer spectra.
$k^{-3/2}$
scaling in the isotropic framework, only the Elsässer spectra.
A subsequent theoretical analysis, made rather simple thanks to EDQNM, is to address pressure fluctuations due to the magnetic field in the Poisson equation. It is found that for the total pressure spectrum, the usual hydrodynamic part depending on
![]() $E_{V}$
and the magnetic part depending on
$E_{V}$
and the magnetic part depending on
![]() $E_{B}$
both scale in
$E_{B}$
both scale in
![]() $k^{-2}$
in the inertial range, whereas the subdominant cross-helical part behaves like
$k^{-2}$
in the inertial range, whereas the subdominant cross-helical part behaves like
![]() $k^{-7/3}$
for the imbalanced case.
$k^{-7/3}$
for the imbalanced case.
Finally, in physical space, the two
![]() $4/3$
rd laws for the total energy and the cross-helicity were assessed numerically with good agreement, at large Reynolds numbers, in decaying MHD turbulence. A noteworthy feature to underline is that both the total energy and the cross-helicity are equally close to the
$4/3$
rd laws for the total energy and the cross-helicity were assessed numerically with good agreement, at large Reynolds numbers, in decaying MHD turbulence. A noteworthy feature to underline is that both the total energy and the cross-helicity are equally close to the
![]() $4/3$
rd prediction, whereas
$4/3$
rd prediction, whereas
![]() $E(k,t)$
and
$E(k,t)$
and
![]() $H_{c}(k,t)$
scale respectively in the inertial range as
$H_{c}(k,t)$
scale respectively in the inertial range as
![]() $k^{-3/2}$
and
$k^{-3/2}$
and
![]() $k^{-5/3}$
. Some developments were proposed in appendix to simplify the evolution equation of the total dissipation rate.
$k^{-5/3}$
. Some developments were proposed in appendix to simplify the evolution equation of the total dissipation rate.
The most important and relevant perspective of this work would be to derive a three-dimensional anisotropic EDQNM model, with
![]() $\boldsymbol{k}$
-dependence, to analyse the anisotropy created by a mean magnetic field at large Reynolds number and possibly to shed some light on the
$\boldsymbol{k}$
-dependence, to analyse the anisotropy created by a mean magnetic field at large Reynolds number and possibly to shed some light on the
![]() $k_{\bot }^{-3/2}$
versus
$k_{\bot }^{-3/2}$
versus
![]() $k_{\bot }^{-5/3}$
controversial topic. All the ingredients are available: the theoretical features for a
$k_{\bot }^{-5/3}$
controversial topic. All the ingredients are available: the theoretical features for a
![]() $\boldsymbol{k}$
-dependent anisotropic EDQNM model (Cambon et al.
Reference Cambon, Mansour and Godeferd1997), and the anisotropic modelling of homogeneous and solenoidal tensors (Briard, Gomez & Cambon Reference Briard, Gomez and Cambon2016), to be extended to the magnetic field.
$\boldsymbol{k}$
-dependent anisotropic EDQNM model (Cambon et al.
Reference Cambon, Mansour and Godeferd1997), and the anisotropic modelling of homogeneous and solenoidal tensors (Briard, Gomez & Cambon Reference Briard, Gomez and Cambon2016), to be extended to the magnetic field.
Appendix A. Additional results in spectral space
In this section, some complementary results are gathered: first, some considerations about the modelling of the magnetic potential spectrum are proposed. Then, numerical results about the residual spectrum
![]() $E_{R}$
are presented.
$E_{R}$
are presented.
A.1 Magnetic potential spectrum
 $A(k,t)$
$A(k,t)$
In this part, it is proposed to briefly analyse the modelling of the magnetic potential spectrum
![]() $A(k,t)$
. This is of theoretical interest since its nonlinear spectral transfer is linked to the third-order correlation
$A(k,t)$
. This is of theoretical interest since its nonlinear spectral transfer is linked to the third-order correlation
![]() $\langle aub\rangle$
: this correlation, written symbolically, was examined in Politano, Gomez & Pouquet (Reference Politano, Gomez and Pouquet2003), and it was notably shown that in the inviscid case, it is exactly related to the dissipation rate of the magnetic helicity.
$\langle aub\rangle$
: this correlation, written symbolically, was examined in Politano, Gomez & Pouquet (Reference Politano, Gomez and Pouquet2003), and it was notably shown that in the inviscid case, it is exactly related to the dissipation rate of the magnetic helicity.
The evolution equation of the magnetic potential
![]() $\boldsymbol{a}$
, defined as
$\boldsymbol{a}$
, defined as
![]() $\boldsymbol{b}=\unicode[STIX]{x1D735}\times \boldsymbol{a}$
, with the Coulomb Gauge
$\boldsymbol{b}=\unicode[STIX]{x1D735}\times \boldsymbol{a}$
, with the Coulomb Gauge
![]() $\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{a}=0$
to make it divergence free, reads
$\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{a}=0$
to make it divergence free, reads
One can define a two-point second-order spectral tensor for the magnetic potential as
whose evolution equation is
The associated nonlinear transfer reads
where
![]() $\unicode[STIX]{x1D61A}_{ijl}^{aub}$
is the following three-point third-order spectral correlation
$\unicode[STIX]{x1D61A}_{ijl}^{aub}$
is the following three-point third-order spectral correlation
Since
![]() $\hat{\unicode[STIX]{x1D608}}_{ij}$
is a solenoidal tensor, it can be decomposed in isotropic MHD as
$\hat{\unicode[STIX]{x1D608}}_{ij}$
is a solenoidal tensor, it can be decomposed in isotropic MHD as
where
![]() ${\mathcal{H}}^{M}$
is the true magnetic helicity density, with
${\mathcal{H}}^{M}$
is the true magnetic helicity density, with
![]() $k^{2}{\mathcal{H}}^{M}={\mathcal{H}}^{B}$
, and
$k^{2}{\mathcal{H}}^{M}={\mathcal{H}}^{B}$
, and
![]() $A(k,t)$
is the magnetic potential spectrum, linked to the magnetic energy spectrum
$A(k,t)$
is the magnetic potential spectrum, linked to the magnetic energy spectrum
![]() $E_{B}(k,t)$
through
$E_{B}(k,t)$
through
It follows that in the inertial range, the magnetic potential spectrum scales in
![]() $A\sim k^{-7/2}$
, as obtained in Galtier et al. (Reference Galtier, Zienicke, Politano and Pouquet1999). An evolution equation for
$A\sim k^{-7/2}$
, as obtained in Galtier et al. (Reference Galtier, Zienicke, Politano and Pouquet1999). An evolution equation for
![]() $A(k,t)$
could be obtained by spherically averaging the equation of
$A(k,t)$
could be obtained by spherically averaging the equation of
![]() $\hat{\unicode[STIX]{x1D608}}_{ii}/2$
.
$\hat{\unicode[STIX]{x1D608}}_{ii}/2$
.
A.2 Residual energy spectrum
 $E_{R}(k,t)$
$E_{R}(k,t)$
The emphasis is put here on the residual energy spectrum
![]() $E_{R}=E_{V}-E_{B}$
. The residual energy spectrum is displayed in figure 11 along with
$E_{R}=E_{V}-E_{B}$
. The residual energy spectrum is displayed in figure 11 along with
![]() $E_{V}(k,t)$
and
$E_{V}(k,t)$
and
![]() $E_{B}(k,t)$
for three different initial conditions: in each case
$E_{B}(k,t)$
for three different initial conditions: in each case
![]() $E_{B}(k,t=0)$
is given by (2.44), and (a)
$E_{B}(k,t=0)$
is given by (2.44), and (a)
![]() $E_{V}(k,t=0)=0$
with
$E_{V}(k,t=0)=0$
with
![]() $\unicode[STIX]{x1D70E}_{B}=2$
, (b)
$\unicode[STIX]{x1D70E}_{B}=2$
, (b)
![]() $E_{V}(k,t=0)=0$
with
$E_{V}(k,t=0)=0$
with
![]() $\unicode[STIX]{x1D70E}_{B}=4$
and (c)
$\unicode[STIX]{x1D70E}_{B}=4$
and (c)
![]() $E_{V}(k,t=0)=E_{B}(k,t=0)$
with
$E_{V}(k,t=0)=E_{B}(k,t=0)$
with
![]() $\unicode[STIX]{x1D70E}_{V}=\unicode[STIX]{x1D70E}_{B}=2$
. It is revealed that for all three cases,
$\unicode[STIX]{x1D70E}_{V}=\unicode[STIX]{x1D70E}_{B}=2$
. It is revealed that for all three cases,
![]() $E_{R}(k,t)$
is negative, which means that there is an excess of magnetic energy at all scales, and scales in
$E_{R}(k,t)$
is negative, which means that there is an excess of magnetic energy at all scales, and scales in
![]() $k^{-2}$
in the inertial range.
$k^{-2}$
in the inertial range.
Moreover, regarding large scales, one can remark in figure 11 that the infrared scaling of
![]() $E_{R}$
, for wavenumbers smaller than
$E_{R}$
, for wavenumbers smaller than
![]() $k_{L}$
, is either
$k_{L}$
, is either
![]() $E_{R}\sim k^{4}$
, when initially
$E_{R}\sim k^{4}$
, when initially
![]() $\unicode[STIX]{x1D70E}_{V}=\unicode[STIX]{x1D70E}_{B}$
(simulations not presented here with
$\unicode[STIX]{x1D70E}_{V}=\unicode[STIX]{x1D70E}_{B}$
(simulations not presented here with
![]() $\unicode[STIX]{x1D70E}_{V}=\unicode[STIX]{x1D70E}_{B}=1$
and
$\unicode[STIX]{x1D70E}_{V}=\unicode[STIX]{x1D70E}_{B}=1$
and
![]() $\unicode[STIX]{x1D70E}_{V}=\unicode[STIX]{x1D70E}_{B}=3$
confirm this observation), or
$\unicode[STIX]{x1D70E}_{V}=\unicode[STIX]{x1D70E}_{B}=3$
confirm this observation), or
![]() $E_{R}\sim k^{\unicode[STIX]{x1D70E}_{B}}$
when
$E_{R}\sim k^{\unicode[STIX]{x1D70E}_{B}}$
when
![]() $E_{V}(k,t=0)=0$
, which is the novelty of this short section.
$E_{V}(k,t=0)=0$
, which is the novelty of this short section.

Figure 11. Residual energy, kinetic energy and magnetic energy spectra
![]() $E_{R}(k,t)$
,
$E_{R}(k,t)$
,
![]() $E_{V}(k,t)$
and
$E_{V}(k,t)$
and
![]() $E_{B}(k,t)$
for various initial conditions, at
$E_{B}(k,t)$
for various initial conditions, at
![]() $Re_{\unicode[STIX]{x1D706}}\simeq 2\times 10^{3}$
, along with the integral, MHD dissipative and Kolmogorov wavenumbers
$Re_{\unicode[STIX]{x1D706}}\simeq 2\times 10^{3}$
, along with the integral, MHD dissipative and Kolmogorov wavenumbers
![]() $k_{L}$
,
$k_{L}$
,
![]() $k_{\unicode[STIX]{x1D702}}^{\text{MHD}}$
and
$k_{\unicode[STIX]{x1D702}}^{\text{MHD}}$
and
![]() $k_{\unicode[STIX]{x1D702}}$
. (a) Initial condition (2.44) with
$k_{\unicode[STIX]{x1D702}}$
. (a) Initial condition (2.44) with
![]() $\unicode[STIX]{x1D70E}_{B}=2$
and
$\unicode[STIX]{x1D70E}_{B}=2$
and
![]() $E_{V}(k,t=0)=0$
. (b) Initial condition (2.44) with
$E_{V}(k,t=0)=0$
. (b) Initial condition (2.44) with
![]() $\unicode[STIX]{x1D70E}_{B}=4$
and
$\unicode[STIX]{x1D70E}_{B}=4$
and
![]() $E_{V}(k,t=0)=0$
. (c) Initial condition (2.44) with
$E_{V}(k,t=0)=0$
. (c) Initial condition (2.44) with
![]() $E_{V}(k,t=0)=E_{B}(k,t=0)$
and
$E_{V}(k,t=0)=E_{B}(k,t=0)$
and
![]() $\unicode[STIX]{x1D70E}_{V}=\unicode[STIX]{x1D70E}_{B}=2$
. (d) Time evolution of the kinetic to magnetic energy ratio
$\unicode[STIX]{x1D70E}_{V}=\unicode[STIX]{x1D70E}_{B}=2$
. (d) Time evolution of the kinetic to magnetic energy ratio
![]() $K_{V}/K_{B}$
for the three previous initial conditions; inset is the spectral ratio
$K_{V}/K_{B}$
for the three previous initial conditions; inset is the spectral ratio
![]() $E_{V}/E_{B}$
for
$E_{V}/E_{B}$
for
![]() $E_{V}(k,t=0)=E_{B}(k,t=0)$
and
$E_{V}(k,t=0)=E_{B}(k,t=0)$
and
![]() $\unicode[STIX]{x1D70E}_{V}=\unicode[STIX]{x1D70E}_{B}=2$
.
$\unicode[STIX]{x1D70E}_{V}=\unicode[STIX]{x1D70E}_{B}=2$
.
The
![]() $k^{-2}$
inertial scaling of
$k^{-2}$
inertial scaling of
![]() $E_{R}$
is in agreement with Grappin et al. (Reference Grappin, Pouquet and Léorat1983) for imbalanced isotropic MHD, and consistent with Müller & Grappin (Reference Müller and Grappin2005) for strong MHD with
$E_{R}$
is in agreement with Grappin et al. (Reference Grappin, Pouquet and Léorat1983) for imbalanced isotropic MHD, and consistent with Müller & Grappin (Reference Müller and Grappin2005) for strong MHD with
![]() $E_{R}(k_{\bot })\sim k_{\bot }^{-2}$
. In Müller & Grappin (Reference Müller and Grappin2004), it is argued that the prediction
$E_{R}(k_{\bot })\sim k_{\bot }^{-2}$
. In Müller & Grappin (Reference Müller and Grappin2004), it is argued that the prediction
![]() $E_{R}\sim k^{-2}$
of Grappin et al. (Reference Grappin, Pouquet and Léorat1983) stems from non-local considerations, which gives in particular
$E_{R}\sim k^{-2}$
of Grappin et al. (Reference Grappin, Pouquet and Léorat1983) stems from non-local considerations, which gives in particular
![]() $k^{3}E_{V}^{2}\sim k^{3}E_{B}E_{R}\Rightarrow k^{3}E_{V}^{2}\sim k^{2}b_{0}^{2}E_{R}$
, where dimensional analysis
$k^{3}E_{V}^{2}\sim k^{3}E_{B}E_{R}\Rightarrow k^{3}E_{V}^{2}\sim k^{2}b_{0}^{2}E_{R}$
, where dimensional analysis
![]() $kE_{B}(k)\sim b_{0}^{2}$
has been used. Further using the IK scaling (3.2) in the previous equation yields
$kE_{B}(k)\sim b_{0}^{2}$
has been used. Further using the IK scaling (3.2) in the previous equation yields
This scaling can also be recovered using a method similar to the one of the IK phenomenology. In (3.1), the dissipation rate
![]() $\unicode[STIX]{x1D716}$
can be defined with
$\unicode[STIX]{x1D716}$
can be defined with
![]() $u^{2}\sim b_{0}^{2}$
instead of
$u^{2}\sim b_{0}^{2}$
instead of
![]() $u^{2}\sim kE$
, and
$u^{2}\sim kE$
, and
![]() $\unicode[STIX]{x1D70F}_{R}=(k^{3}E_{R})^{-1/2}$
instead of
$\unicode[STIX]{x1D70F}_{R}=(k^{3}E_{R})^{-1/2}$
instead of
![]() $\unicode[STIX]{x1D70F}_{V}$
, so that
$\unicode[STIX]{x1D70F}_{V}$
, so that
![]() $\unicode[STIX]{x1D716}\sim b_{0}^{2}\unicode[STIX]{x1D70F}_{A}/\unicode[STIX]{x1D70F}_{R}^{2}\sim b_{0}k^{2}E_{R}$
, which eventually recovers (A 8). The assumption
$\unicode[STIX]{x1D716}\sim b_{0}^{2}\unicode[STIX]{x1D70F}_{A}/\unicode[STIX]{x1D70F}_{R}^{2}\sim b_{0}k^{2}E_{R}$
, which eventually recovers (A 8). The assumption
![]() $u^{2}\sim kE\rightarrow b_{0}^{2}$
appears to be appropriate since the difference between the kinetic and magnetic spectra essentially lies at large scales where
$u^{2}\sim kE\rightarrow b_{0}^{2}$
appears to be appropriate since the difference between the kinetic and magnetic spectra essentially lies at large scales where
![]() $E_{B}$
is stronger than
$E_{B}$
is stronger than
![]() $E_{V}$
, for various initial conditions, as shown in figure 11. Nevertheless, the
$E_{V}$
, for various initial conditions, as shown in figure 11. Nevertheless, the
![]() $k^{-2}$
inertial scaling for the residual energy spectrum is at odds with the isotropic MHD turbulence results of Müller & Grappin (Reference Müller and Grappin2004, Reference Müller and Grappin2005) where
$k^{-2}$
inertial scaling for the residual energy spectrum is at odds with the isotropic MHD turbulence results of Müller & Grappin (Reference Müller and Grappin2004, Reference Müller and Grappin2005) where
![]() $E_{R}\sim k^{-7/3}$
is found. This is because in the latter references, the kinetic energy and magnetic energy spectra scale in
$E_{R}\sim k^{-7/3}$
is found. This is because in the latter references, the kinetic energy and magnetic energy spectra scale in
![]() $E_{V}\sim E_{B}\sim k^{-5/3}$
, unlike the present simulations where
$E_{V}\sim E_{B}\sim k^{-5/3}$
, unlike the present simulations where
![]() $E_{V}\sim E_{B}\sim k^{-3/2}$
: using
$E_{V}\sim E_{B}\sim k^{-3/2}$
: using
![]() $E_{V}\sim k^{-5/3}$
in the previous arguments would consistently yield
$E_{V}\sim k^{-5/3}$
in the previous arguments would consistently yield
![]() $E_{R}\sim k^{-7/3}$
. Note that the exponents of
$E_{R}\sim k^{-7/3}$
. Note that the exponents of
![]() $E_{R}^{-m_{R}}$
and
$E_{R}^{-m_{R}}$
and
![]() $E^{-m_{\text{tot}}}$
verify the relation
$E^{-m_{\text{tot}}}$
verify the relation
![]() $m_{R}=2m_{\text{tot}}-1$
which was recently improved to match solar wind data (Grappin, Müller & Verdini Reference Grappin, Müller and Verdini2016).
$m_{R}=2m_{\text{tot}}-1$
which was recently improved to match solar wind data (Grappin, Müller & Verdini Reference Grappin, Müller and Verdini2016).
In figure 11(d), the kinetic to magnetic energy ratio
![]() $K_{V}/K_{B}$
is presented for the three previous initial conditions: the asymptotic value of
$K_{V}/K_{B}$
is presented for the three previous initial conditions: the asymptotic value of
![]() $K_{V}/K_{B}$
only slightly depends on initial conditions after a few turnover times
$K_{V}/K_{B}$
only slightly depends on initial conditions after a few turnover times
![]() $\unicode[STIX]{x1D70F}_{0}$
, and in all cases, there is an excess of magnetic energy. In the inset of figure 11(d), the spectral ratio
$\unicode[STIX]{x1D70F}_{0}$
, and in all cases, there is an excess of magnetic energy. In the inset of figure 11(d), the spectral ratio
![]() $E_{V}/E_{B}$
is presented for the third initial condition, which clearly illustrates that the excess of magnetic energy is mainly localized at large scales.
$E_{V}/E_{B}$
is presented for the third initial condition, which clearly illustrates that the excess of magnetic energy is mainly localized at large scales.
Finally, the last point to address is the decay of the residual energy
![]() $K_{R}=K_{V}-K_{B}$
. In figure 4, it is revealed that its decay exponent
$K_{R}=K_{V}-K_{B}$
. In figure 4, it is revealed that its decay exponent
![]() $\unicode[STIX]{x1D6FC}_{R}$
follows as well the theoretical predictions (3.6). This is expected, and can be shown in two different ways: (i) writing the continuity of the residual energy spectrum
$\unicode[STIX]{x1D6FC}_{R}$
follows as well the theoretical predictions (3.6). This is expected, and can be shown in two different ways: (i) writing the continuity of the residual energy spectrum
![]() $E_{R}$
in
$E_{R}$
in
![]() $k_{L}=1/L$
provides
$k_{L}=1/L$
provides
according to (A 8), which straightforwardly gives
![]() $\unicode[STIX]{x1D6FC}_{R}=\unicode[STIX]{x1D6FC}$
; and (ii) considering the previous characteristic time scale argument giving
$\unicode[STIX]{x1D6FC}_{R}=\unicode[STIX]{x1D6FC}$
; and (ii) considering the previous characteristic time scale argument giving
![]() $\unicode[STIX]{x1D716}\sim b_{0}u^{2}/L$
, and combining with (3.5), yields again
$\unicode[STIX]{x1D716}\sim b_{0}u^{2}/L$
, and combining with (3.5), yields again
![]() $\unicode[STIX]{x1D6FC}_{R}=\unicode[STIX]{x1D6FC}$
.
$\unicode[STIX]{x1D6FC}_{R}=\unicode[STIX]{x1D6FC}$
.
Appendix B. Details on statistics in physical space
In this appendix, some details about the statistics in physical space are provided, first regarding the evolution equations of the total energy
![]() $K$
and dissipation rate
$K$
and dissipation rate
![]() $\unicode[STIX]{x1D716}$
, and secondly about the
$\unicode[STIX]{x1D716}$
, and secondly about the
![]() $4/5$
th law in isotropic balanced MHD turbulence.
$4/5$
th law in isotropic balanced MHD turbulence.
B.1 Evolution equations of
 $K$
and
$K$
and
 $\unicode[STIX]{x1D716}$
$\unicode[STIX]{x1D716}$
Some details are first given on the evolution equation of the total energy
![]() $K$
. The evolution equations of
$K$
. The evolution equations of
![]() $K_{V}$
and
$K_{V}$
and
![]() $K_{B}$
read
$K_{B}$
read
Since because of homogeneity
![]() $\langle u_{i}b_{j}\unicode[STIX]{x2202}_{j}b_{i}\rangle =-\langle b_{i}b_{j}\unicode[STIX]{x2202}_{j}u_{i}\rangle$
, the evolution equation of the total energy
$\langle u_{i}b_{j}\unicode[STIX]{x2202}_{j}b_{i}\rangle =-\langle b_{i}b_{j}\unicode[STIX]{x2202}_{j}u_{i}\rangle$
, the evolution equation of the total energy
![]() $K$
reads
$K$
reads
which is similar to the equation for the kinetic energy
![]() $K_{V}(t)$
in HIT. Further identifying with the sum of equations (2.37) and (2.38) integrated over the whole wavenumber space provides
$K_{V}(t)$
in HIT. Further identifying with the sum of equations (2.37) and (2.38) integrated over the whole wavenumber space provides
where
![]() $\langle b_{i}b_{j}\unicode[STIX]{x2202}_{j}u_{i}\rangle$
reflects either the production of energy through the Laplace force, or the stretching of the magnetic field. In can be shown that in fully isotropic turbulence, with simple tensorial arguments as in Pope (Reference Pope2000), one has
$\langle b_{i}b_{j}\unicode[STIX]{x2202}_{j}u_{i}\rangle$
reflects either the production of energy through the Laplace force, or the stretching of the magnetic field. In can be shown that in fully isotropic turbulence, with simple tensorial arguments as in Pope (Reference Pope2000), one has
![]() $\langle b_{i}b_{j}\unicode[STIX]{x2202}_{j}u_{i}\rangle =15\langle b_{1}^{2}\,\unicode[STIX]{x2202}_{1}u_{1}\rangle /2$
.
$\langle b_{i}b_{j}\unicode[STIX]{x2202}_{j}u_{i}\rangle =15\langle b_{1}^{2}\,\unicode[STIX]{x2202}_{1}u_{1}\rangle /2$
.
Now, regarding the total energy dissipation rate
![]() $\unicode[STIX]{x1D716}$
. One needs the equations of
$\unicode[STIX]{x1D716}$
. One needs the equations of
![]() $\unicode[STIX]{x1D716}_{V}$
and
$\unicode[STIX]{x1D716}_{V}$
and
![]() $\unicode[STIX]{x1D716}_{B}$
, obtained by deriving with respect to
$\unicode[STIX]{x1D716}_{B}$
, obtained by deriving with respect to
![]() $x_{j}$
the equations (2.1) and (2.2) of
$x_{j}$
the equations (2.1) and (2.2) of
![]() $u_{i}$
and
$u_{i}$
and
![]() $b_{i}$
, and using ensemble averages after multiplication by
$b_{i}$
, and using ensemble averages after multiplication by
![]() $\unicode[STIX]{x2202}_{j}u_{i}$
and
$\unicode[STIX]{x2202}_{j}u_{i}$
and
![]() $\unicode[STIX]{x2202}_{j}b_{i}$
respectively. This yields
$\unicode[STIX]{x2202}_{j}b_{i}$
respectively. This yields
 $$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}\left(\frac{\unicode[STIX]{x1D716}_{V}}{2\unicode[STIX]{x1D708}}\right)+\underbrace{\left\langle \frac{\unicode[STIX]{x2202}u_{i}}{\unicode[STIX]{x2202}x_{j}}\frac{\unicode[STIX]{x2202}u_{i}}{\unicode[STIX]{x2202}x_{l}}\frac{\unicode[STIX]{x2202}u_{l}}{\unicode[STIX]{x2202}x_{j}}\right\rangle }_{\text{(I)}}+\underbrace{\left\langle u_{l}\frac{\unicode[STIX]{x2202}u_{i}}{\unicode[STIX]{x2202}x_{j}}\frac{\unicode[STIX]{x2202}^{2}u_{i}}{\unicode[STIX]{x2202}x_{l}\unicode[STIX]{x2202}x_{j}}\right\rangle }_{\text{(II)}}\nonumber\\ \displaystyle & & \displaystyle \displaystyle \quad =\underbrace{-\left\langle \frac{\unicode[STIX]{x2202}u_{i}}{\unicode[STIX]{x2202}x_{j}}\frac{\unicode[STIX]{x2202}^{2}p^{\ast }}{\unicode[STIX]{x2202}x_{i}\unicode[STIX]{x2202}x_{j}}\right\rangle }_{\text{(III)}}+\underbrace{\left\langle \frac{\unicode[STIX]{x2202}u_{i}}{\unicode[STIX]{x2202}x_{j}}\frac{\unicode[STIX]{x2202}b_{i}}{\unicode[STIX]{x2202}x_{l}}\frac{\unicode[STIX]{x2202}b_{l}}{\unicode[STIX]{x2202}x_{j}}\right\rangle }_{\text{(IV)}}+\underbrace{\left\langle b_{l}\frac{\unicode[STIX]{x2202}u_{i}}{\unicode[STIX]{x2202}x_{j}}\frac{\unicode[STIX]{x2202}^{2}b_{i}}{\unicode[STIX]{x2202}x_{l}\unicode[STIX]{x2202}x_{j}}\right\rangle }_{\text{(V)}}+\underbrace{\unicode[STIX]{x1D708}\left\langle \frac{\unicode[STIX]{x2202}u_{i}}{\unicode[STIX]{x2202}x_{j}}\frac{\unicode[STIX]{x2202}^{3}u_{i}}{\unicode[STIX]{x2202}x_{j}\unicode[STIX]{x2202}x_{l}\unicode[STIX]{x2202}x_{l}}\right\rangle }_{\text{(VI)}},\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}\left(\frac{\unicode[STIX]{x1D716}_{V}}{2\unicode[STIX]{x1D708}}\right)+\underbrace{\left\langle \frac{\unicode[STIX]{x2202}u_{i}}{\unicode[STIX]{x2202}x_{j}}\frac{\unicode[STIX]{x2202}u_{i}}{\unicode[STIX]{x2202}x_{l}}\frac{\unicode[STIX]{x2202}u_{l}}{\unicode[STIX]{x2202}x_{j}}\right\rangle }_{\text{(I)}}+\underbrace{\left\langle u_{l}\frac{\unicode[STIX]{x2202}u_{i}}{\unicode[STIX]{x2202}x_{j}}\frac{\unicode[STIX]{x2202}^{2}u_{i}}{\unicode[STIX]{x2202}x_{l}\unicode[STIX]{x2202}x_{j}}\right\rangle }_{\text{(II)}}\nonumber\\ \displaystyle & & \displaystyle \displaystyle \quad =\underbrace{-\left\langle \frac{\unicode[STIX]{x2202}u_{i}}{\unicode[STIX]{x2202}x_{j}}\frac{\unicode[STIX]{x2202}^{2}p^{\ast }}{\unicode[STIX]{x2202}x_{i}\unicode[STIX]{x2202}x_{j}}\right\rangle }_{\text{(III)}}+\underbrace{\left\langle \frac{\unicode[STIX]{x2202}u_{i}}{\unicode[STIX]{x2202}x_{j}}\frac{\unicode[STIX]{x2202}b_{i}}{\unicode[STIX]{x2202}x_{l}}\frac{\unicode[STIX]{x2202}b_{l}}{\unicode[STIX]{x2202}x_{j}}\right\rangle }_{\text{(IV)}}+\underbrace{\left\langle b_{l}\frac{\unicode[STIX]{x2202}u_{i}}{\unicode[STIX]{x2202}x_{j}}\frac{\unicode[STIX]{x2202}^{2}b_{i}}{\unicode[STIX]{x2202}x_{l}\unicode[STIX]{x2202}x_{j}}\right\rangle }_{\text{(V)}}+\underbrace{\unicode[STIX]{x1D708}\left\langle \frac{\unicode[STIX]{x2202}u_{i}}{\unicode[STIX]{x2202}x_{j}}\frac{\unicode[STIX]{x2202}^{3}u_{i}}{\unicode[STIX]{x2202}x_{j}\unicode[STIX]{x2202}x_{l}\unicode[STIX]{x2202}x_{l}}\right\rangle }_{\text{(VI)}},\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}\left(\frac{\unicode[STIX]{x1D716}_{B}}{2\unicode[STIX]{x1D702}}\right)+\underbrace{\left\langle \frac{\unicode[STIX]{x2202}u_{l}}{\unicode[STIX]{x2202}x_{j}}\frac{\unicode[STIX]{x2202}b_{i}}{\unicode[STIX]{x2202}x_{l}}\frac{\unicode[STIX]{x2202}b_{i}}{\unicode[STIX]{x2202}x_{j}}\right\rangle }_{\text{(IV)}}+\underbrace{\left\langle u_{l}\frac{\unicode[STIX]{x2202}b_{i}}{\unicode[STIX]{x2202}x_{j}}\frac{\unicode[STIX]{x2202}^{2}b_{i}}{\unicode[STIX]{x2202}x_{l}\unicode[STIX]{x2202}x_{j}}\right\rangle }_{\text{(II)}}\nonumber\\ \displaystyle & & \displaystyle \displaystyle \quad =\underbrace{\left\langle \frac{\unicode[STIX]{x2202}u_{i}}{\unicode[STIX]{x2202}x_{l}}\frac{\unicode[STIX]{x2202}b_{i}}{\unicode[STIX]{x2202}x_{j}}\frac{\unicode[STIX]{x2202}b_{l}}{\unicode[STIX]{x2202}x_{j}}\right\rangle }_{\text{(IV)}}+\underbrace{\left\langle b_{l}\frac{\unicode[STIX]{x2202}b_{i}}{\unicode[STIX]{x2202}x_{j}}\frac{\unicode[STIX]{x2202}^{2}u_{i}}{\unicode[STIX]{x2202}x_{l}\unicode[STIX]{x2202}x_{j}}\right\rangle }_{\text{(V)}}+\underbrace{\unicode[STIX]{x1D702}\left\langle \frac{\unicode[STIX]{x2202}u_{i}}{\unicode[STIX]{x2202}x_{j}}\frac{\unicode[STIX]{x2202}^{3}u_{i}}{\unicode[STIX]{x2202}x_{j}\unicode[STIX]{x2202}x_{l}\unicode[STIX]{x2202}x_{l}}\right\rangle }_{\text{(VI)}}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}\left(\frac{\unicode[STIX]{x1D716}_{B}}{2\unicode[STIX]{x1D702}}\right)+\underbrace{\left\langle \frac{\unicode[STIX]{x2202}u_{l}}{\unicode[STIX]{x2202}x_{j}}\frac{\unicode[STIX]{x2202}b_{i}}{\unicode[STIX]{x2202}x_{l}}\frac{\unicode[STIX]{x2202}b_{i}}{\unicode[STIX]{x2202}x_{j}}\right\rangle }_{\text{(IV)}}+\underbrace{\left\langle u_{l}\frac{\unicode[STIX]{x2202}b_{i}}{\unicode[STIX]{x2202}x_{j}}\frac{\unicode[STIX]{x2202}^{2}b_{i}}{\unicode[STIX]{x2202}x_{l}\unicode[STIX]{x2202}x_{j}}\right\rangle }_{\text{(II)}}\nonumber\\ \displaystyle & & \displaystyle \displaystyle \quad =\underbrace{\left\langle \frac{\unicode[STIX]{x2202}u_{i}}{\unicode[STIX]{x2202}x_{l}}\frac{\unicode[STIX]{x2202}b_{i}}{\unicode[STIX]{x2202}x_{j}}\frac{\unicode[STIX]{x2202}b_{l}}{\unicode[STIX]{x2202}x_{j}}\right\rangle }_{\text{(IV)}}+\underbrace{\left\langle b_{l}\frac{\unicode[STIX]{x2202}b_{i}}{\unicode[STIX]{x2202}x_{j}}\frac{\unicode[STIX]{x2202}^{2}u_{i}}{\unicode[STIX]{x2202}x_{l}\unicode[STIX]{x2202}x_{j}}\right\rangle }_{\text{(V)}}+\underbrace{\unicode[STIX]{x1D702}\left\langle \frac{\unicode[STIX]{x2202}u_{i}}{\unicode[STIX]{x2202}x_{j}}\frac{\unicode[STIX]{x2202}^{3}u_{i}}{\unicode[STIX]{x2202}x_{j}\unicode[STIX]{x2202}x_{l}\unicode[STIX]{x2202}x_{l}}\right\rangle }_{\text{(VI)}}.\end{eqnarray}$$
These two equations can be strongly simplified by considering independently the six different groups of terms. First, using homogeneity, incompressibility and classical tensorial algebra given in Pope (Reference Pope2000), one can show that
![]() $\text{(I)}=35\langle (\unicode[STIX]{x2202}_{1}u_{1})^{3}\rangle /2$
. The two
$\text{(I)}=35\langle (\unicode[STIX]{x2202}_{1}u_{1})^{3}\rangle /2$
. The two
![]() $\text{(II)}$
terms are zero because of homogeneity, as found in Betchov (Reference Betchov1963) for the one with
$\text{(II)}$
terms are zero because of homogeneity, as found in Betchov (Reference Betchov1963) for the one with
![]() $b_{i}$
. The pressure term
$b_{i}$
. The pressure term
![]() $\text{(III)}$
is zero because of homogeneity as well. The three
$\text{(III)}$
is zero because of homogeneity as well. The three
![]() $\text{(IV)}$
terms need further investigation through the sixth-order tensor (B 7). The sum of the two
$\text{(IV)}$
terms need further investigation through the sixth-order tensor (B 7). The sum of the two
![]() $\text{(V)}$
terms is also zero because of homogeneity. Finally, the two
$\text{(V)}$
terms is also zero because of homogeneity. Finally, the two
![]() $\text{(VI)}$
dissipative terms can be written as in (B 6), again because of homogeneity, and one has further
$\text{(VI)}$
dissipative terms can be written as in (B 6), again because of homogeneity, and one has further
![]() $\langle \unicode[STIX]{x2202}_{jl}^{2}u_{i}\,\unicode[STIX]{x2202}_{jl}^{2}u_{i}\rangle =\langle \unicode[STIX]{x2202}_{jj}^{2}u_{i}\,\unicode[STIX]{x2202}_{ll}^{2}u_{i}\rangle$
. With these different features, the sum of the two equations yields (B 6).
$\langle \unicode[STIX]{x2202}_{jl}^{2}u_{i}\,\unicode[STIX]{x2202}_{jl}^{2}u_{i}\rangle =\langle \unicode[STIX]{x2202}_{jj}^{2}u_{i}\,\unicode[STIX]{x2202}_{ll}^{2}u_{i}\rangle$
. With these different features, the sum of the two equations yields (B 6).
B.2 Simplification of the equation for
 $\unicode[STIX]{x1D716}$
$\unicode[STIX]{x1D716}$
In this part, the evolution equation of the total dissipation rate
![]() $\unicode[STIX]{x1D716}$
in the framework of balanced IMHDT is addressed, in order to simplify its different terms. After some algebra detailed in the previous part, the evolution equation reads
$\unicode[STIX]{x1D716}$
in the framework of balanced IMHDT is addressed, in order to simplify its different terms. After some algebra detailed in the previous part, the evolution equation reads
 $$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D716}}{\unicode[STIX]{x2202}t} & = & \displaystyle \displaystyle 2\unicode[STIX]{x1D708}\left(\left\langle \frac{\unicode[STIX]{x2202}u_{i}}{\unicode[STIX]{x2202}x_{j}}\frac{\unicode[STIX]{x2202}b_{i}}{\unicode[STIX]{x2202}x_{l}}\frac{\unicode[STIX]{x2202}b_{l}}{\unicode[STIX]{x2202}x_{j}}\right\rangle -\left\langle \frac{\unicode[STIX]{x2202}u_{i}}{\unicode[STIX]{x2202}x_{j}}\frac{\unicode[STIX]{x2202}u_{i}}{\unicode[STIX]{x2202}x_{l}}\frac{\unicode[STIX]{x2202}u_{l}}{\unicode[STIX]{x2202}x_{j}}\right\rangle \right)-2\unicode[STIX]{x1D708}^{2}\left\langle \frac{\unicode[STIX]{x2202}^{2}u_{i}}{\unicode[STIX]{x2202}x_{l}\unicode[STIX]{x2202}x_{l}}\frac{\unicode[STIX]{x2202}^{2}u_{i}}{\unicode[STIX]{x2202}x_{j}\unicode[STIX]{x2202}x_{j}}\right\rangle \nonumber\\ \displaystyle & & \displaystyle +\,2\unicode[STIX]{x1D702}\left(\left\langle \frac{\unicode[STIX]{x2202}u_{i}}{\unicode[STIX]{x2202}x_{j}}\frac{\unicode[STIX]{x2202}b_{i}}{\unicode[STIX]{x2202}x_{l}}\frac{\unicode[STIX]{x2202}b_{j}}{\unicode[STIX]{x2202}x_{l}}\right\rangle -\left\langle \frac{\unicode[STIX]{x2202}u_{l}}{\unicode[STIX]{x2202}x_{j}}\frac{\unicode[STIX]{x2202}b_{i}}{\unicode[STIX]{x2202}x_{l}}\frac{\unicode[STIX]{x2202}b_{i}}{\unicode[STIX]{x2202}x_{j}}\right\rangle \right)-2\unicode[STIX]{x1D702}^{2}\left\langle \frac{\unicode[STIX]{x2202}^{2}b_{i}}{\unicode[STIX]{x2202}x_{l}\unicode[STIX]{x2202}x_{l}}\frac{\unicode[STIX]{x2202}^{2}b_{i}}{\unicode[STIX]{x2202}x_{j}\unicode[STIX]{x2202}x_{j}}\right\rangle \!.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D716}}{\unicode[STIX]{x2202}t} & = & \displaystyle \displaystyle 2\unicode[STIX]{x1D708}\left(\left\langle \frac{\unicode[STIX]{x2202}u_{i}}{\unicode[STIX]{x2202}x_{j}}\frac{\unicode[STIX]{x2202}b_{i}}{\unicode[STIX]{x2202}x_{l}}\frac{\unicode[STIX]{x2202}b_{l}}{\unicode[STIX]{x2202}x_{j}}\right\rangle -\left\langle \frac{\unicode[STIX]{x2202}u_{i}}{\unicode[STIX]{x2202}x_{j}}\frac{\unicode[STIX]{x2202}u_{i}}{\unicode[STIX]{x2202}x_{l}}\frac{\unicode[STIX]{x2202}u_{l}}{\unicode[STIX]{x2202}x_{j}}\right\rangle \right)-2\unicode[STIX]{x1D708}^{2}\left\langle \frac{\unicode[STIX]{x2202}^{2}u_{i}}{\unicode[STIX]{x2202}x_{l}\unicode[STIX]{x2202}x_{l}}\frac{\unicode[STIX]{x2202}^{2}u_{i}}{\unicode[STIX]{x2202}x_{j}\unicode[STIX]{x2202}x_{j}}\right\rangle \nonumber\\ \displaystyle & & \displaystyle +\,2\unicode[STIX]{x1D702}\left(\left\langle \frac{\unicode[STIX]{x2202}u_{i}}{\unicode[STIX]{x2202}x_{j}}\frac{\unicode[STIX]{x2202}b_{i}}{\unicode[STIX]{x2202}x_{l}}\frac{\unicode[STIX]{x2202}b_{j}}{\unicode[STIX]{x2202}x_{l}}\right\rangle -\left\langle \frac{\unicode[STIX]{x2202}u_{l}}{\unicode[STIX]{x2202}x_{j}}\frac{\unicode[STIX]{x2202}b_{i}}{\unicode[STIX]{x2202}x_{l}}\frac{\unicode[STIX]{x2202}b_{i}}{\unicode[STIX]{x2202}x_{j}}\right\rangle \right)-2\unicode[STIX]{x1D702}^{2}\left\langle \frac{\unicode[STIX]{x2202}^{2}b_{i}}{\unicode[STIX]{x2202}x_{l}\unicode[STIX]{x2202}x_{l}}\frac{\unicode[STIX]{x2202}^{2}b_{i}}{\unicode[STIX]{x2202}x_{j}\unicode[STIX]{x2202}x_{j}}\right\rangle \!.\end{eqnarray}$$
It is well known that the triple velocity correlation is linked to the velocity derivative skewness, and one has
![]() $2\langle \unicode[STIX]{x2202}_{j}u_{i}\unicode[STIX]{x2202}_{l}u_{i}\unicode[STIX]{x2202}_{j}u_{l}\rangle =35\langle (\unicode[STIX]{x2202}_{1}u_{1})^{3}\rangle$
. The term in
$2\langle \unicode[STIX]{x2202}_{j}u_{i}\unicode[STIX]{x2202}_{l}u_{i}\unicode[STIX]{x2202}_{j}u_{l}\rangle =35\langle (\unicode[STIX]{x2202}_{1}u_{1})^{3}\rangle$
. The term in
![]() $2\unicode[STIX]{x1D708}^{2}$
is linked to the so-called palinstrophy, and one has
$2\unicode[STIX]{x1D708}^{2}$
is linked to the so-called palinstrophy, and one has
![]() $\langle \unicode[STIX]{x2202}_{jj}^{2}u_{i}\,\unicode[STIX]{x2202}_{ll}^{2}u_{i}\rangle =35\langle (\unicode[STIX]{x2202}_{11}^{2}u_{1})^{2}\rangle$
(Ristorcelli Reference Ristorcelli2006). One can deduce by analogy that the dissipative term in
$\langle \unicode[STIX]{x2202}_{jj}^{2}u_{i}\,\unicode[STIX]{x2202}_{ll}^{2}u_{i}\rangle =35\langle (\unicode[STIX]{x2202}_{11}^{2}u_{1})^{2}\rangle$
(Ristorcelli Reference Ristorcelli2006). One can deduce by analogy that the dissipative term in
![]() $2\unicode[STIX]{x1D702}^{2}$
is
$2\unicode[STIX]{x1D702}^{2}$
is
![]() $\langle \unicode[STIX]{x2202}_{jj}^{2}b_{i}\,\unicode[STIX]{x2202}_{ll}^{2}b_{i}\rangle =35\langle (\unicode[STIX]{x2202}_{11}^{2}b_{1})^{2}\rangle$
, which could be called a magnetic palinstrophy.
$\langle \unicode[STIX]{x2202}_{jj}^{2}b_{i}\,\unicode[STIX]{x2202}_{ll}^{2}b_{i}\rangle =35\langle (\unicode[STIX]{x2202}_{11}^{2}b_{1})^{2}\rangle$
, which could be called a magnetic palinstrophy.
In what follows, we are interested into the three mixed-derivative kinetic-magnetic correlation terms, more complicated to handle than the triple velocity one. For this purpose, we define the sixth-order tensor
In a fully isotropic framework, this tensor has fifteen non-zero components, expressed as products of Kronecker symbols such as
![]() $\unicode[STIX]{x1D6FF}_{ij}\unicode[STIX]{x1D6FF}_{ln}\unicode[STIX]{x1D6FF}_{pq}$
. Because of symmetries in (B 7), only nine terms are independent:
$\unicode[STIX]{x1D6FF}_{ij}\unicode[STIX]{x1D6FF}_{ln}\unicode[STIX]{x1D6FF}_{pq}$
. Because of symmetries in (B 7), only nine terms are independent:
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D60F}_{ijlnpq} & = & \displaystyle c_{1}\unicode[STIX]{x1D6FF}_{ij}(\unicode[STIX]{x1D6FF}_{ln}\unicode[STIX]{x1D6FF}_{pq}+\unicode[STIX]{x1D6FF}_{lp}\unicode[STIX]{x1D6FF}_{nq})+c_{2}(\unicode[STIX]{x1D6FF}_{ip}\unicode[STIX]{x1D6FF}_{jq}\unicode[STIX]{x1D6FF}_{ln}+\unicode[STIX]{x1D6FF}_{iq}\unicode[STIX]{x1D6FF}_{jn}\unicode[STIX]{x1D6FF}_{lp})+c_{3}\unicode[STIX]{x1D6FF}_{np}(\unicode[STIX]{x1D6FF}_{il}\unicode[STIX]{x1D6FF}_{jq}+\unicode[STIX]{x1D6FF}_{iq}\unicode[STIX]{x1D6FF}_{jl})\nonumber\\ \displaystyle & & \displaystyle +\,c_{4}(\unicode[STIX]{x1D6FF}_{il}\unicode[STIX]{x1D6FF}_{jn}\unicode[STIX]{x1D6FF}_{pq}+\unicode[STIX]{x1D6FF}_{ip}\unicode[STIX]{x1D6FF}_{jl}\unicode[STIX]{x1D6FF}_{nq})+c_{5}(\unicode[STIX]{x1D6FF}_{il}\unicode[STIX]{x1D6FF}_{jn}\unicode[STIX]{x1D6FF}_{nq}+\unicode[STIX]{x1D6FF}_{in}\unicode[STIX]{x1D6FF}_{jl}\unicode[STIX]{x1D6FF}_{pq})+c_{6}(\unicode[STIX]{x1D6FF}_{in}\unicode[STIX]{x1D6FF}_{jq}\unicode[STIX]{x1D6FF}_{lp}+\unicode[STIX]{x1D6FF}_{iq}\unicode[STIX]{x1D6FF}_{jp}\unicode[STIX]{x1D6FF}_{ln})\nonumber\\ \displaystyle & & \displaystyle +\,c_{7}\unicode[STIX]{x1D6FF}_{in}\unicode[STIX]{x1D6FF}_{jp}\unicode[STIX]{x1D6FF}_{lq}+c_{8}\unicode[STIX]{x1D6FF}_{ij}\unicode[STIX]{x1D6FF}_{lq}\unicode[STIX]{x1D6FF}_{np}+c_{9}\unicode[STIX]{x1D6FF}_{ip}\unicode[STIX]{x1D6FF}_{jn}\unicode[STIX]{x1D6FF}_{jq}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D60F}_{ijlnpq} & = & \displaystyle c_{1}\unicode[STIX]{x1D6FF}_{ij}(\unicode[STIX]{x1D6FF}_{ln}\unicode[STIX]{x1D6FF}_{pq}+\unicode[STIX]{x1D6FF}_{lp}\unicode[STIX]{x1D6FF}_{nq})+c_{2}(\unicode[STIX]{x1D6FF}_{ip}\unicode[STIX]{x1D6FF}_{jq}\unicode[STIX]{x1D6FF}_{ln}+\unicode[STIX]{x1D6FF}_{iq}\unicode[STIX]{x1D6FF}_{jn}\unicode[STIX]{x1D6FF}_{lp})+c_{3}\unicode[STIX]{x1D6FF}_{np}(\unicode[STIX]{x1D6FF}_{il}\unicode[STIX]{x1D6FF}_{jq}+\unicode[STIX]{x1D6FF}_{iq}\unicode[STIX]{x1D6FF}_{jl})\nonumber\\ \displaystyle & & \displaystyle +\,c_{4}(\unicode[STIX]{x1D6FF}_{il}\unicode[STIX]{x1D6FF}_{jn}\unicode[STIX]{x1D6FF}_{pq}+\unicode[STIX]{x1D6FF}_{ip}\unicode[STIX]{x1D6FF}_{jl}\unicode[STIX]{x1D6FF}_{nq})+c_{5}(\unicode[STIX]{x1D6FF}_{il}\unicode[STIX]{x1D6FF}_{jn}\unicode[STIX]{x1D6FF}_{nq}+\unicode[STIX]{x1D6FF}_{in}\unicode[STIX]{x1D6FF}_{jl}\unicode[STIX]{x1D6FF}_{pq})+c_{6}(\unicode[STIX]{x1D6FF}_{in}\unicode[STIX]{x1D6FF}_{jq}\unicode[STIX]{x1D6FF}_{lp}+\unicode[STIX]{x1D6FF}_{iq}\unicode[STIX]{x1D6FF}_{jp}\unicode[STIX]{x1D6FF}_{ln})\nonumber\\ \displaystyle & & \displaystyle +\,c_{7}\unicode[STIX]{x1D6FF}_{in}\unicode[STIX]{x1D6FF}_{jp}\unicode[STIX]{x1D6FF}_{lq}+c_{8}\unicode[STIX]{x1D6FF}_{ij}\unicode[STIX]{x1D6FF}_{lq}\unicode[STIX]{x1D6FF}_{np}+c_{9}\unicode[STIX]{x1D6FF}_{ip}\unicode[STIX]{x1D6FF}_{jn}\unicode[STIX]{x1D6FF}_{jq}.\end{eqnarray}$$
The three terms of interest in the equation of
![]() $\unicode[STIX]{x1D716}$
can be expressed as
$\unicode[STIX]{x1D716}$
can be expressed as
![]() $2\unicode[STIX]{x1D708}\unicode[STIX]{x1D60F}_{ililjj}+2\unicode[STIX]{x1D702}(\unicode[STIX]{x1D60F}_{ijillj}-\unicode[STIX]{x1D60F}_{iilljj})$
. Unlike the term
$2\unicode[STIX]{x1D708}\unicode[STIX]{x1D60F}_{ililjj}+2\unicode[STIX]{x1D702}(\unicode[STIX]{x1D60F}_{ijillj}-\unicode[STIX]{x1D60F}_{iilljj})$
. Unlike the term
![]() $\text{(I)}$
which involves only the velocity field, it is not possible to express all nine constants
$\text{(I)}$
which involves only the velocity field, it is not possible to express all nine constants
![]() $c_{1},\ldots ,c_{9}$
as functions of one only. Nevertheless, some interesting relations can be found. First, incompressibility provides three equations
$c_{1},\ldots ,c_{9}$
as functions of one only. Nevertheless, some interesting relations can be found. First, incompressibility provides three equations
![]() $2c_{1}+2c_{3}+3c_{8}=0$
,
$2c_{1}+2c_{3}+3c_{8}=0$
,
![]() $2c_{2}+2c_{4}+3c_{9}=0$
and
$2c_{2}+2c_{4}+3c_{9}=0$
and
![]() $2c_{5}+2c_{6}+3c_{7}=0$
. Further using homogeneity, one obtains the crucial result
$2c_{5}+2c_{6}+3c_{7}=0$
. Further using homogeneity, one obtains the crucial result
![]() $\unicode[STIX]{x1D60F}_{ijljli}=0$
– which stems from
$\unicode[STIX]{x1D60F}_{ijljli}=0$
– which stems from
![]() $\langle u_{l}\unicode[STIX]{x2202}_{j}b_{i}\,\unicode[STIX]{x2202}_{il}^{2}b_{j}\rangle =0$
, as already obtained by Betchov (Reference Betchov1963) – which gives
$\langle u_{l}\unicode[STIX]{x2202}_{j}b_{i}\,\unicode[STIX]{x2202}_{il}^{2}b_{j}\rangle =0$
, as already obtained by Betchov (Reference Betchov1963) – which gives
![]() $15c_{8}=24c_{2}+6c_{4}+4c_{5}+16c_{6}$
. Fortunately, all nine constants are not necessary. Indeed, one gets
$15c_{8}=24c_{2}+6c_{4}+4c_{5}+16c_{6}$
. Fortunately, all nine constants are not necessary. Indeed, one gets
The final step is rather tedious and consists into choosing wisely various components of
![]() $\unicode[STIX]{x1D60F}_{ijlnpq}$
to determine the remaining constants. It follows that three simple relations can be found,
$\unicode[STIX]{x1D60F}_{ijlnpq}$
to determine the remaining constants. It follows that three simple relations can be found,
![]() $c_{9}=-2\langle \unicode[STIX]{x2202}_{1}u_{1}\,\unicode[STIX]{x2202}_{3}b_{1}\,\unicode[STIX]{x2202}_{1}b_{3}\rangle$
,
$c_{9}=-2\langle \unicode[STIX]{x2202}_{1}u_{1}\,\unicode[STIX]{x2202}_{3}b_{1}\,\unicode[STIX]{x2202}_{1}b_{3}\rangle$
,
![]() $-2(c_{7}+c_{8}+c_{9})=\langle \unicode[STIX]{x2202}_{1}u_{1}\,(\unicode[STIX]{x2202}_{1}b_{1})^{2}\rangle$
and
$-2(c_{7}+c_{8}+c_{9})=\langle \unicode[STIX]{x2202}_{1}u_{1}\,(\unicode[STIX]{x2202}_{1}b_{1})^{2}\rangle$
and
![]() $2(c_{3}-c_{1})=\langle \unicode[STIX]{x2202}_{1}u_{1}\,(\unicode[STIX]{x2202}_{3}b_{1})^{2}\rangle -\langle \unicode[STIX]{x2202}_{1}u_{1}\,(\unicode[STIX]{x2202}_{1}b_{3})^{2}\rangle$
. Combining all these equations yields the final important results
$2(c_{3}-c_{1})=\langle \unicode[STIX]{x2202}_{1}u_{1}\,(\unicode[STIX]{x2202}_{3}b_{1})^{2}\rangle -\langle \unicode[STIX]{x2202}_{1}u_{1}\,(\unicode[STIX]{x2202}_{1}b_{3})^{2}\rangle$
. Combining all these equations yields the final important results
These two expressions quite simplify the production terms in the equation of the total dissipation rate (B 6).
B.3 The
 $4/5$
th law of isotropic MHD turbulence
$4/5$
th law of isotropic MHD turbulence
In this section, we investigate further the terms labelled
![]() $(\text{i})$
and
$(\text{i})$
and
![]() $(\text{ii})$
, which appear in the evolution equation (5.11) of
$(\text{ii})$
, which appear in the evolution equation (5.11) of
![]() $R+B$
. Three two-point third-order correlations are involved, namely
$R+B$
. Three two-point third-order correlations are involved, namely
which are true tensors. The two first ones are symmetric in their two first indices, and thus easier to handle. It appears that using only the evolution equation of
![]() $R$
, and thus the term
$R$
, and thus the term
![]() $(\text{i})$
, one can recover the
$(\text{i})$
, one can recover the
![]() $4/5$
th law of isotropic MHD turbulence (Politano & Pouquet Reference Politano and Pouquet1998b
; Yousef, Rincon & Schekochihin Reference Yousef, Rincon and Schekochihin2007)
$4/5$
th law of isotropic MHD turbulence (Politano & Pouquet Reference Politano and Pouquet1998b
; Yousef, Rincon & Schekochihin Reference Yousef, Rincon and Schekochihin2007)
as done in Yoshimatsu (Reference Yoshimatsu2012). The main features of the derivation are recalled here, along with some considerations about the term
![]() $(\text{ii})$
.
$(\text{ii})$
.
The term
![]() $(\text{i})$
depends on
$(\text{i})$
depends on
![]() $\unicode[STIX]{x1D719}_{ili}^{(uuu)}-\unicode[STIX]{x1D719}_{ili}^{(bbu)}$
. After some classical algebra (developed in Politano et al. (Reference Politano, Gomez and Pouquet2003), Briard & Gomez (Reference Briard and Gomez2017) for instance) these two tensors can be expressed as
$\unicode[STIX]{x1D719}_{ili}^{(uuu)}-\unicode[STIX]{x1D719}_{ili}^{(bbu)}$
. After some classical algebra (developed in Politano et al. (Reference Politano, Gomez and Pouquet2003), Briard & Gomez (Reference Briard and Gomez2017) for instance) these two tensors can be expressed as
where the subscript
![]() $x$
stands for either
$x$
stands for either
![]() $u$
or
$u$
or
![]() $b$
,
$b$
,
![]() $k_{u}=\langle u_{L}^{2}u_{L}^{\prime }\rangle$
,
$k_{u}=\langle u_{L}^{2}u_{L}^{\prime }\rangle$
,
![]() $k_{b}=\langle b_{L}^{2}u_{L}^{\prime }\rangle$
and the prime
$k_{b}=\langle b_{L}^{2}u_{L}^{\prime }\rangle$
and the prime
![]() $^{\prime }$
on the correlation
$^{\prime }$
on the correlation
![]() $k_{x}$
refers to the spatial derivative
$k_{x}$
refers to the spatial derivative
![]() $k_{x}^{\prime }=\unicode[STIX]{x2202}_{r}k_{x}$
. Using homogeneity, one can further show that
$k_{x}^{\prime }=\unicode[STIX]{x2202}_{r}k_{x}$
. Using homogeneity, one can further show that
![]() $k_{u}=\langle \unicode[STIX]{x1D6FF}u_{L}^{3}\rangle /6$
. Moreover, from the evolution equations (B 1) of
$k_{u}=\langle \unicode[STIX]{x1D6FF}u_{L}^{3}\rangle /6$
. Moreover, from the evolution equations (B 1) of
![]() $K_{V}$
and
$K_{V}$
and
![]() $K_{B}$
, it follows that
$K_{B}$
, it follows that
The evolution equation of
![]() $R$
thus becomes
$R$
thus becomes
Identification with (5.11) provides
where the first of the two relations is usual for HIT. Further dropping the two time derivative and viscous dissipation terms in (B 17), and integrating twice with respect to
![]() $r$
yields the
$r$
yields the
![]() $4/5$
th law (B 14).
$4/5$
th law (B 14).
Some words can be said about the term
![]() $(\text{ii})$
in the equation of
$(\text{ii})$
in the equation of
![]() $B(r,t)$
, which depends on
$B(r,t)$
, which depends on
![]() $\unicode[STIX]{x1D719}_{lii}^{(ubb)}-\unicode[STIX]{x1D719}_{ili}^{(ubb)}$
. The latter tensor can be expressed as
$\unicode[STIX]{x1D719}_{lii}^{(ubb)}-\unicode[STIX]{x1D719}_{ili}^{(ubb)}$
. The latter tensor can be expressed as
where
![]() $A(r)=\langle u_{L}b_{L}b_{L}^{\prime }\rangle$
,
$A(r)=\langle u_{L}b_{L}b_{L}^{\prime }\rangle$
,
![]() $B(r)=\langle u_{N}b_{N}b_{L}^{\prime }\rangle$
,
$B(r)=\langle u_{N}b_{N}b_{L}^{\prime }\rangle$
,
![]() $C(r)=\langle u_{N}b_{L}b_{N}^{\prime }\rangle$
,
$C(r)=\langle u_{N}b_{L}b_{N}^{\prime }\rangle$
,
![]() $D(r)=\langle u_{L}b_{N}b_{N}^{\prime }\rangle$
, with
$D(r)=\langle u_{L}b_{N}b_{N}^{\prime }\rangle$
, with
![]() $A+2B=0$
and
$A+2B=0$
and
![]() $C+D=A+rA^{\prime }/2$
, so that
$C+D=A+rA^{\prime }/2$
, so that
![]() $\unicode[STIX]{x1D719}_{iil}^{(ubb)}=0$
, where the subscript
$\unicode[STIX]{x1D719}_{iil}^{(ubb)}=0$
, where the subscript
![]() $()_{N}$
refers either to
$()_{N}$
refers either to
![]() $()_{2}$
or
$()_{2}$
or
![]() $()_{3}$
. Expanding
$()_{3}$
. Expanding
![]() $(\text{ii})$
yields
$(\text{ii})$
yields
and the quantity
![]() $D-C$
can be linked to
$D-C$
can be linked to
which appears in the calculations of Yoshimatsu (Reference Yoshimatsu2012). Finally, identification between the latter reference and (5.1) provides an additional relation