1 Introduction
Problems of dynamics of fine dispersed particles in the near-Earth space (NES) have been studied for more than 30 years in connection with a problem of anthropogenic pollution of near space by man-made micro-particles (MP). The basic attention is given to the definition of characteristics of man-made micro-particles which are capable of being kept in the near-Earth space for a long time and the conditions of their injection in the NES. These research show that particles with sizes of approximately
$1{-}100~\unicode[STIX]{x03BC}\text{m}$
can have a long-time orbital existence in the NES. At the same time, the basic possibility of the long-time holding of man-made particles with submicron size in the Earth’s vicinity raises doubts because the results of numerical simulation of the motion of particles with sizes of the order of
$0.1{-}1~\unicode[STIX]{x03BC}\text{m}$
showed that the times of orbital existence for MP with the sizes mentioned above are, as a rule, essentially restricted by the influence of disturbances due to the pressure of sunlight for injection at high altitude (Horanyi, Houpis & Mendis Reference Horanyi, Houpis and Mendis1988; Kolesnikov, Chernov & Yakovlev Reference Kolesnikov, Chernov and Yakovlev1999) or by the resistance force of residual gas in the upper atmosphere for low circumterraneous orbits (Merzlyakov Reference Merzlyakov1996; Kolesnikov & Chernov Reference Kolesnikov and Chernov1997).
We have undertaken research of the dynamics of smaller particles with sizes less than
$0.1~\unicode[STIX]{x03BC}\text{m}$
for the first time in Kolesnikov (Reference Kolesnikov2001), Kolesnikov & Chernov (Reference Kolesnikov and Chernov2003). The results of the numerical simulation of the motion of the particles mentioned above in the Earth’s plasmasphere in Kolesnikov (Reference Kolesnikov2001), Kolesnikov & Chernov (Reference Kolesnikov and Chernov2003) have shown that, unlike earlier considered particles with sizes of the order of
$0.1{-}1~\unicode[STIX]{x03BC}\text{m}$
, particles with sizes of less than
$0.1~\unicode[STIX]{x03BC}\text{m}$
(dozens of nanometres) are capable of being kept for a long time in the near-Earth space under certain conditions as a result of the disturbance of the micro-particles’ motion in the NES by the Lorentz force (from the side of the Earth’s magnetic field) acting on the electric charge of the MPs. Thus these particles can be an important factor in the man-made pollution of near space.
In connection with the results mentioned above there is a necessity to carry out a fundamental theoretical study of the conditions of capture of submicron particles by the Earth’s magnetic field by applying the conforming analytical methods. In Kolesnikov, Chernov & Yakovlev (Reference Kolesnikov, Chernov and Yakovlev2007) we showed that the problem of the dynamics of submicron particles in the plasmasphere admits a canonical formulation in the form of a Hamiltonian system for certain model assumptions about number, character and a mode of definition for the disturbing forces acting on the MP. In this case, methods of the theory of Hamiltonian systems which were developed in works by A. N. Kolmogorov, V. I. Arnold, and Yu. Mozer (the so-called KAM theory) (Arnol’d Reference Arnol’d1961; Mozer Reference Mozer1981) can be used for analytical study of the properties of motion. In this paper we will show that satisfaction of the conditions of Mozer’s theorem (which ensures the eternal belonging of current values of osculating elements of MP’s orbit to fixed vicinities of their initial values) (Mozer Reference Mozer1981) can be provided if the conditions of canonical approach are correct in describing the motion of submicron particles in the plasmasphere, together with some additional assumptions about a material, the dimensions and initial orbits of the MPs are satisfied. The possibility of the implementation of the modes of motion mentioned above will be confirmed by the results of the numerical simulation of the dynamics of carbon submicron particles in the Earth’s plasmasphere which is based on the solution of the model and the exact equations of motion.
2 The canonical formulation of the problem of particle motion with a local equilibrium electric charge in the Earth’s plasmasphere
First of all we notice that the general condition for the canonical formulation of the problem of micro-particles in NES is the possibility to represent all forces
$\boldsymbol{F}^{j}$
acting upon a MP in the form Goldstein (Reference Goldstein1953)
$$\begin{eqnarray}\boldsymbol{F}^{j}=-\unicode[STIX]{x1D735}V^{j}\quad \text{or}\quad F_{i}^{j}=-\frac{\unicode[STIX]{x2202}U^{j}}{\unicode[STIX]{x2202}x_{i}}+\frac{\text{d}}{\text{d}t}\frac{\unicode[STIX]{x2202}U^{j}}{\unicode[STIX]{x2202}{\dot{x}}_{i}}\quad (i=1,2,3),\end{eqnarray}$$
where
$V^{j}=V^{j}(x_{1},x_{2},x_{3},t)$
is the usual potential, and
$U^{j}(x_{1},x_{2},x_{3},{\dot{x}}_{1},{\dot{x}}_{2},{\dot{x}}_{3},t)$
is the generalized potential. When a MP moves at sufficiently high altitude, at which one can neglect the drag force of the background gas of the upper atmosphere, the basic forces acting upon the MP are represented by the gravitational force
$\boldsymbol{F}^{gr}$
, solar pressure force
$\boldsymbol{F}^{sp}$
and the Lorentz force
$\boldsymbol{F}^{L}$
. The gravitational force and the force of solar pressure do not depend on velocity (for a spherical MP) and are represented by the usual potentials
$V^{gr}$
and
$V^{sp}$
. At the same time, we showed in Kolesnikov et al. (Reference Kolesnikov, Chernov and Yakovlev2007) that the Lorentz force acting upon the variable electric charge of a MP from the side of the magnetic and electric fields of near-Earth space admits representation with the help of a generalized potential
$U^{L}$
, if appropriate constraints are imposed on the character of the variation of the MP charge in the process of its orbital motion and also on the geometrical features of the magnetic and electric fields of the NES. The first of these constraints consists in validity of the condition of quasi-equilibrium of the MP’s electric charge, which for any position of the MP in the NES should be close to the equilibrium electric charge of a MP resting at this point. In this case, the MP’s electric charge is determined by local values of the parameters of the ambient plasma and depends only on the current coordinates of MP, i.e.
$$\begin{eqnarray}Q=Q(\boldsymbol{r}),\end{eqnarray}$$
where
$\boldsymbol{r}$
is the radius vector of the MP’s current position.
The second constraint (on the geometrical characteristics of the fields) includes the validity of the conditions
$$\begin{eqnarray}\displaystyle & \displaystyle \boldsymbol{B}\bot \unicode[STIX]{x1D735}Q, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \boldsymbol{E}\Vert \unicode[STIX]{x1D735}Q & \displaystyle\end{eqnarray}$$
i.e. the gradient of charge
$Q$
considered in accordance with condition (2.2) as a function of the coordinates should be perpendicular to the vector
$\boldsymbol{B}$
of the magnetic field induction and parallel to the vector
$\boldsymbol{E}$
of the electric field strength. We showed in Kolesnikov et al. (Reference Kolesnikov, Chernov and Yakovlev2007) that, if conditions (2.2)–(2.4) are met, the Lorentz force can be represented by the generalized potential
$$\begin{eqnarray}U^{L}=Y_{1}-\frac{\boldsymbol{v}\boldsymbol{\cdot }\boldsymbol{Y}_{2}}{c},\end{eqnarray}$$
where
$v$
is a velocity of the MP,
$c$
is the velocity of light,
$Y_{1}$
and
$\boldsymbol{Y}_{2}$
are the scalar and vector functions of coordinates that satisfy the equations
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle \unicode[STIX]{x1D735}Y_{1}=Q\unicode[STIX]{x1D735}\unicode[STIX]{x1D711}\\ \displaystyle \text{rot}\,\boldsymbol{Y}_{2}=Q\,\text{rot}\,\boldsymbol{A}.\end{array}\right\}\end{eqnarray}$$
In (2.6)
$\unicode[STIX]{x1D711}$
and
$\boldsymbol{A}$
are the scalar and vector potentials of the electric and magnetic fields acting upon the MP in the NES, respectively. Notice that in the case of constant charge of a micro-particle, the functions
$Y_{1}$
and
$\boldsymbol{Y}_{2}$
are determined by the expressions
$$\begin{eqnarray}Y_{1}=Q\unicode[STIX]{x1D711},\quad \boldsymbol{Y}_{2}=Q\boldsymbol{A},\end{eqnarray}$$
whose substitution into (2.5) leads to the well-known expression for the Lorentz force generalized potential of a particle with constant charge
$$\begin{eqnarray}U^{L}=Q\unicode[STIX]{x1D711}-\frac{Q}{c}\boldsymbol{v}\boldsymbol{\cdot }\boldsymbol{A}.\end{eqnarray}$$
As we showed in Kolesnikov et al. (Reference Kolesnikov, Chernov and Yakovlev2007) the Hamilton function describing the dynamics of a micro-particle with variable charge in the NES is determined by the formula
$$\begin{eqnarray}H=\frac{1}{2m}\mathop{\sum }_{i=1}^{3}\left(P_{i}-\frac{Y_{2i}}{c}\right)^{2}+V^{gr}+V^{pr}+Y_{1},\end{eqnarray}$$
where
$m$
is a mass of MP,
$P_{i}=m{\dot{x}}_{i}+(Y_{2i}/c)$
are components of the generalized momentum vector.
In Kolesnikov et al. (Reference Kolesnikov, Chernov and Yakovlev2007), on the basis of numerical simulation results, we showed that for MP motion in the Earth’s plasmasphere the condition (2.2) is true for micro-particles with radii more than
$0.01~\unicode[STIX]{x03BC}\text{s}$
if their orbits are situated at altitudes more than one and a half times the Earth’s radius from the surface of the Earth.
The geometrical conditions (2.3) and (2.4) are satisfied due to specific features of the plasma spatial distribution in the Earth’s plasmasphere. This distribution is known to be described by the model of a two-component plasma (Hill & Wipple Reference Hill and Wipple1985) consisting of a ‘cold’ component with density
$n_{cold}$
and temperature
$T_{cold}$
, and ‘hot’ component with density
$n_{hot}$
and temperature
$T_{hot}$
. The total plasma density is
$n=n_{cold}+n_{hot}$
. The parameters
$n_{cold}$
,
$T_{cold}$
and
$n_{hot}$
,
$T_{hot}$
are specified by the expressions (Hill & Wipple Reference Hill and Wipple1985)
$$\begin{eqnarray}n_{cold}=\left\{\begin{array}{@{}ll@{}}\displaystyle n^{\ast }-1, & \displaystyle T^{\ast }>1~\text{eV}\\ \displaystyle n^{\ast }, & \displaystyle T^{\ast }<1~\text{eV}\end{array}\right.\quad T_{cold}=\left\{\begin{array}{@{}ll@{}}\displaystyle 1~\text{eV}, & \displaystyle T^{\ast }>1~\text{eV}\\ \displaystyle T^{\ast }, & \displaystyle T^{\ast }<1~\text{eV}\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}n_{hot}=\left\{\begin{array}{@{}ll@{}}\displaystyle 1~\text{cm}^{-3}, & \displaystyle T^{\ast }>1~\text{eV}\\ \displaystyle 0, & \displaystyle T^{\ast }<1~\text{eV}\end{array}\right.\quad T_{hot}=T^{\ast },\quad T^{\ast }>1~\text{eV}\end{eqnarray}$$
Functions
$n^{\ast }(L)$
and
$T^{\ast }(L)$
in (2.10) and (2.11) are determined by the formulas
$$\begin{eqnarray}\displaystyle & \displaystyle n^{\ast }(L)=10^{(15-L)/3.5},~\text{cm}^{-3} & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle T^{\ast }(L)=0.09239L^{2.7073},~\text{eV}, & \displaystyle\end{eqnarray}$$
where
$L$
is the parameter of the local magnetic shell (the McIlwain parameter).
The equilibrium charge of a body, being a function of local density and temperature, does not depend on the longitudinal coordinate along the magnetic field line, which corresponds to satisfaction of condition (2.3). In this way,
$Q=Q(L)$
. The main contribution to the geo-electric field at the altitudes of the plasmasphere is made, as is known, by the electric field of co-rotation
$\boldsymbol{E}_{cor}=1/c(\boldsymbol{r}\times \unicode[STIX]{x1D734})\times \boldsymbol{B}$
where
$\unicode[STIX]{x1D734}$
is the angular velocity vector of the Earth’s rotation. It may be verified without difficulty that if we use as a model of the geomagnetic field the model of a dipole magnetic field with the magnetic moment anti-parallel to the Earth’s rotation axis, then the electric field of co-rotation satisfies condition (2.4).
3 Main result
Let us make a number of extra simplifying assumptions about the MP sizes, their material and MP’s orbits in plasmasphere.
We limit our study to the case of micro-particles with radii of the order of some hundredths of a micrometre. The efficiency of sunlight pressure on a MP is small for particles with the sizes mentioned above (Kolesnikov & Chernov Reference Kolesnikov and Chernov2004), and we can neglect the influence of solar pressure on micro-particle motions in the NES. We shall consider a MP from a material with a low photoemission yield. For such particles in the plasmasphere, the micro-particle potential (and accordingly its charges) varies insignificantly during transit through the Earth’s shadow. The correctness of this statement is confirmed by data from numerical calculations of micro-particle potentials on the concrete trajectory that are presented in figure 1. Thus, in this case, we can also neglect the dynamic effect of the shadowing of a part of the micro-particle’s orbit. At last, we limit our study to the case of micro-particle motions on weakly oblong orbits (with eccentricities
${<}0.3{-}0.4$
) which are situated in the lower part of the plasmasphere with perigee’s altitudes of the order of the Earth’s radius. We observe that on orbits such as those mentioned above, it is possible to neglect the disturbance’s influence of the electric field of co-rotation on micro-particle motions. The correctness of this statement is confirmed by the data of numerical calculations of the dimensionless accelerations on the concrete trajectory that are presented in figure 2 and by results of calculations of the orbit’s parameters which will be outlined below.
Figure 1. The time dependence of the local equilibrium potential of a micro-particle. Initial conditions and carbon micro-particle radius are the same as in figure 3.
With these assumptions, the considered problem becomes one of the motion of the MP with variable electric charge in superposition of the central field of gravitation and the Lorentz force acting on a micro-particle’s electric charge from the dipole magnetic field of the Earth. We note that a dipole approximation is correct for geocentric distances from one and a half up to ten radii of the Earth (Dorman, Smirnov & Tjasto Reference Dorman, Smirnov and Tjasto1971).
Figure 2. The dependences of current values of micro-particle accelerations (in non-dimensional units) under the influence of various disturbed forces on time. 1 – acceleration due to the force of the central gravitational field, 2 – acceleration due to the Lorentz force from the dipole magnetic field of the Earth, 3 – acceleration due to the Lorentz force from the electric field of co-rotation, 4 – acceleration due to sunlight pressure. The dimensionless accelerations are determined by (3.23). Initial conditions and carbon micro-particle radius are the same as in figure 3.
We shall work in a spherical coordinate system
$r,\unicode[STIX]{x1D717},\unicode[STIX]{x1D711}$
with the origin at the Earth’s centre and the polar axis passing through the southern magnetic pole. In this case, the Hamilton function (2.9) can be written as follows
$$\begin{eqnarray}H=\frac{1}{2m}\left[P_{r}^{2}+P_{\unicode[STIX]{x1D717}}^{2}+\frac{1}{r^{2}\sin ^{2}\unicode[STIX]{x1D717}}\left(P_{\unicode[STIX]{x1D711}}+\frac{Y_{2\unicode[STIX]{x1D711}}r\sin \unicode[STIX]{x1D717}}{c}\right)^{2}\right]-\frac{m\unicode[STIX]{x1D707}_{E}}{r},\end{eqnarray}$$
where
$\unicode[STIX]{x1D707}_{E}$
is the gravitational parameter of the Earth.
The value of an electric charge
$Q(L)$
is determined as a result of the numerical solution of the balance equation of the charging currents
$$\begin{eqnarray}J_{tot}(\unicode[STIX]{x1D6F7}_{eq})\equiv J_{p}^{e}+J_{p}^{i}+J_{ph}+J_{field\text{-}emission}=0,\end{eqnarray}$$
here
$\unicode[STIX]{x1D6F7}_{eq}=(1/4\unicode[STIX]{x03C0}\unicode[STIX]{x1D700}_{0})(Q/R)$
is the equilibrium potential,
$J_{p}^{e}$
is the current of plasma electrons,
$J_{p}^{i}$
is the total current of plasma ions,
$J_{ph}$
is the current of photoelectrons and
$J_{field\text{-}emission}$
is the field emission current,
$\unicode[STIX]{x1D700}_{0}$
is the electric constant and
$R$
is particle radius. In the plasmasphere the equilibrium charge is negative therefore the charging currents in (3.2) are determined by the expressions of Kolesnikov et al. (Reference Kolesnikov, Chernov and Yakovlev2007).
Figure 3. Dependence of the semi-major axis of an orbit for a carbon micro-particle with radius 33 nanometres on time. Initial conditions correspond to an orbit of a particle without a charge with a perigee altitude of 9000 km, an eccentricity of 0.145, an angle of inclination of
$30^{\circ }$
, a longitude of ascending node of
$180^{\circ }$
and ascending node-perigee angle of
$270^{\circ }$
. Solid line for the case of equilibrium charge of the micro-particle and two acting forces. Dashed line for general case of 7 forces and a charge which is determined at every step of numerical integration of the system of equations of motion and the micro-particle’s charging.
Figure 4. Dependence of the angle of inclination of an orbit on the plane of the magnetic equator for a carbon micro-particle with radius 33 nanometres on time. Initial conditions correspond to an orbit of a particle without a charge with a perigee altitude of 9000 km, an eccentricity of 0.145, an angle of inclination of
$30^{\circ }$
, a longitude of ascending node of
$180^{\circ }$
and ascending node-perigee angle of
$270^{\circ }$
.
Figure 5. Dependence of the eccentricity of an orbit for a carbon micro-particle with radius 33 nanometres on time. Initial conditions correspond to an orbit of a particle without a charge with a perigee altitude of 9000 km, an eccentricity of 0.145, an angle of inclination of
$30^{\circ }$
, a longitude of ascending node of
$180^{\circ }$
and ascending node-perigee angle of
$270^{\circ }$
. Solid line for the case of equilibrium charge of the micro-particle and two acting forces. Dashed line for general case of 7 forces and a charge which is determined on every step of numerical integration of the system of equations of motion and micro-particle’s charging.
We shall approximate the value of a charge by the following polynomial
$$\begin{eqnarray}Q(L)=Q_{0}\left[1+\mathop{\sum }_{k=1}^{n}\unicode[STIX]{x1D709}_{k}\left(\frac{L-L_{0}}{L}\right)^{k}\right],\end{eqnarray}$$
here
$Q_{0}$
is the charge for
$L=L_{0}$
. We find the expansion coefficient
$\unicode[STIX]{x1D709}_{k}$
by substitution of expression (3.3) into the equation (3.2). It may be shown that an increase of the polynomial degree essentially improves the accuracy of the approximation even for a greater interval of values of
$L$
.
To find an expression for
$Y_{2\unicode[STIX]{x1D711}}$
we shall use dipolar coordinates
$L,\unicode[STIX]{x1D6F7},M$
(Braun Reference Braun1970) and the formula (3.3). Then
$$\begin{eqnarray}Y_{2\unicode[STIX]{x1D711}}H_{\unicode[STIX]{x1D6F7}}=-Q_{0}B_{E}R_{E}^{2}\int \left[1+\mathop{\sum }_{k=1}^{n}\unicode[STIX]{x1D709}_{k}\left(\frac{L-L_{0}}{L}\right)^{k}\right]\frac{1}{L^{2}}\,\text{d}L,\end{eqnarray}$$
here
$H_{\unicode[STIX]{x1D6F7}}$
is Lamé coefficient,
$B_{E}$
is the magnetic field induction in the plane of the magnetic equator
$(\unicode[STIX]{x1D717}=0)$
on the Earth’s surface and
$R_{E}$
is the Earth’s radius (Braun Reference Braun1970). No generality is lost for simplification of the final expressions and we shall restrict ourselves to a case of small eccentricity of an undisturbed elliptic Keplerian orbit and, accordingly, the first three members of the polynomial (3.3). Then, from (3.4) we obtain
$$\begin{eqnarray}Y_{2\unicode[STIX]{x1D711}}=\frac{Q_{0}B_{E}R_{E}}{L\sin ^{3}\unicode[STIX]{x1D717}}\left[\frac{1+\unicode[STIX]{x1D709}_{1}+\unicode[STIX]{x1D709}_{2}}{L}-\frac{L_{0}(\unicode[STIX]{x1D709}_{1}+2\unicode[STIX]{x1D709}_{2})}{2L^{2}}+\frac{\unicode[STIX]{x1D709}_{2}L_{0}^{2}}{3L^{3}}\right].\end{eqnarray}$$
By using the expression for the value of
$B_{E}=M_{E}/R_{E}^{3}$
(
$M_{E}$
is the value of the magnetic dipole) and the connection between spherical and dipolar coordinates, we transform expression (3.1) and write the Hamilton function in the form
$$\begin{eqnarray}H=H_{0}+H_{1}+H_{2},\end{eqnarray}$$
where
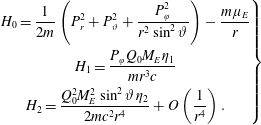$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle H_{0}=\frac{1}{2m}\left(P_{r}^{2}+P_{\unicode[STIX]{x1D717}}^{2}+\frac{P_{\unicode[STIX]{x1D711}}^{2}}{r^{2}\sin ^{2}\unicode[STIX]{x1D717}}\right)-\frac{m\unicode[STIX]{x1D707}_{E}}{r}\\ \displaystyle H_{1}=\frac{P_{\unicode[STIX]{x1D711}}Q_{0}M_{E}\unicode[STIX]{x1D702}_{1}}{mr^{3}c}\\ \displaystyle H_{2}=\frac{Q_{0}^{2}M_{E}^{2}\sin ^{2}\unicode[STIX]{x1D717}\unicode[STIX]{x1D702}_{2}}{2mc^{2}r^{4}}+O\left(\frac{1}{r^{4}}\right).\end{array}\right\}\end{eqnarray}$$
Here
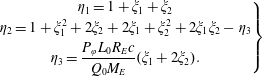$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle \unicode[STIX]{x1D702}_{1}=1+\unicode[STIX]{x1D709}_{1}+\unicode[STIX]{x1D709}_{2}\\ \displaystyle \unicode[STIX]{x1D702}_{2}=1+\unicode[STIX]{x1D709}_{1}^{2}+2\unicode[STIX]{x1D709}_{2}+2\unicode[STIX]{x1D709}_{1}+\unicode[STIX]{x1D709}_{2}^{2}+2\unicode[STIX]{x1D709}_{1}\unicode[STIX]{x1D709}_{2}-\unicode[STIX]{x1D702}_{3}\\ \displaystyle \unicode[STIX]{x1D702}_{3}=\frac{P_{\unicode[STIX]{x1D711}}L_{0}R_{E}c}{Q_{0}M_{E}}(\unicode[STIX]{x1D709}_{1}+2\unicode[STIX]{x1D709}_{2}).\end{array}\right\}\end{eqnarray}$$
For micro-particles and orbits with the parameters mentioned above, all
$\unicode[STIX]{x1D702}_{k}$
are of the order of one. Hence, for the considered case the expressions for the components of the Hamilton function coincide with their expressions for a constant electric charge modulo factor of the order of one (Vavilov & Kolesnikov Reference Vavilov and Kolesnikov1981).
Figure 6. Dependence of the angle of inclination of an orbit to the plane of the magnetic equator for a carbon micro-particle with radius 33 nanometres on time. Initial conditions correspond to an orbit of a particle without a charge with a perigee altitude of 9000 km, an eccentricity of 0.145, an angle of inclination of
$30^{\circ }$
, a longitude of ascending node of
$180^{\circ }$
and ascending node-perigee angle of
$270^{\circ }$
. Solid line for the case of equilibrium charge of micro-particle and two acting forces. Dashed line for the general case of 7 forces and a charge which is determined at every step of numerical integration of the system of equations of motion and micro-particle’s charging.
Figure 7. Dependence of the semi-major axis of an orbit for a carbon micro-particle with radius 27 nanometres on time. Initial conditions correspond to an orbit of a particle without a charge with a perigee altitude of 10 000 km, an eccentricity of 0.1, an angle of inclination of
$40^{\circ }$
, a longitude of ascending node of
$180^{\circ }$
and ascending node-perigee angle of
$270^{\circ }$
. Solid line for the case of equilibrium charge of micro-particle and two acting forces. Dashed line for the general case of 7 forces and a charge which is determined at every step of numerical integration of the system of equations of motion and micro-particle’s charging.
Figure 8. Dependence of the eccentricity of an orbit for a carbon micro-particle with radius 27 nanometres on time. Initial conditions correspond to an orbit of a particle without a charge with a perigee altitude of 10 000 km, an eccentricity of 0.1, an angle of inclination of
$40^{\circ }$
, a longitude of ascending node of
$180^{\circ }$
and ascending node-perigee angle of
$270^{\circ }$
. Solid line for the case of equilibrium charge of micro-particle and two acting forces. Dashed line for general case of 7 forces and a charge which is determined at every step of numerical integration of the system of equations of motion and micro-particle’s charging.
Operating similarly to paper (Vavilov & Kolesnikov Reference Vavilov and Kolesnikov1981), it is possible to show, that in Delaunay variables
$L_{D},G_{D},H_{D},l_{D},g_{D},h_{D}$
(Duboshin Reference Duboshin1964) the Hamilton function is independent of the generalized momentum
$h_{D}$
and, therefore, the coordinate
$H_{D}$
is the integral of motion
$$\begin{eqnarray}H_{D}=H_{D_{0}}.\end{eqnarray}$$
We introduce the dimensionless parameter
$$\begin{eqnarray}\unicode[STIX]{x1D700}=\frac{M_{E}Q_{0}s_{0}^{2}}{mcH_{D_{0}}^{3}},\end{eqnarray}$$
from which it is easy to show that the Hamilton function (3.6) may be written as a finite series in degrees of
$\unicode[STIX]{x1D700}$
$$\begin{eqnarray}H=H_{0}(L_{D})+\unicode[STIX]{x1D700}H_{1}(L_{D},G_{D},l_{D})+\unicode[STIX]{x1D700}^{2}H_{2}(L_{D},G_{D},l_{D},g_{D}),\end{eqnarray}$$
where
$s_{0}^{2}=\unicode[STIX]{x1D6FE}m_{E}$
,
$m_{E}$
is the Earth’s mass,
$\unicode[STIX]{x1D6FE}$
is the gravitational constant and
$$\begin{eqnarray}H_{0}(L_{D})=\frac{s_{0}^{4}}{2L_{D}^{2}}.\end{eqnarray}$$
As has been proved in Vavilov & Kolesnikov (Reference Vavilov and Kolesnikov1981), it is possible to enter new variables
$L_{u},G_{u},l_{u},g_{u}$
in which the Hamilton function takes the form
$$\begin{eqnarray}H_{u}(L_{u},G_{u},l_{u},g_{u})=H_{u0}(L_{u})+\unicode[STIX]{x1D700}H_{u1}(L_{u},G_{u})+\unicode[STIX]{x1D700}^{2}H_{u2}(L_{u},G_{u},l_{u},g_{u})\end{eqnarray}$$
and
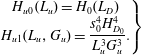$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle H_{u0}(L_{u})=H_{0}(L_{D})\\ \displaystyle H_{u1}(L_{u},G_{u})=\frac{s_{0}^{4}H_{D_{0}}^{4}}{L_{u}^{3}G_{u}^{3}}.\end{array}\right\}\end{eqnarray}$$
In terms of the new variables, the equation of the MP’s motion may be written in the form
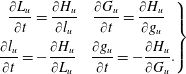$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle \frac{\unicode[STIX]{x2202}L_{u}}{\unicode[STIX]{x2202}t}=\frac{\unicode[STIX]{x2202}H_{u}}{\unicode[STIX]{x2202}l_{u}}\quad \frac{\unicode[STIX]{x2202}G_{u}}{\unicode[STIX]{x2202}t}=\frac{\unicode[STIX]{x2202}H_{u}}{\unicode[STIX]{x2202}g_{u}}\\ \displaystyle \frac{\unicode[STIX]{x2202}l_{u}}{\unicode[STIX]{x2202}t}=-\frac{\unicode[STIX]{x2202}H_{u}}{\unicode[STIX]{x2202}L_{u}}\quad \frac{\unicode[STIX]{x2202}g_{u}}{\unicode[STIX]{x2202}t}=-\frac{\unicode[STIX]{x2202}H_{u}}{\unicode[STIX]{x2202}G_{u}}.\end{array}\right\}\end{eqnarray}$$
Since
$\unicode[STIX]{x2202}H_{u}/\unicode[STIX]{x2202}t\equiv 0$
the trajectories of motion of system (3.15) are situated on isoenergetic surfaces
$$\begin{eqnarray}H_{u}(L_{u},G_{u},l_{u},g_{u})=C.\end{eqnarray}$$
Fixing of the constant
$C$
in (3.16) allows us to express
$L_{u}$
through the variables
$G_{u},l_{u},g_{u}$
. Taking a variable
$l_{u}$
instead of
$t$
as an independent variable, we shall transform (3.15) to the form
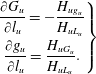$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle \frac{\unicode[STIX]{x2202}G_{u}}{\unicode[STIX]{x2202}l_{u}}=-\frac{H_{ug_{u}}}{H_{uL_{u}}}\\ \displaystyle \frac{\unicode[STIX]{x2202}g_{u}}{\unicode[STIX]{x2202}l_{u}}=\frac{H_{uG_{u}}}{H_{uL_{u}}}.\end{array}\right\}\end{eqnarray}$$
The system of equations (3.17) which defines trajectories of the initial system (3.15) on isoenergetic surfaces (3.16) is also canonical.
We shall consider mapping
$\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D700}}$
of the system of equations (3.17) in a phase surface
$G_{u},g_{u}$
which is defined by moving on trajectories from
$l_{u}=0$
up to
$l_{u}=2\unicode[STIX]{x03C0}$
. Integrating the system of equations (3.17), we shall determine the mapping
$\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D700}}$
explicitly
$$\begin{eqnarray}\displaystyle & \displaystyle G_{u}(2\unicode[STIX]{x03C0})=G_{u}(0)+\unicode[STIX]{x1D700}^{2}f_{1}(G_{u}(0),g_{u}(0)) & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle g_{u}(2\unicode[STIX]{x03C0})=g_{u}(0)+\unicode[STIX]{x1D70D}(G_{u}(0))+\unicode[STIX]{x1D700}^{2}f_{2}(G_{u}(0),g_{u}(0)). & \displaystyle\end{eqnarray}$$
Here
$$\begin{eqnarray}\unicode[STIX]{x1D70D}(G_{u}(0))=\frac{6\unicode[STIX]{x03C0}H_{D_{0}}^{4}}{G_{u}^{4}(0)}.\end{eqnarray}$$
The mapping which is defined by formulas (3.18) and (3.19) satisfies Moser’s theorem (Mozer Reference Mozer1981). Really
$\text{d}\unicode[STIX]{x1D70D}(G_{u}(0))/\text{d}G_{u}(0)\neq 0$
and mapping
$\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D700}}$
– by Liouville’s theorem – preserves the area. Moser’s theorem guarantees infinitely many invariant curves of mapping
$\unicode[STIX]{x1D713}_{\unicode[STIX]{x1D700}}$
for sufficiently small
$\unicode[STIX]{x1D700}$
.
All trajectories of the system (3.15) that start in the poits of an invariant curve produce a two-dimensional invariant torus in four-dimensional phase space. Movements on surfaces of invariant tori are quasi-periodic with two frequencies. Any trajectory starting between two invariant tori on the same energy surface must always remain between these two tori. This guarantees eternal affinity of the current value of a variable
$G_{u}(t)$
to the initial value
$G_{u}(0)$
for any solution of the system (3.15) and sufficiently small
$\unicode[STIX]{x1D700}$
.
Figure 9. Dependence of the angle of inclination of an orbit to the plane of the magnetic equator for a carbon micro-particle with radius 27 nanometres on time. Initial conditions correspond to an orbit of a particle without a charge with a perigee altitude of 10 000 km, an eccentricity of 0.1, an angle of inclination of
$40^{\circ }$
, a longitude of ascending node of
$180^{\circ }$
and ascending node-perigee angle of
$270^{\circ }$
. Solid line for the case of an equilibrium charge of the micro-particle and two acting forces. Dashed line for the general case of 7 forces and a charge which is determined at every step of numerical integration of the system of equations of motion and micro-particle’s charging.
Figure 10. Dependence of the semi-major axis of an orbit for a carbon micro-particle with radius 27 nanometres on time. Initial conditions correspond to an orbit of a particle without a charge with a perigee altitude of 15 000 km, an eccentricity of 0, an angle of inclination of
$35^{\circ }$
, a longitude of ascending node of
$180^{\circ }$
and ascending node-perigee angle of
$270^{\circ }$
. Solid line for the case of equilibrium charge of a micro-particle and two acting forces. Dashed line for the general case of 7 forces and a charge which is determined at every step of numerical integration of the system of equations of motion and micro-particle’s charging.
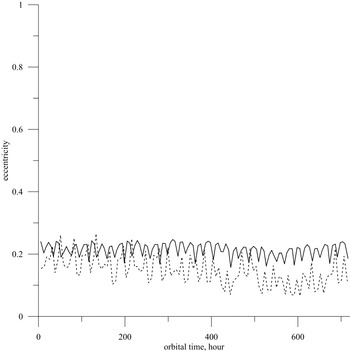
Figure 11. Dependence of the eccentricity of an orbit for a carbon micro-particle with radius 27 nanometres on time. Initial conditions correspond to an orbit of a particle without a charge with a perigee altitude of 15 000 km, an eccentricity of 0, an angle of inclination of
$35^{\circ }$
, a longitude of ascending node of
$180^{\circ }$
and ascending node-perigee angle of
$270^{\circ }$
. Solid line for the case of an equilibrium charge of the micro-particle and two acting forces. Dashed line for the general case of 7 forces and a charge which is determined at every step of numerical integration of the system of equations of motion and micro-particle’s charging.
Figure 12. Dependence of the angle of inclination of an orbit to the plane of the magnetic equator for a carbon micro-particle with radius 27 nanometres on time. Initial conditions correspond to an orbit of a particle without a charge with a perigee altitude of 15 000 km, an eccentricity of 0, an angle of inclination of
$35^{\circ }$
, a longitude of ascending node of
$180^{\circ }$
and ascending node-perigee angle of
$270^{\circ }$
. Solid line for the case of an equilibrium charge of the micro-particle and two acting forces. Dashed line for the general case of 7 forces and a charge which is determined at every step of numerical integration of the system of equations of motion and micro-particle’s charging.
Thus variable
$G_{u}$
(and the variable
$G_{D}$
connected to it) can be considered as a quasi-integral of the system (3.15), in the scope of the suggested model for sufficiently small
$\unicode[STIX]{x1D700}$
. Variables
$L_{u}$
and
$L_{D}$
have similar properties as follows from the integral of energy (3.16). As a result of connection between the Delaunay variables and the osculating elements of the disturbed orbit, eternal affinity of such osculating elements as the semi-major axis, eccentricity and angle of inclination of an orbit to the plane of the magnetic equator to initial values should take place.
The possibility of the realization of modes of micro-particle orbital motions in the plasmasphere with the qualitative properties mentioned above is supported by the results of numerical simulation of the motion of micro-particles with radii of the order of some hundredths of a micrometre in the Earth’s plasmasphere. At the simplifying assumptions for which the Hamilton function (3.1) is written down, the simulation of the micro-particles’ motions in the NES was carried out on the basis of the numerical solution of the equations of micro-particle motion with a local equilibrium electric charge defined by the solution of the equation of current balance (3.2). As an example, in figures 3–5 we can see dependences of the semi-major axis, the inclination and the eccentricity of carbon micro-particle orbits with a radius of 33 nanometres, on time. The MP was injected into the NES in a perigee of an elliptic orbit with a perigee altitude of 9000 km, initial velocity
$5.449~\text{km}~\text{s}^{-1}$
(which corresponds to an eccentricity of 0.145 for a particle without a charge), an angle of inclination of
$30^{\circ }$
, a longitude of ascending node of
$180^{\circ }$
and ascending node-perigee angle of
$270^{\circ }$
. The simulation was carried out over a time interval of 720 hours (1 month). In this case, according to the data presented in figures 3–5, the semi-major axis of the MP’s orbit is actually constant, the inclination oscillates in the range from 30 to
$35^{\circ }$
and the orbit eccentricity oscillates in the range from 0.025 to 0.04. Thus, the obtained simulation data correspond to the results of the analytical study mentioned above. The calculated dependences of the current values of the micro-particle acceleration (in non-dimensional units) under the influence of various disturbed forces on time are given in figure 2 for the time interval of 24 hours. To pass to the dimensionless equations of motion we introduce the following scales of length and time:
$$\begin{eqnarray}\displaystyle & \displaystyle l_{0}=R_{E}=6.371110\times 10^{6}M & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle T_{0}=2\unicode[STIX]{x03C0}\sqrt{\frac{R_{E}^{3}}{\unicode[STIX]{x1D6FE}m_{E}}}=5.06097\times 10^{3}c. & \displaystyle\end{eqnarray}$$
Thus, dimensional acceleration
$\boldsymbol{a}$
is expressed through the dimensionless acceleration
$\boldsymbol{a}^{\prime }$
by the formula
$$\begin{eqnarray}\boldsymbol{a}=\frac{l_{0}}{T_{0}^{2}}\boldsymbol{a}^{\prime }=0.248741\boldsymbol{a}^{\prime }\end{eqnarray}$$
In this case, according to the data of figure 2, the basic forces acting on the MP are the force of the central gravitational field and the Lorentz force due to the interaction of the micro-particle’s charge with the dipole magnetic field of the Earth. This result confirms the correctness of the assumption mentioned above concerning the dominant role of the magnetic component of the Lorentz force to describe the dynamics of the disturbed motion of a MP in the plasmasphere. Finally, for the same time interval the calculated dependence of the local equilibrium potential of a MP on time is presented in figure 1. In the case under consideration, according to the data of figure 1, the MP’s potential changes little during its orbital motion in the NES. The results of our calculations show also that in the case under consideration the equilibrium potential practically coincides with the actual potential of the MP calculated on the basis of the joint solution of the equation of motion and the equation of micro-particle’s charging. Figures 3, 5 and 6 allow us also to compare the evolutions of the semi-major axis, the eccentricity and orbit inclination for parameters mentioned above for two ways of calculation: (i) the central field of gravitation and magnetic component of the Lorentz force are acting on a grain with an electric charge which is assumed to be in equilibrium at every step of the numerical integration of the system of equations of motion; (ii) the full system of 7 forces is acting on a grain, and the system of equations of motion and the micro-particle’s charging are integrated numerically. The full system of forces includes the central gravitational field of the Earth; its perturbation caused by the polar compression of the Earth; the magnetic component of the Lorentz force; the electrical component of the Lorentz force caused by the co-rotation electric field and the convection electric field; the force of solar pressure; and the resistance force arising due to a flow of the background gas. It is seen easily that distinctions exist, but they are small.
Figures 7–12 show the dependences of the semi-major axis, the inclination and the eccentricity of orbit of a carbon micro-particle on time for the same values of longitude of ascending node, ascending node-perigee angle and true anomaly but another values of the grain’s radius, initial altitude (10 000 and 15 000 km), initial velocity (5.175 and
$4.319~\text{km}~\text{s}^{-1}$
) and orbit inclination which are stated in the figure captions. These results allow us to argue that our theoretical model gives a good qualitative description of the evolution of the grains with radii in the several hundredths of a micrometre range if these grains move in some region of the Earth’s plasmasphere.
4 Conclusions
Thus there is the preservation of the form of the MP’s orbit and the preservation of the angle of inclination of the orbit to the plane of the magnetic equator in cases of local equilibrium of the electric charge of a micro-particle with the latter’s radius in the several hundredths of a micrometre range and which moves in the Earth’s plasmasphere. The preservation of the semi-major axis, the angle of inclination of the orbit to the plane of the magnetic equator and the orbit eccentricity are confirmed by the results of the calculations, shown in figures 3–12. The simultaneous small increase in semi-major axis and a decrease in the eccentricity that were observed in, for example figures 10 and 11, do not contradict the statement regarding conservation of the form of the grain’s orbit because this statement means performance of two properties: (i) the sizes of osculating elements of the orbit are in narrow intervals of value, (ii) the orbit does not leave a space area in which it is possible to apply our analytical model.
Acknowledgement
The work is supported by the Russian Foundation of Basic Research, project no. 15-01-05807.
