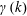1 Introduction
An electron hole in a plasma is a solitary BGK mode (Bernstein, Greene & Kruskal Reference Bernstein, Greene and Kruskal1957) consisting of a positive potential peak self-consistently maintained by phase-space density deficit of trapped electrons (Turikov Reference Turikov1984; Schamel Reference Schamel1986; Eliasson & Shukla Reference Eliasson and Shukla2006; Hutchinson Reference Hutchinson2017). In one dimension, electron holes are the normal nonlinear consequence of growth of an electrostatic instability driven by an unstable electron velocity distribution, for example a two-stream instability. However, it has been known since the earliest simulations (Morse & Nielson Reference Morse and Nielson1969) that in multiple dimensions electron holes either do not form or quickly break up by instability permitted by the additional dimensions; this is referred to as the transverse instability, and observed in many simulations since (Mottez et al. Reference Mottez, Perraut, Roux and Louarn1997; Miyake et al. Reference Miyake, Omura, Matsumoto and Kojima1998; Goldman, Oppenheim & Newman Reference Goldman, Oppenheim and Newman1999; Oppenheim, Newman & Goldman Reference Oppenheim, Newman and Goldman1999; Muschietti et al. Reference Muschietti, Roth, Carlson and Ergun2000; Oppenheim et al. Reference Oppenheim, Vetoulis, Newman and Goldman2001; Singh, Loo & Wells Reference Singh, Loo and Wells2001; Lu et al. Reference Lu, Lembege, Tao and Wang2008). Despite the obvious significance of this instability, since it determines the prevalence and fate of electron holes, satisfactory identification of its mechanism and rigorous analytical determination of its growth rate and threshold have until now been lacking. The current paper now presents this analysis.
Satellite measurements with high time resolution during the past 20 years have established (Matsumoto et al. Reference Matsumoto, Kojima, Miyatake, Omura, Okada, Nagano and Tsutsui1994; Bale et al. Reference Bale, Kellogg, Larsen, Lin, Goetz and Lepping1998; Ergun et al. Reference Ergun, Carlson, McFadden, Mozer, Muschietti, Roth and Strangeway1998; Mangeney et al. Reference Mangeney, Salem, Lacombe, Bougeret, Perche, Manning, Kellogg, Goetz, Monson and Bosqued1999; Pickett et al. Reference Pickett, Chen, Mutel, Christopher, Santolk, Lakhina, Singh, Reddy, Gurnett and Tsurutani2008; Andersson et al. Reference Andersson, Ergun, Tao, Roux, Lecontel, Angelopoulos, Bonnell, McFadden, Larson and Eriksson2009; Wilson et al. Reference Wilson, Cattell, Kellogg, Goetz, Kersten, Kasper, Szabo and Wilber2010; Malaspina et al. Reference Malaspina, Newman, Willson, Goetz, Kellogg and Kerstin2013, Reference Malaspina, Andersson, Ergun, Wygant, Bonnell, Kletzing, Reeves, Skoug and Larsen2014; Vasko et al. Reference Vasko, Agapitov, Mozer, Artemyev and Jovanovic2015; Mozer et al. Reference Mozer, Agapitov, Artemyev, Burch, Ergun, Giles, Mourenas, Torbert, Phan and Vasko2016) that electron holes are widely present in a variety of space plasma regions. They are likely present also, though harder to resolve and observe, in many laboratory plasmas. Therefore it is increasingly pressing to develop a fundamental understanding of their persistence and stability.
Particle in cell (and some Vlasov continuum) simulations have been important in mapping out the phenomena. However, such simulations have not correctly identified the underlying instability mechanism. Figure 1 illustrates an example of a simulation, illustrating a hole and a growing kink in it. The natural idealization of the problem, concentrating on the stability properties rather than on hole formation, is to begin with a pre-formed hole (slab) equilibrium that varies in only one dimension. Simulations of this type have provided valuable insight (Muschietti et al. Reference Muschietti, Roth, Ergun and Carlson1999, Reference Muschietti, Roth, Carlson and Ergun2000; Wu et al. Reference Wu, Lu, Huang and Wang2010), and identified the stabilizing effect of magnetic field. However the transverse ‘focusing’ mechanism, which they hypothesized causes the instability, is not confirmed either by subsequent simulations (Hutchinson Reference Hutchinson2018) or by the present analysis.

Figure 1. Two-dimensional
![]() $(z,y)$
rendering and contours of potential
$(z,y)$
rendering and contours of potential
![]() $\unicode[STIX]{x1D719}$
of an initially one-dimensional hole in the early stages of a transverse instability in a particle-in-cell simulation.
$\unicode[STIX]{x1D719}$
of an initially one-dimensional hole in the early stages of a transverse instability in a particle-in-cell simulation.
Analytic approaches to solving this linear stability problem have previously been at best only partly successful (Schamel Reference Schamel1982, Reference Schamel1987; Jovanović & Schamel Reference Jovanović and Schamel2002). A key difficulty lies in identifying the appropriate eigenmode structure in the direction of equilibrium non-uniformity (Lewis & Symon Reference Lewis and Symon1979). Previous unmagnetized analysis (Schamel Reference Schamel1982) made the inappropriate choice to address symmetric eigenmodes. It is shown here that, in agreement with simulations, the relevant eigenmode is predominantly antisymmetric. Another difficulty is to solve the linearized Vlasov equation by integration along characteristics in regimes that do not yield to simple expansions, in part because of non-uniformity. Previous analyses (Schamel Reference Schamel1982; Jovanović & Schamel Reference Jovanović and Schamel2002) have used expansion in inverse powers of frequency, which is inappropriate for these slowly (and purely) growing modes. The present study instead solves the Vlasov equation by numerical integration at finite complex frequency, showing excellent agreement at small
![]() $\unicode[STIX]{x1D714}$
with a better motivated analytic approximation. A previous study of magnetized holes (Jovanović & Schamel Reference Jovanović and Schamel2002) was, because of its expansions, limited to cases where the wave (
$\unicode[STIX]{x1D714}$
with a better motivated analytic approximation. A previous study of magnetized holes (Jovanović & Schamel Reference Jovanović and Schamel2002) was, because of its expansions, limited to cases where the wave (
![]() $\unicode[STIX]{x1D714}$
) or cyclotron (
$\unicode[STIX]{x1D714}$
) or cyclotron (
![]() $\unicode[STIX]{x1D6FA}$
) frequencies are bigger than the highest bounce frequency of the trapped particles, yet concluded there was instability on the basis of a wave resonance
$\unicode[STIX]{x1D6FA}$
) frequencies are bigger than the highest bounce frequency of the trapped particles, yet concluded there was instability on the basis of a wave resonance
![]() $\unicode[STIX]{x1D714}+m\unicode[STIX]{x1D6FA}\rightarrow 0$
. The present study shows that the low-
$\unicode[STIX]{x1D714}+m\unicode[STIX]{x1D6FA}\rightarrow 0$
. The present study shows that the low-
![]() $k$
transverse instability is stabilized when the cyclotron frequency exceeds the bounce frequency and that the wave frequency is always small, so there is no such resonance except
$k$
transverse instability is stabilized when the cyclotron frequency exceeds the bounce frequency and that the wave frequency is always small, so there is no such resonance except
![]() $m=0$
(which is effectively the one-dimensional case). Prior analytic studies provided no quantitative comparison with simulations. The present study gives quantitative predictions of the fastest growing mode and the previously proposed heuristic criterion (Miyake et al.
Reference Miyake, Omura, Matsumoto and Kojima1998; Muschietti et al.
Reference Muschietti, Roth, Carlson and Ergun2000) for stabilization by magnetic field that agree well with simulations.
$m=0$
(which is effectively the one-dimensional case). Prior analytic studies provided no quantitative comparison with simulations. The present study gives quantitative predictions of the fastest growing mode and the previously proposed heuristic criterion (Miyake et al.
Reference Miyake, Omura, Matsumoto and Kojima1998; Muschietti et al.
Reference Muschietti, Roth, Carlson and Ergun2000) for stabilization by magnetic field that agree well with simulations.
In view of these contrasts, a rather careful development of the mathematics is given here to provide rigor in the derivation, even though some of it has close parallels in the standard analysis of uniform equilibria. Section 2 gives the solution of the linearized Vlasov equation in terms of integrals along unperturbed orbits. Section 3 explains how the Poisson equation gives rise to a generalized eigen-problem and motivates its approximate solution in terms of conservation of momentum which is mathematically equivalent to a variational estimate of the eigenvalue for a shift mode perturbation. Section 4 derives the momentum conservation for unmagnetized plasmas and shows that it is in full agreement with a prior kinematic derivation. This leads to a simple analytic dispersion relation in the long-wavelength limit. Numerical integration at finite frequency gives the growth rate for all wavenumbers. Section 5 performs the analysis for plasmas with a magnetic field in the trapping direction and obtains the corresponding dispersion solutions, showing stabilization for
![]() $\unicode[STIX]{x1D6FA}$
greater than bounce frequency.
$\unicode[STIX]{x1D6FA}$
greater than bounce frequency.
The results are in full agreement with a more descriptive letter recently published by the author (Hutchinson Reference Hutchinson2018). The analysis provides the mathematical justification for the identification of the instability mechanism as being a kinematic one, arising from the transfer of momentum from hole potential to particles (Hutchinson & Zhou Reference Hutchinson and Zhou2016; Zhou & Hutchinson Reference Zhou and Hutchinson2016, Reference Zhou and Hutchinson2017), called jetting.
2 Linearized Vlasov equation
Consider a localized positive potential peak equilibrium
![]() $\unicode[STIX]{x1D719}_{0}(z)$
, the electron hole, to be analysed for linearized electrostatic perturbations. We address only the electron dynamics, taking the ions to be a uniform immobile background. We must retain full-wave treatment in the
$\unicode[STIX]{x1D719}_{0}(z)$
, the electron hole, to be analysed for linearized electrostatic perturbations. We address only the electron dynamics, taking the ions to be a uniform immobile background. We must retain full-wave treatment in the
![]() $z$
-direction, but can Fourier analyse the transverse variation taking a transverse wavenumber
$z$
-direction, but can Fourier analyse the transverse variation taking a transverse wavenumber
![]() $k$
, without loss of generality in the
$k$
, without loss of generality in the
![]() $y$
-direction. So the first-order potential perturbation is harmonic
$y$
-direction. So the first-order potential perturbation is harmonic
Vlasov’s equation is
When linearized in an electrostatic approximation it becomes
which is the rate of change of
![]() $f_{1}$
along the unperturbed orbit in phase space. And
$f_{1}$
along the unperturbed orbit in phase space. And
Integrating (2.3), we get the perturbed distribution:
where the integrand is to be evaluated on the unperturbed orbit, i.e. at
![]() $\boldsymbol{x}(\unicode[STIX]{x1D70F})$
,
$\boldsymbol{x}(\unicode[STIX]{x1D70F})$
,
![]() $\boldsymbol{v}(\unicode[STIX]{x1D70F})$
, which is the characteristic of the linearized equation.
$\boldsymbol{v}(\unicode[STIX]{x1D70F})$
, which is the characteristic of the linearized equation.
The equilibrium distribution is a function of the constants of the unperturbed motion, which are the total parallel energy
![]() $W_{\Vert }=q_{e}\unicode[STIX]{x1D719}+m_{e}v_{\Vert }^{2}/2$
(with
$W_{\Vert }=q_{e}\unicode[STIX]{x1D719}+m_{e}v_{\Vert }^{2}/2$
(with
![]() $z$
the ‘parallel’ direction) and the perpendicular kinetic energy
$z$
the ‘parallel’ direction) and the perpendicular kinetic energy
![]() $W_{\bot }\equiv m_{e}v_{\bot }^{2}/2$
. If a uniform background magnetic field,
$W_{\bot }\equiv m_{e}v_{\bot }^{2}/2$
. If a uniform background magnetic field,
![]() $B_{0}\boldsymbol{e}_{z}$
is present, then
$B_{0}\boldsymbol{e}_{z}$
is present, then
![]() $v_{\bot }^{2}=v_{x}^{2}+v_{y}^{2}$
, but if
$v_{\bot }^{2}=v_{x}^{2}+v_{y}^{2}$
, but if
![]() $B=0$
we can interpret
$B=0$
we can interpret
![]() $v_{\bot }$
as
$v_{\bot }$
as
![]() $v_{y}$
, and ignore
$v_{y}$
, and ignore
![]() $v_{x}$
. So write
$v_{x}$
. So write
And since
![]() $v_{z}(\text{d}\hat{\unicode[STIX]{x1D719}}/\text{d}z)=\text{d}\hat{\unicode[STIX]{x1D719}}/\text{d}\unicode[STIX]{x1D70F}$
,
$v_{z}(\text{d}\hat{\unicode[STIX]{x1D719}}/\text{d}z)=\text{d}\hat{\unicode[STIX]{x1D719}}/\text{d}\unicode[STIX]{x1D70F}$
,
The first term can be integrated by parts to give
assuming that
![]() $\unicode[STIX]{x1D719}_{1}(t=-\infty )=0$
. The leading term is then the ‘adiabatic’ response arising from the variation of a distribution that remains a constant function of total parallel energy
$\unicode[STIX]{x1D719}_{1}(t=-\infty )=0$
. The leading term is then the ‘adiabatic’ response arising from the variation of a distribution that remains a constant function of total parallel energy
![]() $W_{\Vert }$
in response to a potential perturbation giving
$W_{\Vert }$
in response to a potential perturbation giving
![]() $\text{d}W_{\Vert }=q_{e}\unicode[STIX]{x1D719}_{1}$
. The integral term is the non-adiabatic response, which we shall denote
$\text{d}W_{\Vert }=q_{e}\unicode[STIX]{x1D719}_{1}$
. The integral term is the non-adiabatic response, which we shall denote
![]() $\tilde{f}$
.
$\tilde{f}$
.
It is worth noticing that when the unperturbed distribution has a separable isotropic form in energy, for example on all passing orbits when the background is (isotropic) Maxwellian, the
![]() $kv_{y}$
terms disappear because
$kv_{y}$
terms disappear because
But this happens only if the isotropy is in the hole’s rest frame.
3 The unstable shift eigenmode
3.1 Eigen-analysis of the Poisson–Vlasov system
The perturbed Poisson equation (leaving the factor
![]() $\text{e}^{\text{i}(ky-\unicode[STIX]{x1D714}t)}$
implicit) is
$\text{e}^{\text{i}(ky-\unicode[STIX]{x1D714}t)}$
implicit) is
The structure of the linear stability problem is then that we can regard the quantity
![]() ${\tilde{n}}=\int \tilde{f}_{\Vert }\,\text{d}v_{z}$
as a linear functional of
${\tilde{n}}=\int \tilde{f}_{\Vert }\,\text{d}v_{z}$
as a linear functional of
![]() $\hat{\unicode[STIX]{x1D719}}$
determined by the solution of the linearized Vlasov equation. The Poisson equation for given
$\hat{\unicode[STIX]{x1D719}}$
determined by the solution of the linearized Vlasov equation. The Poisson equation for given
![]() $k$
is then a generalized eigen-problem (Lewis & Symon Reference Lewis and Symon1979), of which the complex
$k$
is then a generalized eigen-problem (Lewis & Symon Reference Lewis and Symon1979), of which the complex
![]() $\unicode[STIX]{x1D714}$
is effectively the eigenvalue and the spatial shape of
$\unicode[STIX]{x1D714}$
is effectively the eigenvalue and the spatial shape of
![]() $\hat{\unicode[STIX]{x1D719}}$
is the eigenmode. The non-uniformity of the equilibrium means that the eigenmode structure is of course not a Fourier mode. Determining all the eigenmodes and eigenvalues exactly is difficult, in part because
$\hat{\unicode[STIX]{x1D719}}$
is the eigenmode. The non-uniformity of the equilibrium means that the eigenmode structure is of course not a Fourier mode. Determining all the eigenmodes and eigenvalues exactly is difficult, in part because
![]() ${\tilde{n}}$
is an integral, rather than differential, functional.
${\tilde{n}}$
is an integral, rather than differential, functional.
However, we are not attempting here to identify every mode; only the mechanism and growth rate of a specific type of perturbation observed to occur in simulations, namely the transverse instability. Therefore we concentrate on obtaining a good estimate of the eigenvalue, assuming we have a fair approximation to what the eigenmode shape is. For this purpose, we presuppose what characteristics of the eigenmode the simulations indicate, namely that it is present for small finite values of
![]() $k$
(long transverse wavelength) and the magnitude of its complex frequency is small. To lowest order, then, the eigenmode equation can omit the terms
$k$
(long transverse wavelength) and the magnitude of its complex frequency is small. To lowest order, then, the eigenmode equation can omit the terms
![]() $k^{2}\unicode[STIX]{x1D719}$
and
$k^{2}\unicode[STIX]{x1D719}$
and
![]() ${\tilde{n}}$
, in which case it must approximately satisfy
${\tilde{n}}$
, in which case it must approximately satisfy
It is easy to verify that this linear equation is satisfied by
![]() $\hat{\unicode[STIX]{x1D719}}=-\unicode[STIX]{x0394}(\text{d}\unicode[STIX]{x1D719}_{0}/\text{d}z)$
, a shift mode, which is sometimes called the Goldston mode in soliton and other literature (see e.g. Skryabin (Reference Skryabin2002)). It consists of simply a displacement of the entire hole structure in the
$\hat{\unicode[STIX]{x1D719}}=-\unicode[STIX]{x0394}(\text{d}\unicode[STIX]{x1D719}_{0}/\text{d}z)$
, a shift mode, which is sometimes called the Goldston mode in soliton and other literature (see e.g. Skryabin (Reference Skryabin2002)). It consists of simply a displacement of the entire hole structure in the
![]() $z$
-direction, which is obviously a neighbouring equilibrium, requiring no time derivative terms. In so far as there is a unique solution (modulo a position shift) for a BGK mode (electron hole) with specified distribution function, the shift appears to be the unique solution of this adiabatic equation. In any event, the simulations show that the mode does in fact consist predominantly of a shift, with some other minor distortions.
$z$
-direction, which is obviously a neighbouring equilibrium, requiring no time derivative terms. In so far as there is a unique solution (modulo a position shift) for a BGK mode (electron hole) with specified distribution function, the shift appears to be the unique solution of this adiabatic equation. In any event, the simulations show that the mode does in fact consist predominantly of a shift, with some other minor distortions.
We then take advantage of the fact that an eigen-problem
![]() ${\mathcal{L}}\hat{\unicode[STIX]{x1D719}}=\unicode[STIX]{x1D706}{\mathcal{M}}\hat{\unicode[STIX]{x1D719}}$
where
${\mathcal{L}}\hat{\unicode[STIX]{x1D719}}=\unicode[STIX]{x1D706}{\mathcal{M}}\hat{\unicode[STIX]{x1D719}}$
where
![]() ${\mathcal{L}}$
and
${\mathcal{L}}$
and
![]() ${\mathcal{M}}$
are self-adjoint operatorsFootnote
1
, is equivalent to a variational problem that finds the extremum of the quotient
${\mathcal{M}}$
are self-adjoint operatorsFootnote
1
, is equivalent to a variational problem that finds the extremum of the quotient
![]() $Q=\langle \hat{\unicode[STIX]{x1D719}}{\mathcal{L}}\hat{\unicode[STIX]{x1D719}}\rangle /\langle \hat{\unicode[STIX]{x1D719}}{\mathcal{M}}\hat{\unicode[STIX]{x1D719}}\rangle$
, and that the eigenvalue therefore deviates from the quotient only by terms second order in any deviation of the
$Q=\langle \hat{\unicode[STIX]{x1D719}}{\mathcal{L}}\hat{\unicode[STIX]{x1D719}}\rangle /\langle \hat{\unicode[STIX]{x1D719}}{\mathcal{M}}\hat{\unicode[STIX]{x1D719}}\rangle$
, and that the eigenvalue therefore deviates from the quotient only by terms second order in any deviation of the
![]() $\hat{\unicode[STIX]{x1D719}}$
used in evaluating it from the exact eigenmode. Applying this approach we substitute the shift mode into the full Poisson equation, multiply by
$\hat{\unicode[STIX]{x1D719}}$
used in evaluating it from the exact eigenmode. Applying this approach we substitute the shift mode into the full Poisson equation, multiply by
![]() $\hat{\unicode[STIX]{x1D719}}$
and integrate over space. This process annihilates the adiabatic terms leaving
$\hat{\unicode[STIX]{x1D719}}$
and integrate over space. This process annihilates the adiabatic terms leaving
The value of
![]() $\unicode[STIX]{x1D714}$
that satisfies this equation is then anticipated to be a good approximation to the eigen-frequency of the mode.
$\unicode[STIX]{x1D714}$
that satisfies this equation is then anticipated to be a good approximation to the eigen-frequency of the mode.
3.2 Force balance
A simple physical interpretation of (3.3) is that it is the conservation of momentum: balancing the electric field tension (left-hand side) with the electric force on the non-adiabatic electron perturbation (right-hand side). That makes it an overall approximate ‘kinematic’ constraint. Indeed, this interpretation is one heuristic explanation of the transverse instability mechanism. It is a balance between the effects of ‘jetting’ – the momentum transfer to particles because of the acceleration of the hole (Hutchinson & Zhou Reference Hutchinson and Zhou2016) – (right-hand side), and the stabilizing effects of electric field tension (left-hand side). We shall see shortly that in most circumstances the jetting is the predominant term and the stability boundary is approximately where the jetting is reduced to zero.
We can obtain this equation directly through force considerations without any immediate assumptions about the perturbation eigenmode shape, as follows. Force balance requires the total first-order (
![]() $z$
-direction) force exerted by the electric field to be zero, because the electric field of a solitary potential structure is incapable of sustaining any net momentum transfer. Denoting the charge density by
$z$
-direction) force exerted by the electric field to be zero, because the electric field of a solitary potential structure is incapable of sustaining any net momentum transfer. Denoting the charge density by
![]() $\unicode[STIX]{x1D70C}$
, this is
$\unicode[STIX]{x1D70C}$
, this is
![]() $E_{0}\unicode[STIX]{x1D70C}_{1}$
plus
$E_{0}\unicode[STIX]{x1D70C}_{1}$
plus
![]() $E_{1}\unicode[STIX]{x1D70C}_{0}$
spatially integrated over the hole. These two forces (summed over species) are equal and opposite for a straight (
$E_{1}\unicode[STIX]{x1D70C}_{0}$
spatially integrated over the hole. These two forces (summed over species) are equal and opposite for a straight (
![]() $k=0$
) isolated hole because,
$k=0$
) isolated hole because,
Integrating by parts the final form of (3.4) noting that
![]() $\unicode[STIX]{x1D70C}_{0}$
is a function of
$\unicode[STIX]{x1D70C}_{0}$
is a function of
![]() $\unicode[STIX]{x1D719}_{0}$
, we find
$\unicode[STIX]{x1D719}_{0}$
, we find
A hole with
![]() $y$
-variation (
$y$
-variation (
![]() $k\neq 0$
) has an additional term in
$k\neq 0$
) has an additional term in
![]() $\unicode[STIX]{x1D70C}_{1}$
, arising from
$\unicode[STIX]{x1D70C}_{1}$
, arising from
![]() $\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D719}_{1}/\unicode[STIX]{x2202}y^{2}=-k^{2}\unicode[STIX]{x1D719}_{1}$
. Including it we get
$\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D719}_{1}/\unicode[STIX]{x2202}y^{2}=-k^{2}\unicode[STIX]{x1D719}_{1}$
. Including it we get
The term in the square brackets is manifestly the non-adiabatic charge density
![]() $q_{e}{\tilde{n}}=q_{e}\int \tilde{f}\,\text{d}v$
. Notice that because
$q_{e}{\tilde{n}}=q_{e}\int \tilde{f}\,\text{d}v$
. Notice that because
![]() $\unicode[STIX]{x1D719}_{0}$
is symmetric, this equation selects the antisymmetric part of
$\unicode[STIX]{x1D719}_{0}$
is symmetric, this equation selects the antisymmetric part of
![]() $\unicode[STIX]{x1D719}_{1}$
. For a shift mode it is equivalent to the form
$\unicode[STIX]{x1D719}_{1}$
. For a shift mode it is equivalent to the form
![]() $\int \unicode[STIX]{x1D719}_{1}^{\ast }\tilde{f}\,\text{d}^{3}v\,\text{d}^{3}x$
(whose variational Euler equation is the eigen-problem). The right-hand side becomes
$\int \unicode[STIX]{x1D719}_{1}^{\ast }\tilde{f}\,\text{d}^{3}v\,\text{d}^{3}x$
(whose variational Euler equation is the eigen-problem). The right-hand side becomes
![]() $F_{E}=\unicode[STIX]{x0394}k^{2}\int \unicode[STIX]{x1D716}_{0}(\text{d}\unicode[STIX]{x1D719}_{0}/\text{d}z)^{2}\,\text{d}z$
, which can be thought of as arising from the transfer of
$F_{E}=\unicode[STIX]{x0394}k^{2}\int \unicode[STIX]{x1D716}_{0}(\text{d}\unicode[STIX]{x1D719}_{0}/\text{d}z)^{2}\,\text{d}z$
, which can be thought of as arising from the transfer of
![]() $z$
-momentum in the
$z$
-momentum in the
![]() $y$
-direction via the electric field off-diagonal components of the Maxwell stress tensor (
$y$
-direction via the electric field off-diagonal components of the Maxwell stress tensor (
![]() $(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}y)E_{y}E_{z}$
). It causes the hole to resist kinking as if it had a tension in the
$(\unicode[STIX]{x2202}/\unicode[STIX]{x2202}y)E_{y}E_{z}$
). It causes the hole to resist kinking as if it had a tension in the
![]() $y$
-direction.
$y$
-direction.
4 Unmagnetized plasmas
When there is no magnetic field, the transverse velocity
![]() $v_{y}$
of the equilibrium (unperturbed) orbit is independent of time, and the
$v_{y}$
of the equilibrium (unperturbed) orbit is independent of time, and the
![]() $\unicode[STIX]{x1D70F}$
dependence in the
$\unicode[STIX]{x1D70F}$
dependence in the
![]() $\tilde{f}$
expression (2.8) resides only in
$\tilde{f}$
expression (2.8) resides only in
![]() $\hat{\unicode[STIX]{x1D719}}(z(\unicode[STIX]{x1D70F}))$
and the exponent. In the
$\hat{\unicode[STIX]{x1D719}}(z(\unicode[STIX]{x1D70F}))$
and the exponent. In the
![]() $\unicode[STIX]{x1D70F}$
-integral
$\unicode[STIX]{x1D70F}$
-integral
![]() $y=y(\unicode[STIX]{x1D70F})=y(t)+v_{y}(\unicode[STIX]{x1D70F}-t)$
. We use time subscripts as shorthand for arguments (
$y=y(\unicode[STIX]{x1D70F})=y(t)+v_{y}(\unicode[STIX]{x1D70F}-t)$
. We use time subscripts as shorthand for arguments (
![]() $y(t)\equiv y_{t}$
etc.) and
$y(t)\equiv y_{t}$
etc.) and
![]() $\unicode[STIX]{x1D714}^{\prime }=\unicode[STIX]{x1D714}-kv_{y}$
to denote the frequency felt by the
$\unicode[STIX]{x1D714}^{\prime }=\unicode[STIX]{x1D714}-kv_{y}$
to denote the frequency felt by the
![]() $y$
-moving particle. Then we can write
$y$
-moving particle. Then we can write
where
which is independent of
![]() $t$
, but not of the final position on the orbit
$t$
, but not of the final position on the orbit
![]() $z_{t}$
. All positions and velocities appearing here, and from now on, are for the unperturbed orbit.
$z_{t}$
. All positions and velocities appearing here, and from now on, are for the unperturbed orbit.
4.1 Shift mode perturbed distribution
Now specialize to the case when the eigenmode is the shift mode
![]() $\hat{\unicode[STIX]{x1D719}}(z(\unicode[STIX]{x1D70F}))=-\unicode[STIX]{x0394}(\text{d}\unicode[STIX]{x1D719}_{0}/\text{d}z)$
. Using
$\hat{\unicode[STIX]{x1D719}}(z(\unicode[STIX]{x1D70F}))=-\unicode[STIX]{x0394}(\text{d}\unicode[STIX]{x1D719}_{0}/\text{d}z)$
. Using
we have
For a passing particle it is better to write
![]() $v_{\infty }$
for the velocity at
$v_{\infty }$
for the velocity at
![]() $\unicode[STIX]{x1D70F}\rightarrow \pm \infty$
on the orbit under consideration and then
$\unicode[STIX]{x1D70F}\rightarrow \pm \infty$
on the orbit under consideration and then
![]() $\text{d}v_{z}/\text{d}\unicode[STIX]{x1D70F}=(\text{d}/\text{d}\unicode[STIX]{x1D70F})(v_{z}-v_{\infty })$
so that
$\text{d}v_{z}/\text{d}\unicode[STIX]{x1D70F}=(\text{d}/\text{d}\unicode[STIX]{x1D70F})(v_{z}-v_{\infty })$
so that
The advantage of this form is that
![]() $(v_{z}-v_{\infty })$
is zero outside the hole so the integral has a finite domain. For trapped particles this same form applies provided that
$(v_{z}-v_{\infty })$
is zero outside the hole so the integral has a finite domain. For trapped particles this same form applies provided that
![]() $\unicode[STIX]{x1D714}^{\prime }$
has a positive imaginary part that ensures convergence and eliminates the lower limit contribution. Taking
$\unicode[STIX]{x1D714}^{\prime }$
has a positive imaginary part that ensures convergence and eliminates the lower limit contribution. Taking
![]() $v_{\infty }=0$
is more convenient for trapped particles.
$v_{\infty }=0$
is more convenient for trapped particles.
In any case, the first (integrated) term
![]() $(v_{z}-v_{\infty })$
expresses the effect of an essentially rigid velocity shift of the trapped distribution function, because it gives rise to a term in
$(v_{z}-v_{\infty })$
expresses the effect of an essentially rigid velocity shift of the trapped distribution function, because it gives rise to a term in
![]() $\tilde{f}$
$\tilde{f}$
where
![]() $v_{\text{hole}}=-\text{i}\unicode[STIX]{x1D714}^{\prime }\unicode[STIX]{x1D6E5}=\dot{\unicode[STIX]{x1D6E5}}$
is the hole incremental parallel velocity (observed in the
$v_{\text{hole}}=-\text{i}\unicode[STIX]{x1D714}^{\prime }\unicode[STIX]{x1D6E5}=\dot{\unicode[STIX]{x1D6E5}}$
is the hole incremental parallel velocity (observed in the
![]() $v_{y}$
frame). The term involving
$v_{y}$
frame). The term involving
![]() $v_{y}(\unicode[STIX]{x2202}f_{0}/\unicode[STIX]{x2202}W_{\bot })=\unicode[STIX]{x2202}f_{0}/m_{e}\unicode[STIX]{x2202}v_{y}$
is zero when integrated
$v_{y}(\unicode[STIX]{x2202}f_{0}/\unicode[STIX]{x2202}W_{\bot })=\unicode[STIX]{x2202}f_{0}/m_{e}\unicode[STIX]{x2202}v_{y}$
is zero when integrated
![]() $\text{d}v_{y}$
.
$\text{d}v_{y}$
.
A natural notation for the other term, because it has dimensions of velocity, is to denote it
![]() $\unicode[STIX]{x1D714}^{\prime }\tilde{L}$
with
$\unicode[STIX]{x1D714}^{\prime }\tilde{L}$
with
Although
![]() $\unicode[STIX]{x1D714}^{\prime }\tilde{L}$
is locally of higher order in the transit time, it cannot be simply ignored at positions outside the hole, because all the other terms in
$\unicode[STIX]{x1D714}^{\prime }\tilde{L}$
is locally of higher order in the transit time, it cannot be simply ignored at positions outside the hole, because all the other terms in
![]() $\unicode[STIX]{x1D6F7}$
there are zero. It in fact gives rise to the net perturbation
$\unicode[STIX]{x1D6F7}$
there are zero. It in fact gives rise to the net perturbation
![]() $\tilde{f}$
that crosses the outer boundary of the hole region. In other words, it is the source of the jetting perturbation. Besides which, when we are dealing with situations where
$\tilde{f}$
that crosses the outer boundary of the hole region. In other words, it is the source of the jetting perturbation. Besides which, when we are dealing with situations where
![]() $\unicode[STIX]{x1D714}^{\prime }$
times the transit time is not small, the
$\unicode[STIX]{x1D714}^{\prime }$
times the transit time is not small, the
![]() $\tilde{L}$
term contains all the resulting new behaviour, and it is the thing that is hard to calculate.
$\tilde{L}$
term contains all the resulting new behaviour, and it is the thing that is hard to calculate.
4.2 Shift mode rigid velocity shift contributes no force
It is helpful to eliminate
![]() $\unicode[STIX]{x1D719}_{0}$
from the shift mode expressions by using the orbit equilibrium relation equation (4.3), allowing us to express spatial variations in terms of
$\unicode[STIX]{x1D719}_{0}$
from the shift mode expressions by using the orbit equilibrium relation equation (4.3), allowing us to express spatial variations in terms of
![]() $v_{z}$
. It is also helpful for passing particles to transform distribution
$v_{z}$
. It is also helpful for passing particles to transform distribution
![]() $v_{z}$
-integrals into
$v_{z}$
-integrals into
![]() $v_{\infty }$
-integrals. Then at constant
$v_{\infty }$
-integrals. Then at constant
![]() $z$
(and
$z$
(and
![]() $\unicode[STIX]{x1D719}$
)
$\unicode[STIX]{x1D719}$
)
Moreover, Vlasov’s equation means
![]() $f_{0}(v_{z})=f_{\infty }(v_{\infty })$
.
$f_{0}(v_{z})=f_{\infty }(v_{\infty })$
.
The non-adiabatic density perturbation
![]() ${\tilde{n}}=\int \tilde{f}\,\text{d}^{3}v$
acquires a contribution
${\tilde{n}}=\int \tilde{f}\,\text{d}^{3}v$
acquires a contribution
![]() ${\tilde{n}}_{v}$
from the first term
${\tilde{n}}_{v}$
from the first term
![]() $(v_{z}-v_{\infty })$
of (4.5). However, its contribution to the total force (integrated over the hole) is zero because
$(v_{z}-v_{\infty })$
of (4.5). However, its contribution to the total force (integrated over the hole) is zero because
and so
 $$\begin{eqnarray}\displaystyle \tilde{F}_{v}\equiv \int \!-q_{e}\frac{\text{d}\unicode[STIX]{x1D719}_{0}}{\text{d}z}{\tilde{n}}_{v}\,\text{d}z & = & \displaystyle m_{e}\text{i}\unicode[STIX]{x1D714}^{\prime }\unicode[STIX]{x1D6E5}\int \int v_{z}\frac{\text{d}v_{z}}{\text{d}z}\frac{\unicode[STIX]{x2202}f_{\infty }}{\unicode[STIX]{x2202}v_{\infty }}\left(1-\frac{v_{\infty }}{v_{z}}\right)\text{d}v_{\infty }\,\text{d}z\nonumber\\ \displaystyle & = & \displaystyle m_{e}\text{i}\unicode[STIX]{x1D714}^{\prime }\unicode[STIX]{x1D6E5}\int \frac{\unicode[STIX]{x2202}f_{\infty }}{\unicode[STIX]{x2202}v_{\infty }}\left[\int v_{z}\left(1-\frac{v_{\infty }}{v_{z}}\right)\text{d}v_{z}\right]\text{d}v_{\infty }=0.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \tilde{F}_{v}\equiv \int \!-q_{e}\frac{\text{d}\unicode[STIX]{x1D719}_{0}}{\text{d}z}{\tilde{n}}_{v}\,\text{d}z & = & \displaystyle m_{e}\text{i}\unicode[STIX]{x1D714}^{\prime }\unicode[STIX]{x1D6E5}\int \int v_{z}\frac{\text{d}v_{z}}{\text{d}z}\frac{\unicode[STIX]{x2202}f_{\infty }}{\unicode[STIX]{x2202}v_{\infty }}\left(1-\frac{v_{\infty }}{v_{z}}\right)\text{d}v_{\infty }\,\text{d}z\nonumber\\ \displaystyle & = & \displaystyle m_{e}\text{i}\unicode[STIX]{x1D714}^{\prime }\unicode[STIX]{x1D6E5}\int \frac{\unicode[STIX]{x2202}f_{\infty }}{\unicode[STIX]{x2202}v_{\infty }}\left[\int v_{z}\left(1-\frac{v_{\infty }}{v_{z}}\right)\text{d}v_{z}\right]\text{d}v_{\infty }=0.\end{eqnarray}$$
The same annihilation will occur for any quantity that can be rendered into the form of a spatial integral
![]() $(\text{d}v_{z}/\text{d}z)\text{d}z\rightarrow \text{d}v_{z}$
(the square bracket here, which is zero) when all the
$(\text{d}v_{z}/\text{d}z)\text{d}z\rightarrow \text{d}v_{z}$
(the square bracket here, which is zero) when all the
![]() $z$
-dependence of the integrand is in
$z$
-dependence of the integrand is in
![]() $v_{z}$
. This proof is equally valid for trapped particles as for passing. Therefore for momentum balance purposes we can ignore
$v_{z}$
. This proof is equally valid for trapped particles as for passing. Therefore for momentum balance purposes we can ignore
![]() $\tilde{F}_{v}$
and
$\tilde{F}_{v}$
and
![]() ${\tilde{n}}_{v}$
.
${\tilde{n}}_{v}$
.
The second term of equation (4.5), i.e.
![]() $\unicode[STIX]{x1D714}^{\prime }\tilde{L}$
, is not of this form and gives non-zero total force. From now on, we shall consider only shift modes and use
$\unicode[STIX]{x1D714}^{\prime }\tilde{L}$
, is not of this form and gives non-zero total force. From now on, we shall consider only shift modes and use
![]() $\unicode[STIX]{x1D6F7}$
to denote just
$\unicode[STIX]{x1D6F7}$
to denote just
![]() $\unicode[STIX]{x1D6E5}(m_{e}/q_{e})\unicode[STIX]{x1D714}^{\prime }\tilde{L}$
.
$\unicode[STIX]{x1D6E5}(m_{e}/q_{e})\unicode[STIX]{x1D714}^{\prime }\tilde{L}$
.
4.3 Low-frequency jetting
Major simplification of
![]() $\tilde{L}$
occurs for passing particles when
$\tilde{L}$
occurs for passing particles when
![]() $\unicode[STIX]{x1D714}^{\prime }$
is much smaller than the inverse transit time of the particles through the hole, because then the
$\unicode[STIX]{x1D714}^{\prime }$
is much smaller than the inverse transit time of the particles through the hole, because then the
![]() $\text{e}^{\text{i}\unicode[STIX]{x1D714}^{\prime }(\unicode[STIX]{x1D70F}-t)}$
term can be taken to be unity. We defer integration
$\text{e}^{\text{i}\unicode[STIX]{x1D714}^{\prime }(\unicode[STIX]{x1D70F}-t)}$
term can be taken to be unity. We defer integration
![]() $\text{d}^{2}v_{\bot }$
over the perpendicular velocities and regard
$\text{d}^{2}v_{\bot }$
over the perpendicular velocities and regard
![]() $\unicode[STIX]{x1D714}^{\prime }$
as fixed for now. The resulting contributionFootnote
2
to the perturbed density from the
$\unicode[STIX]{x1D714}^{\prime }$
as fixed for now. The resulting contributionFootnote
2
to the perturbed density from the
![]() $\unicode[STIX]{x2202}f_{0}/\unicode[STIX]{x2202}W_{\Vert }$
term is
$\unicode[STIX]{x2202}f_{0}/\unicode[STIX]{x2202}W_{\Vert }$
term is
 $$\begin{eqnarray}\displaystyle \frac{\text{d}{\tilde{n}}_{p}}{\text{d}^{2}v_{\bot }} & = & \displaystyle \int m_{e}\text{i}\unicode[STIX]{x1D714}^{\prime }\frac{\unicode[STIX]{x2202}f_{0}}{\unicode[STIX]{x2202}W_{\Vert }}\unicode[STIX]{x1D6E5}\text{i}\unicode[STIX]{x1D714}^{\prime }\int _{z_{s}}^{z}(v_{z^{\prime }}-v_{\infty })\frac{\text{d}z^{\prime }}{v_{z^{\prime }}}\,\text{d}v_{z}\nonumber\\ \displaystyle & = & \displaystyle -\unicode[STIX]{x1D714}^{\prime 2}\unicode[STIX]{x1D6E5}\int \frac{\unicode[STIX]{x2202}f_{\infty }}{\unicode[STIX]{x2202}v_{\infty }}\int _{z_{s}}^{z}\left(1-\frac{v_{\infty }}{v_{z^{\prime }}}\right)\text{d}z^{\prime }\,\frac{\text{d}v_{\infty }}{v_{z}}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{\text{d}{\tilde{n}}_{p}}{\text{d}^{2}v_{\bot }} & = & \displaystyle \int m_{e}\text{i}\unicode[STIX]{x1D714}^{\prime }\frac{\unicode[STIX]{x2202}f_{0}}{\unicode[STIX]{x2202}W_{\Vert }}\unicode[STIX]{x1D6E5}\text{i}\unicode[STIX]{x1D714}^{\prime }\int _{z_{s}}^{z}(v_{z^{\prime }}-v_{\infty })\frac{\text{d}z^{\prime }}{v_{z^{\prime }}}\,\text{d}v_{z}\nonumber\\ \displaystyle & = & \displaystyle -\unicode[STIX]{x1D714}^{\prime 2}\unicode[STIX]{x1D6E5}\int \frac{\unicode[STIX]{x2202}f_{\infty }}{\unicode[STIX]{x2202}v_{\infty }}\int _{z_{s}}^{z}\left(1-\frac{v_{\infty }}{v_{z^{\prime }}}\right)\text{d}z^{\prime }\,\frac{\text{d}v_{\infty }}{v_{z}}.\end{eqnarray}$$
Here the lower limit of the
![]() $z^{\prime }$
-integral
$z^{\prime }$
-integral
![]() $z_{s}$
is the start of the orbit, which depends on the sign of
$z_{s}$
is the start of the orbit, which depends on the sign of
![]() $v$
, which we will denote
$v$
, which we will denote
![]() $\unicode[STIX]{x1D70E}_{v}$
.Footnote
3
Contributions come only from places with
$\unicode[STIX]{x1D70E}_{v}$
.Footnote
3
Contributions come only from places with
![]() $v_{z}\neq v_{\infty }$
i.e.
$v_{z}\neq v_{\infty }$
i.e.
![]() $\unicode[STIX]{x1D719}\neq 0$
, so
$\unicode[STIX]{x1D719}\neq 0$
, so
![]() $|z_{s}|$
must exceed the extent of the hole but need not actually be
$|z_{s}|$
must exceed the extent of the hole but need not actually be
![]() $\infty$
. We denote the other end position of an entire spatial integral as
$\infty$
. We denote the other end position of an entire spatial integral as
![]() $z_{f}$
(finish of orbit).
$z_{f}$
(finish of orbit).
The passing particle force is then
 $$\begin{eqnarray}\displaystyle \frac{\text{d}\tilde{F}_{p}}{\text{d}^{2}v_{\bot }} & = & \displaystyle \unicode[STIX]{x1D70E}_{v}\int _{z_{s}}^{z_{f}}-q_{e}\frac{\text{d}\unicode[STIX]{x1D719}_{0}}{\text{d}z}\frac{\text{d}{\tilde{n}}_{p}}{\text{d}^{2}v_{\bot }}\,\text{d}z\nonumber\\ \displaystyle & = & \displaystyle -m_{e}\unicode[STIX]{x1D714}^{\prime 2}\unicode[STIX]{x1D6E5}\unicode[STIX]{x1D70E}_{v}\int _{z_{s}}^{z_{f}}v_{z}\frac{\text{d}v_{z}}{\text{d}z}\int \frac{\unicode[STIX]{x2202}f_{\infty }}{\unicode[STIX]{x2202}v_{\infty }}\int _{z_{s}}^{z}\left(1-\frac{v_{\infty }}{v_{z^{\prime }}}\right)\text{d}z^{\prime }\frac{\text{d}v_{\infty }}{v_{z}}\,\text{d}z\nonumber\\ \displaystyle & = & \displaystyle -m_{e}\unicode[STIX]{x1D714}^{\prime 2}\unicode[STIX]{x1D6E5}\int \frac{\unicode[STIX]{x2202}f_{\infty }}{\unicode[STIX]{x2202}v_{\infty }}\unicode[STIX]{x1D70E}_{v}\int _{z_{s}}^{z_{f}}\frac{\text{d}v_{z}}{\text{d}z}\int _{z_{s}}^{z}\left(1-\frac{v_{\infty }}{v_{z^{\prime }}}\right)\text{d}z^{\prime }\,\text{d}z\,\text{d}v_{\infty }.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{\text{d}\tilde{F}_{p}}{\text{d}^{2}v_{\bot }} & = & \displaystyle \unicode[STIX]{x1D70E}_{v}\int _{z_{s}}^{z_{f}}-q_{e}\frac{\text{d}\unicode[STIX]{x1D719}_{0}}{\text{d}z}\frac{\text{d}{\tilde{n}}_{p}}{\text{d}^{2}v_{\bot }}\,\text{d}z\nonumber\\ \displaystyle & = & \displaystyle -m_{e}\unicode[STIX]{x1D714}^{\prime 2}\unicode[STIX]{x1D6E5}\unicode[STIX]{x1D70E}_{v}\int _{z_{s}}^{z_{f}}v_{z}\frac{\text{d}v_{z}}{\text{d}z}\int \frac{\unicode[STIX]{x2202}f_{\infty }}{\unicode[STIX]{x2202}v_{\infty }}\int _{z_{s}}^{z}\left(1-\frac{v_{\infty }}{v_{z^{\prime }}}\right)\text{d}z^{\prime }\frac{\text{d}v_{\infty }}{v_{z}}\,\text{d}z\nonumber\\ \displaystyle & = & \displaystyle -m_{e}\unicode[STIX]{x1D714}^{\prime 2}\unicode[STIX]{x1D6E5}\int \frac{\unicode[STIX]{x2202}f_{\infty }}{\unicode[STIX]{x2202}v_{\infty }}\unicode[STIX]{x1D70E}_{v}\int _{z_{s}}^{z_{f}}\frac{\text{d}v_{z}}{\text{d}z}\int _{z_{s}}^{z}\left(1-\frac{v_{\infty }}{v_{z^{\prime }}}\right)\text{d}z^{\prime }\,\text{d}z\,\text{d}v_{\infty }.\end{eqnarray}$$
Now we do the
![]() $\text{d}z$
integral by parts, making it
$\text{d}z$
integral by parts, making it
Reversing again the order of integration, we obtain a
![]() $\text{d}v_{\infty }$
integral that can be done by parts
$\text{d}v_{\infty }$
integral that can be done by parts
where
![]() $v_{z0}$
is the absolute value of
$v_{z0}$
is the absolute value of
![]() $v_{z}$
at the separatrix, and
$v_{z}$
at the separatrix, and
![]() $f_{s}$
is the distribution function on the separatrix. The leading term arises from the sign discontinuity of
$f_{s}$
is the distribution function on the separatrix. The leading term arises from the sign discontinuity of
![]() $v_{z}$
at
$v_{z}$
at
![]() $v_{\infty }=0$
. Now
$v_{\infty }=0$
. Now
 $$\begin{eqnarray}\displaystyle \frac{\text{d}}{\text{d}v_{\infty }}\left[v_{z}\left(1-\frac{v_{\infty }}{v_{z}}\right)^{2}\right] & = & \displaystyle \left[\frac{v_{\infty }}{v_{z}}\left(1-\frac{v_{\infty }}{v_{z}}\right)-2\left(1-\frac{v_{\infty }^{2}}{v_{z}^{2}}\right)\right]\left(1-\frac{v_{\infty }}{v_{z}}\right)\nonumber\\ \displaystyle & = & \displaystyle -2+3\frac{v_{\infty }}{v_{z}}-\frac{v_{\infty }^{3}}{v_{z}^{3}}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{\text{d}}{\text{d}v_{\infty }}\left[v_{z}\left(1-\frac{v_{\infty }}{v_{z}}\right)^{2}\right] & = & \displaystyle \left[\frac{v_{\infty }}{v_{z}}\left(1-\frac{v_{\infty }}{v_{z}}\right)-2\left(1-\frac{v_{\infty }^{2}}{v_{z}^{2}}\right)\right]\left(1-\frac{v_{\infty }}{v_{z}}\right)\nonumber\\ \displaystyle & = & \displaystyle -2+3\frac{v_{\infty }}{v_{z}}-\frac{v_{\infty }^{3}}{v_{z}^{3}}.\end{eqnarray}$$
Hence
where
![]() $\unicode[STIX]{x1D70E}_{v}\int _{z_{s}}^{z_{f}}\text{d}z$
is simply
$\unicode[STIX]{x1D70E}_{v}\int _{z_{s}}^{z_{f}}\text{d}z$
is simply
![]() $\int \text{d}z$
. This agreesFootnote
4
with the prior kinematic calculation (Hutchinson & Zhou Reference Hutchinson and Zhou2016), except for the presence of the term
$\int \text{d}z$
. This agreesFootnote
4
with the prior kinematic calculation (Hutchinson & Zhou Reference Hutchinson and Zhou2016), except for the presence of the term
![]() $2f_{s}v_{z0}$
.
$2f_{s}v_{z0}$
.
The trapped particle contribution associated with
![]() $\unicode[STIX]{x2202}f/\unicode[STIX]{x2202}W_{\Vert }$
can be treated using the same sequence of partial integrations except that the
$\unicode[STIX]{x2202}f/\unicode[STIX]{x2202}W_{\Vert }$
can be treated using the same sequence of partial integrations except that the
![]() $v_{\infty }=0$
choice means we cannot adopt
$v_{\infty }=0$
choice means we cannot adopt
![]() $v_{\infty }$
as the velocity integration variable. The past orbit integral now extends to
$v_{\infty }$
as the velocity integration variable. The past orbit integral now extends to
![]() $\unicode[STIX]{x1D70F}=-\infty$
, because the orbit never escapes the hole, but assuming
$\unicode[STIX]{x1D70F}=-\infty$
, because the orbit never escapes the hole, but assuming
![]() $\unicode[STIX]{x1D714}$
to have a positive imaginary part, the integral converges and the lower limit can be ignoredFootnote
5
. The phase-space element
$\unicode[STIX]{x1D714}$
to have a positive imaginary part, the integral converges and the lower limit can be ignoredFootnote
5
. The phase-space element
![]() $(\unicode[STIX]{x2202}f/\unicode[STIX]{x2202}W_{\Vert })\text{d}W_{\Vert }=(\unicode[STIX]{x2202}f/\unicode[STIX]{x2202}v_{z})\,\text{d}v_{z}$
commutes with the
$(\unicode[STIX]{x2202}f/\unicode[STIX]{x2202}W_{\Vert })\text{d}W_{\Vert }=(\unicode[STIX]{x2202}f/\unicode[STIX]{x2202}v_{z})\,\text{d}v_{z}$
commutes with the
![]() $\text{d}z$
integral. We interpret
$\text{d}z$
integral. We interpret
![]() $\text{d}W_{\Vert }$
as implying summing over positive and negative velocities, so we can consider the
$\text{d}W_{\Vert }$
as implying summing over positive and negative velocities, so we can consider the
![]() $\text{d}z$
integral to be over the entire relevant orbit range in the positive direction (avoiding the need for
$\text{d}z$
integral to be over the entire relevant orbit range in the positive direction (avoiding the need for
![]() $\unicode[STIX]{x1D70E}_{v}$
).
$\unicode[STIX]{x1D70E}_{v}$
).
 $$\begin{eqnarray}\displaystyle \frac{\text{d}\tilde{F}_{t}}{\text{d}^{2}v_{\bot }} & = & \displaystyle m_{e}\unicode[STIX]{x1D6E5}\int v_{z}\frac{\text{d}v_{z}}{\text{d}z}\int \text{i}\unicode[STIX]{x1D714}^{\prime }\frac{\unicode[STIX]{x2202}f_{0}}{\unicode[STIX]{x2202}v_{z}}\text{i}\unicode[STIX]{x1D714}^{\prime }\int _{z_{s}}^{z}\,\text{d}z^{\prime }\frac{\text{d}v_{z}}{v_{z}}\,\text{d}z\nonumber\\ \displaystyle & = & \displaystyle -m_{e}\unicode[STIX]{x1D714}^{\prime 2}\unicode[STIX]{x1D6E5}\int \frac{\unicode[STIX]{x2202}f_{0}}{\unicode[STIX]{x2202}v_{z}}\int \frac{\text{d}v_{z}}{\text{d}z}\int _{z_{s}}^{z}\text{d}z^{\prime }\,\text{d}z\,\text{d}v_{z}.\nonumber\\ \displaystyle & = & \displaystyle m_{e}\unicode[STIX]{x1D714}^{\prime 2}\unicode[STIX]{x1D6E5}\int \frac{\unicode[STIX]{x2202}f_{0}}{\unicode[STIX]{x2202}v_{z}}\int v_{z}\,\text{d}z\,\text{d}v_{z}=m_{e}\unicode[STIX]{x1D714}^{\prime 2}\unicode[STIX]{x1D6E5}\int \int \frac{\unicode[STIX]{x2202}f_{0}}{\unicode[STIX]{x2202}v_{z}}v_{z}\,\text{d}v_{z}\,\text{d}z\nonumber\\ \displaystyle & = & \displaystyle m_{e}\unicode[STIX]{x1D714}^{\prime 2}\unicode[STIX]{x1D6E5}\int \left[2f_{s}v_{z0}-\int _{-v_{z0}}^{v_{z0}}f_{0}\,\text{d}v_{z}\right]\text{d}z.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{\text{d}\tilde{F}_{t}}{\text{d}^{2}v_{\bot }} & = & \displaystyle m_{e}\unicode[STIX]{x1D6E5}\int v_{z}\frac{\text{d}v_{z}}{\text{d}z}\int \text{i}\unicode[STIX]{x1D714}^{\prime }\frac{\unicode[STIX]{x2202}f_{0}}{\unicode[STIX]{x2202}v_{z}}\text{i}\unicode[STIX]{x1D714}^{\prime }\int _{z_{s}}^{z}\,\text{d}z^{\prime }\frac{\text{d}v_{z}}{v_{z}}\,\text{d}z\nonumber\\ \displaystyle & = & \displaystyle -m_{e}\unicode[STIX]{x1D714}^{\prime 2}\unicode[STIX]{x1D6E5}\int \frac{\unicode[STIX]{x2202}f_{0}}{\unicode[STIX]{x2202}v_{z}}\int \frac{\text{d}v_{z}}{\text{d}z}\int _{z_{s}}^{z}\text{d}z^{\prime }\,\text{d}z\,\text{d}v_{z}.\nonumber\\ \displaystyle & = & \displaystyle m_{e}\unicode[STIX]{x1D714}^{\prime 2}\unicode[STIX]{x1D6E5}\int \frac{\unicode[STIX]{x2202}f_{0}}{\unicode[STIX]{x2202}v_{z}}\int v_{z}\,\text{d}z\,\text{d}v_{z}=m_{e}\unicode[STIX]{x1D714}^{\prime 2}\unicode[STIX]{x1D6E5}\int \int \frac{\unicode[STIX]{x2202}f_{0}}{\unicode[STIX]{x2202}v_{z}}v_{z}\,\text{d}v_{z}\,\text{d}z\nonumber\\ \displaystyle & = & \displaystyle m_{e}\unicode[STIX]{x1D714}^{\prime 2}\unicode[STIX]{x1D6E5}\int \left[2f_{s}v_{z0}-\int _{-v_{z0}}^{v_{z0}}f_{0}\,\text{d}v_{z}\right]\text{d}z.\end{eqnarray}$$
The term
![]() $2f_{s}v_{z0}$
, which arises from the limits of integration
$2f_{s}v_{z0}$
, which arises from the limits of integration
![]() $\text{d}v_{z}$
at the separatrix, cancels the similar term in the passing particle force expression (4.16). Without that term, the trapped force can be considered to be simply the inertia of the trapped particles.
$\text{d}v_{z}$
at the separatrix, cancels the similar term in the passing particle force expression (4.16). Without that term, the trapped force can be considered to be simply the inertia of the trapped particles.
When
![]() $k=0$
,
$k=0$
,
![]() $\unicode[STIX]{x1D714}^{\prime }=\unicode[STIX]{x1D714}$
, we can integrate
$\unicode[STIX]{x1D714}^{\prime }=\unicode[STIX]{x1D714}$
, we can integrate
![]() $\text{d}^{2}v_{\bot }$
, and no
$\text{d}^{2}v_{\bot }$
, and no
![]() $\unicode[STIX]{x2202}f/\unicode[STIX]{x2202}W_{\bot }$
term need be considered. Then we find
$\unicode[STIX]{x2202}f/\unicode[STIX]{x2202}W_{\bot }$
term need be considered. Then we find
where
![]() $f$
here is the (unperturbed) one-dimensional (
$f$
here is the (unperturbed) one-dimensional (
![]() $v_{z}$
)-distribution function. This force expression is in full agreement with the prior one-dimensional kinematic calculation (Hutchinson & Zhou Reference Hutchinson and Zhou2016).
$v_{z}$
)-distribution function. This force expression is in full agreement with the prior one-dimensional kinematic calculation (Hutchinson & Zhou Reference Hutchinson and Zhou2016).
We observe that since an electron hole has no net electric charge, for immobile ions the sum of the trapped electron charge and the integrated difference of the passing electron charge density from its external value must be zero. This allows us to deduce an alternative expression for the trapped particle number:
4.4 Low-frequency momentum balance including
 $\unicode[STIX]{x2202}f/\unicode[STIX]{x2202}W_{\bot }$
terms
$\unicode[STIX]{x2202}f/\unicode[STIX]{x2202}W_{\bot }$
terms
Let us suppose that the external distribution is isotropic Maxwellian (and the hole is stationary in the Maxwellian frame). Then the
![]() $kv_{y}$
terms in
$kv_{y}$
terms in
![]() $\tilde{f}$
cancel each other for passing particles which has the effect of making one of the
$\tilde{f}$
cancel each other for passing particles which has the effect of making one of the
![]() $\unicode[STIX]{x1D714}^{\prime }$
terms in equation (4.16) just
$\unicode[STIX]{x1D714}^{\prime }$
terms in equation (4.16) just
![]() $\unicode[STIX]{x1D714}$
. No such cancellation occurs for the trapped particles because the sign of
$\unicode[STIX]{x1D714}$
. No such cancellation occurs for the trapped particles because the sign of
![]() $\text{d}f/\text{d}W_{\Vert }$
is reversed: the electron distribution is smaller at smaller
$\text{d}f/\text{d}W_{\Vert }$
is reversed: the electron distribution is smaller at smaller
![]() $v_{z}$
. For shallow holes for trapped particles
$v_{z}$
. For shallow holes for trapped particles
![]() $|\text{d}f/\text{d}W_{\Vert }|\gg |\text{d}f/\text{d}W_{\bot }|$
so the
$|\text{d}f/\text{d}W_{\Vert }|\gg |\text{d}f/\text{d}W_{\bot }|$
so the
![]() $\text{d}f/\text{d}W_{\bot }$
term hardly contributes. A simple way to account for it is to suppose that the distribution is of the Schamel type (Schamel Reference Schamel1979) having a parallel Maxwellian of negative temperature in the trapped region. In that case,
$\text{d}f/\text{d}W_{\bot }$
term hardly contributes. A simple way to account for it is to suppose that the distribution is of the Schamel type (Schamel Reference Schamel1979) having a parallel Maxwellian of negative temperature in the trapped region. In that case,
where
![]() $\unicode[STIX]{x1D6FD}$
is the inverse of the ratio (a negative quantity) of trapped parallel temperature to perpendicular. This ansatz is very convenient because it allows us simply to multiply
$\unicode[STIX]{x1D6FD}$
is the inverse of the ratio (a negative quantity) of trapped parallel temperature to perpendicular. This ansatz is very convenient because it allows us simply to multiply
![]() $kv_{y}(\unicode[STIX]{x2202}f/\unicode[STIX]{x2202}W_{\Vert })$
by
$kv_{y}(\unicode[STIX]{x2202}f/\unicode[STIX]{x2202}W_{\Vert })$
by
![]() $(1+1/|\unicode[STIX]{x1D6FD}|)$
to account for the
$(1+1/|\unicode[STIX]{x1D6FD}|)$
to account for the
![]() $\unicode[STIX]{x2202}f/\unicode[STIX]{x2202}W_{\bot }$
term. This extra factor accompanies all
$\unicode[STIX]{x2202}f/\unicode[STIX]{x2202}W_{\bot }$
term. This extra factor accompanies all
![]() $k^{2}$
terms. For a slow-moving hole,
$k^{2}$
terms. For a slow-moving hole,
![]() $-\unicode[STIX]{x1D6FD}\approx 1+(15/16)\sqrt{\unicode[STIX]{x03C0}T_{e}/e\unicode[STIX]{x1D713}}$
, which is large for a shallow hole (small
$-\unicode[STIX]{x1D6FD}\approx 1+(15/16)\sqrt{\unicode[STIX]{x03C0}T_{e}/e\unicode[STIX]{x1D713}}$
, which is large for a shallow hole (small
![]() $\unicode[STIX]{x1D713}$
). But the quantity
$\unicode[STIX]{x1D713}$
). But the quantity
![]() $1/|\unicode[STIX]{x1D6FD}|\approx 0.346$
is still only a moderate correction for a deep hole
$1/|\unicode[STIX]{x1D6FD}|\approx 0.346$
is still only a moderate correction for a deep hole
![]() $\unicode[STIX]{x1D713}=T_{e}/e$
.
$\unicode[STIX]{x1D713}=T_{e}/e$
.
We still need to integrate over
![]() $v_{y}$
to arrive at the total force. When we do so, first-order
$v_{y}$
to arrive at the total force. When we do so, first-order
![]() $kv_{y}$
terms coming from the cross-products
$kv_{y}$
terms coming from the cross-products
![]() $\unicode[STIX]{x1D714}kv_{y}$
integrate to zero for a symmetric
$\unicode[STIX]{x1D714}kv_{y}$
integrate to zero for a symmetric
![]() $f(v_{y})$
distribution. The passing particle force
$f(v_{y})$
distribution. The passing particle force
![]() $\tilde{F}_{p}$
then is unchanged in form except that only
$\tilde{F}_{p}$
then is unchanged in form except that only
![]() $\unicode[STIX]{x1D714}$
appears in it, not
$\unicode[STIX]{x1D714}$
appears in it, not
![]() $\unicode[STIX]{x1D714}^{\prime }$
. The trapped force
$\unicode[STIX]{x1D714}^{\prime }$
. The trapped force
![]() $\tilde{F}_{t}$
has an
$\tilde{F}_{t}$
has an
![]() $\unicode[STIX]{x1D714}^{2}$
term that adds to the passing as before, plus a
$\unicode[STIX]{x1D714}^{2}$
term that adds to the passing as before, plus a
![]() $k^{2}\langle v_{y}^{2}\rangle$
term that is otherwise of the same form as (4.17).
$k^{2}\langle v_{y}^{2}\rangle$
term that is otherwise of the same form as (4.17).
Consequently, using
![]() $\langle v_{y}^{2}\rangle =T_{y}/m_{e}$
, and considering
$\langle v_{y}^{2}\rangle =T_{y}/m_{e}$
, and considering
![]() $f$
to be the parallel distribution function, the full particle force can be taken as
$f$
to be the parallel distribution function, the full particle force can be taken as
 $$\begin{eqnarray}\displaystyle \tilde{F} & = & \displaystyle -m_{e}\unicode[STIX]{x1D6E5}\int \unicode[STIX]{x1D714}^{2}\left\{\int \left[-2+3\frac{v_{\infty }}{v_{z}}-\left(\frac{v_{\infty }}{v_{z}}\right)^{3}\right]f_{\infty }\,\text{d}v_{\infty }+\int _{-v_{z0}}^{v_{z0}}f\text{d}v_{z}\right\}\nonumber\\ \displaystyle & & \displaystyle \quad +\left(1+\frac{1}{|\unicode[STIX]{x1D6FD}|}\right)k^{2}\frac{T_{y}}{m_{e}}\left\{-2v_{s}f_{s}+\int _{-v_{z0}}^{v_{z0}}f\text{d}v_{z}\right\}\text{d}z.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \tilde{F} & = & \displaystyle -m_{e}\unicode[STIX]{x1D6E5}\int \unicode[STIX]{x1D714}^{2}\left\{\int \left[-2+3\frac{v_{\infty }}{v_{z}}-\left(\frac{v_{\infty }}{v_{z}}\right)^{3}\right]f_{\infty }\,\text{d}v_{\infty }+\int _{-v_{z0}}^{v_{z0}}f\text{d}v_{z}\right\}\nonumber\\ \displaystyle & & \displaystyle \quad +\left(1+\frac{1}{|\unicode[STIX]{x1D6FD}|}\right)k^{2}\frac{T_{y}}{m_{e}}\left\{-2v_{s}f_{s}+\int _{-v_{z0}}^{v_{z0}}f\text{d}v_{z}\right\}\text{d}z.\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & = & \displaystyle -m_{e}\unicode[STIX]{x1D6E5}\int \unicode[STIX]{x1D714}^{2}\left\{\int \left[-1+2\frac{v_{\infty }}{v_{z}}-\left(\frac{v_{\infty }}{v_{z}}\right)^{3}\right]f_{\infty }\,\text{d}v_{\infty }\right\}\nonumber\\ \displaystyle & & \displaystyle \quad +\left(1+\frac{1}{|\unicode[STIX]{x1D6FD}|}\right)k^{2}\frac{T_{y}}{m_{e}}\left\{\int _{-v_{z0}}^{v_{z0}}(f-f_{s})\,\text{d}v_{z}\right\}\text{d}z\nonumber\\ \displaystyle & = & \displaystyle m_{e}\unicode[STIX]{x1D6E5}n_{\infty }\int \left[\unicode[STIX]{x1D714}^{2}h(\unicode[STIX]{x1D712})+\left(1+\frac{1}{|\unicode[STIX]{x1D6FD}|}\right)k^{2}\frac{T_{y}}{m_{e}}g(\unicode[STIX]{x1D712})\right]\text{d}z.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & = & \displaystyle -m_{e}\unicode[STIX]{x1D6E5}\int \unicode[STIX]{x1D714}^{2}\left\{\int \left[-1+2\frac{v_{\infty }}{v_{z}}-\left(\frac{v_{\infty }}{v_{z}}\right)^{3}\right]f_{\infty }\,\text{d}v_{\infty }\right\}\nonumber\\ \displaystyle & & \displaystyle \quad +\left(1+\frac{1}{|\unicode[STIX]{x1D6FD}|}\right)k^{2}\frac{T_{y}}{m_{e}}\left\{\int _{-v_{z0}}^{v_{z0}}(f-f_{s})\,\text{d}v_{z}\right\}\text{d}z\nonumber\\ \displaystyle & = & \displaystyle m_{e}\unicode[STIX]{x1D6E5}n_{\infty }\int \left[\unicode[STIX]{x1D714}^{2}h(\unicode[STIX]{x1D712})+\left(1+\frac{1}{|\unicode[STIX]{x1D6FD}|}\right)k^{2}\frac{T_{y}}{m_{e}}g(\unicode[STIX]{x1D712})\right]\text{d}z.\end{eqnarray}$$
The curly brace expressions have been denoted by the dimensionless functions
![]() $h$
and
$h$
and
![]() $g$
, which depend upon potential
$g$
, which depend upon potential
![]() $\unicode[STIX]{x1D719}$
expressed in terms of
$\unicode[STIX]{x1D719}$
expressed in terms of
![]() $\unicode[STIX]{x1D712}^{2}=-q_{e}\unicode[STIX]{x1D719}/T_{e}=m_{e}v_{z0}^{2}/2T_{e}$
. They are both positive. In so far as the electric field stress is negligible, the dispersion relation is
$\unicode[STIX]{x1D712}^{2}=-q_{e}\unicode[STIX]{x1D719}/T_{e}=m_{e}v_{z0}^{2}/2T_{e}$
. They are both positive. In so far as the electric field stress is negligible, the dispersion relation is
![]() $\tilde{F}=0$
which immediately shows that
$\tilde{F}=0$
which immediately shows that
![]() $\unicode[STIX]{x1D714}^{2}=-(\langle g\rangle /\langle h\rangle )(1+1/|\unicode[STIX]{x1D6FD}|)k^{2}T_{y}/m_{e}$
, where
$\unicode[STIX]{x1D714}^{2}=-(\langle g\rangle /\langle h\rangle )(1+1/|\unicode[STIX]{x1D6FD}|)k^{2}T_{y}/m_{e}$
, where
![]() $\langle g\rangle$
and
$\langle g\rangle$
and
![]() $\langle h\rangle$
are the spatial averages of
$\langle h\rangle$
are the spatial averages of
![]() $g$
and
$g$
and
![]() $h$
. The frequency is therefore pure imaginary, one root being positive, which is a growing unstable perturbation.
$h$
. The frequency is therefore pure imaginary, one root being positive, which is a growing unstable perturbation.
For an unshifted Maxwellian
![]() $f_{\infty }$
, the velocity integrals needed for (4.22) can be carried out. They are
$f_{\infty }$
, the velocity integrals needed for (4.22) can be carried out. They are
and (using (4.19))
For small
![]() $\unicode[STIX]{x1D712}$
the power series is
$\unicode[STIX]{x1D712}$
the power series is
![]() $\text{erfc}(\unicode[STIX]{x1D712})=1-(2/\sqrt{\unicode[STIX]{x03C0}})[\unicode[STIX]{x1D712}-\unicode[STIX]{x1D712}^{3}/3+O(\unicode[STIX]{x1D712}^{5})]$
, so
$\text{erfc}(\unicode[STIX]{x1D712})=1-(2/\sqrt{\unicode[STIX]{x03C0}})[\unicode[STIX]{x1D712}-\unicode[STIX]{x1D712}^{3}/3+O(\unicode[STIX]{x1D712}^{5})]$
, so
![]() $h(\unicode[STIX]{x1D712})=\unicode[STIX]{x1D712}^{2}-(2/\sqrt{\unicode[STIX]{x03C0}})(4/3)\unicode[STIX]{x1D712}^{3}+O(\unicode[STIX]{x1D712}^{4})$
and
$h(\unicode[STIX]{x1D712})=\unicode[STIX]{x1D712}^{2}-(2/\sqrt{\unicode[STIX]{x03C0}})(4/3)\unicode[STIX]{x1D712}^{3}+O(\unicode[STIX]{x1D712}^{4})$
and
![]() $g(\unicode[STIX]{x1D712})=\unicode[STIX]{x1D712}^{2}-(2/\sqrt{\unicode[STIX]{x03C0}})(2/3)\unicode[STIX]{x1D712}^{3}+O(\unicode[STIX]{x1D712}^{4})$
. The ratio
$g(\unicode[STIX]{x1D712})=\unicode[STIX]{x1D712}^{2}-(2/\sqrt{\unicode[STIX]{x03C0}})(2/3)\unicode[STIX]{x1D712}^{3}+O(\unicode[STIX]{x1D712}^{4})$
. The ratio
![]() $g/h\rightarrow 1$
as
$g/h\rightarrow 1$
as
![]() $\unicode[STIX]{x1D712}\rightarrow 0$
; at
$\unicode[STIX]{x1D712}\rightarrow 0$
; at
![]() $\unicode[STIX]{x1D712}=1$
,
$\unicode[STIX]{x1D712}=1$
,
![]() $g/h=1.86$
and
$g/h=1.86$
and
![]() $\langle g\rangle /\langle h\rangle =1.63$
(for a
$\langle g\rangle /\langle h\rangle =1.63$
(for a
![]() $\text{sech}^{4}z$
shape potential).
$\text{sech}^{4}z$
shape potential).
The electric tension force when
![]() $\unicode[STIX]{x1D719}_{0}=\unicode[STIX]{x1D713}\,\text{sech}^{4}(z/4\unicode[STIX]{x1D706}_{D})$
can be evaluated as
$\unicode[STIX]{x1D719}_{0}=\unicode[STIX]{x1D713}\,\text{sech}^{4}(z/4\unicode[STIX]{x1D706}_{D})$
can be evaluated as
Therefore the full dispersion relation is
A crucial observation is that as
![]() $\unicode[STIX]{x1D713}\rightarrow 0$
,
$\unicode[STIX]{x1D713}\rightarrow 0$
,
![]() $g,h\rightarrow \unicode[STIX]{x1D712}^{2}\sim \unicode[STIX]{x1D713}$
, whereas the electric tension scales like
$g,h\rightarrow \unicode[STIX]{x1D712}^{2}\sim \unicode[STIX]{x1D713}$
, whereas the electric tension scales like
![]() $\unicode[STIX]{x1D713}^{2}$
. Therefore for shallow holes (
$\unicode[STIX]{x1D713}^{2}$
. Therefore for shallow holes (
![]() $\unicode[STIX]{x1D713}\ll eT_{e}$
) the
$\unicode[STIX]{x1D713}\ll eT_{e}$
) the
![]() $F_{E}$
term is ignorable. Even for a deep hole such as
$F_{E}$
term is ignorable. Even for a deep hole such as
![]() $\unicode[STIX]{x1D713}=eT_{e}$
, numerical evaluation shows that
$\unicode[STIX]{x1D713}=eT_{e}$
, numerical evaluation shows that
![]() $\int g(\unicode[STIX]{x1D712})\,\text{d}z=0.55\times 4\unicode[STIX]{x1D706}_{D}$
, which makes the
$\int g(\unicode[STIX]{x1D712})\,\text{d}z=0.55\times 4\unicode[STIX]{x1D706}_{D}$
, which makes the
![]() $g$
term 5.4 times larger than
$g$
term 5.4 times larger than
![]() $F_{E}$
. Therefore, for all but exceptionally deep holes,
$F_{E}$
. Therefore, for all but exceptionally deep holes,
![]() $F_{E}$
can be ignored for low-
$F_{E}$
can be ignored for low-
![]() $k$
modes.
$k$
modes.
In summary then, ignoring
![]() $F_{E}$
, the predicted instability at low
$F_{E}$
, the predicted instability at low
![]() $k$
, where the transit, or bounce, time of the electrons is short compared with
$k$
, where the transit, or bounce, time of the electrons is short compared with
![]() $1/\unicode[STIX]{x1D714}^{\prime }$
, is that the imaginary part of the frequency is
$1/\unicode[STIX]{x1D714}^{\prime }$
, is that the imaginary part of the frequency is
where the second square root factor is unity for shallow holes and rises only to 1.48 for
![]() $\unicode[STIX]{x1D713}\simeq T_{e}/e$
. (The real part of the frequency is zero.)
$\unicode[STIX]{x1D713}\simeq T_{e}/e$
. (The real part of the frequency is zero.)
In view of the proportionality of
![]() $\unicode[STIX]{x1D714}_{i}$
and
$\unicode[STIX]{x1D714}_{i}$
and
![]() $k$
, one expects that the fastest growing mode has large
$k$
, one expects that the fastest growing mode has large
![]() $k$
. However, the calculation so far is for low-
$k$
. However, the calculation so far is for low-
![]() $k$
. Therefore the observed growth rate in a simulation or in nature is anticipated to be at the upper end of the
$k$
. Therefore the observed growth rate in a simulation or in nature is anticipated to be at the upper end of the
![]() $k$
-range for which the low-
$k$
-range for which the low-
![]() $k$
approximations apply. We therefore need to analyse the breakdown of the low-
$k$
approximations apply. We therefore need to analyse the breakdown of the low-
![]() $k$
approximations, to find the behaviour of the fastest growing modes.
$k$
approximations, to find the behaviour of the fastest growing modes.
4.5 Full dispersion relation including finite transit time effects
In order to determine the behaviour at high-
![]() $k$
near the instability threshold, we must consider situations where the transit time is comparable to
$k$
near the instability threshold, we must consider situations where the transit time is comparable to
![]() $1/\unicode[STIX]{x1D714}^{\prime }$
. We must therefore abandon the low-
$1/\unicode[STIX]{x1D714}^{\prime }$
. We must therefore abandon the low-
![]() $k$
approximation and fully account for
$k$
approximation and fully account for
![]() $\unicode[STIX]{x1D714}^{\prime }$
in the integral
$\unicode[STIX]{x1D714}^{\prime }$
in the integral
![]() $\tilde{L}$
in (4.7). Rather than pursue further analytical approximation, numerical integration is adopted. Since this requires a quadruple integration over
$\tilde{L}$
in (4.7). Rather than pursue further analytical approximation, numerical integration is adopted. Since this requires a quadruple integration over
![]() $\unicode[STIX]{x1D70F}$
,
$\unicode[STIX]{x1D70F}$
,
![]() $v_{y}$
,
$v_{y}$
,
![]() $v_{z}$
and
$v_{z}$
and
![]() $z$
, which becomes computationally expensive if not done efficiently, it is helpful to recognize that one can actually combine the evaluations corresponding to all positions
$z$
, which becomes computationally expensive if not done efficiently, it is helpful to recognize that one can actually combine the evaluations corresponding to all positions
![]() $z$
into a single orbit integral
$z$
into a single orbit integral
![]() $\text{d}\unicode[STIX]{x1D70F}$
. In other words, one does not have to do a different orbit integral for every position
$\text{d}\unicode[STIX]{x1D70F}$
. In other words, one does not have to do a different orbit integral for every position
![]() $z$
for a certain parallel energy
$z$
for a certain parallel energy
![]() $v_{z}^{2}$
. That integral can be done once, accumulating values for all positions
$v_{z}^{2}$
. That integral can be done once, accumulating values for all positions
![]() $z$
and can be scaled to provide
$z$
and can be scaled to provide
![]() $\tilde{L}$
,
$\tilde{L}$
,
![]() $\unicode[STIX]{x1D6F7}$
and hence
$\unicode[STIX]{x1D6F7}$
and hence
![]() $\tilde{f}$
and the force contribution.
$\tilde{f}$
and the force contribution.
4.5.1 Evaluation of the past orbit integral for passing particles
For passing particles of specified
![]() $v_{\infty }$
, we perform spatial integrals on a uniform
$v_{\infty }$
, we perform spatial integrals on a uniform
![]() $z$
-grid, starting at a negative
$z$
-grid, starting at a negative
![]() $z$
position
$z$
position
![]() $z_{s}$
far enough outside the hole to have its integrand negligible. Call the past orbit time there
$z_{s}$
far enough outside the hole to have its integrand negligible. Call the past orbit time there
![]() $\unicode[STIX]{x1D70F}_{s}=0$
. For each succeeding position
$\unicode[STIX]{x1D70F}_{s}=0$
. For each succeeding position
![]() $z_{j}=z_{s}+j\unicode[STIX]{x1D6FF}z$
, we find its corresponding orbit time as
$z_{j}=z_{s}+j\unicode[STIX]{x1D6FF}z$
, we find its corresponding orbit time as
![]() $\unicode[STIX]{x1D70F}_{j+1}-\unicode[STIX]{x1D70F}_{j}=\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D70F}=\unicode[STIX]{x1D6FF}z(1/v_{j}+1/v_{j+1})/2$
which is an appropriate trapezoid increment for
$\unicode[STIX]{x1D70F}_{j+1}-\unicode[STIX]{x1D70F}_{j}=\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D70F}=\unicode[STIX]{x1D6FF}z(1/v_{j}+1/v_{j+1})/2$
which is an appropriate trapezoid increment for
![]() $\unicode[STIX]{x1D70F}=\int \text{d}z/v$
. The
$\unicode[STIX]{x1D70F}=\int \text{d}z/v$
. The
![]() $v_{j}$
depend only on the known potential
$v_{j}$
depend only on the known potential
![]() $\unicode[STIX]{x1D719}_{j}$
at
$\unicode[STIX]{x1D719}_{j}$
at
![]() $z_{j}$
, and on
$z_{j}$
, and on
![]() $v_{\infty }$
. The next value of
$v_{\infty }$
. The next value of
![]() $\tilde{L}\equiv \int _{\unicode[STIX]{x1D70F}_{s}}^{t}(v-v_{\infty })\text{i}\text{e}^{-\text{i}\unicode[STIX]{x1D714}^{\prime }(\unicode[STIX]{x1D70F}-t)}\,\text{d}\unicode[STIX]{x1D70F}$
is calculated writing
$\tilde{L}\equiv \int _{\unicode[STIX]{x1D70F}_{s}}^{t}(v-v_{\infty })\text{i}\text{e}^{-\text{i}\unicode[STIX]{x1D714}^{\prime }(\unicode[STIX]{x1D70F}-t)}\,\text{d}\unicode[STIX]{x1D70F}$
is calculated writing
![]() $v_{j+1/2}=(v_{j+1}+v_{j})/2$
and using
$v_{j+1/2}=(v_{j+1}+v_{j})/2$
and using
 $$\begin{eqnarray}\displaystyle \tilde{L}_{j+1}-\text{e}^{\text{i}\unicode[STIX]{x1D714}^{\prime }\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D70F}}\tilde{L}_{j} & {\approx} & \displaystyle (v_{j+1/2}-v_{\infty })\int _{\unicode[STIX]{x1D70F}_{j}}^{\unicode[STIX]{x1D70F}_{j+1}}\text{i}\text{e}^{-\text{i}\unicode[STIX]{x1D714}^{\prime }(\unicode[STIX]{x1D70F}-\unicode[STIX]{x1D70F}_{j+1})}\,\text{d}\unicode[STIX]{x1D70F}\nonumber\\ \displaystyle & = & \displaystyle -(v_{j+1/2}-v_{\infty })\frac{1}{\unicode[STIX]{x1D714}^{\prime }}[1-\text{e}^{\text{i}\unicode[STIX]{x1D714}^{\prime }\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D70F}}].\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \tilde{L}_{j+1}-\text{e}^{\text{i}\unicode[STIX]{x1D714}^{\prime }\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D70F}}\tilde{L}_{j} & {\approx} & \displaystyle (v_{j+1/2}-v_{\infty })\int _{\unicode[STIX]{x1D70F}_{j}}^{\unicode[STIX]{x1D70F}_{j+1}}\text{i}\text{e}^{-\text{i}\unicode[STIX]{x1D714}^{\prime }(\unicode[STIX]{x1D70F}-\unicode[STIX]{x1D70F}_{j+1})}\,\text{d}\unicode[STIX]{x1D70F}\nonumber\\ \displaystyle & = & \displaystyle -(v_{j+1/2}-v_{\infty })\frac{1}{\unicode[STIX]{x1D714}^{\prime }}[1-\text{e}^{\text{i}\unicode[STIX]{x1D714}^{\prime }\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D70F}}].\end{eqnarray}$$
This approach preserves accuracy since
![]() $v$
is slowly varying even if
$v$
is slowly varying even if
![]() $\text{e}^{-\text{i}\unicode[STIX]{x1D714}^{\prime }\unicode[STIX]{x1D70F}}$
is not. Thus all values of
$\text{e}^{-\text{i}\unicode[STIX]{x1D714}^{\prime }\unicode[STIX]{x1D70F}}$
is not. Thus all values of
![]() $\tilde{L}_{j}$
and hence of
$\tilde{L}_{j}$
and hence of
![]() $\unicode[STIX]{x1D6F7}$
(4.5) and the contribution to the hole force on the entire uniform
$\unicode[STIX]{x1D6F7}$
(4.5) and the contribution to the hole force on the entire uniform
![]() $z$
-mesh are obtained from one cumulative integral procedure, that gives
$z$
-mesh are obtained from one cumulative integral procedure, that gives
which can then be integrated over the (passing) velocity
![]() $v_{\infty }$
and
$v_{\infty }$
and
![]() $v_{y}$
(and trivially
$v_{y}$
(and trivially
![]() $v_{x}$
).
$v_{x}$
).
4.5.2 Evaluation of the past orbit integral for trapped particles
For trapped particles take
![]() $v_{\infty }=0$
and then denote orbits instead by the quantity
$v_{\infty }=0$
and then denote orbits instead by the quantity
![]() $v_{\unicode[STIX]{x1D713}}=\sqrt{2(-q_{e}\unicode[STIX]{x1D713}+W_{\Vert })/m_{e}}>0$
, which is the orbit speed at
$v_{\unicode[STIX]{x1D713}}=\sqrt{2(-q_{e}\unicode[STIX]{x1D713}+W_{\Vert })/m_{e}}>0$
, which is the orbit speed at
![]() $z=0$
,
$z=0$
,
![]() $\unicode[STIX]{x1D719}=\unicode[STIX]{x1D713}$
, when the parallel energy is the negative quantity
$\unicode[STIX]{x1D719}=\unicode[STIX]{x1D713}$
, when the parallel energy is the negative quantity
![]() $W_{\Vert }({\geqslant}q_{e}\unicode[STIX]{x1D713})$
. To obtain high resolution near the separatrix, it is best to space orbits by equal intervals of
$W_{\Vert }({\geqslant}q_{e}\unicode[STIX]{x1D713})$
. To obtain high resolution near the separatrix, it is best to space orbits by equal intervals of
![]() $\sqrt{-W_{\Vert }}$
. For a given
$\sqrt{-W_{\Vert }}$
. For a given
![]() $v_{\unicode[STIX]{x1D713}}$
the orbit has a finite
$v_{\unicode[STIX]{x1D713}}$
the orbit has a finite
![]() $z$
-extent, and turning points (
$z$
-extent, and turning points (
![]() $v_{z}=0$
) at its ends. Equally spaced
$v_{z}=0$
) at its ends. Equally spaced
![]() $z$
-positions are used, but spanning just the
$z$
-positions are used, but spanning just the
![]() $z$
-extent of the orbit (different for each energy
$z$
-extent of the orbit (different for each energy
![]() $W_{\Vert }$
). Near the ends of the orbit, integration interpolation is optimized by determining
$W_{\Vert }$
). Near the ends of the orbit, integration interpolation is optimized by determining
![]() $\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D70F}$
via
$\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D70F}$
via
![]() $\unicode[STIX]{x1D6FF}t=\unicode[STIX]{x1D6FF}v/\dot{v}$
; but near
$\unicode[STIX]{x1D6FF}t=\unicode[STIX]{x1D6FF}v/\dot{v}$
; but near
![]() $z=0$
using
$z=0$
using
![]() $\unicode[STIX]{x1D6FF}t=\unicode[STIX]{x1D6FF}z/v$
is better. Again
$\unicode[STIX]{x1D6FF}t=\unicode[STIX]{x1D6FF}z/v$
is better. Again
![]() $\unicode[STIX]{x1D70F}$
integrals are combined with
$\unicode[STIX]{x1D70F}$
integrals are combined with
![]() $z$
-integrals over the hole’s spatial extent, by making the
$z$
-integrals over the hole’s spatial extent, by making the
![]() $v_{y}$
integral the outermost and converting the combined
$v_{y}$
integral the outermost and converting the combined
![]() $\text{d}v_{\unicode[STIX]{x1D713}}\text{d}z$
phase-space integral of the orbit contribution over the entire hole into an equivalent
$\text{d}v_{\unicode[STIX]{x1D713}}\text{d}z$
phase-space integral of the orbit contribution over the entire hole into an equivalent
![]() $\text{d}\unicode[STIX]{x1D70F}$
integral round the closed phase-space orbit. Schematically
$\text{d}\unicode[STIX]{x1D70F}$
integral round the closed phase-space orbit. Schematically
![]() $F_{t}=\int \ldots \text{d}\unicode[STIX]{x1D70F}^{\prime }\,\text{d}z\,\text{d}v_{z}\text{d}v_{y}=\int \ldots \text{d}\unicode[STIX]{x1D70F}^{\prime }\,\text{d}\unicode[STIX]{x1D70F}v_{\unicode[STIX]{x1D713}}\,\text{d}v_{\unicode[STIX]{x1D713}}\,\text{d}v_{y}$
.Footnote
6
$F_{t}=\int \ldots \text{d}\unicode[STIX]{x1D70F}^{\prime }\,\text{d}z\,\text{d}v_{z}\text{d}v_{y}=\int \ldots \text{d}\unicode[STIX]{x1D70F}^{\prime }\,\text{d}\unicode[STIX]{x1D70F}v_{\unicode[STIX]{x1D713}}\,\text{d}v_{\unicode[STIX]{x1D713}}\,\text{d}v_{y}$
.Footnote
6
As previously noted, one must assume that
![]() $\unicode[STIX]{x1D714}^{\prime }$
has a positive imaginary part
$\unicode[STIX]{x1D714}^{\prime }$
has a positive imaginary part
![]() $\unicode[STIX]{x1D714}_{i}$
which ensures the backward
$\unicode[STIX]{x1D714}_{i}$
which ensures the backward
![]() $\unicode[STIX]{x1D70F}$
integral giving
$\unicode[STIX]{x1D70F}$
integral giving
![]() $\tilde{L}$
converges. But it is obvious that the contribution from each preceding orbit period is the same except that they are multiplied by successive factors
$\tilde{L}$
converges. But it is obvious that the contribution from each preceding orbit period is the same except that they are multiplied by successive factors
![]() $\exp (\text{i}\unicode[STIX]{x1D714}^{\prime }t_{b})$
, where
$\exp (\text{i}\unicode[STIX]{x1D714}^{\prime }t_{b})$
, where
![]() $t_{b}$
is the orbit (bounce) period. This factor accounts for the attenuation
$t_{b}$
is the orbit (bounce) period. This factor accounts for the attenuation
![]() $\exp (\unicode[STIX]{x1D714}_{i}\unicode[STIX]{x1D70F})$
and the phase change relative to the succeeding period. Therefore it is necessary to perform the integral numerically only around a single period of the orbit; the total including all the prior periods can then be synthesized by multiplying by the infinite sumFootnote
7
:
$\exp (\unicode[STIX]{x1D714}_{i}\unicode[STIX]{x1D70F})$
and the phase change relative to the succeeding period. Therefore it is necessary to perform the integral numerically only around a single period of the orbit; the total including all the prior periods can then be synthesized by multiplying by the infinite sumFootnote
7
:
It does not matter where one chooses to start and stop the single orbit numerically evaluated. For definiteness, choose to start the integral at
![]() $\unicode[STIX]{x1D70F}=0$
saving the cumulative integral
$\unicode[STIX]{x1D70F}=0$
saving the cumulative integral
![]() $L(t)=\int _{0}^{t}v_{z}\text{i}\text{e}^{-\text{i}\unicode[STIX]{x1D714}^{\prime }(\unicode[STIX]{x1D70F}-t)}\,\text{d}\unicode[STIX]{x1D70F}$
. Then take
$L(t)=\int _{0}^{t}v_{z}\text{i}\text{e}^{-\text{i}\unicode[STIX]{x1D714}^{\prime }(\unicode[STIX]{x1D70F}-t)}\,\text{d}\unicode[STIX]{x1D70F}$
. Then take
![]() $\unicode[STIX]{x1D70F}=0$
to be the left end of the orbit (where
$\unicode[STIX]{x1D70F}=0$
to be the left end of the orbit (where
![]() $v_{z}$
changes sign from negative to positive). To construct the first prior orbit for any other position
$v_{z}$
changes sign from negative to positive). To construct the first prior orbit for any other position
![]() $z,v_{z}$
on it, take
$z,v_{z}$
on it, take
![]() $t$
to be the value of
$t$
to be the value of
![]() $\unicode[STIX]{x1D70F}$
during the first orbit at which the numerically calculated orbit passes through that position.
$\unicode[STIX]{x1D70F}$
during the first orbit at which the numerically calculated orbit passes through that position.
Since the hole is reflectionally symmetric, it suffices to calculate only half of the orbit, where
![]() $0<t\leqslant t_{b}/2$
. Starting at the left-hand end and integrating up to the right-hand end is the same as starting at the right and integrating along the negative-
$0<t\leqslant t_{b}/2$
. Starting at the left-hand end and integrating up to the right-hand end is the same as starting at the right and integrating along the negative-
![]() $v$
part of the orbit to the left. The only difference is that the velocity is opposite in sign. The resulting reversal of
$v$
part of the orbit to the left. The only difference is that the velocity is opposite in sign. The resulting reversal of
![]() $\unicode[STIX]{x1D6F7}$
is cancelled by the reflection of the
$\unicode[STIX]{x1D6F7}$
is cancelled by the reflection of the
![]() $z$
position and the consequent reversal of
$z$
position and the consequent reversal of
![]() $\text{d}\unicode[STIX]{x1D719}_{0}/\text{d}z$
. Hence positive and negative velocity parts of the integral give equal contribution to the force. The complete integral for a full prior period ending in the
$\text{d}\unicode[STIX]{x1D719}_{0}/\text{d}z$
. Hence positive and negative velocity parts of the integral give equal contribution to the force. The complete integral for a full prior period ending in the
![]() $0<t\leqslant t_{b}/2$
segment is obtained as the sum of four parts of the orbit:
$0<t\leqslant t_{b}/2$
segment is obtained as the sum of four parts of the orbit:
![]() $(0\rightarrow t),(t-t_{b}\rightarrow -t_{b}/2),(-t_{b}/2\rightarrow -t_{b}/2+t),(-t_{b}/2+t\rightarrow 0)$
. Noting that
$(0\rightarrow t),(t-t_{b}\rightarrow -t_{b}/2),(-t_{b}/2\rightarrow -t_{b}/2+t),(-t_{b}/2+t\rightarrow 0)$
. Noting that
![]() $\int _{-t_{b}}^{t-t_{b}}v_{z}\text{i}\text{e}^{-\text{i}\unicode[STIX]{x1D714}^{\prime }(\unicode[STIX]{x1D70F}-t)}\,\text{d}\unicode[STIX]{x1D70F}=\text{e}^{\text{i}\unicode[STIX]{x1D714}^{\prime }t_{b}}L(t)$
,
$\int _{-t_{b}}^{t-t_{b}}v_{z}\text{i}\text{e}^{-\text{i}\unicode[STIX]{x1D714}^{\prime }(\unicode[STIX]{x1D70F}-t)}\,\text{d}\unicode[STIX]{x1D70F}=\text{e}^{\text{i}\unicode[STIX]{x1D714}^{\prime }t_{b}}L(t)$
,
![]() $\int _{-t_{b}/2}^{t-t_{b}/2}v_{z}\text{i}\text{e}^{-\text{i}\unicode[STIX]{x1D714}^{\prime }(\unicode[STIX]{x1D70F}-t)}\,\text{d}\unicode[STIX]{x1D70F}=-\text{e}^{\text{i}\unicode[STIX]{x1D714}^{\prime }t_{b}/2}L(t)$
and
$\int _{-t_{b}/2}^{t-t_{b}/2}v_{z}\text{i}\text{e}^{-\text{i}\unicode[STIX]{x1D714}^{\prime }(\unicode[STIX]{x1D70F}-t)}\,\text{d}\unicode[STIX]{x1D70F}=-\text{e}^{\text{i}\unicode[STIX]{x1D714}^{\prime }t_{b}/2}L(t)$
and
![]() $\int _{t}^{t_{b}/2}v_{z}\text{i}\text{e}^{-\text{i}\unicode[STIX]{x1D714}^{\prime }(\unicode[STIX]{x1D70F}-t)}\,\text{d}\unicode[STIX]{x1D70F}=\text{e}^{\text{i}\unicode[STIX]{x1D714}^{\prime }(t-t_{b}/2)}L(t_{b}/2)-L(t)$
one finds
$\int _{t}^{t_{b}/2}v_{z}\text{i}\text{e}^{-\text{i}\unicode[STIX]{x1D714}^{\prime }(\unicode[STIX]{x1D70F}-t)}\,\text{d}\unicode[STIX]{x1D70F}=\text{e}^{\text{i}\unicode[STIX]{x1D714}^{\prime }(t-t_{b}/2)}L(t_{b}/2)-L(t)$
one finds
 $$\begin{eqnarray}\displaystyle \int _{t-t_{b}}^{t}v_{z}(\unicode[STIX]{x1D70F})\text{i}\text{e}^{-\text{i}\unicode[STIX]{x1D714}^{\prime }(\unicode[STIX]{x1D70F}-t)}\,\text{d}\unicode[STIX]{x1D70F} & = & \displaystyle \int _{0}^{t}+\int _{t-t_{b}}^{-t_{b}/2}+\int _{-t_{b}/2}^{-t_{b}/2+t}+\int _{-t_{b}/2+t}^{0}v_{z}(\unicode[STIX]{x1D70F})\text{i}\text{e}^{-\text{i}\unicode[STIX]{x1D714}^{\prime }(\unicode[STIX]{x1D70F}-t)}\,\text{d}\unicode[STIX]{x1D70F}\nonumber\\ \displaystyle & = & \displaystyle L(t)+\text{e}^{\text{i}\unicode[STIX]{x1D714}^{\prime }t_{b}}[\text{e}^{\text{i}\unicode[STIX]{x1D714}^{\prime }(t-t_{b}/2)}L(t_{b}/2)-L(t)]\nonumber\\ \displaystyle & & \displaystyle -\,\text{e}^{\text{i}\unicode[STIX]{x1D714}^{\prime }t_{b}/2}L(t)-\text{e}^{\text{i}\unicode[STIX]{x1D714}^{\prime }t_{b}/2}[\text{e}^{\text{i}\unicode[STIX]{x1D714}^{\prime }(t-t_{b}/2)}L(t_{b}/2)-L(t)]\nonumber\\ \displaystyle & = & \displaystyle (1-\text{e}^{\text{i}\unicode[STIX]{x1D714}^{\prime }t_{b}})L(t)+\text{e}^{\text{i}\unicode[STIX]{x1D714}^{\prime }t}(\text{e}^{\text{i}\unicode[STIX]{x1D714}^{\prime }t_{b}/2}-1)L(t_{b}/2).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \int _{t-t_{b}}^{t}v_{z}(\unicode[STIX]{x1D70F})\text{i}\text{e}^{-\text{i}\unicode[STIX]{x1D714}^{\prime }(\unicode[STIX]{x1D70F}-t)}\,\text{d}\unicode[STIX]{x1D70F} & = & \displaystyle \int _{0}^{t}+\int _{t-t_{b}}^{-t_{b}/2}+\int _{-t_{b}/2}^{-t_{b}/2+t}+\int _{-t_{b}/2+t}^{0}v_{z}(\unicode[STIX]{x1D70F})\text{i}\text{e}^{-\text{i}\unicode[STIX]{x1D714}^{\prime }(\unicode[STIX]{x1D70F}-t)}\,\text{d}\unicode[STIX]{x1D70F}\nonumber\\ \displaystyle & = & \displaystyle L(t)+\text{e}^{\text{i}\unicode[STIX]{x1D714}^{\prime }t_{b}}[\text{e}^{\text{i}\unicode[STIX]{x1D714}^{\prime }(t-t_{b}/2)}L(t_{b}/2)-L(t)]\nonumber\\ \displaystyle & & \displaystyle -\,\text{e}^{\text{i}\unicode[STIX]{x1D714}^{\prime }t_{b}/2}L(t)-\text{e}^{\text{i}\unicode[STIX]{x1D714}^{\prime }t_{b}/2}[\text{e}^{\text{i}\unicode[STIX]{x1D714}^{\prime }(t-t_{b}/2)}L(t_{b}/2)-L(t)]\nonumber\\ \displaystyle & = & \displaystyle (1-\text{e}^{\text{i}\unicode[STIX]{x1D714}^{\prime }t_{b}})L(t)+\text{e}^{\text{i}\unicode[STIX]{x1D714}^{\prime }t}(\text{e}^{\text{i}\unicode[STIX]{x1D714}^{\prime }t_{b}/2}-1)L(t_{b}/2).\end{eqnarray}$$
And the full prior time integral from
![]() $-\infty$
to give
$-\infty$
to give
![]() $\tilde{L}$
is obtained by multiplying by (4.30).
$\tilde{L}$
is obtained by multiplying by (4.30).
Then
where the integral
![]() $\text{d}z/v_{z}=\text{d}t$
is over the half-orbit with positive
$\text{d}z/v_{z}=\text{d}t$
is over the half-orbit with positive
![]() $v_{\unicode[STIX]{x1D713}}$
, and an equal contribution also comes from the negative-
$v_{\unicode[STIX]{x1D713}}$
, and an equal contribution also comes from the negative-
![]() $v_{\unicode[STIX]{x1D713}}$
half.
$v_{\unicode[STIX]{x1D713}}$
half.
4.5.3 Results
Implementing these algorithms gives the forces
![]() $F_{t}$
and
$F_{t}$
and
![]() $F_{p}$
for specified general values of
$F_{p}$
for specified general values of
![]() $\unicode[STIX]{x1D713}$
,
$\unicode[STIX]{x1D713}$
,
![]() $k$
and
$k$
and
![]() $\unicode[STIX]{x1D714}$
for some specified potential form
$\unicode[STIX]{x1D714}$
for some specified potential form
![]() $\unicode[STIX]{x1D719}_{0}(z)$
and distribution function
$\unicode[STIX]{x1D719}_{0}(z)$
and distribution function
![]() $f$
. A verification of the numerics is obtained by comparing the values found at
$f$
. A verification of the numerics is obtained by comparing the values found at
![]() $k=0$
,
$k=0$
,
![]() $\text{Re}(\unicode[STIX]{x1D714})=0$
, and
$\text{Re}(\unicode[STIX]{x1D714})=0$
, and
![]() $\text{Im}(\unicode[STIX]{x1D714})$
small, with the analytic expressions leading up to equation (4.18), and employing the forms (4.23) and (4.24).
$\text{Im}(\unicode[STIX]{x1D714})$
small, with the analytic expressions leading up to equation (4.18), and employing the forms (4.23) and (4.24).

Figure 2. Comparison of numerical and analytic calculations of trapped and passing particle forces, for small value of
![]() $\unicode[STIX]{x1D714}_{i}$
and zero
$\unicode[STIX]{x1D714}_{i}$
and zero
![]() $k$
and
$k$
and
![]() $\unicode[STIX]{x1D714}_{r}$
. The forces are real for symmetric
$\unicode[STIX]{x1D714}_{r}$
. The forces are real for symmetric
![]() $v_{y}$
-distributions. (
$v_{y}$
-distributions. (
![]() $\unicode[STIX]{x1D713}$
is measured in units of
$\unicode[STIX]{x1D713}$
is measured in units of
![]() $T_{e}/e$
.)
$T_{e}/e$
.)
As figure 2 indicates, we find essentially exact agreement for the passing particle force
![]() $F_{p}$
, using Maxwellian distributions and a potential
$F_{p}$
, using Maxwellian distributions and a potential
![]() $\unicode[STIX]{x1D719}=\unicode[STIX]{x1D713}\,\text{sech}^{4}(z/4)$
at all values of
$\unicode[STIX]{x1D719}=\unicode[STIX]{x1D713}\,\text{sech}^{4}(z/4)$
at all values of
![]() $\unicode[STIX]{x1D713}$
. However, the trapped particle force requires a self-consistent parallel velocity distribution, which is not readily available analytically except for shallow holes. Using the approximation
$\unicode[STIX]{x1D713}$
. However, the trapped particle force requires a self-consistent parallel velocity distribution, which is not readily available analytically except for shallow holes. Using the approximation
![]() $f(W_{\Vert })=f_{\infty }(0)\exp (-\unicode[STIX]{x1D6FD}W_{\Vert })$
with
$f(W_{\Vert })=f_{\infty }(0)\exp (-\unicode[STIX]{x1D6FD}W_{\Vert })$
with
![]() $-\unicode[STIX]{x1D6FD}=1+(15/16)\sqrt{\unicode[STIX]{x03C0}T_{e}/e\unicode[STIX]{x1D713}}$
, better than 2 % agreement in
$-\unicode[STIX]{x1D6FD}=1+(15/16)\sqrt{\unicode[STIX]{x03C0}T_{e}/e\unicode[STIX]{x1D713}}$
, better than 2 % agreement in
![]() $F_{t}$
is obtained for
$F_{t}$
is obtained for
![]() $\unicode[STIX]{x1D713}<0.02$
, which verifies the integration coding.
$\unicode[STIX]{x1D713}<0.02$
, which verifies the integration coding.

Figure 3. Total particle force
![]() $F_{t}+F_{p}$
, and electric force
$F_{t}+F_{p}$
, and electric force
![]() $F_{E}$
, normalized to
$F_{E}$
, normalized to
![]() $\unicode[STIX]{x1D714}^{2}$
versus wavenumber
$\unicode[STIX]{x1D714}^{2}$
versus wavenumber
![]() $k$
. The dispersion relation is
$k$
. The dispersion relation is
![]() $F_{t}+F_{p}=F_{E}$
.
$F_{t}+F_{p}=F_{E}$
.
As
![]() $k$
is increased from zero the main effect is observed to occur as a reduction of
$k$
is increased from zero the main effect is observed to occur as a reduction of
![]() $F_{t}$
, with only small changes to
$F_{t}$
, with only small changes to
![]() $F_{p}$
. In figure 3 is shown the total particle force and the electric tension force as a function of
$F_{p}$
. In figure 3 is shown the total particle force and the electric tension force as a function of
![]() $k$
for two (fixed) imaginary frequencies
$k$
for two (fixed) imaginary frequencies
![]() $\unicode[STIX]{x1D714}=i\unicode[STIX]{x1D714}_{i}$
. It illustrates the fact that the tension force
$\unicode[STIX]{x1D714}=i\unicode[STIX]{x1D714}_{i}$
. It illustrates the fact that the tension force
![]() $F_{E}$
(drawn for the corresponding
$F_{E}$
(drawn for the corresponding
![]() $\unicode[STIX]{x1D713}$
values and varying
$\unicode[STIX]{x1D713}$
values and varying
![]() $\propto \unicode[STIX]{x1D713}^{2}$
) is a minor correction, probably less important in practice than the approximation arising from taking the trapped distribution to be
$\propto \unicode[STIX]{x1D713}^{2}$
) is a minor correction, probably less important in practice than the approximation arising from taking the trapped distribution to be
![]() $\propto \exp (-\unicode[STIX]{x1D6FD}v_{z}^{2})$
. For small
$\propto \exp (-\unicode[STIX]{x1D6FD}v_{z}^{2})$
. For small
![]() $\unicode[STIX]{x1D714}_{i}$
(figure 3
a), this plot is essentially universal. It gives the small-
$\unicode[STIX]{x1D714}_{i}$
(figure 3
a), this plot is essentially universal. It gives the small-
![]() $k$
dispersion root at the intersection of corresponding curves, where
$k$
dispersion root at the intersection of corresponding curves, where
![]() $kv_{t}/\unicode[STIX]{x1D714}_{i}$
is slightly below 1 in accordance with (4.27). However for larger
$kv_{t}/\unicode[STIX]{x1D714}_{i}$
is slightly below 1 in accordance with (4.27). However for larger
![]() $\unicode[STIX]{x1D714}_{i}$
and correspondingly
$\unicode[STIX]{x1D714}_{i}$
and correspondingly
![]() $kv_{t}$
(figure 3
b), there is no intersection for shallow holes (small
$kv_{t}$
(figure 3
b), there is no intersection for shallow holes (small
![]() $\unicode[STIX]{x1D713}$
) because the curves of
$\unicode[STIX]{x1D713}$
) because the curves of
![]() $F_{t}+F_{p}$
have a minimum above zero. Figure 3(b) also illustrates the existence of a second solution at higher
$F_{t}+F_{p}$
have a minimum above zero. Figure 3(b) also illustrates the existence of a second solution at higher
![]() $k$
for higher
$k$
for higher
![]() $\unicode[STIX]{x1D713}$
values. We shall shortly see that this behaviour arises because of changes of resonance on trapped electrons.
$\unicode[STIX]{x1D713}$
values. We shall shortly see that this behaviour arises because of changes of resonance on trapped electrons.

Figure 4. Dispersion relation showing scaled transverse instability growth rate versus scaled transverse wavenumber, for a wide range of hole potential
![]() $\unicode[STIX]{x1D713}$
. Stationary hole,
$\unicode[STIX]{x1D713}$
. Stationary hole,
![]() $\unicode[STIX]{x1D719}=\unicode[STIX]{x1D713}\text{sech}^{4}(z/4)$
, Maxwellian background, immobile ions. Units of
$\unicode[STIX]{x1D719}=\unicode[STIX]{x1D713}\text{sech}^{4}(z/4)$
, Maxwellian background, immobile ions. Units of
![]() $\unicode[STIX]{x1D6FE}$
,
$\unicode[STIX]{x1D6FE}$
,
![]() $z$
(and
$z$
(and
![]() $k^{-1}$
) and
$k^{-1}$
) and
![]() $\unicode[STIX]{x1D713}$
are respectively
$\unicode[STIX]{x1D713}$
are respectively
![]() $\unicode[STIX]{x1D714}_{p}$
,
$\unicode[STIX]{x1D714}_{p}$
,
![]() $\unicode[STIX]{x1D706}_{De}$
and
$\unicode[STIX]{x1D706}_{De}$
and
![]() $T_{e}/e$
.
$T_{e}/e$
.
The dispersion relation that solves
![]() $F_{t}+F_{p}=F_{E}$
can usefully be displayed in terms of
$F_{t}+F_{p}=F_{E}$
can usefully be displayed in terms of
![]() $\unicode[STIX]{x1D6FE}\equiv \unicode[STIX]{x1D714}_{i}$
as a function of given
$\unicode[STIX]{x1D6FE}\equiv \unicode[STIX]{x1D714}_{i}$
as a function of given
![]() $k$
. This can be accomplished for a stationary hole in a Maxwellian distribution by bisection real root finding because the real part of
$k$
. This can be accomplished for a stationary hole in a Maxwellian distribution by bisection real root finding because the real part of
![]() $\unicode[STIX]{x1D714}$
is zero by symmetry. Both
$\unicode[STIX]{x1D714}$
is zero by symmetry. Both
![]() $k$
and
$k$
and
![]() $\unicode[STIX]{x1D6FE}$
scale like
$\unicode[STIX]{x1D6FE}$
scale like
![]() $\sqrt{\unicode[STIX]{x1D713}}$
, so plotting the resulting
$\sqrt{\unicode[STIX]{x1D713}}$
, so plotting the resulting
![]() $\unicode[STIX]{x1D6FE}/\sqrt{\unicode[STIX]{x1D713}}$
versus
$\unicode[STIX]{x1D6FE}/\sqrt{\unicode[STIX]{x1D713}}$
versus
![]() $k/\sqrt{\unicode[STIX]{x1D713}}$
, as shown in figure 4, gives an almost universal curve, at least for
$k/\sqrt{\unicode[STIX]{x1D713}}$
, as shown in figure 4, gives an almost universal curve, at least for
![]() $\unicode[STIX]{x1D713}\lesssim 0.5$
. (Here and subsequently in presenting numerical results we use non-dimensionalized parameters where units of time are
$\unicode[STIX]{x1D713}\lesssim 0.5$
. (Here and subsequently in presenting numerical results we use non-dimensionalized parameters where units of time are
![]() $1/\unicode[STIX]{x1D714}_{p}$
, of space
$1/\unicode[STIX]{x1D714}_{p}$
, of space
![]() $\unicode[STIX]{x1D706}_{D}$
and of energy
$\unicode[STIX]{x1D706}_{D}$
and of energy
![]() $T_{e}/e$
; that is equivalent to setting
$T_{e}/e$
; that is equivalent to setting
![]() $|q_{e}|=m_{e}=1$
.) The iterative numerical solution breaks down at the upper end of the
$|q_{e}|=m_{e}=1$
.) The iterative numerical solution breaks down at the upper end of the
![]() $k$
-range (
$k$
-range (
![]() $k_{c}$
) where
$k_{c}$
) where
![]() $\unicode[STIX]{x1D714}_{i}$
returns to zero, because the integrals no longer converge. Numerically it breaks down just before
$\unicode[STIX]{x1D714}_{i}$
returns to zero, because the integrals no longer converge. Numerically it breaks down just before
![]() $k_{c}$
, because of imprecision; that is why the curves do not extend all the way back to the
$k_{c}$
, because of imprecision; that is why the curves do not extend all the way back to the
![]() $k$
axis. The forces are evaluated using the same first-order approximation for
$k$
axis. The forces are evaluated using the same first-order approximation for
![]() $\unicode[STIX]{x1D6FD}$
which is inaccurate at
$\unicode[STIX]{x1D6FD}$
which is inaccurate at
![]() $\unicode[STIX]{x1D713}\sim 1$
. That is one reason why the curves only become truly invariant at low
$\unicode[STIX]{x1D713}\sim 1$
. That is one reason why the curves only become truly invariant at low
![]() $\unicode[STIX]{x1D713}$
. Another is that
$\unicode[STIX]{x1D713}$
. Another is that
![]() $F_{E}$
begins to become significant for
$F_{E}$
begins to become significant for
![]() $\unicode[STIX]{x1D713}\sim 1$
. Observe that the slope at the origin also somewhat exceeds the limit value of 1 (indicated by the short solid line) except when
$\unicode[STIX]{x1D713}\sim 1$
. Observe that the slope at the origin also somewhat exceeds the limit value of 1 (indicated by the short solid line) except when
![]() $\unicode[STIX]{x1D713}\ll 1$
. That is consistent with (4.27). The peak growth rate occurs very close to the previously published (Hutchinson Reference Hutchinson2018) estimate
$\unicode[STIX]{x1D713}\ll 1$
. That is consistent with (4.27). The peak growth rate occurs very close to the previously published (Hutchinson Reference Hutchinson2018) estimate
![]() $k=\sqrt{\unicode[STIX]{x1D713}}/8$
. The maximum growth rate, even at low
$k=\sqrt{\unicode[STIX]{x1D713}}/8$
. The maximum growth rate, even at low
![]() $\unicode[STIX]{x1D713}$
somewhat exceeds the prior estimate
$\unicode[STIX]{x1D713}$
somewhat exceeds the prior estimate
![]() $\unicode[STIX]{x1D6FE}/\sqrt{\unicode[STIX]{x1D713}}=1/16$
. This section has thus confirmed that the transverse instability of electron holes (in Maxwellian background plasma) is a kinematic effect arising from the jetting force balance in an accelerating hole; and it has given a detailed mathematical derivation and precise numerical evaluation of coefficients.
$\unicode[STIX]{x1D6FE}/\sqrt{\unicode[STIX]{x1D713}}=1/16$
. This section has thus confirmed that the transverse instability of electron holes (in Maxwellian background plasma) is a kinematic effect arising from the jetting force balance in an accelerating hole; and it has given a detailed mathematical derivation and precise numerical evaluation of coefficients.
5 Magnetized holes
In the presence of a magnetic field (in the
![]() $z$
-direction), the unperturbed orbit is a helix. Because
$z$
-direction), the unperturbed orbit is a helix. Because
![]() $v_{z}$
is not constant, the helix has varying pitch, but since the wave vector is perpendicular to
$v_{z}$
is not constant, the helix has varying pitch, but since the wave vector is perpendicular to
![]() $B$
, that does not matter. Take the perpendicular components of velocity at time
$B$
, that does not matter. Take the perpendicular components of velocity at time
![]() $t$
to be
$t$
to be
![]() $v_{x}(t)=v_{\bot }\cos \unicode[STIX]{x1D703}_{t}$
and
$v_{x}(t)=v_{\bot }\cos \unicode[STIX]{x1D703}_{t}$
and
![]() $v_{y}(t)=v_{\bot }\sin \unicode[STIX]{x1D703}_{t}$
, and write
$v_{y}(t)=v_{\bot }\sin \unicode[STIX]{x1D703}_{t}$
, and write
![]() $\unicode[STIX]{x1D6FA}=eB/m_{e}$
(
$\unicode[STIX]{x1D6FA}=eB/m_{e}$
(
![]() $q_{e}=-e$
so rotation is right-handed about
$q_{e}=-e$
so rotation is right-handed about
![]() $z$
for positive
$z$
for positive
![]() $B$
). Then at a different time
$B$
). Then at a different time
![]() $\unicode[STIX]{x1D70F}$
, the orbit is
$\unicode[STIX]{x1D70F}$
, the orbit is
 $$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}v_{x}(\unicode[STIX]{x1D70F})=v_{\bot }\cos (\unicode[STIX]{x1D703}_{t}+\unicode[STIX]{x1D6FA}[\unicode[STIX]{x1D70F}-t]),\quad v_{y}(\unicode[STIX]{x1D70F})=v_{\bot }\sin (\unicode[STIX]{x1D703}_{t}+\unicode[STIX]{x1D6FA}[\unicode[STIX]{x1D70F}-t]),\\ x(\unicode[STIX]{x1D70F})=x_{t}+(v_{\bot }/\unicode[STIX]{x1D6FA})\{\sin (\unicode[STIX]{x1D703}_{t}+\unicode[STIX]{x1D6FA}[\unicode[STIX]{x1D70F}-t])-\sin \unicode[STIX]{x1D703}_{t}\},\\ y(\unicode[STIX]{x1D70F})=y_{t}+(v_{\bot }/\unicode[STIX]{x1D6FA})\{-\text{cos}(\unicode[STIX]{x1D703}_{t}+\unicode[STIX]{x1D6FA}[\unicode[STIX]{x1D70F}-t])+\cos \unicode[STIX]{x1D703}_{t}\}.\end{array}\right\} & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}v_{x}(\unicode[STIX]{x1D70F})=v_{\bot }\cos (\unicode[STIX]{x1D703}_{t}+\unicode[STIX]{x1D6FA}[\unicode[STIX]{x1D70F}-t]),\quad v_{y}(\unicode[STIX]{x1D70F})=v_{\bot }\sin (\unicode[STIX]{x1D703}_{t}+\unicode[STIX]{x1D6FA}[\unicode[STIX]{x1D70F}-t]),\\ x(\unicode[STIX]{x1D70F})=x_{t}+(v_{\bot }/\unicode[STIX]{x1D6FA})\{\sin (\unicode[STIX]{x1D703}_{t}+\unicode[STIX]{x1D6FA}[\unicode[STIX]{x1D70F}-t])-\sin \unicode[STIX]{x1D703}_{t}\},\\ y(\unicode[STIX]{x1D70F})=y_{t}+(v_{\bot }/\unicode[STIX]{x1D6FA})\{-\text{cos}(\unicode[STIX]{x1D703}_{t}+\unicode[STIX]{x1D6FA}[\unicode[STIX]{x1D70F}-t])+\cos \unicode[STIX]{x1D703}_{t}\}.\end{array}\right\} & & \displaystyle\end{eqnarray}$$
We substitute the orbit parameters into the integral (2.7) and evaluate it. The exponential’s argument becomes
where
![]() $\unicode[STIX]{x1D709}=kv_{\bot }/\unicode[STIX]{x1D6FA}$
. We can then write the
$\unicode[STIX]{x1D709}=kv_{\bot }/\unicode[STIX]{x1D6FA}$
. We can then write the
![]() $\unicode[STIX]{x1D70F}$
-dependence using the Fourier expansion
$\unicode[STIX]{x1D70F}$
-dependence using the Fourier expansion
(and its derivative with respect to the variable
![]() $\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D70F}}=\unicode[STIX]{x1D703}_{t}+\unicode[STIX]{x1D6FA}(\unicode[STIX]{x1D70F}-t)$
). From which we find
$\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D70F}}=\unicode[STIX]{x1D703}_{t}+\unicode[STIX]{x1D6FA}(\unicode[STIX]{x1D70F}-t)$
). From which we find
and
Everything can be taken outside the
![]() $\unicode[STIX]{x1D70F}$
-integral for
$\unicode[STIX]{x1D70F}$
-integral for
![]() $\tilde{f}$
, except the final exponential and the quantity
$\tilde{f}$
, except the final exponential and the quantity
![]() $\hat{\unicode[STIX]{x1D719}}(z(\unicode[STIX]{x1D70F}))$
. So we define the following quantity, which is independent of
$\hat{\unicode[STIX]{x1D719}}(z(\unicode[STIX]{x1D70F}))$
. So we define the following quantity, which is independent of
![]() $t$
(but not
$t$
(but not
![]() $z(t)$
),
$z(t)$
),
where
![]() $z(\unicode[STIX]{x1D70F})=z(t)+\int _{t}^{\unicode[STIX]{x1D70F}}v_{z}(t^{\prime })\,\text{d}t^{\prime }$
. The quantity
$z(\unicode[STIX]{x1D70F})=z(t)+\int _{t}^{\unicode[STIX]{x1D70F}}v_{z}(t^{\prime })\,\text{d}t^{\prime }$
. The quantity
![]() $\unicode[STIX]{x1D6F7}_{m}$
is a partial-domain Fourier transform of
$\unicode[STIX]{x1D6F7}_{m}$
is a partial-domain Fourier transform of
![]() $\hat{\unicode[STIX]{x1D719}}(z(\unicode[STIX]{x1D70F}))$
corresponding to cyclotron harmonic
$\hat{\unicode[STIX]{x1D719}}(z(\unicode[STIX]{x1D70F}))$
corresponding to cyclotron harmonic
![]() $m$
. It also has exactly the same form as the unmagnetized
$m$
. It also has exactly the same form as the unmagnetized
![]() $\unicode[STIX]{x1D6F7}(z)$
with the identification
$\unicode[STIX]{x1D6F7}(z)$
with the identification
![]() $\unicode[STIX]{x1D714}^{\prime }=\unicode[STIX]{x1D714}+m\unicode[STIX]{x1D6FA}$
(instead of
$\unicode[STIX]{x1D714}^{\prime }=\unicode[STIX]{x1D714}+m\unicode[STIX]{x1D6FA}$
(instead of
![]() $\unicode[STIX]{x1D714}^{\prime }=\unicode[STIX]{x1D714}-kv_{y}$
). The remaining space and time
$\unicode[STIX]{x1D714}^{\prime }=\unicode[STIX]{x1D714}-kv_{y}$
). The remaining space and time
![]() $t$
-dependence of
$t$
-dependence of
![]() $\tilde{f}$
(2.8) is then contained in a term
$\tilde{f}$
(2.8) is then contained in a term
![]() $\text{e}^{\text{i}(ky_{t}+\unicode[STIX]{x1D714}t)}$
. The dependence on the gyrophase angle at time
$\text{e}^{\text{i}(ky_{t}+\unicode[STIX]{x1D714}t)}$
. The dependence on the gyrophase angle at time
![]() $t$
,
$t$
,
![]() $\unicode[STIX]{x1D703}_{t}$
, is specified by the velocity
$\unicode[STIX]{x1D703}_{t}$
, is specified by the velocity
![]() $\boldsymbol{v}$
in the argument of
$\boldsymbol{v}$
in the argument of
![]() $f_{1}(\boldsymbol{v},\boldsymbol{x},t)$
. The quantities we need to evaluate, such as the density and force, require us to integrate over all
$f_{1}(\boldsymbol{v},\boldsymbol{x},t)$
. The quantities we need to evaluate, such as the density and force, require us to integrate over all
![]() $\boldsymbol{v}$
, which we can begin to do by integrating over
$\boldsymbol{v}$
, which we can begin to do by integrating over
![]() $\unicode[STIX]{x1D703}_{t}$
. In view of the Bessel function Fourier expansions, we can write
$\unicode[STIX]{x1D703}_{t}$
. In view of the Bessel function Fourier expansions, we can write
which when integrated over
![]() $\unicode[STIX]{x1D703}_{t}$
gives
$\unicode[STIX]{x1D703}_{t}$
gives
![]() $2\unicode[STIX]{x03C0}\text{i}^{m}\text{J}_{\ell }(\unicode[STIX]{x1D709})$
when
$2\unicode[STIX]{x03C0}\text{i}^{m}\text{J}_{\ell }(\unicode[STIX]{x1D709})$
when
![]() $\ell =m$
, but zero otherwise. (Everything else in the
$\ell =m$
, but zero otherwise. (Everything else in the
![]() $\tilde{f}$
integral is independent of
$\tilde{f}$
integral is independent of
![]() $\unicode[STIX]{x1D703}_{t}$
.) Consequently (dropping the
$\unicode[STIX]{x1D703}_{t}$
.) Consequently (dropping the
![]() $t$
suffix as indication of the final orbit position now, so we can use it instead to denote thermal)
$t$
suffix as indication of the final orbit position now, so we can use it instead to denote thermal)
If the perpendicular distribution is Maxwellian
![]() $f_{\bot 0}=(m_{e}/2\unicode[STIX]{x03C0}T_{\bot })\exp (-W_{\bot }/T_{\bot })$
, then the integral with respect to
$f_{\bot 0}=(m_{e}/2\unicode[STIX]{x03C0}T_{\bot })\exp (-W_{\bot }/T_{\bot })$
, then the integral with respect to
![]() $v_{\bot }$
is analytic
$v_{\bot }$
is analytic
![]() $\int _{0}^{\infty }\text{J}_{m}^{2}(\unicode[STIX]{x1D709})v_{\bot }f_{\bot 0}\,\text{d}v_{\bot }=\exp (-\unicode[STIX]{x1D709}_{t}^{2})\text{I}_{m}(\unicode[STIX]{x1D709}_{t}^{2})/2\unicode[STIX]{x03C0}$
, where
$\int _{0}^{\infty }\text{J}_{m}^{2}(\unicode[STIX]{x1D709})v_{\bot }f_{\bot 0}\,\text{d}v_{\bot }=\exp (-\unicode[STIX]{x1D709}_{t}^{2})\text{I}_{m}(\unicode[STIX]{x1D709}_{t}^{2})/2\unicode[STIX]{x03C0}$
, where
![]() $\unicode[STIX]{x1D709}_{t}^{2}=k^{2}T_{\bot }/\unicode[STIX]{x1D6FA}^{2}m_{e}$
, and
$\unicode[STIX]{x1D709}_{t}^{2}=k^{2}T_{\bot }/\unicode[STIX]{x1D6FA}^{2}m_{e}$
, and
![]() $\text{I}_{m}$
is the modified Bessel function. Also
$\text{I}_{m}$
is the modified Bessel function. Also
![]() $\unicode[STIX]{x2202}f_{\bot 0}/\unicode[STIX]{x2202}W_{\bot }=-f_{\bot 0}/T_{\bot }$
. Then there results an expression for the perturbed parallel distribution function
$\unicode[STIX]{x2202}f_{\bot 0}/\unicode[STIX]{x2202}W_{\bot }=-f_{\bot 0}/T_{\bot }$
. Then there results an expression for the perturbed parallel distribution function
We naturally denote the second term (the sum) as
![]() $\tilde{f}_{\Vert }\text{e}^{\text{i}(ky-\unicode[STIX]{x1D714}t)}$
.
$\tilde{f}_{\Vert }\text{e}^{\text{i}(ky-\unicode[STIX]{x1D714}t)}$
.
With this expression we have replaced the integral over perpendicular velocities that was necessary for the unmagnetized case with a sum over
![]() $\unicode[STIX]{x1D6F7}_{m}\text{e}^{-\unicode[STIX]{x1D709}_{t}^{2}}\text{I}_{m}(\unicode[STIX]{x1D709}_{t})$
. Therefore the numerical effort involved in evaluating the force is no greater than what is needed to evaluate the zero field case by numerical integration over the perpendicular distribution (although it is limited to Gaussian perpendicular distributions). Moreover,
$\unicode[STIX]{x1D6F7}_{m}\text{e}^{-\unicode[STIX]{x1D709}_{t}^{2}}\text{I}_{m}(\unicode[STIX]{x1D709}_{t})$
. Therefore the numerical effort involved in evaluating the force is no greater than what is needed to evaluate the zero field case by numerical integration over the perpendicular distribution (although it is limited to Gaussian perpendicular distributions). Moreover,
![]() $\unicode[STIX]{x1D6F7}_{m}$
is essentially exactly the same quantity as the unmagnetized
$\unicode[STIX]{x1D6F7}_{m}$
is essentially exactly the same quantity as the unmagnetized
![]() $\unicode[STIX]{x1D6F7}$
. Regarding
$\unicode[STIX]{x1D6F7}$
. Regarding
![]() $\unicode[STIX]{x1D6F7}(z,\unicode[STIX]{x1D714}^{\prime },W_{\Vert })$
as a function of
$\unicode[STIX]{x1D6F7}(z,\unicode[STIX]{x1D714}^{\prime },W_{\Vert })$
as a function of
![]() $z$
and
$z$
and
![]() $\unicode[STIX]{x1D714}^{\prime }$
, straightforwardly
$\unicode[STIX]{x1D714}^{\prime }$
, straightforwardly
![]() $\unicode[STIX]{x1D6F7}_{m}(z)=\unicode[STIX]{x1D6F7}(z,\unicode[STIX]{x1D714}+m\unicode[STIX]{x1D6FA},W_{\Vert })$
; with
$\unicode[STIX]{x1D6F7}_{m}(z)=\unicode[STIX]{x1D6F7}(z,\unicode[STIX]{x1D714}+m\unicode[STIX]{x1D6FA},W_{\Vert })$
; with
![]() $\unicode[STIX]{x1D714}^{\prime }\rightarrow \unicode[STIX]{x1D714}+m\unicode[STIX]{x1D6FA}$
(instead of
$\unicode[STIX]{x1D714}^{\prime }\rightarrow \unicode[STIX]{x1D714}+m\unicode[STIX]{x1D6FA}$
(instead of
![]() $\unicode[STIX]{x1D714}-kv_{y}$
). The close connection to the unmagnetized calculation can be understood by plotting
$\unicode[STIX]{x1D714}-kv_{y}$
). The close connection to the unmagnetized calculation can be understood by plotting
![]() $\unicode[STIX]{x1D709}_{t}\text{e}^{-\unicode[STIX]{x1D709}_{t}^{2}}\text{I}_{m}(\unicode[STIX]{x1D709}_{t}^{2})$
versus the transverse phase velocity of harmonic
$\unicode[STIX]{x1D709}_{t}\text{e}^{-\unicode[STIX]{x1D709}_{t}^{2}}\text{I}_{m}(\unicode[STIX]{x1D709}_{t}^{2})$
versus the transverse phase velocity of harmonic
![]() $m$
as shown in figure 5. Harmonics are spaced by a velocity increment (in units of the thermal velocity
$m$
as shown in figure 5. Harmonics are spaced by a velocity increment (in units of the thermal velocity
![]() $v_{t}=\sqrt{T_{\bot }/m_{e}}$
) that is
$v_{t}=\sqrt{T_{\bot }/m_{e}}$
) that is
![]() $\unicode[STIX]{x1D6FF}v=1/\unicode[STIX]{x1D709}_{t}=\unicode[STIX]{x1D6FA}/kv_{t}$
. Consequently the sum
$\unicode[STIX]{x1D6FF}v=1/\unicode[STIX]{x1D709}_{t}=\unicode[STIX]{x1D6FA}/kv_{t}$
. Consequently the sum
![]() $\sum _{m}\text{e}^{-\unicode[STIX]{x1D709}_{t}^{2}}\text{I}_{m}(\unicode[STIX]{x1D709}_{t}^{2})=\sum _{m}\unicode[STIX]{x1D709}_{t}\text{e}^{-\unicode[STIX]{x1D709}_{t}^{2}}\text{I}_{m}(\unicode[STIX]{x1D709}_{t}^{2})\unicode[STIX]{x1D6FF}v$
, when
$\sum _{m}\text{e}^{-\unicode[STIX]{x1D709}_{t}^{2}}\text{I}_{m}(\unicode[STIX]{x1D709}_{t}^{2})=\sum _{m}\unicode[STIX]{x1D709}_{t}\text{e}^{-\unicode[STIX]{x1D709}_{t}^{2}}\text{I}_{m}(\unicode[STIX]{x1D709}_{t}^{2})\unicode[STIX]{x1D6FF}v$
, when
![]() $\unicode[STIX]{x1D709}_{t}>1$
, represents a kind of finite-difference approximation to the integral
$\unicode[STIX]{x1D709}_{t}>1$
, represents a kind of finite-difference approximation to the integral
![]() $\int \unicode[STIX]{x1D709}_{t}\text{e}^{-\unicode[STIX]{x1D709}_{t}^{2}}\text{I}_{m}(\unicode[STIX]{x1D709}_{t}^{2})\,\text{d}v_{m}$
, where
$\int \unicode[STIX]{x1D709}_{t}\text{e}^{-\unicode[STIX]{x1D709}_{t}^{2}}\text{I}_{m}(\unicode[STIX]{x1D709}_{t}^{2})\,\text{d}v_{m}$
, where
![]() $v_{m}=m/\unicode[STIX]{x1D709}_{t}$
is regarded as a continuous variable for given
$v_{m}=m/\unicode[STIX]{x1D709}_{t}$
is regarded as a continuous variable for given
![]() $\unicode[STIX]{x1D709}_{t}$
. Figure 5 shows how quickly the values of the harmonic sum approximates the integral over a Gaussian perpendicular velocity distribution as the magnetic field becomes smaller.
$\unicode[STIX]{x1D709}_{t}$
. Figure 5 shows how quickly the values of the harmonic sum approximates the integral over a Gaussian perpendicular velocity distribution as the magnetic field becomes smaller.

Figure 5. Illustration of the Bessel function harmonic sum approximating a transverse Maxwellian distribution.
At low values of
![]() $\unicode[STIX]{x1D709}_{t}({<}1)$
(high magnetic field), only one or two harmonics give any substantial contribution. In the infinite-field limit, when only the
$\unicode[STIX]{x1D709}_{t}({<}1)$
(high magnetic field), only one or two harmonics give any substantial contribution. In the infinite-field limit, when only the
![]() $m=0$
harmonic matters (and
$m=0$
harmonic matters (and
![]() $\text{I}_{0}(0)=1$
), we return to the one-dimensional motion expression:
$\text{I}_{0}(0)=1$
), we return to the one-dimensional motion expression:
which amounts to setting effectively
![]() $k=0$
. As
$k=0$
. As
![]() $\unicode[STIX]{x1D6FA}$
is decreased from infinity (
$\unicode[STIX]{x1D6FA}$
is decreased from infinity (
![]() $\unicode[STIX]{x1D709}_{t}$
raised from zero), the
$\unicode[STIX]{x1D709}_{t}$
raised from zero), the
![]() $m=\pm 1$
terms next become important. And for
$m=\pm 1$
terms next become important. And for
![]() $\unicode[STIX]{x1D709}_{t}\ll 1$
, since
$\unicode[STIX]{x1D709}_{t}\ll 1$
, since
![]() $\text{e}^{-\unicode[STIX]{x1D709}_{t}^{2}}\text{I}_{m}(\unicode[STIX]{x1D709}_{t}^{2})\simeq (\unicode[STIX]{x1D709}_{t}^{2}/2)^{m}/m!$
, the higher-
$\text{e}^{-\unicode[STIX]{x1D709}_{t}^{2}}\text{I}_{m}(\unicode[STIX]{x1D709}_{t}^{2})\simeq (\unicode[STIX]{x1D709}_{t}^{2}/2)^{m}/m!$
, the higher-
![]() $m$
terms are negligible (although up to at least
$m$
terms are negligible (although up to at least
![]() $m=4$
are kept in the numerics to retain precision). Noting
$m=4$
are kept in the numerics to retain precision). Noting
![]() $\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D714}^{\prime })=(m_{e}\unicode[STIX]{x1D6E5}/q_{e})\unicode[STIX]{x1D714}^{\prime }\tilde{L}(\unicode[STIX]{x1D714}^{\prime })$
, in (5.9) the
$\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D714}^{\prime })=(m_{e}\unicode[STIX]{x1D6E5}/q_{e})\unicode[STIX]{x1D714}^{\prime }\tilde{L}(\unicode[STIX]{x1D714}^{\prime })$
, in (5.9) the
![]() $m=1$
relevant coefficient for small
$m=1$
relevant coefficient for small
![]() $\unicode[STIX]{x1D714}$
is
$\unicode[STIX]{x1D714}$
is
![]() $m\unicode[STIX]{x1D6FA}\unicode[STIX]{x1D6F7}_{m}\text{e}^{-\unicode[STIX]{x1D709}_{t}^{2}}\text{I}_{m}(\unicode[STIX]{x1D709}_{t}^{2})=(m_{e}\unicode[STIX]{x1D6E5}/q_{e})\tilde{L}\unicode[STIX]{x1D6FA}^{2}\unicode[STIX]{x1D709}_{t}^{2}$
$m\unicode[STIX]{x1D6FA}\unicode[STIX]{x1D6F7}_{m}\text{e}^{-\unicode[STIX]{x1D709}_{t}^{2}}\text{I}_{m}(\unicode[STIX]{x1D709}_{t}^{2})=(m_{e}\unicode[STIX]{x1D6E5}/q_{e})\tilde{L}\unicode[STIX]{x1D6FA}^{2}\unicode[STIX]{x1D709}_{t}^{2}$
![]() $/2=(m_{e}\unicode[STIX]{x1D6E5}/q_{e})\tilde{L}k^{2}v_{t}^{2}/2$
, whose only dependence on
$/2=(m_{e}\unicode[STIX]{x1D6E5}/q_{e})\tilde{L}k^{2}v_{t}^{2}/2$
, whose only dependence on
![]() $\unicode[STIX]{x1D6FA}$
enters through
$\unicode[STIX]{x1D6FA}$
enters through
![]() $\tilde{L}(\unicode[STIX]{x1D714}^{\prime })$
, that is through finite transit time effects. The particle force becomes
$\tilde{L}(\unicode[STIX]{x1D714}^{\prime })$
, that is through finite transit time effects. The particle force becomes
 $$\begin{eqnarray}\displaystyle \tilde{F} & = & \displaystyle -\text{i}\int q_{e}\frac{\text{d}\unicode[STIX]{x1D719}_{0}}{\text{d}z}\left[\frac{\unicode[STIX]{x2202}f_{\Vert 0}}{\unicode[STIX]{x2202}W_{\Vert }}\unicode[STIX]{x1D714}\mathop{\sum }_{m=0,\pm 1}[\unicode[STIX]{x1D6F7}_{m}\text{e}^{-\unicode[STIX]{x1D709}_{t}^{2}}\text{I}_{m}(\unicode[STIX]{x1D709}_{t}^{2})]\right.\nonumber\\ \displaystyle & & \displaystyle \quad +\left.\left(\frac{\unicode[STIX]{x2202}f_{\Vert 0}}{\unicode[STIX]{x2202}W_{\Vert }}+\frac{f_{\Vert 0}}{T_{\bot }}\right)\mathop{\sum }_{m=\pm 1}m\unicode[STIX]{x1D6FA}[\unicode[STIX]{x1D6F7}_{m}\text{e}^{-\unicode[STIX]{x1D709}_{t}^{2}}\text{I}_{m}(\unicode[STIX]{x1D709}_{t}^{2})]\right]\,\text{d}v_{z}\,\text{d}z\nonumber\\ \displaystyle & \simeq & \displaystyle -m_{e}\unicode[STIX]{x1D6E5}\int q_{e}\frac{\text{d}\unicode[STIX]{x1D719}_{0}}{\text{d}z}\!\left[\frac{\unicode[STIX]{x2202}f_{\Vert 0}}{\unicode[STIX]{x2202}W_{\Vert }}\unicode[STIX]{x1D714}^{2}\text{i}\tilde{L}(\unicode[STIX]{x1D714})+\frac{\unicode[STIX]{x2202}f_{\Vert t}}{\unicode[STIX]{x2202}W_{\Vert }}\left(1+\frac{1}{|\unicode[STIX]{x1D6FD}|}\right)\frac{1}{2}k^{2}v_{t}^{2}\mathop{\sum }_{\pm 1}\text{i}\tilde{L}(m\unicode[STIX]{x1D6FA}+\unicode[STIX]{x1D714})\right]\text{d}v_{z}\,\text{d}z,\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \tilde{F} & = & \displaystyle -\text{i}\int q_{e}\frac{\text{d}\unicode[STIX]{x1D719}_{0}}{\text{d}z}\left[\frac{\unicode[STIX]{x2202}f_{\Vert 0}}{\unicode[STIX]{x2202}W_{\Vert }}\unicode[STIX]{x1D714}\mathop{\sum }_{m=0,\pm 1}[\unicode[STIX]{x1D6F7}_{m}\text{e}^{-\unicode[STIX]{x1D709}_{t}^{2}}\text{I}_{m}(\unicode[STIX]{x1D709}_{t}^{2})]\right.\nonumber\\ \displaystyle & & \displaystyle \quad +\left.\left(\frac{\unicode[STIX]{x2202}f_{\Vert 0}}{\unicode[STIX]{x2202}W_{\Vert }}+\frac{f_{\Vert 0}}{T_{\bot }}\right)\mathop{\sum }_{m=\pm 1}m\unicode[STIX]{x1D6FA}[\unicode[STIX]{x1D6F7}_{m}\text{e}^{-\unicode[STIX]{x1D709}_{t}^{2}}\text{I}_{m}(\unicode[STIX]{x1D709}_{t}^{2})]\right]\,\text{d}v_{z}\,\text{d}z\nonumber\\ \displaystyle & \simeq & \displaystyle -m_{e}\unicode[STIX]{x1D6E5}\int q_{e}\frac{\text{d}\unicode[STIX]{x1D719}_{0}}{\text{d}z}\!\left[\frac{\unicode[STIX]{x2202}f_{\Vert 0}}{\unicode[STIX]{x2202}W_{\Vert }}\unicode[STIX]{x1D714}^{2}\text{i}\tilde{L}(\unicode[STIX]{x1D714})+\frac{\unicode[STIX]{x2202}f_{\Vert t}}{\unicode[STIX]{x2202}W_{\Vert }}\left(1+\frac{1}{|\unicode[STIX]{x1D6FD}|}\right)\frac{1}{2}k^{2}v_{t}^{2}\mathop{\sum }_{\pm 1}\text{i}\tilde{L}(m\unicode[STIX]{x1D6FA}+\unicode[STIX]{x1D714})\right]\text{d}v_{z}\,\text{d}z,\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
where terms of order
![]() $\unicode[STIX]{x1D714}/\unicode[STIX]{x1D6FA}$
and higher are neglected,
$\unicode[STIX]{x1D714}/\unicode[STIX]{x1D6FA}$
and higher are neglected,
![]() $\unicode[STIX]{x2202}f_{\Vert t}/\unicode[STIX]{x2202}W_{\Vert }$
denotes the trapped distribution’s slope, and the passing
$\unicode[STIX]{x2202}f_{\Vert t}/\unicode[STIX]{x2202}W_{\Vert }$
denotes the trapped distribution’s slope, and the passing
![]() $m=\pm 1$
contribution cancels by isotropy. This is identical to (4.22) except insofar as the argument of
$m=\pm 1$
contribution cancels by isotropy. This is identical to (4.22) except insofar as the argument of
![]() $\tilde{L}$
is changed. Since
$\tilde{L}$
is changed. Since
![]() $\tilde{L}$
is constant in the short transit time limit, instability there is not stabilized by magnetic field. The low-
$\tilde{L}$
is constant in the short transit time limit, instability there is not stabilized by magnetic field. The low-
![]() $k$
instability growth rate is still positive and given by (4.27) unless
$k$
instability growth rate is still positive and given by (4.27) unless
![]() $\unicode[STIX]{x1D6FA}$
is at least of order the predominant bounce frequency
$\unicode[STIX]{x1D6FA}$
is at least of order the predominant bounce frequency
![]() $\unicode[STIX]{x1D714}_{b}$
, so as to change
$\unicode[STIX]{x1D714}_{b}$
, so as to change
![]() $\tilde{L}(\unicode[STIX]{x1D6FA}+\unicode[STIX]{x1D714})$
. For definiteness we take
$\tilde{L}(\unicode[STIX]{x1D6FA}+\unicode[STIX]{x1D714})$
. For definiteness we take
![]() $\unicode[STIX]{x1D714}_{b}=\sqrt{\unicode[STIX]{x1D713}}/2$
, which is the (dimensionless) bounce frequency in a
$\unicode[STIX]{x1D714}_{b}=\sqrt{\unicode[STIX]{x1D713}}/2$
, which is the (dimensionless) bounce frequency in a
![]() $\unicode[STIX]{x1D713}\,\text{sech}^{4}z/4$
hole for trapped particles at the bottom of the potential energy well.
$\unicode[STIX]{x1D713}\,\text{sech}^{4}z/4$
hole for trapped particles at the bottom of the potential energy well.
What is required for stabilization is that (for small
![]() $\unicode[STIX]{x1D714}=\text{i}\unicode[STIX]{x1D714}_{i}$
) the value (which is real) of
$\unicode[STIX]{x1D714}=\text{i}\unicode[STIX]{x1D714}_{i}$
) the value (which is real) of
![]() $\sum _{m=\pm 1}\int \text{i}\tilde{L}(m\unicode[STIX]{x1D6FA}+\text{i}\unicode[STIX]{x1D714}_{i})(\text{d}\unicode[STIX]{x1D719}_{0}/\text{d}z)\,\text{d}z(\text{d}f_{\Vert t}/\text{d}W_{\Vert })\,\text{d}v_{z}$
, for trapped particles be reversed, or else reduced sufficiently that the combination with the electric field tension is reversed, so that the dispersion relation
$\sum _{m=\pm 1}\int \text{i}\tilde{L}(m\unicode[STIX]{x1D6FA}+\text{i}\unicode[STIX]{x1D714}_{i})(\text{d}\unicode[STIX]{x1D719}_{0}/\text{d}z)\,\text{d}z(\text{d}f_{\Vert t}/\text{d}W_{\Vert })\,\text{d}v_{z}$
, for trapped particles be reversed, or else reduced sufficiently that the combination with the electric field tension is reversed, so that the dispersion relation
![]() $\tilde{F}_{p}=-\tilde{F}_{t}+F_{E}$
cannot be satisfied.
$\tilde{F}_{p}=-\tilde{F}_{t}+F_{E}$
cannot be satisfied.
The total consequence of magnetization can be conveniently documented by creating a contour plot of the total force
![]() $\tilde{F}_{t}+\tilde{F}_{p}-F_{E}$
over the relevant domain of
$\tilde{F}_{t}+\tilde{F}_{p}-F_{E}$
over the relevant domain of
![]() $\unicode[STIX]{x1D714}_{i}=\unicode[STIX]{x1D6FE}$
and
$\unicode[STIX]{x1D714}_{i}=\unicode[STIX]{x1D6FE}$
and
![]() $k$
. The sum of cyclotron harmonics replaces the
$k$
. The sum of cyclotron harmonics replaces the
![]() $\int \text{d}v_{y}$
and is used to evaluate the force for the entire hole. Only the zero contour of a series of contour plots for different
$\int \text{d}v_{y}$
and is used to evaluate the force for the entire hole. Only the zero contour of a series of contour plots for different
![]() $\unicode[STIX]{x1D6FA}$
is shown in figure 6, since zero value occurs at the solution of the dispersion relation (when there is one). The labels are the values of
$\unicode[STIX]{x1D6FA}$
is shown in figure 6, since zero value occurs at the solution of the dispersion relation (when there is one). The labels are the values of
![]() $\unicode[STIX]{x1D6FA}/\unicode[STIX]{x1D714}_{b}$
. Once again, this is a nearly universal figure for the
$\unicode[STIX]{x1D6FA}/\unicode[STIX]{x1D714}_{b}$
. Once again, this is a nearly universal figure for the
![]() $\text{sech}^{4}(z/4)$
hole, at least at low
$\text{sech}^{4}(z/4)$
hole, at least at low
![]() $\unicode[STIX]{x1D713}$
where the
$\unicode[STIX]{x1D713}$
where the
![]() $\unicode[STIX]{x1D6FD}$
approximation for the trapped energy distribution is accurate.
$\unicode[STIX]{x1D6FD}$
approximation for the trapped energy distribution is accurate.

Figure 6. The zero contours of
![]() $F_{p}+F_{t}-F_{E}$
for magnetized holes labelled with the increasing values of
$F_{p}+F_{t}-F_{E}$
for magnetized holes labelled with the increasing values of
![]() $\unicode[STIX]{x1D6FA}/\unicode[STIX]{x1D714}_{b}$
. The contours give the dispersion relation
$\unicode[STIX]{x1D6FA}/\unicode[STIX]{x1D714}_{b}$
. The contours give the dispersion relation
![]() $\unicode[STIX]{x1D6FE}(k)$
. Magnetic stabilization of the transverse instability occurs as
$\unicode[STIX]{x1D6FE}(k)$
. Magnetic stabilization of the transverse instability occurs as
![]() $\unicode[STIX]{x1D6FA}/\unicode[STIX]{x1D714}_{b}\simeq 0.7$
is approached.
$\unicode[STIX]{x1D6FA}/\unicode[STIX]{x1D714}_{b}\simeq 0.7$
is approached.
Stabilization arises from a reversal of
![]() $\tilde{F}_{t}$
, which can be understood by examining the contributions to the trapped force from different trapped energy particles. Figure 7 shows how the contribution to trapped force from different parallel energy orbits varies for different real parts (
$\tilde{F}_{t}$
, which can be understood by examining the contributions to the trapped force from different trapped energy particles. Figure 7 shows how the contribution to trapped force from different parallel energy orbits varies for different real parts (
![]() $\unicode[STIX]{x1D714}_{r}$
) of
$\unicode[STIX]{x1D714}_{r}$
) of
![]() $\unicode[STIX]{x1D714}^{\prime }$
in (4.32). It is expressed as
$\unicode[STIX]{x1D714}^{\prime }$
in (4.32). It is expressed as
![]() $\text{d}F_{t}/\text{d}(-W_{\Vert })^{1/2}$
versus
$\text{d}F_{t}/\text{d}(-W_{\Vert })^{1/2}$
versus
![]() $(-W_{\Vert })^{1/2}$
, so that the total force is the area under the curve, integrated from zero to
$(-W_{\Vert })^{1/2}$
, so that the total force is the area under the curve, integrated from zero to
![]() $\sqrt{\unicode[STIX]{x1D713}}$
(the right-hand end). The application to a magnetized case is that the cyclotron harmonic trapped force contribution is equal to the same integral but with
$\sqrt{\unicode[STIX]{x1D713}}$
(the right-hand end). The application to a magnetized case is that the cyclotron harmonic trapped force contribution is equal to the same integral but with
![]() $\unicode[STIX]{x1D714}_{r}=\unicode[STIX]{x1D6FA}$
. So this plot represents how the (
$\unicode[STIX]{x1D714}_{r}=\unicode[STIX]{x1D6FA}$
. So this plot represents how the (
![]() $m=\pm 1$
) trapped force depends on parallel energy. The behaviour is dominated by resonances between the frequency
$m=\pm 1$
) trapped force depends on parallel energy. The behaviour is dominated by resonances between the frequency
![]() $\unicode[STIX]{x1D714}_{r}$
and the bounce frequency of the particles (and its harmonics, since the bounce orbits are anharmonic). The bounce frequency varies from zero for marginally trapped particles (
$\unicode[STIX]{x1D714}_{r}$
and the bounce frequency of the particles (and its harmonics, since the bounce orbits are anharmonic). The bounce frequency varies from zero for marginally trapped particles (
![]() $W_{\Vert }=0$
) to the value
$W_{\Vert }=0$
) to the value
![]() $\unicode[STIX]{x1D714}_{b}=\sqrt{\unicode[STIX]{x1D713}}/2$
for the deepest trapped particles
$\unicode[STIX]{x1D714}_{b}=\sqrt{\unicode[STIX]{x1D713}}/2$
for the deepest trapped particles
![]() $-W_{\Vert }=\unicode[STIX]{x1D713}$
. The resonant energy corresponds to the place where the curve passes rapidly through zero. For the unmagnetized case, contributions for
$-W_{\Vert }=\unicode[STIX]{x1D713}$
. The resonant energy corresponds to the place where the curve passes rapidly through zero. For the unmagnetized case, contributions for
![]() $kv_{y}=\unicode[STIX]{x1D714}_{r}$
are represented by the same plot.
$kv_{y}=\unicode[STIX]{x1D714}_{r}$
are represented by the same plot.

Figure 7. Contributions to the trapped particle force for specific real and imaginary parts of
![]() $\unicode[STIX]{x1D714}^{\prime }$
, as a function of trapped energy. The real part
$\unicode[STIX]{x1D714}^{\prime }$
, as a function of trapped energy. The real part
![]() $\unicode[STIX]{x1D714}_{r}$
corresponds to
$\unicode[STIX]{x1D714}_{r}$
corresponds to
![]() $\unicode[STIX]{x1D6FA}$
. The effects of bounce resonances dominate the variation at higher
$\unicode[STIX]{x1D6FA}$
. The effects of bounce resonances dominate the variation at higher
![]() $\unicode[STIX]{x1D714}_{r}$
. Resonances are sharper at lower
$\unicode[STIX]{x1D714}_{r}$
. Resonances are sharper at lower
![]() $\unicode[STIX]{x1D714}_{i}$
, (b), than at higher, (a).
$\unicode[STIX]{x1D714}_{i}$
, (b), than at higher, (a).
Low
![]() $\unicode[STIX]{x1D714}_{r}$
is resonant only at very low bounce frequency, which means low
$\unicode[STIX]{x1D714}_{r}$
is resonant only at very low bounce frequency, which means low
![]() $|W_{\Vert }|$
: marginally trapped particles at the left-hand end of the plot. Thus the areas under curves 1 and 2 in figure 7(a) are dominated by regions to the right of the resonances, where
$|W_{\Vert }|$
: marginally trapped particles at the left-hand end of the plot. Thus the areas under curves 1 and 2 in figure 7(a) are dominated by regions to the right of the resonances, where
![]() $\text{d}F_{t}/\text{d}(-W)^{1/2}$
is positive. Curves 3 and 4 show the fundamental resonance approaching the centre of the energy range; so significant contribution is beginning to arise from regions to the left of the fundamental resonance where
$\text{d}F_{t}/\text{d}(-W)^{1/2}$
is positive. Curves 3 and 4 show the fundamental resonance approaching the centre of the energy range; so significant contribution is beginning to arise from regions to the left of the fundamental resonance where
![]() $\text{d}F_{t}/\text{d}(-W)^{1/2}$
is negative. Curves 5 and 6 show the transition to the state where the negative contributions exceed the positive, and curve 8 corresponds to
$\text{d}F_{t}/\text{d}(-W)^{1/2}$
is negative. Curves 5 and 6 show the transition to the state where the negative contributions exceed the positive, and curve 8 corresponds to
![]() $\unicode[STIX]{x1D714}_{r}=\sqrt{\unicode[STIX]{x1D713}}/2$
where the resonance is exactly at the right-hand end of the energy range: particles at the bottom of the potential well. It has a clearly predominant negative integrated force. For the higher frequencies, e.g. 8 and 9, it is easy to see the second (and higher) bounce-frequency harmonic resonance effects in the left-hand one third of the energy range.
$\unicode[STIX]{x1D714}_{r}=\sqrt{\unicode[STIX]{x1D713}}/2$
where the resonance is exactly at the right-hand end of the energy range: particles at the bottom of the potential well. It has a clearly predominant negative integrated force. For the higher frequencies, e.g. 8 and 9, it is easy to see the second (and higher) bounce-frequency harmonic resonance effects in the left-hand one third of the energy range.
All these qualitative statements depend little on the choice of other parameters. The hole depth
![]() $\unicode[STIX]{x1D713}$
determines the energy range of the plot; the imaginary part of
$\unicode[STIX]{x1D713}$
determines the energy range of the plot; the imaginary part of
![]() $\unicode[STIX]{x1D714}^{\prime }$
,
$\unicode[STIX]{x1D714}^{\prime }$
,
![]() $\unicode[STIX]{x1D714}_{i}$
, determines the sharpness of the resonance, as is seen by comparing figures 7(a) with 7(b). Low
$\unicode[STIX]{x1D714}_{i}$
, determines the sharpness of the resonance, as is seen by comparing figures 7(a) with 7(b). Low
![]() $\unicode[STIX]{x1D714}_{i}$
requires fine energy mesh to resolve accurately. Once
$\unicode[STIX]{x1D714}_{i}$
requires fine energy mesh to resolve accurately. Once
![]() $\unicode[STIX]{x1D714}_{r}>\unicode[STIX]{x1D714}_{b}$
the first bounce harmonic resonance disappears but stability remains, showing that cyclotron damping per se is not the stabilization mechanism, since no particles are then resonant.
$\unicode[STIX]{x1D714}_{r}>\unicode[STIX]{x1D714}_{b}$
the first bounce harmonic resonance disappears but stability remains, showing that cyclotron damping per se is not the stabilization mechanism, since no particles are then resonant.
6 Summary
The transverse instability of an electron hole in an isotropic Maxwellian background plasma arises not because of orbit transverse ‘focusing’ but because of the overall hole force balance arising from the kinematic parallel jetting (energization) of particles. The shift mode is the relevant low-frequency perturbation eigenmode, proportional to the spatial derivative of the hole potential. It is demonstrated that a linearized Vlasov–Poisson calculation of the jetting force gives expressions identical at low frequency to those recently derived by more elementary analysis. Previous stability analyses of symmetric eigenmodes are irrelevant to the long-wavelength shift mode which kinks the hole, because the shift mode is antisymmetric. A rigorous linear analysis of the dispersion relation of the shift mode has been completed for a slowly moving electron hole, ignoring ion motion. The instability is purely growing and
![]() $\unicode[STIX]{x1D6FE}(k)$
has been found and expressed in essentially universal form (figure 4). The peak growth rate occurs, for a
$\unicode[STIX]{x1D6FE}(k)$
has been found and expressed in essentially universal form (figure 4). The peak growth rate occurs, for a
![]() $\unicode[STIX]{x1D713}\,\text{sech}^{4}(z/4\unicode[STIX]{x1D706}_{D})$
hole potential, at
$\unicode[STIX]{x1D713}\,\text{sech}^{4}(z/4\unicode[STIX]{x1D706}_{D})$
hole potential, at
![]() $k\unicode[STIX]{x1D706}_{D}\simeq \sqrt{e\unicode[STIX]{x1D713}/T_{e}}/8$
, with a value (in the absence of magnetic field) slightly above
$k\unicode[STIX]{x1D706}_{D}\simeq \sqrt{e\unicode[STIX]{x1D713}/T_{e}}/8$
, with a value (in the absence of magnetic field) slightly above
![]() $\unicode[STIX]{x1D6FE}=\unicode[STIX]{x1D714}_{p}\sqrt{e\unicode[STIX]{x1D713}/T_{e}}/16$
, in good confirmation of the recent estimates (Hutchinson Reference Hutchinson2018) based on the same kinematic mechanism. The magnetized case has also been analysed (figure 6), showing that stabilization occurs at
$\unicode[STIX]{x1D6FE}=\unicode[STIX]{x1D714}_{p}\sqrt{e\unicode[STIX]{x1D713}/T_{e}}/16$
, in good confirmation of the recent estimates (Hutchinson Reference Hutchinson2018) based on the same kinematic mechanism. The magnetized case has also been analysed (figure 6), showing that stabilization occurs at
![]() $\unicode[STIX]{x1D6FA}\simeq 0.7\unicode[STIX]{x1D714}_{b}$
where
$\unicode[STIX]{x1D6FA}\simeq 0.7\unicode[STIX]{x1D714}_{b}$
where
![]() $\unicode[STIX]{x1D714}_{b}=\unicode[STIX]{x1D714}_{p}\sqrt{e\unicode[STIX]{x1D713}/T_{e}}/2$
is the bounce frequency of deeply trapped electrons. Stabilization occurs because the jetting force on the trapped electrons reverses its sign across the resonance between the bounce and cyclotron frequencies (figure 7). The same sort of reversal effect is responsible for suppressing the unmagnetized instability when
$\unicode[STIX]{x1D714}_{b}=\unicode[STIX]{x1D714}_{p}\sqrt{e\unicode[STIX]{x1D713}/T_{e}}/2$
is the bounce frequency of deeply trapped electrons. Stabilization occurs because the jetting force on the trapped electrons reverses its sign across the resonance between the bounce and cyclotron frequencies (figure 7). The same sort of reversal effect is responsible for suppressing the unmagnetized instability when
![]() $kv_{t}\gtrsim \unicode[STIX]{x1D714}_{b}$
. This upper
$kv_{t}\gtrsim \unicode[STIX]{x1D714}_{b}$
. This upper
![]() $k$
-limit suggests that holes with transverse extent less than approximately
$k$
-limit suggests that holes with transverse extent less than approximately
![]() $4\unicode[STIX]{x03C0}\unicode[STIX]{x1D706}_{D}\sqrt{T_{e}/e\unicode[STIX]{x1D713}}$
should not suffer this instability. As (4.27) shows, it is the transverse temperature
$4\unicode[STIX]{x03C0}\unicode[STIX]{x1D706}_{D}\sqrt{T_{e}/e\unicode[STIX]{x1D713}}$
should not suffer this instability. As (4.27) shows, it is the transverse temperature
![]() $T_{y}$
that determines the low-
$T_{y}$
that determines the low-
![]() $k$
growth rate. Particle-in-cell simulations observe that the transverse temperature can alter the observed growth rate, but have not yet established the dependence systematically enough to test the analytical prediction.
$k$
growth rate. Particle-in-cell simulations observe that the transverse temperature can alter the observed growth rate, but have not yet established the dependence systematically enough to test the analytical prediction.
There remain some discrepancies between the present analysis and simulation observations. In Maxwellian plasmas it has been documented in Hutchinson (Reference Hutchinson2018) that a higher magnetic field
![]() $\unicode[STIX]{x1D6FA}\simeq 1.5\sqrt{\unicode[STIX]{x1D713}}/2$
than predicted here is needed for complete stability. That might perhaps be explained by the simulation potential being more peaked than
$\unicode[STIX]{x1D6FA}\simeq 1.5\sqrt{\unicode[STIX]{x1D713}}/2$
than predicted here is needed for complete stability. That might perhaps be explained by the simulation potential being more peaked than
![]() $\text{sech}^{4}(z/4\unicode[STIX]{x1D706}_{D})$
or by trapped electron distributions differing from the negative-temperature Maxwellian form used here. But it might also indicate a shortcoming in the assumption made here that the eigenmode is a pure shift mode. It is possible that a distorted or more complicated mode might remain less stable near the shift mode’s marginal stability.
$\text{sech}^{4}(z/4\unicode[STIX]{x1D706}_{D})$
or by trapped electron distributions differing from the negative-temperature Maxwellian form used here. But it might also indicate a shortcoming in the assumption made here that the eigenmode is a pure shift mode. It is possible that a distorted or more complicated mode might remain less stable near the shift mode’s marginal stability.
Simulations with non-Maxwellian background plasma (Goldman et al.
Reference Goldman, Oppenheim and Newman1999; Oppenheim et al.
Reference Oppenheim, Newman and Goldman1999; Newman et al.
Reference Newman, Goldman, Spector and Perez2001; Oppenheim et al.
Reference Oppenheim, Vetoulis, Newman and Goldman2001; Berthomier et al.
Reference Berthomier, Muschietti, Bonnell, Roth and Carlson2002; Lu et al.
Reference Lu, Lembege, Tao and Wang2008; Wu et al.
Reference Wu, Lu, Huang and Wang2010) have also observed instabilities of different character and shorter
![]() $y$
-wavelength even above this higher-field stability limit. And holes of limited transverse dimensions are observed by spacecraft even in regions where
$y$
-wavelength even above this higher-field stability limit. And holes of limited transverse dimensions are observed by spacecraft even in regions where
![]() $\unicode[STIX]{x1D6FA}>\unicode[STIX]{x1D714}_{b}$
, as well as in lower magnetic field regions. These facts are not explained by the current transverse instability analysis. Maxwellian shape
$\unicode[STIX]{x1D6FA}>\unicode[STIX]{x1D714}_{b}$
, as well as in lower magnetic field regions. These facts are not explained by the current transverse instability analysis. Maxwellian shape
![]() $f(v)$
was deliberately chosen here to give an unequivocally stable background and rule out instability enhancement by the untrapped background. The present analysis can readily be extended to address such cases as anisotropic bi-Maxwellians. In any case, the ‘whistler’ or ‘streaked’ instabilities observed at high magnetic field in codes are not pure shift modes, and probably require different assumptions about eigenstructure, such as those of Vetoulis & Oppenheim (Reference Vetoulis and Oppenheim2001).
$f(v)$
was deliberately chosen here to give an unequivocally stable background and rule out instability enhancement by the untrapped background. The present analysis can readily be extended to address such cases as anisotropic bi-Maxwellians. In any case, the ‘whistler’ or ‘streaked’ instabilities observed at high magnetic field in codes are not pure shift modes, and probably require different assumptions about eigenstructure, such as those of Vetoulis & Oppenheim (Reference Vetoulis and Oppenheim2001).
Acknowledgements
I am grateful to C. Zhou for our many thoughtful discussions of electron hole kinematics, and to the anonymous reviewer of a previous paper who alerted us to the ideas in § 3.1. X. Chen helped by checking some of the algebra. This work was partially supported by NASA grant NNX16AG82G.