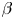1. The problem
The effects of climate change are already manifesting and the existing portfolio of clean energy sources has not been deployed quickly enough to broadly reduce greenhouse gas emissions. Controlled nuclear fusion is a safe and dispatchable source of energy, produces no greenhouse gas emissions and generates minimal radiological waste. It is a possible solution to the world's urgent need for clean energy, provided that it is developed and deployed rapidly in order to make a difference on the time scales necessary to have an impact on climate change.
Within this framework, SPARC – see Creely et al. (Reference Creely, Greenwald, Ballinger, Brunner, Canik, Doody, Fülöp, Garnier, Granetz and Gray2020), Rodriguez-Fernandez et al. (Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020) and references therein – is a proposed high-field, medium-size tokamak operating with deuterium–tritium (DT) fuel, superconducting coils and ion cyclotron range-of-frequencies (ICRF) auxiliary heating. The SPARC project aims at building a machine based on conservative, well-established physics assumptions. SPARC aims to achieve $Q > 2$![]() (where the dimensionless fusion gain $Q$
(where the dimensionless fusion gain $Q$![]() is defined as the fusion power $W_{{\rm fus}}$
is defined as the fusion power $W_{{\rm fus}}$![]() generated in the plasma divided by the external heating power absorbed in the plasma, i.e. the sum $W_{{\rm aux}} + W_{{\rm ohm}}$
generated in the plasma divided by the external heating power absorbed in the plasma, i.e. the sum $W_{{\rm aux}} + W_{{\rm ohm}}$![]() of auxiliary power $W_{{\rm aux}}$
of auxiliary power $W_{{\rm aux}}$![]() and ohmic power $W_{{\rm ohm}}$
and ohmic power $W_{{\rm ohm}}$![]() ) with unambiguous margin over break-even ($Q = 1$
) with unambiguous margin over break-even ($Q = 1$![]() ), itself a critical next step on the path to commercial fusion energy. A list of main plasma parameters for current SPARC design includes: major radius $R_{0} = 1.87$
), itself a critical next step on the path to commercial fusion energy. A list of main plasma parameters for current SPARC design includes: major radius $R_{0} = 1.87$![]() m, minor radius $a_{p} = 0.57$
m, minor radius $a_{p} = 0.57$![]() m, vacuum toroidal magnetic field on axis $B_{T} = 12.2$
m, vacuum toroidal magnetic field on axis $B_{T} = 12.2$![]() T, plasma current $I_{p} = 8.7$
T, plasma current $I_{p} = 8.7$![]() MA, elongation at the separatrix (defined as the cross-sectional area divided by $\pi a_{p}^{2}$
MA, elongation at the separatrix (defined as the cross-sectional area divided by $\pi a_{p}^{2}$![]() ) $k_{{\rm sep}} = 1.97$
) $k_{{\rm sep}} = 1.97$![]() , $\delta _{{\rm sep}} = 0.54$
, $\delta _{{\rm sep}} = 0.54$![]() triangularity at the separatrix, ICRF power $W_{{\rm aux}} \leq 25$
triangularity at the separatrix, ICRF power $W_{{\rm aux}} \leq 25$![]() MW (via $^{3}{\rm He}$
MW (via $^{3}{\rm He}$![]() minority and second-harmonic tritium absorption; Lin, Wright & Wukitch Reference Lin, Wright and Wukitch2020) and plasma current flat-top duration $\varDelta t_{{\rm flat}} = 10$
minority and second-harmonic tritium absorption; Lin, Wright & Wukitch Reference Lin, Wright and Wukitch2020) and plasma current flat-top duration $\varDelta t_{{\rm flat}} = 10$![]() s (Creely et al. Reference Creely, Greenwald, Ballinger, Brunner, Canik, Doody, Fülöp, Garnier, Granetz and Gray2020).
s (Creely et al. Reference Creely, Greenwald, Ballinger, Brunner, Canik, Doody, Fülöp, Garnier, Granetz and Gray2020).
A recent, successful test (Chandler Reference Chandler2021) of a $20$![]() T high-temperature superconductor (HTS) (Bruzzone et al. Reference Bruzzone, Fietz, Minervini, Novikov, Yanagi, Zhai and Zheng2018) magnet has sparked the interest in SPARC, as a HTS enables high strength of $B_{T}$
T high-temperature superconductor (HTS) (Bruzzone et al. Reference Bruzzone, Fietz, Minervini, Novikov, Yanagi, Zhai and Zheng2018) magnet has sparked the interest in SPARC, as a HTS enables high strength of $B_{T}$![]() . It is claimed (Creely et al. Reference Creely, Greenwald, Ballinger, Brunner, Canik, Doody, Fülöp, Garnier, Granetz and Gray2020) that HTS allows the following:
. It is claimed (Creely et al. Reference Creely, Greenwald, Ballinger, Brunner, Canik, Doody, Fülöp, Garnier, Granetz and Gray2020) that HTS allows the following:
(i) To operate at high volume-averaged electron density ($\langle n_{e} \rangle = 3 \times 10^{20}$
 m$^{-3}$
m$^{-3}$ ) and electron temperature ($\langle T_{e}\rangle = 7$
) and electron temperature ($\langle T_{e}\rangle = 7$ keV), while still enforcing significant margin to the Greenwald limit $f_{G} \equiv {\pi a^{2} \langle n_{e}\rangle (10^{20}\,{\rm m}^{-3})}/{0.9 I_{p}\ ({\rm MA})} = 0.37 < 1$
keV), while still enforcing significant margin to the Greenwald limit $f_{G} \equiv {\pi a^{2} \langle n_{e}\rangle (10^{20}\,{\rm m}^{-3})}/{0.9 I_{p}\ ({\rm MA})} = 0.37 < 1$ on $\langle n_{e}\rangle$
on $\langle n_{e}\rangle$ , Troyon limit $\beta _{N} \equiv {a B_{T} \beta _{T}}/{I_{p}\ ({\rm MA})} = 1.0 < 3$
, Troyon limit $\beta _{N} \equiv {a B_{T} \beta _{T}}/{I_{p}\ ({\rm MA})} = 1.0 < 3$ on $\beta _{T} \equiv {2 \mu _{0} \langle p\rangle }/{B_{T}^{2}}$
on $\beta _{T} \equiv {2 \mu _{0} \langle p\rangle }/{B_{T}^{2}}$ (in %, $\langle p\rangle$
(in %, $\langle p\rangle$ being the volume average of the pressure $p$
being the volume average of the pressure $p$ ) and the disruptive kink limit on the edge safety factor $q^{*} \equiv {5a^{2}R_{0}B_{T}[1+k_{{\rm sep}}^{2}(1+2\delta _{{\rm sep}}^{2}-1.2\delta _{{\rm sep}}^{3})]}/{2I_{p}\ ({\rm MA})} = 3.05 > 2.2$
) and the disruptive kink limit on the edge safety factor $q^{*} \equiv {5a^{2}R_{0}B_{T}[1+k_{{\rm sep}}^{2}(1+2\delta _{{\rm sep}}^{2}-1.2\delta _{{\rm sep}}^{3})]}/{2I_{p}\ ({\rm MA})} = 3.05 > 2.2$ (Sorbom et al. Reference Sorbom, Ball, Palmer, Mangiarotti, Sierchio, Bonoli, Kasten, Sutherland, Barnard and Haakonsen2015).
(Sorbom et al. Reference Sorbom, Ball, Palmer, Mangiarotti, Sierchio, Bonoli, Kasten, Sutherland, Barnard and Haakonsen2015).(ii) To achieve $Q > 2$
 because of the favourable dependence of fusion power with $B_{T}^{4}$
because of the favourable dependence of fusion power with $B_{T}^{4}$ . Should SPARC exceed its goal and achieve still higher gain – e.g. $Q = 11$
. Should SPARC exceed its goal and achieve still higher gain – e.g. $Q = 11$ and $Q = 9$
and $Q = 9$ in Creely et al. (Reference Creely, Greenwald, Ballinger, Brunner, Canik, Doody, Fülöp, Garnier, Granetz and Gray2020) and Rodriguez-Fernandez et al. (Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020), respectively – it would also address many novel challenges in the research on burning plasmas, i.e. those reactor-relevant plasmas where the heating power $W_{\alpha } = {W_{{\rm fus}}}/{5} = {Q(W_{{\rm aux}} + W_{{\rm ohm}})}/{5}$
in Creely et al. (Reference Creely, Greenwald, Ballinger, Brunner, Canik, Doody, Fülöp, Garnier, Granetz and Gray2020) and Rodriguez-Fernandez et al. (Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020), respectively – it would also address many novel challenges in the research on burning plasmas, i.e. those reactor-relevant plasmas where the heating power $W_{\alpha } = {W_{{\rm fus}}}/{5} = {Q(W_{{\rm aux}} + W_{{\rm ohm}})}/{5}$ from the fusion-produced $\alpha$
from the fusion-produced $\alpha$ 's (Scott et al. Reference Scott, Kramer, Tolman, Snicker, Varje, Särkimäki, Wright and Rodriguez-Fernandez2020) exceeds $W_{{\rm aux}} + W_{{\rm ohm}}$
's (Scott et al. Reference Scott, Kramer, Tolman, Snicker, Varje, Särkimäki, Wright and Rodriguez-Fernandez2020) exceeds $W_{{\rm aux}} + W_{{\rm ohm}}$ . A list of these challenges includes, for example, the control of the thermal stability of the fusion burn, the verification of the predicted robustness (Tolman et al. Reference Tolman, Loureiro, Rodrigues, Hughes and Marmar2019) of high-field tokamak plasmas like in SPARC (Scott et al. Reference Scott, Kramer, Tolman, Snicker, Varje, Särkimäki, Wright and Rodriguez-Fernandez2020) and IGNITOR (Bombarda et al. Reference Bombarda, Coppi, Airoldi, Cenacchi and Detragiache2004) against instabilities involving Alfvèn eigenmodes triggered by fusion-produced $\alpha$
. A list of these challenges includes, for example, the control of the thermal stability of the fusion burn, the verification of the predicted robustness (Tolman et al. Reference Tolman, Loureiro, Rodrigues, Hughes and Marmar2019) of high-field tokamak plasmas like in SPARC (Scott et al. Reference Scott, Kramer, Tolman, Snicker, Varje, Särkimäki, Wright and Rodriguez-Fernandez2020) and IGNITOR (Bombarda et al. Reference Bombarda, Coppi, Airoldi, Cenacchi and Detragiache2004) against instabilities involving Alfvèn eigenmodes triggered by fusion-produced $\alpha$ 's, the assessment of the impact of ripple on the $\alpha$
's, the assessment of the impact of ripple on the $\alpha$ 's (Scott et al. Reference Scott, Kramer, Tolman, Snicker, Varje, Särkimäki, Wright and Rodriguez-Fernandez2020) and the optimization of detection and mitigation of vertically unstable current quench in a reactor-relevant environment (Sweeney et al. Reference Sweeney, Creely, Doody, Fülöp, Garnier, Granetz, Greenwald, Hesslow, Irby and Izzo2020).
's (Scott et al. Reference Scott, Kramer, Tolman, Snicker, Varje, Särkimäki, Wright and Rodriguez-Fernandez2020) and the optimization of detection and mitigation of vertically unstable current quench in a reactor-relevant environment (Sweeney et al. Reference Sweeney, Creely, Doody, Fülöp, Garnier, Granetz, Greenwald, Hesslow, Irby and Izzo2020).(iii) To extrapolate quickly the results obtained to the design of an economically viable power plant. In contrast, overcoming the electricity cost of running the magnets in a power plant may be difficult if the toroidal field coils are made of copper, as envisaged, for example, in IGNITOR. SPARC is slated for completion in 2025, i.e. many years in advance on the much larger ITER with its Nb-alloy low-temperature superconductors.
Both physics and engineering in SPARC try to be as conventional as possible so that minimum extrapolation is required, the novelty being the HTS magnet technology. SPARC is designed with considerable margin in plasma performance in order to ensure that the machine's mission is feasible even given the uncertainties in performance projections. To start with, performance projections for SPARC are based largely on the ITER Physics Basis (Shimada et al. Reference Shimada, Campbell, Mukhovatov, Fujiwara, Kirneva, Lackner, Nagami, Pustovitov, Uckan and Wesley2007). Moreover, the results of simulations appear to be robust against uncertainties in pedestal predictions, such as in cases where pedestals are degraded as a consequence of high gas puffing that may be needed to reach target densities. Finally, SPARC has no neutral beam. Then, toroidal plasma rotation is expected to only have contributions from self-generated residual turbulent stresses, i.e. intrinsic rotation; the latter is likely to lead to a small increase in performance through perpendicular flow shear stabilization of core turbulence. Conservatively, it is assumed that there will be no rotation overall. Optimistic predictions have been obtained through both a zero-dimensional approach based on empirical scaling laws and 1.5-dimensional time-dependent solutions of the transport equations based on first principles. The results of these two independent workflows agree significantly with each other (Creely et al. Reference Creely, Greenwald, Ballinger, Brunner, Canik, Doody, Fülöp, Garnier, Granetz and Gray2020; Rodriguez-Fernandez et al. Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020).
No matter how conservative, however, these predictions are still affected by various uncertainties. Firstly, there is a scatter in the confinement scaling relationship. Secondly, the assumed value $Z_{{\rm eff}} = 1.5$![]() of the effective charge is likely to be a reasonable one at high values of $\langle n_{e} \rangle$
of the effective charge is likely to be a reasonable one at high values of $\langle n_{e} \rangle$![]() ; however, impurity concentrations vary significantly in existing machines, and so introduce considerable uncertainty when projecting to SPARC. Thirdly, sawteeth are predicted to occur; but the prediction of sawtooth period and dynamics is highly uncertain. Fourthly, both L-mode and H-mode operation are envisaged in SPARC; ICRF heating power is set to the level required to sustain the H-mode at the operational density, accounting for the heating due to the $\alpha$
; however, impurity concentrations vary significantly in existing machines, and so introduce considerable uncertainty when projecting to SPARC. Thirdly, sawteeth are predicted to occur; but the prediction of sawtooth period and dynamics is highly uncertain. Fourthly, both L-mode and H-mode operation are envisaged in SPARC; ICRF heating power is set to the level required to sustain the H-mode at the operational density, accounting for the heating due to the $\alpha$![]() 's to maintain the plasma above the L–H power threshold. The L–H transition is assumed to occur at the very beginning of the flat top (Rodriguez-Fernandez et al. Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020), i.e. about $8$
's to maintain the plasma above the L–H power threshold. The L–H transition is assumed to occur at the very beginning of the flat top (Rodriguez-Fernandez et al. Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020), i.e. about $8$![]() s after the beginning of the discharge (Creely et al. Reference Creely, Greenwald, Ballinger, Brunner, Canik, Doody, Fülöp, Garnier, Granetz and Gray2020). However, the physics of the L–H transition is still an area of active research and predictions of the power required to transition have considerable uncertainty. Furthermore, a detailed description of the average impurity mix that will be present in SPARC H-mode plasmas is beyond current predictive capabilities because source rates depend on details of plasma–wall interactions and edge transport. Finally, the diffusion and convection particle coefficients for thermal $^{4}$
s after the beginning of the discharge (Creely et al. Reference Creely, Greenwald, Ballinger, Brunner, Canik, Doody, Fülöp, Garnier, Granetz and Gray2020). However, the physics of the L–H transition is still an area of active research and predictions of the power required to transition have considerable uncertainty. Furthermore, a detailed description of the average impurity mix that will be present in SPARC H-mode plasmas is beyond current predictive capabilities because source rates depend on details of plasma–wall interactions and edge transport. Finally, the diffusion and convection particle coefficients for thermal $^{4}$![]() He are kept constant during the simulations, and the $^{4}$
He are kept constant during the simulations, and the $^{4}$![]() He effective particle confinement time is ${\approx }4$
He effective particle confinement time is ${\approx }4$![]() times the energy confinement time, which is equivalent to postulating that edge-localized modes ensure efficient ash removal. In particular, the time-dependent evolution of particle density and temperatures for ions and electrons is described with the help of both an analytical model for neoclassical transport and a sophisticated, quasi-linear model for the turbulent transport fluxes in the plasma between the pedestal near the edge and a region surrounding the magnetic axis; an ad hoc treatment of on-axis transport is implemented near the magnetic axis. The detailed analysis presented in Rodriguez-Fernandez et al. (Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020) (figure 7) shows that the plasma becomes a burning plasma within the first $2$
times the energy confinement time, which is equivalent to postulating that edge-localized modes ensure efficient ash removal. In particular, the time-dependent evolution of particle density and temperatures for ions and electrons is described with the help of both an analytical model for neoclassical transport and a sophisticated, quasi-linear model for the turbulent transport fluxes in the plasma between the pedestal near the edge and a region surrounding the magnetic axis; an ad hoc treatment of on-axis transport is implemented near the magnetic axis. The detailed analysis presented in Rodriguez-Fernandez et al. (Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020) (figure 7) shows that the plasma becomes a burning plasma within the first $2$![]() s of the current flat top. However, this analysis ignores the possible plasma trajectory needed to access (and subsequently sustain) the H-mode, which may require higher auxiliary power $W_{{\rm aux}}$
s of the current flat top. However, this analysis ignores the possible plasma trajectory needed to access (and subsequently sustain) the H-mode, which may require higher auxiliary power $W_{{\rm aux}}$![]() than the assumed value of $11$
than the assumed value of $11$![]() MW for some early portion of the flat top. Given the considerable values of both ion and electron temperatures predicted already at the beginning of the flat top and the large value of $Q$
MW for some early portion of the flat top. Given the considerable values of both ion and electron temperatures predicted already at the beginning of the flat top and the large value of $Q$![]() predicted 2 s later, this uncertainty is of considerable importance, as it is precisely the detailed unsteady evolution in the first 2 s of flat top that raises $Q$
predicted 2 s later, this uncertainty is of considerable importance, as it is precisely the detailed unsteady evolution in the first 2 s of flat top that raises $Q$![]() .
.
The likelihood of this unsteady scenario at the beginning of the flat top depends crucially on the choices made when solving the time-dependent transport equations. In turn, these choices are affected by the known difficulties of present heat transport models in predicting turbulence and associated transport. Unfortunately, past experience in time-dependent simulation of IGNITOR (Bombarda et al. Reference Bombarda, Coppi, Airoldi, Cenacchi and Detragiache2004) – where ${{{\rm d}}I_{p}}/{{{\rm d}}t} \approx 2.8$![]() MA s$^{-1}$
MA s$^{-1}$![]() in the ramp-up, ${W_{{\rm aux}}}/{W_{{\rm ohm}}} \leq 1$
in the ramp-up, ${W_{{\rm aux}}}/{W_{{\rm ohm}}} \leq 1$![]() and the toroidal electric field is strongly non-uniform – is scarcely useful when it comes to SPARC, where ${{{\rm d}}I_{p}}/{{{\rm d}}t} \approx 1.1$
and the toroidal electric field is strongly non-uniform – is scarcely useful when it comes to SPARC, where ${{{\rm d}}I_{p}}/{{{\rm d}}t} \approx 1.1$![]() MA s$^{-1}$
MA s$^{-1}$![]() and ${W_{{\rm aux}}}/{W_{{\rm ohm}}} \gg 1$
and ${W_{{\rm aux}}}/{W_{{\rm ohm}}} \gg 1$![]() (Creely et al. Reference Creely, Greenwald, Ballinger, Brunner, Canik, Doody, Fülöp, Garnier, Granetz and Gray2020). Such uncertainties make it difficult to assess the self-consistency of this unsteady scenario independently, even if this assessment is highly desirable. Generally speaking, the less an independent assessment depends on a particular detailed model for energy and impurity transport, sawteeth, L–H mode transition, etc., the better. In this paper we discuss a possible basis for such assessment.
(Creely et al. Reference Creely, Greenwald, Ballinger, Brunner, Canik, Doody, Fülöp, Garnier, Granetz and Gray2020). Such uncertainties make it difficult to assess the self-consistency of this unsteady scenario independently, even if this assessment is highly desirable. Generally speaking, the less an independent assessment depends on a particular detailed model for energy and impurity transport, sawteeth, L–H mode transition, etc., the better. In this paper we discuss a possible basis for such assessment.
2. Thermal runaway
We assume the following ordering:
where $\tau _{{\rm MHD}} = O ( 10^{-7} )$![]() s, $\tau _{e} = O ( 10^{-4} )$
s, $\tau _{e} = O ( 10^{-4} )$![]() s, $\tau _{i} = O ( 10^{-2} )$
s, $\tau _{i} = O ( 10^{-2} )$![]() s, $\tau _{{\rm sd}} = O ( 10^{-2} )$
s, $\tau _{{\rm sd}} = O ( 10^{-2} )$![]() , $\tau _{E} \approx 0.77$
, $\tau _{E} \approx 0.77$![]() s, $\tau _{{\rm saw}} \approx 1$
s, $\tau _{{\rm saw}} \approx 1$![]() s, $\tau _{{\rm ramp}} \approx I_{p} \vert {{{\rm d}}I_{p}}/{{{\rm d}}t}\vert ^{-1} \approx 8$
s, $\tau _{{\rm ramp}} \approx I_{p} \vert {{{\rm d}}I_{p}}/{{{\rm d}}t}\vert ^{-1} \approx 8$![]() s and $\varDelta t_{{\rm flat}} = 10$
s and $\varDelta t_{{\rm flat}} = 10$![]() s are the typical time scale of ideal magnetohydrodynamics (MHD), the electron–electron collision time, the ion–ion collision time, the typical time scale of slowing down of fusion-produced $\alpha$
s are the typical time scale of ideal magnetohydrodynamics (MHD), the electron–electron collision time, the ion–ion collision time, the typical time scale of slowing down of fusion-produced $\alpha$![]() 's, the energy confinement time, the sawtooth period, the time scale of the current ramp-up before the flat top and the flat-top duration, respectively. As for $\tau _{{\rm MHD}}$
's, the energy confinement time, the sawtooth period, the time scale of the current ramp-up before the flat top and the flat-top duration, respectively. As for $\tau _{{\rm MHD}}$![]() , $\tau _{e}$
, $\tau _{e}$![]() and $\tau _{i}$
and $\tau _{i}$![]() , these are reasonable orders of magnitude for high-field tokamak plasmas. As for $\tau _{{\rm sd}}$
, these are reasonable orders of magnitude for high-field tokamak plasmas. As for $\tau _{{\rm sd}}$![]() , in a plasma with such a large particle density like SPARC we may reasonably take a value near to its value in IGNITOR, which is $= 0.05$
, in a plasma with such a large particle density like SPARC we may reasonably take a value near to its value in IGNITOR, which is $= 0.05$![]() s (Bombarda et al. Reference Bombarda, Coppi, Airoldi, Cenacchi and Detragiache2004). We take the values of $\tau _{E}$
s (Bombarda et al. Reference Bombarda, Coppi, Airoldi, Cenacchi and Detragiache2004). We take the values of $\tau _{E}$![]() , $\tau _{{\rm ramp}}$
, $\tau _{{\rm ramp}}$![]() and $\varDelta t _{{\rm flat}}$
and $\varDelta t _{{\rm flat}}$![]() from § 3, figure 3 and table 1 of Creely et al. (Reference Creely, Greenwald, Ballinger, Brunner, Canik, Doody, Fülöp, Garnier, Granetz and Gray2020), respectively. We take the value of $\tau _{{\rm saw}}$
from § 3, figure 3 and table 1 of Creely et al. (Reference Creely, Greenwald, Ballinger, Brunner, Canik, Doody, Fülöp, Garnier, Granetz and Gray2020), respectively. We take the value of $\tau _{{\rm saw}}$![]() from Rodriguez-Fernandez et al. (Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020); in the words of this work, the first sawtooth crash occurs soon after the plasma enters into H-mode, the L–H transition is assumed to happen at the very beginning of the flat top and the first sawtooth crash occurs soon after the plasma enters into H-mode.
from Rodriguez-Fernandez et al. (Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020); in the words of this work, the first sawtooth crash occurs soon after the plasma enters into H-mode, the L–H transition is assumed to happen at the very beginning of the flat top and the first sawtooth crash occurs soon after the plasma enters into H-mode.
The inequalities $\tau _{{\rm MHD}} < \tau _{{\rm sd}} < \tau _{E}$![]() in (2.1) allow us both to describe the evolution of the plasma as a succession of MHD equilibria which evolve according to laws ruling magnetic flux, particle and energy flows, etc., and to neglect the time delay of the heating of the plasma due to the collisions of $\alpha$
in (2.1) allow us both to describe the evolution of the plasma as a succession of MHD equilibria which evolve according to laws ruling magnetic flux, particle and energy flows, etc., and to neglect the time delay of the heating of the plasma due to the collisions of $\alpha$![]() 's with electrons and ions with respect to the production of $\alpha$
's with electrons and ions with respect to the production of $\alpha$![]() 's due to fusion reactions. Now, the density $n_{\alpha } (\boldsymbol {x}, t)$
's due to fusion reactions. Now, the density $n_{\alpha } (\boldsymbol {x}, t)$![]() of $\alpha$
of $\alpha$![]() 's produced per unit time at a given point and at the time $t$
's produced per unit time at a given point and at the time $t$![]() is proportional to $T(\boldsymbol {x} , t)^{2}$
is proportional to $T(\boldsymbol {x} , t)^{2}$![]() . Then, the density $P_{\alpha } = P_{\alpha } (\boldsymbol {x} , t)$
. Then, the density $P_{\alpha } = P_{\alpha } (\boldsymbol {x} , t)$![]() of fusion heating power at the time $t$
of fusion heating power at the time $t$![]() (where $W_{\alpha } (t) = \int P_{\alpha } (\boldsymbol {x}, t)\,{{\rm d}}\boldsymbol {x}$
(where $W_{\alpha } (t) = \int P_{\alpha } (\boldsymbol {x}, t)\,{{\rm d}}\boldsymbol {x}$![]() and all volume integrations are performed on the plasma volume $V$
and all volume integrations are performed on the plasma volume $V$![]() here and below) is proportional to $n_{\alpha } (\boldsymbol {x} , t)$
here and below) is proportional to $n_{\alpha } (\boldsymbol {x} , t)$![]() with negligible time delay, and is therefore also $\propto O(T(\boldsymbol {x} , t)^{2})$
with negligible time delay, and is therefore also $\propto O(T(\boldsymbol {x} , t)^{2})$![]() . The resulting strong dependence of $W_{\alpha }$
. The resulting strong dependence of $W_{\alpha }$![]() on $T$
on $T$![]() implies that when $Q$
implies that when $Q$![]() becomes larger than $5$
becomes larger than $5$![]() – namely when $W_{\alpha } > W_{{\rm aux}} + W_{{\rm ohm}}$
– namely when $W_{\alpha } > W_{{\rm aux}} + W_{{\rm ohm}}$![]() , i.e. fusion becomes the dominant heating mechanism – a thermal runaway occurs: a positive feedback involves $W_{\alpha }$
, i.e. fusion becomes the dominant heating mechanism – a thermal runaway occurs: a positive feedback involves $W_{\alpha }$![]() and $T$
and $T$![]() , and starts from a relatively colder state where fusion is negligible to a hotter state where energy losses are basically compensated by fusion. Following Mayoral et al. (Reference Mayoral, Buttery, Jones, Kiptily, Sharapov, Mantsinen, Coda, Sauter, Eriksson and Nguyen2004), the words ‘thermal runaway’ mean that ‘a change in plasma energy results in a change of $P_{\alpha }$
, and starts from a relatively colder state where fusion is negligible to a hotter state where energy losses are basically compensated by fusion. Following Mayoral et al. (Reference Mayoral, Buttery, Jones, Kiptily, Sharapov, Mantsinen, Coda, Sauter, Eriksson and Nguyen2004), the words ‘thermal runaway’ mean that ‘a change in plasma energy results in a change of $P_{\alpha }$![]() […] greater than the increase of the loss power’. At first sight, it makes sense to speak of thermal runaway here, as the latter occurs in Mayoral et al. (Reference Mayoral, Buttery, Jones, Kiptily, Sharapov, Mantsinen, Coda, Sauter, Eriksson and Nguyen2004) for $Q = 8$
[…] greater than the increase of the loss power’. At first sight, it makes sense to speak of thermal runaway here, as the latter occurs in Mayoral et al. (Reference Mayoral, Buttery, Jones, Kiptily, Sharapov, Mantsinen, Coda, Sauter, Eriksson and Nguyen2004) for $Q = 8$![]() , which is less than the value $Q = 9$
, which is less than the value $Q = 9$![]() envisaged for SPARC (Rodriguez-Fernandez et al. Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020). However, the results in Mayoral et al. (Reference Mayoral, Buttery, Jones, Kiptily, Sharapov, Mantsinen, Coda, Sauter, Eriksson and Nguyen2004) are extrapolated starting from results in pure deuterium plasma, and no such extrapolation is actually free from ambiguities (Guazzotto & Betti Reference Guazzotto and Betti2019). Thus, with a slight abuse of notation we are just going to refer to the transition from $Q < 5$
envisaged for SPARC (Rodriguez-Fernandez et al. Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020). However, the results in Mayoral et al. (Reference Mayoral, Buttery, Jones, Kiptily, Sharapov, Mantsinen, Coda, Sauter, Eriksson and Nguyen2004) are extrapolated starting from results in pure deuterium plasma, and no such extrapolation is actually free from ambiguities (Guazzotto & Betti Reference Guazzotto and Betti2019). Thus, with a slight abuse of notation we are just going to refer to the transition from $Q < 5$![]() to $Q > 5$
to $Q > 5$![]() as ‘thermal runaway’ below. A thermal runaway is a process where the slightest, initial perturbation of temperature gets amplified more and more as time goes by. Stability against perturbations of $T$
as ‘thermal runaway’ below. A thermal runaway is a process where the slightest, initial perturbation of temperature gets amplified more and more as time goes by. Stability against perturbations of $T$![]() corresponds therefore to lack of thermal runaway; if $Q$
corresponds therefore to lack of thermal runaway; if $Q$![]() is initially ${<}5$
is initially ${<}5$![]() and if thermal runaway never occurs then $Q < 5$
and if thermal runaway never occurs then $Q < 5$![]() at all times.
at all times.
Let us investigate thermal runaway in detail. We follow step by step the approach originally invoked in Di Vita (Reference Di Vita2010) for the analysis of an IGNITOR plasma, and try to apply it to a SPARC scenario. Simulations of SPARC discharges envisage low values of both $\beta$![]() and dimensionless collisionality $\nu _{*}$
and dimensionless collisionality $\nu _{*}$![]() – see e.g. figures 5(b) and 5(d) of Creely et al. (Reference Creely, Greenwald, Ballinger, Brunner, Canik, Doody, Fülöp, Garnier, Granetz and Gray2020). According to (15) and (16) of Rogister & Li (Reference Rogister and Li1992) – which follow from the Fokker–Planck equation – and in agreement with the inequalities $\tau _{{\rm MHD}} \ll \tau _{e} < \tau _{i} < \tau _{E}$
– see e.g. figures 5(b) and 5(d) of Creely et al. (Reference Creely, Greenwald, Ballinger, Brunner, Canik, Doody, Fülöp, Garnier, Granetz and Gray2020). According to (15) and (16) of Rogister & Li (Reference Rogister and Li1992) – which follow from the Fokker–Planck equation – and in agreement with the inequalities $\tau _{{\rm MHD}} \ll \tau _{e} < \tau _{i} < \tau _{E}$![]() in (2.1), the typical time scales of thermalization (namely ‘relaxation to a Maxwellian of the distribution function’) of ions and electrons in a weakly collisional, axisymmetric, toroidal, low-$\beta$
in (2.1), the typical time scales of thermalization (namely ‘relaxation to a Maxwellian of the distribution function’) of ions and electrons in a weakly collisional, axisymmetric, toroidal, low-$\beta$![]() turbulent plasma region between magnetic surfaces with poloidal flux $\psi$
turbulent plasma region between magnetic surfaces with poloidal flux $\psi$![]() and $\psi + d\psi$
and $\psi + d\psi$![]() are much shorter than the typical time scales of particle and energy transport in the direction parallel to $\nabla \psi$
are much shorter than the typical time scales of particle and energy transport in the direction parallel to $\nabla \psi$![]() . This constraint holds at all times during the plasma discharge, and regardless of the detailed mechanism underlying transport. As for SPARC (Rodriguez-Fernandez et al. Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020), it is supposed that $Z_{{\rm eff}} = 1.5$
. This constraint holds at all times during the plasma discharge, and regardless of the detailed mechanism underlying transport. As for SPARC (Rodriguez-Fernandez et al. Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020), it is supposed that $Z_{{\rm eff}} = 1.5$![]() , that the accumulation of thermal $^{4}$
, that the accumulation of thermal $^{4}$![]() He ash is negligible and that the $^{3}$
He ash is negligible and that the $^{3}$![]() He fraction required by ICRF does not exceed 5 % at all times. Moreover, it turns out that ion temperature $T_{i}$
He fraction required by ICRF does not exceed 5 % at all times. Moreover, it turns out that ion temperature $T_{i}$![]() and $T_{e}$
and $T_{e}$![]() are approximately equal everywhere at all times (we write $T_{i} = T_{e} = T$
are approximately equal everywhere at all times (we write $T_{i} = T_{e} = T$![]() below) and that the total boostrap current is ${\approx }12$
below) and that the total boostrap current is ${\approx }12$![]() % of the plasma current $I_{p}$
% of the plasma current $I_{p}$![]() during the flat top. Furthermore, SPARC has no non-inductive current drive. (Admittedly, no explicit discussion of the impact of sawteeth is considered in Rogister & Li (Reference Rogister and Li1992). However, the inequality $\tau _{{\rm saw}} < \tau _{{\rm ramp}} \approx \varDelta t _{{\rm flat}}$
during the flat top. Furthermore, SPARC has no non-inductive current drive. (Admittedly, no explicit discussion of the impact of sawteeth is considered in Rogister & Li (Reference Rogister and Li1992). However, the inequality $\tau _{{\rm saw}} < \tau _{{\rm ramp}} \approx \varDelta t _{{\rm flat}}$![]() in (2.1) and the fact that the relative impact of sawteeth on both $W_{{\rm fus}}$
in (2.1) and the fact that the relative impact of sawteeth on both $W_{{\rm fus}}$![]() and $Q$
and $Q$![]() is never ${>}10$
is never ${>}10$![]() % (Rodriguez-Fernandez et al. Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020) allow us to neglect sawteeth below.) Thus, the result of Rogister & Li (Reference Rogister and Li1992) implies that we may safely assume that the distribution functions of ions and electrons are locally Maxwellian in SPARC at all times (even if with time-dependent values of $n_{e}$
% (Rodriguez-Fernandez et al. Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020) allow us to neglect sawteeth below.) Thus, the result of Rogister & Li (Reference Rogister and Li1992) implies that we may safely assume that the distribution functions of ions and electrons are locally Maxwellian in SPARC at all times (even if with time-dependent values of $n_{e}$![]() , $T$
, $T$![]() , etc.); by ‘locally’ we mean: ‘as far as we are interested in phenomena occurring between magnetic surfaces labelled with $\psi$
, etc.); by ‘locally’ we mean: ‘as far as we are interested in phenomena occurring between magnetic surfaces labelled with $\psi$![]() and $\psi + d\psi$
and $\psi + d\psi$![]() on a time scale much shorter than the typical time scales related to the transport of energy and particles’. Momenta of Maxwellian distribution functions include the temperature, the energy, the entropy and other usual quantities of thermodynamics, and the familiar relationships of thermodynamics linking temperature, entropy, etc., hold locally. The condition where the latter relationships hold at all times within a small mass element (e.g. the mass of plasma contained within the magnetic surfaces $\psi$
on a time scale much shorter than the typical time scales related to the transport of energy and particles’. Momenta of Maxwellian distribution functions include the temperature, the energy, the entropy and other usual quantities of thermodynamics, and the familiar relationships of thermodynamics linking temperature, entropy, etc., hold locally. The condition where the latter relationships hold at all times within a small mass element (e.g. the mass of plasma contained within the magnetic surfaces $\psi$![]() and $\psi + d\psi$
and $\psi + d\psi$![]() ) of a system (like a tokamak plasma) even if the system as a whole is not at thermodynamic equilibrium is referred to as ‘local thermodynamic equilibrium’ (LTE) in the literature. In contrast with fluids, where short-range, interparticle collisions usually ensure validity of LTE, LTE is uncommon in plasmas (Pegoraro Reference Pegoraro1994). When it comes to investigating systems far from thermodynamic equilibrium, it is often assumed that Onsager symmetry relationships between phenomenological coefficients (including electron diffusivities, electrical resistivity, etc.) hold (DeGroot & Mazur Reference DeGroot and Mazur1962). The impact of Onsager symmetry – if valid – on the description of transport processes in tokamaks is discussed in Hinton & Hazeltine (Reference Hinton and Hazeltine1976), but tokamak plasmas usually do not satisfy Onsager symmetry (Balescu Reference Balescu1991; Di Vita Reference Di Vita1991; Brusati & Di Vita Reference Brusati and Di Vita1993). Physically, however, LTE still puts a constraint on the evolution of the discharge regardless of the detailed mechanism underlying transport. Actually, thermodynamics leads to an inequality involving ${{{\rm d}}T}/{{{\rm d}}t}$
) of a system (like a tokamak plasma) even if the system as a whole is not at thermodynamic equilibrium is referred to as ‘local thermodynamic equilibrium’ (LTE) in the literature. In contrast with fluids, where short-range, interparticle collisions usually ensure validity of LTE, LTE is uncommon in plasmas (Pegoraro Reference Pegoraro1994). When it comes to investigating systems far from thermodynamic equilibrium, it is often assumed that Onsager symmetry relationships between phenomenological coefficients (including electron diffusivities, electrical resistivity, etc.) hold (DeGroot & Mazur Reference DeGroot and Mazur1962). The impact of Onsager symmetry – if valid – on the description of transport processes in tokamaks is discussed in Hinton & Hazeltine (Reference Hinton and Hazeltine1976), but tokamak plasmas usually do not satisfy Onsager symmetry (Balescu Reference Balescu1991; Di Vita Reference Di Vita1991; Brusati & Di Vita Reference Brusati and Di Vita1993). Physically, however, LTE still puts a constraint on the evolution of the discharge regardless of the detailed mechanism underlying transport. Actually, thermodynamics leads to an inequality involving ${{{\rm d}}T}/{{{\rm d}}t}$![]() and ${{{\rm d}}p}/{{{\rm d}}t}$
and ${{{\rm d}}p}/{{{\rm d}}t}$![]() in systems at LTE, the ‘general evolution criterion’ (GEC). The proof of the GEC invokes no Onsager symmetry – see both Glansdorff & Prigogine (Reference Glansdorff and Prigogine1964) and (1.5) of Di Vita (Reference Di Vita2010) for a detailed discussion. In turn, the GEC leads to the following necessary criterion (Di Vita Reference Di Vita2010) for the stability against perturbation of $T$
in systems at LTE, the ‘general evolution criterion’ (GEC). The proof of the GEC invokes no Onsager symmetry – see both Glansdorff & Prigogine (Reference Glansdorff and Prigogine1964) and (1.5) of Di Vita (Reference Di Vita2010) for a detailed discussion. In turn, the GEC leads to the following necessary criterion (Di Vita Reference Di Vita2010) for the stability against perturbation of $T$![]() , i.e. for a lack of thermal runaway:
, i.e. for a lack of thermal runaway:
where integration is performed on the plasma volume and we have introduced the ohmic power density $P_{{\rm ohm}} (\boldsymbol {x} , t)$![]() , the auxiliary power density $P_{{\rm aux}} (\boldsymbol {x} , t)$
, the auxiliary power density $P_{{\rm aux}} (\boldsymbol {x} , t)$![]() and the total heating power density $P_{h} (\boldsymbol {x} , t) \equiv P_{\alpha } (\boldsymbol {x} , t) + P_{{\rm ohm}} (\boldsymbol {x} , t) + P_{{\rm aux}} (\boldsymbol {x} , t)$
and the total heating power density $P_{h} (\boldsymbol {x} , t) \equiv P_{\alpha } (\boldsymbol {x} , t) + P_{{\rm ohm}} (\boldsymbol {x} , t) + P_{{\rm aux}} (\boldsymbol {x} , t)$![]() (in analogy with $P_{\alpha } (\boldsymbol {x} , t)$
(in analogy with $P_{\alpha } (\boldsymbol {x} , t)$![]() ) such that $W_{{\rm ohm}} (t) = \int P_{{\rm ohm}} (\boldsymbol {x} , t) \,{{\rm d}}\boldsymbol {x}$
) such that $W_{{\rm ohm}} (t) = \int P_{{\rm ohm}} (\boldsymbol {x} , t) \,{{\rm d}}\boldsymbol {x}$![]() and $W_{{\rm aux}} (t) = \int P_{{\rm aux}} (\boldsymbol {x} , t)\,{{\rm d}}\boldsymbol {x}$
and $W_{{\rm aux}} (t) = \int P_{{\rm aux}} (\boldsymbol {x} , t)\,{{\rm d}}\boldsymbol {x}$![]() ; here and in the following, moreover, we denote with $a_{0} (t)$
; here and in the following, moreover, we denote with $a_{0} (t)$![]() , $\langle a \rangle (t)$
, $\langle a \rangle (t)$![]() and $a_{b} (t)$
and $a_{b} (t)$![]() the maximum value of the generic physical quantity $a (\boldsymbol {x} , t )$
the maximum value of the generic physical quantity $a (\boldsymbol {x} , t )$![]() across the plasma cross-section at a given time $t$
across the plasma cross-section at a given time $t$![]() , the average $({1}/{V})\int a \,{{\rm d}}\boldsymbol {x}$
, the average $({1}/{V})\int a \,{{\rm d}}\boldsymbol {x}$![]() of $a$
of $a$![]() on the plasma volume $V (t)$
on the plasma volume $V (t)$![]() and the boundary value of $a$
and the boundary value of $a$![]() , respectively. (The proof of (2.2a–c) relies also on the assumptions $P_{hb} = 0$
, respectively. (The proof of (2.2a–c) relies also on the assumptions $P_{hb} = 0$![]() (Di Vita & Brusati Reference Di Vita and Brusati1995), ${{{\rm d}}T_{b}}/{{{\rm d}}t} = 0$
(Di Vita & Brusati Reference Di Vita and Brusati1995), ${{{\rm d}}T_{b}}/{{{\rm d}}t} = 0$![]() and ${{{\rm d}}p_{b}}/{{{\rm d}}t} = 0$
and ${{{\rm d}}p_{b}}/{{{\rm d}}t} = 0$![]() as well as of small ${{{\rm d}} \nabla T}/{{{\rm d}}t}$
as well as of small ${{{\rm d}} \nabla T}/{{{\rm d}}t}$![]() ; the latter assumption makes sense as far as we limit ourselves to scenarios with constant temperature peaking factor ${T_{0}}/{\langle T\rangle }$
; the latter assumption makes sense as far as we limit ourselves to scenarios with constant temperature peaking factor ${T_{0}}/{\langle T\rangle }$![]() (Creely et al. Reference Creely, Greenwald, Ballinger, Brunner, Canik, Doody, Fülöp, Garnier, Granetz and Gray2020).) Remarkably, (2.2a–c) involves total time derivatives only, and may therefore describe unsteady (and possibly moving) plasmas.
(Creely et al. Reference Creely, Greenwald, Ballinger, Brunner, Canik, Doody, Fülöp, Garnier, Granetz and Gray2020).) Remarkably, (2.2a–c) involves total time derivatives only, and may therefore describe unsteady (and possibly moving) plasmas.
Physically, (2.2a–c) means that if a perturbation raises $P_{h}$![]() somewhere, then $T$
somewhere, then $T$![]() must increase locally (this limiting the increase in $T^{-1}P_{h}$
must increase locally (this limiting the increase in $T^{-1}P_{h}$![]() ) so that the resulting increase in $\vert \nabla T \vert$
) so that the resulting increase in $\vert \nabla T \vert$![]() raises the heat flux towards the external world and compensates the increase in $P_{h}$
raises the heat flux towards the external world and compensates the increase in $P_{h}$![]() in the energy balance. In the opposite direction, if a perturbation lowers $T$
in the energy balance. In the opposite direction, if a perturbation lowers $T$![]() somewhere so that the resulting decrease in $\vert \nabla T \vert$
somewhere so that the resulting decrease in $\vert \nabla T \vert$![]() lowers the heat flux towards the external world and the associated heat loss, then $P_{h}$
lowers the heat flux towards the external world and the associated heat loss, then $P_{h}$![]() must decrease in order to compensate the reduction in heat loss, and the increase in $T^{-1}P_{h}$
must decrease in order to compensate the reduction in heat loss, and the increase in $T^{-1}P_{h}$![]() is limited once again. Then, (2.2a–c) agrees with Le Châtelier's principle (Landau & Lifshitz Reference Landau and Lifshitz1959). The latter principle provides us with a physical meaning of the result of Rogister & Li (Reference Rogister and Li1992), which is basically an upper bound on the thermalization time scale (an increasing function of $T$
is limited once again. Then, (2.2a–c) agrees with Le Châtelier's principle (Landau & Lifshitz Reference Landau and Lifshitz1959). The latter principle provides us with a physical meaning of the result of Rogister & Li (Reference Rogister and Li1992), which is basically an upper bound on the thermalization time scale (an increasing function of $T$![]() ). Once a mechanism for energy transport is given, indeed, this upper bound provides an upper bound on $T$
). Once a mechanism for energy transport is given, indeed, this upper bound provides an upper bound on $T$![]() itself. If the plasma is stable against perturbation of $T$
itself. If the plasma is stable against perturbation of $T$![]() then (2.2a–c) holds and too strong a heating leads just to an increase in heat flux towards the external world. If $W_{\alpha }$
then (2.2a–c) holds and too strong a heating leads just to an increase in heat flux towards the external world. If $W_{\alpha }$![]() is negligible and (2.2a–c) holds at the beginning of the discharge then no thermal runaway occurs as far as (2.2a–c) holds. (For example, any increase in $T_{0}$
is negligible and (2.2a–c) holds at the beginning of the discharge then no thermal runaway occurs as far as (2.2a–c) holds. (For example, any increase in $T_{0}$![]() at fixed $T_{b}$
at fixed $T_{b}$![]() raises $\vert \nabla T \vert$
raises $\vert \nabla T \vert$![]() , hence the heat flux, thus preventing further heating and barring the path towards further development of thermal runaway.) Thus, successful achievement of a burning plasma starting from a colder plasma when $W_{\alpha }$
, hence the heat flux, thus preventing further heating and barring the path towards further development of thermal runaway.) Thus, successful achievement of a burning plasma starting from a colder plasma when $W_{\alpha }$![]() is negligible is only possible when (2.2a–c) is violated. Since (2.2a–c) is a necessary condition for the lack of thermal runaway, its violation is a sufficient condition for the occurrence of thermal runaway. In particular, we may highlight scenarios for $W_{{\rm aux}} ( t )$
is negligible is only possible when (2.2a–c) is violated. Since (2.2a–c) is a necessary condition for the lack of thermal runaway, its violation is a sufficient condition for the occurrence of thermal runaway. In particular, we may highlight scenarios for $W_{{\rm aux}} ( t )$![]() which are relevant to thermal runaway. This is the crucial result of our discussion. We stress the point that it follows from Rogister & Li (Reference Rogister and Li1992); then, it holds regardless of the detailed microscopic description of the physical processes ruling energy transport.
which are relevant to thermal runaway. This is the crucial result of our discussion. We stress the point that it follows from Rogister & Li (Reference Rogister and Li1992); then, it holds regardless of the detailed microscopic description of the physical processes ruling energy transport.
Further analysis requires two final considerations. Firstly, let us focus our attention on the steady-state flat top of a tokamak plasma discharge which lasts long enough to ensure $T_{i} = T_{e} = T$![]() . For such discharge, where both $V$
. For such discharge, where both $V$![]() and $W_{{\rm ohm}}$
and $W_{{\rm ohm}}$![]() are constant, the quantity $\int ({P_{h}}/{T})\,{{\rm d}}\boldsymbol {x}$
are constant, the quantity $\int ({P_{h}}/{T})\,{{\rm d}}\boldsymbol {x}$![]() acts as a Lyapunov function for all perturbations of the steady state according to (2.2a–c), so that stability against perturbations of $T$
acts as a Lyapunov function for all perturbations of the steady state according to (2.2a–c), so that stability against perturbations of $T$![]() requires that the steady state corresponds to a constrained minimum of the contribution $\int ({P_{h}}/{T})\,{{\rm d}}\boldsymbol {x}$
requires that the steady state corresponds to a constrained minimum of the contribution $\int ({P_{h}}/{T})\,{{\rm d}}\boldsymbol {x}$![]() of heating processes to the entropy production rate (Di Vita Reference Di Vita2010). For JET such minimization has been successfully utilized in the description of the ohmic ($P_{h} = P_{{\rm ohm}}$
of heating processes to the entropy production rate (Di Vita Reference Di Vita2010). For JET such minimization has been successfully utilized in the description of the ohmic ($P_{h} = P_{{\rm ohm}}$![]() ) discharge no. 24888, where $\varDelta t_{{\rm flat}} = 60$
) discharge no. 24888, where $\varDelta t_{{\rm flat}} = 60$![]() s; the same is true for discharges no. 24963 (with LHCD) and no. 25264 (ELM-free H-mode, high $\beta$
s; the same is true for discharges no. 24963 (with LHCD) and no. 25264 (ELM-free H-mode, high $\beta$![]() , high bootstrap) where the constraint $T_{i} = T_{e}$
, high bootstrap) where the constraint $T_{i} = T_{e}$![]() could be removed and $T_{e}$
could be removed and $T_{e}$![]() replaced $T$
replaced $T$![]() (Di Vita & Brusati Reference Di Vita and Brusati1995). Secondly, thermal runaway is not the only example of lack of stability; the L–H transition is obviously another example, even with negligible $P_{\alpha }$
(Di Vita & Brusati Reference Di Vita and Brusati1995). Secondly, thermal runaway is not the only example of lack of stability; the L–H transition is obviously another example, even with negligible $P_{\alpha }$![]() . A sudden rise of $T_{b}$
. A sudden rise of $T_{b}$![]() related to the onset of a pedestal lowers the last term on the right-hand side of (2.2a–c), thus facilitating its violation. However, this lies outside the aim of the present work, which focuses rather on the SPARC scenario in the first 2 s of the flat top, when the plasma is always supposed to be in H-mode.
related to the onset of a pedestal lowers the last term on the right-hand side of (2.2a–c), thus facilitating its violation. However, this lies outside the aim of the present work, which focuses rather on the SPARC scenario in the first 2 s of the flat top, when the plasma is always supposed to be in H-mode.
3. A scenario of SPARC
Condition (2.2a–c) being a necessary condition for stability against perturbations of $T$![]() , we are free to select the perturbation which (2.2a–c) is to be tested against. We choose a perturbation with typical time scale $\tau$
, we are free to select the perturbation which (2.2a–c) is to be tested against. We choose a perturbation with typical time scale $\tau$![]() such that $\tau _{{\rm MHD}} < \tau < \tau _{{\rm sd}}$
such that $\tau _{{\rm MHD}} < \tau < \tau _{{\rm sd}}$![]() . This choice allows us to get rid of fast MHD fluctuations; it allows also all quantities in (2.2a–c) to refer explicitly to the generic MHD equilibrium at the time $t$
. This choice allows us to get rid of fast MHD fluctuations; it allows also all quantities in (2.2a–c) to refer explicitly to the generic MHD equilibrium at the time $t$![]() , in agreement with the familiar description of the plasma evolution as a succession of MHD equilibria. If no thermal runaway occurs and the plasma relaxes to a stable, steady state, then (2.2a–c) makes such relaxed state to correspond to a constrained minimum of $\int ({P_{h}}/{T})\,{{\rm d}}\boldsymbol {x}$
, in agreement with the familiar description of the plasma evolution as a succession of MHD equilibria. If no thermal runaway occurs and the plasma relaxes to a stable, steady state, then (2.2a–c) makes such relaxed state to correspond to a constrained minimum of $\int ({P_{h}}/{T})\,{{\rm d}}\boldsymbol {x}$![]() , as shown above. In the unsteady discharge of IGNITOR (Bombarda et al. Reference Bombarda, Coppi, Airoldi, Cenacchi and Detragiache2004), in contrast, $Q > 5$
, as shown above. In the unsteady discharge of IGNITOR (Bombarda et al. Reference Bombarda, Coppi, Airoldi, Cenacchi and Detragiache2004), in contrast, $Q > 5$![]() is envisaged near the end of the current rise, taking full advantage of a strong rate of ohmic heating. By the end of this transient phase, the electric field is strongly inhomogeneous: it is low at the centre of the plasma column, where it is consistent with relatively high values of $T$
is envisaged near the end of the current rise, taking full advantage of a strong rate of ohmic heating. By the end of this transient phase, the electric field is strongly inhomogeneous: it is low at the centre of the plasma column, where it is consistent with relatively high values of $T$![]() , and remains high at the edge of the plasma column. Accordingly, $P_{{\rm ohm}}$
, and remains high at the edge of the plasma column. Accordingly, $P_{{\rm ohm}}$![]() becomes far from negligible in the outer region of the plasma, so that $\int ({P_{h}}/{T})\,{{\rm d}}\boldsymbol {x}$
becomes far from negligible in the outer region of the plasma, so that $\int ({P_{h}}/{T})\,{{\rm d}}\boldsymbol {x}$![]() grows and (2.2a–c) is violated. More generally, violation of (2.2a–c) is more difficult if ${{{\rm d}}V}/{{{\rm d}}t}> 0$
grows and (2.2a–c) is violated. More generally, violation of (2.2a–c) is more difficult if ${{{\rm d}}V}/{{{\rm d}}t}> 0$![]() (e.g. due to an increase in the Shafranov shift, which in turn may follow from an increasing value of the poloidal beta). This is far from surprising, as expanding plasmas cool down. In contrast, both ${{{\rm d}}V}/{{{\rm d}}t} < 0$
(e.g. due to an increase in the Shafranov shift, which in turn may follow from an increasing value of the poloidal beta). This is far from surprising, as expanding plasmas cool down. In contrast, both ${{{\rm d}}V}/{{{\rm d}}t} < 0$![]() (e.g. due to adiabatic heating) and increasing of $T_{b}$
(e.g. due to adiabatic heating) and increasing of $T_{b}$![]() (e.g. due to the onset of a pedestal related to H-mode) are useful in violating (2.2a–c).
(e.g. due to the onset of a pedestal related to H-mode) are useful in violating (2.2a–c).
We invoke (2.2a–c) in order to assess the feasibility of a SPARC scenario proposed in Rodriguez-Fernandez et al. (Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020) for the flat top; suitable values of $W_{{\rm aux}} + W_{\alpha }$![]() ensure that the L–H mode transition occurs. The uncertainties discussed in § 1 leave our discussion unaffected, as (2.2a–c) holds regardless of the detailed microscopic physics. Figure 3 of Creely et al. (Reference Creely, Greenwald, Ballinger, Brunner, Canik, Doody, Fülöp, Garnier, Granetz and Gray2020) shows that the flat top starts and ends at $t = t_{i} \approx 7$
ensure that the L–H mode transition occurs. The uncertainties discussed in § 1 leave our discussion unaffected, as (2.2a–c) holds regardless of the detailed microscopic physics. Figure 3 of Creely et al. (Reference Creely, Greenwald, Ballinger, Brunner, Canik, Doody, Fülöp, Garnier, Granetz and Gray2020) shows that the flat top starts and ends at $t = t_{i} \approx 7$![]() and $t = t_{i} + 10$
and $t = t_{i} + 10$![]() s, respectively, where $t = 0$
s, respectively, where $t = 0$![]() corresponds to the beginning of the discharge. In the words of Rodriguez-Fernandez et al. (Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020), ‘the analysis presented next ignores the possible plasma trajectory needed to access (and subsequently sustain) the H-mode, which may require higher auxiliary power than assumed here […] for some early portion of the current flat top’; then, we focus our attention on the first 2 s of the flat top, displayed as a blue-shaded area in figure 7 of Rodriguez-Fernandez et al. (Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020). For the sake of clarity, we introduce the dimensionless time variable $z \equiv {(t - t_{i})}/{t_{{\rm saw}}}$
corresponds to the beginning of the discharge. In the words of Rodriguez-Fernandez et al. (Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020), ‘the analysis presented next ignores the possible plasma trajectory needed to access (and subsequently sustain) the H-mode, which may require higher auxiliary power than assumed here […] for some early portion of the current flat top’; then, we focus our attention on the first 2 s of the flat top, displayed as a blue-shaded area in figure 7 of Rodriguez-Fernandez et al. (Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020). For the sake of clarity, we introduce the dimensionless time variable $z \equiv {(t - t_{i})}/{t_{{\rm saw}}}$![]() ($t_{{\rm saw}} = 1$
($t_{{\rm saw}} = 1$![]() s on SPARC; Rodriguez-Fernandez et al. Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020) so that we focus on $0 \leq z \leq 2$
s on SPARC; Rodriguez-Fernandez et al. Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020) so that we focus on $0 \leq z \leq 2$![]() . Both figure 7 and p. 2 of Rodriguez-Fernandez et al. (Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020) show that $Q ( z = 2 ) = 11 > 5$
. Both figure 7 and p. 2 of Rodriguez-Fernandez et al. (Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020) show that $Q ( z = 2 ) = 11 > 5$![]() . We shall see that $Q ( z = 0 ) < 5$
. We shall see that $Q ( z = 0 ) < 5$![]() ; thus, a value $z_{Q}$
; thus, a value $z_{Q}$![]() of $z$
of $z$![]() exists such that $0 < z_{Q} < 2$
exists such that $0 < z_{Q} < 2$![]() and $Q ( z_{Q} ) = 5$
and $Q ( z_{Q} ) = 5$![]() . Let us divide all terms in (2.2a–c) by $\int ({P_{h}}/{T})\,{{\rm d}}\boldsymbol {x}$
. Let us divide all terms in (2.2a–c) by $\int ({P_{h}}/{T})\,{{\rm d}}\boldsymbol {x}$![]() and write
and write

where we have dropped the dependence on $z$![]() of the dimensionless quantities $A$
of the dimensionless quantities $A$![]() , $B$
, $B$![]() , $C$
, $C$![]() , etc., for simplicity. We shall see that $C ( z = 0 ) < 0$
, etc., for simplicity. We shall see that $C ( z = 0 ) < 0$![]() ; thus, thermal runaway in the interval $0 < z < 2$
; thus, thermal runaway in the interval $0 < z < 2$![]() is only possible if $C$
is only possible if $C$![]() becomes positive at some time in this interval, i.e. if a value $z_{C}$
becomes positive at some time in this interval, i.e. if a value $z_{C}$![]() of $z$
of $z$![]() exists such that $0 < z_{C} < 2$
exists such that $0 < z_{C} < 2$![]() and $C ( z_{C} ) = 0$
and $C ( z_{C} ) = 0$![]() . The achievement of $Q > 5$
. The achievement of $Q > 5$![]() predicted in Rodriguez-Fernandez et al. (Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020) requires thermal runaway, and (3.1a–c) – which follows from the results of Rogister & Li (Reference Rogister and Li1992) – allows no thermal runaway as far as $C < 0$
predicted in Rodriguez-Fernandez et al. (Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020) requires thermal runaway, and (3.1a–c) – which follows from the results of Rogister & Li (Reference Rogister and Li1992) – allows no thermal runaway as far as $C < 0$![]() . In turn, the results of Rogister & Li (Reference Rogister and Li1992) are general properties of weakly collisional, low-$\beta$
. In turn, the results of Rogister & Li (Reference Rogister and Li1992) are general properties of weakly collisional, low-$\beta$![]() , turbulent axisymmetric plasmas, including precisely the plasma of SPARC described in Rodriguez-Fernandez et al. (Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020). Thus, the predictions of Rodriguez-Fernandez et al. (Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020) are compatible with the general results of Rogister & Li (Reference Rogister and Li1992) and may therefore be self-consistent provided that
, turbulent axisymmetric plasmas, including precisely the plasma of SPARC described in Rodriguez-Fernandez et al. (Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020). Thus, the predictions of Rodriguez-Fernandez et al. (Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020) are compatible with the general results of Rogister & Li (Reference Rogister and Li1992) and may therefore be self-consistent provided that
Let us compute $z_{C}$![]() and $z_{Q}$
and $z_{Q}$![]() in the scenario presented in Rodriguez-Fernandez et al. (Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020) (see table 1) in order to check whether (3.2a–c) is satisfied.For this purpose, we follow a five-step procedure, which generalizes the procedure followed in Di Vita (Reference Di Vita2010) for the analysis of IGNITOR to the SPARC-relevant case $W_{{\rm aux}} > 0$
in the scenario presented in Rodriguez-Fernandez et al. (Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020) (see table 1) in order to check whether (3.2a–c) is satisfied.For this purpose, we follow a five-step procedure, which generalizes the procedure followed in Di Vita (Reference Di Vita2010) for the analysis of IGNITOR to the SPARC-relevant case $W_{{\rm aux}} > 0$![]() :
:
(i) We write $T$
 and $n_{e}$
and $n_{e}$ as functions of $\boldsymbol {x}$
as functions of $\boldsymbol {x}$ and of the temporal coordinate $z$
and of the temporal coordinate $z$ as (Coppi et al. Reference Coppi, Airoldi, Bombarda, Cenacchi, Detragiache and Sugiyama2001)
(3.3a,b)\begin{equation} \left.\begin{gathered} T ( \boldsymbol{x} , z ) = T_{0} (z) \left[1-y( \boldsymbol{x} , z )^{2}\right]^{\nu_{T}(z)-1}+T_{b};\\ n_{e} ( \boldsymbol{x} ,z ) = n_{e0} (z)\left[1-y( \boldsymbol{x} , z )^{2}\right]^{\nu_{n}(z)-1}+n_{eb}, \end{gathered}\right\} \end{equation}where $0 \leq y( \boldsymbol {x} , z ) \equiv {(\psi (\boldsymbol {x},z) - \psi _{b})}/{(\psi _{0} - \psi _{b})} \leq 1$
as (Coppi et al. Reference Coppi, Airoldi, Bombarda, Cenacchi, Detragiache and Sugiyama2001)
(3.3a,b)\begin{equation} \left.\begin{gathered} T ( \boldsymbol{x} , z ) = T_{0} (z) \left[1-y( \boldsymbol{x} , z )^{2}\right]^{\nu_{T}(z)-1}+T_{b};\\ n_{e} ( \boldsymbol{x} ,z ) = n_{e0} (z)\left[1-y( \boldsymbol{x} , z )^{2}\right]^{\nu_{n}(z)-1}+n_{eb}, \end{gathered}\right\} \end{equation}where $0 \leq y( \boldsymbol {x} , z ) \equiv {(\psi (\boldsymbol {x},z) - \psi _{b})}/{(\psi _{0} - \psi _{b})} \leq 1$
 is a dimensionless radius. According to (3.3a,b), the peaking factors $({T_{0}}/{\langle T\rangle })(z)$
is a dimensionless radius. According to (3.3a,b), the peaking factors $({T_{0}}/{\langle T\rangle })(z)$ and ${n_{e0}}/{\langle n_{e}\rangle } (z)$
and ${n_{e0}}/{\langle n_{e}\rangle } (z)$ of the profiles of temperature and particle density (Rodriguez-Fernandez et al. Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020) are just ${T_{0}}/{\langle T\rangle }(z) = \nu _{T}(z)$
of the profiles of temperature and particle density (Rodriguez-Fernandez et al. Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020) are just ${T_{0}}/{\langle T\rangle }(z) = \nu _{T}(z)$ and ${n_{e0}}/{\langle n_{e}\rangle } (z) = \nu _{n}(z)$
and ${n_{e0}}/{\langle n_{e}\rangle } (z) = \nu _{n}(z)$ provided that $T_{b} \ll T_{0} (z)$
provided that $T_{b} \ll T_{0} (z)$ and $n_{eb} \ll n_{e0} (z)$
and $n_{eb} \ll n_{e0} (z)$ , respectively. Had we chosen Gaussian profiles, similar relationships would hold, but nothing essential would change in the following.
, respectively. Had we chosen Gaussian profiles, similar relationships would hold, but nothing essential would change in the following.(ii) We describe all quantities listed in table 1 as functions of $z$
 with the help of polynomial fittings starting from the values for $z = 0$
with the help of polynomial fittings starting from the values for $z = 0$ , $1$
, $1$ and $2$
and $2$ . These values are either taken from Creely et al. (Reference Creely, Greenwald, Ballinger, Brunner, Canik, Doody, Fülöp, Garnier, Granetz and Gray2020) and Rodriguez-Fernandez et al. (Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020) or extrapolated from them (see the notes in table 1). Admittedly, three values of $z$
. These values are either taken from Creely et al. (Reference Creely, Greenwald, Ballinger, Brunner, Canik, Doody, Fülöp, Garnier, Granetz and Gray2020) and Rodriguez-Fernandez et al. (Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020) or extrapolated from them (see the notes in table 1). Admittedly, three values of $z$ are likely to be just too few; all the same, we are going to show they are enough to prove the impact of suitable timing of auxiliary heating on the achievement of a burning plasma. More detailed computations require more points and are the topic of future work.
are likely to be just too few; all the same, we are going to show they are enough to prove the impact of suitable timing of auxiliary heating on the achievement of a burning plasma. More detailed computations require more points and are the topic of future work.(iii) We use $W_{\alpha } (z)$
 and $W_{\textrm {ohm}} (z)$
and $W_{\textrm {ohm}} (z)$ as normalization constants for $P_{\alpha } \propto n_{D} n_{T} T^{2} \propto n_{e}^{2} T^{2}$
as normalization constants for $P_{\alpha } \propto n_{D} n_{T} T^{2} \propto n_{e}^{2} T^{2}$ and $P_{\textrm {ohm}} \propto T^{{3}/{2}}$
and $P_{\textrm {ohm}} \propto T^{{3}/{2}}$ , respectively, $n_{D}$
, respectively, $n_{D}$ and $n_{T}$
and $n_{T}$ being the density of deuterium and tritium ions, respectively, so that $p = (n_{e} + n_{D} + n_{T})T$
being the density of deuterium and tritium ions, respectively, so that $p = (n_{e} + n_{D} + n_{T})T$ , $n_{D} = n_{T}$
, $n_{D} = n_{T}$ in the DT fuel and $n_{i} \equiv n_{D} + n_{T} = 0.85 n_{e}$
in the DT fuel and $n_{i} \equiv n_{D} + n_{T} = 0.85 n_{e}$ everywhere at all times – see p. 13 of Creely et al. (Reference Creely, Greenwald, Ballinger, Brunner, Canik, Doody, Fülöp, Garnier, Granetz and Gray2020). The normalization to $W_{\textrm {ohm}}$
everywhere at all times – see p. 13 of Creely et al. (Reference Creely, Greenwald, Ballinger, Brunner, Canik, Doody, Fülöp, Garnier, Granetz and Gray2020). The normalization to $W_{\textrm {ohm}}$ encompasses possible neoclassical contributions to the electric conductivity. Our approach makes sense at least if relative variations of $\nu _{T}(z)$
encompasses possible neoclassical contributions to the electric conductivity. Our approach makes sense at least if relative variations of $\nu _{T}(z)$ and $\nu _{n}(z)$
and $\nu _{n}(z)$ in time are small in comparison with relative variations of $T_{0} (z)$
in time are small in comparison with relative variations of $T_{0} (z)$ and $n_{e0}(z)$
and $n_{e0}(z)$ , just like in table 1.
, just like in table 1.(iv) As for $W_{\textrm {aux}}$
 , the results concerning the absorbed ICRF power density by different species as a function of major radius in SPARC – see figure 4(a) of Rodriguez-Fernandez et al. (Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020) – allow us to assume for simplicity that $P_{\textrm {aux}}$
, the results concerning the absorbed ICRF power density by different species as a function of major radius in SPARC – see figure 4(a) of Rodriguez-Fernandez et al. (Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020) – allow us to assume for simplicity that $P_{\textrm {aux}}$ is uniform and ${>}0$
is uniform and ${>}0$ for $0 \leq y \leq y_{\textrm {aux}}$
for $0 \leq y \leq y_{\textrm {aux}}$ and vanishes for $y_{\textrm {aux}} \leq y \leq 1$
and vanishes for $y_{\textrm {aux}} \leq y \leq 1$ at all values of $z$
at all values of $z$ , for some $y_{\textrm {aux}}$
, for some $y_{\textrm {aux}}$ such that $0 \leq y_{\textrm {aux}} \leq 1$
such that $0 \leq y_{\textrm {aux}} \leq 1$ .
.(v) Once $T ( \boldsymbol {r} , z )$
 , $n_{e} ( \boldsymbol {r} ,z )$
, $n_{e} ( \boldsymbol {r} ,z )$ , $W_{\alpha } (z)$
, $W_{\alpha } (z)$ , $W_{\textrm {ohm}} (z)$
, $W_{\textrm {ohm}} (z)$ , $W_{\textrm {aux}} (z)$
, $W_{\textrm {aux}} (z)$ and $V (z)$
and $V (z)$ are known, computation of $C (z)$
are known, computation of $C (z)$ , $Q (z)$
, $Q (z)$ , $z_{C}$
, $z_{C}$ and $z_{Q}$
and $z_{Q}$ is lengthy but straigthforward. For example:
(3.4)\begin{equation} \int \frac{P_{h}}{T} {{\rm d}}\boldsymbol{x}= \frac{W_{\alpha}}{T_{0}}\frac{1 + 2 \alpha_{n} + 2 \alpha_{T}}{1 + 2 \alpha_{n} + \alpha_{T}}+ \frac{W_{{\rm ohm}}}{T_{0}}\frac{2 + 3 \alpha_{T}}{2 + \alpha_{T}} +\frac{W_{{\rm aux}}}{T_{0}}\frac{1-(1-y_{{\rm aux}}^{2})^{1-\alpha_{T}}}{y_{{\rm aux}}^{2}(1 - \alpha_{T})}, \end{equation}where $\alpha _{T} \equiv \nu _{T}-1$
is lengthy but straigthforward. For example:
(3.4)\begin{equation} \int \frac{P_{h}}{T} {{\rm d}}\boldsymbol{x}= \frac{W_{\alpha}}{T_{0}}\frac{1 + 2 \alpha_{n} + 2 \alpha_{T}}{1 + 2 \alpha_{n} + \alpha_{T}}+ \frac{W_{{\rm ohm}}}{T_{0}}\frac{2 + 3 \alpha_{T}}{2 + \alpha_{T}} +\frac{W_{{\rm aux}}}{T_{0}}\frac{1-(1-y_{{\rm aux}}^{2})^{1-\alpha_{T}}}{y_{{\rm aux}}^{2}(1 - \alpha_{T})}, \end{equation}where $\alpha _{T} \equiv \nu _{T}-1$
 , $\alpha _{n} \equiv \nu _{n}-1$
, $\alpha _{n} \equiv \nu _{n}-1$ , we have dropped the dependence on $z$
, we have dropped the dependence on $z$ everywhere for simplicity and (3.4) reduces to (11) of Di Vita (Reference Di Vita2010) for $W_{\textrm {aux}} \rightarrow 0$
everywhere for simplicity and (3.4) reduces to (11) of Di Vita (Reference Di Vita2010) for $W_{\textrm {aux}} \rightarrow 0$ . Boundaries affect (3.1a–c) through the contribution of $T_{b}$
. Boundaries affect (3.1a–c) through the contribution of $T_{b}$ to $c_{2}$
to $c_{2}$ only, as $P_{hb} = 0$
only, as $P_{hb} = 0$ (Di Vita & Brusati Reference Di Vita and Brusati1995).
(Di Vita & Brusati Reference Di Vita and Brusati1995).
Table 1. A scenario of SPARC in the first two seconds of flat top.

$^{1}$![]() In keV.
In keV.
$^{2}$![]() Dimensionless.
Dimensionless.
$^{3}$![]() In $10^{20}\,\textrm {m}^{-3}$
In $10^{20}\,\textrm {m}^{-3}$![]() .
.
$^{4}$![]() In MW.
In MW.
$^{5}$![]() Figure 7(a) of Rodriguez-Fernandez et al. (Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020).
Figure 7(a) of Rodriguez-Fernandez et al. (Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020).
$^{6}$![]() As $\langle T\rangle _{z=0} = (\nu _{T}^{-1} \cdot T_{0})_{z=0}$
As $\langle T\rangle _{z=0} = (\nu _{T}^{-1} \cdot T_{0})_{z=0}$![]() .
.
$^{7}$![]() Page 13 of Creely et al. (Reference Creely, Greenwald, Ballinger, Brunner, Canik, Doody, Fülöp, Garnier, Granetz and Gray2020), table 3 of Rodriguez-Fernandez et al. (Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020).
Page 13 of Creely et al. (Reference Creely, Greenwald, Ballinger, Brunner, Canik, Doody, Fülöp, Garnier, Granetz and Gray2020), table 3 of Rodriguez-Fernandez et al. (Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020).
$^{8}$![]() As $n_{e}^{-1} n_{i} \equiv 0.85$
As $n_{e}^{-1} n_{i} \equiv 0.85$![]() – p. 13 of Creely et al. (Reference Creely, Greenwald, Ballinger, Brunner, Canik, Doody, Fülöp, Garnier, Granetz and Gray2020) – and $(n_{e})_{z=0} = 2 \times 10^{20}\,\textrm {m}^{-3}$
– p. 13 of Creely et al. (Reference Creely, Greenwald, Ballinger, Brunner, Canik, Doody, Fülöp, Garnier, Granetz and Gray2020) – and $(n_{e})_{z=0} = 2 \times 10^{20}\,\textrm {m}^{-3}$![]() – figure 7(a) of Rodriguez-Fernandez et al. (Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020).
– figure 7(a) of Rodriguez-Fernandez et al. (Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020).
$^{9}$![]() As $(n_{io})_{z=0} = \langle n_{i}\rangle _{z=0}$
As $(n_{io})_{z=0} = \langle n_{i}\rangle _{z=0}$![]() – figure 7(a) of Rodriguez-Fernandez et al. (Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020).
– figure 7(a) of Rodriguez-Fernandez et al. (Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020).
$^{10}$![]() As $(\nu _{n})_{z=0} = (\langle n_{e}\rangle ^{-1} n_{e0})_{z=0}$
As $(\nu _{n})_{z=0} = (\langle n_{e}\rangle ^{-1} n_{e0})_{z=0}$![]() , $n_{e}^{-1} n_{i} \equiv 0.85$
, $n_{e}^{-1} n_{i} \equiv 0.85$![]() – p. 13 of Creely et al. (Reference Creely, Greenwald, Ballinger, Brunner, Canik, Doody, Fülöp, Garnier, Granetz and Gray2020) – and $(n_{io})_{z=0} = \langle n_{i}\rangle _{z=0}$
– p. 13 of Creely et al. (Reference Creely, Greenwald, Ballinger, Brunner, Canik, Doody, Fülöp, Garnier, Granetz and Gray2020) – and $(n_{io})_{z=0} = \langle n_{i}\rangle _{z=0}$![]() .
.
$^{11}$![]() As $P_{\textrm {aux}} > 0$
As $P_{\textrm {aux}} > 0$![]() between $R_{\min } = 1.8$
between $R_{\min } = 1.8$![]() m and $R_{\min } = 2.1$
m and $R_{\min } = 2.1$![]() m – figure 4(a) of Rodriguez-Fernandez et al. (Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020) – and $2y_{\textrm {aux}} = {(R_{\max }-R_{\min })}/{R_{0}}$
m – figure 4(a) of Rodriguez-Fernandez et al. (Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020) – and $2y_{\textrm {aux}} = {(R_{\max }-R_{\min })}/{R_{0}}$![]() .
.
$^{12}$![]() As $(W_{\textrm {ohm}})_{z=0} = (W_{\textrm {ohm}})_{z=2} (T_{0})_{z=0}^{{3}/{2}} (T_{0})_{z=2}^{-({3}/{2})} {(1 + \frac {3}{2} (\alpha _{T})_{z=2})}/{(1 + \frac {3}{2} (\alpha _{T})_{z=0})}$
As $(W_{\textrm {ohm}})_{z=0} = (W_{\textrm {ohm}})_{z=2} (T_{0})_{z=0}^{{3}/{2}} (T_{0})_{z=2}^{-({3}/{2})} {(1 + \frac {3}{2} (\alpha _{T})_{z=2})}/{(1 + \frac {3}{2} (\alpha _{T})_{z=0})}$![]() .
.
$^{13}$![]() As $(W_{\alpha })_{z=0} = (W_{\alpha })_{z=2} (n_{i0})_{z=0}^{2} (T_{0})_{z=0}^{2}(n_{i0})_{z=2}^{-2} (T_{0})_{z=2}^{-2} (1 + 2 (\alpha _{n})_{z=2}+ 2 (\alpha _{T})_{z=2})(1 + 2 (\alpha _{n})_{z=0}+ 2 (\alpha _{T})_{z=0})^{-1}$
As $(W_{\alpha })_{z=0} = (W_{\alpha })_{z=2} (n_{i0})_{z=0}^{2} (T_{0})_{z=0}^{2}(n_{i0})_{z=2}^{-2} (T_{0})_{z=2}^{-2} (1 + 2 (\alpha _{n})_{z=2}+ 2 (\alpha _{T})_{z=2})(1 + 2 (\alpha _{n})_{z=0}+ 2 (\alpha _{T})_{z=0})^{-1}$![]() .
.
$^{14}$![]() Table 1 of Rodriguez-Fernandez et al. (Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020).
Table 1 of Rodriguez-Fernandez et al. (Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020).
$^{15}$![]() Figure 7(a) of Rodriguez-Fernandez et al. (Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020).
Figure 7(a) of Rodriguez-Fernandez et al. (Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020).
$^{16}$![]() As $\langle T\rangle _{z=1} = (\nu _{T}^{-1} T_{0})_{z=1}$
As $\langle T\rangle _{z=1} = (\nu _{T}^{-1} T_{0})_{z=1}$![]() .
.
$^{17}$![]() Page 13 of Creely et al. (Reference Creely, Greenwald, Ballinger, Brunner, Canik, Doody, Fülöp, Garnier, Granetz and Gray2020), table 3 of Rodriguez-Fernandez et al. (Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020).
Page 13 of Creely et al. (Reference Creely, Greenwald, Ballinger, Brunner, Canik, Doody, Fülöp, Garnier, Granetz and Gray2020), table 3 of Rodriguez-Fernandez et al. (Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020).
$^{18}$![]() As $(n_{e0})_{z=1} = 2.7 \times 10^{20}\,\textrm {m}^{-3}$
As $(n_{e0})_{z=1} = 2.7 \times 10^{20}\,\textrm {m}^{-3}$![]() – figure 7(a) of Rodriguez-Fernandez et al. (Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020) – and $n_{e}^{-1} n_{i} \equiv 0.85$
– figure 7(a) of Rodriguez-Fernandez et al. (Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020) – and $n_{e}^{-1} n_{i} \equiv 0.85$![]() – p. 13 of Creely et al. (Reference Creely, Greenwald, Ballinger, Brunner, Canik, Doody, Fülöp, Garnier, Granetz and Gray2020).
– p. 13 of Creely et al. (Reference Creely, Greenwald, Ballinger, Brunner, Canik, Doody, Fülöp, Garnier, Granetz and Gray2020).
$^{19}$![]() As $\langle n_{e}\rangle _{z=1} = 2.7 \times 10^{20}\,\textrm {m}^{-3}$
As $\langle n_{e}\rangle _{z=1} = 2.7 \times 10^{20}\,\textrm {m}^{-3}$![]() – figure 7(a) of Rodriguez-Fernandez et al. (Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020) – and $n_{e}^{-1} n_{i} \equiv 0.85$
– figure 7(a) of Rodriguez-Fernandez et al. (Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020) – and $n_{e}^{-1} n_{i} \equiv 0.85$![]() – p. 13 of Creely et al. (Reference Creely, Greenwald, Ballinger, Brunner, Canik, Doody, Fülöp, Garnier, Granetz and Gray2020).
– p. 13 of Creely et al. (Reference Creely, Greenwald, Ballinger, Brunner, Canik, Doody, Fülöp, Garnier, Granetz and Gray2020).
$^{20}$![]() As $(\nu _{n})_{z=1} = (\langle n_{e}\rangle ^{-1} n_{e0})_{z=1}$
As $(\nu _{n})_{z=1} = (\langle n_{e}\rangle ^{-1} n_{e0})_{z=1}$![]() , $n_{e}^{-1} n_{i} \equiv 0.85$
, $n_{e}^{-1} n_{i} \equiv 0.85$![]() – p. 13 of Creely et al. (Reference Creely, Greenwald, Ballinger, Brunner, Canik, Doody, Fülöp, Garnier, Granetz and Gray2020) – and $(n_{io})_{z=1} = \langle n_{i}\rangle _{z=1}$
– p. 13 of Creely et al. (Reference Creely, Greenwald, Ballinger, Brunner, Canik, Doody, Fülöp, Garnier, Granetz and Gray2020) – and $(n_{io})_{z=1} = \langle n_{i}\rangle _{z=1}$![]() .
.
$^{21}$![]() As $P_{\textrm {aux}} > 0$
As $P_{\textrm {aux}} > 0$![]() between $R_{\min } = 1.8$
between $R_{\min } = 1.8$![]() and $R_{\min } = 2.1$
and $R_{\min } = 2.1$![]() m – figure 4(a) of Rodriguez-Fernandez et al. (Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020) – and $2y_{\textrm {aux}} = {(R_{\max }-R_{\min })}/{R_{0}}$
m – figure 4(a) of Rodriguez-Fernandez et al. (Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020) – and $2y_{\textrm {aux}} = {(R_{\max }-R_{\min })}/{R_{0}}$![]() .
.
$^{22}$![]() As $(W_{\textrm {ohm}})_{z=1} = (W_{\textrm {ohm}})_{z=2} (T_{0})_{z=1}^{{3}/{2}} (T_{0})_{z=2}^{-({3}/{2})} {(1 + \frac {3}{2} (\alpha _{T})_{z=2})}/{(1 + \frac {3}{2} (\alpha _{T})_{z=1})}$
As $(W_{\textrm {ohm}})_{z=1} = (W_{\textrm {ohm}})_{z=2} (T_{0})_{z=1}^{{3}/{2}} (T_{0})_{z=2}^{-({3}/{2})} {(1 + \frac {3}{2} (\alpha _{T})_{z=2})}/{(1 + \frac {3}{2} (\alpha _{T})_{z=1})}$![]() .
.
$^{23}$![]() As $(W_{\alpha })_{z=1} = (W_{\alpha })_{z=2} (n_{i0})_{z=1}^{2} (T_{0})_{z=1}^{2}(n_{i0})_{z=2}^{-2} (T_{0})_{z=2}^{-2} (1 + 2 (\alpha _{n})_{z=2}+ 2 (\alpha _{T})_{z=2})(1 + 2 (\alpha _{n})_{z=1}+ 2 (\alpha _{T})_{z=1})^{-1}$
As $(W_{\alpha })_{z=1} = (W_{\alpha })_{z=2} (n_{i0})_{z=1}^{2} (T_{0})_{z=1}^{2}(n_{i0})_{z=2}^{-2} (T_{0})_{z=2}^{-2} (1 + 2 (\alpha _{n})_{z=2}+ 2 (\alpha _{T})_{z=2})(1 + 2 (\alpha _{n})_{z=1}+ 2 (\alpha _{T})_{z=1})^{-1}$![]() .
.
$^{24}$![]() Table 1 of Rodriguez-Fernandez et al. (Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020).
Table 1 of Rodriguez-Fernandez et al. (Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020).
$^{25}$![]() As $(T_{0})_{z=2} = (\nu _{T})_{z=2} \langle T\rangle _{z=2}$
As $(T_{0})_{z=2} = (\nu _{T})_{z=2} \langle T\rangle _{z=2}$![]() .
.
$^{26}$![]() Table 2 of Creely et al. (Reference Creely, Greenwald, Ballinger, Brunner, Canik, Doody, Fülöp, Garnier, Granetz and Gray2020).
Table 2 of Creely et al. (Reference Creely, Greenwald, Ballinger, Brunner, Canik, Doody, Fülöp, Garnier, Granetz and Gray2020).
$^{27}$![]() Page 13 of Creely et al. (Reference Creely, Greenwald, Ballinger, Brunner, Canik, Doody, Fülöp, Garnier, Granetz and Gray2020), table 3 of Rodriguez-Fernandez et al. (Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020).
Page 13 of Creely et al. (Reference Creely, Greenwald, Ballinger, Brunner, Canik, Doody, Fülöp, Garnier, Granetz and Gray2020), table 3 of Rodriguez-Fernandez et al. (Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020).
$^{28}$![]() Figure 8(a) of Rodriguez-Fernandez et al. (Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020).
Figure 8(a) of Rodriguez-Fernandez et al. (Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020).
$^{29}$![]() Table 2 of Creely et al. (Reference Creely, Greenwald, Ballinger, Brunner, Canik, Doody, Fülöp, Garnier, Granetz and Gray2020).
Table 2 of Creely et al. (Reference Creely, Greenwald, Ballinger, Brunner, Canik, Doody, Fülöp, Garnier, Granetz and Gray2020).
$^{30}$![]() As $(\nu _{n})_{z=2} = (\langle n_{e}\rangle ^{-1} n_{e0})_{z=2}$
As $(\nu _{n})_{z=2} = (\langle n_{e}\rangle ^{-1} n_{e0})_{z=2}$![]() , $n_{e}^{-1} n_{i} \equiv 0.85$
, $n_{e}^{-1} n_{i} \equiv 0.85$![]() – p. 13 of Creely et al. (Reference Creely, Greenwald, Ballinger, Brunner, Canik, Doody, Fülöp, Garnier, Granetz and Gray2020) – and $(n_{io})_{z=2} = 1.15 \langle n_{i}\rangle _{z=2}$
– p. 13 of Creely et al. (Reference Creely, Greenwald, Ballinger, Brunner, Canik, Doody, Fülöp, Garnier, Granetz and Gray2020) – and $(n_{io})_{z=2} = 1.15 \langle n_{i}\rangle _{z=2}$![]() . Here $(\nu _{n})_{z=2} < 1.3$
. Here $(\nu _{n})_{z=2} < 1.3$![]() , the value provided on p. 9 of Rodriguez-Fernandez et al. (Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020); this may be a overpessimistic assumption.
, the value provided on p. 9 of Rodriguez-Fernandez et al. (Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020); this may be a overpessimistic assumption.
$^{31}$![]() As $P_{\textrm {aux}} > 0$
As $P_{\textrm {aux}} > 0$![]() between $R_{\min } = 1.8$
between $R_{\min } = 1.8$![]() and $R_{\min } = 2.1$
and $R_{\min } = 2.1$![]() m – figure 4(a) of Rodriguez-Fernandez et al. (Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020) – and $2y_{\textrm {aux}} = {(R_{\max }-R_{\min })}/{R_{0}}$
m – figure 4(a) of Rodriguez-Fernandez et al. (Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020) – and $2y_{\textrm {aux}} = {(R_{\max }-R_{\min })}/{R_{0}}$![]() .
.
$^{32}$![]() $= Q_{z=2}^{-1} (W_{\textrm {fus}})_{z=2} - (W_{\textrm {aux}})_{z=2}$
$= Q_{z=2}^{-1} (W_{\textrm {fus}})_{z=2} - (W_{\textrm {aux}})_{z=2}$![]() with $Q_{z=2} = 11$
with $Q_{z=2} = 11$![]() , $(W_{\textrm {fus}})_{z=2} = 140$
, $(W_{\textrm {fus}})_{z=2} = 140$![]() MW – table 2 of Creely et al. (Reference Creely, Greenwald, Ballinger, Brunner, Canik, Doody, Fülöp, Garnier, Granetz and Gray2020), figure 7(b) and p. 2 of Rodriguez-Fernandez et al. (Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020).
MW – table 2 of Creely et al. (Reference Creely, Greenwald, Ballinger, Brunner, Canik, Doody, Fülöp, Garnier, Granetz and Gray2020), figure 7(b) and p. 2 of Rodriguez-Fernandez et al. (Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020).
$^{33}$![]() $= {(W_{\textrm {fus}})_{z=2}}/{5}$
$= {(W_{\textrm {fus}})_{z=2}}/{5}$![]() with $(W_{\textrm {fus}})_{z=2} = 140$
with $(W_{\textrm {fus}})_{z=2} = 140$![]() MW – figure 7(b) and p. 2 of Rodriguez-Fernandez et al. (Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020).
MW – figure 7(b) and p. 2 of Rodriguez-Fernandez et al. (Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020).
$^{34}$![]() Table 1 of Rodriguez-Fernandez et al. (Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020).
Table 1 of Rodriguez-Fernandez et al. (Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020).
For the sake of simplicity we ignore changes in plasma geometry, i.e. we assume $R_{0}$![]() , $a_{p}$
, $a_{p}$![]() , $\kappa _{\textrm {sep}}$
, $\kappa _{\textrm {sep}}$![]() , $\delta _{\textrm {sep}}$
, $\delta _{\textrm {sep}}$![]() and $V$
and $V$![]() to be constant so that $V \approx 2\,\%$
to be constant so that $V \approx 2\,\%$![]() (Creely et al. Reference Creely, Greenwald, Ballinger, Brunner, Canik, Doody, Fülöp, Garnier, Granetz and Gray2020) of ITER volume ($830\,\textrm {m}^{3}$
(Creely et al. Reference Creely, Greenwald, Ballinger, Brunner, Canik, Doody, Fülöp, Garnier, Granetz and Gray2020) of ITER volume ($830\,\textrm {m}^{3}$![]() ; Shimada et al. Reference Shimada, Campbell, Mukhovatov, Fujiwara, Kirneva, Lackner, Nagami, Pustovitov, Uckan and Wesley2007); admittedly, this is an optimistic assumption as $V$
; Shimada et al. Reference Shimada, Campbell, Mukhovatov, Fujiwara, Kirneva, Lackner, Nagami, Pustovitov, Uckan and Wesley2007); admittedly, this is an optimistic assumption as $V$![]() expands due to increasing Shafranov shift and expansion cools the plasma, but it seems reasonable as far as we are dealing with the flat top. Generalization to the case of moving plasma is cumbersome but straigthforward. (Should, for example, a scenario provide us with a known $({{\textrm {d}}V}/{{\textrm {d}}t})(t) > 0$
expands due to increasing Shafranov shift and expansion cools the plasma, but it seems reasonable as far as we are dealing with the flat top. Generalization to the case of moving plasma is cumbersome but straigthforward. (Should, for example, a scenario provide us with a known $({{\textrm {d}}V}/{{\textrm {d}}t})(t) > 0$![]() , we could divide both sides of (2.2a–c) by ${{\textrm {d}}V}/{V \,{\textrm {d}}t}$
, we could divide both sides of (2.2a–c) by ${{\textrm {d}}V}/{V \,{\textrm {d}}t}$![]() and rewrite both (3.1a–c) and (3.2a–c) by replacing $z$
and rewrite both (3.1a–c) and (3.2a–c) by replacing $z$![]() with a natural independent coordinate $\ln V$
with a natural independent coordinate $\ln V$![]() .) Following Creely et al. (Reference Creely, Greenwald, Ballinger, Brunner, Canik, Doody, Fülöp, Garnier, Granetz and Gray2020), and in analogy with a previous analysis of an IGNITOR scenario with $W_{\textrm {aux}} = 0$
.) Following Creely et al. (Reference Creely, Greenwald, Ballinger, Brunner, Canik, Doody, Fülöp, Garnier, Granetz and Gray2020), and in analogy with a previous analysis of an IGNITOR scenario with $W_{\textrm {aux}} = 0$![]() (Di Vita Reference Di Vita2010), we consider no pellet. The latter analysis has shown that the feasibility of a burning plasma strongly depends on $T_{b}$
(Di Vita Reference Di Vita2010), we consider no pellet. The latter analysis has shown that the feasibility of a burning plasma strongly depends on $T_{b}$![]() (Di Vita Reference Di Vita2010). We have performed a scan of $T_{b}$
(Di Vita Reference Di Vita2010). We have performed a scan of $T_{b}$![]() (Rodriguez-Fernandez et al. Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020) while investigating two scenarios (figure 1) in the range $0 \leq z \leq 2$
(Rodriguez-Fernandez et al. Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020) while investigating two scenarios (figure 1) in the range $0 \leq z \leq 2$![]() . The first scenario (dubbed I) is the SPARC scenario of table 1 where $W_{\textrm {aux}} = 11$
. The first scenario (dubbed I) is the SPARC scenario of table 1 where $W_{\textrm {aux}} = 11$![]() MW at all times. The second scenario (dubbed II) is just like I, but with a modified timing of $W_{\textrm {aux}}$
MW at all times. The second scenario (dubbed II) is just like I, but with a modified timing of $W_{\textrm {aux}}$![]() : $W_{\textrm {aux}} (z = 0)= 1$
: $W_{\textrm {aux}} (z = 0)= 1$![]() MW, $W_{\textrm {aux}} (z=1) = 25$
MW, $W_{\textrm {aux}} (z=1) = 25$![]() MW (25 MW is the maximum coupled auxiliary heating power allowed in SPARC design; Creely et al. Reference Creely, Greenwald, Ballinger, Brunner, Canik, Doody, Fülöp, Garnier, Granetz and Gray2020) and $W_{\textrm {aux}}(z=2) = 11$
MW (25 MW is the maximum coupled auxiliary heating power allowed in SPARC design; Creely et al. Reference Creely, Greenwald, Ballinger, Brunner, Canik, Doody, Fülöp, Garnier, Granetz and Gray2020) and $W_{\textrm {aux}}(z=2) = 11$![]() MW; polynomial interpolation among these values provides us with $W_{\textrm {aux}} (z)$
MW; polynomial interpolation among these values provides us with $W_{\textrm {aux}} (z)$![]() in the whole range $0 \leq z \leq 2$
in the whole range $0 \leq z \leq 2$![]() . In II, figure 1 shows that a rising $W_{\textrm {aux}}$
. In II, figure 1 shows that a rising $W_{\textrm {aux}}$![]() accompanies the growth of $W_{\alpha }$
accompanies the growth of $W_{\alpha }$![]() (and the related rise of $T_{0}$
(and the related rise of $T_{0}$![]() , not displayed in the figure) until $z = 1$
, not displayed in the figure) until $z = 1$![]() , then decreases after $W_{\alpha }$
, then decreases after $W_{\alpha }$![]() has ‘taken off’; in contrast, $W_{\textrm {aux}}$
has ‘taken off’; in contrast, $W_{\textrm {aux}}$![]() is constant in I. Figure 2 and figures 3 and 4 display $C (z)$
is constant in I. Figure 2 and figures 3 and 4 display $C (z)$![]() at various values of $T_{b}$
at various values of $T_{b}$![]() – taken from figures 3(b) and 6(d) of Rodriguez-Fernandez et al. (Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020) – and $Q(z) - 5$
– taken from figures 3(b) and 6(d) of Rodriguez-Fernandez et al. (Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020) – and $Q(z) - 5$![]() for I and II,respectively.
for I and II,respectively.

Figure 1. Vertical axis: $W_{\textrm {ohm}}$![]() (MW, shared by scenarios I and II and labelled with crosses), $W_{\alpha }$
(MW, shared by scenarios I and II and labelled with crosses), $W_{\alpha }$![]() (MW, shared by scenarios I and II and labelled with pluses), $W_{\textrm {aux}}$
(MW, shared by scenarios I and II and labelled with pluses), $W_{\textrm {aux}}$![]() (MW, scenario I and labelled with dots) and $W_{\textrm {aux}}$
(MW, scenario I and labelled with dots) and $W_{\textrm {aux}}$![]() (MW, scenario II and labelled with dashes). Horizontal axis: dimensionless time variable $z$
(MW, scenario II and labelled with dashes). Horizontal axis: dimensionless time variable $z$![]() , where $z = 0$
, where $z = 0$![]() and $z = 2$
and $z = 2$![]() correspond to the beginning and the end of the first $2$
correspond to the beginning and the end of the first $2$![]() s of SPARC flat top, respectively (see text). In scenario II, the growth of $W_{\textrm {aux}}$
s of SPARC flat top, respectively (see text). In scenario II, the growth of $W_{\textrm {aux}}$![]() accompanies the growth of $W_{\alpha }$
accompanies the growth of $W_{\alpha }$![]() up to the time $z = 1$
up to the time $z = 1$![]() when $T_{0}$
when $T_{0}$![]() achieves its maximum (see table 1).
achieves its maximum (see table 1).

Figure 2. Scenario I. Vertical axis: dimensionless $Q(z)-5$![]() (labelled with continuous line) and dimensionless $C(z)$
(labelled with continuous line) and dimensionless $C(z)$![]() at $T_{b} = 2$
at $T_{b} = 2$![]() keV (labelled with crosses), $T_{b} = 4$
keV (labelled with crosses), $T_{b} = 4$![]() keV (labelled with pluses), $T_{b} = 5$
keV (labelled with pluses), $T_{b} = 5$![]() keV (labelled with dashes). Horizontal axis: dimensionless time variable $z$
keV (labelled with dashes). Horizontal axis: dimensionless time variable $z$![]() (see figure 1). The range of the zeroes of $C(z)$
(see figure 1). The range of the zeroes of $C(z)$![]() is $1.3 \leq z_{C} \leq 1.4$
is $1.3 \leq z_{C} \leq 1.4$![]() , and $Q(z)= 5$
, and $Q(z)= 5$![]() at $z = z_{Q} \approx 0.3$
at $z = z_{Q} \approx 0.3$![]() , i.e. $z_{C} > z_{Q}$
, i.e. $z_{C} > z_{Q}$![]() and (3.2a–c) is violated regardless of $T_{b}$
and (3.2a–c) is violated regardless of $T_{b}$![]() . Thus, scenario I is compatible with the requirements of Rogister & Li (Reference Rogister and Li1992) in no case.
. Thus, scenario I is compatible with the requirements of Rogister & Li (Reference Rogister and Li1992) in no case.

Figure 3. Scenario II. Vertical axis: dimensionless $Q(z)-5$![]() (labelled with continuous line) and dimensionless $C(z)$
(labelled with continuous line) and dimensionless $C(z)$![]() at $T_{b} = 2$
at $T_{b} = 2$![]() keV (labelled with crosses), $T_{b} = 4$
keV (labelled with crosses), $T_{b} = 4$![]() keV (labelled with pluses), $T_{b} = 5$
keV (labelled with pluses), $T_{b} = 5$![]() keV (labelled with dashes). Horizontal axis: dimensionless time variable $z$
keV (labelled with dashes). Horizontal axis: dimensionless time variable $z$![]() (see figure 1). If $T_{b} < 4$
(see figure 1). If $T_{b} < 4$![]() keV then (3.2a–c) is still violated, but if $T_{b} > 4$
keV then (3.2a–c) is still violated, but if $T_{b} > 4$![]() keV it is satisfied (see also figure 4) and scenario II is compatible with Rogister & Li (Reference Rogister and Li1992).
keV it is satisfied (see also figure 4) and scenario II is compatible with Rogister & Li (Reference Rogister and Li1992).
Regardless of $T_{b}$![]() , it turns out that $C(z=0) <0$
, it turns out that $C(z=0) <0$![]() and $Q(z=0) < 5$
and $Q(z=0) < 5$![]() in both I and II, as anticipated.
in both I and II, as anticipated.
As for I, figure 2 shows that $z_{C} > z_{Q}$![]() . The warning in Rodriguez-Fernandez et al. (Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020) quoted above concerning the need for detailed analysis of auxiliary heating for some early portion of the current flat top is therefore well justified: a scenario which assumes a constant $W_{\textrm {aux}}$
. The warning in Rodriguez-Fernandez et al. (Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020) quoted above concerning the need for detailed analysis of auxiliary heating for some early portion of the current flat top is therefore well justified: a scenario which assumes a constant $W_{\textrm {aux}}$![]() and predicts that $Q > 5$
and predicts that $Q > 5$![]() may be in contrast with the general results of Rogister & Li (Reference Rogister and Li1992), and therefore may be not self-consistent.
may be in contrast with the general results of Rogister & Li (Reference Rogister and Li1992), and therefore may be not self-consistent.
As for II, figure 3 and its zoomed detail (figure 4) show that $z_{C} < z_{Q}$![]() provided that $T_{b} > 4$
provided that $T_{b} > 4$![]() keV, a value which is still compatible with the results displayed in figure 6(d) of Rodriguez-Fernandez et al. (Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020). Admittedly, computations in this modified scenario have been performed after changing $W_{\textrm {aux}}$
keV, a value which is still compatible with the results displayed in figure 6(d) of Rodriguez-Fernandez et al. (Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020). Admittedly, computations in this modified scenario have been performed after changing $W_{\textrm {aux}}$![]() only, all other things being equal; even if this procedure is not fully self-consistent, however, it is enough to suggest that modulation of auxiliary heating in time during the initial phase of flat top may greatly increase the feasibility of a burning plasma in SPARC. Our result for the minimum temperature pedestal required for $Q > 5$
only, all other things being equal; even if this procedure is not fully self-consistent, however, it is enough to suggest that modulation of auxiliary heating in time during the initial phase of flat top may greatly increase the feasibility of a burning plasma in SPARC. Our result for the minimum temperature pedestal required for $Q > 5$![]() somehow differs from the conclusions concerning resilience of SPARC plasma performances against pedestal degradation displayed in figure 6(c) of Rodriguez-Fernandez et al. (Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020); this is just as expected, as far as the latter conclusions are concerned with the successful accomplishment of SPARC mission (the achievement of $Q > 2$
somehow differs from the conclusions concerning resilience of SPARC plasma performances against pedestal degradation displayed in figure 6(c) of Rodriguez-Fernandez et al. (Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020); this is just as expected, as far as the latter conclusions are concerned with the successful accomplishment of SPARC mission (the achievement of $Q > 2$![]() ), while we focused rather on the (even more difficult) achievement of a $Q> 5$
), while we focused rather on the (even more difficult) achievement of a $Q> 5$![]() plasma.
plasma.
4. Conclusions
Recently, successful operation of a 20 T, HTS magnet has been reported (Chandler Reference Chandler2021). This result paves the way for the construction of SPARC, a proposed high-field tokamak (Creely et al. Reference Creely, Greenwald, Ballinger, Brunner, Canik, Doody, Fülöp, Garnier, Granetz and Gray2020; Rodriguez-Fernandez et al. Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020) with superconducting coils (Bruzzone et al. Reference Bruzzone, Fietz, Minervini, Novikov, Yanagi, Zhai and Zheng2018) and ion cyclotron radiofrequency heating (ICRH) (Lin et al. Reference Lin, Wright and Wukitch2020) which aims at achieving a fusion gain $Q$![]() larger than 2 in a DT plasma starting from well-established assumptions on both physics and engineering; most assumptions of SPARC, indeed, are largely based on the ITER Physics Basis (Shimada et al. Reference Shimada, Campbell, Mukhovatov, Fujiwara, Kirneva, Lackner, Nagami, Pustovitov, Uckan and Wesley2007). SPARC is slated for completion in 2025, i.e. many years in advance on the much larger ITER with its Nb-alloy low-temperature superconductors. Its results are therefore relevant to the rapid development and deployment of nuclear fusion as a source of clean energy and can make a difference on the time scales necessary to have an impact on climate change. Different simulations of SPARC performances agree in predicting successful achievement of $Q > 2$
larger than 2 in a DT plasma starting from well-established assumptions on both physics and engineering; most assumptions of SPARC, indeed, are largely based on the ITER Physics Basis (Shimada et al. Reference Shimada, Campbell, Mukhovatov, Fujiwara, Kirneva, Lackner, Nagami, Pustovitov, Uckan and Wesley2007). SPARC is slated for completion in 2025, i.e. many years in advance on the much larger ITER with its Nb-alloy low-temperature superconductors. Its results are therefore relevant to the rapid development and deployment of nuclear fusion as a source of clean energy and can make a difference on the time scales necessary to have an impact on climate change. Different simulations of SPARC performances agree in predicting successful achievement of $Q > 2$![]() , and even of $Q > 5$
, and even of $Q > 5$![]() under conservative assumptions concerning the physics (Rodriguez-Fernandez et al. Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020); in the latter case, SPARC can also address many challenges in burning plasma research – including burn control, burning plasma self-organization, interactions between $\alpha$
under conservative assumptions concerning the physics (Rodriguez-Fernandez et al. Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020); in the latter case, SPARC can also address many challenges in burning plasma research – including burn control, burning plasma self-organization, interactions between $\alpha$![]() particles and MHD modes, divertor physics and disruption prediction and mitigation (Creely et al. Reference Creely, Greenwald, Ballinger, Brunner, Canik, Doody, Fülöp, Garnier, Granetz and Gray2020). In particular, the transition from a $Q \ll 5$
particles and MHD modes, divertor physics and disruption prediction and mitigation (Creely et al. Reference Creely, Greenwald, Ballinger, Brunner, Canik, Doody, Fülöp, Garnier, Granetz and Gray2020). In particular, the transition from a $Q \ll 5$![]() condition (with negligible heating due to $\alpha$
condition (with negligible heating due to $\alpha$![]() particles) to a $Q > 5$
particles) to a $Q > 5$![]() state (where the $\alpha$
state (where the $\alpha$![]() particles govern plasma heating) implies a fast rise of both ion and electron temperatures in the simulations of high-field tokamaks like SPARC (Creely et al. Reference Creely, Greenwald, Ballinger, Brunner, Canik, Doody, Fülöp, Garnier, Granetz and Gray2020; Rodriguez-Fernandez et al. Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020) and IGNITOR (Bombarda et al. Reference Bombarda, Coppi, Airoldi, Cenacchi and Detragiache2004) (we take both temperatures to be equal, say to $T$
particles govern plasma heating) implies a fast rise of both ion and electron temperatures in the simulations of high-field tokamaks like SPARC (Creely et al. Reference Creely, Greenwald, Ballinger, Brunner, Canik, Doody, Fülöp, Garnier, Granetz and Gray2020; Rodriguez-Fernandez et al. Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020) and IGNITOR (Bombarda et al. Reference Bombarda, Coppi, Airoldi, Cenacchi and Detragiache2004) (we take both temperatures to be equal, say to $T$![]() , in these high-density plasmas); given the strong dependence of the fusion power on temperature, we read this fast rise as a thermal runaway.
, in these high-density plasmas); given the strong dependence of the fusion power on temperature, we read this fast rise as a thermal runaway.
As usual when it comes to controlled nuclear fusion research, however, these predictions are still affected by various uncertainties, no matter how conservative their underlying assumptions. As for SPARC, such uncertainties involve, for example, particle and energy transport, sawteeth and the amount of auxiliary heating required for sustaining a H-mode. As for the latter, in turn, the detailed simulation described in Rodriguez-Fernandez et al. (Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020) ignores the possible plasma trajectory needed to access (and subsequently sustain) the H-mode, which may require higher auxiliary power $W_{\textrm {aux}}$![]() than the assumed value of 11 MW for some early portion of the current flat top. Even for powerful computational tools like those based on the highly sophisticated gyro-Landau fluid (TGLF-SAT1) quasilinear model in Rodriguez-Fernandez et al. (Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020), of course, the validity of the resulting predictions is ultimately limited by the validity of approximations like, for example, those concerning impurity concentrations (Creely et al. Reference Creely, Greenwald, Ballinger, Brunner, Canik, Doody, Fülöp, Garnier, Granetz and Gray2020), which is difficult to check a priori. An assessment of the feasibility of a burning ($Q > 5$
than the assumed value of 11 MW for some early portion of the current flat top. Even for powerful computational tools like those based on the highly sophisticated gyro-Landau fluid (TGLF-SAT1) quasilinear model in Rodriguez-Fernandez et al. (Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020), of course, the validity of the resulting predictions is ultimately limited by the validity of approximations like, for example, those concerning impurity concentrations (Creely et al. Reference Creely, Greenwald, Ballinger, Brunner, Canik, Doody, Fülöp, Garnier, Granetz and Gray2020), which is difficult to check a priori. An assessment of the feasibility of a burning ($Q > 5$![]() ) plasma in SPARC which depends on detailed models of particle and energy transport as little as possible is therefore highly desirable.
) plasma in SPARC which depends on detailed models of particle and energy transport as little as possible is therefore highly desirable.
For this purpose, we take advantage of the general discussion of Rogister & Li (Reference Rogister and Li1992) concerning weakly collisional, low-$\beta$![]() , turbulent axisimmetric plasmas like the plasma of SPARC. It boils down to the conclusion that the thermalization time scales for ions and electrons in the plasma bounded by adjacent magnetic surfaces are much shorter than the typical time scales of particle and energy transport in the direction perpendicular to these surfaces. Crucially, this result depends on no detailed model of transport. Moreover, it allows us to define locally a temperature, an entropy density and all other familiar quantities of thermodynamics, which are linked to each other by the usual relationships of thermodynamics. The validity of these relationships locally at all times puts a constraint (Glansdorff & Prigogine Reference Glansdorff and Prigogine1964) on the time evolution of the system as a whole, in agreement with Le Châtelier's principle (Landau & Lifshitz Reference Landau and Lifshitz1959). If, furthermore, the system is a high-field tokamak plasma which undergoes no thermal runaway, then this constraint takes the form of an inequality (2.2a–c) involving the total time derivatives of both the total heating power ($\textrm {ohmic} + \textrm {auxiliary} + \alpha$
, turbulent axisimmetric plasmas like the plasma of SPARC. It boils down to the conclusion that the thermalization time scales for ions and electrons in the plasma bounded by adjacent magnetic surfaces are much shorter than the typical time scales of particle and energy transport in the direction perpendicular to these surfaces. Crucially, this result depends on no detailed model of transport. Moreover, it allows us to define locally a temperature, an entropy density and all other familiar quantities of thermodynamics, which are linked to each other by the usual relationships of thermodynamics. The validity of these relationships locally at all times puts a constraint (Glansdorff & Prigogine Reference Glansdorff and Prigogine1964) on the time evolution of the system as a whole, in agreement with Le Châtelier's principle (Landau & Lifshitz Reference Landau and Lifshitz1959). If, furthermore, the system is a high-field tokamak plasma which undergoes no thermal runaway, then this constraint takes the form of an inequality (2.2a–c) involving the total time derivatives of both the total heating power ($\textrm {ohmic} + \textrm {auxiliary} + \alpha$![]() ) and the related entropy production. Any description of the time evolution of a weakly collisional, low-$\beta$
) and the related entropy production. Any description of the time evolution of a weakly collisional, low-$\beta$![]() , turbulent, axisymmetric, high-field tokamak plasma (like SPARC) which does not achieve $Q > 5$
, turbulent, axisymmetric, high-field tokamak plasma (like SPARC) which does not achieve $Q > 5$![]() in a given time interval must satisfy (2.2a–c) at all times in such a time interval, no matter what the physical mechanism underlying transport is like. Now, a simulation of SPARC predicts that $Q > 5$
in a given time interval must satisfy (2.2a–c) at all times in such a time interval, no matter what the physical mechanism underlying transport is like. Now, a simulation of SPARC predicts that $Q > 5$![]() within the first 2 s of the flat top – see figure 7(a) of Rodriguez-Fernandez et al. (Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020). This is only possible if (2.2a–c) is violated at some time in this time interval, as no thermal runaway is possible as far as (2.2a–c) holds.
within the first 2 s of the flat top – see figure 7(a) of Rodriguez-Fernandez et al. (Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020). This is only possible if (2.2a–c) is violated at some time in this time interval, as no thermal runaway is possible as far as (2.2a–c) holds.
Our discussion shows that (2.2a–c) allows independent assessment of the feasibility of burning plasmas in high-field tokamaks. More precisely, it allows one to check if the time evolution of the plasma which turns out to be the result of numerical computations based on given physical assumptions concerning transport, impurities, etc., is compatible with the constraints imposed by low-$\beta$![]() turbulence. Following an approach already utilized in the analysis of IGNITOR (Di Vita Reference Di Vita2010), we check if a SPARC-relevant scenario outlined in Rodriguez-Fernandez et al. (Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020) – with its time-dependent values of ohmic, auxiliary and fusion power and its time-dependent profiles of particle densities and temperatures – violates (2.2a–c) as $Q > 5$
turbulence. Following an approach already utilized in the analysis of IGNITOR (Di Vita Reference Di Vita2010), we check if a SPARC-relevant scenario outlined in Rodriguez-Fernandez et al. (Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020) – with its time-dependent values of ohmic, auxiliary and fusion power and its time-dependent profiles of particle densities and temperatures – violates (2.2a–c) as $Q > 5$![]() . Only in this case, indeed, can the thermal runaway actually occur. Basically, this is a self-consistency check of the simulation which we take as a given input, and relies therefore on no assumption concerning energy transport, impurities,etc.
. Only in this case, indeed, can the thermal runaway actually occur. Basically, this is a self-consistency check of the simulation which we take as a given input, and relies therefore on no assumption concerning energy transport, impurities,etc.
It turns out that the result of the test depends on the temperature pedestal and on the modulation of auxiliary heating in time. Admittedly, the former enters (2.2a–c) as an independent variable in input (we have performed a scan of pedestal temperature; Rodriguez-Fernandez et al. Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020), rather than as an output of some model of plasma–wall interaction as required by a fully self-consistent treatment. All the same, our analysis is still meaningful as it highlights a feature of SPARC which is common to different burning plasma experiments, from IGNITOR (Di Vita Reference Di Vita2010) to ITER (Navratil Reference Navratil2001): the higher the pedestal, the easier the achievement of large values of $Q$![]() . This result is far from surprising, given the favourable role played, for example, by H-mode when it comes to energy confinement.
. This result is far from surprising, given the favourable role played, for example, by H-mode when it comes to energy confinement.
Even at high pedestal, however, no thermal runaway is possible if $W_{\textrm {aux}} = 11$![]() MW at all times. In contrast, if we start from a low value of $W_{\textrm {aux}}$
MW at all times. In contrast, if we start from a low value of $W_{\textrm {aux}}$![]() ($= 1$
($= 1$![]() MW) at the beginning of the flat top, then we raise $W_{\textrm {aux}}$
MW) at the beginning of the flat top, then we raise $W_{\textrm {aux}}$![]() up to 25 MW (the maximum design value for ICRH power on SPARC; Creely et al. Reference Creely, Greenwald, Ballinger, Brunner, Canik, Doody, Fülöp, Garnier, Granetz and Gray2020) after 1 s so that the growth of $W_{\textrm {aux}}$
up to 25 MW (the maximum design value for ICRH power on SPARC; Creely et al. Reference Creely, Greenwald, Ballinger, Brunner, Canik, Doody, Fülöp, Garnier, Granetz and Gray2020) after 1 s so that the growth of $W_{\textrm {aux}}$![]() accompanies the growth of temperature and fusion power, and finally decrease it down to 11 MW 2 s after the beginning of the flat top, then the scenario of Rodriguez-Fernandez et al. (Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020) is compatible with the results of Rogister & Li (Reference Rogister and Li1992) during the first 2 s of the flat top and a value of $Q = 11$
accompanies the growth of temperature and fusion power, and finally decrease it down to 11 MW 2 s after the beginning of the flat top, then the scenario of Rodriguez-Fernandez et al. (Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020) is compatible with the results of Rogister & Li (Reference Rogister and Li1992) during the first 2 s of the flat top and a value of $Q = 11$![]() can actually be achieved, provided that the pedestal temperature is ${>}4$
can actually be achieved, provided that the pedestal temperature is ${>}4$![]() keV, a value still compatible with the analysis of Rodriguez-Fernandez et al. (Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020). Again, our treatment is not fully self-consistent, as we have modified the time evolution of $W_{\textrm {aux}}$
keV, a value still compatible with the analysis of Rodriguez-Fernandez et al. (Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020). Again, our treatment is not fully self-consistent, as we have modified the time evolution of $W_{\textrm {aux}}$![]() by hand while leaving all other quantities unaffected; all the same, our discussion is still meaningful as it confirms the suggestion of Rodriguez-Fernandez et al. (Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020) that achieving $Q > 5$
by hand while leaving all other quantities unaffected; all the same, our discussion is still meaningful as it confirms the suggestion of Rodriguez-Fernandez et al. (Reference Rodriguez-Fernandez, Howard, Greenwald, Creely, Hughes, Wright, Holland, Lin and Sciortino2020) that achieving $Q > 5$![]() is possible provided that $W_{\textrm {aux}}$
is possible provided that $W_{\textrm {aux}}$![]() rises above 11 MW in an early portion of the flat top. This is not surprising, as suitable timing of heating in a rapidly evolving plasma is likely to be crucial – just like it used to be in IGNITOR – see Di Vita (Reference Di Vita2010) and references therein. When it comes to drive the plasma towards large values of $Q$
rises above 11 MW in an early portion of the flat top. This is not surprising, as suitable timing of heating in a rapidly evolving plasma is likely to be crucial – just like it used to be in IGNITOR – see Di Vita (Reference Di Vita2010) and references therein. When it comes to drive the plasma towards large values of $Q$![]() , auxiliary heating definitely plays a much more relevant role in SPARC than in IGNITOR. According to our analysis, a simultaneous growth of absorbed auxiliary power and of temperature, hence of fusion power, has the highest effectiveness in triggering the thermal runaway which drives the plasma away from its initial state where fusion power is negligible towards a condition where fusion power is dominant. Remarkably, the fact that the initial state is unstable to the highest degree against a perturbation of $T$
, auxiliary heating definitely plays a much more relevant role in SPARC than in IGNITOR. According to our analysis, a simultaneous growth of absorbed auxiliary power and of temperature, hence of fusion power, has the highest effectiveness in triggering the thermal runaway which drives the plasma away from its initial state where fusion power is negligible towards a condition where fusion power is dominant. Remarkably, the fact that the initial state is unstable to the highest degree against a perturbation of $T$![]() when an externally applied heating evolves in time together with the evolving $T$
when an externally applied heating evolves in time together with the evolving $T$![]() is retrieved also outside plasma physics, namely in unmagnetized mixtures of reacting gases (see, for example, the discussion of these mixtures in Brear et al. (Reference Brear, Nicoud, Talei, Giauque and Hawkes2012) when the quantity $D_{Q}$
is retrieved also outside plasma physics, namely in unmagnetized mixtures of reacting gases (see, for example, the discussion of these mixtures in Brear et al. (Reference Brear, Nicoud, Talei, Giauque and Hawkes2012) when the quantity $D_{Q}$![]() in its (2.26) is ${>}0$
in its (2.26) is ${>}0$![]() ); this is not surprising, as in both cases stability is described by Le Châtelier's principle.
); this is not surprising, as in both cases stability is described by Le Châtelier's principle.
In spite of these encouraging results, our analysis is still in its infancy. Firstly, a more detailed description of the time evolution of the plasma is definitely required (we have just taken the values of electron temperature, fusion power, etc., from a few published papers). Secondly, the possible impact of pellet injection remains to be discussed. Thirdly, we have yet described no L–H transition, an obvious example of loss of stability; this is a task for future research. Finally, we have assumed that the plasma volume is constant. This is a reasonable assumption as far as the flat top is concerned; however, the impact of non-constant geometry is far from negligible (for example, expansion due to an increase of Shafranov shift may cool the plasma). However, the fact that our fundamental relationship (2.2a–c) contains only total time derivatives of thermodynamic quantities makes the generalization of our discussion to the case of moving plasmas straightforward. Finally, the agreement of our results (high-temperature pedestals and suitably modulated ICRH facilitate the achievement of $Q > 5$![]() ) with both previous results and physical intuition suggests that the approach described here may provide a useful tool for the analysis of the time evolution of burning plasmas in SPARC.
) with both previous results and physical intuition suggests that the approach described here may provide a useful tool for the analysis of the time evolution of burning plasmas in SPARC.
Acknowledgements
Motivation and encouragement of Dr A. Amato and Dr G. Campa of Ansaldo Energia, Genoa, Italy are gratefully acknowledged.
Editor Tünde Fülöp thanks the referees for their advice in evaluating this article.
Declaration of interests
The author reports no conflict of interest.