1 Introduction
What level of spending during retirement do people consider desirable, given their lifetime budget constraints? How does this level compare to spending during working life? Is there a minimum level of retirement spending which people want to maintain at all costs? The answers to these questions allow us to take an informed stand on an important issue that many economists and policy-makers are concerned with: that people may not prepare adequately for retirement (Thaler, Reference Thaler1994; Banks et al., Reference Banks, Richard, Richard and Carl1998; Bernheim et al., Reference Beshears, Choi, Laibson and Madrian2000; Munnell et al., 2006; Lusardi and Mitchell, Reference Lusardi and Mitchell2007; Skinner, Reference Skinner2007; Fornero et al., Reference Gomes and Alexander2009). The answers to the above questions are furthermore important for several countries that are currently considering reforming their pension systems, since any pension reform plan requires information about adequate old-age consumption levels.
There are several existing approaches for determining adequate levels of old-age consumption. First, in a study that reports that a non-negligible fraction of the British population might be at risk of an inadequately low standard of living during retirement, Banks et al. (Reference Banks, Richard and Carl2005a) argue that a minimal requirement for an adequate old-age spending may be that it exceeds the poverty line. Second, an adequate spending level during retirement may be seen as one that does not fall short of a certain benchmark fraction of (annual) income during active life, such as 67 or 80 or 100% (Palmer, Reference Palmer1994; Moore and Mitchell, Reference Moore and Mitchell1997; Banks et al., Reference Banks, Richard and Carl2005a). The great advantage of these two approaches is that they are straightforward to operationalize. Furthermore, the meaning of both adequacy measures is very intuitive. The disadvantage is that they are not based on individual preferences.
This disadvantage is addressed by a further approach that we may dub the preference-based calibration approach. This approach postulates a particular utility function, typically a time-separable form of constant relative risk aversion (CRRA) utility. Making specific assumptions about the parameters of this function as well as about other relevant variables such as interest rates and equity returns allows the analyst to calibrate optimal consumption choices during old age and during working life. According to the calibration approach, actually observed choices are considered adequate if they come sufficiently close to these calibrated choices. This approach is pursued in, for instance, the study of Scholz et al. (Reference Scholz, Ananth and Surachai2006), which finds that many people appear to either save optimally for retirement or, in many cases, to over-save. The calibration approach is compelling since it explicitly takes into account information about individual preferences when computing an adequate level of old-age consumption. However, this approach requires strong assumptions about the functional forms and parameter values of preferences, although solid information about appropriate functional forms and parameter values that best correspond to individuals' true preferences is not available in many cases.Footnote 1, Footnote 2
In sum, there is no consensus about what constitutes an adequate level of retirement consumption. Rather, the identification of the most appropriate approach for determining a benchmark level for adequate retirement consumption remains an open issue (Banks et al., Reference Banks, Carl, Zoë and Gemma2002).
In this paper, we aim to advance the existing literature by investigating the adequacy of old-age consumption based on a different approach, inspired by work on risk and time preference elicitation through surveys (Barsky et al., Reference Bernheim, Forni, Gokhale and Kotlikoff1997; Kapteyn and Teppa, Reference Kapteyn and Teppa2003). We elicit measures of intertemporal and risk preferences based on survey questions that are explicitly framed in terms of retirement preparation. This allows us to infer adequate ratios of old-age to working-life consumption, as well as minimum absolute adequate consumption levels during retirement.
Two features of our novel survey design stand out. First, we tailor the survey questions individually to each respondent's financial situation, based on prior information about a respondent's socio-economic characteristics, such as total household income. This makes our questions meaningful in the context of the respondent's personal situation. Second, none of our questions requires respondents to understand any technical aspects of retirement preparation, such as the concept of compound interest or inflation.
Our specifically designed internet survey module was conducted in two countries: with the American Life Panel (ALP) at RAND in the U.S. and with the CentERpanel (CP) in The Netherlands. The U.S. embodies a country where individuals bear a substantial amount of responsibility for their own retirement preparation, while The Netherlands is a country with a typical European-style welfare state and a pension system that offers generous replacement rates.Footnote 3 In particular, the after-tax income replacement rate for an average earner amounts to about 85% in The Netherlands. In contrast, it amounts to only about 50% in the U.S. (OECD, 2007). Our paper, therefore, also sheds light on the question of whether notions of an adequate standard of living during retirement differ across such contrasting institutional setups and, if so, to what degree.
A main advantage of the survey approach is that it allows for learning directly about individual preferences since it does not impose specific functional forms or parameter values. Furthermore, the survey approach allows for testing whether the prescriptions of the calibration approach or any other approach are consistent with the preferences that individuals express themselves. As for any other approach, the survey approach has its own disadvantages. Most notably, we need to assume that respondents understand our questions and are motivated to answer them properly.
Overall, our study presents a novel way to elicit policy-relevant preference information that is based on individually tailored surveys. Our claim is not that the survey approach dominates any other method of investigating the nature of adequate retirement consumption levels. Rather, we view our study as providing a new and complementary perspective on the ongoing discussion about adequate standards of living during retirement.
Our main findings are as follows. First, neglecting any risk associated with retirement spending, we find that ex-ante desirable ratios of old-age to working-life spending are surprisingly high; they exceed 80% for a majority of respondents in both the U.S. and The Netherlands. Second, we investigate the lower limits on old-age spending below which individuals would not want to fall in any case, and we estimate minimum income replacement rates for each income quintile. For the U.S., these minimum replacement rates amount to about 95% for respondents in the lowest income quintile and gradually decrease to about 45% for respondents in the top income quintile. In The Netherlands, this gradient is weaker and minimum replacement rates range between 75 and 60%. This weaker gradient in The Netherlands may partly reflect the much tighter income distribution there.Footnote 4
Our results about desirable ratios of old-age to working-age income and about lower bounds of old-age spending are useful for inferring adequate wealth accumulation and portfolio strategies. Information about desirable old-age consumption levels has become increasingly important in many countries due to the shrinking number of people that are covered by defined-benefit pension schemes (Banks et al., Reference Banks, Richard and Carl2005b). The importance of this information is forcefully underlined in a number of recent studies (see, e.g., Fornero et al., Reference Fornero, Annamaria and Chiara2009).
The rest of the paper is organized as follows. Section 2 provides information about our samples. Section 3 presents our results on ex-ante adequate old-age spending in the absence of risk. Section 4 brings risk into play. Section 5 concludes.
2 The Data
2.1 The Dutch CP
The Dutch CP is hosted by the data collection agency CentERdata at Tilburg University, and the data used for the presented analysis are publicly available from CentERdata. The CP consists of a sample of members who regularly fill out internet-based questionnaires, typically on weekends. There are two types of questionnaires. First, panel members are regularly asked about socio-economic characteristics of their household within the framework of the so-called DNB Household Survey. We use this information to tailor our questions to the respondent's personal financial situation. Second, panel members are invited to answer special-topic questionnaire modules such as ours from time to time.
An outstanding feature of the CP is that it is representative for the overall Dutch population. Since internet penetration may be systematically lower in some subgroups of the population, CentERdata provides households that do not own a computer or internet connection with an add-on device that allows them to access internet via television. It also provides a television if necessary.
Our questionnaire was conducted in March 2007. We presented the survey to panel members who were older than 25 and who were either the household's main breadwinner or his or her spouse. We did not exclude retired panel members. Based on these selection criteria, 835 panel members answered our questionnaire. The actual number of responses per question varies between 590 and 835.
2.2 The ALP
The ALP at the RAND institution was modeled after the CP, and grants public access to the data used in this paper. As in the case of the CP, ALP members regularly answer questions on general socio-economic characteristics. There are two main differences between the ALP and the CP. First, the ALP is not fully representative of the overall U.S. population. Second, to provide respondents with a psychological incentive to answer the questions carefully, ALP members are paid an amount of $2 per interview minute. In contrast, CP-members are paid per completed survey module and the amount depends on the number of years a household has been a member of the panel and is lower than the amount paid to ALP members.
In the case of the ALP, our questionnaire was fielded in November 2007. Using the same selection criteria as in the case of the CP, 847 panel members answered our questionnaire. The actual number of responses per question varies between about 600 and 847.
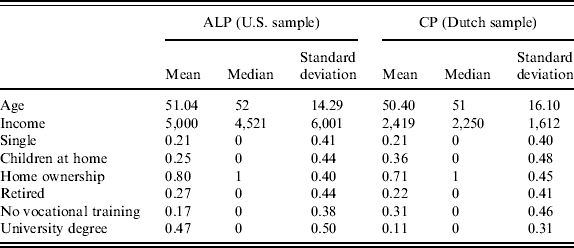
Table 1 shows descriptive statistics for our two samples. The income variable refers to total household income per month after taxes. The respondents' highest degree of professional education is indicated by the two dummy variables ‘no vocational training’ and ‘university degree’. The excluded category is the middle one, i.e. if both dummy variables are zero, the corresponding respondent's highest professional degree is a vocational degree. The variable ‘children at home’ indicates whether any children are living at the respondent's home. The figures in Table 1 show that ALP respondents are slightly richer and better educated than the average American. In contrast, the CP is – by construction – representative for the Dutch population along many socioeconomic characteristics.
Table 1. Descriptive statistics

Note: Total number of respondents is 847 for the ALP (U.S. sample) and 835 for the CP (Dutch sample). Income refers to monthly income and is measured in year-2007 U.S. dollars for the ALP and in year-2007 euros for the CP.
3 Adequate old-age spending in the absence of risk
We address the question of what represents an adequate standard of living during retirement from an ex-ante anticipatory perspective. This perspective corresponds to a preference-based approach that basically underlies all of standard economic theory. From the ex-ante perspective, the question of what represents an adequate standard of living during retirement relates to the trade-off between spending during working life and spending during old age. In the interest of keeping our questionnaire as transparent and simple as possible, our survey questions on this trade-off neglect any form of risk. Furthermore, we do not consider any variation of spending within working life or within retirement. This would lead to rather difficult questions and, as a consequence, would reduce the reliability of respondents' answers (Dillman, Reference Dillman2000). Hence, we concentrate on how average spending levels during retirement compare to average spending levels during working life.
Specifically, we present each respondent i a total number of six options of monthly working-life and retirement spending levels (c w,ik, c r,ik), k=1, 2, …, 6. The consumption levels c w,ik and c r,ik represent absolute amounts. Respondents are asked to indicate which option they like most. The defining property of each option is the ratio c kr,i/c w,ik, which we set at 50, 64, 76, 88, 100 and 140% (up to rounding) for k=1, 2, …, 6, respectively. This includes the range of spending ratios that are commonly viewed as potentially adequate. All six options are characterized by an identical present value of lifetime consumption (see below).
It is important to stress that we show respondents absolute amounts of money, not percentages. We do so since respondents may find imagining exactly what these percentage numbers would mean for their personal situation difficult. We do not inform respondents that the ratios c r,ik/c w,ik correspond to the particular percentage numbers mentioned above.
On a first screen, respondents only see four options corresponding to spending ratios of 64, 76, 88, and 100%, respectively (see Table 2 for an example). This is meant to avoid respondents having to process an excessive amount of information on one screen. Only if a respondent chooses a ratio of 64 or 100% do we ask on a follow-up screen if he or she would actually prefer the chosen option to that associated with a ratio of 50 or 140%, respectively.
Table 2. Options for life cycle spending profiles (example)

Note: This table is part of the survey question eliciting desired life cycle spending profiles. Respondents see a table like this after having read the introductory text stated in Appendix B. The numbers in the table are based on a respondent's total after-tax household income. Here, the numbers refer to a monthly income of 3,000 U.S. dollars.
The calculation of the individual spending profiles (c w,ik, c r,ik) is outlined in Appendix A. These profiles are determined according to the following requirements:
(i) All options are tailored to respondents' income. In particular, the option with the highest working-life spending level c w,i k on the first screen approximately equals total household income after taxes.
(ii) The present value of all six presented spending profiles (c w,ik, c r,ik) is identical (see Appendix A).
These requirements ensure that all presented options appear realistic to the respondents in light of their personal financial situation. In particular, we rule out that any of the values of c w,ik on the first screen exceeds the respondent's current household income in order to not alienate respondents to whom such options would appear infeasible. All presented numbers are rounded to entire multiples of 50 or 20 units of the corresponding currency.Footnote 5
After reading an introductory text (see Appendix B), respondents see a table such as Table 2. The numbers in the table depend on the respondent's total household income. In Table 2, the numbers correspond to a monthly household income after taxes of 3,000 U.S. dollars. Table 2 refers to an interest rate of 1%.Footnote 6 After having indicated their favorite profile, respondents are presented with a second table, corresponding to an interest rate of 6%. In this second table, the ratios of the spending levels are identical. However, for a higher interest rate, achieving a given level of retirement spending requires giving up less working-life spending. As a result, the distances between the numbers in the first column are smaller and the distances in the second column are larger, compared to Table 2.
In the introductory text to Table 2, respondents are told to include ‘all your expenditures, such as food, clothing, accommodation, insurance, traveling etc.’ We did not provide an exhaustive list of all potential items here, since such a lengthy list would make the question awkward to most respondents, reducing their motivation to read the question and to provide an answer (Dillman, Reference Dillman2000). Rather, we use the incomplete illustrative list mentioned above. It ends with ‘etc.’ to indicate that other such expenses should be included as well. If individuals are concerned about consumption smoothing, it is important to include education expenditures for children, mortgage payments, out-of-pocket medical expenditures, and, potentially, also planned bequests. While we cannot be sure that all our respondents really thought about all these items, we believe that our question provides a reasonable trade-off between accuracy and simplicity.Footnote 7 In the interest of simplicity, our question also neglects that expenditures may vary within working life or old age.
It is important to stress that a respondent choosing her most-preferred profile (c w,ik, c r,ik) from Table 2 need not have an understanding of compound interest rate calculations, inflation or any other technical detail. Our inference based on respondents' answers only depends on the assumption that individuals have well-defined preferences over spending profiles such as shown in Table 2. The assumption that individuals have well-defined preferences is much weaker than the assumption that individuals are able to make utility maximizing choices. People may well know what spending profile they would like to achieve, but they may not be able to implement it, due to, e.g., financial illiteracy.
As mentioned in the introduction, the seminal papers on the elicitation of time preferences through survey questions are Barsky et al. (Reference Barsky, Juster, Kimball and Shapiro1997) and Kapteyn and Teppa (Reference Kapteyn and Teppa2003) . In principle, the setup in these two papers is similar to oursFootnote 8, but there are two key differences. First, the questions in Barsky et al. (Reference Barsky, Juster, Kimball and Shapiro1997) and Kapteyn and Teppa (Reference Kapteyn and Teppa2003) are neither worded nor framed in the context of retirement preparation. Second, our questions are substantially less difficult since they are individually tailored to a respondent's personal financial situation and since the information we provide is easy to process. This makes the questions more meaningful to respondents and reduces cognitive load.
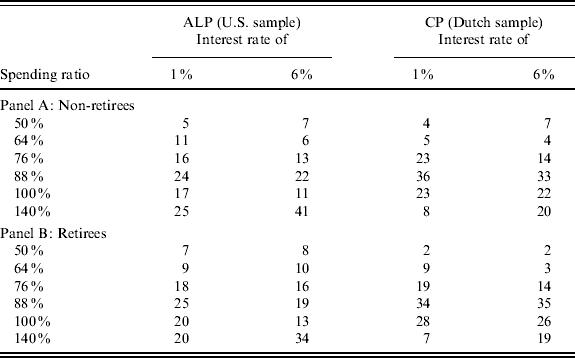
Our results about desired consumption profiles are shown in Table 3. The upper panel shows the result for the subsample of non-retirees, whereas the lower panel shows the result for the subsample of retired respondents. We find that the distribution of chosen spending ratios does not differ between the two subsamples for both the ALP and the CP.Footnote 9
Table 3. Distribution of preferred life cycle spending ratios for non-retirees and retirees

Note: The table shows the distribution of desired life cycle spending ratios. A spending ratio of 50% means that retirement consumption is half of working life consumption, etc. The numbers in the table indicate percentages of observations. The total number of non-retirees is 576 for the ALP and 539 for the CP. The total number of retirees is 211 for the ALP and 169 for the CP.
The key observations are the following. First, irrespective of the sample and the level of the interest rate, only very few respondents prefer a spending profile corresponding to a ratio of 50 or 64%. Second, there is substantial mass concentrated on the options corresponding to spending ratios of 76, 88 and 100%. Third, the 140% option is very popular in the U.S., but not in The Netherlands, at an interest rate of 1%. Finally, consistent with economic theory, the 140% option is much more popular for an interest rate of 6% than for an interest rate of 1% in both countries.
In order to explore the reliability of the elicited data, we randomized the order of the response options. Respondents were randomly assigned to one of two treatments. Half of the respondents saw the numbers arranged in the order as in Table 2, where the order of the spending ratios is decreasing. The other half saw the numbers arranged with an increasing order of spending ratios. We do not find any evidence that our results differ across randomization treatments.
It is noteworthy that economic theory predicts that, for a given individual, the spending ratio should not be lower for the 6% scenario than for the 1% scenario. We find that, in both samples, only 12% of the respondents violate this prediction. This compares favorably to Barsky et al. (Reference Barsky, Juster, Kimball and Shapiro1997) where 21% changed the slope of the desired consumption path in the wrong direction.Footnote 10
The differences in the distributions of preferred spending ratios between the U.S. and the Dutch sample are statistically significant.Footnote 11 This mainly reflects the fact that the 140% option is much more popular in the U.S. The pattern that a substantial fraction of Americans desire an upward sloping consumption profile is consistent with the finding in Hurd and Rohwedder (Reference Hurd and Rohwedder2008) that a similar fraction of individuals in their U.S.-based sample exhibit de-facto increasing spending profiles around retirement. This may be explained by the fact that Americans may find postponing consumption (e.g. in the form of traveling) until retirement as a complement to leisure more desirable. This is in line with the fact that the number of vacation days is typically much lower in the U.S. than in The Netherlands.Footnote 12 As a result, people working in the U.S. may find delaying spending power until retirement – when they have the time to enjoy leisure and traveling – more valuable relative to their Dutch colleagues. However, it should also be kept in mind that our samples are not fully comparable since the ALP is not fully representative for the U.S. population. Thus, the above results could partly also reflect differences between samples rather than intrinsic differences between the Americans and the Dutch.
Table 4 reports ordinary least squares (OLS) regressions for the chosen spending profiles. The dependent variable is the value of the chosen ratio c r,i/c w,i for an interest rate of 1%, and we regress this variable on dummies for income quintilesFootnote 13 (omitting the bottom quintile), age, and other sociodemographic variables. In the case of the ALP sample, the dummy variable for the fifth income quintile is the only significant explanatory variable. Its effect is rather small: the point estimate indicates that the desired consumption ratio is 8% lower for a member of the fifth income quintile, everything else equal. For the CP sample, only the dummy variables for children living at home and for a university degree are significantly related to the chosen spending profile. These effects are also rather small, amounting both to minus 4%, respectively. When running other specifications, including ordered probit regressions, we obtain very similar results.
Table 4. OLS regressions for preferred spending ratios

Note: Dependent variable is the preferred ratio of retirement to working life spending, amounting to either 50, 64, 76, 88, 100, or 140%. In case of the ALP, income quintile bounds refer to the Current Population Survey, not our dataset. In case of the CP, quintile bounds refer to our dataset. One, two and three asterisks denote significance at the 10, 5, and 1% level, respectively. Robust standard errors are indicated in parentheses.
The main conclusion drawn from the results discussed in this section is that a substantial fraction of the population prefers spending ratios that exceed 80% of working life spending. This applies to both The Netherlands and the U.S. In the case that old-age spending is exposed to risk, our finding would apply to certainty equivalence values of old-age spending.
4 Bringing risk into play
In this study, we conceptualize risk from the perspective of a lower limit on old-age spending below which an individual would not want to fall in almost any case. This represents a particularly simple framework for thinking about risk since it does not require evaluating any risk-return trade-off. Such a framework corresponds to the logic of poverty thresholds as well as to preferences with habit formation or Stone–Geary utility functions.Footnote 14 Information on such a minimum acceptable level of old-age spending is very useful for thinking about adequate retirement preparation. It specifies a benchmark spending level that an individual may want to exceed, from an ex-ante point of view, with a very high probability. Thus, such a benchmark helps to identify adequate asset allocation strategies for individual retirement accounts. It also implies an overall lower bound on adequate savings for retirement.
Our question on minimum acceptable old-age spending levels is shown in Appendix B. For the ALP, the 25th, 50th and 75th percentile of the answers amount to 2,000, 3,000 and 4,000 year-2007 U.S. dollars per month, respectively. The 25th, 50th and 75th percentiles of the ratio of the answers to total monthly household income after taxes amount to 0.48, 0.73, and 0.95, respectively. For the CP, the respective absolute numbers are 1,200, 1,600 and 2,000 year-2007 euros per month. The respective ratios of the answers to total household income after taxes are 0.56, 0.72 and 0.88.
Table 5 shows median regressions where we regress minimum acceptable spending levels on dummies for income quintiles (omitting the bottom quintile), age and other sociodemographic variables.Footnote 15 It is noteworthy that in a standard model with CRRA preferences, the concept of a minimum acceptable standard of living is not meaningful. However, there are positive minimum acceptable spending levels in the case of Stone–Geary or habit formation preferences. In the case of Stone–Geary preferences, the minimum spending levels would be independent of household income. Thus, under Stone–Geary preferences we would expect the coefficients on the income quintile dummies to be zero. In the case of standard habit formation preferences (see e.g., Gomes and Michaelides, Reference Gomes and Alexander2003), habit levels – and thus minimally acceptable spending levels – would increase one by one with (permanent) income. Therefore, we would expect the coefficients of the income quintile dummies to match the increase of income levels between those quintiles. In the case of lexicographic loss aversion preferences of Binswanger (Reference Binswanger2007, Reference Binswanger2010), habit levels increase with income, but less than proportionally. Under these preferences, we would expect coefficients for income quintiles that entail increases in spending levels that are smaller than the corresponding increases in income levels.
Table 5. Median regressions for minimum acceptable old-age spending levels

Note: The dependent variable is indicated in the column headers. Minimum acceptable spending levels are measured in year-2007 U.S. dollars for the ALP (U.S. sample) and in year-2007 euros for the CP (Dutch sample). In case of the ALP, income quintile bounds refer to the Current Population Survey, not our dataset. In case of the CP, quintile bounds refer to our dataset. ‘Minimum replacement ratio’ refers to the ratio of the minimum acceptable spending level to current total household income after taxes. One, two, and three asterisks denote significance at the 10, 5, and 1% level, respectively. Robust standard errors are indicated in parentheses.
The first two columns of Table 5 show the results for median regressions with the level of minimum acceptable old-age spending as the dependent variable. The results show that income primarily determines the minimally acceptable spending level.Footnote 16 To inspect the relationship between income and minimum acceptable old-age spending more closely, it is useful to use the regression results to calculate predicted minimum spending levels for each income quintile. We do so for a non-single household aged 50 who is not retired.Footnote 17 Furthermore, we set the values of the dummy variables for children, home ownership, no vocational training and for having a university degree to zero.
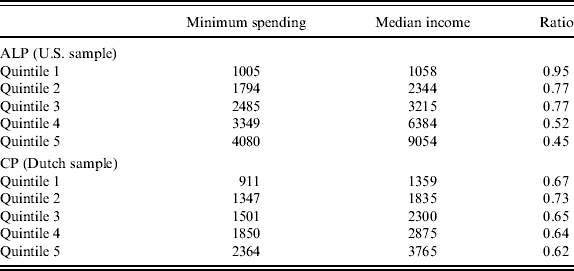
The predicted minimum spending levels are shown in Table 6. The upper panel refers to the ALP and the measurement units are year-2007 U.S. dollars. The lower panel refers to the CP and the units are year-2007 euros. The first column in each of the two panels shows the calibrated monthly minimum spending levels. The second column simply reports the monthly median after-tax incomes in our samples for each income quintile. The third column reports the ratio of predicted minimum spending to median income for each quintile. The striking pattern in Table 6 is that the increments in minimum spending levels are smaller than the increments in income. This pattern is consistent with a model of habit formation in which the habit level increases with income but less than proportionally, as in the model of Binswanger (Reference Binswanger2007, Reference Binswanger2010).
Table 6. Predicted minimum acceptable old-age spending levels and minimum replacement rates
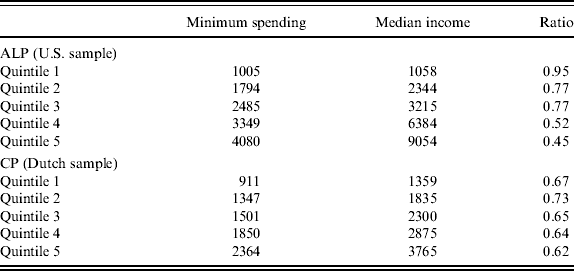
Note: Predictions are based on the regressions in the first and second column of Table 5. Minimum acceptable spending levels per month are calculated setting age to 50, and the dummy variables for single children, home ownership, retired, no vocational training, and for having a university degree to zero. In case of the ALP, income quintile bounds refer to the Current Population Survey, not our dataset. In case of the CP, quintile bounds refer to our dataset. Numbers in the upper panel represent year-2007 U.S. dollars. Numbers in the lower panel represent year-2007 euros. The ratio in the third column reports the value of dividing minimum spending by median income as indicated in the first and second column, respectively.
The pattern of decreasing ratios of spending levels to income is particularly pronounced for the U.S. There, the ratios range from 95 to 45%. In contrast, in The Netherlands, they only range between 75 and 60%. The much smaller range in The Netherlands may in part reflect the much tighter income distribution there. In the U.S., the median income of the first and fifth quintile amount to 33 and 282% of the median income of the middle quintile, respectively. In The Netherlands, the respective numbers are only 59 and 164%.
The pattern in Table 6 also suggests that in order to finance their minimally acceptable old-age spending, richer individuals need to save proportionally less than poorer individuals. Furthermore, the results suggest that low-income people are of particular concern. In the U.S., for the lowest income quintile, the minimum needs during retirement are almost as high as the median income for this quintile. In a privatized defined contribution pension system, financing this need would require high savings (in relative terms). Since current income is low for individuals in the first income quintile, there is, however, little scope for high savings. This suggests that redistribution (through Social Security) plays an important role for assuring an adequate level of retirement spending for low-income households.
An alternative way of analyzing how minimum needs vary with income is to run a regression where the left-hand side variable is minimum acceptable spending levels normalized by current income. This is shown in the last two columns of Table 5. Again, it appears very clearly that these normalized future minimum needs decrease with income and this decrease is particularly pronounced for the U.S. sample. This pattern is also supported by formal statistical analysis. We run several tests for equality of the income quintile coefficients; equality is always strongly rejected (at the 1% level) for both samples.
Few of the other sociodemographic variables are consistently significant in Table 5. In particular, it is noteworthy that home ownership never turns out significant.Footnote 18 At first sight, this may be somewhat surprising, since current home ownership may be a good predictor of home ownership during retirement. If all mortgages are repaid until retirement, then one would expect home owners to indicate lower retirement needs, everything else equal. In our estimations, we do not see this effect. There are two potential explanations for this. First, home ownership is highly correlated with income since the demand curve for owning a house is crucially affected by income; indeed, if we run regressions where we exclude any income variables on the right-hand side, home ownership turns out to be highly significant (not shown). Second, current home ownership may be a good predictor of homeownership during retirement only for those individuals that are sufficiently close to retirement. Consistent with this, we find that needs are lower for home owners if the sample is reduced to individuals with age above 60. However, we find this effect only for the American sample and it is only significant at the 10% level.
A variable that is significant in most specifications is the dummy variable for being retired. This suggests that retired people realize that they have greater minimum needs than anticipated before retirement.
Our results may prove helpful in designing adequate asset allocation strategies, since any asset allocation strategy maps into a distribution of available resources during retirement. Our calibrations help identify adequate portfolio strategies in that, say, the 10th percentile of the resulting distribution of monthly spending should exceed the values in the first column of Table 6. Furthermore, the numbers in Table 6 may be useful for thinking about adequate benefit levels in a mandatory pension system.
5 Conclusion
In this paper, we use a specifically designed internet survey, conducted in the U.S. and The Netherlands, to address the question of what represents an adequate standard of living during old age. We address this question from an ex-ante point of view, consistent with the perspective suggested by economic theory.
We find that a large majority of individuals aims to achieve a spending profile where, under normal circumstances, old-age spending exceeds 80% of working-life spending. Bringing risk into play, there is clear evidence that individuals do not want to fall below a certain lower limit of old-age spending. We use respondents' answers to calibrate minimum income replacement rates for each income quintile. For the U.S. sample, these range between 95% for the lowest income quintile and 45% for the highest. For The Netherlands, these rates fall between 75 and 60%.
Our elicited values of minimally desirable spending levels may be used for calibrating desirable risk management strategies. For this, one may proceed along the line of Binswanger (Reference Binswanger2007) who provides a simple framework for the analysis of risk management strategies in the domain of retirement preparation and pension design. In particular, one may infer critical lower bounds on wealth accumulation and estimate optimal contribution and benefit levels for a pension system.
In future research, our approach using an individually tailored and randomized survey design for eliciting information on preferences could be combined with data on further dimensions of individuals' circumstances – ranging from physical to mental and psychological circumstances – in order to understand the heterogeneity of retirement preferences better (see, e.g., Banks, Reference Banks2006). Furthermore, our approach can be applied in various other domains that are important for policy. For example, consider information on individual preferences with respect to the trade-off between lower contributions to the welfare state and higher levels of risk borne by private individuals. Such information is relevant for the identification of a desirable design of social policy as well as of desirable macroeconomic policies. Carefully elicited information on people's preferences will stimulate the interaction between theoretical and empirical researchers, will make the policy discourse richer, and may ultimately lead to better policies.
Appendix A: Derivation of spending profiles of section 3
We discuss here the calculation of the spending profiles (c w,ik, c r,ik) that underlie the analysis in Section 3. For the derivation of these profiles we make a number of simplifying assumptions. A respondent's working life is assumed to start at the age of 25. Furthermore, we assume that respondents retire at age 65 in case of the ALP and at 61 in case of the CP.Footnote 19 We neglect mortality risk and assume that death occurs with certainty after age 85.Footnote 20
The present value of the profile (c w,ik, c r,ik) for respondent i is then given by
R denotes the retirement age and amounts to either 65 or 61. r denotes the real risk-free interest rate. (Respondents are first asked to choose their favorite spending profile for an interest rate of 1% and then for an interest rate of 6%.) PVY i denotes a hypothetical present value of lifetime income for respondent i. It is determined according to
Y i represents respondent i's total annual household income after taxes and after deduction of contributions to existing mandatory pension systems. We do observe Y i from previous survey modules.
Two features of (1) require explanation. First, we use 98 Y i instead of Y i for the calculation of the hypothetical present value of income. This is done to assure that the number corresponding to the highest c w,ik on the first screen does not exceed Y i even after rounding (which may mean upward rounding). Second, we need to explain the presence of the number 0.64. Our calculation of PVY i implicitly assumes that retirement income equals 64% of working-life income. This assumption is hypothetical. It implies that if c w,ik is equal to current income, then c r,ik/c w,ik is equal to 0.64. This is thus the case for the option with the highest c w,ik on the first screen, where c w,ik is approximately equal to Y i. Our implicit reasoning behind this is that the observed income Y i is net of contributions to currently existing mandatory pension systems. These contributions may be sufficient to achieve an income replacement rate of 64 percent in a fully funded pension system.Footnote 21
We should point out that the assumptions made for calculating the profiles (c w,ik, c r,ik) do not imply any assumptions about actual savings behavior of respondents. Our purpose is uniquely to show respondents spending profiles that are feasible under the above assumptions in order to learn which of the feasible profiles they would like most.
Appendix B: Wording of survey questions
B.1 Life cycle spending profiles
The introductory text to our life cycle spending profile questions is as follows:Footnote 22
Below you find four options of how you could spend your money over your lifetime. For each option the first column indicates how much your household could spend on average per month from age 25 until retirement. Thus, this refers to your total (working) age from age 25 until retirement, not just the remaining (working) age. The second column indicates how much your household could spend during retirement. Please think of all your expenditures, such as food, clothing, accommodation, insurance, traveling, etc. Assume that the numbers below show what you can spend after having already paid for taxes. Assume also that prices of the things you spend your money on remain the same in the future as today (no inflation). If you had a choice, which option would you like most? Footnote 23
This text is then followed by a table such as Table 2, as explained in Section 3. In Table 2, the numbers correspond to a monthly income after taxes of 3,000 U.S. dollars.
B.2 Minimum acceptable old-age spending
The question on minimum acceptable old-age spending reads as follows.
This question refers to the overall level of spending that applies to you and your partner during retirement. What is a minimal level of monthly spending that you never want to fall below during retirement, at all costs? Please think of all your expenditures, such as food, clothing, accommodation, insurance, etc. Assume that prices of the things you spend your money on remain the same in the future as today (no inflation).
It is noteworthy that this question is framed in a way that we should expect answers to differ across countries if they are characterized by different institutions. For instance, the answers to this question may differ between countries with different health insurance schemes.
Specifically, in The Netherlands, health insurance is compulsory for everyone. It is supplied by private insurance companies and premiums are paid by each insured individual herself. Health insurance pays for most doctor visits and pharmaceuticals as well as for hospital stays up to 1 year. Furthermore, every resident is covered by a public long-term care insurance scheme (dubbed AWBZ) that covers nursing homes and long-term hospital stays. The U.S. Medicare system requires a 20% copayment for hospital stays, a feature that has no counterpart in The Netherlands. Covering this copayment requires an extra (non-mandatory) so-called Medigap insurance. (The requirement of a copayment drops if Medicaid covers care costs.)