Overview of model assumptions

The PIMS is a simulation modeling framework developed by the PBGC ‘designed to quantify the uncertainty that surrounds pension insurance’ and to be used as a tool to characterize potential distributions of pension insurance claims on the PBGC and, importantly, the agency's surplus (or deficit)Footnote ¹. The PBGC is clear that the system is not a predictive system intended to identify point estimates of the future financial condition of the agency but to provide ranges of simulated distributions of outcomes (Ibid.). The system has been designed and maintained by the agency (presumably with input from outside parties, contractors, and other stakeholders via various direct interactions with the model as well as via technical reviews such as this one) to give an understanding of how pension plans insured by the PBGC behave under various shocks to internal and external parameters (which characterize economic and other conditions), including being able ‘accurately [to] portray underfunding among the insured universe under a wide variety of economic conditions’ as long as the assumptions, constraints and reflections of pension plan, and governing rule data are accurate. Of course, modeling decisions about granularity of the system components and data used and measured must have been made, and the system cannot be possibly expected to capture all possible relevant inputs or reflect all possible scenarios.

The system accommodates inputs from a subsample of large insured pensions including actuarial inputs such as current plan demographics and benefit formulas, data on the financial condition of sponsors, fund portfolio compositions and the PBGC's own financial position. We understand that, typically, PIMS simulations (say 5,000 or 10,000 in number of draws over different economic scenarios) are used, say, to project 10 years of future economic events in the financial markets (PBGC 2011). First, interest rates, stock returns, and related variables (e.g., inflation, wage growth, and multiplier increases in flat-dollar plans) are drawn according to the stochastic equations listed in Table 1. In the model, it appears that the 30-year Treasury bond is presumed to follow a random walk while corporate bond yields, which are viewed as highly correlated over time, are mean reverting to historical estimates of their spread over Treasury yields of comparable maturity. Real rates are assumed to be a constant level (e.g., 1.64%), and inflation is calculated as the as the spread between nominal and real rates. The term structure of interest rates does not directly enter into the equations, per se (Overview 2011).

Table 1. PIMS equations

Source: ‘Pension insurance modeling system: PIMS system description’. Version 1.0, revision 9/22/2010.

Returns on equities seem to be modeled as mean reverting to a long run average value estimated from historical data (e.g., 10.4% plus noise according to one historical document, or 8.6% or 8.2% according to other documents) using data ranging from 1926, which is when the famous Stock, Bonds, Bills, and Inflation (SBBI) data from Ibbotson begin (PBGC FY 2012 Exposure Report, hereafter referred to as Exposure Report). Innovations are drawn IID over time, presumably from a calibrated multivariate Gaussian distribution. Correlations between stock returns and bond yields appear strictly to be based on historical estimates from the time period 1973–2007 (Exposure Report), with the implication being that of contemporaneous negative correlation between stock returns and bond yields (also as shown in the 2012 Exposure Report, the model assumes a positive correlation between Treasury Bond returns and stocks). Plan asset returns are determined by a two-factor model that combines stock return premia over nominal rates and bond premia, both adjusted for sensitivities to these premia via estimates of beta as in a two-factor market model, against which plan asset returns are regressed. Note that in a one-factor case, this model might be thought of as the time series estimation equation made famous by the Capital Asset Pricing Model of Sharpe (Reference Sharpe1964). It is important to note that the PBGC has indicated that it has Form 5500 data on reported plan asset allocations, which it incorporates. My comments below on the changing nature of plan allocations must be conditioned with this information. Historically, asset mixes of plan portfolios have assumed roughly to be a 60% allocation to equities and 40% allocation to bonds (Buck Consultants 2012) or ‘a weighting based on the average of the estimated rate mixtures: 48% stock market returns, 23% long-term Treasury bond returns, 30% long-term Treasury bond yield and a −2.5 basis points additive adjustment’. (Exposure Report: 17) With the inclusion of actual Form 5500 data, the model can incorporate important potential diversification characteristics as outlined below. However, modeling the increased span of risks introduced in this manner also may require more sophisticated models than the two-factor model described above.

Simulations of the model first appear to presume that sponsors make the minimum statutory contributions implied by the tax code. If a sponsor goes bankrupt in the simulation, it does not contribute from the previous year. The PBGC adjusts premia based on sponsor historical choices to fund plans above the minimum in avoidance of higher premiums. PIMS simulations allow plan participants to retire, leave the firm and to die according to actuarial data and assumptions. Benefits and salaries for a given age and service time grow with inflation plus a productivity factor (Overview 2011 and see Table 1).

As mentioned above, sponsor health is measured by equity-to-debt ratios, cash flows, firm equity, and employment levels. Here, equity-to-debt and cash flow ratios are mean-reverting to long run historical averages. Employment and firm equity are essentially modeled as correlated random walks. Innovations in the equations for sponsors appearing in Table 1 are assumed to be correlated to one another and to innovations in financial market returns, with correlations estimated from history. Finally, bankruptcy is modeled as a random function with parameters estimated by historical bankruptcies and data on the health of companies over the period 1980–1998 (Exposure Report). These data are not industry-specific. If a firm goes bankrupt at the same time a plan is less than 80% funded, the plan represents a loss and is included in average loss calculations across simulations and scenarios (Exposure Report). Formerly, the model incorporated parameter uncertainty by including estimations as part of the simulation procedures by estimating certain parameters within simulation iterations. Currently parameter uncertainty is no longer accounted for.

PIMS capital market assumptions vs. the assumptions of others

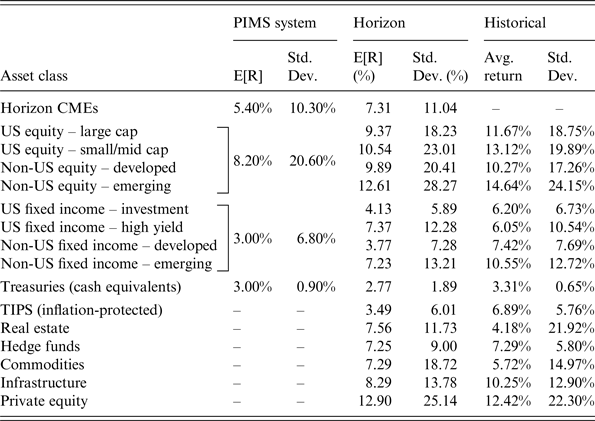
Table 2 outlines the baseline capital market expectations used/produced by the PIMS system. It also provides a listing of the capital market assumptions recently compiled by Horizon Actuarial Services, LLC in its annual survey of 17 large multi-employer consultanciesFootnote ². While the assumptions utilized by plans insured by the PBGC themselves are not available (at least to me), and the use of third party capital market assumptions is fraught with its own problems, not the least of which is the prima facie problem that the respondents are service providers to plan sponsors and are paid by them, they serve to raise several important issues for consideration. In addition, it is reasonable to assume that when these advisors, as likely fiduciaries under both the Advisors Act of 1940 and under ERISA, provide their expectations which likely serve as a base for sponsor assumptions, these consultancies are required to provide their advice in an un-conflicted manner as required under the law, and these consultancies advise both single-employer and multi-employer plans in their fiduciary advisory capacities. Also, they use a wide variety of models that are forward-looking as well as historical data.

Table 2. Capital market expected returns and volatilities: PIMS vs. others

Source: Author's calculations.

The results in Table 2 indicate a substantial discrepancy between the expected returns used in the PIMS system (where we note that we have multiple sources describing the PIMS assumptions)Footnote ³ and those of large consultancies that either serve or are like those that serve the plans insured by the PBGC. Part of the discrepancy surely arises directly from the fact that consultancies have different approaches to assessing future capital market investment performance. Apparently, some use forward-oriented models such as a form of the dividend discount model for equity returns (for example, possibly accumulating some measure of earnings growth, earnings yield or dividend yield, and expected return from multiples expansion as well as inflation expectations). Certainly some use historical data or at least calibrate their models based on historical data. Such forward-looking models might allow initial conditions important for the accommodation and inclusion time-varying expected returns, critical for the calculation of funding ratios and for many conceivable outputs of the model to be incorporated.

Also, while information is sparse on how all 17 consultancies compute their forecasts, the importance of this discrepancy is that if plan sponsors base their allocations on them, as a result their allocations are potentially more complex that what the two-factor model for plan assets may suggest. Also, the mere fact that reasonable analysts can rely on different models for asset returns at least raises the issue of testing of robustness by the PBGC with respect to its own assumptions regarding its two-factor model.

As we show later, evidence that corporate plans allocate much differently than presumed by the PBGC seems undeniable. They allocate to more asset classes that are represented in the US stock/bond two-factor model assumption, and some of those allocations are to classes of assets that are highly likely to be exposed to risks simply outside the risks of US domestic stocks and bonds. Thus, as apparent in the unconditional expected returns, risks and correlations assumptions presented in Table 2, higher volatilities for foreign classes and classes outside the narrow confines of the PIMS assumption would likely result in higher volatilities and more extreme outcomes, were the alterative presumptions to be more accurate. Moreover, since the volatility attribution implied by the stock/bond assumption clearly indicates that this asset allocation, which has arisen historically in the financial industry (and academic literatureFootnote ⁴) as components in the so-called ‘balanced’ portfolio, is in fact not at all balanced. Its risk is heavily dominated by the risk of the equity component of the assumption. All this said, we hasten to add that the assumptions of the average consultant may not accurately reflect the forecasts of reasonable models. In Section 4 below, we turn to models that, in a forward-looking way, calibrate market expectations.

PIMS capital market assumptions and the stochastic character of asset prices

Since no later than the work of Mandelbrot, Fama, and others, the non-Gaussian character of asset prices has been a topic of intense study in academia and industry. The gist of that body of research and practice suggests that asset returns are have greater extremes than presumed by the type of stochastic assumption embedded in the PIMS system. In addition, at least one source of that heavy-tailed character is the time-varying nature and auto-correlated nature of first and higher moments. The PIMS model assumptions on one hand incorporate a form of this autocorrelation (e.g., the well-known autocorrelation of bond yields). On the other hand, they appear to ignore the time-varying nature of volatility in the short and long runs.

There are numerous ways to illustrate this critical point. The approach we take here is first to illustrate basic levels of predictability in asset returns. We do this graphically (Figure 1, Panels A and B), although much research has demonstrated how both reduced form and more structural approaches may be estimated econometrically.Footnote ⁵ We then make the point that volatility is time-varying using implied volatilities in the form of the VIX (Figure 2), ex post realized volatilities over the long run (Figure 3, Panels A and B), demonstrating the strongly different implications for the assumption of time-varying volatility for outcomes with a greater frequency of extremes in simulations.

Figure 1. (colour online) (A) Treasury yields as predictors of future returns. (B) Dividend yields as predictors of future returns. Source: Shiller (Reference Shiller2013).

Figure 2. (colour online) Implied S&P 500 volatility (VIX). Source: CBOE (2013).

Figure 3. (colour online) (A) Realized large US firm market capitalization stock index return volatility. (B) Implications of PIMS model assumptions vs. realized large US firm market capitalization stock index return volatility. Source: Author's calculations.

Since PBGC insurance both conceptually and as modeled in PIMS is expected to pay at times when plans are underfunded and sponsors are in distress, having a more accurate representation of equity market extremes seems quite important. Moreover, the diversification benefits normally attributed to asset allocation varies with time and with market volatility. We show below – again, graphically (Figures 4 and 5) – how the correlation between stocks and bonds varies across both business and volatility cycles.

Figure 4. (colour online) Implied S&P 500 correlations. Source: Author's calculations.

Figure 5. (colour online) (A) Realized correlations between US large cap stocks and 20-year Treasury returns. (B) Realized correlations between US large cap stocks and 20-year Treasury returns with block-bootstrapped 95% C.I.s. Source: Author's calculations.

To illustrate the first point, Figure 1, Panel A relates starting 5-year Treasury yields (same axes) to future annualized returns on Treasuries from January 1955–January 2013, and Figure 1, Panel B relates the current dividend yield on US Large Cap stocks (reflected most recently in the S&P 500) over the period January 1871–January 2013. Both graphs make two strong points, ones that the academic literature has spent considerable effort in understanding over approximately the last three decades. First, the graphs imply that it is impossible to assert that either equity returns are simply random walks with IID innovations or that bond returns are simply mean reverting with IID innovations. Also, since the entire term structure of interest rates clearly is important for model outcomes across the future time span of simulations, it might be highly useful to incorporate factor models for the term structure. Second, the investment opportunity set is highly time-varying and correlates strongly with simple instruments (for instance, the period correlation between d/p and subsequent 7-year return in Figure 1, Panel B is just under 70%). Especially since insurance claims are a strong function of these two forcing variables in the PIMS system and since they track economic conditions, it may be useful to incorporate this notion into the assumptions of the model.

Another feature of real-world data that today does not appear to be as controversial as it was when first introduced is the property of asset returns to have fat tails, highly autocorrelated conditional volatilities and time-varying implied volatilities that reflect the pricing of systematic risk. Again, there may be innumerable ways to make this point, and one guesses that there may be thousands of academic and practitioner papers and dissertations written on the topic, but we again here take a graphical approach (later we build a simulation model that accommodates time-varying volatility). Figure 2 presents the Chicago Board of Options Exchange VIX index over the period January 2007–December 2012 (CBOE 2013), and Figure 3, Panel A presents ex post realized volatility estimated over 18-month rolling windows. Both graphs tell a similar story of time-varying volatility with that variation corresponding to business and market cycles over a recent period of market disruption and, in fact, in the very long run (at least by US standards). Moreover, 99% of positive daily changes in the VIX index correlate with negative S&P 500 index returns. That is, equity values are negatively correlated with increases in volatility. Finally, over the long run, cycles like those apparent in the recent financial crisis are reflected in realized volatility. Again, while sophisticated modeling assumptions and technologies capturing this effect may take many different forms, the graphs point out clearly that the modeling assumptions of the PIMS system may usefully incorporate conditional heteroskedasticity in asset returns, or at least for equity returns, likely the most important source of systematic variability in plan and in fact corporate solvency, on average.

To illustrate this point, Figure 3, Panel B incorporates our understanding of the PIMS equity return assumptions from Table 1 in modeling simulated returns that are either random walks like those from the PIMS model (which we label ‘IID’) or a calibrated random walk (cleverly labeled ‘Calibrated’) using in-sample estimates of the period represented by each point on the graph for actual returns. Apparent in this graph is that the actual spikes in volatility arising in the real world are not reflected in the IID approach of the PIMS model estimated based on long-run, constant variance assumptions. Moreover, while local calibration helps over the rolling horizons of the model (and it should, as it benefits from perfect hindsight!), it is not able to match the observed spikes in volatility in the historical record. The implication of these figures is that, again, because volatility is so strongly inversely correlated with bad outcomes for asset valuations, in our view a model of insurance may fruitfully incorporate these effects.

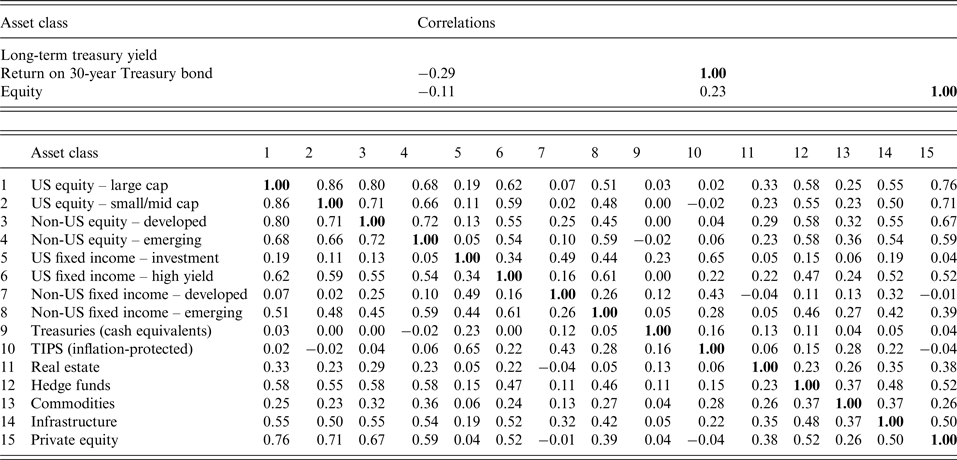
Unfortunately, it turns out that spikes in volatility due, in our view, both to characteristics of asset returns themselves and possibly to ancillary effects (like runs on liquidity that arise during financial crises and times of systemic stress) have happened commonly throughout modern human history (e.g., see Kindleberger and Aliber Reference Kindleberger and Allber2011). One way among many to understand this effect is to think simply how components of classes of assets like those to which insured plans have exposure relate in their variations to the classes as a whole. Consider, for example, the traditional portfolio theoretic measure, R². The fundamental definition of R² for an asset in an investment context is as the ratio of its systematic (e.g., market) risk to its total risk which is the sum of systematic and idiosyncratic, non-market risk. The previous figures indicate that the numerator and the first part of the denominator, systematic or market risk, change over time and with widespread pricing of equity risk, and, at times, spike. Unless idiosyncratic risk compensates for changes in systematic risk, R ²s may vary as well. Moreover, formulaically, R ² is defined as the square of correlation between the asset and the asset class being modeled. That is, just when the diversification power of lower-than-higher correlations are most important, they may be fleeting. Altogether, this indicates that just when assumptions about constant correlations may be important, they may actually go up. This effect may be especially important to the PBGC because sponsor contributions are functions of financial distress of sponsor firms, which is likely correlated with shocks common to equities. Even more, PBGC assets may themselves be subject to this behavior, making claims (and other difficult outcomes) and their backstop move more negatively in bad times. To illustrate this point, Figure 4 plots the implied correlations of the S&P 500 components via the term structure of the CBOE S&P 500 implied correlation indexesFootnote ⁶, JCJ, KCJ, and ICJ, over time, in which it is notable that correlations implied by options prices are both time-varying and correlated with volatility spikes in the previous graphs. Finally, Figure 5, Panels A and B plot rolling realized correlations between and index of US large cap stocks (represented most recently by the S&P 500) with 20-year Treasury returns, without and with 95% confidence intervals. While the PIMS model assumptions presume a fairly strong negative correlation between stock and bond yields, and a positive correlation between stock and Treasury bond returns, it is clear at least from the perspective of Figure 5, this last presumption may be appropriate only at certain times. It may be useful to note that the times of particularly negative observed correlations in Figure 5 often arise over estimation periods covering intervals of market distress, perhaps making the PIMS stock/bond return correlation assumption a bit removed from market experience. Again, more generally, it may be beneficial for the PIMS system to incorporate time-varying second moments in a multivariate context for asset returns, particularly if, as discussed in the next section, the system would be moving toward consideration of more asset classes than just the components of the stock/bond portfolio in the modeling of plan allocations.

PIMS and capital market expectations models

As we highlighted above, there are strong differences between the capital market assumptions for the simple asset classes of the PIMS model and the assumptions of large consultancies assumed to be providing investment advice to the sponsors of insured plans. To assess further the PIMS assumptions about equities, we estimate two additional models for future asset returns, focusing on equity returns: The dividend discount model and a model based upon dividend yield as an instrument which accommodates the time-varying nature of expected returns in the academic and practitioner literature. With respect to future expected returns on bonds, the evidence in Figures 1a and 1b relating yields to future returns over time indicates that, based on the assumption of current yields being unbiased predictors of future returns (an assailable presumption, but a reasonable one here as long as residual correlations are maintained), future bond returns might actually be quite a bit lower than presumed by the PIMS systems, based upon our assessment. While this indication is not a direct comment about the modeling character of the system, it points out a difference that arises based upon modeling choices of the system.

Asset and risk-based allocations of pension plans and their implications

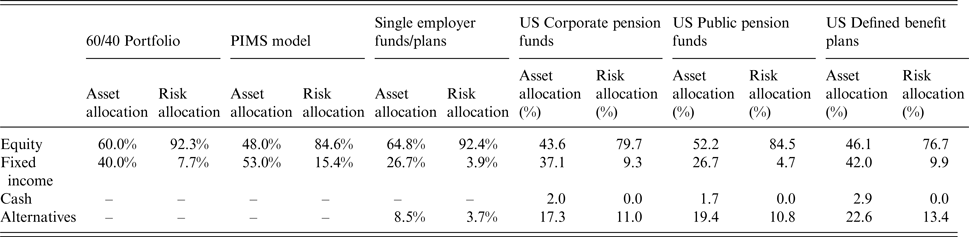
Next we demonstrate that the asset allocation of the PIMS system, which in a sense presumes a domestic stock/bond split, does not comport with the allocation of many plans today or with trends in plan allocations and, thus, may not reflect the actual risk of plans on average. The risks of those plans differ substantially from that of the so-called ‘balanced’ approach of the famous 60/40 allocation, which is in the PIMS model essentially a US-based model, based on its two-factor model assumption. First, Table 3 provides allocations across a fairly highly aggregated depiction of asset classes from various sources in the PIMS documentation set as well as for US corporate plans, US public plans and a sample of US defined benefit plans (the largest 100 corporate plans in 2012), according to Pensions and Investments Research (2013). The column labeled PIMS Model refers to the allocations reported to me assumed in the Exposure Report, and the columns labeled Single Employer Funds/Plans represent a summary and subjective aggregation of the allocations reported in the PBGC Annual Report for 2012. The columns labeled as corporate and public plans are also those that appear for 2011 in Figure 6, Panels A–C from the P&I annual plan surveys.

Figure 6. (colour online) (A) Allocation trends of US corporate pension plans. (B) Allocation trends of US public pension plans. (C) Alternative asset allocation trends of US corporate pension plans, public pension plans and university endowments and foundations. Source: Pensions & Investments Research (2013).

Table 3. Capital market expected correlations: PIMS vs. horizon

Source: Author's calculations.

Table 3 indicates that the US stock/bond assumption of the two-factor PIMS assumption for plan assets quite different from plan allocations across the board which recently have lower levels of equity allocations than the assumption of PIMS. In addition, the allocations observed for plans in the real world are more diversified into alternatives. Moreover, as indicated above, the PIMS model assumptions are calibrated to US data, again an assumption which does not match reality, although due to the aggregations in Table 3, those subtleties are averaged away. The bottom line is that pension plans insured by the PBGC have potentially drastically different allocations (implying vastly different effective capital market assumptions) than the PIMS system contemplates, either on a dollar basis or on a ‘risk allocation’ or variance contribution basis (see Table 4). In addition, with the inclusion of increasing allocations to alternative investments (see Figure 6, Panel C, for instance), PBGC insured plans are taking on risks not even contemplated by the PIMS model. It is useful to note that in one sense, the over-allocation in the model assumptions to equity risks may actually be conservative if less accurate than matching observed allocations reported by plans on Form 5500 might be. Domestic equity risk dominates the risk allocation of the 60/40 allocation historically and in the capital market assumptions-based Table 3. More diversified plans may in fact have fewer incidences of underfunding as a result if those alternative allocations do indeed end up providing diversification benefits on average and at times of general market distress.

Table 4. Asset allocations and risk (variance contribution) allocations assumed by PIMS and selections of pension plans

Source: Author's calculations.