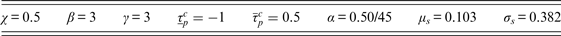Introduction
The current economic crisis has put funded pension schemes under serious stress. The collapse of equity markets and the sharp decline of interest rates have worsened the financial position of funded pension schemes. In the case of defined benefit (DB) pensions, this has undermined the backing of future pension liabilities. This holds especially true in the Netherlands, which features one of the biggest funded pension schemes in the world.
However, the great recession is not the only bad news for pension funds. The perspective of an ageing population that applies to many industrialized countries may be even more important. It implies that pension funds will become more vulnerable to longevity and capital market shocks. At the same time, with the pension base shrinking in relative terms, it becomes more difficult to absorb such shocks by pension contributions. This explains the quest for pension reform.
This paper addresses a specific type of pension reform, namely the transition from a funded DB scheme towards a funded defined contribution (DC) scheme. In particular, it compares a funded pension scheme that provides defined benefits with an equally generous pension scheme that provides benefits that are responsive to capital market shocks. The focus is on two types of efficiency effects: intergenerational risk sharing and labour market distortions.
The paper thus explores the question whether the welfare gains from intergenerational risk sharing in a collective DB scheme outweigh the welfare losses from labour supply distortions? In order to assess these two elements, this paper constructs a model with overlapping generations of households and a pension scheme. The pension scheme is either an individual DC scheme or a collective DB scheme. Participation in the pension scheme is mandatory. The economy we model is a small open economy, in line with the economy of the Netherlands. Hence, we abstract from feedbacks on the rate of return that may occur in a closed economy, but which may be largely absent in a small open economy.
Households in the model decide on their labour supply, their private saving and their investment in risky equity, except for households who have retired; retired generations are not allowed to participate on the labour market. Household income is stochastic, directly because of the investments in risky equity and indirectly because the DB pension scheme absorbs capital market shocks into the pension contribution rate. Further, we assume that households have non-stochastic lives. We abstract from lifetime risk and lifetime insurance because they do not seem to be a distinctive element in the comparison between DB and DC pensions.Footnote 1
There is only one risk factor in the model of this paper: equity risk. We argue that this does not reduce the applicability of the paper to the real world for several reasons. First, equity risk is by far the most important risk factor. Second, equity risk may be interpreted as representative for other capital market risks as well, such as inflation risk and interest rate risk. Third, if our approach leads us to underestimate the role of risk, we underestimate both the gains from risk sharing and the costs of labour market distortions; the balance between the two will be less severely affected.
There is some earlier literature on the subject. As to the model, relevant are Krueger and Kubler (Reference Krueger and Kubler2006), Bodie et al. (Reference Bodie, Merton and Samuelson1992) and Gomes et al. (Reference Gomes, Kotlikoff and Viceira2008). As to the welfare effects of funded pension schemes, Bovenberg et al. (Reference Bovenberg, Koijen, Nijman and Teulings2007) and Gollier (Reference Gollier2008) should be mentioned. Closest to the current paper is Bonenkamp and Westerhout (Reference Bonenkamp and Westerhout2014). This paper also addresses the trade-off between intergenerational risk sharing and labour supply distortions. There are two important differences with that paper, though. First, their model is a two-period overlapping-generations model, whereas we use 13 periods to describe the life cycle of households. Our richer setup allows us to assess the welfare aspects of the uniformity principle – a standard feature of DB pension schemes, something that cannot be done with a two-period model. Second, in modelling the DB pension scheme, we adopt a positive approach rather than a normative approach (Bonenkamp and Westerhout (Reference Bonenkamp and Westerhout2014) model the pension scheme as an optimizing scheme). This lends our estimate of both the sign and the magnitude of the welfare effect of a DB pension scheme more relevant for the policy discussion in the Netherlands.
The structure of our paper is as follows. The next section sets up our model. Section 3 discusses the calibration of the model. Section 4 then discusses our results. It provides an assessment of the effects of the introduction of a collective DB scheme upon the average and spread of consumption and labour supply and upon welfare. It also offers a decomposition of the welfare effect into the effects of the various elements that underlie it. The final section makes some concluding remarks.
The model
Features of the model
Our model consists of overlapping generations of households and a collective pension fund. The following features are attached to the economy. First, the economy is small relative to the outside world. That is, domestic policies do not affect the interest rate and the equity rate of return, which are determined on world capital markets. Second, goods supply and labour demand are perfectly elastic. Third, although good prices and gross wages are given, the price of leisure is endogenous due to the connection between the labour market and the pension scheme.
The capital market
Our model distinguishes two financial products: risk-free bonds and risky equity. Risk-free bonds earn a (gross) return R b , whereas equity earns a return R s . The return on the risky asset, R s , follows a lognormal white noise process. The excess return, e s , on the risky asset is defined as
$$e_s (t) = R_s (t) - R_b. $$
In equation (1), index b points to the risk-free asset (bonds) and s to the risky asset (equity). The expected value of the excess return on equity, E[e
s
(t)], will be denoted as μ
s
, its variance, E[(e
s
(t) − E[e
s
(t)])2], as
$\sigma _s^2 $
.
The assumptions of a constant mean and variance of the equity return, of a completely risk-free interest rate and of independence of equity returns over time are standard. They are not undisputed, however. In particular, the assumption of independence of equity returns over time conflicts with the notion that equity returns exhibit mean reversion (Campbell and Viceira (Reference Campbell and Viceira2002)). To the extent that this is true, our calculations will overstate the volatility of equity returns. We will therefore as part of a sensitivity analysis also run a simulation with a lower equity return volatility.
Population
Our model features overlapping generations of households: each period a new generation enters the economy and the oldest generation leaves the economy. Households enter the economy at the age of 20 and may work up to the age of 65. From that age onwards, they receive a pension until they die at the age of 85. The unit period of our model equals 5 years. In the model, we will use j r to denote the retirement age (10) and j e to denote the maximum age (13). We assume that each cohort has size one.
The DB pension scheme
We model the collective DB pension scheme in our model along the lines of the pension scheme that may be considered representative for the Netherlands. The pensions offered by the majority of the schemes in the Netherlands are of the average wage type: workers accumulate pension rights based on their gross wage income. Participation in the scheme is obligatory, but not beyond the control of households. In particular, the building up of pension rights and the payment of pension contributions are both related to the individual household's labour supply.
Pension benefits are unresponsive to capital market shocks and these shocks are absorbed by pension funds through adjusting the pension contribution rate. The absorption is only partial. Hence, it takes some time for the pension scheme to eliminate funding deficits or surpluses. This reflects the risk sharing between generations which is a central feature of the Dutch pension schemes. Importantly, pension fund policies are not necessarily optimal in the sense of maximizing the utility function of a typical generation or a group of generations. The following expression describes aggregate contributions to the pension scheme:
$$x_p (t) = \tau (t)y_g (t) = \tau (t)\mathop \sum \limits_{i = 1}^{\,j_r - 1} (5 - v(i,t))p_l (t),$$
where x p (t) denotes aggregate pension contributions, τ the pension contribution rate and y g (t) aggregate gross wage income. v and 5 − v stand for leisure and labour supply respectively and p l (t) stands for the wage rate. Similarly, the equation for aggregate pensions sums the equivalents for retired generations,
$$y_p (t) = \mathop \sum \limits_{i = j_r} ^{\,j_e} y_p (i,t),$$
where y p (t) denotes aggregate pensions and y p (j,t) pensions of cohort j in period t.
The pensions of the DB scheme are unrelated to capital market returns. Next, the pension benefits are of the average wage type, i.e., they are based on the wage income earned in the working phase of the life cycle. More specifically, every unit of gross labour income adds α units to the stock of pension rights. Furthermore, the stock of pension rights is indexed with respect to the rate of productivity or wage growth, so that wage growth does not affect the pension replacement ratio, i.e., the ratio between the pension benefit level and the wage rate. During the retirement phase, pension income continues to be indexed to labour productivity
$$y_p (\,j,t) = \left\{ {\matrix{ {0,} \hfill & {{\rm for}\;j = 1,} \hfill \cr {\rho [y_p (\,j - 1,t - 1) + \alpha (5 - v(\,j - 1,t - 1))p_l (t - 1)],} \hfill & {{\rm for}\;2 \le j \le j_r,} \hfill \cr {\rho y_p (\,j - 1,t - 1),} \hfill & {{\rm for}\;j_r \lt j \le j_e,} \hfill \cr}} \right.$$
with ρ the productivity growth factor, i.e., one plus the rate of productivity growth.
The accumulation of the financial wealth of the pension scheme is uncertain in advance, given that the scheme allocates its financial wealth over risky equity and risk-free bonds. The following expression captures the accumulation of financial wealth:
$$a_f^p (t + 1) = R_b \left[ {a_f^p (t) + x_p (t) - y_p (t)} \right] + e_s (t + 1)a_s^p (t).$$
Here,
$a_f^p $
denotes financial wealth of the pension scheme and
$a_s^p $
the investment by the scheme into equity.
Inherent to the combination of a risky portfolio investment strategy and guaranteed pension benefits is a mismatch between financial wealth and liabilities. This is reflected in the funding ratio, q, which is defined as the ratio of financial wealth to pension liabilities, lp
$$q(t) = \displaystyle{{a_f^p (t)} \over {l^p (t)}}.$$
Pension liabilities are defined as the pensions that have so far been accumulated:
$$l^p (t) = \mathop \sum \limits_{i = j_r} ^{\,j_e} \mathop \sum \limits_{l = 0}^{\,j_e - i} \left( {\displaystyle{\rho \over {R_b}}} \right)^l y_p (i,t) + \mathop \sum \limits_{i = 1}^{\,j_r - 1} \mathop \sum \limits_{l = j_r - i}^{\,j_e - i} \left( {\displaystyle{\rho \over {R_b}}} \right)^l y_p (i,t).$$
These pension rights are fully indexed with labour productivity. They are grouped into two terms. The first term reflects the pension rights of the households who have already retired from the labour market; they collect pensions from that point in time until they die. The second term counts the pension rights of generations of working age; they will only start collecting pensions when they retire.
We split the pension contribution rate into three components: the cost recovery component, denoted τd , the catching-up component, denoted τc , and the equity premium component, denoted τs :
$$\tau (t) = \tau ^d (t) + \tau ^c (t) + \tau ^s (t).$$
We will discuss these components in turn. The first component in equation (8), τd , denotes the contribution that is made to cover new pension rights,
$$\tau ^d (t) = \displaystyle{{\mathop \sum \nolimits_{i = 1}^{\,j_r - 1} (5 - v(i,t))p_r (i,t)} \over {y_g (t)}},$$
where p r , the pension right per unit of labour supply, will be discussed below.
The second component is the catching-up contribution, τc , which is non-zero only when the funding ratio of the pension scheme deviates from its target of 100%. The catching-up component of the pension contribution rate follows in principle from the idea that the pension scheme reduces its funding deficit to χ times its value at the beginning of the period. However, we impose that this component does not become too small or too large:
$$\tau ^c \left( t \right) = \max \; \left( {\underline{\tau} ^c, \min \; \left( {\chi \left[ {\displaystyle{{ - \left( {q(t) - 1} \right)l^p \left( t \right)} \over {y_g (t)}}} \right],\bar \tau ^c} \right)} \right).$$
The expression for the equity premium component is as follows:
$$\tau ^s (t) = \displaystyle{{ - \mu _s a_s^p (t)} \over {R_b y_g (t)}}.$$
This equity premium component is negative. It reflects the equity premium that the pension scheme earns due to its investment in equity.
We take as given the investment strategy of the pension scheme. In particular, we specify that the pension fund invests a fixed fraction of its financial wealth into equity. This investment behaviour of the pension scheme has two consequences. First, it increases the expected rate of return due to the equity premium, which allows the pension scheme to reduce the pension contribution rate, as we have seen in discussing equation (11). Second, the investment in equity renders the pension contribution rate a stochastic variable. For both reasons, the pension scheme distorts the labour supply decision of households. The equity premium component increases labour supply, whereas the catching up component increases or decreases it, depending on the sign of the shock in the rate of equity return. In general, the two do not cancel against each other. A third type of distortion is due to the uniformity principle. This uniformity principle implies that younger workers pay contributions that are higher than actuarially fair and vice versa for older workers. The uniformity principle thus distorts the labour supply decisions of both younger and older workers, although in different directions.
Households
An individual of age j maximizes expected utility over the remaining lifetime, U, which adds per-period utility flows in all remaining periods after discounting with the time preference factor δ. Expectations have to be formed because future consumption is uncertain:
$$U(\,j,t) = E_t \mathop \sum \limits_{i = j}^{\,j_e} \delta ^{ - \left( {i - j} \right)} u(i,t).$$
In this equation E t denotes the expectations operator that calculates expectations, conditional upon information that is available in period t. Per-period utility, u, is a function of the consumption of commodities, c, and of leisure, v:
$$\eqalign{& u(j,t) = \displaystyle{1 \over {1 - \gamma }}{\left(c(j,t) + \phi \displaystyle{{v{{(j,t)}^{1 - \beta }}} \over {1 - \beta }}\right)^{1 - \gamma }} \quad {\rm and} \cr & \quad \phi \gt 0, \quad \beta \gt 1, \quad \gamma \gt 0.} $$
Here, 1/γ is the elasticity of intertemporal substitution (γ is the coefficient of relative risk aversion), 1/β the price elasticity of leisure demand and ϕ the utility weight of leisure. The marginal per-period utility of leisure becomes infinite as leisure approaches zero, which guarantees positive leisure. To obtain that leisure is equal to or smaller than the maximum available time (normalized to five), we will include a Kuhn−Tucker constraint in the optimization procedure.
The specification of per-period utility in equation (13), linear in commodity consumption and concave in leisure, is similar to the specification in Greenwood et al. (Reference Greenwood, Hercowitz and Huffman1988). It implies that leisure demand is unresponsive to changes in financial wealth. Furthermore, it implies that the consumption of commodities will have a minimum, c l , equal to −ϕv 1 − β /(1 − β). It can be shown that c l is non-negative and increasing in hours worked. Because of the latter, we call this labour-induced consumption. Related, we will call c − c l above labour-induced consumption. As the marginal utility of the above labour-induced consumption becomes infinite as it decreases to zero, c − c l is strictly positive. The parameter γ then denotes the risk aversion with respect to above labour-induced consumption. The coefficient of relative risk aversion with respect to total consumption equals γc/(c + ϕv 1 − β /(1 − β)), which is strictly larger than γ. Numerically, the difference is not very relevant, however.
The asset accumulation equation describes the development of household financial wealth, a f , through time:
$$a_f (\,j + 1,t + 1) = R_b (a_f (\,j,t) + y(\,j,t) - c(\,j,t) + e_s (t + 1)a_{\,fs} (\,j,t).$$
Equation (14) signals that households receive non-capital income y, and invest their savings in bonds and equity. a fs denotes the household's investment in risky equity. Regarding the timing of transactions, we use as convention that all variables (transactions, demographic changes and stocks) are measured at the start of a period.
Non-capital income equals labour income y w in the working phase of the life cycle, 1 ⩽ j < j r and pension income y p in the retirement phase j r ⩽ j ⩽ j e .
$$y(\,j,t) = \left\{ {\matrix{ {y_w (\,j,t),} \hfill & {{\rm for}\;1 \le j \lt j_r,} \hfill \cr {y_p (\,j,t),} \hfill & {{\rm for}\;j_r \le j \le j_e.} \hfill \cr}} \right.$$
Labour income depends on labour time, the wage rate p l and the pension contribution rate. τ.
$$y_w (\,j,t) = (1 - \tau (t))(5 - v(\,j,t))p_l (t).$$
The household's problem is now to maximize expected intertemporal utility (12), subject to the asset accumulation equation (14), the initial amount of financial wealth, a f , and a Kuhn−Tucker condition that ensures that leisure does not exceed the time endowment of the household. Instruments of this optimization problem are the consumption of goods and equity investments in all years of the life cycle and the consumption of leisure in all years of the working phase (leisure equals the time endowment 5 in the retirement periods). The complete solution to this optimization problem can be found in Appendix AFootnote 2 . Here we only state the first-order conditions and rewrite them into equations for equity demand, leisure demand and the consumption of goods. As explained above, the leisure decision is independent of the consumption and portfolio decision and will be discussed first.
Leisure
Elaborating the first-order condition for leisure generates an equation for leisure demand:
$$v\left( {\,j,t} \right) = \max \; \left\{ {\left[ {\displaystyle{1 \over \varphi} p_v \left( t \right)} \right]^{ - \; \displaystyle{1 \over \beta}}, 5} \right\}.$$
This equation shows that leisure demand reacts negatively to the price of leisure. The price of leisure is the marginal reward for supplying labour, taking into account not just the net wage rate but also future pension income to the extent that it can be imputed to current labour. It will be defined below precisely. Note that, due to our per-period utility function, leisure demand does not depend on the household's financial or total wealth position. This accords with empirical evidence (Lumsdaine and Mitchell (Reference Lumsdaine and Mitchell1999)). Next, note that, due to the inclusion of the max operator in equation (17), leisure demand does not exceed five, the available amount of time per period.
The price of leisure consists of three components:
$$p_v (\,j,t) = p_l (t) - \tau (t)p_l (t) + p_r (\,j,t).$$
The first is the gross wage rate p l and the second the pension contribution. The third component of the price of leisure measures the discounted value of future pension income that can be attributed to the marginal hour of work, p r
$$p_r (\,j,t) = \alpha p_l (t)\mathop \sum \limits_{h = j_r} ^{\,j_e} \left( {\displaystyle{\rho \over {R_b}}} \right)^{\left( {h - j} \right)}. $$
This component is also proportional to the wage rate.
Equation (18) shows that if τp l coincided with p r , the pension scheme would exert no effect upon labour supply. This is not the case for three reasons. First, one effect of the investment by the pension fund in equity is that the pension fund can charge a lower contribution rate. Another effect is that shocks in the rate of return on equity (defined as realizations in deviation from the mean) imply a positive or negative catching-up component in the contribution rate. Thirdly, the pension fund in our model does not levy contributions that are actuarially fair, but levies contributions according to the uniformity principle. This means that people of different age face the same contribution rate, although the build-up of pension rights is different. This uniform contribution acts as a tax on young employees and a subsidy on old employees because future pension income that can be attributed to the marginal hour of work, p r , increases with age.
All three factors drive a wedge between τp l and p r and imply that the price of leisure p v is larger or smaller than the wage rate p l . This induces households to increase or decrease their labour supply. Along these channels, the pension scheme distorts labour supply behaviour.
Equity investment
Households are exposed to equity return risk along different channels. The first, most obvious direct channel is through their own equity investments. The second way is indirectly through the pension fund equity investments. Indeed, equity return shocks are absorbed in the pension contribution rate, which changes the net income of households. Moreover, the catching up part of the pension contribution affects labour supply and thus labour income, which is a third channel through which the consumption of goods is exposed to equity return risk.
Households optimize their total equity risk exposure each period; there are no non-negativity constraints on the demand for equity. The portfolio share ω s of equity investments in total household wealth (to be defined below) can be approximatedFootnote 3 by:
$$\omega _s (\,j,t) = \displaystyle{{\mu _s} \over {\gamma \sigma _s^2}}. $$
Equation (20) tells us two things. First, the portfolio allocation over equity and bonds is the same for all ages. Second, the equation shows that equity investment is increasing in the equity premium μ
s
, decreasing in the variance
$\sigma _s^2 $
and decreasing in the coefficient of relative risk aversion γ.
The household's exposure to equity risk is the product of the portfolio share in equation (20) and total household wealth, a. The latter consists of three elements: financial wealth, a f , accumulated pension rights, a p , and human wealth, a n , i.e., the expected discounted value of future labour income, diminished with labour-induced consumption.
$$a(\,j,t) \equiv a_f (\,j,t) + a_p (\,j,t) + a_n (\,j,t).$$
Human wealth relates to non-stochastic gross wage income and stochastic pension contributions. Hence, it acts partly as bonds and partly as equity. The exposure to equity risk in equation (20) relates to both direct and indirect investments. Hence, if a pension reform makes human wealth more equity-like, then households will reduce their direct investment in equity such that the condition in equation (20) continues to hold (like in Bodie et al. (Reference Bodie, Merton and Samuelson1992)).
It is well-known that investing a constant fraction of total household wealth implies investing 100% or more of financial wealth in the beginning of the life cycle. This model aspect is clearly unrealistic. However, this need not be worrisome for two reasons. First, a large part of saving is done through the pension scheme that will be less hampered by this type of borrowing constraints; the role of private saving is small. Second, the assumption that households do not face capital market imperfections applies to both the case with and without a DB pension scheme, so that it would not directly affect the comparison of the two cases.
Consumption of goods and welfare
Like investment in equity, above labour-induced consumption, c − c l , is proportional with total household wealth in the optimal program. Hence, consumption can be formulated as linear in total household wealth:
$$c(\,j,t) = c_l (\,j,t) + \pi (\,j,t)a(\,j,t),$$
where π denotes a proportionality factor, which is elaborated in Appendix A.
Without leisure, consumption would be proportional to total wealth as in the standard life-cycle model. The life-cycle pattern of commodities consumption deviates from the pattern of this standard model, due to the interaction with leisure demand. In particular, the household consumes more (fewer) commodities than prescribed by the standard model in years in which his labour supply is relatively high (low). Our utility specification thus brings about a positive correlation between consumption and labour supply. Hence, consumption and current income are more strongly correlated than in the standard life-cycle model, which may explain part of the excess sensitivity of consumption puzzle (Flavin (Reference Flavin1981)).
Corresponding to the optimal household program is an expression for indirect utility, the maximum level of expected utility. Substituting the derived expression for optimal consumption of goods (22) into the expected utility function gives the expression for indirect utility as a function of total household wealth:
$$V(\,j,t) = \displaystyle{{\pi (\,j,t)^{ - \gamma}} \over {1 - \gamma}} a(\,j,t)^{1 - \gamma}. $$
Welfare analysis
We analyse the effect of reform upon efficiency or welfare of the whole society by combining the changes in welfare of all generations. Converting the change in welfare for a generation to its equivalent variation, social welfare then follows by simply adding up. Basically, this is the approach developed by Auerbach and Kotlikoff (Reference Auerbach and Kotlikoff1987), applied in a stochastic context. It explores whether the reform in question is a potential Pareto-improvement, i.e., whether the utility gains of those who benefit from the policy reform are sufficiently large to potentiallyFootnote 4 compensate the cohorts that lose from the reform.
In calculating the equivalent variation for a specific generation of the pension reform, we have to distinguish between current generations, i.e., generations alive at the time of reform, and future generations. For a current generation j, the equivalent variation is calculated by equating indirect utility before the reform, V 0(j,t 0), to indirect utility after the reform, V 1(j,t 0). Here, we use superscripts 0 and 1 to refer to the economy before and after the reform, respectively. We add time index t 0 to make explicit that the equivalent variation is calculated at the time of pension reform.
We thus have the following implicit equation for the equivalent variation of current generations:
$$\displaystyle{{\pi ^0 (k)^{ - \gamma}} \over {1 - \gamma}} (a^0 (k,t_0 ) + ev(k,t_0 ))^{1 - \gamma} = \displaystyle{{\pi ^1 (k)^{ - \gamma}} \over {1 - \gamma}} (a^1 (k,t_0 ))^{1 - \gamma} $$
and (t 0 − j e + 1⩽k⩽t 0), where we use k = t − j to denote a generation's period of birth.
There are two ways to calculate the equivalent variation of a change in welfare for a future generation (Demange (Reference Demange2002)). The interim view calculates for each possible state of the economy the equivalent variation that would leave a generation in that state of the economy indifferent between the status quo and the case of policy reform. The ex-ante view calculates the equivalent variation of a future generation that would leave this generation indifferent on average. In line with Gollier (Reference Gollier2008), we adopt the ex-ante concept. This gives us one equivalent variation per future generation.
For future generations, we thus calculate the equivalent variations by equating indirect utility before the reform with the expected value of indirect utility after the reform. After the pension reform, the indirect utility of a future generation depends on the state of the economy at the time this generation is born. By equating expected indirect utilities, we thus calculate the amount of wealth that would make this future generation on average indifferent between not reforming and reforming. As regards notation, in order to make explicit that the indirect utility of future generations before the pension reform is dependent on the state of the economy, we condition total household wealth upon the state of the economy, denoted as S. Further, we measure the equivalent variation of future generations at the time they enter the economy (age 1). The equivalent variation is then defined as follows:
$$\displaystyle{{\pi ^0 (1)^{ - \gamma}} \over {1 - \gamma}} (a^0 (1,k) + ev(1,k))^{1 - \gamma} = E_{t_0} \left[ {\displaystyle{{\pi ^1 (1)^{ - \gamma}} \over {1 - \gamma}} (a^1 (1,k)\vert S)^{1 - \gamma}} \right],\quad k \gt t_0. $$
Finally, the aggregate equivalent variation follows by adding up the equivalent variations of current and future generations:
$$AEV(t_0 ) = \mathop \sum \limits_{i = 1}^{\,j_e} ev(t_0 + 1 - i,t_0 ) + \mathop \sum \limits_{i = 1}^\infty R_b ^{ - i} ev(1,t_0 + i).$$
Now, the policy reform is welfare-improving if AEV(t 0) > 0. If AEV(t 0) < 0, then the policy reform is welfare-reducing.
Calibration of the model
This section discusses the values for the model parameters. We start with parameters that relate to the rates of return on financial markets. The risk-free rate (R b − 1) takes a value of 0.104. This implies an annual interest rate of 2%, which matches the post-war EU average for government bonds (Broer (Reference Broer2010)). The equity premium is set to μ s = 0.103 and the standard deviation of the return on equity to σ s = 0.368. The annual equivalent of the equity premium is 2.0%. We choose a value for the equity premium which is below empirical estimates (Broer (Reference Broer2010)) as with common figures for the coefficient of risk aversion and the volatility of equity returns, there would be a much too high investment in equity. The annual equivalent of the standard deviation is 15%. This is about equal to the standard deviation of US stocks (Campbell and Viceira (Reference Campbell and Viceira2002)) and matches the value adopted by Cui et al. (Reference Cui, Jong and Ponds2011). The productivity growth rate is set at (ρ − 1) = 0.088. The annual equivalent of this value is 1.7%, which is about the same as the long-run estimates for the EU and USA presented in Broer (Reference Broer2010).
Table 1. Model parameters
As regards the parameters that describe household preferences, the utility parameter ϕ is used to calibrate leisure time v at 2.5 during the working ages in between ages 20 and 65. The elasticity of intertemporal substitution is fixed at 0.33 (γ = 3). This value is within the range obtained by Epstein and Zin (Reference Epstein and Zin1991). We choose the rate of time preference such that initially the growth rate of individual consumption equals the rate of labour productivity growth. This gives a value for δ slightly below one: 0.993. The price elasticity of leisure equals −1/β = − 1/3. This corresponds with a labour supply elasticity of one-third, which is in the range of empirical estimates (Blundell and Macurdy (Reference Blundell and Macurdy1999)).
The pension fund charges a fraction χ = 0.5 of the funding deficit over the total contribution base. This corresponds with actual policies in the Netherlands that require pension funds to eliminate 10% of their funding deficit per year. On a 5-year basis, this is 40%, which is close to our assumption χ = 0.5. The accrual rate α is 0.50/45 a year, i.e., the replacement rate, the ratio between pension income and labour income, is 50%, which can be built up in the 45 years of working life. Pension funds equate the portfolio composition of their financial wealth to the portfolio share of the aggregate of households for the economy without a DB pension scheme. This boils down to a portfolio share of equity of about 68%.
Although our model has only one risk factor, the rate of return on equity, the model cannot be solved recursively. To obtain a recursive form, we adopt the method of parametrized expectations to derive an expression for human wealth, a n (i), in terms of the state of the economy. See Appendix B for further discussion.
The ex-ante welfare calculations are based on 10,000 different stochastic paths (and their antithetic counterparts). Fifteen stochastic paths could not be used because the modelled feedback mechanism did not deliver stable developments. So we ended up with 9,985 stochastic paths (and the antithetic counterparts).
Stochastic simulations
This section discusses the effects of introducing a DB pension scheme. We start with comparing steady-state results. In particular, we show the unconditional expected developments of consumption, income and wealth of a steady-state generation. Following up on that, we will explore how accounting for transitional effects changes the social welfare effect. A decomposition of the welfare effect shows the role of intergenerational risk sharing and that of labour market distortions.
Consumption and wealth in the steady state
The age profiles of the means of the steady-state distributions of financial wealth, human wealth and total wealth are represented in Figure 1. The left panel displays the case with an individual pension scheme, while the right panel that of a DB scheme. The x-axis gives the age and the y-axis the wealth components of households of that age. For the purpose of illustration, all presented variables are detrended for productivity growth.
Figure 1. Age profiles of average household wealth and its components.
The left panel shows the usual characteristics of a life-cycle profile. Human wealth is highest when households enter the labour market and falls gradually to zero over the working phase. Wealth accumulated in the individual pension fund displays an inverted V-pattern: it accumulates during the working phase and is decumulated in the retirement phase.
The right panel reveals that the profile of pension wealth in the DB case resembles very much that of pension wealth in the individual DC case. This indicates that savings through the individual DC scheme are replaced with savings through the DB pension scheme; the role of private saving is negligible.
Figure 2 presents the age profiles of the means of the distribution of consumption and non-capital income. Consumption is constant during working ages, as during retirement. This follows from our choice to detrend variables for productivity growth (and the calibration of the model such that individual consumption grows with the rate of labour productivity growth). Interestingly, upon retirement, consumption drops. This is due to the combination of mandatory retirement and non-separable preferences for consumption and leisure. Retirement forces the household to increase leisure; the reduction of consumption goes hand in hand with a reduction of labour supply.
Figure 2. Age profiles of average consumption and income.
Comparing the DB case with the DC case learns that the average consumption is higher in the DB case, both in the working phase and in the retirement phase. In the working phase, consumption is about 4% higher in the case of a DB pension fund; during retirement, the difference is about 2%. This reflects the welfare gain that is due to intergenerational risk sharing. As in Gollier (Reference Gollier2008) and in Bonenkamp and Westerhout (Reference Bonenkamp and Westerhout2014), risk sharing lowers the amount of risk attached to saving, given the returns on saving. Optimizing households subsequently rebalance their portfolios by increasing the investment in equity. This raises the average portfolio rate of return and allows a higher level of average consumption.
Figure 3 exhibits the mean and the 5% and 95% quantiles of the distribution of consumption. The effect of intergenerational risk sharing is clearly visible: consumption at the age of 20 is non-stochastic in the individual DC case, but stochastic in the DB case. Moving through the life cycle, the difference becomes smaller, but remains. At the age of 60, the 90% interval equals 0.37 in the individual DC case and 0.52 in the DB case. Similarly, at the age of 85, the figures are 0.45 and 0.48, respectively.
Figure 3. Distribution of the consumption age profiles.
Figure 4 sends out a similar message. The figure shows the same three aspects, now of the distribution of labour supply, in the individual DC case and in the DB case. The difference in the variations of results is now even more extreme than in the case of consumption: only in the DB case is labour supply stochastic. A comparison of the two panels shows two additional things.
Figure 4. Distribution of the employment age profiles.
First, labour supply is larger in the DB case. The reason is that risk sharing increases the investment in equity; the larger equity premium allows for a reduction of the pension contribution rate, which induces households to increase their labour supply; on average, it is 1.8% higher over the working phase of the life-cycle. Second, the age profile of labour supply is slightly increasing in the DB case. This reflects the uniformity principle due to which labour supply is implicitly taxed at young ages and implicitly subsidized at old ages. Because of this the labour supply effect increases from 1.3% at age 20 to 2.2% at age 65.
The steady-state generations enjoy a welfare gain of 19. This is equivalent to a 1.5% increase of consumption. This means that a 1.5% increase of consumption of this generation at all ages in all states of nature would imply the same increase in welfare as its participation in the DB pension scheme. The total welfare gain, which accounts for transitional generations and steady-state generations, is a little higher, i.e., 1.8%. We conclude that transitional dynamics are relevant, but not dominating.
The welfare gain we calculate for the introduction of a DB pension scheme is somewhat smaller than that in Bonenkamp and Westerhout (Reference Bonenkamp and Westerhout2014) who report a welfare gain of 2.9%. That the results are different, is not surprising as the models are different. In particular, we think a two-period setup as in their paper may be too rough for a numerical assessment of the welfare gain of a DB pension scheme. Our figure of 1.8% is also smaller than that of Cui et al. (Reference Cui, Jong and Ponds2011) who find a welfare gain of 2.3% of consumption. Again, this result is not surprising as the models are different. Moreover, their paper abstracts from labour supply distortions. We will come back to this when we provide a decomposition of our welfare effect into its components.
A decomposition of the welfare gain
The mean of the distribution of consumption is over the whole life cycle higher in the economy with a DB pension fund than in the economy with a DC pension fund. This indicates that an economy with a DB pension fund generates higher welfare than an economy with DC pension schemes. For workers, average consumption is about 3.4% higher; for pensioners, it is about 1.9% higher.
An interesting question is to what extent the different factors contribute to this welfare gain? In order to find answers to these questions, this section presents a decomposition of the welfare gain. In particular, we investigate two types of hypothetical DB pension schemes. The first one is a DB pension scheme that, unlike earlier, assumes that the recovery cost component of the pension contribution rate matches the value of accumulated pension rights – say, a DB pension scheme without the uniformity principle – and that labour supply is exogenous. The second hypothetical DB scheme is like the first hypothetical DB scheme, but assumes endogenous labour supply. Hence, a move from individual DC schemes towards the first hypothetical scheme identifies the welfare gain from risk sharing, the move from the first to the second hypothetical DB scheme identifies the welfare loss from endogenous labour supply reactions to changes in the pension contribution rate and the move from the second hypothetical DB scheme to the original DB scheme identifies the welfare loss from the uniformity principle.
This decomposition yields that the gain from intergenerational risk sharing is 141% of the total welfare gain. The welfare loss due to less labour supply distortions through the contribution rate equal 40% and the loss due to the uniformity principle 1% of the total welfare gain. The gain from risk sharing is thus more than double the losses that are due to the two types of labour supply distortions. That the welfare effect due to the uniformity principle is small has to do with the magnitude of the difference between the interest rate and the rate of growth (the rate of labour productivity growth). The difference is 0.3% only (the difference between 2.0% and 1.7%).
Risk sharing alone has an effect equal to 141% of the total welfare gain, which we calculated to be the equivalent of 1.8% of consumption. Risk sharing thus amounts to 2.5% of consumption. This effect is of the same order of magnitude as the effect in Cui et al. (Reference Cui, Jong and Ponds2011). We can also relate the impact of labour supply distortions to the earlier literature. In particular, Bonenkamp and Westerhout (Reference Bonenkamp and Westerhout2014) calculate the impact of labour supply distortions at 11% of the pure effect of risk sharing. This is significantly smaller than our result: 29% (41/141). According to our calculations, this cannot be explained by the fact that only the present paper accounts for the uniformity principle. We speculate that the result is due to a number of factors, such as the number of model periods in the papers (2 versus 13) and the values of parameters such as the labour supply elasticity and the coefficient of relative risk aversion. To provide a detailed analysis of the contribution of all possible factors, is beyond the scope of this paper, however.
Appendix C reports on a sensitivity analysis which we have performed in order to assess the robustness of the results obtained thus far. Overall, we conclude that our quantitative results are not robust to all parameter changes. In particular, alternative assumptions on the degree of risk aversion, the equity premium and the volatility of equity returns have a big impact upon the outcomes; even the sign of the welfare effect may change. On the other hand, the effect of alternative assumptions about the values of other parameters is much smaller. In general, we conclude that introduction of a DB scheme which combines better intergenerational risk with labour supply distortions will be welfare-improving.
Ex-post versus ex-ante effects
The stochastic nature of our model has an important implication. That introduction of a DB scheme improves welfare according to our calculations, is an ex-ante result. Ex-post, things may turn out differently. In particular, a generation may be born after a series of adverse shocks have hit the DB pension scheme. In this case, (mandatory) participation in a collective DB scheme may be worse than participating in an individual DC scheme. As an illustration, we calculate the distribution of welfare for a generation born 20 years after the reform. For this generation, the reform is in expectation welfare-improving. However, there is ex-post a probability of no less than 43% that the reform turns out to be welfare-reducing. This indicates that it would be difficult to introduce a DB scheme without imposing mandatory participation, even if the scheme is found to increase welfare.
Conclusions
This paper has found that a collective DB pension scheme dominates an individual DC scheme from a welfare point of view. In particular, the welfare gains from intergenerational risk sharing are found to be generally larger than the welfare losses due to distorted labour supply decisions.
Our paper can be extended in several directions. One option is to generalize the pension scheme into a scheme with both DB and DC elements, for example by introducing conditional and age-specific indexation of pensions and pension rights. In addition, our analysis concerns a small open economy. Although this is a reasonable assumption when it comes to an analysis of the economy of the Netherlands, in other cases the assumption is not so obvious. In a closed-economy context, pension schemes may crowd out private investment by lowering aggregate savings. This reduces the welfare gains from pension schemes and may even turn the gain into a loss (Krueger and Kubler Reference Krueger and Kubler2006).
Supplementary material
To view supplementary material for this article, please visit http://dx.doi.org/10.1017/S1474747215000074.
