2. DYNAMICAL MODEL AND COMPUTATION OF LPOS

2.1. Dynamical Model

The dynamical model used in this work is the Circular Restricted Three-Body Problem (CRTBP). By adopting a normalized set of units, the equations of motion of CRTBP expressed in the Earth-Moon barycentric synodic frame are (Szebehely, Reference Szebehely1967)

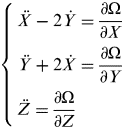(1)$$\left\{ \matrix{\ddot X - 2\dot Y = \displaystyle{{\partial \Omega} \over {\partial X}} \cr \ddot Y + 2\dot X = \displaystyle{{\partial \Omega} \over {\partial Y}} \cr {\rm} \ddot Z = \displaystyle{{\partial \Omega} \over {\partial Z}} } \right.$$

with

(2)$$\Omega = \displaystyle{1 \over 2}(X^2 + Y^2 ) + \displaystyle{{1 - \mu} \over {R_1}} + \displaystyle{\mu \over {R_2}} + \displaystyle{1 \over 2}\mu (1 - \mu ),$$

where μ=M ₂/(M ₁+M ₂) is the mass parameter of CRTBP, here for the Earth-Moon system, μ≈0·01215. R ₁ and R ₂ are the distances from the spacecraft to the Earth and the Moon, respectively

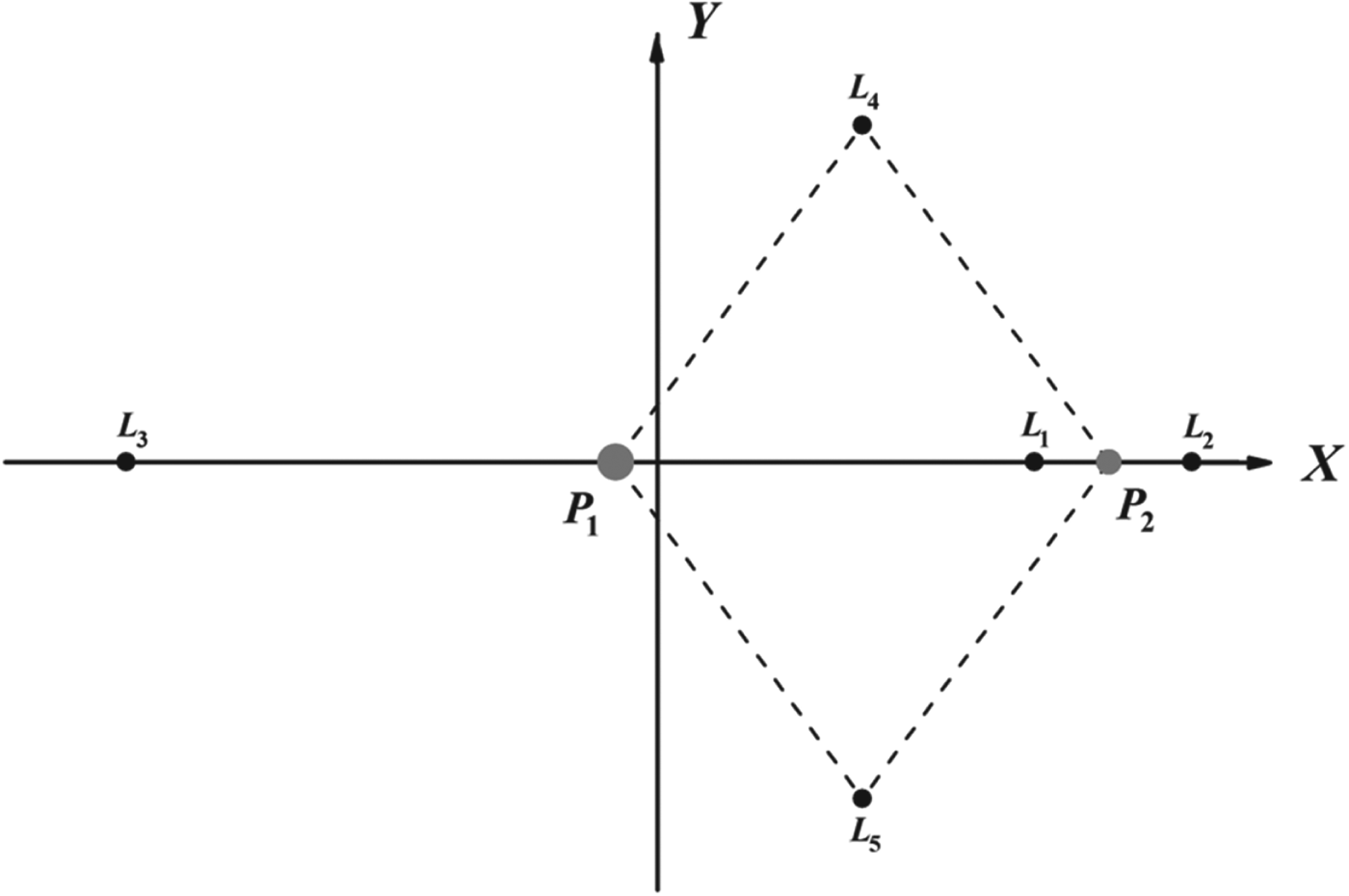
(3)$$\left\{ \matrix{R_1 = [(X + \mu )^2 + Y^2 + Z^2 ]^{1/2} \cr R_2 = [(X - 1 + \mu )^2 + Y^2 + Z^2 ]^{1/2} } \right.$$

The equations of motion of CRTBP admit five well-known equilibrium points in the synodic coordinate system (as shown in Figure 1). The five equilibrium points, also known as the libration points, are all located in the plane of motion of the primaries, with three collinear points L _1,2,3 located on the X-axis, and two triangular ones L _4,5 forming two equilateral triangles with the primaries.

Figure 1. Equilibrium points of CRTBP in the Earth-Moon synodic coordinate system.

The dynamical properties around the libration points are abundant, which offer many new orbits and applications to space missions, such as providing low energy transfers between the Earth and the Moon (Lei et al., Reference Lei, Xu and Sun2013a) or forming navigation architectures for space exploration. In this work, the LPOs around the Earth-Moon equilibrium points are selected as candidate orbits to build the constellation architecture for our proposed satellite navigation system.

2.2. Computation Of The LPOs

Generally speaking, there are two kinds of LPOs, the periodic orbits and the quasi-periodic orbits. Around the three collinear libration points L ₁, L ₂ and L ₃, the periodic orbits are halo orbits, planar Lyapunov orbits and vertical Lyapunov orbits, and the quasi-periodic orbits are Lissajous orbits and Quasi-Halo orbits. While for the two triangular libration points L ₄ and L ₅, there are three kinds of periodic orbits: the planar long periodic orbits, planar short periodic orbits and the vertical periodic orbits. Similarly, there also exist quasi-periodic orbits around the triangular libration points.

There are various methods of constructing these LPOs, including numerical differential correction (Gómez et al., Reference Gómez, Llibre, Martínez and Simó2001a;Reference Gómez, Llibre, Martínez and Simób) and analytic construction (Richardson, Reference Richardson1980; Jorba and Masdemont, Reference Jorba and Masdemont1999). As a large number of LPOs need to be constructed for constellation design, a high-efficiency computational method is indispensable. After trying several different ways of computation, a semi-analytical computational method is finally adopted in this work to construct the LPOs. Firstly, the analytical solutions of different LPOs truncated at a relatively high order are constructed by the Lindstedt-Poincaré (L-P) method. Here we shall only give the final expressions. The construction details and meanings of different coefficients can all be found in the References (Lei et al., Reference Lei, Xu, Hou and Sun2013b; Lei and Xu, Reference Lei and Xu2013c).

For LPOs around L _1,2,3,

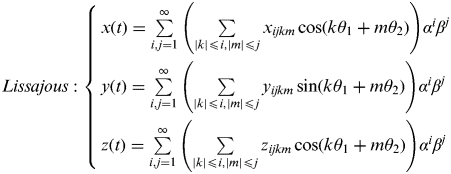(4)$$Lissajous:{\rm} \left\{ \matrix{x(t) = \sum\limits_{i,j = 1}^\infty {\left( {\sum\limits_{|k| \leqslant i,|m| \leqslant j} {x_{ijkm} \cos (k\theta _1 + m\theta _2 )}} \right)} \alpha ^i \beta ^j \cr y(t) = \sum\limits_{i,j = 1}^\infty {\left( {\sum\limits_{|k| \leqslant i,|m| \leqslant j} {y_{ijkm} \sin (k\theta _1 + m\theta _2 )}} \right)} \alpha ^i \beta ^j \cr z(t) = \sum\limits_{i,j = 1}^\infty {\left( {\sum\limits_{|k| \leqslant i,|m| \leqslant j} {z_{ijkm} \cos (k\theta _1 + m\theta _2 )}} \right)} \alpha ^i \beta ^j } \right.$$

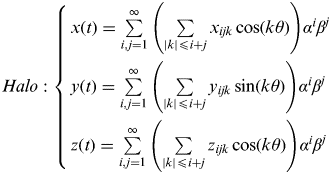(5)$$Halo:{\rm} \left\{ \matrix{x(t) = \sum\limits_{i,j = 1}^\infty {\left( {\sum\limits_{|k| \leqslant i + j} {x_{ijk} \cos (k\theta )}} \right)} \alpha ^i \beta ^j \cr y(t) = \sum\limits_{i,j = 1}^\infty {\left( {\sum\limits_{|k| \leqslant i + j} {y_{ijk} \sin (k\theta )}} \right)} \alpha ^i \beta ^j \cr z(t) = \sum\limits_{i,j = 1}^\infty {\left( {\sum\limits_{|k| \leqslant i + j} {z_{ijk} \cos (k\theta )}} \right)} \alpha ^i \beta ^j } \right.$$

For LPOs around L _4,5,

(6)$$\left\{ \matrix{x(t) = \sum\limits_{i,j,k = 1}^\infty {\left\{ {\sum\limits_{|l| \leqslant i,|m| \leqslant j,|n| \leqslant k} {\left[ \matrix{C_{ijklmn}^x \cos (l\theta _1 + m\theta _2 + n\theta _3 ) + \cr S_{ijklmn}^x \sin (l\theta _1 + m\theta _2 + n\theta _3 )} \right]}} \right\}\alpha ^i \beta ^j \gamma ^k} \cr y(t) = \sum\limits_{i,j,k = 1}^\infty {\left\{ {\sum\limits_{|l| \leqslant i,|m| \leqslant j,|n| \leqslant k} {\left[ \matrix{C_{ijklmn}^y \cos (l\theta _1 + m\theta _2 + n\theta _3 ) + \cr S_{ijklmn}^y \sin (l\theta _1 + m\theta _2 + n\theta _3 )} \right]}} \right\}\alpha ^i \beta ^j \gamma ^k} \cr z(t) = \sum\limits_{i,j,k = 1}^\infty {\left\{ {\sum\limits_{|l| \leqslant i,|m| \leqslant j,|n| \leqslant k} {\left[ \matrix{C_{ijklmn}^z \cos (l\theta _1 + m\theta _2 + n\theta _3 ) + \cr S_{ijklmn}^z \sin (l\theta _1 + m\theta _2 + n\theta _3 )} \right]}} \right\}\alpha ^i \beta ^j \gamma ^k} } \right.$$

It should be noted that when the in-plane amplitude α=0 in Equation (4), the Lissajous orbits reduce to the vertical Lyapunov orbits and when the out-of-plane amplitude β=0, they reduce to the planar Lyapunov orbits.

Once the coefficients in the above equations have been determined recursively by the L-P procedure, expressions for different LPOs can be obtained directly by substituting the amplitude parameter. Then with the initial conditions provided by these high-order analytical solutions, a RKF78 integrator is employed to numerically integrate the orbit for appropriate units of time. In this way, LPOs can be computed quickly and efficiently for constellation design purposes and some typical plots of LPOs computed by this method are presented in Figures 2 and 3 respectively for the collinear and triangular case.

Figure 2. Typical orbits of LPOs around the Earth-Moon collinear libration point. Upper left: Lissajous orbit. Upper right: planar Lyapunov orbit. Lower left: vertical Lyapunov orbit. Lower right: Halo orbit. All of the orbits are computed by the semi-analytical method.

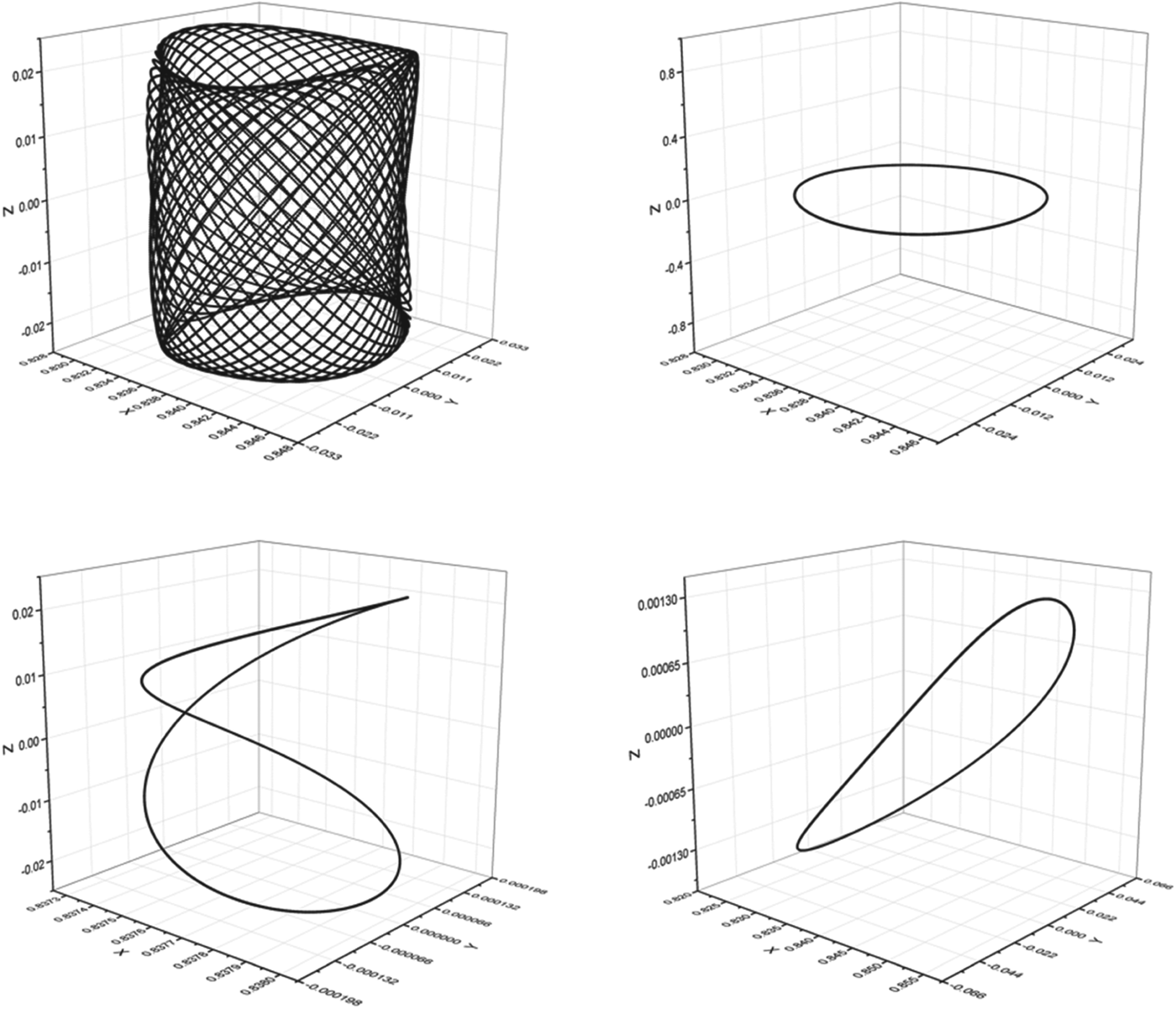
Figure 3. Typical orbits of LPOs around the Earth-Moon triangular libration point. Upper left: planar long periodic orbit. Upper right: planar short periodic orbit. Lower left: vertical periodic orbit. Lower right: quasi-periodic orbit. All of the orbits are computed by the semi-analytical method.

3. SATELLITE CONSTELLATION COVERAGE AND GEOMETRY

Constellation coverage performance is regarded as a primary criterion for satellite constellation design. Here for the libration point satellite navigation system, it is also the primary consideration. From the above description, it is known that the proposed navigation system employs the Liaison technique to perform autonomous navigation, so the geometry of the constellation can be more flexible, because only one libration point satellite in view is enough to provide navigation capability. Also, as the size and shape of LPOs are correlated with autonomous orbit determination accuracy, constellation design of the libration point satellite navigation system should be based on a comprehensive consideration of constellation coverage and autonomous orbit determination performance. Considering the existing navigation systems have already been able to provide an excellent coverage on Earth and the proposed system is primarily designed for lunar exploration, the coverage here is specific to lunar orbits, which can have various orbital characteristics.

Consider a lunar orbiter moving on a circular orbit, with inclination i and right ascension of the ascending node Ω. The position vector of the lunar orbiter at a given time can be expressed in a Moon-centred inertial (MCI) frame as

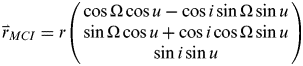(7)$$\overset{\lower-0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}\hskip-5pt {r} _{MCI} = r\left( {\matrix{ {\cos \Omega \cos u - \cos i\sin \Omega \sin u} \cr {\sin \Omega \cos u + \cos i\cos \Omega \sin u} \cr {\sin i\sin u} \cr}} \right)$$

where r is the orbital radius of the circular orbit, u is the argument of latitude at the given time.

As the LPOs are customarily expressed in the Earth-Moon barycentric synodic reference frame, it requires a coordinate transformation between the inertial frame and the synodic frame. The rotation matrix from the MCI frame to the Moon-centred rotating frame, denoted by R_z(t), is given by

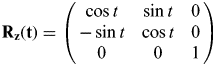(8)$${\bf R}_{\bf z} {\bf (t)} = \left( {\matrix{ {\cos t} & {\sin t} & 0 \cr { - \sin t} & {\cos t} & 0 \cr 0 & 0 & 1 \cr}} \right)$$

It has been assumed that the two frames coincide at t=0, and the transformation time t is in the normalized unit so as to simplify the rotation matrix to the above form. Then the coordinate transformation from the MCI frame to the Earth-Moon barycentric synodic reference frame can be expressed as

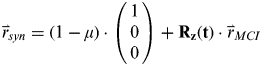(9)$$\overset{\lower-0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}\hskip-5pt {r} _{syn} = (1 - \mu ) \cdot \left( {\matrix{ 1 \cr 0 \cr 0 \cr}} \right) + {\bf R}_{\bf z} {\bf (t)} \cdot \overset{\lower-0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}\hskip-5pt {r} _{MCI} $$

where $\overset{\lower-0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}\hskip-5pt {r} _{syn} $ is the position vector expressed in the synodic frame, and μ is the mass parameter of the Earth-Moon system. Substituting the expression of $\overset{\lower-0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}\hskip-5pt {r} _{MCI} $ into the above equation, it can be deduced, after some calculations, that

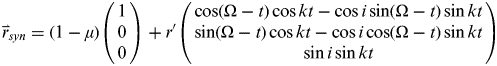(10)$$\overset{\lower-0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}\hskip-5pt {r} _{syn} = (1 - \mu )\left( {\matrix{ 1 \cr 0 \cr 0 \cr}} \right) + r'\left( {\matrix{ {\cos (\Omega - t)\cos kt - \cos i\sin (\Omega - t)\sin kt} \cr {\sin (\Omega - t)\cos kt - \cos i\cos (\Omega - t)\sin kt} \cr {\sin i\sin kt} \cr}} \right)$$

where r′ is the normalized orbital radius of the circular orbit, k is a scaling factor between the argument of latitude u and normalized time t, which is defined by

(11)$$u = kt,{\rm} k = \sqrt {\displaystyle{\mu \over {r'^3}}} $$

Comparing the second term on the right side of Equation (10) with the expression of $\vec r_{MCI} $ given by Equation (7), it can be found that the right ascension of the ascending node is now varying with time in the synodic frame, which means a circular lunar orbit in the MCI frame becomes a spherical zone seen from the synodic frame and the expression for the spherical zone can be written as

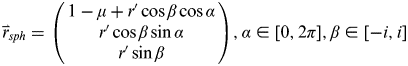(12)$$\overset{\lower-0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}\hskip-5pt {r} _{sph} = \left( {\matrix{ {1 - \mu + r'\cos \beta \cos \alpha} \cr {r'\cos \beta \sin \alpha} \cr {r'\sin \beta} \cr}} \right),{\rm} \alpha \in [0,{\rm} 2\pi ],{\rm} \beta \in [ - i,{\rm} i]$$

From the above relation, it can be easily deduced that the size and shape of different spherical zones are only related to the orbital radius and inclination of circular lunar orbits. When two lunar orbits have the same orbital radius, the spherical zone of the more inclined one will cover the spherical zone with smaller inclination. Consequently, the constraint of continuous global coverage for users that are in lunar orbits becomes the equivalent coverage to different spherical zones in the synodic frame.

Consider a libration point satellite constellation with the navigation satellites located on different LPOs around the Earth-Moon L ₁, L ₂, L ₄ and L ₅. The LPOs around L ₃ are not selected because they are on the far side of the Earth and make no contribution for lunar orbit coverage. Then the satellite constellation can be determined as follows to fulfil the continuous global coverage requirement:

1. 1) Compute the spherical zone. For a given circular lunar orbit with inclination i and radius r′, use Equation (12) to obtain the corresponding spherical zone;

2. 2) Construct the LPO. Select a first libration point L _i, i=1, 2, 4, 5, and compute LPOs around this point using the semi-analytical method mentioned before;

3. 3) Identify the continuous coverage region. For the previously computed LPOs, identify the region on the spherical zone which can be continuously covered by the libration point satellite in its whole orbit period;

4. 4) Check for the global coverage requirement. If the existing constellation has already been able to achieve continuous global coverage for the whole spherical zone, the construction procedure is over. Otherwise, select a different libration point and repeat the above two steps until the constellation which can maximize the continuous coverage region has been found.

Candidate constellations which fulfil the continuous global coverage requirement can be found after such a search process and, because of the special requirement described in Step 3, there is no constraint for the relative phase difference between LPOs.

What should be noted is that only the periodic LPOs are investigated in this work for the consideration of spatial repeatability of the constellation configuration. It is also assumed that only one navigation satellite is operating in the vicinity of every libration point so as to simplify the geometry of the system.

4. ARCHITECTURE ANALYSIS OF THE CANDIDATE CONSTELLATIONS

According to the search process described before, an architecture analysis of the libration point satellite navigation system will be performed in this section. Candidate orbits for the navigation satellites operating around different libration points are summarised in Table 1. Candidate configurations primarily considered in this work include: 1) Earth-Moon L _1,2 constellation with two satellites located respectively around Earth-Moon L ₁ and L ₂; 2) Earth-Moon L _2,4,5 constellation with three satellites located respectively around Earth-Moon L ₂, L ₄ and L ₅; and 3) Earth-Moon L _1,2,4,5 constellation with four satellites located respectively around Earth-Moon L ₁, L ₂, L ₄ and L ₅. Only these three kinds of configurations are considered, for the reason that they are the simplest and most representative architecture for each case, and it will be seen later that the latter two cases can already achieve continuous global coverage for a variety of lunar orbits.

Table 1. Candidate orbits for the libration point navigation satellites.

4.1. Earth-Moon L_1,2 Constellation

As a starting point, we first consider the simplest constellation with two navigation satellites operating in the periodic LPOs around the Earth-Moon L ₁ and L ₂, respectively. In order to investigate the coverage performance of this constellation, orbits of the user satellites must be determined first. Assume the user satellites are located in circular lunar orbits with inclination i and altitude h, varying in the range of

(13)$$i \in [0 \deg, {\rm} 90 \deg ],{\rm} h \in [100 \; {\rm km},{\rm} 2000 \; {\rm km}]$$

As was described in Section 3, a circular lunar orbit looks like a spherical zone when looking from the synodic frame and the height of the spherical zone is positively correlated with the inclination of the orbit. When a lunar orbiter has a polar inclination (i=90°), the spherical zone becomes a spherical surface, which covers all other spherical zones with the same radius and smaller inclinations.

For the Earth-Moon L _1,2 two-satellite constellation, it is an intuitive thought that this constellation cannot achieve continuous coverage for the region perpendicular to the line joining the two libration points, which has been verified by the numerical simulation result, as shown in Figure 4. This is given no more consideration for this case. Actually, it can be concluded that it is impossible to achieve continuous global coverage for any lunar orbits, which is not restricted to the L _1,2 case.

Figure 4. Earth-Moon L _1,2 constellation coverage performance. Left: spherical zone of a lunar polar orbit. Right: planar projection of the spherical zone. The red parts in the figure represent the region which can not be continuously covered by the libration point satellite, and the green parts represent the region that can be continuously covered. It is obvious that the region perpendicular to the line joining the two libration points is the blind area for the two-satellite constellation.

4.2. Earth-Moon L_2,4,5 Constellation

Consider the Earth-Moon L _2,4,5 three-satellite constellation, which employs two satellites operating in the vicinity of the Earth-Moon triangular libration points. The planar long periodic orbits, planar short periodic orbits and vertical periodic orbits around the triangular libration points are available now. In order to determine the appropriate architecture that can fulfil the continuous global coverage requirement, LPOs of the navigation satellites are discretized first. Assuming a periodic LPO is discretized into N patch points, then a region on the spherical zone of a lunar orbit is said to be continuously covered by the navigation satellite, on condition that all the N points are visible to that region. For LPOs around the collinear libration points and triangular libration points, the discrete number N is selected respectively as Table 2.

Table 2. Discrete number of different LPOs.

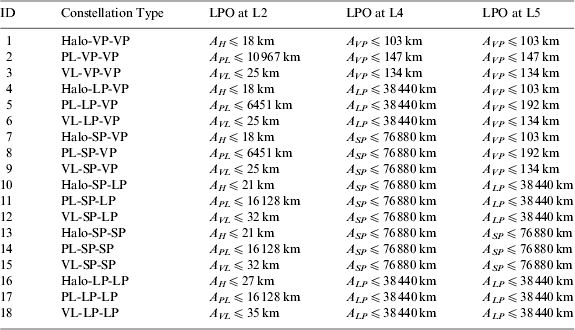
Then for the circular lunar orbits which are in the same range given by Equation (13), an exhaustive search process stated before is adopted to determine the appropriate Earth-Moon L _2,4,5 constellation architecture. The final results show that the Earth-Moon L _2,4,5 three-satellite constellation is feasible and all the appropriate configurations that fulfil the continuous global coverage requirement are listed in Table 3.

Table 3. Appropriate configurations of the Earth-Moon L _2,4,5 constellation*.

* The variables A _H, A_PL, A_VL, A_VP, A_LP and A _SP in the table are amplitude parameters respectively representing for: the out-of-plane amplitude of the halo orbit, the in-plane amplitude of the planar Lyapunov orbit, the out-of-plane amplitude of the vertical Lyapunov orbit, the out-of-plane amplitude of the vertical periodic orbit, the in-plane amplitude of the planar long periodic orbit and the in-plane amplitude of the planar short periodic orbit. All these amplitudes are parameters in the analytical expressions of LPOs.

It can be seen from the above results that there exists an upper bound value for the amplitude parameter of every feasible configuration. As long as the amplitude constraint is satisfied, the corresponding constellation can achieve continuous global coverage for all lunar orbits with arbitrary inclination and orbital radius changing in the range of 100 km to 2000 km, and an intuitive coverage performance of the Earth-Moon L _2,4,5 constellation is presented in Figure 5. Note that the region which is unable to be continuously covered by the Earth-Moon L _1,2 two-satellite constellation can be covered by the triangular libration point satellites now.

Figure 5. Earth-Moon L _2,4,5 constellation coverage performance. Left: spherical zone of a lunar polar orbit. Right: planar projection of the spherical zone. The green parts in the figure represent the region which can be continuously covered by one libration point satellite, and the blue parts represent the region that can be continuously covered by two libration point satellites. There is no blind area for the Earth-Moon L _2,4,5 three-satellite constellation.

4.3. Earth-Moon L_1,2,4,5 Constellation

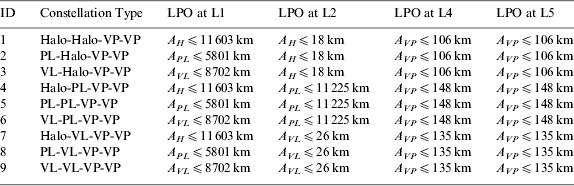
Although the Earth-Moon L _2,4,5 constellation can already achieve the continuous global coverage requirement, it can be seen from Figure 5 that only a small part of the spherical zone is continuously covered by more than one navigation satellite, which is not a prominent criterion in a consideration of system stability. Thus it is a natural idea to add another satellite. Here, for the Earth-Moon L _1,2,4,5 constellation, we consider adding a fourth satellite operating in the vicinity of L ₁. By adopting a similar search process, the appropriate four-satellite constellation architecture can be found, and the final results are listed in Table 4.

Table 4. Appropriate configurations of the Earth-Moon L _1,2,4,5 constellation.

It should be noted that only the results of vertical periodic orbits around L _4,5 are listed here for the triangular libration point satellites, for the reason that the result will be just similar for the planar long periodic orbit and planar short periodic orbit cases. Comparing the above results with the first three rows in Table 3, it can be found that the upper bound value for the amplitude of the same LPO in the Earth-Moon L _1,2,4,5 constellation is larger than that of the Earth-Moon L _2,4,5 case, which means the number of feasible LPOs will be increased. Moreover, as had been expected, the coverage performance of the Earth-Moon L _1,2,4,5 four-satellite constellation will also be improved.

From Figure 6, it can be clearly seen that more regions can be covered by more than one libration point satellites compared with the three-satellite constellation case. Although the coverage performance can still be improved by adding more navigation satellites, we do not cover that here to preserve the simplicity of the constellation architecture.

Figure 6. Earth-Moon L _1,2,4,5 constellation coverage performance. Left: spherical zone of a lunar polar orbit. Right: planar projection of the spherical zone. The green, blue and cyan parts in the figure respectively represent the region that can be continuously covered by one libration point satellite, two libration point satellites and three libration point satellites.

5. AUTONOMOUS ORBIT DETERMINATION FOR THE LPOS

It is known that scalar satellite-to-satellite tracking data can be used to perform autonomous orbit determination. Because of the strong asymmetry of the three-body force field, a LPO with specific size and shape can only have a single orientation with respect to the Earth and the Moon, which means a spacecraft in a LPO can track other spacecraft using crosslink range measurements and determine the absolute positions of both spacecraft simultaneously without any mathematical constraints. This linked, autonomous orbit determination method is known as Liaison Navigation which was first proposed by Hill et al. (Reference Hill, Born and Lo2005b). Hill has conducted a systematic study on the autonomous orbit determination for LPOs in his PhD dissertation (Hill, Reference Hill2007). Here, as part of the navigation architecture analysis, a Liaison Navigation simulation is also performed to verify the autonomous orbit determination accuracy for these candidate libration point satellite constellations.

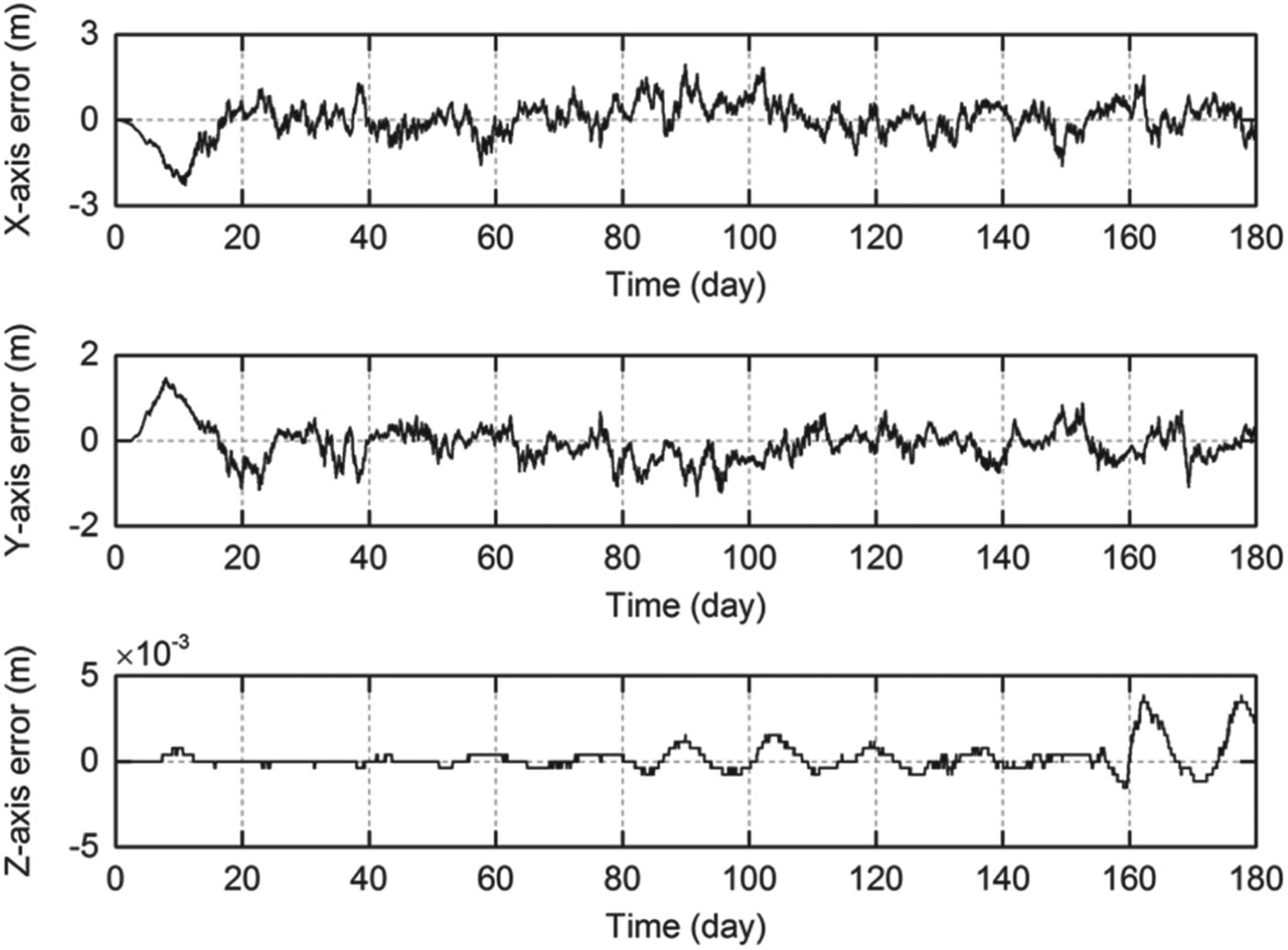
By assuming a 0·3 m inter-satellite ranging precision, which is acceptable for current techniques, we first come to the orbit determination of Earth-Moon L _2,4,5 three-satellite constellation. With the semi-analytical LPO solutions used as nominal orbits, a typical plot of 180 days' autonomous orbit determination results obtained by an extended Kalman filter is shown in Figure 7. The plot shown here is for a L ₂ navigation satellite, for the L ₁ or the L _4,5 case, the result is similar.

Figure 7. 180 days' Autonomous orbit determination result for a L ₂ navigation satellite. Upper plot: x-position error in the 180 days' period. Middle plot: y-position error in the 180 days' period. Lower plot: z-position error in the 180 days' period.

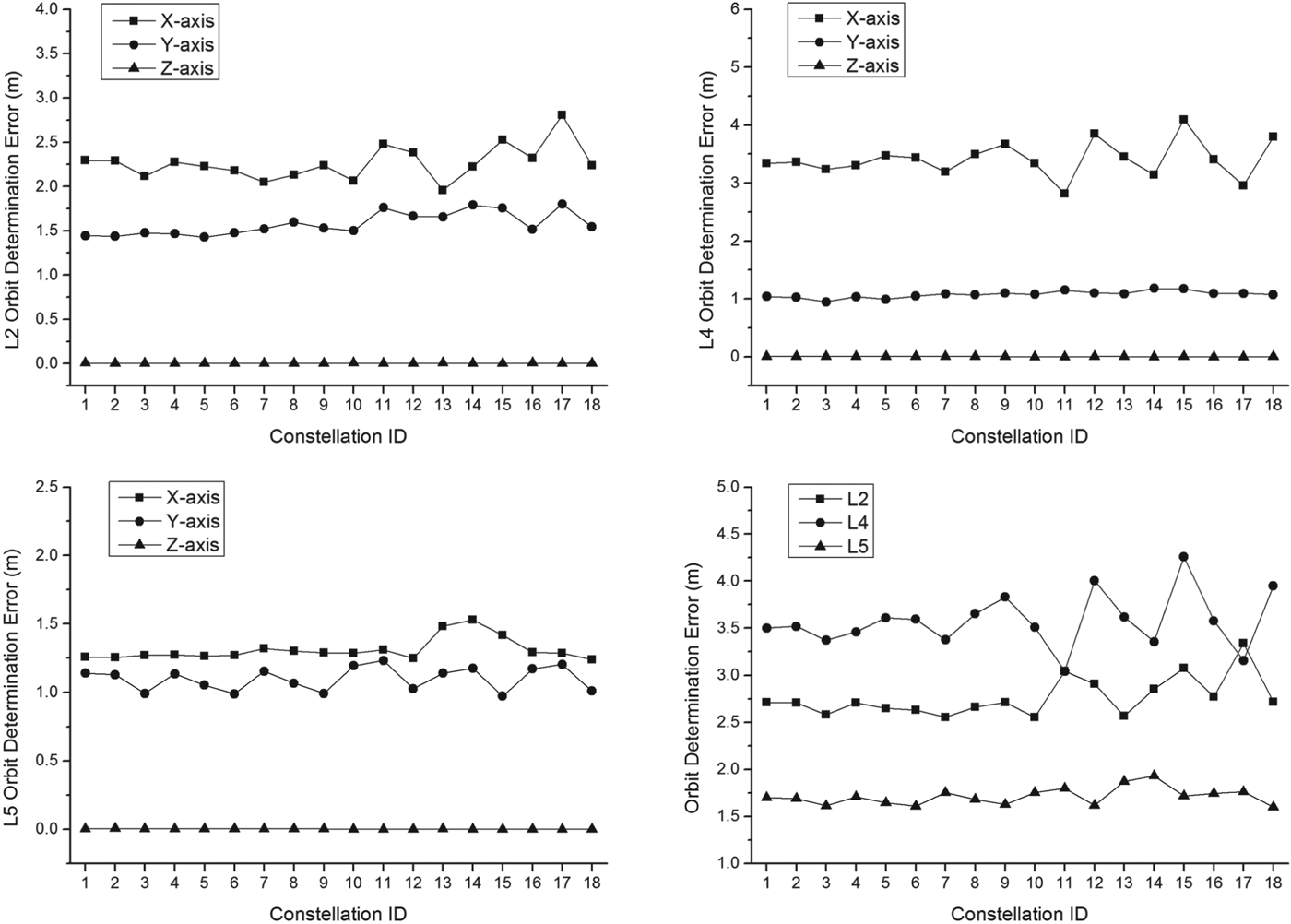
It can be seen from Figure 7 that the position of a libration point satellite is autonomously determined within 3 m error in the 180 days period. With the help of Liaison navigation, orbits of the navigation satellites can be determined accurately and autonomy of the libration point navigation system can be greatly increased. For all the 18 candidate three-satellite constellations, the autonomous orbit determination accuracies are verified by this process and maximum orbit determination errors in 180 days for each case are presented in Figure 8.

Figure 8. Autonomous orbit determination performance of the Earth-Moon L _2,4,5 three-satellite constellations. Upper left: autonomous orbit determination accuracy of the L ₂ orbiter. Upper right: autonomous orbit determination accuracy of the L ₄ orbiter. Lower left: autonomous orbit determination accuracy of the L ₅ orbiter. Lower right: total orbit determination accuracy of the three libration point orbiters.

From the above results, it can be found that the autonomous orbit determination accuracy of the Earth-Moon L _2,4,5 three-satellite constellation is within a few metres for all of the 18 candidate configurations. Also, the out-of-plane orbit determination accuracy seems always to exhibit a better performance, which may be concerned with the intrinsic characteristics of LPOs. According to the autonomous orbit determination results, the optimal architecture for the Earth-Moon L _2,4,5 three-satellite constellation is the Vertical Lyapunov Orbit - Vertical Periodic Orbit - Vertical Periodic Orbit (ID=3) configuration.

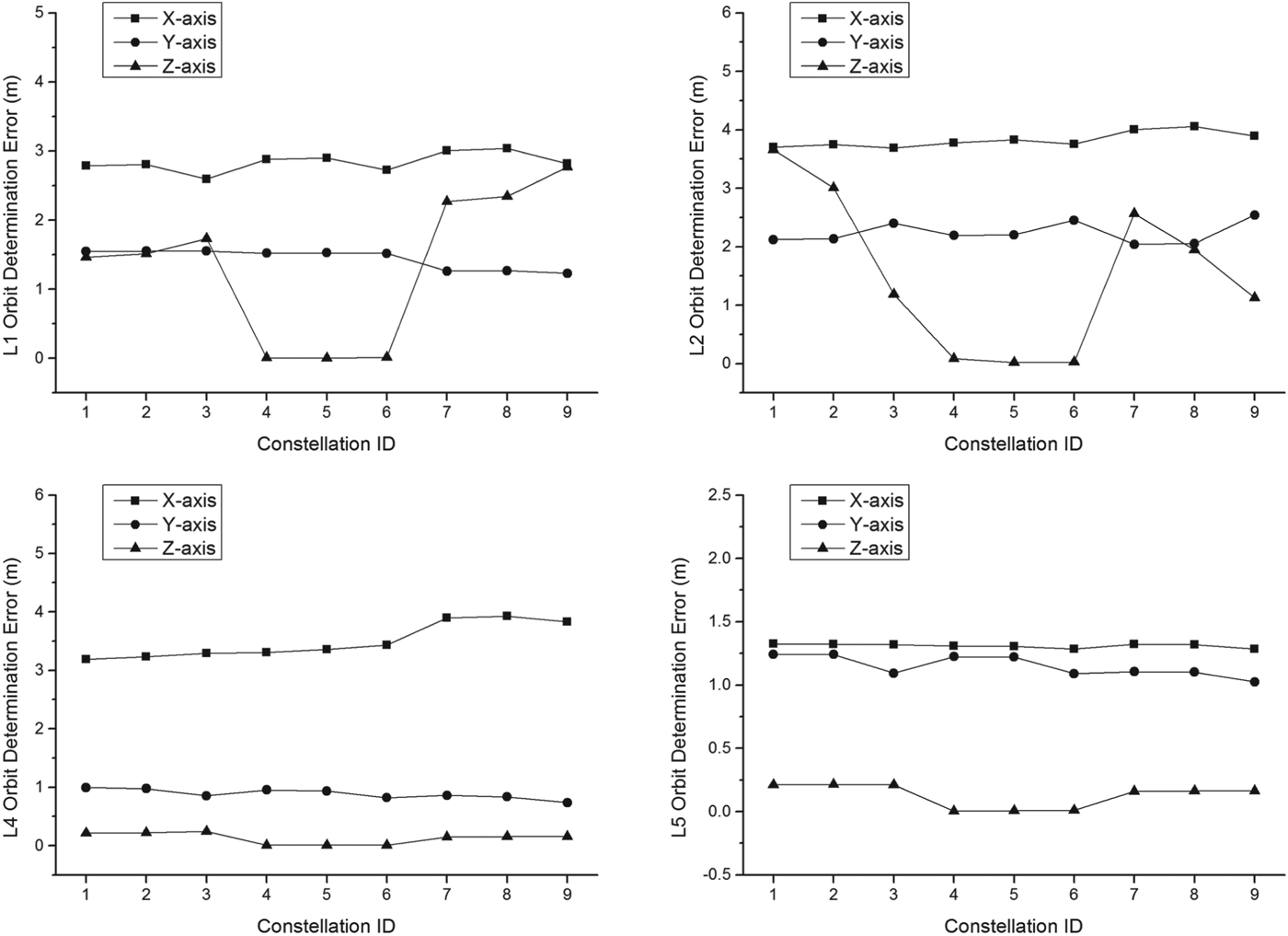
Likewise, the orbit determination performance of the Earth-Moon L _1,2,4,5 four-satellite constellation is also verified by the Liaison navigation technique and maximum orbit determination errors in 180 days are illustrated in Figure 9.

Figure 9. Autonomous orbit determination performance of the Earth-Moon L _1,2,4,5 four-satellite constellations. Upper left: autonomous orbit determination accuracy of the L ₁ orbiter. Upper right: autonomous orbit determination accuracy of the L ₂ orbiter. Lower left: autonomous orbit determination accuracy of the L ₄ orbiter. Lower right: autonomous orbit determination accuracy of the L ₅ orbiter.

Similarly with the three-satellite constellation, autonomous orbit determination performance of the Earth-Moon L _1,2,4,5 four-satellite case is also satisfactory seen from the above results. Considering the overall constellation position error, the optimal Earth-Moon L _1,2,4,5 four-satellite architecture is the Vertical Lyapunov Orbit - Planar Lyapunov Orbit - Vertical Periodic Orbit - Vertical Periodic Orbit (ID=6) configuration.

6. CONCLUSIONS AND DISCUSSIONS

This paper presents a detailed study on the architecture of the libration point satellite navigation system. In order to achieve continuous global coverage for lunar orbits, three candidate constellations are specifically analysed. The final results indicate that the Earth-Moon L _2,4,5 three-satellite constellation and the Earth-Moon L _1,2,4,5 four-satellite constellation are the simplest feasible architectures to form the libration point satellite navigation system, with the latter having a better coverage performance. Considering the strong asymmetry of the three-body force field, an autonomous navigation technique, known as Liaison navigation, is also adopted by the libration point satellites. After a comprehensive consideration of coverage ability and autonomous orbit determination accuracy, two optimal architectures are finally obtained by a thorough numerical simulation.

In further discussions, the main superiorities of the proposed libration point satellite navigation system can be concluded as follows:

1. a. The proposed system will provide a better navigation capability for deep-space exploration missions in the future;

2. b. The proposed system can combine with existing navigation satellites near Earth, which can improve the autonomy of these navigation systems;

3. c. In fact, the proposed system can also be extended to other libration points, such as the Sun-Mars libration points, with a similar procedure.

This paper serves as a first step for libration point navigation system design. Specific examination of the navigation performance for lunar exploration and station-keeping techniques for libration point navigation satellites will be investigated in future work.