1. INTRODUCTION
The collision risk of ship-ship encounters is a key issue that must be accounted for in ship navigation safety. Many risk analysis models and methodologies have been proposed for analysing accident risk both in general and in maritime transportation in particular. For an overview of current research, see Li et al. (Reference Li, Meng and Qu2012). Additionally, Debnath and Chin (Reference Debnath and Chin2010) and Goerlandt and Montewka (Reference Goerlandt and Montewka2015a) describe some recent frameworks for analysing risk in maritime transportation. Qu et al. (Reference Qu, Meng and Li2011), and Goerlandt et al. (Reference Goerlandt, Montewka, Kuzmin and Kujala2015) have also made contributions in the study of risk frameworks.
Some studies that evaluate encounter risk, such as that by Goerlandt et al. (Reference Goerlandt, Montewka, Kuzmin and Kujala2015) propose a theoretical framework for effective ship collision risk, and the authors point out that a ship-ship encounter is a complicated process (Laureshyn et al., Reference Laureshyn, Svensson and Hydén2010). It is indeed a complex operational process that is dynamically changing and its characteristics need to be continuously measured (Goerlandt et al., Reference Goerlandt, Montewka, Kuzmin and Kujala2015). In other research (Zhang et al., Reference Zhang, Goerlandt, Montewka and Kujala2015; Zhang et al., Reference Zhang, Goerlandt, Kujala and Wang2016), the risk of near-miss collisions is ranked by a formulated index, Vessel Collision Risk Operator (VCRO), which can track encounter procedures and includes the effect of ship size though consideration of the ship domain.
The previously mentioned research made significant progress in the field of ship-ship collision assessment. However, there are still several limitations within risk analysis methods proposed by these studies, specifically regarding the complex situation of how to best consider ship-ship encounters, an issue which has not yet been resolved. Most previous studies only consider the encounter risk from the perspective of a single ship, rather than from the whole system that involves both ships involved in a given encounter. Other studies simply consider the risk of both ships to be equal even if the systematic risk is considered to some degree (Goerlandt and Montewka, Reference Goerlandt and Montewka2015a). Additionally, although the factor of ship size has been taken into consideration in the VCRO metric, the ship size difference has historically been ignored (Zhang et al., Reference Zhang, Goerlandt, Kujala and Wang2016). Thus, the VCRO assumes that the vessels involved, which have different sizes and manoeuvrability, have the same value. This does not reflect reality in most cases. Consequently, traditional VCRO risk assessment becomes significantly less effective when the sizes of encountered ships have a large difference, as opposed to a fairly accurate assessment when the difference between their sizes is much smaller. In the former scenario, the difference in ship sizes cannot be ignored. Further, it is not sufficient to judge risk by only considering the current state of factors. Since ships keep moving in a continual state, the ship movement state during ship-ship encounters should be monitored continuously to achieve better assessment of encountered risk.
This paper proposes a systematic method for collision risk assessment that formulates ship-ship collisions in a systematic manner from the view of both ships involved in the encounter. In the proposed model, multiple states of ship-ship encounters that reflect not only the current state, but also the previous state and the state change rate are involved. An improved risk indicator based on VCRO is proposed by considering the difference of ship domain in the risk assessment and thus overcoming the existing shortcomings of VCRO regarding the false assumptions that have historically led to ignoring ship size differences. The systematic framework of risk proposed here is combined with an improved risk indicator based on VCRO to assess the risk of collision through analysing the risk of ship-ship encounters under specific conditions, such as differences in ship size and differences in state change rate. By applying the systematic risk framework and risk indicator, the risks of collision can be ranked more precisely. The conflict risk analysis presented here is the extension of the near-miss detection concept which could, in principle, be used for operational purposes to assess the traffic situation and detect possible critical situations in real time.
2. RISK PERSPECTIVE
There have been many studies on the collision risk of ships. This research attempts to use a systematic perspective to study the risk to a system composed of two encountering ships in order to establish an approach to track the dynamic risk of encountered ships.
2.1. Systematic perspective in dynamic risk
Based on the concepts of risk and probability studied in previous research (Kaplan and Garrick, Reference Kaplan and Garrick1981), the collision risk during an encounter between ship a and ship b can be defined as:
$$Risk(ship_{a},ship_{b})=\{s_{ab},p_{ab}c_{ab}\}$$
here s ab is the collision scenario of ship a and b, s ab is the probability of the collision scenario, and c ab is the consequence of the collision scenario, i = 1, 2 … n.
Equation (1) indicates the fundamental factors that should be considered in ship-ship encounter risk assessment. However, it fails to clearly describe how to track and assess the encounter process by accounting for details which are always in a state of dynamic change.
During the process of risk assessment for ship-ship encounters, the pair of ships that encounter each other can be thought of as a system, and that system state can be described by ship movement parameters, which change dynamically. The systematic process and its complexities were studied by Goerlandt et al. (Reference Goerlandt, Montewka, Kuzmin and Kujala2015). A ship-ship encounter involves the simultaneous presence of two vessels in a finite area and is widely considered as an elementary aspect of maritime traffic environments (Debnath and Chin, Reference Debnath and Chin2010; Laureshyn et al., Reference Laureshyn, Svensson and Hydén2010). It is a continuous process characterised by dynamically changing states, and Goerlandt et al. (Reference Goerlandt, Montewka, Kuzmin and Kujala2015) claimed that this perspective is well suited for operational settings where risk is continuously assessed in changing conditions.
Goerlandt et al. (Reference Goerlandt, Montewka, Kuzmin and Kujala2015) also indicate there are some challenges in assessing risk using the proposed systematic approach. First, the dynamic nature of the system requires that the identification of dynamic states should be measured continuously, then transformed and mapped to collision risk. Second, certain static factors like vessel size can influence the risk interpretation, which relates to a situation being experienced as a whole as opposed to considering isolated parts of the situation (Brown, Reference Brown2012).
From the preceding description, we can know ship encounters are always complex processes because there are many factors that may influence risk assessment. Since the relative motion between the encountered vessels is constantly changing and in turn causing changes in many risk factors, it is clear that determining the risk from only one side is not sufficient.
In this study, the systematic risk perspective for ship pairs is presented in the following equation based on the previous discussion on risk and the work of Goerlandt et al. (Reference Goerlandt, Montewka, Kuzmin and Kujala2015),
$$R\sim I(SQ\lpar SS_{1},SS_{2}),CS\rpar \to E\vert BK$$
Here, CS refers to collision consequence, SS 1 is the system state of the first vessel, and SS 2 is the system state of the second vessel. Equation (2) states that Risk R is described by indicator I, reflecting an interpretation of the possible occurrence of an Event (E), based on a mental projection in light of a number of Situational Qualities (SQs) and collision consequence (CS). Finally, BK represents background knowledge.
2.2. VCRO and system state in ship-ship encounters
In the marine traffic field, various methods have been proposed for analysing accidental risk and safety. Zhang et al. (Reference Zhang, Goerlandt, Montewka and Kujala2015) apply a risk operator (VCRO), an indicator based on the distance between the two ships encountered, the relative speed of the ships, and the difference between the headings of the ships as the indicator for risk detection. This work is significantly improved by taking ship domain and Minimum Distance to Collision (MDTC) into consideration (Zhang et al., Reference Zhang, Goerlandt, Kujala and Wang2016).
The dynamic nature of the system requires the identification of dynamic states which can be continuously measured. Therefore, it is necessary to define a method to provide such a continuous measurement for dynamic states. In this study, VCRO is selected as the metric to describe the dynamic states.
VCRO is an indicator-based method to rank ship encounters for detecting possible near-miss encounters. In constructing the mathematical model of the VCRO, its functional form is deduced from the qualitative relations that the individual factors are considered to have in relation to the conflict severity. VCRO is calculated based on relative distance, relative speed, and intersection angle. These factors change dynamically and can be measured in a time series. Therefore, VCRO can represent a dynamic system state and its changes if the ship pair is considered as a system during a ship-ship encounter.
3. VESSEL COLLISION RISK OPERATOR
As indicated by earlier studies (Zhang et al., Reference Zhang, Goerlandt, Montewka and Kujala2015; Zhang et al., Reference Zhang, Goerlandt, Kujala and Wang2016), VCRO works well in validating ranking and prioritising encounters in the northern Baltic Sea. However, there are still some issues. The primary issue is that VCRO ignores the size differences of the ships involved in the encounter, which may lead to an incorrect explanation of risk assessment due to the fact that the ship domain of large ships is typically larger than that of small ships. Additionally, regarding the calculation of safety distance, an elliptical domain is adopted in Zhang et al. (Reference Zhang, Goerlandt, Kujala and Wang2016), which is a simple and static domain model that cannot reflect dynamic safety distance well. In this section, the uncertainty and consequences associated with ship size issues are analysed. Moreover, an improved ship domain model is applied to calculate safety distance that enhances the risk ranking ability of VCRO.
3.1. Problems associated with VCRO
Due to intensive demand from the oil trade and high volumes of passenger trips, there is a large marine transportation system in the Baltic Sea. Meanwhile, the geography of the area surrounding the Baltic Sea, specifically the Gulf of Finland, is relatively narrow, which causes ship-ship encounters to occur frequently. In previous studies, risk encountered by vessels has been ranked according to VCRO and k-means clustering as shown in Figure 1(a). As indicated in both the figure and reviewed literature, this ranking methodology ignores the ship size difference discussed in Zhang et al. (Reference Zhang, Goerlandt, Kujala and Wang2016).
Figure 1. Ship collision risk analysis in the Northern Baltic Sea in July, 2011. (a) Ship encounter risk analysis (Zhang et al., Reference Zhang, Goerlandt, Montewka and Kujala2015) (b) Ship near-miss encounter with different ship size.
Taking ship size difference into consideration, VCRO shows some obvious differences in the ship encounter scenarios. As shown in Figure 1(b), red spots mark the near-miss encounters with different ship sizes in an area of the northern Baltic Sea in July of 2011, whereas Figure 1(a) shows the marine traffic risk analysis in the same area (Zhang et al., Reference Zhang, Goerlandt, Montewka and Kujala2015). The encounter cases are classified by criteria of identification conditions such as distance less than 0.5 nm, and difference of ship length more than 50 m, which indicates that large differences in ship size often cause differences in risk assessment during certain ship encounter scenarios. The identification conditions are established based on marine traffic statistics in the Baltic Sea and are used to identify the pairs of ships involved in encounters; not included in the data are small operated vessels in ports such as tugs and pilot boats, etc.
Some near-miss encounters are detected according to encounter identification conditions and they are denoted by red spots in Figure 1(b). There are 172 near-miss encounters where the ships involved had vastly different sizes during the July 2011 study period. This shows an apparent difference in risk assessment from the perspective of both ships in a given encounter. As evidenced in Figure 1, these situations are not unusual in maritime traffic. Therefore, analysis and modelling techniques that consider the effect of ship size in ship encounters where the ships involved have vastly different sizes are necessary and meaningful in practice.
3.2. Ship domain consideration in VCRO
Ship domain is considered in VCRO models to calculate safety distance (Zhang et al., Reference Zhang, Goerlandt, Kujala and Wang2016), however the elliptical ship domain model used in the previous model does not account for a dynamic ship domain and is thus less effective in tracking ships' dynamic states. The Kijima and Furukawa model (Kijima and Furukawa, Reference Kijima and Furukawa2003) is thus adopted in this study to represent dynamic ship states.
3.2.1. Ship domain
A ship domain is defined by Goodwin (Reference Goodwin1975) as the area around the vessel which the navigator would like to keep free of other vessels for safety reasons. Usually ship domains can be categorised by their shapes; for example, circular, elliptical and polygonal domains are common (Wang et al., Reference Wang, Meng, Xu and Wang2009). Kijima and Furukawa (Reference Kijima and Furukawa2003) proposed a new ship domain modelled as shown in Figure 2, which is a dynamic ship domain model, and the factors like ship dimensions, manoeuvrability, encounter situations and target ship states are accounted for.
Figure 2. Ship domain according to the Kijima model (Reference Kijima and Furukawa2003). After Wang et al. (Reference Wang, Meng, Xu and Wang2009).
The ship domain has a certain importance for classifying encounters in terms of their severity, as the violation of domains implies a certain proximity which navigators typically want to avoid. Moreover, it should be considered together with other situational characteristics.
In addition, usage of ship domain in ship encounter risk classification is quite limited. In a meeting between ships, the larger ship has the larger domain. This means that for the larger vessel in a given encounter, a situation may be classified as dangerous for the larger vessel, but not for the smaller vessel where the situation may still be evaluated as safe. This issue triggers the problem of risk fusion from a systematic view that is further discussed in Section 4.
3.2.2. Safety distance
Considering that the distance between vessels alone does not describe the complexity of the encounter, the safety distance is defined to describe the distance that the observed ship is away from the safety domain boundary of the observing ship. This definition of distance is used because navigators keep a larger distance between vessels of different sizes, as discussed in Section 3.1.
In the mathematical model, this relation is accounted for by making VCRO inversely proportional to the distance.
$$ VCRO\sim f\!\lpar (x-l_{\alpha})^{-1}\rpar $$
Here x is defined as the distance between the two ships, and l α is defined as the position of the safety domain considering the course difference α of the ships (see Figure 3). The safety domain is estimated via the Kijima and Furukawa model (Wang et al., Reference Wang, Meng, Xu and Wang2009), then
$$\alpha =\arccos \left(\displaystyle{{y_{2}-y_{1}}\over{\sqrt[2]{(x_{2}-x_{1})^{2}+(y_{2}-y_{1})}^{2}}}\right)-\varphi$$
$$\left\{ {\matrix{ {l_\alpha = {\left( {\displaystyle{{1 + {\tan }^2\alpha } \over {\displaystyle{1 \over {S_b^2 }} + \displaystyle{{{\tan }^2\alpha } \over {R_{bf}^2 }}}}} \right)}^{1/2},} & {{\rm if}\;0^\circ \le \varphi _r \le {90}^\circ \;{\rm or}\;{270}^\circ \le \varphi _r < {360}^\circ } \cr {l_\alpha = {\left( {\displaystyle{{1 + {\tan }^2\alpha } \over {\displaystyle{1 \over {S_b^2 }} + \displaystyle{{{\tan }^2\alpha } \over {R_{ba}^2 }}}}} \right)}^{1/2},} & {{\rm if}\;{90}^\circ < \varphi _r < {270}^\circ } \cr } } \right.$$
$$d=x-l_{\alpha }$$
Figure 3. The distance between a pair of ships from the observing ship.
Here, S b is the latitudinal radii of the domain, and R bf , R ba are the longitudinal radii of the areas in the fore and aft domains, respectively.
Finally, the new VCRO equation is improved by taking the dynamic ship domain into consideration (Zhang et al., Reference Zhang, Goerlandt, Kujala and Wang2016):
$$VCRO\sim \lpar (x-l_{\alpha})^{-1},y,g(z)\rpar $$
According to Zhang et al. (Reference Zhang, Goerlandt, Kujala and Wang2016), VCRO can be calculated by
$${VCRO}\lpar \hbox{x,y,z,l} \rpar = \lpar k\cdot(x-l_{\alpha})^{-1}\cdot y\rpar \sum_{i=1}^{\rm n}m_{i}\sin(i\cdot z)$$
where l
α is defined by Equation (5), x is the distance between the two ships, y is the relative speed, and z is the phase. The n value is equal to 17 as decided on by sampling accuracy limitation. The coefficients are calculated and listed in Table 1. The value of k is in an interval mapping to interval of relative speed from zero to maximum that change the range of the ship domain. Let
$\bar{k}$
be the mean of k, then
$\bar{k}=k_{1}$
when
$0^{\circ}\le \alpha \le {90}^{\circ}$
, and
$\bar{k}=k_{2}$
when
${90}^{\circ}<\alpha \le 180^{\circ}$
. α is demonstrated in Figure 3.
Table 1. Coefficient calculation results.
4. SYSTEMATIC RISK ASSESSMENT WITH THE IMPROVED VCRO
4.1. Systematic risk in ship collisions
From Equation (1), we can see that the risk of collision for two ships in an encounter depends on the possibility and consequence of a collision. It is known that the possibility of ship collision can be analysed via indictors that integrate risk-related parameters. Generally, the consequences of ship collisions are influenced by many factors such as speed, size, vessel type, angle and position at which the collision occurred. In this study, the principle of risk research is based on the following fundamental view: the potential vessel conflict risks can be ranked by dynamic state tracking and monitoring based on detecting possible near-miss encounters.
There are different opinions regarding the effect of consequence in encounter risk assessment. Bukhari et al. (Reference Bukhari, Tusseyeva and Kim2013) and Goerlandt et al. (Reference Goerlandt, Montewka, Kuzmin and Kujala2015) describe a belief in which only probability should be accounted for, whereas Mou et al. (Reference Mou, Tak and Van der Ligteringen2010) account for both probability and consequence. In this paper, the encounter scenario studied occurs frequently in waterways, and the latter opinion is adopted. In general, as found by expert interviews reported in Van Iperen (Reference Van Iperen2012), this requires a more extensive contextualisation of the encounter, where other factors such as other traffic in the area, the meteorological conditions and the vessel sizes and types are considered. This is because navigational situations are experienced collectively; that is, navigators interpret the collision risk of many different encounter situations and decide, for each, on the necessity of collision avoidance actions based on the proximity of the interacting vessels, their characteristics and the prevailing geospatial and meteorological conditions (Chauvin and Lardjane, Reference Chauvin and Lardjane2008). The weather and geography factors are beyond the scope of data collection in this study. When crews judge collision risk during ship-ship encounters in the context of a near-miss situation in open sea, the information they can obtain directly and immediately includes ship size and ship type as provided by AIS data (Harati-Mokhtari et al., Reference Harati-Mokhtari, Wall, Brooks and Wang2007). The factors related to ship manoeuvrability, like speed, course, etc., have been included in indicators of collision possibility. Hence, the most relevant factors affecting consequences of collisions from the viewpoint of ship operators are ship size and type. In other words,
$$c_{ab}\sim \{size,type\}$$
From another perspective, it is not sufficient to judge encounter status only via current state since ships are constantly in a dynamic state. When ships are close to one another, VCRO may increase quickly even though the initial value of VCRO is small. That means the collision risk increases rapidly. Meanwhile, when encountered ships keep away, VCRO may decrease rapidly. Although the current VCRO may be large, the actual collision risk decreases rapidly. This means that crews should pay more attention to the encounter scenarios that cause VCRO to incrementally increase. Therefore, it is necessary to define the change rate of system state. Through observing the change rate,
$\Delta VCRO\lpar n\rpar $
, the trend of ship-ship encounters can be monitored, and then one can judge changes in risk development.
As summarised previously, the equation for the risk of ship collision can be expressed as
$$R\sim I\lpar ship_{1},ship_{2}\rpar = \{(VCRO_{ship1}, {VCRO}_{ship2},\Delta VCRO(n))\vert (size,type)\}$$
4.2. Collision risk in ship-ship systems
From previous discussion and Equation (10), three factors should be taken into key consideration, those being the risk perceived by both ships in the encounter, the current state and state change rate, and the ship size and type that are both related to the potential collision consequence. Each of these three key factors are studied in this section, followed by a proposal for a systematic risk assessment method.
4.2.1. VCRO perceived by both ships in an encounter
Difference in ship size is one of the main causes of inconsistency in the judgment of risk. If the two ships in a given encounter have inconsistent judgment regarding the potential collision risk, they may respond and manoeuvre differently, likely resulting in increased risk of collision. This is in part because ships of different size require different ranges in terms of ship domain. This becomes particularly evident when the sizes of ships involved in an encounter are quite different.
Generally speaking, the risk from a systematic viewpoint for two ships of different sizes in a given encounter should be less than the maximum from the perspective of the bigger ship and be greater than the minimum from the perspective of the smaller ship. This is consistent with Equation (10), which determines collision risk according to both collision probability and consequences.
Following the aforementioned general principles, an arithmetic average criterion is suggested for the integration of VCRO as follows:
$${VCRO}_{merge}=\displaystyle{{{VCRO}_{ship1}+{VCRO}_{ship2}}\over{2}}$$
VCRO reflects the near-miss state during ship-ship encounters, and VCRO needs to change constantly because ship-ship encounter situations are in states of dynamic change. Since VCRO may increase or decrease rapidly due to ship proximity, the near-miss collision risk may rapidly increase or decrease accordingly. In addition to considering the current VCRO, one must also consider the change rate from a systematic perspective to determine the ship risk trends which are critical to understanding changes in risk development. This means that crews should pay attention to not only the VCRO value that is related to near-miss collision probability, but also to the VCRO change rate.
Accordingly, the VCRO change rate is defined as:
$$\Delta VCRO(n)=VCRO(T)-VCRO(T-n)$$
Here T is the current time, and n refers to the number of time intervals that have previously passed.
A logical way to classify VCRO change rate is by trend. For example, the VCRO change rate can be classified with five categories, such as fast increase, increase, no change, decrease, and fast decrease. The time unit is minutes according to the AIS data sampling procedure.
Thus, under the conditions of systematic risk, Equation (10) becomes
$$Risk(t)=\{Risk(VCRO_{merge},\Delta VCRO(t))\mid C_{ab}\}$$
4.2.2. Category of ship size
Ship size and type can be derived from AIS data. In this study, the influence of ship pair size difference is given more careful consideration. The vessel size dimensions of the ships navigating in the Northern Baltic Sea considered in this study's dataset are extracted and clustered. Table 1 shows the results in May and June of 2011. The total number of ships is 1576, not including tugs and pilot vessels that operated solely in ports, as well as passenger vessels with length less than 35 metres. The statistical results of the clustering procedure with K-means method (Hartigan and Wong, Reference Hartigan and Wong1979) indicate the ships can be divided into three categories as follows: large, medium, and small.
Based on Table 2, the ship pair involved in the encounter can be classified as small-small, small-medium, small-large, medium-medium, medium-large, and large-large. The information on ship pair size can be used to judge the degree of severity of a potential ship-ship collision.
Table 2. Ship size clustering results (Zhang et al., Reference Zhang, Goerlandt, Kujala and Wang2016).
4.2.3. Risk assessment and fuzzy logic
In considering the following three key factors, the risk perspective from both ships in the encounter, the current state and state change rate, and the ship size and type that are related to potential collision consequence, an assessment framework and method are proposed to assess ship-ship collision risk in a systematic way.
In the process of risk judgment, knowledge from experts is usually necessary to assess risk appropriately according to VCRO and the change rate of VCRO, as well as the ship types and sizes of those in the encounter. Fuzzy logic is a suitable method to replicate this expert knowledge system. In this paper, fuzzy logic is used to judge collision risk by considering various risk factors as a means to replicate knowledge and judgment from expert opinion. The risk assessment framework is shown in Figure 4.
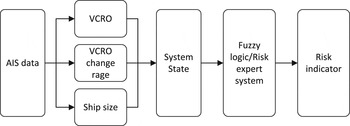
Figure 4. Risk assessment framework.
Fuzzy rules are the key for establishing fuzzy models. Fuzzy rules can be obtained from human experts who are not objective and reliably consistent at all times. The approach of data-driven construction of fuzzy rules has been proposed in some past studies (Goerlandt and Montewka, Reference Goerlandt and Montewka2015a; Setnes, Reference Setnes2000).
Following the data-driven fuzzy rule extraction approach, some parameters, such as ship size and type, can be classified with fuzzy clustering methods (Hartigan and Wong, Reference Hartigan and Wong1979) and then fuzzy classification results can be obtained in the following steps. Based on Equations (10) and (12), in the fuzzy rules, the antecedents consist of the factors of merged VCRO, VCRO change rate, and size of the ships in the encounter. Following these methods, fuzzy rules can be extracted from data by means of fuzzy clustering in the product space of inputs and outputs where each cluster corresponds to a fuzzy IF-THEN rule in Takagi-Sugeno (TS) fuzzy model,
$$R_{i}:IF\ {VCRO}_{merge}\ {is}\ A_{i1}, \Delta VCRO\ {is} A_{i2},{Size}_{shippair}\ {is}\ A_{i3},\ THEN\ risk\ is\ a_{i}^{T}X+b_{i}$$
X is defined as
${\lsqb VCRO}_{merge}\comma \; \Delta VCRO\comma \; {Size}_{shippair}\rsqb $
. The risk category is divided into five levels, which are: no conflict severity, low conflict severity, medium conflict severity, high conflict severity, and highest conflict severity. Then the factors merged VCRO, VCRO change rate, size of ships in the encounter, risk category of VCRO and corresponding risk categories can be classified using a fuzzy clustering method, and the corresponding fuzzy partition is achieved to construct the fuzzy rules.
5. CASE STUDY AND DISCUSSION
In this section, one typical case of ship encounters involving ships of different sizes is analysed. As mentioned earlier, many studies ignored the situation of ship-ship encounters involving ships of very different sizes. The example shown in Figures 5(a) and 5(b) demonstrates such a situation of a ship-ship encounter. During the encounter, both ships judge risk differently.
Figure 5. Case 1 - differences between models by considering safety domain.
In Figures 5(a) and 5(b), an encounter scenario detected in AIS data from July 2011 in the Northern Baltic Sea area is selected from the database of encounters (Zhang et al., Reference Zhang, Goerlandt, Montewka and Kujala2015), and their resulting VCRO values are calculated. Each encounter is described in eight sub-figures in order of the trajectories of the vessels, Safety Distance, Relative Speed, and Phase, in Figure 5(a); VCRO in the first ship, VCRO in the second ship, VCRO in the old model, and VCRO in the new model proposed in this paper, Figure 5(b). The trajectories of the vessels engaged in the encounter are shown, where the ‘x’ indicates the starting locations of each vessel, the ‘o’ indicates their final location, and the red ‘*’ indicates the location at which the ships have the minimum distance from each other. The curve composed of the ‘x’ symbols signifies the trajectory of the first ship, and the curve composed of the ‘+’ symbols shows the trajectory of the second ship.
In Figure 5, the two vessels considered are as follows: IMO9299898 is a crude oil tanker from Greece with a length of 249 metres and IMO8603547 is a general cargo vessel with a length of 104 metres. These ships are interacting in a crossing encounter where one vessel maintains course and speed while the other performs a course change, obviously taking place after the encounter. According to Equations (11) and (13),
$$\eqalign{ {VCR}_{Ship1}^{max} &=\max \lcub {VCRO}\lpar t,ship1 \rpar \rcub =791, \cr {VCRO}_{Ship2}^{max} & =\max \lcub {VCRO}\lpar t,ship2 \rpar \rcub =95, \cr {VCRO}_{merge}^{max} =\max \lcub {merge}\lpar & {VCRO}\lpar t,ship1\rpar , {VCRO}\lpar t,ship2 \rpar \rpar \rcub =443, \cr {VCRO}_{old}^{max} &=\max \lcub {VCRO}_{old}(t) \rcub =101.} $$
The old model indicates the VCRO is 101 for both ships, whereas the new model indicates a VCRO value of 791 for IMO9299898, and 95 for IMO8603547. The merged VCRO is 443. The minimum passing distance during the encounter is −0·056 NM, which is less than the safety domain for IMO9299898.
The distance is calculated based on ship domain defined as safety distance, which indicates the distance between one ship and the safety domain border of the other ship. A negative value means the ship is in the safety domain of the other ship.
Obviously, both vessels are aware of the risk during the encounter as can be seen from the course change after the encounter and the small minimum distance. Meanwhile, the VCRO from one ship is likely too large or too small. A VCRO of 93 means the risk in the encounter is not severe at all, even if the other vessel is a tanker, but a VCRO of 798 means the encounter is severe in risk and an evasive manoeuvre is mandatory. From the trajectories of both vessels, the merged VCRO of 233 means the encounter does involve risk to which high attention must be paid.
The preceding analysis is only focused on the moment where the occurrence of the risk is largest, but there is no investigation of dynamic risk changes, and analysis of risk trends are also absent. In fact, during the process of a ship-ship encounter, risk assessment is continuously performed. According to Equation (12), time series of VCRO change rates can be calculated as shown in Table 3.
Table 3. Time series of VCRO change rates during ship-ship encounter.
Fuzzy rules of risk assessment can be established based on the statistics of a large number of ship-ship encounters. In general, the three parameters, VCRO, VCRO change rate and ship pair size, can be classified as corresponding categories shown in Table 4 that refer to the classification of Zhang et al. (Reference Zhang, Goerlandt, Kujala and Wang2016).
Table 4. Parameter category.
The fuzzy rules can be established from fuzzy clustering analysis such as fuzzy k-means method together with expert knowledge (Tang et al., Reference Tang, Liu, Zou, Zhang and Wang2017). With a fixed number of categories, the fuzzy rule extraction process can be simplified and ignore the procedure of clusters merging.
Fuzzy classification of VCRO, VCRO change rate and ship pair size are shown in Figure 6. Through statistical procedures and classification of encounter scenarios in the Baltic Sea, some fuzzy rules to assess near-miss risk are acquired, and some of them are shown in Table 5.
Figure 6. Fuzzy clustering of parameters.
Table 5. Example of fuzzy rules for risk classification.
According to these fuzzy rules, the risk of processes in Table 3 can be tracked by Table 6.
Table 6. Risk assessment during ship-ship encounter.
Thus, through monitoring dynamic changes in ship-ship encounter, the details of changes in risk can be tracked and analysed. This overcomes the disadvantages of the prior VCRO that only considers the maximum value from which it is difficult to track and judge the risk trend.
Overall, through the risk classification model established in this paper, the risk state can be monitored systematically. As a result, a systematic approach is proposed to assess ship-ship encounter near-miss risk more effectively. Moreover, the new VCRO proposed here is more reasonable than the previous VCROs because the size of ship is taken into consideration. Therefore the new method can indicate cases where the distance between ships is shorter than the ship domain. The VCRO of two vessels in a given encounter may be different because the different ship sizes will affect the respective ship domain range and hence the safety distances. In judging the encounter severity, it is necessary to merge both VCRO values, a consideration which is well-handled by the new VCRO model.
6. CONCLUSIONS
This article discusses the mechanism of marine traffic safety and its application in scenarios of ship-ship encounters. The risk of encountered ships from a systematic perspective is studied in this article based on the consideration of a ship-ship encounter as a system composed of both ships in that encounter. As a result, a systematic risk assessment framework and a method for integrating risks is proposed, which overcomes the disadvantages of the prior VCRO that only considers the maximum value from which it is difficult to track and judge the risk trend. To validate the proposed models, a case study considering ship near-miss encounters involving ships of different sizes in the northern Baltic Sea was conducted. The case study analysis shows that the problem studied in this paper is quite common in practice. In terms of validation, more cases linking VCRO with risk of collision are expected to be performed in future research.
Although ship type is classified as one of the main factors in a risk assessment, the effect of ship type on safety has not been researched in depth here as it is beyond the scope of this study. In future study, the application of the proposed method is necessary to enhance the capability of risk assessment by collecting more data such as ship size and type on ship encounter scenarios in practice.
ACKNOWLEDGEMENTS
The authors would like to acknowledge the National Natural Science Foundation of China (Grant nos. 51138003, 51329801), and Hi-Tech Research and Development Program of China (Grant no. 2014BAG03B04) for financial supporting to this research.
