Hostname: page-component-745bb68f8f-lrblm Total loading time: 0 Render date: 2025-02-06T08:11:37.133Z Has data issue: false hasContentIssue false
  • English
  • Français

Ship's Fuzzy Domain – a Criterion for Navigational Safety in Narrow Fairways

Published online by Cambridge University Press:  26 June 2008

Zbigniew Pietrzykowski
Zbigniew Pietrzykowski*
Affiliation:
(Maritime University of Szczecin)
*
(Email: z.pietrzykowski@am.szczecin.pl)
Rights & Permissions [Opens in a new window]

Abstract

The concept of ship's domain plays an important role in navigating a ship. It is a criterion of safety in the process of making decisions by the navigator – in analyzing and assessing a navigational situation and in performing the right manoeuvre. This concept is particularly useful in restricted areas, including narrow fairways, which results from the fact that in such waters a manoeuvring area is restricted so that the criterion of the closest point of approach (CPA) cannot be used. This author has analyzed definitions of ship's domain and methods of its determination found in the literature on the subject. Then a method of navigational safety assessment using the fuzzy domain concept is proposed in reference to a ship in a restricted area. The concept and method of determination have been, respectively, defined and described. The method is based on relevant navigators' knowledge. The methods and tools for knowledge acquisition and representation make use of artificial intelligence. Ships and navigational areas of various size have been considered.

Keywords

Navigational safetyShip's domainRestricted area
Type
Research Article
Information
The Journal of Navigation , Volume 61 , Issue 3 , July 2008 , pp. 499 - 514
Copyright
Copyright © The Royal Institute of Navigation 2008

1. INTRODUCTION

The concept of ship's domain has been used in marine traffic engineering since the 1960s. By using the ship's domain we can quickly identify and assess a navigational situation, which translates into supporting and working out navigational decisions. This refers to both restricted and open sea areas.

A restricted (confined) water area is often defined as a water area in which the wave system generated by a vessel moving full-ahead is disturbed. What happens in a restricted area is that a ship often cannot choose a route freely. It has to comply strictly with safety regulations and take into account local conditions (restriction of one of the three dimensions determining the ship's distance to other objects).

The restrictions of a manoeuvring area make the criterion of the closest point of approach (CPA), applicable in collision avoidance systems, difficult to use. The criterion of ship's domain may be an alternative to CPA in assessing navigational safety. The factors considered while assessing a navigational situation, therefore affecting the shape and size of ship's domain, are as follows:

  • • ship size,

  • • ship's manoeuvring characteristics,

  • • parameters of the area the ship is manoeuvring in,

  • • hydrological and meteorological conditions,

  • • ship's speed and relative speeds of other ships,

  • • traffic intensity in an area,

  • • accuracy of position determination,

  • • level of training, knowledge and experience of navigators.

The variety of factors affecting the shape and size of ship's domain make the latter difficult to determine. Therefore, it is important to utilize the competencies and experience of navigators. The domains and methods of their determination proposed by various authors differ from one another, as the various factors affecting navigational safety are taken into account to varying extent.

2. SHIP'S DOMAIN

Some of the most common definitions of the ship's domain have been given by Fuji (Fuji, Reference Fujii and Tanaka1971), Goodwin (Goodwin, Reference Goodwin1975) and Coldwell (Coldwell, Reference Coldwell1983). The ship's domain by Fuji: “Most of the navigators of the following ships avoid entering the surrounding domain of the fore-going ship”. The ship's domain by Goodwin: “The surrounding effective waters which the navigator of a ship wants to keep clear of others ships or fixed objects”. The ship's domain by Coldwell: “The surrounding effective waters which the typical navigator actually keeps clear, considering the existence of other ships”.

It is interesting how Zhao (Zhao, Wu, Wang, Reference Zhao, Wu and Wang1993) comments on these definitions. He notes that “they all refer to a water area around a vessel which is needed to ensure the safety of navigation and to avoid collision”. It is worthy of note that the concept of domain is understood, directly or indirectly, as an ‘effective’ area around a ship that the navigator maintains clear of other objects. We can therefore claim that the quoted authors define an effective domain. Its shape and size is determined by the officer of the watch who considers a number of factors (ship's speed and length, sea area, traffic density, etc.). This means the domain boundary varies depending on a current navigational situation. Such a domain may be referred to as the dynamic domain. Entering the ship's domain is interpreted as a threat to navigational safety. This attitude is equivalent with adopting a two-step classification of a navigational situation.

To sum up, let us say that the analyzed definitions of the domain refer to the effective and dynamic domain, one that allows us to evaluate a navigational situation on a two class scale. The basic problem is to define the crisp domain boundary, dividing the area around a ship into dangerous and safe areas.

2.1. Domain shape and size

The ship's domain (DS) is determined by its boundary B DS. Two- and three-dimensional domains are proposed in the literature. The former define an area around the ship. Two-dimensional domains can be circular, rectangular, elliptical, polygonal or other more complex 2D figures. Three-dimensional domains include ship's draft and air draft (ship's height above its waterline). These most often have a shape of a sphere, ellipsoid or cuboid.

Two-dimensional domains have been considered here. Assuming a specific level of discretization of relative bearing (e.g. Δ∠K=1°), we can describe the ship's domain boundary B DS by a curve passing through n points p Di (i=1, 2, … , n), lying on the relative bearings ∠K i at distances d DSKi from the centre of the ship (e.g. centre of the waterplane):

(1)
B_{DS} \equals \lcub p_{D\setnum{1}} \comma p_{D\setnum{2}} \comma \ldots \comma p_{Dn} \rcub

The size of ship's domain DS on particular relative bearings is then described as follows:

(2)
D_{S} \lpar \angle K_{i} \rpar \les d_{DSKi} \quad i \equals 1\comma 2\comma \ldots \comma n

It is essential to know which method for the determination of domain boundary is adopted. This refers to the shape and size of the domain as well as its interpretation.

2.2. Methods of Ship's Domain Determination

Three groups of methods for ship's domain determination can be distinguished: statistical, analytical and artificial intelligence. All the three types share one feature: they tend to utilize navigators' knowledge, both procedural and declarative. These methods have various forms: facts (statistical methods), theories from various disciplines (analytical methods) rules, decision trees, fuzzy inference systems or artificial neural networks that are taught from a set of gathered data (artificial intelligence methods).

Originally, statistical methods were used for determining a ship's domain. In such methods, ships' positions and movement trajectories are registered, and an area around the ship that navigators maintain clear of other navigational objects is determined. The domain boundary is defined by Fuji and Coldwell as the distance from the central ship at which the density of passing ships reaches a local maximum value. The domain boundary by Goodwin is defined as a distance at which the total number of ships is smaller then the number would be if the domain did not exist.

In reference to the three definitions above, we can consider the effective domain, i.e. an area that the navigator keeps clear of other objects. These objects are other vessels of various size or stationary objects. This is a basis enabling the approximation of the domain shape to a two-dimensional figure by applying analytical formulas. For example, in (Zhao, Wu, Wang, Reference Zhao, Wu and Wang1993) the domain has the shape of an ellipsis described with lengths of its major and minor axes.

Analytical methods are based on an analytical description of domain boundaries as a function of variables describing a given ship (central ship) and other objects. These methods enable the consideration of selected factors affecting navigational safety. These factors include, among others, geometrical dimensions, speeds or/and relative speeds of other vessels. The work (Wawruch, R, Reference Wawruch1998) presents an analytical description of domain size for rectangular and elliptical domains:- their dynamical length and width. The approach has been modified with a concept of relative domain for a target vessel, proposed in (Smierzchalski, R, Weintrit, A., Reference Smierzchalski and Weintrit1999). Based on the determined dynamical length and width of a ship, its hexagonal domain is defined for a ship' speed or relative speed.

The formulated analytical formulas have been justified by kinematical and dynamical properties of objects, regulations in force and the principles of good sea practice. We can assume that in the case of analytical methods the effective domain is also determined, understood as an area around the ship that the navigator keeps clear of other objects.

Methods of artificial intelligence (AI) are very useful and effective in representing the declarative – descriptive knowledge of navigators that results from their competence and experience. These methods are aimed at the acquisition and use of experts' knowledge by using adequate tools. Among artificial intelligence tools in use most commonly mentioned are fuzzy logic, artificial neural networks and evolutionary algorithms.

One of the first applications of fuzzy logic in a decision model for ship encounter situations was included in the work of James (James, Reference James1986). That study did not directly refer to the problem of ship domain determination. It presented a description of a decision process that aimed at collision avoidance through the defining of an objective function and constraints in the form of fuzzy sets. These sets were “safe” passing distance and “small” course change, represented by membership functions μG and μC. The arguments were, respectively, values of passing distance and the shift of the ship movement trajectory relative to the original one (trajectory before the manoeuvre), considered as a course change. The membership function values determined in the 0 to 1 interval the degree of argument membership (distances) to fuzzy sets “safe” passing distance and “small” course change. On this basis it was possible to work out a decision on a manoeuvre in a manner corresponding to a navigator's reasoning and behaviour.

Zhao (Zhao, Wu, Wang, Reference Zhao, Wu and Wang1993) proposed a definition of ship domain using the theory of fuzzy sets. His proposal introduced a ship fuzzy domain boundary. This determines an area defined by ship domain and a line with points for which the function of membership to the set “safe distance” is 0·5. It was assumed that only if the area defined by the ship fuzzy domain boundary were to be interrupted, would the navigator's action be necessary.

3. SHIP FUZZY DOMAIN

James' and Zhao's concepts were developed in (Pietrzykowski, Reference Pietrzykowski1999, Reference Pietrzykowski2002). The “classical” definition of ship domain adopts the classification into two zones: dangerous and safe – ship domain and the area outside it. It is characteristic of the human being that s/he distinguishes a larger number of zones that are expressed in linguistic terms: safe, less safe, dangerous etc. Depending on the situation the human tries to maintain a selected zone clear of other objects. Similarly, depending on the situation, the navigator steering a ship attempts to keep the ship in an area that has a preset level of navigational danger (safety) and is supposed to be clear of other objects.

3.1. Definition of Ship Fuzzy Domain

The ship fuzzy domain is defined as an area around a ship which the navigator of the ship should maintain clear of other vessels and objects, the shape and size of which depend on an adopted level of navigational safety, understood as a degree of membership of a navigational situation to the fuzzy set ‘dangerous navigation’.

According to the definition of a fuzzy set, the ship fuzzy domain D SF on the relative bearing ∠K i is described as follows:

(3)
D_{SFKi} \equals \lcub \mu _{{DSFKi}} \lpar d_{Ki} \rpar \comma d_{Ki} \rcub

where:

d Ki – 

distance from ship waterplane centre; d Ki∊〈0, ∝) [m]

μDSFKi – 

function of membership to the set “dangerous navigation” on the relative bearing ∠K i; μDSFKi∊〈0, 1〉

Assuming that the ship fuzzy domain D SF on the relative bearing ∠K i is described by the membership function μDSFKi, we can express the navigational safety level γ in a situation when the other object is on this heading at a distance d Ki by this formula:

(4)
\gamma \equals \mu _{DSFKi} \lpar d_{Ki} \rpar

Graphically, an interpretation of the ship fuzzy domain is illustrated in Figure 1.

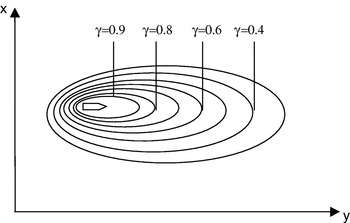
Figure 1. Ship fuzzy domain; domain boundaries for various levels of navigational safety γ. (γ∊<0, 1>); γ=0 – very safe situation; γ=1 – very dangerous situation (collision).

Considering the above, we can state that the presented definition of fuzzy domain:

  • • is in accordance with previously presented definitions, i.e. it defines an area around the ship that should be clear of other objects,

  • • extends previous definitions of the domain by taking into consideration various values of navigational safety (multi-degree scale) that may be attributed linguistic terms such as very dangerous, dangerous, safe, very safe etc.,

  • • does not describe the effective domain, because it describes an area that the navigator wishes to maintain clear of other objects depending on the accepted level of safety,

  • • describes the dynamical domain.

Thus the determined fuzzy domain makes up a criterion for assessment of a navigational situation, the criterion that enables continuous assessment of the situation (level of safety is described by the degree of membership to the fuzzy set “dangerous navigation”), i.e. also the trend of safety level change.

For a decision maker the relation between the fuzzy domain and the effective domain is important. If we consider the process of making decisions concerning ship movement control by the navigator as formulated by James, the objective function is described by a fuzzy domain, while its constraint is “small course change”. This means that the effective domain is a compromise between the defined goal, i.e. safe passing of another object, and the mentioned constraint.

The basis for defining a ship fuzzy domain is the representation of navigators' knowledge that enables the determination of a navigational safety level for any navigational situation.

3.2. The Level of Ship's Navigational Safety in Narrow Fairway

The assessment of a situation that may result in identifying it as dangerous is related with the determination of navigational safety level – the value of navigational safety measure. The measure can have the form of this functional:

(5)
P \equals F\lpar B\comma R\comma S\comma M\rpar

where:

B – 

area parameters,

R – 

vessel parameters,

S – 

parameters of position determination system,

M – 

environmental parameters.

The works (Pietrzykowski, Reference Pietrzykowski1997), (Pietrzykowski, Dubowik, Reference Pietrzykowski and Dubowik1998), (Dziedzic, Pietrzykowski, Uriasz, Reference Dziedzic, Pietrzykowski and Uriasz2000). (Pietrzykowski, Uriasz, Reference Pietrzykowski and Uriasz2003), proposed a method of determining navigational safety level based on the representation of expert navigators' knowledge, using artificial neural networks with fuzzy logic. These networks make up a universal approximating system, representing multi-dimensional data sets, with capabilities of learning and adapting to changing environmental conditions. After the learning process, they allow assessment of a navigational situation with the criteria used by navigators.

Learning data are facts gathered during expert research (simulation and questionnaires): parameters characterizing a navigational situation (such as ship state vector parameters) and the assessments of navigational safety of registered situations.

The network was tasked to execute the representation (Figure 2)

(6)
\gamma \equals f\lpar \Delta y\comma \Delta \phi \comma \omega \rpar

where:

Δy – 

distance to the fairway axis

Δφ – 

deviation from the preset course defined by the fairway axis

ω=

rate of turn

Figure 2. An illustration of a ship moving in a restricted area.

The research carried out made use of a ship handling simulator NMS90, and was supplemented with expert studies, in which the assessments of navigational situations performed by navigators were recorded during simulated ship movements. The following simulation conditions were adopted:

  • • the ship was handled by the rudder, no engine or thruster was used,

  • • environmental conditions were very good (good visibility, no current or wind, no waves)

  • • ship's speed was 7 to 8 knots.

The observers – navigators – were assessing a navigational situation with their own individual criteria, at 10 seconds intervals, using the 0 to 10 scale:

  • • 0 was attributed to a very safe situation,

  • • 10 was attributed to a very dangerous situation.

During the simulation all parameters of ship movement were automatically recorded, including the deviation from the fairway axis Δφ, the distance to the fairway axis Δy and the ship's rate of turn ω. Negative values of these parameters represented, respectively, deviation to port from the course defined by the fairway axis, going to port of the fairway axis and the rate of anticlockwise turn. Then the assessments were standardized to the [0, 1] interval.

The above mentioned network was used for navigational safety assessment. The process of learning of the neural network with fuzzy logic was performed. The values of network response make up a measure of navigational danger level γ. For the assumed evaluation interval<0, 1>the 0 value denotes a high level of navigational safety – (very) safe situation, while the value 1 denotes a very dangerous situation (collision).

Figure 3 shows the values of navigational safety γ for the bulk carrier “Freight”, 95·5 m long, 18·2 m in breadth, draft 5·5 m, proceeding in a restricted area at 8 knots and the present rate of turn ω equalling −5°/min, depending on the distance to the fairway axis and the deviation from the preset course. This provides a basis for the determination of areas around the ship that have a preset level of navigational safety – ship fuzzy domain.

Figure 3. Values of navigational safety level for the m/s “Freight” (ω=−5 o/min); Δφ – deviation from the from the preset course; Δy – distance to the fairway axis.

3.3. The Method of Determining a Ship Fuzzy Domain in a Narrow Fairway

Areas of a ship fuzzy domain with a preset navigational safety level in the case of a straight fairway section are determined by respective half planes, constrained by a straight boundary line, containing the ship's centre of gravity (Pietrzykowski, Reference Pietrzykowski2002). (See Figure 4).

Figure 4. Navigational situations within a straight fairway section a) situation (1); b) situation (2); c) superimposed situations (1) and (2).

At a preset distance between the fairway centre line and its limit x o and for an assumed navigational safety level γ=μγ(Δy, Δφ), the mentioned half planes are bounded by the straight lines:

(7)
\eqalign{ \tab l_{\setnum{1}} \minus {\rm for\ a\ navigational\ situation\ }\lpar 1\rpar \colon \ \Delta _{y\setnum{1}} \equals x_{\setnum{1}} \minus x_{\setnum{0}}, \rmDelta _{\phi \setnum{1}} \equals \alpha_{\setnum{1}} \cr \tab l_{\setnum{2}} \minus {\rm for\ a\ navigational\ situation\ }\lpar 2\rpar \colon \ \Delta _{y\setnum{2}} \equals x_{\setnum{2}} \minus x_{\setnum{0}}, \rmDelta _{\phi \setnum{2}} {\rm \equals \ }\alpha_{\setnum{2}} \cr}

The half plane bounded by the straight line li, containing the ship's centre of gravity is denoted as lĩ. To illustrate the ship fuzzy domain, the Cartesian system was adopted as a reference system, with its origin at the ship's gravity centre. If we consider n half lanes lĩ for the safety level γ, part of the ship fuzzy domain D RSγ in the IV-th quarter of the coordinate system is described by this relation:

(8)
D_{{RS}\gamma }^{IV} \equals \bigcap\limits_{i \equals \setnum{1}}^{n} {l_{\tilde{i}}}

Making similar steps for the other quarters, we can determine, respectively, partial domains D RSγI, D RSγII, D RSγIII. Therefore, the ship fuzzy domain for the safety level γ is expressed by this formula:

(9)
D_{{RS}\gamma } \equals \bigcap\limits_{j \equals \setnum{1}}^{\setnum{4}} {D_{\hskip-1{RS}\gamma }^{\hskip1j} } \equals \bigcap\limits_{i_{j} \equals \setnum{1}}^{n_{j} } {l_{i_{j} }^{\sim}}

where:

l_{i_{j} }^{\sim}  – 

i-th half plane of the quarter j,

n j  – 

number of half planes of the quarter j.

This presented method enables the determination of a ship's fuzzy domain for a given level of navigational safety. With ship's rate of turn (ROT) taken into account, we can determine the dynamical fuzzy domain whose shape and size are significantly affected by the ROT.

3.4. Ship Fuzzy Domain in a Narrow Fairway

From the author's research data the fuzzy domain of the bulk carrier m/s Freight was determined. Figures 5a and 5b show, respectively, straight lines bounding the area of fuzzy domain D RSγIV of that ship and the fuzzy domain D RSγ for navigational safety level γ=0·7.

Figure 5. Fuzzy domain of the bulk carrier m/s Freight (rate of turn ω=0°/min):a) straight lines bounding the area of fuzzy domain D 0,7IV; b) ship fuzzy domain D RS0,7.

Similarly, the fuzzy domain for different navigational levels can be defined (Figure 6a). The ship's rate of turn can also be considered, which for navigation in a restricted area is very important. The effect of rate of turn on the shape and size of the fuzzy domain is depicted in Figure 6b.

Figure 6. Fuzzy domain of the m/s Freight proceeding along a straight fairway section: a) for the rate of turn ω=0°/min and navigational safety level γ=0·3, 0·5, 0·7, 0·9; b) for the navigational safety level γ=0·9 (the rate of turn: 0 and 50°/min).

To sum up, it can be said that a ship fuzzy domain is a dynamical domain describing areas around the ship that the navigator wants to keep clear of other objects, depending on the adopted level of navigational safety.

4. ANALYSIS OF THE FUZZY DOMAIN

The fuzzy domain of the m/s Freight was examined for various levels of navigational safety (Pietrzykowski, Reference Pietrzykowski2002). The detailed analysis included:

  • • domain boundaries – distances from the ship's centre of the waterline to fuzzy domain boundaries for various values of navigational safety γ=0·2, 0·3, … 0·9 on all relative bearings at 10° discretization steps (see Figure 7),

  • • domain areas; to this end the forward and aft parts were identified – from abeam to, respectively, the bow and stern of the ship.

Figure. 7. Ship fuzzy domain for various relative bearings ∠K and navigational safety γ=0·5.

4.1. Fuzzy Domain Boundaries

In order to analyze the boundaries of ship fuzzy domain for various levels of navigational safety γ the regression analysis was applied:

(10)
y \equals ln\lpar d_{j} \lpar \gamma \rpar \rpar \equals a_{j} \plus b_{j} x

where:

d j(γ) – 

distances of a fuzzy boundary of ship domain for various levels of safety γ on the j-th relative bearing.

From the results obtained we can say there are no grounds to reject the hypothesis on the exponential regression between the values of navigational safety and distances from the corresponding fuzzy domain boundaries for all examined relative bearings.

Figure 8 shows the results of model estimation for relative bearings −90° and +90° (port and starboard beam) and the adopted confidence level 95%. This proves that the navigators used the logarithmic scale while estimating navigational safety and reflects the decision making process analysis performed in the works (James, Reference James1986, Reference James1993). This is important for the improvement of fuzzy domain determination if various ships and various environmental conditions are to be considered.

Figure 8. Regression model for relative bearings ∠K j: a) −90°; b) +90°.

4.2. Fuzzy Domain Area

The size of the fuzzy domain for various navigational safety values were similarly examined. The areas analysed were those of the whole fuzzy domain (1) and its two parts ahead of the beam (2) and two parts astern of the beam (3) (Figure 9). Table 1. gives the results of the regression analysis for the model in this form:

(11)
y \equals ln\lpar p_{k} \lpar \gamma \rpar \rpar \equals a_{k} \plus b_{k} x\quad k \equals 1\comma 2\comma 3

where:

p k(γ) – 

area of the ship fuzzy domain for various navigational levels γ;

k=1 – 

whole domain; k=2 – forward domain; k=3 – aft domain.

Figure 9. The area of a fuzzy domain for various values of safety level γ=0·2; 0·3; … 0·9.

Table 1. Correlation coefficients and estimated parameters of the linear regression for the forward, aft and whole domains.

From the results obtained we can say there are no grounds to reject the hypothesis on the exponential regression between the values of navigational safety and the areas of fuzzy domain: its forward and aft parts and the whole domain. The results obtained confirm the fact that a human being uses the logarithmic scale while assessing the safety level. The relation between safety level and domain size has been found to be noticeable. The observed relation may facilitate the process of fuzzy domain determination and verification.

The results obtained using the knowledge extracted from expert navigators confirm that the method used was the right one and they bring closer the principles of safety level estimation in the process of decision making by navigators.

5. EFFECT OF SHIP AND AREA PARAMETERS ON THE SHAPE AND SIZE OF THE SHIP FUZZY DOMAIN

The manoeuvre examined was performed in a narrow passage by a ship with length overall 156·68 m, breadth 24·0 m and draft 9·30 m, proceeding at 7 to 8 knots. The parameters of two areas are given in Table 2. Simulated conditions were those described in section 3·3.

Table 2. Area parameters.

5.1. Effect of Area Parameters on the Shape and Size of the Ship Fuzzy Domain

Research was done to acquire the navigators' knowledge used in assessing a navigational situation in which a ship proceeds in a restricted area.

Artificial neural networks with fuzzy logic were used for the representation of that knowledge. Thus it was possible to determine the navigational safety level for various situations of a ship moving within the examined areas (Figure 10). Then fuzzy domains of the examined ship were determined in areas 1 and 2 (Figure 11).

Figure 10. Assessment of navigational safety level for various ship's deviations from the fairway centre line and shifts from the preset course: a) area 1; b) area 2.

Figure 11. Ship fuzzy domain for various navigational safety levels γ: a) restricted area 1; b) restricted area 2.

In the case of a fairway 100 metres in width it was possible to determine fuzzy domains for navigational safety γ in the range 〈0·3, 0·9〉, while for a fairway 200 metres wide the range was 〈0·2, 0·9〉.

The comparison of the domains shows that the criteria of situation assessment were changed. The change, in fact, consisted of adjusting the shape and size of the fuzzy domain to the size of the area. Consequently, the domain size was reduced because the area width was smaller.

The lengths and widths of a fuzzy domain for various safety levels are presented in Figure 12. The results again provide no basis to reject the hypothesis on exponential regression between the values of navigational safety and lengths and widths of ship fuzzy domains in both examined areas. The domain areas were also examined for various levels of navigational safety γ=0·2, 0·3, … 0·9 (Figure. 13). As for the domain lengths and widths, also here no grounds were found to reject the hypothesis on exponential regression (11) between the values of safety level and the areas of ship fuzzy domain in both sailing areas.

Figure 12. Lengths and widths of ship fuzzy domain for various values of navigational safety γ in areas 1 and 2: a) length; b) width.

Figure 13. Areas of ship fuzzy domain for various values of navigational safety γ in restricted areas 1 and 2.

5.2. Effect of ship parameters on the shape and size of the ship fuzzy domain

The simulation and expert research previously described allowed a comparison of the effect of ship size on the shape and size of the domain. To this end the above mentioned ships moving within a 200 metre wide area were considered (see Table 2, area 2). The ships' parameters are given in Table 3. Figure 14 depicts the lengths and widths of a fuzzy domain of both ships for various levels of navigational safety. Figure 15 presents graphs representing the domains of both ships for various navigational levels.

Figure 14. Lengths and widths of a fuzzy domain of ships for various values of navigational safety γ in a restricted area 2 with a width of 200 metres: a) domain length; b) domain width.

Figure 15. Areas of ship fuzzy domain for various levels of navigational safety γ in a restricted area 2 with a width of 200 metres.

Table 3. Ships' parameters.

6. CONCLUSIONS

This article deals with possibilities of assessing ship's navigational safety with the use of a fuzzy domain. The concept of ship fuzzy domain has been defined. The method for the determination of ship fuzzy domain in a restricted area has been presented. In order to determine a ship fuzzy domain, first navigators' knowledge, indispensable for identification and assessment of a navigational situation, has to be acquired and represented.

Navigators' knowledge can be acquired through expert research. Artificial neural networks with fuzzy logic offer tools for the representation of such knowledge. These networks are capable of learning and make up a universal approximating tool for functions with many variables. After the learning process, they make it possible to assess a situation according to criteria used by navigators. The transformation of a simple representation of the network response into the domain display enables fast interpretation of a navigational situation, which may improve the process of decision making.

The determined ship fuzzy domain is a dynamical domain and it describes the areas around a ship that the navigator wants to maintain clear of other objects, depending on the adopted level of navigational safety. The presented fuzzy domain of a ship takes into consideration criteria for assessing a navigational situation that are used by navigators and that significantly affect the shape and size of an area around the ship that should be clear of other objects.

The proposed method of the determination of ship fuzzy domain in a restricted area allows the consideration of ship and sailing area parameters which affect the shape and size of the domain. It is also possible to take into account the parameters of ship state vector (e.g. turn of rate).

The results shown confirm the fact that the human being uses the logarithmic scale while assessing navigational safety level. A clear relation has been found between safety level and domain size. This may facilitate the process of fuzzy domain determination and verification for ships of various size in restricted areas of different width.

The fuzzy domain can be used for supporting decisions made by navigators. In the process of decision making aimed at ship movement control, the navigator takes into consideration specific goals and constraints. The fuzzy domain describes an objective (safety criterion) that, with existing constraints, allows to formulate an optimization task: determination of ship movement trajectory according to criteria used by navigators.

References

REFERENCES

Coldwell, T. G. (1983). Marine traffic behaviour in restricted waters. The Journal of Navigation, 36, 430–444.CrossRefGoogle Scholar
Dziedzic, T., Pietrzykowski, Z., Uriasz, J. (2000). Knowledge-based System for Evaluation of Ship's Navigational Safety. In: Proc. of Ist Conf. COMPIT 2000, Potsdam, 132–140.Google Scholar
Fujii, Y., Tanaka, K. (1971). Traffic capacity, The Journal of Navigation, 24, 543–552.Google Scholar
Goodwin, E. M. (1975), A statistical study of ship domains. Journal of Navigation, 28, 328–344.CrossRefGoogle Scholar
James, M. (1986). Modelling the decision process in computer simulation of ship navigation. The Journal of Navigation, 39, 32–49.Google Scholar
James, M., The timing of collision avoidance manoeuvres: descriptive mathematical models, The Journal of Navigation, 47, 1993, 259–272.Google Scholar
Pietrzykowski, Z. (1997). Applications of neuro-fuzzy networks for identifications of distress situations in vessel traffic in restricted areas. In: Proc. of 7th International Scientific and Technical Conference on Sea Traffic Engineering, Szczecin, 131–142 (in Polish).Google Scholar
Pietrzykowski, Z., Dubowik, W. (1998). Neuro-fuzzy networks for identification of distress situations in restricted area vessel traffic. Scientific Papers Maritime University of Szczecin, 55, 79–96, (in Polish).Google Scholar
Pietrzykowski, Z. (1999). Ship fuzzy domain in assessment of navigational safety in restricted areas. In: Proc. of 3rd Navigational Symposium, Gdynia, I, 253–264 (in Polish).Google Scholar
Pietrzykowski, Z. (2002), The analysis of a ship fuzzy domain in a restricted area, IFAC Conference Computer Applications in Marine Systems CAMS'2001, Elsevier Science Ltd 2002.Google Scholar
Pietrzykowski, Z., Uriasz, J. (2003), Methods of artificial intelligence in navigational safety assessment of ship encounters, Proc. of Computer and Information Technology Applications in the Maritime Industries COMPIT 2003, Hamburg 2003, 40–47.Google Scholar
Smierzchalski, R, Weintrit, A. (1999). Domains of navigational objects as an aid to route planing in collision situation at sea. In: Proc. of 3rd Navigational Symposium, Gdynia, I, 265–279, (in Polish).Google Scholar
Wawruch, R (1998), Vessel traffic control systems, Scientific Papers Gdynia Maritime University, 6, 28–47 (in Polish).Google Scholar
Zhao, J, Wu, Z., Wang, F. (1993). Comments of ship domains. The Journal of Navigation, 46, 422–436.Google Scholar
Figure 0

Figure 1. Ship fuzzy domain; domain boundaries for various levels of navigational safety γ. (γ∊<0, 1>); γ=0 – very safe situation; γ=1 – very dangerous situation (collision).

Figure 1

Figure 2. An illustration of a ship moving in a restricted area.

Figure 2

Figure 3. Values of navigational safety level for the m/s “Freight” (ω=−5 o/min); Δφ – deviation from the from the preset course; Δy – distance to the fairway axis.

Figure 3

Figure 4. Navigational situations within a straight fairway section a) situation (1); b) situation (2); c) superimposed situations (1) and (2).

Figure 4

Figure 5. Fuzzy domain of the bulk carrier m/s Freight (rate of turn ω=0°/min):a) straight lines bounding the area of fuzzy domain D0,7IV; b) ship fuzzy domain DRS0,7.

Figure 5

Figure 6. Fuzzy domain of the m/s Freight proceeding along a straight fairway section: a) for the rate of turn ω=0°/min and navigational safety level γ=0·3, 0·5, 0·7, 0·9; b) for the navigational safety level γ=0·9 (the rate of turn: 0 and 50°/min).

Figure 6

Figure. 7. Ship fuzzy domain for various relative bearings ∠K and navigational safety γ=0·5.

Figure 7

Figure 8. Regression model for relative bearings ∠Kj: a) −90°; b) +90°.

Figure 8

Figure 9. The area of a fuzzy domain for various values of safety level γ=0·2; 0·3; … 0·9.

Figure 9

Table 1. Correlation coefficients and estimated parameters of the linear regression for the forward, aft and whole domains.

Figure 10

Table 2. Area parameters.

Figure 11

Figure 10. Assessment of navigational safety level for various ship's deviations from the fairway centre line and shifts from the preset course: a) area 1; b) area 2.

Figure 12

Figure 11. Ship fuzzy domain for various navigational safety levels γ: a) restricted area 1; b) restricted area 2.

Figure 13

Figure 12. Lengths and widths of ship fuzzy domain for various values of navigational safety γ in areas 1 and 2: a) length; b) width.

Figure 14

Figure 13. Areas of ship fuzzy domain for various values of navigational safety γ in restricted areas 1 and 2.

Figure 15

Figure 14. Lengths and widths of a fuzzy domain of ships for various values of navigational safety γ in a restricted area 2 with a width of 200 metres: a) domain length; b) domain width.

Figure 16

Figure 15. Areas of ship fuzzy domain for various levels of navigational safety γ in a restricted area 2 with a width of 200 metres.

Figure 17

Table 3. Ships' parameters.