1. INTRODUCTION
Precise surveying works are usually carried out using geodetic-grade, dual-frequency GPS systems. Unfortunately, these systems are expensive and cannot be afforded by many small business organizations. Low-cost, single-frequency, carrier-phase-capable GPS receivers provide an affordable solution; however, their accuracy degrades significantly under high multipath condition and/or high differential ionospheric delay. With the rapid improvements in the satellites constellation and the availability of precise products, such as precise ephemeris and ionospheric correction maps produced by the International GNSS Service (IGS) or the National Oceanic and Atmospheric Administration (NOAA), it should now be feasible to derive accurate solutions using low-cost single-frequency GPS receivers. Multipath disturbance however appreciably reduces GPS accuracies and will remain a major challenge. Multipath disturbance affects solutions derived by precise point positioning, relative positioning and kinematic positioning. It is difficult to model multipath disturbance mathematically due to its localized nature and due to its being environmentally dependent. Several studies have been initiated to check the possibilities of improving the accuracy of the positioning solution derived from single-frequency GPS receivers. Masella [Reference Masella, Gonthier and Dumaine1] tested the capability of implementing a low-cost single-frequency receiver for real-time kinematic (RTK) applications. Rizos et al. [Reference Rizos, Han and Han2] and Alkan et al., [Reference Alkan, El-Rabbany and Saka3] investigated the potential use of the Canadian Marconi Allstar OEM GPS single-frequency receiver board for surveying applications. The value of wavelet analysis has recently been demonstrated in various geodetic applications, including GPS data processing and geoid computations. Fu et al. [Reference Fu and Rizos4] applied the Daubechies orthonormal wavelet family to GPS data processing. Aram et al. [Reference Aram, El-Rabbany and Krishnan5] tackled the identification of the multipath effect on data collected by a single-frequency GPS receiver. This paper investigates the possibility of using single-frequency GPS sensors in static mode over different baselines (up to 65 km). To improve the accuracy of the single-frequency systems in multipath environments, we propose the use of a mitigation technique based on wavelet analysis using Daubechies family wavelets. Wavelet analysis using db8-wavelets is used to decompose the code minus carrier residuals into a low-frequency bias and high-frequency noise terms. The analysis identifies the amount of multipath disturbance in each observed satellite's signal. The best satellites (in terms of multipath standard deviation values) are used to compute the final positions. The Magellan AC12 low-cost single-frequency GPS receiver was extensively tested in static mode. It is shown that accuracies within 5 cm are routinely obtained for baselines up to 65 km under various multipath environments.
2. MULTIPATH IDENTIFICATION METHODOLOGY
This research proposes a new approach to identify multipath-contaminated L1 measurements through wavelet analysis. First, the difference between the code and carrier-phase measurements is estimated, leaving essentially twice the ionospheric delay, multipath and system noise. The ionospheric delay is largely removed by using high-resolution ionospheric delay maps produced by NOAA. The remaining residuals contain mainly low-frequency multipath, if they exist, and high-frequency system noise, which are decomposed using Daubechies family wavelets (db8). The following sections detail the implemented identification methodology.
2.1. Computation of code-minus-carrier residuals
The code-minus-carrier residual is computed by subtracting the L1 carrier-phase from the L1 pseudorange measurements. Equations (1) and (2) represent the pseudorange (P) and carrier phase (Φ) observations respectively [Reference El-Rabbany7].
![\eqalign{ P\lpar t\rpar \equals \tab \rho \lpar t\comma t \minus \tau \rpar \plus c\left[ {dt_{i} \lpar t\rpar \minus dt^{\hskip 1pt j} \lpar t \minus \tau \rpar } \right] \plus d_{trop} \plus d_{ion} \cr \tab \plus c\left[ {d_{i} \lpar t\rpar \plus d^{j} \lpar t \minus \tau \rpar } \right] \plus d_{mp} \plus \varepsilon _{p} \cr}](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151022065409686-0811:S0373463309990373_eqn1.gif?pub-status=live){kind=small}
![\eqalign{ \rmPhi \lpar t\rpar \equals \tab \rho \lpar t\comma t \minus \tau \rpar \plus c\left[ {dt_{i} \lpar t\rpar \minus dt^{\hskip 1pt j} \lpar t \minus \tau \rpar } \right] \plus \lambda N \cr \tab \plus d_{trop} \minus d_{ion} \plus c\left[ {\delta _{i} \lpar t\rpar \plus \delta ^{j} \lpar t \minus \tau \rpar } \right] \plus \delta _{mp} \plus \varepsilon _{\rmPhi } \cr}](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151022065409686-0811:S0373463309990373_eqn2.gif?pub-status=live){kind=small}
When we take the difference (code-carrier) between the two observables, relativistic effects and the effects of geometry, tropospheric delay, satellite and receiver clock errors, and antenna phase centre variations are eliminated. The terms that remain include the multipath effect in both the carrier phase (δmp) and the code measurements (d mp), twice the ionospheric effect (d ion), the ambiguity term (λN), the hardware delay and the receiver noise, as shown in Equation (3):
![\eqalign{ P \minus \rmPhi \approx \tab \, 2d_{ion} \minus \lambda N \plus c\left[ {d_{i} \lpar t\rpar \plus d^{\hskip 2pt j} \lpar t \minus \tau \rpar } \right] \plus d_{mp} \cr \tab \plus \varepsilon _{p} \minus c\left[ {\delta _{i} \lpar t\rpar \plus \delta ^{j} \lpar t \minus \tau \rpar } \right] \minus \delta _{mp} \minus \varepsilon _{\rmPhi } \cr}](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151022065409686-0811:S0373463309990373_eqn3.gif?pub-status=live){kind=small}
The carrier phase multipath and noise are negligible when compared to the code multipath and noise [Reference Braash, Parkinson and Spilker6] and could be removed from Equation (3). The differential hardware delay is very stable over time and can be removed from the equation by taking the mean of the residual. In addition, carrier-phase system noise (εΦ) is much smaller than the corresponding code noise (εp) and, as such, can be removed from Equation (3). As a result, Equation (3) can be simplified as shown in Equation (4):
The terms in Equation (4) represent twice the ionospheric effect, and the C/A code multipath and noise, offset by a constant DC-component due to the carrier phase ambiguity [Reference Langley, Teunissen and Kleusberg8]. When the measurement is clean and has no cycle slips, the range due to the differential integer ambiguity is constant over time and hence the effect of integer cycle ambiguity can be removed by subtracting the mean of the residuals. The remaining residual is then represented by Equation (5):
After removing the ambiguity term, the remaining residual now mainly represents the multipath and twice the ionospheric effect as low frequency errors beside some other high frequency noises. Figure 1 shows the PRN31 residual collected using the AC12 single-frequency GPS receiver at point Ryerson. Point Ryerson is surrounded by tall buildings and road signs and additional multipath was introduced by parked vehicles. The residual for PRN31 shows large fluctuations at large magnitudes. These large fluctuations indicate a dominant multipath effect on the residual as compared to the slowly varying ionospheric delay. The peak-to-peak variation for this satellite is about 3·5 metres.
Figure 1. Residuals for PRN31, observed at station Ryerson.
2.2. Ionospheric correction
Ionospheric disturbance is the largest source of GPS measurement error. In this study, the L1 ionospheric error was largely accounted for using the high resolution USTEC ionospheric maps produced by NOAA [Reference Rowell9]. USTEC ASCII files contain the vertical Total Electron Content (VTEC) and the slant line-of-sight electron content (STEC) for each satellite. The files are produced every 15 minutes, and cover all the satellites in view within the spatial coverage. The maps have a spatial resolution of 1°×1° and cover regions across the United States extending from latitude 10° to 60° North, and from longitude 50° to 150° West [10]. The expected accuracy of the USTEC maps is in the range of 1 to 3 TEC units. The differential vertical TEC has an average root mean square error of 1·7 TEC units, which is equivalent to less than 30 cm of signal delay at the GPS L1 frequency, while the differential slant TEC has an average root mean square error of 2·4 TEC units, which is equivalent to less than 40 cm of signal delay at the GPS L1 frequency [Reference Rowell9].
2.3. Procedures used to reduce ionospheric delay
To compute the L1 ionospheric correction necessary for the data collected by the single-frequency receiver at each location in this study, it is first necessary to compute the TEC values that correspond to the locations of the data collection points and match the time and rate of data collection. Unfortunately, the selected data collection points may not lie exactly on the TEC grid provided by NOAA; therefore TEC values were interpolated using a two-dimensional spatial interpolation procedure. Time must also be considered. The USTEC grid file may not correspond exactly to the time and rate of data collection. This problem was overcome by time interpolating the TEC values using the Lagrange interpolation method [Reference Yousif and El-Rabbany11]. The L1 ionospheric correction interpolated from the USTEC model was used to account for the ionospheric delay in Equation (5) to generate quasi-ionosphere-free residuals. Such residuals were then used as inputs for multipath identification using wavelet analysis. Figure 2 shows an example of the pseudorange residuals before and after applying the ionospheric correction.
Figure 2. Residuals for PRN31 before and after removing the ionospheric effect, observed at Ryerson.
3. PROPOSED ALGORITHM: MULTI-RESOLUTION ANALYSIS BASED ON THE DAUBECHIES FAMILY
No general criteria are available to guide the selection of the appropriate wavelet for analyzing a certain type of data. This is because the selection of the wavelet requires knowledge of the exact behaviour of the signal at hand (frequency-band), and this knowledge is unlikely to be available. The selection of the wavelet that best fits a specific signal remains a research topic of its own [Reference Satirapod and Rizos12]. In general terms, however, it has been proved that GPS bias terms such as multipath and ionospheric delay behave like low-frequency noise, while GPS measurement noise behaves like high frequency noise [Reference Fu and Rizos4]. As these basic principles indicate that multipath is concentrated in the narrow low-frequency band, a high frequency resolution needs to be identified. Therefore, multi-resolution analysis based on the Daubechies family (dbN) was chosen to approximate the multipath values for all the datasets collected during the field observations of the observed satellites. dbN is a series of compactly supported orthogonal wavelets. N specifies the order of the mother wavelet and is related to the number of coefficients necessary to represent the associated low-pass and high-pass filters in the dyadic filter tree implementation. The “db” is the “surname” of the wavelet. The Daubechies basis is the cornerstone of many wavelet applications today.
In this research, db8 is selected as the mother wavelet and the decomposition level is considered to be six. The main consideration is being able to filter out as much of the higher frequency observation noise as possible to be left mainly with the low-frequency multipath bias. To achieve this, the remaining residuals were fed into the proposed algorithm (db8-level 6) to approximate the multipath values. The input data (i.e., the remaining residuals) were decomposed into low-frequency bias and high-frequency noise for each observed satellite. This decomposition process is accomplished by successive high-pass and low-pass filtering of the residuals (time domain signals). Each residual is first passed through a half band high-pass filter h[n] and a low-pass filter l[n]. This filtering process was followed by a sub-sampling operation. The signal (residual) was sub-sampled by two, i.e., half of the samples on the signal were discarded because they are considered redundant according to Nyquist's rule. This process completed one decomposition level, and is expressed mathematically in Equations (6) and (7):
where Res high [k] and Res low [k] are the outputs of the high-pass and low-pass filters, respectively, after sub-sampling by a factor of two. This decomposition process results in half the time resolution, and twice the frequency resolution. The process was then repeated for further decomposition. At each subsequent level, the filtering and sub-sampling yield half the number of points (and hence half the time resolution) and half the frequency band spanned, doubling the frequency resolution. The process is shown in Figure 3.
Figure 3. Multi-resolution analysis scheme (after [Reference Satirapod and Rizos12]).
3.1. Wavelets approximation results
Figure 4 shows the wavelet decomposition tree using the db8 wavelet at six decomposition levels. In this figure, S represents the input signal, a1 through a6 are the details from level 1 to 6, and d1 through d6 are the respective approximations.
Figure 4. Wavelet decomposition tree for db8-level 6.
Figure 5 shows the wavelet multipath approximation results obtained for PRN01 residuals observed at point PIER as a result of passing the residuals into the db8 wavelet using the six decomposition levels. As it is clear that the successive approximations became less noisy and resulted in higher frequency resolution, level 6 was adopted for approximating the multipath disturbance in the observations. Figure 6 shows the approximated multipath for PRN01 using db8 (level 6). The approximated multipath is represented as a smooth trace superimposed on the input residual which exhibits more fluctuations. This satellite was setting during the observation period (elevation angles between 37° and 0°). The standard deviation of the approximated multipath is 0·7529 m.
Figure 5. Wavelet approximation levels for PRN01 residual.
Figure 6. Approximated multipath for PRN01 residual using level 6.
To validate the reliability of the proposed algorithm, the db8 wavelet was used to decompose the residuals for the L1 data obtained from the dual-frequency receiver. The multipath approximated by the wavelet approach was compared with the multipath determined by TEQC software for the same dual-frequency data. The results showed good agreement between the two methods, and verified the suitability of the proposed wavelet algorithm for identifying multipath effect in satellites signals (see Figure 7).
Figure 7. Multipath for PRN01 determined by wavelet and TEQ for L1 dual-frequency data.
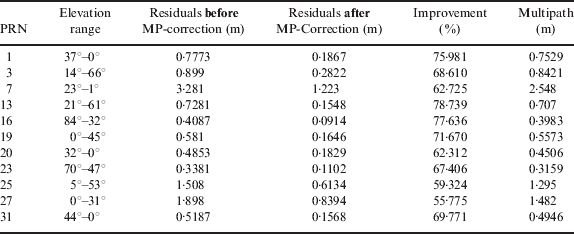
The final step was to derive a criterion on which to base the rejection of a particular satellite. The criterion was based on each signal's standard deviation of the approximated multipath. Signals with the largest multipath standard deviation values were excluded from the final data processing and computation of the coordinates of the observed points. The standard deviations of all residuals before and after applying the multipath corrections were also computed to show the improvement achieved when the multipath identified by the wavelet algorithm was removed from the signal. Table 1 shows the standard deviations for the residuals, approximated multipath and elevation angles for each observed satellite. The table clearly confirms the relationship between satellite elevation and multipath effect.
Table 1. Standard Deviations for code residuals before and after multipath correction and the approximated multipath using db8-Wavelet-PIER.
4. RESULTS AND DISCUSSION
In this research, single- and dual-frequency GPS receivers were used to simultaneously collect static data using the same antenna. The Magellan AC12 low-cost single-frequency GPS receiver and the NovAtel ProPack-V3 geodetic-grade dual-frequency GPS receiver were connected to a common antenna via an antenna splitter to collect the data simultaneously. The latter receiver was used, along with the Bernese software, to generate reference coordinates at all occupied points. Data were collected at a recording rate of 1 Hz for 2 hours in static mode at several locations under various multipath environments with different baselines with lengths ranging from 10 to 49 km. This was done to ensure that enough observations were collected to meet the objective of the proposed research. Collected data were processed using two different processing software packages, namely Trimble Total Control (TTC) and the Bernese software.
The efficiency of the wavelet-based multipath identification technique developed in this research was verified by comparing the station coordinates obtained with the single-frequency receiver with the reference coordinates. The station coordinates were first computed using all satellites in view. Multipath-contaminated satellites were then isolated and the station coordinates were computed again. Figure 8 shows sample results derived from the AC12 single-frequency receiver for station Ryerson (downtown Toronto, 21 km baseline) before isolating multipath-contaminated satellites, while Figure 9 shows the results after isolating multipath-contaminated satellites. Note that the vertical scale for Figure 8 is in metres, while it is in centimetres for Figure 9. Point Ryerson was observed under severe multipath conditions which result from the many reflecting objects surrounding the GPS antenna. In addition, more than 50% of the observed satellites were at very low elevations during the observation period (as shown in Table 1). This led to deterioration in the estimated position, which was essentially based on code observations (see Figure 8).
Figure 8. Point Ryerson coordinates differences (from known coordinates) before isolating multipath contaminated satellites.
Figure 9. Point Ryerson coordinates differences (from known coordinates) after isolating multipath contaminated satellites.
The positioning accuracy was improved substantially when multipath-contaminated satellites were isolated. As shown in Figure 9, the positioning accuracy improved to the decimetre level when the TTC software was used, while it improved to the centimetre level when the Bernese software was used. Since both software packages used the same input parameters, the relative accuracy degradation could be attributed to incorrect fixing of the ambiguity parameters by the TTC software.
Figure 10 compares the positioning results obtained for point Ryerson when two different reference stations, namely Toronto and Pwel, were used. The corresponding baseline lengths were 21 km and 49 km, respectively. As expected, the positioning accuracy degrades as the baseline increases. This is essentially caused by the larger differential ionospheric delay between the end points of the longer baseline. This accuracy level, however, can still meet the requirements of many geomatics applications.
Figure 10. Ryerson coordinates differences using Bernese software.
5. CONCLUSIONS
Precise positioning using single-frequency GPS receivers under various multipath environments have been extensively investigated in this research. The L1 code-minus-carrier residuals, with ionospheric delay removed, were estimated for each satellite, leaving essentially multipath and system noise. A wavelet-based multipath identification technique was successfully implemented to identify the code multipath in the residuals of the single frequency system. The efficiency of the proposed multipath identification technique was demonstrated through the improvement in the user position estimation at various locations with moderate to high multipath environments. It has been shown that the positioning accuracy of the single frequency system was improved by a factor of two when wavelet-identified multipath-contaminated satellites were isolated from the final data processing. The improvement is more significant when the multipath error is large. The achieved results convincingly demonstrated the efficiency of the wavelet analysis technique in identifying the multipath-contaminated satellite signal with only L1 data available. This technique furnished the ground to isolate the multipath-contaminated satellites from the baseline processing, which results in speeding up the ambiguity resolution and improving the accuracy of the estimated baseline components.
Various static baselines with lengths ranging from 10 to 49 km were processed with both the Bernese and the TTC software packages to validate our proposed multipath identification strategy and to examine the performance of the single-frequency low-cost systems. The end points of the baselines were located at various multipath environments. Prior to removing the multipath-contaminated satellites, the obtained accuracy of the horizontal components ranged from 0·21 m to 15·7 m, while the accuracy of the vertical component ranged from 1·2 m to 9·3 m. This, however, was improved to an average of 0·16 cm and 5·2 cm for both the horizontal and vertical components, respectively, after isolating the multipath-contaminated satellites identified with our wavelet-based method.
