1. INTRODUCTION
In 2004 the General Lighthouse Authorities (GLA) outlined their strategy for AtoNs with a vision out to 2020. In particular, this study examines whether the vision remains valid when developments in INS are taken into account. The GLAs have a common mission statement: “to deliver a reliable, efficient and cost effective AtoN service for the benefit and safety of all mariners”. The vision recognises the continued importance of lit buoys and beacons and emphasises the need for continued development and use of electronic navigational systems, including satellite navigation, the Automatic Identification System (AIS), racons and terrestrial radionavigation services. Lighthouses, major floating aids, fog signals and unlit beacons/buoys will be decreasingly used for general navigation, but may have an increasing role in some areas, because of changes in traffic and new hazards.
In conditions of good visibility, visual AtoNs continue to be universally used by vessels. They are sometimes used as the main positional reference but more often, particularly for SOLAS vessels, are used as secondary aids to give confidence to radionavigation derived positional information and also to provide visual cues for manoeuvring actions and visual feedback on the result of such actions. In poor visibility, GPS and radar become the major navigational tools, supported by AIS, log, (gyro) compass and depth indicator. With these tools, particularly when supported with an electronic chart or chart radar, some masters may be tempted to allow their vessels to continue at similar operational speeds, whatever the conditions of visibility. Although such practices put undue confidence on the availability and accuracy of GPS, it occurs because of a mixture of commercial pressures for meeting docking times, an over-confidence in the capabilities of GPS (and radar), and presumably, a certain amount of bravado.
Despite their great usefulness in conditions of good to moderate visibility, visual AtoNs have poor to zero effectiveness in low visibility and therefore they are not an ideal backup to electronic AtoNs. Improved integrity of electronic aids could allow the possibility of safe navigation in zero visibility in many or all circumstances. Such improved integrity could also reduce the numbers of visual AtoNs that need to be sustained – because of their overall usefulness they would probably not become totally redundant.
Inertial navigation is the technique of measuring the displacement from an initial position by measuring acceleration and rate of turn using accelerometers and gyros. Acceleration is integrated twice to obtain displacement, whereas the gyros are used to maintain a reference frame by measuring how much the axes have rotated. An Inertial Navigation System is typically formed using three orthogonal axes of accelerometers and gyroscopes to form an Inertial Measurement Unit (IMU). The INS contains a navigation computer that integrates the output from the IMU and transforms the measurements into useful measurements of position, velocity and orientation. The primary advantage of using INS for navigation is that it is entirely autonomous. It works without the need to send or receive signals which can be blocked or interfered with. INS is now almost standard equipment for military navigation for aircraft, ships, missiles and spacecraft [Reference Schmidt6].
Inertial navigation systems are not currently used in most commercial marine applications. This has been because of their historically high cost and the lack of any convincing cost benefit analyses for these applications. Additionally, there has not been a high profile accident where a subsequent investigation showed that it would have been prevented solely by the mandatory use of INS; therefore there has been no external or political pressure for the introduction of INS.
Navigation equipment mandatory carriage requirements for shipping have historically been introduced sensor by sensor as the requirement and the technological solutions have become clear. Mechanical logs, magnetic compasses, gyrocompasses and GPS are all good examples of this. The requirements for radar and more recently AIS are more unusual examples, in that there is a required integration with other sensors. However, for these two examples, the integration is at a basic level – there is no mutual enhancement of a navigation solution nor are there any requirements for cross-sensor integrity measurements. The possible incorporation of an inertial sensor into a commercial marine navigation system is at a greater level of integration. For this reason it has the potential to produce a system with the following benefits:
• An improved navigational solution, with position and velocity estimates available at a rapid update rate with a lower noise content than is obtainable from existing ship systems.
• Additional automatic warnings that other sensors, including GNSS, have failed or are giving reduced navigational accuracy.
• Maintenance of an acceptable navigation solution in the event of a failure or degradation of other sensors.
In addition to any potential safety benefits that an INS based system could bring, the shipping industry would also be attracted to a system that would reduce fuel costs. An INS may be able to assist in this, for instance by allowing an advanced autopilot to make automatic decisions concerning the optimum yaw limits to achieve the lowest fuel consumption for a given speed, depending on the actual sea conditions. Small, but consistently and demonstrably achieved fuel reductions would create an immediate demand for such a system. Even a 1% fuel saving can amount to tens of thousands of Euros a year for a large ship.
This study has attempted to assess the performance of three different grades of INS during a GNSS outage, by both simulation analysis and dedicated sea trials.
2. PREDICTED PERFORMANCE – COVARIANCE ANALYSIS
As part of the assessment, the study included a theoretical performance overview of three different types of IMUs: navigation grade, tactical grade and low cost. This section is not intended to provide exact performance specifications for the different types of sensors, as this would be impossible to achieve without performing hundreds of trials in different conditions and environments using real sensors. This section is, however, used to give an indication of the performance that may be achieved using three different sensor grades. The covariance analysis is used to give a rough order of magnitude indication of the errors experienced using different IMUs. The sensors that are considered are as follows:
• Honeywell HG9900 navigation grade IMU
• Northrop Grumman (Litton) LN200 tactical grade IMU
• BAE Systems SiIMU01 low cost IMU
These sensors are used as an indication of the performance typically obtained for the different grades of sensor. The Honeywell HG9900 is a navigation grade sensor that is used in thousands of aircraft worldwide. Similarly the Northrop Grumman LN200 is a mass produced tactical grade IMU. The BAE Systems SiIMU has been selected as the MEMS grade/low cost grade sensor as it is representative of the type of performance that is expected to be available in the near future at low cost.
Prior to the sea trials which were conducted later in the project, a real trajectory was obtained from a GPS-equipped car when travelling from Leicester, UK to Nottingham. There are many different environments that an IMU may be used in such as land, air and marine. The positioning performance will vary in each of these environments principally as a result of dynamics, but also as a result of other factors such as environmental conditions. For the vehicle trajectory, the journey involved a combination of urban conditions in Leicester and Nottingham city centres, and also major trunk road conditions including a dual carriage way. The maximum speed reached on the journey was 70 mph.
2.1. Stand Alone Performance
To begin the analysis, each of the IMUs is assumed to be initialised with a position accuracy of 1 m and a velocity accuracy of 0·02 m/s. The attitude accuracy is obtained using a coarse alignment algorithm. For the MEMS grade sensor, this approach cannot be used, therefore the initial roll and pitch is obtained using the autonomous coarse alignment, and the initial heading is set to be 2° which is consistent with the type of performance obtained from an aiding sensor such as a magnetometer. The initial errors can be improved by performing a static alignment, however, this is not considered here. The results of the covariance analysis for different periods of time are given in Table 1.
Table 1. Standalone INS 1-sigma horizontal position error in metres.

Table 1 shows the range in positioning performance that is achieved from the different sensors. The navigation grade sensor clearly provides the highest positioning accuracy, as would be expected. The HG9900 is described as having proven 0·8 nmi/hr performance which is equivalent to approximately 1·5 km/h. The figure given in Table 1 for 50 minutes duration is consistent with this value, as the error growth is non-linear. Values are only provided in Table 1 up to 50 minutes because of the duration of the vehicle journey. However, an extra trial was performed using a 10 minute static period at the beginning of the dataset. This resulted in a position error of 1236 m after 60 minutes which is consistent with the 0·8 nmi/hr performance quoted by the manufacturers.
For the tactical grade system, the IMU positioning accuracy after 30 seconds was computed to be 10 m. Tactical grade IMUs are designed to operate over very short time intervals, which would be less than 30 seconds for most tactical applications. The figure shows that the error growth increases significantly after this time with the position error greater than 1 km after 10 minutes. For time periods greater than 10 minutes, the position error is too large for the majority of positioning applications. The 30 second and 1 minute positioning accuracies are consistent with papers such as [Reference Petovello4] where less than 10 metre accuracy is achieved over intervals of 60 s. No published information is available on time periods greater than 1 minute to validate the results given in Table 1 since such positioning errors are too large for the majority of applications.
The performance of the MEMS SiIMU is shown in Table 1 to be 26 m after 30 seconds, and 102 metres after 60 seconds. After only 2 minutes, the position error increases to approximately 0·5 km. Again, positioning accuracy of this magnitude is too large for the majority of applications. The positioning accuracy of MEMS grade sensors has been examined in, for example, [Reference Salychev, Voronov, Cannon, Nayak and Lachapelle5] and [Reference Hide1] by analysing the position drift in a GPS-aided system when GPS measurements are not available. In [Reference Hide1], average positioning accuracies of approximately 7·5 m after a 30 second outage were achieved in a land vehicle environment. However, these results were obtained in an environment where horizontal acceleration was induced in the vehicle specifically to align the IMU sensor. Similarly, [Reference Salychev, Voronov, Cannon, Nayak and Lachapelle5] obtained 20 m position error after 20 seconds using a BEI Systron Donner Motionpak. However, these results were obtained in an airborne environment, where again, dynamics of the host vehicle ensure that horizontal acceleration is introduced to restrict the drift of some of the errors. Therefore, the results for the SiIMU shown in Table are considered to be consistent with available publications.
The estimated INS positioning errors shown in Table 1 demonstrate the vast difference in performance that is obtained from the different grades of IMU. The results provide an approximate indication of the magnitude of the errors that are experienced as a result of various IMU error sources.
Position and velocity aided performance
Covariance analysis can also be used to assess the performance of an INS when external measurements are available. In addition to reducing position and velocity errors, the position and velocity updates are also used to update the attitude errors and the sensor errors. This is referred to as the dynamic alignment. Figure 1 illustrates the attitude error resulting from these updates. A significant period of the results shown in Figure 1 is between 1500 and 2000 seconds. In this period, the dynamics of the vehicle are relatively stable. This is because during this period, the vehicle is travelling on a major road at relatively constant velocity. This demonstrates that the attainable performance from an INS is significantly related to the types of external updates available and the vehicle dynamics.

Figure 1. SiIMU estimated attitude performance using position and velocity aiding.
3. SEA TRIALS
To support the assessment of different grades of IMU, a trial was conducted in Plymouth Sound in July 2006. The vessel Marco was used for the trial and is shown in Figure 2. The figure shows the position of the NovAtel GPS antenna used for the trial. The antenna is located on the bow of the vessel on a pole braced by two further poles to keep the antenna rigid. The IMUs were located in the front cabin of the vessel approximately as shown in the figure.

Figure 2. The vessel Marco.
The vessel trajectory consisted of an initial series of figure of eight manoeuvres (required to align the INS, which is particularly important for the low cost sensors), followed by a series of three survey lines performed within the Plymouth breakwater lasting approximately 10–15 minutes each. The vessel then moved out past the breakwater to perform an additional two survey lines. The vessel then travelled back past the breakwater to the mooring. The total length of the dataset is approximately two and three-quarter hours, including stationary periods at the start and end of approximately 20 minutes and 5 minutes respectively. The sea state during the trial was calm with similar conditions experienced both inside and outside the breakwater.
3.1. Sea Trial Equipment
The following equipment was installed on the boat:
• Applanix POS-RS: (consisting of Honeywell CIMU, NovAtel OEM4 GPS receiver, NovAtel 600 antenna). The Applanix POS-RS is a GPS and INS integrated system custom made for the IESSG at the University of Nottingham. The POS-RS is similar to other Applanix products such as the Applanix POS-AV which is a system developed for aerial survey applications; however the POS-RS uses a much higher specification IMU. The POS-RS comprises the IMU, a GPS antenna and a 19” rack mounted computer containing the GPS receiver. A laptop computer is used to control operation using a TCP/IP connection. The Honeywell Commercial Inertial Measurement Unit (CIMU) is a high-accuracy navigation-grade IMU designed for survey, pipeline and mining markets. The unit consists of 3 digital laser gyros and 3 quartz-flex accelerometers. The gyro bias is specified as
 . It is the largest of the IMUs discussed here, having a volume of ~4,300 cm3 and a weight of ~4·9 kg. The approximate cost of the IMU alone is €90,000. The high performance of the IMU means that low drift rates result in high accuracy navigation even when GPS measurements are not available. The system uses a dual frequency NovAtel OEM4 GPS receiver and antenna. The POS-RS records and time tags the raw IMU data at 200 Hz, and is capable of outputting a real-time integrated navigation solution at the same data rate.
. It is the largest of the IMUs discussed here, having a volume of ~4,300 cm3 and a weight of ~4·9 kg. The approximate cost of the IMU alone is €90,000. The high performance of the IMU means that low drift rates result in high accuracy navigation even when GPS measurements are not available. The system uses a dual frequency NovAtel OEM4 GPS receiver and antenna. The POS-RS records and time tags the raw IMU data at 200 Hz, and is capable of outputting a real-time integrated navigation solution at the same data rate.• Honeywell HG1700. The HG1700 manufactured by Honeywell is a tactical grade IMU comprising 3 ring laser gyros and 3 quartz beam accelerometers. The unit a volume of ~540 cm3 and weight of ~725 g. The model used for this trial is the HG1700AG58 which is specified with 1°/hr gyros and an accelerometer bias of 1 mg. The approximate cost of the HG1700AG58 is €20,000.
• Crossbow IMU300CC. The IMU300CC is a low-cost IMU, manufactured by Crossbow. All of the six sensing elements within the IMU are solid-state MEMS devices. The 3 accelerometers use differential capacitance to sense acceleration, while the 3 angular rate sensors are vibratory in nature and use Coriolis force to measure angular rate independently of acceleration. The performance of the IMU is one of the lowest that is used for navigation applications, with initial gyro biases specified as <±2 degrees per second. The unit is comparatively small and lightweight (volume ~500 cm3, weight ~600 g). The approximate cost of the IMU300CC is €2600.
The Applanix POS-RS comprises an IMU and POS Computer System (PCS). The PCS contains the GPS receiver and hard disk for data logging. A time synchronisation card from NavSys was used to time stamp the data from the Honeywell HG1700, with the time stamped data logged using a notebook PC. The data from the Crossbow IMU300CC was time stamped and logged using the University of Nottingham's time stamping PC. All IMU data is assumed to be time stamped with millisecond accuracy. The configuration of the IMU sensors and data loggers is shown in Figure 3.

Figure 3. IMU and data loggers installed in Marco.
The POS-RS is used with the Applanix POSPac post-processing software to compute a position, velocity and orientation solution. POSPac uses the integration architecture commonly referred to as loose coupling where GPS position and velocity is computed using an independent Kalman filter, and an integration Kalman filter is then used to estimate the errors in the INS. POSPac also implements a Kalman filter smoothing algorithm for the GPS/INS integration which is used when post-processing. Kalman filter smoothing can provide a significant performance improvement for GPS/INS integrated systems. The manufacturer's specification is shown in Table 2.
Table 2. Applanix POS-RS attitude accuracy.

The results in the following sections are generated using GPS and INS integration software developed at the IESSG, University of Nottingham. The software provides the capability to integrate GPS and INS measurements from any type of IMU with different GPS data using loose or tight coupling. Although the software works in post-processing, the algorithms that are implemented can be applied in real-time to provide the same results. The states modelled in the Kalman filter are:
• Position error, velocity error, attitude error
• Accelerometer bias, gyro bias, gyro scale factor
These are typical states that are estimated in commercial systems such as the Applanix POS-MV. Other states such as lever arm error between the IMU and the GPS antenna are not estimated since this is usually required as a one-off estimation when the system is installed in the vessel.
Sea Trial Results
Since the aim of this section is to provide an analysis of the performance of GPS and INS integrated systems for marine applications, a reference trajectory was generated using the Applanix POSPac post-processing software which uses the CIMU integrated with RTK GPS from the NovAtel OEM4 receiver. The 1 Hz reference data for this RTK processing was obtained from the nearby Ordnance Survey reference station at Plymouth. These results are the best that can be achieved since they use the benefit of post-processing using a combination of forward and backward processing.
The data from the different tested IMUs was integrated using the University of Nottingham's GPS/INS integration software. The IMU data is integrated for an initial period of 90 minutes. After this time, GPS aiding is artificially removed and the INS is used as the sole means of navigation for a range of time intervals from 30 seconds to 60 minutes. This is then repeated for five different outages starting at different times, and therefore covering parts of the trajectory with different dynamics characteristics. In the charts showing all five of these outages, they are referred to as Series 1 to 5.
The following sections show the results from these outage tests for the three different IMUs described above, integrated with RTK GPS measurements (carrier phase) or Differential GPS (DGPS) measurements (code only). In all cases the GPS solutions are at a rate of 1 Hz. It should be emphasised that both the RTK and the DGPS results refer to post-processed solutions, rather than the use of any real-time over the air services. The post-processed DGPS uses the raw pseudorange measurements from the vessel and a fixed reference receiver to produce a solution that is analogous to that from a real-time system, but which avoids the experimental problems associated with installing real-time equipment and receiving the DGPS correction broadcasts. Similarly, the RTK solution comes from post-processing, using raw (carrier phase) measurements from the vessel and a reference receiver, but using the more complex algorithms associated with the use of carrier phase data in a kinematic mode. As noted previously, the method of post-processing in each case is suitable for use in a real-time environment, but has not yet been coded into a real-time executable program.
CIMU and RTK GPS (Loose coupled)
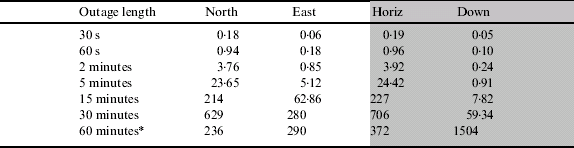
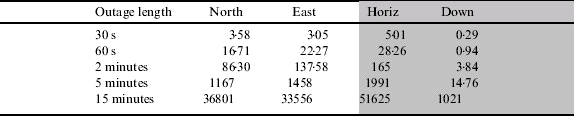
Table 3 shows the position error at the end of the GPS outage for different outage lengths for the Honeywell CIMU integrated with RTK GPS. The results shown are the average of the five different outages to provide a statistical assessment of the error as a function of time. The table shows that the INS is able to provide metre level horizontal positioning during an outage of up to 60 seconds. The vertical position error in the down axis is shown to be accurate to within 1 metre during an outage of up to 5 minutes. The Honeywell CIMU is a navigation grade IMU that should provide 1 nautical mile per hour performance (nmi/hr≈1852 m/hr). Table 3 shows that this performance is met.
Table 3. Average position error for different outage lengths for the CIMU with RTK GPS (* average of 3 outages only).
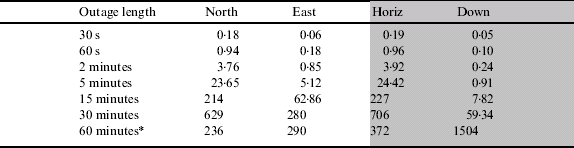
Figure 4 shows the position error over time for the outage that resulted in the largest error. The figure shows the characteristic of the error over time. For the horizontal channels (north and east) the error demonstrates Schuler oscillation (with the characteristic period of 84 minutes) where the horizontal error is approximately bounded with time. The vertical channel has a different characteristic since the error is unbounded with time.

Figure 4. Position error during one RTK GPS gap for the CIMU.
Figure 5 shows a representation of the variation of the five outages analysed for different outage lengths. From this figure, the position error for different outage lengths can be identified, and equivalently, the length of time a particular level of position accuracy can be maintained can be read. For example, a maximum position of 100 m is maintained for 10 minutes (600 seconds).

Figure 5. Horizontal position error for the CIMU integrated with RTK GPS for different outages.
CIMU and DGPS (Loose coupled)
The University of Nottingham software is capable of integrating the measurements using the tight integration algorithm. Where there are greater than three satellites in view (as in this instance), the loose and tight integration algorithms should demonstrate similar results. An early test demonstrated a small improvement through using tight integration, thought to be a result of maintaining the full statistical information in the single filter. Since the differences between the results from the two integration algorithms are not significant when a full constellation of satellites is available, only the loose integration filter is considered in this paper. This is further justified since most of the current commercial systems available use the loose integration algorithm.
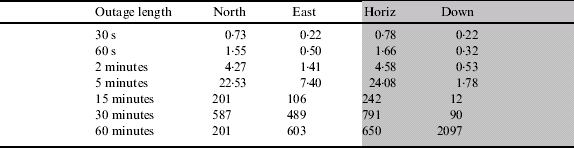
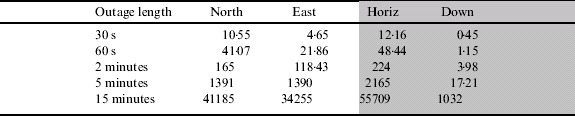
Table 4 shows the position performance of the CIMU during an outage after it has been integrated with DGPS positions rather than RTK positions. The table shows that the position errors are overall slightly larger (approximately 10%) for most outage lengths. For shorter outages, the error increase is more significant but this is expected since at the beginning of the outage, the initial position error will be larger due to using less accurate (D) GPS aiding.
Table 4. Position error for different outage lengths for the CIMU loosely coupled with DGPS.

HG1700 and RTK GPS
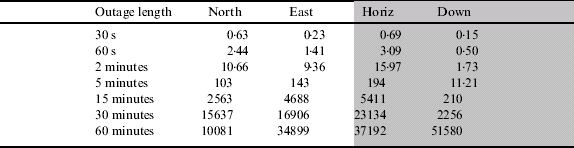
Table 5 shows the outage performance for the HG1700 after being updated using RTK GPS positions. The table shows that the position error growth is significantly more rapid than with the navigation grade CIMU which is as expected. For example, the HG1700 maintains a position accuracy of approximately 5 m for 60 seconds, whereas this accuracy is maintained for more than two minutes for the CIMU. Furthermore, for the HG1700, position accuracy degrades to approximately 5 km by 15 minutes whereas for the CIMU, better than 1 km is maintained for the full hour. The results from the five different outages are shown in Figure 6.

Figure 6. Horizontal position error for the HG1700 integrated with RTK GPS for different outages.
Table 5. Position error for different outage lengths for the HG1700 loosely coupled with RTK.
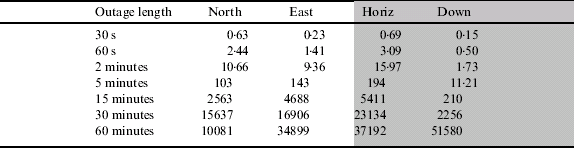
HG1700+DGPS (Loose coupled)
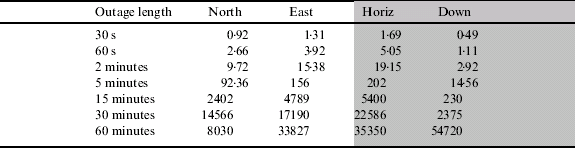
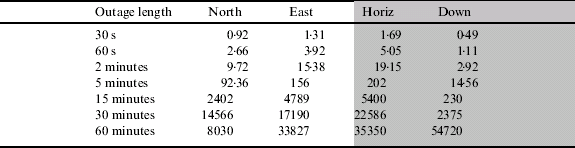
Table 6 shows the position error during a GPS outage for the HG1700 when it has been integrated with DGPS measurements. As with the CIMU, the position error is larger than for the RTK cases for nearly all outage lengths, principally as a result of the initial position error at the beginning of the outage, but also as a result of the estimation of some of the other parameters such as attitude error and inertial sensor errors.
Table 6. Position error for different outage lengths for the HG1700 loosely coupled with DGPS.
IMU300 and RTK
This section evaluates the performance of the Crossbow IMU300 integrated with RTK GPS. The IMU300 is significantly lower accuracy (and lower cost) than the other sensors investigated in this paper. This has a direct impact on the position accuracy when GPS measurements are unavailable. The main disadvantage of a low cost IMU is the poor performance of the gyros which has an impact on the attitude accuracy (and hence position accuracy) that can be maintained. For low cost IMUs, the estimation of inertial sensor errors as well as navigation errors is critical to maintain performance during outages. Low cost IMUs therefore require constant updates from aiding sensors such as GPS.
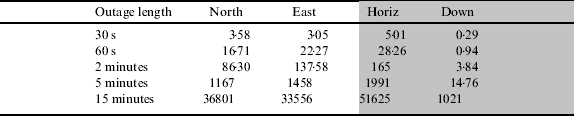
Table 7 shows the position error during different GPS outage periods for the IMU300. Position errors are only investigated up to 15 minutes due to their rapid drift over time. From the table it is shown that 5 m horizontal accuracy is only maintained for up to 30 seconds compared to the HG1700 that can provide better than 5 m for 60 seconds, and the CIMU up to 120 seconds. Similarly, after 2 minutes, position errors of 165 m are achieved with the IMU300 whereas this level of accuracy can be maintained for almost 5 minutes with the HG1700. Again, accuracy in the down axis is significantly better than horizontal performance with position accuracy of better than 15 m after 5 minutes achieved.
Table 7. Position error for different outage lengths for the IMU300 loosely coupled with RTK.
The error characteristics of the IMU300 are shown over time in Figure 7 for the worst case outage found when computing the statistics in Table 7. The figure shows position performance up to 30 minutes to demonstrate that there appears to be some Schuler-type oscillation apparent in the East axis, however the position errors are of the order of 50 km. In the North axis, the Schuler oscillation is not clear and it is likely that due to the large drifts experienced in both position and attitude errors, the position solution will grow without bound. The results from the 5 different outages are shown in Figure 8.

Figure 7. Position error during one RTK GPS gap for IMU300.

Figure 8. Horizontal position error for the IMU300 integrated with RTK GPS for different outages.
IMU300 and DGPS
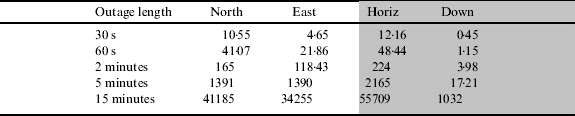
Table 8 shows the position error over time when integrating the IMU300 with DGPS measurements before the outage. It is clear from this table that the position error is significantly larger than when integrating with RTK measurements. For example, after 60 seconds, 48 m accuracy is maintained after DGPS whereas using RTK, position accuracy is 28 m. This is likely to be due to the less accurate estimation of the inertial sensor errors caused by integrating with less accurate DGPS position measurements. The increase in position error is apparent for all outage lengths.
Table 8. Position error for different outage lengths for the IMU300 loosely coupled with DGPS.
Sensor Performance Summary
The sea trials described above have investigated the performance of three different IMUs integrated with DGPS and RTK measurements. The performance of the INS-only solution has been investigated where GPS measurements are temporarily unavailable. Figure 9 shows the results from all three IMUs on a single chart for comparison purposes. The results obtained are consistent with current commercial systems that are available using the three different grades of IMU investigated (see for example, [Reference Hide and Moore2] and [Reference Petovello4]). The results are also consistent with the predicted results from the covariance analysis described earlier, given the assumptions used for initial position, velocity and attitude error. The results of the sea trials show an improvement over the predicted results from covariance analysis primarily because of the improvement in attitude accuracy and as a result of estimating the inertial sensor errors.

Figure 9. Horizontal position error comparison for all 3 IMUs.
Both the sea trials and the covariance analyses have shown that a vast difference in performance is obtained between a high accuracy navigation grade IMU, a tactical grade IMU and a MEMS IMU. This difference in performance is directly related to the cost of the IMU, but also some impact has been identified as a result of the aiding measurements used, in this case using updates from RTK or DGPS, as well as the integration algorithm used.
4. SUITABILITY OF INS FOR MARINE APPLICATIONS
A fundamental advantage of an inertial sensor is that it is ship based and independent of external systems. In this respect it is similar to radar – they both give relative positional data. Therefore they both need to be referenced to absolute position to give ground referenced data. A perfectly accurate INS would only need to have its reference position entered once. It could then be used indefinitely to report position. All real INS equipment suffers from errors and therefore reference positions must be regularly inserted. The better the INS, the less often this has to be performed. Even an expensive military grade Ships Inertial Navigation System (SINS) based on spinning wheel gyros will suffer a (published) 1 nautical mile error in 18 hours; although systems used on strategic submarines may have a rather higher accuracy. Therefore, in practice an IMU can only be seen as a backup for relatively short term outages of a primary electronic position fix system, such as GNSS.
The analyses presented in this paper have given practical illustrations of what happens to the position accuracy of an INS integrated with GNSS when GNSS fails. Not surprisingly, the expected accuracy of the position estimate degrades with time. It depends on the fundamental accuracy of the INS sensor and the degree to which biases can be compensated by the constant calibration with GNSS position prior to the time of its loss.
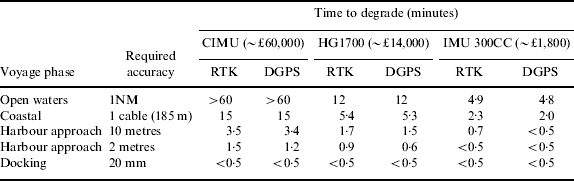
What is significant is the length of time of a GNSS failure that the system has to work through and what the acceptable positional accuracy is at the end of the failure period. Acceptable positional accuracy, depending on the voyage phase, has been considered in the full report of this study [3]. If the performance measured as part of the trials is typical when measured on other vessels, then Table 9 indicates the expected outages that could be met by the different INS configurations, tested for the four voyage stages.
Table 9. Time taken to exceed positional accuracy requirements after a failure of GNSS.
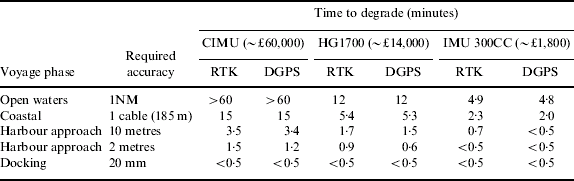
It is clear that none of these options is suitable to maintain navigation accuracy during a prolonged outage of GNSS. However, the following observations can be made:
• For coastal areas, 15 minutes of good accuracy would be maintained using a CIMU-based system, giving good time for the watch to be increased and preparations made for traditional navigational techniques to be employed. In particular, if ground fixed radar-conspicuous objects are available it gives ample time for the bridge staff to lock the radar chart or map onto these, allowing the radar to be used for absolute position fixing to an accuracy of about 1 cable or better. In practice, this would be accompanied by increased frequency of positioning using visual sights.
• For the harbour approach phase, accuracy to 10 metres would be obtained for 3·5 minutes from a CIMU-based system. This would give time for an experienced user to reference the radar to conspicuous ground fixed targets, provided these were available and pre-determined as part of the passage planning process. In practice, rather more time is available before the accuracy degrades to typical radar accuracies. These are of the order of 1% of the maximum displayed range, limiting to no better than 30 metres at short range. This is clearly inferior to the accuracy of GNSS and therefore it will be necessary to take this into account in the navigation of the vessel subsequent to GNSS failure.
• For coastal areas, accuracy to 1 cable would be achievable from the HG1700 for 5·3 minutes. This also gives time for an experienced operator to switch to a radar based position reference, provided there were suitable conspicuous ground fixed radar targets available and predetermined in the passage plan.
• For coastal areas the IMU 300CC would only give about 2 minutes of continuing accuracy. However, it still increases the possibility of an orderly fallback to the use of radar and traditional visual sighting techniques.
• For docking and where sub-10 metre accuracy is required, INS coupled with GNSS does not appear to offer a practical solution. Perhaps the only solution in these circumstances is a local position fix system, using RF or laser technologies. Although technically feasible, it would pose a significant problem to get agreement on an international basis for a standardised system to be installed in many ports.
• For ocean areas, the CIMU and the HG1700 give protection for appreciable outages (over 1 hour for the CIMU and 15 minutes for the HG1700).
Unfortunately, the price/performance ratios of the CIMU and HG1700 make it unlikely that they could become an acceptable solution, even though what is meant by affordable is obviously debatable. It is perhaps difficult to justify that the price of a backup to GNSS should cost considerably more than the original equipment. Perhaps it could therefore be argued that the additional cost of an integrated INS/GNSS should be of the order of €1500–3000. The IMU 300CC is within this bracket, although it is difficult to argue that it has a useful performance for this application. However, a future MEMS-based INS with the performance of the CIMU or HG1700 but with a price similar to the IMU 300CC could prove to be a useful addition to a ship's navigation system. Whether, and when, such a situation might arise is very difficult to predict. Certainly, MEMS development is currently an area of intense research, so it should be expected that significant advances will be made. However, the limitations of the technology might ultimately prevent this situation.
Even if such a future system gives the affordable possibility of an orderly positional fallback to using radar in coastal regions when GNSS fails, it does not appear to justify reducing AtoNs beyond what is outlined by the General Lighthouse Authorities in its 2004 publication “Strategy for AtoNs with a Vision out to 2020”. This is because radar can already be used in this manner, without the need for INS, and therefore its possible use would already have been factored into the deliberations of the plan.
CONCLUSIONS
The conclusions of the study can be summarised as follows:
• Although INS may offer tangible advantages to improve a ship's navigation it is unlikely that its adoption alone would lead to a reduction in the need for AtoNs.
• Because the duration of a GNSS outage is indefinable, INS cannot be considered as a primary backup to GNSS.
• Its main safety advantage is in allowing accurate navigation for a defined time after GNSS failure to enable the navigation of the ship to revert to alternative techniques in an orderly manner.
• When GNSS is available it is speculated that the extra motion information obtainable from INS could prove useful to enhance the performance of autopilots, thereby reducing fuel consumption.
• The INS units considered in the study do not appear to provide any useful reversionary capability when used in applications needing accuracies of much better than 10 metres.
ACKNOWLEDGEMENTS
The authors are grateful to Sonardyne International Ltd for the use of the vessel Marco for the sea trials discussed in this study.