1. INTRODUCTION
Marine development and monitoring often require highly precise kinematic positions of surveying platforms such as vessels and buoys (Geng et al., Reference Geng, Teferle, Meng and Dodson2010; Park and Cho, Reference Park and Cho2012; Watson, Reference Watson2005). These derived positions can be critical to maritime applications, for example, in dynamic positioning and measuring tidal variation. Therefore, highly precise positioning techniques have been attracting increasing attention in the maritime community. Currently, Global Navigation Satellite Systems (GNSS) can provide a position service in a global reference frame, and have been widely used in geophysical measurements and precision positioning applications (Alkan and Öcalan, Reference Alkan and Öcalan2013; Shi et al., Reference Shi, Yuan, Cai and Wang2017; Jin and Park, Reference Jin and Park2006; Jin et al., Reference Jin and Qian2017). As one of the GNSS precise positioning techniques, Precise Point Positioning (PPP) uses un-differenced observations at a single user station to obtain global decimetre- to millimetre-level position accuracy (Zumberge et al., Reference Zumberge, Heflin, Jefferson, Watkins and Webb1997). Hence, it is normally recognised that PPP is free from the constraint of baseline lengths and can be a cost-effective solution for marine platform position determination.
The PPP technique is usually carried out by utilising dual-frequency Ionosphere-Free (IF) code and carrier phase observation combinations (Kouba and Héroux, Reference Kouba and Héroux2001). Over the past two decades, dual-frequency IF PPP has been proven capable of providing centimetre to millimetre accuracy in static mode and decimetre to centimetre accuracy in kinematic mode (Pan et al., Reference Pan, Cai, Santerre and Zhang2017a). Currently, dual-frequency observations are mainly used for PPP. Without IF combination, the ionospheric error has to be dealt with in the case of single-frequency PPP, and dual-frequency PPP always outperforms single-frequency PPP when the position solutions are converged (Lou et al., Reference Lou, Zheng, Gu, Wang, Guo and Feng2016). Not all GNSS currently have enough available satellites to implement triple-frequency PPP alone. Furthermore, the inconsistency of satellite clocks based on different ionosphere-free carrier phase combinations is another issue to be solved for triple-frequency PPP (Pan et al., Reference Pan, Zhang, Li, Liu and Li2017b; Pan et al., Reference Pan, Li, Zhang, Li, Lu, Zhao and Liu2017c). For the dual-frequency IF PPP technique, although the position accuracy and convergence time of integer PPP with fixed ambiguities are superior to float PPP with real ambiguities (Ge et al., Reference Ge, Gendt, Rothacher, Shi and Liu2008; Collins, Reference Collins2008; Laurichesse and Mercier, Reference Laurichesse and Mercier2007), the ambiguity resolution success rate of PPP can be challenged by many factors such as severe multipath and poor satellite geometry, which can be the typical navigation environment (Collins et al., Reference Collins, Henton, Mireault, Heroux, Schmidt, Dragert and Bisnath2009; Shi, Reference Shi2012; Geng and Bock, Reference Geng and Bock2014). However, the dual-frequency float PPP based on IF combination is easy to implement and reliable for maritime precise positioning.
The navigation performance of PPP depends on the quality of correction products including their accuracy and precision (Fund et al., Reference Fund, Perosanz, Testut and Loyer2013). One of the most commonly used precise products for satellite orbit and clocks is from the International GNSS Service (IGS) with different latencies, ranging from three hours for the ultra-rapid (observed half), to 17 hours for the rapid, and 13 days for the final products (Kouba, Reference Kouba2009). Although these products normally have good quality, they are used for post-processing PPP. With the broad need of Real-Time (RT) PPP applications, the advent of RT precise orbit and clock correction streams allows PPP to shift from post-processing to providing RT solutions. Although the IGS provides RT ultra-rapid (predicted half) products for RT applications, they have to be re-estimated using a network of reference stations by fixing the corresponding IGS predicted satellite orbits due to the poor accuracy of predicted satellite clocks (Hauschild and Montenbruck, Reference Hauschild and Montenbruck2009). Some researchers have also proposed PPP using Satellite Based Augmentation System (SBAS) correction products to implement RT kinematic positioning (Heßelbarth and Wanninger, Reference Heßelbarth and Wanninger2013; Li et al., Reference Li, Jia, Zhao, Cheng, Liu and Ding2016). However, the position accuracy of SBAS aided PPP is limited by the poor accuracy of SBAS correction products when compared with the IGS correction products. In April 2013, the IGS launched an open-access Real-Time Service (RTS) for RT PPP applications. The accuracy of RT satellite orbit and clock products distributed as the State Space Representation format from Radio Commission for Maritime Services (RTCM-SSR) are better than those of the RT ultra-rapid (predicted half) products (Elsobeiey and Al-Harbi, Reference Elsobeiey and Al-Harbi2016). The Analysis Centres (ACs), such as the German Research Centre for Geosciences (GFZ) and Centre National d'Etudes Spatiales (CNES), can also provide the streams in RTCM-SSR format for RT PPP (Li et al., Reference Li, Ge, Dai, Ren, Fritsche and Wickert2015; Shi et al., Reference Shi, Yuan, Cai and Wang2017). In addition, a number of private commercial companies provide RT correction products in RTCM-SSR, such as Fugro and Veripos. Furthermore, the precise RT correction products in RTCM-SSR format are also recognised by the International Maritime Organization (IMO) for RT maritime PPP applications (IMO, 2004).
Currently, the investigation of PPP for maritime applications is mainly based on the Global Positioning Service (GPS) (Geng et al., Reference Geng, Teferle, Meng and Dodson2010; Alkan and Öcalan, Reference Alkan and Öcalan2013; Eldiasty and Elsobeiey, Reference Eldiasty and Elsobeiey2015). The BeiDou Navigation Satellite System (BDS) is the third navigation satellite system, offering an independent regional service now and a global positioning service by 2020 (CSNO, 2013). By the end of 2016, there were 14 satellites with full operational capability including five Geostationary Earth Orbit (GEO) satellites, six satellites in Inclined Geosynchronous Orbit (IGSO) and three satellites in Medium altitude Earth Orbit (MEO). At present, BDS can provide full coverage in the Asia-Pacific region, and the IMO has decided to accept BDS as one of the satellite navigation providers. Although it is widely accepted that the combination of multiple constellations is positive to the position accuracy and convergence time of PPP, to the authors' knowledge, the performance evaluation of maritime RT PPP using BDS or BDS/GNSS is not clear. Therefore, it is necessary to evaluate the performance of maritime PPP based on BDS and BDS/GNSS in the Asia-Pacific region. Meanwhile, it is now feasible to investigate the maritime positioning performance of RT BDS/GNSS PPP, due to the availability of RT satellite corrections distributed as RTCM-SSR streams.
This paper focuses on a maritime performance evaluation of BDS/GNSS RT kinematic PPP. Firstly, we present the mathematical model of dual-frequency IF PPP. In particular, the differences between RT satellite products and final precise products including GPS, BDS and the Russian GLONASS are analysed, and a detailed tropospheric estimation method is introduced. Furthermore, the adjustment model of BDS/GNSS PPP adopts the Robust Sequential Least Squares (RSLSQ) method by introducing a weighting function (Yang et al., Reference Yang, He and Xu2001) to estimate the rover parameters with the characterisation of a stochastic model. Secondly, the performance of BDS/GNSS PPP is evaluated using real world maritime kinematic data, including single and multi-constellation GNSS. Some conclusions and remarks are summarised at the end of the paper.
2. MATHEMATICAL MODEL OF PPP
This section presents the mathematical model of BDS/GNSS PPP. After a short description of the dual-frequency IF PPP model, RT satellite correction using RTCM-SSR and the tropospheric estimation are introduced in detail. Then, the adjustment model and the stochastic model are introduced to estimate rover parameters based on the RSLSQ method.
2.1. IF PPP model
The dual-frequency IF combination is widely used by PPP models, which can be simplified as (Zumberge et al., Reference Zumberge, Heflin, Jefferson, Watkins and Webb1997):
 $$P^s_{IF}=\displaystyle{{f^2_1}\over{f^2_1-f^2_2}}P^s_{1}-\displaystyle{{f^2_2}\over{f^2_1-f^2_2}} P^s_2=\rho^s+\delta\rho^s+dt_r+dt^s+d^s_{trop}+\varepsilon_{P^s_{IF}} $$
$$P^s_{IF}=\displaystyle{{f^2_1}\over{f^2_1-f^2_2}}P^s_{1}-\displaystyle{{f^2_2}\over{f^2_1-f^2_2}} P^s_2=\rho^s+\delta\rho^s+dt_r+dt^s+d^s_{trop}+\varepsilon_{P^s_{IF}} $$ $$\Phi^s_{IF}=\displaystyle{{f^2_1}\over{f^2_1-f^2_2}}\Phi^s_{1}-\displaystyle{{f^2_2}\over{f^2_1-f^2_2}} \Phi^s_2=\rho^s+\delta\rho^s+dt_r+dt^s+d^s_{trop}+N^s_{IF}+B^s_{IF}+\varepsilon_{\Phi^s_{IF}} $$
$$\Phi^s_{IF}=\displaystyle{{f^2_1}\over{f^2_1-f^2_2}}\Phi^s_{1}-\displaystyle{{f^2_2}\over{f^2_1-f^2_2}} \Phi^s_2=\rho^s+\delta\rho^s+dt_r+dt^s+d^s_{trop}+N^s_{IF}+B^s_{IF}+\varepsilon_{\Phi^s_{IF}} $$
where f i(i = 1, 2) are the carrier phase frequencies in Hertz and P i and Φi denote the code and phase observation at the i-th frequency in metres, respectively. The superscript s refers to the satellite, and the subscript IF means the IF combination. ρ denotes the geometric distance between satellite and receiver in metres, δρ is the satellite orbit error in metres and dt r and dt s represent the receiver and satellite clock error in metres, respectively. d trop is the troposphere delay error in metres. N IF and B IF denote the IF integer phase ambiguity and the IF initial phase delay in metres, respectively. ![]() ${\varepsilon}_{P_{IF}}$ and
${\varepsilon}_{P_{IF}}$ and ![]() ${\varepsilon}_{\Phi_{IF}}$ represent the multipath and receiver noise for the IF code and phase in metres, respectively.
${\varepsilon}_{\Phi_{IF}}$ represent the multipath and receiver noise for the IF code and phase in metres, respectively.
The more observation error sources are corrected or mitigated, the higher the position accuracy and a faster convergence time can be obtained. The first order of ionosphere delay can be eliminated from Equations (1) and (2). Meanwhile, the relativity effects, the phase wind-up, as well as the site displacement effects, including solid earth tides, ocean tides and polar tides, must be corrected through the empirical models (Kouba, Reference Kouba2009). The satellite-induced Differential Code Bias (DCB) can be eliminated by forming either a L1/L2 or B1/B2 IF combination (Kouba, Reference Kouba2009; Guo et al., Reference Guo, Zhang, Wang and Ren2016). Elevation- and frequency-dependent corrections are applied for BDS code systematic biases (Wanninger and Beer, Reference Wanninger and Beer2015). For the carrier phase, the initial phase delays cannot be cancelled and will be mapped into ambiguities. This mapping will not be an issue since the ambiguities are estimated with the position coordinates and receiver clock error as a lumped term and treated as real solutions (Guo et al., Reference Guo, Zhang, Wang and Ren2016). In addition, the satellites' orbit, the satellites' clock and the troposphere delay should be corrected to achieve RT maritime PPP, which will be analysed next.
2.2. Real-time satellite orbit and clock corrections
Unlike the final precise products from the IGS, the RT precise products in RTCM-SSR format are the corrections referring to the broadcast ephemeris. The broadcast ephemeris refers to the Earth-Centred-Earth Fixed (ECEF) coordinate system. However, the RT corrections are given in the orbital coordinate system (radial-track, along-track and cross-track), so the RT corrections must be transformed from the orbital coordinate system to the ECEF coordinate system. The RT satellite clock corrections are streamed in the form of polynomial coefficients C 0, C 1, C 2, and high rate clock message correction hrclk, which also refer to the current broadcast ephemeris. Therefore, the current RT precise satellite orbit and clock can be calculated as follows (RTCM, 2013):
 $$\left[\matrix{\delta_r\cr\delta_a\cr\delta_c}\right]_t= \left[\matrix{\delta_r\cr\delta_a\cr\delta_c}\right]_{t_0}+ \left[\matrix{\dot{\delta}_r\cr\dot{\delta}_a\cr\dot{\delta}_c}\right]\cdot \lpar t-t_0\rpar $$
$$\left[\matrix{\delta_r\cr\delta_a\cr\delta_c}\right]_t= \left[\matrix{\delta_r\cr\delta_a\cr\delta_c}\right]_{t_0}+ \left[\matrix{\dot{\delta}_r\cr\dot{\delta}_a\cr\dot{\delta}_c}\right]\cdot \lpar t-t_0\rpar $$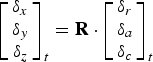 $$\left[\matrix{\delta_x\cr\delta_y\cr\delta_z}\right]_t= {\bf R}\cdot \left[\matrix{\delta_r\cr\delta_a\cr\delta_c}\right]_t $$
$$\left[\matrix{\delta_x\cr\delta_y\cr\delta_z}\right]_t= {\bf R}\cdot \left[\matrix{\delta_r\cr\delta_a\cr\delta_c}\right]_t $$
where δ r, δ a and δ c are the radial-track, along-track and cross-track corrections, respectively. t 0 and t are the issue of data and the current epoch, respectively. ![]() $\dot{\delta}_{r}$,
$\dot{\delta}_{r}$, ![]() $\dot{\delta}_{a}$ and
$\dot{\delta}_{a}$ and ![]() $\dot{\delta}_{c}$ are the rate of radial-track, along-track, and cross-track corrections, respectively. δ x, δ y and δ z are the orbital corrections in the ECEF coordinate system, R is the transformation matrix and r and
$\dot{\delta}_{c}$ are the rate of radial-track, along-track, and cross-track corrections, respectively. δ x, δ y and δ z are the orbital corrections in the ECEF coordinate system, R is the transformation matrix and r and ![]() $\dot{r}$ are the satellite position and velocity vectors, respectively (RTCM, 2013). t c is the RT precise satellite clock correction and C 0, C 1 and C 2 are the polynomial coefficients of RT satellite clock corrections. The Phase Centre Offsets (PCO) should be corrected, if the satellite orbit corrections refer to the centre of mass of satellite antennae.
$\dot{r}$ are the satellite position and velocity vectors, respectively (RTCM, 2013). t c is the RT precise satellite clock correction and C 0, C 1 and C 2 are the polynomial coefficients of RT satellite clock corrections. The Phase Centre Offsets (PCO) should be corrected, if the satellite orbit corrections refer to the centre of mass of satellite antennae.
Precise satellite orbits and clocks are essential prerequisites for a PPP service and their performance in terms of accuracy and time latency decides to some extent the capacity of the system services (Li et al., Reference Li, Ge, Dai, Ren, Fritsche and Wickert2015). Therefore, the quality of RT corrections is key in ensuring the performance of PPP. The RT RTCM-SSR corrections used in this study are from the GNSS centre of Wuhan University CLK93 Mountpoint. The update interval for the satellite correction products is 5 s. The satellite orbit corrections refer to the phase centre of satellite antennae. The RT RTCM-SSR correction streams broadcast over the Internet using the Networked Transport of RTCM via Internet Protocol (NTRIP). In order to evaluate the quality of RT corrections from CLK93, the difference is compared between the RT precise products and the final precise products from GFZ in the Day Of Year (DOY) 73, 2016, aiming at ensuring that the stochastic weighting model of RT PPP is consistent with the quality of RT correction products. The evaluation method for satellites' orbit and clock based on a one day solution is adopted because the final precise products from GFZ are a stable and trustworthy reference for evaluating the quality of RT precise orbit and clock products. Meanwhile, the Root Mean Square (RMS) of errors of the satellite orbit and the Standard Deviation (STD) of errors of the satellite clock are two indicators to evaluate the quality of RT satellite orbit and clock, respectively.
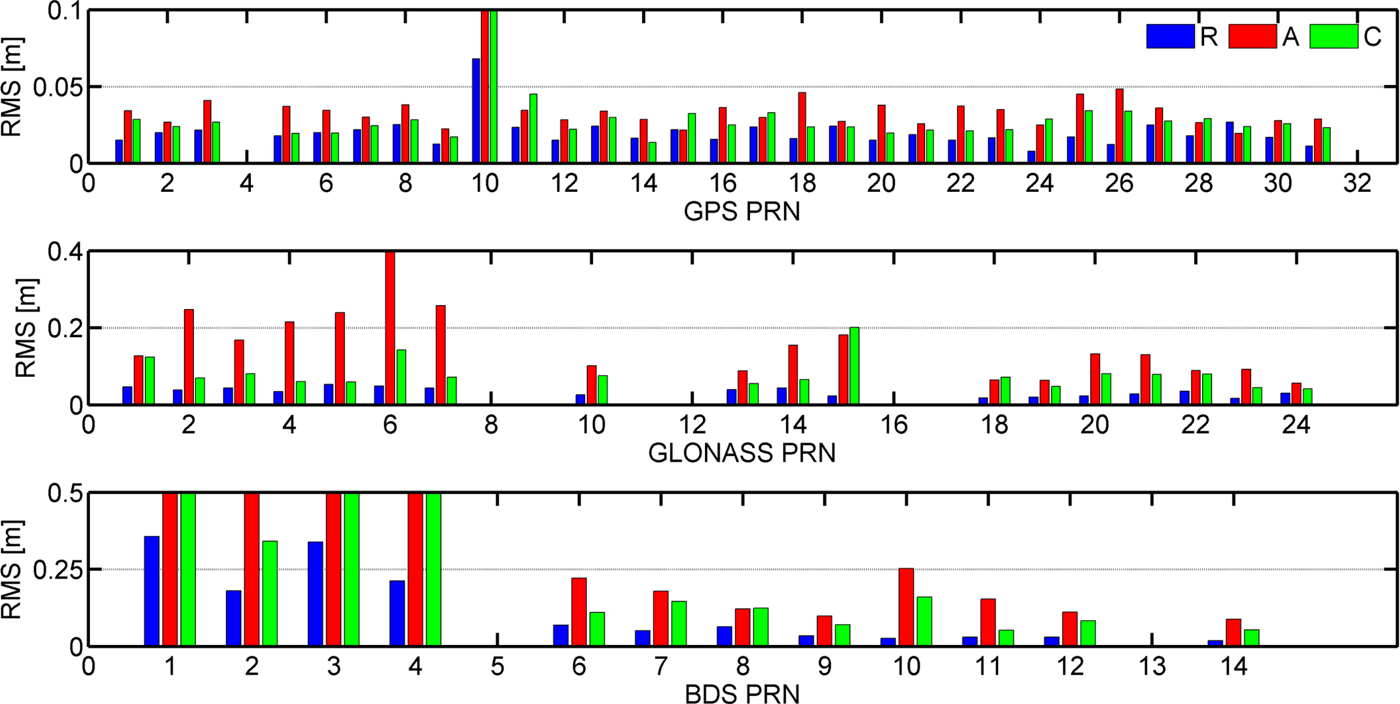
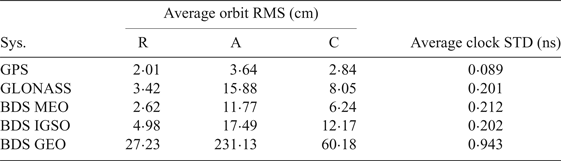
Figure 1 shows the RMS values of 24 hour overlap for each satellite in the along-track, cross-track and radial-track directions. For the GPS satellites, the RMS values are generally better than 3 cm in the radial-track and cross-track direction, and better than 4 cm in the along-track direction. For the GLONASS satellites, the RMS values in the radial-track are better than 4 cm, and the RMS values in the cross-track direction are more than twice as much as the radial-track RMS values. The BDS MEO satellites have a similar orbit difference to GLONASS satellites, and the RMS values of BDS IGSO satellites are twice as large as for the BDS MEO. For the BDS GEO satellites, the orbit RMS values are significantly enlarged to 27·23 cm, 60·18 cm and 231·13 cm in the radial-track, cross-track and along-track directions, as shown in Table 1. Therefore, the RMS values of GEO satellites in each direction are much larger than for the other satellites, especially in the along-track direction. One explanation is that the GEO satellites do not move significantly in the along-track direction with respect to the ground stations, resulting in a rather weak geometrical constellation (Li et al., Reference Li, Ge, Dai, Ren, Fritsche and Wickert2015). Although it can be found that the RMS values in the along-track direction for all satellites are the largest among the three directions, the positioning users are less sensitive to the errors in the along-track and cross-track directions.
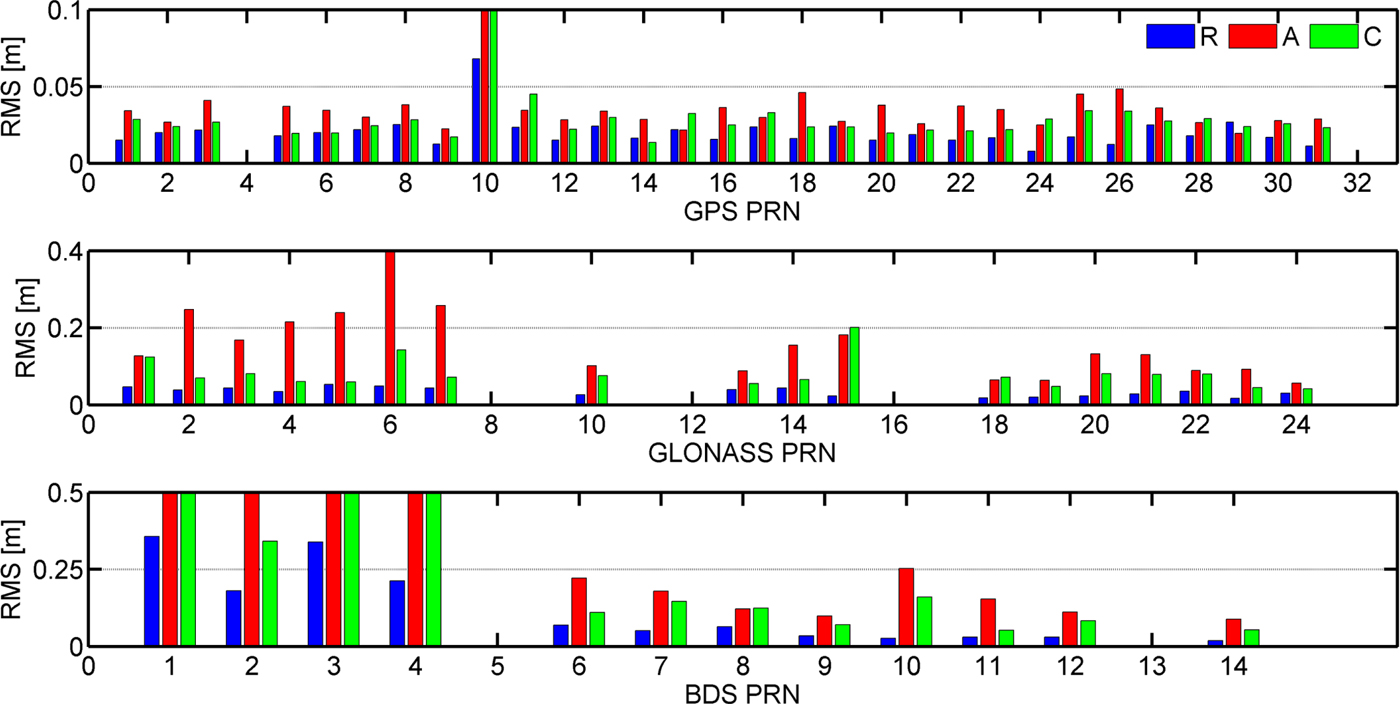
Figure 1. RMS values of 24hour orbit differences in radial, cross, and along for GPS, BDS and GLONASS.
Table 1. Statistics of RT satellites orbit and clock for GPS, BDS, and GLONASS

Figure 2 shows the STD values of 24 hour overlap for each satellite to assess the quality of RT clock products. The STDs of clock differences are calculated by removing the common clock bias with respect to all satellites, therefore the STD values are equal to the RMS values in this case. The constant satellite clock bias which is different from satellite to satellite can be absorbed by ambiguity items and will not affect PPP position solutions (Li et al., Reference Li, Ge, Dai, Ren, Fritsche and Wickert2015). The STDs of GPS RT clock errors are less than 0·1 ns. The STD of GLONASS clocks is twice as large as for GPS. For the BDS satellites, the STD values of IGSO and MEO clocks have a similar accuracy to GLONASS; however, the STD of BDS GEO satellites clock is enlarged to 0·943 ns, which will degrade the users' position accuracy.
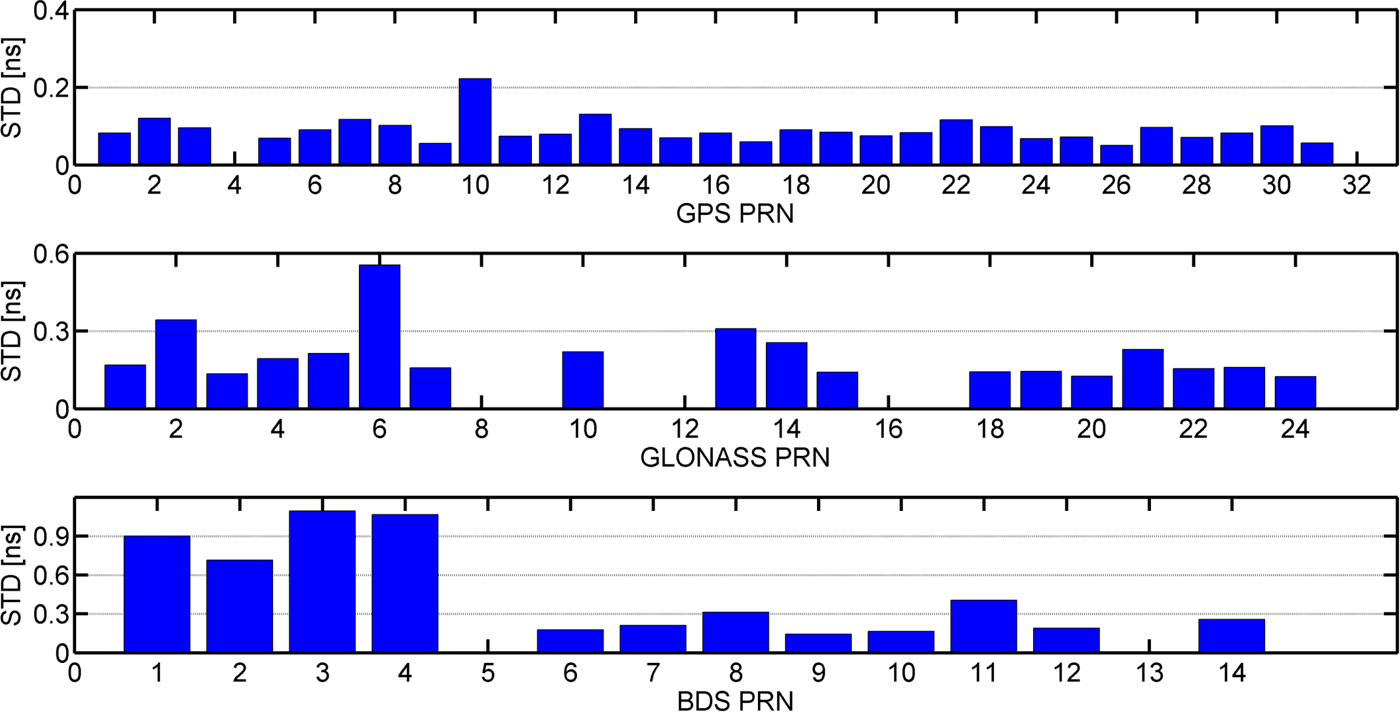
Figure 2. STD values of 24 hour clock differences for GPS, BDS and GLONASS.
From Figure 1 and Table 1, it can be seen that the quality of RT GPS products is similar to that found by Wang et al. (Reference Wang, Li, Ge, Neitzel, Wang and Yuan2018), therefore, the quality of RT correction products can meet the requirement for GPS PPP. Although GLONASS, BDS MEO and BDS IGSO in the radial-track direction are better than 5cm, the STDs of RT clocks are twice as large than for GPS. Meanwhile, BDS GEO satellites have larger orbit and clock errors than the other satellites, thus, the BDS GEO satellites should be assigned smaller weights than the other satellites. Therefore, the weight of different satellite types should be adjusted based on the differences of correction product quality. It is noted that the satellites which are not shown in
Figures 1 and 2 are lacking in RT precise products or final precise products.
2.3. Troposphere estimation method
The atmospheric error of PPP includes two parts, the ionospheric error and the tropospheric error. For the ionospheric error, the first order term can be eliminated by IF combination, and the remainder will be considered as part of a stochastic observation error. As another major atmospheric error, the tropospheric error can be separated into a dominant hydrostatic part and a smaller wet part, in which the hydrostatic part can be modelled with accuracy up to a few millimetres (Bevis et al., Reference Bevis, Businger, Herring, Rocken, Anthes and Ware1992), while the wet part should be estimated with other parameters. Currently, the maritime tropospheric estimation mainly adopts the Global Mapping Function (GMF) (Boehm et al., Reference Boehm, Niell, Tregoning and Schuh2006), while the efforts of Niell Mapping Function (NMF) and forecast Vienna Mapping Function 1 (VMF1-FC) (Boehm et al., Reference Boehm, Kouba and Schuh2009) have not been investigated for maritime PPP. Furthermore, considering the azimuthal inhomogeneity of the troposphere, a more precise troposphere delay model, including a gradient member for maritime troposphere estimation, can be modelled as follows (Chen and Herring, Reference Chen and Herring1997):
The description and handling method of each symbol in Equation (7) is given in Table 2, el and az denote elevation angle and azimuth angle, respectively. Meanwhile, the residual tropospheric error is also considered as a part of a stochastic observation error. The maritime PPP performance based on NMF and VMF1-FC is analysed in Section 3.
Table 2. Handling strategy of troposphere delay for maritime real-time PPP

2.4. Adjustment model
When the observation errors have been corrected, the position coordinates can be precisely resolved. Assuming that there are n satellites available, the measurement equation can be written as follows:
 $$\left[\matrix{\tilde{{\bf P}}_{{\bf IF}}\cr\tilde{\bf \Phi}_{{\bf IF}}}\right]= \left[\matrix{{\bf G} & {\bf M}_{{\bf RC}} & {\bf M}_{{\bf T}} & {\bf 0}\cr{\bf G} & {\bf M}_{{\bf RC}} & {\bf M}_{{\bf T}} & {\bf I}}\right]\left[\matrix{{\bf x}\cr{\bf clk}\cr{\bf \beta} \cr{\bf n}_{{\bf IF}}}\right]+{\bf R}\to {\bf V}={\bf H}{\bf \Delta}+{\bf R} $$
$$\left[\matrix{\tilde{{\bf P}}_{{\bf IF}}\cr\tilde{\bf \Phi}_{{\bf IF}}}\right]= \left[\matrix{{\bf G} & {\bf M}_{{\bf RC}} & {\bf M}_{{\bf T}} & {\bf 0}\cr{\bf G} & {\bf M}_{{\bf RC}} & {\bf M}_{{\bf T}} & {\bf I}}\right]\left[\matrix{{\bf x}\cr{\bf clk}\cr{\bf \beta} \cr{\bf n}_{{\bf IF}}}\right]+{\bf R}\to {\bf V}={\bf H}{\bf \Delta}+{\bf R} $$ $${\bf R}=\left(k^S_s\cdot\left[\matrix{ k^S_c\cdot \sigma^2_{UDRE}+\sigma^2_{trop}+k^S_o\cdot \sigma^2_{\hat{P}_{IF}} & k^S_c\cdot \sigma^2_{UDRE}+\sigma^2_{trop} \cr k^S_c\cdot \sigma^2_{UDRE}+\sigma^2_{trop} & k^S_c\cdot \sigma^2_{UDRE}+\sigma^2_{trop}+k^S_o\cdot \sigma^2_{\hat{\Phi}_{IF}} }\right]\right)\otimes {\bf I} $$
$${\bf R}=\left(k^S_s\cdot\left[\matrix{ k^S_c\cdot \sigma^2_{UDRE}+\sigma^2_{trop}+k^S_o\cdot \sigma^2_{\hat{P}_{IF}} & k^S_c\cdot \sigma^2_{UDRE}+\sigma^2_{trop} \cr k^S_c\cdot \sigma^2_{UDRE}+\sigma^2_{trop} & k^S_c\cdot \sigma^2_{UDRE}+\sigma^2_{trop}+k^S_o\cdot \sigma^2_{\hat{\Phi}_{IF}} }\right]\right)\otimes {\bf I} $$
where ![]() $\tilde{{\bf P}}_{{\bf IF}}$ and
$\tilde{{\bf P}}_{{\bf IF}}$ and ![]() $\tilde{\bf{\Phi}}_{{\bf IF}}$ are the n × 1 IF code and phase observation residuals, respectively.
$\tilde{\bf{\Phi}}_{{\bf IF}}$ are the n × 1 IF code and phase observation residuals, respectively. ![]() ${\bf \Delta}$ is the correction vector to the a priori parameters,
${\bf \Delta}$ is the correction vector to the a priori parameters, ![]() ${\bf x}=\lsqb \delta x\ \delta y\ \delta z\rsqb ^{T}$ are the position corrections with n × 3 observation matrix G and
${\bf x}=\lsqb \delta x\ \delta y\ \delta z\rsqb ^{T}$ are the position corrections with n × 3 observation matrix G and ![]() ${\bi clk}=[dt\ ISB]^{T}$ are the receiver clock corrections with n×3 design matrix
${\bi clk}=[dt\ ISB]^{T}$ are the receiver clock corrections with n×3 design matrix ![]() ${\bf M}_{\rm RC}$. For any row of the
${\bf M}_{\rm RC}$. For any row of the ![]() ${\bf M}_{\rm RC},$ the element in the first column is 1, the second column is 1 for BDS, and the third is 1 for GLONASS, otherwise it is 0. ISB is the Inter System Bias vector of BDS and GLONASS to GPS.
${\bf M}_{\rm RC},$ the element in the first column is 1, the second column is 1 for BDS, and the third is 1 for GLONASS, otherwise it is 0. ISB is the Inter System Bias vector of BDS and GLONASS to GPS. ![]() ${\bf \beta}=[d_{\rm w}\ G_{N}\ G_{E}]^{T}$ are the troposphere corrections with n×3 design matrix
${\bf \beta}=[d_{\rm w}\ G_{N}\ G_{E}]^{T}$ are the troposphere corrections with n×3 design matrix ![]() ${\bf M}_{{\bf T}}$ from Equation (7).
${\bf M}_{{\bf T}}$ from Equation (7). ![]() $ {\bi n}_{\bi IF}$is the n×1 correction vector to the real ambiguities and I is the identity matrix with rank n. R is the variance-covariance for the observation noise, ⊗ is the Kronecker product operator and σ UDRE, σ trop,
$ {\bi n}_{\bi IF}$is the n×1 correction vector to the real ambiguities and I is the identity matrix with rank n. R is the variance-covariance for the observation noise, ⊗ is the Kronecker product operator and σ UDRE, σ trop, ![]() $\sigma_{\tilde{P}_{IF}}$ and
$\sigma_{\tilde{P}_{IF}}$ and ![]() $ \sigma_{\tilde{\Phi}_{IF}}$ are the STDs of residual range, troposphere, IF code and IF phase noise. k is the weight coefficient, the superscript S means the satellite system for GPS, BDS, and GLONASS, and the subscript s, c and o denote the satellite system, satellite corrections and observations, respectively. It is noted that all satellite systems are referred to a GPS time scale. A UTC-GPS time offset of 17 s is used for GLONASS within the analysis period, while a 14 s BDS-GPS time offset applies for BDS.
$ \sigma_{\tilde{\Phi}_{IF}}$ are the STDs of residual range, troposphere, IF code and IF phase noise. k is the weight coefficient, the superscript S means the satellite system for GPS, BDS, and GLONASS, and the subscript s, c and o denote the satellite system, satellite corrections and observations, respectively. It is noted that all satellite systems are referred to a GPS time scale. A UTC-GPS time offset of 17 s is used for GLONASS within the analysis period, while a 14 s BDS-GPS time offset applies for BDS.
With the proposed mathematical model Equation (8) and stochastic model Equation (9), we can use the RSLSQ to estimate the position coordinates, as shown in Equation (10). The RSLSQ has a positive effect on resistance against the abnormal observation by adjusting the stochastic model by Equations (11) and (12).
 $$\alpha_i = \left\{\matrix{ 1 & \vert \tilde{V}_i\vert \le k_0 \cr \displaystyle{{k_0}\over{\vert \tilde{V}_i\vert }}\left(\displaystyle{{k_1-\vert \tilde{V}_i\vert }\over{k_1-K_0}}\right)^2 & k_0 \lt \vert {\tilde V}_i \vert \le k_1 \cr 10^{-8} & \vert {\tilde V}_i \vert \gt k_1 }\right.$$
$$\alpha_i = \left\{\matrix{ 1 & \vert \tilde{V}_i\vert \le k_0 \cr \displaystyle{{k_0}\over{\vert \tilde{V}_i\vert }}\left(\displaystyle{{k_1-\vert \tilde{V}_i\vert }\over{k_1-K_0}}\right)^2 & k_0 \lt \vert {\tilde V}_i \vert \le k_1 \cr 10^{-8} & \vert {\tilde V}_i \vert \gt k_1 }\right.$$ where ![]() ${\bi Q}_{{\bf \Delta}}$ is the variance-covariance matrix for
${\bi Q}_{{\bf \Delta}}$ is the variance-covariance matrix for ![]() ${\bf \Delta}$, and
${\bf \Delta}$, and ![]() $\bar{{\bf R}}$ is the equivalent observation variance to R, α i is the variance-covariance amplification factor and
$\bar{{\bf R}}$ is the equivalent observation variance to R, α i is the variance-covariance amplification factor and ![]() ${\tilde V}_i$$ denotes the standardised residual. k 0 and k 1 are the thresholds, and the practical values are 1·0–1·5 and 3·0–4·5, respectively (Zhang et al., Reference Zhang, Guo, Li and Zuo2012).
${\tilde V}_i$$ denotes the standardised residual. k 0 and k 1 are the thresholds, and the practical values are 1·0–1·5 and 3·0–4·5, respectively (Zhang et al., Reference Zhang, Guo, Li and Zuo2012).
In addition to error correction models, the proper stochastic models are also crucial for PPP performance evaluation. The stochastic model should account for the state noise and the observation noise, respectively. For the state noise, the Random Walk (RW) sigma of receiver coordinates and receiver clock offsets are empirically set to ![]() $10\,{\rm m}/\sqrt{s}$ and
$10\,{\rm m}/\sqrt{s}$ and ![]() $10^{2}\, {\rm m} /\sqrt{s}$, respectively. The values of
$10^{2}\, {\rm m} /\sqrt{s}$, respectively. The values of ![]() $10^{-6}\, \hbox{m}/\sqrt{s}$ and
$10^{-6}\, \hbox{m}/\sqrt{s}$ and ![]() $10^{-7}\, \hbox{m}/\sqrt{s}$ are set as the RW sigma for the troposphere and its gradient (Jokinen et al., Reference Jokinen, Feng, Milner, Schuster, Ochieng, Hide, Moore and Hill2011). The stochastic model of observation noise is explained in Equation (9). The STDs of code and phase observations for GPS and BDS are set to 0·5 m and 3 mm, respectively. The STDs of the GLONASS code and phase are set to 0·8 m and 3 mm, respectively. Meanwhile, among many widely-used stochastic models (Jin et al., Reference Jin, Wang and Park2005; Li et al., Reference Li, Ge, Dai, Ren, Fritsche and Wickert2015), we select the elevation dependent weighting model for PPP (Geng et al., Reference Geng, Teferle, Meng and Dodson2010; Guo et al., Reference Guo, Zhang, Wang and Ren2016; Wang et al., Reference Wang, Li, Ge, Neitzel, Wang and Yuan2018). Specifically, the IF observation variance at elevation θ is
$10^{-7}\, \hbox{m}/\sqrt{s}$ are set as the RW sigma for the troposphere and its gradient (Jokinen et al., Reference Jokinen, Feng, Milner, Schuster, Ochieng, Hide, Moore and Hill2011). The stochastic model of observation noise is explained in Equation (9). The STDs of code and phase observations for GPS and BDS are set to 0·5 m and 3 mm, respectively. The STDs of the GLONASS code and phase are set to 0·8 m and 3 mm, respectively. Meanwhile, among many widely-used stochastic models (Jin et al., Reference Jin, Wang and Park2005; Li et al., Reference Li, Ge, Dai, Ren, Fritsche and Wickert2015), we select the elevation dependent weighting model for PPP (Geng et al., Reference Geng, Teferle, Meng and Dodson2010; Guo et al., Reference Guo, Zhang, Wang and Ren2016; Wang et al., Reference Wang, Li, Ge, Neitzel, Wang and Yuan2018). Specifically, the IF observation variance at elevation θ is ![]() $\sigma^{2}_{X_{IF}}=\sigma^{2}_{X_{0\comma IF}}\cdot \lpar 1+1/\sin^{2}\theta\rpar$ with
$\sigma^{2}_{X_{IF}}=\sigma^{2}_{X_{0\comma IF}}\cdot \lpar 1+1/\sin^{2}\theta\rpar$ with ![]() $ \sigma^{2}_{X_{0\comma IF}}$ being the STD of GPS IF observation; the subscript X denotes P or Φ. The other stochastic models selection can be found in Jin et al. (Reference Jin, Wang and Park2005) and Li et al. (Reference Li, Ge, Dai, Ren, Fritsche and Wickert2015). It is noted that k o is decided by the ratio of the observation precision referring to GPS. σtrop is set to 1 cm. The σUDRE for the STD of GPS range residual is set to 0·15 m. Since the accuracy of BDS and GLONASS satellite orbits and clocks are relatively lower than GPS, their range residuals are down-weighted. The BDS MEO, the BDS IGSO and the GLONASS residuals are twice as large as for GPS, and the BDS GEO range residual is a tenth larger than the range residual of GPS, which is regarded as the satellite corrections weight coefficient of k c. The system weight of k s for GPS, BDS and GLONASS are set to 1, 2 and 2, respectively.
$ \sigma^{2}_{X_{0\comma IF}}$ being the STD of GPS IF observation; the subscript X denotes P or Φ. The other stochastic models selection can be found in Jin et al. (Reference Jin, Wang and Park2005) and Li et al. (Reference Li, Ge, Dai, Ren, Fritsche and Wickert2015). It is noted that k o is decided by the ratio of the observation precision referring to GPS. σtrop is set to 1 cm. The σUDRE for the STD of GPS range residual is set to 0·15 m. Since the accuracy of BDS and GLONASS satellite orbits and clocks are relatively lower than GPS, their range residuals are down-weighted. The BDS MEO, the BDS IGSO and the GLONASS residuals are twice as large as for GPS, and the BDS GEO range residual is a tenth larger than the range residual of GPS, which is regarded as the satellite corrections weight coefficient of k c. The system weight of k s for GPS, BDS and GLONASS are set to 1, 2 and 2, respectively.
Furthermore, we adopted the widely-used method, that is, the Melbourne-Wübbena (MW) and Geometry-Free (GF) combination to detect cycle slips (Zhang et al., Reference Zhang, Guo, Li and Zuo2012). If cycle slips are detected, we reset the variances of ambiguities.
3. EXPERIMENT AND RESULTS
In order to sufficiently evaluate RT kinematic BDS/GNSS PPP performance using RTCM-SSR for maritime positioning, we carried out a kinematic experiment based on real-world marine data. First, single constellation RT PPP performance was analysed by comparing with PPP using final precise products. Particularly, we focused on BDS PPP. Secondly, the performance of RT multi-constellation PPP was evaluated to show its superiority for maritime positioning. Meanwhile, the observation residuals were used as an important index to evaluate the multi-constellation PPP model (Pan et al., Reference Pan, Cai, Santerre and Zhang2017a). Finally, the mapping function models of troposphere estimation including GMF, NMF, and VMF1-FC were investigated for maritime PPP performance.
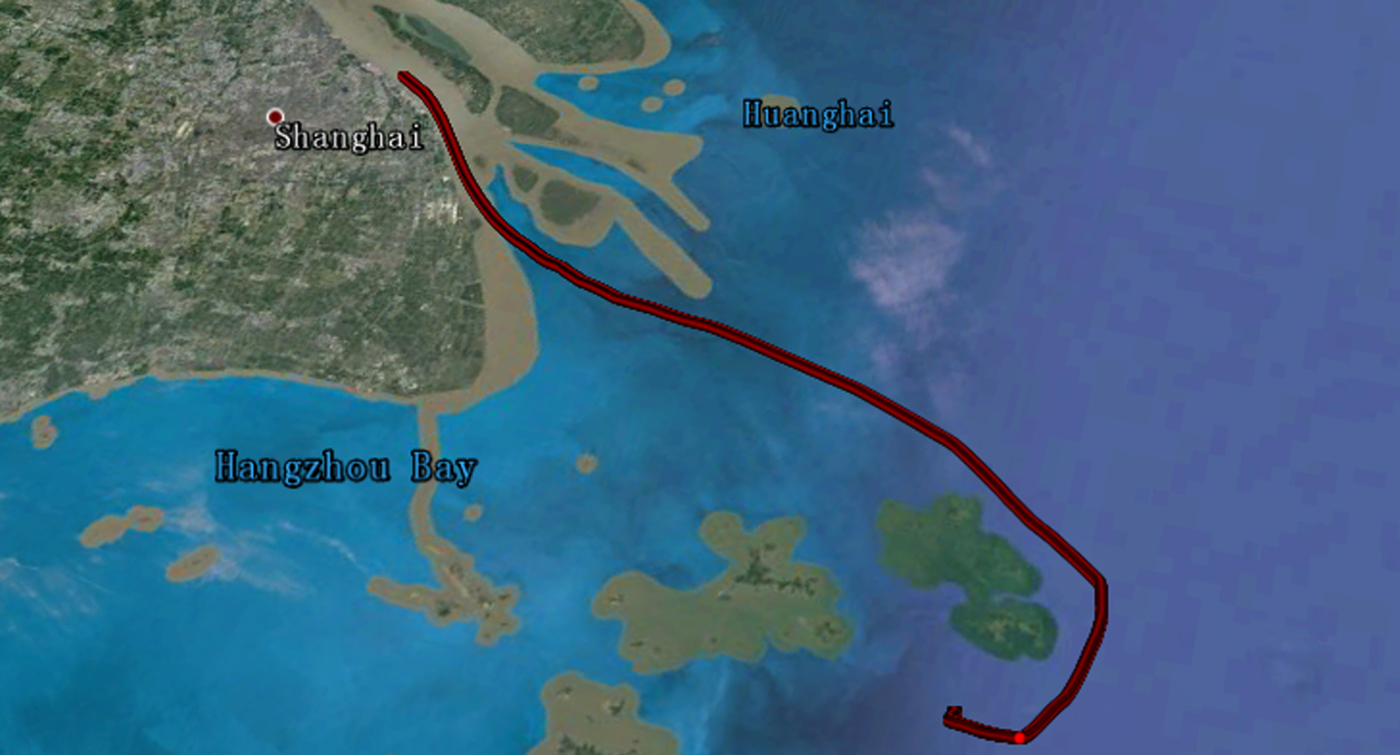
Table 3 summarises the detailed processing strategy for BDS/GNSS PPP. The performance was evaluated by the metrics of position accuracy and convergence time. It should be noted that the reference of position solutions (with an accuracy of cm-level) were obtained by network Real-Time Kinematic (RTK) processing. Meanwhile, in order to ensure that the performance evaluation was reliable, we selected data within the range of network RTK, which corresponds to a 12 hour experiment on 13 March 2016. The motion trajectory was about 137·936 km which started at 31°22′N, 121°38′E, ended at 30°36′N, 122°44′E and the average speed of the experimental ship was 6·2 knots, as shown by the red line in Figure 3.
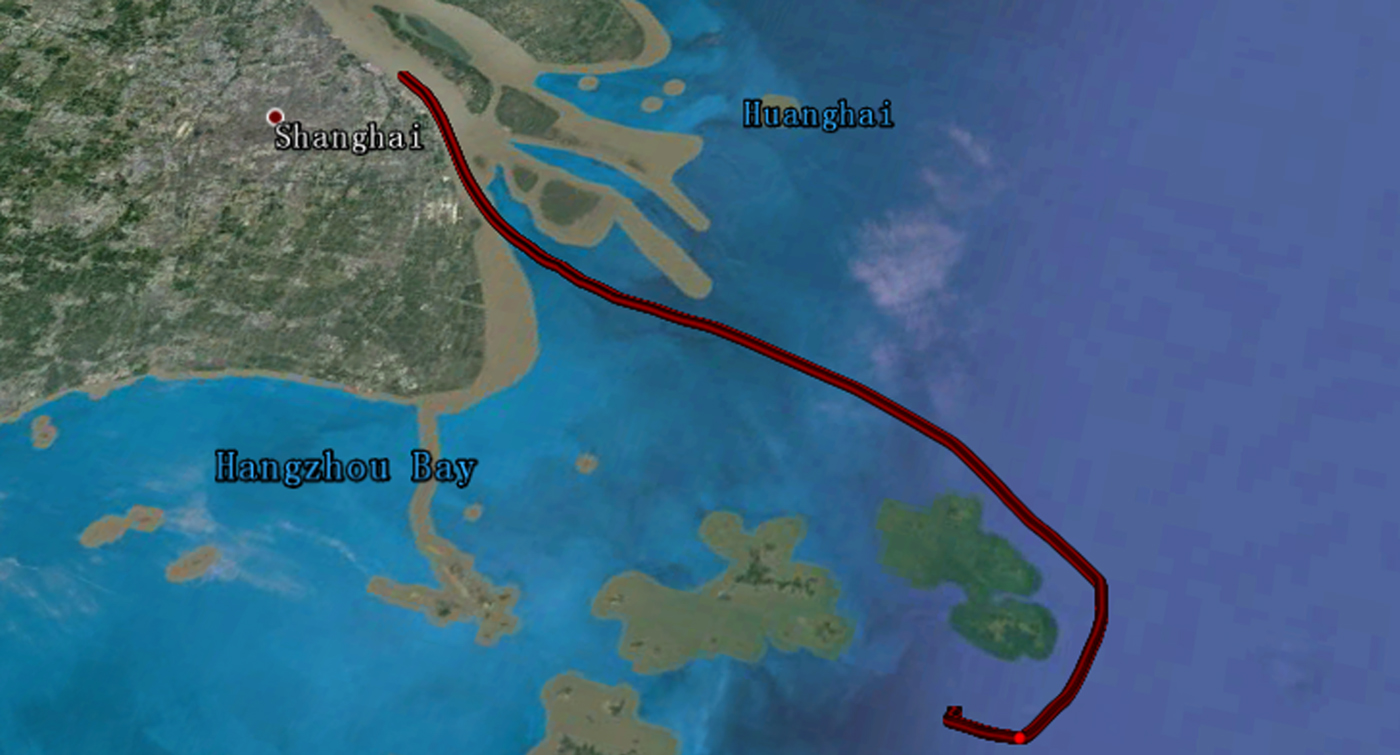
Figure 3. Motion trajectory of the ship.
Table 3. BDS/GNSS maritime PPP processing strategy

For the 12 hour kinematic maritime experiment, the convergence time was defined as the horizontal position error converging to 50 cm for a continuous time span of twenty epochs (Li and Zhang, Reference Li and Zhang2014), and the RMS of position error was calculated from the converged epoch to the end of the experiment in the ambiguity-float mode. In addition, we did not consider the latency effect of transmission RT corrections in the experiment, because the datasets were processed after the fact, that is, post-processing, but “as if” in real-time, strictly with the RTCM-SSR products available at the time of observation.
3.1. Single constellation performance
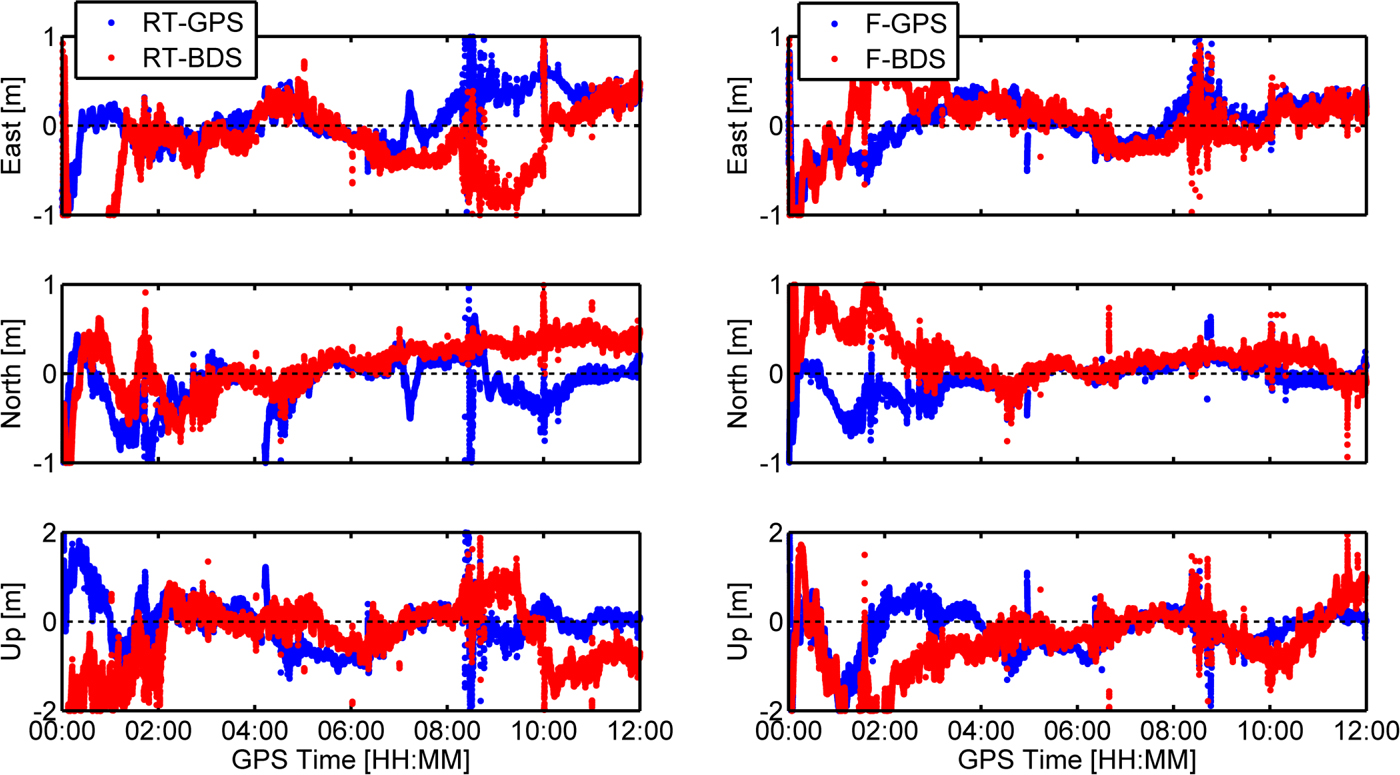
The position errors in the east, north and up components of single constellation using RTCM-SSR (denoted as RT-PPP) and final precise products (denoted as F-PPP) are shown in Figure 4. For RT-PPP, both GPS and BDS can achieve sub-decimetre level position accuracy in the horizontal plane and decimetre level in the vertical direction, while BDS has a slower convergence time. Compared with RT-PPP, the F-PPP using single constellation has a higher position accuracy and faster convergence time, as shown in the right of Figure 4. The reason is that the accuracy of final precise products is higher than RT precise products. BDS F-PPP also has a slower convergence time than GPS because of the relatively slow change of the BDS GEO and IGSO satellite geometry (Lu et al., Reference Lu, Li, Zus, Heinkelmann, Dick, Ge, Wickert and Schuh2017).
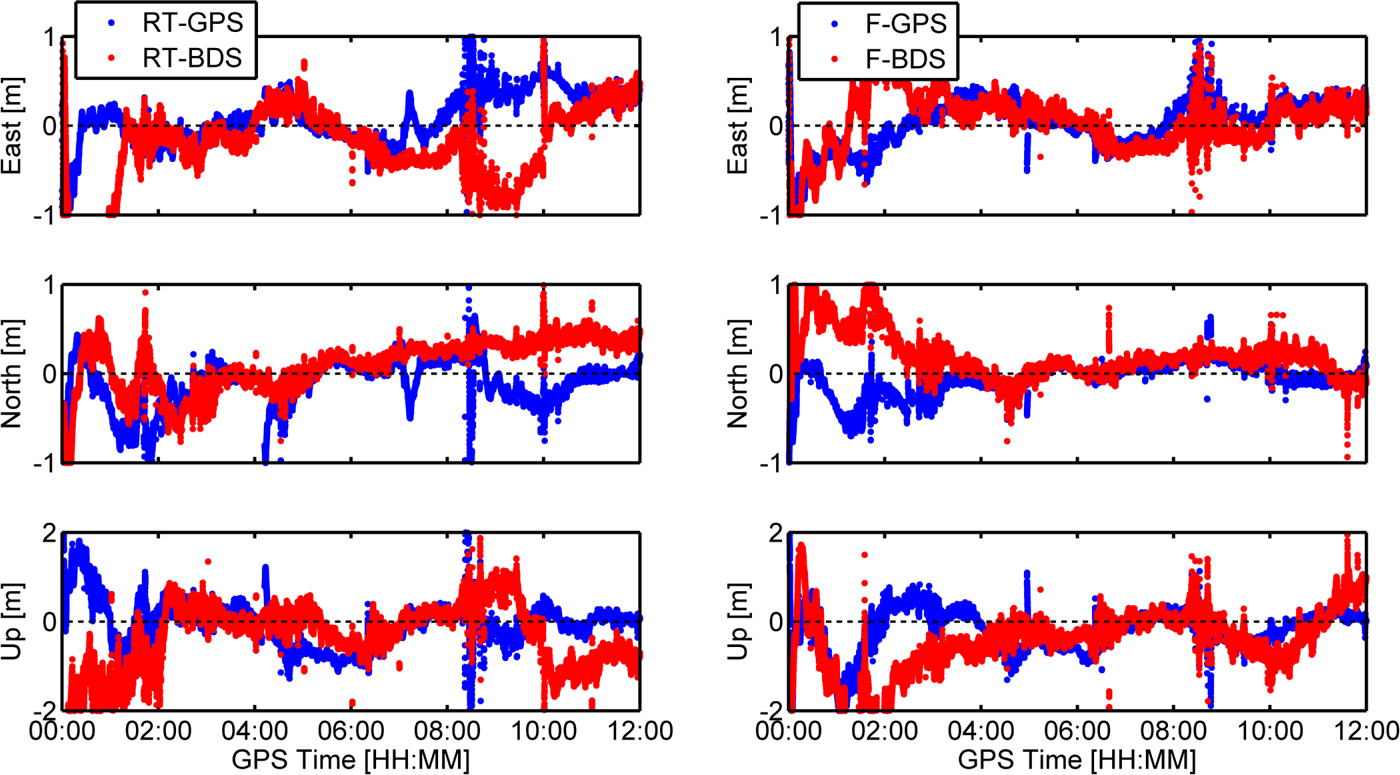
Figure 4. Kinematic position errors in the east, north, and up direction for GPS and BDS. The panels from left to right are RT-PPP and F-PPP, respectively.
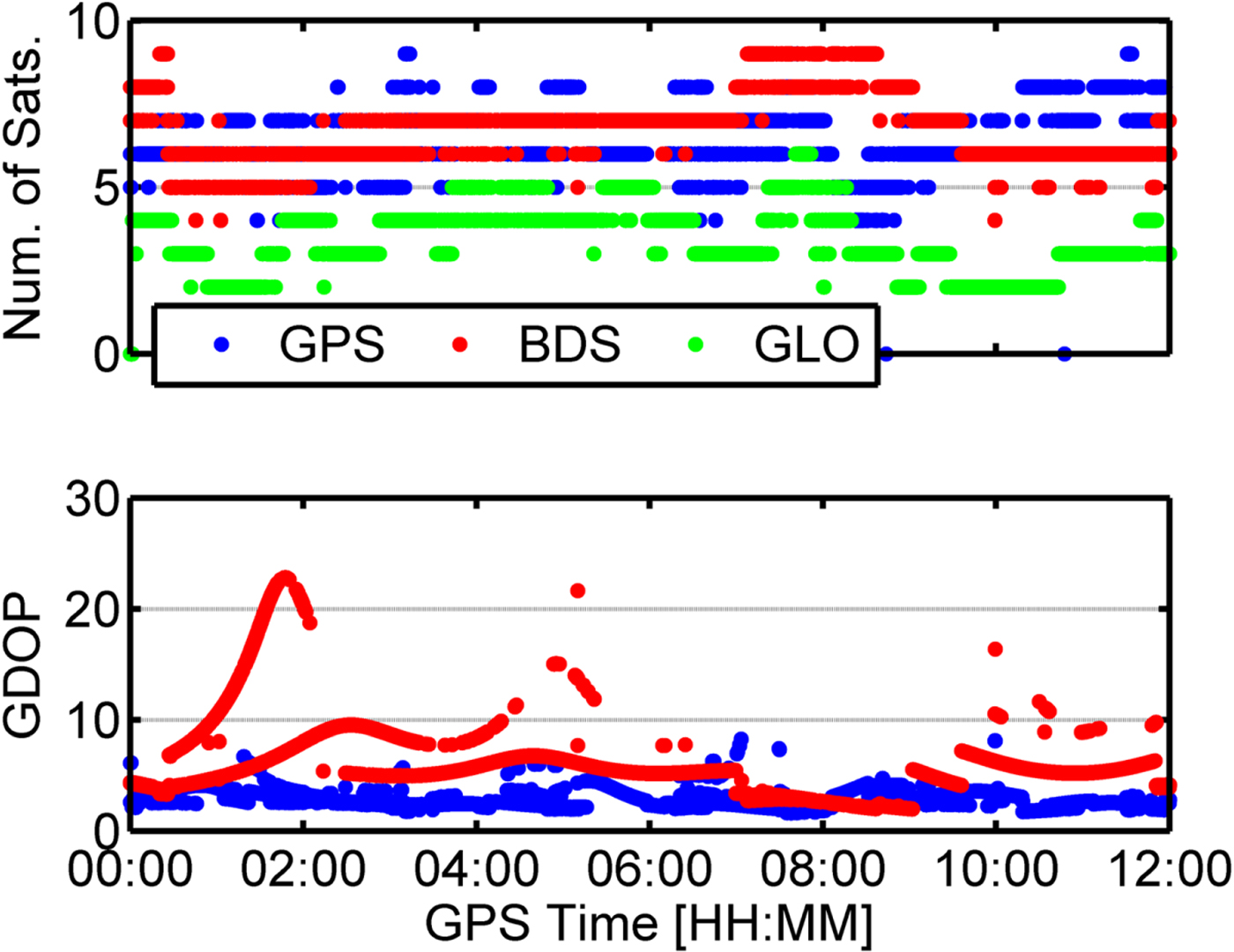
In order to further illustrate the differences of performance between GPS and BDS, Figure 5 shows the number of available satellites and the Geometrical Dilution of Precision (GDOP) values for RT GPS and BDS, respectively. It can be seen that there are always five or six available BDS satellites for the first two hours, and the GDOP values are always much larger than for GPS. A sudden drop of available satellites in Figure 5 can also be observed, and the GDOP values change frequently. In order to achieve consistency of the data and model, the satellite is excluded when the Signal to Noise Ratio (SNR) value is less than 30 dB/Hz, or the a priori standardised residual is larger than 3 or the post-fit IF code and phase residuals are respectively larger than 15 m and 0·15 m. Therefore, the slow convergence time of BDS PPP was caused by the poor satellite geometry distribution and RT satellite corrections quality as shown in Figures 1 and 2. In addition, Figure 5 shows that the available number of GLONASS satellites was always less than five. The statistics of navigation performances for single constellation are shown in Table 4. CT in Table 4 means the Convergence Time and RT and F mean RT-PPP and F-PPP, respectively.
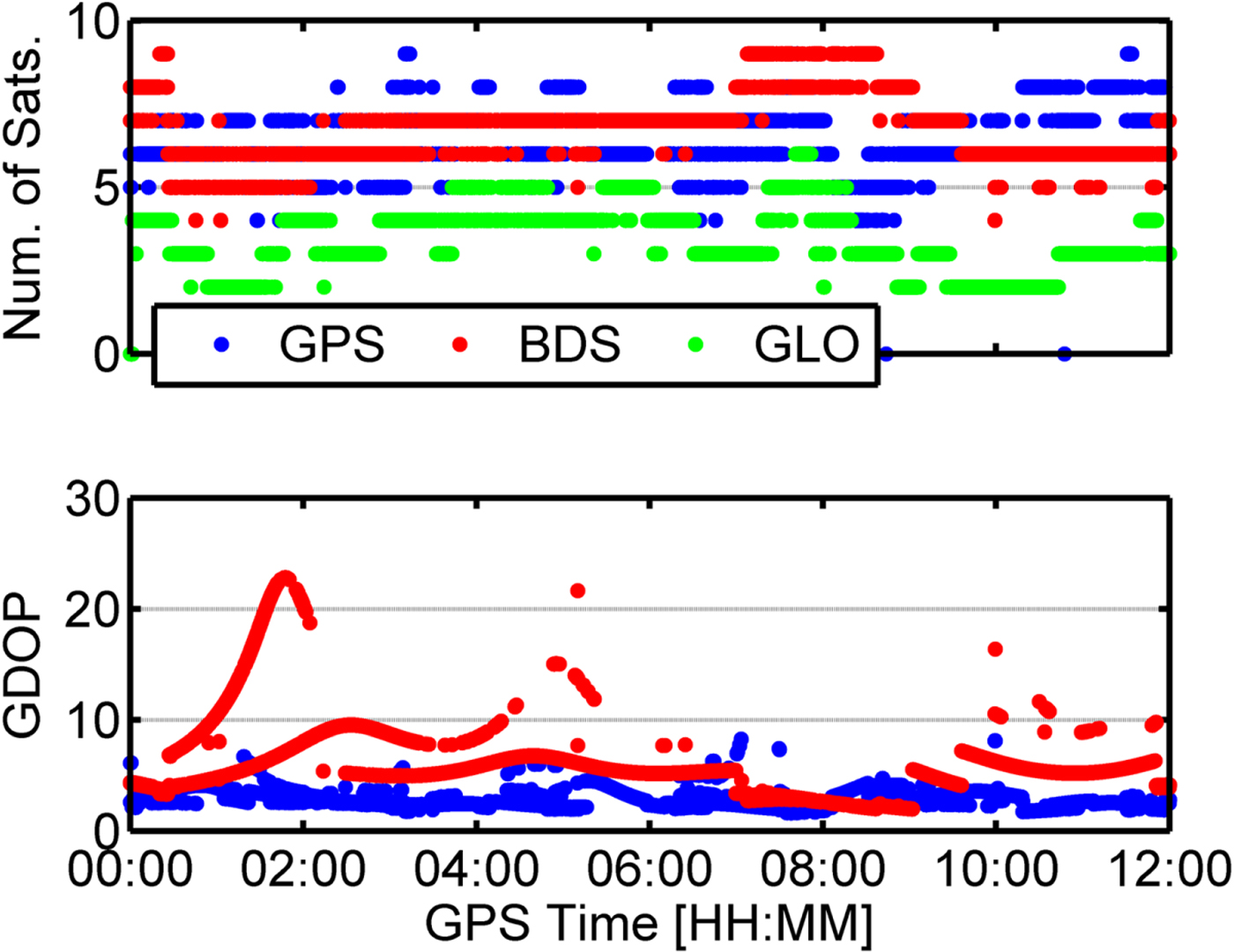
Figure 5. Number of available satellites and GDOP values for GPS and BDS.
Table 4. RMS of navigation performance statistics for single constellation

From Figures 4 and 5, it can be observed that the position errors of a single constellation dramatically increased when the number of available satellites was low or the GDOP is large (at 10:00 for BDS in the left panel of Figure 4).
3.2. Multi-constellation PPP performance
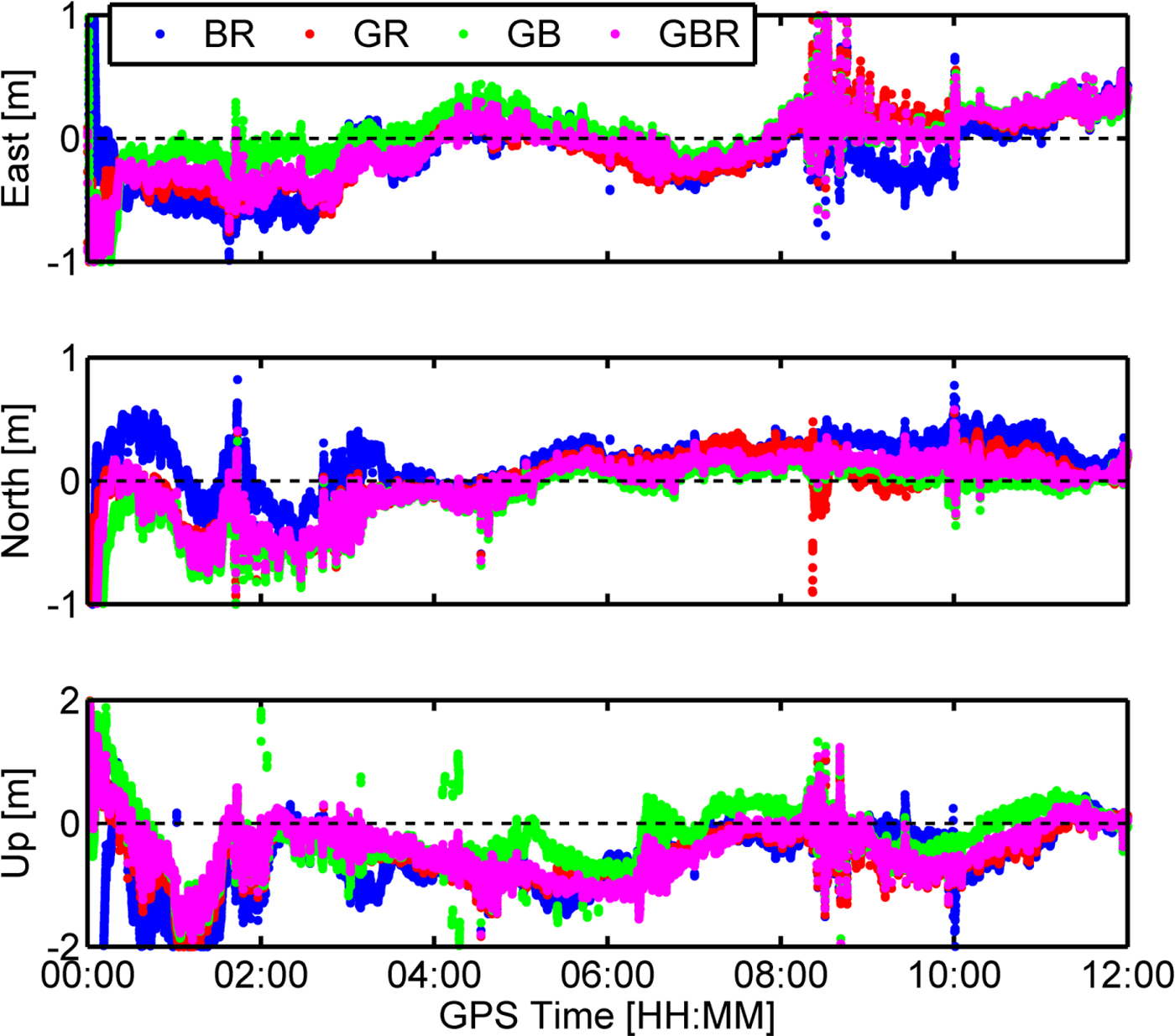
In order to demonstrate the effectiveness of multi-constellation maritime RT PPP in improving position accuracy and convergence time. Figures 6 and 7 present position errors and GDOP values from all the possible combinations of GPS, GLONASS and BDS.
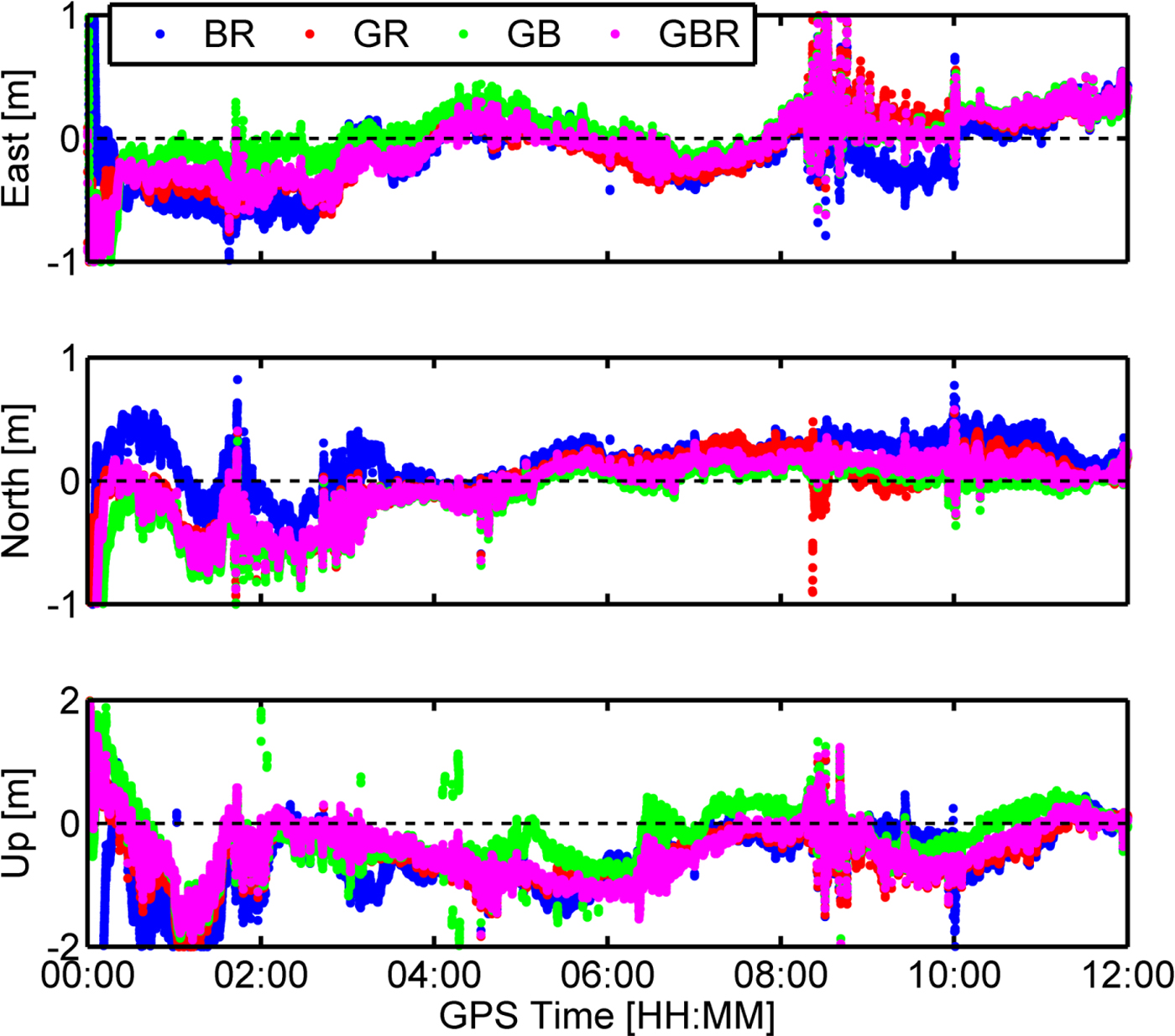
Figure 6. Position errors in east, north, and up direction for multi-GNSS. G, B, and R mean GPS, BDS, and GLONASS, respectively.
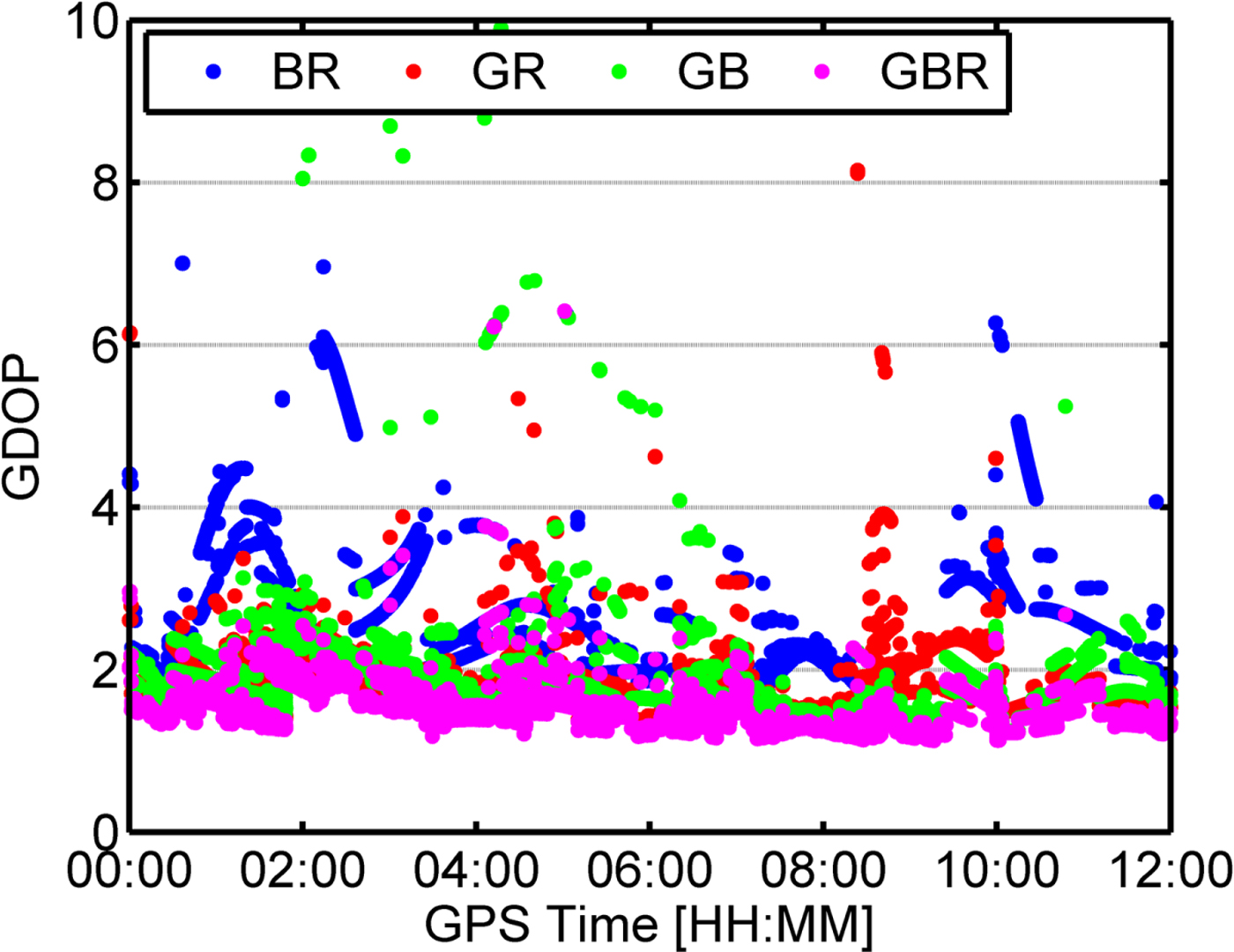
Figure 7. GDOP for multi-GNSS. G, B, and R mean GPS, BDS, and GLONASS, respectively.
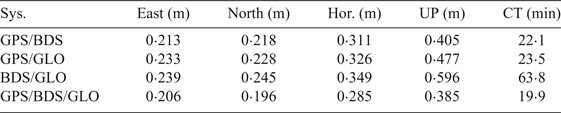
Compared with the single constellation results, the multi-constellation approach has a higher position accuracy and faster convergence time. For the dual-constellation combination, BDS/GPS had a faster convergence time and higher position accuracy than GPS/GLONASS because BDS had more available satellites and better geometry distribution than GLONASS. Meanwhile, the inter-frequency bias of GLONASS was regarded as a random term, thus, we gave little weight to the GLONASS observations which also limited the performance of GPS/GLONASS. Although BDS/GLONASS had a faster convergence time than BDS, the convergence time of BDS/GLONASS still reached up to 63·8 minutes, which is much slower than GPS/GLONASS. The relatively slow convergence time of BDS/GLONASS can be explained by larger GDOP values and worse BDS RT precise products quality than GPS. Therefore, BDS/GPS has the best performance among the dual-constellation configurations. Furthermore, the convergence time, the position accuracy and the GDOP value are further improved after adding the GLONASS observations. It can be concluded that the performance of multi-constellation PPP benefits from an increased number of satellites and improved satellite geometry. Meanwhile, some outliers can be mitigated and the position solutions are smoothed for BDS/GNSS PPP. Table 5 shows the performance statistics of multi-constellation PPP.
Table 5. RMS of navigation performance statistics for multi-constellations

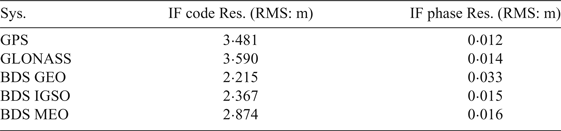
Although multi-constellation PPP gave a better performance, there are still large biased position errors in Figure 6, such as the position solutions between 08:00 and 09:00. In order to assess the maritime kinematic multi-constellation PPP model, the three-constellation observation residuals including IF code and phase are given in Figure 8 and Figure 9, respectively. It can be seen that the IF phase residuals of GPS and GLONASS range from −0·1 mm to 0·1 m, and for BDS range from −0·15 m to 0·15 m. It can also be observed that the IF phase residuals of BDS GEO are the largest, while GPS, GLONASS, BDS IGSO and BDS MEO have similar average IF phase residuals RMS, as shown in Table 6. This is because BDS GEO has the worst RT satellite precise products. Meanwhile, the BDS GEO IF phase residuals are unusual between 08:00 and 09:00, and the position errors increase dramatically, as shown in Figure 6. Furthermore, from Figures 8 and 10, it can be seen that the elevation-dependent weighting stochastic model is suitable for the IF phase observations. However, because the magnitude of IF phase residuals are generally at the centimetre level, the IF phase residuals are easily affected by the accuracy of RT satellite precise products, as shown for the BDS GEO satellites in Figure 8. Overall, the RMS values of IF phase residuals are smaller than 0·016 m for GPS, GLONASS, BDS IGSO and BDS MEO, and no systematic errors can be found in the residuals, suggesting that various errors and biases of the IF phase observations have been properly handled in the kinematic multi-constellation PPP model.
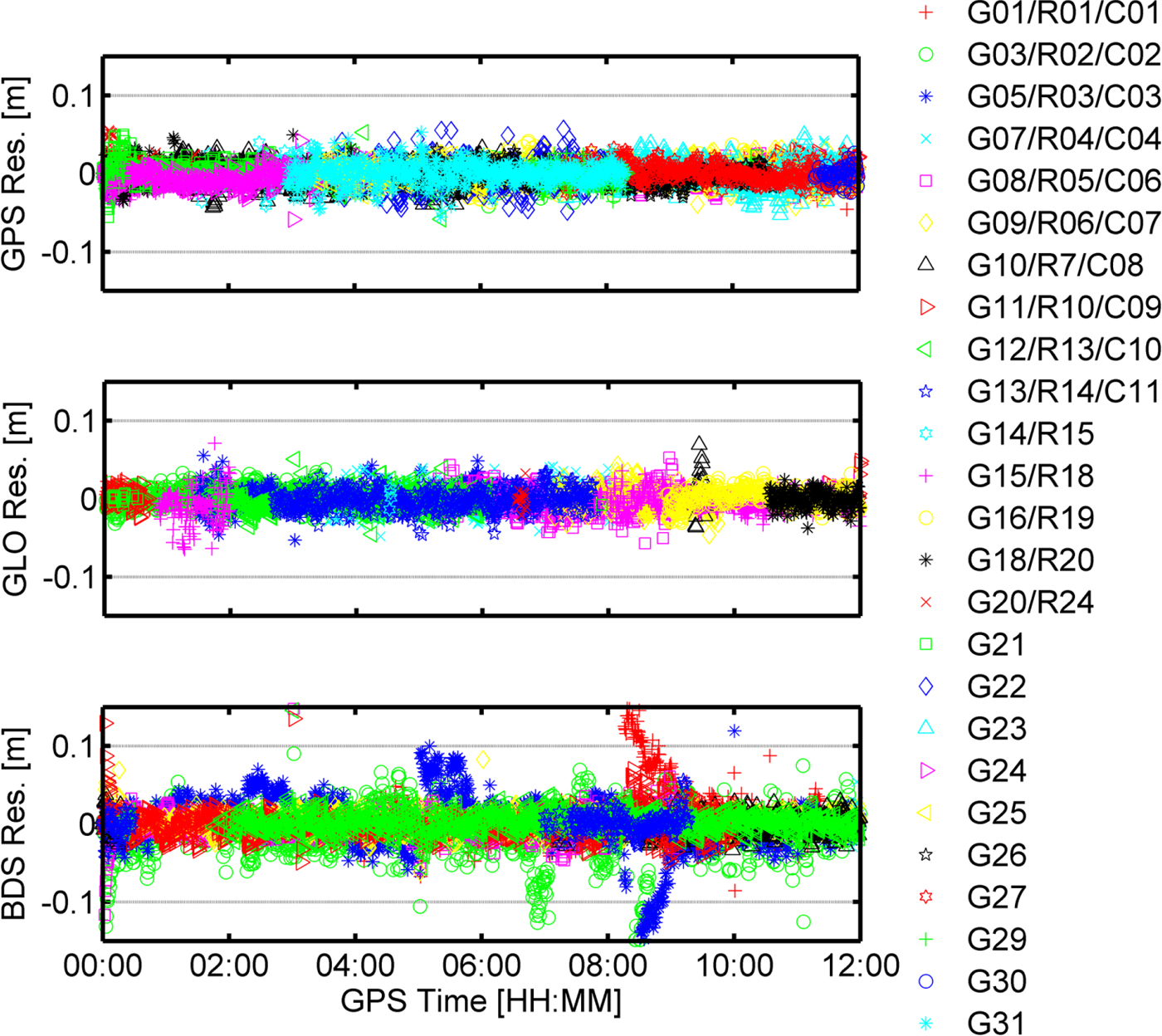
Figure 8. IF phase residuals for GPS, BDS, and GLONASS.

Figure 9. IF code residuals for GPS, BDS, and GLONASS.
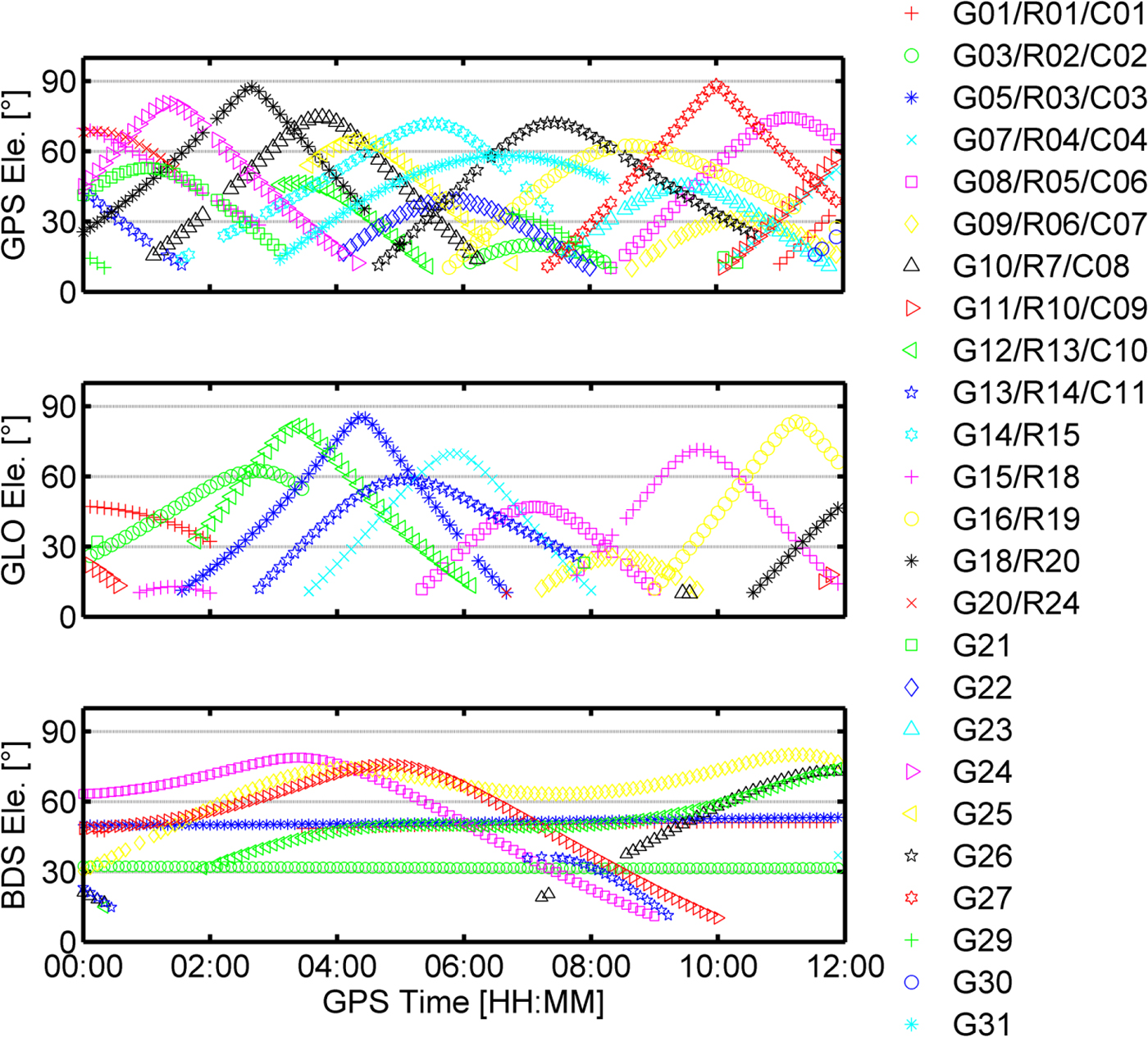
Figure 10. Elevation angle for the GPS, BDS, and GLONASS, respectively.
Table 6. RMS of residuals for GPS, BDS, and GLONASS based on multi-GNSS

Compared with the IF phase residuals, the IF code residuals of GPS, BDS and GLONASS are much larger and have no systematic errors, as shown in Figure 9. Both the IF phase and the IF code residuals have the same un-modelled errors for each satellite including satellite orbit, satellite clock and troposphere error. As the code observation noises and multipath errors are much larger than the phase, and the high-order ionosphere error is much smaller, the IF code residuals mainly reflect IF observation noises and multipath errors. The large observation noise and multipath errors may affect the position accuracy and convergence time of PPP (Seepersad and Bisnath, Reference Seepersad and Bisnath2015). Meanwhile, in order to ensure the positioning continuity, the satellites with large observation noises and multipath errors cannot be excluded for kinematic maritime PPP when the number of available satellites is less than seven for GPS/BDS/GLONASS PPP. Figure 10 gives the elevation angles for GPS, BDS and GLONASS. From Figures 9 and 10, it can also be verified that the elevation-dependent weighting model is suitable for IF code observations.
3.3. PPP performance based on different troposphere mapping functions
Currently, the NMF, the GMF and the VMF1-FC mapping functions can achieve RT troposphere estimation. The tropospheric estimation method is mentioned in Table 2, while the applicability with regard to maritime PPP of NMF and VMF1-FC have not been investigated. Furthermore, the convergence time of PPP is highly dependent on the estimation of tropospheric delays (Shi et al., Reference Shi, Xu, Guo and Gao2014), thus, the BDS/GNSS PPP performance based on the above typical RT tropospheric estimation models are compared for a comprehensive performance evaluation.
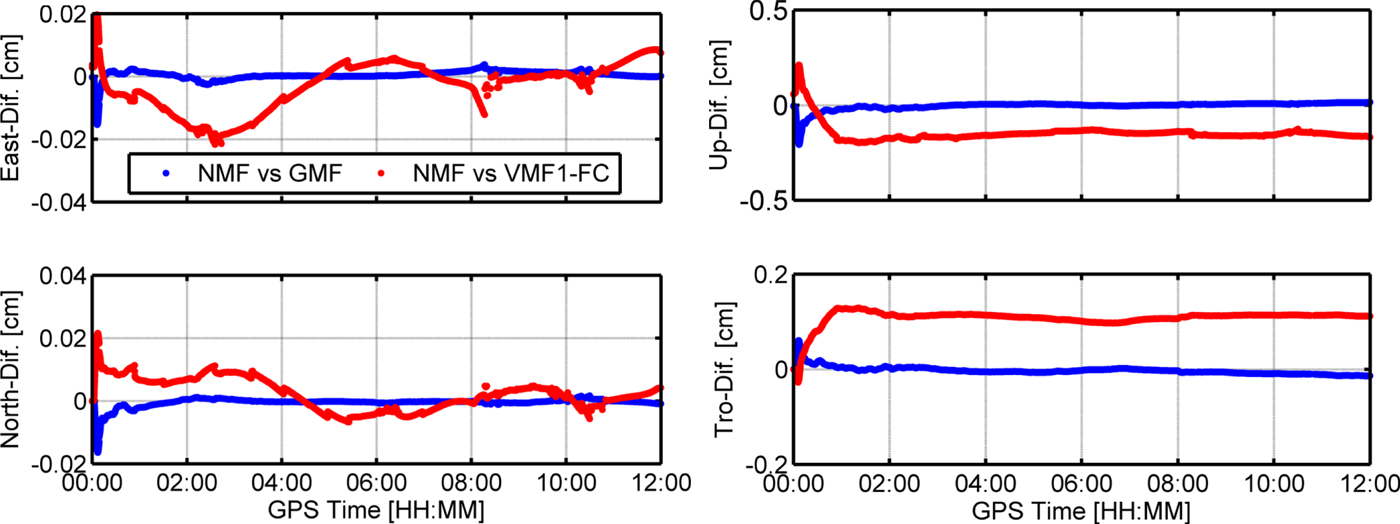
As we lack maritime RT troposphere reference values, the differences are compared to analyse the effects of three RT mapping functions on the estimation of position coordinates and troposphere. Figure 11 shows the differences of wet part troposphere and position coordinates based on different mapping functions. It can be found that the NMF and the GMF have a similar effect on the estimation of troposphere and position coordinates for maritime PPP, and the up component position of VMF1-FC has about a 2 millimetre difference from the other mapping functions. Therefore, we conclude that the three mapping functions mentioned above have the same effect on the estimation of troposphere and position coordinates.
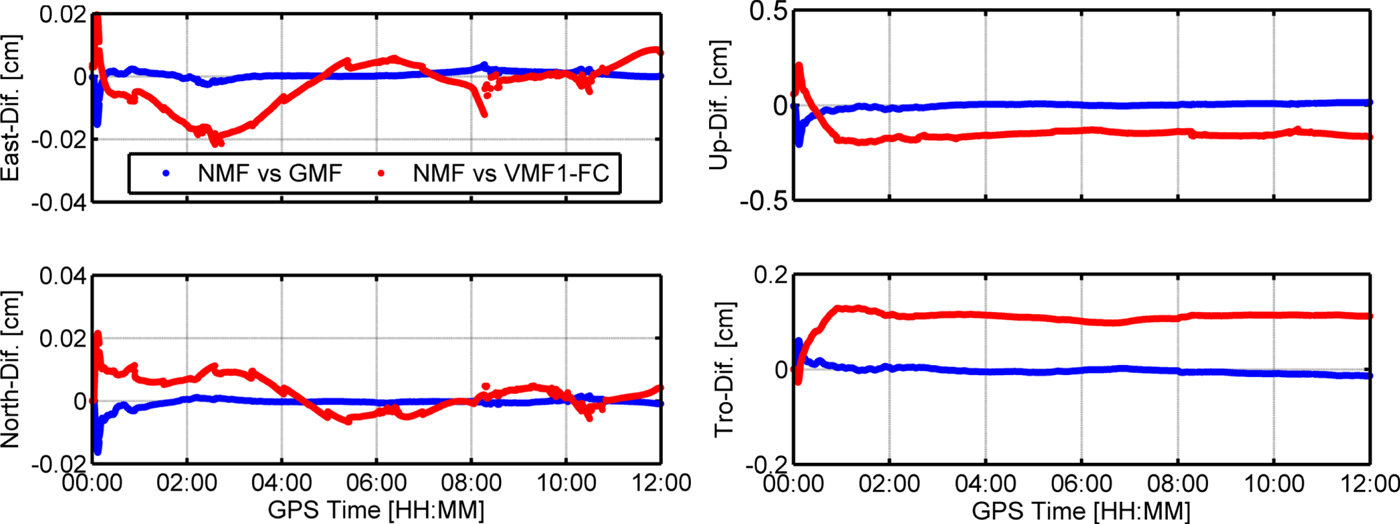
Figure 11. Differences of troposphere and position based on different mapping functions. The panels from left to right are East, North, Up and Troposphere.
4. CONCLUSIONS
BDS is a navigation satellite system that offers an independent regional service now and a global positioning service by 2020. Multi-constellation PPP integrating BDS has significant potential to improve position accuracy and reduce the convergence time in the Asia-Pacific region for maritime positioning. This study has investigated the performances of BDS and BDS/GNSS RT PPP for maritime positioning based on 12 hour kinematic real-world data.
Our marine data has shown that, in single constellation mode, BDS can provide similar RT precise positioning services to GPS for maritime applications. BDS performances in terms of convergence time and position accuracy are still slightly worse than GPS. The performance of BDS is expected to be further improved when more accurate orbit and clock products and more satellite redundancy become available. Compared with single constellation mode, BDS/GPS has the best performance among the dual-constellation configurations. Meanwhile, the integration of BDS and GLONASS to GPS reduces the convergence time by 22·8%, while the position accuracy is improved by 24·6% and 20·6% in the horizontal plane and vertically, respectively. Some outliers in the single constellation mode can be mitigated when the BDS/GNSS observations are processed simultaneously. Therefore, multi-constellation PPP can significantly improve position accuracy and reduce convergence time for maritime applications. However, the position errors dramatically increase when the phase residuals are unusual, which is caused by an inaccurate stochastic model description. Therefore, the position accuracy and the convergence time of maritime kinematic BDS/GNSS PPP can potentially be improved by applying an accurate stochastic model. We further tested the effect of different troposphere models, that is, the NMF, the GMF, and the VMF1-FC, on maritime PPP. It has been shown that the maximum difference of wet part troposphere and position coordinates based on different mapping functions is at the millimetre level. Therefore, the NMF, the GMF and the VMF1-FC are all suitable for maritime PPP.
It is noted that these results are based on limited data; more data samples for RT BDS/GNSS maritime PPP need to be collected under different navigational conditions. Therefore, extensive experiments have to be conducted including single constellation, multi-constellation combination, and PPP performance based on different tropospheric mapping functions. In addition, in order to ensure continuous high precision positioning for maritime PPP based on BDS/GNSS, the maritime multipath errors mitigation method, the strategy for maintaining PPP during outages of RT precise products and re-initialisation need to be further studied.
ACKNOWLEDGMENTS
This research was jointly funded by National Natural Science Foundation of China (Nos. 61773132, 61633008, 61374007, 61304235), the 7th Generation Ultra Deep Water Drilling Unit Innovation Project sponsored by Chinese Ministry of Industry and Information Technology, the Fundamental Research Funds for Central Universities (No. HEUCFP201768), and the Post-Doctoral Scientific Research Foundation, Heilongjiang Province (No. LBH-Q15033).