1. INTRODUCTION
The space segment of the China Satellite Navigation System consists of Geostationary Earth Orbit (GEO), Inclined Geosynchronous Earth Orbit (IGSO) and Medium Earth Orbit (MEO) satellites (Zhou et al., Reference Zhou, Hu and Wu2010). To ensure high precision in position determination, the measurement of GEO satellite orbits must also be highly precise, and the technologies used to measure these orbits has become key.
Based on Two-Way Satellite Time and Frequency Transfer (TWSTFT), the original idea for orbit determination, “determination of satellite orbit by transfer”, was proposed by the National Time Service Center, Chinese Academy of Sciences (Li et al., Reference Li, Yang, Ai, Shi, Qiao and Feng2009). This method is adopted in the Chinese Area Positioning System (CAPS). The ranging accuracy is better than one cm, and the precision of orbit determination is better than two m. The precision of orbit determination is improved greatly (Li et al., Reference Li, Yang, Ai, Shi, Qiao and Feng2009; Ai et al., Reference Ai, Shi, Wu, Li and Guo2009). Only ranging data are adopted in precise orbit determination (POD), orbit error in the radial direction can be restricted, but not in the transverse direction. Therefore, the precision of orbit determination in the radial direction is higher than the transverse by one level (Huang et al., Reference Huang, Hu, Zhang, Zhang, Guo, Wang and Shi2011).
The base of VLBI is the high precision, high-resolution measurement of angles (Zheng, Reference Zheng1999). Only the down-signals from the target to different sites need observing, with the time delay difference between the two ranges being processed to get the position of the target. It is sensitive to the angular change between the line-of-sight and the baseline, which complements the range measurement (Huang et al., Reference Huang, Hu, Zhang, Zhang, Guo, Wang and Shi2011; Yan et al., Reference Yan, Ping, Li, Cao, Huang and Fung2010).
The “differenced ranges between master station and slave stations by transfer” method has been proposed as a new type of observation. It has been shown that POD and prediction of precision using the combination of the “receiving own station-disseminated signals” data (ranging data) and the “differenced ranges between master-slave stations” data is higher than one using only ranging observation (Cao et al., Reference Cao, Yang, Li, Yang and Feng2012; Yang et al., Reference Yang, Li, Yang, Feng and Cao2012). However, the angular resolution and the baseline length are not optimum, which causes the angular resolution and the restriction in the transverse direction to be weakened (Li et al., Reference Li, Cheng, Feng, Li and Li2007), since the master station is located in the centre of all the stations. In this paper, a new method of “differenced ranges between slave-slave stations by transfer” has been developed, as a new combination of observations by transfer, which conquers the weakness of differenced observation between master-slave stations. It has more and longer baselines and higher angular resolution.
2. PRINCIPLE OF DIFFERENCED OBSERVATION BETWEEN SLAVE-SLAVE STATIONS BY TRANSFER
The principle of observation for “determination of satellite orbit by transfer” is that precise time signals from atomic clocks at ground stations modelled with different pseudo-noise code sequences are disseminated with the same carrier frequencies. The time signals are transferred via satellite transponder and received by receivers at stations in such a way that the time delay on the propagation path can be determined (Li et al., Reference Li, Yang, Ai, Shi, Qiao and Feng2009). Each station can both disseminate and receive signals from the satellite. Therefore, receiving own-station disseminated signal data and other-station disseminated signal data can be obtained at every station.
For the CAPS project, the signals disseminated by the master station, transferred via satellite transponder, will be received at receivers at all stations. Meanwhile, the signal disseminated by the slave stations can be received at the master station and own station. There are also the observations receiving own station-disseminated signals and slave station-disseminated signals at the master station, and observations receiving master station-disseminated signals and own station-disseminated signals at the slave stations.
Then there are the observations receiving own station-disseminated signals at the master station, and observations receiving master station-disseminated signals at slave stations. The two different signal observations have the same up path, which is the path from the master to the satellite. If we subtract the same up-path range from the observations, the remainders are the ranges from the satellite to the master station and to the slave stations, respectively. We can then obtain the range difference from satellite to master and slave station, which forms a differenced observation between master-slave stations by transfer (Cao et al., Reference Cao, Yang, Li, Yang and Feng2012; Yang et al., Reference Yang, Li, Yang, Feng and Cao2012). Meanwhile, the clock offset between master-slave stations is deducted from the master-slave differenced observation as the system error.
Furthermore, if we subtract the up paths from the master-slave i and master-slave j, then the differenced observation from satellite to slave stations is constructed. That is the principle of “differenced observation between slave-slave stations by transfer”. The clock offset between slave stations i and j is also deducted from the slave-slave differenced observation as the system error. (Figure 1)
Figure 1. Principle for differenced observation between slave-slave, master-slave stations by transfer.
The principle of the differenced observation between slave-slave stations by transfer is quite similar to the VLBI observation (Huang et al., Reference Huang, Hu, Zhang, Zhang, Guo, Wang and Shi2011; Yan et al., Reference Yan, Ping, Li, Cao, Huang and Fung2010), since slave stations i and j receive the same signal from the transponder on the satellite. It is essentially a new angular observation.
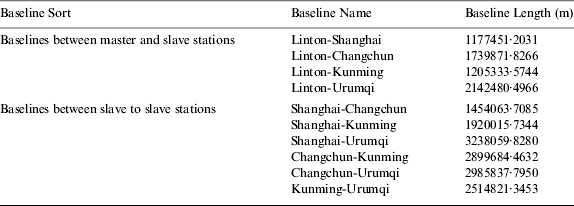
The baselines for differenced observation are N(N−1)/2 if there are N stations in the measurement system. With (N−1) baselines for master-slave stations, there are (N−2) (N−1)/2 baselines for slave-slave stations. There are four differenced baselines between master-slave stations for a measurement system with five stations. However, the differenced observations between slave-slave stations have two more baselines and the longest one has increased up to 3238·059 km. Figure 2 and Table 1 shows all the differenced baselines between slave-slave stations, master-slave stations for the existing CAPS project.
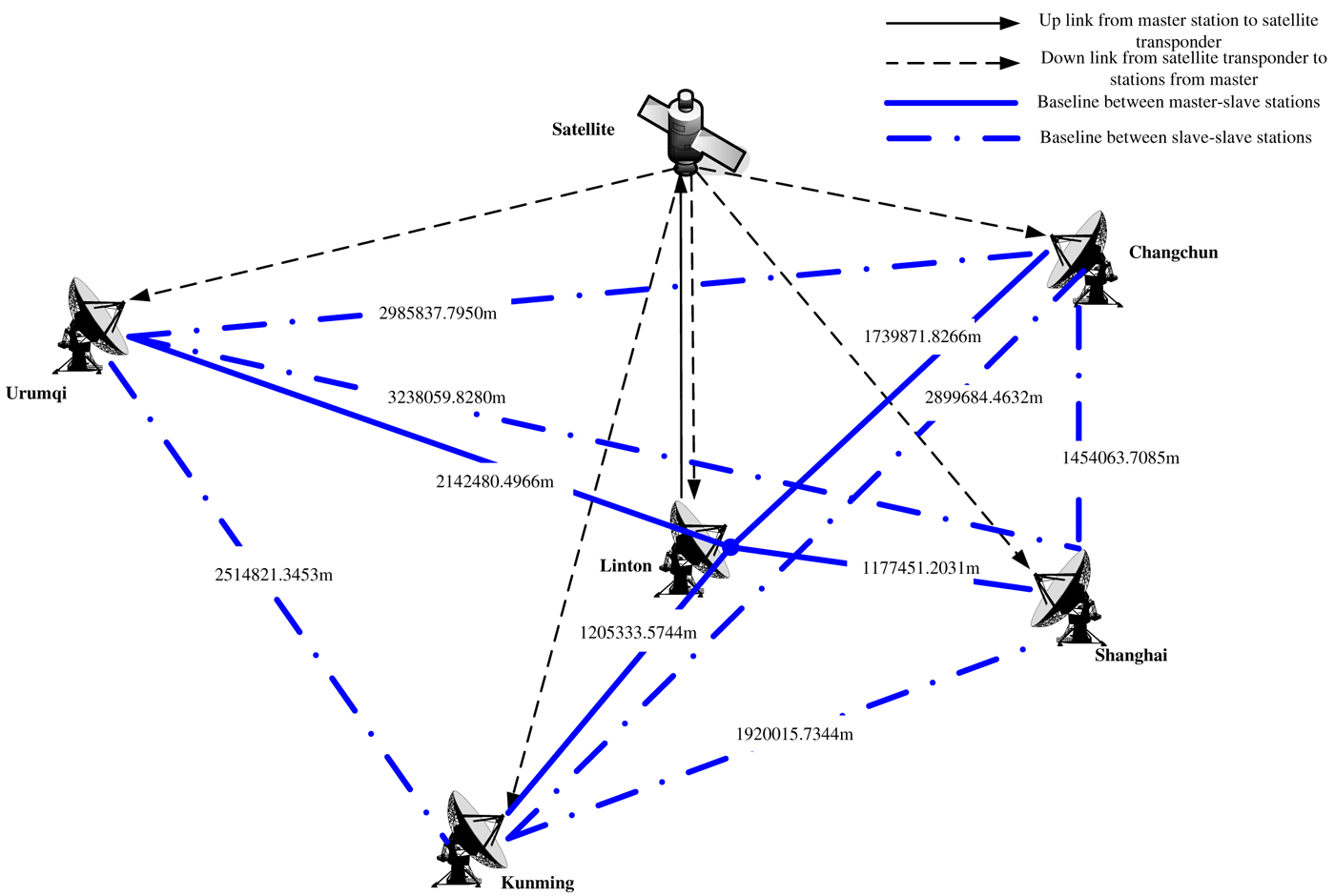
Figure 2. Baselines of slave-slave, master-slave stations by transfer.
Table 1. Baselines between master-slave stations, slave-slave stations.
Both the differenced observations between slave-slave stations and between master-slave stations are characteristic of quasi-VLBI measurement, but the differenced observations between slave-slave stations have more and longer baselines, higher angular resolution and more combination data.
The relation of time delay for the signals can be expressed as
$$\left\{ \matrix{R_{i0} (t_0 ) = R_0^u (t_0 ) + O_0^u + I_0^e + \tau _s + R_i^d (t_0 ) + O_i^d + I_{i0}^r + \Delta T_i + \Delta \tau _{sag}^{o - i} {\rm} \cr R_{\,j0} (t_0 ) = R_0^u (t_0 ) + O_0^u + I_0^e + \tau _s + R_j^d (t_0 ) + O_j^d + I_{\,j0}^r + \Delta T_j + \Delta \tau _{sag}^{o - j} \cr R_{00} (t_0 ) = R_0^u (t_0 ) + O_0^u + I_0^e + \tau _s + R_0^d (t_0 ) + O_0^d + I_{00}^r {\rm} } \right.$$Where 0 is the serial number of the master station, meaning Linton station in the CAPS, with u and d meaning up link and down link. i, j mean the serial number of the slave stations, two of the Shanghai, Changchun, Kunming and Urumqi stations.
t 0 is the moment of signal arriving at satellite from master station.
R i0(t 0), R j0(t 0) and R 00(t 0) are the reading of the Time Interval Counter (TIC) receiving signals from master station at station i, station j and master station respectively.
R 0u(t 0) is the geometrical time delay from phase centre of antenna of master station to satellite barycentre.
O 0u is the additional time delay of ionosphere at master station for the up link.
I 0e is the transmitter time delay at master station.
τ s is the signals time delay of satellite transponder.
R id(t 0), R jd(t 0) and R 0d(t 0) are the geometrical time delay from satellite barycentre to phase centre of antenna of station i, station j and master station respectively.
O id, Ojd and O 0d are the additional time delay of ionosphere for the down link at station i, station j and master station respectively.
I i0r, I j0r and I 00r are the time delay of receiver received signals from master station at station i, station j and master station respectively.
ΔT i and ΔT j are the clock offset related to atomic clock of master station at station i and station j respectively.
Δτ sago−i and Δτ sago−j are the Sagnac effect of received signals from master station at station i and station j respectively.
The expression of differenced observation between slave-slave stations by transfer can be obtained from Equation (1).
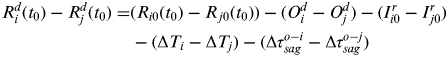$$\eqalign{R_i^d (t_0 ) - R_j^d (t_0 ) = & (R_{i0} (t_0 ) - R_{\,j0} (t_0 )) - (O_i^d - O_j^d ) - {\rm} (I_{i0}^r - I_{\,j0}^r ) \cr & - (\Delta T_i - \Delta T_j ) - (\Delta \tau _{sag}^{o - i} - \Delta \tau _{sag}^{o - j} )} $$The left side is the time delay of differenced observation between slave-slave stations at moment t 0. (R i0(t 0)−R j0(t 0)) is the reading difference for the paths from the master station to station i and station j respectively. (O id−O jd) is the ionosphere delay difference for the down link to slave stations i and j respectively, which can be corrected by the ionosphere model formula (Li et al., Reference Li, Cheng, Feng, Li and Li2007); (I i0r−Ij0r) is the difference of system error for the station i and j receiving signals from master station; (ΔT i−ΔT j) is the difference of clock offset between the slave stations i and j, which can be calculated by TWSTFT between master and slave station i, master and slave station j. (Δτ sago−i−Δτ sago−j) is the correction caused by the Sagnac effect.
From the principle and derivation of the differenced observation between slave-slave stations, the clock offset between slave stations and the system error has enormous effects for the differenced observation. Thus derivation of the clock offset between slave stations and system error has been discussed in detail.
3. DERIVATION OF THE CLOCK OFFSET BETWEEN SLAVE STATIONS AND SYSTEM ERROR
The precise time synchronism at remote clocks is available for “determination of satellite orbit by transfer”. According to TWSTFT, once a pair of observations (the receiver at station i receives the signal from master and the receiver at station j receives the signal from station i) has been obtained, the clock offset can be calculated. Taking the Sagnac effect, the time delay caused by the satellite velocity, ionosphere delay, time delay of transmitting and receiving channel into consideration, the formula for derivation of the clock offset between master station and slave station i becomes
$$\Delta T_i = \displaystyle{1 \over 2}(R_{i0} - R_{0i} ) + \displaystyle{1 \over 2}[(I_i^e - I_{i0}^r ) - (I_0^e - I_{0i}^r )] + \displaystyle{1 \over 2}[(O_0^d - O_0^u ) - (O_i^d - O_i^u )] + \Delta \tau _{sag}^{0 - i} + \Delta \mathop \dot {\rho} {^{0 - i}} $$Also, the clock offset between master station and slave station j can be expressed as
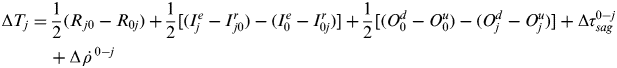$$\Delta T_j = \displaystyle{1 \over 2}(R_{\,j0} - R_{0j} ) + \displaystyle{1 \over 2}[(I_j^e - I_{\,j0}^r ) - (I_0^e - I_{0j}^r )] + \displaystyle{1 \over 2}[(O_0^d - O_0^u ) - (O_j^d - O_j^u )] + \Delta \tau _{sag}^{0 - j} + \Delta \mathop \dot {\rho} {^{0 - j}} $$The first item in the right side of Equation (3) is the readings difference between station i receiving signal from master station and the master station receiving signal from station i, which is a combination of the observations. The second item is the correction caused by the transmitting and receiving channels of instruments at both stations. The third item is the correction caused by the ionosphere delay. The correction caused by the Sagnac effect (Wu et al., Reference Wu, Li, Yang, Lei, Chen, Cheng and Feng2012) is at the fourth position. The last item is the correction from the satellite velocity. The origin of TWSTFT error contains transmitting and receiving delay, the time delay of satellite transponder, the time delay for the path, the instability of the clock, the resolution of time measurement and so on (Ye et al., Reference Ye, Shi and Lou2011).
The expressions in Equation (3) are as follows. (O id−O iu) is the ionosphere delay difference between the down link and up link at station i. (O 0d−O 0u) is the ionosphere delay difference between the down link and up link at master station. (I 0e−I 0ir) is the system error difference between transmitting channel delay and receiving one at master station, and (I ie−Ii 0r) is the according system error difference at slave station i.
Therefore, the clock offset between slave stations i and j can be expressed as
$$\eqalign{\Delta T_i - \Delta T_j = & \displaystyle{1 \over 2}[(R_{i0} - R_{0i} ) - (R_{\,j0} - R_{0j} )] + (\Delta \tau _{sag}^{0 - i} - \Delta \tau _{sag}^{0 - j} ) \cr &+ (\Delta \mathop \dot {\rho} {^{0 - i}} - \Delta \mathop \dot {\rho} {^{0 - j}} ) + \displaystyle{1 \over 2}[(O_j^d - O_j^u ) - (O_i^d - O_i^u )] \cr &+ \displaystyle{1 \over 2}[(I_i^e - I_{i0}^r ) - (I_0^e - I_{0i}^r ) - (I_j^e - I_{\,j0}^r ) + (I_0^e - I_{0j}^r )]} $$If the former four items in Equation (5) can be expressed as a, then the expression is valid.
$$\Delta T_i - \Delta T_j = a + \displaystyle{1 \over 2}[(I_i^e - I_{i0}^r ) - (I_0^e - I_{0i}^r ) - (I_j^e - I_{\,j0}^r ) + (I_0^e - I_{0j}^r )]$$Since there is also system error (I i0r−I j0r) in Equation (2), we combine the items referring to system error in Equation (2), which is the derivation of differenced observation between slave-slave stations.
$$\eqalign{ - & {\rm} (I_{i0}^r - I_{\,j0}^r ) - (\Delta T_i - \Delta T_j ) \cr = & - {\rm} (I_{i0}^r - I_{\,j0}^r ) - \left\{ a + \displaystyle{1 \over 2}[(I_i^e - I_{i0}^r ) - (I_0^e - I_{0i}^r ) - (I_j^e - I_{\,j0}^r ) + (I_0^e - I_{0j}^r )]\right\} \cr = & - a - \displaystyle{1 \over 2}(I_{i0}^r + I_i^e ) + \displaystyle{1 \over 2}(I_{\,j0}^r + I_j^e ) - \displaystyle{1 \over 2}(I_0^e + I_{0j}^r ) - \displaystyle{1 \over 2}(I_0^e + I_{0i}^r )} $$The last four items in Equation (7) can all be measured by the instrument measurement. Ten minutes in every hour are used to measure the system error for all stations. The measurement process is as follows.
There are six channels at the master station, as Figure 3 depicts. (I 0e+I 0jr) is the system error measured for the channel of receiving j station-disseminated signal at the master station. (I 0e+I 0ir) is the system error measured for the channel of receiving i station-disseminated signal at master station.
Figure 3. Channels at master and slave stations.
There are only three channels for the slave stations. (I i0r+I ie) is the system error for the second channel at slave station i, that is the channel for receiving the master station-disseminated signal. (I j0r+I je) is the system error for the second channel at slave station j, that is the channel for receiving the master station-disseminated signal.
From the discussion and derivation of clock offset and system error, the differenced observation between slave-slave stations by transfer can be changed to Equation (8):
$$\eqalign{ & R_i^d (t_0 ) - R_j^d (t_0 ) = (R_{i0} (t_0 ) - R_{\,j0} (t_0 )) - (O_i^d - O_j^d ) - (\Delta \tau _{sag}^{o - i} - \Delta \tau _{sag}^{o - j} ) \cr & - a - \displaystyle{1 \over 2}(I_{i0}^r + I_i^e ) + \displaystyle{1 \over 2}(I_{\,j0}^r + I_j^e ) - \displaystyle{1 \over 2}(I_0^e + I_{0j}^r ) - \displaystyle{1 \over 2}(I_0^e + I_{0i}^r )} $$4. DISCUSSION
In order to confirm the performance of the quasi-VLBI observation for a GEO satellite's orbit determination, several experiments have been conducted. The differenced observation between slave-slave stations by transfer have been performed using the pseudo-range observation of SINOSAT-1 satellite with C-band from 6 to 13 June 2005. Moreover, the orbit determination and prediction results have been compared between slave-slave station solely receiving own station-disseminated signal and slave-slave station by combination of ranging observation with the differenced observation between slave stations.
The sum of transmitting and receiving delay in each channel is measured every hour at the master station and slave stations. The clock offset between slave-slave stations can be obtained from Equation (7). As a consequence, the differenced observation between slave-slave stations can be obtained from Equation (8).
The adopted astronomical constants, reference system, dynamical and measurement models are referred to International Earth Rotation Service (IERS) 1996. The dynamical perturbation models are (1) gravitational attractions of the non-spherical Earth (Earth gravity model JGM3, truncated to 10th degree and order), (2) three-body gravitational attractions of the Sun and Moon, (3) relativistic perturbation, (4) gravitational attractions of solid-Earth tides and oceanic tides, (5) radiation pressure of the Sun, (6) earthshine radiation pressure, (7) perturbation of Earth's rotational deformation and (8) empirical radial-transverse-normal accelerations.
The measurement models are (1) Saastamoinen-Niell atmospheric refraction, (2) the correction of the barycentre of the satellite, (3) the displacement of the station due to the solid-Earth tide, (4) the effects of the secular tidal term on the station coordinates, (5) the effects of the loading of the oceanic tides on station coordinates, and (6) the effect of the Earth's rotational deformation on station coordinates.
The reference systems are (1) the mean equator (x-y plane) and mean spring equinox (the direction of the x-axis) at J2000.0, (2) ITRF2000 for the coordinates of the stations and their velocities of motion, (3) the procession model IAU1976, (4) the 1980 nutation model and IERS nutation correction, and (5) the planetary ephemeris DE403/LE403 (Li et al., Reference Li, Qiao and Feng2006).
The orbit determination slip arc has been chosen as 1·5 days, shifting about one day every time. Orbit comparison between the consecutive orbit arcs has tested the precision of POD. Since a manoeuvre was conducted on the SINOSAT-1 satellite on 14 June 2005, the last orbit arc chosen was 13 June 2005 to 0800 14 June 2005.
The strategy for the orbit determination using observations receiving own station-disseminated signals is as follows. The sets of parameters, including six sets for satellite orbit parameters, six sets for solar radiation coefficient, 12 sets for experimental acceleration, and 12 sets for transponder delay, are estimated. Moreover, the sum of bias of each station is restricted to zero (Li et al., Reference Li, Yang, Ai, Shi, Qiao and Feng2009).
In addition, the strategy for orbit determination using a combination of one receiving own station-disseminated signal and differenced observation between slave-slave stations is chosen as follows. Apart from the above parameters, the biases for the differenced baseline are determined also to absorb the remaining system error. Likewise, the sum of bias of each station is restricted to zero (Li et al., Reference Li, Yang, Ai, Shi, Qiao and Feng2009). Table 2 shows the observing numbers and observing root mean square (RMS) for orbit determination in arc duration for two kinds of orbit strategy.
Table 2. Accuracy of observations of 1·5 days data for Sino-1 satellite.
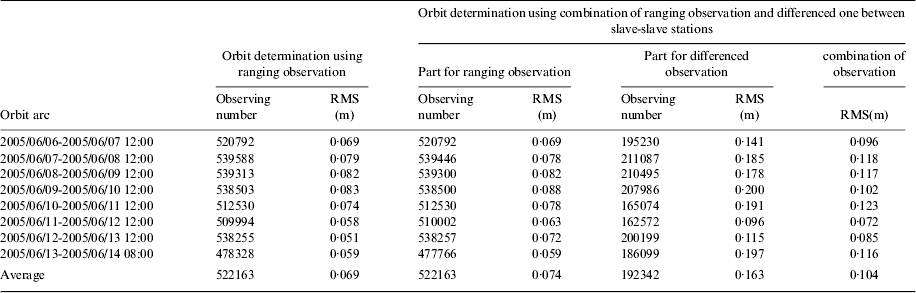
It is shown in Table 2 that the residual for differenced observation between slave stations is about 0·163 m, while for ranging data it is about 0·074 m. As a result of the formation of differenced data referring to the two stations on one baseline, the residual for differenced data is about twice that for ranging data. The residual is about 0·1 m, for both orbit determination using only observation receiving own station-disseminated signal, and the orbit determination using the combination. The orbit reflects the observation very well.
The precision of orbit determination is estimated by an orbit overlap of half a day. The orbit differences in the overlap arcs have also been provided in Table 3.
Table 3. Orbit differences in the overlap of orbit arcs (unit: m).
The R, T and N are respectively the orbit differences in radial, along-track and cross-track direction. H denotes the difference in the transverse direction, which is the square sum of the T and N difference. P denotes the difference in position of the GEO satellite. URE is the user range error.
From Table 3, the orbit difference is about 0·333 m for the radial direction, 0·890 m for the along-track direction and 1·560 m for the cross-track direction, with the transverse difference being 1·822 m during the overlap of 0·5 day using only ranging observation. After the combination of ranging data and differenced calculation between slave stations, the orbit difference in radial, along-track and cross-track directions is respectively 0·283, 0·694 and 0·915 m, with the transverse difference decreasing by 0·646 m. Therefore, the transverse and horizontal parts have a tendency to decrease using a combination of ranging data and differenced observation.
Meanwhile, URE for orbit determination using combination data is about 0·318 m, which can satisfy the navigation users' need. This value has dropped by 0·065 m comparing with that using only ranging data. In addition, the orbit difference has a decrease of 0·623 m after combination orbit determination. The precision accuracy in orbit difference and URE using combination data is higher than that using only ranging data.
From the above discussion, it can be concluded that the differenced observations between slave-slave stations by transfer can be formed using the existing modes. The transverse orbit accuracy, orbit difference and URE are all restricted after combining the differenced observation and observation receiving the own station-disseminated signal in POD.
An additional experiment has been completed to test the orbit prediction precision using a combination of differenced observation between slave-slave stations and ranging data. The orbit determined using only ranging data is also predicted. The long arc orbit precision (O-C) comparison was conducted between results of just ranging data and results using the combination of ranging and differenced data between slave stations. The prediction precision (O-C) of one day, two days, four days and five days based on an orbit arc from 7 to 8 June 1200, are given in Table 4 and Figure 4.
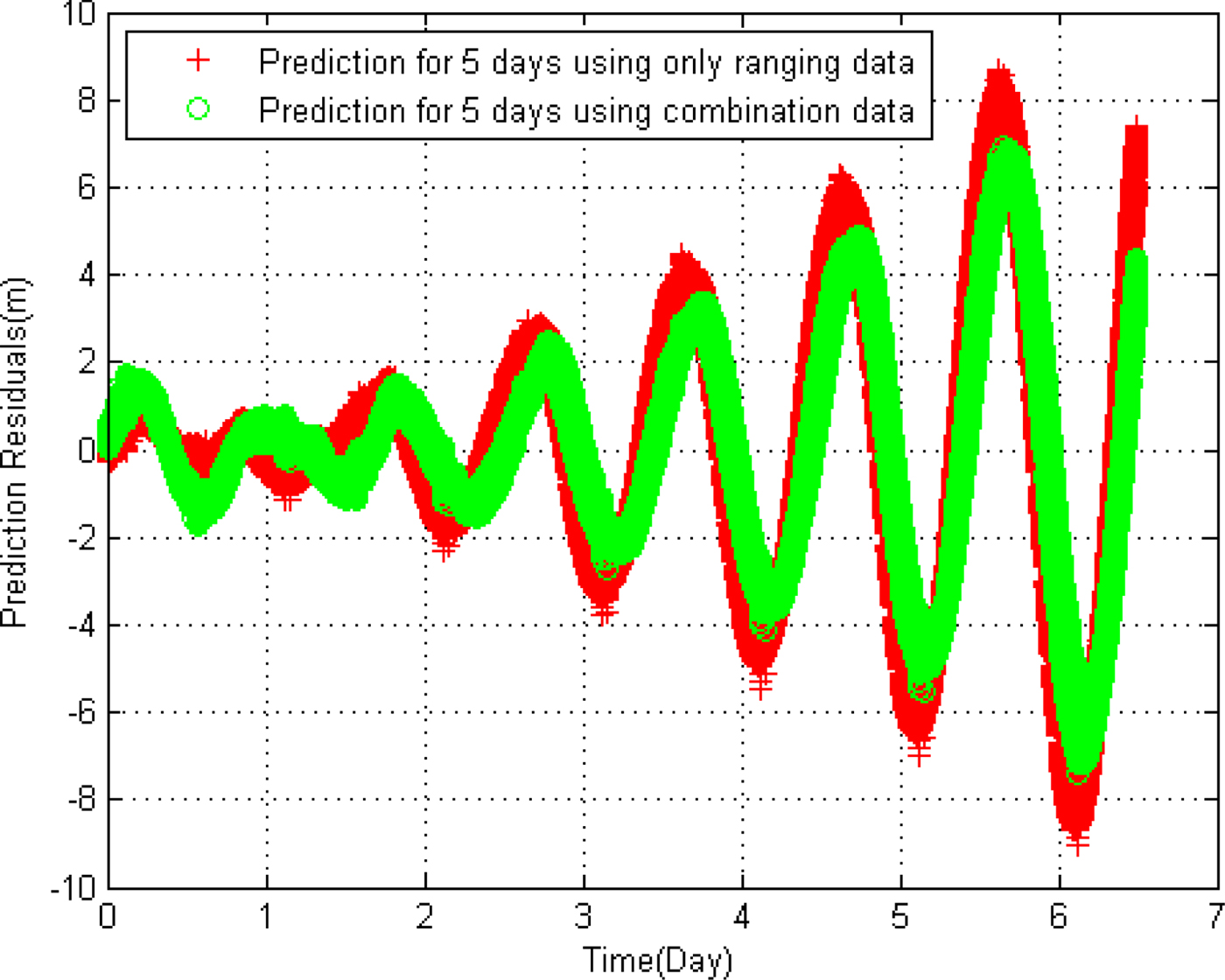
Figure 4. Residuals of orbit prediction of 5 days.
Table 4. Orbit prediction precision (O-C) for 1·5 days orbit arc (unit: m).
Using an observation arc of 1·5 days, the orbit is predicted for five days. Using a combination observation of ranging and differenced data, the predicted orbit accuracy is about 1·032 m over a period of two days, 1·899 m over a period of four days and 2·522 m over a period of five days. Meanwhile, using only ranging data, the predicted accuracy is about 1·243, 2·400 and 2·522 m, respectively.
With the above analysis, it is demonstrated that the prediction precision for orbit determination using the combination of ranging data and differenced data between slave-slave stations is higher than the precision using only ranging data. The differenced observation between slave-slave stations can be used to improve long-arc prediction accuracy.
5. CONCLUSIONS
The derivation and principle of differenced observation between slave-slave stations have been presented. We have analysed the clock offset and system error explicitly, since the differenced observation would be greatly influenced by these two items. Joint orbit determination and orbit prediction were expected to yield improved results using C-band ranging data from 6 to 13 June 2005 and differenced data. The differenced observation between slave-slave stations can be used to improve long-arc POD accuracy. The orbit accuracy in the transverse direction and URE are improved using the joint method.
There are still some problems to be solved with the differenced observation between slave stations, such as the optimization of the system accuracy and time signal arriving at the satellite, the weight choice for observations using the joint process, the orbit determination for just quasi-VLBI observation, orbit in spanning manoeuvre and orbit recovery (Yang et al., Reference Yang, Li, Feng, Guo, Shi, Ai, Wu and Qiao2009) for GEO satellite and so on.
The differenced observation between slave-slave stations is a new type of combination of the existing modes in the CAPS. It is a quasi-VLBI observation with higher angular resolution and provides a constraint on the orbit in the transverse direction. Moreover, it would be unaffected by the master station, unlike the differenced observation between master-slave stations. This will also be used in future with the development of an angular measurement subsystem for the navigation of satellites.
ACKNOWLEDGEMENT
This work was carried out under the support of the National Natural Science Foundation of China Key Program (Grant No. 11033004, No. 11173026 and No. 41104021); West Light Foundation of the Chinese Academy of Sciences (Grant No. 2007LH01).
