2. POSITIONING MODEL WITH MULTI-CONSTELLATION GNSS SATELLITES

The influence of receiver noise, clock error, tidal and relativity error are significantly reduced through observation DD processing. For positioning systems that employ Code Division Multiple Access (CDMA) coding techniques, such as GPS, Galileo and BDS, the same frequencies are used by all satellites from the same system. When only considering tropospheric and ionosphere delays, the DD carrier phase observation equations are as follows:

(1)$$\lambda _1 {\rm \Delta} \nabla \varphi _1 = {\rm \Delta} \nabla \rho - {\rm \Delta} \nabla I_1 + {\rm \Delta} \nabla T + \lambda _1 {\rm \Delta} \nabla N_1 $$

(2)$$\lambda _2 {\rm \Delta} \nabla \varphi _2 = {\rm \Delta} \nabla \rho - {\rm \Delta} \nabla I_2 + {\rm \Delta} \nabla T + \lambda _2 {\rm \Delta} \nabla N_2 $$

For Frequency Division Multiple Access (FDMA) coding systems such as GLONASS, the observations coming from different satellites employ different frequencies (Glonass, I. C. D, Reference Glonass2002; Wanninger, Reference Wanninger2012; Pratt et al., Reference Pratt, Burke and Misra1998), thus the carrier phase DD observation equations can be presented as:

(3)$$\lambda _1^p {\rm \Delta} \nabla \varphi _1 = {\rm \Delta} \nabla \rho - {\rm \Delta} \nabla I_1 + {\rm \Delta} \nabla T + \lambda _1^p {\rm \Delta} \nabla N_1 + (\lambda _1^p - \lambda _1^r ){\rm \Delta} N_1^r $$

(4)$$\lambda _2^p {\rm \Delta} \nabla \varphi _2 = {\rm \Delta} \nabla \rho - {\rm \Delta} \nabla I_2 + {\rm \Delta} \nabla T + \lambda _2^p {\rm \Delta} \nabla N_2 + (\lambda _2^p - \lambda _2^r ){\rm \Delta} N_2^r $$

In Equations (1) to (4) Δ∇(·) is the double difference operator between satellites and receivers. λ ₁ and λ ₂ are the wavelengths for signal carriers L ₁ and L ₂. φ ₁ and φ ₂ are the carrier measurements on L ₁ and L ₂. ρ is the geometrical distance between the satellite and the receiver. I ₁ and I ₂ are the ionosphere delays on L ₁ and L ₂. T is the tropospheric delay. N ₁ and N ₂ are the unknown integer ambiguities of both carriers. In Equations (3) and (4), p and r are the index number of the reference and non-reference satellites in the GLONASS system respectively. ΔN _i^r is the receiver single difference integer ambiguity for frequency i of the reference satellite. Methods proposed by Wang (Reference Wang2000) and Walsh and Daly (Reference Walsh and Daly1996) may be used to resolve for the single difference ambiguity of the GLONASS system. Having fixed the single difference ambiguities, we may assume that GPS, Galileo, BDS and GLONASS systems employ the same DD integer ambiguity resolution model. Equations (1) and (2) or Equations (3) and (4) may be combined to form the ionosphere-free observation equation to eliminate the ionosphere effect when neglecting the second order terms of the ionosphere bias (Ge et al., Reference Ge, Gendt, Rothacher, Shi and Liu2008; Loyer et al., Reference Loyer, Perosanz, Mercier, Capdeville and Marty2012; Hoque and Jakowski, Reference Hoque and Jakowski2007), as shown below:

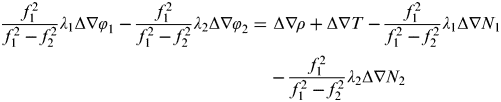(5)$$\displaystyle{{\,f_1^2} \over {\,f_1^2 - f_2^2}} \lambda _1 {\rm \Delta} \nabla \varphi _1 - \displaystyle{{\,f_1^2} \over {\,f_1^2 - f_2^2}} \lambda _2 {\rm \Delta} \nabla \varphi _2 = {\kern 1pt} {\rm \Delta} \nabla \rho + {\rm \Delta} \nabla T - \displaystyle{{\,f_1^2} \over {\,f_1^2 - f_2^2}} \lambda _1 {\rm \Delta} \nabla N_1 - \displaystyle{{\,f_1^2} \over {\,f_1^2 - f_2^2}} \lambda _2 {\rm \Delta} \nabla N_2 $$

f ₁ and f ₂ are frequencies of L ₁ and L ₂ respectively. The DD ambiguities Δ∇N ₁ and Δ∇N ₂ are both included in Equation (5). In practice, the wide-lane DD ambiguity Δ∇N _w (Δ∇N _w=Δ∇N ₁−Δ∇N ₂) of the longer wavelength is usually worked out first. Thus Equation (5) will be left with the basic DD ambiguity (Δ∇N ₁ or Δ∇N ₂) only. They are then treated as unknown parameters together with baseline coordinates to be solved through multi-epoch observation equations.

The number of available satellites from a single satellite system is significantly reduced in dense urban areas due to complicated surrounding environments, which leads to poor positioning accuracy or even position fixing failure. In such cases, a combination of multi-constellation GNSS satellites that shares the same baseline vector with unknown parameters helps to solve for a better position fix. Each system determines the reference satellites independently to overcome the problem of different frequencies used by different systems. Therefore at least two satellites from the same system must be observed in order to solve for a position fix. Once an ambiguity resolution is achieved, the position for a single epoch may be obtained using Equation (6).

(6)$$ \eqalign { V = & BX - L{\kern 1pt} = \left({\matrix{ {a^{1,k_G}} & {b^{1,k_G}} & {c^{1,k_G}} \cr \vdots & \vdots & \vdots \cr {a^{m,k_R}} & {b^{m,k_R}} & {c^{m,k_R}} \cr \vdots & \vdots & \vdots \cr {a^{n,k_C}} & {b^{n,k_C}} & {c^{n,k_C}} \cr \vdots & \vdots & \vdots \cr}} \right)\left( {\matrix{ {\delta x} \cr {\delta y} \cr {\delta z} \cr}} \right) \cr & - \left( {\matrix{ {{\rm \Delta} \nabla (\rho _0^{1,k_G} + T^{1,k_G} + \varepsilon _{IF}^{1,k_G} ) + \lambda _{G,IF} {\rm \Delta} \nabla (N_{IF}^{1,k_G} - \varphi _{IF}^{1,k_G} )} \cr \vdots \cr {{\rm \Delta} \nabla (\rho _0^{m,k_R} + T^{m,k_R} + \varepsilon _{IF}^{m,k_R} ) + \lambda _{R,IF}^m {\rm \Delta} \nabla (N_{IF}^{m,k_R} - \varphi _{IF}^{m,k_R} )} \cr \vdots \cr {{\rm \Delta} \nabla (\rho _0^{n,k_C} + T^{n,k_C} + \varepsilon _{IF}^{n,k_C} ) + \lambda _{C,IF} {\rm \Delta} \nabla (N_{IF}^{n,k_C} - \varphi _{IF}^{n,k_C} )} \cr \vdots \cr}} \right)} $$

Where V is the residual vector. B is the design matrix. X is the unknown baseline-vector parameters to be estimated. L is the observation vector. a, b, c are the coefficients of the unknown parameters δx, δy δz of each error equation respectively. k _G, k_R k_C are the satellite index numbers of GPS, GLONASS and BDS respectively. m and n are the beginning index of GLONASS and BDS satellites. Suppose that i indicates the index of non-reference, we have the following correspondence:

$$\left\{ {\matrix{ {1 \leqslant i \lt m,\quad GPS} \cr {m \leqslant i \lt n{\kern 1pt}, \quad GLONASS} \cr {i \geqslant n{\kern 1pt}, \quad BDS} \cr}} \right.$$

ρ ₀ is the approximate range between the satellite and the receiver. λ _G,_IF, λ _R,IF^m, λ _C,_IF are the ionosphere-free wavelength combinations of GPS, GLONASS (the m-index satellite) and BDS. φ _IF, ε_IF, N_IF are the ionosphere-free carrier phase observations, residuals and ambiguities, of which ε _IF for GLONASS includes the equivalent range term of the single difference ambiguity for the reference satellites.

Equation (6) could be used to solve for single epoch positioning after fixing the carrier phase DD ambiguities. With only three unknown coordinates, a minimum of three observation equations is needed, thus at least three satellite pairs are required. Any further equations would be regarded as redundant observations, which may increase positioning accuracy on one hand, but on the other hand might increase the correlation between equations and reduce positioning stability.

3. EVALUATION OF THE OBSERVATION STRUCTURE OF MULTI-CONSTELLATION-BASED POSITIONING

In dense urban environments, observable satellites from ground GNSS stations are generally unevenly distributed due to signal obstruction. This results in positioning instability in the blocked area. For example, if the satellites to the north of the station were blocked, the positioning result in the north and south direction would be unstable; if only high elevation satellites were observable from the station, then the height accuracy would fluctuate. Currently, PDOP values are generally used to describe the quality of satellite distributions. For the nth observable satellite at a station, its coordinates are denoted as (Xⁿ, Yⁿ, Zⁿ), station coordinates are (X _i, Y_i, Z_i), the design matrix can be expressed as Equation (7) (Borre and Strang, Reference Borre and Strang1997):

(7)$$A = \left[ {\matrix{ { - \hskip 2pt\displaystyle{{X^1 - X_i} \over {\rho _i^1}}} & { - \hskip 2pt \displaystyle{{Y^1 - Y_i} \over {\rho _i^1}}} & {- \hskip 2pt \displaystyle{{Z^1 - Z_i} \over {\rho _i^1}}} & 1 \cr { - \hskip 2pt \displaystyle{{X^2 - X_i} \over {\rho _i^2}}} & { - \hskip 2pt \displaystyle{{Y^2 - Y_i} \over {\rho _i^2}}} & { - \hskip 2pt \displaystyle{{Z^2 - Z_i} \over {\rho _i^2}}} & 1 \cr \vdots & \vdots & \vdots & 1 \cr { - \hskip 2pt \displaystyle{{X^n - X_i} \over {\rho _i^n}}} & { - \hskip 2pt \displaystyle{{Y^n - Y_i} \over {\rho _i^n}}} & { - \hskip 2pt \displaystyle{{Z^n - Z_i} \over {\rho _i^n}}} & 1 \cr}} \right]$$

Then the co-factor matrix would be Q=(A^T·A)⁻¹ and $PDOP = \sqrt {Q(1,1) + Q(2,2) + Q(3,3)} $. PDOP is a straightforward reflection of the distribution evenness and discreteness of the visible satellites and proves to be a good accuracy evaluation criterion in non-differencing positioning. However in DD positioning, the relative distributions among the reference and non-reference satellites should be considered together with the independent distribution described by PDOP.

Each pair of satellites refers to a carrier phase DD observation equation. Hence the correlations between the observation equations reflect the geometric distribution of the satellite pairs. The more scattered the satellite pairs, the smaller the correlation between the observation equations. If a strong correlation was detected between the observation equations, it would be assumed that there is a lack of sufficient observations, which can seem to be an ill-conditioned problem (Chang et al., Reference Chang, Wang and Chang2009; Farooq and Salhi, Reference Farooq and Salhi2011; Wang et al., Reference Wang, Rizos and Lim2006). A condition number provides an effective evaluation method to a system of its ill-conditioned level when resolving for ill-conditioned system parameters. The condition number is described below.

For an observation equation V=BX−L, its least squares solution can be expressed as Equation (8) (Mikhail and Ackermann, Reference Mikhail and Ackermann1976; Ge et al., Reference Ge, Gendt, Dick and Zhang2005):

(8)$$\hat X = (B^T PB)^{ - 1} B^T PL$$

Of which V is the residual vector, B is the design matrix, P is the weight matrix, L is the observation vector, and X is the unknown-parameter vector, whereas in this paper it is the unknown baseline-vector parameters, $\hat X$ is the least squares solution of X.

If N=B^TPB is denoted as the coefficient matrix of the normal equation, Equation (8) may be rewritten as

(9)$$\hat X = N^{ - 1} W$$

where W=B^TPL.

As mentioned by Farooq and Salhi (Reference Farooq and Salhi2011) and Wang et al. (Reference Wang, Rizos and Lim2006), the unknown parameter vector X will bring in an error term δX when the normal matrix N and constant matrix W each contain an error term δN and δW. The corresponding relationship is as below:

(10)$$\displaystyle{{||\delta {\bi X}||} \over {||{\bi X}||}} \leqslant \displaystyle{{{\rm cond}({\bi N})} \over {1 - {\rm cond}({\bi N})\displaystyle{{||\delta {\bi N}||} \over {{\kern 1pt} ||{\bi N}||}}}}\left( {\displaystyle{{||\delta {\bi W}||} \over {||{\bi W}||}} + {\kern 1pt} {\kern 1pt} \displaystyle{{||\delta {\bi N}||} \over {||{\bi N}||}}} \right){\kern 1pt} $$

Of which cond(N)=||N^{− 1}||·||N|| is the condition number of matrix N; ||·|| is the spectrum norm operator. We can see from Equation (10) that the condition number reflects the impact of the relative disturbance of the normal matrix N and constant W on parameter estimations. When the condition number of the normal equation N is large (i.e. serious ill-conditioned normal equation), the parameter solution would still contain a large error even if disturbance were small in N and W. Therefore, the condition number is commonly used as an evaluation factor for the ill-condition of a parameter estimation model (Cline et al., Reference Cline, Moler, Stewart and Wilkinson1979; Hansen, Reference Hansen1992), and we can further use it to evaluate the observation structure in the carrier phase DD GNSS positioning.

A set of combined GPS/BDS/GLONASS short baseline observation data (data rate of 1 s for a continuous 1000 epochs) was collected at Southeast University, China on 17 March 2013 to assess and validate the effectiveness of PDOP and condition number on evaluating the stability of positioning solutions. During this period, a total number of eight GPS satellites, seven BDS satellites and seven GLONASS satellites could be observed. The sky plot of these GNSS satellites can be seen in Figure 1. The reason for using a short baseline is so that we can avoid the impact of other errors, so that we can analyse purely the impact of the observation structure. In data processing the reference satellites are chosen independently for three GNSS constellations, thus five satellites are randomly selected for the trial forming 56, 21 and 21 combinations respectively for each GNSS system. The statistical analysis of the PDOP values, condition numbers and positioning stability for every combination are shown in Figure 2 and Table 1. The PDOP values and the condition numbers are the means of the values from all epochs. The standard deviation (STD) indicates the positioning stability of the positioning result during the trial period.

Figure 1. Sky plot of the whole observation period.

Figure 2. STD of GPS/BDS/GLONASS positioning, PDOP values and condition numbers.

Table 1. Correlation coefficients of PDOP, condition number and standard deviation for GPS/BDS/GLONASS.

The correlation (i.e. the correlation coefficient, is used to measure the degree of correlation between two variables; the closer the correlation coefficient is to 1 or −1 the greater the correlation) between PDOP, condition number and standard deviation of each system is estimated and listed in Table 1.

From Figure 2 and Table 1, it could be concluded that whether it is the 56 different combinations of GPS or 21 combinations of BDS or GLONASS, the condition number proves to be a better indicator of the positioning stability. The correlation coefficient of the condition number and positioning standard deviation reach 0·920, 0·986 and 0·963 respectively for each system. Therefore the correlation statistics shown in Table 1 indicate that the condition number is a more reliable indicator of the positioning stability than the PDOP when the same numbers of satellites are observed.

A more detailed analysis of the effectiveness of the condition number with the positioning stability is shown in Figure 3, where the worst set of the mean condition number from the combinations mentioned above is picked and analysed.

Figure 3. GPS/BDS/GLONASS positioning result with maximum mean condition number.

Figure 3 indicates that a large condition number results in poor positioning stability. In this case all the observation structures from the three systems become worse. That is to say the condition number is increasing. The positioning error and fluctuation also increase, reaching decimetre level, which further demonstrates that the condition number is a valid indicator of positioning stability.

4. USING MINIMUM CONDITION NUMBER TO DETERMINE THE OPTIMAL OBSERVATION STRUCTURE

It is apparent that reducing the ill-conditioned level of the observation equation plays a vital role in improving positioning accuracy and stability. Many publications have discussed this matter from a mathematical point of view, such as ridge estimation and singular value decomposition method (Li et al., Reference Li, Shen and Feng2010; Wen et al., Reference Wen, Wang and Norman2012; Shen and Li, Reference Shen and Li2007). Its principles lie in decreasing the ill-posed characteristics of the covariance matrix by modifying the normal equation. Yet most of these methods focus on transforming the existing covariance matrix rather than its fundamental source, i.e., the structure of the observation equation.

The determination of the reference satellites is an essential part of solving for the carrier phase double difference positioning solution. A common procedure would be selecting reference satellites with the maximum elevation, due to concerns of reduced observation precision caused by atmospheric delay between stations with long baselines. Yet short or even very short baselines are still very common in daily applications. In these cases, the station-difference observations at different elevations show no obvious difference. Hence no noticeable impact on the observation equation could be recognised from the different elevation reference satellites. Nonetheless, relatively fewer satellites could be observed in harsh observation environments. The different selection of reference satellites would therefore result in significant changes to satellite pair distribution. We can see from Equation (8) that the positioning accuracy is not only relevant to the accuracy of observations L, but also affected by the design matrix B. Variance matrix D is commonly used for the evaluation of positioning accuracy, as shown below:

(11)$$D = \sigma _0 \cdot Q = \sigma _0 \cdot (B^T PB)^{ - 1} $$

Of which σ ₀ is the posterior mean square error of unit weight, whose value is decided by the observation accuracy. From Equation (11), we can see that the positioning accuracy might change by altering the design matrix from selecting different reference satellites, while Equation (10) indicates that the condition number of the co-factor matrix Q reflects the system resistance to error. Thus the condition number proves to be a valid criterion for selecting reference satellites. Or it can be interpreted that in harsh environments, observation structure is more important compared with the difference of observations due to the different choice of the reference satellites.

In GNSS carrier phase DD positioning, an accurate ambiguity fix could be solved for after a long observation period. It would then be fed back into the observation equation to produce a single epoch positioning solution. For a DD ambiguity that has already been fixed, the DD ambiguity of each satellite pair could be attained after transforming the corresponding matrix. For example, the equation for transforming the DD ambiguity for reference satellite No. 2 into the DD ambiguity for reference satellite No. 3 is as below:

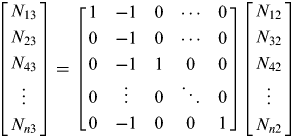(12)$$\left[ {\matrix{ {N_{13}} \cr {N_{23}} \cr {N_{43}} \cr \vdots \cr {N_{n3}} \cr}} \right] = \left[ {\matrix{ 1 & { - 1} & 0 & \cdots & 0 \cr 0 & { - 1} & 0 & \cdots & 0 \cr 0 & { - 1} & 1 & 0 & 0 \cr 0 & \vdots & 0 & \ddots & 0 \cr 0 & { - 1} & 0 & 0 & 1 \cr}} \right]\left[ {\matrix{ {N_{12}} \cr {N_{32}} \cr {N_{42}} \cr \vdots \cr {N_{n2}} \cr}} \right]$$

The effect of the condition number-based method can be simplified as in Figure 4 and Figure 5, where the green circle and the red circle stand for the reference and non-reference satellites respectively. Figure 4 represents the conventional maximum elevation method (MAEA method for short in this paper), while Figure 5 represents the minimum condition number method (MICN method for short in this paper) proposed in this paper. As we can see, the MICN method is dedicated to make the best distribution of satellite pairs, so that the calculating system has much improved structure in the DD positioning.

Figure 4. Outline effect of the MAEA method.

Figure 5. Outline effect of the MICN method.

In the practical application of the condition number for the reference satellite selection, the length of the baseline needs to be taken into account. That is to say we need set a certain cut-off elevation angle for the reference satellites. This is due to the atmospheric delay, satellite ephemeris and other residual errors. For different baseline length, the accuracies of station-difference observations from the same elevation satellites are also different. The longer the baseline is, the lower the accuracy of the observations. If a satellite with low-accuracy observation is treated as the reference satellite, large errors will be introduced into the positioning results (Wang et al., Reference Wang, Stewart and Tsakiri1998; Gendt et al., Reference Gendt, Dick, Reigber, Tomassini, Liu and Ramatschi2003; Ge et al., Reference Ge, Gendt, Rothacher, Shi and Liu2008). We can use an experiential index for guidance on this. When the baseline is longer than 50 km, an angle between 35° and 40° can be used as the cut-off elevation angle for the selection of the reference satellite. When the baseline is between 20 km than 50 km, an angle between 25° and 35° can be used. If a baseline is less than 20 km, we can set the cut-off angle between 15° and 25°. Of course, this is just a suggestive indicator. In practice, it can be adjusted according to the actual situation.

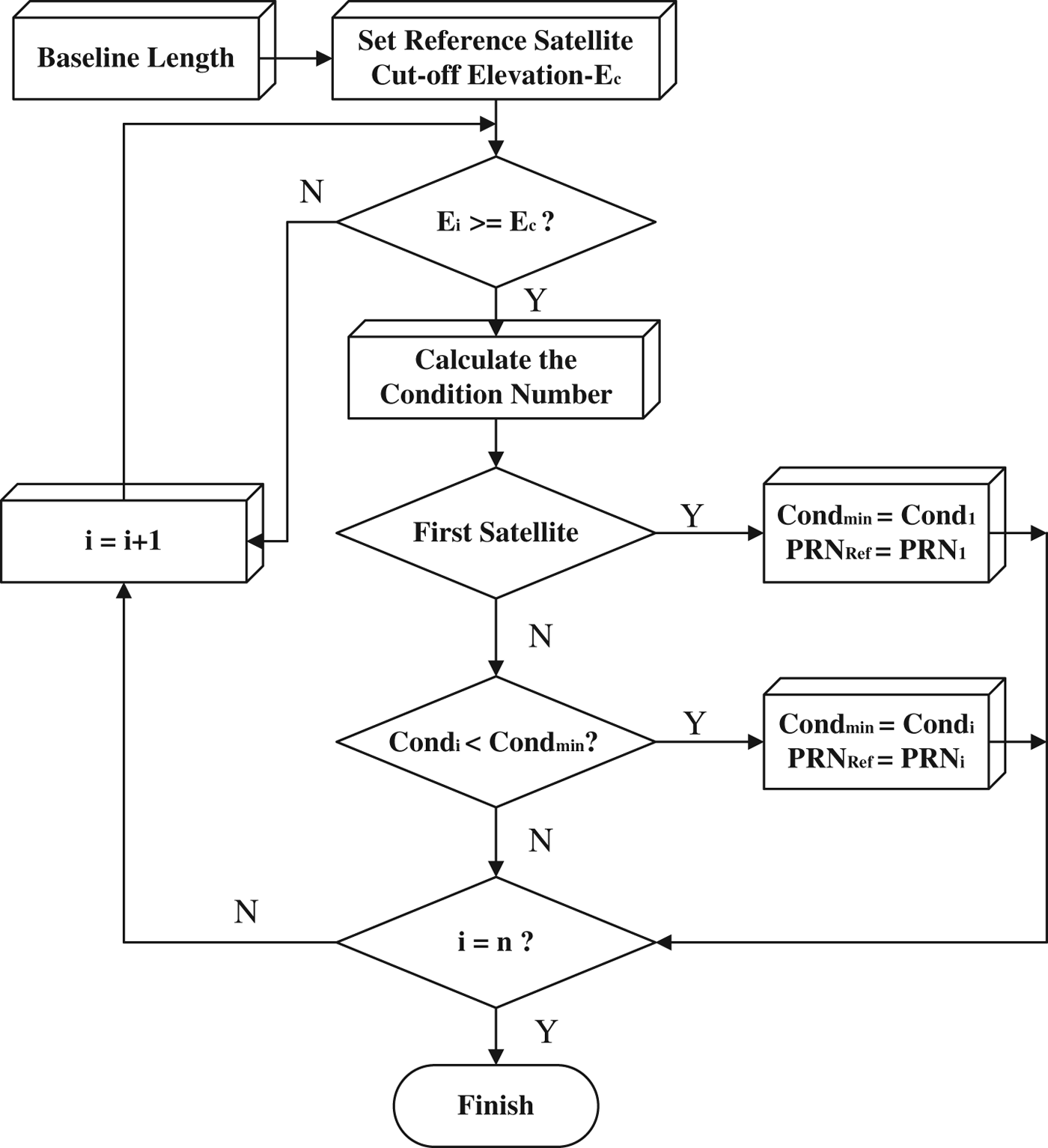
As the satellites are in constant motion, so the satellite observation structure is changing all the time. Therefore, in the process of positioning, the choice of reference satellite also needs updating. We can make an iterative assessment every 5–10 minutes, so that we can always find the qualifying reference satellite, which makes the minimum condition number for the calculation system. It needs to be noted that the three reference satellites are integrally solved so as to find the optimal combination. The following steps specifically define the calculation loop:

1. (1) According to the baseline length, set a cut-off elevation angle for the selection of reference satellites;

2. (2) Calculate the condition number of norm matrix when each qualified satellite is treated as a reference satellite in order. Then we can select the satellite with the minimum condition number as the reference satellite;

3. (3) Judge whether the reference satellite determined in Step (2) is the same as the prior reference satellite. If they are different, we need transfer the DD ambiguities according to Equation (11);

4. (4) Repeat Step (2) and Step (3) by a time interval (such as 5 to 10 minutes);

5. (5) If the time duration has not yet approached the time interval set in Step (4) and the reference satellite does not meet the condition of cut-off elevation angle, repeat all the above steps.

The above procedure is further illustrated in Figure 6.

Figure 6. Flowchart of the observation structure optimization based on the MICN method.

In Figure 6, i is the satellite index; E _c is the cut-off elevation angle of reference satellites; E _i is the elevation angle of satellite i; n is the satellite number; Cond _min is the minimum condition number; Cond _i is the condition number when satellite i is treated as the reference, PRN _Ref and PRN _i are the PRN numbers of the reference satellite and the ith satellite respectively.

The new method proposed in this paper may take a little more time than the MAEA method due to the circular computations. When the numbers of candidate reference satellites from each GNSS are all six, each search of reference satellites will take our normal Personal Computer (PC) (CPU: 3·3 GHz, RAM: 3·19 G) 4 ms on average for the new method. So small a computational burden has very little negative effect on practical application.

5. METHODOLOGY VALIDATION IN HARSH ENVIRONMENTS

The number of observable satellites increases significantly when a combination of multi-constellations is used for positioning (Figure 7 shows the global distribution of GPS/BDS/GLONASS at a certain epoch), thus signal blockage caused by the surrounding environment would not lead to insufficient observable satellites. However, it will change the satellite spatial distribution and affect GNSS positioning accuracy and stability. Besides, in different geo-locations, the situations will be different. Especially in high-latitude areas, such as in the UK, Norway, Finland and so on, the satellite observation environment is more complex because just a few satellites pass through the very high-latitude areas. This leads to the situation that there is always a large vacancy on the visible satellites sky plot in the high-latitude area (Meng et al., Reference Meng, Roberts, Dodson, Cosser, Barnes and Rizos2004). This paper simulates azimuth shielding, elevation shielding and strip shielding of satellites commonly seen in GNSS application. This mainly includes 270° internal building shielding, strip shielding in strip foundation work or in urban canyons, and construction foundation or building patio environment with a large cut-off elevation shielding. Each kind of blockage will be tried in a medium-latitude area and a high-latitude area, and in this paper Nanjing (about latitude 32°N) in China and Nottingham (about latitude of 53°N) in the UK are selected to represent the two different latitudes. The experimental data acquired in Nanjing is the same as the data used in Section 3, and the GPS/BDS/GLONASS data (1 s interval) in Nottingham was collected in the University of Nottingham on 26 October 2013. The lengths of the short baselines used are all about 3 km.

Figure 7. Distribution of GPS/BDS/GLONASS.

For each trial, the positioning results obtained by applying the conventional MAEA method and the proposed MICN method for observation structure determination are compared. The positioning results, condition number and PDOP values are statistically calculated for each case.

Trial 1: Figure 8 shows one of the worst cases for GNSS applications. A typical scenario is 270° azimuth shielding, and in such circumstances we can only observe about a quarter of the satellites. The sky plots in the two places are shown in Figure 8. The shielding effects of each situation with two methods (MAEA and MICN) are illustrated in Figure 9. The visible satellite number, mean PDOP value and condition number are listed in Table 2.

Figure 8. Sky plots indicating 270° blockage.

Figure 9. Positioning error distribution for 270° blockage.

Table 2. Satellite number, condition number, positioning result and PDOP value for 270° blockage.

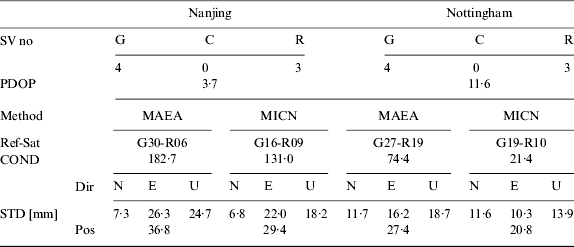
*: G is short for GPS, C for COMPASS (BDS), R for GLONASS, Dir for Direction, Pos for Position; same below.

In the Nanjing experiment, satellites G30 and R06 were selected for the MAEA method as shown in Figure 8, and the satellites selected for the new method were G16 and R09. The mean condition number for each method is 182·7 and 131·0 respectively. The observation structure was significantly improved by the new method and positioning accuracy was improved by 20·2%. In the Nottingham experiment, G27 and R19 were selected for the MAEA method; while G19 and R10 were selected for the MICN method. The overall positioning accuracy was improved by 24·1%. From Figure 8(b), we can see that the non-reference satellites were separated evenly around the reference satellites in the east-west direction, so the positioning accuracy in the east-west direction was improved by 36·4%.What is more, the larger elevation and smaller elevation satellites were also separated more evenly around the reference satellites, so the up-direction positioning accuracy was also improved by around 25%. As shown above, by implementing the condition number-based method for determining the reference satellites in the obstructed and unevenly distributed environments, with increased satellite utilisation as well as a result of using the optimal observation equation, more accurate positioning results and better stability could be achieved.

Trial 2: This is to simulate the application scenarios such as positioning in a deep valley where satellites below certain elevation angles could not be observed. Figure 10 shows the sky plots in two different locations with a cut-off elevation angle of 50°. Their directional accuracy statistics are shown in Figure 11 (a) and (b). Satellite numbers, condition number, positioning accuracy and mean PDOP are listed in Table 3.

Figure 10. Sky plots for a cut-off elevation angle of 50°.

Figure 11. Positioning error distribution for 50 degrees elevation cut-off angle.

Table 3. Satellite number, condition number, positioning result and PDOP value for 50° elevation cut-off angle.

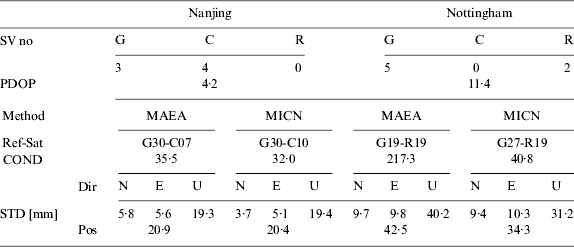
From results shown in Figure 11 (a) and Table 3, we can see that the new method shows no significant improvement on observation structure and positioning accuracy in the Nanjing experiment. This is mainly because the satellites are more evenly distributed in elevation shielding scenarios. Therefore the MICN method and the MAEA method of optimising observation structure are fundamentally the same in such cases. In the Nottingham experiment, there were few satellites in the north of the visible satellites sky plot and the distribution of satellites was extremely uneven. The mean PDOP reached 11·4. From Figure 11 (b) and Table 3 we can see that the MICN method improved the positioning accuracy, especially in the up direction by 22%.

Trial 3: Visual strips and strip shielding scenarios are a combination of directional and elevation blockage. Visual bands usually occur in strip foundation work or in urban canyons. The chosen sky plots for this scenario in the two places are shown in Figure 12(a) and Figure 12(b). The directional accuracies are as Figure 13. Positional accuracy, satellite number, condition number and mean PDOP values are listed in Table 4.

Figure 12. Sky plots of east-west blockage.

Figure 13. Positioning error distribution for east-west blockage.

Table 4. Satellite number, condition number, positioning result and PDOP of east-west blockage.

The visualization band in the blockage scenario shown in Figure 13(a) and Figure 13(b) is very narrow. In the Nanjing experiment, the reference satellites selected with the MAEA method were G30 and C07, while satellite C10 was selected as the BDS reference satellite for the MICN method. The positional accuracy and stability have been improved significantly in both north and up directions. The positional accuracy has been improved by 29·7% compared to the conventional method. A similar improvement has been achieved in the Nottingham experiment, in which the positional accuracy improved by 35·7%.

From the above experiments in the two places, we can conclude that the MICN method demonstrates a much better improvement for the observation structure when positioning in harsh observation environments, especially for the up direction. Actually, in harsh observation environments, the satellites with maximum elevation angles are generally not the most central satellites. With the MICN method, reference satellites are chosen to make the whole satellite pairs in an optimal distribution.