1. INTRODUCTION
Autonomous Underwater Vehicles (AUVs) are being extensively used by the scientific, oil and gas, and military communities (Liu et al., Reference Liu, Cui and Li2010; Zheng et al., Reference Zheng, Wang and Wu2013). Real-time tracking control is a fundamentally important issue for AUV systems, achieved by the use of adequate position sensors and generally by the adoption of advanced control approaches. However, how to effectively control an AUV to precisely track the desired vehicle trajectory is still a challenging problem. The existing tracking control methods for AUVs can be classified as follows:
1.1. Proportional-Integral-Derivative (PID) control strategy
PID control strategy (De Paula and Ferreira, Reference De Paula and Ferreira2012; Antonelli et al., Reference Antonelli, Chiaverini, Sarkar and West2001) is the most commonly used approach for mobile robot tracking control. It is widely used for linear control systems with a single input and single output, but for systems with multiple inputs and multiple outputs, the control effect is not ideal. As the AUV dynamic model is non-linear, both model parameters and ocean disturbances are uncertain and the traditional PID control effect has disadvantages.
1.2. Backstepping Control Strategy
The backstepping kinematic controller has been widely used in mobile robot tracking control (Yang and Luo, Reference Yang and Luo2004; Tsai et al., Reference Tsai, Wang and Chang2004) and it also adapted to AUV use (Jon et al., Reference Jon, Asgeir and Kristin2008). The main idea of the backstepping algorithm is to define a velocity controller that stabilizes the closed-loop system (Sharma et al., Reference Sharma, Gregory, Johnson and Dixon2012). It can deal with large initial state errors, but has major disadvantages. Large state errors can cause large control velocity and sharp speed jumps when a sudden tracking error occurs. This means that the required acceleration and forces are very large, and even infinite, may exceed the vehicle's control constraints and is usually impossible to implement practically.
1.3. Neural Network Control Method
The neural network control method (Kodogiannis, Reference Kodogiannis2003; Pepijn et al., Reference Pepijn, Colinvan and Daniel2005; Bagheri et al., Reference Bagheri, Karimi and Amanifard2010) is also used widely in controlling dynamic systems. No exact underwater vehicle model is required and an AUV's nonlinearities can be coped with. However, the problem with this approach is that the neural network model requires on-line and off-line learning in order to make the AUV perform properly. This learning procedure is computationally expensive and may not be fit for a real-time situation (Luo and Yang, Reference Luo and Yang2008).
1.4. Sliding Mode Control Method
It is well known that most physical systems have certain non-linear and various uncertainties and complex hydrodynamic forces are also relatively difficult to calculate. Sliding mode control has been proved to be able to tackle system uncertainties and external disturbances robustly. So it is usually used for dynamic tracking control of AUV (Khadija et al., Reference Khadija, Majda and Said2012; Wallace et al., Reference Wallace, Max and Edwin2008; Pan et al., Reference Pan, Seok and Yong1999). However, one major disadvantage of the sliding mode approach is the high frequency of chattering (Dongkyoung, Reference Dongkyoung2011; Bagheri and Moghaddam, Reference Bagheri and Moghaddam2009; Santhakumar and Asokan, Reference Santhakumar and Asokan2010). This high frequency chattering can cause high heat losses in the system and premature wear in thrusters. In addition, the chattering may arouse unmodelled high-frequency dynamics, which in turn destroy system performance.
1.5. Fuzzy Control Approaches
The fuzzy control approach (Wai, Reference Wai2007; Ishaque et al., Reference Ishaque, Abdullah, Ayob and Salam2010, Reference Ishaque, Abdullah, Ayob and Salam2011; Miller et al., Reference Miller, Flowers and Bevly2012) is employed for controlling uncertain or strongly nonlinear systems without knowing the precise system model. The fuzzy control approach does not need on-line or off-line learning and the computation procedure is relatively simple. The major handicap for fuzzy control is in the formulation of the fuzzy rules. The approach needs a complicated learning mechanism or a specific performance decision table designed by trial-and-error based on human knowledge. Its applications still present certain limitations.
Each of the tracking control methods for AUV discussed has advantages and disadvantages, so it is difficult to use a single method to deal with all the problems. In this paper, for the problems of speed jumps and the thruster control constraints for AUV tracking control, we present a kinematic/dynamic control system based on a velocity controller with biological neurons and an adaptive sliding mode controller. First, a novel velocity controller based on biological neurons is constructed, the velocity control outputs produced by the velocity controller are used as the control inputs of the adaptive sliding mode controller, which is designed on the vehicle position error and the biological neural dynamics model to guarantee that the position error is asymptotically stable and eliminates the sharp speed jumps when the tracking error changes suddenly. Then an adaptive sliding mode controller is used to generate the control torque, which is designed to drive the AUV and make the linear and angular velocities of the AUV converge to the reference velocities. Our proposal is chatter-free and robust under dynamic uncertainties and disturbances, because an adaptive algorithm is used in the sliding mode controller (Zhang et al., Reference Zhang, Qi and Pang2009; Antonelli et al., Reference Antonelli, Chiaverini, Sarkar and West2001; Ding and Wang, Reference Ding and Wang2009). Simulation studies have verified that the proposed control system is able to realize real-time dynamic tracking of an AUV and has better performance than the traditional backstepping method.
The remainder of this paper is organised as follows: In Section 2, we present the six degree-of-freedom kinematics and dynamics model of an AUV. In Section 3, thruster configuration and force allocation of one type of AUV are introduced, called Autonomous Remote Vehicle (ARV). In Section 4, the kinematic/dynamic hybrid control strategy is given in detail. Then, simulation results are presented in Section 5, which include an AUV tracking a broken line and a helical line trajectory in three dimensional space. A comparison between the novel hybrid control strategy and the conventional backstepping control method is presented in this section. Finally, the work is concluded in Section 6.
2. KINEMATICS AND DYNAMICS MODELLING OF AUV
2.1. Kinematic Modelling of AUV
It is normal to classify an AUV's coordinate system into a global coordinate system and a local coordinate system. The spatial position and orientation state vector in the global coordinate system can be expressed as η. The spatial linear velocity and angular velocity state vector in the local coordinate system can be expressed as q. The three dimensional AUV coordinate systems are shown in Figure 1.
Figure 1. AUV Coordinate systems.
We consider that all kinematics equality constraints are independent of time. The position state vector η and the velocity state vector q have the following relations:
$$\dot \eta = J(\eta )q$$where J ∈ R 6×6 represents the transformation matrix from the local coordinate system to the global coordinate system. It has been discussed in many papers (Dongkyoung, Reference Dongkyoung2011; Serdar et al., Reference Serdar, Bradley and Ron2010).
2.2. Dynamics Modelling of AUV
The three dimensional six degree-of-freedom dynamics equations of AUV can be expressed as follows (Dongkyoung, Reference Dongkyoung2011; Serdar et al., Reference Serdar, Bradley and Ron2010):
$$\eqalign{ & M\dot q + C(\dot q)q + D(\dot q)q + g(\eta ) = \tau + w \cr & \tau = BT} $$where M ∈ R 6×6 is the inertia matrix; C ∈ R 6×6 is the centrifugal terms and Coriolis matrix; D ∈ R 6×6 is the hydrodynamic damping matrix; g ∈ R 6 is the vector of gravity and buoyancy; τ ∈ R 6 is the control forces and torques on the AUV centre; w is the control forces and torques caused by unknown disturbance including unstructured and modelled dynamics in the local coordinate system; B is the matrix of forces configuration; T is the forces produced by thruster.
From Equation (2), we can obtain dynamics equality in the global coordinate system through coordinate transformation 
$\dot \eta = J(\eta )q$.
$$f = M_\eta (\eta )\ddot \eta + C_\eta (q,\eta )\dot \eta + D_\eta (q,\eta )\dot \eta + g_\eta (\eta ) = J^{ - T} \tau $$where M η (η)=J−TMJ− 1, 
$C_\eta (q,\eta ) = J^{ - T} [C - MJ^{ - 1} \dot J]J^{ - 1}\!\!$, D η (q,η)=J−TDJ− 1, g η (η)=J−Tg.
3. THRUSTER CONFIGURATION AND FORCE ALLOCATION OF AUV
In this paper, we use a particular type of AUV model for simulation. It is from the Laboratory of Underwater Vehicles and Intelligent Systems, Shanghai Maritime University, and will be described in detail below.
There is no lateral thruster in our AUV, so v=0 in the velocity state vector. Usually the model is decoupled and controllable in three degrees-of-freedom (surge, heave and yaw). The reduced position state vector η=[x y z ψ]T and velocity state vector q=[u w r]T.
The dynamics modelling of the AUV can also be simplified as follows (Lapierre and Jouvencel, Reference Lapierre and Jouvencel2008; Edin and Geoff, Reference Edin and Geoff2004; Zhu et al., Reference Zhu, Liu and Hu2011):
$$(m - X_{\dot u} )\dot u + X_u u + X_{uu} u|u| = \tau _X $$
$$(m - Z_{\dot w} )\dot w + Z_w w + Z_{ww} w|w| = \tau _Z $$
$$(I_Z - N_{\dot r} )\dot r + N_r r + N_{rr} r|r = \tau _N $$The AUV has four thrusters; two thrusters are in the horizontal plane and the other two are in vertical plane. Figure 2 shows its structure. A brief sketch of the vehicle's thruster configuration is shown in Figure 3. The dynamic equation of the AUV can be written by Equation (7), based on the thrusters' distribution.
Figure 2. Structure of AUV.
Figure 3. Thruster configuration.
We can deduce the relationship between the normalized form of torque and the normalized form of thruster forces as follows:
$$\tau = \left[ {\matrix{ {\tau _X} \cr {\tau _Z} \cr {\tau _N} \cr}} \right] = \left[ {\matrix{ K & K & 0 & 0 \cr 0 & 0 & K & K \cr {KR} & { - KR} & 0 & 0 \cr}} \right]\left[ {\matrix{ {T_1} \cr {T_2} \cr {T_3} \cr {T_4} \cr}} \right]$$
$$\tau _{Zm} = 2KT_m $$
$$\tau _{Zm} = 2KT_m $$
$$\tau _{Nm} = 2KRT_m $$
$$\left[ {\matrix{ {\displaystyle{{\tau _X} \over {\tau _{Xm}}}} \cr {\displaystyle{{\tau _Z} \over {\tau _{Zm}}}} \cr {\displaystyle{{\tau _N} \over {\tau _{Nm}}}} \cr}} \right] = \left[ {\matrix{ {\displaystyle{1 \over 2}} & {\displaystyle{1 \over 2}} & 0 & 0 \cr 0 & 0 & {\displaystyle{1 \over 2}} & {\displaystyle{1 \over 2}} \cr {\displaystyle{1 \over 2}} & { - \displaystyle{1 \over 2}} & 0 & 0 \cr}} \right]\left[ {\matrix{ {\displaystyle{{T_1} \over {T_m}}} \cr {\displaystyle{{T_2} \over {T_m}}} \cr {\displaystyle{{T_3} \over {T_m}}} \cr {\displaystyle{{T_4} \over {T_m}}} \cr}} \right] \Leftrightarrow \left[ {\matrix{ {\bar \tau _X} \cr {\bar \tau _Z} \cr {\bar \tau _N} \cr}} \right] = \overline {B} \cdot \left[ {\matrix{ {\skew3\overline{T}_1} \cr {\overline{T}_2} \cr {\overline{T}_3} \cr {\overline{T}_4} \cr}} \right] \Leftrightarrow \bar \tau = \overline{B} \cdot \overline{T}$$where τ are the values of the surge and heave forces and the yaw torque respectively. K is a constant. R is the distance between the two vertical thrusters. τ m=[τ XmτZm τNm]T are maximum values of the surge and heave forces and the yaw torque for the AUV respectively. [T 1T 2T 3T 4]T are the forces of the four thrusters individually. T m represents the max force of an individual thruster. 
$\bar \tau $ is the normalized form of 
$\tau, \overline{T} = \left[ {\matrix{ {\overline{T}_1} & {\overline T_2} & {\matrix{ {\overline T_3} & {\overline T_4} \cr}} \cr}} \right]^T $ is the normalized form of T=[T 1T 2T 3T 4]T, 
$-1\! \leqslant \bar \tau _i \leqslant 1, i = X,Z,N,- 1 \leqslant {\overline T}_i \leqslant 1, i = 1,2,3,4$.
4. HYBRID CONTROL STRATEGY FOR AUV
The trajectory tracking problem of an AUV can be described as: Given an AUV dynamical model and a continuous bounded time varying reference trajectory, design a control law that ensures asymptotically exact tracking of the reference trajectory. This paper focuses on the problem of speed jumps and the thruster control constraints for AUV tracking control. A novel control system is presented in Figure 4, which combines a velocity controller with biological neurons and an adaptive sliding mode controller (Dongkyoung, Reference Dongkyoung2011).
Figure 4. The novel control system scheme.
4.1. Kinematic Velocity Controller
A backstepping algorithm is employed in the velocity controller to produce the expected velocity. For the AUV model in three dimensional space, the desired position state and velocity state can be described as η d=[x dyd zd ψd]T and q d=[u dwd rd]T, the actual position state and velocity state can be described as η=[x y z ψ]T and q=[u w r]T. The position state error in the global coordinate system is defined as e=η−η d=[e xey ez eψ]T. The development of tracking control is to let trajectory η follow the reference trajectory η d smoothly and let the e converge to zero. The position state error in the local coordinate system can be expressed as:
$$e' = [\matrix{ {e_1} & {e_2} & {e_3} & {e_4} \cr} ]^T = J^T e = J^T [\matrix{ {e_x} & {e_y} & {e_z} & {e_\psi} \cr} ]^T $$
$${\rm where}\ J = \left[ {\matrix{ {\cos \psi} & { - \sin \psi} & 0 & 0 \cr {\sin \psi} & {\cos \psi} & 0 & 0 \cr 0 & 0 & 1 & 0 \cr 0 & 0 & 0 & 1 \cr}} \right]$$The backstepping algorithm (Zhang et al., Reference Zhang, Velinsky and Feng1997) is defined as follows:
$$\left\{ \matrix{{u = u_d + k_v (e_1 \cos \psi + e_2 \sin \psi )} \cr { r = r_d + k_\psi \sin \left( {\displaystyle{{e_4} \over 2}} \right) + 2u_d \left( {e_2 \cos \displaystyle{{\psi _d + \psi} \over 2} - e_1 \sin \displaystyle{{\psi _d + \psi} \over 2}} \right)} \cr {w = w_d + k_z e_3} } \right.$$where k v, kψ, kz are constant.
By analysing the performance of the velocity controller based on the backstepping approach, this controller smooths the sharp speed jumps when tracking errors change suddenly. This means that the required acceleration and forces/torques are very large and may even be infinite, which may exceed the vehicle's control constraint and it is usually practically impossible. However, the biological neural model has characteristics such as stability, bounded activity and smooth response, that may allow it to be used to produce a bounded and smooth auxiliary signal related to tracking errors to improve the real-time velocity commands. Thus we add a biological neuron model to the velocity controller.
Hodgkin and Huxley (Reference Hodgkin and Huxley1952) proposed a model for a patch of membrane in a biological neural system using electrical circuit elements. The model then developed and gave rise to many model variations and applications. A biological neuron model was first proposed by Grossberg (Reference Grossberg1988). The shunting equation is described as:
$$C_m \displaystyle{{dV_m} \over {dt}} = - (E_p + V_m )g_p + (E_{Na} - V_m )g_{Na} - (E_k + V_m )g_k $$where C m is the membrane capacitance. The parameters E k, E na and E p are the Nernst potentials for potassium ions, sodium ions, and negative drain current in the membrane, respectively. g k, gNa and g p are the conductance of potassium, sodium and negative pole, respectively. The above parameters can be simplified:
$$\eqalign{ C_m\!=\!1, V\!=\!E_p+V_m, A\!=\!g_p, B\!=\!E_{Na}+E_p, D\!=\!E_k-E_p, S(t)^+\!=\!g_{Na}, S(t)^-\!=\!g_K}.$$Then the shunting equation can be written as follow:
$$\dot V = - AV + (B - V)S(t)^ + - (D + V)S(t)^ - $$where V is the neural activity (membrane potential) of the neuron. Parameters A, B and D are the passive decay rate, the upper and lower bounds of the neural activity, respectively. The variables S + and S− represent the excitatory and inhibitory input to a neuron, respectively. The shunting dynamic of an individual neuron can be modelled by this equation. The state responses of the models are limited to the finite interval [−D, B] because of the auto gain-regulation of the model. So we can infer the shunting equation to the following form:
$$\dot V_i = - AV_i + (B - V_i )f\,(e_i ) - (D + V_{_i} )g(e_i )$$where i is the neuron index, f(e i)=max(e i, 0), g(e i)=max(−e i, 0). It is guaranteed that the neural activity will stay in this interval for any value of the excitatory and inhibitory inputs. The stability and convergence of the shunting model can be rigorously proved by Lyapunov stability theory (Slotine and Li, Reference Slotine and Li1991). It is continuous and smooth. We put the biological neuron model into the traditional velocity controller, so that Equation (13) can be written as:
$$\left\{ \matrix{u = u_d + k_v (V_1 \cos \psi + V_2 \sin \psi ) \cr r = r_d + k_\psi \sin \left( {\displaystyle{{V_4} \over 2}} \right) + 2u_d \left( {V_2 \cos \displaystyle{{\psi _d + \psi} \over 2} - V_1 \sin \displaystyle{{\psi _d + \psi} \over 2}} \right) \cr w = w_d + k_z V_3 } \right.$$where V i (i=1, 2, 3, 4) represent the outputs of the biological neuron model related to the tracking errors e′ respectively. Because of the smooth and bounded activity of the shunting model, the sharp speed jumps are inhibited effectively. Thus, the outputs of the velocity controller will become smooth even if the tracking errors change suddenly. The performance of the velocity controller is significantly improved.
4.2. Dynamic Sliding Mode Controller
Since sliding mode control can offer many properties, such as fast dynamic response, insensitivity to parametric variations and external disturbance rejection, it has been widely used to control nonlinear dynamic systems. It can also be employed to control AUV (Khadija et al., Reference Khadija, Majda and Said2012; Wallace et al., Reference Wallace, Max and Edwin2008). The sliding mode controller generates forces and torques τ=[τ XτZ τN]T in the AUV, which drive the AUV states towards a sliding mode surface, and then switch on that surface. The forces and torques are applied to AUV to produce actual velocity q. So we can easily get the actual states η by Equation (1).
We choose the sliding mode surface:
$$s = \left( {\displaystyle{d \over {dt}} + \Lambda} \right)^2 \left( {\int {edt}} \right) = \dot e + 2\Lambda e + \Lambda ^2 \int {edt} $$where e=q c−q=[e ueω er]T is the error between the virtual velocity generated by the velocity controller and the actual velocity of the AUV. Furthermore, there is
$$\dot s = \ddot e + 2\Lambda \dot e + \Lambda ^2 e = \ddot e + 2\Lambda (\dot q_c - \dot q) + \Lambda ^2 e$$where the system is operating on the sliding mode surface, Equation (19) equals zero.
$$\dot s = \ddot e + 2\Lambda \dot e + \Lambda ^2 e = \ddot e + 2\Lambda (\dot q_c - \dot q) + \Lambda ^2 e = 0$$ Equation (2) is simplified as 
$M\dot q + Cq + Dq + g = \tau $. Put this into Equation (20).
$$\ddot e + 2\Lambda (\dot q_c - M^{ - 1} )=( {(\tau - Cq - Dq - g)}) + \Lambda ^2 e = 0$$Here, the system dynamic term τ is simply divided into two parts: estimated term and unknown term:
$$\tau = \hat \tau + \tilde \tau $$So the equivalent control law can be concluded as
$$\tau _{eq} = \hat M\left( {\dot q_c + \displaystyle{{\ddot e} \over {2\Lambda}} + \displaystyle{\Lambda \over 2}e} \right) + \hat Cq + \hat Dq + \hat g$$where 
$\hat M,\hat C,\hat D,\hat g$ are estimated terms. Considering the difficulty of computing ë, we introduce a feedback control method of acceleration error
$$\ddot e = - k\dot e$$The conventional sliding mode algorithm is designed as follows:
$$\tau = \tau _{eq} + k\,{\mathop{\rm sgn}} (s)$$To eliminate the chattering problem caused by the discontinuous term, an adaptive term is added in the control law to replace the switching term in Equation (25).
$$\tau _{ad} = \tilde \tau _{est} + Ks$$where 
$\tilde \tau _{est} $ is an adaptive term that estimates the unknown term 
$\tilde \tau $. The update rate of 
$\tilde \tau _{est} $ is as follows:
$${\dot {\tilde \tau}}_{est} = \Gamma s $$We then produce a new siding mode controller, called the adaptive sliding mode controller. The total control law can be defined as:
$$\tau = \tau _{eq} + \tau _{ad} = \tau _{eq} + \tilde \tau _{est} + Ks $$5. SIMULATION
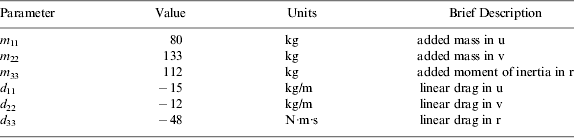
The trajectory tracking for the AUV is simulated based on the conventional backstepping control method and the novel hybrid control strategy in this section. The reference trajectories are a broken line and a helical line in three-dimensional space. A comparison between the simulation results of the two control methods is presented. The aim of the comparison is to illustrate that the novel hybrid control strategy has advantages over the conventional backstepping control method in driving the AUV onto a desired trajectory, and that there is no problem with speed jumps and thruster control constraints for the proposed hybrid control strategy. The hydrodynamic parameters of the AUV are given in Table 1.
Table 1. AUV hydrodynamic parameters.
From Figure 4, we can easily obtain position error e=η−η d. We then obtain e′ from Equation (12). e′ is used as the input of the velocity controller, the output is the expected velocity q c=[u cvc rc]T. We use velocity error e″=q−q c=[e ueω er]T as the sliding mode controller's input, the output is torques τ=[τ XτZ τN]T. Put into Equation (11), the result is the normalized form of forces 
$\overline T = \left[ {\matrix{ {\overline T_1} \enspace {\overline T_2} \enspace {\matrix{ {\overline T_{\rm 3}} \enspace {\overline T_{\rm 4}} \cr}} \cr}} \right]^T $. The forces and torques are applied to the AUV to produce actual velocity q=[u v r]T. Thus we can easily get the actual states η=[x y z ψ]T by Equation (1).
5.1. Broken Line Trajectory Tracking
A typical broken line trajectory is studied first. Its equation is a random function. The three dimensional state vector of the AUV can be expressed as η(t)=[x(t) y(t) z(t) ψ(t)]T, and the actual initial state is η(0)=[6 0 0 0]T. Assume the desired state of the AUV is
$$\left\{ \matrix{x_d (t) = 0{\cdot}3*t + 3,\enspace y_d (t) = 0{\cdot}3*t{\rm},\enspace {\rm} z_d (t) = 0{\cdot}3*t{\rm},\enspace {\rm} \psi _d (t) = \displaystyle{\pi \over 4}\quad\quad 0 \lt t \lt 10 \cr x_d (t) = 0{\cdot}3*(t - 10) + 6{\rm},\enspace y_d (t) = 3{\rm}, {\rm}\enspace z_d (t) = 3{\rm},\enspace {\rm} \psi _d (t) = 0\quad\quad\quad 10 \leqslant t \lt 20 \cr x_d (t) = 0{\cdot}3*(t - 20) + 9,\enspace y_d (t) = 0{\cdot}3*(t - 20) + 3,\enspace z_d (t) = 0{\cdot}3*(t - 20) + 3,\cr\quad\quad\quad\enspace\psi _d = \displaystyle{\pi \over 4}\quad t \geqslant 20 } \right.$$The simulation result of trajectory tracking is shown in Figure 5. The blue dotted line represents the traditional backstepping method and red solid line represents the novel hybrid control strategy. From Figure 5 we can see that it takes a short time to catch up the desired trajectory smoothly for the two methods. Figure 6 shows the two methods both produce error jumps at initial time and at random points. However, the velocity responses are obviously different for the different track control methods. For the traditional backstepping method, sharp speed jumps occur when tracking errors change suddenly at initial time and at random points. For example, the virtual surge speed of the traditional backstepping method jumps to more than 5 m/s at initial time, but for the novel hybrid method this is less than 2 m/s in Figure 7. This means that the required acceleration and forces or moments will exceed their control constraint values at the velocity jump points for the traditional backstepping approach, which is practically impossible. For the hybrid control strategy, due to the shunting characteristics of the biological neuron model, the sharp speed jumps are effectively inhibited. Thus, the outputs of the velocity controller will become smoother even if the tracking errors change suddenly.
Figure 5. Broken line trajectory tracking.
Figure 6. Tracking error.
Figure 7. The velocity of the AUV.
Figure 8 shows normalized thruster forces. For the traditional backstepping approach, the tracking controller outputs do not meet the thruster control constraint (
$ - 1\! \leqslant\! \overline T\! \leqslant\! + 1$), for instance, the normalized thruster force 
$\overline T_{\rm 1} $ of the traditional backstepping method jumps to over ten at the tenth second, but for the hybrid method is less than one. This means that thruster forces in the traditional backstepping approach exceed their maximum values, which is practically impossible. Conversely, the hybrid control method does not exhibit this problem. No control value exceeds its maximum; thus the proposed neurodynamics control strategy is more effective.
Figure 8. The forces of thrusters.
In addition, from Figures 5 to 8, it can be seen that the hybrid control method is chatter-free and robust under dynamic uncertainties and disturbance because the adaptive sliding mode algorithm is used.
5.2. Helical Line Trajectory Tracking
A typical helical trajectory is studied first. The three dimensional state vector of the AUV can be expressed as η(t)=[x(t) y(t) z(t) ψ(t)]T. Assume the desired state is x d(t)=sin(0·5*t), y d(t)=−cos(0·5*t), z d(t)=0·2*t, ψ d(t)=0·5*t; the actual initial state η(0)=[x(0) y(0) z(0) ψ(0)]T=[−0·5 0·5 0 0]T.
The simulation result of trajectory tracking is shown in Figure 9. The blue dotted line represents the traditional backstepping method and the red solid line represents the hybrid control strategy. From Figure 9 we can see that it takes a short time to catch up the desired trajectory smoothly for the two methods. Figure 10 shows the two strategies both produce error jumps at initial time, but the velocity responses are obviously different. From Figure 11, the virtual velocity based on the traditional backstepping approach gives rise to sharp speed jumps when tracking errors change suddenly. For example, the virtual heave speed jumps to more than 0·8 m/s at initial time, but for the hybrid method it is less than 0·2 m/s. This means that the required acceleration and forces or moments will exceed their control constraint values at the velocity jump points for the traditional backstepping approach, which is practically impossible. Compared with the traditional backstepping approach, the virtual velocities of the hybrid method are smooth without any sharp jumps.
Figure 9. Helical line trajectory tracking.
Figure 10. Tracking error.
Figure 11. The velocity of the AUV.
Normalized thruster forces are shown in Figure 12. For the traditional backstepping approach, the tracking controller outputs do not meet the thruster control constraint (
$ - 1 \leqslant \overline T \leqslant + 1$). For instance, the normalized thruster force 
$\overline T_{\rm 3} $ of the traditional backstepping method jumps to three at initial time, but the novel hybrid method is less than 0·5. This means that thruster forces of the traditional backstepping method exceed their maximum values, which is impossible to achieve. For the hybrid control method, no control value exceeds their maximum, and all control values based on the biological neuron model are smaller than the maximum. This proves the efficiency of the proposed hybrid strategy.
Figure 12. The forces of thrusters.
In addition, from Figures 9 to 12, it can be seen that the hybrid control method is chatter-free and robust under dynamic uncertainties and disturbances because the adaptive sliding mode algorithm is used in the hybrid controller.
6. CONCLUSIONS
In this paper, a kinematic/dynamics control system based on a velocity controller with biological neurons and an adaptive sliding mode controller is presented for tracking control of an AUV. The biological neuron model can obviously inhibit the sharp speed jumps that commonly exist in the conventional backstepping method. Thus it avoids the required acceleration and forces or moments exceeding their control constraint values at the velocity jump points. Also, we employed an adaptive algorithm to the sliding mode controller; an adaptive term is added into the control law to replace the switching term. Thus the adaptive sliding mode control strategy is chatter-free and robust under dynamic uncertainties and disturbances.
The simulation studies have verified that the proposed novel control system is able to realize the dynamic tracking of an AUV and has better performance than the traditional backstepping method.
ACKNOWLEDGEMENT
This project is supported by the National Natural Science Foundation of China (51279098), Research Fund of Ministry Transport of China (2011-329-810-440) and the Project of Shanghai Municipal Education Commission (13ZZ123).
