1. INTRODUCTION
With the development and modernisation of global and regional Global Satellite Navigation Systems (GNSS), an increasing number of satellites and navigation signals are becoming available. It is expected that combining signals from different GNSSs will improve positioning accuracy, availability and reliability, especially in obstructed environments where the number of observed satellites for each system are limited (Ji et al. Reference Ji, Chen, Ding, Chen, Zhao and Hu2010; Deng et al., Reference Deng, Tang, Liu and Shi2014; He et al., Reference He, Li, Yang, Xu, Guo and Wang2014; Nadarajah and Teunissen, Reference Nadarajah and Teunissen2014; Paziewski and Wielgosz, Reference Paziewski and Wielgosz2014; Teunissen et al., Reference Teunissen, Odolinski and Odijk2014; Li et al., Reference Li, Ge, Dai, Fritsche, Wickert and Schuh2015; Odolinski et al., Reference Odolinski, Teunissen and Odijk2015; Quan et al., Reference Quan, Lau, Roberts and Meng2016). Recently, 12 Global Positioning System (GPS) Block IIF satellites have been launched into orbit, all of which are currently operational (GPS.gov, 2018). By the end of 2017, 18 Galileo Full-Operational Capability (FOC) satellites had also been launched next to the four In-Orbit Validation (IOV) satellites (MGEX.igs, 2018a). In addition to these new GPS and Galileo satellites, three new Quasi-Zenith Satellite System (QZSS) satellites were launched into orbit in 2017 after the launch of the first satellite Michibiki or QZS-1 on September 2010 (MGEX.igs, 2018b). To ensure compatibility and interoperability with modernised GPS satellites, Galileo satellites are capable of broadcasting navigation signals on carrier phase frequencies that overlap with GPS L1, and L5 and QZSS satellites transmit the same navigation signals (that is, L1C/A, L1C, L2C, and L5) as GPS (Hofmann-Wellenhof et al., Reference Hofmann-Wellenhof, Lichtenegger and Wasle2007). This allows for tightly combined processing or inter-system double-differencing of observations from GPS, Galileo and QZSS. In such a case, Galileo and QZSS satellites can be used as if they were additional GPS satellites and thus additional Double-Differenced (DD) observations can be created with respect to loosely combined or classical double-differencing of observations from each system independently, resulting in improved integer ambiguity resolution and positioning results (Odijk and Teunissen, Reference Odijk and Teunissen2013a; Paziewski and Wielgosz, Reference Paziewski and Wielgosz2015; Liu et al., Reference Liu, Shu, Xu, Qian, Zhang and Zhang2017; Odijk et al., Reference Odijk, Nadarajah, Zaminpardaz and Teunissen2017; Paziewski and Wielgosz, Reference Paziewski and Wielgosz2017; Wu et al., Reference Wu, Zhang, Liu, Ni and Yu2017; Gao et al., Reference Gao, Meng, Gao, Pan and Wang2018; Kubo et al., Reference Kubo, Tokura and Pullen2018; Li et al., Reference Li, Geng, Guo, Zhou and Lin2018; Tian et al., Reference Tian, Liu, Ge and Neitzel2018).
However, when the tightly combined approach is introduced, the phase and code between-receiver Differential Inter-System Biases (DISBs) that originate from the differences in the receiver hardware delays affecting signals from different GNSS systems (Montenbruck et al., Reference Montenbruck, Hauschild and Hessels2011) must be accounted for. The knowledge of time-varying characteristics and influencing factors of DISBs are prerequisites for the optimal realisation of tightly combined relative positioning. Previous studies have revealed that the phase and code DISBs between overlapping frequencies that are shared by different GNSS systems are receiver-type dependent. They are absent when identical types of multi-GNSS receivers are used at both ends of a baseline. In contrast, they are generally present and cannot be neglected for baselines with different receiver types. Fortunately, it is also shown that the DISBs are very stable in the time domain, which provides the possibility of a priori calibration and correction of these biases (Odijk and Teunissen, Reference Odijk and Teunissen2013a; Reference Odijk and Teunissen2013b; Yuan and Zhang, Reference Yuan and Zhang2014; Paziewski and Wielgosz, Reference Paziewski and Wielgosz2015). Deprez and Warnant (Reference Deprez and Warnant2016a; Reference Deprez and Warnant2016b) found that the activation of multipath filters for Trimble NetR9 receivers might have an impact on GPS-Galileo (L1-E1 and L5-E5a) code DISBs but have no effect on the phase DISBs. They also showed that the phase DISBs might be affected by a firmware upgrade. However, they only presented their initial results and did not provide full details. Tsuji et al. (Reference Tsuji, Matsuo, Furuya, Yamao and Kamakari2016) demonstrated that GPS-Galileo-QZSS phase DISBs are not affected by change of antennae, reboot of receivers, upgrade of receiver's firmware and temperature for a cluster of receivers (JAVAD SIGMA, LEICA GRX1200 + GNSS, TOPCON NET-G3, and Trimble NetR9). However, their results were based on the specific receivers (including receiver firmware versions) used in the experiments and probably do not fully read across to results from other receivers. In this work, it has been found that the reboot of receivers and the type of the observations may have an impact on the GPS-Galileo-QZSS phase DISBs, which will be shown in Section 4. In addition, a comprehensive investigation regarding the impact of the receiver firmware upgrade and the activation of anti-multipath filter on the DISBs was carried out. Some new results are presented for both the phase and code DISBs for different GNSS system pairs (GPS-Galileo and GPS-QZSS), different frequencies (L1-E1 and L5-E5a), and different receiver types (Trimble NetR9 and Javad TRE-G3T DELTA). Finally, as a method to evaluate the interoperability of Galileo and QZSS with GPS, this paper also conducts a performance comparison of epoch-by-epoch relative positioning between loosely and tightly combined models with observations from current GPS/Galileo/QZSS constellations, in which the recently launched Galileo and QZSS satellites will also be included.
This paper focuses on an influencing factors analysis of DISB estimates and performance assessment of tightly combined GPS, Galileo and QZSS relative positioning for short baselines with only single-epoch observations. The tightly combined observational model, which assumes a single GPS reference satellite for all observations from GPS, Galileo and QZSS is introduced. The influencing factors (including reboot of receivers, the upgrade of receiver firmware, the activation of an anti-multipath filter and the type of observations) of DISBs between overlapping frequencies that are shared by GPS, Galileo, and QZSS (that is, GPS/Galileo/QZSS L1-E1-L1/L2-L2/ L5-E5a-L5) are then comprehensively analysed. Finally, the performance of single-epoch tightly combined GPS, Galileo and QZSS relative positioning using single-frequency (GPS/Galileo/QZSS L1-E1-L1) and dual-frequency (GPS/Galileo/QZSS L1-E1-L1 and L5-E5a-L5) observations are evaluated by a formal as well as an empirical analysis, consisting of the Ambiguity Dilution Of Precision (ADOP), Bootstrapping Success Rate (BSR), ratio values, empirical ambiguity resolution success rate and positioning accuracy.
The paper is organised as follows. Section 2 presents the methodology of DISB estimation and correction for zero and short baselines. Section 3 provides an overview of GNSS data collection. Section 4 presents a comprehensive analysis of the influencing factors of DISBs. Section 5 presents a performance evaluation of tightly combined GPS, Galileo and QZSS single-epoch relative positioning using single-frequency and dual-frequency observations. Finally, some conclusions are given in Section 6.
2. METHODOLOGY
This section briefly introduces the Loosely Combined Model (LCM), and the inter-system DD model or Tightly Combined Model (TCM) corresponding to the estimation and correction of DISB parameters for zero or short baselines. As the atmospheric delays, including ionospheric delays and tropospheric delays, can generally be mitigated to a negligible level when forming DD observations for short baselines, they will be omitted for formula simplification.
Assuming that two receivers k and l simultaneously track satellites s G = 1G, 2G…m G and s * = 1*, 2*…m * on overlapping frequencies i = 1, 2… f, where m G and m * are the number of satellites from GPS and constellation * (The symbol * is E for Galileo and Q for QZSS) respectively, the undifferenced phase and code observation equations for receiver k and GPS satellite s G on frequency i then read (Hofmann-Wellenhof et al., Reference Hofmann-Wellenhof, Lichtenegger and Wasle2007):
$$\eqalign{\phi_{k\comma i}^{s_G} &=\rho_k^{s_G} +dt_k -dt^{s_G }+\lambda_i \lpar {\delta_{k\comma i}^G +\varphi_{k\comma i} -\delta_i^{s_G} -\varphi_i^{s_G} +N_{k\comma i}^{s_G}}\rpar +\varepsilon_{k\comma i}^{s_G} \cr P_{k\comma i}^{s_G} &=\rho_k^{s_G} +dt_k -dt^{s_G }+d_{k\comma i}^G -d_i^{s_G} +e_{k\comma i}^{s_G}} $$
where 
$\phi_{k\comma i}^{s_{G}}$ and 
$P_{k\comma i}^{s_{G}}$ are the phase and code measurements in metres, respectively; 
$\rho_{k}^{s_{G}}$ is the geometric distance between the satellite and receiver antenna; dt k is receiver clock bias; 
$dt^{s_{G}}$ is the satellite clock bias; λ i is the wavelength; 
$\delta_{k\comma i}^{G}$ and 
$\delta_{i}^{s_{G}}$ are the phase hardware delay in the receiver and satellite, respectively; φ k, i and 
$\varphi_{i}^{s_{G}}$ are the initial phase bias in the receiver and satellite, respectively; 
$d_{k\comma i}^{G}$ and 
$d_{i}^{s_{G}}$ are the code hardware delays in the receiver and satellite, respectively; 
$N_{k\comma i}^{s_{G}}$ is the ambiguity and 
$\varepsilon_{k\comma i}^{s_{G}}$ and 
$e_{k\comma i}^{s_{G}}$ are all other errors including the measurement noise. Note that the subscript G means that 
$\delta_{k\comma i}^{G}$ and 
$d_{k\comma i}^{G}$ are related to the GPS system rather than a particular GPS satellite.
Similarly, the undifferenced phase and code observation equations for receiver k and satellite s * on frequency i then read:
$$\eqalign{\phi_{k\comma i}^{s_\ast} & =\rho_k^{s_\ast } +dt_k -dt^{s_\ast }+\lambda_i \lpar {\delta_{k\comma i}^\ast +\varphi_{k\comma i} -\delta_i^{s_\ast } -\varphi_i^{s_\ast } +N_{k\comma i}^{s_\ast } }\rpar +d_{TO} +\varepsilon_{k\comma i}^{s_\ast } \cr P_{k\comma i}^{s_\ast } &=\rho_k^{s_\ast } +dt_k -dt^{s_\ast }+d_{k\comma i}^\ast -d_i^{s_\ast } +d_{TO} +e_{k\comma i}^{s_\ast }} $$where d TO is the time offset between GPS and constellation *.
2.1. Intra-system DD observations with LCM
When LCM or an intra-system DD model is considered, the satellite-specific errors, the receiver-specific errors and the time offset are all eliminated. The intra-system DD observations can be given as follows:
$$\eqalign{\phi_{kl\comma i}^{1_G s_G}&=\rho_{kl}^{1_G s_G} +\lambda_i N_{kl\comma i}^{1_G s_G}+\varepsilon_{kl\comma i}^{1_G s_G} \cr \phi_{kl\comma i}^{1_\ast s_\ast} &=\rho_{kl}^{1_\ast s_\ast} +\lambda_i N_{kl\comma i}^{1_\ast s_\ast} +\varepsilon_{kl\comma i}^{1_\ast s_\ast} \cr P_{kl\comma i}^{1_G s_G} &=\rho_{kl}^{1_G s_G} +e_{kl\comma i}^{1_G s_G} \cr P_{kl\comma i}^{1_\ast s_\ast} &=\rho_{kl}^{1_\ast s_\ast} +e_{kl\comma i}^{1_\ast s_\ast}} $$where s G ≥ 2G and s * ≥ 2*.
2.2. Estimation of phase and code DISBs with TCM
When TCM or an inter-system DD model is considered, the phase and code hardware delays in the receiver cannot be cancelled out. The inter-system DD observations can be given as follows (Odijk and Teunissen, Reference Odijk and Teunissen2013a; Paziewski and Wielgosz, Reference Paziewski and Wielgosz2014):
$$\eqalign{\phi_{kl\comma i}^{1_G s_G}&=\rho_{kl}^{1_G s_G} +\lambda_i N_{kl\comma i}^{1_G s_G}+\varepsilon_{kl\comma i}^{1_G s_G} \cr \phi_{kl\comma i}^{1_G s_\ast} &=\rho_{kl}^{1_G s_\ast} +\lambda_i \lpar N_{kl\comma i}^{1_G s_\ast} +\bar{\delta}_{kl\comma i}^{G\ast} \rpar +\varepsilon_{kl\comma i}^{1_G s_\ast} \cr P_{kl\comma i}^{1_G s_G} &=\rho_{kl}^{1_G s_G} +e_{kl\comma i}^{1_G s_G} \cr P_{kl\comma i}^{1_G s_\ast} &=\rho_{kl}^{1_G s_\ast} +d_{kl\comma i}^{G\ast} +e_{kl\comma i}^{1_G s_\ast}} $$
where s G ≥ 2G and s * ≥ 1*. Note that 
$d_{kl\comma i}^{G\ast}$ is the code DISB parameter and 
$\bar {\delta }_{kl\comma i}^{G\ast} =\delta_{kl\comma i}^{G\ast} +N_{kl\comma i}^{1_{G} 1_{\ast}}$ the lumped phase DISB parameter, which is composed of the phase DISB parameter (
$\delta_{kl\comma i}^{G\ast} \rpar $ and DD ambiguity between pivot satellites of GPS and system *. According to Equation (4), the phase and code DISBs can be estimated separately for each of the overlapping frequencies in a “instantaneous” (single-epoch) solution or in a “session” solution.
2.3. Correction of phase and code DISBs with TCM
Previous studies have shown that the DISBs are generally very stable in the time domain. In such cases, they can be a priori calibrated and corrected to strengthen the adjustment model. The DD observations corresponding to the correction of DISB parameters then read (Odijk and Teunissen, Reference Odijk and Teunissen2013a; Paziewski and Wielgosz, Reference Paziewski and Wielgosz2014):
$$\eqalign{\phi_{kl\comma i}^{1_G s_G}&=\rho_{kl}^{1_G s_G}+\lambda_i N_{kl\comma i}^{1_G s_G}+\varepsilon_{kl\comma i}^{1_G s_G} \cr \hat {\phi }_{kl\comma i}^{1_G s_\ast} &=\phi_{kl\comma i}^{1_G s_\ast} -\lambda_i \hat {\delta }_{kl\comma i}^{G\ast} =\rho_{kl}^{1_G s_\ast} +\lambda_i N_{kl\comma i}^{1_G s_\ast} +\varepsilon_{kl\comma i}^{1_G s_\ast} \cr P_{kl\comma i}^{1_G s_G} &=\rho_{kl}^{1_G s_G} +e_{kl\comma i}^{1_G s_G} \cr \hat {P}_{kl\comma i}^{1_G s_\ast} &=P_{kl\comma i}^{1_G s_\ast} -\hat {d}_{kl\comma i}^{G\ast} =\rho_{kl}^{1_G s_\ast} +e_{kl\comma i}^{1_G s_\ast}} $$
where s G ≥ 2G and s * ≥ 1*, 
$\hat {P}_{kl\comma i}^{1_{G} s_{\ast}}$ is a DD code observation with code DISB corrected, and 
$\hat {\phi}_{kl\comma i}^{1_{G} s_{\ast}}$ is a DD phase observation with phase DISB corrected. The inter-system DD observation equations for GPS, Galileo, and QZSS in Equation (5) are all relative to pivot satellite 1G, which means that additional satellites are available compared to the standard intra-system DD model or loosely combined model. This strengthens the model and benefits ambiguity resolution and position estimation.
In the data processing procedure of DISB estimation (Equation (4)) and precise positioning (Equations (3) and (5)), the observational model is resolved with a least squares adjustment. Regarding the stochastic model, the exponential elevation weighting function by Euler and Goad (Reference Euler and Goad1991) was used:
$$\sigma \lpar \theta\rpar =\sigma_0 \left(1+10\exp \left(\displaystyle{{-\theta }\over {10}}\right)\right)$$where σ(θ) is the Standard Deviation (STD) of the undifferenced observation; θ is the elevation of the satellite; σ 0 is the zenith-referenced a priori code and phase STD. In this contribution, they are 3 mm and 0·3 m for phase and code, respectively (Odolinski et al., Reference Odolinski, Teunissen and Odijk2014a; Reference Odolinski, Teunissen and Odijk2014b; Reference Odolinski, Teunissen and Odijk2015).
3. DATA COLLECTION
The analyses herein are based on zero and short baseline data collected from Curtin University, Wuhan University and the Multi-GNSS Experiment (MGEX).
3.1. Curtin University experiment
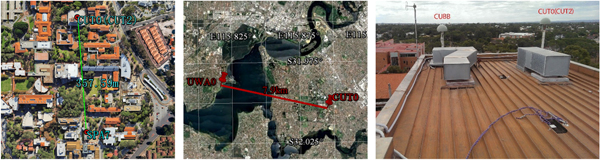
Observations from five GNSS stations (CUT0, CUT2, CUBB, SPA7, and UWA0) from the Curtin GNSS network were used in the following analysis. Figure 1 shows the observation conditions and GNSS antennae used in zero and short baseline experiments from the Curtin GNSS network. Table 1 outlines the characteristics of receivers used in the experiments.
Figure 1. Observation conditions and GNSS antennae (http://www.igs.org/images/site/CUT0_1.jpg) used in zero and short baseline experiments at Curtin University.
Table 1. Characteristics of multi-GNSS receivers used in the Curtin University experiment
3.2. Wuhan University experiment
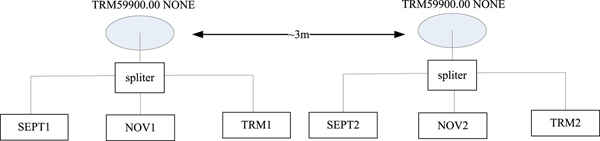
Observations collected at six stations (TRM1, SEP1, NOV1, TRM2, SEP2 and NOV2) on the roof of School of Geodesy and Geomatics building at Wuhan University from 30 March to 2 April 2017 were used in the following analysis. Figure 2 shows the observation conditions and GNSS antennae (TRM59900.00 NONE) used in the experiment and the configuration of the receivers and antennae are shown in Figure 3. Table 2 shows the characteristics of receivers used in the experiments. Four sessions (S1, S2, S3 and S4) of observation data were collected and all the receivers were rebooted after data collection in each session (the time-span was about one day for each session).
Figure 2. Observation conditions and GNSS antennae used in zero and short baseline experiment at Wuhan University.
Figure 3. Configuration of multi-GNSS receivers and antennae.
Table 2. Characteristics of multi-GNSS receivers used in the Wuhan University experiment
3.3. MGEX experiment
Raw observations collected at zero baseline SIN1 (Trimble NetR9 v5.10)-SIN0 (JAVAD TRE_G3TH DELTA v3.6.2) from MGEX at Singapore were also used in the following analysis. The antenna type used in the experiment was a LEIAR25.R3 LEIT.
4. INFLUENCING FACTORS OF PHASE AND CODE DISBS
The between-receiver DISB originates from the difference in the receiver hardware delays affecting signals from different GNSS systems. It depends on not only hardware but also the correlation algorithm inside the receiver, for example, the digital signal processing and signal-processing in the firmware (Montenbruck et al., Reference Montenbruck, Hauschild and Hessels2011). In this section, the influencing factors on the DISB estimates such as the receiver reboot, the receiver firmware upgrade, the activation of an anti-multipath filter and the observations types, will be analysed. Observations of zero and short baselines collected at Curtin University, Wuhan University and MGEX with 30 s sampling interval and 10° elevation cut-off angle were used in the data processing. The phase and code DISBs epoch-by-epoch with known receiver positions based on the observation model in Equation (4) were first collected. Then the phase and code DISB values were derived by averaging the single-epoch solutions over the whole time-span.
4.1. Impact of receiver reboot on DISB estimates
GNSS receivers are shut down and rebooted repeatedly when they are used for navigation and positioning by surveyors. If DISBs vary with the reboot of the involved GNSS receivers, the a priori-calibrated DISBs should not be used as corrections for subsequent positioning. In such cases, the DISBs can only be estimated and modelled during a continuous observation period in real-time. This will severely constrain the use of tightly combined models for multi-GNSS relative positioning.
Observation data collected at Wuhan University were used to investigate the impact of receiver reboot on DISB estimates. The estimated phase and code DISBs before and after a receiver reboot are shown in Table 3. It is observed that for receiver pairs of Trimble NetR9 and Septentrio PolaRx5, the phase and code DISBs remain invariable after a receiver reboot. However, an obvious change is observed in the phase DISBs for GPS/Galileo L1-E1 after a receiver reboot. Taking a receiver pair of NOV1 and TRM1 as an example, the L1-E1 phase DISBs are 0·477, 0·383 and −0·072 cycles, respectively. Similar results were also observed for a receiver pair of NOV2 and TRM2. It should be noted that several experiments of this kind were conducted and similar results were observed. In contrast, Tsuji et al. (Reference Tsuji, Matsuo, Furuya, Yamao and Kamakari2016) demonstrated that the GPS-Galileo-QZSS phase DISBs for a cluster of receivers, such as JAVAD SIGMA, LEICA GRX1200+GNSS, TOPCON NET-G3 with respect to Trimble NetR9 were not affected by reboot of receivers. Taking this into account, it is assumed that the results may be due to the correlation algorithm inside the specific NovAtel Propak6 receivers used in the experiments. The receivers may assign different initial phase biases in the receiver for GPS/Galileo L1-E1 signals whereas they assign identical initial phase biases for GPS/Galileo L5-E5a, and GPS/QZSS L1/L2/L5 signals. In such cases, the initial phase biases in the receiver for GPS/Galileo L1-E1 signals cannot be cancelled out through double-differencing, which further results in varying phase DISBs after receiver rebooting. However, further investigation is still required to confirm if this phenomenon is also present in other NovAtel Propak6 receivers or other receiver types.
Table 3. Phase and code DISBs for Septentrio PolaRx5 and NovAtel Propak6 with respect to Trimble NetR9
4.2. Impact of receiver firmware upgrade on DISB estimates
The digital signal processing and signal processing in the firmware can be a source of significant signal delays. Fortunately, they are completely deterministic and not affected by external factors such as temperature variations and ageing. Also, this type of delay should be identical for receivers of the same type with the same firmware (Melgard et al., Reference Melgard, Tegedor, de Jong, Lapucha and Lachapelle2013). The digital signal processing inside the receiver, on which the between-receiver DISBs would be dependent, may alter as soon as the firmware upgrade has been done (Zhang and Teunissen, Reference Zhang and Teunissen2016). This means that the receiver firmware upgrade may also impact on DISB values. In this subsection, the influence of the receiver firmware upgrade on the estimated DISBs will be investigated using observations collected from Trimble NetR9 and Javad TRE_G3T DELTA at Curtin University.
The estimated phase DISBs for zero baseline CUT2-CUT0 from Day Of Year (DOY) 183 to DOY 185, 2015 are shown in Figure 4. The firmware of the Trimble NetR9 receiver at CUT2 was upgraded from v5.01 to v5.03 around 01:00 GPS Time (GPST), DOY 184 whereas the firmware of the Trimble NetR9 receiver at CUT0 remained unchanged (v5.01) during all the experiments. It was observed that the phase DISBs were estimated with an average of approximately −0·001 and 0 cycles for GPS/Galileo L1-E1 and L5-E5a phase DISBs, respectively. However, after the firmware upgrade, the average values of estimated GPS/Galileo L1-E1 and L5-E5a phase DISBs changed to approximately 0·211 and 0·470 cycles, respectively. Moreover, the corresponding STDs were approximately 0·007 ~ 0·008 cycles, which is within the noise of phase and code observations and verifies the stability of phase DISBs in each observational session before and after firmware upgrade. The results demonstrate that a firmware upgrade can have an impact on the phase DISB estimates. Meanwhile, it can be concluded that the phase DISBs may be non-zero even for receivers of the same type but with different firmware versions.
Figure 4. The estimated GPS/Galileo phase DISBs for zero baseline CUT2-CUT0 from DOY 183 to DOY 185, 2015 before and after receiver firmware upgrade.
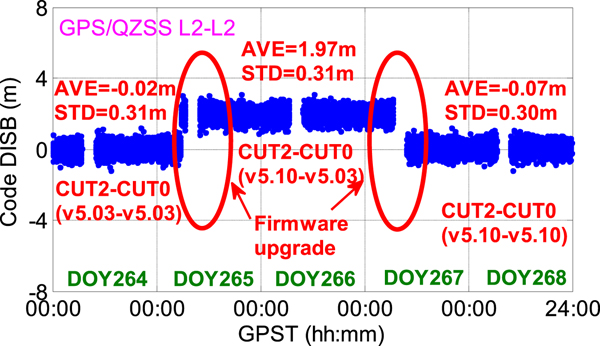
The code DISBs for CUT2-CUT0 were estimated from DOY 264 to DOY 268, 2015 as shown in Figure 5. It is observed that the average values of the estimated GPS/QZSS L2-L2 code DISB vary from approximately −0·02 to 1·97 m after the firmware upgrade of CUT2 from v5.03 to v5.10 at around 05:30 GPST, DOY 265. It is also shown that the average values of estimated GPS/QZSS L2-L2 code DISB vary from approximately 1·97 to −0·07 m after the firmware upgrade of CUT0 from v5.03 to v5.10 at around 06:30 GPST, DOY 267. Moreover, the corresponding STDs were approximately 0·3 m, which is within the noise of code observations and verifies the stability of code DISBs in each observational session before and after firmware upgrade. These results demonstrate that the firmware upgrade can have an impact on the code DISB estimates as well.
Figure 5. The estimated GPS/QZSS L2-L2 code DISBs for zero baseline CUT2-CUT0 from DOY 264 to DOY 268, 2015 before and after receiver firmware upgrade.
In addition, the impact of firmware upgrade on DISBs was also observed for Javad TRE-G3T DELTA receivers. Figure 6 shows the estimated phase DISBs for short baseline SPA7-CUBB (both Javad TRE-G3T DELTA) from DOY 340 to DOY 342, 2015. It can be seen clearly that the estimated GPS/Galileo L1-E1 phase DISB varies from approximately 0 to 0·498 cycles after the firmware upgrade of SPA7 from v3.6.3 to v3.7.0 at around 08:40 GPST, DOY 341.
Figure 6. The estimated GPS/Galileo L1-E1 phase DISBs for short baseline SPA7-CUBB from DOY 340 to DOY 342, 2015 before and after receiver firmware upgrade.
The phase and code DISB estimates can also remain invariant after a receiver firmware upgrade, which is not shown in this paper. It can be concluded from the above results that the upgrade of firmware inside the receivers may have an impact on the estimated phase and code DISBs, which should be considered when the tightly combined model is used in multi-GNSS relative positioning applications.
Note that the reason for the three interruptions in Figure 4 (from approximately 00:10 to 03:25 GPST, 07:52 to 10:28 GPST on DOY 183, and 05:44 to 11:27 GPST on DOY 184) and Figure 6 (from approximately from approximately 20:21 GPST DOY 340 to 00:56 GPST DOY 341) is that no Galileo satellite was tracked around these time spans. The five interruptions in Figure 5 were caused by the absence of QZSS observations.
4.3. Impact of the activation of an anti-multipath filter on DISB estimates
Modern commercial receivers can generally provide multipath filtering to reduce the impact of multipath effects in harsh environments. Observation data collected at Wuhan University (Sessions S3 and S4, in which the multipath filter was set on and off, respectively) are used to investigate the impact of activation of multipath filters on the DISB estimates. Phase and code DISBs for Trimble NetR9 with multipath filter on and off are shown in Table 4. It can be observed that the activation of a multipath filter can lead to significant changes in the code DISB estimates for all the overlapping frequencies whereas the phase DISBs remain invariable. Taking a receiver pair of SEPT1 and TRM1 for example, the code DISBs vary from 0·34, −4·51, −0·08, −0·50, and −0·11 to −1·79, −6·12, −1·58, −3·76, −1·71 m after the activation of the multipath filter, respectively. In addition, it was found that the activation of an anti-multipath filter for a Septentrio PolaRx5 does not result in variation in the phase and code DISBs, which is not shown in this paper. Such results demonstrate that the activation of an anti-multipath filter may result in a variation of GPS/Galileo/QZSS code DISB estimates. A similar phenomenon regarding the GPS/Galileo L1-E1 and L5-E5a code DISBs was also observed in Deprez and Warnant (Reference Deprez and Warnant2016a; Reference Deprez and Warnant2016b).
Table 4. Phase and code DISBs for Trimble NetR9 with multipath filter on and off
4.4. Impact of the observation types on DISB estimates
Modern multi-GNSS receivers can provide phase and code observations for several different signal channels at a certain frequency. Carrier phases tracked on different signal channels or modulation bands of the same frequency may differ in phase by 1/4 (for example, GPS: P/Y-code-derived L2 phase versus L2C-based phase) or, in some exceptional cases, by other fractional parts of a cycle (RINEX 3.02, 2012). Moreover, Differential Code Bias (DCB) also exists between code observations on different signal channels of the same frequency. Consequently, different DISB values may be derived when observations from different signal channels are used.
Raw observations collected at zero baseline SIN1 (Trimble NetR9 v5.10)-SIN0 (Javad TRE_G3TH DELTA v3.6.2) from MGEX on 29 February 2016 (from 00:00 to 24:00 GPST), were processed to analyse the impact of observation types on the DISB estimates. Phase and code DISBs derived using observations from different signal channels are shown in Table 5 and the DISB series are shown in Figure 7. It is observed that the use of observations from different signal channels results in significant discrepancy (approximately 0·250 and 0·253 cycles, respectively) for GPS/QZSS L1-L1 and L2-L2 phase DISBs. On the other hand, the discrepancy (approximately 0·06 and 0·55 m, respectively) in the code DISB estimates seems to be not obvious considering the relatively high STDs of code DISB series. Such results demonstrate that the use of prior-calibrated DISB estimates should correspond to the observations types. Note that the interruption from 10:34 to 10:54 GPST was caused by the absence of QZSS observations.
Figure 7. Phase and code DISBs derived using observations from different signal channels.
Table 5. Phase and code DISBs derived using observations from different signal channels
5. PERFORMANCE ASSESSMENT OF TIGHTLY COMBINED GPS, GALILEO AND QZSS RELATIVE POSITIONING
Although the DISB values are affected by the influencing factors as demonstrated in Section 4, they are invariant and remain stable if the configuration of the two involved receivers is not changed. In such cases, the performance of multi-GNSS relative positioning can be improved with DISB calibration and correction in terms of ambiguity resolution and position estimation. In this section, this will be tested using short baseline (separated by approximately 7·9 km) GPS, Galileo and QZSS observations collected between stations UWA0 (Septentrio PolaRx5) and CUT0 (Trimble NetR9) from the Curtin GNSS network (as shown in Figure 1). The Trimble NetR9 and Septentrio PolaRx5 receivers were connected to a TRM59800.00 SCIS antenna and a JAVRINGANT_DM SCIS antenna, respectively. The observations were collected at a 30 s sampling interval and 10° elevation cut-off angle.
In the data processing procedure, position and integer estimation was conducted epoch-by-epoch. The correctly fixed integer ambiguities were first derived by using all the available GPS, Galileo and QZSS observations over the whole time-span with fixed baseline coordinates. These true ambiguities were then used as a reference to compute an instantaneous empirical success rate, which is defined as the number of accepted and correctly fixed epochs divided by the total number of epochs, to verify the performance of ambiguity resolution (Odolinski et al., Reference Odolinski, Teunissen and Odijk2014a; Reference Odolinski, Teunissen and Odijk2014b). Note that the Least-squares AMBiguity Decorrelation Adjustment (LAMBDA) method was used for ambiguity resolution and the Fixed Critical-value Ratio Test (FCRT) as well as the Fixed Failure-rate Ratio Test (FFRT) were used for ambiguity validation (Teunissen and Verhagen, Reference Teunissen and Verhagen2009; Verhagen and Teunissen, Reference Verhagen and Teunissen2013). We set the corresponding FCRT to a standard value of 1/3 and FFRT with a user defined failure rate (P f) of 1%.
Raw GNSS data collected on 27 September 2018 (from 00:00 to 24:00 GPST) was processed to verify the performance of tightly combined GPS/Galileo/QZSS positioning with single-frequency (L1-E1-L1) and dual-frequency (L1-E1-L1 and L5-E5a-L5) observations. GPS Block IIF satellites with the highest elevation cut-off angle were used as common pivot satellites for GPS, Galileo and QZSS. Moreover, the phase and code DISBs were a priori calibrated using observations collected on 18 August 2018, as listed in Table 6.
Table 6. Calibrated phase and code DISBs using observations collected on 18 August 2018
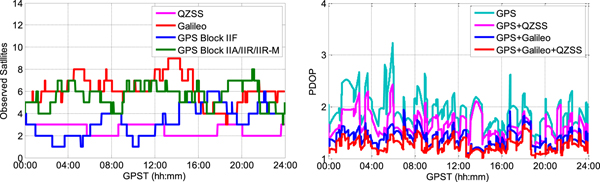
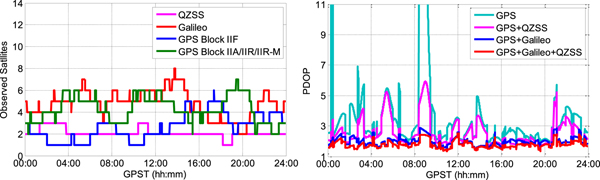
Figure 8 shows the sky plot (top) and availability (bottom) of GPS, Galileo, and QZSS satellites on 27 September 2018 above a 10° elevation cut-off angle. It was observed that three QZSS, 20 Galileo and 12 GPS Block IIF satellites could be tracked during the day. Figures 9 and 10 show the number of satellites tracked above 10° and 20° elevation cut-off angles and the corresponding Position Dilution of Precision (PDOP) series, respectively. It was observed that the observed GPS Block IIF and QZSS satellites above 10° and 20° elevation cut-off angles were both no less than one over the day and the available Galileo satellites were two to eight. Moreover, the average tracked satellites (GPS, Galileo and QZSS) during the day were 17·1 and 13·6, and the corresponding average PDOPs were 1·26 and 1·78, respectively.
Figure 8. Sky plot (top) and availability (bottom) of GPS, Galileo, and QZSS satellites on September 27, 2018 above 10° elevation cut-off angle. Note that the Block IIF satellites are represented by the blue colour and other blocks are represented by the green colour.
Figure 9. Number of satellites tracked above a 10° elevation cut-off angle and the corresponding PDOP series.
Figure 10. Number of satellites tracked above a 20° elevation cut-off angle and the corresponding PDOP series.
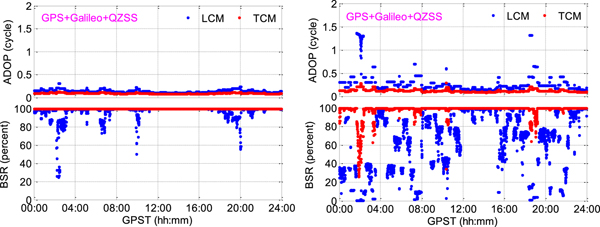
Figure 11 shows the epoch-by-epoch ADOP and BSR for LCM and TCM with single-frequency observations under 10° and 20° elevation cut-off angles. It was observed that the single-epoch ADOP time series of TCM was obviously smaller than LCM. Meanwhile, the BSR of TCM was significantly increased with respect to LCM. In the case of a 10° elevation cut-off angle, the mean ADOP decreased from 0·158 to 0·126 cycles and the mean BSR increased from 96·5% to 99·7%. If the elevation cut-off angle was 20°, the mean ADOP decreased from 0·190 to 0·138 cycles and the mean BSR increased from 88·4% to 99·1%. The improvement was more significant under a 20° elevation cut-off angle due to fewer observed satellites.
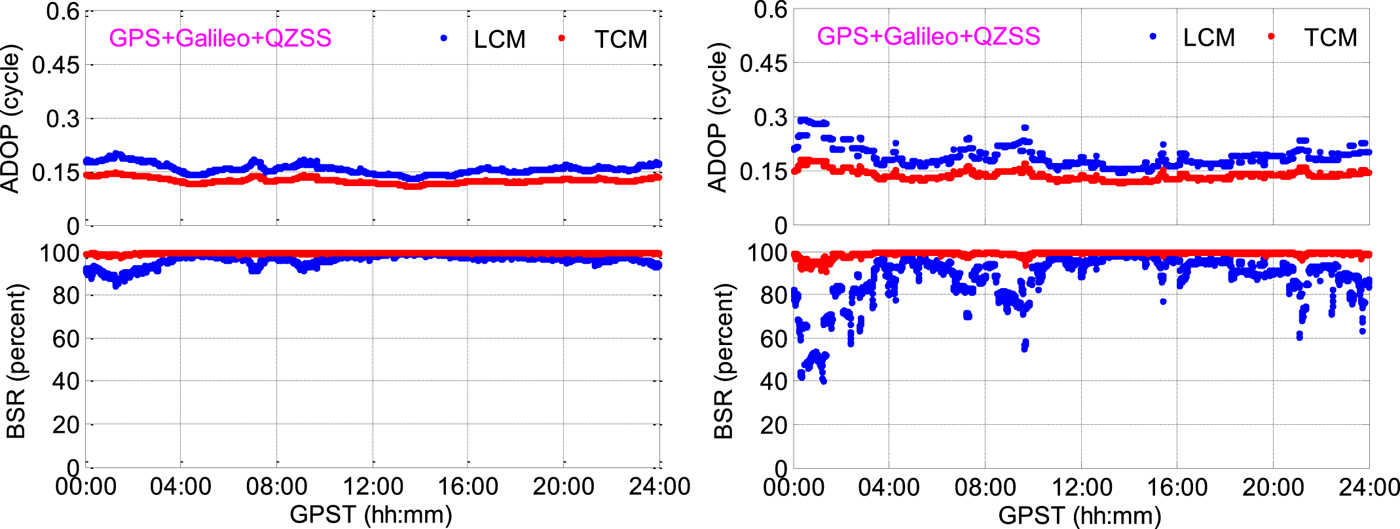
Figure 11. Epoch-by-epoch ADOP and BSR for LCM and TCM with single-frequency observations under 10° (left) and 20° (right) elevation cut-off angles.
The epoch-by-epoch ADOP and BSR for LCM and TCM with dual-frequency observations under 30° and 40° elevation cut-off angles were computed as shown in Figure 12. It is also demonstrated that TCM can provide a much smaller ADOP and higher BSR. For a 30° elevation cut-off angle, the mean ADOP decreased from 0·139 to 0·090 cycles and the mean BSR increased from 97·2% to 100·0%. For a 40° elevation cut-off angle, the mean ADOP decreased from 0·286 to 0·121 cycles and the mean BSR increased from 63·3% to 98·0%. Such results demonstrated that under current GPS, Galileo and QZSS constellations, the TCM can deliver a relatively high BSR with dual-frequency observations even with a 40° elevation cut-off angle.
Figure 12. Epoch-by-epoch ADOP and BSR for LCM and TCM with dual-frequency observations under 30° (left) and 40° (right) elevation cut-off angles.
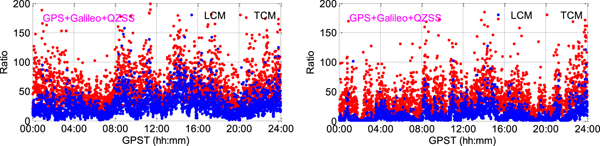
The ratio values, which are defined as the quadratic norm of a suboptimal solution divided by that of the optimal solution (Euler and Schaffrin, Reference Euler and Schaffrin1991; Verhagen, Reference Verhagen2004), were derived to analyse the ambiguity performance as well. Figures 13 and 14 show the epoch-by-epoch ratio values for LCM and TCM with single-frequency GPS/Galileo/QZSS observations under 10° and 20° elevation cut-off angles and dual-frequency observations under 30° and 40° elevation cut-off angles, respectively. It is clear that TCM can deliver much higher ratio values, which will result in a theoretical higher empirical ambiguity resolution success rate and reliability.
Figure 13. Epoch-by-epoch ratio values for LCM and TCM with single-frequency observations under 10° (left) and 20° (right) elevation cut-off angles.
Figure 14. Epoch-by-epoch ratio values for LCM and TCM with dual-frequency observations under 30° (left) and 40° (right) elevation cut-off angles.
Table 7 shows the epoch-by-epoch empirical ambiguity resolution performance of LCM, TCM and GPS only models with different integer ambiguity validation strategies (FCRT with u = 1/3, and FFRT with P f = 1%) under different elevation cut-off angles (10°, 20°, 30° and 40°). It was observed that under current constellations, the average number of observed satellites with a 10° elevation cut-off angle were 8·9, 11·5, 15·1 and 17·6 for GPS, GPS/QZSS, GPS/Galileo and GPS/Galileo/QZSS, respectively. If an integer ambiguity validation strategy of FCRT with u = 1/3 is adopted, the single-frequency solutions can provide empirical ambiguity resolution success rates of approximately 39·6%, 66·9%, 99·0% and 99·8% for GPS only, loosely combined GPS/QZSS, GPS/Galileo and GPS/Galileo/QZSS, respectively. If the elevation cut-off angle is 20°, the corresponding average number of observed satellites were 6·9, 9·0, 11·7 and 13·8, respectively and the corresponding empirical success rates were approximately 20·2%, 35·1%, 91·7% and 97·6%, respectively. Such results demonstrate the potential of combining GPS/Galileo/QZSS observations for single-epoch precise relative positioning with current constellations. Similar results were also observed with dual-frequency solutions. Furthermore, it was observed that whether the combination is GPS/Galileo, GPS/QZSS or GPS/Galileo/QZSS, the TCM can deliver much higher empirical ambiguity resolution success rates with respect to the LCM, especially under environments where the observed satellites for each system are limited and only single-frequency observations are available. For positioning using GPS, Galileo and QZSS single-frequency observations with FCRT u = 1/3, the empirical ambiguity resolution success rates of TCM were increased by approximately 0·2%, 2·4%, 26·3% and 49·5% with respect to LCM under elevation cut-off angles of 10°, 20°, 30° and 40° respectively. When dual-frequency GPS, Galileo and QZSS observations were used, the empirical ambiguity resolution success rates were increased by approximately 0·0%, 0·0%, 1·6% and 27·1%, respectively. The improvement (approximately 49·5%) is most evident in the case of a 40° elevation cut-off angle with single frequency observations. Similar results were also obtained for an ambiguity validation strategy of FFRT P f = 1%.
Table 7. Empirical success rate (percent) with FCRT u = 1/3, and FFRT P f = 1%. Number of epochs 2,880. SF (Single-Frequency) refers to L1/E1/L1 whereas DF (Dual-Frequency) refers to L1/E1/L1 and L5/E5a/L5. In the third column, the numbers in the brackets represent the average observed satellites for GPS, GPS/QZSS, GPS/Galileo, and GPS/Galileo/QZSS, respectively. In columns 8, 11, and 14, “Imp.” means empirical success rate improvement of TCM with respect to LCM.
Table 8 shows empirical STDs of float and correctly fixed single-epoch positioning errors in the North, East and Up directions. It was observed that two orders of magnitude improvement were achieved from float to correctly fixed solutions. Moreover, the STDs for correctly-fixed solutions were basically identical to the different processing strategies whereas significant improvements were observed for float solutions. For positioning with single-frequency observations under a 20° elevation cut-off angle, the STDs were reduced from [47·8, 66·4, 194·2] (GPS only solution) to [45·1, 58·8, 147·7], [31·4, 38·3, 89·3], and [31·3, 36·7, 85·3] cm for loosely combined GPS/QZSS, GPS/Galileo, and GPS/Galileo/QZSS solutions, respectively. Moreover, the TCM can further reduce STDs to [40·3, 50·1, 129·6], [30·1, 36·1, 85·2] and [28·0, 32·9, 77·3] cm with respect to the LCM. Although higher accuracy of the float solutions does not mean higher final positioning accuracy, they have an undeniable impact on the reliability of the ambiguity resolution.
Table 8. STDs of float and correctly-fixed (in the brackets) single-epoch positioning errors in the North, East and Up directions. Number of epochs 2,880. SF (Single-Frequency) refers to L1/E1/L1 whereas DF (Dual-Frequency) refers to L1/E1/L1 and L5/E5a/L5. GJ, GE and GEJ represent GPS/QZSS, GPS/Galileo and GPS/Galileo/QZSS, respectively.
Particularly, the positioning errors for different models with single-frequency observations under a 20° elevation cut-off angle were presented as shown in Figure 15. It can be clearly observed that the loosely combined GPS/QZSS, GPS/Galileo and GPS/Galileo/QZSS solutions can provide fewer float and wrongly fixed solutions, and more correctly fixed solutions with respect to GPS only solutions. Furthermore, similar results were also observed for TCM with respect to LCM. Such results clearly confirm the benefits of the TCM.
Figure 15. Positioning errors with single-frequency observations under a 20° elevation cut-off angle.
6. CONCLUSIONS
In this paper the influencing factors of DISBs between overlapping frequencies of different GNSS systems have been investigated and a performance assessment of tightly combined GPS, Galileo and QZSS relative positioning using single-epoch single-frequency (GPS/Galileo/QZSS L1-E1-L1) and dual-frequency (GPS/Galileo/QZSS L1-E1-L1 and L5-E5a-L5) observations under current constellations has been presented. The influencing factors of DISBs between overlapping frequencies that are shared by GPS, Galileo and QZSS were first analysed. For the first time it was found that the GPS/Galileo L1-E1 phase DISBs for NovAtel Propak6 and Trimble NetR9 receiver pairs may change after a receiver reboot, which should be considered when achieving DISB corrections for tightly combined positioning. This may be due to the correlation algorithm inside the specific NovAtel Propak6 receivers used in the experiments and further investigation is still required to confirm if this phenomenon is also present in other NovAtel Propak6 receivers or other receiver types. Moreover, the upgrade of receiver firmware, the activation of anti-multipath filters and the type of the observations were also found to have an impact on the DISB estimates, which should also be carefully considered in practical applications. Finally, the performance of single-epoch tightly combined GPS, Galileo and QZSS relative positioning using single-frequency and dual-frequency observations were also evaluated by a formal as well as an empirical analysis, consisting of ADOP, BSR, ratio values, the empirical ambiguity resolution success rate and the positioning accuracy. It was demonstrated that with current constellations, loosely combined GPS, Galileo and QZSS solutions can provide much higher empirical ambiguity resolution success rates and accuracy of float solutions with respect to GPS only solutions. In the case of a 10° elevation cut-off angle, loosely combined GPS/Galileo/QZSS solutions can deliver empirical ambiguity resolution success rates of approximately 99·8% and 97·6%, and approximately 100·0% and 100·0% with single and dual frequency observations, respectively. Furthermore, it was also shown that when DISBs were a priori calibrated and corrected, the TCM can deliver much higher BSR and ratio values, and a lower ADOP with respect to classical LCM. Meanwhile, the empirical ambiguity resolution success rate and positioning accuracy were remarkably improved as well, especially under environments where the number of observed satellites for each system are limited and only single-frequency observations are available. In such cases, the improvement of the empirical ambiguity resolution success rate can reach up to approximately 20%~ 50%.
ACKNOWLEDGEMENTS
This work is supported by the National Natural Science Foundation of China (No. 41774031), the National Science Fund for Distinguished Young Scholars (No. 41825009), the Fundamental Research Founds for National University, China University of Geosciences (Wuhan) (No. G1323541876), and Wuhan science and technology project (2018010401011270). The authors would also like to acknowledge the Curtin GNSS research centre and the Multi-GNSS Experiment (MGEX) for providing the GNSS data.
