2.1. Halo orbits

Halo orbits have been extensively studied in the literature, from both (semi-)analytical and numerical approaches (Richardson, Reference Richardson1980; Gómez, Reference Gómez2001). Due to the symmetry of the CRTBP, there are two families of halo orbit around each CLP – the north family and the south family (Jorba and Masdemont, Reference Jorba and Masdemont1999). They are symmetric to each other with respect to the x–y plane. Shown in Figure 1 are some examples of the north and south halo families around the points L1 and L2. Figure 2(a) shows the x–z projection of the south halo orbits around L1 and L2, along with the asterisks marking the uppermost points of the halo orbits. Originating from the critical planar Lyapunov orbit, the out-of-plane amplitude of the halo orbits first increases and then decreases, and the halo orbits of both L1 and L2 gradually approach the Moon, with their projections on the x–z plane gradually looking like straight lines. Using the z coordinate of the uppermost point as the amplitude parameter, Figure 2(b) shows the curves of the halo orbit's period. As can be seen, for L1 halo orbits, with the increase of out-of-plane displacement, the period first increases slightly. When the L1 halo orbits are getting closer to the Moon, the out-of-plane displacement decreases rapidly and so does the period. The basic behaviour of L2 halo family is very similar to that of the L1 halo family. For the halo orbits computed by us, the period of the L1 halo orbit ranges from about 8 days to 12 days. The period of the L2 halo orbit ranges from a little bit more than 4 days to approximately 15 days. Because we are going to choose orbits with the same period, we restrict the halo orbits in this work to have periods ranging from 8 days to 12 days.

Figure 1. The northern (red) and southern (blue) halo families about the Earth–Moon L1 (left) and L2 (right).

Figure 2. (a) The x–z projection of the south halo orbits and (b) the relationship between periods and z-amplitude at perilune.

2.2. DROs

A DRO is a special kind of periodic orbit in the CRTBP. In astronomy, people prefer to call them ‘quasi-satellite orbits’ and some natural small bodies move on these orbits (Kinoshita and Nakai, Reference Kinoshita and Nakai2007; Marcos and Marcos, Reference Marcos and Marcos2016). In celestial mechanics, the DRO family also has the name of family f in Strömgren's classification (Szebehely, Reference Szebehely1967). Although different names are used, they all represent the same family of orbits. In the Moon-centred synodic frame, Figure 3(a) shows some example DROs with different sizes. The black line in Figure 3(b) shows the curve of period versus amplitude of this family. The amplitude is defined as the distance between the Moon and the left vertical intersection of the DRO with the x axis. The period increases monotonically with the amplitude, from less than 1 day to more than 25 days. We denote the monodromy matrix associated with the DROs as M. Its eigenvalues are usually of the form $\{1,1,\lambda _1,\lambda _1^{-1},\lambda _2,\lambda _2^{-1}\}$ (Gómez et al., Reference Gómez, Masdemont and Simó1998). We can define the stability indices as $s_i=\lambda _i+\lambda _i^{-1}$, i=1,2, so that the orbits are stable if |s _i| < 2 and unstable if one of |s _i| > 2 (Arnold, Reference Arnold2013). The red lines in Figure 3(b) show the two stability curves for this family. Obviously all the DROs shown in Figure 3 are stable in the CRTBP of the Earth–Moon system. One remark is that very large DROs are no longer stable in the real Earth–Moon system due to various perturbations (Xu and Xu, Reference Xu and Xu2009), but still DROs with sizes as large as 67,000 km with practical stability (for space missions) can be found (Bezrouk and Parker, Reference Bezrouk and Parker2017).

Figure 3. (a) DRO family; (b) period versus x amplitude (black) and stability indices of DROs (red).

The planar DROs are in the Moon's orbit plane, having good coverage of the lunar surface except for the poles. In order to also cover the poles, a small out-of-plane amplitude should be added to the planar DROs. There are two ways to generate a spatial orbit: one is to use the vertical m-bifurcation orbits (Hou and Liu, Reference Hou and Liu2013) bifurcating from critical planar DROs; the other is to simply add a small out-of-plane deviation to the planar DRO (Liu et al., Reference Liu, Hou, Tang and Liu2014; Bezrouk and Parker, Reference Bezrouk and Parker2017). The difference is that the former generates an exact periodic orbit while the latter usually generates a quasi-periodic orbit. As an example, Figure 4(a) shows two spatial periodic orbits (belonging to a 5- (blue) and 6-bifurcation (red) periodic family) bifurcating from the planar DRO orbit. Figure 4(b) shows a spatial quasi-periodic orbit by adding a deviation of 7000 km along the z direction. Since we only deal with periodic orbits in this study, we prefer the first way to generate a three-dimensional periodic orbit for the following analysis. A few more words are given about the m-bifurcation orbits. An m-bifurcation orbit in the planar DRO family is not a bifurcation orbit itself, but becomes a bifurcation one when it orbits m times (Henrard, Reference Henrard2002). So a 5-bifurcation planar DRO orbit travels five times in the x–y plane and a 6-bifurcation planar DRO orbit travels six times in the x–y plane. A new family of spatial periodic orbits appears, starting from the m-bifurcation orbit. We call the family an m-bifurcation periodic family. The ones shown in Figure 4(a) belong to the 5- and 6-bifurcation periodic family, respectively. More details on how to compute the m-bifurcation family can be found in the literature (Hou et al., Reference Hou, Xin and Feng2018).

Figure 4. Spatial DROs generated by m-bifurcation (a) and by simply adding a small out-of-plane deviation (b).

3.1. Coordinate definition

Figure 5 shows the Moon-centred coordinate used in our coverage analysis. The x axis points from the Earth to the Moon, the z axis is perpendicular to the Moon's orbital plane, and the y axis completes the right-hand rule. The longitude/latitude is defined as the angle λ/φ in Figure 5, with λ ∈ [0°, 360°) and φ ∈ [ − 90°, 90°]. The north polar region is defined as φ ∈ [60°, 90°], and the south polar region is defined as φ ∈ [ − 90°, − 60°]. The elevation angle h between a point P on the Moon's surface and the CN satellite is also defined in Figure 5. A critical value of the elevation angle, h ₀, is selected. The value h ₀ is the minimum elevation angle for the visibility check. If h ≥ h ₀, the CN satellite is visible to P, otherwise it is not visible. Since the Moon is atmosphereless, in our work, the value of h ₀ is taken as 0°.

Figure 5. Illustration of the coordinates used in our analysis and the elevation angle h.

3.2. CTP and SCP

The CTP of a region refers to the time that the region is covered by at least one CN satellite divided by the total simulation time. The region is continuously covered if the CTP equals 100%.

The SCP indicates the ratio of the Moon's continuous one-fold coverage area to the total lunar surface. The continuous one-fold coverage area means the region where there is always at least one CN satellite visible. In order to compute the SCP, we discretise the lunar surface along both the longitude and latitude directions with a certain interval. To save computational time, we first set the interval as 10°. Once a CN constellation is found to be able to cover 100% of the lunar surface with such a coarse grid, we check whether the SCP is still 100% with a finer grid interval of 1°.

The area of each grid is approximately R ²cosφ ΔφΔλ, where R is the radius of the Moon, and Δφ = Δλ = 10° or 1°. The formula to calculate the SCP is:

$${\rm SCP}=\frac{\sum_{i\in{S}} \delta{R^2\cos\varphi_{i}\,\Delta\varphi\Delta\lambda}}{\sum_{i\in{S}} {R^2\cos\varphi_{i}\,\Delta\varphi\Delta\lambda}},\quad \delta=\begin{cases} 0, & {\rm CTP}<100\%,\\ 1, & {\rm CTP}=100\%, \end{cases}$$

where S indicates the grid for the whole lunar surface. For north or south polar region coverage, the same SCP value can be defined, with S replaced by the north or south polar area.

4.1. The case of one CN satellite

We study the north halo orbits around the L2 points first. The coverage property of the south halo orbits around the L2 points should be symmetric with the results of the north halo orbits. Therefore, we only study the north halo orbits here. Figure 6 shows the CTP map of the lunar surface for L2 north halo orbits with different out-of-plane amplitudes. From left to right and from top to bottom, the maximum out-of-plane displacement is 0 km, 1000 km, 10,000 km, 30,000 km, 50,000 km, 70,000 km, 77,828·208 km, 75,000·944 km and 67,056·001 km.

Figure 6. CTP map for a satellite moving on an L2 north halo orbit.

The bright yellow regions are the one-fold coverage areas while the dark blue ones are areas in which the CN satellite is never seen. Regions with other colours indicate that the CN is partially visible. Numbers on the lines represent the CTP. For example, 0·8 means that this region is covered for 80% of one orbital period.

For small out-of-plane amplitude halo orbits, they are closer to the L2 point, so the CN satellite is always visible to the far side of the Moon but never visible to the near side. With the period reducing, the out-of-plane amplitude increases. For the north halo orbits, the apoapsis is above the x–y plane, so they have better (worse) coverage of the northern (southern) area. Results in Figure 6 suggest the use of shorter-period halo orbits with large out-of-plane amplitude in the CN constellation if we need coverage of the polar region. For halo orbits around the L1 point, similar phenomena can be expected and the details are omitted.

4.2. The case of two CN satellites

Now we extend the analysis to the case of two CN satellites. There are in total 10 possible combinations, as listed in Table 1. Due to symmetry, cases 1, 3, 5 and 7 are symmetric to cases 2, 4, 6 and 8, respectively. As a result, we only need to discuss six cases in total, that is, cases 1, 3, 5, 7, 9 and 10.

Table 1. The 10 kinds of CN constellations with two CN satellites on halo orbits.

For each case, there are two free parameters to describe the CN constellation: one is the period T (or the amplitude) of the halo orbits; the other is the initial phase difference Δτ between the two CN satellites. To illustrate the initial phase difference, we divide each halo orbit into N segments with a fixed time interval (in this part, N=100). That is, the time interval between two nearby points is T/N. For L1 south halo orbits and L2 north halo orbits, starting from the uppermost point, we use one parameter τ _j = j/N (j=0, 1, …, N-1) to describe different points on the halo orbit. For the L1 north halo orbits and L2 south halo orbits, starting from the lowermost point, we use the same parameter to describe different points on the orbit. That is to say, when τ = 0, the satellite is at the uppermost point if the orbit is an L1 south or an L2 north halo orbit, and is at the lowermost point if the orbit is an L1 north or an L2 south halo orbit. The definition of the reference point when τ = 0 remains the same in the following analysis and will not be repeated again. At the initial epoch, suppose the position of the first CN satellite on the halo orbit is τ₁, and the position of the second CN satellite on the halo orbit is τ₂, then the initial phase difference is defined as Δτ_1,2 = τ₂ − τ₁. Obviously, Δτ_1,2 ∈ [0, 1]. There are in total six cases to be investigated, and for each case there are two free parameters. Thus figures such as Figure 6 are no longer valid to present the results, so we choose the SCP to show the results, as shown by Figure 7. For each fixed value of T, we survey the parameter Δτ_1,2 in [0, 1] to get the maximum value of the SCP.

Figure 7. Maximum SCP of different cases of two-satellite constellation moving on halo orbits.

The results are shown in Figure 7, where the abscissa represents the period of the CN constellation, and the ordinate represents the maximum SCP value that the CN constellation can have. The lines with red triangles represent the maximum SCP of the north polar region, the black lines represent the maximum SCP of the south polar region, and the green line represents the maximum SCP of the equatorial region.

An obvious fact from Figure 7 is that the north polar region can be covered completely in cases 1, 3 and 5 and the south polar region can be covered completely in case 7. Cases 2, 4, 6 and 8 are symmetric to cases 1, 3, 5 and 7, so the north or south polar region can be completely covered in these cases. Hamera et al. (Reference Hamera, Mosher, Gefreh, Paul, Slavkin and Trojan2008) proposed a constellation similar to case 4, i.e. two satellites in an L2 south halo orbit, to provide continuous south pole coverage. Another fact is that continuous one-fold coverage of both the north and the south polar regions is impossible with only two satellites on halo orbits.

4.3. The case of three CN satellites

There are 20 options for the three-satellite CN constellation in total. They are listed in Table 2. However, considering the symmetry, only the first 10 cases are necessary to be studied.

Table 2. The 20 kinds of CN constellation with three CN satellites on halo orbits.

For each case, there are three free parameters to describe the CN constellation: the period T, and the initial phase differences Δτ_1,2 and Δτ_1,3. Similar to the case of two satellites, we can survey Δτ_1,2 and Δτ_1,3 in [0, 1] and find the maximum SCP, as shown in Figure 8. It can be found that for all cases the north polar region can be covered continuously. In cases 5 and 10, the north and the south polar regions can be simultaneously covered.

Figure 8. Maximum SCP of different cases of three-satellite constellation moving on halo orbits.

One example three-satellite 10-day constellation is shown in Figure 9(a). The three satellites move on L1N, L2N and L2S, respectively. As a result, this is an example of case 10. The period of this example constellation is T=10 days. The initial phases are τ₁ = 0, τ₂ = 0 and τ₃ = 0.5. Figure 9(b) shows the CTP map. Obviously, the two polar regions are covered continuously while equatorial regions are only partially covered. An animation of the coverage in one orbital period is given in supplementary files. Figure 10 shows some snapshots of the coverage during one orbital period, where the blue region indicates the coverage gap. It is obvious that the coverage gap remains close to the equatorial region and moves from east to west. From the following analysis, we know that this coverage gap can be perfectly compensated by CN satellites moving on DROs, since these orbits also move from east to west around the Moon and have good coverage of the equatorial regions.

Figure 9. One example three-satellite constellation and its CTP.

Figure 10. Some snapshots of the coverage during one orbital period.

4.4. The case of four CN satellites

Next we extend the results to four satellites. There are 35 kinds of constellations in total. Due to symmetry, 19 of them are necessary to be studied. They are listed in Table 3. Cases 1 to 19 are studied. The other cases are symmetric to them. To be specific, case i is symmetric to case i−19 when 20 ≤ i ≤ 25; case i is symmetric to case i−18 when 26 ≤ i ≤ 29; and case i is symmetric to case i−17 when 30 ≤ i ≤ 35.

Table 3. The 35 kinds of CN constellation with four CN satellites on halo orbits.

For each case, there are four free parameters: the period T, and the initial phase differences Δτ_1,2, Δτ_1,3 and Δτ_1,4. We first set a coarse grid interval as 10°. Similar to the above, we can survey Δτ_1,2, Δτ_1,3 and Δτ_1,4 in [0, 1] and get the maximum value of SCP, as shown in Figure 11 (corresponding to the coarse grid interval).

Figure 11. Maximum SCP of different cases of four-satellite constellation moving on halo orbits.

In most cases, global coverage cannot be achieved, but in cases 9, 17 and 19, at several certain periods 100% global coverage could be achieved. However, when a finer grid interval of 1° is used, none of them can perfectly reach 100%. As shown in Figure 12, the blue line indicates the results of the coarse grid interval, and the red line indicates the results of the fine grid interval. Several points on the blue lines reach 100% but they cannot reach 100% on the red lines. Therefore, four satellites on halo orbits could provide nearly global coverage of the lunar surface but not perfectly 100%.

Figure 12. Comparison of maximum SCP of cases 9, 17 and 19 for the coarse and fine grid intervals.

5.1. Planar DROs

From Section 2.2, we know that planar DROs are in the Moon's orbital plane, so they have good coverage of the Moon's equatorial region but poor coverage of the polar regions. The coverage characteristics of one, two and three DRO satellites (period 10 days) are shown in Figure 13. The satellites are moving on the same DRO but with a phase difference. For readers to check the result, the initial conditions of this DRO is given in the Moon-centred synodic coordinates as

$$\vec{r}({\rm km})=(-53{,}080{\cdot}461369,0,0)^T, \quad \vec{v}({\rm km/s})=(0,0{\cdot}490681,0)^T .$$

One DRO satellite can provide less than 50% coverage of the equatorial region. Two satellites on a DRO can provide a CTP larger than 90% for the equatorial region. To completely cover the equatorial region, at least three satellites are needed. It is found that three satellites equally phased on a DRO can continuously cover 99·8% of the lunar surface. An obvious fact from Figure 13 is that the polar caps cannot be covered, due to the fact that the planar DROs are used. This problem can be solved in two ways: one way is to utilise the spatial DROs to provide coverage of the polar regions; another way is to combine the planar DROs with halo orbits. The latter will be discussed later.

Figure 13. CTP map for one, two and three satellites moving on a 10-day DRO.

5.2. Spatial DROs

As illustrated in Section 2.2, we use spatial periodic DROs in this section to perform the coverage analysis. We pick up some members of the 5- and 6-bifurcation DRO families (see Figure 4(a)). The same as what we did in Section 4.4, for each fixed T, we survey Δτ_1,2, Δτ_1,3 and Δτ_1,4 in [0, 1] to find the maximum SCP value. Studies show that the whole lunar surface can be continuously covered in this case if the lunar surface is discretised by 10° × 10°. Figure 14(a) and 14(b) shows the corresponding four-satellite results for the 5-bifurcation and 6-bifurcation families, respectively. However, SCP will not achieve 100% when the lunar surface is discretised by 1° × 1°. As can be seen from Figure 15, the maximum SCP has decreased to less than 100%. In Figure 15(b), the maximum SCP is about 99·975% when the period is about 64·5 day. As a result, the conclusion is that a four-satellite constellation on a DRO is able to cover nearly the whole lunar surface. It should be noted that the period of spatial DROs is far more than that of planar DROs. This is because the spatial DROs are 5- or 6-bifurcation of planar DROs. That means the total period of a spatial DRO is 5 or 6 times of the planar period of a spatial DRO.

Figure 14. Maximum SCP of four-satellite constellation moving on a DRO.

Figure 15. Comparison of maximum SCP of the four-satellite constellation moving on the spatial DRO for the coarse and fine grid intervals.

6.1. Three halo satellites and one planar DRO satellite

Since we only have one DRO satellite, the configuration of the constellation is up to the choice of the three halo satellites. The same as the case in Section 4.3, there are 20 cases of constellations in total, as described by Table 2. Also, only the first 10 cases need to be studied due to symmetry.

There are four free parameters to describe the CN constellation for each case: the period T, and the initial phase differences Δτ_1,2 between the halo CN satellites 1 and 2, Δτ_1,3 between the halo CN satellites 1 and 3, and Δτ_1,4 between the halo CN satellite 1 and the DRO CN satellite. For the DRO, the starting point of the phase lies on the Earth–Moon line between the Earth and the Moon. We can survey Δτ_1,2, Δτ_1,3 and Δτ_1,4 in [0, 1] and find the maximum SCP of the north polar, south polar and equatorial regions and of the whole lunar surface. The results are shown in Figure 16. According to Figure 16, it seems that case 10 performs best in terms of whole lunar surface coverage. However, even for this best case, the maximum SCP is about 99·8%, a little bit less than 100%. This means that the configuration of three halo satellites and one DRO satellite cannot completely fulfil the goal of one-fold coverage of the whole lunar surface. We need another DRO satellite to fulfil this goal.

Figure 16. Maximum SCP of different cases of four-satellite constellation composed of three halo satellites and one DRO satellite.

6.2. Three halo satellites and two planar DRO satellites

For the five-satellite CN constellation, a complete survey of different cases is beyond our current computation ability and is not necessary. Inspired by the results shown in Figure 9, we know that the goal of the DRO is to compensate for the coverage of the equatorial region. By fixing the initial relative geometry of three halo satellites in Figure 9 unchanged, and by adjusting the relative geometry of the two DRO satellites, it is very easy for us to find a constellation that can continuously cover the whole lunar surface. One example is shown in Figure 17.

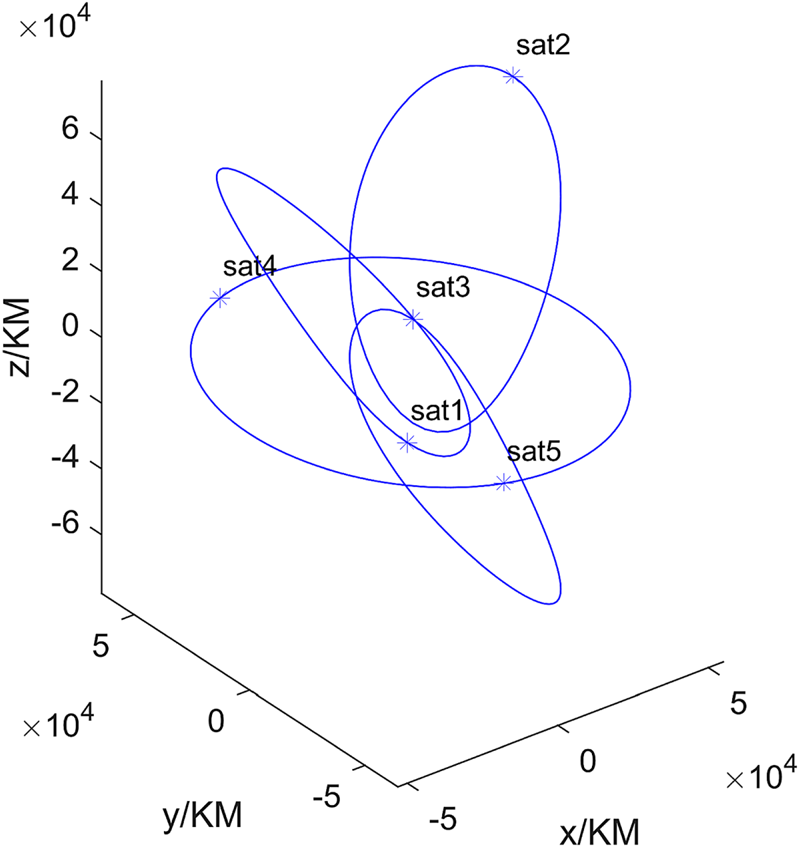
Figure 17. A final five-satellite hybrid constellation.

The period of this example constellation is 10 days. The initial phase of each satellite is τ₁ = 0, τ₂ = 0, τ₃ = 0.5, τ₄ = 0.2 and τ₅ = 0.8. The ‘invisible’ region in Figure 9 is perfectly compensated by the two DRO satellites. When a finer grid interval 1° is used, the SCP is still 100%. One advantage of such a hybrid CN constellation is that it has a better observation geometry than the one that uses only the halo orbits or only the DROs.

As examples to confirm the coverage ability of our final constellation, we choose two positions on the lunar surface and calculate the visible satellites during one period (10 days). One is located at (0°, 80°), which is in the polar region. Another is located at (90°, − 40°), which is in the middle latitude region. A visibility analysis is performed and the results are shown in a stacked bar graph, as can be seen in Figure 18. Obviously, in both cases, at least one satellite is visible, i.e. the one-fold coverage is 100%. The two-fold coverage is not 100% but most of the time at least two satellites are visible.

Figure 18. Visibility analysis of two locations on the Moon's surface for the five-satellite hybrid constellation shown in Figure 17.

One remark is made here. The hybrid CN constellation in Figure 16 is given in the simple CRTBP model. It is periodic (in this case, the period is 10 days). As a result, if its SCP in one orbital period is 100%, then the SCP will always be 100%. Of course, a strict periodic CN constellation configuration is impossible in reality due to various perturbations. Nevertheless, we can expect quasi-periodic orbits close to these periodic orbits in reality so the SCP analysis of this hybrid constellation is a good approximation of the real case. Another remark is that the halo orbits in Figure 17 are unstable and require orbit control. How to control these orbits is beyond the scope of the current paper, but, according to previous studies, the station-keeping cost of such halo orbits is small – about 7·79 m/s annual cost according to Davis et al. (Reference Davis, Bhatt, Howell, Jang, Whitley, Clark, Guzzetti, Zimovan and Barton2017).