1. INTRODUCTION
In order to cater for the general increase in air traffic, there is an immediate need for a more efficient approach to air navigation, including landing and surface movement in all conditions. In addition to physical, technological, procedural and environmental constraints on capacity, there are problems associated with the operational environment, including the contextual factors surrounding the provision of ATM and Control (ATM/ATC), such as weather conditions. Currently low visibility conditions can cause a dramatic reduction in airport capacity. For example, a major European airport operated in low visibility procedures currently presents flight planning problems over Europe on average for two consecutive days. The reduction in airport capacity is partly due to the difficulty of manoeuvring aircraft on the ground since, at present, most taxiing is carried out visually.
Significant research and development effort is being directed at the use of Global Navigation Satellite System (GNSS)-based air navigation in support of the phases of flight up to CAT-I precision approaches, to meet increasing capacity demands without compromising safety. The extension of the use of GNSS for landing and surface movement is encapsulated in the Ground Based Augmentation System (GBAS) concept. The adoption of GNSS for approach, landing and surface movement without the limitations associated with the ILS should enable a welcome improvement of accessibility to airports and thus contribute to the alleviation of capacity problems.
Although the potential benefits of GNSS in terms of capacity, efficiency and mitigation of environmental impact are clear, its introduction to aviation must not compromise safety. A key element of operational safety is the definition of the performance requirements for a particular phase of aircraft operation. This is a pre-requisite to determining whether a given navigation system is suitable for that phase of operation. For phases of flight up to, but excluding airport surface movement (ASM), performance requirements are typically derived based on the performance of legacy navigation systems. For example, one of the approaches for the derivation of the GNSS-based performance requirements for CAT-III precision approaches is based on translating the operational performance requirements of the Instrument Landing System (ILS) to GBAS (Eurocae, 2007; Schuster et al. Reference Schuster and Ochieng2010).
On the airport, surface movement radar (SMR) is currently the basic means for ATC surface surveillance. However, radar only provides an approximate position of the aircraft and, by itself, does not provide the required accuracy to identify or prevent runway incursions, let alone allow surface movement under zero visibility conditions. In order to meet future safety and capacity demands, novel support systems, such as the projected Advanced Surface Movement Guidance and Control Systems (ASMGCS) are thus required. ASMGCS are expected to fulfil four primary functions (ICAO, 2001):
• Surveillance: Capture of the information on aircraft, vehicles and objects within the coverage area and under specified operational conditions, and update of data needed for guidance and control.
• Routing: Provision of assignment of a route to individual aircraft and vehicles, which provides safe and efficient movement from its current position to the intended final position.
• Guidance: Provision of guidance necessary for movements through clear and continuous indications allowing pilots and vehicle drivers to maintain their positions on intended routes and for situational awareness.
• Control: Provision of a safe and efficient means of managing movements and planning for required movements, detection of conflicts/incursions and provision of solutions.
Ultimately, the safety requirements of a given operation define the requirements placed upon each of the elements involved in the operation. In the context of airport surface movement, at the highest level, the safety of the operation is determined by the adequacy of the combined airport and aircraft infrastructures to perform the proposed taxiing manoeuvre. On the ground-side, this includes an adequate airport layout and an appropriate Ground Management System (GMS) – including safety barriers. On the aircraft-side, this includes appropriate navigation and flight-management systems (including pilots and safety barriers). Navigation systems onboard the aircraft may include the use of equipment outside the aircraft. This process is captured in Figure 1. It is the combined performance of airport and aircraft infrastructure that determines whether a given taxiing operation is supported and safe.
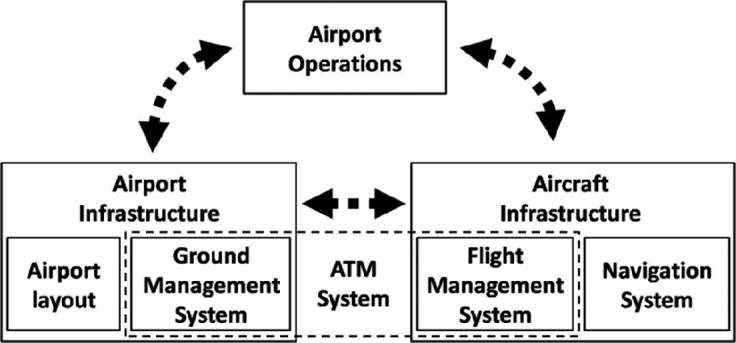
Figure 1. High-level architecture of aircraft ground operations.
The difference of ASM with respect to the remaining phases of operation is the lack of high-performance legacy navigation instruments to support ASM. This lack presents particular challenges for operations under zero visibility, given the proximity of other aircraft and buildings. Furthermore, as a result, there are no established and validated system performance requirements for high-performance ASM operations under zero-visibility conditions. These system performance requirements must thus be derived from basic safety considerations. The difference with respect to previous work (RTCA, 1999) is that the approach taken in this paper is based upon basic safety considerations that are directly extrapolated from those for CAT-III precision approaches, which have been validated by many years of operational experience. This ensures not only a coherent probabilistic framework, but also that ASM under zero-visibility is (at least) as safe as CAT-III precision approaches.
1.1. Zero-Visibility Operations
In this paper, in order to develop the aircraft infrastructure requirements for a truly gate-to-gate service, aircraft movement on the airport surface under zero visibility conditions is analysed. Zero-visibility requires an aircraft infrastructure able to guide the aircraft safely from one point on the airport to another, following instructions of the Ground Management System (GMS), without using external visual references. Instructions from the GMS can be thought of as a series of waypoints (with real-time updates) provided to the Flight Management System (FMS). Each waypoint has associated instructions, such as speed limits. The navigation system computes the aircraft position in relation to the airport layout. The FMS then combines the information from the navigation system and the GMS instructions to provide instructions to the Flight Control System (FCS) to guide the aircraft. The FCS here in the most general sense includes the pilot(s) and/or auto-pilot(s).
1.2. Safety
In this paper, safety is expressed as a probability that the aircraft will accidentally exceed the airport surface boundaries and/or collide with an airport obstacle (i.e. another aircraft, vehicle or building). This probability is a function of the available error margins with respect to nominal operation and the combined performance of the individual elements of the aircraft and airport infrastructures, expressed as a total system error. Nominal operation here refers to the operation of an aircraft according to its intended trajectory, e.g. by accurately tracking taxiway centre lines.
The tolerable error margins depend upon the airport layout and aircraft physical design (i.e. dimensions), as discussed in Section 2, both of which are assumed to be known. Using safety as the key driver, the tolerable error margins are used to determine the total tolerable system error (see Section 3). Making various assumptions about the performance of the aircraft FMS, this paper then analyses the navigation system performance requirements (Section 4). The results are compared with existing requirements (as far as available) from the International Civil Aviation Organisation (ICAO, 2001) and the Radio Technical Commission for Aeronautics (RTCA, 1999).
2. AIRPORT LAYOUT
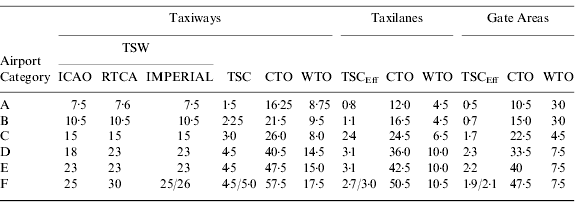
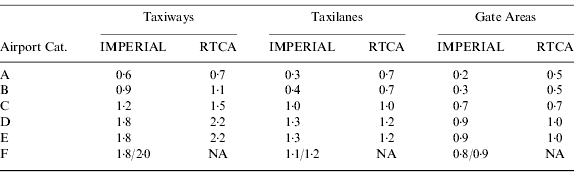
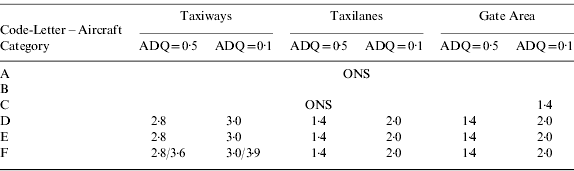
Airports are divided into six categories: A to F (ICAO, 1999), as shown in Table 1. A different convention is used by the RTCA (RTCA, 1999). However, for clarity, the ICAO coding is used throughout this paper. The table is essentially divided into two types of airports: private airports (code letters A and B) and commercial airports (code letters C to F). Each category of airport can accommodate aircraft up to the specified under-carriage widths and wingspans. For example a CAT-E airport can accommodate aircraft of CAT C, D and E (but not F). This is to ensure that certain minimum error margins are met as discussed in Section 2.1.
Table 1. Airport/Aircraft categories and specifications (ICAO, 1999).

2.1. ICAO and RTCA design requirements
The taxiing operation on an airport consists of a number of phases, each associated with a given travel surface, with maximum allowed speeds, and are divided into three categories: taxiways (with maximum speeds of 50 knots – 20 knots for curved taxiways and 80 knots for exit taxiways), taxilanes (with a maximum speed of 10 knots) and gate areas (with a maximum speed of 10 knots).
The ICAO and the RTCA have specified minimum design requirements in terms of various parameters regarding each of these travel surfaces, summarised in ICAO (2005). For taxiways, the design requirements are expressed in terms of a minimum Travel Surface Width (TSW) for a given Undercarriage Width (UW), yielding a minimum Travel Surface Clearance (TSC). The TSC is the distance between the outer wheels of the undercarriage and the taxiway edge when the aircraft is tracking the centreline, and is simply given by:
For taxilanes and gate areas, the relevant parameter is not the TSC since the hard surface extends up to the surrounding obstacles (i.e. other aircraft and buildings), but the Wingtip-To-(nearest-)Object (WTO) distance. This is directly related to the minimum Centre-line-To-Object (CTO) distance and the maximum Wing Span (WS) requirements. The CTO is the lateral distance from the centreline to the outer limit of a so-called containment region, mandated to be obstacle-free (RTCA, 1999). The WTO corresponds to the deviation from the centreline that could result in a collision with a surrounding obstacle:
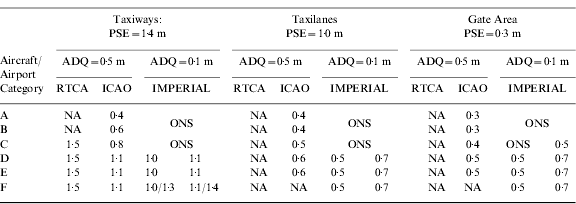
The various parameters are shown in Figure 2. Table 2 summarises the design requirements for the various travel surfaces as given in RTCA (1999) and ICAO (1999) together with those adopted in this paper, where maximum UW and WS from Table 1 are assumed. Also shown are the TSCEff, which are effective TSCs for the Taxilane and Gate Areas, discussed later in this paper. It should be noted that the TSW for CAT-F (RTCA) appears to be inconsistent with the TSC and the maximum WS requirements.
The values for CAT-F (Imperial College London – IMPERIAL), computed using Equation 1, depend upon the assumed TSC: the two values given are 4·5 m (ICAO, 1999) and 5·0 m (RTCA, 1999). It should be noted that for taxiways, the WTO are significantly larger than the TSC such that a departure from the taxiways does not immediately constitute a hazardous risk. This confirms that the limiting requirement for the taxiways is the TSC.
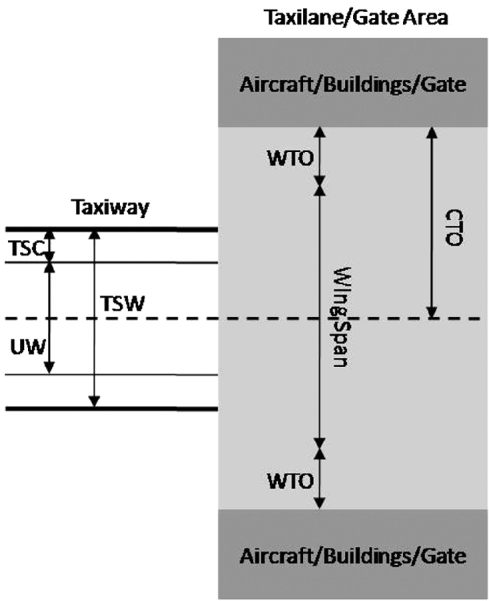
Figure 2. Travel surface design parameters.
Table 2. Airport travel surface design requirements.
In the next section, these design requirements are used as a basis to compute the total performance requirements a system must meet to be able to support movement on these travel surfaces under zero-visibility conditions.
3. TOTAL SYSTEM PERFORMANCE
Total system performance for airport surface movement is expressed as the probability that an aircraft exceeds the travel surface dimensions and/or collides with other aircraft and/or buildings. This probability is a measure of the safety of the taxiing operation. Once the safety requirements are established (Section 3.1), the total system error requirements can be computed under some general assumptions about the error distribution (as described in Section 3.2). The approach in this paper (referred to as IMPERIAL) uses the basic safety considerations to determine navigation system performance requirements.
3.1. Safety
This paper makes the assumption that the safety requirements for surface movement are not less stringent than for CAT-III landings. The latter are specified as a maximum allowed probability of 1E-6 of exceeding the lateral limits of the landing box (EASA, 2003; FAA, 1999). Note that the RTCA (1999) assumes that the TSC corresponds to the TSE at 4-σ, without further justification, leading to a probability of exceeding the lateral limits of 6·3E-5, larger than 1E-6.
3.2. Total System Error (TSE) Requirements
Using as input the safety requirements from the previous section and the tolerable error margins presented in Section 2.1, the allowed TSE is computed as the tolerable overall system error such that the probability in the tails of the distribution exceeding the travel surface limits are less than or equal to the safety requirements. In the case of taxiways, this corresponds to a TSE larger than the TSC, and in the case of taxilanes and gate areas to a TSE larger than the WTO. In order to derive the most stringent TSE, this paper uses the largest undercarriage width for a given airport category. Due to the lack of adequate measurements, the shape of the error distribution is unknown and assumed to be Gaussian. However the same approach can be used for any other distribution. For a Gaussian distribution, the total system error for the taxiways is computed as:
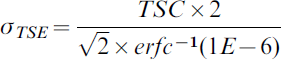
where the factor 2 in the numerator is included to express the results at 95% and:
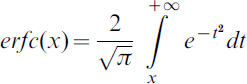
For the taxilanes and gate areas, the relevant parameter is the WTO. However, the TSC for the taxiways cannot simply be replaced by the WTO, since exceeding either the WTO or the TSC have very different safety consequences. Since safety is the primary driver in establishing the requirements, an assumption is made in this paper that the overall safety factor should be the same for all phases of surface movement. This implies that the ratio between the deviation required to collide with an object (WTO) and the deviation required to leave the travel surface (TSC) should be the same, leading to the definition of an effective travel surface for the taxilanes and gate areas as:
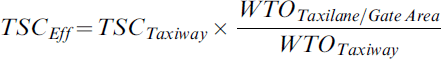
The results are summarised in Table 2. The current approach differs from that in RTCA (1999), where the justification for the effective TSC is based upon a qualitative argument that reduced separation and lower taxiing speeds are expected to lead to a reduction in the TSC. The final TSE requirements are shown in Table 3. The requirements derived in this paper are generally more stringent than those obtained in RTCA (1999). This can essentially be attributed to the larger probability of exceeding the travel surface allowed in RTCA (1999) compared to this paper, which adopts existing safety requirements for CAT-III landings.
Table 3. TSE Requirements in metres (95%). (NA=not available).
4. NAVIGATION SYSTEM PERFORMANCE REQUIREMENTS
The maximum tolerable NSE depends upon the tolerable limits of the various other error sources contributing towards the TSE (described in the previous section). The “total system” in the general sense is composed of the aircraft and pilot, as well as the airport travel surface. Onboard the aircraft it consists of a navigation system unit as well as a steering system (either automatic or including the pilot) which translates the navigation information into physical actions to direct the plane. Additionally, the overall system includes a “map”, relating the position from the navigation unit to the physical position on the airport. Each of these components has associated uncertainties. The navigation unit computes the position with a given accuracy, the NSE, while the steering system translates the navigation information into physical actions with a given error, the so-called path-steering error (PSE). Lastly, the ‘map’ uncertainties are expressed in terms of Aeronautical Data Quality (ADQ). Assuming that these three error sources are independent and normally distributed, we thus have the following relationship:
In order to compute the NSE requirements from the TSE requirements, ADQ and PSE requirements must be known. These are addressed in the next two sections.
4.1. Aeronautical Data Quality
ADQ are specified in (ICAO, 1999) as 0·5 m for taxiway intersections and centrelines as well as gate areas. These values were adopted in this paper as the basis in the computation of the NSE requirements, although it is shown in Section 4.3 that an improvement in the ADQ requirements could potentially significantly relax the NSE requirements for the taxilanes and gate areas. Therefore, consideration should be given to improving the ADQ specifications for those travel surfaces.
4.2. Path Steering Error
Data from Heathrow airport under best visibility conditions presented in Cassell et al (Reference Cassell, Bradfield and Smith1997) yield PSE for CAT-C to -E aircraft of 1·4 m for the straight sections of the taxiways, and 2·0 m for the curved sections of the taxiways. No data have been found for taxilanes and gate areas. However, it should be noted that the PSE is essentially a function of three factors: the aircraft angular offset with respect to the centreline, the aircraft speed and the aircraft (here including pilot and/or control system) reaction rate. The angular offsets and aircraft reaction rates are independent of the travel surface type. Therefore it is reasonable to assume that the ratio of the PSEs for the taxiways and taxilanes (resp. gate areas) is proportional to the ratio of the maximum speeds of taxiing of the taxiways and taxilanes (resp. gate areas). The PSEs for the taxilanes and the gate area are then computed as:
• PSEtaxilane=1·0 m
• PSEgate area=0·3 m
The assumption is made that the initial turn towards the gate area is part of the taxilane phase of operation and as such the taxilane PSE is derived from the curved taxiway PSE. If the initial turn to the gate area were considered part of the gate area, taxiing under zero visibility conditions in the gate area would not be achieved with current PSE. Furthermore, it should be noted that if the TSE of curved taxiways was the same as that of straight taxiways, TSE requirements could not be met with the current PSE. However, it is assumed in this paper that there is an additional margin for the TSC (and hence the TSE) on the curved taxiway sections (as can typically be observed at airports), such that the PSE of straight taxiway sections is in fact the limiting factor.
For CAT-A and -B aircraft no PSE data are available. However, smaller aircraft are expected to have smaller PSE as a result of better manoeuvrability. This paper derives the PSE of smaller aircraft assuming that it is proportional to the maximum undercarriage widths:
• CAT-A: PSEtaxiway=0·7 m; PSEtaxilane=0·5 m; PSEgate area=0·15 m.
• CAT-B: PSEtaxiway=0·9 m; PSEtaxilane=0·7 m; PSEgate area=0·2 m
4.3. Navigation System Error
Using the ADQ and PSE, the allowed NSE can be computed using Equation (6). The results are shown in Table 4. As can be seen, CAT-A and CAT-B airports are unable to support surface movement under zero visibility conditions with current ADQ and PSE requirements. If the PSE were improved by 50%, and the ADQ reduced to 0·1 m, CAT-A and CAT-B airports would be able to support surface movement under zero visibility conditions with NSE requirements of 0·2 m and 0·3 m respectively. For CAT-C airports, this paper finds that surface movement guidance under zero-visibility conditions is not supported unless the ADQ and the PSE are significantly improved. Despite the different assumptions made by the ICAO and this paper, the agreement between the final results is generally good for CAT-D to CAT-F airports.
Table 4. Navigation System Error (NSE) Requirements (95%). (ONS=Operation Not Supported; NA=Not Available).
4.4. Integrity & Continuity Requirements
ICAO (2002) specifies safety requirements in terms of a target level of safety (TLS), which expresses the risk of a fatal accident during the entire operation of an aircraft from the point it leaves the gate until it arrives at its destination gate. This risk should not exceed 1E-7, and the surface movement operation is attributed 10% of that figure. Moreover, statistically, only 1 out of 50 events are fatal accidents, leading to a total allowed event risk of 5E-7 per surface movement operation. This is further divided between the various functions of ASMGCS and between the departure and arrival phases, taking into account exposure times of 0·5 minutes for the exit taxiway (ETWY), 6 minutes for the normal taxiway (TWY), and 3 minutes for the taxilane (TL) and gate area (GA) combined.
Using these exposure times, the total exposure time for the arrival phase is 9·5 minutes, compared to 6 minutes for the departure phase, where the assumption was made that for the latter the TL/GA area exposure time is not applicable. This is due to the fact that the aircraft is pushed back by means of a ground vehicle and is therefore not under its own control. Note that the values obtained in Table 5 differ from the values presented in RTCA (1999) and Cassell et al (Reference Cassell, Bradfield and Smith1997), where the individual event risks attributed to the departure and arrival phases are not directly proportional to the exposure times.
Table 5. Event Risks.
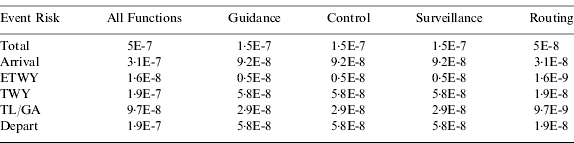
The event risks are divided into continuity and integrity risks, and are each allocated 50% in RTCA (1999), where the assumption is then made that pilot intervention mitigates the overall risk. For continuity, it is deemed that a pilot's actions are unable to mitigate the risks in only 1 out of 10 000 cases for all phases of surface movement. For integrity, it is deemed that pilots are unable to mitigate the risks in 1 out of 20 for the taxilanes and gate areas and 1 out of 10 for the remaining phases of operation. In this paper, the assumption is made that integrity risks cannot be mitigated at all by the pilot under zero-visibility conditions since there is no external visual reference that would allow the pilot to identify the problem. Making these assumptions, the tolerable continuity and integrity risks of the navigation system are computed as:

and:
where the factor of 0·5 reflects the allocation of 50% of the overall event risk to the CR and the IR. The results are summarised in Table 6.
Table 6. Navigation System Continuity & Integrity Risks (this paper).

A key performance indicator of integrity is the alert limit (AL), which defines the maximum limit of the NSE that must not be exceeded without the system providing an alert within the time-to-alert (TTA). It is related to the integrity risk as follows:

Using the NSE requirements from Table 4 together with the integrity risk requirements from Table 6, the AL is computed as:
where:
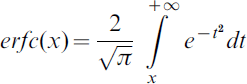
The results are shown in Table 7. CAT-A and CAT-B airport surface movement is not supported for reasons discussed previously in this paper. Operations on CAT-C airports are limited as a result of the maximum tolerated PSE, which is too large for current surface design requirements. Only with improved ADQ and at the lower speeds in the gate area are the PSE smaller than the maximum values imposed by the TSE. For CAT-D to -F airports, the most stringent requirements with current ADQ are AL=1·4 m. These alert limits can be further relaxed if the ADQ are improved.
Table 7. Alert Limit Requirements. (ONS=Operation Not Supported).
A further key performance indicator of integrity is the TTA. It specifies the maximum tolerable time interval between the onset of a failure and the time of annunciation. At the onset of the failure, in the worst-case scenario the aircraft is closer to the obstacle by a distance corresponding to the alert limit, d AL. The total distance travelled by the aircraft during this time-interval in the worst-case scenario (i.e. with the aircraft travelling at its maximum allowed speed) is simply given by:
Once the alert is issued the aircraft takes a certain time t reaction to react, during which time it covers a distance
This reaction time corresponds to the overall time between which the alert is issued and the brakes are applied. In the case of pilot-in-the-loop, the total reaction time will be the sum of the pilot reaction time and the reaction time of the control system. In the case of automatic braking, the total reaction time is only determined by the reaction time of the control system since it can be assumed that the reaction time of the autopilot is negligible. The aircraft can then be brought to a halt within a stopping distance given by:
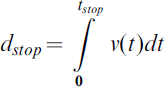
where t stop is given by:
In case of a potential collision risk, the aircraft would use its maximum deceleration power a max in the above equation. The aircraft would thus cover a total distance between the time at which a failure occurs and the time at which it comes to a complete stop given by:
This can be re-written as:
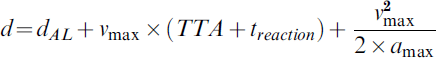
Assuming that the along-track distance to the nearest obstacle is at least as large as the WTO, that reaction times are 2·75 seconds (pilot+brake control-system) and 0·75 seconds (auto-pilot+brake control-system), as well as typical deceleration values of 2·4 m/s2 (RTCA, 1999), the required TTA can be computed as a function of v max. The results are shown in Figure 3. It is clear from these figures that maximum speeds of 10 kts currently allowed in the gate area are not adequate for taxiing under zero-visibility conditions. For CAT-C airports, a TTA of 1 second would yield maximum tolerable aircraft speeds of ~1·5 kts (pilot-in-the-loop) or ~2·9 kts (auto-pilot). For CAT-D to -F airports, the corresponding values are ~2·9 kts (pilot-in-the-loop) and ~5·1 kts (auto-pilot).

Figure 3. TTA versus maximum speed in gate area.
A TTA of 2 seconds would yield maximum speeds for CAT-C airports of ~1·2 kts (pilot-in-the-loop) and ~1·9 kts (auto-pilot) and for CAT-D to -F airports of ~2·3 kts (pilot-in-the-loop) and ~3·7 kts (auto-pilot). In line with the most stringent requirements for CAT-III precision landings, a TTA of 1 second was adopted as the final requirement. The maximum tolerable speeds in the gate area associated with this choice are summarised in Table 8.
Table 8. Maximum tolerable aircraft speeds in gate area.

5. CONCLUSIONS
This paper has reviewed and independently derived the navigation system performance requirements for the surface movement guidance function under zero visibility conditions. The derivation of the performance requirements is based upon operational considerations and basic safety requirements extrapolated from CAT-III precision approaches, which have been validated by many years of operational experience. This ensures a coherent probabilistic framework, and guarantees that ASM under zero-visibility is (at least) as safe as CAT-III precision approaches.
The approach in this paper assumes that airports meet the airport design and operational requirements specified in ICAO (2005). With the assumption of typical PSE (improved PSE for curved taxiways) and maximum allowed taxiing speeds as well as current requirements on the ADQ, the conclusion is that surface movement under zero visibility conditions can only be supported at airports CAT-D to -F, for which the most stringent requirements derived in this paper are summarised in Table 9. The requirements were shown to be significantly more stringent than those for CAT-III landings, primarily due to the relatively large PSE.
Table 9. Surface Movement Signal-In-Space Navigation System Performance Requirements (airport categories D to F).

An improvement in ADQ (through better surveying of the reference points) and in the PSE (e.g. through improved steering techniques or reduced taxiing speeds) may potentially allow an ASMGCS to provide the surface movement guidance functionality for CAT-C airports, and to relax the navigation system performance requirements for airport categories D to F. Since the PSE has the largest impact upon, and can be traded with, the NSE requirements (similar to being able to trade the FTE in flight with the NSE for CAT-III approaches, as described in Schuster et al, Reference Schuster and Ochieng2010), it is important that future work carefully validates the assumptions on the PSE. The performance requirements derived in this paper were compared with existing requirements (where available) by the ICAO and the RTCA and shown to be generally somewhat more stringent than previously assumed. The analysis of tolerable taxiing speeds in the gate area under zero-visibility conditions shows that a reduction to significantly lower levels than currently tolerable maxima is required to maintain adequate safety standards.
ACKNOWLEDGMENTS
This work was undertaken within the ANASTASIA project, funded under the EC Sixth Framework Program. The authors acknowledge contributions of ANASTASIA partners and the generous contribution of the EC.














