1. Introduction
In recent years, a large number of studies have provided substantial evidence that institutional quality is an important determinant of economic growth.Footnote 1 Rodrik et al. (Reference Rodrik, Subramanian and Trebbi2004) even go so far as to claim that ‘institutions rule’, i.e. that institutional quality trumps other determinants of growth. Other studies indicate that not all types of institutions are equally conducive to growth and that factors such as human capital are also important (Glaeser et al., Reference Glaeser, La Porta, Lopez-de-Silanes and Shleifer2004; Acemoglu et al., Reference Acemoglu and Johnson2005). The main reason to expect institutional quality to contribute to growth is that it entails productivity-enhancing incentives and decreased transaction costs through reduced uncertainty of economic transactions (Kingston and Caballero, Reference Kingston and Caballero2009). As North (Reference North1990: 110) puts it: ‘Third World countries are poor because the institutional constraints define a set of payoffs to political/economic activity that does not encourage productive activity.’
To improve institutional quality, a country must go through a series of institutional changes and thereby a period of institutional instability.Footnote 2 While high-quality institutions are growth enhancing because they reduce uncertainty and transaction costs, and entail incentives for productive behaviour, the growth effects of institutional change and instability are theoretically ambiguous. On the one hand, instability that entails change conducive to growth in the long run may come with transitional costs of a size that hamper growth in the short run. On the other hand, if the status quo is associated with what Olson (Reference Olson1982) called institutional sclerosis, institutional change as well as instability per se may also have positive effects on growth.
In this study, we try to estimate the growth effects of institutional instability. To isolate the instability effect, and to mitigate the problem of omitted variable bias, we control for the level and medium-run trend in institutional quality. To our knowledge, such an analysis has not been undertaken before. We analyse 132 countries over four five-year periods from 1984 to 2004 and construct new measures of institutional quality and instability based on annual data from the political risk index from the International Country Risk Guide (ICRG). The index consists of 12 components. To avoid testing partially correlated indices against each other, and to alleviate well-known problems of composite institutional indicators, we use principal components analysis (PCA) to construct three orthogonal dimensions of different types of institutional quality from the 12 components. By examining how these three dimensions correlate with other existing institutional measures, we show that the resulting dimensions can be interpreted as measures of legal quality, regulatory policy and social congruence. Institutional instability is measured as the coefficient of variation in each of these dimensions of institutional quality within each five-year period.
Previous studies that use measures of political (i.e. government or regime) instability generally find a negative relationship with investments or growth.Footnote 3 Studies looking at policy instability, mainly at the effects of macroeconomic variation on macroeconomic outcomes, likewise mostly find a negative relationship.Footnote 4 Hence, there is a growing body of literature that deals with the growth effects of political instability or the instability of economic policy and/or macroeconomic variables. The novelty of our approach rests in focusing on institutions rather than on the effects of macroeconomic or political instability, and in investigating the concurrent growth effects of institutional quality and instability. Our main findings are that institutional quality is positively linked to growth, but that the effect of institutional instability depends on economic development and institutional type.Footnote 5
Pierson (Reference Pierson, Shapiro, Skowronek and Galvin2006) notes that the standard definition of institutions as ‘the humanly devised constraints that shape human interaction’ (North, Reference North1990: 3) also includes policies. Indeed, an index such as the Economic Freedom Index produced by the Fraser Institute, which is often used to quantify institutions, actually measures a mix of stable institutions (such as property rights and the integrity of the legal system) and variable policies (such as average tariff rates), as pointed out by Sobel and Coyne (Reference Sobel and Coyne2011). Our empirical strategy, described in section 3, provides a way of separating the two, as the growth effects of policy instability may be different from the growth effects of institutional instability.
The paper is structured as follows. In the next section, we present some brief theoretical considerations and hypotheses about the relationship between institutional quality and instability, on the one hand, and growth, on the other. Next, we describe the data used and our empirical strategy. In section 4, we present our main results, and in section 5, we perform a number of robustness tests. Here we also discuss and attempt to handle potential reverse-causality problems. Section 6 concludes.
2. Theoretical considerations
North (Reference North1990) states:
The major role of institutions in a society is to reduce uncertainty by establishing a stable (but not necessarily efficient) structure to human interaction. The overall stability of an institutional framework makes complex exchange possible across both time and space. . . . [T]his set of stability features in no way guarantees that the institutions relied upon are efficient, although stability may be a necessary condition for human interaction, it is certainly not a sufficient condition for efficiency (North, Reference North1990: 6, 83–84).
Along these lines, we define institutional quality as the degree to which institutions reduce uncertainty for economic decision-makers and offer incentives for productive and innovative behaviour. Higher certainty implies lower transaction costs, which makes economic projects more profitable and hence more likely to be undertaken. By affecting the expectations of economic agents, it also allows agents to use a longer time horizon, through the stability that institutions provide. By offering incentives for productive behaviour, high-quality, or efficient, institutions stimulate individuals to engage in actions where the private return is close to the social return (Demsetz, Reference Demsetz1967).
Institutional quality is multidimensional, and higher certainty and incentives for productive behaviour may arise on the basis of many institutional characteristics, not least those relating to the protection of private property rights. Some examples of such characteristics are: generality (that equals are treated equally), transparency in public decision-making, accountability in public decision-making, stability and, importantly, an expectation that the main institutional decisions will be properly implemented and enforced. In such a setting, people are relatively more willing to engage in more advanced economic transactions, including interactions over longer periods of time and with more agents, as they can form a reasonable expectation that if instances of opportunism and cheating by others occur, the offenders will be punished and hence be less likely in the first place to engage in such treacherous behaviour.Footnote 6 Thus, by giving political and economic actors incentives to behave honestly and predictably, high-quality institutions help ensure that consequences of economic undertakings are more easily foreseen and that incentives stimulate productive rather than unproductive behaviour (see Baumol, Reference Baumol1990).
As noted by North in the quote above, stability is not enough for efficiency. To improve institutional quality, institutions must be changed, causing at least some instability. While the growth effects of institutional quality seem clear cut, those of institutional instability are theoretically ambiguous. On the one hand, based on the reasoning above, we expect a negative effect from the mere fact that instability increases uncertainty, increases transaction costs and shortens the time horizon for producers, investors and innovators. Institutional quality entails stability for economic decision-makers, and institutional stability entails stability in the institutional quality that entails stability for economic decision-makers, thereby reinforcing the stability already expected to be conducive to growth. Thus, institutional instability, even when caused by institutional improvements, could entail transitional costs that lower growth in the short and medium run. Hence, a J-curve-like growth effect could arise from uncertainty in a period where confidence in institutional innovations is built.
On the other hand, we see several mechanisms through which institutional instability may affect growth rates positively. First, the possibility of institutional sclerosis described by Olson (Reference Olson1982) suggests that institutional instability may diminish the influence of interest groups with rent-seeking behaviour. Already Adam Smith (Reference Smith1776 [1930]: 130) noted that ‘[p]eople of the same trade seldom meet together, even for merriment and diversion, but the conversation ends in a conspiracy against the publick, or in some contrivance to raise prices.’ Milton Friedman (Reference Friedman1962: ch. 8) remarks that this tendency of business interests to try to limit competition has often taken the form of influencing political decision-makers such that economic institutions are created that benefit certain companies and industries, to the detriment of competition and innovation. Indeed, Coates et al. (Reference Coates, Heckelman and Wilson2010, Reference Coates, Heckelman and Wilson2011) and Horgos and Zimmermann (Reference Horgos and Zimmermann2009) provide recent evidence of this type of interest-group influence. Thus, institutional instability could be beneficial for growth by changing the balance of power, thereby preventing or removing Olsonian institutional sclerosis.
Second, Hayek (Reference Hayek1973, Reference Hayek and Hayek1978) and Knight and Johnson (Reference Knight and Johnson2007) could be taken to suggest that regardless of the short-run effect of institutional instability, institutions are improved through a process of experimentation. Naturally, direct reforms are sometimes growth-enhancing, but this presupposes knowledge about how particular reforms work. This knowledge may need to be produced in an institutional trial-and-error process. In other words, noting that the economic environment continuously changes, such piecemeal experimentation could often reflect institutional adjustments which entail instability but which may result in higher institutional quality and, on net, higher growth rates, at least in the long run.
Finally, as it is reasonable to say that institutions work through expectations, it may be the case that the effect of institutional instability on growth depends on the trend: if instability occurs along a positive trend, instability may be interpreted as a sign of improvement. If Collier (Reference Collier2008) is right in asserting that actual institutions in the poorest countries on average are better than they are perceived to be by international investors, instability along a positive trend may be particularly important in a developing context, as it draws investors’ attention to institutional improvement in a country previously dismissed as too uncertain an environment for investments. On the other hand, instability along a negative trend may cause not only uncertainty but also signal that institutions are deteriorating.
Thus, the theoretical link between institutional instability and growth is ambiguous: arguments based on uncertainty and transitional costs suggest a negative link. On the other hand, if institutional instability is connected to institutional change in a setting with institutional sclerosis à la Olson (Reference Olson1982), Hayekian experimentation and with expectations of improvement, the link may be positive.Footnote 7 To sum up, it is evident that an empirical test of the growth effects of institutional instability must allow for complexity in the findings. More specifically, it should:
Acknowledge the multidimensionality of institutional quality;
Allow effects of instability to vary depending on the trend in institutional quality; and
Allow effects to vary between rich and poor countries.
The next section describes how our empirical strategy tries to meet these challenges.
3. Data and empirical method
The dependent variable and control variables
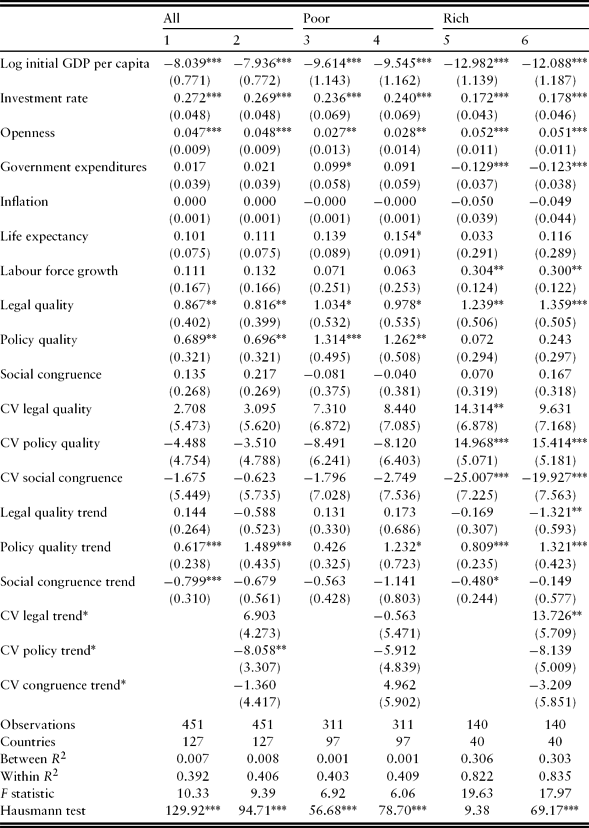
Following Temple (Reference Temple1999: 131–132), we run panel regressions with time- and country-fixed effects and growth of real gross domestic product (GDP) per capita as the dependent variable, averaged over five-year periods. There is no complete agreement on what control variables to include in growth regressions, but we use an extensive set including initial GDP, investment rate, openness (as measured by trade shares), government size, inflation, life expectancy and labour force growth. This includes the most commonly used control variables in the growth literature except education, omitted here to economize on data.Footnote 8 (In section 5, we do include education as a robustness test, and note that it does not affect our main results.) This full set of control variables is included in all regressions, even when not shown to save space. Table 1 gives variable description and sources for the data we use, and Table A1 in Appendix A contains descriptive statistics. In the next section, we describe our variables of interest, measuring institutional quality and instability.
Table 1. Variable definitions

Variables of interest: institutional quality and institutional instability
Aron (Reference Aron2000: 115) stresses the importance of using institutional measures carefully, as many studies in the growth literature employ an ‘often-arbitrary aggregation of different components’ (see de Haan, Reference de Haan2007). We share this concern, and as will be described, we use PCA to minimize this problem.
To construct a measure of institutional quality and instability, we use the ICRG (International Country Risk Guide, 2008), which is the only measure of institutional quality that suits the requirements to test the theory. Containing yearly data since 1984 for a large number of countries, the data allow us to quantify instability using the coefficient of variation over time within four five-year periods; note that this metric is scale invariant. The full dataset from the ICRG consists of three dimensions, quantifying political risk, economic risk and financial risk. Because the latter two consist mainly of economic outcomes such as international GDP ranking, inflation, foreign debt and current account balance, we use the political risk index to construct measures of institutional quality.
The overall political risk index is composed of 12 components listed in Table 2. These are aggregated with equal weights into a single index.Footnote 9 As stressed by Aron (Reference Aron2000), aggregating different components is inappropriate given the multidimensionality of institutional quality: some of the 12 different components differ substantially from each, and a growth effect from instability in the aggregated index would not reveal what is driving the result. On the other hand, some of the 12 components are conceptually similar and highly correlated, and it is not advisable to test these against each other. These problems can in principle be alleviated in two different ways: (1) by manually separating components into theoretically informed groups from which to form conceptually separate indices; and (2) by using an algorithm exploiting the empirical associations between components to form indices that are statistically separable. On the one hand, solution (1) has the benefit of providing readily interpretable data, as they are based on the theoretical preconception of its author. However, this solution does not solve the problems of statistical separability and suffers from necessarily being constructed from an arbitrary weighting scheme, and from relying on the validity of the constitutive theoretical conception. Additionally, solution (1) may tempt the researcher to cherry-pick components that generate interesting results. Solution (2), on the other hand, may under some circumstances fail to provide meaningful index structures. The ideal solution is, obviously, when solution (2) yields an index structure and dimensionality that makes theoretical sense. We therefore choose solution (2) and argue that the solution indeed is theoretically consistent and interpretable.Footnote 10
Table 2. The components of the political risk index of the ICRG

To avoid imposing a one-dimensional structure with a potentially arbitrary weighting scheme on the data, we therefore use PCA to form a number of institutional indicators from the 12 components in the political risk index. By doing so, we maximize variation and avoid testing partially correlated indices against each other. Using PCA lets the structure of the data determine how components are pooled to form separate indices instead of forcing a specific organization on the data. The results of the PCA are reported in Table 3.
Table 3. Principal components analysis (PCA): loadings and uniqueness
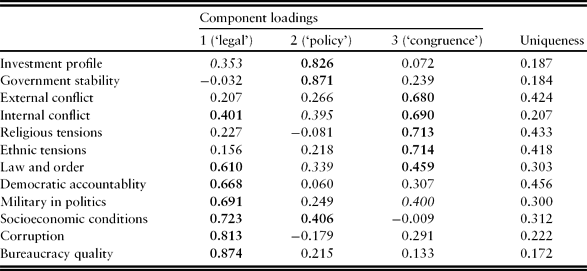
Notes: Loadings in bold are referred to in the text as ‘heavy’ loadings, i.e. the major influences on the PCA scores. Loadings in italics refer to indices with intermediate influence. The component solution has been rotated using the Varimax technique.
Table 3 shows that the 12 components of the political risk index do not load onto a single factor but split quite nicely into three underlying dimensions explaining approximately 70% of the variation of the original data. We thus avoid one of the main problems of choosing solution (2).
The use of PCA entails two potential problems: (1) that one risks throwing away valuable information even though the analysis provides a best fit of the data; and (2) that component solutions may be difficult to interpret by not conforming to any established theory. Yet, given that the fourth component has an eigenvalue of only 0.8 and the constituting components of the political risk index derive from dichotomous data, the precision of the PCA – an R 2 of 0.7 – can be deemed satisfactory.Footnote 11 As for the second potential problem, that the results from the PCA may be difficult to interpret, we note that, in our case, the three dimensions turn out to be rather informative.
The first dimension is interpreted quite easily, as it loads heavily on Law and order, Democratic accountability, Military in politics, Socioeconomic conditions, Corruption and Bureaucratic quality, all of which either measure the quality and capacity of the legal system or consequences and reflections of such quality and capacity. Furthermore, the correlation between our first dimension and the second area of the Economic Freedom of the World Index (EFI), Legal structure and security of property rights (often treated as the most transparent and arguably the ‘cleanest’ measure of the rule of law; see Gwartney and Lawson, Reference Gwartney and Lawson2007), is 0.77, making it intuitively sensible to interpret this dimension as a ‘legal dimension’ of institutional quality.
The second dimension includes heavy loadings of countries’ Investment profile and their Government stability. The correlation between this dimension and area five of the EFI, Regulation of credit, labour and business, is 0.42, while the partial correlation, when controlling for area two of the EFI, is 0.34. Adding the two areas of the EFI to the PCA shows that area two exclusively loads onto a factor including the same ICRG components as the first dimension (with a loading of 0.78), which we term a legal dimension, while area five loads moderately onto the first dimension and heavily onto the second dimension (loading 0.63). We therefore interpret the second dimension as a measure of the quality of regulatory policy, in short a ‘policy dimension’.
In Table A2 in Appendix A, we present the complete correlations between our two PCA dimensions and areas two and five of the EFI. The first dimension, which we interpret as the legal dimension, correlates highly with the corresponding dimension of the Economic Freedom Index not only in levels but also in variation.Footnote 12 Furthermore, our second dimension, the policy dimension, correlates highly with the corresponding dimension of the Economic Freedom Index (EFI5), and our third dimension is uncorrelated with these, as it should be.
The third dimension, finally, consists of heavy loadings of the ICRG components on External and Internal conflict, Religious and Ethnic tensions and Law and order, and correlates at –0.37 with the ethnic diversity index from Alesina et al. (Reference Alesina, Devleeschauwer, Easterly, Kurlat and Wazciarg2003). This final index can therefore readily be interpreted as a measure of both actual and latent conflicts and tensions in society, including socio-political instability and social unrest (see Alesina and Perotti, Reference Alesina and Perotti1996). We thus call this dimension ‘social congruence’.
Finally, to arrive at a set of measures of institutional instability, we calculate the coefficients of variation of the resulting principal components within each five-year period using the variance and averages of institutional quality. Thereby we also allow the heterogeneity of the instability inherent in the data to determine our indicators.
An illustration
As an illustration of what the three indices obtained from the PCA actually measure, we explore their correlations with the well-known Gastil index. The three indices all correlate with the Gastil index at 0.59, 0.45 and 0.27, respectively, and the Gastil index in turn correlates with the overall political risk index at 0.77.
The PCA indices can be used to clarify the potential pitfalls of not treating institutional quality as a multidimensional concept, and the need to separate quality and instability. To take an example, Denmark receives the second-largest score in the latest period for legal quality and is the fifth most stable country in that area. However, it is only number 71 in terms of the quality of policy and number 80 in terms of social congruence, and receives relatively unstable scores on both these dimensions, placed at number 50 and 71, respectively. Panama, on the other hand, is placed at number 52 on the legal dimension but has the seventh most stable legal environment. These countries exemplify how quality and stability are only imperfectly associated: the correlation between legal quality and legal instability is –0.50, that between policy quality and policy instability is –0.61, and that between the level of social congruence and its stability is –0.40.
The main points of our strategy are illustrated in Figure 1, where we plot the scores of legal quality for Denmark, Malaysia, the USA and Venezuela. First, Danish legal quality has been high and very stable across the entire period 1984–2004, while American legal quality has been of almost the same quality, but as the figure illustrates, somewhat more volatile. Simply comparing quality at the beginning of the period may therefore give a slightly biased impression of actual institutional performance in the two countries, although the differences may seem relatively minor. Second, comparing Malaysia and Venezuela accentuates this point, as the two countries had almost equal legal quality around 1990. The legal quality of the Venezuelan system has, on the other hand, been less stable than its Malaysian counterpart across the entire period and has obviously been characterized by a long-run downward trend. Yet, if either the initial level of 1990 or the average is used, one is likely to overestimate the positive impact of Venezuela's legal institutions compared with Malaysia, a disparity reflected in the difference between the Venezuelan average annual growth rate during 1984–2004 of –0.36% and the Malaysian average of 3.2% in the same period. Likewise, comparing the instability of the institutions of the two countries can be misleading, as Malaysia has seen instability around a relatively stable long-run level while the instability of Venezuelan institutions is a reflection of a steady deterioration. One therefore ideally has to take into account both the level, the medium-run trend of the quality of such institutions as well as its instability in order to get a full estimate of the institutional impact.

Figure 1. Legal quality 1984–2004, giving four examples. For interpretative convenience, we have rescaled indices in this figure to be within the same interval as the original International Country Risk Guide (ICRG) components
Estimation strategy
We estimate regressions as in equation 1, where Gr is the growth rate of real GDP per capita, and X is a set of standard controls; D are time- and country-fixed effects and ε is a noise term. In order to separate the potential effects as discussed above, we include three groups of variables:
Q, which is the set of measures of institutional quality from the PCA;
CVQ, capturing institutional instability as the coefficients of variation of Q across each five-year period; and
TRQ, which is a categorical variable based on Kendall's Tau, a set of non-parametric trends measures, that we add to be able to separate institutional instability and change.
When interpreting these effects, one must therefore keep in mind that what our trends measure is strictly categorical and allows only for separate effects between situations where the trend is positive, i.e. conditional on institutions improving (trend = 1), when the trend is negative, i.e. where institutions are worsening (trend = –1), or when the trend is roughly constant (trend = 0).
In further analysis, we expand the specification to equation 2 and add an interaction term between CVQ and TRQ as specified in equation 2.Footnote 13
Although our main focus is on CVQ, we need to include Q and TRQ in the specification at all times. As the correlations noted above suggest, these elements (variation, level and trend) are statistically separable, but they remain sufficiently strongly associated that excluding one or both would be likely to cause an omitted variable bias. We thus note that this problem means that previous estimates in the literature may suffer from such a bias. In addition, by including the trend we gain more precise information about under what conditions institutional instability matters for growth.
The control variables in our specification are factors that are broadly used in the empirical growth literature. In all regressions, the X vector consists of the logarithm of initial GDP per capita to account for conditional convergence, government expenditures as percentage of total GDP, openness (imports plus exports as percentage of total GDP), the investment share of GDP, inflation, life expectancy and labour force growth. As such, we capture the most important non-institutional determinants of economic growth while still keeping the specification sufficiently parsimonious to include a large and diverse set of countries (in line with Barro, Reference Barro1997). As we are thereby running the risk of spurious results due to omitted variables bias, we offer a set of robustness tests in which we include five additional variables.
Our full sample covers 127 countries with a political risk rating in at least one of the four time periods 1984–1989, 1989–1994, 1994–1999 and 1999–2004; the countries are listed in Table A3 of Appendix A. Growth is measured as the five-year average, as are all control variables except initial GDP per capita. Forty of these countries have a GDP per capita above 14,000 USD in at least one period, which we define as our high-income subsample for which determinants of growth and institutional impacts may differ from the full sample and the poor subsample (see Keefer and Knack, Reference Knack and Keefer1995; de Haan and Siermann, Reference de Haan and Siermann1996). We split the sample, as citizens and market actors in high-income countries have access to more complete insurance markets, financial instruments in deeper markets as well as better market information, and are therefore substantially better suited to handle institutional instability without real losses in the short to medium run.Footnote 14 The rich subsample roughly corresponds to the current group of Organisation for Economic Co-operation and Development (OECD) member countries.
4. Institutions and growth: empirical results
Using the data described above, we derive a series of fixed-effects generalized least squares estimates. Results are reported for the full sample and for two subsamples of countries with a GDP per capita below and above 14,000 USD, respectively. This corresponds to dividing the sample into a large group (n = 100) of poor and middle-income countries and a smaller group (n = 40) of rich countries (including the OECD and equally rich countries, including countries that become rich during the period). The regression results, linking the three institutional features to growth, are presented in Table 4.
Table 4. Growth effects of institutional quality, instability and trend – using the three principal components analysis (PCA) indices
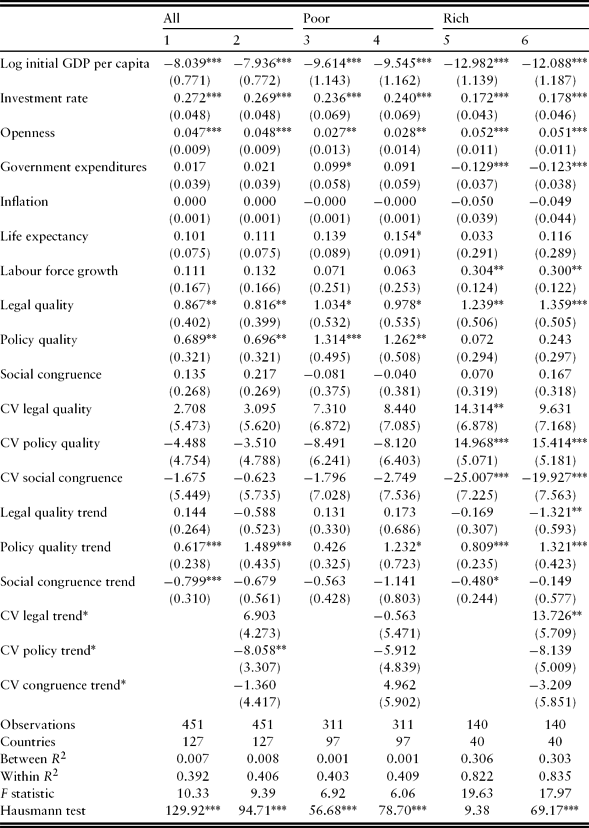
Notes: All regressions are generalized least squares (GLS) with country and period as fixed effects. Standard errors are in parentheses and CV denotes coefficient of variation. * Significant at 10%, ** significant at 5%, *** significant at 1%.
The signs of our control variables are typically as expected: investments and openness are positively associated with growth, initial GDP displays a negative association, indicating convergence, while government expenditures are weakly (but not robustly) positively associated with growth in poor countries and significantly negatively so in rich countries (see Schaltegger and Torgler, Reference Schaltegger and Torgler2006; Bergh and Henrekson, Reference Bergh and Henrekson2011). Labour force growth is positive and significant in the rich subsample, while life expectancy seems to matter more in the poorer part of the sample.
As for the level of institutional quality, the findings clearly point towards the importance of legal quality: in both samples it turns out to be positive and statistically significant. In the full and the poor part of the sample, policy quality is also positive and significant. In the subsample consisting of low- and middle-income countries, these two dimensions appear roughly of equal importance: a one standard deviation change in legal quality is ceteris paribus associated with a growth increase of approximately one percentage point (roughly the difference between present-day legal quality in Jordan and Lithuania, and between Serbia and India in policy quality). In the high-income subsample, the effect is slightly larger: a one standard deviation change to legal institutions in rich countries (the difference between present-day Spain and Norway) is associated with an increase of growth of approximately 72% of a standard deviation, or 1.3 percentage points, all other things being equal.Footnote 15
Regarding our main variable of interest, institutional instability, a positive sign for the CV coefficients implies support for Olson's (Reference Olson1982) concern with excessive stability, whereas a negative sign implies a negative effect of increased transaction costs due to a rise in uncertainty. In general, the results indicate a rather complex pattern. In the rich countries, instability of legal quality and policy quality is positively associated with growth, but this is not the case in poor countries. Also, in rich countries, instability of social congruence is negatively related to growth.
The associations between institutional instability and growth in rich countries are not only statistically significant but also of economic significance. For example, a one standard deviation increase in legal instability in rich countries, roughly the difference between extremely stable Finland and Belgium, is associated with an improvement in the growth rate of about one-third of a standard deviation. Conversely, a one standard deviation change in the instability of social congruence, the difference between present-day Denmark and Austria, is associated with a medium-run growth decline of almost one-half of a standard deviation.
Furthermore, the results in odd-numbered columns show that the trend in policy quality exhibits a significantly positive association with growth, which is robust in rich countries, indicating that such changes have short-run effects, whereas the long-run level of policy quality is of no significant relevance in developed countries (the point estimate on policy quality is not significantly different from zero).
Table 5 reports both the interactions between trends and instability measures (to the left in the table) and also the effects of trends, given the level of instability: the 25th percentile, i.e. low instability, at average instability, and the 75th percentile, high instability (to the right in the table). For example, the upper left-hand panel reports the effects of instability of legal quality, evaluated at negative, neutral and positive trends of legal quality. The upper right-hand panel instead evaluates the effects of the trend in legal quality as evaluated at relative stability (the 25th percentile), average instability, and at a relatively high level of instability (the 75th percentile). All standard errors in the table are evaluated at the denoted value of the interacting variable (see Brambor et al., Reference Brambor, Clark and Golder2006).
Table 5. Evaluating interactions

Notes: All regressions are generalized least squares (GLS) with country and period as fixed effects. Standard errors are in parentheses and CV denotes coefficient of variation. Control variables are used throughout but are not reported for reasons of space. High instability refers to 75th percentile CV; low instability refers to 25th percentile CV. * Significant at 10%, ** significant at 5%, *** significant at 1%.
The results show that instability around positive trends of legal quality is positively associated with growth in rich countries while instability around negative trends is insignificant. The effects of policy instability are also positive, yet only in rich countries and only when associated with negative or neutral trends. In rich countries, policy instability is thus on average inconsequential when the level is improving.
The findings for poor countries are entirely contrary, as the instability of policy quality is negatively associated with growth when accompanied by a positive trend, but not robustly so at neutral or negative trends. As such, these results suggest that the contrary theoretical explanations outlined in section 2 may have differential importance in poor and rich countries. Finally, the results show that the instability of social congruence – i.e. the random occurrence of unrest – is negatively associated with growth regardless of its medium-run trend.
To illustrate the structure and pertinence of such results, Figure 2 shows the regression coefficient for the instability of legal quality evaluated at different trends in institutional quality in the rich subsample. As the trend goes from negative to constant and to improving, the growth effect of instability of legal quality goes from negative to positive. Yet, as evident from the 95% confidence intervals, only the latter, positive effect is statistically significant, suggesting that institutional instability is conducive to growth in rich countries only when the legal quality is improving.Footnote 16

Figure 2. Partial effect of the instability of legal quality on growth in rich countries depending on the trend in institutional quality, based on Table 5. By ‘worsening’ is meant that the trend for institutional quality is negative, etc. The dashed lines show the 95% confidence interval
Turning to an evaluation of the growth effects of trends in institutional quality (all right-hand panels), we find that trends in legal quality are only significantly and negatively associated with growth when the decline is along a very stable path (i.e. around the 25th percentile). These effects only seem to occur in rich countries, as there are no significant effects in poor countries. Likewise, the effects of trends in policy quality, although weakly significant in the table, on closer inspection turn out to be insignificant in poor countries (standard errors in the table are evaluated at zero instability, which we actually do not observe in the sample). For rich countries, though the point estimates differ, we cannot say with certainty that the positive growth effects of improving policy quality differ whether the medium-run trend is stable or not. Finally, instability of social congruence is, in contrast, negatively related to growth in rich – but again not in poor – countries.
Some of these effects are quantitatively rather large. The instability of legal quality, for example, is associated with no growth effects when the quality of the legal system is not changing or if it is deteriorating (negative or neutral trends). Yet, when instability occurs along a positive trend, a one-standard deviation change in the coefficient of variation of legal quality is associated with an increase in the growth rate of half a standard deviation. The effects of instability of policy quality, when accompanied by deteriorating levels, and instability of social congruence, are of approximately the same magnitude.
Calculating the average transitional gain of a positive trend in policy quality through a five-year period from the present estimates suggests that they approximate 200 USD per capita per year in rich countries, and approximately zero in poor countries. However, such trends are often accompanied by instability, while instability can also arise on its own. The similar medium-run gain of having instability in legal quality is roughly 450 USD per capita, the gain from instability of policy quality around negative trends is roughly 400 USD, while instability in institutions related to social congruence induces a medium-run cost of approximately 350 USD per capita, averaged across a five-year period. Yet, this exercise crucially underlines that we cannot evaluate the gains and costs of instability or those of trends in institutional quality without considering whether instability is associated with improvements, deteriorations, or takes place around a stable long-run level. Before concluding, we address the potential fragility of our main results.
5. Robustness tests
Additional indices and outliers
First, we test whether the main results are robust to including the level and coefficient of variation of four alternative indicators of institutional quality: the Gastil index of political rights and civil liberties, Henisz's (Reference Henisz2002) ‘Political Constraints V’ indicator of veto player strength, the Polity IV index of democracy, and the Herfindahl index of the legislature as an index of the level of political competition. These alternatives mainly pick up variations in political institutions, while we argue that the ICRG indices mainly capture economic and judicial institutions (see Munck and Verkuilen, Reference Munck and Verkuilen2002). By including alternative indicators with established interpretations we test whether our results simply proxy for effects of, e.g., democracy or constraints on policy-makers, although we also note that the simultaneous inclusion of alternative institutional measures most probably causes some variance inflation. We limit ourselves to these indices, as they are the only other institutional measures with a sufficient amount of years covered.
We perform all types of robustness analysis with the full specification, although we only report the institutional coefficients in Tables A4 and A5 of Appendix A; these should be compared with columns 4 and 6 of Table 4. For the poor countries, out of 36 coefficients (nine for each of the four indices), 25 have the same sign and statistical significance as before. For the rich countries, the corresponding figure is 20 out of 36, implying less robustness, although we should stress that the problems of variance inflation when including multiple institutional indicators seem particularly acute in this sample. The result that only legal quality is significant in rich countries while both legal quality and policy quality are significant in poor countries also turns out to be robust when excluding outliers, as do the results pertaining to instability and institutional trends. The tables show that most main findings are largely robust to including the quality and coefficient of variation of the Gastil index, the Political Constraints V index, the Polity IV index and the Herfindahl index.Footnote 17 The only non-robust result in rich countries appears to be that the positive effects of legal instability, as evaluated at the sample mean, are not robust to including the Herfindahl index, although neither its level, trend nor its instability are close to significance.
Second, we test what happens when potential outlier observations are removed from the sample and whether the results are robust to excluding the observations with the best and worst institutions. We use a jack-knife exercise in which we exclude single regions and countries with few observations; in general, the main results are reconfirmed. In the full sample, the effect of the instability of policy quality fails significance when excluding observations from either the post-communist countries, Sub-Saharan Africa, the Middle East and North African region, Asia or countries with less than three observations in the dataset. What is more, excluding the Sub-Saharan African countries – i.e., the absolutely poorest countries in the sample – yields the legal quality index insignificant. However, in the rich subsample, all results remain robust in a jack-knife.
Third, we acknowledge a potential problem of omitted variables bias with the use of a parsimonious model specification. In Tables A6–A8 we therefore check the robustness of our results to the inclusion of further controls (the standard baseline of control variables still included): investment price, which we include instead of the investment rate; two human capital variables (the share of population with at least secondary schooling, and average years of schooling in the population); fertility; and a dummy for terms of trade crisis. We find that terms of trade crises are important (and negative) for growth in poor countries, while fertility is weakly significant in the rich subsample, also with a negative sign.
In general, our main results pertaining to institutional quality are robust – including the positive growth effects from policy quality trends and negative effects of trends in social congruence. In rich countries, results pertaining to policy and social congruence instability remain robust while the effects of legal instability appear less robust.
Handling possible endogeneity
As a final issue, we try to control for possible endogeneity and simultaneity in two ways.Footnote 18 As is almost always the case, we note that the institutional measures may lag rather than lead growth rates for several reasons. First, simple arguments could be made why institutions might improve when the economy grows (see Chong and Calderón, Reference Chong and Calderón2000). For example, the quality of legal systems and public bureaucracies could be constrained by available resources, in which case growth would lead to better institutions in the long run by alleviating this constraint. Second, we note the risk when using subjective or quasi-subjective indices that evaluations of institutional quality are affected by expectations of economic growth in the immediate future. If these expectations are on average correct, higher growth rates in the short run would simply be reflected in our measures of institutional quality instead of causing actual quality. In this case, we would expect this reflection to show up in higher investment rates to the extent that the expectations are shared by the market to which the ICRG primarily delivers its risk assessments.
To investigate causality in a tentative way, we first include lagged growth rates, based on the simple argument that if higher growth rates cause rather than follow higher institutional quality and affect institutional stability, a lagged dependent variable would pick up at least some of this effect by being the actual cause of institutional differences. If some estimates are due to simultaneity or reverse causality, we would expect to see those estimates become smaller and statistically weaker. Yet, the estimates, which we report in Table A9 in Appendix A, in general do not suggest that endogeneity is a major concern even though the inclusion of a lagged dependent variable induces a degree of downwards Nickell bias. In the full sample, we find no significant differences although the point estimates of trends in policy quality and social congruence are slightly smaller. The results in the rich subsample are entirely unaffected while the instability of policy quality in the poor subsample is rendered insignificant. With few exceptions, this exercise therefore does not suggest major endogeneity problems. With respect to the possibility that our estimates suffer from simultaneity bias due to institutional indices reflecting market expectations, the exclusion of investment rates does not affect our estimates of institutional effects (not shown). Given that such expectations would most probably show up in the investment rate instead of affecting productivity, we do not believe that this is a major worry.
Our second test is an attempt to instrument for our variables of interest. We must note that, as is often the case, our search for valid instrumental variables that account for the variation of institutional quality and instability over time has proven to be unsuccessful. In particular, as all our main estimates are obtained with country- and time-fixed effects, we cannot rely on the advances in instrumentation from the recent literature on long-run development, as all potential instrumental variables would need to define medium-run institutional changes. The best instrumental variables we could find proved to be lagged measures of institutional quality derived from the PCA and lagged growth rates; but these primarily explain the cross-country variation while leaving almost all within-country variation unexplained. The same problem pertained when we switched to either a random-effects generalized least squares (GLS) estimator or pooled ordinary least squares (OLS) with panel-corrected standard errors. As these choices allowed us to identify institutional differences by time-invariant factors, it proved substantially easier to find statistically valid candidates for instruments. However, while legal quality can be instrumented satisfactorily in more than one way, our search for instrumental variables for instability measures was unsuccessful. In particular, identification across the spectrum of trends – what appeared as a mediating factor in Table 5 – was not possible, implying that these instruments exhibited a significant bias towards zero (Dunning, Reference Dunning2008).Footnote 19
We nevertheless found one set of additional practicable instruments for legal quality and its instability in the rich subsample. We therefore report the instrumental variable estimates of legal quality, policy quality and social congruence in column 4 of Table A9, where instruments are lagged growth, lagged institutional quality and voting patterns in the United Nations General Assembly (from Voeten, Reference Voeten2004). We find that only legal quality appears important; as usual, the instrumented estimate is somewhat larger despite good identification statistics, although we cannot reject that it is the same as the simple estimate in previous tables. In column 5, we instead provide the instrumented estimates of legal quality and its instability, instrumented by lagged growth, lagged legal quality and social congruence (hence excluded) and the investment price level. We again find insignificantly larger but robust estimates with good identification statistics. As such, these exercises do not point to major endogeneity problems – if anything, our simpler estimates may arguably give relatively conservative estimates of the importance of institutional quality and instability.
As the main results are relatively robust to a set of feasible tests, especially with regard to the important role of institutional quality, and especially in rich countries, we move on to discussing the implications of the findings in the final section.
6. Conclusions
The burgeoning literature on economic growth has in recent years documented a close association between institutional quality and economic development. However, to achieve high quality of institutions that, for example, protect property rights or constrain political decision-making, countries need to go through periods of institutional change and instability: few countries are born with great institutions. Even among rich countries, some have more volatile institutions than others, yet economic theory provides only ambiguous insights as to how institutional change and instability might affect the economy in the medium run. While uncertainty about the future institutional framework intuitively would be associated with larger transaction costs and force economic actors to adopt a relatively short time horizon, thus being harmful to growth, it could also reflect positive institutional adjustments to shifting circumstances that would clear away uncertainty.
Consequently, this paper has explored the full association between institutional quality, institutional instability, institutional trends and economic growth. We employ the political risk index from the ICRG to form three indices aggregated from its 12 constituting components by the use of PCA. We choose to deal with institutional measurement problems to overcome the problem that if aggregated indices hide multiple dimensions, estimates of their effects are likely to suffer a downward bias. The empirical results based on a panel of 127 countries observed across four five-year periods between 1984 and 2004 support a sizeable effect of high-quality institutions on growth in both poor and rich countries. The effects of institutional instability and change, however, are more context dependent and harder to interpret. Employing the three composite indices measuring legal quality, policy quality and social congruence, the main results indicate that policy improvements are positively related to growth in rich countries, and that policy instability hampers growth in poor countries. Furthermore, a stable level of social tensions seems to be better than a less stable level.
Lack of good instruments or other ways to handle potential endogeneity problems prevents us from fully examining the direction of causality in these relationships. Also, the scarcity of institutional indicators available on a yearly basis means that our results should be considered as rather tentative. Given these limitations, it is still interesting to note that instability of legal quality (around positive medium-run trends) and policy quality (around negative and neutral trends) is on average conducive to economic growth in relatively rich countries. While these results should be particularly carefully interpreted, they are compatible with the idea that institutional instability can mitigate negative growth effects of Olsonian institutional sclerosis. Our results can also be interpreted as supporting the positive effects of institutional adjustments in the spirit of Hayek. In any case, the simplistic view that stable institutions always are better for growth than institutional instability seems not to hold.
Appendix A
Table A1. Descriptive statistics

Table A2. Correlations between the three principal components analysis (PCA) dimensions and areas two and five of the EFI

Notes: EFI refers to the Economic Freedom of the World Index (Gwartney and Lawson, Reference Gwartney and Lawson2007).
Table A3. Countries included in our sample

Notes: Countries in italics are included in the high-income subsample.
Table A4. Growth effects of institutional quality, instability and trend – using the three principal components analysis (PCA) indices along with alternative institutional indicators

Notes: All regressions are generalized least squares (GLS) with country and period as fixed effects. Standard errors are in parentheses and CV denotes coefficient of variation. * Significant at 10%, ** significant at 5%, *** significant at 1%.
Table A5. Growth effects of institutional quality, instability and trend – using the three principal components analysis (PCA) indices along with alternative institutional indicators and excluding outliers and tails

Notes: All regressions are generalized least squares (GLS) with country and period as fixed effects. Standard errors are in parentheses and CV denotes coefficient of variation. * Significant at 10%, ** significant at 5%, *** significant at 1%.
Table A6. Growth effects of institutional quality, instability and trend – using the three principal components analysis (PCA) indices

Notes: All regressions are generalized least squares (GLS) with country and period as fixed effects. Standard errors are in parentheses and CV denotes coefficient of variation. Control variables are used throughout but are not reported for reasons of space. * Significant at 10%, ** significant at 5%, *** significant at 1%.
Table A7. Growth effects of institutional quality, instability and trend – using the three principal components analysis (PCA) indices

Notes: All regressions are generalized least squares (GLS) with country and period as fixed effects. Standard errors are in parentheses and CV denotes coefficient of variation. Control variables are used throughout but are not reported for reasons of space. * Significant at 10%, ** significant at 5%, *** significant at 1%.
Table A8. Growth effects of institutional quality, instability and trend – using the three principal components analysis (PCA) indices

Notes: All regressions are generalized least squares (GLS) with country and period as fixed effects. Standard errors are in parentheses and CV denotes coefficient of variation. Control variables are used throughout but are not reported for reasons of space. * Significant at 10%, ** significant at 5%, *** significant at 1%.
Table A9. Growth effects of institutional quality, including lagged growth and instrumental variables (IV)

Notes: All regressions are generalized least squares (GLS) with fixed effects. Standard errors are in parentheses and CV denotes coefficient of variation. Instruments in column 4 are lagged growth, lagged institutional quality (all three measures) and voting shares in the UN General Assembly with the USA and Russia/Soviet Union. We instrument all three institutional measures, yet results are insignificantly different when only one measure is instrumented at a time. Column 5 instead instruments for legal quality and its instability, using lagged growth, lagged legal quality, social congruence and the investment price level; the two latter are instruments for legal instability. Instrumented variables are in bold. * Significant at 10%, ** significant at 5%, *** significant at 1%.
Appendix B
The components of the International Country Risk Guide's political risk index (a full description can be found at http://www.prsgroup.com/icrg_methodology.aspx):
A. Government stability
Assesses the government's ability to carry out its declared programme(s), and its ability to stay in office. The risk rating assigned is the sum of three subcomponents: Government unity, Legislative strength and Popular support.
B. Socioeconomic conditions
Assesses the socioeconomic pressures at work in society that could constrain government action or fuel social dissatisfaction. There are three subcomponents: Unemployment, Consumer confidence and Poverty.
C. Investment profile
Assesses factors affecting the risk to investment that are not covered by other political, economic and financial risk components. The subcomponents are: Contract viability/Expropriation, Profits repatriation and Payment delays.
D. Internal conflict
Political violence in the country and its actual or potential impact on governance. The subcomponents are: Civil war/Coup threat, Terrorism/political violence and Civil disorder.
E. External conflict
Assesses the risk to the incumbent government from foreign action, ranging from non-violent external pressure (diplomatic pressures, withholding of aid, trade restrictions, territorial disputes, sanctions, etc.) to violent external pressure (cross-border conflicts to all-out war).
The subcomponents are: War, Cross-border conflict and Foreign pressures.
F. Corruption
Assesses corruption within the political system. No subcomponents.
G. Military in politics
Assesses the degree of military participation in politics and the higher level of political risk associated with such interventions. No subcomponents.
H. Religious tensions
Assesses religious tensions from the domination of society and/or governance by a single religious group that seeks to replace civil law by religious law and to exclude other religions from the political and/or social process and the suppression of religious freedom. No subcomponents.
I. Law and order
The Law subcomponent is an assessment of the strength and impartiality of the legal system. The Order subcomponent is an assessment of popular observance of the law.
J. Ethnic tensions
Assesses the degree of tension within a country attributable to racial, nationality, or language divisions.
K. Democratic accountability
Assesses how responsive government is to its people, on the basis that the less responsive it is, the more likely it is that the government will fall, peacefully in a democratic society, but possibly violently in a non-democratic one. Assessment is done by classifying countries using the following types of governance:
Alternating democracy, Dominated democracy, De facto one-party state, De jure one-party state, and Autarchy.
L. Bureaucracy quality
Assesses the institutional strength and quality of the bureaucracy. Countries that lack the cushioning effect of a strong bureaucracy are considered worse because a change in government can be traumatic in terms of policy formulation and day-to-day administrative functions.