1. Introduction
What development societies take in historical terms hinges, it may be argued, on their capacities and their incentives to introduce or adopt new technologies, not only in processing economic resources, but also with respect to hygiene, medicine, and warfare. The incentives may be contingent on the particular conditions of the societies' geographic environment – a conjecture, recently popularized by Diamond (Reference Diamond1997). But the institutions that societies are able to create also matter for the incentives, and even more so the capacity, to develop, support, and handle innovative technologies. This idea has been shared, despite controversial views in other respects, by such diverse authors as Veblen (Reference Veblen1899, Reference Veblen1914) and F. A. Hayek (Reference Hayek and Hayek1967a, Reference Hayek and Hayek1967b, Reference Hayek1971, Reference Hayek1979, Epilogue; Reference Hayek1988) in his later work. Like Veblen, Hayek developed a Darwinian, naturalistic view on both human institutions and their implications for economic history. Such an approach differs fundamentally from more recent works on competitive economic growth in the very long run in which the idea of competition between human societies is dressed up as a story of optimal choices that societies are supposed to make on the basis of hypothetic aggregate utility functions (cf. Acemoglu, Johnson, and Robinson, Reference Acemoglu, Johnson and Robinson2001; Galor and Moav, Reference Galor and Moav2002).
Unldike Veblen, Hayek tried to cast his conjectures in the form of a more abstract group selection argument, borrowing notions from eugenics (Carr-Saunders, Reference Carr-Saunders1922) and sociobiology (Wynne-Edwards, Reference Wynne-Edwards1962) that emerged more recently. In his theory of societal evolution he emphasized the unique human potential for cultural adaptations through collective, ‘cultural’ learning processes specific to the respective human societies or groups. He claimed that the often unconscious, collective, cultural learning processes form an ontological layer in the development of societies ‘between instinct and reason’ (Hayek, Reference Hayek1971). With regard to its historical origin and evolutionary pace this layer is situated, Hayek argued, between the layers of intentional human choice on the one hand and natural selection on the other. It is at this layer, he believed, that – as an unintended, collective outcome – ‘rules of conduct’ (Hayek, Reference Hayek and Hayek1967a) emerge as basic institutions. Through their impact on incentives and capacities to trade, accumulate, and innovate they should affect population growth and economic prosperity, which, in turn, are the variables driving the group selection process.
However, Hayek's naturalistic group selection approach left many details open. Later commentators therefore argued that there are some vague, incomplete, or even inconsistent features in his view of group selection (Gray, Reference Gray1984; Vanberg, Reference Vanberg1986; Hodgson, Reference Hodgson1991; Witt, Reference Witt, Birner and Van Zijp1994). Although the debate on Hayek's theory of societal evolution has continued (see Bianchi, Reference Bianchi, Birner and van Zijp1994; Vanberg, Reference Vanberg1997; Caldwell, Reference Caldwell2000; Rizzello, Reference Rizzello2000), the role of his group selection argument has not been satisfactorily clarified. The core problem of any group selection hypothesis is the possibility that individual behavior contributing to a selection advantage for the group as a whole is potentially subject to free-riding. Such pro-social behavior usually demands individual sacrifices. Benefitting from, but not contributing to, theses sacrifices – i.e. free-riding – is therefore the individually more favorable strategy whenever this is possible.
In a natural selection environment in which both pro-social behavior and free-riding are genetically determined and inheritable, free-riding has a differential reproductive advantage, if there is no way for group members to discriminate against or exclude free-riders. Their propagation in the gene pool of the group threatens to undermine and eventually wipe out the pro-social behavior that established the selection advantage for the group in the first place. It has been argued that the share of carriers of pro-social behavior in the gene pool of a whole population (made up of several groups) may nonetheless increase. The condition for this to happen is that natural selection between groups in the population favors the growth of groups with strong pro-social behavior sufficiently over that of groups of free-riders (cf. e.g. Sober and Wilson, Reference Sober and Wilson1998; Field, Reference Field2001; Henrich, Reference Henrich2004). Yet, such a process is not sustainable as no group can expand in size indefinitely.
It is highly doubtful, however, whether a natural selection environment is indeed relevant to the discussion of theories about more modern human societies differing in, and competing on the basis of, the institutions that have emerged from their cultural learning processes. In a natural selection environment, the only criterion is differential reproductive success of human groups or societies (whether determined by genetic factors alone or by inherited and acquired, cultural features simultaneously, cf. Boyd and Richerson, Reference Boyd and Richerson1985; Henrich, Reference Henrich2004). Yet in more recent times, changes in institutions and technology and their demographic and/or economic effects happen at time scales significantly shorter than the several human generations that are necessary for natural selection to develop a shaping effect. Moreover, economic progress seems to have enabled most human societies, except a few, traditional ones at the fringes of the developed world, to reach a state of ‘reproductive affluence’. This means that the relationships between group success in terms of (military) power, wealth, or income on the one hand and reproductive success/population growth on the other are no longer as clear as in the natural selection model.
In later formulations of his theory of societal evolution, Hayek (Reference Hayek1988) seems to have acknowledged these facts. He argues that in more modern times, the drivers of group selection and differential growth of societies are imitation and migration. Institutions of more successful societies tend to be imitated by less successful ones. In addition, there is a substantial migration from less successful societies to more successful ones, and an assimilation of migrants into successful societies. However, if this is true, the conditions for pro-social behavior need to be explained differently from the genetic and co-evolutionary approach, because both imitation and targeted (not just random) migration rest at least in part on individual, cognitive reflection and decision making that belong to the ontological layer of human reasoning and rational choice.
The present paper tries to make progress with respect to such an explanation. A game-theoretic model is proposed that accounts for the motivations underlying the adoption of pro-social rules of conduct in the presence of a free-riding temptation. The core feature in this model is a mechanism of acquiring attitudes based on observational learning on the one hand and the rational weighing of own strategies against the experience of other players with newly recognized alternatives on the other. Under these conditions, the chances for the emergence and dissemination of socially contingent attitudes ranging from opportunistic free riding to aggressive moralism towards, and punishment of, rule-breaking behavior can be analyzed. Allowing the interaction probabilities to be biased in a way that favors local subgroups interactions, an additional critical mass condition can be derived without invoking the assumption of a genetic disposition for conformism as in Henrich and Boyd (Reference Henrich and Boyd1998). The critical mass condition turns out to be decisive for the emergence and dissemination of pro-social rules of conduct as an institution in groups that gives these groups a competitive advantage in group ‘selection’.
The reduction to a game-theoretic framework inevitably has to abstract from the details of the historical record of the competition between societies and to argue on the basis of somewhat artificial, idealizing assumptions. Nonetheless, it may help to clarify some generic condition of how societies are able to create and maintain institutions conducive to societal evolution. The paper proceeds as follows. In Section 2, Hayek's views on societal evolution are briefly summarized. A crucial step in developing the logic of ‘group’ selection in more detail is the specification of the cultural learning processes allowing for cognitive insight and inference. We borrow here from social cognitive learning theory, which is briefly outlined in Section 3. Section 4 presents a game-theoretic model for the analysis of the evolutionary process. The results derived from the model are discussed in Section 5. They highlight the role of rules of conduct for the differential growth or decline of different groups, the equivalent in the abstract model of different human societies. Although these results are based on several simplifications, they still allow a more detailed appraisal of Hayek's theoretical conjectures. Section 6 offers a brief conclusion.
2. Spontaneous order and societal evolution
When, in the later part of his academic works, Hayek was developing the foundations of his social philosophy, he was increasingly attracted to evolutionary thought and the Darwinian idea of natural selection operating, in the particular form of group selection, on the human society.Footnote 1 Like his entire social philosophy, his theory of societal evolution is informed by the understanding that the capacity of individual human cognition – despite its uniqueness in nature – is limited. In the domain of societal and economic interactions, the fact that individual knowledge is incomplete, imperfect, and hypothetical in nature has two important implications.
One is that human agents never fully grasp the influence that their own actions have on the scope for, and the limits to, the behavior of other agents. To a certain extent, these effects are transmitted, in an impersonal form, through the price mechanism as is well-known to economists. The other, related, implication is that human agents regularly have difficulties in anticipating the full range of possible behaviors with which they may be confronted by other members of society. The lack of reliable expectations about the outcome of interactions, which might paralyze the willingness to engage in them, is prevented by the emergence of an impersonal system of rules of conduct (Hayek, Reference Hayek and Hayek1967a). Since the complexity of both the price mechanism and systems of rules of conduct make it extremely difficult for the human mind to comprehend both, they cannot be the result of deliberate design and choice. Rather, these forms of coherent behavior, i.e. the ‘spontaneous order’, must have emerged from the interactions of all members of society as a largely unintended and unplanned outcome.
The coordination of individual behavior in the economic and political context is thus seen as a phenomenon similar to the inter-individual coordination that turns up in, and is brought about by, language, tradition, morality, custom, and law.Footnote 2 Eager to establish an approach that is built on the ‘twin ideas of spontaneous order and evolution’, Hayek (Reference Hayek1979) distinguishes between three ontological layers at which the development of human society takes place. The first layer is that of biological evolution during human phylogeny. At this level, primitive forms of social behavior, values, and attitudes became genetically fixed as a result of natural selection processes. The criterion that governed that genetic adaptation was fitness for survival under the particular conditions prevailing in the environment. An observable order of social interactions emerged as a result of which sociobiology provides the explanatory model. Once they were genetically established, these attitudes and values have continued to be part of the natural endowment of modern humans, even though biological selection pressure has now been largely relaxed. The second layer of evolution is that of human intelligence and its products, i.e. knowledge and the numerous ways of recording, transmitting, and processing it. The systematic propagation, elaboration, and storing of knowledge, which is independent of the existence of any individual human brain, has made possible an enormously accelerated scientific and technological progress and a mastery of nature as no other species has ever achieved it.
The two layers of evolution mentioned so far – ‘instinct and reason’ – are widely acknowledged as rather independent, and significantly differing sources of evolution in the human domain. However, Hayek claims – and he considered this the genuine contribution of his own theory – that there is a third, and frequently overlooked, ontological layer of evolution, a layer between instinct and reason at which cultural evolution takes place (Hayek, Reference Hayek1971, Reference Hayek1988: chapter 1). From this cultural evolutionary process, the rules of conduct, morals, and traditions emerge that shape human interactions into the orderly forms of civilization.
The cultural evolutionary process goes on, Hayek holds, since the times of the small bands characteristic of the early stages of human phylogeny. In all these times orderly patterns of behavior have been learnt, passed on, and adapted in cultural, not genetic, transmission without much reflection of their meaning. They have been developed into cultural norms without deliberate planning or control. While historical accidents determine what new forms of rule-following behavior arise within the group, which of these survive and are successful is not a matter of chance, but of a selection process. More precisely this is a process of group selection where different rules may allow differential growth of the groups as a result of, e.g., more successful procreation and integration of outsiders. A growing population fosters specialization and the division of labor, which, in turn, favor groups with the superior rules. By the same logic, groups that do not adopt appropriate rules, whether by inventing or by imitating them, are likely to decline. Through this selection process, the rules of conduct, norms, and morals that eventually prevail are suited for the survival of an increasing number of members of the group.
Hayek thus interprets natural selection as occurring not only between competing species but also between competing groups of humans – and later entire societies – defined by common cultural norms. However, the actual transmission process differs between the case of competing species and the case of competing human societies. At the layer of evolution between instinct and reason Hayek envisages a cultural learning process in which a kind of collective intelligence is accumulated in a population in the form of rules of behavior. Compared to the process of genetic variation that occurs through generational change, rules of conduct and cultural norms can be acquired and transmitted much faster. As the population size has grown significantly in the more recent times, the rules themselves have become more and more differentiated and abstract. They have eventually led to the anonymous extended order of the world-wide interconnected markets that, Hayek (Reference Hayek1988: chapter 3) argues, have made civilization and exceptional prosperity possible.
In its somewhat sketchy state, Hayek's theory of societal evolution and spontaneous order leaves several questions open. The selective transmission of group-specific rules of conduct is argued to result from ‘cultural learning’ and imitation – both seen as largely unconscious processes. But how, precisely, are these supposed to work? To what extent do they interact with genetic fitness and reproductive success (as they are interpreted to do, e.g., in the theory of co-evolution of genes and culture in Boyd and Richerson, Reference Boyd and Richerson1985)? Similarly, with respect to his group selection hypothesis, it is unclear how that kind of selection is supposed to work. Is it a modified version of ‘Social Darwinism’ (as Gray, Reference Gray1984: 140–145 has called it) in which the differential growth of competing groups is to be attributed to comparative advantages in producing descendants or attracting members from competing groups into the own group?Footnote 3
3. Observational learning and the rules of conduct
A way to improve the foundations of a theory of societal evolution based on the notion of collective, cultural learning processes situated ‘between instinct and reason’ is to elaborate in more detail the process of learning and its social or cultural contingencies. As will be argued in this section, learning has a social dimension and this dimension is decisive for understanding the spontaneous emergence of rules of conduct as a tacitly shared feature within groups of intensely interacting individuals. The point to start from are the limitations of human perception, information processing, and knowledge. Individual decision makers cannot completely grasp the multitude of imaginable series of choices that unfold into the future. Perceptions, and even more so, cognitive reflections are selective. They are based on partial and fallible knowledge of what is relevant for evaluating alternatives. Given that choices can only be made between alternatives that have been recognized, it seems only natural, therefore, to ask to what extent, and in which way, individual choice may be biased by selective knowledge acquisition and recall.
A key role is played here by selective attention processes which, in turn, depend on three features of information offered to the mind.Footnote 4 The first is sensory strength and frequency of the stimuli carrying the information. The second feature is whether similarities or an identity with already known elements/patterns can be recognized. (For this purpose relevant patterns stored in the memory must be activated by appropriate cues on an associative basis.) The third feature is the affective or emotional value of recognized similarities/identities in the sense of an association with earlier rewarding, neutral, or aversive experience. The cues instrumental for memorizing patterns and identifying incoming information also occur in larger and more complex systems called frames. These are employed in classificatory and associative activities and allow knowledge to be represented in a meaningful way. The associative capacity of the human mind is able to create longer and longer associative chains with increasingly more complex sets of frames from a limited number of probable genetically coded cues. This development starts in individual socialization, in the learning of language, and in the identification of meaning. As a consequence, the human mind always ‘frames’ information with already existing interpretation patterns (knowledge representations) even on the level of deliberate reasoning and thus produces mental attitudes of a sometimes fairly rigid nature.
The necessarily selective cognitive development, although entirely internal to the individual and in this sense subjective, is molded in social processes of communication with other agents (Bandura Reference Bandura1986, ch. 2). In the communication process, individuals tend to develop similarities in interpretation patterns and frames. Communication circles have an ‘agenda setting’ effect, which modifies in a self-reinforcing way that is similar for all, the frequency with which particular information is – at the expense of potentially rivaling information – exchanged and attracts attention. In addition, agents who belong to the same social environment are exposed to the same symbolic representation of knowledge, which often suggests similar mental attitudes. They therefore tend to agree more closely about what are rewarding or aversive experiences. Despite the subjectivity of the individuals' unique cognitive history, these common features mean that a tacit, collectively shared, bias can occur within groups of intensely interacting individuals, a bias that influences what actions are selectively perceived, and what are not, as alternatives.
There is thus a socially shaped bias in the individuals' perception of their choice sets. Common beliefs and interpretations emerge tacitly and similarly for the agents in the population. The agents do not normally recognize the fact that, due to their selective information processing, potential choices go unnoticed, because the cognitive system that processes some information cannot at the same time reflect on how that information is processed. As a consequence, the tacit commonalities in perceiving and framing information are neither consciously chosen nor available for deliberate design. Although a precondition of reasoning, they cannot in their entirety themselves be subject to reason. They originate from the innate limitations of the human cognitive system, but, as they develop in a process of social cognitive learning, they are not in themselves genetically determined, that is a matter of instinct. As a basic element of (population-specific) culture they indeed belong to the layer ‘between instinct and reason’.
Tacitly socially shared constraints in the perception of alternatives can be expected to result in some similarities of individual choices. There is little motivation to deviate from such similarities as long as the individually experienced consequences of similar behavior do not systematically diverge – which is unlikely to happen given the coherence also of response patterns implied by the similarities in the framing of information and in mental attitudes. For this reason, individual learning from experience should not, in principle, cancel out the effects of tacit cognitive commonalities. In fact, in the form of observational learning, the process of learning from behavioral feed back has itself a social dimension that reinforces, and creates further, cognitive commonalities (cf. Bandura Reference Bandura1986; chapter 2). The actions chosen by the agents and the consequences they experience can usually be observed by others. Those others can thus expand their knowledge about actions and consequences without bearing the risks and costs of experimenting themselves. Inferences with respect to success or failure of certain actions may appear the more meaningful to those agents, the more significant the respective actions of others qualify as models of behavior (which they do when occurring in a sufficiently stereotypical and persistent manner).
Because of its vicarious character, the ‘model’ of behavior given by some agent(s) and the associated consequences are likely to attract significant attention. Within one and the same population of intensely communicating agents, observational learning focuses on much the same ‘model’ and, therefore, tends to produce correlated results. This, in turn, ensures that such a ‘model’ becomes an important part of collectively shared knowledge. New and old members of a population – as well as the scientific observer – identify the behavioral regularity and its contingencies and consequences more easily than the underlying cognitive commonalities in the subjective sphere. For this reason, generalizations tend to be made at the phenomenological level: the commonly observed behavioral regularity starts to figure as a ‘social model’, to use Bandura's terminology, and the more frequently some social model occurs in a population, the more convincingly it may be inferred to be a representation of a ‘rule of conduct’ in Hayek's terminology.Footnote 5
While tacit, socially shared, cognitive frames are instrumental to the emergence of rules of conduct, the actual variety of subjective knowledge and interpretations may be decisive for understanding the further development of those rules, their perseverance or decline. Variety results, first, from the particularities of the individual learning histories, from ambiguities in associating meaning with one and the same information, or simply from misconceptions. Second, it results from reflection, inventive thinking, and from accidental discovery of choices not perceived earlier, which enable the agents to create novel choices and actions and to widen their knowledge experimentally. At the individual level, subjective variety allows the agents to gradually shift cognitive constraints and to deviate from earlier patterns of behavior, possibly even from established rules of conduct. Variety of behavior within the population thus increases, and rules may be violated. This is very likely to arouse the attention of other group members who directly observe the deviation, and a communication process is likely to be triggered by which the news of novel choices and actions disseminate. Success or failure of the deviating behavior crucially hinges on the reaction of the social environment, i.e. on how, and on how many, group members respond to the deviation. Given the form and intensity of the collective reaction, however, the group members may be induced to start a (re-) appraisal of their own behavior in the light of the innovator's vicarious success or failure. As long as the population members at least roughly agree on what is a success or a failure, the innovator's fate tends to, respectively, induce or inhibit corresponding behavior adjustments by imitation (Bandura, Reference Bandura1986: chapter 7).
The consequences of the innovator's deviation are thus contingent on two different effects. One is the direct effect represented by individual response of those group members being faced with the innovator as their opponent and with her or his deviating behavior – a strategic response that lends itself to a game-theoretic analysis. The other, indirect effect is induced by those group members who do not directly interact with the innovator but, after observing success or failure of her or his innovative strategy in the interaction with others, change their own behavior autonomously. This effect is a matter of observational learning. Both these reactions will be discussed in more detail in the next section. They jointly decide on whether behavioral variety is increasing or decreasing. They may well stabilize the actual degree of variance within narrow bounds. At the same time, both cognitive commonalities and behavioral regularities within the population, i.e. the rules of conduct, may be subject to continuing change.Footnote 6
4. The analytic representation of ‘rules of conduct’ and ‘groups’
When a member of a group is observed to deviate from a rule of conduct (or prevailing social model), the outcome of such a transgression is likely to arouse the attention of other group members. As argued in the preceding section, the outcome is determined by the responses of the members of the population involved in direct interactions with the innovator. It ultimately depends on what the currently prevailing rules of conduct imply as a response to deviant behavior. A dependency like this suggests a game-theoretic analysis. In such an analysis, a rule of conduct can be given the meaning of an equilibrium point of the underlying game. Accordingly, the question of what kind of rule of conduct emerges and persists, or changes, can be reformulated as the question of what solution originates from certain types of games, given the particular behavioral hypotheses about strategy choices and observational learning.
A typical example of a ‘rule of conduct’ within a group of interacting agents is the ‘convention’ resulting as equilibrium point in a coordination game (see, e.g., Boyer and Orléan, Reference Boyer, Orléan and Witt1993; Young, Reference Young1993) or the non-cooperative solution in a one-shot prisoner's dilemma game. Since the latter, in contrast to the former, has a devastating impact on societal evolution, it represents the case of a destructive rule of conduct that Hayek seems to have neglected – perhaps because he believed that societies unable to prevent the spreading of destructive rules of conduct are bound to decline and eventually disappear. Indeed, if such a rule of conduct becomes endemic in a society whenever social dilemmas occur, this is likely to threaten both the productivity and the competitiveness of that society. Hence, the focus will here be on the generic conditions under which, in social dilemma situations, either pro-social, cooperative ‘rules of conduct’ or destructive ones will emerge within a society. To make the case as strong as possible, conditions coming close to those in large, anonymous societies will be assumed.
Thus, imagine a large group of players who cannot recognize each others' performance. Let always two players be drawn at random to engage in a one-shot prisoner's dilemma game (pd-game). As is well known, if all players chose their strategies rationally (given the way they selectively perceive their choices), the result would be mutual defection. However, an entirely isolated interaction as in a one-shot pd-game may be a rather rare situation, even in large societies. For pd-games that are sufficiently frequently repeated to be recognized by each player as a series requiring interconnected strategic choices, it is well known from the ‘folk theorem’ that every solution from continued defection to continued cooperation can result as a solution of the repeated game. Yet, this continued social dilemma may be considered an equally extreme case as the pure one-shot game and, hence, not representative either of the way in which social dilemmas occur in large societies.
A more realistic, intermediate case will therefore be assumed here to explore how pro-social, cooperative rules of conduct for social dilemmas can emerge. This is the case of a singular interaction (still an encounter without recall) in which, however, the spatial proximity or the institutional set-up allow both players to ‘get after’ their opponent at some cost, if they want to. Getting after the opponent here means taking a singular subsequent action rewarding or punishing the opponent, e.g. by expressing gratitude with a small gift or by beating up someone who has betrayed, or by suing an opponent in court even if there is no chance to recuperate the expenses.Footnote 7 Thus, consider a symmetric pd-game with two randomly matched players i and j that is extended into two-stages as follows. In the opening stage, a choice has to be made between the moves c (cooperate) and d (defect) simultaneously. In a second, closing stage, the pay-offs of the choices in the first stage are revealed and the option to react, e.g. by imposing a penalty costly to both players on the opponent is given to both players. To keep things simple, let there be just two simultaneous moves in the second stage, p (punishing the opponent) and a (accepting the outcome of the first stage without taking the response option).Footnote 8 By assumption, the interaction between the two players in this particular two-stage game then ends, and the pay-offs for the second stage are revealed. Hence, each player has two choices in the opening stage and four contingent choices in the closing stage. The two-stage game is characterized by eight contingent strategies per player and sixteen outcomes or combinations of strategies of both players (see the extensive form of the game in Figure 1).Footnote 9

Figure 1. Prisoner's Dilemma with Punishment Option in Extensive Form (for omitted contingent strategies see Footnote 8)
Let the contingent strategies for player i be denoted by {x, y} where x ∈ {c, d} and y ∈ {a|x, p|x}. The outcomes accruing to the players from their contingent strategies are determined by summing the pay-offs of the first and second stage of the game. With respect to the first stage, the standard pd-game order relation on the pay-offs is assumed. If T (‘temptation’) denotes defection while the opponent cooperates, R (‘reward’) denotes mutual cooperation, P (‘punishment’) denotes mutual defection, and S (‘sucker's pay-off’) denotes cooperation while the opponent defects, this means that
With regard to the second stage pay-offs, it will be assumed that no additional costs arise to any player by choosing move a. However, choosing move p, usually invokes costs on both sides, i.e. on those who take punishing measures and on those being punished. To consider the least favorable case, let the costs Cp incurred by a punishing player be larger than the cost Co incurred by the punished opponent. Moreover, to push the argument to its limits and to make conditions for the emergence of cooperation as hard as possible, assume that punishment causes such heavy costs that in addition to relation (1) the following holds
The game-theoretic setting developed so far is designed to discuss what rule of conduct will emerge in social dilemmas under what conditions. A different, but related, question is whether different rules of conduct affect the survival and growth of the groups that adopt them. To be able to deal with this question the individualistic game-theoretic framework needs to be extended by a proper analytic representation of the concept of ‘groups’ or ‘societies’ (the terms used interchangeably here).
In the context of modern human societies, ‘group selection’, i.e. a differential growth of group size, is more a matter of differences in migration rates between groups or societies than a matter of differential reproductive success. Migration presupposes two things: a spatial dimension in which groups are separated from each other and some minimal form of spatial interconnectedness or neighborhood within groups. In an abstract way, these conditions may be captured by assuming that a human population made up of n agents, indexed i = 1,. . .n, is scattered over a spatial dimension. For expository convenience, let n be a large, but constant, odd number. To simplify the analysis of the diffusion of new strategies, a one-dimensional space is sometimes assumed in game-theoretic models (Boyer and Orléan, Reference Boyer, Orléan and Witt1993; Eshel, Sansone, and Shaked, Reference Eshel, Sansone and Shaked1999) so that the interacting agents are represented by n points on a line. Without loss of generality, the line can be arranged into a closed circle so that no bordering cases need to be considered. In this abstract setting, the population on the circle may either be taken to represent a single group, provided it is structured in such a way that proximity between group members matters, or the union of all groups or societies. Both representations will be used further below. For the present let us look into the latter case more closely.
If the spatial distribution of all groups is represented by the circle, each single group in the union corresponds to a closed subset of points on (a segment of) the circle. This means that each agent i has more or less close neighbors to the left and to the right that are either members of her own or other groups. The spatial proximity of any two agents i and j can be expressed by the number of points between them. If each agent belongs to just one group, all groups together form a complete partitioning of the circle. Agents are assumed to interact with each other with a probability that depends on spatial proximity (the very reason why space is accounted for here). To strengthen the argument, suppose that the interaction probability hinges on proximity alone, i.e. not on group membership, and that the agents are unable to discriminate between individuals even within their group (the least favorable assumptions for the emergence of a cooperative rule of conduct). It seems reasonable then that the probability of an agent i being matched with any other agent j in an interaction decreases with the distance between i and j. It may become zero once a critical distance r, (n – 1)/2 ≥ r ≥ 1, to the left or to the right of agent i is exceeded. (Interactions of an agent i with other agents have an equal chance of occuring on the left side or the right side of i).
Consider an agent who is h points away from i, either to the left or to the right. The probability pi,h of an interaction of agent i with that agent can then be given as
On either side of agent i, Σh pi,h =![]() . For reasons that will become apparent later (see the appendix) it is useful to define a neighborhood N adjacent to agent i on one side by a segment of k points on the circle. By summing over (3) one gets
. For reasons that will become apparent later (see the appendix) it is useful to define a neighborhood N adjacent to agent i on one side by a segment of k points on the circle. By summing over (3) one gets
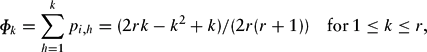
with 0 < Φk ≤ ![]() for 1 ≤ k ≤ r. Φk gives the probability for an interaction of agent i within a neighborhood of size k to the right or to the left.
for 1 ≤ k ≤ r. Φk gives the probability for an interaction of agent i within a neighborhood of size k to the right or to the left.
5. The evolution of rules of conduct and the differential growth of groups
On the basis of the assumptions introduced in the previous section, the two core problems of Hayek's theory of societal evolution can now be discussed in more detail. The first problem revolves around the question of what rules of conduct will emerge and survive within groups during societal evolution. More specifically, can pro-social behavior really be expected if societal evolution is faced with social dilemmas? In terms of the two stage pd-game above, this objection translates into the question: are there any cooperative contingent strategies able to emerge and survive and, if so, under what conditions? Obviously, both emergence and survival hinge on the state of the environment, i.e. the initial composition of strategies present in a population. This is called the ‘occupancy effect’ in evolutionary biology.Footnote 11 The effect is of crucial importance also in the context of a socially learned behavior.
As has been explained above, collectively shared cognitive constraints can only give rise to, and observational learning can only operate on, behavioral regularities to the extent to which they can be observed in the population. In the game-theoretic model, this means that, in order to learn about the (dis-)advantage of some so far unknown contingent strategy, there must be an innovator who introduces it into the population in the first place. The comparative (dis-)advantage is then revealed by a difference in the outcomes accruing to the innovator's strategy on the one hand and the (established) strategy of the opponent on the other. Consequently, to assess the prospects for the cooperative rules of conduct to indeed survive and disseminate in the repeated playing of the game, we can explore whether, and in what occupancy setting, these combinations of strategies persist.
The criterion that can be used for this assessment is the ‘evolutionary stability’ of a particular strategy in a game played by the members of a population.Footnote 12 An evolutionary stable strategy is a strategy that, if prevailing in a group, cannot be invaded by a deviating strategy s. More precisely, denote two (possibly mixed) strategies by e and s, and their expected pay-off by E(π(l, m)), where l, m ∈ {e, s}. Then, e is an evolutionary stable strategy if and only if either E(π (e, e)) > E(π (s, e)) or E(π (e, e)) = E(π (s, e)) and E(π (e, s)) > E(π (s, s)). Accordingly, consider a single group initially characterized by all players playing one and the same strategy.Footnote 13 When, in such a situation, an innovator appears and plays a deviating strategy, several responses are triggered. These responses jointly determine the social learning process and the result in terms of survival or decline of the originally prevailing strategy (i.e. its evolutionary stability).
First, the innovator her/himself learns about the outcome of her/his experiment and reacts to the outcome in her/his future interactions. Since the further development hinges on this reaction, a hypothesis is needed here. A plausible one is the following:
Assumption 1
A player following a new strategy continues to do so as long as this does not result in a lower pay-off than the strategy previously prevailing in the group. If a lower pay-off is obtained, the player switches to the strategy previously prevailing after a few trials resulting in a lower average pay-off.
Second, the innovator's opponent faces a new outcome and may respond to it in future interactions. Third, since the deviation is also likely to attract attention elsewhere in the population, the innovator's experiment becomes an object of observational learning. This means that the pay-off realized with the deviant strategy is also observed by members of the population who have not been directly confronted (and are probably not in close proximity to the innovator). They may rate the vicarious pay-off against that of the currently prevailing strategy. Sooner or later this can induce spontaneous strategy changes (imitation) elsewhere in the population. Again an explicit hypothesis is needed:
Assumption 2
Players who either are directly confronted with, or observe from outside, a new strategy introduced to the group adopt it:
– with probability zero, if it yields a pay-off no higher than that of the strategy previously prevailing;
– with a probability ≥ 0 that varies monotonously with a difference ≥ 0 between the pay-off of the new strategy and that of the previously prevailing strategy.
Assumptions 1 and 2 taken together imply a stochastic replication process. Among the realizations it can take over time, those converging to one of the following stable states are of particular interest here. The innovative strategy can:
• invade the population and disseminate without being adopted by the whole population; in the limiting case only the innovator keeps to it (‘partial invasion’);
• invade and fully disseminate through adoption by the innovator's opponents or through imitation (‘complete invasion’);
• fail to even gain a foothold, if even the innovator abandons it (‘failure’).
On the basis of these explications and assumptions and the logic underlying the notion of an evolutionary stable strategy, the question of whether pro-social, cooperative rules of conduct can indeed emerge and survive within groups during societal evolution can be given the following answer:Footnote 14
Proposition 1
A strategy that is newly introduced by an innovator results in partial invasion, complete invasion, or failure as denoted in Table 1, depending on what strategy prevails in the population.
TABLE 1. Survival and Dissemination of Rivaling Strategies (order numbers refer to the proof)

Since a rule of conduct has been above given, the meaning of an equilibrium point of the underlying game, Proposition 1 implies that, if the new strategy fails to invade, the previously prevailing strategy remains the rule of conduct for the social dilemma in the group. Conversely, if the new strategy completely invades, it becomes the new rule of conduct. Table 1 highlights a few remarkable features of the evolutionary process. A first one is the asymmetry between cooperative and defectionist strategies. Consider the ‘permissive’ cooperative strategy {c; a| c}, {c; a| d} and the ‘aggressive’ cooperative strategy {c; a| c}, {c; p| d}. Under the chosen initial conditions neither of them can even gain a foothold, not to speak of successful dissemination, in an all defectionist social environment (the reasons for this difference are discussed in the appendix). Defection as innovation, by contrast, has much better chances of invading an all cooperative group and of driving pro-social, cooperative behavior to extinction. However, this finding – quite destructive for the chances of a pro-social rule of conduct – needs qualifications. It hinges on a special initial condition as will be explained momentarily.
Another remarkable feature is that there are significant differences in terms of evolutionary stability between the permissive cooperative strategy and the aggressive one. Despite the high costs incurred by punishing an opponent when playing the aggressive cooperative strategy, i.e. to cooperate in the first stage and punish opponent after experiencing defection, this strategy is not equally vulnerable to invasion as the permissive cooperative strategy is. In fact, the latter rule of conduct has no chance of surviving. This seems an important finding: cooperation as a rule of conduct in social dilemmas can resist subversive, defectionist deviations provided it comes in an aggressive form.
The question of what rules of conduct will emerge and survive during societal evolution to which Proposition 1 refers is not the only one relevant for Hayek's theory of societal evolution. A second, equally important, element of his theory, to which we now turn, is the hypothesis of a differential growth process during societal evolution which favors groups adopting pro-social behavior as a rule of conduct. To account for this hypothesis requires to distinguish groups which can grow differentially in the first place. In the previous section, it has been suggested that this can be done by representing a group by a closed subset of points (a segment) of a circle where the circle represents the union of two or more groups. As will turn out now, the possibility of forming distinct groups within a population indeed modifies the selection environment significantly by reducing the advantage of defectionist strategies over pro-social, cooperative strategies that are characteristic of the case of undifferentiated populations.
Consider a group formed by players adjacent to each other in a segment of the circle. Let all members of that group simultaneously introduce a strategy that deviates from the strategy played by the rest of all players. If ‘group selection’ is a process of differential growth of groups, the question arises whether the deviating group is able to profit in terms of its sizeFootnote 15 from its innovation. More specifically, under what conditions is it possible that a group collectively introducing one of the pro-social, cooperative strategies into an otherwise defecting population is favored by group selection? Under the chosen assumptions, the following answer can be provided:Footnote 16
Proposition 2
An aggressive cooperative strategy collectively introduced by a group of players to a defectionist population can result in partial or even complete invasion of the population by this new strategy, if the group size exceeds a critical mass k* > (n–1)/2.
Proposition 2 implies that group selection can favor a group with pro-social, cooperative behavior in social dilemmas even though that group has to interact with groups with defecting behavior. Hence, a cooperative strategy need not be the rule of conduct from the very beginning in order to be an evolutionary stable strategy. This implication of Proposition 2 seems to support Hayek's optimistic view of societal evolution overcoming the perils of social dilemmas. However, it is bound to two strong conditions being satisfied.
First, pro-social, cooperative behavior must be paired with aggressiveness against attempts to exploit cooperation (‘aggressive moralism’). Pro-social behavior must go so far as to be willing to bear the extra costs of punishing a defecting opponent by playing the aggressive strategy {c; p| d}. Proposition 2 does not hold for the permissive cooperative strategy {c; a| d} which fails to be able to invade an otherwise defectionist population, even if introduced by an entire group of agents. Second, the group of aggressive cooperators needs to be large enough so that the relative frequency of being forced to punish and thus to incur the corresponding costs is for each member of the group still bearable. If the group does not make for the majority of the population, the individually born costs of retaliation are too high for the new cooperative strategy to be individually maintained according to Assumption 1. These two contingencies seriously qualify the logical basis for hoping that cooperation can prevail as the rule of conduct for social dilemmas.
6. Conclusions
The theory of societal evolution based by F.A. Hayek in his later work on a group selection argument leaves several important questions open. After identifying the major problems, an attempt has been made in the present paper to dwell on the behavioral foundation of cultural evolution by reference to social cognitive learning theory. On this basis an extended prisoner's dilemma game has been suggested that allows to be more specific with respect to what ‘group selection’ means and under what conditions it can favor pro-social behavior in social dilemmas. The analysis has shown that groups (which, moreover, need to have a critical size) are essential: unless pro-social, cooperative strategies already prevail from the very beginning, they only have a chance to emerge in a non-cooperative world, if collectively adopted by agents belonging to such groups. The cooperative gains such groups can realize may induce migration into those groups and, thus, allow the groups to grow differentially. As was shown, at least in the present model set up, a pro-social, cooperative rule of conduct needs to be paired with a certain ‘aggressiveness’ in order to be able to survive and grow, more precisely, a willingness to bear the costs of punishing attempts to exploit pro-social behavior.
Appendix
A proof of proposition 1 based on the (static) criterion of evolutionary stability can be sketched as follows (in the sequence of the order numbers in the cells of Table 1):
1 Defection strategy entering a population playing permissive cooperation strategy: initially, the innovator obtains T > R with certainty. However, if the defection strategy disseminates, the frequency of {d; a | d} being encountered with {d; a | d} increases and the pay off of defectionist strategy converges to P < R. Since returning to the cooperative strategy would entail R when encountering {c; a | c} and S when playing against {d; a | c}, no player having adopted the defectionist strategy ever switches back to cooperation by Assumption 1. The initially prevailing permissive strategy {c; a | c}, {c; a | d} obtains R when playing against itself and S against the defection strategy. The defection strategy realizes P > S when playing against itself and T > R against the permissive strategy. This means that {c; a | c} and {c; a | d} are dominated under all circumstances. Hence, by Assumption 2, there is a finite waiting time until all players have adopted the defection strategy.
2 Defection strategy entering a population playing aggressive cooperati‘n strategy: initially, the innovator obtains T − Co < R by the order relations (1) and (2). If the defection strategy disseminates, a pay off P > T − Co becomes more frequent. Since returning to cooperation would entail R when playing against the aggressive cooperators and S − Cp when playing against the defectionists, the innovator's future behavior by Assumption 1 hinges on whether defection becomes a frequently played strategy in the population. Consider the initially prevailing aggressive cooperation strategy obtaining R when playing against itself and S − Cp as the innovator's opponent. The player most likely to encounter the innovator and, hence, to switch from cooperation to defection is the innovator's neighbor. Let E(πc) denote the expected outcome of the cooperative strategy and E(πd) the expected outcome of the defectionist strategy. Due to the local structure of interactions reflected by equation (4), the immediate neighbor of the innovating player gets
In case of switching, the neighbor gets Equating both expected values and solving yields
Equating both expected values and solving yields since 0 > T − Co − R > S − Cp − P because of order relations (1) and (2). Hence, it cannot be excluded that the probability Φ1 happens to satisfy the condition Φ1* < Φ1 ≤
since 0 > T − Co − R > S − Cp − P because of order relations (1) and (2). Hence, it cannot be excluded that the probability Φ1 happens to satisfy the condition Φ1* < Φ1 ≤![\begin{equation*}
\rp _1^* = [{ T} - { C}_{ o} - { R}]/[{ T} - { C}_{ o} - { R} + { S} - { C}_{ p} - { P}] < 1/2,\end{equation*}](data:image/gif;base64,R0lGODlhAQABAIAAAMLCwgAAACH5BAAAAAAALAAAAAABAAEAAAICRAEAOw==)
 . (Note, however, that since Φ1 = 1/(r + 1), the condition is the less likely satisfied the larger r.) If so, there is a finite waiting time for the neighbor player to switch to defection according to Assumption 2. If the innovator maintains the new strategy for long enough, incurring the opportunity loss R − (T − Co) in each play, the expected outcome may at best converge to P through the neighbor's switching. Since R > P > T − Co, the innovator may eventually return to the incumbent strategy according to Assumption 1. However, if a neighbor has already switched such a move would amount simply to changing places with the neighbor. While it cannot be excluded that the defection strategy disseminates, if this happens at all, it may therefore be a matter of cyclical convergence. In case 0 < Φ1 ≤ Φ1*, by contrast, switching is excluded so that for the corresponding parameter values defection as an innovation cannot survive.
. (Note, however, that since Φ1 = 1/(r + 1), the condition is the less likely satisfied the larger r.) If so, there is a finite waiting time for the neighbor player to switch to defection according to Assumption 2. If the innovator maintains the new strategy for long enough, incurring the opportunity loss R − (T − Co) in each play, the expected outcome may at best converge to P through the neighbor's switching. Since R > P > T − Co, the innovator may eventually return to the incumbent strategy according to Assumption 1. However, if a neighbor has already switched such a move would amount simply to changing places with the neighbor. While it cannot be excluded that the defection strategy disseminates, if this happens at all, it may therefore be a matter of cyclical convergence. In case 0 < Φ1 ≤ Φ1*, by contrast, switching is excluded so that for the corresponding parameter values defection as an innovation cannot survive.3 Permissive cooperation strategy entering a population playing defection strategy: by order relation (1) the innovator is initially certain of obtaining S < P. Since returning to defection entails P, by Assumption 1 the innovator returns to defection after playing a limited number of times {c; a | d}. The prevailing defectionist strategy obtains P > S against itself and T > S as the innovator's opponent, so that, by Assumption 2, no player other than the innovator will ever adopt the cooperative strategy.
4 Permissive cooperation strategy entering a population playing aggressive cooperation strategy: when playing against the prevailing strategy, the innovative strategy is indistinguishable. Hence, by Assumptions 1 and 2, none of the players could be induced to adopt the new strategy.
5 Aggressive cooperation strategy entering a population playing defection strategy: initially, the innovator realizes S − Cp < P. If the defection strategy disseminates, a pay off R > P becomes more frequent. Since returning to defection would entail P when playing against the defectors and T − Co when playing against aggressive cooperators, the innovator's future behavior according to Assumption 1 hinges on whether aggressive cooperation becomes a frequently played strategy in the population. Consider the initially prevailing defection strategy obtaining P when playing against itself and T − Co as the innovator's opponent. By switching to the aggressive cooperative strategy S − Cp can be realized against defectionists and R > T − Co against cooperating players. Again a critical value
can be derived. This means that no value Φ1 ∈ (0,![\begin{equation*}
\Phi _1^{**} = [{ S} - { C}_{ p} - { P}]/[{ S} - { C}_{ p} - { P} + { T} - { C}_{ o} - { R}] > {\textstyle\frac{1}{2}}
\end{equation*}](data:image/gif;base64,R0lGODlhAQABAIAAAMLCwgAAACH5BAAAAAAALAAAAAABAAEAAAICRAEAOw==)
 ) exists such that a switch would be advantageous. Since the innovator is to return to playing defection by Assumption 1, the aggressive cooperation strategy cannot survive.
) exists such that a switch would be advantageous. Since the innovator is to return to playing defection by Assumption 1, the aggressive cooperation strategy cannot survive.6 Aggressive cooperation strategy entering a population playing the permissive cooperation strategy: when playing against the incumbent strategy, the innovative strategy is indistinguishable. Hence, by Assumptions 1 and 2, none of the players could be induced to adopt the new strategy.
The proof of proposition 2 can be sketched as follows:
Assume all players in a segment of the circle that represents the group with at least two members simultaneously introduce the aggressive cooperative strategy. Accordingly, n > 2. Outside the group, defection is the prevailing strategy. A group member's pay-off from an interaction depends on whether it is an in-group or an out-group interaction. The group members at the edge of the segment on the circle profit least from the cooperation gain since, by assumption, they interact equally likely on either side. Cooperative players at the edge are therefore most likely to switch back to defection. The expected outcome of playing the aggressive cooperative strategy for such a player is
given that the innovating group has k+1 members.
Should that player switch back to defection, the expected outcome would be
Equating both values and solving yields
Hence, by equation (4) no number k ≤ r exists so that E(πd) ≤ E(πc). By Assumption 2, the cooperative players at the edge of the segment on the circle are to switch back in finite time to defection, while none of their neighbors not belonging to the group is likely to imitate the innovation. If k > ![]() , however, the respective expected outcomes are
, however, the respective expected outcomes are
![\begin{array}{l}
{ E}({ \pi }_{ c} ) = {\textstyle\frac{1}{2}}\,{ R} + \rp _{ k} ({ S} - { C}_{ p} ) + \big({\textstyle\frac{1}{2}} - \rp _{ k}\big)\,{ R}\,{\rm and} \\[4pt]
{ E}({ \pi }_{ d} ) = {\textstyle\frac{1}{2}}({ T} - { C}_{ o} ) + \rp _k \,{ P} + \big({\textstyle\frac{1}{2}} - \rp _{ k}\big)({ T} - { C}_{ o} ). \\
\end{array}](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151027131442168-0327:S1744137407000823_eqnU8.gif?pub-status=live)
In view of order relations (1) and (2), this means that E(πc) > E(πd). A critical number of group members k* > (n − 1)/2 exists such that, once k* has been exceeded, all players initially following the defection strategy will eventually switch to the aggressive cooperation strategy.




