2.1 Formulation based on the autocovariance of generalised flow stresses

Following Goldstein & Leib (Reference Goldstein and Leib2008), time-averaged, Favre-averaged mean-flow and fluctuation variables are introduced,

(2.1a-d ) $$\begin{eqnarray}\unicode[STIX]{x1D70C}^{\prime }=\unicode[STIX]{x1D70C}-\overline{\unicode[STIX]{x1D70C}},\quad p^{\prime }=p-\overline{p},\quad h^{\prime }=h-\overline{h},\quad v_{i}^{\prime }=v_{i}-\overline{v}_{i},\end{eqnarray}$$

where $\unicode[STIX]{x1D70C},p,v$ and $h$ refer to density, pressure, velocity and enthalpy respectively; primes denote fluctuations, and bars and tildes correspond to time and Favre averaging.

By defining the new dependent variables

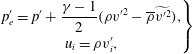(2.2) $$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\displaystyle p_{e}^{\prime }=p^{\prime }+\frac{\unicode[STIX]{x1D6FE}-1}{2}(\unicode[STIX]{x1D70C}v^{\prime 2}-\overline{\unicode[STIX]{x1D70C}}\widetilde{v^{\prime 2}}),\\ \displaystyle u_{i}=\unicode[STIX]{x1D70C}v_{i}^{\prime },\end{array}\right\} & & \displaystyle\end{eqnarray}$$

the governing Navier–Stokes equations are exactly rearranged to

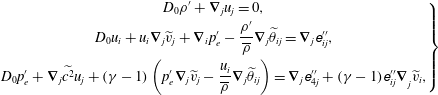(2.3) $$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\displaystyle D_{0}\unicode[STIX]{x1D70C}^{\prime }+\unicode[STIX]{x1D735}_{j}u_{j}=0,\\ \displaystyle D_{0}u_{i}+u_{i}\unicode[STIX]{x1D735}_{j}\widetilde{v}_{j}+\unicode[STIX]{x1D735}_{i}p_{e}^{\prime }-\frac{\unicode[STIX]{x1D70C}^{\prime }}{\overline{\unicode[STIX]{x1D70C}}}\unicode[STIX]{x1D735}_{j}\widetilde{\unicode[STIX]{x1D703}}_{ij}=\unicode[STIX]{x1D735}_{j}\unicode[STIX]{x1D626}_{ij}^{\prime \prime },\\ \displaystyle D_{0}p_{e}^{\prime }+\unicode[STIX]{x1D735}_{j}\widetilde{c^{2}}u_{j}+(\unicode[STIX]{x1D6FE}-1)\left(p_{e}^{\prime }\unicode[STIX]{x1D735}_{j}\widetilde{v}_{j}-\frac{u_{i}}{\overline{\unicode[STIX]{x1D70C}}}\unicode[STIX]{x1D735}_{j}\widetilde{\unicode[STIX]{x1D703}}_{ij}\right)=\unicode[STIX]{x1D735}_{j}\unicode[STIX]{x1D626}_{4j}^{\prime \prime }+(\unicode[STIX]{x1D6FE}-1){\unicode[STIX]{x1D626}_{ij}^{\prime \prime }\unicode[STIX]{x1D735}}_{j}\widetilde{v}_{i},\end{array}\right\} & & \displaystyle\end{eqnarray}$$

where

(2.4a,b ) $$\begin{eqnarray}\unicode[STIX]{x1D735}_{j}=\frac{\unicode[STIX]{x2202}\cdot }{\unicode[STIX]{x2202}y_{j}},\quad D_{0}=\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}\cdot +\unicode[STIX]{x1D735}_{j}(\widetilde{v}_{j}\cdot )\end{eqnarray}$$

and

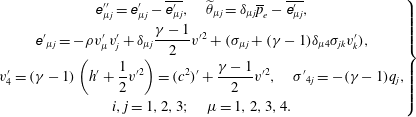(2.5) $$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\displaystyle \unicode[STIX]{x1D626}_{\unicode[STIX]{x1D707}j}^{\prime \prime }=\unicode[STIX]{x1D626}_{\unicode[STIX]{x1D707}j}^{\prime }-\overline{\unicode[STIX]{x1D626}_{\unicode[STIX]{x1D707}j}^{\prime }},\quad \widetilde{\unicode[STIX]{x1D703}}_{\unicode[STIX]{x1D707}j}=\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D707}j}\overline{p}_{e}-\overline{\unicode[STIX]{x1D626}_{\unicode[STIX]{x1D707}j}^{\prime }},\\ \displaystyle {\unicode[STIX]{x1D626}^{\prime }}_{\unicode[STIX]{x1D707}j}=-\unicode[STIX]{x1D70C}v_{\unicode[STIX]{x1D707}}^{\prime }v_{j}^{\prime }+\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D707}j}\frac{\unicode[STIX]{x1D6FE}-1}{2}v^{\prime 2}+(\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D707}j}+(\unicode[STIX]{x1D6FE}-1)\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D707}4}\unicode[STIX]{x1D70E}_{jk}v_{k}^{\prime }),\\ \displaystyle v_{4}^{\prime }=(\unicode[STIX]{x1D6FE}-1)\left(h^{\prime }+\frac{1}{2}v^{\prime 2}\right)=(c^{2})^{\prime }+\frac{\unicode[STIX]{x1D6FE}-1}{2}v^{\prime 2},\quad {\unicode[STIX]{x1D70E}^{\prime }}_{4j}=-(\unicode[STIX]{x1D6FE}-1)q_{j},\\ i,j=1,2,3;\quad \unicode[STIX]{x1D707}=1,2,3,4.\end{array}\right\} & & \displaystyle\end{eqnarray}$$

In the above equations, Einstein summation is implied, $\unicode[STIX]{x1D70E}_{ij}$ and $q_{j}$ are the viscous stress and heat flux respectively, $\widetilde{c^{2}}$ is the square of the mean-flow sound speed, which is used to define the corresponding fluctuation, $\widetilde{\unicode[STIX]{x1D703}}_{ij}$ is the total mean-flow stress tensor and $\unicode[STIX]{x1D626}_{\unicode[STIX]{x1D707}j}^{\prime \prime }$ is the generalised fluctuating stress tensor. It should be noted that the latter $(4\times 3)$ tensor includes both the fluctuating Reynolds stresses and the fluctuating enthalpy vector. This is the same term that appears as a separate source component in other formulations of the generalised acoustic analogy (Goldstein Reference Goldstein2002, Reference Goldstein2003, Reference Goldstein2011).

By introducing the far-field microphone and the jet flow coordinates, $\boldsymbol{x}$ and $\boldsymbol{y}$ respectively, the spectral density of the far-field pressure signal can be expressed as the acoustic integral

(2.6) $$\begin{eqnarray}S(\boldsymbol{x},\unicode[STIX]{x1D714})=\int _{V_{y}}\int _{V_{\unicode[STIX]{x1D6E5}}}\hat{\unicode[STIX]{x1D619}}_{\unicode[STIX]{x1D707}jkl}(\boldsymbol{y},\unicode[STIX]{x1D71F},\unicode[STIX]{x1D714})\hat{\unicode[STIX]{x1D6FE}}_{\unicode[STIX]{x1D707}j}(\boldsymbol{y},\unicode[STIX]{x1D714}|\boldsymbol{x})\hat{\unicode[STIX]{x1D6FE}}_{kl}^{\ast }(\boldsymbol{y}+\unicode[STIX]{x1D71F},\unicode[STIX]{x1D714}|\boldsymbol{x})\,\text{d}\unicode[STIX]{x1D71F}\,\text{d}\boldsymbol{y}\end{eqnarray}$$

of the generalised stress tensor autocovariance

(2.7) $$\begin{eqnarray}\hat{\unicode[STIX]{x1D619}}_{\unicode[STIX]{x1D707}jkl}(\boldsymbol{y},\unicode[STIX]{x1D71F},\unicode[STIX]{x1D714})=\int \unicode[STIX]{x1D619}_{\unicode[STIX]{x1D707}jkl}(\boldsymbol{y},\unicode[STIX]{x1D71F},\unicode[STIX]{x1D70F})\text{e}^{-\text{i}\unicode[STIX]{x1D714}\unicode[STIX]{x1D70F}}\,\text{d}\unicode[STIX]{x1D70F}.\end{eqnarray}$$

Here, $\unicode[STIX]{x1D619}_{\unicode[STIX]{x1D707}jkl}(\boldsymbol{y},\unicode[STIX]{x1D71F},\unicode[STIX]{x1D70F})=\overline{{\unicode[STIX]{x1D626}^{\prime \prime }}_{\unicode[STIX]{x1D707}j}(\boldsymbol{y},\unicode[STIX]{x1D70F}){\unicode[STIX]{x1D626}^{\prime \prime }}_{kl}^{\ast }(\boldsymbol{y}+\unicode[STIX]{x1D71F},t+\unicode[STIX]{x1D70F})}$ is the generalised stress tensor autocovariance in the time domain, where the overbar means averaging over time $t$ , $i,j=1,2,3$ and $\unicode[STIX]{x1D707},k=1,2,3,4$ .

It is the time-domain generalised stress tensor autocovariance that can, in principle, be provided from unsteady flow simulations. However, since it is a fourth rank tensor defined over the entire $(6+1)$ -dimensional space–time domain, computation of this quantity is a challenge.

Using the standard Fourier transformation formulae, the same quantity can be related to the frequency-domain representation of the stresses,

(2.8) $$\begin{eqnarray}\hat{\unicode[STIX]{x1D619}}_{ijkl}(\boldsymbol{y},\unicode[STIX]{x1D71F},\unicode[STIX]{x1D714})=\overline{\hat{\unicode[STIX]{x1D626}}_{ij}^{\prime \prime }(\boldsymbol{y},\unicode[STIX]{x1D714})\hat{\unicode[STIX]{x1D626}}_{kl}^{\prime \prime \ast }(\boldsymbol{y}+\unicode[STIX]{x1D71F},\unicode[STIX]{x1D714})},\quad \text{where }\hat{\unicode[STIX]{x1D626}}_{ij}(\boldsymbol{y},\unicode[STIX]{x1D714})=\int \unicode[STIX]{x1D626}_{ij}(\boldsymbol{y},\unicode[STIX]{x1D70F})\text{e}^{-\text{i}\unicode[STIX]{x1D714}\unicode[STIX]{x1D70F}}\,\text{d}\unicode[STIX]{x1D70F}.\end{eqnarray}$$

The other part of the far-field sound integral (2.6) is the propagator operator,

(2.9) $$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\displaystyle \hat{\unicode[STIX]{x1D6FE}}_{ij}(\boldsymbol{y},\unicode[STIX]{x1D714}|\boldsymbol{x})=\unicode[STIX]{x1D735}_{i}\hat{u} _{j}^{a}(\boldsymbol{y},\unicode[STIX]{x1D714}|\boldsymbol{x})+\hat{p}^{a}(\boldsymbol{y},\unicode[STIX]{x1D714}|\boldsymbol{x})\unicode[STIX]{x1D735}_{j}\widetilde{v}_{i}(\boldsymbol{y}),\\ \displaystyle \hat{\unicode[STIX]{x1D6FE}}_{4j}(\boldsymbol{y},\unicode[STIX]{x1D714}|\boldsymbol{x})=-\unicode[STIX]{x1D735}_{j}\hat{p}^{a}(\boldsymbol{y},\unicode[STIX]{x1D714}|\boldsymbol{x}),\end{array}\right\} & & \displaystyle\end{eqnarray}$$

which depends on the corresponding adjoint vector Green’s function, ( $\hat{\boldsymbol{u}}^{a}(\boldsymbol{y},\unicode[STIX]{x1D714}|\boldsymbol{x})$ , $\hat{p}^{a}(\boldsymbol{y},\unicode[STIX]{x1D714}|\boldsymbol{x})$ ). The adjoint vector Green’s function is directly related to the direct tensor Green’s function in accordance with the reciprocal theorem between the solution of the direct sound radiation and the adjoint sound scattering problem (e.g. see Tam & Auriault Reference Tam and Auriault1998; Karabasov Reference Karabasov2010). Compared with solution of the direct sound radiation problem, solution of the adjoint problem for a small number of far-field microphone locations relative to the number of source points is computationally advantageous. In the frequency domain, the latter is determined by the following adjoint linearised Euler equations:

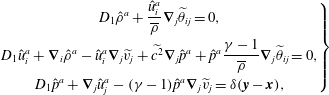(2.10) $$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\displaystyle D_{1}\hat{\unicode[STIX]{x1D70C}}^{a}+\frac{\hat{u} _{i}^{a}}{\overline{\unicode[STIX]{x1D70C}}}\unicode[STIX]{x1D735}_{j}\widetilde{\unicode[STIX]{x1D703}}_{ij}=0,\\ \displaystyle D_{1}\hat{u} _{i}^{a}+\unicode[STIX]{x1D735}_{i}\hat{\unicode[STIX]{x1D70C}}^{a}-\hat{u} _{i}^{a}\unicode[STIX]{x1D735}_{j}\widetilde{v}_{j}+\widetilde{c^{2}}\unicode[STIX]{x1D735}_{j}\hat{p}^{a}+\hat{p}^{a}\frac{\unicode[STIX]{x1D6FE}-1}{\overline{\unicode[STIX]{x1D70C}}}\unicode[STIX]{x1D735}_{j}\widetilde{\unicode[STIX]{x1D703}}_{ij}=0,\\ \displaystyle D_{1}\hat{p}^{a}+\unicode[STIX]{x1D735}_{j}\hat{u} _{j}^{a}-(\unicode[STIX]{x1D6FE}-1)\hat{p}^{a}\unicode[STIX]{x1D735}_{j}\widetilde{v}_{j}=\unicode[STIX]{x1D6FF}(\boldsymbol{y}-\boldsymbol{x}),\end{array}\right\} & & \displaystyle\end{eqnarray}$$

where

(2.11) $$\begin{eqnarray}D_{1}=\text{i}\unicode[STIX]{x1D714}\cdot +\widetilde{v}_{j}\unicode[STIX]{x1D735}_{j}(\cdot ).\end{eqnarray}$$

The solution of these equations can be found by numerically solving the above equations with the delta function source term replaced by an appropriate open-domain radiation boundary condition corresponding to a sink in the far-field observer location (Karabasov & Hynes Reference Karabasov and Hynes2006). The current work, following Tam & Auriault (Reference Tam and Auriault1998) and Semiletov et al. (Reference Semiletov, Karabasov, Chintagunta and Markesteijn2015), uses a simplified semianalytical locally parallel flow approximation to solve the sound mean-flow propagation problem. Briefly, under the locally parallel flow approximation, the jet flow is divided into a series of non-overlapping sections along the jet streamwise coordinate. Each of the sections is streamwise averaged to correspond to a piecewise constant flow field in terms of the streamwise coordinate which becomes a function of radius only, i.e. $\widetilde{v}=(\widetilde{v}(r),0,0),\widetilde{c}=\widetilde{c}(r)$ , of the cylindrical–polar coordinate basis in the jet $\boldsymbol{y}=(r,\unicode[STIX]{x1D703},z)$ . For each jet section, periodic boundary conditions are assumed in the streamwise $z$ direction. After such simplifications, the linearised Euler equations can be decomposed into equations for each azimuthal mode separately. This leads to an ordinary differential equation of Rayleigh type for the amplitude of each mode as a function of radius to be solved numerically. Overall, the solution for the amplitudes will be a function of both radius and axial location because of the local mean-flow velocity profile used.

It can be remarked that in a number of previous publications (Afsar, Sescu & Leib Reference Afsar, Sescu and Leib2016; Goldstein & Leib Reference Goldstein and Leib2016), including some earlier work of the present authors (Karabasov et al. Reference Karabasov, Afsar, Hynes, Dowling, McMullan, Prokora, Page and McGuirk2010, Reference Karabasov, Bogey and Hynes2013), the importance of a fully evolving flow/sound propagation model for far-field jet noise predictions was stressed. While the effect of a more accurate definition of the Green’s function, taking jet flow evolution effects into account, compared with the locally parallel flow model will be a subject of future investigations, the present work is the first in the literature where the effective source term is evaluated directly from LES, avoiding the approximations of previous models. Hence, it is possible that the far-field acoustic solutions, which were obtained in the earlier works as convolution products of the Green’s function propagator with an approximate model of the seven-dimensional space–time source term, could have a larger sensitivity to the evolving jet mean-flow details compared with the present approach which is approximation-free.

2.2 Formulation based on the volume integral approach

The same far-field power spectral density (2.6) can be expressed as a complex conjugate of the far-field pressure,

(2.12) $$\begin{eqnarray}S(\boldsymbol{x},\unicode[STIX]{x1D714})=\overline{\hat{p}(\boldsymbol{x},\unicode[STIX]{x1D714})\hat{p}^{\ast }(\boldsymbol{x},\unicode[STIX]{x1D714})},\end{eqnarray}$$

where $\hat{p}(\boldsymbol{x},\unicode[STIX]{x1D714})$ is the frequency-domain pressure signal at the far-field microphone location and the overbar indicates statistical ensemble averaging.

In turn, the frequency-domain pressure signal can be expressed as a volume integral of the source and the vector adjoint Green’s function that satisfies (2.10) and (2.11). After some rearrangement involving a few integrations by parts, this leads to

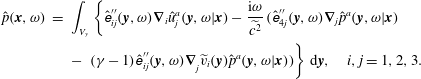(2.13) $$\begin{eqnarray}\displaystyle \hat{p}(\boldsymbol{x},\unicode[STIX]{x1D714}) & = & \displaystyle \int _{V_{y}}\left\{\hat{\unicode[STIX]{x1D626}}_{ij}^{\prime \prime }(\boldsymbol{y},\unicode[STIX]{x1D714})\unicode[STIX]{x1D735}_{i}\hat{u} _{j}^{a}(\boldsymbol{y},\unicode[STIX]{x1D714}|\boldsymbol{x})-\frac{\text{i}\unicode[STIX]{x1D714}}{\widetilde{c^{2}}} (\!\hat{\unicode[STIX]{x1D626}}_{4j}^{\prime \prime }(\boldsymbol{y},\unicode[STIX]{x1D714})\unicode[STIX]{x1D735}_{j}\hat{p}^{a}(\boldsymbol{y},\unicode[STIX]{x1D714}|\boldsymbol{x})\right.\nonumber\\ \displaystyle & & \displaystyle -\,\left.(\unicode[STIX]{x1D6FE}-1){{\hat{\unicode[STIX]{x1D626}}^{\prime \prime }}_{ij}(\boldsymbol{y},\unicode[STIX]{x1D714})\unicode[STIX]{x1D735}}_{j}\widetilde{v}_{i}(\boldsymbol{y})\hat{p}^{a}(\boldsymbol{y},\unicode[STIX]{x1D714}|\boldsymbol{x})\!)\right\}\,\text{d}\boldsymbol{y},\quad i,j=1,2,3.\end{eqnarray}$$

Let us assume that $\boldsymbol{e}_{1}$ is the Cartesian coordinate in the streamwise (jet flow) direction, $(\boldsymbol{e}_{2},\boldsymbol{e}_{3})$ are in the transverse plane and $(\boldsymbol{e}_{1},\boldsymbol{e}_{2})$ are in plane with the far-field microphone.

There are three types of noise sources that can be identified in (2.13): (i) the fluctuating Reynolds stress $\hat{\unicode[STIX]{x1D626}}_{ij}^{\prime \prime }(\boldsymbol{y},\unicode[STIX]{x1D714})$ , (ii) the fluctuating stagnation enthalpy stress $(\unicode[STIX]{x1D714}/\widetilde{c^{2}})\hat{\unicode[STIX]{x1D626}}_{4j}^{\prime \prime }(\boldsymbol{y},\unicode[STIX]{x1D714})$ and (iii) a term associated with the non-divergent mean-flow velocity field $(\unicode[STIX]{x1D714}(\unicode[STIX]{x1D6FE}-1)/\widetilde{c^{2}}){\hat{\unicode[STIX]{x1D626}}_{ij}^{\prime \prime }(\boldsymbol{y},\unicode[STIX]{x1D714})\unicode[STIX]{x1D735}}_{j}\widetilde{v}_{i}(\boldsymbol{y})$ .

For an axisymmetric mean flow, the 3D integral can be further decomposed into a series of two-dimensional azimuthal modes,

(2.14) $$\begin{eqnarray}\displaystyle & & \displaystyle \hat{p}(\boldsymbol{x},\unicode[STIX]{x1D714})=\mathop{\sum }_{n}\hat{p}^{(n)}(\boldsymbol{x},\unicode[STIX]{x1D714})=\mathop{\sum }_{n}\int _{V_{y_{\unicode[STIX]{x1D702}}}}\left\{\right.\!\hat{\unicode[STIX]{x1D626}}_{ij}^{\prime \prime (n)}(\boldsymbol{y}_{\boldsymbol{\unicode[STIX]{x1D702}}},\unicode[STIX]{x1D714})\unicode[STIX]{x1D735}_{i}\hat{u} _{j}^{a(n)}(\boldsymbol{y}_{\boldsymbol{\unicode[STIX]{x1D702}}},\unicode[STIX]{x1D714}|\boldsymbol{x})\nonumber\\ \displaystyle & & \displaystyle \qquad -\,\hat{\unicode[STIX]{x1D626}}_{4j}^{\prime \prime (n)}(\boldsymbol{y}_{\boldsymbol{\unicode[STIX]{x1D702}}},\unicode[STIX]{x1D714})\unicode[STIX]{x1D735}_{j}\hat{p}^{a(n)}(\boldsymbol{y}_{\boldsymbol{\unicode[STIX]{x1D702}}},\unicode[STIX]{x1D714}|\boldsymbol{x})-(\unicode[STIX]{x1D6FE}-1)\hat{\unicode[STIX]{x1D626}}_{ij}^{\prime \prime (n)}(\boldsymbol{y}_{\boldsymbol{\unicode[STIX]{x1D702}}},\unicode[STIX]{x1D714})\unicode[STIX]{x1D735}_{j}\widetilde{v}_{i}(\boldsymbol{y}_{\boldsymbol{\unicode[STIX]{x1D702}}})\hat{p}^{a(n)}(\boldsymbol{y}_{\boldsymbol{\unicode[STIX]{x1D702}}},\unicode[STIX]{x1D714}|\boldsymbol{x})\!\left.\right\}\,\text{d}\boldsymbol{y}_{\boldsymbol{\unicode[STIX]{x1D702}}},\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$

using the standard definition of the Fourier transform in the azimuthal direction,

(2.15) $$\begin{eqnarray}f^{(n)}(\boldsymbol{y}_{\boldsymbol{\unicode[STIX]{x1D702}}})=\int _{0}^{2\unicode[STIX]{x03C0}}\text{e}^{\text{i}n\unicode[STIX]{x1D703}}f(z,r,\unicode[STIX]{x1D703})\,\text{d}\unicode[STIX]{x1D703}.\end{eqnarray}$$

Here, $(\boldsymbol{y}_{\boldsymbol{\unicode[STIX]{x1D702}}},\unicode[STIX]{x1D703})=(r,z,\unicode[STIX]{x1D703})$ is a local cylindrical–polar coordinate basis in the jet, where $r$ and $\unicode[STIX]{x1D703}$ are the radial and azimuthal angle components and $z$ coincides with the jet axis. Vectors with superscript $(n)$ correspond to the $(r,z)$ components of the cylindrical–polar system. The modal representation is useful for reducing computer storage overheads when recording the stresses in the 3D jet volume since for axisymmetric jets it is only a relatively small number of modes (compared with the points of the LES grid) that can contribute efficiently to the acoustic integral.

Apparently, the method of computing the far-field spectral density based on the 3D volume integral formulation (2.12)–(2.14) is mathematically identical to the standard formulation (2.6)–(2.9). However, there is no calculation of the generalised stress tensor autocovariance involved in the former volume integral formulation, which leads to a considerable saving of computer memory resources compared with the standard approach. Table 1 compares the computer memory costs for recording the fluctuating stresses required for the volume integral formulation (2.6)–(2.9) with those of computing the generalised autocovariance stress tensor for the formulation (2.12)–(2.14). The figures are based on the jet case example to be considered in § 3. For simplicity, all numbers are normalised by the computational cost of the volume integral approach. It should be noted that even for a limited number of tensor components, the computation of the autocovariance function is five orders of magnitude more expensive than with the integral volume approach.

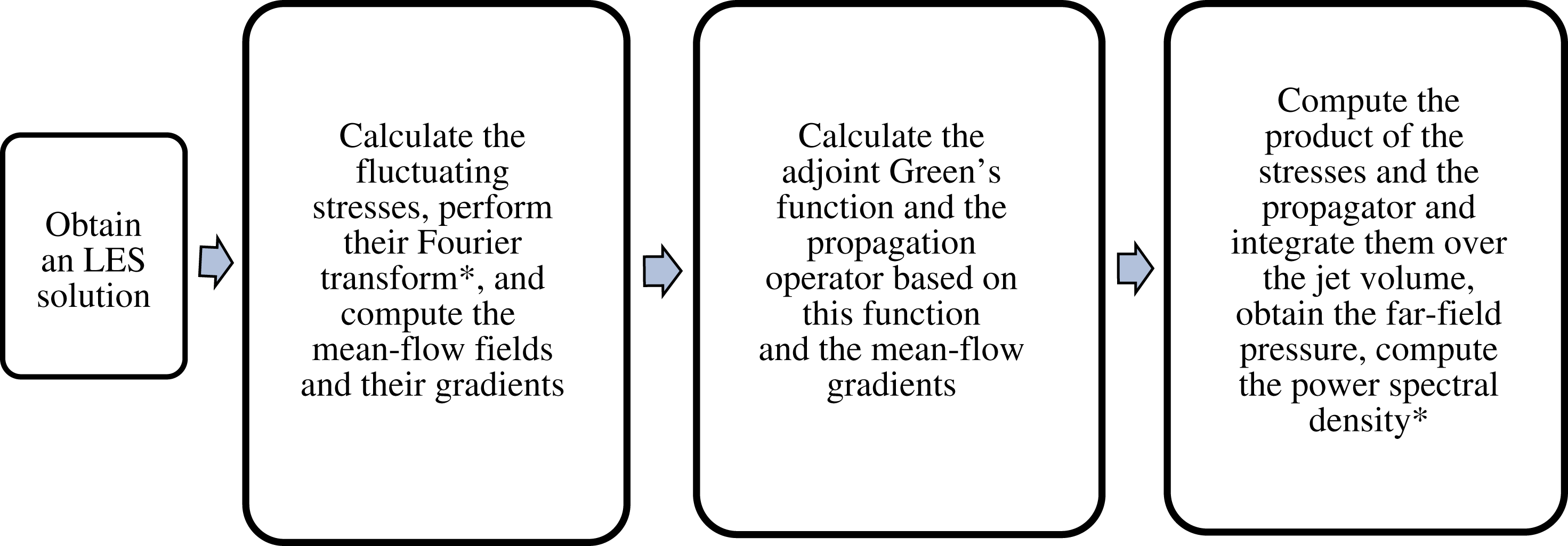
Figure 1. Flow diagram of the volume integral method based on the generalised acoustic analogy; * indicates the use of signal processing techniques to compensate for a finite duration of the LES time signal.

The total computer storage required with the current implementation of the volume integral method for the jet case considered is around 4 TB, which figure could be reduced by performing all preprocessing operations on the fly.

The implementation of the volume integral approach involves the following steps (figure 1).

1. (1) Perform an LES simulation.

2. (2) Calculate all 12 components of the fluctuating stress tensor, $\unicode[STIX]{x1D626}_{\unicode[STIX]{x1D707}j}^{\prime \prime }$ , in the jet volume by applying (2.5).

3. (3) Fourier transform the stress components in time and in the azimuthal direction, record the several discrete frequencies and modes needed; for the processing of the LES time signals, use the signal processing theory (Welch Reference Welch1967): (i) break each fluctuating stress signal into several subintervals with 50% overlap, (ii) Fourier transform each set and (iii) record them as several independent frequency-domain realisations of the stresses.

4. (4) Calculate the mean jet flow properties.

5. (5) For each frequency and mode required, calculate the adjoint Green’s function, $\hat{u} ^{a(n)}(\boldsymbol{y}_{\boldsymbol{\unicode[STIX]{x1D702}}},\unicode[STIX]{x1D714}\mid \boldsymbol{x}),\hat{p}^{a(n)}(\boldsymbol{y}_{\boldsymbol{\unicode[STIX]{x1D702}}},\unicode[STIX]{x1D714}\mid \boldsymbol{x})$ .

6. (6) For each set of the frequency-domain stress fields recorded, integrate the source over the 2D volume, $V_{y_{\unicode[STIX]{x1D702}}}$ , and sum over all modes to obtain the far-field pressure signal (2.14) for each realisation.

7. (7) Calculate the power spectral density by averaging over all realisations of the frequency-domain stress fields available (2.12).

2.3 Volume integral formulation and effective source decomposition

Table 1. Computer memory costs of different implementations of the Goldstein generalised acoustic analogy.

Compared with the standard generalised acoustic analogy approach (2.12)–(2.14), which links the effective sources in the jet to the far-field sound power, the same direct correspondence is not explicit for the current volume integral formulation. Indeed, the current approach first relates the fluctuating stress terms in the jet to the far-field pressure and then relates the far-field pressure to the far-field sound.

To demonstrate how the analysis of far-field noise sources in the jet is also possible within the suggested volume integral approach, let us first decompose the far-field pressure integral into the contributions of individual modes and the corresponding modes of the vector adjoint Green’s function terms using (2.14). For each mode, the far-field pressure integral can be further broken down into the contributions of different source components,

(2.16) $$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\displaystyle \hat{p}_{\unicode[STIX]{x1D626}_{ij}}^{(n)}(\boldsymbol{x},\unicode[STIX]{x1D714})=\int _{V_{y}}\hat{\unicode[STIX]{x1D626}}_{ij}^{\prime \prime (n)}(\boldsymbol{y}_{\boldsymbol{\unicode[STIX]{x1D702}}},\unicode[STIX]{x1D714})\unicode[STIX]{x1D735}_{i}\hat{u} _{j}^{a(n)}(\boldsymbol{y}_{\boldsymbol{\unicode[STIX]{x1D702}}},\unicode[STIX]{x1D714}|\boldsymbol{x})\,\text{d}\boldsymbol{y}_{\boldsymbol{\unicode[STIX]{x1D702}}},\\ \displaystyle \hat{p}_{\unicode[STIX]{x1D626}_{4j}}^{(n)}(\boldsymbol{x},\unicode[STIX]{x1D714})=\int _{V_{y}}\hat{\unicode[STIX]{x1D626}}_{4j}^{\prime \prime (n)}(\boldsymbol{y}_{\boldsymbol{\unicode[STIX]{x1D702}}},\unicode[STIX]{x1D714})\unicode[STIX]{x1D735}_{j}\hat{p}^{a(n)}(\boldsymbol{y}_{\boldsymbol{\unicode[STIX]{x1D702}}},\unicode[STIX]{x1D714}|\boldsymbol{x})\,\text{d}\boldsymbol{y}_{\boldsymbol{\unicode[STIX]{x1D702}}},\\ \displaystyle \hat{p}_{\unicode[STIX]{x1D735}_{j}\widetilde{v}_{i}}^{(n)}(\boldsymbol{x},\unicode[STIX]{x1D714})=\int _{V_{y}}(\unicode[STIX]{x1D6FE}-1)\hat{\unicode[STIX]{x1D626}}_{ij}^{\prime \prime (n)}(\boldsymbol{y}_{\boldsymbol{\unicode[STIX]{x1D702}}},\unicode[STIX]{x1D714})\unicode[STIX]{x1D735}_{j}\widetilde{v}_{i}(\boldsymbol{y}_{\boldsymbol{\unicode[STIX]{x1D702}}})\hat{p}^{a(n)}(\boldsymbol{y}_{\boldsymbol{\unicode[STIX]{x1D702}}},\unicode[STIX]{x1D714}|\boldsymbol{x})\,\text{d}\boldsymbol{y}_{\boldsymbol{\unicode[STIX]{x1D702}}}.\end{array}\right\} & & \displaystyle\end{eqnarray}$$

The contributions due to the fluctuating Reynolds stresses can be further decomposed into

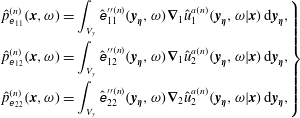(2.17) $$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\displaystyle \hat{p}_{\unicode[STIX]{x1D626}_{11}}^{(n)}(\boldsymbol{x},\unicode[STIX]{x1D714})=\int _{V_{y}}\hat{\unicode[STIX]{x1D626}}_{11}^{\prime \prime (n)}(\boldsymbol{y}_{\boldsymbol{\unicode[STIX]{x1D702}}},\unicode[STIX]{x1D714})\unicode[STIX]{x1D735}_{1}\hat{u} _{1}^{a(n)}(\boldsymbol{y}_{\boldsymbol{\unicode[STIX]{x1D702}}},\unicode[STIX]{x1D714}|\boldsymbol{x})\,\text{d}\boldsymbol{y}_{\boldsymbol{\unicode[STIX]{x1D702}}},\\ \displaystyle \hat{p}_{\unicode[STIX]{x1D626}_{12}}^{(n)}(\boldsymbol{x},\unicode[STIX]{x1D714})=\int _{V_{y}}\hat{\unicode[STIX]{x1D626}}_{12}^{\prime \prime (n)}(\boldsymbol{y}_{\boldsymbol{\unicode[STIX]{x1D702}}},\unicode[STIX]{x1D714})\unicode[STIX]{x1D735}_{1}\hat{u} _{2}^{a(n)}(\boldsymbol{y}_{\boldsymbol{\unicode[STIX]{x1D702}}},\unicode[STIX]{x1D714}|\boldsymbol{x})\,\text{d}\boldsymbol{y}_{\boldsymbol{\unicode[STIX]{x1D702}}},\\ \displaystyle \hat{p}_{\unicode[STIX]{x1D626}_{22}}^{(n)}(\boldsymbol{x},\unicode[STIX]{x1D714})=\int _{V_{y}}\hat{\unicode[STIX]{x1D626}}_{22}^{\prime \prime (n)}(\boldsymbol{y}_{\boldsymbol{\unicode[STIX]{x1D702}}},\unicode[STIX]{x1D714})\unicode[STIX]{x1D735}_{2}\hat{u} _{2}^{a(n)}(\boldsymbol{y}_{\boldsymbol{\unicode[STIX]{x1D702}}},\unicode[STIX]{x1D714}|\boldsymbol{x})\,\text{d}\boldsymbol{y}_{\boldsymbol{\unicode[STIX]{x1D702}}},\end{array}\right\} & & \displaystyle\end{eqnarray}$$

and so on.

By disabling all source terms except from any user-defined stress and mode component of the pressure integral $\hat{p}(\boldsymbol{x},\unicode[STIX]{x1D714})$ , the contribution of this particular source term in the far-field power spectra $\hat{P}(\boldsymbol{x},\unicode[STIX]{x1D714})$ can be calculated.

Furthermore, the effect of cross-products in the power spectra integral can be ignored; that is, only symmetric terms of the generalised stress tensor autocovariance, $\unicode[STIX]{x1D619}_{\unicode[STIX]{x1D707}j\unicode[STIX]{x1D707}j}$ , are important for the far-field sound. The source symmetry property is consistent with observations made for other high-speed axisymmetric jets (e.g. compare with $\unicode[STIX]{x1D619}_{1111}$ , $\unicode[STIX]{x1D619}_{2222}$ , $\unicode[STIX]{x1D619}_{3333}$ , $\unicode[STIX]{x1D619}_{1212}$ , $\unicode[STIX]{x1D619}_{1313}$ and $\unicode[STIX]{x1D619}_{2323}$ main source components considered in Karabasov et al. (Reference Karabasov, Afsar, Hynes, Dowling, McMullan, Prokora, Page and McGuirk2010)) and the sound power spectra can be decomposed into the contributions of individual terms,

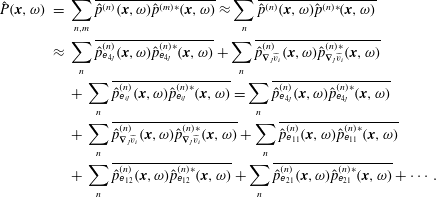(2.18) $$\begin{eqnarray}\displaystyle \hat{P}(\boldsymbol{x},\unicode[STIX]{x1D714}) & = & \displaystyle \mathop{\sum }_{n,m}\overline{\hat{p}^{(n)}(\boldsymbol{x},\unicode[STIX]{x1D714})\hat{p}^{(m)\ast }(\boldsymbol{x},\unicode[STIX]{x1D714})}\approx \mathop{\sum }_{n}\overline{\hat{p}^{(n)}(\boldsymbol{x},\unicode[STIX]{x1D714})\hat{p}^{(n)\ast }(\boldsymbol{x},\unicode[STIX]{x1D714})}\nonumber\\ \displaystyle & {\approx} & \displaystyle \mathop{\sum }_{n}\overline{\hat{p}_{\unicode[STIX]{x1D626}_{4j}}^{(n)}(\boldsymbol{x},\unicode[STIX]{x1D714})\hat{p}_{\unicode[STIX]{x1D626}_{4j}}^{(n)\ast }(\boldsymbol{x},\unicode[STIX]{x1D714})}+\mathop{\sum }_{n}\overline{\hat{p}_{\unicode[STIX]{x1D735}_{j}\widetilde{v}_{i}}^{(n)}(\boldsymbol{x},\unicode[STIX]{x1D714})\hat{p}_{\unicode[STIX]{x1D735}_{j}\widetilde{v}_{i}}^{(n)\ast }(\boldsymbol{x},\unicode[STIX]{x1D714})}\nonumber\\ \displaystyle & & \displaystyle +\,\mathop{\sum }_{n}\overline{\hat{p}_{\unicode[STIX]{x1D626}_{ij}}^{(n)}(\boldsymbol{x},\unicode[STIX]{x1D714})\hat{p}_{\unicode[STIX]{x1D626}_{ij}}^{(n)\ast }(\boldsymbol{x},\unicode[STIX]{x1D714})}=\mathop{\sum }_{n}\overline{\hat{p}_{\unicode[STIX]{x1D626}_{4j}}^{(n)}(\boldsymbol{x},\unicode[STIX]{x1D714})\hat{p}_{\unicode[STIX]{x1D626}_{4j}}^{(n)\ast }(\boldsymbol{x},\unicode[STIX]{x1D714})}\nonumber\\ \displaystyle & & \displaystyle +\,\mathop{\sum }_{n}\overline{\hat{p}_{\unicode[STIX]{x1D735}_{j}\widetilde{v}_{i}}^{(n)}(\boldsymbol{x},\unicode[STIX]{x1D714})\hat{p}_{\unicode[STIX]{x1D735}_{j}\widetilde{v}_{i}}^{(n)\ast }(\boldsymbol{x},\unicode[STIX]{x1D714})}+\mathop{\sum }_{n}\overline{\hat{p}_{\unicode[STIX]{x1D626}_{11}}^{(n)}(\boldsymbol{x},\unicode[STIX]{x1D714})\hat{p}_{\unicode[STIX]{x1D626}_{11}}^{(n)\ast }(\boldsymbol{x},\unicode[STIX]{x1D714})}\nonumber\\ \displaystyle & & \displaystyle +\,\mathop{\sum }_{n}\overline{\hat{p}_{\unicode[STIX]{x1D626}_{12}}^{(n)}(\boldsymbol{x},\unicode[STIX]{x1D714})\hat{p}_{\unicode[STIX]{x1D626}_{12}}^{(n)\ast }(\boldsymbol{x},\unicode[STIX]{x1D714})}+\mathop{\sum }_{n}\overline{\hat{p}_{\unicode[STIX]{x1D626}_{21}}^{(n)}(\boldsymbol{x},\unicode[STIX]{x1D714})\hat{p}_{\unicode[STIX]{x1D626}_{21}}^{(n)\ast }(\boldsymbol{x},\unicode[STIX]{x1D714})}+\cdots \,.\end{eqnarray}$$

The former property can be referred to as mutual orthogonality of the individual source components with respect to the far-field sound power. It should be noted that it does not only require symmetry of the autocorrelation source tensor but also orthogonality of the source modes for the far-field noise solution, which was also previously discussed in the jet noise literature (Goldstein & Leib Reference Goldstein and Leib2016). In § 4, it will be demonstrated how both of these conditions are satisfied for the SILOET jet case.

Besides, if the density distribution of any particular source component corresponding to a given stress term needs to be analysed in the jet volume, this can also be achieved by noting, for example, that

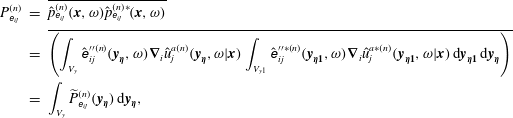(2.19) $$\begin{eqnarray}\displaystyle P_{\unicode[STIX]{x1D626}_{ij}}^{(n)} & = & \displaystyle \overline{\hat{p}_{\unicode[STIX]{x1D626}_{ij}}^{(n)}(\boldsymbol{x},\unicode[STIX]{x1D714})\hat{p}_{\unicode[STIX]{x1D626}_{ij}}^{(n)\ast }(\boldsymbol{x},\unicode[STIX]{x1D714})}\nonumber\\ \displaystyle & = & \displaystyle \overline{\left(\int _{V_{y}}\hat{\unicode[STIX]{x1D626}}_{ij}^{\prime \prime (n)}(\boldsymbol{y}_{\boldsymbol{\unicode[STIX]{x1D702}}},\unicode[STIX]{x1D714})\unicode[STIX]{x1D735}_{i}\hat{u} _{j}^{a(n)}(\boldsymbol{y}_{\boldsymbol{\unicode[STIX]{x1D702}}},\unicode[STIX]{x1D714}|\boldsymbol{x})\int _{V_{y1}}\hat{\unicode[STIX]{x1D626}}_{ij}^{\prime \prime \ast (n)}(\boldsymbol{y}_{\boldsymbol{\unicode[STIX]{x1D702}}\mathbf{1}},\unicode[STIX]{x1D714})\unicode[STIX]{x1D735}_{i}\hat{u} _{j}^{a\ast (n)}(\boldsymbol{y}_{\boldsymbol{\unicode[STIX]{x1D702}}\mathbf{1}},\unicode[STIX]{x1D714}|\boldsymbol{x})\,\text{d}\boldsymbol{y}_{\boldsymbol{\unicode[STIX]{x1D702}}\mathbf{1}}\,\text{d}\boldsymbol{y}_{\boldsymbol{\unicode[STIX]{x1D702}}}\right)}\nonumber\\ \displaystyle & = & \displaystyle \int _{V_{y}}\widetilde{P}_{\unicode[STIX]{x1D626}_{ij}}^{(n)}(\boldsymbol{y}_{\boldsymbol{\unicode[STIX]{x1D702}}})\,\text{d}\boldsymbol{y}_{\boldsymbol{\unicode[STIX]{x1D702}}},\end{eqnarray}$$

where $\widetilde{P}_{\unicode[STIX]{x1D626}_{ij}}^{(n)}(\boldsymbol{y}_{\boldsymbol{\unicode[STIX]{x1D702}}})$ is the corresponding source density function, given by

(2.20) $$\begin{eqnarray}\widetilde{P}_{\unicode[STIX]{x1D626}_{ij}}^{(n)}(\boldsymbol{y}_{\boldsymbol{\unicode[STIX]{x1D702}}})=\unicode[STIX]{x1D735}_{i}\hat{u} _{j}^{a(n)}(\boldsymbol{y}_{\boldsymbol{\unicode[STIX]{x1D702}}},\unicode[STIX]{x1D714}|\boldsymbol{x})\overline{\hat{\unicode[STIX]{x1D626}}_{ij}^{\prime \prime (n)}(\boldsymbol{y}_{\boldsymbol{\unicode[STIX]{x1D702}}},\unicode[STIX]{x1D714})\left(\int _{V_{y1}}\hat{\unicode[STIX]{x1D626}}_{ij}^{\prime \prime \ast (n)}(\boldsymbol{y}_{\boldsymbol{\unicode[STIX]{x1D702}}\boldsymbol{ 1}},\unicode[STIX]{x1D714})\unicode[STIX]{x1D735}_{i}\hat{u} _{j}^{a\ast (n)}(\boldsymbol{y}_{\boldsymbol{\unicode[STIX]{x1D702}}\boldsymbol{ 1}},\unicode[STIX]{x1D714}|\boldsymbol{x})\,\text{d}\boldsymbol{y}_{\boldsymbol{\unicode[STIX]{x1D702}}\mathbf{1}}\right)}.\end{eqnarray}$$

It should be noted also that although, inside the integral, (2.20) implicitly includes the fourth rank autocovariance tensor, $\hat{\unicode[STIX]{x1D619}}_{ijij}^{(n)}(\boldsymbol{y}_{\boldsymbol{\unicode[STIX]{x1D702}}},\boldsymbol{y}_{\boldsymbol{\unicode[STIX]{x1D702}}\mathbf{1}},\unicode[STIX]{x1D714})=\overline{\hat{\unicode[STIX]{x1D626}}_{ij}^{\prime \prime (n)}(\boldsymbol{y}_{\boldsymbol{\unicode[STIX]{x1D702}}},\unicode[STIX]{x1D714})\hat{\unicode[STIX]{x1D626}}_{ij}^{\prime \prime \ast (n)}(\boldsymbol{y}_{\boldsymbol{\unicode[STIX]{x1D702}}\mathbf{1}},\unicode[STIX]{x1D714})}$ , the latter expensive function does not need to be recorded. Indeed, the computation of the effective source density, $\widetilde{P}_{\unicode[STIX]{x1D626}_{ij}}^{(n)}(\boldsymbol{y})$ , only requires the storage of several realisations of turbulent stresses $\hat{\unicode[STIX]{x1D626}}_{ij}^{\prime \prime (n)}(\boldsymbol{y}_{\boldsymbol{\unicode[STIX]{x1D702}}},\unicode[STIX]{x1D714})$ and the vector adjoint Green’s function $\unicode[STIX]{x1D735}_{i}\hat{u} _{j}^{a}(\boldsymbol{y}_{\boldsymbol{\unicode[STIX]{x1D702}}},\unicode[STIX]{x1D714}|\boldsymbol{x})$ for azimuthal modes and frequencies of interest as outlined in § 3.2. The effective source density $\widetilde{P}_{\unicode[STIX]{x1D626}_{ij}}^{(n)}(\boldsymbol{y})$ can then be reconstructed in the entire 3D jet volume as follows: (i) calculate the inner integral $\int _{V_{y1}}\hat{\unicode[STIX]{x1D626}}_{ij}^{\prime \prime \ast (n)}(\boldsymbol{y}_{\boldsymbol{\unicode[STIX]{x1D702}}\mathbf{1}},\unicode[STIX]{x1D714})\unicode[STIX]{x1D735}_{i}\hat{u} _{j}^{\ast a}(\boldsymbol{y}_{\boldsymbol{\unicode[STIX]{x1D702}}\mathbf{1}},\unicode[STIX]{x1D714}|\boldsymbol{x})\,\text{d}\boldsymbol{y}_{\boldsymbol{\unicode[STIX]{x1D702}}\mathbf{1}}$ for each realisation of the stress field, (ii) multiply the result by all possible realisation values of the stress field $\hat{\unicode[STIX]{x1D626}}_{ij}^{\prime \prime (n)}(\boldsymbol{y}_{\boldsymbol{\unicode[STIX]{x1D702}}},\unicode[STIX]{x1D714})$ and (iii) ensemble average over the combined number of realisations and multiply by the Green’s function, $\unicode[STIX]{x1D735}_{i}\hat{u} _{j}^{a(n)}(\boldsymbol{y}_{\boldsymbol{\unicode[STIX]{x1D702}}},\unicode[STIX]{x1D714}|\boldsymbol{x})$ .

3.1 Jet case definition and flow solution validation

For validation of the new volume integral method developed, jet conditions from the Rolls-Royce Strategic Investment in Low-carbon Engine Technology (SILOET) experiment performed in the Noise Test Facility (NTF) of QinetiQ are considered (SILOET Programme Rolls-Royce private data). The conditions correspond to a high-speed single-stream subsonic isothermal jet flow issuing from a convergent profiled nozzle. Details of the jet case are summarised in table 2. Two conditions are considered: a zero coflow (the static jet case) and a coflow velocity $U_{c}$ in the jet streamwise direction corresponding to $M_{c}=0.3$ , where $M_{c}=U_{c}/c_{\infty }$ .

Table 2. Parameters of the Rolls-Royce SILOET jet case.

The flow solutions have been obtained with the MILES CABARET solver (Faranosov et al. Reference Faranosov, Goloviznin, Karabasov, Kondakov, Kopiev and Zaitsev2013; Semiletov & Karabasov Reference Semiletov and Karabasov2013, Reference Semiletov and Karabasov2014b ,Reference Semiletov and Karabasov a ) on a hexahedral cylindrical grid of circa $21\times 10^{6}$ cells in total. For unsteady flow modelling, the governing Navier–Stokes equations are solved in the framework of the monotonically integrated LES (MILES) method (Fureby & Grinstein Reference Fureby and Grinstein2002). The MILES implementation used is based on the low-dissipative and low-dispersive CABARET method (Goloviznin & Samarskii Reference Goloviznin and Samarskii1998; Karabasov & Goloviznin Reference Karabasov and Goloviznin2009; Chintagunta, Naghibi & Karabasov Reference Chintagunta, Naghibi and Karabasov2018) on a hexahedral cylindrical grid of circa $21\times 10^{6}$ cells in total. Numerical simulations have been performed over approximately 560 time units (TUs), which includes approximately 200 TUs of the initial solution spin-out time. Here, one TU corresponds to the time required for an eddy to travel over one jet diameter, $\text{TU}=D_{j}/U_{j}$ .

The computational domain is covered with a cylindrical-type computational grid with a Cartesian bloc along the centreline. The grid includes the jet flow downstream of the nozzle exit and spans over approximately 100 jet diameters axially and 30 jet diameters radially. For open boundaries, a combination of characteristic non-reflecting boundary conditions and grid stretching is used to minimise spurious reflections. The standard no-slip adiabatic boundary condition is applied on the nozzle walls. Upstream of the nozzle exit, the computational domain includes part of the nozzle and spreads over five jet diameters.

Most of the grid cells are clustered in the shear-layer region which is the most important zone for noise generation. Figure 2 shows details of the grid spacing distribution along the jet lipline and radially. The grid has a sufficient resolution for acoustic wave propagation up to $St\sim 1{-}2$ over the first 8–15 jet diameters from the nozzle exit, where $St=fD_{j}/U_{j}$ is the Strouhal number defined by the nozzle diameter.

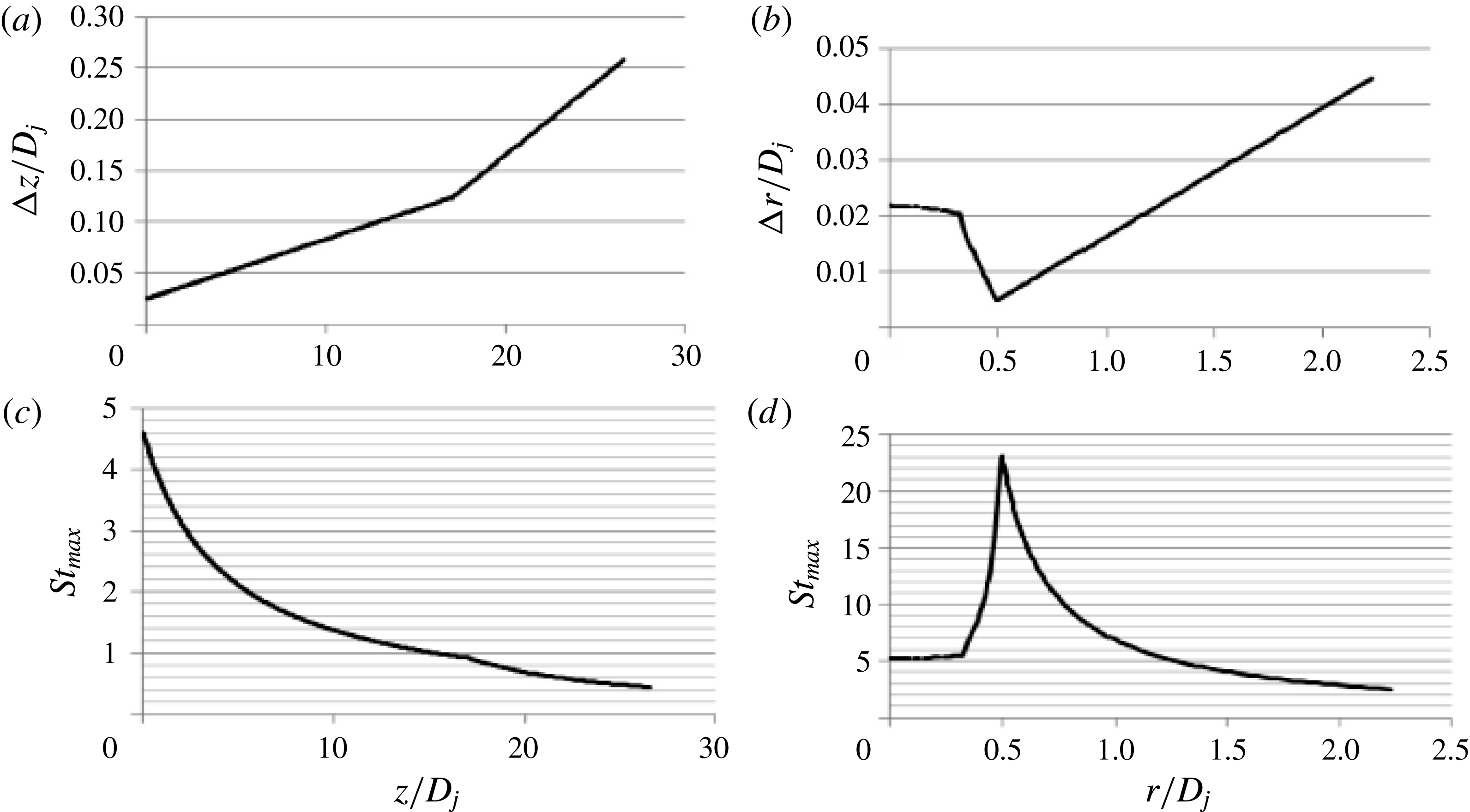
Figure 2. Cell size distribution in the axial and radial directions, (a) and (b), and the corresponding highest resolved acoustic frequencies, (c) and (d).

At the nozzle lip, the grid cell sizes in the radial, streamwise and azimuthal directions are $\unicode[STIX]{x0394}r=0.005D_{j},\unicode[STIX]{x0394}z=0.025D_{j},r\unicode[STIX]{x0394}\unicode[STIX]{x1D703}=0.0245D_{j}$ respectively. This resolution is likely to be too coarse to capture the boundary layer at the nozzle exit and, while no boundary layer modelling was attempted since there are no flow measurements available inside the nozzle from the experiment, this resulted in an initially laminar jet condition in the LES solution. It should be noted that use of the laminar jet inflow condition not only relies on the fast transition of the flow solution to turbulence in accordance with the shear-layer instability development downstream of the nozzle exit but also ignores the fact that the jet flow at such a high Reynolds number is always turbulent at the nozzle exit. Hence, the current idealised treatment of the jet inflow conditions makes the jet development dependent on the numerical method details, which may not be ideal according to the existing jet noise literature (Bogey, Marsden & Bailly Reference Bogey, Marsden and Bailly2012; Bres et al. Reference Bres, Jaunet, Le Rallic, Jordan, Colonius and Lele2015). A subject of future work will be to obtain a more accurate LES solution for the same jet case with account for a realistic turbulent jet inflow condition, for example based on the wall-modelled LES approach (Bres et al. Reference Bres, Jaunet, Le Rallic, Jordan, Colonius and Lele2015). In the meantime, it should be pointed out that similar idealised laminar inflow jet conditions were used in other publications on isolated jets (Bres et al. Reference Bres, Nichols, Lele, Ham, Schlinker, Reba and Simonich2012; Ingraham & Bridges Reference Ingraham and Bridges2017; Leib, Ingraham & Bridges Reference Leib, Ingraham and Bridges2017) without reporting any drastic effect of the initially laminar condition on the downstream jet flow development that defines the far-field noise spectra and acoustic sensitive jet flow properties such as the fourth-order velocity autocorrelation functions. Most recently, Markesteijn & Karabasov (Reference Markesteijn and Karabasov2018) used the MILES CABARET method for computing NASA jets corresponding to set point 7 and 3 conditions at Reynolds numbers of around $10^{6}$ on graphics processing units (GPUs) to reduce the LES run time. The GPU LES solutions obtained with the imposition of a laminar inflow jet condition were compared with the solutions obtained by introducing a numerical turbulence grid upstream of the nozzle exit to capture the same velocity fluctuations at the nozzle exit as reported in the NASA experiment. In both cases, with and without imposing the initial disturbances at the nozzle exit, the obtained LES solutions showed similar good agreement with the experiment in predicting the rest of the flow field and the far-field noise spectra.

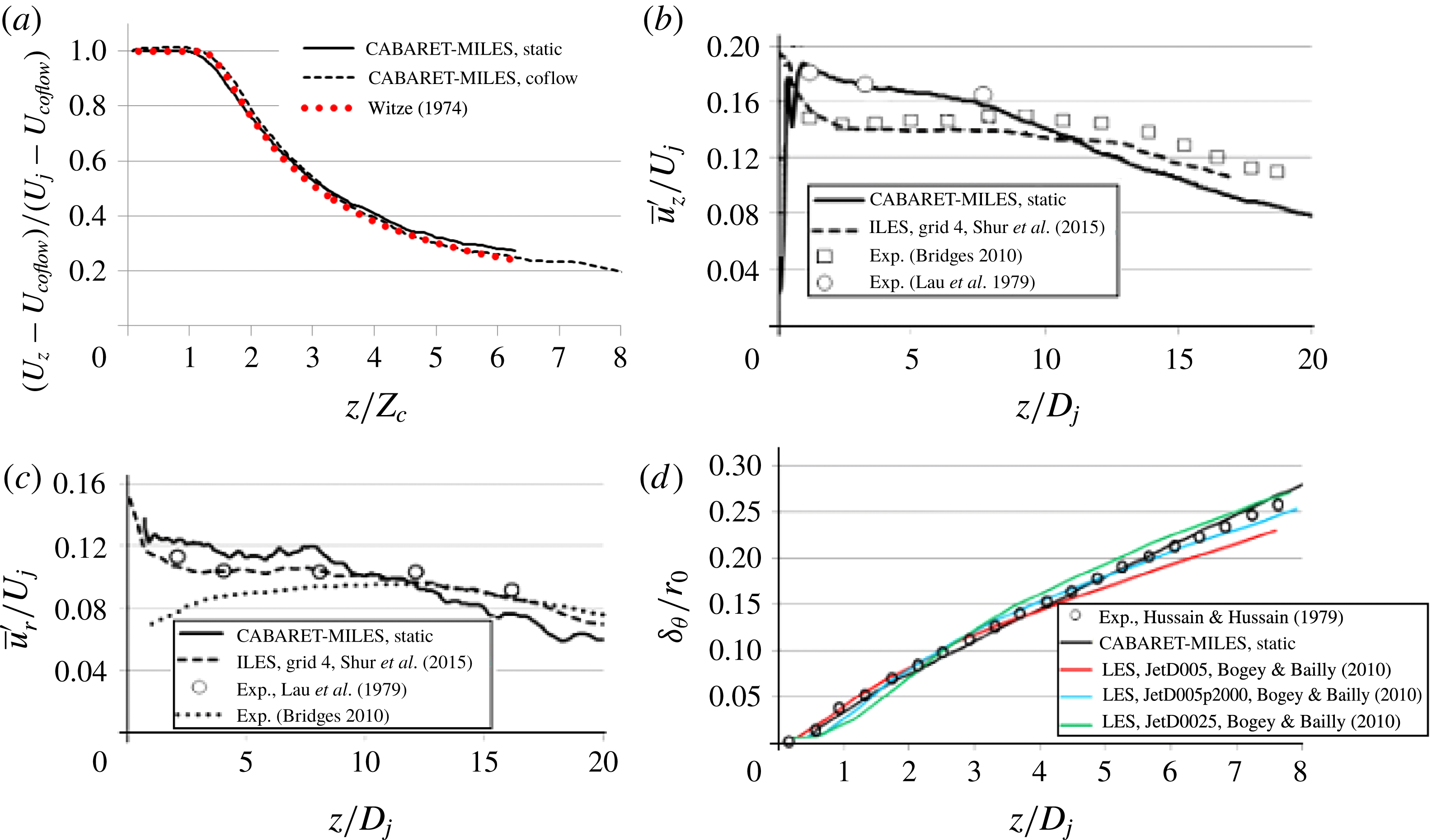
Figure 3. Comparison of the CABARET SILOET flow solution with the experimental and computational data available: centreline mean-flow velocity profile (a), lipline profile of the axial velocity fluctuation (b), lipline profile of the radial velocity fluctuation (c) and streamwise profile of the shear-layer thickness (d).

Figure 3 shows the results of the validation of the presented CABARET SILOET flow solutions in comparison with the experimental data available in the literature.

Figure 3(a) compares the centreline profile of the axial mean-flow velocity component with the function $(\overline{v}_{z}/U_{j})=1-\unicode[STIX]{x1D626}^{\unicode[STIX]{x1D6FC}/(1-z/Z_{0})}$ , where $Z_{0}$ is the potential core length of the jet and $\unicode[STIX]{x1D6FC}=1.43$ is the Witze empirical parameter, which describes a similitude jet profile, as commonly accepted in high-speed jet flow experiments (Witze Reference Witze1974).

Figures 3(b) and 3(c) compare the current LES solutions for jet lipline distributions of the streamwise and transverse velocity component fluctuations with the experimental data from Lau, Morris & Fisher (Reference Lau, Morris and Fisher1979), Bridges & Wernet (Reference Bridges and Wernet2003) and Bridges (Reference Bridges2010) as well as with the implicit LES solution obtained on a similar resolution grid ( ${\sim}20\times 10^{6}$ grid cells) from Shur et al. (Reference Shur, Spalart, Strelets and Travin2015) which corresponds to jet conditions of the Boeing experiment (Viswanathan Reference Viswanathan2004).

To further analyse the current SILOET LES solution in the noise sensitive shear-layer region, following Bogey & Bailly (Reference Bogey and Bailly2010), the streamwise profile of the shear-layer momentum thickness

(3.1) $$\begin{eqnarray}\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D703}}=\int _{0}^{r_{0.04}}\frac{\overline{v}_{z}}{\overline{U}_{c}}\left(1-\frac{\overline{v}_{z}}{\overline{U}_{c}}\right)\,\text{d}r\end{eqnarray}$$

is considered, where $\overline{v}_{z}$ is the local axial mean-flow velocity, $\overline{U}_{c}$ is the corresponding axial velocity value at the jet centreline and $r_{0.04}$ is defined so that $\overline{v}_{z}(r_{0.04})=0.04\overline{U}_{c}$ .

Figure 3(d) compares the above quantity computed from the present LES solution with the experimental data available from Hussein, Capp & George (Reference Hussein, Capp and George1994). In addition, LES solutions from several references digitised from Bogey & Bailly (Reference Bogey and Bailly2010) are shown on the same plot. In the latter case, these solutions correspond to various shear-layer resolutions at the nozzle exit ( $r/D_{j}=0.005$ and 0.0025, denoted by JetD005 and JetD0025 respectively) and with and without additional boundary layer tripping inside the pipe nozzle (JetD005p2000 and JetD005 respectively). In each case, the normalisation based on the jet radius at the nozzle exit ${r_{0}=D}_{j}/2$ is applied.

Notably, in all cases, the present CABARET SILOET simulation is in good agreement with the referenced experimental and computational data.

To conclude the LES validation section, the turbulent velocity spectra from the current jet flow solution for a few representative points in the shear layer are extracted and their slope is compared with the $-5/3$ that is representative of the inertial range of turbulence cascade in accordance with Kolmogorov’s theory (Pope Reference Pope2000). Because of the limited length of time history available from the LES solution, the spectra are calculated in accordance with the standard signal postprocessing method (Welch Reference Welch1967) to improve the statistical convergence. Again, the original signal is divided into several subsample signals with 50 % overlap. Each subsample signal is Fourier-transformed with a Hanning window applied and the final spectra are obtained by averaging over all sections. This is the same signal postprocessing technique as is used in the implementation of the volume integral method outlined in §§ 2.2 and 2.3. The results are presented in figure 4, which shows that the current LES solution captures the $-5/3$ slope over at least one octave of the turbulent velocity spectra, as expected from a high-Reynolds-number flow.

At this point, it may be concluded that the laminar inflow jet condition approximation used for the current LES solution did not lead to a significant change in the jet flow dynamics downstream of the nozzle exit in comparison with the existing literature. Therefore, despite the approximation made, the quality of the current LES flow solution is reasonable in terms of its further input in the acoustic analogy modelling that is the core part of the current publication.

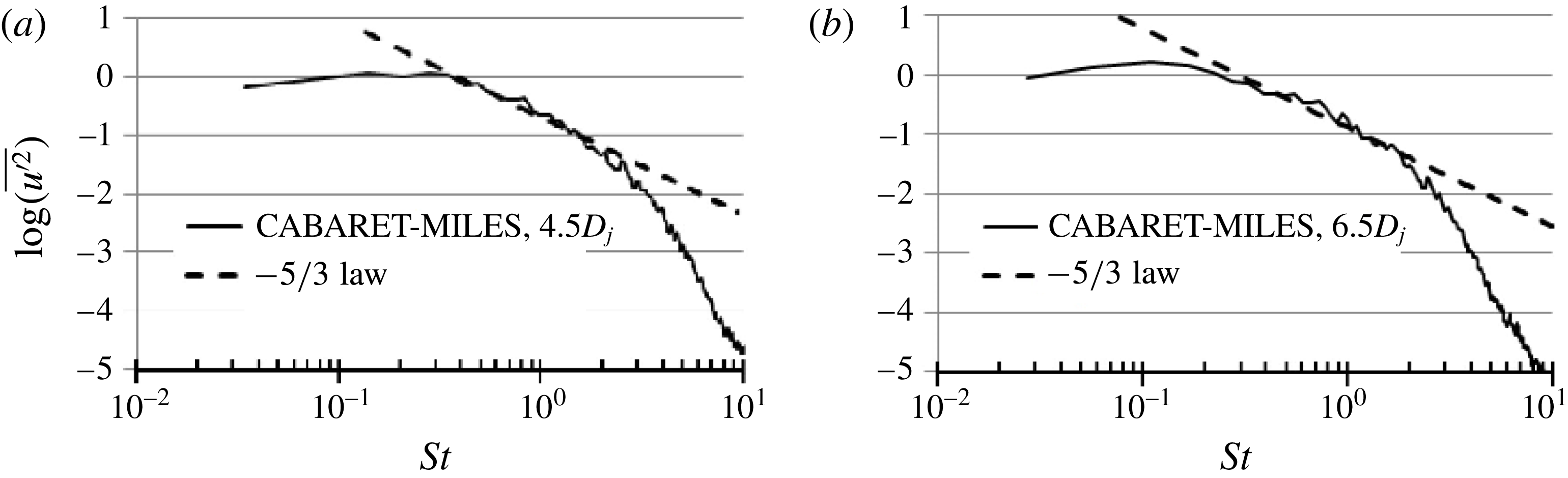
Figure 4. CABARET SILOET results for the turbulent velocity spectra at two representative jet lipline locations.

3.2 Far-field noise spectra predictions and comparison with the Ffowcs Williams–Hawkings method

Having selected a sufficiently large cylindrical part of the computational domain (25  $D_{j}$ axially times 2 $D_{j}$ radially) downstream of the nozzle exit, all components of the generalised fluctuating turbulent stresses $\unicode[STIX]{x1D626}_{\unicode[STIX]{x1D707}j}^{\prime \prime }$ are extracted from the LES solution and decomposed into 10 azimuthal modes and 50 frequencies within $0.05<St<3$ . The resulting stress fields are substituted in the volume integral formulation of the generalised acoustic analogy (2.12), (2.14) to compute the far-field noise spectra and compare the results with the far-field microscope measurements from the SILOET experiment. The far-field microphone data correspond to a distance of 120 $D_{j}$ from the centre of the nozzle exit.

For statistical averaging of the fluctuating stress signals obtained from LES, 20 subintervals with 50 % overlap are used. The computational cost of the volume integral solution is mainly due to computation of the integral sums for the multiple realisations of the LES stress fields required, since the computation of the semianalytical Green’s function is extremely fast. The total cost of applying the volume integral method to calculate the far-field noise is a small fraction of the computational cost of the LES solution ( ${\sim}20$  min on a workstation compared with a few weeks on a large computer cluster with hundreds of parallel processes respectively).

In terms of computer memory, the major cost of the volume integral method is due to the recording of the various realisations of the 12 generalised stress components in the 3D jet volume. However, since the stresses only need to be recorded for a discrete number of frequencies, while the Fourier transformation is performed during the simulation run, and the flow solution is required for a limited number of azimuthal modes, the total cost is only marginally larger compared with that of standard 3D surface integral methods.

To cross-verify the far-field noise predictions of the volume integral formulation of the Goldstein generalised acoustic analogy, the same LES solution is applied in the framework of the penetrable formulation of the Ffowcs Williams–Hawkings (FW–H) surface integral method. The method is based on computing the acoustic integrands corresponding to the ‘thickness’ and ‘dipole’ terms on a control surface that confines the jet with all important noise sources (di Francescantonio Reference di Francescantonio1997; Brentner & Farassat Reference Brentner and Farassat1998) and propagating the solution to the far field using the analytical free-space Green’s function. Under the assumption that all significant noise sources are included inside the control surface, the external quadrupole sources are ignored. Following Shur et al. (Reference Shur, Spalart, Strelets and Travin2015), a sufficient number of closing discs $({\sim}10)$ at approximately 25 jet diameters downstream of the nozzle exit are used. An average far-field prediction of the results obtained with the same conical-shaped control surface with different closing discs (figure 5) was used to filter out the pseudosound effect due to vorticity waves crossing the control surface. Upstream of the nozzle exit, the control surface confines the nozzle lip and is left open. Furthermore, since the solution of the penetrable formulation of the FW–H method is known to be sensitive to the location of the integration surface, several (denoted as ‘sets’ in figure 5) were considered before the optimum one (set no. 2) was selected to make sure that the acoustic integration surface was located within the region of a sufficient grid resolution while sufficiently far away from the vorticity-rich zones. To process the time signal at the far-field microphone location, the same signal processing method based on a Fourier transform with subsample averaging (Welch Reference Welch1967) was applied as in the volume integral method based on the acoustic analogy.

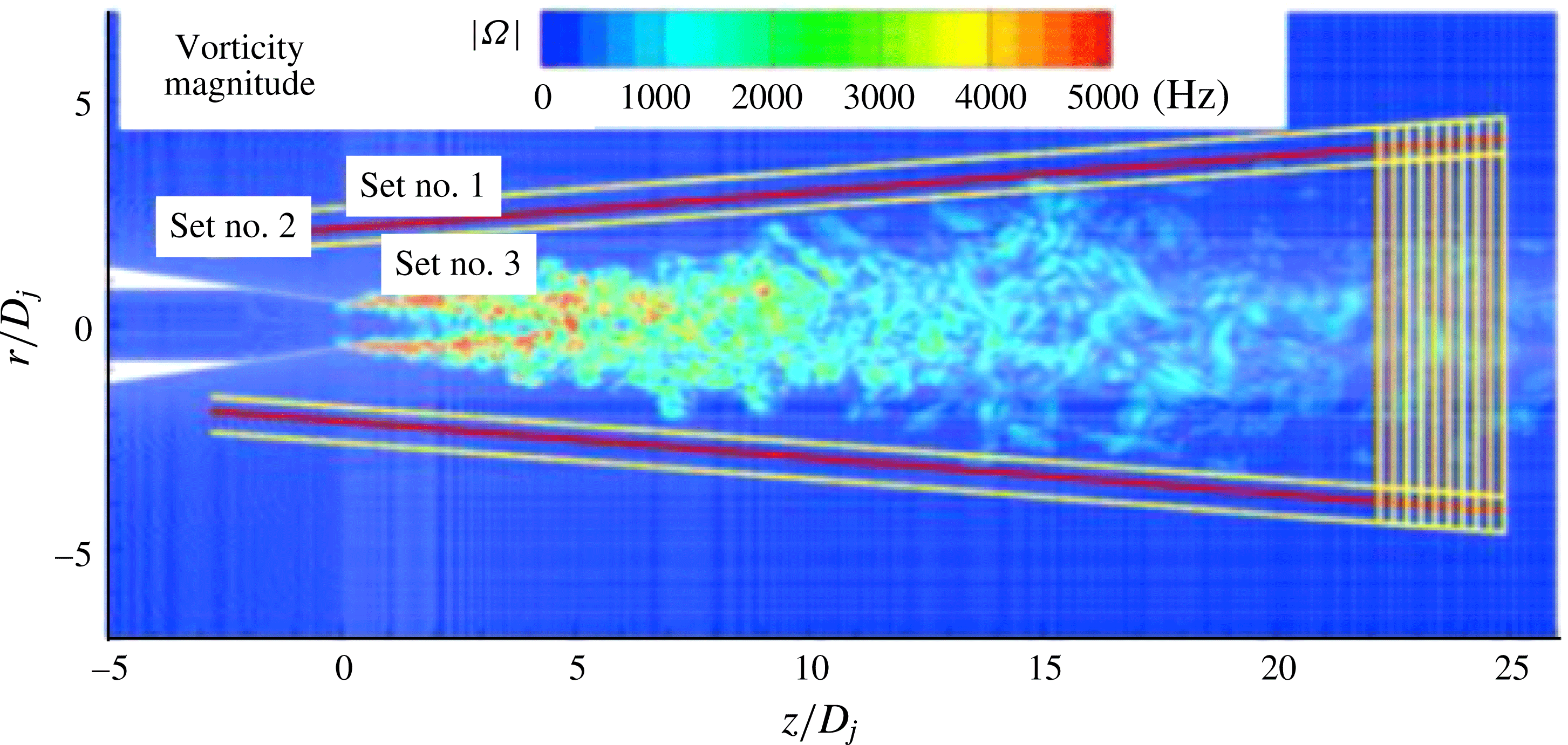
Figure 5. Location of integration surfaces used with the Ffowcs Williams–Hawkings method relative to a typical distribution of the instantaneous vorticity magnitude in the SILOET jet.

Figure 6 compares the sound power spectral density (PSD) obtained with the Goldstein generalised acoustic analogy implementation (2.12), (2.14) and with those of the FW–H method. Both predictions are within 2–3 dB of the experiment from $St\sim 0.1{-}0.2$ to $St\sim 2{-}3$ for polar angles $30^{\circ }{-}90^{\circ }$ to the jet axis.

It should be noted that, for the $30^{\circ }$ angle to the jet, frequencies lower than $St\sim 0.2$ are attenuated for both the FW–H and the acoustic analogy solution (resulting in a ${\sim}4$  dB error with respect to the experiment). This attenuation is probably due to the insufficient LES grid resolution at the end of the potential core of the SILOET jet. This is also in accordance with the results of Markesteijn & Karabasov (Reference Markesteijn and Karabasov2018), who examined the grid sensitivity of the MILES CABARET solutions with the FW–H method on several LES grids of circa $60{-}80\times 10^{6}$ cells with various refinements for similar high-speed jet cases. Besides, for the same $30^{\circ }$ angle to the jet flow, the acoustic analogy solution appears to be less accurate in the medium-frequency range, $0.2<St<0.4$ , in comparison with the FW–H prediction which is virtually ‘spot on’ for a $30^{\circ }$ angle, e.g. remains within 0.5–1 dB accuracy with respect to the experiment for $0.2<St<1.5$ . One explanation for the discrepancy could be the simplified locally parallel flow approximation that was applied for solving the sound mean-flow propagation problem in the current acoustic analogy implementation. Hence, future work will be devoted to implementing a more sophisticated evolving mean-flow propagation model within the suggested volume integral approach. For example, further steps may involve a numerical solution of the adjoint linearised Euler equations for the fully evolving jet flow following the method of Karabasov & Hynes (Reference Karabasov and Hynes2006), and using non-parallel flow asymptotics within the semianalytical approach suggested by Afsar et al. (Reference Afsar, Sescu, Sassanis and Lele2017). On the other hand, it should also be recalled that, in comparison with the FW–H solution, there is no single calibration parameter involved in defining the integration domain of the acoustic analogy method. Hence, the current predictions of the acoustic analogy method were not at all ‘calibrated’ compared with the FW–H solution based on the optimal control integration surface. This means that the 0.5–1 dB accuracy achieved with the FW–H method for the $30^{\circ }$ angle noise spectrum predictions on the current 21 million LES grid could be slightly fortuitous and future work should also involve improving the LES grid resolution for the current jet case.

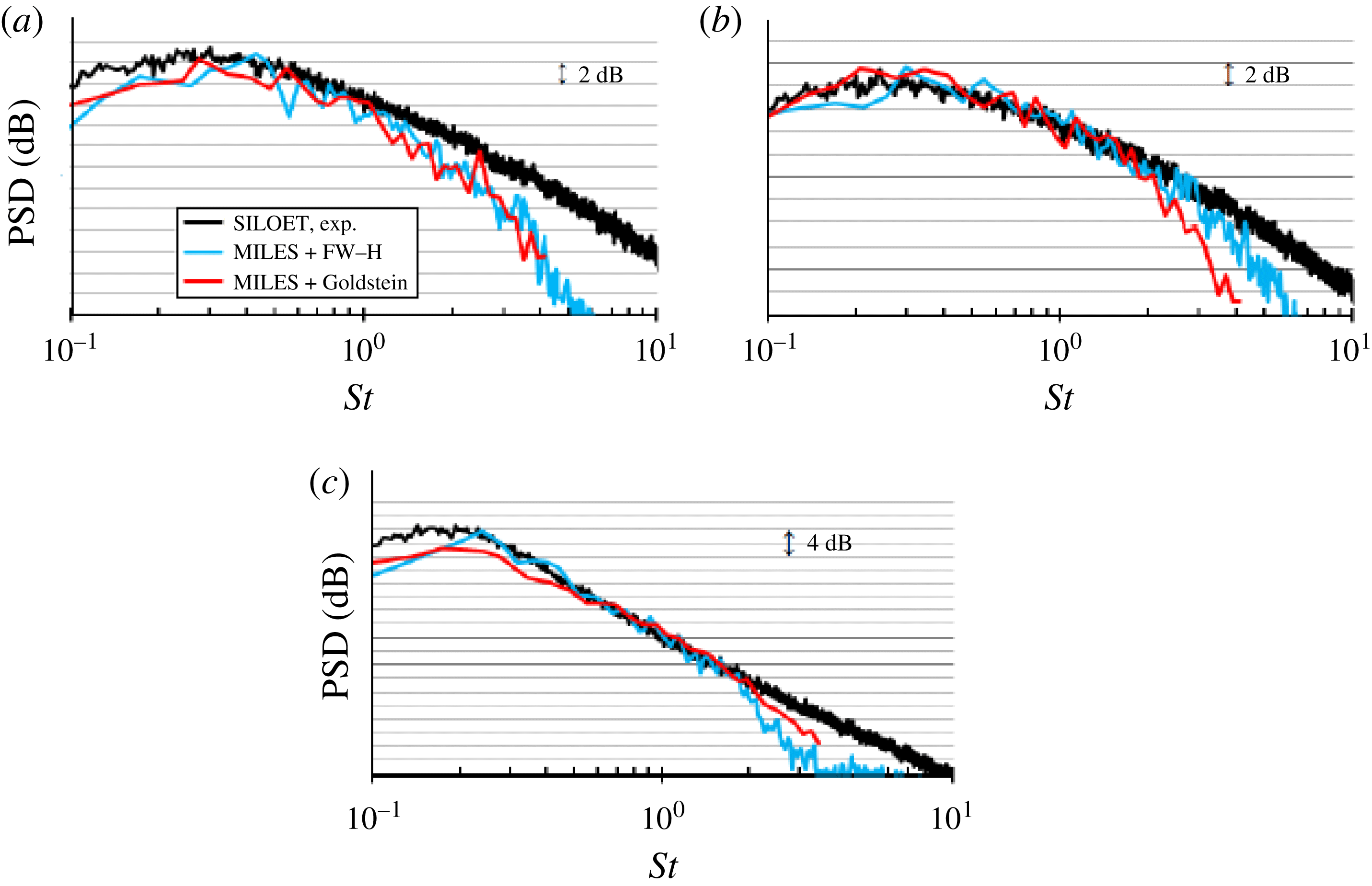
Figure 6. Validation of the far-field noise spectra predictions of the volume integral acoustic analogy method in comparison with the experiment and the reference FW–H solution for the isothermal static SILOET jet: $90^{\circ }$ polar angle (a), $60^{\circ }$ polar angle (b), $90^{\circ }$ and $30^{\circ }$ (c) polar angle to the jet flow.

To demonstrate the importance of the absence of calibration parameters for jet noise predictions, the second SILOET jet case, which corresponds to a coflow in the jet streamwise direction at $M_{c}=0.3$ , is considered. Similarly to the static jet case, the CABARET solution is first obtained for the SILOET jet flow case taking the coflow effect into account. The LES solution is then applied for the volume integral formulation as well as for the penetrable FW–H formulation without any additional calibration of either of the acoustic modelling methods. For the FW–H method, this means using the same acoustic control surface in the coflow case as in the previous static jet case.

Figure 7 compares the sound spectra predictions by both methods and with the experiment for $90^{\circ }$ observer location. There is a strong amplification of the FW–H solution notable at low frequencies, which is a manifestation of spurious pseudosound waves that were not sufficiently abated in this case. It should be noted that there are recipes in the FW–H literature (e.g. Shur et al. Reference Shur, Spalart and Strelets2005) regarding how to adjust the acoustic surface location depending on the jet operating conditions to filter out the pseudosound effects, but these recipes are empirical in nature. In comparison with these, the noise spectra predictions of the current volume integral method based on the acoustic analogy are within 2–3 dB of the experiment for both the static and the coflow jet conditions without any empirical calibration needed.

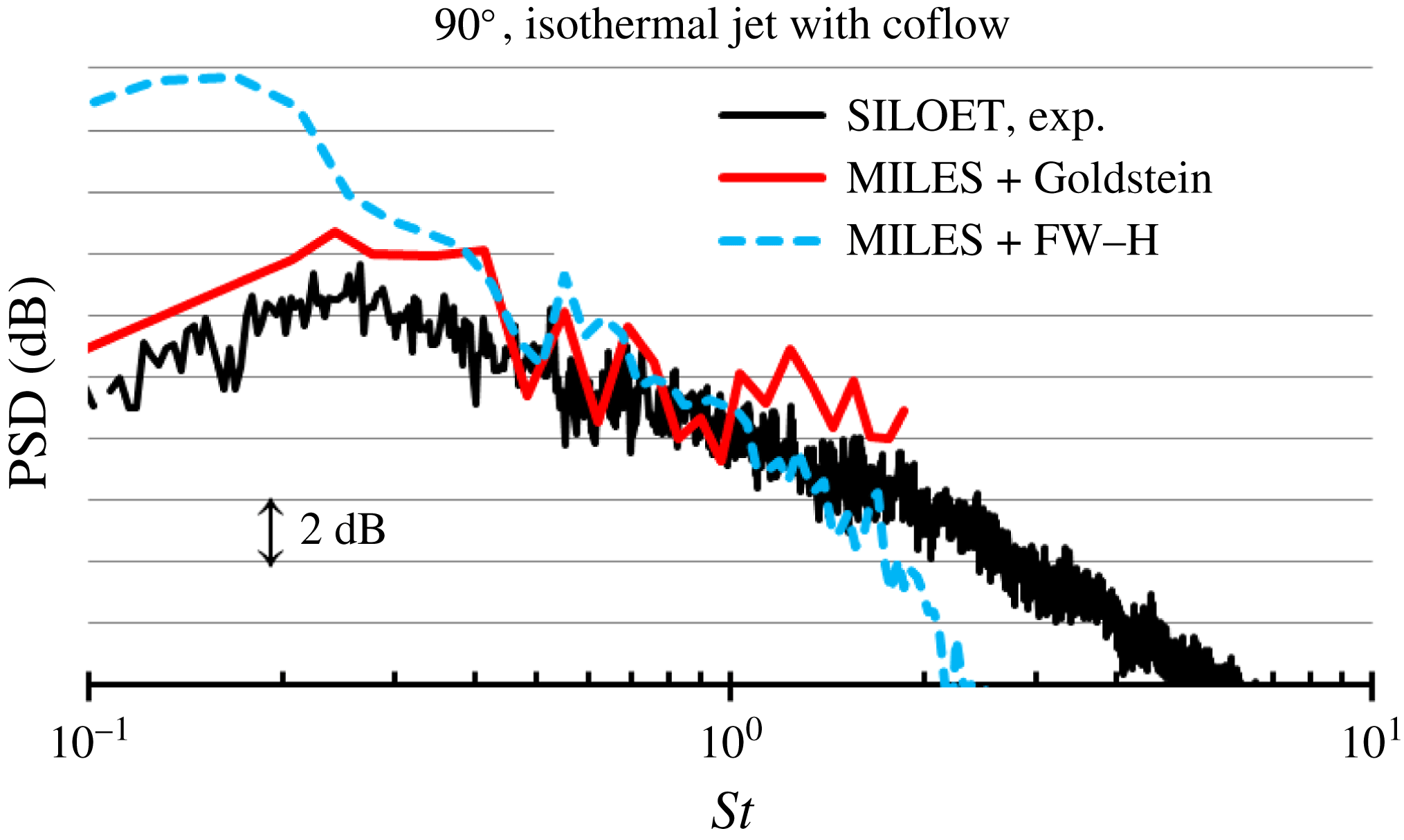
Figure 7. Far-field noise spectra of the isothermal SILOET jet with the coflow for $90^{\circ }$ polar angle: comparison of the volume integral method predictions with those of the FW–H method and with the experiment.

4.1 Contribution of the source volume to the far-field noise

Figure 8 shows the far-field spectra predictions based on various subdomains of the original integration volume for $90^{\circ }$ microphone angle. Each of the small parts of the original control volume has a cylindrical shape and starts at the nozzle exit. The radius and the streamwise extent of the control volume are varied one at a time. The change of the far-field sound spectra due to decrease of the integration domain in the streamwise direction down to the cylindrical volume $(2\times 4)D_{j}$ (radially times axially) is demonstrated in figure 8(a), and the same for the radial direction down to $(0.75\times 25)D_{j}$ (radially times axially) is shown in figure 8(b). In both cases, as the size of the source volume decreases, the low frequencies become attenuated whereas the frequencies higher than $St\sim 0.4$ remain almost unaffected by the control volume change applied. Furthermore, starting from a certain elongated cylinder shape of the source volume, which is approximately $(1.5\times 10)D_{j}$ (radially times axially), that is, approximately a factor of 2 larger than the jet plume dimensions (the potential core length of the SILOET jet is approximately 5.5 $D_{j}$ ), the same relative change of the control volume in the radial or streamwise direction leads to approximately the same noise spectra. For example, the effect of the change of control volume in the radial direction from 1.5 $D_{j}$ to 0.75 $D_{j}$ on the low part of the frequency spectra is approximately the same as that of the change in the streamwise direction from 15 $D_{j}$ to 6 $D_{j}$ . Results of varying the size of the integration volume for the $30^{\circ }$ angle spectra (not shown) demonstrate the same effect. This suggests that the effective source shape, which in terms of the autocovariance of fluctuating turbulent stresses (2.6) corresponds to the source correlation volume, changes approximately in proportion to the jet dimensions. The effective source shrinks for high-frequency sound and the high-frequency sources tend to be more compactly located closer to the nozzle exit and the jet lipline area compared with the low frequencies.

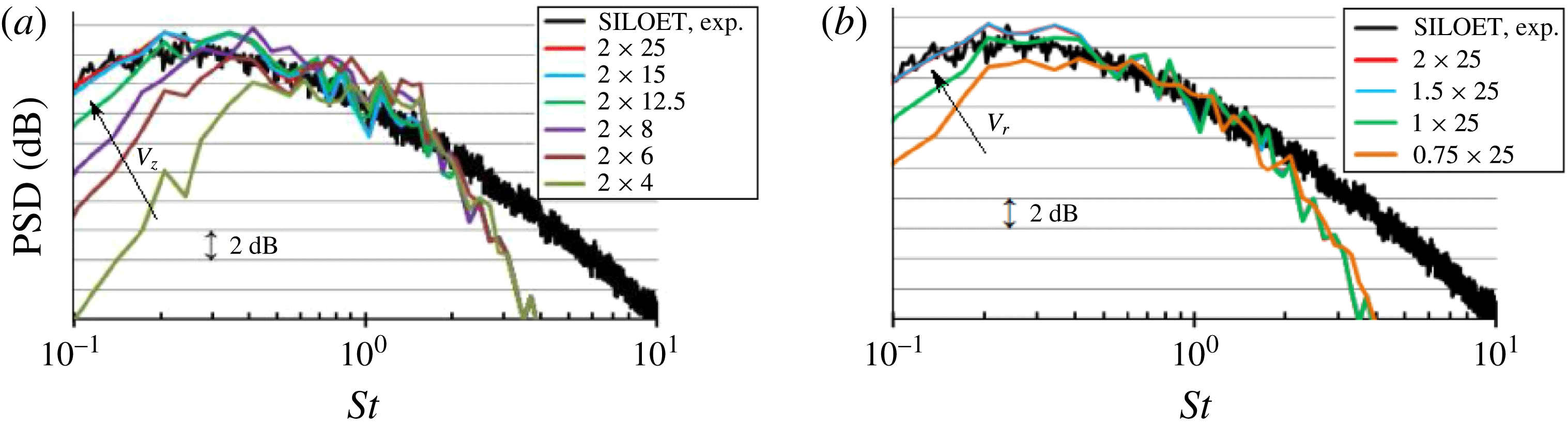
Figure 8. Effect of shrinking the cylindrical source integration domain on the far-field noise spectra at $90^{\circ }$ observer angle: varying the source volume in the streamwise direction $V_{z}$ (a) and the radial direction $V_{r}$ (b).

4.2 Orthogonality of different source components for far-field power noise spectra

Figure 9 shows far-field noise spectra predictions for two typical microphone angles based on the complete source integration volume with and without neglecting some of the mixed terms in the acoustic integral to investigate the effect of mutual orthogonality of individual source terms.

The total spectra solution and the reference experimental data are included in the same panels for comparison. The two approximate solutions shown correspond to (i) assuming the orthogonality of different azimuthal modes $\sum _{n}\overline{\hat{p}^{(n)}(\boldsymbol{x},\unicode[STIX]{x1D714})\hat{p}^{(n)\ast }(\boldsymbol{x},\unicode[STIX]{x1D714})}$ and (ii) further assuming the orthogonality of different source terms $\sum _{n}\overline{\hat{p}_{\unicode[STIX]{x1D626}_{4j}}^{(n)}(\boldsymbol{x},\unicode[STIX]{x1D714})\hat{p}_{\unicode[STIX]{x1D626}_{4j}}^{(n)\ast }(\boldsymbol{x},\unicode[STIX]{x1D714})}+\sum _{n}\overline{\hat{p}_{\unicode[STIX]{x1D735}_{j}\widetilde{v}_{i}}^{(n)}(\boldsymbol{x},\unicode[STIX]{x1D714})\hat{p}_{\unicode[STIX]{x1D735}_{j}\widetilde{v}_{i}}^{(n)\ast }(\boldsymbol{x},\unicode[STIX]{x1D714})}+\sum _{n}\overline{\hat{p}_{\unicode[STIX]{x1D626}_{ij}}^{(n)}(\boldsymbol{x},\unicode[STIX]{x1D714})\hat{p}_{\unicode[STIX]{x1D626}_{ij}}^{(n)\ast }(\boldsymbol{x},\unicode[STIX]{x1D714})}$ for the far-field sound power spectra in (2.18). It should be noted that both of the approximate solutions are within 1–2 dB of the total spectra for most frequencies, which confirms the validity of the assumption of mutual orthogonality for different stress term components in the SILOET jet case.

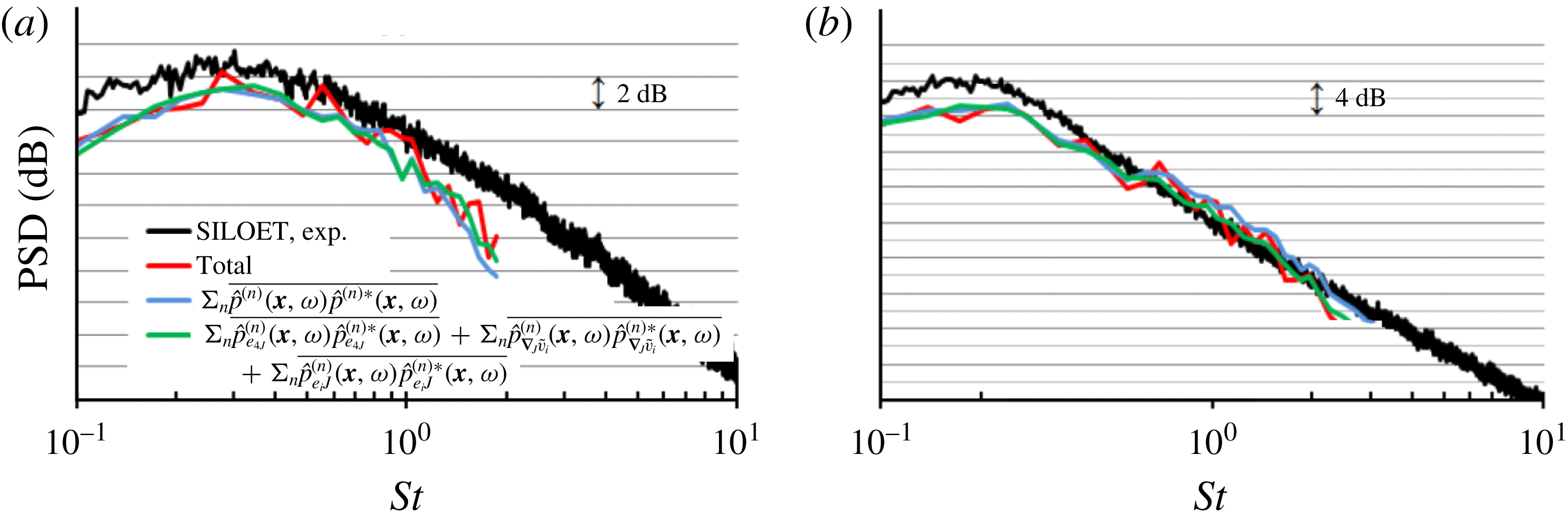
Figure 9. Orthogonality of individual source term components for far-field sound spectra at $60^{\circ }$ (a) and $30^{\circ }$ angle (b) to the jet flow. The predictions shown correspond to the total spectra, the spectra solutions with the assumption of orthogonality of different azimuthal modes of the source, and the assumption of orthogonality of different stress terms.

4.3 Effect of the source type and directivity on far-field noise

Figure 10 shows the contributions to the far-field noise spectra produced by various turbulent fluctuating stresses in comparison with the total spectra. There are contributions of various components of the fluctuating Reynolds stresses, $\unicode[STIX]{x1D626}_{ij}^{\prime \prime }$ , considered $(i,j=1,2,3)$ , where $\boldsymbol{e}_{1}$ is the Cartesian coordinate in the jet flow direction, $(\boldsymbol{e}_{2},\boldsymbol{e}_{3})$ are in the transverse plane and $(\boldsymbol{e}_{1},\boldsymbol{e}_{2})$ are in plane with the far-field microphone, as discussed in § 2.2. The contributions of the enthalpy fluctuation term, $\hat{\unicode[STIX]{x1D626}}_{4j}^{\prime \prime }(\boldsymbol{y},\unicode[STIX]{x1D714})$ , and the term that includes the velocity divergence, ${\hat{\unicode[STIX]{x1D626}}_{ij}^{\prime \prime }(\boldsymbol{y},\unicode[STIX]{x1D714})\unicode[STIX]{x1D735}}_{j}\widetilde{v}_{i}(\boldsymbol{y})$ , are also shown. The integration domain corresponds to the entire jet source volume.

Figure 10(a) shows that for $90^{\circ }$ microphone angle, the contribution of the enthalpy term and the velocity divergence term to the far-field noise is negligible compared with the fluctuating Reynolds stresses. This is the generalised stress term which corresponds to the Lighthill quadrupole noise source. Fluctuating Reynolds stresses remain the dominant noise component terms for other polar angles as well. However, the directivity of the dominant Reynolds stress component changes depending on the polar angle. For example, the $\unicode[STIX]{x1D626}_{22}^{\prime \prime }$ stress component is most important at $90^{\circ }$ angle, $\hat{\unicode[STIX]{x1D626}}_{22}^{\prime \prime },\hat{\unicode[STIX]{x1D626}}_{21}^{\prime \prime },\hat{\unicode[STIX]{x1D626}}_{12}^{\prime \prime },\hat{\unicode[STIX]{x1D626}}_{11}^{\prime \prime }$ all become significant for $60^{\circ }$ , and $\hat{\unicode[STIX]{x1D626}}_{11}^{\prime \prime },\hat{\unicode[STIX]{x1D626}}_{12}^{\prime \prime },\hat{\unicode[STIX]{x1D626}}_{21}^{\prime \prime }$ are important for $30^{\circ }$ . The relative contribution of the Reynolds stress components also depends on the sound frequency. For example, the relative importance of $\unicode[STIX]{x1D626}_{12}^{\prime \prime }$ increases at high frequencies, while $\unicode[STIX]{x1D626}_{21}^{\prime \prime }$ is most important at low frequencies and small angles to the jet flows. The contribution of the out-of-plane components remains negligible for all angles and frequencies.

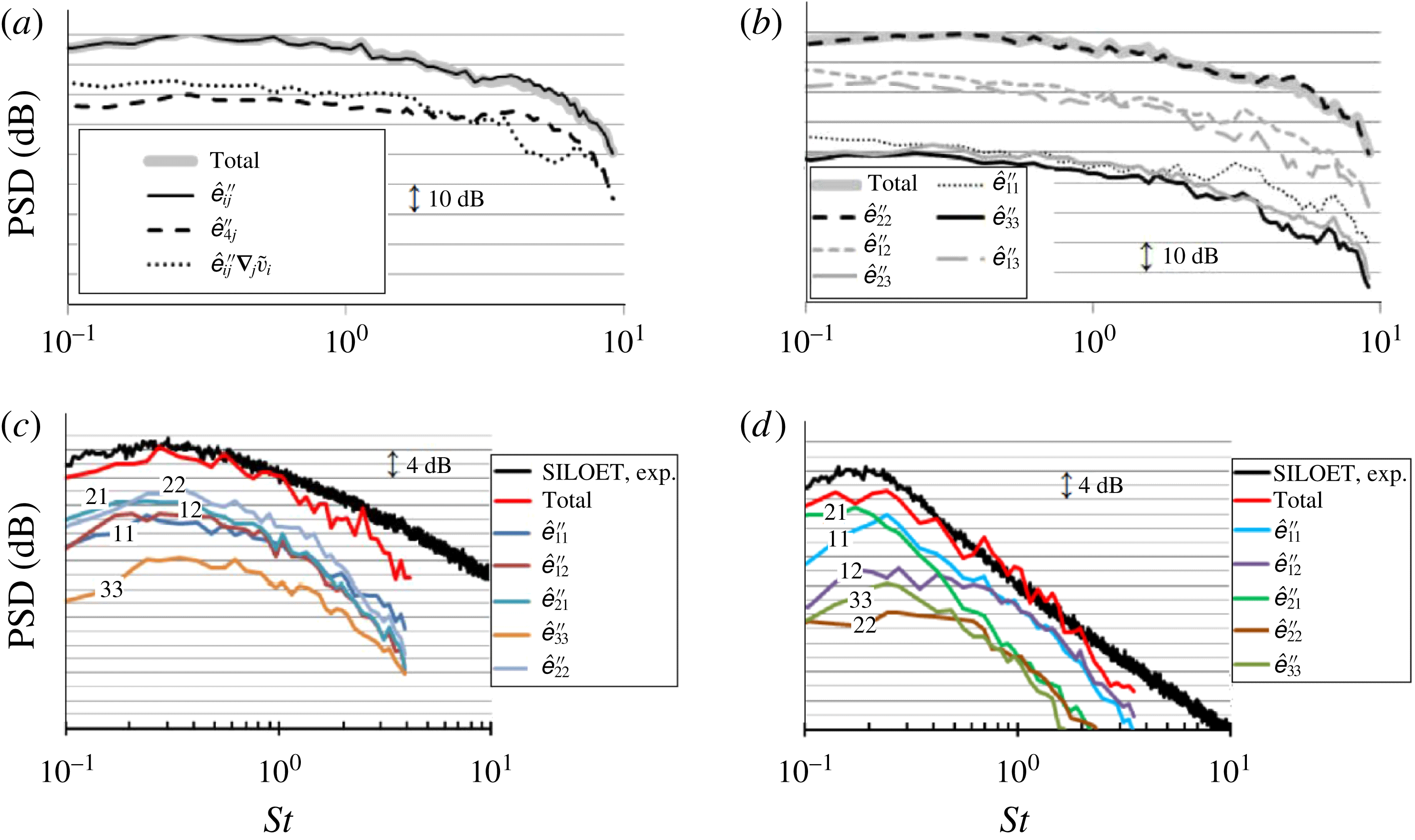
Figure 10. Contributions of individual fluctuating stresses to far-field noise spectra: comparison of the fluctuating Reynolds stress term with the fluctuating enthalpy and the velocity divergence terms for $90^{\circ }$ polar angle (a), comparison of various components of the fluctuating Reynolds stress term for $90^{\circ }$ polar angle (b), comparison of various components of the fluctuating Reynolds stress term for $60^{\circ }$ polar angle (c) and comparison of various components of the fluctuating Reynolds stress term for $30^{\circ }$ polar angle (d).

4.4 Contribution of the azimuthal source modes to the far-field noise

Figure 11 shows the contributions of different modes of the fluctuating Reynolds stresses to the far-field noise spectra for different polar angles. The total spectra solutions based on the same complete integration volume and the experimental data are shown on the same plots for comparison.

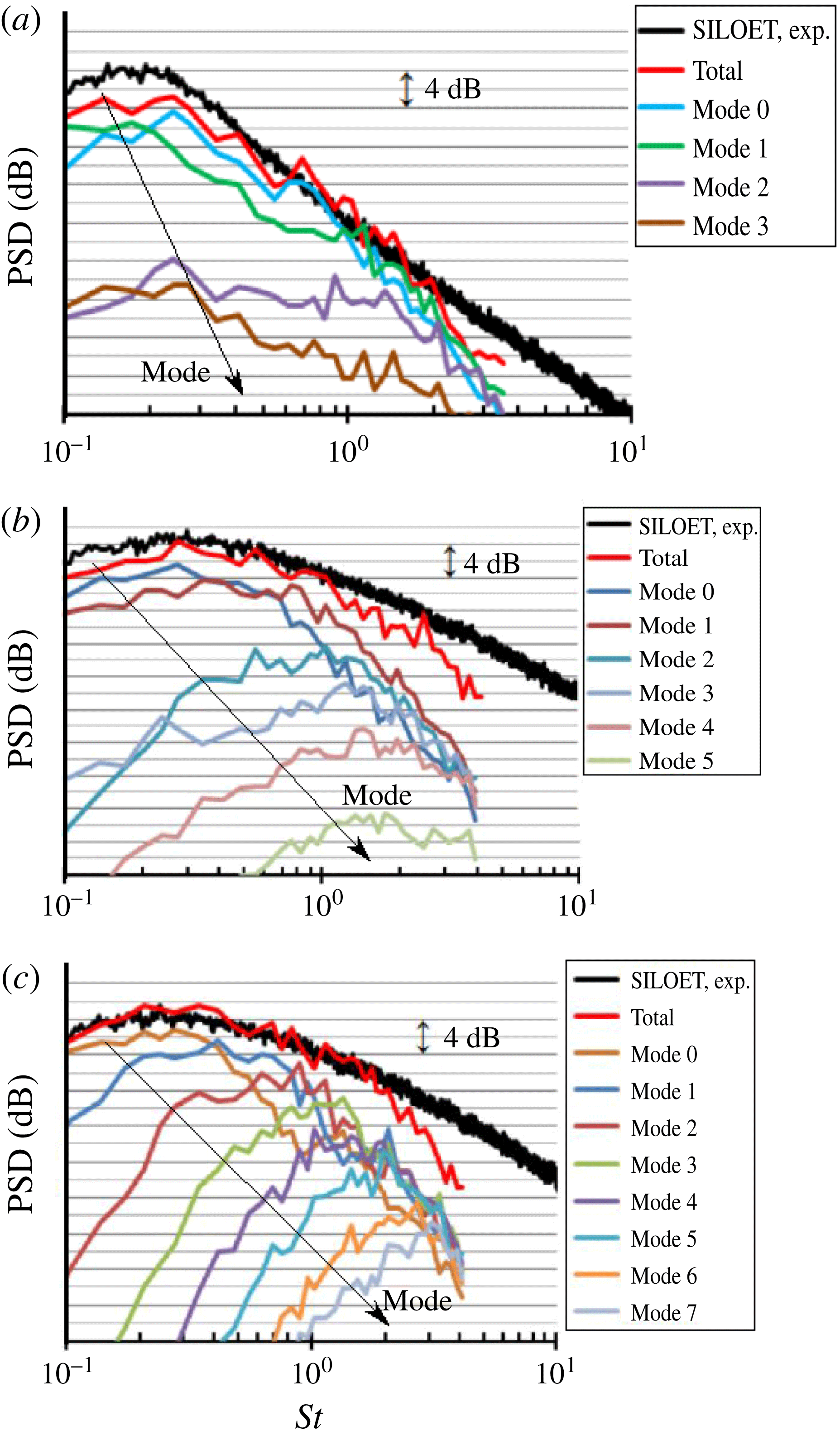
Figure 11. Contributions to the far-field noise spectra from different azimuthal modes of the fluctuating Reynolds stresses for $30^{\circ }$ (a), $60^{\circ }$ (b) and $90^{\circ }$ (c) polar angle to the jet flow.

For the $30^{\circ }$ angle to the jet flow, the axisymmetric azimuthal mode, $n=0$ , is the most dominant component in the frequency range $0.2<St<0.8$ , where $St\sim 0.2$ corresponds to the lowest numerical frequencies, which are numerically captured for sound spectra predictions at this polar angle (see the discussion in § 3). This observation is in agreement with existing experiments Cavalieri et al. (Reference Cavalieri, Rodriguez, Jordan, Colonius and Gervais2013), which show that it is the zero-order azimuthal mode, $n=0$ , that mostly contributes to jet noise at the $30^{\circ }$ polar angle.

For high polar angles, $60^{\circ }$ and $90^{\circ }$ to the jet flow, the first asymmetric azimuthal mode, $n=1$ , becomes increasingly important starting from mid frequencies, $St\geqslant 0.4$ . As the sound frequency increases, the importance of other high-order modes also increases. The increase in relative importance of high-order modes with frequency is most notable at the $90^{\circ }$ polar angle compared with small angles to the jet flow. For example, at $St=1$ and $30^{\circ }$ polar angle, there are only a few significant modes, $n=0$ and 1, that contribute to the far-field noise spectra efficiently, while for the $60^{\circ }$ polar angle, it is the $n=1$ mode that is most significant, and for the $90^{\circ }$ angle, it is the modes $n=1$ and 2 that contribute to the far-field noise effectively. All of this is also consistent with the analysis presented in Goldstein (Reference Goldstein1975) and Goldstein et al. (Reference Goldstein, Sescu and Afsar2012), who showed that the $n=0$ mode is highly directional, and hence does not significantly contribute to the $90^{\circ }$ noise spectrum. Notably, the effect of high-order azimuthal modes on sound spectra at large polar angles to the jet flow, which is captured by the current calibration-free implementation of the generalised acoustic analogy, would be difficult to reproduce by approaches based on modelling of coherent large-scale structures that stem from the instability wave theory.

4.5 Effect of the mean-flow sound propagation on the far-field noise

In addition to the effect of the source integration volume and individual source components, the effect of mean-flow sound propagation is an important contributor to the far-field noise. In this subsection, the effect of the Green’s function on the far-field solution is analysed by comparing the noise predictions obtained with the locally parallel solution and those obtained with the free-space solution which completely ignores the jet refraction effect. In each case, the integration volume and the noise source description are fixed to be the same and correspond to a complete set of the fluctuating stresses, $\unicode[STIX]{x1D626}_{\unicode[STIX]{x1D707}j}^{\prime \prime }$ , of the Goldstein generalised acoustic analogy.

Both noise spectra solutions, with and without taking the mean-flow effect into account, are integrated in the frequency band $0.05<St<2$ and compared with the corresponding overall sound pressure level (OASPL) data from the SILOET experiment.

The results are given in table 3, which shows the differences between the reference OASPL data and the two far-field predictions of the volume integral method based on the Goldstein generalised acoustic analogy with and without considering the mean-flow propagation effect as a function of the polar angle. The error for the solution that includes the corresponding Green’s function that takes into account the mean-flow effect remains within 0.5–2.2 dB. Compared with this, the error of the same volume integral method based on the free-space Green’s function monotonically grows with decrease of the polar angle and reaches 6 dB for $30^{\circ }$ microphone angle. It should be noted that the error can be expected to be much larger at the higher Mach numbers corresponding to take-off conditions. This error growth signifies the importance of mean-flow propagation effects for small angles of noise radiation to the jet flow. The latter is in agreement with the existing jet noise literature that discusses the effect of mean-flow sound propagation modelling on noise spectra predictions at small angles to the jet flow (compare with figure 16 from Karabasov et al. (Reference Karabasov, Afsar, Hynes, Dowling, McMullan, Prokora, Page and McGuirk2010) and figure 12(a,b) from Karabasov et al. (Reference Karabasov, Bogey and Hynes2013)).

For comparison, the same table also shows the OASPL error, which corresponds to an integral volume implementation of the classical Lighthill acoustic analogy based on the LES solution of a high-speed jet case from Bogey, Bailly & Juve (Reference Bogey, Bailly and Juve2001). For this case, there are no experimental data available and the reference ‘true solution’ was defined by computing the LES solution inside a large control surface and then integrating the latter to the far field using the Kirchhoff method. Using the digitised data from Bogey et al. (Reference Bogey, Bailly and Juve2001), the Lighthill acoustic analogy error was then specified as the difference between the reference ‘true solution’ and the OASPL predictions of the Lighthill acoustic analogy solution. It should be noted that the latter error fluctuates between $+2.5$  dB and $-5$  dB and does not show any particular trend with the polar angle.

Table 3. Dependence of the OASPL error on the acoustic model and the polar angle.