2. Drop impact experiments

To analyse the influence of the surface tension and viscosity of liquid, five liquids are used: pure ethanol (ethanol), deionized water (water), 1:1 glycerol–water mixture (glycerol 6 mPa s), 1:1.3 glycerol–water mixture (glycerol 10 mPa s) and 1:3 glycerol–water mixture (glycerol 51 mPa s). The liquid density ${\it\rho}$ , viscosity ${\it\mu}$ and surface tension ${\it\gamma}$ are reported in table 1.

We selected three smooth surfaces with an arithmetic average roughness $R_{a}<0.5~{\rm\mu}\text{m}$ : glass, steel and parafilm. The parafilm substrate is prepared on slide glass with a plastic paraffin film (PARAFILM M, Sigma-Aldrich). The rough surfaces are sandpaper (Silicon Carbide Paper, Buehler) with different grit sizes (P120, P240, P600 and P2500), a monolayer of glass beads sintered to a glass surface (GB) and a sandblasted glass slide (SB). The roughness is measured by a contact profilometer (Surftest-211, Mitutoyo) equipped with a $5~{\rm\mu}\text{m}$ radius diamond-tipped stylus. The roughness $R_{a}$ for the different surfaces is given in table 2.

The wettability in equilibrium conditions is characterized by the contact angle of the droplet. The contact angle ${\it\theta}_{eq}$ is determined with a $3~{\rm\mu}\text{l}$ sessile droplet in equilibrium (no movement) after gentle deposition from a needle. The equilibrium contact angle is obtained from a polynomial fit to the outline of the liquid–vapour interface (table 3). At equilibrium conditions, glass and steel are wetting surfaces for all liquids, while parafilm is wetting for ethanol and non-wetting for water and glycerol.

Droplets are generated at a flat-tipped needle by means of the pendant method. The syringe pump pushes the liquid at the rate of $20~{\rm\mu}\text{l}~\text{min}^{-1}$ though the needle until a single droplet detaches. The drop impact is recorded in shadowgraphy using a high-speed camera (10 000 f.p.s., $7.38~{\rm\mu}\text{m}$ spatial resolution and $5~{\rm\mu}\text{s}$ exposure time). The impact velocity is varied by varying the height of the needle above the surface. The impact velocity is increased until splashing (prompt splash) starts to occur. The impact conditions are given in table 1. Droplet impact for each measuring condition is repeated at least three times. A custom-made image analysis MATLAB code is used to measure the initial droplet diameter $D_{0}$ , the impact velocity $V_{i}$ , the spreading diameter $D(t)$ , the dynamic contact angle ${\it\theta}_{D}(t)$ , the maximum spreading diameter $D_{max}$ at $t_{max}$ and the dynamic contact angle at maximum spreading ${\it\theta}_{D}(t_{max})$ . The dynamic contact angle is obtained from the image by applying a goniometric mask (Biolè & Bertola Reference Biolè and Bertola2015) on the region of $100~{\rm\mu}\text{m}$ vertically above the surface line. As an example, figure 1 shows the typical time evolution of the spreading ratio ${\it\beta}(t)=D(t)/D_{0}$ , the dynamic contact angle ${\it\theta}_{D}(t)$ , as well as the maximum spreading ratio ${\it\beta}_{max}$ and the dynamic contact angle at maximum spreading ${\it\theta}_{D}(t_{max})$ for three liquids on a steel surface with $V_{i}\sim 1.0~\text{m}~\text{s}^{-1}$ .

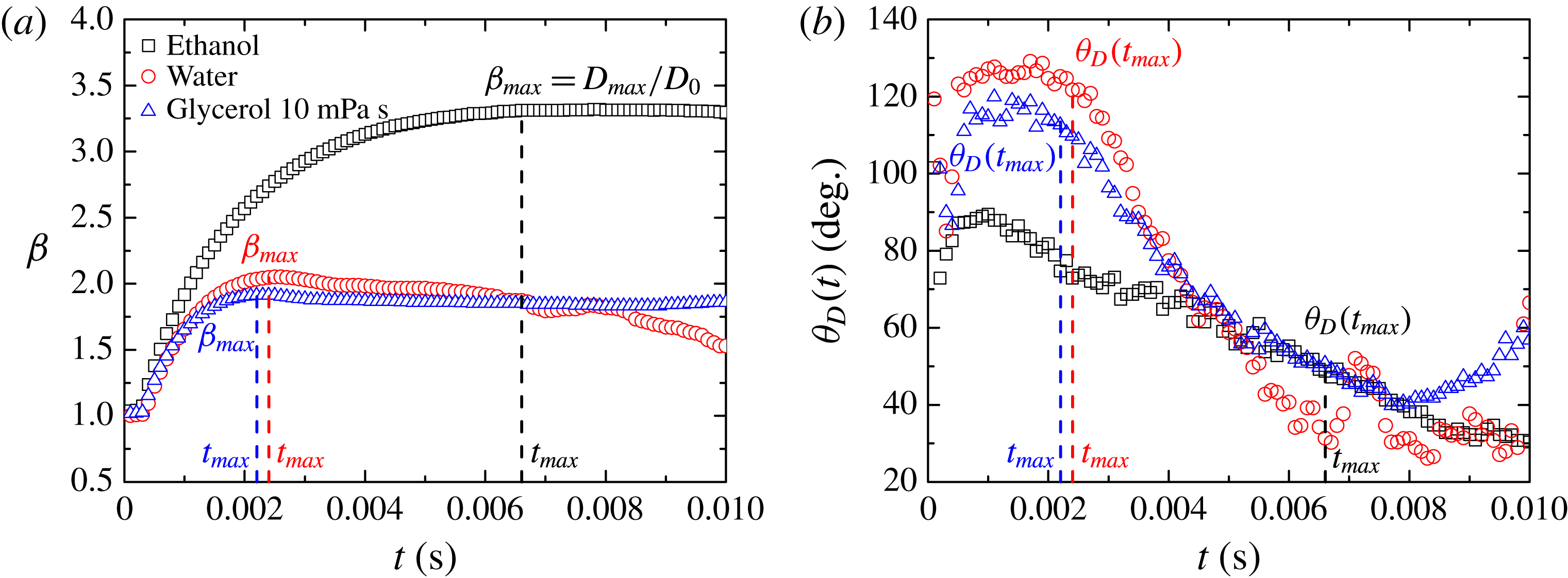
Figure 1. Time evolution of (a) the spreading ratio and (b) the dynamic contact angle for different liquids. The vertical lines indicate the time at maximal spreading.

Figure 2. Snapshots of droplets impacting on a steel surface at maximal spreading as a function of impact velocity ( $V_{i}=0.2{-}1.8~\text{m}~\text{s}^{-1}$ ): (a) ethanol, (b) water, (c) glycerol $10~\text{mPa}~\text{s}$ .

Figure 3. Maximum spreading ratio versus impact velocity. (a) Different liquids on different smooth surfaces. (b) Influence of viscosity (smooth surfaces). (c) Influence of roughness (liquid $=$ water).

Figure 2 shows snapshots of ethanol, water and glycerol 10 mPa s impacting on a smooth steel surface at maximum spreading for different impact velocities ( $V_{i}=0.2{-}1.8~\text{m}~\text{s}^{-1}$ ). The maximum spreading ratio ${\it\beta}_{max}$ increases with impact velocity for all three liquids. Ethanol spreads further and reaches its maximum spreading later in time than water and glycerol. The dynamic contact angle at maximum spreading, also indicated in the figure, is approximately constant over the impact velocity range. We report the average values of the dynamic contact angle at maximum spreading in table 3. The dynamic contact angle of ethanol lies in the range of $44^{\circ }$ – $63^{\circ }$ , which is higher than the equilibrium contact angle ( $21^{\circ }$ ). Water and glycerol also show a higher dynamic contact angle ( $94^{\circ }$ – $123^{\circ }$ ) than the equilibrium contact angle ( $22^{\circ }$ – $61^{\circ }$ ) for glass and steel, while for parafilm the equilibrium and dynamic contact angles are equal (approximately $110^{\circ }$ ). For completeness, the time at maximum spreading, $t_{max}$ , is indicated in the images, which decreases with impact velocity.

There is a clear distinction in the maximum spreading ratio ${\it\beta}_{max}$ between the different liquids on the smooth surfaces (glass, steel and parafilm) as a function of the impact velocity (figure 3 a). Given a specific liquid, the maximum spreading ratio is almost identical for all of the smooth surfaces. Accordingly, we argue that the liquid, not the substrate, plays the most important role. Ethanol shows the highest maximum spreading, while glycerol shows the lowest maximum spreading. The maximum spreading of water shows a transition between the glycerol at low impact velocity and the ethanol at high impact velocity. At low impact velocity, the spreading is similar for water and glycerol as their values of surface tension are similar. We may conclude that the nature of the substrate has only a small influence on the spreading and, with a proper rescaling by the surface wettability, we will show that this influence disappears (see below).

Figure 3(b) shows the maximum spreading ratio for liquids of increasing viscosity: water and water–glycerol mixtures 6, 10 and 51 mPa s respectively. The liquid viscosity limits the spreading at high velocity, but does not influence the spreading at low velocity, where all curves tend to acquire similar values.

Figure 3(c) shows the maximum spreading ratio for water on rough surfaces: four sandpapers of different roughnesses, monolayered sintered glass beads (GB) and sandblasted glass (SB). Although the surfaces have different roughness and equilibrium wetting characteristics, the maximum spreading ratio is almost identical for all of them and is equal to the spreading ratio on a smooth surface. We therefore conclude that the roughness of the substrate has a rather small influence on the spreading. We will further show that, when we rescale the curves for different liquids and substrates taking into account the dynamic wetting behaviour at low velocity, all curves collapse onto a single curve.

3. Scaling of the maximum spreading diameter

When considering the energy balance of a droplet impacting on a solid substrate, the kinetic energy, the capillary energy and the viscous dissipation have to be taken into account. During impact, the spreading droplet deforms until it reaches its maximum diameter $D_{max}$ within a few milliseconds. The capillary energy can then be written as $E_{{\it\gamma}}\sim {\it\gamma}D_{max}^{2}$ and the energy dissipated by viscous forces as $E_{{\it\mu}}\sim {\it\mu}V_{i}D_{max}^{5}/D_{0}^{3}$ (Madejski Reference Madejski1976; Collings et al. Reference Collings, Markworth, McCoy and Saunders1990). In the capillary limit, we can assume that kinetic energy is transformed into capillary energy, $E_{k}\sim E_{{\it\gamma}}$ . In this regime, the maximum spreading ratio scales as ${\it\beta}_{max}\sim We^{1/2}$ (Bechtel et al. Reference Bechtel, Bogy and Talke1993; Eggers et al. Reference Eggers, Fontelos, Josserand and Zaleski2010). In the viscous limit, the kinetic energy is totally transformed into viscous energy, $E_{k}\sim E_{{\it\mu}}$ . Then, the maximum spreading ratio scales as ${\it\beta}_{max}\sim Re^{1/5}$ (Madejski Reference Madejski1976; Chandra & Avedisian Reference Chandra and Avedisian1991). The scaling of ${\it\beta}_{max}\sim We^{1/2}$ implies that, at zero impact velocity, the spreading ratio equals zero, which is physically impossible ( ${\it\beta}_{max}$ ${\geqslant}$ 1). At low impact velocity, the spreading ratio does not tend to zero, but levels off to a limiting value, which is referred to in the following as ${\it\beta}_{V_{i}\rightarrow 0}$ (figure 4).

The spreading ratio ${\it\beta}_{V_{i}\rightarrow 0}$ is determined by approximating the measured data by the function

where $A$ , $B$ , $C$ and ${\it\beta}_{V_{i}\rightarrow 0}$ are fitting parameters. Figure 4 shows that (3.1) describes the measured data for liquid droplets on a steel surface satisfactorily. Table 4 gives the values for ${\it\beta}_{V_{i}\rightarrow 0}$ on different substrates and for different liquids.

Figure 4. Example of the determination of the maximum spreading ratio at zero impact velocity ${\it\beta}_{V_{i}\rightarrow 0}$ by fitting (3.1) to the measured data.

When we assume that the spreading droplet attains the form of a spherical cap while it keeps a constant volume (Berthier & Beebe Reference Berthier and Beebe2007), the spreading ratio ${\it\beta}_{V_{i}\rightarrow 0}$ can be related to a contact angle ${\it\theta}_{V_{i}\rightarrow 0}$ . It is necessary to discern between the cases for a hydrophilic surface ( ${\it\theta}_{V_{i}\rightarrow 0}<90^{\circ }$ ) and a hydrophobic surface ( ${\it\theta}_{V_{i}\rightarrow 0}>90^{\circ }$ ). The spreading ratio is given by

This equation allows determination of a contact angle ${\it\theta}_{V_{i}\rightarrow 0}$ given a value of ${\it\beta}_{V_{i}\rightarrow 0}$ . Figure 5(a) compares the dynamic contact angle ${\it\theta}_{D}(t_{max})$ , determined from experiments, and the contact angle ${\it\theta}_{V_{i}\rightarrow 0}$ , determined from ${\it\beta}_{V_{i}\rightarrow 0}$ using (3.2). Regardless of a constant offset, the contact angle ${\it\theta}_{V_{i}\rightarrow 0}$ predicts fairly well the measured contact angles during dynamic wetting ${\it\theta}_{D}(t_{max})$ . The offset is attributed to an empty volume in the spherical cap model (see figure 5 a,b), since the real droplet shape does not totally resemble a spherical cap but rather acquires the form of a pancake. The missing volume leads to an underprediction of the contact angle by the spherical cap model.

The aim of this analysis is to demonstrate that dynamic wetting plays an important role in the spreading at low velocities, and that the dynamic wetting as characterized by the dynamic contact angle ${\it\theta}_{D}$ has to be taken into account in predicting the maximum spreading. The analysis above shows that the capillary energy related to ${\it\theta}_{V_{i}\rightarrow 0}$ or to ${\it\beta}_{V_{i}\rightarrow 0}$ has to be incorporated in the maximum spreading model.

Figure 5. (a) Comparison of the dynamic contact angle ${\it\theta}_{D}(t_{max})$ (from experiments) and the contact angle ${\it\theta}_{V_{i}\rightarrow 0}$ determined from ${\it\beta}_{V_{i}\rightarrow 0}$ using (3.2). (b,c) Spherical cap representation of a droplet with height $h$ , radius $R$ , maximum droplet diameter $D$ and corresponding contact angle ${\it\theta}$ : (b) ${\it\theta}<90^{\circ }$ , (c)  ${\it\theta}>90^{\circ }$ .

To do so, we add the capillary energy $E_{{\it\gamma}0}\sim {\it\gamma}D_{V_{i}\rightarrow 0}^{2}$ in the low-velocity limit, where $D_{V_{i}\rightarrow 0}={\it\beta}_{V_{i}\rightarrow 0}D_{0}$ . Then, the energy balance reads

which leads to

Equation (3.4) shows that we can still assume a scaling with $We^{1/2}$ after a correction for dynamic wetting using the maximum spreading ratio at zero velocity ${\it\beta}_{V_{i}\rightarrow 0}$ as from (3.1). After correction, the maximum spreading should still scale with $We^{1/2}$ and $Re^{1/5}$ at low and high velocities respectively. Similarly to Laan et al. (Reference Laan, de Bruin, Bartolo, Josserand and Bonn2014), the interpolation between the low- and high-impact-velocity regimes can be written as

The function $f$ allows a smooth cross-over between the two limits where only one fitting parameter is required to successfully describe the data and is based on the first-order Padé approximation (Laan et al. Reference Laan, de Bruin, Bartolo, Josserand and Bonn2014)

Figure 6 shows the rescaled measured data $({\it\beta}_{max}^{2}-{\it\beta}_{V_{i}\rightarrow 0}^{2})^{1/2}$ versus the Weber number. We observe that all rescaled data, for all liquids and all substrates (roughness, nature), collapse onto a single curve. In addition, using this approach it is shown that, for low impact velocities the maximum spreading ratio approaches ${\it\beta}_{V_{i}\rightarrow 0}$ and for high impact velocities, we find once more the $Re^{1/5}$ scaling. Moreover, the transition from low impact velocity towards high impact velocity is a function of $We^{1/2}$ . The curve as predicted by (3.6) ( $A=7.6$ ) describes the data very well. The larger error bars at low velocity are due to the logarithmic scaling.

This result shows that we universally rescale the maximum spreading ratio for different liquids and substrates into a single description, when the dynamic wettability is taken into account accurately.

Figure 6. The rescaled maximum spreading ratio as a function of the Weber number in a log–log plot for all liquids and smooth and rough surfaces. The dotted line is the first-order Padé approximation (3.6).