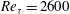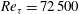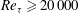1. Introduction
The scaling of turbulent wall-bounded flows with Reynolds number has been the subject of much recent interest and debate (Marusic et al.
Reference Marusic, McKeon, Monkewitz, Nagib, Smits and Sreenivasan2010; Smits, McKeon & Marusic Reference Smits, McKeon and Marusic2011a
; Smits & Marusic Reference Smits and Marusic2013), and new experiments have expanded considerably the range of Reynolds numbers available for study. For example, examinations of pipe flow have reported mean flow data at values of
![]() $\mathit{Re}_{{\it\tau}}$
as high as 530 000 (Zagarola & Smits Reference Zagarola and Smits1998; McKeon et al.
Reference McKeon, Li, Jiang, Morrison and Smits2004), where
$\mathit{Re}_{{\it\tau}}$
as high as 530 000 (Zagarola & Smits Reference Zagarola and Smits1998; McKeon et al.
Reference McKeon, Li, Jiang, Morrison and Smits2004), where
![]() $\mathit{Re}_{{\it\tau}}$
is the friction Reynolds number, with turbulence data at values up to 98 000 (Hultmark et al.
Reference Hultmark, Vallikivi, Bailey and Smits2012, Reference Hultmark, Vallikivi, Bailey and Smits2013; Rosenberg et al.
Reference Rosenberg, Hultmark, Vallikivi, Bailey and Smits2013). For boundary layer flows under laboratory conditions, the corresponding values are 70 000 (Winter & Gaudet Reference Winter and Gaudet1973) and 19 000 (Mathis, Hutchins & Marusic Reference Mathis, Hutchins and Marusic2009), although some limited but valuable turbulence data were acquired at 69 000 in the LCC facility by Winkel et al. (Reference Winkel, Cutbirth, Ceccio, Perlin and Dowling2012), and at 650 000 in the neutral atmospheric boundary layer by Hutchins et al. (Reference Hutchins, Chauhan, Marusic, Monty and Klewicki2012).
$\mathit{Re}_{{\it\tau}}$
is the friction Reynolds number, with turbulence data at values up to 98 000 (Hultmark et al.
Reference Hultmark, Vallikivi, Bailey and Smits2012, Reference Hultmark, Vallikivi, Bailey and Smits2013; Rosenberg et al.
Reference Rosenberg, Hultmark, Vallikivi, Bailey and Smits2013). For boundary layer flows under laboratory conditions, the corresponding values are 70 000 (Winter & Gaudet Reference Winter and Gaudet1973) and 19 000 (Mathis, Hutchins & Marusic Reference Mathis, Hutchins and Marusic2009), although some limited but valuable turbulence data were acquired at 69 000 in the LCC facility by Winkel et al. (Reference Winkel, Cutbirth, Ceccio, Perlin and Dowling2012), and at 650 000 in the neutral atmospheric boundary layer by Hutchins et al. (Reference Hutchins, Chauhan, Marusic, Monty and Klewicki2012).
The available laboratory data are limited in Reynolds number primarily because of experimental difficulties. Conducting high Reynolds number experiments usually requires large and often expensive facilities, and for scaling studies the flows need to be of high quality and employ high-resolution instrumentation. Here, we use a pressurized facility, the Princeton High Reynolds Number Test Facility (HRTF), to generate very high Reynolds number flat-plate boundary layers. We report results obtained at a maximum Reynolds number based on the momentum thickness of 235 000, which is believed to be higher than that investigated in any previous laboratory study featuring well-controlled initial and boundary conditions. The HRTF is the counterpart to the Princeton Superpipe facility, which has been extensively used to examine very high Reynolds number pipe flows. Here, we present the first data from this unique boundary layer wind tunnel, which, together with novel nanoscale flow sensors, will enable us to investigate canonical flat-plate boundary layers over an unprecedented range of Reynolds numbers.
The friction Reynolds number,
![]() $\mathit{Re}_{{\it\tau}}=u_{{\it\tau}}{\it\delta}/{\it\nu}$
, provides a common standard for comparisons among wall-bounded flows. Here,
$\mathit{Re}_{{\it\tau}}=u_{{\it\tau}}{\it\delta}/{\it\nu}$
, provides a common standard for comparisons among wall-bounded flows. Here,
![]() $u_{{\it\tau}}=\sqrt{{\it\tau}_{w}/{\it\rho}}$
is the friction velocity,
$u_{{\it\tau}}=\sqrt{{\it\tau}_{w}/{\it\rho}}$
is the friction velocity,
![]() ${\it\tau}_{w}$
is the wall shear stress,
${\it\tau}_{w}$
is the wall shear stress,
![]() ${\it\rho}$
and
${\it\rho}$
and
![]() ${\it\nu}$
are fluid density and kinematic viscosity, respectively, and
${\it\nu}$
are fluid density and kinematic viscosity, respectively, and
![]() ${\it\delta}$
is the boundary layer thickness
${\it\delta}$
is the boundary layer thickness
![]() ${\it\delta}_{99}$
, or the pipe radius
${\it\delta}_{99}$
, or the pipe radius
![]() $R$
, or the half-height of the channel
$R$
, or the half-height of the channel
![]() $h$
. This Reynolds number, also known as the von Kármán number, characterizes the range of scales present in the flow, and avoids the use of more specific velocity and length scales such as the free-stream velocity
$h$
. This Reynolds number, also known as the von Kármán number, characterizes the range of scales present in the flow, and avoids the use of more specific velocity and length scales such as the free-stream velocity
![]() $U_{\infty }$
, the bulk velocity
$U_{\infty }$
, the bulk velocity
![]() $\langle U\rangle$
, the momentum thickness
$\langle U\rangle$
, the momentum thickness
![]() ${\it\theta}$
, or the displacement thickness
${\it\theta}$
, or the displacement thickness
![]() ${\it\delta}^{\ast }$
.
${\it\delta}^{\ast }$
.
For turbulent wall-bounded flows at sufficiently large Reynolds numbers, we expect that for
![]() $y^{+}=yu_{{\it\tau}}/{\it\nu}\gg 1$
and
$y^{+}=yu_{{\it\tau}}/{\it\nu}\gg 1$
and
![]() $y/{\it\delta}\ll 1$
, the mean velocity
$y/{\it\delta}\ll 1$
, the mean velocity
![]() $U$
behaves logarithmically according to
$U$
behaves logarithmically according to
(Millikan Reference Millikan1938), where
![]() $U^{+}=U/u_{{\it\tau}}$
,
$U^{+}=U/u_{{\it\tau}}$
,
![]() $y$
is the wall-normal distance,
$y$
is the wall-normal distance,
![]() ${\it\kappa}$
is the von Kármán constant, and
${\it\kappa}$
is the von Kármán constant, and
![]() $B$
is the additive constant for the mean velocity. The values of
$B$
is the additive constant for the mean velocity. The values of
![]() ${\it\kappa}$
reported in the past have varied over a considerable range, with values as low as 0.38 in a boundary layer (Österlund et al.
Reference Österlund, Johansson, Nagib and Hites2000) and as high as 0.42 in a pipe (McKeon et al.
Reference McKeon, Li, Jiang, Morrison and Smits2004). A recent study by Bailey et al. (Reference Bailey, Vallikivi, Hultmark and Smits2014) showed that for pipe flow
${\it\kappa}$
reported in the past have varied over a considerable range, with values as low as 0.38 in a boundary layer (Österlund et al.
Reference Österlund, Johansson, Nagib and Hites2000) and as high as 0.42 in a pipe (McKeon et al.
Reference McKeon, Li, Jiang, Morrison and Smits2004). A recent study by Bailey et al. (Reference Bailey, Vallikivi, Hultmark and Smits2014) showed that for pipe flow
![]() ${\it\kappa}=0.40\pm 0.02$
, where the uncertainty estimate reflects the many sources of error that make it difficult to find
${\it\kappa}=0.40\pm 0.02$
, where the uncertainty estimate reflects the many sources of error that make it difficult to find
![]() ${\it\kappa}$
more precisely even when the friction velocity is well known. For boundary layers one would expect an even larger variation due to the difficulty in estimating
${\it\kappa}$
more precisely even when the friction velocity is well known. For boundary layers one would expect an even larger variation due to the difficulty in estimating
![]() $u_{{\it\tau}}$
.
$u_{{\it\tau}}$
.
The pipe flow measurements by Zagarola & Smits (Reference Zagarola and Smits1998) and McKeon et al. (Reference McKeon, Li, Jiang, Morrison and Smits2004) revealed that the start of the log-law region in the mean flow, commonly assumed to be located at
![]() $y^{+}=30{-}50$
, was actually located much further from the wall at
$y^{+}=30{-}50$
, was actually located much further from the wall at
![]() $y^{+}=600$
, or even
$y^{+}=600$
, or even
![]() $y^{+}=1000$
. In boundary layers, George & Castillo (Reference George and Castillo1997) argued that the inner limit was located at
$y^{+}=1000$
. In boundary layers, George & Castillo (Reference George and Castillo1997) argued that the inner limit was located at
![]() $y^{+}\approx 300$
, whereas Wei et al. (Reference Wei, Fife, Klewicki and McMurtry2005) suggested a Reynolds-number-dependent lower limit and Nagib, Chauhan & Monkewitz (Reference Nagib, Chauhan and Monkewitz2007) reported a value of
$y^{+}\approx 300$
, whereas Wei et al. (Reference Wei, Fife, Klewicki and McMurtry2005) suggested a Reynolds-number-dependent lower limit and Nagib, Chauhan & Monkewitz (Reference Nagib, Chauhan and Monkewitz2007) reported a value of
![]() $y^{+}=200$
. As to the outer limit, values in the literature range from
$y^{+}=200$
. As to the outer limit, values in the literature range from
![]() $y/{\it\delta}=0.08$
to 0.3, with Marusic et al. (Reference Marusic, Monty, Hultmark and Smits2013) suggesting a value of 0.15. With an inner limit of
$y/{\it\delta}=0.08$
to 0.3, with Marusic et al. (Reference Marusic, Monty, Hultmark and Smits2013) suggesting a value of 0.15. With an inner limit of
![]() $y^{+}=300$
, and an outer limit of
$y^{+}=300$
, and an outer limit of
![]() $y/{\it\delta}=0.15$
, a decade of logarithmic variation in the mean velocity of a boundary layer is not expected to occur until
$y/{\it\delta}=0.15$
, a decade of logarithmic variation in the mean velocity of a boundary layer is not expected to occur until
![]() $\mathit{Re}_{{\it\tau}}=20\,000$
, which is the upper limit of the detailed data sets that have so far been available for boundary layers.
$\mathit{Re}_{{\it\tau}}=20\,000$
, which is the upper limit of the detailed data sets that have so far been available for boundary layers.
As to the behaviour of the turbulence, Townsend (Reference Townsend1976) and Perry, Henbest & Chong (Reference Perry, Henbest and Chong1986) suggested that a logarithmic behaviour in streamwise and wall-parallel fluctuations should also occur in the region where (1.1) holds, if the Reynolds number is large enough. That is, for the streamwise velocity fluctuations
![]() $u$
, we would expect
$u$
, we would expect
where
![]() $u^{2+}=\overline{u^{2}}/u_{{\it\tau}}^{2}$
,
$u^{2+}=\overline{u^{2}}/u_{{\it\tau}}^{2}$
,
![]() $A_{1}$
is the Townsend–Perry constant, and
$A_{1}$
is the Townsend–Perry constant, and
![]() $B_{1}$
is the additive constant for the variance. This logarithmic behaviour was first observed experimentally in pipe flow over a significant wall-normal extent by Hultmark et al. (Reference Hultmark, Vallikivi, Bailey and Smits2012), where it only became evident for
$B_{1}$
is the additive constant for the variance. This logarithmic behaviour was first observed experimentally in pipe flow over a significant wall-normal extent by Hultmark et al. (Reference Hultmark, Vallikivi, Bailey and Smits2012), where it only became evident for
![]() $y/R<0.12$
once
$y/R<0.12$
once
![]() $\mathit{Re}_{{\it\tau}}\geqslant 20\,000$
, with a spatial extent that increased with Reynolds number. Marusic et al. (Reference Marusic, Monty, Hultmark and Smits2013) suggested that this scaling also applies in boundary layers, and proposed a universal value of
$\mathit{Re}_{{\it\tau}}\geqslant 20\,000$
, with a spatial extent that increased with Reynolds number. Marusic et al. (Reference Marusic, Monty, Hultmark and Smits2013) suggested that this scaling also applies in boundary layers, and proposed a universal value of
![]() $A_{1}=1.26$
.
$A_{1}=1.26$
.
In deriving (1.2), Townsend appealed to his attached eddy hypothesis, where the turbulent eddy length scales are assumed to be proportional to
![]() $y$
with a population density proportional to
$y$
with a population density proportional to
![]() $y^{-1}$
. Meneveau & Marusic (Reference Meneveau and Marusic2013) used this hypothesis to show that if the summands are assumed to be statistically independent (as in the case of non-interacting eddies), the
$y^{-1}$
. Meneveau & Marusic (Reference Meneveau and Marusic2013) used this hypothesis to show that if the summands are assumed to be statistically independent (as in the case of non-interacting eddies), the
![]() $p$
th root of moments of velocity fluctuations is expected to behave according to
$p$
th root of moments of velocity fluctuations is expected to behave according to
where
![]() $A_{p}$
and
$A_{p}$
and
![]() $B_{p}$
are constants, at least at fixed Reynolds number. They examined the validity of this generalized logarithmic law in boundary layers with
$B_{p}$
are constants, at least at fixed Reynolds number. They examined the validity of this generalized logarithmic law in boundary layers with
![]() $\mathit{Re}_{{\it\tau}}$
up to 19 000, and found that the behaviour of high-order moments was sub-Gaussian, and that there may be a universal value of
$\mathit{Re}_{{\it\tau}}$
up to 19 000, and found that the behaviour of high-order moments was sub-Gaussian, and that there may be a universal value of
![]() $A_{p}$
.
$A_{p}$
.
It is evident from this previous work that high Reynolds number data reveal intriguing trends in the scaling of the mean flow and the turbulence. At the same time it is clear that for boundary layers high-quality turbulence data over any extensive range of Reynolds numbers is limited to values of
![]() $\mathit{Re}_{{\it\tau}}<20\,000$
, and it appears that this might be the lower limit of what is possibly the start of an asymptotic behaviour (Smits & Marusic Reference Smits and Marusic2013). In order to extend the boundary layer observations beyond this value, we now describe a new experimental study that examines turbulent boundary layer behaviour for
$\mathit{Re}_{{\it\tau}}<20\,000$
, and it appears that this might be the lower limit of what is possibly the start of an asymptotic behaviour (Smits & Marusic Reference Smits and Marusic2013). In order to extend the boundary layer observations beyond this value, we now describe a new experimental study that examines turbulent boundary layer behaviour for
![]() $2600\leqslant \mathit{Re}_{{\it\tau}}\leqslant 72\,500$
. Here, we focus on the behaviour of the mean flow, the variance, and the higher-order moments of the streamwise velocity fluctuations. The spectral behaviour is reported separately by Vallikivi, Ganapathisubramani & Smits (Reference Vallikivi, Ganapathisubramani and Smits2015). We will, wherever possible, compare the boundary layer data with the results of pipe flow at similar Reynolds numbers.
$2600\leqslant \mathit{Re}_{{\it\tau}}\leqslant 72\,500$
. Here, we focus on the behaviour of the mean flow, the variance, and the higher-order moments of the streamwise velocity fluctuations. The spectral behaviour is reported separately by Vallikivi, Ganapathisubramani & Smits (Reference Vallikivi, Ganapathisubramani and Smits2015). We will, wherever possible, compare the boundary layer data with the results of pipe flow at similar Reynolds numbers.
2. Experimental methods
The measurements were conducted in the HRTF at the Princeton University Gas Dynamics Laboratory. The HRTF is a closed-loop wind tunnel that uses air at pressures up to 220 atm as the working fluid. The tunnel has a maximum speed of
![]() $12~\text{m}~\text{s}^{-1}$
and free-stream turbulence intensity levels between 0.3 and 0.6 %. It has two working sections, each 2.44 m long with a 0.49 m inner diameter, as shown in figure 1(a). The facility is described in further detail by Jiménez, Hultmark & Smits (Reference Jiménez, Hultmark and Smits2010).
$12~\text{m}~\text{s}^{-1}$
and free-stream turbulence intensity levels between 0.3 and 0.6 %. It has two working sections, each 2.44 m long with a 0.49 m inner diameter, as shown in figure 1(a). The facility is described in further detail by Jiménez, Hultmark & Smits (Reference Jiménez, Hultmark and Smits2010).

Figure 1. The Princeton HRTF. (a) Tunnel layout; (b) flat-plate details.
A 2.06 m flat-plate model with an elliptic leading edge was mounted in the downstream test section of the wind tunnel. A 1 mm square tripwire, located 76 mm from the leading edge, was used to trip the boundary layer. A single measurement station was used, located 1.82 m downstream of the tripwire (figure 1
b). The aluminum surface of the plate was polished to a mirror finish. The surface roughness was estimated using an optical microscope and comparator plates and found to be less than
![]() $0.15~{\rm\mu}\text{m}$
, corresponding to
$0.15~{\rm\mu}\text{m}$
, corresponding to
![]() $k_{rms}^{+}<0.4$
at the highest Reynolds number studied, so that for all conditions the plate was assumed to be hydraulically smooth.
$k_{rms}^{+}<0.4$
at the highest Reynolds number studied, so that for all conditions the plate was assumed to be hydraulically smooth.
The pressure distribution in the circular test section was adjusted using a ‘blister’ insert attached to the tunnel wall on the opposite side of the plate, as shown in figure 1(b). The pressure distribution was measured using 18 streamwise and 15 spanwise pressure taps, and the insert was adjusted to minimize the pressure gradient. The local streamwise pressure gradient parameter
![]() $K_{p}=({\it\nu}/U_{\infty }^{2})(\text{d}U_{\infty }/\text{d}x)=({\it\nu}/{\it\rho}u_{{\it\tau}}^{3})(\text{d}p/\text{d}x)$
was found to be less than
$K_{p}=({\it\nu}/U_{\infty }^{2})(\text{d}U_{\infty }/\text{d}x)=({\it\nu}/{\it\rho}u_{{\it\tau}}^{3})(\text{d}p/\text{d}x)$
was found to be less than
![]() $1\times 10^{-8}$
for all cases (Vallikivi, Hultmark & Smits Reference Vallikivi, Hultmark and Smits2013; Vallikivi Reference Vallikivi2014). This value is an order of magnitude smaller than that reported in some previous studies (for example, DeGraaff & Eaton (Reference DeGraaff and Eaton2000) reported
$1\times 10^{-8}$
for all cases (Vallikivi, Hultmark & Smits Reference Vallikivi, Hultmark and Smits2013; Vallikivi Reference Vallikivi2014). This value is an order of magnitude smaller than that reported in some previous studies (for example, DeGraaff & Eaton (Reference DeGraaff and Eaton2000) reported
![]() $K_{p}<1.1\times 10^{-7}$
), and therefore the flow was assumed to be free of pressure gradient effects.
$K_{p}<1.1\times 10^{-7}$
), and therefore the flow was assumed to be free of pressure gradient effects.
2.1. NSTAP measurements
In the current study, two nanoscale thermal anemometry probes (NSTAPs) were used, one with filament length
![]() $\ell =60~{\rm\mu}\text{m}$
and cross-section
$\ell =60~{\rm\mu}\text{m}$
and cross-section
![]() $0.1~{\rm\mu}\text{m}\times 2~{\rm\mu}\text{m}$
, and a second one with
$0.1~{\rm\mu}\text{m}\times 2~{\rm\mu}\text{m}$
, and a second one with
![]() $\ell =30~{\rm\mu}\text{m}$
and cross-section
$\ell =30~{\rm\mu}\text{m}$
and cross-section
![]() $0.08~{\rm\mu}\text{m}\times 1.5~{\rm\mu}\text{m}$
. The fabrication, validation and behaviour of these sensors are described in detail by Bailey et al. (Reference Bailey, Kunkel, Hultmark, Vallikivi, Hill, Meyer, Tsay, Arnold and Smits2010), Vallikivi et al. (Reference Vallikivi, Hultmark, Bailey and Smits2011) and Vallikivi & Smits (Reference Vallikivi and Smits2014).
$0.08~{\rm\mu}\text{m}\times 1.5~{\rm\mu}\text{m}$
. The fabrication, validation and behaviour of these sensors are described in detail by Bailey et al. (Reference Bailey, Kunkel, Hultmark, Vallikivi, Hill, Meyer, Tsay, Arnold and Smits2010), Vallikivi et al. (Reference Vallikivi, Hultmark, Bailey and Smits2011) and Vallikivi & Smits (Reference Vallikivi and Smits2014).
The sensors were operated using a Dantec Streamline Constant Temperature Anemometry system with a 1:1 bridge, keeping the heated filament at a temperature of about 450 K. The frequency response, determined from a square wave test, was always above 150 kHz in still air, increasing to more than 300 kHz in the flow. The data were digitized using a 16-bit A/D board (NI PCI-6123) at a rate of 300 kHz and low-pass filtered using an eighth-order Butterworth filter at 150 kHz. The sensor was traversed in the wall-normal direction using a stepper motor traverse with a Numeric Jena LIK22 encoder with a resolution of
![]() $0.05~{\rm\mu}\text{m}$
. The initial wall-normal distance
$0.05~{\rm\mu}\text{m}$
. The initial wall-normal distance
![]() $y_{0}$
of the probe was measured using a depth-measuring microscope (Titan Tool Supply Inc.) with an accuracy of
$y_{0}$
of the probe was measured using a depth-measuring microscope (Titan Tool Supply Inc.) with an accuracy of
![]() $5~{\rm\mu}\text{m}$
.
$5~{\rm\mu}\text{m}$
.
The NSTAPs were calibrated using a 0.4 mm Pitot tube together with two 0.4 mm static pressure taps located in the pipe wall at the same streamwise location. The Pitot tube measurements were corrected for static tap Reynolds number effects and viscous effects using the correlations proposed by McKeon & Smits (Reference McKeon and Smits2002) and McKeon et al. (Reference McKeon, Li, Jiang, Morrison and Smits2003), respectively. Fourteen calibration points were used, and the calibration was performed before and after each profile measurement. A fourth-order polynomial fit was used to find the calibration coefficients. The ambient fluid temperature change during a given profile ranged from 0.7 to 10.0 °C over the full Reynolds number range, and the data were corrected using the temperature correction outlined by Hultmark & Smits (Reference Hultmark and Smits2010).
NSTAP data were acquired for
![]() $2600<\mathit{Re}_{{\it\tau}}<72\,500$
, corresponding to
$2600<\mathit{Re}_{{\it\tau}}<72\,500$
, corresponding to
![]() $8400<\mathit{Re}_{{\it\theta}}<235\,000$
(where
$8400<\mathit{Re}_{{\it\theta}}<235\,000$
(where
![]() $\mathit{Re}_{{\it\theta}}=U_{\infty }{\it\theta}/{\it\nu}$
). The tunnel was pressurized for all cases and the experimental conditions are listed in table 1 (cases 1–7). Here,
$\mathit{Re}_{{\it\theta}}=U_{\infty }{\it\theta}/{\it\nu}$
). The tunnel was pressurized for all cases and the experimental conditions are listed in table 1 (cases 1–7). Here,
![]() $p_{a}$
denotes the ambient pressure,
$p_{a}$
denotes the ambient pressure,
![]() $\ell ^{+}$
is the wire length in viscous units (
$\ell ^{+}$
is the wire length in viscous units (
![]() $=\!\ell u_{{\it\tau}}/{\it\nu}$
),
$=\!\ell u_{{\it\tau}}/{\it\nu}$
),
![]() $y_{0}$
is the initial wall-normal distance and
$y_{0}$
is the initial wall-normal distance and
![]() $y_{0}^{+}=y_{0}u_{{\it\tau}}/{\it\nu}$
. The data were sampled for 60 s in cases 1–6 and for 20 s in case 7, corresponding to convection lengths of more than 20 000 and
$y_{0}^{+}=y_{0}u_{{\it\tau}}/{\it\nu}$
. The data were sampled for 60 s in cases 1–6 and for 20 s in case 7, corresponding to convection lengths of more than 20 000 and
![]() $5000{\it\delta}$
, respectively. Convergence was tested by comparing the magnitudes of the moments evaluated over the full sampling time with those obtained over half the sampling time. Even for the 10th-order moment, the differences were within 3 %.
$5000{\it\delta}$
, respectively. Convergence was tested by comparing the magnitudes of the moments evaluated over the full sampling time with those obtained over half the sampling time. Even for the 10th-order moment, the differences were within 3 %.
Table 1. Experimental conditions for boundary layer measurements:
![]() $p_{a}$
is the ambient tunnel pressure,
$p_{a}$
is the ambient tunnel pressure,
![]() $y_{0}$
is the initial distance from the wall, and
$y_{0}$
is the initial distance from the wall, and
![]() $u_{{\it\tau}}$
is derived using the correlation proposed by Fernholz & Finley (Reference Fernholz and Finley1996). Cases 1–7: NSTAP data with sensor length
$u_{{\it\tau}}$
is derived using the correlation proposed by Fernholz & Finley (Reference Fernholz and Finley1996). Cases 1–7: NSTAP data with sensor length
![]() $\ell$
. Cases 8–14: Pitot probe data with diameter
$\ell$
. Cases 8–14: Pitot probe data with diameter
![]() $d_{p}$
.
$d_{p}$
.

It can be seen from table 1 that at the higher Reynolds number even the NSTAP probe has insufficient spatial resolution. To minimize bias errors due to spatial filtering, the correction by Smits et al. (Reference Smits, Monty, Hultmark, Bailey, Hutchins and Marusic2011b
) was applied to the variance. Smits et al. showed that this correction works well for
![]() $\ell ^{+}$
up to 153, considerably greater than the maximum value found here (
$\ell ^{+}$
up to 153, considerably greater than the maximum value found here (
![]() $=\!75$
). Any data on the variance where the spatial filtering correction exceeded 5 % are shown with grey symbols in figure 4. Note that spatial resolution has its major effect in the near-wall region, and even at the highest Reynolds numbers the correction is less than 5 % for
$=\!75$
). Any data on the variance where the spatial filtering correction exceeded 5 % are shown with grey symbols in figure 4. Note that spatial resolution has its major effect in the near-wall region, and even at the highest Reynolds numbers the correction is less than 5 % for
![]() $200{\it\nu}/u_{{\it\tau}}<y=0.003{\it\delta}$
. For the higher-order moments, no equivalent correction method exists, so all higher-order data points where the correction on the variance exceeded 5 % were removed from the data set. In addition to spatial filtering, there is the uncertainty in initial wall location
$200{\it\nu}/u_{{\it\tau}}<y=0.003{\it\delta}$
. For the higher-order moments, no equivalent correction method exists, so all higher-order data points where the correction on the variance exceeded 5 % were removed from the data set. In addition to spatial filtering, there is the uncertainty in initial wall location
![]() $y_{0}$
(about
$y_{0}$
(about
![]() $5~{\rm\mu}\text{m}$
), which needs to be borne in mind when examining the results for
$5~{\rm\mu}\text{m}$
), which needs to be borne in mind when examining the results for
![]() $y^{+}<100$
at high Reynolds numbers.
$y^{+}<100$
at high Reynolds numbers.
2.2. Pitot tube measurements
In addition to the NSTAP data, Pitot tube measurements were taken for
![]() $2800<\mathit{Re}_{{\it\tau}}<65\,000$
, corresponding to
$2800<\mathit{Re}_{{\it\tau}}<65\,000$
, corresponding to
![]() $9400<\mathit{Re}_{{\it\theta}}<223\,000$
. The experimental conditions for these cases are given in table 1 (cases 8–14). A Pitot probe with an outer diameter of
$9400<\mathit{Re}_{{\it\theta}}<223\,000$
. The experimental conditions for these cases are given in table 1 (cases 8–14). A Pitot probe with an outer diameter of
![]() $d_{p}=0.20~\text{mm}$
was used, in conjunction with two 0.4 mm static pressure taps in the plate. The pressure difference was measured using a DP15 Validyne pressure transducer with a 1.40 kPa range which was calibrated against a manometer standard. As for the NSTAP measurements, the initial wall distance of the Pitot probe
$d_{p}=0.20~\text{mm}$
was used, in conjunction with two 0.4 mm static pressure taps in the plate. The pressure difference was measured using a DP15 Validyne pressure transducer with a 1.40 kPa range which was calibrated against a manometer standard. As for the NSTAP measurements, the initial wall distance of the Pitot probe
![]() $y_{0}$
was measured using a depth-measuring optical microscope and the probe was traversed in the wall-normal direction using a stepper motor traverse with a resolution of
$y_{0}$
was measured using a depth-measuring optical microscope and the probe was traversed in the wall-normal direction using a stepper motor traverse with a resolution of
![]() $0.05~{\rm\mu}\text{m}$
. The Pitot tube measurements were corrected following Bailey et al. (Reference Bailey, Hultmark, Monty, Alfredsson, Chong, Duncan, Fransson, Hutchins, Marusic, McKeon, Nagib, Örlü, Segalini, Smits and Vinuesa2013), including the static tap correction by McKeon et al. (Reference McKeon, Li, Jiang, Morrison and Smits2003), viscous and shear corrections by Zagarola & Smits (Reference Zagarola and Smits1998), and the near-wall correction by MacMillan (Reference MacMillan1957). The data for wall distances smaller than
$0.05~{\rm\mu}\text{m}$
. The Pitot tube measurements were corrected following Bailey et al. (Reference Bailey, Hultmark, Monty, Alfredsson, Chong, Duncan, Fransson, Hutchins, Marusic, McKeon, Nagib, Örlü, Segalini, Smits and Vinuesa2013), including the static tap correction by McKeon et al. (Reference McKeon, Li, Jiang, Morrison and Smits2003), viscous and shear corrections by Zagarola & Smits (Reference Zagarola and Smits1998), and the near-wall correction by MacMillan (Reference MacMillan1957). The data for wall distances smaller than
![]() $2d_{p}$
were neglected, as in the pipe flow experiments described by Bailey et al. (Reference Bailey, Vallikivi, Hultmark and Smits2014). Further details on the experimental techniques are given by Vallikivi (Reference Vallikivi2014).
$2d_{p}$
were neglected, as in the pipe flow experiments described by Bailey et al. (Reference Bailey, Vallikivi, Hultmark and Smits2014). Further details on the experimental techniques are given by Vallikivi (Reference Vallikivi2014).
2.3. Friction velocity
To determine
![]() $u_{{\it\tau}}$
and the skin friction coefficient
$u_{{\it\tau}}$
and the skin friction coefficient
![]() $C_{f}=2u_{{\it\tau}}^{2}/U_{\infty }^{2}$
, a number of different methods were used. First, the 0.2 mm Pitot probe when in contact with the wall was used as a Preston tube (Patel Reference Patel1965; Zagarola, Williams & Smits Reference Zagarola, Williams and Smits2001). Second, the Clauser chart technique (Clauser Reference Clauser1956) was used, where the log-law was fitted to the velocity profiles using the constants
$C_{f}=2u_{{\it\tau}}^{2}/U_{\infty }^{2}$
, a number of different methods were used. First, the 0.2 mm Pitot probe when in contact with the wall was used as a Preston tube (Patel Reference Patel1965; Zagarola, Williams & Smits Reference Zagarola, Williams and Smits2001). Second, the Clauser chart technique (Clauser Reference Clauser1956) was used, where the log-law was fitted to the velocity profiles using the constants
![]() ${\it\kappa}=0.40$
and
${\it\kappa}=0.40$
and
![]() $B=5.1$
recommended by Coles (Reference Coles1956). These results were compared to the skin friction correlation proposed by Fernholz & Finley (Reference Fernholz and Finley1996), as well as data from one of the few direct measurements of skin friction using a drag plate at high Reynolds number (Winter & Gaudet Reference Winter and Gaudet1973) (see figure 2). For comparison, values from DeGraaff & Eaton (Reference DeGraaff and Eaton2000) found using the Clauser chart are also shown.
$B=5.1$
recommended by Coles (Reference Coles1956). These results were compared to the skin friction correlation proposed by Fernholz & Finley (Reference Fernholz and Finley1996), as well as data from one of the few direct measurements of skin friction using a drag plate at high Reynolds number (Winter & Gaudet Reference Winter and Gaudet1973) (see figure 2). For comparison, values from DeGraaff & Eaton (Reference DeGraaff and Eaton2000) found using the Clauser chart are also shown.

Figure 2. Boundary layer skin friction coefficient
![]() $C_{f}$
: ○, Preston tube; ▫, Clauser fit for Pitot data sets; ▪, Clauser fit for NSTAP data sets (Clauser Reference Clauser1956); *, DeGraaff & Eaton (Reference DeGraaff and Eaton2000); solid line, Fernholz & Finley (Reference Fernholz and Finley1996); dashed line, Winter & Gaudet (Reference Winter and Gaudet1973). Error bars indicate
$C_{f}$
: ○, Preston tube; ▫, Clauser fit for Pitot data sets; ▪, Clauser fit for NSTAP data sets (Clauser Reference Clauser1956); *, DeGraaff & Eaton (Reference DeGraaff and Eaton2000); solid line, Fernholz & Finley (Reference Fernholz and Finley1996); dashed line, Winter & Gaudet (Reference Winter and Gaudet1973). Error bars indicate
![]() $\pm 5\,\%$
.
$\pm 5\,\%$
.
All
![]() $C_{f}$
estimates except for the Preston tube data had a standard deviation less than 3 % compared to the Fernholz correlation. In addition, the Fernholz correlation closely matches the average value obtained by the other methods, and it agrees well with the force plate measurements by Winter & Gaudet (Reference Winter and Gaudet1973) over the same Reynolds number range. Hence, we used the value of
$C_{f}$
estimates except for the Preston tube data had a standard deviation less than 3 % compared to the Fernholz correlation. In addition, the Fernholz correlation closely matches the average value obtained by the other methods, and it agrees well with the force plate measurements by Winter & Gaudet (Reference Winter and Gaudet1973) over the same Reynolds number range. Hence, we used the value of
![]() $u_{{\it\tau}}$
determined from the Fernholz correlation for all subsequent data analysis.
$u_{{\it\tau}}$
determined from the Fernholz correlation for all subsequent data analysis.
2.4. Pipe flow data for comparison
We compare the turbulent boundary layer data with that from fully developed turbulent pipe flow obtained by Hultmark et al. (Reference Hultmark, Vallikivi, Bailey and Smits2012, Reference Hultmark, Vallikivi, Bailey and Smits2013). The cases used for comparison are listed in table 2, and cover
![]() $3300\leqslant \mathit{Re}_{{\it\tau}}\leqslant 98\,000$
.
$3300\leqslant \mathit{Re}_{{\it\tau}}\leqslant 98\,000$
.
Table 2. Pipe flow data for comparison, from Hultmark et al. (Reference Hultmark, Vallikivi, Bailey and Smits2013).

3. Results and discussion
In presenting the results, we use a single notation
![]() ${\it\delta}$
to denote the outer length scale, that is, the boundary layer thickness for boundary layer data and the pipe radius for pipe flow data.
${\it\delta}$
to denote the outer length scale, that is, the boundary layer thickness for boundary layer data and the pipe radius for pipe flow data.
3.1. Mean flow
The mean velocity profiles for the boundary layer are shown in figure 3. The agreement between the NSTAP and Pitot profiles is within 1.3 %, well within the uncertainty on
![]() $U$
(estimated to be
$U$
(estimated to be
![]() ${<}\!2.2\,\%$
). The mean velocity behaviour and scaling in boundary layers may be compared to the behaviour in pipe flow by referring to the extensive discussions of pipe flows given by Zagarola & Smits (Reference Zagarola and Smits1998), McKeon et al. (Reference McKeon, Li, Jiang, Morrison and Smits2004), Hultmark et al. (Reference Hultmark, Vallikivi, Bailey and Smits2013) and Bailey et al. (Reference Bailey, Vallikivi, Hultmark and Smits2014), and so this will not be repeated here. Suffice it to say that both flows show an extended region of logarithmic behaviour, although for the boundary layer this behaviour starts closer to the wall compared to pipe flows, where the log-law only appears for
${<}\!2.2\,\%$
). The mean velocity behaviour and scaling in boundary layers may be compared to the behaviour in pipe flow by referring to the extensive discussions of pipe flows given by Zagarola & Smits (Reference Zagarola and Smits1998), McKeon et al. (Reference McKeon, Li, Jiang, Morrison and Smits2004), Hultmark et al. (Reference Hultmark, Vallikivi, Bailey and Smits2013) and Bailey et al. (Reference Bailey, Vallikivi, Hultmark and Smits2014), and so this will not be repeated here. Suffice it to say that both flows show an extended region of logarithmic behaviour, although for the boundary layer this behaviour starts closer to the wall compared to pipe flows, where the log-law only appears for
![]() $y^{+}>600{-}800$
. The middle of the log-layer, located at
$y^{+}>600{-}800$
. The middle of the log-layer, located at
![]() $y^{+}=3\mathit{Re}_{{\it\tau}}^{0.5}$
according to Marusic et al. (Reference Marusic, Monty, Hultmark and Smits2013), served as a conservative lower bound for fitting the logarithmic portion of the profile, and for all cases the log-layer was found to extend to about
$y^{+}=3\mathit{Re}_{{\it\tau}}^{0.5}$
according to Marusic et al. (Reference Marusic, Monty, Hultmark and Smits2013), served as a conservative lower bound for fitting the logarithmic portion of the profile, and for all cases the log-layer was found to extend to about
![]() $0.15{\it\delta}$
. Due to the many uncertainties in the evaluation of the slope (and friction velocity in the boundary layer), it is not possible to determine any differences in the von Kármán constant between pipes and boundary layers (Bailey et al.
Reference Bailey, Vallikivi, Hultmark and Smits2014). The constants proposed by Coles (Reference Coles1956) (
$0.15{\it\delta}$
. Due to the many uncertainties in the evaluation of the slope (and friction velocity in the boundary layer), it is not possible to determine any differences in the von Kármán constant between pipes and boundary layers (Bailey et al.
Reference Bailey, Vallikivi, Hultmark and Smits2014). The constants proposed by Coles (Reference Coles1956) (
![]() ${\it\kappa}=0.40$
and
${\it\kappa}=0.40$
and
![]() $B=5.1$
) give an equally good fit for both flows.
$B=5.1$
) give an equally good fit for both flows.

Figure 3. Boundary layer mean velocity profiles. (a) Inner coordinates; (b) inner coordinates, each profile shifted by
![]() ${\rm\Delta}U^{+}=5$
; (c) outer coordinates. Symbols as given in table 1. In (a,b) solid black lines show (1.1) with
${\rm\Delta}U^{+}=5$
; (c) outer coordinates. Symbols as given in table 1. In (a,b) solid black lines show (1.1) with
![]() ${\it\kappa}=0.40$
and
${\it\kappa}=0.40$
and
![]() $B=5.1$
; thin solid lines show
$B=5.1$
; thin solid lines show
![]() $U^{+}=y^{+}$
.
$U^{+}=y^{+}$
.
Table 3 lists the boundary layer thickness
![]() ${\it\delta}={\it\delta}_{99}$
, displacement thickness
${\it\delta}={\it\delta}_{99}$
, displacement thickness
![]() ${\it\delta}^{\ast }$
, momentum thickness
${\it\delta}^{\ast }$
, momentum thickness
![]() ${\it\theta}$
, and shape factor
${\it\theta}$
, and shape factor
![]() $H={\it\delta}^{\ast }/{\it\theta}$
for each case. All bulk properties were found to decrease with Reynolds number in the expected manner, as observed by DeGraaff & Eaton (Reference DeGraaff and Eaton2000) and others, and they are discussed in more detail by Vallikivi et al. (Reference Vallikivi, Hultmark and Smits2013) and Vallikivi (Reference Vallikivi2014).
$H={\it\delta}^{\ast }/{\it\theta}$
for each case. All bulk properties were found to decrease with Reynolds number in the expected manner, as observed by DeGraaff & Eaton (Reference DeGraaff and Eaton2000) and others, and they are discussed in more detail by Vallikivi et al. (Reference Vallikivi, Hultmark and Smits2013) and Vallikivi (Reference Vallikivi2014).
3.2. Variances
In figure 4, profiles of the streamwise variances
![]() $u^{2+}$
are shown in inner coordinates, with the boundary layer data on the left and the pipe flow data on the right. Points in the boundary layer data where the spatial filtering correction is greater than 5 % are indicated by grey symbols. The two flows show a broadly similar behaviour with a distinct inner peak at approximately the same wall-normal position. The inner peak appears to be invariant with Reynolds number, with a non-dimensional magnitude
$u^{2+}$
are shown in inner coordinates, with the boundary layer data on the left and the pipe flow data on the right. Points in the boundary layer data where the spatial filtering correction is greater than 5 % are indicated by grey symbols. The two flows show a broadly similar behaviour with a distinct inner peak at approximately the same wall-normal position. The inner peak appears to be invariant with Reynolds number, with a non-dimensional magnitude
![]() $u_{I}^{2+}=8.4\pm 0.8$
for the boundary layer data, which agrees with the pipe data within experimental error. However, the inner peak values for the boundary layer are only resolved for the three lowest Reynolds numbers tested (
$u_{I}^{2+}=8.4\pm 0.8$
for the boundary layer data, which agrees with the pipe data within experimental error. However, the inner peak values for the boundary layer are only resolved for the three lowest Reynolds numbers tested (
![]() $2622\leqslant \mathit{Re}_{{\it\tau}}\leqslant 8261$
). Thus, the data cannot resolve the question regarding the scaling of the inner peak at higher Reynolds numbers.
$2622\leqslant \mathit{Re}_{{\it\tau}}\leqslant 8261$
). Thus, the data cannot resolve the question regarding the scaling of the inner peak at higher Reynolds numbers.

Figure 4. Variance profiles in inner coordinates: (a) boundary layer; (b) pipe. Symbols as given in tables 1 and 2. Grey symbols indicate boundary layer data where the spatial filtering exceeds 5 % according to the correction by Smits et al. (Reference Smits, Monty, Hultmark, Bailey, Hutchins and Marusic2011b ).
Table 3. Boundary layer bulk and integral properties, with
![]() $C_{f}$
obtained using Fernholz & Finley (Reference Fernholz and Finley1996) correlation; see also table 1.
$C_{f}$
obtained using Fernholz & Finley (Reference Fernholz and Finley1996) correlation; see also table 1.

The data indicate that an outer peak emerges at approximately the same Reynolds number for the two flows. The outer peak magnitude,
![]() $u_{II}^{2+}$
, was found for each Reynolds number (for the three lowest Reynolds numbers there is no peak, and so the inflection point was used instead), and the results shown in figure 5 demonstrate that the magnitudes of the outer peaks are very similar in boundary layer and pipe flows.
$u_{II}^{2+}$
, was found for each Reynolds number (for the three lowest Reynolds numbers there is no peak, and so the inflection point was used instead), and the results shown in figure 5 demonstrate that the magnitudes of the outer peaks are very similar in boundary layer and pipe flows.

Figure 5. Magnitudes of the outer peak in
![]() $u^{2+}$
: ▫, boundary layer; ○, pipe; filled symbols,
$u^{2+}$
: ▫, boundary layer; ○, pipe; filled symbols,
![]() $\mathit{Re}_{{\it\tau}}>20\,000$
; ♢, atmospheric boundary layer (Metzger, McKeon & Holmes Reference Metzger, McKeon and Holmes2007); - - - -,
$\mathit{Re}_{{\it\tau}}>20\,000$
; ♢, atmospheric boundary layer (Metzger, McKeon & Holmes Reference Metzger, McKeon and Holmes2007); - - - -,
![]() $u_{II}^{2+}=0.63\ln (\mathit{Re}_{{\it\tau}})+0.33$
(Pullin, Inoue & Saito Reference Pullin, Inoue and Saito2013); – ⋅ – ⋅ –,
$u_{II}^{2+}=0.63\ln (\mathit{Re}_{{\it\tau}})+0.33$
(Pullin, Inoue & Saito Reference Pullin, Inoue and Saito2013); – ⋅ – ⋅ –,
![]() $u_{II}^{2+}=0.42\ln (\mathit{Re}_{{\it\tau}})+2.82$
(Pullin et al.
Reference Pullin, Inoue and Saito2013);
$u_{II}^{2+}=0.42\ln (\mathit{Re}_{{\it\tau}})+2.82$
(Pullin et al.
Reference Pullin, Inoue and Saito2013);
Pullin et al. (Reference Pullin, Inoue and Saito2013) presented an analysis that supports a logarithmic increase in the outer peak value
![]() $u_{II}^{2+}$
with Reynolds number, with two possible relations depending on the relation governing the location of the peak: either
$u_{II}^{2+}$
with Reynolds number, with two possible relations depending on the relation governing the location of the peak: either
![]() $u_{II}^{2+}=0.42\ln (\mathit{Re}_{{\it\tau}})+2.82$
, or
$u_{II}^{2+}=0.42\ln (\mathit{Re}_{{\it\tau}})+2.82$
, or
![]() $u_{II}^{2+}=0.63\ln (\mathit{Re}_{{\it\tau}})+0.33$
. Figure 5 shows that these relations are in generally good agreement with the data, although our analysis gives slightly different curve fits (
$u_{II}^{2+}=0.63\ln (\mathit{Re}_{{\it\tau}})+0.33$
. Figure 5 shows that these relations are in generally good agreement with the data, although our analysis gives slightly different curve fits (
![]() $u_{II}^{2+}=0.49\ln (\mathit{Re}_{{\it\tau}})+1.7$
in pipes and
$u_{II}^{2+}=0.49\ln (\mathit{Re}_{{\it\tau}})+1.7$
in pipes and
![]() $u_{II}^{2+}=0.47\ln (\mathit{Re}_{{\it\tau}})+2.0$
in boundary layers). The data broadly support the hypothesis of Pullin et al. that at the limit of infinite Reynolds number the wall-normal turbulent transport of turbulent energy declines and the turbulence is asymptotically attenuated across the whole outer layer. Hence, with increasing Reynolds number, the locations of the inner peak (at constant
$u_{II}^{2+}=0.47\ln (\mathit{Re}_{{\it\tau}})+2.0$
in boundary layers). The data broadly support the hypothesis of Pullin et al. that at the limit of infinite Reynolds number the wall-normal turbulent transport of turbulent energy declines and the turbulence is asymptotically attenuated across the whole outer layer. Hence, with increasing Reynolds number, the locations of the inner peak (at constant
![]() $y^{+}$
) and the outer peak (varying as
$y^{+}$
) and the outer peak (varying as
![]() $\ln \mathit{Re}_{{\it\tau}}$
) are both moving closer to the wall in physical coordinates, and so the asymptotic state of the wall layer is a slip-flow bounded by a vortex sheet at the wall (Pullin et al.
Reference Pullin, Inoue and Saito2013).
$\ln \mathit{Re}_{{\it\tau}}$
) are both moving closer to the wall in physical coordinates, and so the asymptotic state of the wall layer is a slip-flow bounded by a vortex sheet at the wall (Pullin et al.
Reference Pullin, Inoue and Saito2013).
Figure 6 shows that in outer coordinates the variances do not collapse as well in boundary layers as they do in pipes, and a clear trend with increasing Reynolds numbers can be observed, especially at the lower Reynolds numbers. The mixed scaling
![]() $(u_{{\it\tau}}U_{\infty })^{0.5}$
, introduced for boundary layers by DeGraaff & Eaton (Reference DeGraaff and Eaton2000), did not noticeably improve the collapse, and so it was not pursued further.
$(u_{{\it\tau}}U_{\infty })^{0.5}$
, introduced for boundary layers by DeGraaff & Eaton (Reference DeGraaff and Eaton2000), did not noticeably improve the collapse, and so it was not pursued further.

Figure 7. Mean velocity profiles (empty symbols) and turbulence intensities (filled symbols) for
![]() $\mathit{Re}_{{\it\tau}}\approx 20\,000$
(a,b),
$\mathit{Re}_{{\it\tau}}\approx 20\,000$
(a,b),
![]() $Re_{{\it\tau}}\approx 40\,000$
(c,d),
$Re_{{\it\tau}}\approx 40\,000$
(c,d),
![]() $Re_{{\it\tau}}\approx 70\,000$
(e,f) in the boundary layer (a,c,e) and the pipe (b,d,f). Symbols as given in tables 1 and 2. Lines: - - - -, limits of logarithmic region (
$Re_{{\it\tau}}\approx 70\,000$
(e,f) in the boundary layer (a,c,e) and the pipe (b,d,f). Symbols as given in tables 1 and 2. Lines: - - - -, limits of logarithmic region (
![]() $y^{+}=400$
and
$y^{+}=400$
and
![]() $y^{+}=0.15\mathit{Re}_{{\it\tau}}$
for the boundary layer,
$y^{+}=0.15\mathit{Re}_{{\it\tau}}$
for the boundary layer,
![]() $y^{+}=800$
and
$y^{+}=800$
and
![]() $y^{+}=0.15\mathit{Re}_{{\it\tau}}$
for the pipe); ——, (1.1) with
$y^{+}=0.15\mathit{Re}_{{\it\tau}}$
for the pipe); ——, (1.1) with
![]() ${\it\kappa}=0.40,B=5.1$
, and (1.2) with
${\it\kappa}=0.40,B=5.1$
, and (1.2) with
![]() $A_{1}=1.24,B_{1}=1.48$
.
$A_{1}=1.24,B_{1}=1.48$
.
For
![]() $\mathit{Re}_{{\it\tau}}>20\,000$
, the logarithmic behaviour described by (1.2) is observed in the boundary layer profiles for
$\mathit{Re}_{{\it\tau}}>20\,000$
, the logarithmic behaviour described by (1.2) is observed in the boundary layer profiles for
![]() $y^{+}\gtrsim 400$
. This logarithmic behaviour can be seen more clearly when the data are restricted to
$y^{+}\gtrsim 400$
. This logarithmic behaviour can be seen more clearly when the data are restricted to
![]() $\mathit{Re}_{{\it\tau}}>20\,000$
and
$\mathit{Re}_{{\it\tau}}>20\,000$
and
![]() $y^{+}>100$
. The Townsend–Perry constant
$y^{+}>100$
. The Townsend–Perry constant
![]() $A_{1}=1.24$
and additive constant
$A_{1}=1.24$
and additive constant
![]() $B_{1}=1.48$
were taken from the results in pipe flow (Hultmark et al.
Reference Hultmark, Vallikivi, Bailey and Smits2013). The slope appears to be very similar in boundary layer and pipe flows, as found by Marusic et al. (Reference Marusic, Monty, Hultmark and Smits2013) (who used
$B_{1}=1.48$
were taken from the results in pipe flow (Hultmark et al.
Reference Hultmark, Vallikivi, Bailey and Smits2013). The slope appears to be very similar in boundary layer and pipe flows, as found by Marusic et al. (Reference Marusic, Monty, Hultmark and Smits2013) (who used
![]() $A_{1}=1.26$
), but for boundary layers there seems to be some variation with Reynolds number in the additive constant. The uncertainty limits on these constants are unknown at present.
$A_{1}=1.26$
), but for boundary layers there seems to be some variation with Reynolds number in the additive constant. The uncertainty limits on these constants are unknown at present.
3.3. Logarithmic regions in the mean and the variance
Profiles of the mean velocity and the variances are shown cross-plotted together in figure 7. The dashed lines correspond to
![]() $y^{+}=400$
and
$y^{+}=400$
and
![]() $y/{\it\delta}=0.15$
in the boundary layer, and
$y/{\it\delta}=0.15$
in the boundary layer, and
![]() $y^{+}=800$
and
$y^{+}=800$
and
![]() $y/{\it\delta}=0.15$
in the pipe. Both the mean velocity and the variances follow a logarithmic behaviour within these limits, but the mean velocity in the boundary layer case seems to follow a logarithmic variation down to
$y/{\it\delta}=0.15$
in the pipe. Both the mean velocity and the variances follow a logarithmic behaviour within these limits, but the mean velocity in the boundary layer case seems to follow a logarithmic variation down to
![]() $y^{+}\approx 100$
. This result indicates the presence of an intermediate range below
$y^{+}\approx 100$
. This result indicates the presence of an intermediate range below
![]() $y^{+}\approx 400$
in boundary layers, and below
$y^{+}\approx 400$
in boundary layers, and below
![]() $y^{+}\approx 800$
in pipes, where the boundary layer variances deviate from the logarithmic behaviour in a manner very similar to that described in Hultmark (Reference Hultmark2012) for pipe flows. This region corresponds approximately to the mesolayer described by Afzal (Reference Afzal1982, Reference Afzal1984), George & Castillo (Reference George and Castillo1997), Sreenivasan & Sahay (Reference Sreenivasan, Sahay and Panton1997), Wosnik, Castillo & George (Reference Wosnik, Castillo and George2000) and Wei et al. (Reference Wei, Fife, Klewicki and McMurtry2005) in boundary layers, and the power law region described by McKeon et al. (Reference McKeon, Li, Jiang, Morrison and Smits2004) in pipes. George & Castillo (Reference George and Castillo1997) suggested that in this region the mean velocity has reached a seemingly logarithmic behaviour but the effects of viscosity are still evident in the behaviour of the turbulent stress terms. Wei et al. (Reference Wei, Fife, Klewicki and McMurtry2005) identified the mesolayer with the region where the stress gradients are close to zero, and the viscous force balances the pressure force in pipe flow or the mean advection in the turbulent boundary layer. The present results are at a sufficiently high Reynolds number to distinguish the mesolayer clearly from the logarithmic region where all viscous effects are negligible, but a more precise statement needs a consideration of the spectral behaviour, which is given by Vallikivi et al. (Reference Vallikivi, Ganapathisubramani and Smits2015).
$y^{+}\approx 800$
in pipes, where the boundary layer variances deviate from the logarithmic behaviour in a manner very similar to that described in Hultmark (Reference Hultmark2012) for pipe flows. This region corresponds approximately to the mesolayer described by Afzal (Reference Afzal1982, Reference Afzal1984), George & Castillo (Reference George and Castillo1997), Sreenivasan & Sahay (Reference Sreenivasan, Sahay and Panton1997), Wosnik, Castillo & George (Reference Wosnik, Castillo and George2000) and Wei et al. (Reference Wei, Fife, Klewicki and McMurtry2005) in boundary layers, and the power law region described by McKeon et al. (Reference McKeon, Li, Jiang, Morrison and Smits2004) in pipes. George & Castillo (Reference George and Castillo1997) suggested that in this region the mean velocity has reached a seemingly logarithmic behaviour but the effects of viscosity are still evident in the behaviour of the turbulent stress terms. Wei et al. (Reference Wei, Fife, Klewicki and McMurtry2005) identified the mesolayer with the region where the stress gradients are close to zero, and the viscous force balances the pressure force in pipe flow or the mean advection in the turbulent boundary layer. The present results are at a sufficiently high Reynolds number to distinguish the mesolayer clearly from the logarithmic region where all viscous effects are negligible, but a more precise statement needs a consideration of the spectral behaviour, which is given by Vallikivi et al. (Reference Vallikivi, Ganapathisubramani and Smits2015).
3.4. Higher-order moments
We now consider the behaviour of the higher-order moments of the streamwise velocity fluctuations (up to 10th order). Because no established correction for spatial filtering on higher-order moments exists, data with more than 5 % spatial filtering on the variances, as indicated by the spatial filtering correction, were excluded from the analysis.
To make direct comparisons between boundary layer and pipe flows, six cases with matching Reynolds numbers were chosen: cases 1–3 and 5–7 given in table 1 for the boundary layer, and cases 1–6 given in table 2 for the pipe. These cases correspond to
![]() $\mathit{Re}_{{\it\tau}}\approx$
3000, 5000, 10 000, 20 000, 40 000, and 70 000, and they are summarized in table 4. The higher-order moments for the pipe are reported here for the first time, although they are based on the data collected by Hultmark et al. (Reference Hultmark, Vallikivi, Bailey and Smits2013).
$\mathit{Re}_{{\it\tau}}\approx$
3000, 5000, 10 000, 20 000, 40 000, and 70 000, and they are summarized in table 4. The higher-order moments for the pipe are reported here for the first time, although they are based on the data collected by Hultmark et al. (Reference Hultmark, Vallikivi, Bailey and Smits2013).
Table 4. Cases chosen for comparing boundary layer (current data) and pipe flow (Hultmark et al. Reference Hultmark, Vallikivi, Bailey and Smits2013).

Figure 8 shows, for a representative boundary layer case, the probability density function
![]() $P(u)$
(p.d.f.), and the premultiplied probability density function
$P(u)$
(p.d.f.), and the premultiplied probability density function
![]() $u^{2p}P(u)$
, where
$u^{2p}P(u)$
, where
![]() $2p=[2,6,10]$
indicates the
$2p=[2,6,10]$
indicates the
![]() $p$
th even moment. Each moment is the area under the corresponding curve, and the data appear to be statistically converged. We see a clear deviation around the maximum value in the p.d.f. from a Gaussian behaviour, as well as deviations from symmetry in the premultiplied p.d.f.s.
$p$
th even moment. Each moment is the area under the corresponding curve, and the data appear to be statistically converged. We see a clear deviation around the maximum value in the p.d.f. from a Gaussian behaviour, as well as deviations from symmetry in the premultiplied p.d.f.s.

Figure 8. Probability density functions for the boundary layer at
![]() $\mathit{Re}_{{\it\tau}}=70\,000$
,
$\mathit{Re}_{{\it\tau}}=70\,000$
,
![]() $y^{+}=800$
. (a) ●,
$y^{+}=800$
. (a) ●,
![]() $P(u)$
; ——, Gaussian distribution. (b)
$P(u)$
; ——, Gaussian distribution. (b)
![]() $u^{2p}P(u)$
; ▪,
$u^{2p}P(u)$
; ▪,
![]() $2p=2$
; ◂,
$2p=2$
; ◂,
![]() $2p=6$
; ▴,
$2p=6$
; ▴,
![]() $2p=10$
.
$2p=10$
.
The skewness
![]() $S=\langle u^{3}\rangle /\langle u^{2}\rangle ^{3/2}$
is shown in figure 9. Both flows exhibit a very similar behaviour, with the skewness slightly positive near the wall for
$S=\langle u^{3}\rangle /\langle u^{2}\rangle ^{3/2}$
is shown in figure 9. Both flows exhibit a very similar behaviour, with the skewness slightly positive near the wall for
![]() $y^{+}<200$
and becoming negative further away from the wall. For the boundary layer, the skewness is well collapsed in inner coordinates over the region
$y^{+}<200$
and becoming negative further away from the wall. For the boundary layer, the skewness is well collapsed in inner coordinates over the region
![]() $100<y^{+}<0.15\mathit{Re}_{{\it\tau}}$
, and we see all profiles change sign at
$100<y^{+}<0.15\mathit{Re}_{{\it\tau}}$
, and we see all profiles change sign at
![]() $y^{+}\approx 200$
and reach a value of
$y^{+}\approx 200$
and reach a value of
![]() $S\approx -0.1$
before becoming more negative in the wake, where they collapse well in outer coordinates. In contrast, the pipe flow profiles show a small Reynolds number dependence over the log region, and the collapse in the wake region in terms of outer layer coordinates is not as clean as that seen in the boundary layer data.
$S\approx -0.1$
before becoming more negative in the wake, where they collapse well in outer coordinates. In contrast, the pipe flow profiles show a small Reynolds number dependence over the log region, and the collapse in the wake region in terms of outer layer coordinates is not as clean as that seen in the boundary layer data.

Figure 9. Skewness in inner coordinates (a,b) and outer coordinates (c,d) for cases given in table 4. (a,c) Boundary layer; (b,d) pipe.
The kurtosis
![]() $K=\langle u^{4}\rangle /\langle u^{2}\rangle ^{2}$
is shown in figure 10. Again, the behaviour for the two flows is very similar, with perhaps some small dependence on the Reynolds number in the outer region (although this could also be the result of some unresolved spatial filtering effects).
$K=\langle u^{4}\rangle /\langle u^{2}\rangle ^{2}$
is shown in figure 10. Again, the behaviour for the two flows is very similar, with perhaps some small dependence on the Reynolds number in the outer region (although this could also be the result of some unresolved spatial filtering effects).

Figure 10. Kurtosis in inner coordinates (a,b) and outer coordinates (c,d) for cases given in table 4. (a,c) Boundary layer; (b,d) pipe.
The
![]() $p$
th roots of the
$p$
th roots of the
![]() $p$
th even moments
$p$
th even moments
![]() $\langle (u^{+})^{2p}\rangle ^{1/p}$
are shown in figure 11 for
$\langle (u^{+})^{2p}\rangle ^{1/p}$
are shown in figure 11 for
![]() $2p=2$
, 6, and 10 (the data for
$2p=2$
, 6, and 10 (the data for
![]() $2p=4$
, 8, and 12 show the same trends). In inner coordinates, the behaviour is qualitatively similar to that seen in the variances, with an inner peak at about
$2p=4$
, 8, and 12 show the same trends). In inner coordinates, the behaviour is qualitatively similar to that seen in the variances, with an inner peak at about
![]() $y^{+}=15$
that is either increasing very slowly with Reynolds number or not at all, a blending region over the range
$y^{+}=15$
that is either increasing very slowly with Reynolds number or not at all, a blending region over the range
![]() $30<y^{+}<300$
, followed by a logarithmic region. The results from the boundary layer and the pipe agree well throughout most of the flow, with the only differences appearing in the outer layer due to the different outer boundary conditions, as expected. Some minor differences can also be seen in the near-wall region, around
$30<y^{+}<300$
, followed by a logarithmic region. The results from the boundary layer and the pipe agree well throughout most of the flow, with the only differences appearing in the outer layer due to the different outer boundary conditions, as expected. Some minor differences can also be seen in the near-wall region, around
![]() $y^{+}\approx 15$
, where the pipe flow displays a slightly higher peak value, possibly due to smaller spatial filtering effects since
$y^{+}\approx 15$
, where the pipe flow displays a slightly higher peak value, possibly due to smaller spatial filtering effects since
![]() $\ell ^{+}$
is smaller for the pipe than the boundary layer (see table 4). Finally, it appears that the inner limit of the logarithmic range for pipes occurs at higher values of
$\ell ^{+}$
is smaller for the pipe than the boundary layer (see table 4). Finally, it appears that the inner limit of the logarithmic range for pipes occurs at higher values of
![]() $y^{+}$
than in boundary layers, similar to what was observed for the variances.
$y^{+}$
than in boundary layers, similar to what was observed for the variances.

Figure 11. Higher-order even moments
![]() $2p=2$
, 6, and 10 for boundary layer (filled symbols) and pipe flow (empty symbols). Data in inner coordinates (a,c,e) for all cases given in table 4. Same data in outer coordinates (b,d,f) for
$2p=2$
, 6, and 10 for boundary layer (filled symbols) and pipe flow (empty symbols). Data in inner coordinates (a,c,e) for all cases given in table 4. Same data in outer coordinates (b,d,f) for
![]() $\mathit{Re}_{{\it\tau}}\geqslant 20\,000$
and
$\mathit{Re}_{{\it\tau}}\geqslant 20\,000$
and
![]() $y^{+}>100$
. Solid line, (1.3) with
$y^{+}>100$
. Solid line, (1.3) with
![]() $A_{p}$
and
$A_{p}$
and
![]() $B_{p}$
derived from the pipe flow profile at
$B_{p}$
derived from the pipe flow profile at
![]() $\mathit{Re}_{{\it\tau}}=70\,000$
(where
$\mathit{Re}_{{\it\tau}}=70\,000$
(where
![]() $A_{p}=[1.13;2.48;3.44]$
and
$A_{p}=[1.13;2.48;3.44]$
and
![]() $B_{p}=[1.17;3.31;6.73]$
accordingly).
$B_{p}=[1.17;3.31;6.73]$
accordingly).
Figure 11 also displays the data in outer coordinates for the three highest Reynolds numbers (
![]() $\mathit{Re}_{{\it\tau}}\geqslant 20\,000$
). As seen in the variances, the higher moments show good agreement between boundary layer and pipe flows. With increasing moment, the agreement improves, and the range of logarithmic behaviour increases.
$\mathit{Re}_{{\it\tau}}\geqslant 20\,000$
). As seen in the variances, the higher moments show good agreement between boundary layer and pipe flows. With increasing moment, the agreement improves, and the range of logarithmic behaviour increases.
The constants
![]() $A_{p}$
and
$A_{p}$
and
![]() $B_{p}$
in (1.3) were found by regression fit to each profile, that is, separately for each flow, Reynolds number, and moment. To test the consequences of choosing a particular range for the curve fit, different ranges were used for fitting, with the inner limit varying as
$B_{p}$
in (1.3) were found by regression fit to each profile, that is, separately for each flow, Reynolds number, and moment. To test the consequences of choosing a particular range for the curve fit, different ranges were used for fitting, with the inner limit varying as
![]() $y_{min}^{+}=[3\mathit{Re}_{{\it\tau}}^{0.5};200;400;600;800]$
while keeping a constant outer limit at
$y_{min}^{+}=[3\mathit{Re}_{{\it\tau}}^{0.5};200;400;600;800]$
while keeping a constant outer limit at
![]() $(y/{\it\delta})_{max}=0.15$
(the results were not sensitive to reasonable variations in the outer limit). A minimum of four points in each profile were used for determining the constants, otherwise the profile was discarded as not having a sufficiently extensive logarithmic region.
$(y/{\it\delta})_{max}=0.15$
(the results were not sensitive to reasonable variations in the outer limit). A minimum of four points in each profile were used for determining the constants, otherwise the profile was discarded as not having a sufficiently extensive logarithmic region.
The variation of the slope
![]() $A_{p}$
with
$A_{p}$
with
![]() $p$
is shown in figure 12. For Gaussian statistics,
$p$
is shown in figure 12. For Gaussian statistics,
![]() $A_{p}$
would vary as
$A_{p}$
would vary as
![]() $A_{1}[(2p-1)!!]^{1/p}$
, where
$A_{1}[(2p-1)!!]^{1/p}$
, where
![]() $A_{1}$
is the Townsend–Perry constant and
$A_{1}$
is the Townsend–Perry constant and
![]() $!!$
denotes double factorial. It is evident that for boundary layer and pipe flows all the constants have a sub-Gaussian behaviour, as observed by Meneveau & Marusic (Reference Meneveau and Marusic2013) for boundary layers at lower Reynolds numbers. For smaller
$!!$
denotes double factorial. It is evident that for boundary layer and pipe flows all the constants have a sub-Gaussian behaviour, as observed by Meneveau & Marusic (Reference Meneveau and Marusic2013) for boundary layers at lower Reynolds numbers. For smaller
![]() $y_{min}^{+}$
values, there is a clear Reynolds number dependence in
$y_{min}^{+}$
values, there is a clear Reynolds number dependence in
![]() $A_{p}$
between cases, as well as a dependence on
$A_{p}$
between cases, as well as a dependence on
![]() $y_{min}^{+}$
. For both flows,
$y_{min}^{+}$
. For both flows,
![]() $A_{p}$
was found to become independent of
$A_{p}$
was found to become independent of
![]() $\mathit{Re}_{{\it\tau}}$
for
$\mathit{Re}_{{\it\tau}}$
for
![]() $y_{min}^{+}\gtrsim 400$
. The limit
$y_{min}^{+}\gtrsim 400$
. The limit
![]() $y_{min}^{+}=3\mathit{Re}_{{\it\tau}}^{0.5}$
used by Meneveau & Marusic (Reference Meneveau and Marusic2013) underestimates the inner limit at low
$y_{min}^{+}=3\mathit{Re}_{{\it\tau}}^{0.5}$
used by Meneveau & Marusic (Reference Meneveau and Marusic2013) underestimates the inner limit at low
![]() $\mathit{Re}_{{\it\tau}}$
while overestimating it at high
$\mathit{Re}_{{\it\tau}}$
while overestimating it at high
![]() $\mathit{Re}_{{\it\tau}}$
, and so it appears that either a constant inner limit or one with a very weak
$\mathit{Re}_{{\it\tau}}$
, and so it appears that either a constant inner limit or one with a very weak
![]() $\mathit{Re}_{{\it\tau}}$
dependence is more appropriate for both flows. A good representation of the asymptotic value of the slope is given empirically by
$\mathit{Re}_{{\it\tau}}$
dependence is more appropriate for both flows. A good representation of the asymptotic value of the slope is given empirically by
![]() $A_{p}\sim A_{1}(2p-1)^{1/2}$
for both pipe and boundary layer (
$A_{p}\sim A_{1}(2p-1)^{1/2}$
for both pipe and boundary layer (
![]() $A_{1}=1.24$
, as before).
$A_{1}=1.24$
, as before).

Figure 12. Constant
![]() $A_{p}$
for even moments
$A_{p}$
for even moments
![]() $2p$
, for the fitting range
$2p$
, for the fitting range
![]() $y^{+}=[y_{min}^{+},0.15Re_{{\it\tau}}]$
. Left: boundary layer; right: pipe. Line colors given in table 4. ——, expected Gaussian variation
$y^{+}=[y_{min}^{+},0.15Re_{{\it\tau}}]$
. Left: boundary layer; right: pipe. Line colors given in table 4. ——, expected Gaussian variation
![]() $A_{p}=A_{1}[(2p-1)!!]^{1/p}$
; - - - -, empirical fit
$A_{p}=A_{1}[(2p-1)!!]^{1/p}$
; - - - -, empirical fit
![]() $A_{p}=A_{1}(2p-1)^{1/2}$
.
$A_{p}=A_{1}(2p-1)^{1/2}$
.
It appears that if a large enough value of
![]() $y_{min}^{+}$
is chosen,
$y_{min}^{+}$
is chosen,
![]() $A_{p}$
is independent of Reynolds number in pipe and boundary layer flows. The only outlier, the highest Reynolds number case for the boundary layer, has a slightly lower value of
$A_{p}$
is independent of Reynolds number in pipe and boundary layer flows. The only outlier, the highest Reynolds number case for the boundary layer, has a slightly lower value of
![]() $A_{p}$
, but this could be due to experimental error, which is expected to be greatest at the highest Reynolds number.
$A_{p}$
, but this could be due to experimental error, which is expected to be greatest at the highest Reynolds number.
The behaviour of the additive constant
![]() $B_{p}$
is more difficult to establish, due to its high sensitivity to the magnitude of the moments. In pipes the constant appears to be independent of Reynolds number, whereas in boundary layers a weak dependence is observed in most cases. In contrast, Meneveau & Marusic (Reference Meneveau and Marusic2013) found a much stronger dependence, possibly caused by using
$B_{p}$
is more difficult to establish, due to its high sensitivity to the magnitude of the moments. In pipes the constant appears to be independent of Reynolds number, whereas in boundary layers a weak dependence is observed in most cases. In contrast, Meneveau & Marusic (Reference Meneveau and Marusic2013) found a much stronger dependence, possibly caused by using
![]() $3\mathit{Re}_{{\it\tau}}^{0.5}$
as the inner limit on the curve fit. Interestingly, for the current data set
$3\mathit{Re}_{{\it\tau}}^{0.5}$
as the inner limit on the curve fit. Interestingly, for the current data set
![]() $B_{p}$
reached a constant value for the three highest Reynolds number cases when
$B_{p}$
reached a constant value for the three highest Reynolds number cases when
![]() $y_{min}^{+}\geqslant 600$
was used as inner limit, which could suggest that high-order moments are still affected by viscosity for smaller
$y_{min}^{+}\geqslant 600$
was used as inner limit, which could suggest that high-order moments are still affected by viscosity for smaller
![]() $y^{+}$
. However, these trends are probably within experimental error, and no strong conclusions can be made.
$y^{+}$
. However, these trends are probably within experimental error, and no strong conclusions can be made.
4. Conclusions
Zero-pressure-gradient turbulent boundary layer measurements for
![]() $2600<\mathit{Re}_{{\it\tau}}<72\,500$
were compared with previously acquired pipe flow data at similar Reynolds numbers. These Reynolds numbers covered a sufficient range to enable identification of some apparently asymptotic trends. For
$2600<\mathit{Re}_{{\it\tau}}<72\,500$
were compared with previously acquired pipe flow data at similar Reynolds numbers. These Reynolds numbers covered a sufficient range to enable identification of some apparently asymptotic trends. For
![]() $\mathit{Re}_{{\it\tau}}\geqslant 20\,000$
, the mean velocity and variance profiles showed extended logarithmic regions, with very similar constants in both flows. The two logarithmic regions coincide over the region
$\mathit{Re}_{{\it\tau}}\geqslant 20\,000$
, the mean velocity and variance profiles showed extended logarithmic regions, with very similar constants in both flows. The two logarithmic regions coincide over the region
![]() $400\lesssim y^{+}\lesssim 0.15\mathit{Re}_{{\it\tau}}$
. The inner limit may not be a perfect constant but may be subject to a weak Reynolds number dependence (certainly less than
$400\lesssim y^{+}\lesssim 0.15\mathit{Re}_{{\it\tau}}$
. The inner limit may not be a perfect constant but may be subject to a weak Reynolds number dependence (certainly less than
![]() $\mathit{Re}_{{\it\tau}}^{0.5}$
), and it is further explored by Vallikivi et al. (Reference Vallikivi, Ganapathisubramani and Smits2015) when considering the spectral behaviour.
$\mathit{Re}_{{\it\tau}}^{0.5}$
), and it is further explored by Vallikivi et al. (Reference Vallikivi, Ganapathisubramani and Smits2015) when considering the spectral behaviour.
Higher-order even moments also show a logarithmic behaviour over the same physical space as the mean velocity and the variances, and the slope of the line appears to become independent of Reynolds number for the same region, defined by
![]() $400\lesssim y^{+}\lesssim 0.15\mathit{Re}_{{\it\tau}}$
for both boundary layer and pipe flows. These bounds define a Reynolds number of
$400\lesssim y^{+}\lesssim 0.15\mathit{Re}_{{\it\tau}}$
for both boundary layer and pipe flows. These bounds define a Reynolds number of
![]() $\mathit{Re}_{{\it\tau}}\approx 27\,000$
where this region extends over a decade in
$\mathit{Re}_{{\it\tau}}\approx 27\,000$
where this region extends over a decade in
![]() $y^{+}$
, underlining the need to obtain data at Reynolds numbers comparable to those obtained here if one wants to study scaling behaviours.
$y^{+}$
, underlining the need to obtain data at Reynolds numbers comparable to those obtained here if one wants to study scaling behaviours.
Acknowledgements
The authors would like to thank B. McKeon and acknowledge J. Allen for their help in the design and construction of the flat-plate apparatus and the pressure gradient blister, G. Kunkel, R. Echols and S. Bailey for conducting preliminary tests, and B. Ganapathisubramani and W. K. George for many insightful discussions and suggestions. This work was made possible by support received through ONR grant N00014-13-1-0174, program manager R. Joslin, and NSF grant CBET-1064257, program managers H. Winter and D. Papavassiliou.