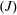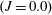1 Introduction
In scramjet engine combustors, fuel is injected normally through sonic jets from wall orifices into a supersonic cross-flow of air, which is a simple and efficient injection scheme for combustor design. A significant body of work has been conducted, as summarized in the previous reviews (Karagozian Reference Karagozian2010; Mahesh Reference Mahesh2013). Many experimental investigations have been carried out to understand the mechanisms of the jet injected into a supersonic cross-flow, including detailed velocity (Santiago & Dutton Reference Santiago and Dutton1997) and wall-pressure measurements (Everett et al. Reference Everett, Woodmansee, Dutton and Morris1998), penetration height (Portz & Segal Reference Portz and Segal2006) and time-resolved flow visualizations (Gruber et al. Reference Gruber, Nejad, Chen and Dutton1997; Sun et al. Reference Sun, Zhang, Zhao, Zhao and Liang2013) and analysis of mixing characteristics (Ben-Yakar, Mungal & Hanson Reference Ben-Yakar, Mungal and Hanson2006; Gamba & Mungal Reference Gamba and Mungal2015) with non-reactive and combustible gaseous jets. These measurements showed the overall jet flow features and the dynamics of the jet shear layer and shocks along with intensive flow data that can be used to validate numerical predictions. Because of the difficulties in measuring the complex high-speed unsteady flow fields, experimental data are mainly obtained for certain transverse and longitudinal two-dimensional (2D) slices of the flow field.
Figure 1. A three-dimensional view of the near-field mean flow and shock structures of a sonic jet into a supersonic cross-flow. (a) Dickmann & Lu (Reference Dickmann and Lu2009), (b) Liang et al. (Reference Liang, Sun, Liu and Yang2018).
A widely accepted flow topology of a transverse jet through an under-expanded sonic injection from a wall surface to a supersonic cross-flow is illustrated in figure 1. The flow field involves complex three-dimensional (3D) unsteady shocks, separation, wall-bounded turbulence, vortical structures and their interactions (Dickmann & Lu Reference Dickmann and Lu2009). A barrel shock around the plume terminated by a Mach disk and a bow shock is generated ahead of the jet. This causes boundary-layer separation upstream of the injection and leads to the formation of a horseshoe vortex. A local leeward separation bubble and a secondary shock are presented. Recently Liang et al. (Reference Liang, Sun, Liu and Yang2018) identified that a reflected shock deflects the collision shock and the collision shock intersects with the barrel shock, as shown in figure 1(b), which clarifies knowledge about the shock-wave structures in the jet wake. The formation of a major counter-rotating vortex pair (CVP) and horseshoe vortices from the jet interaction with supersonic cross-flows has been well explained in the previous studies (Karagozian Reference Karagozian2010; Mahesh Reference Mahesh2013). Our recent research clarified the upper trailing CVP (Sun & Hu Reference Sun and Hu2018b ) and the surface lower trailing CVP (Sun & Hu Reference Sun and Hu2018a ).
Recently a number of detailed numerical simulations have been conducted to obtain the detailed flow field and to analyse the behaviour of coherent structures. Kawai & Lele (Reference Kawai and Lele2010) and Rana, Thomber & Drikakis (Reference Rana, Thomber and Drikakis2011) performed large-eddy simulations (LES) of sonic jets with
$J=1.7$
in a supersonic stream and their results demonstrated Kelvin–Helmholtz (KH) instabilities in the interface of the jet shear layer confronted with the main airstream. Won et al. (Reference Won, Jeung, Parent and Choi2010) used detached-eddy simulation (DES) to reveal vortex evolution under the jet conditions of the experiment of Ben-Yakar et al. (Reference Ben-Yakar, Mungal and Hanson2006). Chai, Iyer & Mahesh (Reference Chai, Iyer and Mahesh2015) conducted LES on jets in a supersonic cross-flow. Although the above simulations have shown the flow field in the boundary layer, neither the effects of jet interaction on the supersonic boundary layer, nor the turbulence evolution in the boundary layer of the jet wakes has been well revealed in the literature. Especially when
$J$
is not large, the previous calculations (Kawai & Lele Reference Kawai and Lele2010; Rana et al.
Reference Rana, Thomber and Drikakis2011; Chai et al.
Reference Chai, Iyer and Mahesh2015) did not display an apparent change of the turbulence state in the jet wake. As is well known, the turbulence state in the boundary layer influences strongly both the skin friction and heat transfer; therefore, it is important to understand any change of the turbulence in the boundary layer around the jet. Previous experiments have not clarified this topic. Reynolds-averaged Navier–Stokes (RANS) simulations cannot provide detailed information of turbulent flow, while LES requires modelling of the subgrid scales of turbulence since LES cannot resolve all the scales. This is also the reason why the previous LES studies did not judge the turbulence in the boundary layer directly. In the present work, direct numerical simulation (DNS) is used to obtain detailed information on the turbulence around the jet in the boundary layer based on the previous simulation (Sun & Hu Reference Sun and Hu2018b
). The significance of this investigation lies in the identification of the turbulence state in the supersonic boundary layer around the transverse jet, which has been overlooked by previous studies.
This paper is organized as follows. The computational grid, the algorithm, the simulation conditions and the validation are discussed in § 2. A description of the instantaneous boundary-layer flow field is presented in § 3.1. Then § 3.2 gives the mean flow field and properties of turbulent kinetic energy (TKE) and root-mean-square (r.m.s.) velocity distributions. Analysis of streamlines which illustrate flow-field characteristics related to the change of local turbulence is presented in § 4. A preliminary experimental study is presented in § 5 and the main description is given in appendices A and B since the experiment validation is qualitative. A summary is given in § 6.
2 Flow conditions and numerical set-up
2.1 Supersonic and jet inflow conditions
All simulations in this paper solve the unsteady 3D compressible Navier–Stokes equations directly without any modelling, using an in-house DNS code. The code has been developed and applied to studies of instability, transition and turbulence in high-speed flows (Sandham et al. Reference Sandham, Schlein, Wagner, Willems and Steelant2014; Sandham Reference Sandham2016). Here we provide a brief description of the main features of the code and explain the simulation conditions for the present study. The detailed governing equations of mass, momentum and total energy conservation for a 3D flow field can be found in Touber (Reference Touber2010) and thus are not repeated here.
The air inflow parameters (shown in table 1) are set in accordance with the
$Ma=2.7$
experiments of Sun et al. (Reference Sun, Zhang, Zhao, Zhao and Liang2013) with stagnation pressure
$P_{0}=101\,325~\text{Pa}$
and stagnation temperature
$T_{0}=300~\text{K}$
. The supersonic inflow 99 % boundary-layer thickness, which is the same for all simulations, is estimated to be
$\unicode[STIX]{x1D6FF}_{i}=5.12~\text{mm}$
, with the compressible (including density variations) boundary-layer displacement thickness
${\unicode[STIX]{x1D6FF}_{i}}^{\ast }=1.75~\text{mm}$
and the momentum thickness
$\unicode[STIX]{x1D703}=0.38~\text{mm}$
and corresponding Reynolds numbers
$Re_{\unicode[STIX]{x1D6FF}\ast }=15\,367$
and
$Re_{\unicode[STIX]{x1D703}}=3337$
, respectively. A sketch of the computational domain can be found in the previous papers (Sun & Hu Reference Sun and Hu2018a
,Reference Sun and Hu
b
) and for brevity is omitted here.
Two momentum flux ratios
$J=2.3$
and
$J=5.5$
of air injection are modelled. Both cases lead to a sonic jet with stagnation temperature
$T_{0i}=300~\text{K}$
. The jet properties are shown in table 2. Since the turbulent levels originating from the jet orifice in the experiments are not known, a uniform profile across the jet orifice is implemented without any disturbance. It might be argued that turbulence would not be thoroughly resolved in the jet; however, it is believed that the overall behaviour of coherent structures in the jet and boundary layer will not be affected by this assumption (Sun & Hu Reference Sun and Hu2018a
,Reference Sun and Hu
b
).
Table 1. Air flow conditions for the simulations, including the Mach number
$(Ma)$
, stagnation temperature (
$T_{0}$
), stagnation pressure (
$P_{0}$
), dimensional boundary-layer 99 % thickness (
$\unicode[STIX]{x1D6FF}_{i}$
), momentum thickness (
$\unicode[STIX]{x1D703}$
) and Reynolds number (
$Re_{\unicode[STIX]{x1D703}}$
) at the inflow.
Table 2. Jet conditions for the simulations, including jet-to-cross-flow momentum ratio
$(J)$
, orifice diameter
$(D)$
, Mach number (
$Ma_{j}$
), stagnation temperature (
$T_{0j}$
) and stagnation pressure (
$P_{0j}$
).
2.2 Computational domain and boundary conditions
The use of a digital filter to generate the inflow boundary condition significantly reduces the length required for boundary-layer development (Xie & Castro Reference Xie and Castro2008), but nevertheless there should be enough distance provided in the simulation to allow the boundary layers to adjust to an equilibrium state upstream of the jet. Wang et al. (Reference Wang, Sandham, Hu and Liu2015) found that a distance of 12 times the inflow boundary-layer thickness is enough to obtain realistic turbulent mean and r.m.s. profiles from the digital filter inflow generator used. Accordingly, the initial length is set to be
$L_{i}=12.7\unicode[STIX]{x1D6FF}_{i}\approx 65~\text{mm}$
for a fully developed turbulence generation. The jet mixing length is set to
$L_{m}=90~\text{mm}$
including the near field (denoted as JISC section 1) with 10 mm upstream and 40 mm downstream of the jet and the far field (denoted as JISC section 2) with 40 mm downstream of JISC section 1. Therefore, the total length of the physical domain is
$L_{x}=155~\text{mm}$
. The wall-normal extent of the domain is 18 mm, and a span of 14 mm is used. The jet is centred 75 mm downstream of the inlet with an orifice diameter of
$D=2~\text{mm}$
. The grid used in the current simulation is kept the same as in the set-up in our previous work (Sun & Hu Reference Sun and Hu2018a
,Reference Sun and Hu
b
). As analysed, the grid set-up ensures a fine DNS resolution in the near-wall region and a quasi-DNS (QDNS) resolution in the jet and the mainstream due to the unknown information about the smallest scales in the jet plume, as denoted by Sandham, Johnstone & Jacobs (Reference Sandham, Johnstone and Jacobs2017).
Large buffer layers with non-reflective outside boundaries are introduced with lengths of 15 mm, 11 mm and 12 mm at the outlet, on both the sides and the upper boundaries, respectively. The grid is smoothly stretched in the buffer layers towards the boundaries. The buffer layers, with coarsened mesh, help to damp fluctuations and minimize any possible reflections from the boundaries. Non-slip and adiabatic boundary conditions are enforced on the wall. An integrated characteristic boundary condition (Thompson Reference Thompson1987) is applied at the inflow, and an outflow condition with an integrated characteristic scheme is applied to the spanwise, top and outflow boundaries, which are located on the outer edge of the buffer layers. The jet orifice is defined directly in the surface wall uniform grid and set to a sonic condition with
$J=2.3$
and
$J=5.5$
, respectively.
2.3 Numerical methods and validation
This in-house code (Sandham, Li & Yee Reference Sandham, Li and Yee2002) uses a fourth-order central difference scheme for the spatial derivatives and a third-order explicit Runge–Kutta scheme for time advancement. The code makes use of an entropy splitting of the Euler terms and the Laplacian formulation of the viscous terms to improve the stability of the non-dissipative central scheme. To better resolve the steep variations in flow field around the injected jet, we developed a hybrid scheme which combines the entropy splitting central scheme with a fourth-order central-upwind weighted essentially non-oscillatory (WENO-CU4) scheme and is applied in the areas with high gradients (Sun & Hu Reference Sun and Hu2018b ).
The digital filter inflow generation method of Xie & Castro (Reference Xie and Castro2008) is used to provide inflow boundary conditions to generate a more realistic turbulent boundary layer, from predefined mean and r.m.s. profiles. The mean inflow profiles are generated from a similarity solution of the compressible boundary layer using the same approach as in Wang et al. (Reference Wang, Sandham, Hu and Liu2015). The inflow r.m.s. values are taken from the DNS results of Schlatter & Orlu (Reference Schlatter and Orlu2010) for a similar Reynolds number.
Turbulent boundary-layer mean profiles and distributions of r.m.s. values at
$x/D=-7.5$
(corresponding to the position at 60 mm downstream of the inlet) have been evaluated, giving a good agreement with the existing data (Sun & Hu Reference Sun and Hu2018a
,Reference Sun and Hu
b
). The approximate penetration boundary based on a concentration identification was obtained and compared with the empirical correlation. It was found that the current penetration result agrees well with previous experimental correlations for both
$J=5.5$
and
$J=2.3$
(Sun & Hu Reference Sun and Hu2018a
). The jet trajectory of
$J=5.5$
and
$J=2.3$
was extracted from the streamline originating from the centre of the jet exit on the time-averaged symmetry plane. It was compared with Schetz & Billig’s (Reference Schetz and Billig1966) prediction and showed reasonably good agreement (Sun & Hu Reference Sun and Hu2018a
). The above comparison validated the approach and the current simulation.
3 Numerical results and analysis
All simulations were performed on Archer, the UK’s National Supercomputer. Each simulation requires approximately 540 000 processor core hours for flow development and collecting statistics over 100 non-dimensional time units (
$D/U_{\infty }$
).
3.1 Instantaneous flow structures
Contours of typical instantaneous density fields for the supersonic boundary layer without and with the jet injection are compared in figure 2. Figure 2(a) reveals detailed structures of the boundary layer and unsteady jet penetration. The bow shock, barrel shock and separation bubbles introduced by the jet are well identified in the simulations. The upstream separation shock is not as strong as the other shocks. Upstream of the jet, a separation zone is observed and marked by the isolines of
$u/U_{\infty }=0.0$
. The vortical structures, displayed by local density variations, around the jet break down to form the well-developed small turbulent eddies downstream. Analysis of the jet structure can be found in the previous literature, and therefore is not detailed here. The present study focuses on the boundary-layer developments downstream of the jet. It is found that the jet interacts with the upcoming boundary layer intensively and the interaction is still strong in the downstream region in the centreline plane
$(z/D=0)$
. Figure 2(b) gives the flow field on the plane
$z/D=3.0$
for all cases. From this side view, the vortices in the boundary layer of both
$J=5.5$
and
$J=2.3$
cases are observed to have been suppressed, especially for
$J=5.5$
. The vortical structures are attenuated, and start to reorganize (denoted as recovery in this paper) after a long distance in the region downstream of the jet. For
$J=5.5$
, this recovery distance is longer, and part of the boundary layer even approaches the laminar state, which means that higher
$J$
leads to a more intensive vortex decay and even a relaminarization downstream of the jet.
Figure 2. Density contours at
$z/D=0.0$
(a) and
$z/D=3.0$
(b) planes of the jet interacting with the incoming boundary layer. The red solid lines are the isolines of
$u/U_{\infty }=0.0$
.
Figure 3. Density contours on
$y/D=0.08$
(a) and
$y/D=1.0$
(b) planes for different cases (
$J=0$
, 2.3, 5.5 from top to bottom). The red solid lines are the isolines of
$u/U_{\infty }=0.0$
.
To clearly identify the development of the turbulence in the boundary layer downstream of the jet, the near-wall streaks in the turbulent flow field are shown and analysed. The density contours at the same wall-normal distances (
$y/D=0.08$
and
$y/D=1.0$
) for
$J=0$
, 2.3 and 5.5 are shown in figure 3 from a top view. Alternate low-magnitude (dark colour) and high-magnitude (light colour) density regions are observed in figure 3(a), which are caused by the near-wall streaks in the boundary layer. The flow field of the jet interaction cases demonstrates different flow characteristics compared to the flat plate. We can see that the classic streaks are developed along the streamwise direction in the undisturbed boundary layer of the flat plate upstream of the jet orifices. For
$J=2.3$
and
$J=5.5$
, the quasi-streamwise streaky structures crush into the separation region upstream of the jet. On the lateral of the jet, the streaks are interrupted by the bow shock induced by the jet. For both
$J=2.3$
and
$J=5.5$
cases, downstream of the jet lateral separation region, the vortical structures displayed by local density variations in the boundary layer are greatly weakened and almost disappear, accompanied by increased density (shown in grey-white colour). In the far field of
$x/D>10.0$
, it can be seen from figure 3(a) that the boundary-layer turbulence in the lateral downstream of the jet at
$y/D=0.08$
of
$J=2.3$
has a quick recovery and small streaks intermittently appear in the wall-bounded flow. For
$J=5.5$
, it is observed at
$y/D=0.08$
that the turbulence decreases more noticeably than for
$J=2.3$
.
Figure 3(b) shows density contours on the
$y/D=1.0$
plane for all cases from a top view. Downstream of the jet lee, the high-speed flow impacts the shock waves generated by the collision of the flow running around the jet barrel. The collision shock waves are clearly shown in density contours on
$y/D=1.0$
slices and they are twisted by the unsteady turbulent structures in the jet lee. The boundary layer interacts with the shock generated by the collision of the flow around the jet barrel. It is clear that these collision shocks induce the herringbone separation shown in figure 3(a). It is seen that the herringbone separation region is confined laterally and also in the wall-normal direction since its size decreases significantly at
$y/D=1.0$
(figure 3
a) compared to at
$y/D=0.08$
(figure 3
a). Flow over the separation reattaches downstream of the cross point of the separation branches. From figure 3(b), it is seen that the herringbone separation zone exists in a limited region and the high-speed flow in the lateral (
$z/D>3.0$
or
$z/D<-3.0$
) of the jet seems not to be affected by the herringbone zone. The region is affected slightly by the collision shock waves. The flow behind the collision shock falls into the reattachment zone and after a certain distance the streaky structures reorganize near the symmetry plane, as shown in figure 3(a). A comparison of figure 3(a) and figure 3(b), especially for
$J=2.3$
, shows that at
$y/D=0.08$
the streaks are regenerated earlier than
$y/D=1.0$
, which suggests that the turbulence in the inner layer of the lateral boundary layer recovers more quickly than in the outer layer. A comparison between
$J=5.5$
and
$J=2.3$
shows that higher
$J$
leads to a more intensified suppression phenomenon on the wall-bounded flow. For
$J=5.5$
the intensified suppression causes the lateral flow to stay in a weakened turbulence state that has not been fully recovered even near the exit, which is
$40D$
downstream of the jet. For both
$J=2.3$
and
$J=5.5$
cases, the central region downstream of the collision shock-affected region remains in a turbulence state with augmented intensity characterized by the twisted and corrugated streaks. In the jet lateral the streaks are intermittent and smooth, especially for the
$J=5.5$
case, which is the character of low-intensity turbulence. This phenomenon demonstrates that the collision flow in the jet lee central zone leads to a local turbulence with larger intensity in the boundary layer than the jet lateral. A preliminary experimental observation on the slices of the flow field in appendix B confirms the jet lateral suppression phenomenon and the central augmentation phenomenon observed in figure 3.
Figure 4. Isosurface of the streamwise velocity
$(u/U_{\infty }=0.4)$
fields of the jet interaction with the incoming boundary layer: (a)
$J=0.0$
, (b)
$J=2.3$
, (c)
$J=5.5$
.
Figure 5. Isosurface of the streamwise velocity
$(u/U_{\infty }=0.55)$
fields of the jet interaction with the incoming boundary layer: (a)
$J=0.0$
, (b)
$J=2.3$
, (c)
$J=5.5$
.
Isosurfaces of the streamwise velocity in the 3D flow field coloured by the wall-normal distance are illustrated and compared in figures 4 and 5. For the flat plate
$(J=0.0)$
, we can clearly see the classic elongated streamwise vortices in the isosurface of
$u/U_{\infty }=0.4$
, which maintains similar characteristics within the whole domain. A mean velocity of
$u/U_{\infty }=0.4$
usually corresponds to an inner layer location in the boundary layer, as was shown in Sun, Hu & Sandham (Reference Sun, Hu and Sandham2017). The streaky structures concentrate in the inner part of the flat-plate boundary layer and have no large liftup. For the
$J=2.3$
and
$J=5.5$
cases, the structures are similar to the flat-plate case upstream of the jet. Further downstream the near-wall streaks develop into a completely new pattern which exhibits a suppression of the streaky structures. The phenomenon is especially prominent for the
$J=5.5$
case. The isosurfaces of
$u/U_{\infty }=0.55$
given in figure 5 show the large-scale structures in the outer part of the boundary layer. Structures of the
$J=0.0$
case (figure 5
a) show that many packets grow from the near-wall region to a higher wall-normal location. These structures occur with local mass and energy exchange between the inner layer and the outer layer. In figure 5(c) for the
$J=5.5$
case, we can hardly see any packet structures in the lateral downstream of the separation bubble ahead of the jet orifice, which reflects a suppression of turbulence when the flow goes across the jet windward separation region. Usually when the packet structures occur less, the exchange between the inner layer and the outer layer would suffer (Sun et al.
Reference Sun, Hu and Sandham2017). Compared with the
$J=0.0$
case, jet interaction modifies the boundary layer and weakens the exchange process in the inner layer with the outer layer. Downstream of the jet leeward separation at
$x/D>10.0$
, coherent structures in the near-wall region are regenerated during the recovery process and packet structures in the outer part of the boundary layer seem to grow with the recovery.
From the results shown in figures 4 and 5, we can find that the turbulence in the far field is affected by the history effect of the turbulence decay in the vicinity of the jet. Higher
$J$
leads to a more intensive interaction and a more apparent turbulence decay, which needs a longer distance to recover. In the jet leeward region near the centreline, turbulence is not suppressed since the jet interaction with the main stream enhances the local turbulence intensity, especially when the collision shock has an intensified interaction with the boundary layer.
3.2 Mean flow properties and quantitative analysis on turbulent kinetic energy and Reynolds shear stress
This section further analyses the turbulence formation mechanism in the boundary layer around the jet with turbulent statistics. Since averaging over 100 characteristic times is still not enough to obtain smooth profiles of high-order statistics, data are further averaged over the region
$z/D\in [3.0,3.5]$
. It is assumed that the boundary layer is approximately homogeneous in this spanwise zone and is not affected by the leeward separation zone; therefore averaging in the spanwise direction across
$z/D\in [3.0,3.5]$
away from the jet is considered to be reasonable.
Profiles normal to the wall are extracted at several locations upstream and downstream of the jet to compare with the results at the same locations for the flat-plate case, as is illustrated in figure 6 for the streamwise velocity. In the vicinity downstream of the jet, where strong interaction is expected underneath the jet with the boundary layer, the velocity downstream of the jet is larger over most of the boundary layer than in the flat-plate case, and the downstream velocity profiles become fuller as
$J$
increases. It is interesting that at
$x/D=5$
the inner-layer velocity (
$y/D<0.15$
, shown in figure 7
a) of
$J=5.5$
is larger than
$J=2.3$
and
$J=0.0$
, while at
$x/D=35$
the inner-layer velocity (
$y/D<0.15$
shown in figure 7
b) is virtually the same for the three cases. This implies that in the far field downstream of the jet, the inner-layer velocity (
$y/D<0.15$
) for both
$J=2.3$
and
$J=5.5$
almost recovers to the shape of the fully developed turbulent boundary layer of the
$J=0.0$
case (flat plate), while the outer layer is not fully recovered.
Figure 8 gives the development of the boundary-layer 99 % thickness
$\unicode[STIX]{x1D6FF}_{99}$
, the 90 % thickness
$\unicode[STIX]{x1D6FF}_{90}$
and the displacement thickness
$\unicode[STIX]{x1D6FF}^{\ast }$
along the streamwise direction for all cases. There
$U_{e}$
is taken as the free-stream velocity at
$y/D=3.0$
. This is not an accurate estimation but it provides a useful comparison to understand the evolution of the boundary-layer thickness. It is not surprising to see that the boundary-layer thickness of the jet cases has an obvious drop downstream of the jet. Since there is a strong interaction region at
$4.0<x/D<20.0$
, an inaccurate prediction for the boundary-layer thickness
$\unicode[STIX]{x1D6FF}_{99}$
is shown in figure 8. After
$x/D=20.0$
, it is seen that the boundary-layer thickness of the jet cases is smaller than the flat-plate
$(J=0.0)$
case, which reflects the decrease of the boundary-layer thickness in the jet lateral downstream of the windward separation. The boundary-layer thickness even drops below
$0.8D$
after the jet for the
$J=5.5$
case. It is found that
$\unicode[STIX]{x1D6FF}_{90}$
is not sensitive to the jet interaction and could reflect the decrease of the boundary layer in the jet lateral side. The displacement thickness,
$\unicode[STIX]{x1D6FF}^{\ast }$
can also be used to characterize the growth of the boundary layer,
$$\begin{eqnarray}\unicode[STIX]{x1D6FF}^{\ast }=\int _{0}^{\infty }\left(1-\frac{\unicode[STIX]{x1D70C}}{\unicode[STIX]{x1D70C}_{e}}\frac{u}{U_{e}}\right)\text{d}y.\end{eqnarray}$$
Here the displacement thickness of different cases is compared in figure 8(c), and it is seen that
$\unicode[STIX]{x1D6FF}^{\ast }$
of the
$J=5.5$
case is the smallest downstream of the jet orifice. This phenomenon corresponds to the experimental nanoparticle laser scattering (NPLS) images given in appendix B where the boundary-layer thickness decreases in the jet lateral.
Figure 6. Mean velocity profiles at different streamwise locations based on averaging over
$z/D\in [3.0,3.5]$
, normalized by inflow free-stream velocity: (a)
$x/D=-10.0$
, (b)
$x/D=5.0$
, (c)
$x/D=20.0$
, (d)
$x/D=35.0$
.
Figure 7. Mean velocity profiles at different streamwise locations in logarithmic coordinates, based on averaging over
$z/D\in [3.0,3.5]$
, normalized by the inflow free-stream velocity.
Figure 8. Boundary-layer thicknesses
$\unicode[STIX]{x1D6FF}_{99}$
,
$\unicode[STIX]{x1D6FF}_{90}$
and
$\unicode[STIX]{x1D6FF}^{\ast }$
along the streamwise direction based on averaging over
$z/D\in [3.0,3.5]$
, where
$U_{e}$
is taken as the free-stream velocity at
$y/D=3.0$
.
Time-averaged skin friction along the wall in the domain
$z/D\in [3.0,3.5]$
is shown in figure 9. Usually the skin friction considering compressibility effects can be calculated, following Young’s (Reference Young1989) assumption, as
$c_{f}/c_{fi}\approx (1+0.1165M_{\infty }^{2})^{-0.622}$
for an adiabatic wall. Here
$c_{fi}$
denotes the skin friction at the same Reynolds number in the incompressible boundary layer by assuming a
$1/7$
th power law. If we calculate
$Re_{x}$
from
$\unicode[STIX]{x1D6FF}^{vd}=0.37xRe_{x}^{-0.2}$
(the superscript
$vd$
means the value under the van Driest transform (van Driest Reference van Driest1956)) and
$c_{fi}$
is obtained as
$c_{ft}=0.0592Re_{x}^{-0.2}$
, we get
$c_{f}\approx 0.00209$
at
$x/D=-7.5$
for the flat plate. The prediction is comparable to the numerical calculation
$c_{f}\approx 0.00188$
.
The skin friction for different cases follows the theoretical result for a flat-plate turbulent boundary layer up to
$x/D=-10.0$
, which indicates that the artificial inflow condition develops to a fully turbulent boundary layer before the jet. The skin friction coefficient decreases suddenly over
$-10.0<x/D<-2.0$
in the separation region ahead of the jet. In the region
$-2.0<x/D<-0$
, the skin friction coefficient recovers across the jet lateral separation. The wall pressure (shown in figure 9
b) rises in this region due to the bow shock effect. Downstream of the location
$x/D=-1.0$
for
$J=2.3$
and
$x/D=-2.0$
for
$J=5.5$
, wall pressure falls corresponding to an expansion in the supersonic flow. It is worth mentioning that the wall pressure starts to decease ahead of the jet, which means that the expansion starts upstream of the jet, not only in the jet lee, as seen in figure 9(b). For
$x/D>7.5$
, the wall-pressure gradient is positive, which corresponds to the recovery process. In the region
$3.0<x/D<8.0$
for
$J=2.3$
and
$3.0<x/D<10.0$
for
$J=5.5$
, the skin friction coefficient decreases and reaches a local minimum. Downstream of this region, the skin friction quickly recovers towards an equilibrium state for
$J=2.3$
, while the recovery for
$J=5.5$
is much slower. At the location
$x/D=40.0$
near the physical domain exit, the skin friction coefficient for both jet cases approaches the flat-plate value, which indicates that the inner-layer flow almost recovers to the fully developed turbulent boundary layer within the domain. These results are consistent with the analysis for streaks shown in figures 3–5 and velocity profiles in figures 6 and 7. It is identified that the expansion process exists across the jet separation bubble. As is well known, a sudden expansion suppresses the turbulence in the supersonic flows (Sun et al.
Reference Sun, Hu and Sandham2017), which could be the reason that the streaks are weakened and the skin friction coefficient falls.
Figure 9. Skin friction coefficient (a) and wall pressure (b) distributions along the wall averaged for the zone
$z/D\in [3.0,3.5]$
.
Figure 10. Contours of the Mach number (a,c) and static pressure (b,d) on different wall-parallel planes for the
$J=5.5$
case. Streamlines are superimposed on the Mach number contours. The white solid line superimposed on the contour plots represents
$u/U_{\infty }=0.0$
.
Further analysis of the mean flow is presented in figures 10 and 11, which show the contours of static pressure and Mach number at various locations. It is seen that the pressure downstream of the separation region in front of the jet decreases until the flow runs to the collision shock waves. Streamlines on the Mach number contours shown in figure 10 reflect a divergence in the lateral around the jet which corresponds to an expansion. A low-pressure zone exists in the jet lateral due to the blockage and expansion effects from the jet. The flow in the jet lateral is supersonic and the collision shock is induced. Cross-flow runs around the jet and impinges together in the jet lee, which leads to a local pressure increment due to the collision effects. Studies of the supersonic boundary-layer flow over an expansion corner (Arnette, Samimy & Elliott Reference Arnette, Samimy and Elliott1998) showed that sudden expansion would lead to local turbulence decay. The separation region behind the collision shocks in the jet lee on the
$y/D=0.08$
plane has a large size, but almost disappears on
$y/D=0.5$
, which means that the separation is restricted to
$y/D\leqslant 0.5$
. The recirculating flow within the separation zone on the
$y/D=0.08$
slice reattaches in a V-shaped reattachment region. The supersonic flow at the
$y/D=0.5$
slice around the jet impinges into a concentrated flow behind the collision shocks. The reattached supersonic flow and the impinging flow near the wall lead to a pressure increment in the downstream region of the leeward separation bubble, as shown in figure 10.
The TKE contours on different wall-parallel planes for
$J=5.5$
are plotted in figure 11, which shows the whole flow field including the jet wake and the far field. It is seen that the TKE in the separation region ahead of the jet is increased compared to the TKE upstream on both
$y/D=0.08$
and
$y/D=0.5$
planes. Downstream of the windward separation bubble, the TKE reduces significantly, which corresponds to the process of lateral supersonic flow running around the jet orifice. Downstream of the windward separation bubble, the TKE reduces significantly, which corresponds to the expansion process of the lateral supersonic flow running around the jet orifice. In the far field of the jet lateral, the TKE shows a slow recovery. The herringbone separation zone behind the collision shocks has a lower TKE level due to the recirculating flow. Outside of the herringbone zone, the TKE increases noticeably due to the shock interaction with the boundary layer and the reattachment of the jet leeward flow, which is the typical feature of boundary layer–shock wave interactions (Andreopoulos, Agui & Briassulis Reference Andreopoulos, Agui and Briassulis2000; Touber & Sandham Reference Touber and Sandham2011). Above the herringbone zone
$(y/D>0.5)$
, the TKE is intensified due to the interaction of the collision shocks and the flow impingement. In the region downstream in the jet far field, the TKE is higher in the centreline than that on the lateral along the span.
Figure 11. TKE contours on different wall-parallel planes of the
$J=5.5$
case. The white solid line superimposed on the contour plots represents
$u/U_{\infty }=0.0$
.
Representative TKE profiles averaged over
$z/D\in [3.0,3.5]$
along the streamwise direction are given in figures 12 and 13. Results for the flat-plate case are also plotted for comparison. At
$x/D=5.0$
, the TKE is much higher for both jet cases due to the intensive interaction of the jet with the boundary-layer flow. As shown in figure 11, the TKE at
$x/D=5.0$
is smaller than that within the zone of
$-2.0<x/D<3.0$
since the flow over the windward separation region has a higher TKE, which indicates that TKE reduction occurs after the windward separation. It is also seen that the jet lateral supersonic streamlines diverge in figure 10 at
$x/D=5.0$
, which corresponds to the expansion process and leads to the turbulence decay. At
$x/D=20.0$
, the TKE reduction continues and a ravine with low TKE magnitude forms between the inner layer and the outer layer. This phenomenon is more obvious for the
$J=5.5$
case (see the blue arrow points in figure 12
d) at
$x/D=35.0$
although the boundary layer is recovering. In the inner layer, the TKE is increased for both jet cases compared to the flat-plate case, which indicates that the near-wall turbulence remains at a higher level after the flow goes across the jet windward separation region. The ravine in the TKE profile is very clear compared to the flat-plate case, which reveals a significant TKE decay near the inner layer. In the outer layer, the interaction between the jet and the boundary-layer flow exists and the local TKE magnitude deviates significantly from the flat-plate case. As the boundary layer grows, the TKE ravine extends to the outer layer due to the history effect of the turbulence suppression near the jet orifice. Recalling the analysis for figures 2–5, the disappearance of the streaky structure reflects the local turbulence laminarization, which originates from the significant turbulence decay near the jet orifice. Figure 13 shows the TKE averaged over the zone
$z/D\in [-0.5,0.5]$
in the boundary layer at
$x/D=35.0$
. It is seen that the TKE is kept at a high level due to the interaction of the collision shock and the impingement of the lateral supersonic flow running around the jet, as analysed for figures 10 and 11. Corresponding to figures 2–5, along the streamwise domain within
$z/D\in [-0.5,0.5]$
, an abundance of turbulence is generated and the turbulent vortical structures create the high-level TKE downstream of the jet.
Figure 12. TKE profile predictions at different locations along the belt
$z/D\in [3.0,3.5]$
, normalized by the square of the inflow free-stream velocity: (a)
$x/D=-10.0$
, (b)
$x/D=5.0$
, (c)
$x/D=20.0$
, (d)
$x/D=35.0$
.
Figure 13. TKE profiles at
$x/D=35.0$
averaged over
$z/D\in [-0.5,0.5]$
, normalized by the square of the inflow free-stream velocity.
Figure 14 shows the evolution of r.m.s. velocity components at different streamwise locations for the
$J=5.5$
case compared with the profiles on the flat plate. At
$x/D=5.0$
, velocity fluctuations of
$\langle u^{\prime }v^{\prime }\rangle$
are suppressed in the inner layer of
$y^{+}<20$
. In the outer layer, turbulence is enhanced significantly due to the interaction of the jet with the boundary-layer flow. Comparing the r.m.s. velocity components at
$x/D=20.0$
and
$x/D=35.0$
, it is clearly seen that the turbulence in the inner layer recovers to the same level as for the flat-plate flow; however, it is still not recovered thoroughly in other parts of the boundary layer due to the history effect of the turbulence decay in the vicinity of the jet. It is obvious that a ravine (indicated by the arrow in figure 14
d) exists in the profile of the shear stress even at
$x/D=35.0$
compared to the flat-plate case. Since the shear stress is mainly associated with large-scale structures, it is consistent with figures 4 and 5, which shows that the large structures are less coherent in the lateral downstream of the jet. The reduction of the turbulence level between the inner and outer layers highlights a weakening of the large-scale structures in the jet lateral flow. Owing to the turbulence suppression in this region, the exchange of turbulence energy between the inner layer and the outer layer is reduced, which results in a turbulent energy accumulation in the inner layer since the turbulence in the inner layer stays in local equilibrium, as seen in the profiles of figure 12. The exchange intensity of turbulence energy between the inner layer and the outer layer is reduced. The r.m.s. velocity components at
$x/D=35.0$
averaged in
$z/D\in [-0.5,0.5]$
are kept at a high level and no indication of decay exists in the profiles of the
$J=5.5$
case compared to the flat-plate case, as shown in figure 15, which reveals that the turbulence stress retains a strong intensity along the streamwise domain within
$z/D\in [-0.5,0.5]$
downstream of the jet.
Figure 14. R.m.s. velocity profiles at different locations averaged over
$z/D\in [3.0,3.5]$
, plotted in wall unit coordinates, normalized by the inflow free-stream velocity: (a)
$x/D=-10.0$
, (b)
$x/D=5.0$
, (c)
$x/D=20.0$
, (d)
$x/D=35.0$
. Solid lines represent the flat-plate case, and dash-dotted lines represent the
$J=5.5$
case. R.m.s. velocities of the streamwise (▵), wall-normal (♦) and spanwise (▸) components, together with the Reynolds shear stress (●), are shown.
Figure 15. R.m.s. velocity profile predictions at
$x/D=35.0$
in the belt
$z/D\in [-0.5,0.5]$
, normalized by the inflow free-stream velocity. Solid lines represent the
$J=5.5$
case and dash-dotted lines represent the flat-plate case for r.m.s. velocities of the streamwise (▵), wall-normal (♦) and spanwise (▸) components, together with the Reynolds shear stress (●).
The evolutions of the TKE and the shear stress
$\langle u^{\prime }v^{\prime }\rangle$
along
$y/D=0.08$
and
$y/D=0.6$
in the domain
$z/D\in [3.0,3.5]$
are shown in figures 16 and 17, respectively, where a similar trend of the different evolution processes for jet cases can be seen. The amplification of the TKE and
$\langle u^{\prime }v^{\prime }\rangle$
near the jet orifice is due to the interaction of the jet bow shock with the boundary layer (Andreopoulos et al.
Reference Andreopoulos, Agui and Briassulis2000), which results in the windward separation region in front of the jet. It is interesting to see that the absolute magnitudes of both the TKE and
$\langle u^{\prime }v^{\prime }\rangle$
start to decease ahead of the jet, which corresponds to the analysis of the pressure distribution in figure 9(b). From figures 16 and 17, we can see that the evolution of the TKE and
$\langle u^{\prime }v^{\prime }\rangle$
depends on the momentum flux ratio
$J$
. As
$J$
increases, the peak values of TKE and
$\langle u^{\prime }v^{\prime }\rangle$
decrease in the lateral downstream of the jet. The
$\langle u^{\prime }v^{\prime }\rangle$
value is reduced to almost zero along
$y/D=0.6$
for
$J=5.5$
, indicating that turbulence is greatly suppressed and even laminarization happens. The magnitude of the TKE and
$\langle u^{\prime }v^{\prime }\rangle$
decreases to local minima soon after the separation at
$y/D=0.08$
, then gradually redevelops outwards. Along
$y/D=0.08$
downstream of the jet orifice, the peak of the TKE and
$\langle u^{\prime }v^{\prime }\rangle$
first occurs around
$x/D=18.0$
for
$J=2.3$
, where the inner layer is basically recovered; while at
$y/D=0.6$
for
$J=2.3$
, the peak of the TKE and
$\langle u^{\prime }v^{\prime }\rangle$
first occurs around
$x/D=25.0$
, suggesting that the outer boundary layer takes a longer distance to recover than the inner layer. Compared to
$J=2.3$
, the peak of the TKE and
$\langle u^{\prime }v^{\prime }\rangle$
of
$J=5.5$
appears further downstream, which means that wall turbulence regeneration in the near-wall region is slower for higher
$J$
. For
$J=2.3$
, the process of regeneration of wall turbulence takes place within a shorter distance than
$J=5.5$
, which again can be attributed to the interaction induced by the jet plume with the boundary layer. Compared to
$J=2.3$
, the peak of the TKE and
$\langle u^{\prime }v^{\prime }\rangle$
of
$J=5.5$
appears further downstream, which means that wall turbulence regeneration in the near-wall region is slower for higher
$J$
.
Figure 16. TKE along the streamwise direction at (a)
$y/D=0.08$
and (b)
$y/D=0.6$
in the domain
$z/D\in [3.0,3.5]$
for different cases, normalized by the square of the inflow free-stream velocity.
Figure 17. The velocity
$\langle u^{\prime }v^{\prime }\rangle$
along the streamwise direction at (a)
$y/D=0.08$
and (b)
$y/D=0.6$
in the domain
$z/D\in [3.0,3.5]$
of different cases, normalized by the square of the inflow free-stream velocity.
4 Streamline analysis and flow topology
Figure 18 shows several representative time-averaged streamlines and the isosurface of
$Ma=0.6$
. The isosurface of
$Ma=0.6$
reflects the windward separation bubble ahead of the jet orifice. In figure 18, the streamlines originate from the inflow at
$y/D=1.0$
upstream of the jet orifice. The streamlines, coloured by the local wall-normal distance, demonstrate the motion of the supersonic cross-flow around the jet plume, especially the motion in the wall-normal direction. As shown in figure 18(a), when the incoming flow is obstructed by the jet plume, the streamlines wrap around the jet orifice and are pushed to higher wall-normal positions and lifted away from the wall by the separation bubble ahead of the jet. Owing to the existence of a low-pressure region in the jet lee, flow around the jet plume moves from the edge of the separation region to the jet lee. During this process, the flow experiences several stages, which are well demonstrated by the streamlines. Streamlines firstly move towards the wall from the top of the separation bubble when travelling across the separation region, which indicates a flow reattachment from the top of the separation bubble to the wall. During this process, the flow experiences an expansion due to the reattachment in a supersonic flow. This expansion is denoted as reattachment expansion, which is consistent with the analysis of the wall pressure shown in figure 9(b). After the reattachment, streamlines run further around the jet orifice and keep expanding due to the existence of the low-pressure zone in the jet lee, as can be seen from figure 18(b), where streamlines are coloured by the local pressure. Downstream of the jet orifice, streamlines are twisted by the well-known CVP and concentrate in the jet lee and further rotate downstream to the jet far field, which were well discussed in our previous work (Sun & Hu Reference Sun and Hu2018c
). To summarize, supersonic boundary-layer flow around the jet orifice experiences at least two expansions, the reattachment expansion and the jet lateral expansion, which inevitably change the turbulence state in the supersonic boundary layer.
Figure 18. Streamlines originating from the plane
$y/D=1.0$
in the cross-flow of the
$J=5.5$
case, and the isosurface of
$Ma=0.6$
, both coloured by (a) the local wall-normal distance and (b) the local pressure.
Figure 19. Pressure, pressure gradient and Mach number distributions along the streamline selected in figure 18(b) of the
$J=5.5$
case.
Figure 20. Streamlines originating from jet wake flow coloured by the local wall-normal distance (a) and local pressure (b) of the
$J=5.5$
case.
A representative streamline originated from
$y/D=1.0$
on the incoming cross-flow plane is selected, as highlighted in figure 18(b), to show the state that the flow experiences. The pressure and corresponding streamwise pressure gradient along this streamline are given in figure 19(a). The Mach number along the streamline is shown in figure 19(b). Firstly it is seen that the Mach number is always larger than
$1.0$
along the whole streamline, which demonstrates that the supersonic flow condition is kept in the whole near field. The negative pressure gradient can be divided into two parts. The first part is a quick expansion region
$(0.0<x/D<2.1)$
with a large favourable pressure gradient, which corresponds to the reattachment expansion, and the second part
$(2.1<x/D<7.3)$
is a gentler expansion region, corresponding to the lateral expansion. As has been analysed in the previous work (Gao et al.
Reference Gao, Liang, Sun and Zhao2017), the expansion in supersonic flow leads to a favourable pressure gradient and the reduction of Reynolds shear stress induced by the favourable pressure gradient can be analysed from the Reynolds stress transport equations. After some algebraic manipulations (details can be found in Dussauge & Gaviglio (Reference Dussauge and Gaviglio1987)), the transport equation for
$\widetilde{u_{i}^{\prime }u_{j}^{\prime }}$
is obtained as
$$\begin{eqnarray}\frac{\text{D}}{\text{D}t}\widetilde{u_{i}^{\prime }u_{j}^{\prime }}=\frac{\displaystyle \overline{\unicode[STIX]{x1D70C}^{\prime }u_{j}^{\prime }}\frac{\unicode[STIX]{x2202}\bar{p}}{\unicode[STIX]{x2202}x_{i}}+\overline{\unicode[STIX]{x1D70C}^{\prime }u_{i}^{\prime }}\frac{\unicode[STIX]{x2202}\bar{p}}{\unicode[STIX]{x2202}x_{j}}}{\bar{\unicode[STIX]{x1D70C}}^{2}}+\frac{\displaystyle \overline{u_{i}^{\prime }\frac{\unicode[STIX]{x2202}p^{\prime }}{\unicode[STIX]{x2202}x_{j}}}+\overline{u_{j}^{\prime }\frac{\unicode[STIX]{x2202}p^{\prime }}{\unicode[STIX]{x2202}x_{i}}}}{\bar{\unicode[STIX]{x1D70C}}}.\end{eqnarray}$$
For the mean pressure-gradient contribution to pressure fluctuations (the second term on the right-hand side of (4.1)), the following model by Lumley (Reference Lumley and Yih1979) is used:
$$\begin{eqnarray}\left(\overline{u_{i}^{\prime }\frac{\unicode[STIX]{x2202}p^{\prime }}{\unicode[STIX]{x2202}x_{j}}}+\overline{u_{j}^{\prime }\frac{\unicode[STIX]{x2202}p^{\prime }}{\unicode[STIX]{x2202}x_{i}}}\right)_{\overline{p}}=0.3\left(\frac{\overline{T^{\prime }u_{i}^{\prime }}}{\tilde{T}}\frac{\unicode[STIX]{x2202}\bar{p}}{\unicode[STIX]{x2202}x_{j}}+\frac{\overline{T^{\prime }u_{j}^{\prime }}}{\tilde{T}}\frac{\unicode[STIX]{x2202}\bar{p}}{\unicode[STIX]{x2202}x_{i}}-\frac{2}{3}\frac{\overline{T^{\prime }u_{k}^{\prime }}}{\tilde{T}}\frac{\unicode[STIX]{x2202}\bar{p}}{\unicode[STIX]{x2202}x_{k}}\unicode[STIX]{x1D6FF}_{ij}\right)\!.\end{eqnarray}$$
When the flow encounters a streamwise favourable pressure gradient
$(\unicode[STIX]{x2202}\bar{p}/\unicode[STIX]{x2202}x<0)$
, as
$\unicode[STIX]{x2202}\bar{p}/\unicode[STIX]{x2202}y$
is close to zero near the wall, the contribution of the pressure fluctuation term is negative (
$\unicode[STIX]{x1D6FF}_{ij}=0$
when
$i\neq j$
). Thus the right-hand side of (4.1) is negative. For a steady flow,
$\text{D}(\widetilde{u_{i}^{\prime }u_{j}^{\prime }})/\text{D}t$
is simplified to
$\widetilde{u_{k}}[\unicode[STIX]{x2202}(\widetilde{u_{i}^{\prime }u_{j}^{\prime }})/\unicode[STIX]{x2202}x_{k}]$
, which gives the change of the Reynolds shear stresses along a time-averaged streamline. As a consequence, a negative right-hand side of (4.1) indicates that the Reynolds shear stresses decrease in the streamwise direction when the flow travels through a favourable pressure gradient region. As analysed above, the phenomenon of local turbulence reduction is associated with the decrease of Reynolds shear stresses. Based on the numerical results and the above analysis, it is concluded that the double expansion in the supersonic flow leads to the turbulence decay in the lateral boundary layer downstream of the jet.
In figure 20, streamlines passing the horizontal line of
$y/D=0.5$
at
$x/D=10.0$
in the jet wakes are given. Figure 20 demonstrates the streamline movement in the jet lateral boundary layer. The streamlines running around the jet lateral converge towards the jet leeward centreline. Streamlines adjacent to the jet orifice are tilted and folded by the jet leeward 3D flow. It is seen that flow in the jet wake shows strong rotation due to the surface trailing CVP, which is induced by the reattachment flow over the jet lee herringbone separation. This phenomenon has been well analysed in our previous paper (Sun & Hu Reference Sun and Hu2018a
). The impingement and the surface trailing rotating flow significantly increase the turbulence intensity in the boundary layer, which leads to an increment of turbulence fluctuation downstream of the jet leeward separation and in the far field, revealing a different character from the lateral side. Analysis of the TKE and r.m.s. velocities has reflected the turbulence state in the centreline wake. The streaky structures near the centreline wakes in figure 3 are also associated with these interactions. Figure 20 also shows that the streamlines from the cross-flow run through the lateral zone in the vicinity of the jet, which means that the far-field boundary-layer flow is related to the near-field lateral region which has a suppressed turbulence state. There is no doubt that the immediate turbulence decay in the jet near-field boundary layer would affect the downstream boundary layer due to the history effect.
Figure 21 gives an oblique view and a top view of the double expansion with isosurfaces of
$Ma=0.6$
and
$2.9$
superimposed by pressure contours, which demonstrates that the supersonic boundary-layer flow experiences double expansion around the sonic jet which leads to turbulence decay in the vicinity of the jet lateral. The first expansion corresponds to the reattachment expansion. The streamlines go across the windward separation bubble ahead of the jet and reattach to the wall, experiencing an expansion in the supersonic flow. The second expansion represents the lateral expansion which occurs in the lateral vicinity to the jet orifice. As shown in figure 21(a), the barrel shock detaches from the wall surface and creates the low-pressure region which absorbs the lateral flow, which was well analysed in our previous work (Sun & Hu Reference Sun and Hu2018b
). The streamlines follow the lateral side of the barrel shock and run into the low-pressure region behind the jet, experiencing a lateral expansion in the supersonic flow. The double expansion leads to the apparent turbulence decay in the lateral of the jet. The streamlines from the cross-flow run through this lateral region (as shown in figure 20) and suffer from the suppressed turbulence state, which results in the slow recovery of the outer boundary layer in the far field.
Figure 21. The double expansion for a supersonic boundary-layer flow around the jet of the
$J=5.5$
case, superimposed by pressure contours. (a) Oblique view, (b) top view.
5 Preliminary experiments to confirm the turbulence decay phenomenon
All the results of these activities are described in appendices A and B. The experiments are conducted to investigate the supersonic turbulent boundary layer with a transverse jet by using the NPLS technique. The instantaneous images and the averaged data from NPLS images both confirm the existence of the turbulence decay phenomena in reality. The experimental validation is preliminary and indicative for several reasons. Firstly, there is no particle fed in the injection. The dark colour in the jet regime probably represents no particle, which does not reflect the density variation in the flow field. The jet plume also expands and extends in the spanwise direction, which means that the density field reflected by the NPLS image is polluted by the jet injectants and gives invalid density variation and inaccurate turbulence state. According to the NPLS images shown in figure 24, the spanwise zone
$z/D\in [-5,5]$
near to the jet orifice is contaminated by the non-particle flow and the local turbulence state is unknown. This means that the near-field zone
$z/D\in [-3.5,3.5]$
in which we are interested cannot be well revealed. The comparison between the simulation and the experiment cannot be made directly. This problem is difficult to solve. Even though we conduct a particle image velocimetry (PIV) test to obtain the velocity field, there are few particles in the near-field zone and it is impossible to calculate an accurate velocity. We can only observe the turbulence state in the lateral boundary layer which has a distance long enough away from the jet orifice and in the far-field boundary layer where the cross-flow has carried enough particles to reflect the density variation. Secondly, the density variation does not correspond to the turbulent velocity fluctuation directly. As Martin (Reference Martin2007) pointed out, even assuming the pressure fluctuations are negligible in a turbulent boundary layer, the strong Reynolds analogy gives
$$\begin{eqnarray}\frac{\unicode[STIX]{x1D70C}^{\prime }}{\bar{\unicode[STIX]{x1D70C}}}=(\unicode[STIX]{x1D6FE}-1)Ma^{2}\frac{u^{\prime }}{\bar{u}},\end{eqnarray}$$
which means
$\unicode[STIX]{x1D70C}^{\prime }/\bar{\unicode[STIX]{x1D70C}}$
is not proportional to
$u^{\prime }/\bar{u}$
since the local Mach number still needs to be determined. Thus the density fluctuation obtained from NPLS images is only indirect evidence for turbulence. Thirdly, the NPLS experiment only acquires certain transverse and longitudinal 2D slices of the flow field. The 3D configuration of the jet plume and its interaction with the supersonic cross-flow are difficult to reveal by slices. The turbulence state inferred from the NPLS images is not easily related to the turbulence change near the jet.
Anyway, the current NPLS experiments basically demonstrate the turbulence suppression caused by the jet in the supersonic cross-flow. Meanwhile the experimental verification is far from a complete or thorough validation. The current simulations and the experiment provide a challenging and open topic for other researchers. Any possible advanced optical technique could be tested for this complex flow phenomenon, especially if the near-wall region in the vicinity of the jet orifice could be well measured. As discussed above, this is very hard.
6 Conclusions
In the present study, direct numerical simulations are conducted to uncover physical aspects of a transverse sonic jet injected into a supersonic cross-flow at Mach number 2.7, focusing on the supersonic boundary-layer flow characteristics subjected to the sonic jet. Simulations are run for two jet-to-cross-flow momentum flux ratios of 2.3 and 5.5. A flat-plate boundary layer without a jet (
$J=0.0$
) is also simulated for comparison.
The simulation provides the instantaneous and averaged flow features in the supersonic boundary layer with the sonic jet injection. It is found that, in the near-wall region, favourable pressure gradients exist and turbulent coherent structures are weakened significantly in the vicinity of the jet and the state is retained in the downstream recovery region on the lateral of the jet, where the boundary-layer thickness decreases significantly with an increased
$J$
. Turbulence in the central region behind the jet is amplified due to the collision of the cross-flow running around the jet and its interaction with the boundary layer.
A characteristic reduction in the TKE and shear stress profiles in the boundary layer along the streamwise direction in the lateral near-wall region is found and compared to the flat-plate case. The shear stress decreases significantly and the turbulence in the outer layer of the supersonic boundary layer decays sharply and is consistently suppressed along the streamwise direction in the lateral. The decay blocks the exchange of energy between the inner layer and the mainstream, and leads to a quick recovery in the inner boundary layer and a slow recovery in the outer layer. In the far-field boundary layer, the TKE is higher in the jet centreline than the lateral along the span. Higher jet momentum flux ratio leads to a more intense turbulence suppression in the lateral downstream.
Analysis of cross-flow streamlines exhibits a double-expansion character around the sonic jet which leads to turbulence decay in the vicinity of the jet lateral. The first expansion is the reattachment expansion, which occurs in the reattachment region downstream of the windward separation bubble induced by the jet. The second expansion is the lateral expansion, which occurs in the lateral side of the barrel shock. The double expansion leads to the turbulence reduction and the weakening of the coherent structures in the jet near field and affects the turbulence in the far-field boundary layer due to history effects.
A preliminary experiment based on the nanoparticle laser scattering technique is conducted for
$J=5.5$
. The instantaneous experimental results reveal that the boundary-layer thickness in the lateral region downstream of the jet decreases and also reflect the local turbulence reduction. From an overall view of the averaged and r.m.s. data of the NPLS images, it is found that the intensity of the density fluctuation decreases in the jet lateral side, which indicates the existence of turbulence decay phenomenon in the near-wall lateral flow downstream of the jet.
Acknowledgements
Our sincere thanks go to Professor N. D. Sandham of the University of Southampton for providing the SBLI DNS code and for helpful discussions on the data analysis. This work is funded by the National Science Foundation of China (grants 11472305 and 11522222) and the Outstanding Youth Fund of the National University of Defense Technology. Supercomputer time provided by the UK Engineering and Physical Sciences Research Council under the project Thermal and Reactive Flow Simulation on High-End Computers (grant no. EP/J016381/1) is gratefully acknowledged.
Appendix A
This paper uses nanoparticle-based planar laser scattering (NPLS) technology (developed by Zhao et al. (Reference Zhao, Yi, Tian and Cheng2009)) to conduct the experiments. The NPLS system is composed of a double-pulsed Nd:YAG laser with wavelength of 532 nm and pulse energy of 520 mJ per 6 ns, a IMPERX charge-coupled device (CCD) camera of
$4000~\text{pixel}\times 2672~\text{pixel}$
, a nanoparticle generator, a computer and a synchronizer. The nanoparticles are seeded in the supersonic flow and act as the tracer, and their relaxation time is 66.3 ns and effective diameter is 42.5 nm, as given by Zhao et al. (Reference Zhao, Yi, Tian and Cheng2009). It is reasonable that the nanoparticles follow the fluctuation of small-scale turbulence in the low-noise supersonic flow tunnel (Wang & Wang Reference Wang and Wang2016). The maximum resolution of the system reaches
$10~\unicode[STIX]{x03BC}\text{m}~\text{pixel}^{-1}$
. Experiments are conducted in a Mach 2.7 suction-type supersonic wind tunnel. The test section of the wind tunnel is 400 mm long with a cross-sectional size of
$200~\text{mm}\times 200~\text{mm}$
. Test models are mounted horizontally in the test section. The model is a flat plate with a circular injector (diameter
$D$
is 2 mm), as shown in figure 22. We assume that the origin of the coordinate system lies on the centre of the orifice, and that resolution on slice
$z=0~\text{mm}$
is
$0.0259~\text{mm}~\text{pixel}^{-1}$
for a side-view visualization, and resolution on slice
$y=2~\text{mm}$
(
$y/D=1.0$
) and slice
$y=4~\text{mm}$
(
$y/D=2.0$
) is
$0.0332~\text{mm}~\text{pixel}^{-1}$
and
$0.0344~\text{mm}~\text{pixel}^{-1}$
for a top-view visualization, respectively.
Figure 22. Schematic of the experimental set-up in the supersonic flow tunnel.
As shown in figure 22, a roughness belt with size of
$10~\text{mm}\times 190~\text{mm}$
is placed 10 mm downstream of the leading edge to shift the inflow boundary layer from the laminar to the turbulent state. The method can be found in Wang & Wang (Reference Wang and Wang2016). To ensure that the boundary layer is fully developed, a long flat plate with length 250 mm is set upstream of the jet orifice. The
$x$
-axis is set along the centreline of the flat plate.
The air inflow parameters are set in accordance with
$Ma=2.7$
with stagnation pressure
$P_{0}=101\,325~\text{Pa}$
, stagnation temperature
$T_{0}=300~\text{K}$
and the corresponding unit Reynolds number is
$Re_{l}=8.96\times 10^{6}$
. The high-spatiotemporal-resolution NPLS image of the incoming turbulent boundary layer is given in figure 23, from which the coherent structures reflected by density variations in the inner part and the outer part of the turbulent boundary layer could be distinguished. The velocity data in the wall boundary layer at
$x=-10~\text{mm}$
from the PIV measured field and a theoretical prediction as described by Touber (Reference Touber2010)) are compared. From the comparison the 99 % boundary-layer thickness is estimated as
$\unicode[STIX]{x1D6FF}=6.0~\text{mm}$
, which is basically consistent with the current simulation.
Figure 23. The flat-plate boundary layer without the jet imaged by NPLS.
Nitrogen gas injection without nanoparticles is used and the jet properties are set to correspond to the injection parameters as shown in table 3. The stagnation pressure is higher than the set-up in the simulation since the jet orifice has a pressure loss and the mass flow discharge coefficient is approximately 0.86. The given stagnation pressure assures that
$J$
is basically equal to 5.5.
Table 3. Nitrogen jet condition for the experiment, including the jet-to-cross-flow momentum ratio
$(J)$
, orifice diameter
$(D)$
, Mach number (
$M_{j}$
), stagnation temperature (
$T_{0j}$
) and stagnation pressure (
$P_{0j}$
).
Appendix B
Figure 24 gives the representative NPLS images of the instantaneous density variation structures with the sonic jet into the
$Ma=2.7$
supersonic cross-flow. The large-scale structures, the bow shock, the separated shock and the boundary layer upstream of the jet can be observed. Chaotic turbulent structures in the boundary layer upstream of the jet can be well identified. The boundary layer downstream of the orifice is also visible in figure 24(b). Since the nitrogen jet carries no nanoparticles, the coherent structures displayed by the nanoparticles in the wake flow come from the cross-flow. It is found that the jet interacts with the upcoming boundary layer significantly. The turbulent structures crush into the separation region upstream of the jet. In the lateral of the jet, the structure of a horseshoe vortex is also identified which originates from the upstream separation induced by the bow shock. In the lateral of the jet, the outline of the horseshoe vortex originated from the upstream separation induced by the bow shock is reflected by the density variations, which has been well revealed by the oil-flow tracing technique (Liu et al.
Reference Liu, Sun, Liang, Cai and Wang2018). Downstream of the separation region, it is seen that the cross-flow runs around the jet and impinges into the trailing wake region.
Figure 24. Instantaneous density variation structure of the sonic jet into the supersonic cross-flow with different slices of the flow field: (a)
$z/D=0.0$
, (b)
$z/D=5.0$
(
$z=10~\text{mm}$
), (c)
$y/D=1.0$
(
$y=2~\text{mm}$
) and (d)
$y/D=2.0$
(
$y=4~\text{mm}$
) slices.
In the vicinity downstream of the jet leeward separation, the wake structures in dark colour cannot be well identified since the flow might originate from the non-particle jet. At the
$y/D=1.0$
(
$y=2~\text{mm}$
) slice, it is identified that the intensity of the turbulence in the lateral side downstream of the jet orifice is lower than the flow upstream of the jet in the boundary layer, as enclosed in the dashed red ellipse. The phenomena reveal two characters in the lateral boundary layer. The first is that the boundary-layer thickness in the lateral downstream of the jet is decreased. This is due to the quick reattachment of the supersonic flow downstream of the windward separation, as indicated by the simulation. The second is that the turbulence in the jet lateral is suppressed. In the centre downstream of the jet wake, the grey coherent structures occur in the jet lee, which represents that the cross-flow runs around the jet and concentrates in the jet lee and leads to a local turbulence amplification. The turbulent coherent structures downstream of the jet wake extend in the spanwise zone and affect the lateral boundary layer. The effect of the wake turbulence is also an important factor for the turbulence recovery of the lateral boundary layer from the suppression near to the jet.
Figure 25. Averaged and r.m.s. streamwise flow structures of the sonic jet into the supersonic cross-flow on the
$y/D=1.0$
and 2.0 slices. The
$z/D=0.0$
(
$z=0~\text{mm}$
) and
$z/D=6.0$
(
$z=12~\text{mm}$
) lines on the slices are selected. (a) Averaged NPLS images on
$y/D=1.0$
; (b) averaged NPLS images on
$y/D=2.0$
, (c) r.m.s. of NPLS images on
$y/D=1.0$
, and (d) r.m.s. of NPLS images on
$y/D=2.0$
.
Figure 26. Density fluctuation intensity at (a)
$z/D=6.0$
(
$z=12~\text{mm}$
) and (b)
$z/D=0.0$
(
$z=0~\text{mm}$
) on
$y/D=1.0$
(
$y=2~\text{mm}$
),
$y/D=2.0$
(
$y=4~\text{mm}$
) slice, respectively. The smoothed line obtained by averaging 1000 points for the original data is superimposed.
Averaged and r.m.s. of the NPLS images are calculated and shown in figure 25. The colour of the NPLS image reflects the density (
$\unicode[STIX]{x1D70C}$
) change on the slice, as concluded by Zhao et al. (Reference Zhao, Yi, Tian and Cheng2009). In the jet wake it clearly shows that an impingement occurs in the jet leeward and a V-shaped wake exists. R.m.s. images reflect the local density fluctuation, denoted as
$\unicode[STIX]{x1D70C}_{rms}$
and averaged images reflect the local density intensity
$\bar{\unicode[STIX]{x1D70C}}$
. In the vicinity of the jet orifice, it is hard to evaluate the local density fluctuation since there are no particles in the injectants. That is why we cannot give the density fluctuation in the domain of
$-3.5<z/D<3.5$
directly to make comparison with the simulated data. In the lateral side, the zone of
$z/D>5.0$
could be treated as a region non-polluted by the injectants. It is recognized that the local density fluctuation in the zone
$z/D>5.0$
of the lateral boundary layer is clearly revealed. The density fluctuation in the jet wakes in the centre downstream of the jet with
$z/D>5.0$
is also clearly revealed.
The location at
$z/D=6.0$
has a long enough distance away from the jet centre, which ensures that the location is not affected by the non-particle flow from the jet. Figure 26 gives the
$\unicode[STIX]{x1D70C}_{rms}/\bar{\unicode[STIX]{x1D70C}}$
distribution along
$z/D=6.0$
and
$z/D=0.0$
at
$y/D=1.0$
and
$y/D=2.0$
corresponding to figure 25. In figure 26(a), the peak value of
$\unicode[STIX]{x1D70C}_{rms}/\bar{\unicode[STIX]{x1D70C}}$
corresponds to the jet windward separation. The magnitude of this at
$y/D=1.0$
starts to decrease when the flow goes across the separation region. From figure 26, we can see that
$\unicode[STIX]{x1D70C}_{rms}/\bar{\unicode[STIX]{x1D70C}}$
at
$z/D=6.0$
decreases to a minimum value at nearly
$x/D=20.0$
(
$x=40~\text{mm}$
), indicating that local density fluctuation is reasonably suppressed. A careful observation shows that the minimum
$\unicode[STIX]{x1D70C}_{rms}/\bar{\unicode[STIX]{x1D70C}}$
intensity in the boundary layer is reduced by approximately 9.8 % of the intensity in the upstream boundary layer. In the downstream region of
$x/D=20.0$
,
$\unicode[STIX]{x1D70C}_{rms}/\bar{\unicode[STIX]{x1D70C}}$
starts to increase, which reflects a local density fluctuation recovery due to the development of the lateral boundary layer and the spanwise extension of the wake flow. At
$y/D=2.0$
the phenomenon is lagged since at this height the local boundary-layer thickness decreases and it takes a longer distance to recover when compared to
$y/D=1.0$
. At
$z/D=0.0$
, the magnitude of the density fluctuation in the flow downstream of the orifice is higher than that upstream of the orifice, which can be attributed to the strong flow interaction by the collision of the cross-flows. In the zone of
$-5.0<z/D<5.0$
due to the non-particle flow related to the jet, the density fluctuation is not valid in figure 26(b).
This experiment basically confirms the existence of the turbulence delay phenomenon in the lateral supersonic boundary layer around the jet orifice, and reveals the turbulence amplification in the jet wake near-wall flow.
