1. Introduction
Fluid flows in stars and planets, which are typically subject to rotation, can be driven by internal thermal forcing (Spiegel Reference Spiegel1971; Aurnou et al. Reference Aurnou, Calkins, Cheng, Julien, King, Nieves, Soderlund and Stellmach2015; Jones Reference Jones2015) and/or by external mechanical forcings due to the gravitational coupling with orbital companions (Ogilvie Reference Ogilvie2014; Le Bars, Cébron & Le Gal Reference Le Bars, Cébron and Le Gal2015). Despite the common rotational constraint, thermal convection and mechanically driven flows are traditionally treated as two separate branches in rotating fluid dynamics (Chandrasekhar Reference Chandrasekhar1961; Greenspan Reference Greenspan1968).
Owing to the periodicity of orbital motions, mechanical forcings such as precession (Hollerbach & Kerswell Reference Hollerbach and Kerswell1995; Noir et al. Reference Noir, Brito, Aldridge and Cardin2001), libration (Aldridge & Toomre Reference Aldridge and Toomre1969) and tides (Ogilvie & Lin Reference Ogilvie and Lin2004) can drive oscillatory motions in rotating fluids, known as inertial modes or inertial waves restored by the Coriolis force (Greenspan Reference Greenspan1968). On the other hand, it has been long recognized that rotating convection close to the onset is in the form of quasi-steady columnar rolls (Busse Reference Busse1970; Jones, Soward & Mussa Reference Jones, Soward and Mussa2000). At low Prandtl number (![]() ${\textit {Pr}} < 1$), however, it was found that the onset of convection can be in the form of an oscillatory inertial mode at leading order (Zhang Reference Zhang1994), suggesting that rotating convection and mechanically driven rotating flows are closely related. Indeed, a recent monograph by Zhang & Liao (Reference Zhang and Liao2017) provided a set of unified asymptotic theories for the linear onset of convection and linear responses to mechanical forcings in rotating fluids based on an expansion of inertial waves. In this paper, we show that some aspects of the nonlinear dynamics of rotating convection can be understood within the framework of inertial wave interactions, as developed in mechanically driven rotating flows (Kerswell Reference Kerswell2002; Le Bars et al. Reference Le Bars, Cébron and Le Gal2015).
${\textit {Pr}} < 1$), however, it was found that the onset of convection can be in the form of an oscillatory inertial mode at leading order (Zhang Reference Zhang1994), suggesting that rotating convection and mechanically driven rotating flows are closely related. Indeed, a recent monograph by Zhang & Liao (Reference Zhang and Liao2017) provided a set of unified asymptotic theories for the linear onset of convection and linear responses to mechanical forcings in rotating fluids based on an expansion of inertial waves. In this paper, we show that some aspects of the nonlinear dynamics of rotating convection can be understood within the framework of inertial wave interactions, as developed in mechanically driven rotating flows (Kerswell Reference Kerswell2002; Le Bars et al. Reference Le Bars, Cébron and Le Gal2015).
Rotating flows can become unstable through the so-called triadic resonance (Le Bars et al. Reference Le Bars, Cébron and Le Gal2015), i.e. a base flow with frequency ![]() $\omega _0$ and azimuthal wavenumber
$\omega _0$ and azimuthal wavenumber ![]() $m_0$ can excite two inertial waves whose frequencies
$m_0$ can excite two inertial waves whose frequencies ![]() $\omega _1,\omega _2$ and azimuthal wavenumbers
$\omega _1,\omega _2$ and azimuthal wavenumbers ![]() $m_1, m_2$ match the resonance conditions (Bretherton Reference Bretherton1964; Kerswell Reference Kerswell2002):
$m_1, m_2$ match the resonance conditions (Bretherton Reference Bretherton1964; Kerswell Reference Kerswell2002):
(Here we present the resonance conditions in a spherical geometry. In an unbounded domain, the second condition should read ![]() $\boldsymbol{k}_1\pm \boldsymbol{k}_2=\boldsymbol{k}_0$, where
$\boldsymbol{k}_1\pm \boldsymbol{k}_2=\boldsymbol{k}_0$, where ![]() $\boldsymbol{k}$ is the wavevector.) Such an instability has been observed both experimentally and numerically in a variety of rotating flows driven by mechanical forcings (see Kerswell Reference Kerswell2002; Le Bars et al. Reference Le Bars, Cébron and Le Gal2015, and references therein), but never reported before in rotating convection systems. Motivated by geophysical and astrophysical applications, rotating convection has been studied extensively both for planar models (see recent review by Plumley & Julien (Reference Plumley and Julien2019)) and for spherical models (e.g. Aubert et al. Reference Aubert, Brito, Nataf, Cardin and Masson2001; Christensen Reference Christensen2002; Gastine, Wicht & Aubert Reference Gastine, Wicht and Aubert2016; Kaplan et al. Reference Kaplan, Schaeffer, Vidal and Cardin2017; Guervilly, Cardin & Schaeffer Reference Guervilly, Cardin and Schaeffer2019), yet the nonlinear dynamics and turbulent regime remain to be fully understood (Aurnou et al. Reference Aurnou, Calkins, Cheng, Julien, King, Nieves, Soderlund and Stellmach2015).
$\boldsymbol{k}$ is the wavevector.) Such an instability has been observed both experimentally and numerically in a variety of rotating flows driven by mechanical forcings (see Kerswell Reference Kerswell2002; Le Bars et al. Reference Le Bars, Cébron and Le Gal2015, and references therein), but never reported before in rotating convection systems. Motivated by geophysical and astrophysical applications, rotating convection has been studied extensively both for planar models (see recent review by Plumley & Julien (Reference Plumley and Julien2019)) and for spherical models (e.g. Aubert et al. Reference Aubert, Brito, Nataf, Cardin and Masson2001; Christensen Reference Christensen2002; Gastine, Wicht & Aubert Reference Gastine, Wicht and Aubert2016; Kaplan et al. Reference Kaplan, Schaeffer, Vidal and Cardin2017; Guervilly, Cardin & Schaeffer Reference Guervilly, Cardin and Schaeffer2019), yet the nonlinear dynamics and turbulent regime remain to be fully understood (Aurnou et al. Reference Aurnou, Calkins, Cheng, Julien, King, Nieves, Soderlund and Stellmach2015).
Recent numerical simulations (Horn & Schmid Reference Horn and Schmid2017) and laboratory experiments (Aurnou et al. Reference Aurnou, Bertin, Grannan, Horn and Vogt2018) of rotating convection in a cylinder using liquid gallium (![]() ${\textit {Pr}} \approx 0.025$) observed multi-modal interactions, yet the underlying mechanism remains to be elucidated. Lam, Kong & Zhang (Reference Lam, Kong and Zhang2018) numerically studied rotating convection in a sphere with
${\textit {Pr}} \approx 0.025$) observed multi-modal interactions, yet the underlying mechanism remains to be elucidated. Lam, Kong & Zhang (Reference Lam, Kong and Zhang2018) numerically studied rotating convection in a sphere with ![]() $Pr=0.0023$ at moderate Ekman numbers and found that the nonlinear interaction of various thermal inertial waves leads to a weakly turbulent state, though no evidence of triadic resonances was shown. Here we show, through numerical simulations at lower Ekman numbers, that the primary convective mode at low
$Pr=0.0023$ at moderate Ekman numbers and found that the nonlinear interaction of various thermal inertial waves leads to a weakly turbulent state, though no evidence of triadic resonances was shown. Here we show, through numerical simulations at lower Ekman numbers, that the primary convective mode at low ![]() ${\textit {Pr}}$ (relevant to liquid metals) can excite a pair of inertial modes through the triadic resonance in a rotating sphere, leading to more complex convective motions. Increasing the thermal forcing leads to a turbulent state that shows signatures of inertial waves. Our study may offer a new pathway to study rotating turbulent convection within the framework of inertial wave turbulence (Godeferd & Moisy Reference Godeferd and Moisy2015; Le Reun et al. Reference Le Reun, Favier, Barker and Le Bars2017).
${\textit {Pr}}$ (relevant to liquid metals) can excite a pair of inertial modes through the triadic resonance in a rotating sphere, leading to more complex convective motions. Increasing the thermal forcing leads to a turbulent state that shows signatures of inertial waves. Our study may offer a new pathway to study rotating turbulent convection within the framework of inertial wave turbulence (Godeferd & Moisy Reference Godeferd and Moisy2015; Le Reun et al. Reference Le Reun, Favier, Barker and Le Bars2017).
2. Numerical model
We consider the canonical problem of Boussinesq convection in a sphere of radius ![]() $r_o$, which rotates at
$r_o$, which rotates at ![]() $\boldsymbol{\varOmega} = \varOmega \hat{\boldsymbol{z}}$. Convection is driven by a uniform heat source
$\boldsymbol{\varOmega} = \varOmega \hat{\boldsymbol{z}}$. Convection is driven by a uniform heat source ![]() $S$ under a gravitational field
$S$ under a gravitational field ![]() $\boldsymbol{g} = -g_o \boldsymbol{r}/r_o$. The problem was first formulated by Chandrasekhar (Reference Chandrasekhar1961) and is governed by the following dimensionless equations in the rotating frame:
$\boldsymbol{g} = -g_o \boldsymbol{r}/r_o$. The problem was first formulated by Chandrasekhar (Reference Chandrasekhar1961) and is governed by the following dimensionless equations in the rotating frame:
where ![]() $\boldsymbol{u}$ is the fluid velocity,
$\boldsymbol{u}$ is the fluid velocity, ![]() $p$ is the reduced pressure,
$p$ is the reduced pressure, ![]() $T$ is the total temperature and
$T$ is the total temperature and ![]() $T_b=(1-r^2)/2$ is the dimensionless basic temperature without convection. The system is defined by three non-dimensional parameters, i.e. the Ekman number
$T_b=(1-r^2)/2$ is the dimensionless basic temperature without convection. The system is defined by three non-dimensional parameters, i.e. the Ekman number ![]() $E$, the Rayleigh number
$E$, the Rayleigh number ![]() ${Ra}$ and the Prandtl number
${Ra}$ and the Prandtl number ![]() ${\textit {Pr}}$:
${\textit {Pr}}$:
where ![]() $\nu$ is the kinematic viscosity,
$\nu$ is the kinematic viscosity, ![]() $\kappa$ is the thermal diffusivity,
$\kappa$ is the thermal diffusivity, ![]() $\alpha$ is the thermal expansion coefficient and
$\alpha$ is the thermal expansion coefficient and ![]() $\beta =S/(3\kappa )$ characterizes the temperature gradient without convection. In rotating flows, another important non-dimensional parameter is the Rossby number, which is defined as
$\beta =S/(3\kappa )$ characterizes the temperature gradient without convection. In rotating flows, another important non-dimensional parameter is the Rossby number, which is defined as
In our model, the Rossby number ![]() $Ro$ is an output parameter and is determined by the dimensional root mean square velocity
$Ro$ is an output parameter and is determined by the dimensional root mean square velocity ![]() $U_{rms}$ in the simulation domain.
$U_{rms}$ in the simulation domain.
The fully nonlinear governing equations of the system are numerically solved using a spectral method based on expansions of spherical harmonics in the angular direction and Jones–Worland polynomials in the radial direction (Marti & Jackson Reference Marti and Jackson2016). We use the no-slip boundary condition and a fixed-temperature (![]() $T=0$) condition on the spherical boundary. Simulations are initiated from small random velocity perturbations or from a saturated state at lower
$T=0$) condition on the spherical boundary. Simulations are initiated from small random velocity perturbations or from a saturated state at lower ![]() $Ra$.
$Ra$.
This study explores rotating convection in the parameter regime of low Ekman numbers (![]() $10^{-6}\le E\le 10^{-5}$) and low Prandtl numbers (
$10^{-6}\le E\le 10^{-5}$) and low Prandtl numbers (![]() $10^{-3}\le Pr\le 10^{-2}$). The Rayleigh number varies from the slightly supercritical to the turbulent convection regime. The resulting Rossby number ranges from
$10^{-3}\le Pr\le 10^{-2}$). The Rayleigh number varies from the slightly supercritical to the turbulent convection regime. The resulting Rossby number ranges from ![]() $10^{-3}$ to
$10^{-3}$ to ![]() $3\times 10^{-2}$, suggesting that convection is rotationally dominated in all of the simulations. We use numerical truncations of
$3\times 10^{-2}$, suggesting that convection is rotationally dominated in all of the simulations. We use numerical truncations of ![]() $N=63$,
$N=63$, ![]() $L=M=127$ for the simulations near the onset, and increase the truncations up to
$L=M=127$ for the simulations near the onset, and increase the truncations up to ![]() $N=191$,
$N=191$, ![]() $L=M=383$ for the turbulent convection, where
$L=M=383$ for the turbulent convection, where ![]() $N$,
$N$, ![]() $L$ and
$L$ and ![]() $M$ are truncations of the radial polynomials, degree and order of spherical harmonics, respectively. The convergence of the numerical solutions is warranted by checking energy spectra and by doubling the truncations for some cases.
$M$ are truncations of the radial polynomials, degree and order of spherical harmonics, respectively. The convergence of the numerical solutions is warranted by checking energy spectra and by doubling the truncations for some cases.
3. Results
Figure 1 shows the Fourier transform of the time series of the radial velocity at a fixed position (![]() $r=0.59$) in the equatorial plane for various
$r=0.59$) in the equatorial plane for various ![]() $Ra$ at
$Ra$ at ![]() $E=10^{-6}$ and
$E=10^{-6}$ and ![]() ${\textit {Pr}}=0.001$. For
${\textit {Pr}}=0.001$. For ![]() $Ra=1.5\times 10^{7}\approx 1.4 Ra_c$, where
$Ra=1.5\times 10^{7}\approx 1.4 Ra_c$, where ![]() $Ra_c$ is the critical Rayleigh number for the onset of convection, the frequency spectrum shows a pronounced peak at
$Ra_c$ is the critical Rayleigh number for the onset of convection, the frequency spectrum shows a pronounced peak at ![]() $\omega /\varOmega =0.25$, which corresponds to an oscillatory convective mode at low
$\omega /\varOmega =0.25$, which corresponds to an oscillatory convective mode at low ![]() ${\textit {Pr}}$ (Zhang Reference Zhang1994). In figure 1(a), there is also an obvious peak at
${\textit {Pr}}$ (Zhang Reference Zhang1994). In figure 1(a), there is also an obvious peak at ![]() $\omega /\varOmega \approx 0.5$, twice the frequency of the primary mode. Similar doubling in frequency has been observed in recent numerical simulations (Horn & Schmid Reference Horn and Schmid2017) and laboratory experiments (Aurnou et al. Reference Aurnou, Bertin, Grannan, Horn and Vogt2018) using liquid metal in a rotating cylinder. As we shall show later, the doubling in frequency is accompanied by a doubling in the azimuthal wavenumber as well, which may result from the nonlinear self-interaction of the primary mode. (The nonlinear term of a flow
$\omega /\varOmega \approx 0.5$, twice the frequency of the primary mode. Similar doubling in frequency has been observed in recent numerical simulations (Horn & Schmid Reference Horn and Schmid2017) and laboratory experiments (Aurnou et al. Reference Aurnou, Bertin, Grannan, Horn and Vogt2018) using liquid metal in a rotating cylinder. As we shall show later, the doubling in frequency is accompanied by a doubling in the azimuthal wavenumber as well, which may result from the nonlinear self-interaction of the primary mode. (The nonlinear term of a flow ![]() $\boldsymbol{u} \propto \exp ({\mathrm i (\omega t+m \phi )})$ potentially has two components:
$\boldsymbol{u} \propto \exp ({\mathrm i (\omega t+m \phi )})$ potentially has two components: ![]() $m_0=0,\ \omega _0=0$ and
$m_0=0,\ \omega _0=0$ and ![]() $m_2=2m,\ \omega _2=2\omega$.) For
$m_2=2m,\ \omega _2=2\omega$.) For ![]() $Ra=1.7\times 10^{7}\approx 1.6Ra_c$, apart from similar peaks observed in figure 1(a), the spectrum exhibits two distinct peaks with similar amplitudes at
$Ra=1.7\times 10^{7}\approx 1.6Ra_c$, apart from similar peaks observed in figure 1(a), the spectrum exhibits two distinct peaks with similar amplitudes at ![]() $\omega /\varOmega =0.09$ and 0.16, respectively (figure 1b). These two peaks and the primary peak at
$\omega /\varOmega =0.09$ and 0.16, respectively (figure 1b). These two peaks and the primary peak at ![]() $\omega /\varOmega =0.25$ satisfy the triadic resonance condition, i.e.
$\omega /\varOmega =0.25$ satisfy the triadic resonance condition, i.e. ![]() $\omega _1 \pm \omega _2=\omega _0$, suggesting a possible resonant triad between the primary convective mode and a pair of free modes.
$\omega _1 \pm \omega _2=\omega _0$, suggesting a possible resonant triad between the primary convective mode and a pair of free modes.

Figure 1. Fourier transform of the radial velocity ![]() $u_r$ at a fixed position (
$u_r$ at a fixed position (![]() $r=0.59$) in the equatorial plane at
$r=0.59$) in the equatorial plane at ![]() $E=10^{-6}$ and
$E=10^{-6}$ and ![]() ${\textit {Pr}}=0.001$, but various
${\textit {Pr}}=0.001$, but various ![]() $Ra$. Frequencies are normalized by the rotation frequency
$Ra$. Frequencies are normalized by the rotation frequency ![]() $\varOmega$.
$\varOmega$.
Figure 2 shows the kinetic energy contained in different azimuthal wavenumbers ![]() $m$ for the case in figure 1(b). We can see from the time-averaged spectrum that the energy is dominated by the
$m$ for the case in figure 1(b). We can see from the time-averaged spectrum that the energy is dominated by the ![]() $m=4$ component, with subsequent major contributions from the
$m=4$ component, with subsequent major contributions from the ![]() $m=0,1,3$ and
$m=0,1,3$ and ![]() $8$ components. Figure 2(b) shows the time evolution of the kinetic energy for the aforementioned components. After a transient stage, the
$8$ components. Figure 2(b) shows the time evolution of the kinetic energy for the aforementioned components. After a transient stage, the ![]() $m=4$ component starts to grow and becomes the dominant one, which corresponds to the primary convective mode. As the primary mode becomes saturated, the
$m=4$ component starts to grow and becomes the dominant one, which corresponds to the primary convective mode. As the primary mode becomes saturated, the ![]() $m=0$ and
$m=0$ and ![]() $m=8$ components also develop and saturate. The
$m=8$ components also develop and saturate. The ![]() $m=0$ component represents a steady zonal flow, while
$m=0$ component represents a steady zonal flow, while ![]() $m=8$ is twice the azimuthal wavenumber of the primary mode. Both
$m=8$ is twice the azimuthal wavenumber of the primary mode. Both ![]() $m=0$ and
$m=0$ and ![]() $m=8$ components can be attributed to the nonlinear interaction of the convective mode with itself (Zhang & Liao Reference Zhang and Liao2017). More interestingly, at
$m=8$ components can be attributed to the nonlinear interaction of the convective mode with itself (Zhang & Liao Reference Zhang and Liao2017). More interestingly, at ![]() $\varOmega t/(2{\rm \pi} )\approx 1000$, the
$\varOmega t/(2{\rm \pi} )\approx 1000$, the ![]() $m=1$ and
$m=1$ and ![]() $m=3$ components start to grow exponentially with the same growth rate and then saturate to similar levels, again pointing to a possible triadic resonance between the primary mode
$m=3$ components start to grow exponentially with the same growth rate and then saturate to similar levels, again pointing to a possible triadic resonance between the primary mode ![]() $m=4$ and two free modes of
$m=4$ and two free modes of ![]() $m=1$ and
$m=1$ and ![]() $m=3$.
$m=3$.

Figure 2. (a) Time-averaged kinetic energy spectrum as a function of the azimuthal wavenumber ![]() $m$ at
$m$ at ![]() $E=10^{-6}$,
$E=10^{-6}$, ![]() ${\textit {Pr}}=0.001$ and
${\textit {Pr}}=0.001$ and ![]() $Ra=1.7\times 10^7$. (b) Time evolution of the kinetic energy contained in different
$Ra=1.7\times 10^7$. (b) Time evolution of the kinetic energy contained in different ![]() $m$, for the five largest components (represented by circles) in panel (a). Time is in the unit of the rotation period.
$m$, for the five largest components (represented by circles) in panel (a). Time is in the unit of the rotation period.
In order to confirm that both ![]() $\omega$ and
$\omega$ and ![]() $m$ simultaneously satisfy the triadic resonance conditions, we decompose the velocity field into different
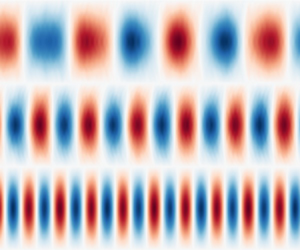
$m$ simultaneously satisfy the triadic resonance conditions, we decompose the velocity field into different ![]() $m$ components and then analyse the time evolution of each component. Figure 3 shows the time evolution of the radial velocity along a fixed vertical line for the
$m$ components and then analyse the time evolution of each component. Figure 3 shows the time evolution of the radial velocity along a fixed vertical line for the ![]() $m=1,3,4$ and
$m=1,3,4$ and ![]() $8$ components, respectively, for the case in figure 2. As the
$8$ components, respectively, for the case in figure 2. As the ![]() $m=0$ component represents a steady zonal flow, it is not shown in figure 3. One can see that each
$m=0$ component represents a steady zonal flow, it is not shown in figure 3. One can see that each ![]() $m$ component corresponds to a single frequency mode, and the
$m$ component corresponds to a single frequency mode, and the ![]() $m=1,3$ and 4 modes have the simplest structure along the axis of rotation. We extract the frequencies of each mode by fitting the time series with a sinusoidal function and find
$m=1,3$ and 4 modes have the simplest structure along the axis of rotation. We extract the frequencies of each mode by fitting the time series with a sinusoidal function and find ![]() $\omega /\varOmega =0.1624$, 0.0899, 0.2529 for the
$\omega /\varOmega =0.1624$, 0.0899, 0.2529 for the ![]() $m=1$, 3, 4 modes, respectively (see table 1), which clearly satisfy the triadic resonance conditions in both
$m=1$, 3, 4 modes, respectively (see table 1), which clearly satisfy the triadic resonance conditions in both ![]() $\omega$ and
$\omega$ and ![]() $m$. These results convincingly demonstrate that the primary convective mode with
$m$. These results convincingly demonstrate that the primary convective mode with ![]() $m=4$ excites two free modes with
$m=4$ excites two free modes with ![]() $m=1$ and 3 through the triadic resonance. We also find that the
$m=1$ and 3 through the triadic resonance. We also find that the ![]() $m=8$ mode has a frequency of
$m=8$ mode has a frequency of ![]() $\omega /\varOmega =0.5058$, doubling both
$\omega /\varOmega =0.5058$, doubling both ![]() $m$ and
$m$ and ![]() $\omega$ of the primary mode, as we mentioned before.
$\omega$ of the primary mode, as we mentioned before.

Figure 3. Time evolution of the radial velocity along a fixed vertical line with the distance to the rotation axis ![]() $s=0.5$ for the case in figure 2. The velocity field has been decomposed into components with different azimuthal wavenumber
$s=0.5$ for the case in figure 2. The velocity field has been decomposed into components with different azimuthal wavenumber ![]() $m$.
$m$.
Table 1. Examples of the triadic resonance at different control parameters and involved modes. Here ![]() $\omega _{{ns}}$ is the frequency obtained from numerical simulations and
$\omega _{{ns}}$ is the frequency obtained from numerical simulations and ![]() $\omega _{{in}}$ is the frequency of purely inviscid inertial modes. Frequencies are in the unit of the rotation frequency and positive (negative) values correspond to prograde (retrograde) modes. For each case, a movie showing the radial velocity of the interacting modes in the equatorial plane is also provided in the supplementary movies.
$\omega _{{in}}$ is the frequency of purely inviscid inertial modes. Frequencies are in the unit of the rotation frequency and positive (negative) values correspond to prograde (retrograde) modes. For each case, a movie showing the radial velocity of the interacting modes in the equatorial plane is also provided in the supplementary movies.

Table 1 lists three examples of triadic resonances and involved modes (see also supplementary movies available at https://doi.org/10.1017/jfm.2020.1050 for the radial velocity of interacting modes in the equatorial plane) at different control parameters. We can see that the triadic resonance can excite modes with either lower or higher wavenumbers and frequencies with respect to the primary modes, providing a mechanism for the bi-directional energy transfer. For instance, at ![]() $E=10^{-5}$,
$E=10^{-5}$, ![]() ${\textit {Pr}}=0.01$ and
${\textit {Pr}}=0.01$ and ![]() $Ra=3.3\times 10^6$, a low-frequency (
$Ra=3.3\times 10^6$, a low-frequency (![]() $\omega /\varOmega =0.0918$) prograde mode of
$\omega /\varOmega =0.0918$) prograde mode of ![]() $m=3$ excites a pair of retrograde modes with higher frequencies (
$m=3$ excites a pair of retrograde modes with higher frequencies (![]() $\omega /\varOmega =0.3596$ and 0.2678) and wavenumbers (
$\omega /\varOmega =0.3596$ and 0.2678) and wavenumbers (![]() $m=10$ and 13). Note that the primary mode in this case shows a multi-cellular pattern of the radial structure (Net, Garcia & Sánchez Reference Net, Garcia and Sánchez2008), whereas the primary mode in figure 3 shows a mono-cellular pattern of the radial structure (see supplementary movies). In this case, we also observe cyclic growth and collapse of the unstable modes (figure 4a,b), which is a typical behaviour of the triadic resonance (Lin, Noir & Jackson Reference Lin, Noir and Jackson2014; Barker Reference Barker2016). We can see that higher-wavenumber modes are excited on top of the
$m=10$ and 13). Note that the primary mode in this case shows a multi-cellular pattern of the radial structure (Net, Garcia & Sánchez Reference Net, Garcia and Sánchez2008), whereas the primary mode in figure 3 shows a mono-cellular pattern of the radial structure (see supplementary movies). In this case, we also observe cyclic growth and collapse of the unstable modes (figure 4a,b), which is a typical behaviour of the triadic resonance (Lin, Noir & Jackson Reference Lin, Noir and Jackson2014; Barker Reference Barker2016). We can see that higher-wavenumber modes are excited on top of the ![]() $m=3$ primary mode during the growth phase (figure 4c). As the energy in the growing modes becomes comparable to the zonal flow (
$m=3$ primary mode during the growth phase (figure 4c). As the energy in the growing modes becomes comparable to the zonal flow (![]() $m=0$), the flow suddenly collapses to chaotic small scales (figure 4d), known as resonant collapse of inertial modes, which was first observed by McEwan (Reference McEwan1970) in a precessing cylinder. The collapse is followed by a relaminarization (figure 4e), and then the cycle repeats. The whole process is reminiscent of the triadic resonant instability observed in several mechanically driven rotating flows (see Le Bars et al. Reference Le Bars, Cébron and Le Gal2015, and references therein).
$m=0$), the flow suddenly collapses to chaotic small scales (figure 4d), known as resonant collapse of inertial modes, which was first observed by McEwan (Reference McEwan1970) in a precessing cylinder. The collapse is followed by a relaminarization (figure 4e), and then the cycle repeats. The whole process is reminiscent of the triadic resonant instability observed in several mechanically driven rotating flows (see Le Bars et al. Reference Le Bars, Cébron and Le Gal2015, and references therein).

Figure 4. The growth and collapse of the unstable modes at ![]() $E=10^{-5}$,
$E=10^{-5}$, ![]() ${\textit {Pr}}=0.01$ and
${\textit {Pr}}=0.01$ and ![]() $Ra=3.3\times 10^6$. (a) Time series of the radial velocity at a fixed point. (b) Time series of the kinetic energy contained in different
$Ra=3.3\times 10^6$. (a) Time series of the radial velocity at a fixed point. (b) Time series of the kinetic energy contained in different ![]() $m$ components. (c–e) Snapshots of the radial velocity in the equatorial plane at the instants indicated by the inverted black triangles in panel (b).
$m$ components. (c–e) Snapshots of the radial velocity in the equatorial plane at the instants indicated by the inverted black triangles in panel (b).
Table 1 also lists the frequencies of purely inviscid inertial modes in a sphere, which have similar spatial structures as the modes observed from numerical simulations. We note that the observed frequencies are slightly shifted from the inviscid frequencies due to the viscous effect, the detuning effect (Kerswell Reference Kerswell2002) and the coupling with the thermal equation (Zhang Reference Zhang1994). Here we report a few cases in which the interacting modes can be clearly identified. For large ![]() $Ra$ and low
$Ra$ and low ![]() $E$, triadic resonances can simultaneously excite several pairs of modes, which makes it more difficult to identify individual modes. However, the mechanism appears to be generic as long as the onset of convection is in the form of an oscillatory thermal inertial mode, which generally exists at
$E$, triadic resonances can simultaneously excite several pairs of modes, which makes it more difficult to identify individual modes. However, the mechanism appears to be generic as long as the onset of convection is in the form of an oscillatory thermal inertial mode, which generally exists at ![]() $Pr<1$ (Zhang Reference Zhang1994).
$Pr<1$ (Zhang Reference Zhang1994).
Further increasing ![]() $Ra$ leads to several modes interacting and eventually to a turbulent state. Figure 5 shows an example of turbulent flows at
$Ra$ leads to several modes interacting and eventually to a turbulent state. Figure 5 shows an example of turbulent flows at ![]() $E=10^{-6}$,
$E=10^{-6}$, ![]() ${\textit {Pr}}=0.001$ and
${\textit {Pr}}=0.001$ and ![]() $Ra=5.0\times 10^7$. The Rossby number in this case is calculated to be
$Ra=5.0\times 10^7$. The Rossby number in this case is calculated to be ![]() $Ro=2.9\times 10^{-2}$, suggesting that turbulence convection is strongly influenced by the rotation. The axial vorticity (figure 5a) exhibits both small-scale and large-scale structures elongated along the rotation axis. These large-scale vortices located near the equator would merge into a single vortex at the centre when the stress-free boundary condition is used (Lin & Jackson Reference Lin and Jackson2020). Figure 5(b) shows the time evolution of the axial velocity along two dashed lines in figure 5(a), which exhibits wave-like behaviours with typical frequencies within the spectrum of inertial waves (see also figure 1c). Figure 5(c) shows the energy spectrum as a function of the azimuthal wavenumber
$Ro=2.9\times 10^{-2}$, suggesting that turbulence convection is strongly influenced by the rotation. The axial vorticity (figure 5a) exhibits both small-scale and large-scale structures elongated along the rotation axis. These large-scale vortices located near the equator would merge into a single vortex at the centre when the stress-free boundary condition is used (Lin & Jackson Reference Lin and Jackson2020). Figure 5(b) shows the time evolution of the axial velocity along two dashed lines in figure 5(a), which exhibits wave-like behaviours with typical frequencies within the spectrum of inertial waves (see also figure 1c). Figure 5(c) shows the energy spectrum as a function of the azimuthal wavenumber ![]() $m$. We can see from the spectrum that there is a dominant toroidal
$m$. We can see from the spectrum that there is a dominant toroidal ![]() $m=0$ component, which represents a strong mean zonal flow. For smaller scales (
$m=0$ component, which represents a strong mean zonal flow. For smaller scales (![]() $20\lesssim m \lesssim 200$), we see that the energy spectrum follows a power law of
$20\lesssim m \lesssim 200$), we see that the energy spectrum follows a power law of ![]() $m^{-2}$, which is reminiscent of the energy spectrum of inertial wave turbulence driven by elliptical instability (Le Reun et al. Reference Le Reun, Favier, Barker and Le Bars2017). The power law
$m^{-2}$, which is reminiscent of the energy spectrum of inertial wave turbulence driven by elliptical instability (Le Reun et al. Reference Le Reun, Favier, Barker and Le Bars2017). The power law ![]() $m^{-2}$ is also predicted by Zhou (Reference Zhou1995) using a phenomenological approach for rotating turbulence. These observations suggest that the interaction of inertial waves plays an important role even in the turbulent regime, though further investigations are required in future.
$m^{-2}$ is also predicted by Zhou (Reference Zhou1995) using a phenomenological approach for rotating turbulence. These observations suggest that the interaction of inertial waves plays an important role even in the turbulent regime, though further investigations are required in future.

Figure 5. (a) A snapshot of the axial vorticity in the equatorial plane (left) and in a meridional plane (right). (b) Time evolution of the axial velocity along the white (top panel) and black (bottom panel) dashed lines in panel (a). (c) Energy spectra as a function of the azimuthal wavenumber ![]() $m$. Here
$m$. Here ![]() $E=10^{-6}$,
$E=10^{-6}$, ![]() ${\textit {Pr}}=0.001$ and
${\textit {Pr}}=0.001$ and ![]() $Ra=5.0\times 10^7$.
$Ra=5.0\times 10^7$.
4. Conclusion
We have shown for the first time that triadic resonances are taking place in a rotating convection system. The convective modes can excite either a pair of inertial waves with lower frequencies and wavenumbers or a pair with higher frequencies and wavenumbers, depending on the structure of the primary mode. This provides a possible mechanism for bi-directional energy transfer. The turbulent regime also shows signatures of inertial waves, and is reminiscent of inertial wave turbulence as observed in mechanically driven rotating flows. This study paves the way to study the nonlinear dynamics and turbulence in rotating convection within the framework of inertial wave interactions.
This study suggests that thermally (at low ![]() $Pr$) and mechanically (e.g. tides, precession and libration) driven rotating flows share many features even in the nonlinear and turbulent regime, which may have significant implications for some fundamental problems in geophysical and astrophysical fluid dynamics. Both convection (Jones Reference Jones2015) and mechanical forcings (Le Bars et al. Reference Le Bars, Cébron and Le Gal2015) are thought to be possible driven mechanisms for the generation of the Earth's and planetary magnetic fields through the dynamo process. It is possible that dynamos driven by two different mechanisms also share many features in certain parameter regimes and can be studied within the same framework. In stars and giant planets, the interaction between convection and tides is of great importance for calculating the efficiency of tidal dissipation, yet the problem remains poorly understood (Ogilvie Reference Ogilvie2014). Turbulent convection is usually treated as an effective viscosity in damping the tidal flow (Zahn Reference Zahn1989; Vidal & Barker Reference Vidal and Barker2020). However, given small
$Pr$) and mechanically (e.g. tides, precession and libration) driven rotating flows share many features even in the nonlinear and turbulent regime, which may have significant implications for some fundamental problems in geophysical and astrophysical fluid dynamics. Both convection (Jones Reference Jones2015) and mechanical forcings (Le Bars et al. Reference Le Bars, Cébron and Le Gal2015) are thought to be possible driven mechanisms for the generation of the Earth's and planetary magnetic fields through the dynamo process. It is possible that dynamos driven by two different mechanisms also share many features in certain parameter regimes and can be studied within the same framework. In stars and giant planets, the interaction between convection and tides is of great importance for calculating the efficiency of tidal dissipation, yet the problem remains poorly understood (Ogilvie Reference Ogilvie2014). Turbulent convection is usually treated as an effective viscosity in damping the tidal flow (Zahn Reference Zahn1989; Vidal & Barker Reference Vidal and Barker2020). However, given small ![]() $Pr$ in the convective zone of rotating stars and giant planets, both convection and tides can drive inertial waves, which would be interacting simultaneously and make it more difficult to estimate the efficiency of tidal dissipation in these systems.
$Pr$ in the convective zone of rotating stars and giant planets, both convection and tides can drive inertial waves, which would be interacting simultaneously and make it more difficult to estimate the efficiency of tidal dissipation in these systems.
In this paper, we consider rotating convection in a whole sphere. It is also of great interests to consider the problem in a spherical shell, in which the behaviours of inertial waves are complicated by the critical latitudes and wave attractors (Rieutord, Georgeot & Valdettaro Reference Rieutord, Georgeot and Valdettaro2001). Therefore, interactions of thermal inertial waves in a spherical shell may exhibit more complex dynamics, which will be considered in future.
Supplementary movies
Supplementary movies are available at https://doi.org/10.1017/jfm.2020.1050.
Acknowledgements
The author would like to thank P. Marti for providing the numerical code, A. Jackson for comments on an early draft of this paper, A. Barker for useful discussions and the anonymous referees for their helpful comments. This study was supported by the B-type Strategic Priority Program of the CAS (XDB41000000), an NSFC grant (41904066), and the pre-research project on Civil Aerospace Technologies of CNSA (D020308) and the Macau Foundation. Simulations were performed on the Taiyi cluster supported by the Center for Computational Science and Engineering of Southern University of Science and Technology.
Declaration of interests
The author reports no conflict of interest.