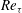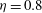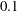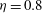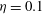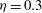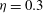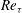1 Introduction and purpose
Transition to turbulence in most wall-bounded shear flows is subcritical as it features a competition between a linearly stable laminar regime and the turbulent regime. Cylindrical Poiseuille flow (cPf), plane Couette flow (pCf) and plane Poiseuille flow (pPf) fall into this category and have puzzled researchers and engineers for a long time. Both cPf and pCf are considered linearly stable for any Reynolds number
$Re$
. As for pPf, the base flow is linearly unstable only for values of
$Re$
much above the first values where turbulence can be sustained in experiments (Schmid & Henningson Reference Schmid and Henningson2001). Transition in these flows is hence characterised by sensitivity to finite-amplitude perturbations only, and thus by hysteresis. The lowest end of the transitional range features intermittent coherent structures referred to as ‘puffs’ in the cPf (Wygnanski & Champagne Reference Wygnanski and Champagne1973) and ‘oblique stripe patterns’ in pPf (Tsukahara et al.
Reference Tsukahara, Seki, Kawamura, Tochio and Humphrey2005) and pCf (Duguet, Schlatter & Henningson Reference Duguet, Schlatter and Henningson2010). They correspond to spatial alternations of turbulent and quasilaminar regions. In the case of cPf, the geometry makes this alternation essentially one-dimensional, and a critical Reynolds number has been predicted (Avila et al.
Reference Avila, Moxey, de Lozar, Avila, Barkley and Hof2011) in the thermodynamic limit of infinitely long domain and observation times. This special point delimits statistically the regime of transient localised turbulence from that of spatial turbulence proliferation. This suggests that the dynamics of isolated turbulent structures is the key to the statistical characterisation of laminar–turbulent transition. Compared to cPf, planar shear flows such as pCf and pPf show spatial extension in one additional (spanwise) direction. This gives rise to complex large-scale flows involved in the formation of the oblique stripe patterns (Duguet & Schlatter Reference Duguet and Schlatter2013). Many questions remain open regarding their growth mechanisms, robustness and lifetime (Manneville Reference Manneville2015). There has been no direct determination of the global Reynolds number threshold for transition to sustained turbulence using the method proposed for cPf (Avila et al.
Reference Avila, Moxey, de Lozar, Avila, Barkley and Hof2011), despite recent success in adapting this approach to one-dimensional periodic representations of Couette flows (Shi, Avila & Hof Reference Shi, Avila and Hof2013).
In the present article, we suggest a possible connection between the canonical geometries of pPf and cPf. We investigate several intermediate flow configurations with the hope of revealing links between the turbulent structures observed in the transitional regime. We thus consider the annular Poiseuille flow (aPf), the flow between two coaxial cylinders driven by a pressure gradient parallel to the cylinder’s common axis. This set-up is used in many industrial situations such as heat exchangers, cooling of nuclear plants. Annular Poiseuille flow is one of the simplest incompressible flow systems featuring skewed velocity profiles. The main geometrical parameter of aPf is the radius ratio
${\it\eta}=r_{i}/r_{o}$
, where
$r_{i}$
and
$r_{o}$
stand respectively for inner and outer radii, as in the Taylor–Couette flow (TCf) literature. The limit
${\it\eta}\rightarrow 1$
corresponds to pPf. Our objective is the parametric investigation of the transitional regime of aPf for decreasing
${\it\eta}$
. The limit
${\it\eta}\approx 0$
has sometimes been regarded in the literature as a modified cPf (Mott & Joseph Reference Mott and Joseph1968). Both geometries differ strongly, even in the limit
${\it\eta}\rightarrow 0$
, because of the presence of the inner rod in aPf. Laminar profiles in aPf are known to be linearly unstable for all
${\it\eta}$
(
$0<{\it\eta}\leqslant 1$
) above a critical Reynolds number
$Re_{L}({\it\eta})$
(Cotrell & Pearlstein Reference Cotrell and Pearlstein2006; Heaton Reference Heaton2008). Despite the relatively high values for the linear instability thresholds, there is experimental evidence that actual transition to turbulence can occur for
$Re\ll Re_{L}$
(Walker, Whan & Rothfus Reference Walker, Whan and Rothfus1957), i.e. transition is of a subcritical type. Together with the common one-dimensional extension and symmetries, this justifies why cPf can be expected to display the same transition phenomenology as aPf in the limit
${\it\eta}\rightarrow 0$
. Our interest is therefore the parametric knowledge of the transitional regime of aPf for varying
${\it\eta}$
, which would bridge together the limiting cases of cPf and pPf. For
${\it\eta}=1$
, the critical Reynolds number coincides exactly with that for pPf, whereas for
${\it\eta}\rightarrow 0$
,
$Re_{L}$
diverges as
${\it\eta}^{-1}\log {\it\eta}$
, inducing linear stability as in cPf (Heaton Reference Heaton2008). High-
$Re$
turbulent statistics have been previously reported in simulations and experiments for different radius ratios (see e.g. Chung, Rhee & Sung Reference Chung, Rhee and Sung2002; Rodriguez-Corredor et al.
Reference Rodriguez-Corredor, Bizhani, Ashrafuzzaman and Kuru2014). Surprisingly little is known yet about the transitional regime. Walker et al. (Reference Walker, Whan and Rothfus1957) (W57) measured the friction factor for the outer cylinder for low to moderate
${\it\eta}=0.025$
–0.5 (they did not report measurements on the inner cylinder side) as well as for cPf and pPf. Based on the variations of the friction factor, they suggested lower and upper end values of
$Re$
for the transitional regime, reported in table 1 in terms of lower critical bulk Reynolds number
$Re_{m}$
(defined in the next section). The orders of magnitude of
$Re$
for the onset of transition are consistent, for both
${\it\eta}=0$
and
$1$
, with recent estimations of the global critical Reynolds numbers for cPf (Avila et al.
Reference Avila, Moxey, de Lozar, Avila, Barkley and Hof2011) and pPf (Tsukahara et al.
Reference Tsukahara, Kawaguchi, Kawamura, Tillmark, Alfredsson, Schlatter and Henningson2010). The results of W57 strengthen the hypothesis that despite evident geometrical differences the phenomenology of aPf interpolates between those of pPf and cPf. It is thus natural to also expect laminar–turbulent coexistence at the onset of the hysteretic regime of aPf.
The present study is a parametric investigation of aPf, varying both the aspect ratio
${\it\eta}$
and the Reynolds number (more specifically the friction Reynolds number
$Re_{{\it\tau}}$
which is a well-defined parameter for pressure-driven flows). We report here for the first time numerical evidence for various types of laminar–turbulent structures in the low-
$Re$
parameter regime.
Table 1. Parameters for the turbulent simulations: radius ratio
${\it\eta}$
, friction Reynolds number
$Re_{{\it\tau}}$
, corresponding mean bulk Reynolds number
$Re_{m}$
, maximum observation time, range of streamwise domain lengths in outer and inner units, and experimental critical values for
$Re_{m}$
reported in Walker et al. (Reference Walker, Whan and Rothfus1957).
2 Numerical method and parameters
We consider here the axial flow between two coaxial cylinders, driven by a constant and uniform pressure gradient
$\text{d}p/\text{d}x=-(2/d)({\it\tau}_{o}+{\it\eta}{\it\tau}_{i})/(1+{\it\eta})$
in the axial direction denoted by
$x$
. Here
$d=r_{o}-r_{i}$
is the gap between the inner and outer cylinders,
${\it\tau}_{i}$
and
${\it\tau}_{o}$
are the mean wall shear rate at the inner and outer wall, respectively. We adopt the conventional cylindrical coordinate system
$(r,{\it\theta},x)$
and define
$y=r-r_{i}$
as the wall-normal distance measured from the inner wall. The velocity components are described by (
$u_{r}$
,
$u_{{\it\theta}}$
,
$u_{x}$
). The flow obeys the incompressible Navier–Stokes equations. A sketch of the geometry is shown in figure 1(a). Velocity profiles of the laminar solutions are reported for values of
${\it\eta}$
ranging from 1 to
$10^{-5}$
in figure 1(b). Periodic boundary conditions are imposed in the
$x$
and
${\it\theta}$
directions while no-slip is satisfied at both the inner and outer walls. The governing Navier–Stokes equations are discretised using finite differences, and time integration is carried out using a combination of second-order Crank–Nicolson and Adams–Bashforth schemes. Further information about the numerical method employed here can be found in Abe, Kawamura & Matsuo (Reference Abe, Kawamura and Matsuo2001). Four values of the radius ratio
${\it\eta}=0.1$
, 0.3, 0.5 and 0.8 have been considered. We begin by simulating fully turbulent flow at
$Re_{{\it\tau}}:=u_{{\it\tau}}d/2{\it\nu}=150$
for each value of
${\it\eta}$
, where
$u_{{\it\tau}}=\sqrt{({\it\tau}_{o}+{\it\eta}{\it\tau}_{i})/(1+{\it\eta})/{\it\rho}}$
is the friction velocity averaged between the two walls,
${\it\nu}$
is the kinematic viscosity, and
${\it\rho}$
is the density.
$Re_{{\it\tau}}$
is then decreased in small discrete steps down to the target value. Our parametric exploration was carried out in the range
$80\geqslant Re_{{\it\tau}}\geqslant 56$
for
${\it\eta}=0.3$
–0.8, and reached
$Re_{{\it\tau}}=46$
for
${\it\eta}=0.1$
. In order to capture spatially intermittent regimes, a long streamwise domain of
$L_{x}^{+}~(=L_{x}u_{{\it\tau}}/{\it\nu})\approx 8200$
is necessary. For
${\it\eta}=0.1$
below
$Re_{{\it\tau}}=56$
, a longer domain of
$L_{x}^{+}\approx 16\,500$
, corresponding to
$180d$
for
$Re_{{\it\tau}}=46$
, was found necessary. The minimum and maximum values of
$L_{x}^{+}$
are reported for convenience in table 1. The full azimuthal extent depends on
${\it\eta}$
, e.g.
$(L_{{\it\theta}}|_{in},L_{{\it\theta}}|_{out})=(2{\rm\pi}r_{i},2{\rm\pi}r_{o})=(6.28d,12.56d)$
at
${\it\eta}=0.5$
. The computational grid consists of
$N_{y}=128$
points in the wall-normal direction for all
${\it\eta}$
. In the streamwise direction, we used
$N_{x}=4096$
for
${\it\eta}=0.1$
below
$Re_{{\it\tau}}=56$
and
$N_{x}=2048$
for higher
${\it\eta}$
and
$Re_{{\it\tau}}$
. The azimuthal grid number also depends on
${\it\eta}$
and was chosen as follows:
$(N_{{\it\theta}},{\it\eta})=(1024,0.8),(512,0.5/0.3)$
, (256, 0.1). The grid is uniform in
$x$
and
${\it\theta}$
but non-uniform in the wall-normal direction in a manner similar to Moin & Kim (Reference Moin and Kim1982). Statistically steady states were achieved in all cases after transients shorter than our minimum observation time of
$tu_{{\it\tau}}^{2}/{\it\nu}\approx 9000$
(approximatively
$900d/u_{m}$
). Finally, the mean bulk Reynolds number
$Re_{m}=u_{m}d/{\it\nu}$
and its instantaneous fluctuations are estimated only in the steady regime, where
$u_{m}$
is the bulk velocity.
Figure 1. Schematic diagram (a) and laminar velocity profiles (b) of annular Poiseuille flow.
3 Results
In order to demonstrate laminar–turbulent coexistence in aPf, we begin by displaying in figure 2 the turbulent fraction
$F_{t}$
, parametrised by
${\it\eta}$
. Its time-averaged value
$\langle F_{t}\rangle$
is plotted as a function of the mean bulk Reynolds number
$Re_{m}$
for easier comparison with other shear flows.
$F_{t}$
measures the instantaneous amount of turbulence in the flow. If
$F_{t}=0$
the flow is laminar everywhere, whereas when
$F_{t}\sim 1$
the flow is considered fully turbulent. In practice
$F_{t}$
is computed from velocity data on the
$x{-}{\it\theta}$
cylinder at midgap. Laminar regions are identified by monitoring whether
$|u_{r}/u_{{\it\tau}}|<0.25$
at each (
${\it\theta},x$
) position independently of
$Re$
, with no significant qualitative dependence on the threshold value. Standard deviations of both
$F_{t}$
and
$Re_{m}$
are displayed as error bars in figure 2. In order to test the dependence on the wall-normal direction
$y$
, the statistics of
$F_{t}$
were also computed closer to the inner and outer cylinders. Again, despite slight shifts of the mean values of
$F_{t}$
the picture remains qualitatively unchanged, therefore we omit these results here.
Whereas
$F_{t}$
is close to unity for
$Re_{m}\geqslant 2250$
, in the range
$1500\leqslant Re_{m}\leqslant 2000$
it fluctuates around a mean value smaller than 0.8, indicating sustained laminar–turbulent coexistence. Moreover, the non-vanishing fluctuations suggest spatiotemporal intermittency. Whereas the results differ quantitatively little among values of
${\it\eta}\geqslant 0.3$
, the time-averages of
$F_{t}$
– as well as its fluctuations – stand out in the case of low
${\it\eta}=0.1$
:
$F_{t}$
takes high values
${\geqslant}0.8$
even for
$Re_{m}$
as low as 1900, and continuously drops to zero over a very narrow interval of values of
$Re_{m}\approx 1650{-}1700$
. Note that the amount of statistics and the computational power needed for an accurate determination of the critical values of
$Re_{m}({\it\eta})$
is several orders of magnitude beyond the present computational capability. This is mainly due to the very large domains needed to accommodate a large number of interacting localised patches near onset, as well as to the huge time scales involved (Avila et al.
Reference Avila, Moxey, de Lozar, Avila, Barkley and Hof2011).
$\langle F_{t}\rangle$
should therefore not be interpreted as an order parameter, as in non-equilibrium phase transitions, because the thermodynamic limit becomes harder to reach as the critical point
$Re_{c}$
is approached from above. In the following, we classify large-scale coherent structures typical of each value of
${\it\eta}$
, estimate visually whether they resemble the puffs and stripes of cPf and pPf, and show how they are connected to each other through variations of
${\it\eta}$
.
Figure 2. Turbulent fraction as a function of the mean bulk Reynolds number
$Re_{m}$
for each value of
${\it\eta}$
. Laminar and turbulent regions are sorted according to
$|u_{r}/u_{{\it\tau}}|$
(
$\text{laminar}<0.25<\text{turbulent}$
). Error bars correspond to the standard mean deviations of
$F_{t}$
and
$Re_{m}$
over the observation times considered here.
Figure 3. Instantaneous visualisation for
$Re_{{\it\tau}}=72$
and
${\it\eta}=0.8$
. (a) Three-dimensional visualisation of streamwise velocity fluctuations (red,
$u_{x}^{\prime }>3$
; blue,
$u_{x}^{\prime }<-3$
); (b) two-dimensional contours of instantaneous
$u_{r}^{\prime }$
at midgap. In all figures, the main flow is from left to right. The corresponding large-scale flow around helical turbulence are visualised using arrows in (b).
3.1 Helical turbulence for
${\it\eta}=0.8$
and
${\it\eta}=0.5$
The typical equilibrium structures observed in aPf for high
${\it\eta}=0.8$
are first described here. A three-dimensional visualisation of instantaneous streamwise velocity fluctuations at
$Re_{{\it\tau}}=72$
(
$Re_{m}=2060$
) is shown in figure 3(a). Figure 3(b) displays two-dimensional contours of wall-normal velocity in an
$x{-}{\it\theta}$
cylinder at midgap. We use
$z=r{\it\theta}$
as a modified coordinate unfolding the pipe geometry in figure 3 and the figures hereafter. We also display in figure 3(b) the large-scale flow at the same locations using vectors, computed using a low-pass spectral filter selecting all azimuthal and axial wavenumbers smaller than 4. For
${\it\eta}=0.8$
, we found a spatially periodic arrangement of oblique turbulent regions. Visualisations of turbulent fluctuations closer to the inner or outer wall show negligible differences since
$L_{{\it\theta}}|_{in}\approx L_{{\it\theta}}|_{out}$
and curvature effects are small. These bands have a well-defined pitch angle of approximately
$24^{\circ }\pm 4^{\circ }$
with the streamwise direction, depending on the
$y$
location at which it is measured. As in Duguet & Schlatter (Reference Duguet and Schlatter2013), the large-scale flow evaluated at midgap points in a direction almost parallel to the turbulent bands. The pattern is very reminiscent of the laminar–turbulent stripe patterns arising in pPf or from the barber-pole turbulent structures found in TCf for higher
${\it\eta}$
(Coles Reference Coles1965; Prigent et al.
Reference Prigent, Grégoire, Chaté, Dauchot and van Saarloos2002). This pattern wraps endlessly around the inner cylinder because of the azimuthal periodicity. We call this structure a ‘helical stripe’ in order to distinguish it from the stripe pattern in pPf and pCf. The large-scale flow possesses both streamwise and spanwise velocity components. From figure 3(b) it is clear that this large-scale flow also satisfies an approximate helical symmetry, and the corresponding (signed) helix angle can be used to characterise the chirality of the turbulent pattern. For
$Re_{{\it\tau}}=72$
, the streamwise and azimuthal extents of the turbulent intervals can be evaluated to
$25d$
and
$12d$
, respectively. Such dimensions are directly comparable to those in pPf (Tsukahara et al.
Reference Tsukahara, Kawaguchi, Kawamura, Tillmark, Alfredsson, Schlatter and Henningson2010). For
$Re_{{\it\tau}}<72$
, the extent of the turbulent region stays unchanged whereas the laminar intervals between the turbulent regions expand in the streamwise direction, again echoing most observations in pPf.
Figure 4. Instantaneous visualisation for
$Re_{{\it\tau}}=56$
and
${\it\eta}=0.5$
. (a) Three-dimensional visualisation of azimuthal velocity fluctuations (red,
$u_{{\it\theta}}^{\prime }>1$
; blue,
$u_{{\it\theta}}^{\prime }<-1$
); (b) two-dimensional contours of instantaneous
$u_{r}^{\prime }$
at midgap. Same colour coding as in figure 3(b).
Figure 4(a) now shows a three-dimensional visualisation of azimuthal velocity for
${\it\eta}=0.5$
at
$Re_{{\it\tau}}=56$
(
$Re_{m}=1538$
). This confirms that helical turbulence is robust and can be observed even for stronger wall curvatures. The velocity contours at midgap, shown in figure 4(b), reveal a turbulent helix with a pitch of
$15^{\circ }\pm 3^{\circ }$
steeper compared to the cases
${\it\eta}=0.8$
and
$1$
. For comparison, earlier studies of pPf have reported a regular turbulent stripe pattern with a spanwise spacing of at least
$12d$
and an inclination angle of
$21^{\circ }{-}25^{\circ }$
(Tsukahara et al.
Reference Tsukahara, Seki, Kawamura, Tochio and Humphrey2005, Reference Tsukahara, Kawaguchi, Kawamura, Tillmark, Alfredsson, Schlatter and Henningson2010; Tuckerman et al.
Reference Tuckerman, Kreilos, Schrobsdorff, Schneider and Gibson2014). For further comparison, we note that for
${\it\eta}=0.5$
outer and inner circumferences are
$(L_{{\it\theta}}|_{in},L_{{\it\theta}}|_{out})=(6.28d,12.56d)$
. Comparable spanwise dimensions would not be large enough to sustain stripes in the planar case. This suggests that the annular geometry and the wall curvature make helical stripe patterns more robust, at the price of steeper angles never reported in the planar case.
Figure 5. Instantaneous visualisations for
$Re_{{\it\tau}}=56$
and
${\it\eta}=0.3$
: (a,d), three-dimensional visualisation of instantaneous
$u_{x}^{\prime }$
; (b,e), contours of instantaneous
$u_{r}^{\prime }$
and vector at midgap same as figure 3(b); (c,f), azimuthally averaged wall-normal velocity along the
$x$
axis. The time lapse between (d–f) and (a–c) is
$88.7d/u_{m}$
.
3.2 Helical puff for
${\it\eta}=0.3$
We consider now aPf with a lower radius ratio
${\it\eta}=0.3$
, for which
$(L_{{\it\theta}}|_{in},L_{{\it\theta}}|_{out})=(2.7d,9.0d)$
. Flow visualisations for
$Re_{{\it\tau}}=80$
show almost featureless turbulence on the inner wall while the flow appears intermittent on the outer wall. Further decrease of
$Re_{{\it\tau}}$
to 64 leads again to a clear stripe pattern, now characterised by stronger intermittency, judging from the temporal fluctuations of
$F_{t}$
. The interesting regime occurs for
$Re_{{\it\tau}}=56~(Re_{m}=1655)$
. Flow visualisation in figure 5 for
$Re_{{\it\tau}}=56~(Re_{m}=1655)$
shows, for all velocity components, that the helical structure is still recognisable with a pitch of
$9^{\circ }\pm 3^{\circ }$
, but it is now localised in the streamwise direction. Despite its evident chirality, the helical structure is thus closer to a puff-like shape. The streamwise length of this new localised structure, approximatively half the periodic domain length
$L_{x}=74d$
, fluctuates little with time, and the localisation is robust (figure 5
a,d). Analysis of the large-scale flow suggests that the helical puff rotates azimuthally around the inner rod as it propagates downstream (see figure 5
b,e). Velocity profiles that are not averaged in the azimuthal direction show two active zones of turbulent fluctuations. Azimuthally averaged radial velocity profiles in turn show a singly connected zone of turbulent fluctuations, again occupying on average half the domain length (figure 5
c,f). From such profiles one could deduce that the upstream front is not sharper than the downstream front, hence violating the upstream/downstream asymmetry typical of turbulent puffs found in cPf and in aPf for
${\it\eta}=0.1$
. However, we note from figure 5(b,e) that the large-scale flow is at all times strongest near the upstream front, but only in a narrow range of azimuthal angles. Hence the helical puff displays a more subtle upstream/downstream asymmetry partially hidden by its chiral shape. At the downstream front, the large-scale velocity field on the midgap cylinder shows that fluid both enters the puff and exits it depending on the azimuthal coordinate, implying a non-trivial mass balance at the interface. For
$Re_{{\it\tau}}<56$
, this helical puff was observed to relaminarise after less than
$10^{3}$
time units (in units of
$d/u_{m}$
). Such coherent structures have never been observed before in annular geometries. In particular, the present computation suggests that helical puffs are marginally low-
$Re$
structures and represent the simplest form of turbulence for this geometry. Oblique stripes of finite extent have been reported in pPf, also at marginally low values of
$Re$
(Xiong et al.
Reference Xiong, Tao, Chen and Brandt2015) but it is not clear whether they are robust isolated structures or transients. They do not possess chirality, hence the different parts of the turbulent region do not interact with each other as is the case for the helical case. We note that localised helical structures have not been observed in the present computations for higher
${\it\eta}$
. The exact range of existence and the lifetimes of these helical puffs, both as a function of
$Re$
and
${\it\eta}$
, deserve further investigation.
3.3 Turbulent puffs for
${\it\eta}=0.1$
Finally, we consider the case of smaller
${\it\eta}$
and analyse a few simulations of aPf for
${\it\eta}=0.1$
as
$Re_{{\it\tau}}$
is gradually decreased. Despite the presence of a rigid rod at the axis, the present phenomenology is very close to that reported in investigations of cPf (Moxey & Barkley Reference Moxey and Barkley2010), confirming early speculation. For
$Re_{{\it\tau}}\geqslant 80$
, the whole flow is turbulent. However, the time-averaged value of
$F_{t}$
for
$Re_{{\it\tau}}=64$
(
$Re_{m}=1864$
) is 0.8, indicating that short localised laminar pockets occur intermittently (Avila & Hof Reference Avila and Hof2013). Reducing
$Re_{{\it\tau}}$
further to 56 (
$Re_{m}=1710$
), we recognise the classical intermittent sequences of turbulent puffs with sharp upstream fronts. The temporal dynamics of this train of turbulent puffs is complex despite the mild fluctuations of the observable
$F_{t}$
. This steady flow regime shows recurring sequences of instabilities (self-replications) and recombinations (merging) of individual localised puffs. In agreement with experimental observations of pipe flow by Samanta, de Lozar & Hof (Reference Samanta, de Lozar and Hof2011), the term ‘pattern’ is here no longer justified as no clear wavelength emerges, as opposed to the higher-
${\it\eta}$
cases. Further decrease to
$Re_{{\it\tau}}=52$
displays relaminarisation or replication events (over longer time scales) but no merging events, see figure 6(a–f). This dynamics featuring only individual puffs is identical to the regime just above the critical point in cPf (Avila et al.
Reference Avila, Moxey, de Lozar, Avila, Barkley and Hof2011; Shimizu et al.
Reference Shimizu, Manneville, Duguet and Kawahara2014). Further decrease of
$Re_{{\it\tau}}$
to 48 shows only puffs with finite lifetimes, but no replication events, suggesting (in the thermodynamic limit) that
$Re_{{\it\tau}}$
lies here below the critical point. The original streamwise extent of each puff before its possible relaminarisation is approximately
$20d$
. Because of the finite domain used in simulations, the disappearance of a single puff causes a typical fluctuation downwards of
$F_{t}$
. Besides, the lifetimes of individual turbulent puffs in this regime are known to increase very rapidly (typically as double exponential) with
$Re$
(Avila et al.
Reference Avila, Moxey, de Lozar, Avila, Barkley and Hof2011). It is hence expected that simulations over observation times several orders of magnitude longer would, for the lowest values of
$Re_{{\it\tau}}$
, lead to fully laminar flow with
$F_{t}=0$
. The values of
$\langle F_{t}\rangle \approx 0.1{-}0.2$
indicated in figure 2 for the lowest values of
$Re_{{\it\tau}}$
can hence be expected to converge to zero with increasing simulation time, making the
$Re$
-dependence of
$\langle F_{t}\rangle$
sharper at onset.
Figure 6. Instantaneous visualisations for
$Re_{{\it\tau}}=52$
and
${\it\eta}=0.1$
: (a,d), three-dimensional visualisation of instantaneous
$u_{x}^{\prime }$
; (b,e), contours of instantaneous
$u_{r}^{\prime }$
at midgap with the same colour range as figure 3(b); (c,f), azimuthally averaged streamwise velocity along the
$x$
axis. The time lapse between (a–c) and (d–f) is
$197d/u_{m}$
.
4 Discussion
Localised turbulent structures of transitional annular pipe flow have been investigated using direct numerical simulation for decreasing radius ratio
${\it\eta}$
. Robust helical stripe patterns similar to pPf have been identified for
${\it\eta}=0.8$
and
$0.5$
. At lower radius ratio,
${\it\eta}=0.3$
, sustained turbulence appears first in the form of helical stripe patterns with stronger fluctuations. The pitch angle of such patterns decreases with decreasing
${\it\eta}$
. At
${\it\eta}=0.3$
, at marginally low
$Re$
, the flow relaminarises partly. A new form of robust streamwise-localised helical pattern, the helical puff, emerges. This indicates a possible change towards a new phenomenology as
${\it\eta}$
is further decreased. Indeed, for smaller
${\it\eta}$
(0.1 and probably also below), the large-scale flow becomes axisymmetric, and the turbulent fluctuations occur in finite-length turbulent patches similar to equilibrium puffs in cPf. This similarity can be surprising, because the presence of the inner rod makes the geometry of aPf quite different from that of cPf: boundary layers are present near the inner rod. Besides, the laminar base flows in figure 1(b) display little quantitative differences between the cases
${\it\eta}=1$
and
${\it\eta}=0.1$
: the maximum streamwise velocity occurs respectively at
$y/d=0.5$
and
$0.4$
(and 0.2 for
${\it\eta}$
as low as
$10^{-5}$
). The geometry of aPf hence definitely differs from that of cPf but the transitional phenomenology is similar. The mean turbulent fraction
$\langle F_{t}\rangle$
near onset – obtained from a small number of realisations only and over limited observation times – displays for
${\it\eta}=0.1$
a steep but continuous variation with
$Re_{m}$
. The discontinuity observed for higher
${\it\eta}$
is most likely due to finite-size effects. Let us now use all these results to discuss expectations within the thermodynamic limit formalism. A similar decrease was reported in the heuristic model for cPf by Barkley (Reference Barkley2011), where
$\langle F_{t}\rangle \sim (Re-Re_{c})^{{\it\beta}}$
, consistently with the critical exponent
${\it\beta}\approx 0.27$
of directed percolation in one spatial dimension, see also Lemoult et al. (Reference Lemoult, Shi, Avila, Jalikop, Avila and Hof2016). While the present data for aPf at low
${\it\eta}$
is obviously insufficient to support this trend, all our observations suggest a scenario similar to cPf. This suggests that the statistical analysis of Avila et al. (Reference Avila, Moxey, de Lozar, Avila, Barkley and Hof2011) and Barkley (Reference Barkley2011) to determine the critical point
$Re_{c}$
, based on balancing mean waiting times for laminarisation and replication of individual puffs, should in principle be applicable to
${\it\eta}\leqslant 0.1$
. Whether this approach can be extended to higher
${\it\eta}$
requires further evidence. In the other limit
${\it\eta}\rightarrow 1$
, the two-dimensional directed percolation scenario has recently been advanced from large pPf experimental set-ups (Sano & Tamai Reference Sano and Tamai2016).
$\langle F_{t}\rangle$
obeys a similar scaling but a larger value of
${\it\beta}$
(in theory
${\it\beta}\approx 0.58$
). The similarity between the helical structures found for
${\it\eta}\geqslant 0.3$
and pPf (
${\it\eta}\rightarrow 1$
) suggests a dynamical cross-over between one-dimensional and two-dimensional directed percolation, occurring over a range of values of
${\it\eta}$
between 0.1 and 0.3. The new type of localised helical structure identified at low
$Re_{{\it\tau}}$
for
${\it\eta}=0.3$
might already belong to such a cross-over range. The computational or experimental cost of such an investigation would be enormous and this is obviously beyond the scope of this paper. Another related question concerns the mechanisms breaking the mean axisymmetry of single puffs and leading to chirality as
${\it\eta}$
increases, addressed by focusing on the influence of curvature on the large-scale flow.
Acknowledgements
T.I. was supported by a Grant-in-Aid from JSPS (Japan Society for the Promotion of Science) Fellowship no. 26-7477. The present simulations were performed on SX-9 at the Cyberscience Centre of Tohoku University and on SX-ACE at the Cybermedia Centre of Osaka University. We thank JSPS and CNRS (Centre National de la Recherche Scientifique) for additional financial support.
