Hostname: page-component-745bb68f8f-kw2vx Total loading time: 0 Render date: 2025-02-12T10:02:39.588Z Has data issue: false hasContentIssue false
  • English
  • Français

Three-dimensional stability of natural convection flows in inclined square enclosures

Published online by Cambridge University Press:  13 January 2025

Henry K Shen Open the ORCID record for Henry K Shen [Opens in a new window] ,
Wisam K. Hussam Open the ORCID record for Wisam K. Hussam [Opens in a new window]  and
Gregory J. Sheard Open the ORCID record for Gregory J. Sheard [Opens in a new window]
Henry K Shen*
Affiliation:
Department of Mechanical and Aerospace Engineering, Monash University, VIC 3800, Australia
Wisam K. Hussam
Affiliation:
Department of Mechanical and Aerospace Engineering, Monash University, VIC 3800, Australia Department of Mechanical Engineering, College of Engineering, Australian University, West Mishref, Safat 13015, Kuwait
Gregory J. Sheard
Affiliation:
Department of Mechanical and Aerospace Engineering, Monash University, VIC 3800, Australia
*
†Email address for correspondence: henry.shen@monash.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

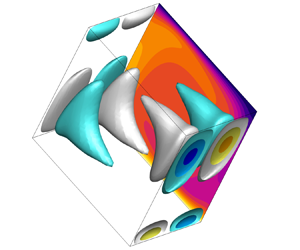
The three-dimensional stability of two-dimensional natural convection flows in a heated, square enclosure inclined to the horizontal is investigated numerically. First, the computational procedure is validated by comparison of base flow solutions to results reported in literature across a range of inclinations. A bi-global linear stability analysis is then conducted to investigate the stability of these two-dimensional base flows to infinitesimal three-dimensional perturbations, and the effect that buoyancy forces (defined by a buoyancy number $R_N$) and enclosure inclination $\theta$ have on these stability characteristics. The flow is first observed to become three-dimensionally unstable at buoyancy number $R_N = 213.8$ when $\theta$ is $180^\circ$; this increases to $R_N = 2.54 \times 10^4$ at inclination $\theta =58^\circ$. It is found that the two-dimensional base flow is more unstable to three-dimensional perturbations with the critical $R_N$ corresponding to three-dimensional instability being significantly lower than its two-dimensional counterpart across all considered inclinations except $83^\circ \leq \theta \leq 88^\circ$, where the most unstable mode is a two-dimensional oscillatory mode that develops in the boundary layers along the conducting walls. Eight different leading three-dimensional instability modes are identified, with inclinations $58^\circ \leq \theta < 88^\circ$ transitioning through an oscillatory mode, and inclinations $88^\circ \leq \theta \leq 180^\circ$ transitioning through a stationary mode. The characteristics of the primary instability modes corresponding to inclinations $88^\circ \leq \theta \leq 179^\circ$ indicate the presence of a Taylor–Görtler instability.

JFM classification

Geophysical and Geological Flows: Baroclinic flows Convection: Buoyancy-driven instability Convection: Convection in cavities
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 1003 , 25 January 2025 , A8
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Acharya, S. & Tsang, C.H. 1985 Natural convection in a fully partitioned, inclined enclosure. Numer. Heat Transfer 8 (4), 407–428.CrossRefGoogle Scholar
Adachi, T. 2006 Stability of natural convection in an inclined square duct with perfectly conducting side walls. Intl J. Heat Mass Transfer 49 (13–14), 2372–2380.CrossRefGoogle Scholar
Al-Suhaibani, Z., Ali, M. & Almuzaiqer, R. 2024 Tilt angle effect on natural convection heat transfer from an inclined array of square cylinders. Energies 17 (7), 1516.CrossRefGoogle Scholar
Barkley, D. & Henderson, R.D. 1996 Three-dimensional Floquet stability analysis of the wake of a circular cylinder. J. Fluid Mech. 322, 215–241.CrossRefGoogle Scholar
Blackburn, H.M. & Sheard, G.J. 2010 On quasiperiodic and subharmonic Floquet wake instabilities. Phys. Fluids 22 (3), 031701.CrossRefGoogle Scholar
Chandra, M. & Verma, M.K. 2011 Dynamics and symmetries of flow reversals in turbulent convection. Phys. Rev. E 83 (6), 067303.CrossRefGoogle ScholarPubMed
Chen, H.T. & Chou, J.C. 2006 Investigation of natural-convection heat transfer coefficient on a vertical square fin of finned-tube heat exchangers. Intl J. Heat Mass Transfer 49 (17–18), 3034–3044.CrossRefGoogle Scholar
Citro, V., Luchini, P., Giannetti, F. & Auteri, F. 2017 Efficient stabilization and acceleration of numerical simulation of fluid flows by residual recombination. J. Comput. Phys. 344, 234–246.CrossRefGoogle Scholar
Corvaro, F., Paroncini, M. & Sotte, M. 2012 PIV and numerical analysis of natural convection in tilted enclosures filled with air and with opposite active walls. Intl J. Heat Mass Transfer 55 (23–24), 6349–6362.CrossRefGoogle Scholar
Dimopoulos, D. & Pelekasis, N. 2012 Three-dimensional stability of free convection vortices in the presence of a magnetic field. Fluid Dyn. Res. 44 (3), 031405.CrossRefGoogle Scholar
Dušek, J., Le Gal, P. & Fraunié, P. 1994 A numerical and theoretical study of the first Hopf bifurcation in a cylinder wake. J. Fluid Mech. 264, 59–80.CrossRefGoogle Scholar
Fusegi, F., Farouk, B., Hyun, J.M. & Kuwahara, K. 1990 A direct numerical simulation of periodic natural convection in differentially heated cubical enclosure. In Proc. Intl Symp. on Engineering Turbulence Modeling and Measurements (ed. W. Rodi & E.N. Ganić), pp. 261–268. Elsevier.Google Scholar
Gill, A.E. 1966 The boundary-layer regime for convection in a rectangular cavity. J. Fluid Mech. 26 (3), 515–536.CrossRefGoogle Scholar
Grayer, H., Yalim, J., Welfert, B.D. & Lopez, J.M. 2020 Dynamics in a stably stratified tilted square cavity. J. Fluid Mech. 883, A62.CrossRefGoogle Scholar
Henkes, R.A.W.M. & Le Quéré, P. 1996 Three-dimensional transition of natural-convection flows. J. Fluid Mech. 319, 281–303.CrossRefGoogle Scholar
Hier Majumder, C.A., Yuen, D.A. & Vincent, A.P. 2004 Four dynamical regimes for a starting plume model. Phys. Fluids 16 (5), 1516–1531.CrossRefGoogle Scholar
Inaba, H. & Fukuda, T. 1984 Natural convection in an inclined square cavity in regions of density inversion of water. J. Fluid Mech. 142, 363–381.CrossRefGoogle Scholar
Ivey, G.N. 1984 Experiments on transient natural convection in a cavity. J. Fluid Mech. 144, 389–401.CrossRefGoogle Scholar
Janssen, R.J.A. & Henkes, R.A.W.M. 1996 Instabilities in three-dimensional differentially-heated cavities with adiabatic horizontal walls. Phys. Fluids 8 (1), 62–74.CrossRefGoogle Scholar
Jiang, L., Sun, C. & Calzavarini, E. 2019 Robustness of heat transfer in confined inclined convection at high Prandtl number. Phys. Rev. E 99 (1), 013108.CrossRefGoogle ScholarPubMed
Kangni, A., Vasseur, P. & Bilgen, E. 1995 Natural convection in inclined enclosures with multiple conducting partitions. J. Thermophys. Heat Transfer 9 (2), 270–277.CrossRefGoogle Scholar
Karniadakis, G.E., Israeli, M. & Orszag, S.A. 1991 High-order splitting methods for the incompressible Navier–Stokes equations. J. Comput. Phys. 97 (2), 414–443.CrossRefGoogle Scholar
Karniadakis, G.E. & Triantafyllou, G.S. 1992 Three-dimensional dynamics and transition to turbulence in the wake of bluff objects. J. Fluid Mech. 238, 1–30.CrossRefGoogle Scholar
Landau, L.D. & Lifshitz, E.M. 1976 Mechanics, 3rd edn. Pergamon Press.Google Scholar
Le Quéré, P. & Alziary de Roquefort, T. 1985 Transition to unsteady natural convection of air in differentially heated vertical cavities. In Fourth Int. Conf. on Numerical Methods in Laminar and Turbulent Flow (ed. C. Taylor), pp. 841–852. Pineridge Press.Google Scholar
Le Quéré, P. & Behnia, M. 1998 From onset of unsteadiness to chaos in a differentially heated square cavity. J. Fluid Mech. 359, 81–107.CrossRefGoogle Scholar
Lehoucq, R.B., Sorensen, D.C. & Yang, C. 1998 ARPACK Users’ Guide: Solution of Large-scale Eigenvalue Problems with Implicitly Restarted Arnoldi Methods. SIAM.CrossRefGoogle Scholar
Mayeli, P., Tsai, T. & Sheard, G.J. 2022 Linear stability analysis of horizontal convection under a Gay-Lussac type approximation. Intl J. Heat Mass Transfer 182, 121929.CrossRefGoogle Scholar
Medelfef, A., Henry, D., Bouabdallah, A. & Kaddeche, S. 2019 Bifurcations from steady to quasi-periodic flows in a laterally heated cavity filled with low Prandtl number fluids. J. Fluid Mech. 861, 223–252.CrossRefGoogle Scholar
Murali, S., Ng, Z.Y. & Sheard, G.J. 2022 Stability of flow in a channel with repeated flow-facing wedge-shaped protrusions. J. Fluid Mech. 941, A59.CrossRefGoogle Scholar
Ng, Z.Y., Vo, T. & Sheard, G.J. 2018 Stability of the wakes of cylinders with triangular cross-sections. J. Fluid Mech. 844, 721–745.CrossRefGoogle Scholar
Oteski, L., Duguet, Y., Pastur, L. & Le Quéré, P. 2015 Quasiperiodic routes to chaos in confined two-dimensional differential convection. Phys. Rev. E 92 (4), 043020.CrossRefGoogle ScholarPubMed
Page, M.A. 2011 Combined diffusion-driven and convective flow in a tilted square container. Phys. Fluids 23 (5), 056602.CrossRefGoogle Scholar
Paolucci, S. & Chenoweth, D.R. 1989 Transition to chaos in a differentially heated vertical cavity. J. Fluid Mech. 201, 379–410.CrossRefGoogle Scholar
Peacock, T., Stocker, R. & Aristoff, J.M. 2004 An experimental investigation of the angular dependence of diffusion-driven flow. Phys. Fluids 16 (9), 3503–3505.CrossRefGoogle Scholar
Phillips, O.M. 1970 On flows induced by diffusion in a stably stratified fluid. Deep-Sea Res. Oceanogr. Abstr. 17, 435–443.CrossRefGoogle Scholar
Provansal, M., Mathis, C. & Boyer, L. 1987 Bénard–von Kármán instability: transient and forced regimes. J. Fluid Mech. 182, 1–22.CrossRefGoogle Scholar
Quon, C. 1976 Diffusively induced boundary layers in a tilted square cavity: a numerical study. J. Comput. Phys. 22 (4), 459–485.CrossRefGoogle Scholar
Ramanan, N. & Homsy, G.M. 1994 Linear stability of lid-driven cavity flow. Phys. Fluids 6 (8), 2690–2701.CrossRefGoogle Scholar
Ravi, M.R., Henkes, R.A.W.M. & Hoogendoorn, C.K. 1994 On the high-Rayleigh-number structure of steady laminar natural-convection flow in a square enclosure. J. Fluid Mech. 262, 325–351.CrossRefGoogle Scholar
Rayleigh, Lord 1916 LIX. On convection currents in a horizontal layer of fluid, when the higher temperature is on the under side. Lond. Edinb. Dublin Phil. Mag. J. Sci. 32 (192), 529–546.CrossRefGoogle Scholar
Ryan, K., Butler, C.J. & Sheard, G.J. 2012 Stability characteristics of a counter-rotating unequal-strength Batchelor vortex pair. J. Fluid Mech. 696, 374–401.CrossRefGoogle Scholar
Sapardi, A.M., Hussam, W.K., Pothérat, A. & Sheard, G.J. 2017 Linear stability of confined flow around a 180-degree sharp bend. J. Fluid Mech. 822, 813–847.CrossRefGoogle Scholar
Sharma, A., Chen, C.R. & Lan, N.V. 2009 Solar-energy drying systems: a review. Renew. Sustain. Energy Rev. 13 (6–7), 1185–1210.CrossRefGoogle Scholar
Sheard, G.J. 2011 Wake stability features behind a square cylinder: focus on small incidence angles. J. Fluids Struct. 27 (5–6), 734–742.CrossRefGoogle Scholar
Sheard, G.J., Fitzgerald, M.J. & Ryan, K. 2009 Cylinders with square cross-section: wake instabilities with incidence angle variation. J. Fluid Mech. 630, 43–69.CrossRefGoogle Scholar
Sheard, G.J., Leweke, T., Thompson, M.C. & Hourigan, K. 2007 Flow around an impulsively arrested circular cylinder. Phys. Fluids 19 (8), 083601.CrossRefGoogle Scholar
Shishkina, O. & Horn, S. 2016 Thermal convection in inclined cylindrical containers. J. Fluid Mech. 790, R3.CrossRefGoogle Scholar
Torres, J.F., Henry, D., Komiya, A., Maruyama, S. & Hadid, H.B. 2013 Three-dimensional continuation study of convection in a tilted rectangular enclosure. Phys. Rev. E 88 (4), 043015.CrossRefGoogle Scholar
de Vahl Davis, G. 1983 Natural convection of air in a square cavity: a bench mark numerical solution. Intl J. Numer. Meth. Fluids 3 (3), 249–264.CrossRefGoogle Scholar
Vo, T., Montabone, L., Read, P.L. & Sheard, G.J. 2015 Non-axisymmetric flows in a differential-disk rotating system. J. Fluid Mech. 775, 349–386.CrossRefGoogle Scholar
Wang, P., Zhang, Y. & Guo, Z. 2017 Numerical study of three-dimensional natural convection in a cubical cavity at high Rayleigh numbers. Intl J. Heat Mass Transfer 113, 217–228.CrossRefGoogle Scholar
Wang, Q., Liu, H., Verzicco, R., Shishkina, O. & Lohse, D. 2021 Regime transitions in thermally driven high-Rayleigh number vertical convection. J. Fluid Mech. 917, A6.CrossRefGoogle Scholar
Wunsch, C. 1970 On oceanic boundary mixing. Deep-Sea Res. Oceanogr. Abstr. 17, 293–301.CrossRefGoogle Scholar
Xin, S. & Le Quéré, P. 2001 Linear stability analyses of natural convection flows in a differentially heated square cavity with conducting horizontal walls. Phys. Fluids 13 (9), 2529–2542.CrossRefGoogle Scholar
Xin, S. & Le Quéré, P. 2002 An extended Chebyshev pseudo-spectral benchmark for the 8 : 1 differentially heated cavity. Intl J. Numer. Meth. Fluids 40 (8), 981–998.CrossRefGoogle Scholar
Xin, S. & Le Quéré, P. 2006 Natural-convection flows in air-filled, differentially heated cavities with adiabatic horizontal walls. Numer. Heat Transfer A: Appl. 50 (5), 437–466.CrossRefGoogle Scholar
Zwirner, L., Emran, M.S., Schindler, F., Singh, S., Eckert, S., Vogt, T. & Shishkina, O. 2022 Dynamics and length scales in vertical convection of liquid metals. J. Fluid Mech. 932, A9.CrossRefGoogle Scholar
Zwirner, L., Khalilov, R., Kolesnichenko, I., Mamykin, A., Mandrykin, S., Pavlinov, A., Shestakov, A., Teimurazov, A., Frick, P. & Shishkina, O. 2020 The influence of the cell inclination on the heat transport and large-scale circulation in liquid metal convection. J. Fluid Mech. 884, A18.CrossRefGoogle Scholar
Supplementary material: File

Shen et al. supplementary movie

Animations of oscillatory instability modes; Mode 1, Mode 2 and Mode 3.
Download Shen et al. supplementary movie(File)
File 2.3 MB