2 Mathematical model

We consider a two-dimensional droplet of density $\unicode[STIX]{x1D70C}$ and viscosity $\unicode[STIX]{x1D707}$ deposited on a non-uniformly heated surface, as shown in figure 1. Under the assumptions of lubrication approximation, the Navier–Stokes equations are reduced to a single partial differential equation for the thickness $h$ of the droplet. Although this approximation assumes small slope of the liquid–gas interface, it is usually employed to describe partial wetting systems. Its applicability was studied and small differences of a few per cent were found when compared with solutions of the Navier–Stokes equation for contact angles as large as $40^{\circ }$ (Goodwin & Homsy Reference Goodwin and Homsy1991; Perazzo & Gratton Reference Perazzo and Gratton2004).

Figure 1. Sketch of the problem: a two-dimensional droplet of thickness $h(x,t)$ resting on a non-uniformly heated surface. The temperature induces a gradient of the surface tension which drives the liquid towards the region with the highest surface energy. The droplet is surrounded by a constant film thickness with an initial (equilibrium) thickness $h_{film}$ (Mac Intyre et al. Reference Mac Intyre, Gomba and Perazzo2016).

The flow field $u(x,z,t)$ is governed by the momentum balance equation (Oron et al. Reference Oron, Davis and Bankoff1997; Craster & Matar Reference Craster and Matar2009)

(2.1) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D707}\frac{\unicode[STIX]{x2202}^{2}u}{\unicode[STIX]{x2202}z^{2}}-\frac{\unicode[STIX]{x2202}p}{\unicode[STIX]{x2202}x}=0, & & \displaystyle\end{eqnarray}$$

and the flow continuity

(2.2) $$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x2202}h}{\unicode[STIX]{x2202}t}+\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x}\left(\int _{0}^{h}u\,\text{d}z\right)=0, & & \displaystyle\end{eqnarray}$$

where $h=h(x,t)$ is the thickness profile of the drop. The second term in (2.1) is given by

(2.3) $$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x2202}p}{\unicode[STIX]{x2202}x}=\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x}\left(-\unicode[STIX]{x1D6FE}\frac{\unicode[STIX]{x2202}^{2}h}{\unicode[STIX]{x2202}x^{2}}-\unicode[STIX]{x1D6F1}(h)+\unicode[STIX]{x1D70C}gh\right), & & \displaystyle\end{eqnarray}$$

$\unicode[STIX]{x1D6FE}$ being the surface tension and $g$ the gravity. The term $\unicode[STIX]{x1D6F1}(h)$ represents the disjoining–conjoining pressure defined by (Oron et al. Reference Oron, Davis and Bankoff1997; Schwartz & Roy Reference Schwartz and Roy2004)

(2.4) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F1}(h)=\unicode[STIX]{x1D705}\left[\left(\frac{h_{\ast }}{h}\right)^{n}-\left(\frac{h_{\ast }}{h}\right)^{m}\right],\quad n>m>1. & & \displaystyle\end{eqnarray}$$

The thickness of the energetically favoured molecular film is represented by $h_{\ast }$ and $\unicode[STIX]{x1D705}$ is related to the static contact angle $\unicode[STIX]{x1D703}$ by (Schwartz & Eley Reference Schwartz and Eley1998)

(2.5) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D705}=\frac{\unicode[STIX]{x1D6FE}\tan ^{2}\unicode[STIX]{x1D703}\,(n-1)(m-1)}{2(n-m)\,h_{\ast }}. & & \displaystyle\end{eqnarray}$$

The contact angle $\unicode[STIX]{x1D703}$ is defined as the angle at the inflection point for large drops (Schwartz & Eley Reference Schwartz and Eley1998; Gomba & Homsy Reference Gomba and Homsy2009). Once $\unicode[STIX]{x1D703}$ is chosen, the value of $\unicode[STIX]{x1D705}$ is determined and, therefore $\unicode[STIX]{x1D703}$ quantifies the strength of the molecular interaction between the liquid and the substrate (the relationship among $\unicode[STIX]{x1D705}$ , the Hammaker constants and $\unicode[STIX]{x1D703}$ is discussed in Solomentsev & White (Reference Solomentsev and White1999) and Mac Intyre et al. (Reference Mac Intyre, Gomba and Perazzo2016)).

The definition in (2.4) has been largely employed to model the effects of molecular interactions. Here, we focus on two different types of molecular potential. On the one hand, the case $(n,m)=(3,2)$ that represents the competition of London–van der Waals ( $n=3$ ) and ionic–electrostatics forces ( $m=2$ ) (Schwartz & Eley Reference Schwartz and Eley1998; Gotkis et al. Reference Gotkis, Ivanov, Murisic and Kondic2006). The dependence with $m=2$ , valid for thickness much lower than the Debye length, was verified in experiments of water (polar liquid) films on glass, quartz and mica (Derjaguin & Churaev Reference Derjaguin and Churaev1974). The term with $m=3$ is an exact classical result obtained by summing individual London–van der Waals interactions between molecules. On the other hand, the case $(n,m)=(4,3)$ that correctly describes retarded and non-retarded effects in London–van der Waals interactions, as in experiments with tetradecane on quartz and hexane on metals (Derjaguin & Churaev Reference Derjaguin and Churaev1974; Derjaguin, Rabinovich & Churaev Reference Derjaguin, Rabinovich and Churaev1978; Starov et al. Reference Starov, Velarde and Radke2007). The term with $n=4$ is an exact expression that results from considering retardation effects in London–van der Waals interactions (Oron & Bankoff Reference Oron and Bankoff2001; Glasner & Witelski Reference Glasner and Witelski2003; Starov et al. Reference Starov, Velarde and Radke2007). Summarizing, the pairs $(3,2)$ and $(4,3)$ model the molecular interactions for polar and non-polar liquids, respectively.

Equation (2.1) is subject to two boundary conditions: no slip at the solid substrate and tangential Marangoni stress along the liquid–air interface (Ehrhard & Davis Reference Ehrhard and Davis1991); that is

(2.6) $$\begin{eqnarray}\displaystyle & \displaystyle u(x,0,t)=0, & \displaystyle\end{eqnarray}$$

(2.7) $$\begin{eqnarray}\displaystyle & \displaystyle \left.\unicode[STIX]{x1D707}\frac{\unicode[STIX]{x2202}u}{\unicode[STIX]{x2202}z}\right|_{z=h}=\frac{\text{d}\unicode[STIX]{x1D6FE}}{\text{d}x}=\frac{\text{d}\unicode[STIX]{x1D6FE}}{\text{d}T}\frac{\text{d}T}{\text{d}x}. & \displaystyle\end{eqnarray}$$

The surface tension $\unicode[STIX]{x1D6FE}$ is linear in the temperature $T(x,h)$ at the air–liquid interface (Eötvös Reference Eötvös1886; Guggenheim Reference Guggenheim1945)

(2.8) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FE}=\unicode[STIX]{x1D6FE}_{0}-\unicode[STIX]{x1D70E}(T-T_{0}), & & \displaystyle\end{eqnarray}$$

where $\unicode[STIX]{x1D6FE}_{0}$ is the surface tension at $T=T_{0}$ and $\unicode[STIX]{x1D70E}$ a positive constant. Based on experimental data (Brzoska et al. Reference Brzoska, Brochard-Wyart and Rondelez1993; Chen et al. Reference Chen, Troian, Darhuber and Wagner2005), it is reasonable to assume that the conduction is the main heat transfer mechanism within the drop (i.e. Péclet number $Pe=HU/\unicode[STIX]{x1D6FF}\ll 1$ ) and the conductivity of the liquid is high (i.e. Biot number $Bi=Hq_{\infty }/\unicode[STIX]{x1D705}_{t}\ll 1$ ). Here, $H$ is the maximum droplet thickness, $U$ the migration velocity, $\unicode[STIX]{x1D6FF}$ the liquid thermal diffusivity, $q_{\infty }$ the interfacial heat transfer coefficient and $\unicode[STIX]{x1D705}_{t}$ the liquid thermal conductivity. Consequently, the unknown temperature $T$ is related to the linear temperature profile at the substrate $T_{s}(x)$ by means of $T(x,h)=T_{s}(x)$ (Ehrhard & Davis Reference Ehrhard and Davis1991; Gomba & Homsy Reference Gomba and Homsy2010) and the boundary condition at the drop air interface becomes

(2.9) $$\begin{eqnarray}\displaystyle \left.\unicode[STIX]{x1D707}\frac{\unicode[STIX]{x2202}u}{\unicode[STIX]{x2202}z}\right|_{z=h}=\frac{\text{d}\unicode[STIX]{x1D6FE}}{\text{d}T}\frac{\text{d}T_{s}}{\text{d}x}=\unicode[STIX]{x1D70E}\frac{T_{H}-T_{C}}{L}=\unicode[STIX]{x1D70F}, & & \displaystyle\end{eqnarray}$$

$\unicode[STIX]{x1D70F}$ being a positive constant and $L$ the distance of application of the two temperature.

We set the scale in both space directions as $h_{c}=x_{c}=a$ , where $a=\sqrt{\unicode[STIX]{x1D6FE}_{0}/\unicode[STIX]{x1D70C}g}$ is the capillary length, and define the characteristic time as $t_{c}=3\unicode[STIX]{x1D707}a/\unicode[STIX]{x1D6FE}_{0}$ . Equation (2.2) for the thickness $h(x,t)$ becomes

(2.10) $$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x2202}h}{\unicode[STIX]{x2202}t}+\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x}\left[h^{3}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x}\left(\frac{\unicode[STIX]{x2202}^{2}h}{\unicode[STIX]{x2202}x^{2}}+K\left[\left(\frac{h_{\ast }}{h}\right)^{n}-\left(\frac{h_{\ast }}{h}\right)^{m}\right]-Gh\right)+Bh^{2}\right]=0, & & \displaystyle\end{eqnarray}$$

where the constants are

(2.11a,b ) $$\begin{eqnarray}\displaystyle K=\frac{\tan ^{2}\unicode[STIX]{x1D703}\,(n-1)(m-1)}{2(n-m)h_{\ast }},\quad B=\frac{3a\unicode[STIX]{x1D70F}}{2\unicode[STIX]{x1D6FE}_{0}}, & & \displaystyle\end{eqnarray}$$

and $h_{\ast }$ is in units of $a$ . The term which models the gravity effect is multiplied by the constant $G=x_{c}^{2}\unicode[STIX]{x1D70C}g/\unicode[STIX]{x1D6FE}_{0}$ , which in the selected scale results in

(2.12) $$\begin{eqnarray}\displaystyle G=\left\{\begin{array}{@{}ll@{}}1 & \text{with gravity}\\ 0 & \text{without gravity}.\end{array}\right. & & \displaystyle\end{eqnarray}$$

The evolution equation (2.10) includes capillary, gravity, disjoining and Marangoni effects. This fourth-order differential equation is solved using finite element technique in the COMSOL Multiphysics environment, and is subject to periodic boundary conditions at both extreme of the domain for the height of the droplet $h$ and pressure  $p$ . A convergence analysis was carried out to check the accuracy of the calculations, and the results were satisfactory compared with those obtained using a finite difference technique (Gomba & Homsy Reference Gomba and Homsy2010).

The initial condition in the following simulations corresponds to the profile of a static droplet of area $A$ when the temperature gradient is zero. We employ the static profiles reported by Mac Intyre et al. (Reference Mac Intyre, Gomba and Perazzo2016) for a molecular potential with $(n,m)=(4,3)$ and by Gomba & Homsy (Reference Gomba and Homsy2009), Perazzo, Mac Intyre & Gomba (Reference Perazzo, Mac Intyre and Gomba2014) for $(n,m)=(3,2)$ . Those analytic solutions are scaled using molecular constant $\unicode[STIX]{x1D705}$ and, in order to change the scale appropriately, we have to set the thermodynamic contact angle $\unicode[STIX]{x1D703}$ in the parameter $K$ in (2.11) (Mac Intyre et al. Reference Mac Intyre, Gomba and Perazzo2016). The profile of the droplet is allowed to change dynamically over time and the contact angle $\unicode[STIX]{x1D703}$ plays the role of parametric value. Given that the scale in $x$ and $z$ axes is $a$ , $\unicode[STIX]{x1D703}$ has the same value in both dimensional and dimensionless variables.

Table 1 summarize the relevant physical parameters, together with the typical values found in experiments. Based on these parameters, we estimate the range for $B$ as $0.002\leqslant B\leqslant 0.05$ . A word about the value of the precursor film thickness is appropriate. When the ratio of the maximum height to the precursor film thickness increases, the use of realistic values for $h_{\ast }$ in problems with moving contact lines is impractical because it requires cell sizes of the order of $h_{\ast }$ , as shown in Gaskell et al. (Reference Gaskell, Jimack, Sellier and Thompson2004). Then, most of the simulations are solved using $h_{\ast }\geqslant 5\times 10^{-3}\,a$ .

Figure 2. Evolution of the thickness profile for a droplet with cross-sectional area $A=10$ , contact angle $\unicode[STIX]{x1D703}=4^{\circ }$ , thermal gradient $B=0.01$ and $(n,m)=(4,3)$ . The corresponding profiles for $(n,m)=(3,2)$ are almost identical to these ones. Here $h_{\ast }=0.01$ . The dashed blue line is the analytic solution for the rear profile given by (3.2).

Table 1. Orders of magnitude of the relevant physical parameters (Brochard-Wyart Reference Brochard-Wyart1989; Brzoska et al. Reference Brzoska, Brochard-Wyart and Rondelez1993; Schwartz & Eley Reference Schwartz and Eley1998; Chen et al. Reference Chen, Troian, Darhuber and Wagner2005; Pratap et al. Reference Pratap, Moumen and Subramanian2008).

3 Small contact angle: film regime

3.1 Absence of gravity, $G=0$

The film regime occurs for small contact angles. Therefore, we have that $\tan ^{2}\unicode[STIX]{x1D703}\sim 0$ , which implies that the molecular action is negligible (Chaudhury & Chakraborty Reference Chaudhury and Chakraborty2015). Experimental results for Marangoni films by Fote, Slade & Feuerstein (Reference Fote, Slade and Feuerstein1977) have shown that non-polar liquids under microgravity develop a linear profile. Similarly, Sur et al. (Reference Sur, Bertozzi and Behringer2003) have shown experimentally a linear profile connecting the advancing ridges with the fluid in the container. Gomba & Homsy (Reference Gomba and Homsy2010) have reported a linear profile numerically and demonstrated an analytical expression for this evolution for polar liquids.

Figure 2 shows the numerical solution of (2.10) for a non-polar liquid with $\unicode[STIX]{x1D703}=4^{\circ }$ and $G=0$ . After a short transient stage, the front develops a characteristic capillary ridge and the bulk adopts a linear profile which slope decreases in time. Note that the bump forms because the contact line moves slower than the fluid being pumped in from behind by the Marangoni stress. Due to independence of molecular interaction, non-polar liquids exhibits almost identical behaviour to polar liquids. As time increases, the droplet elongates, its maximum height decreases and the volume under the linear profile grows.

The numerical solutions of the differential equation retaining all terms show that the long rear part of the drop develops a linear profile. To describe it analytically, we assume null curvature in this region so that the capillary effect can be neglected and, due to the fact that the molecular forces are negligible, equation (2.10) becomes

(3.1) $$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x2202}h}{\unicode[STIX]{x2202}t}+\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x}(Bh^{2})=0. & & \displaystyle\end{eqnarray}$$

Then, the thickness profile is constant along of the characteristic $\text{d}x/\text{d}t=2Bh$ , which means that a point with height $h$ moves to the right with speed $2Bh$ . As a result, the linear profile is (Gomba & Homsy Reference Gomba and Homsy2010)

(3.2) $$\begin{eqnarray}\displaystyle h=\frac{x-x_{0}}{2Bt}, & & \displaystyle\end{eqnarray}$$

where $x_{0}$ is a constant related to the initial position of the rear contact line. Figure 2 shows the comparison between the numerical solution of the full equation (2.10) with (3.2). The high agreement justifies the omission of surface tension and disjoining pressure terms in (3.1). Figure 3 shows the evolution of the front $x_{f}$ for several values of $\unicode[STIX]{x1D703}$ and $B$ with both polar and non-polar liquids. At long times, the curves converge to the asymptotic curve $x_{f}/h_{m}\sim t^{1/2}$ independently of the molecular interaction. Note that as the value of $B$ is increased, the duration of the transient stage is reduced.

Figure 3. Evolution of the front $x_{f}$ for several values of $\unicode[STIX]{x1D703}$ and $B$ with both molecular potentials. Here, $A=10$ , $h_{\ast }=0.01$ , $G=0$ and $h_{m}$ is the maximum of the profile.

The bulk region of the droplet can be approximated by a triangular profile, and then its area $A$ is (Gomba & Homsy Reference Gomba and Homsy2010)

(3.3) $$\begin{eqnarray}\displaystyle A=\frac{w(x_{f}-x_{a})}{2(2Bt)}=\frac{w^{2}}{4Bt}, & & \displaystyle\end{eqnarray}$$

with $x_{a}$ the location of the receding contact line and $w=x_{f}-x_{a}$ the droplet width. Then, the width is $w=(4ABt)^{1/2}$ and, therefore, the footprint of the droplet increases with time, as shown in figure 4. In addition, we can see that while the slope of the linear profile is independent of $A$ , as predicted by (3.2), the velocity of the front increases with $A$ and the position $x_{a}$ is almost constant.

Figure 4. Evolution of the thickness profile for several values of $A$ at two different times: $t=9000$ (dashed lines) and $t=19\,000$ (solid lines). The contact angle is $\unicode[STIX]{x1D703}=3^{\circ }$ , $B=0.01$ , $h_{\ast }=0.01$ , $G=0$ and $(n,m)=(4,3)$ . The linear profile is given by (3.2).

3.2 Effect of gravity, $G=1$

Figure 5 shows the evolution of the thickness profile under the same conditions as in figure 2 but with $G=1$ . The initial profile, compressed in the $z$ direction due to gravity, evolves to the asymptotic linear profile (3.2). Nevertheless, gravity has a role at the leading front: comparing with the evolution shown in figure 2, we can see that the presence of gravity decreases the height of the capillary ridge and smooths the valley immediately behind it.

Figure 5. Evolution of the thickness profile for a droplet with $A=10$ , $\unicode[STIX]{x1D703}=4^{\circ }$ , $B=0.01$ , $G=1$ , $(n,m)=(4,3)$ and $h_{\ast }=0.01$ . The dashed blue line is the analytic solution (3.2). Similar behaviour is observed for a molecular potential with $(n,m)=(3,2)$ .

The most remarkable effect of gravity is on the velocity of the front, as shown in figure 6. Given that the initial profiles for $G=1$ and $G=0$ have the same initial front position, in figure 6(a) we observe that the profile with $G=1$ takes more time to reach the asymptotic linear shape than the case $G=0$ . Figure 6(b) shows the evolution of the front position for $G=1$ and $G=0$ . The final velocity, $\text{d}x_{f}/\text{d}t=2Bh(x_{f})$ , is monotonically reached in both cases, but it decreases with time for $G=0$ , while the velocity increases for $G=1$ . Similarly to the case with $G=0$ , the velocity for $G=1$ is independent of the molecular potential and the speed increases with $A$ and $B$ .

Figure 6. (a) Comparison of the thickness evolution with gravity $G=1$ (dashed blue line) and without gravity $G=0$ (black line). The position of the initial front is the same in both droplets. (b) Position of the front $x_{f}$ versus time $t$ for droplets with $\unicode[STIX]{x1D703}=3^{\circ }$ , $A=10$ , $h_{\ast }=0.01$ , $B=0.01$ and several combination of $(n,m)$ and $G$ . For the dotted line, $A=50$ .

4 Intermediate contact angle: transition regime

4.1 Absence of gravity, $G=0$

The transition regime appears for intermediate values of the contact angle $\unicode[STIX]{x1D703}$ . In contrast with previous section, here the effects of the molecular potential and the Marangoni stress are of the same order. We observe two different dynamics: a droplet breaks into two or more smaller volumes, as reported Gomba & Homsy (Reference Gomba and Homsy2010), or it evolves to a steady profile that migrates with a constant velocity without breakups.

Figure 7 shows the evolution of the thickness profile for $(n,m)=(3,2)$ , $\unicode[STIX]{x1D703}=15^{\circ }$ and $G=0$ . As described in Gomba & Homsy (Reference Gomba and Homsy2010), the fluid breaks up into smaller droplets and the behaviour is quite complex. Nevertheless, we observe that before breakup, the droplet adopts a transient stage consisting in a linear profile followed by a (short length) almost-flat thickness $h_{e}$ (see $t=4000$ in the figure). We will show that this thickness determines the later dynamics of the flow.

Figure 7. Evolution of the thickness profile with $\unicode[STIX]{x1D703}=15^{\circ }$ , $G=0$ , $h_{\ast }=0.01$ , $B=0.03$ and $(n,m)=(3,2)$ . The droplet with initial cross-sectional area $A=10$ breaks into smaller droplets.

In figure 8, we keep all the parameters of the previous figure but we change the pair of the molecular potential to $(n,m)=(4,3)$ . Here, instead of the rupture observed for polar liquids, we observe that an steady profile is adopted after a transition stage. The initial shape evolves into a flat droplet with a capillary ridge at the front, which migrates with a constant velocity. This droplet shape has not been reported before.

Figure 8. Evolution of the thickness profile with $\unicode[STIX]{x1D703}=15^{\circ }$ , $G=0$ , $h_{\ast }=0.01$ , $(n,m)=(4,3)$ , $B=0.03$ and $A=10$ . The change of the molecular potential stabilizes the profile.

Thus, in the transition regime a constant height $h_{e}$ emerges, and the dynamics of the flow depends on the stability of that thickness. In the next two subsections, we analyse the parametric dependence of $h_{e}$ and also the occurrence of breakups. Finally, we explore the effect of gravity.

4.1.1 Migration of flat droplets

We first analyse flat droplets, i.e. steady solutions that do not break up, move with a constant velocity and present a characteristic flat thickness $h_{e}$ . Figure 9(a) shows the profiles for $\unicode[STIX]{x1D703}=15^{\circ }$ , $A=10$ and several values of $B$ at $t=2.4\times 10^{4}$ , when the steady profile is completely developed. As $B$ increases, the width of the profile $w$ and the velocity of the droplet $U$ increases, while the thickness $h_{e}$ decreases. Note that the area below the capillary ridge enlarges as $B$ diminishes and, when most of the fluid is within the capillary ridge, the profile does not present a flat film, such as in the case with $B=0.01$ . In figure 9(b) we set $\unicode[STIX]{x1D703}=18^{\circ }$ . If we compare these profiles with those with $\unicode[STIX]{x1D703}=15^{\circ }$ , we observe that for the same values of $B$ , a larger $\unicode[STIX]{x1D703}$ implies a shorter $w$ , and larger values for $h_{e}$ and $U$ .

Figure 9. Profiles at $t=2.4\times 10^{4}$ in the evolution of a droplet with $A=10$ , $G=0$ , $h_{\ast }=0.01$ , $(n,m)=(4,3)$ and initial contact angle (a) $\unicode[STIX]{x1D703}=15^{\circ }$ , and (b) $\unicode[STIX]{x1D703}=18^{\circ }$ . We observe that the thickness $h_{e}$ , the width $w$ and the velocity $U$ depends on the thermal gradient $B$ .

Simulations show that $w$ increases with $A$ , while $h_{e}$ is independent of $A$ . Dimensional analysis and parametric studies on $K$ , $B$ and $A$ allows us to determine how the different parameters are related. We find that the dependence of $h_{e}$ on $K$ and $B$ is given by

(4.1) $$\begin{eqnarray}\displaystyle h_{e}\propto KB^{-2/3}\propto \tan ^{2}\unicode[STIX]{x1D703}\,B^{-2/3}. & & \displaystyle\end{eqnarray}$$

Figure 10(a) shows a good agreement between (4.1) and the numerical data for several combinations of the parameters. To understand how $w$ depends on $A$ , $K$ and $B$ , we approximate the area $A$ by:

(4.2) $$\begin{eqnarray}\displaystyle A=\int h\,\text{d}x\sim h_{e}\,w, & & \displaystyle\end{eqnarray}$$

and therefore the width follows the power law

(4.3) $$\begin{eqnarray}\displaystyle w\propto \frac{A}{K}B^{2/3}\propto \frac{A}{\tan ^{2}\unicode[STIX]{x1D703}}B^{2/3}. & & \displaystyle\end{eqnarray}$$

This expression is successfully tested in figure 10(b). Also, the numerical results show that when $A$ is increased, the width $w$ increases but the thickness $h_{e}$ remains constant, as expected from (4.1) and (4.3).

Figure 10. Dependence of (a) $h_{e}$ and (b) $w$ on the parameters of the problem $B$ , $\unicode[STIX]{x1D703}$ and $A$ . The dashed lines are the derived analytical expressions.

As mentioned, the droplets finally move with a constant velocity $U$ . To estimate $U$ , we assume that the solution is well represented by a travelling wave of the form $h(x,t)\equiv h(\unicode[STIX]{x1D702})$ , with $\unicode[STIX]{x1D702}=x-Ut$ . After integration, equation (2.10) becomes

(4.4) $$\begin{eqnarray}\displaystyle h^{3}\frac{\text{d}^{3}h}{\text{d}\unicode[STIX]{x1D702}^{3}}+Kh^{3}\frac{\text{d}}{\text{d}\unicode[STIX]{x1D702}}\left[\left(\frac{h_{\ast }}{h}\right)^{n}-\left(\frac{h_{\ast }}{h}\right)^{m}\right]-Gh^{3}\frac{\text{d}h}{\text{d}\unicode[STIX]{x1D702}}+Bh^{2}-Uh={\mathcal{V}}, & & \displaystyle\end{eqnarray}$$

with ${\mathcal{V}}$ a constant of integration. At the flat film, where $h=h_{e}$ , the first and third derivatives are negligible, i.e.

(4.5) $$\begin{eqnarray}\displaystyle \left.\frac{\text{d}h}{\text{d}\unicode[STIX]{x1D702}}\right|_{h=h_{e}}=\left.\frac{\text{d}^{3}h}{\text{d}\unicode[STIX]{x1D702}^{3}}\right|_{h=h_{e}}=0, & & \displaystyle\end{eqnarray}$$

and then,

(4.6) $$\begin{eqnarray}\displaystyle U=Bh_{e}-\frac{{\mathcal{V}}}{h_{e}}. & & \displaystyle\end{eqnarray}$$

Similarly, at $h=h_{\ast }$ , the same conditions (4.5) apply, and (4.4) becomes

(4.7) $$\begin{eqnarray}\displaystyle U=Bh_{e}\left(1+\left(\frac{h_{\ast }}{h_{e}}\right)\right). & & \displaystyle\end{eqnarray}$$

Assuming $h_{\ast }/h_{e}\ll 1$ , the velocity of migration is $U=Bh_{e}$ , which using (4.1) becomes

(4.8) $$\begin{eqnarray}\displaystyle U\propto KB^{1/3}\propto \tan ^{2}\unicode[STIX]{x1D703}\,B^{1/3}. & & \displaystyle\end{eqnarray}$$

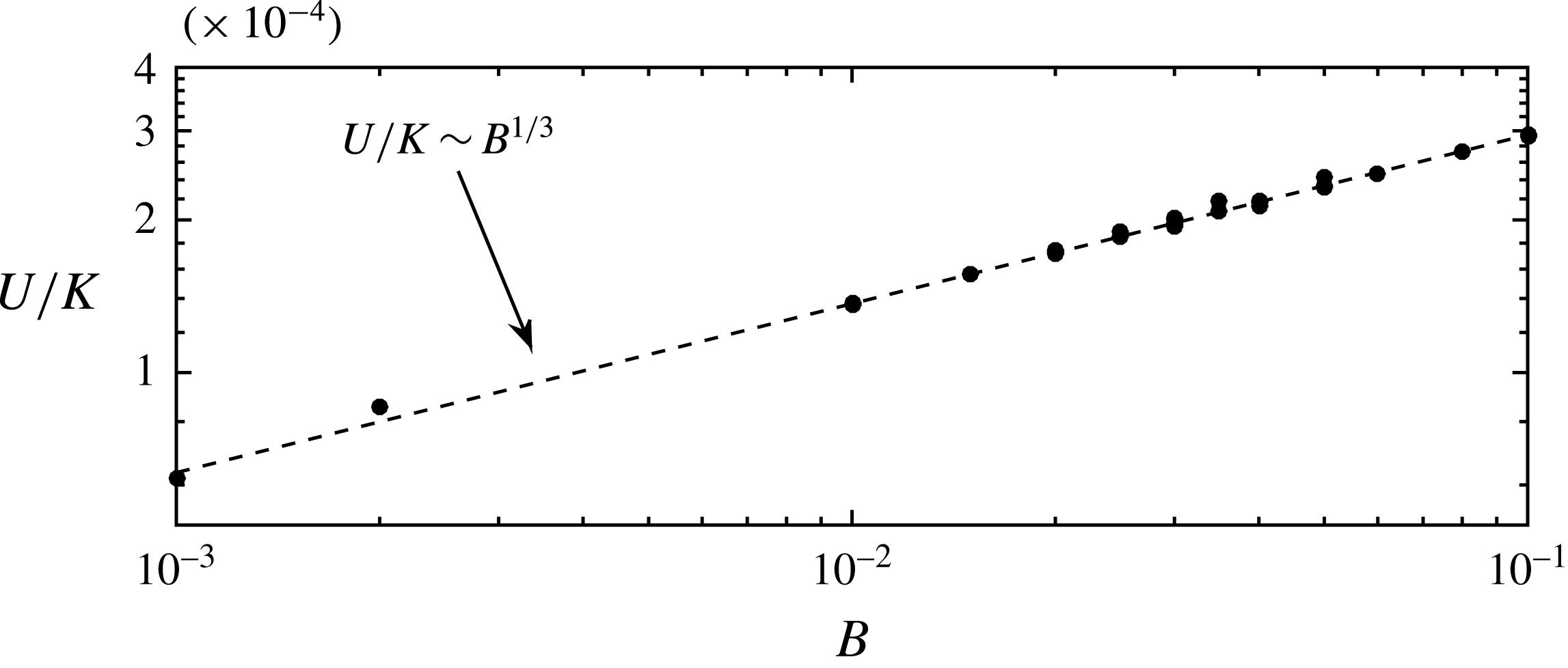
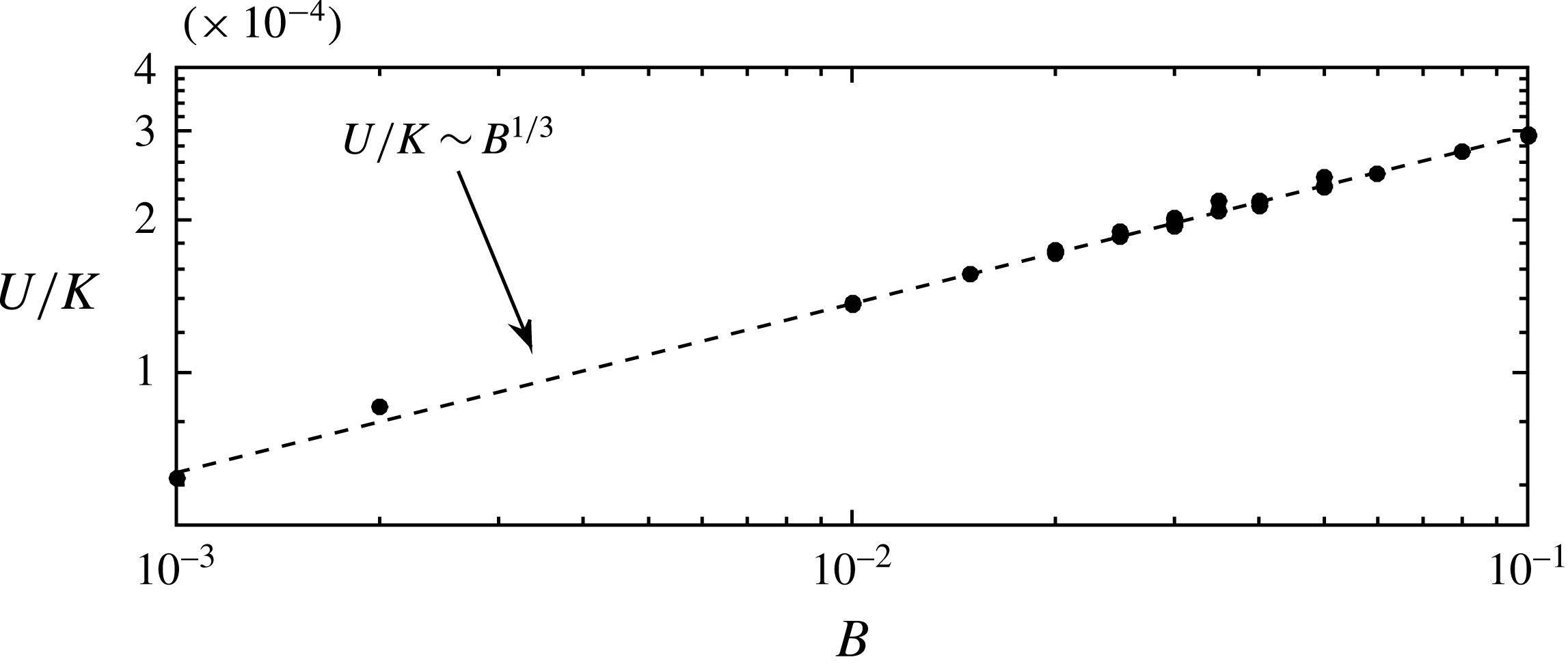
Figure 11 confirms this dependence of $U$ on the parameters $K$ and $B$ .

Figure 11. Dependence of the velocity $U$ for several combination of the parameters $B$ and $K$ . The law (4.8) is valid for the intermediate flow regime when droplets moves steady without ruptures, as shown in figure 9.

4.1.2 Occurrence of breakup

For intermediate contact angles, most of the cases with polar liquids break up into smaller droplets during the migration, while the rupture process with non-polar liquids was only observed for the highest values of $B$ . Figure 12(a) shows the breakup of a droplet for $B=0.05$ and $(n,m)=(4,3)$ . Although rupture is present, it only occurs for late times and in few points when compared with the cases with $(n,m)=(3,2)$ . On the contrary, figure 12(b) shows a multiple droplet breakup occurring for $B=0.01$ and $(n,m)=(3,2)$ . Therefore, simulations show that the molecular potentials and the Marangoni force clearly play a role in the stability of the flat film.

Figure 12. Evolution of the thickness profile with $\unicode[STIX]{x1D703}=10^{\circ }$ , $A=10$ , $h_{\ast }=0.01$ and $G=0$ . (a) Non-polar liquid, $(n,m)=(4,3)$ and thermal gradient $B=0.05$ . (b) Polar liquid, $(n,m)=(3,2)$ and $B=0.01$ .

The molecular potential, i.e. the nature of polar or non-polar liquid, manages the stability of the flat film. In order to understand the rupture process, we implement a linear stability analysis assuming that $h=h_{e}+\unicode[STIX]{x1D709}$ , with $\unicode[STIX]{x1D709}\ll h_{e}$ . After linearization, equation (2.10) becomes

(4.9) $$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}}{\unicode[STIX]{x2202}t}+\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x}\left[h_{e}^{3}\left(\frac{\unicode[STIX]{x2202}^{3}\unicode[STIX]{x1D709}}{\unicode[STIX]{x2202}x^{3}}+K^{\prime }\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}}{\unicode[STIX]{x2202}x}\right)\right]+2Bh_{e}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}}{\unicode[STIX]{x2202}x}=0, & & \displaystyle\end{eqnarray}$$

with

(4.10) $$\begin{eqnarray}\displaystyle K^{\prime }=K\left(m\frac{h_{\ast }^{m}}{h_{e}^{m+1}}-n\frac{h_{\ast }^{n}}{h_{e}^{n+1}}\right). & & \displaystyle\end{eqnarray}$$

We replace $\unicode[STIX]{x1D709}\sim \exp (\text{i}kx+\unicode[STIX]{x1D714}t)$ and obtain the following dispersion equation

(4.11) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D714}=-2\text{i}Bh_{e}k-h_{e}^{3}k^{2}(k^{2}-K^{\prime }). & & \displaystyle\end{eqnarray}$$

A stable constant thickness $h_{e}$ has to satisfy $Re[\unicode[STIX]{x1D714}]<0$ , i.e.

(4.12) $$\begin{eqnarray}\displaystyle k>\sqrt{K}\left(m\frac{h_{\ast }^{m}}{h_{e}^{m+1}}-n\frac{h_{\ast }^{n}}{h_{e}^{n+1}}\right)^{1/2}, & & \displaystyle\end{eqnarray}$$

and the mode with the largest growth rate is

(4.13) $$\begin{eqnarray}\displaystyle k_{m}=\sqrt{\frac{K}{2}}\left(m\frac{h_{\ast }^{m}}{h_{e}^{m+1}}-n\frac{h_{\ast }^{n}}{h_{e}^{n+1}}\right)^{1/2}. & & \displaystyle\end{eqnarray}$$

Figure 13 shows the dispersion relationship for different values of $\unicode[STIX]{x1D703}$ and both molecular potentials. Comparing cases with the same value of $B$ and $A$ , the growth rate is always notably smaller for the pair $(n,m)=(4,3)$ than for the $(n,m)=(3,2)$ . Also, the minimum unstable wavelength is larger for the case $(n,m)=(4,3)$ . Thus, non-polar liquids needs longer times and larger domains to develop an instability.

Figure 13. Relation of dispersion (4.11) for different combination of the parameters. The thickness $h_{e}$ is estimated in the transition stage. Same colour is used for cases with same $\unicode[STIX]{x1D703}$ and $A$ .

To estimate the distance between droplets, we implement a Fourier analysis of the thickness profile. Figure 14 shows the Fourier transform of the thickness profiles obtained for $(n,m)=(3,2)$ and different values of $B$ . The position of the vertical line, that indicates the maximum wavelength amplitude $\unicode[STIX]{x1D706}_{m}^{n}$ , agrees well with the theoretical value $\unicode[STIX]{x1D706}_{m}^{t}=2\unicode[STIX]{x03C0}/k_{m}$ as shown in table 2. Thus, the number of droplets and the distance between them can be predicted from a linear stability analysis.

Table 2. Comparison of theoretical $\unicode[STIX]{x1D706}_{m}^{t}$ , equation (4.13) and numerical $\unicode[STIX]{x1D706}_{m}^{n}$ wavelengths.

Figure 14. Fourier transform of the thickness profile with a molecular potential $(n,m)=(3,2)$ and three different values of $B$ . The vertical line points the maximum wavelength $\unicode[STIX]{x1D706}_{m}^{n}$ .

4.2 Effect of gravity, $G=1$

Figure 15 shows the evolution of the thickness profile for $\unicode[STIX]{x1D703}=15^{\circ }$ , $B=0.01$ , $G=1$ and both molecular potentials. Gravity compresses the profiles in the $z$ direction, softens the valley that appears immediately behind the capillary ridge and increases the width of the initial profile (compare with the profiles in figures 7 and 9). More interesting, under the action of gravity the breakups are not observed.

Figure 15. Evolution of the thickness profile for a droplet with $\unicode[STIX]{x1D703}=15^{\circ }$ , $A=10$ , $G=1$ , $h_{\ast }=0.01$ and $B=0.01$ . (a) Non-polar liquid, $(n,m)=(4,3)$ . (b) Polar liquid, $(n,m)=(3,2)$ .

We study how gravity affects the stability of flat profiles. A linear stability analysis shows that the growth rate is now given by

(4.14) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D714}=-2\text{i}Bh_{e}k-h_{e}^{3}k^{2}(k^{2}-(K^{\prime }-G)), & & \displaystyle\end{eqnarray}$$

and then, a uniform film $h_{e}$ is stable if the wavenumber satisfies

(4.15) $$\begin{eqnarray}\displaystyle k>(K^{\prime }-G)^{1/2}. & & \displaystyle\end{eqnarray}$$

Figure 16 shows that the effect of $G$ is to decrease the real part of the growth rate $\unicode[STIX]{x1D714}$ and the mode $k_{m}$ . Thus, situations where breakup is observed with $G=0$ may not present ruptures with $G=1$ , as in the cases for $B=0.03$ and $(n,m)=(3,2)$ shown in figures 7 and 17. Nevertheless, figure 17 shows that breakup for $G=1$ and polar liquids may occur for larger values of $B$ . Breakup of a polar liquid in the presence of gravity can be understood in the following way: assuming that the relation $h_{e}\propto B^{-\unicode[STIX]{x1D6FD}}$ (with $\unicode[STIX]{x1D6FD}>0$ ) is still valid when $G=1$ (later this is confirmed), if the thermal gradient $B$ increases, the thickness of the stable film $h_{e}$ decreases. Then, from (4.10) $K^{\prime }$ increases and finally, from (4.15), the smallest wavenumber of a stable mode becomes larger. Briefly, an increase of $B$ is destabilizing. Added to this, when $B$ is increased, the region with $h=h_{e}$ widens ( $w$ enlarges) and it is easier to fit unstable modes inside the drop.

Figure 16. Effect of gravity on the growth rate. Here, $\unicode[STIX]{x1D703}=15^{\circ }$ and $h_{e}=0.07$ . The maximum of $\unicode[STIX]{x1D714}$ and the largest unstable $k$ decrease when $G=1$ compared with the case $G=0$ .

Figure 17. Profiles at $t=2.7\times 10^{4}$ in the evolution of a droplet with initial contact angle $\unicode[STIX]{x1D703}=15^{\circ }$ , $A=10$ , $G=1$ , $h_{\ast }=0.01$ and $(n,m)=(3,2)$ . In contrast with the observed evolution for the case with $G=0,$ here the case with $B=0.01$ does not present a breakup when gravity is considered.

Gravity also changes the dependence of $h_{e}$ on the parameters. Figure 18(a) shows $h_{e}/K$ against $B$ for $G=1$ for the two explored potentials (we also include cases with $G=0$ to illustrate the difference in the exponent of the power law). For $G=1$ , the simulations show that the dependence of $h_{e}$ on $K$ and $B$ is

(4.16) $$\begin{eqnarray}\displaystyle h_{e}\propto K\,B^{-3/5}\propto \tan ^{2}\unicode[STIX]{x1D703}\,B^{-3/5}. & & \displaystyle\end{eqnarray}$$

Since for a given value of $\unicode[STIX]{x1D703}$ , $K$ is higher for non-polar than for polar liquids, the value of $h_{e}$ is higher for the pair $(n,m)=(4,3)$ . Then, equation (4.7) predicts that the velocity of migration is higher for non-polar liquids than for polar liquids. Effectively, figure 18(b) shows that both $h_{e}$ and $U$ are larger for the pair $(n,m)=(4,3)$ .

Figure 18. (a) Dependence of the thickness $h_{e}$ for several combinations of $B$ and $\unicode[STIX]{x1D703}$ . (b) Evolution of the thickness profile with $\unicode[STIX]{x1D703}=22^{\circ }$ , $A=10$ , $G=1$ , $h_{\ast }=0.01$ , $B=0.03$ and both molecular potentials.

5 Large contact angles: droplet regime

5.1 Absence of gravity, $G=0$

For large contact angles, the value of $K$ increases and the molecular potential becomes strong enough to keep the initial shape of the droplet during the migration. In the droplet regime, the Marangoni stress displaces the droplet with constant velocity $U$ without stretching it. Brzoska et al. (Reference Brzoska, Brochard-Wyart and Rondelez1993) and Chen et al. (Reference Chen, Troian, Darhuber and Wagner2005) show experimentally that droplets migrate keeping their initial shape. In their experiments, the velocity increases with the footprint $R$ of the wet surface, but different liquids present differences in the dependence of $U$ on $R$ . This leads us to think that the type of the molecular force should modify the velocity of migration. Figure 19 shows the evolution of the thickness profile for a droplet with area $A=10$ , initial contact angle $\unicode[STIX]{x1D703}=25^{\circ }$ and thermal gradient $B=0.01$ , for both molecular potentials. Effectively, the velocity of migration changes with the polarity of the liquid.

Figure 19. Evolution of the thickness profile for (a) non-polar liquid, $(n,m)=(4,3)$ and (b) polar liquid, $(n,m)=(3,2)$ , until $t=4.8\times 10^{4}$ . The effect of the potential avoids drop stretching due to Marangoni stress. Here, $\unicode[STIX]{x0394}t=6\times 10^{3}$ , $\unicode[STIX]{x1D703}=25^{\circ }$ , $A=10$ , $G=0$ , $h_{\ast }=0.01$ and $B=0.01$ .

In this regime, front and rear contact lines move with the same constant velocity $U$ . Brzoska et al. (Reference Brzoska, Brochard-Wyart and Rondelez1993) and Chen et al. (Reference Chen, Troian, Darhuber and Wagner2005) have shown that the velocity is proportional to $B$ and inversely proportional to the viscosity. Gomba & Homsy (Reference Gomba and Homsy2010) demonstrated, by means of dimensional analysis, that the velocity for droplets with $(n,m)=(3,2)$ supports this experimental conclusion. The latter authors constructed two $\unicode[STIX]{x1D6F1}^{\ast }$ groups and, using numerical results, explored the relationship between them. They found that the velocity is given by

(5.1) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F1}_{1}^{\ast }=\frac{U}{Bh_{\ast }}\propto (\unicode[STIX]{x1D6F1}_{2}^{\ast })^{\unicode[STIX]{x1D6FD}}, & & \displaystyle\end{eqnarray}$$

with $\unicode[STIX]{x1D6FD}=0.4$ for the case $(n,m)=(3,2)$ and $G=0$ . Here, we generalize the previous result considering that the pair $(n,m)$ could change depending on the type of liquid. Then, we define the dimensionless number

(5.2) $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F1}_{2}^{\ast }=\left(\frac{(n-1)(m-1)}{2(n-m)}\right)^{1/2}\frac{A\tan \unicode[STIX]{x1D703}}{h_{\ast }^{2}}. & & \displaystyle\end{eqnarray}$$

Figure 20 shows $U/Bh_{\ast }$ versus $A\tan \unicode[STIX]{x1D703}/h_{\ast }^{2}$ for several combinations of the parameters $(n,m)$ , $A$ , $\unicode[STIX]{x1D703}$ , $B$ and $h_{\ast }$ . Interestingly, the exponent in (5.1) is $\unicode[STIX]{x1D6FD}=0.40$ , independently of the pair $(n,m)$ . Therefore, the pre-factor in (5.2) is responsible of the different velocity for each liquid.

Figure 20. Dependence of the velocity $U$ for several combination of the parameters $(n,m)$ , $A$ , $\unicode[STIX]{x1D703}$ , $B$ and $h_{\ast }$ .

5.2 Effect of gravity, $G=1$

Gravity produces similar results to those observed in previous regimes. Figure 21 shows the evolution of a droplet with $A=10$ , $\unicode[STIX]{x1D703}=25^{\circ }$ , $B=0.01$ and $G=1$ , for both molecular potentials. Here, the initial profile is wider and has a lower height than the corresponding case with $G=0$ . When the thermal gradient is applied, the droplet slightly modified its shape. After a short time, the droplet migrates with a steady profile, but its velocity is smaller than the case with $G=0$ , as shown in figures 19 and 21.

Figure 21. Evolution of the thickness profile for (a) $(n,m)=(4,3)$ and (b) $(n,m)=(3,2)$ , until $t=6.6\times 10^{4}$ . Here, $\unicode[STIX]{x0394}t=1.1\times 10^{4}$ , $\unicode[STIX]{x1D703}=25^{\circ }$ , $A=10$ , $G=1$ , $h_{\ast }=0.01$ and $B=0.01$ .

Figure 22 shows $U/Bh_{\ast }$ versus $A\tan \unicode[STIX]{x1D703}/h_{\ast }^{2}$ for several combination of the parameters $(n,m)$ , $A$ , $\unicode[STIX]{x1D703}$ , $B$ , $h_{\ast }$ and $G$ . Gravity has an noticeable effect on the power law exponent. Effectively, for $G=1$ ( $G=0$ ), the exponent is $\unicode[STIX]{x1D6FD}=0.45$ ( $\unicode[STIX]{x1D6FD}=0.40$ ), with $\unicode[STIX]{x1D6FD}$ independent of $n$ and $m$ . Due to the fact that the exponents are different in each case, the results suggest that the droplet could migrate with a larger velocity for $G=1$ than for $G=0$ . In addition, we can see from the figure that for a given value of $G$ , polar liquids migrate always with a velocity $U$ smaller than non-polar ones.

Figure 22. Dependence of the velocity $U$ for several combinations of the parameters $(n,m)$ , $A$ , $\unicode[STIX]{x1D703}$ , $B$ , $h_{\ast }$ and $G$ .

6 Discussions and conclusions

In this paper, the fate of droplets subject to a thermocapillary driving force is investigated numerically with a particular emphasis on the effects of the form of the molecular interaction potential and gravity. The droplet dynamics model is based on the lubrication approximation and the resulting partial differential equation is solved in the finite element package COMSOL. The study confirms earlier observations that three regimes exist depending on the value of the contact angle.

For small contact angles, the film regime is observed for which the droplet stretches with the advancing contact line moving substantially faster than the receding one, leading to an increasing droplet footprint and a decreasing maximum thickness. The balance between viscous and Marangoni stresses produces a linear profile behind the capillary ridge at the front, analogous to the self-similar solution observed for falling films on solid substrates (Huppert Reference Huppert1982; Gomba et al. Reference Gomba, Diez, González and Gratton2005, Reference Gomba, Diez, Gratton, González and Kondic2007). This regime is well described by the similarity solution given by Gomba & Homsy (Reference Gomba and Homsy2010) irrespective of the molecular interaction potential which is a consequence of the fact that for small contact angles, the contribution of the disjoining pressure term is negligible. The effect of gravity is to delay the development of this similarity solution which is still reached for larger times but with a decreased height of the capillary ridge at the advancing contact line. The asymptotic velocity of the front is given by $U=\sqrt{BA/t}$ .

For intermediate values of the contact angle, the transition regime occurs. In this regime, the droplet either travels with a constant profile which is different from the initial one or breaks up into a series of smaller droplets. In the former case, the droplet is found to travel with a constant velocity which scales as the $1/3$ power of the thermocapillary driving stress and is proportional to $K$ , i.e. small differences in the contact angle produce noticeable effects on the velocity, as shown in figure 9. In the latter case, the outcome is found to be strongly dependent of the molecular interaction potential. For polar liquids with a disjoining pressure given by the pair $(n,m)=(3,2)$ , breakup occurs more readily than for non-polar liquids with a disjoining pressure for which $(n,m)=(4,3)$ . In other words, it takes a smaller value of the driving thermocapillary stress to break up the initial droplets into smaller ones for polar liquids than for non-polar ones. This feature is explained by a linear stability analysis of the uniform film which develops as the droplet evolves in the intermediate regime. This linear stability analysis reveals that the maximum growth rate of the instability is larger for polar liquids, $(n,m)=(3,2)$ than for non-polar ones and occurs for shorter wavelengths. In other words, the instability for non-polar liquids takes longer times and larger distances to develop. The stability analysis also allows a prediction of the number of droplets the parent droplet breaks up into and the distance between them. The effect of gravity on the growth of the instability is to decrease the maximum growth rate and shift it to larger wavelengths.

For larger values of the contact angle, the model confirms earlier observations that the droplet travels with a constant profile and at constant speed towards the colder part of the substrate. The travelling velocity is found to be greater for non-polar than for polar liquids and scales linearly with the thermocapillary driving force with or without gravity. Interestingly, the exponent of the law is found to be independent of model of the disjoining pressure term, i.e. independent of $n$ and $m$ , but it depends on the gravity. We expect that for a different combination of parameters, the travelling velocity will be greater for the case with gravity. The effect of gravity in that case is to modify slightly the droplet profile as it travels on the substrate. Table 3 summarizes the description of the velocities of droplets for each regime, for polar and non-polar liquids and considering or not the effect of gravity.

Table 3. Velocity of droplets for each regime depending on the molecular and gravitational effects. The velocities for the transition regime are for cases without breakups.

The results allow us to discuss the points raised in § 1 about experimental observations. These are: (i) the saturation in the curve $U$ versus $R$ , (ii) the elongation of large droplets and (iii) the non-occurrence of breakups.

Brzoska et al. (Reference Brzoska, Brochard-Wyart and Rondelez1993) show in their figure $2$ the velocity of the droplets versus the footprint, $R$ . While for the smallest droplets in the experiments ( $1<R<4$ ), the velocity follows a roughly linear dependence on $R$ , from $R\geqslant 4$ the experimental curve suggests that the velocity starts to converge to a saturation value. The authors attribute the change in the curve to the effect of gravity, despite the fact that gravity is expected to have an effect from smaller values of $R$ , i.e. for $R\geqslant 1$ .

Our results show that gravity is not needed to explain the change in the behaviour of $U$ , and that gravity effectively has an effect from $R=1$ . Under non-gravity conditions, it is observed that as $A$ is increased, the velocity first follows a dependence with $A^{0.4}$ in the droplet regime, to later saturate to a velocity $U\propto KB^{1/3}$ when flat droplets emerge due to the presence of the Marangoni stress (§ 4.1.1). When gravity is included to match experimental conditions, droplets with $R<1$ also displace with a velocity $U\propto A^{0.4}$ because the effect of gravity is negligible. Middle size droplets ( $1<R<4$ ) move with $U\propto A^{0.45}$ , and larger droplets migrate with a velocity $U\propto KB^{2/5}$ .

Figure 23 shows $U$ versus $R$ (both dimensionless), in the same fashion as in the experimental works. Let us first focus on the curve for $G=1$ . Notice that for $R<1$ we have $U\propto R^{0.72}$ . For $1<R<4$ , $U\propto R^{0.45}$ which is easily explained because as gravity is not negligible, $A\propto R$ . Finally, for $R>4$ the velocity saturates. The inset of figure 23 shows the same data in a regular plot: the points with $1<R<4$ resembles the ‘almost linear’ dependence observed in the experiments for $R<4$ . The saturation of $U$ for $R\approx 4$ is observed for both $G=1$ and $G=0$ , as occurs in experiments. Therefore, the saturation of $U$ is due to the change of the dynamics from droplet to transition regimes, and not to the action of gravity.

Figure 23. Log–log plot of the velocity against the footprint of the droplets (both are dimensionless, $B=0.008$ , $\unicode[STIX]{x1D703}=13^{\circ }$ ). The plot clearly shows three different behaviours for $U$ when $G=1$ . For $R<1$ , gravity is negligible and $U\propto R^{0.72}$ . For $1<R<4$ , $U\propto R^{0.45}$ due to the action of gravity. Larger droplets present a saturation with a velocity $U=Bh_{e}$ when the dynamics switches from ‘droplet’ to ‘transition’ regime. For $G=0$ , $U$ also presents a saturation at $R\approx 4$ , as in the experiments. The inset shows the same data, in regular coordinates, as in figure 2 of Brzoska et al. (Reference Brzoska, Brochard-Wyart and Rondelez1993).

Brzoska et al. (Reference Brzoska, Brochard-Wyart and Rondelez1993) also tracked the shape of the perimeter of the moving droplet, and observed that smaller ones almost keep their initial shape, while larger ones elongate in the direction of displacement. In figure 6 of their work, the authors present the ratio of the elongation on the initial radius against the initial radius: the relative elongation is stronger for larger volume droplets. Our simulations show, effectively, that the relative elongation is larger for $R>4$ without the need for the action of gravity. Again, the change is due to the transition from ‘droplet’ to ‘transition’ regime.

Another important issue connected with the elongation of the droplet is the non-occurrence of the breakup in experiments, as predicted by Gomba & Homsy (Reference Gomba and Homsy2010). Here, we show that, when a non-polar liquid is considered, the droplet elongates but does not break up into smaller droplets, as shown in § 4. The instability of the bulk region behind the bump is found to be sensitive both to the effects of gravity and the polarity of the liquid. As shown in figure 16, polar liquids present a larger growth rate than non-polar ones. Furthermore, as the shorter unstable mode of a polar liquid is smaller than the corresponding one for non-polar liquids, the instability of the latter requires larger domains than the former to develop, i.e. more stretched droplets. Gravity has a similar effect, reducing both the growth rate (the maximum growth rate $\unicode[STIX]{x1D714}_{max}=h_{e}^{3}(K^{\prime }-G)^{2}/4$ ), and the shorter unstable mode, $k_{c}=(K^{\prime }-G)^{1/2}$ . In conclusion, the polar nature of the liquid is an important parameter to consider to correctly account for the experimental results. Experimentalists should employ polar liquids or stronger thermal gradients in order to observe, under gravity conditions, the breakup of drops.

Summarizing, this study provides new insights on the fate of partially wetting droplets subject to a non-uniform, linearly varying temperature field. It also provides new guidelines on how to select fluid properties and operating conditions to achieve a desired wetting outcome which may be of importance, for example, in the context of droplet actuation in open microfluidics devices.