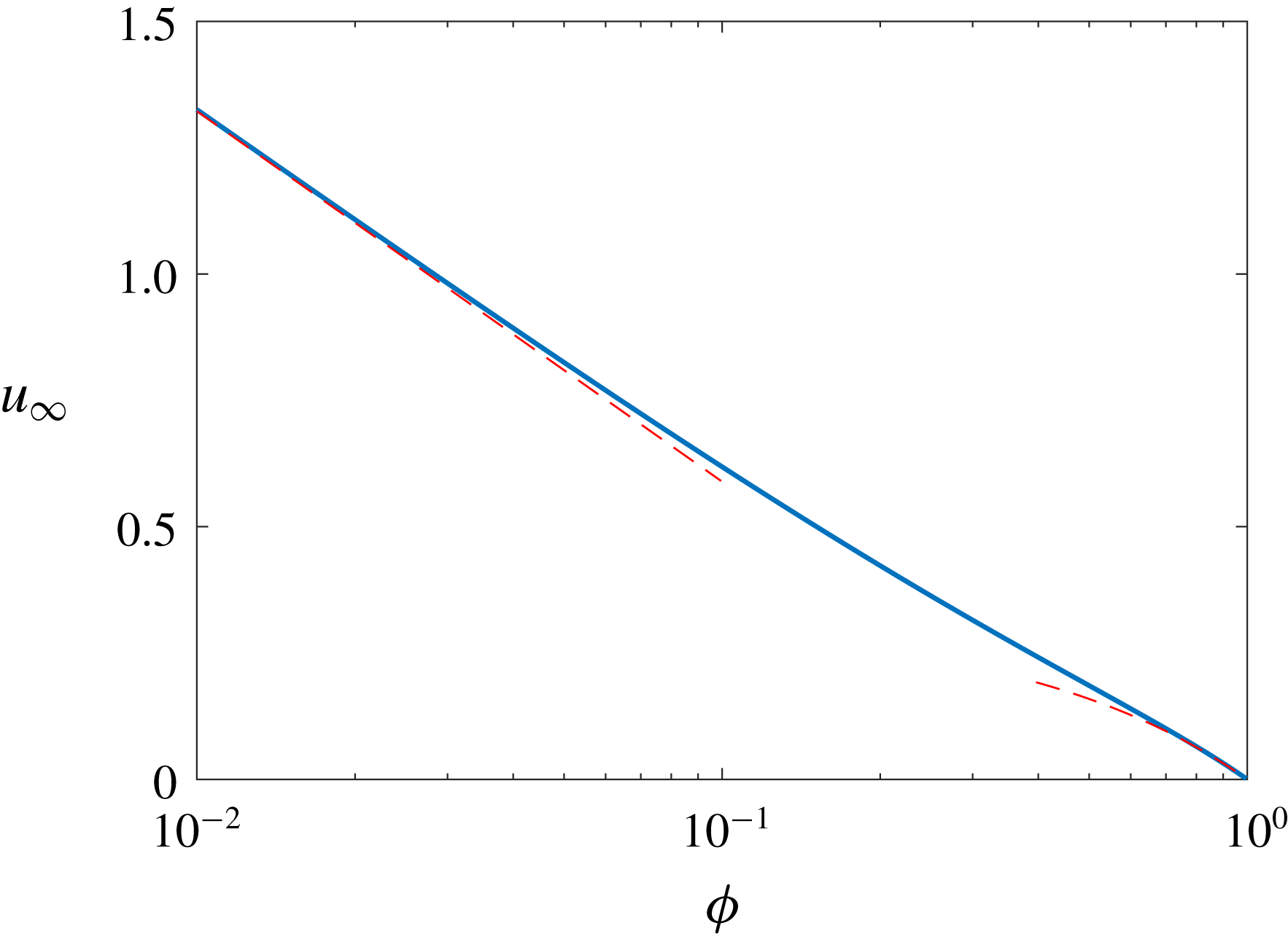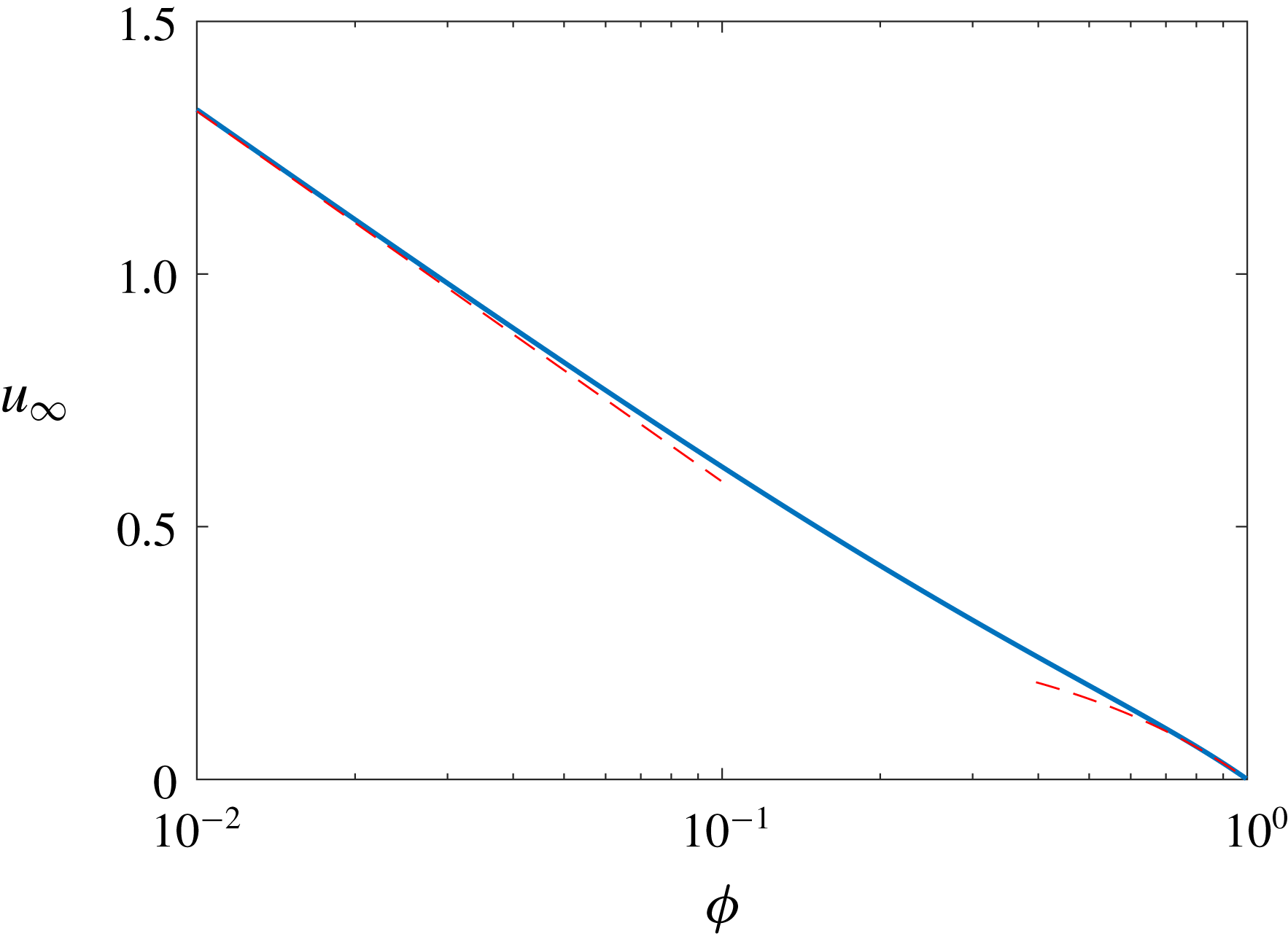1 Introduction
This is a follow-up to the recent paper of Yariv (Reference Yariv2018) which deals with thermocapillary flows between superhydrophobic surfaces that are made up of highly conducting grooved arrays in which zero-protrusion-angle cylindrical bubbles are trapped – a scenario originally addressed by Baier, Steffes & Hardt (Reference Baier, Steffes and Hardt2010). Yariv (Reference Yariv2018) considered the longitudinal problem, where a macroscopic temperature gradient is applied along the grooves. In that event, the solid-phase temperature simply coincides with the macroscopic profile which corresponds to the applied gradient. The associated Marangoni forces then generate longitudinal liquid flow. Heat advection with that flow, moreover, results in the formation of an excess-temperature field, above and beyond the macroscopic profile; Marangoni forces associated with the latter field trigger cross-sectional flow.
The above picture of transport phenomena is simplified by translational invariance, whereby both the excess temperature and velocity components are independent of the longitudinal coordinate. Moreover, the problem enjoys a partial decoupling, where the longitudinal flow is independent of both the excess temperature and cross-sectional flow. That independence has allowed Yariv (Reference Yariv2018) to identify a linkage between the longitudinal case and pressure-driven flows. This linkage generalises a result obtained by Baier et al. (Reference Baier, Steffes and Hardt2010) in the deep-channel limit, showing that at large distances from the bounding surfaces the longitudinal velocity approaches a far-field uniform value which is proportional to the slip length pertaining to the comparable shear flow over one of these surfaces.
The present contribution is concerned with the transverse problem, where the macroscopic temperature gradient is applied perpendicular to the grooves. In contrast to the longitudinal problem, the assumption of a highly conducting solid does not result here in an effectively prescribed temperature distribution. Consider indeed the macroscopic distribution associated with the imposed macroscopic gradient, where the temperature increases linearly with distance in the applied-gradient direction. Although that distribution is valid deep inside the solid, it clearly violates the no-flux condition at the portions of the solid–gas interface which are not parallel to the imposed gradient, see figure 1(a). Thus, while the solid temperature profile is still independent of that in the liquid, it has to be solved for the given groove geometry, thereby resulting in an awkward dependence upon the shape of the grooves. Because the temperature profile in the liquid phase must follow that in the solid phase along their common interfaces, it would also exhibit such an anomalous dependence, and then so would the ensuing flow. The resulting sensitivity to the detailed geometry of the microstructure has no parallel in ‘conventional’ pressure-driven flows about superhydrophobic surfaces, where the liquid ‘sees’ only the liquid–air interface and is ‘unaware’ of the shape and depth of the air cavities lying beyond it. (Assuming, of course, that a Cassie state is indeed attained. The validity of that assumption clearly depends upon the shape of the cavity (Quéré Reference Quéré2005, Reference Quéré2008).)
Fortunately, Baier et al. (Reference Baier, Steffes and Hardt2010) identified a case for which the above sensitivity disappears. Thus, when the slats are long relative to their width (as is the case in realistic systems) the temperature distribution at the end of each slat is essentially divorced from the macroscopic one. The slat-end distribution then only needs to satisfy Laplace’s equation and a no-flux condition, and is accordingly uniform at leading order. Consistency with the imposed gradient is attained by constant increments of the uniform temperature value, from one slat to another, with the ratio of said increment to the array pitch being equal to the imposed-gradient magnitude.
Even within that simplified framework, the transport problem is significantly more complicated than the one in the longitudinal problem. To elucidate the difference between the two problems, it is convenient to consider the case of vanishingly small Marangoni number, where heat advection is negligible. In the longitudinal problem, the temperature profile in the liquid then simply coincides with the macroscopic profile. In the transverse problem, however, the linearly varying macroscopic profile is incompatible with the requirement of temperature continuity at the solid–liquid interfaces, where the temperature is uniform. It follows that the temperature profile in the liquid must be solved for. Given this difference between the longitudinal and transverse problems, it does not seem possible to establish a general linkage to pressure-driven flows, analogous to the one identified by Yariv (Reference Yariv2018) in the longitudinal problem. In particular, there is no reason to expect that, in the deep-channel limit, the far-field velocity would be simply proportional to the appropriate slip length, as was the case in the longitudinal problem.
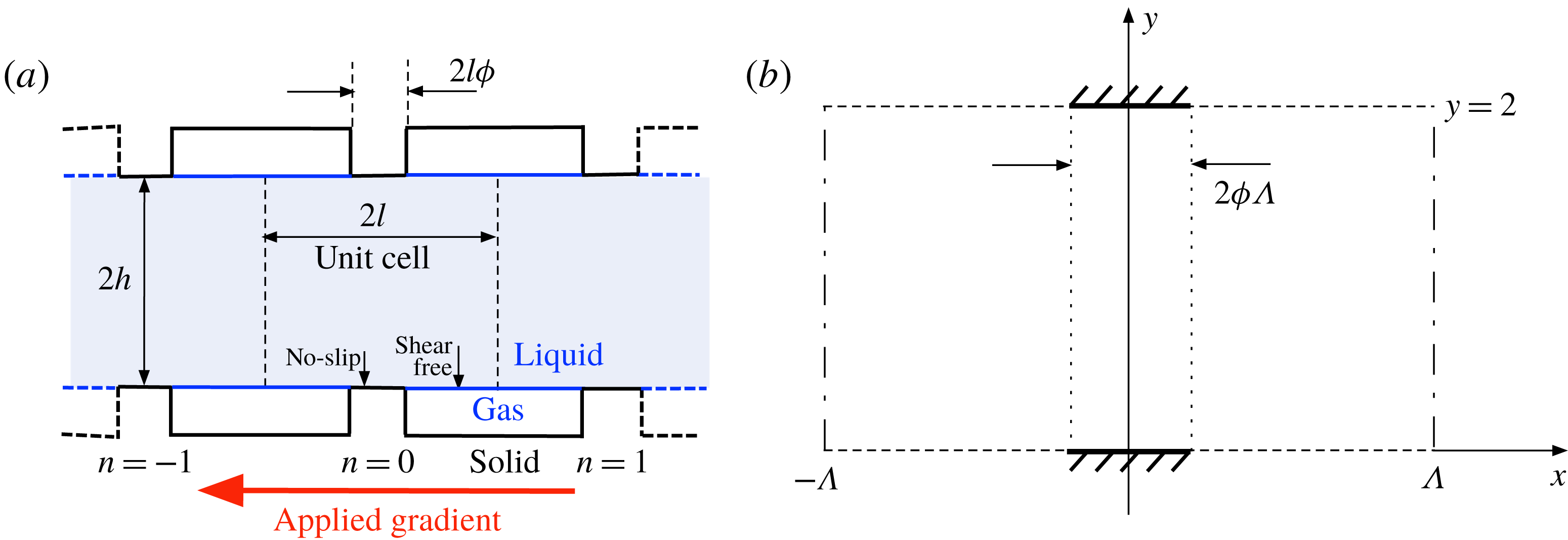
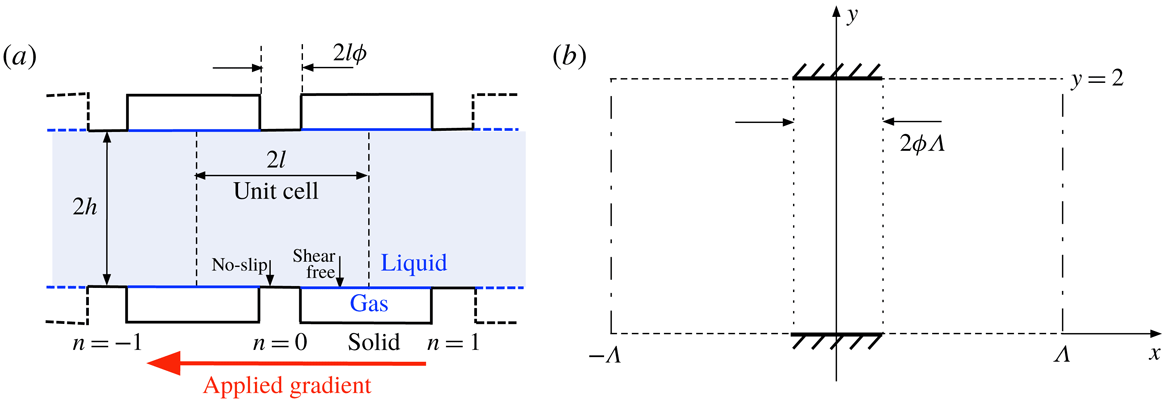
Figure 1. (a) Schematic of the dimensional channel geometry; (b) Schematic of the dimensionless unit-cell geometry.
Given these obstacles, Baier et al. (Reference Baier, Steffes and Hardt2010) resorted to numerical solutions when addressing the transverse problems. Our goal here is to confront that problem using a combination of matched asymptotic expansions and conformal mapping techniques in several relevant geometric limits, the most important being that of deep channels. With heat advection being neglected, the thermal problem is uncoupled from the flow. It follows that the problem reduces to a sequence of two linear problems, the first governing the temperature distribution in the liquid, and the second, animated by Marangoni forces due to that distribution, governing the engendered two-dimensional flow. The associated dimensionless problems are governed by two geometric parameters characterising the grooves array, namely the pitch-to-depth ratio
$\unicode[STIX]{x1D6EC}$
and the solid fraction
$\unicode[STIX]{x1D719}$
. Our goal is to determine the net volumetric flux through the two-dimensional channel.
Following the formulation of the general problem in § 2, we identify in § 3 an analogy between the harmonic conjugate of the temperature field and a complementary shear-driven flow. Making use of the Lorentz reciprocal theorem (Happel & Brenner Reference Happel and Brenner1965) we then obtain an integral representation for the volumetric flux. This general result is followed by separate asymptotic analyses which lead to useful approximations for the flux in different geometric limits. The limit of deep channels,
$\unicode[STIX]{x1D6EC}\ll 1$
, which is discussed in § 4, constitutes the main part of the present contribution. In that limit, a combination of matched asymptotic expansions and conformal mapping leads, via use of Lorentz’s reciprocity, to an expression for the far-field velocity, akin to that obtained by Baier et al. (Reference Baier, Steffes and Hardt2010) in the longitudinal problem. The second limit we consider (§ 5) is that of shallow channels,
$\unicode[STIX]{x1D6EC}\gg 1$
; it is based upon the familiar Hele-Shaw approximation that has been employed extensively in pressure-driven flows between superhydrophobic surfaces (Feuillebois, Bazant & Vinogradova Reference Feuillebois, Bazant and Vinogradova2009). The third limit addressed herein (§ 6) is that of small solid fraction,
$\unicode[STIX]{x1D719}\ll 1$
, where the flux exhibits a logarithmic singularity that resembles the one appearing in pressure-driven flows (Yariv Reference Yariv2017). We conclude in § 7, suggesting two future generalisations of the present work.
2 Problem formulation
The geometry considered herein is portrayed in figure 1(a). A layer of liquid (viscosity
$\unicode[STIX]{x1D707}$
) is confined between two parallel superhydrophobic surfaces, spaced a distance
$2h$
apart. Each surface is made up of an infinite array (period
$2l$
) of flat-edged slats, each of width
$2l\unicode[STIX]{x1D719}$
; equivalently, one can say that it is made up of an infinite array of grooves, each of width
$2l(1-\unicode[STIX]{x1D719})$
. Air is trapped in a stable Cassie state within each of these grooves, with the (presumed flat) liquid–air menisci being pinned at the corners of the slats. The liquid domain is accordingly bounded by two (planar) compound surfaces.
Our interest is in the heat transport and flow which are animated by the application of an external temperature gradient of magnitude
$G$
perpendicular to the grooves, assuming that the interfacial-tension coefficient of the liquid–air menisci varies linearly with the temperature, with a slope
$\unicode[STIX]{x1D70E}_{T}$
.
2.1 Normalisation and unit cell
Using
$h$
as a length unit we employ the Cartesian coordinates
$(x,y,z)$
with the
$x$
-axis running perpendicular to the grooves, anti-parallel to the applied gradient, and the liquid domain lying within
$0<y<2$
. The geometry is accordingly periodic in the
$x$
-direction, the dimensionless semi-period being
$\unicode[STIX]{x1D6EC}=l/h$
. The plane
$x=0$
is chosen as that passing between the centres of an opposing pair of solid slats. (Note the different choice of origin in Yariv Reference Yariv2017.) The dimensionless geometry is portrayed in figure 1(b). It is convenient to label the slats such that the plane passing through the centre of the
$n$
th slat (with
$n\in \mathbb{Z}$
) is
$x=2n\unicode[STIX]{x1D6EC}$
.
We employ
$Gh$
as a temperature unit for defining the dimensionless temperature
$t$
, a function of
$x$
and
$y$
. Since the temperature is defined to within an arbitrary additive constant, we may assume – with no loss of generality – that
$t$
is an odd function of
$x$
. In particular, the externally imposed gradient is represented by the linear macroscopic variation,
$$\begin{eqnarray}t=-x,\end{eqnarray}$$
which applies ‘deep’ within the solid substrate. Assuming long slats, the temperature at the end of the
$n$
th slat (and in particular at the associated solid–liquid interface) is uniform, namely
$$\begin{eqnarray}t\equiv -2n\unicode[STIX]{x1D6EC}.\end{eqnarray}$$
Since the liquid motion is driven by Marangoni stresses at the surfaces, we employ
$-G\unicode[STIX]{x1D70E}_{T}$
as a stress unit (positive in the common case of negative
$\unicode[STIX]{x1D70E}_{T}$
). With the intrinsic length scale in the flow direction being
$l$
, it is natural to use
$-G\unicode[STIX]{x1D70E}_{T}l/\unicode[STIX]{x1D707}$
as the velocity unit. The two-dimensional velocity field is
$\boldsymbol{u}=\hat{\boldsymbol{e}}_{x}u+\hat{\boldsymbol{e}}_{y}v$
, with
$u$
and
$v$
being functions of
$x$
and
$y$
.
Owing to the obvious periodicity of
$\boldsymbol{u}$
, it is sufficient to consider the liquid domain restricted to the unit cell
$|x|<\unicode[STIX]{x1D6EC}$
. Given the symmetry about the mid-plane
$y=1$
, the domain of interest is further restricted to the ‘semi-cell’
$0<y<1$
.
2.2 Thermal problem
Neglecting heat advection, the temperature is governed by Laplace’s equation,
$$\begin{eqnarray}\unicode[STIX]{x1D6FB}^{2}t=0\quad \text{for }-\unicode[STIX]{x1D6EC}<x<\unicode[STIX]{x1D6EC},\quad 0<y<1.\end{eqnarray}$$
At
$y=0$
it satisfies (i) the temperature-continuity condition at the solid–liquid interface, which, upon making use of (2.2) reads
$$\begin{eqnarray}t=0\quad \text{for }|x|<\unicode[STIX]{x1D719}\unicode[STIX]{x1D6EC};\end{eqnarray}$$
and (ii) the no-flux condition at the liquid–air interface,
$$\begin{eqnarray}\frac{\unicode[STIX]{x2202}t}{\unicode[STIX]{x2202}y}=0\quad \text{for }\unicode[STIX]{x1D719}\unicode[STIX]{x1D6EC}<|x|<\unicode[STIX]{x1D6EC}.\end{eqnarray}$$
At
$y=1$
it satisfies the symmetry condition
$$\begin{eqnarray}\frac{\unicode[STIX]{x2202}t}{\unicode[STIX]{x2202}y}=0\quad \text{at }y=1,\end{eqnarray}$$
while at the lateral ends of the semi-cell it satisfies
$$\begin{eqnarray}t=\mp \unicode[STIX]{x1D6EC}\quad \text{at }x=\pm \unicode[STIX]{x1D6EC}\quad \text{for }0<y<1,\end{eqnarray}$$
representing the imposed macroscopic gradient.
It is convenient to define the periodic function
$\unicode[STIX]{x1D703}$
via the relation
$$\begin{eqnarray}t(x,y)=-x+\unicode[STIX]{x1D703}(x,y).\end{eqnarray}$$
With
$t$
being an odd function of
$x$
, so must be
$\unicode[STIX]{x1D703}$
. The ‘excess temperature’
$\unicode[STIX]{x1D703}$
satisfies the same boundary-value problem as
$t$
, with two exceptions: the homogeneous condition (2.4) is replaced by the inhomogeneous condition,
$$\begin{eqnarray}\unicode[STIX]{x1D703}=x\quad \text{for }|x|<\unicode[STIX]{x1D719}\unicode[STIX]{x1D6EC},\end{eqnarray}$$
while the jump condition (2.7) becomes
$$\begin{eqnarray}\unicode[STIX]{x1D703}=0\quad \text{at }x=\pm \unicode[STIX]{x1D6EC}\quad \text{for }0<y<1.\end{eqnarray}$$
With advection being neglected, the thermal problem is uncoupled from the flow problem which we consider next.
2.3 Flow problem
The flow is governed by the continuity equation,
$$\begin{eqnarray}\frac{\unicode[STIX]{x2202}u}{\unicode[STIX]{x2202}x}+\frac{\unicode[STIX]{x2202}v}{\unicode[STIX]{x2202}y}=0,\end{eqnarray}$$
and the Stokes equations,
$$\begin{eqnarray}\frac{\unicode[STIX]{x2202}p}{\unicode[STIX]{x2202}x}=\unicode[STIX]{x1D6FB}^{2}u,\quad \frac{\unicode[STIX]{x2202}p}{\unicode[STIX]{x2202}y}=\unicode[STIX]{x1D6FB}^{2}v,\end{eqnarray}$$
in which
$p$
is the pressure field. At
$y=0$
the flow satisfies impermeability,
$$\begin{eqnarray}v=0.\end{eqnarray}$$
In addition, it satisfies there a no-slip condition at the edge of the solid slat,
$$\begin{eqnarray}u=0\quad \text{for }|x|<\unicode[STIX]{x1D719}\unicode[STIX]{x1D6EC},\end{eqnarray}$$
as well as the Marangoni condition at the liquid–air interfaces,
$$\begin{eqnarray}\frac{\unicode[STIX]{x2202}u}{\unicode[STIX]{x2202}y}=\unicode[STIX]{x1D6EC}^{-1}\frac{\unicode[STIX]{x2202}t}{\unicode[STIX]{x2202}x}=\unicode[STIX]{x1D6EC}^{-1}\left(\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}}{\unicode[STIX]{x2202}x}-1\right)\quad \text{for }\unicode[STIX]{x1D719}\unicode[STIX]{x1D6EC}<|x|<\unicode[STIX]{x1D6EC}.\end{eqnarray}$$
The symmetry about
$y=1$
implies the relations
$$\begin{eqnarray}v=\frac{\unicode[STIX]{x2202}u}{\unicode[STIX]{x2202}y}=0\quad \text{at }y=1.\end{eqnarray}$$
Noting that
$u$
is an even function of
$x$
, while
$v$
is an odd one, the periodicity conditions adopt the form
$$\begin{eqnarray}v=\frac{\unicode[STIX]{x2202}u}{\unicode[STIX]{x2202}x}=0\quad \text{at }x=\pm \unicode[STIX]{x1D6EC}\quad \text{for }0<y<1.\end{eqnarray}$$
The preceding equations are supplemented by the condition of pressure periodicity,
$$\begin{eqnarray}p(x=\unicode[STIX]{x1D6EC},y)=p(x=-\unicode[STIX]{x1D6EC},y)\quad \text{for }0<y<1,\end{eqnarray}$$
representing the absence of a macroscopic pressure gradient. (Note that in the longitudinal problem this absence is reflected in the longitudinal velocity being governed by Laplace’s equation.) The Stokes equation (2.12b
) and the symmetry conditions (2.17) imply that
$p$
is uniform at
$x=\pm \unicode[STIX]{x1D6EC}$
; since it is defined to within an additive constant, we may set it to zero at
$x=0$
with no loss of generality. We conclude that
$p$
is an odd function of
$x$
, whereby (2.18) becomes
$$\begin{eqnarray}p(x=\unicode[STIX]{x1D6EC})=0\quad \text{for }0<y<1.\end{eqnarray}$$
The preceding structure of two consecutive linear problems is reminiscent of classical thermocapillary problems involving drops and bubbles (Young, Goldstein & Block Reference Young, Goldstein and Block1959; Subramanian Reference Subramanian1981). With a vanishing Marangoni number, the dimensionless problem is governed by two geometric parameters, namely the semi-period
$\unicode[STIX]{x1D6EC}=l/h$
and the solid fraction
$\unicode[STIX]{x1D719}$
. Our interest is not in the detailed solution, but rather in the mean velocity,
$$\begin{eqnarray}\bar{u}=\int _{0}^{1}u(x,y)\,\text{d}y,\end{eqnarray}$$
which coincides with (half of) the volumetric flux through the channel (per unit length in the
$z$
-direction), This quantity, which is necessarily independent of
$x$
, can only depend upon
$\unicode[STIX]{x1D6EC}$
and
$\unicode[STIX]{x1D719}$
.
2.4 Integral force balance
Integration of the
$x$
-momentum balance (2.12a
) using the two-dimensional variants of the divergence and gradient theorems yields, upon making use of the pertinent symmetries about
$x=0$
and the homogeneous conditions (2.16)–(2.18),
$$\begin{eqnarray}\int _{-\unicode[STIX]{x1D719}\unicode[STIX]{x1D6EC}}^{\unicode[STIX]{x1D719}\unicode[STIX]{x1D6EC}}\left.\frac{\unicode[STIX]{x2202}u}{\unicode[STIX]{x2202}y}\right|_{y=0}\,\text{d}x+2\int _{\unicode[STIX]{x1D719}\unicode[STIX]{x1D6EC}}^{\unicode[STIX]{x1D6EC}}\left.\frac{\unicode[STIX]{x2202}u}{\unicode[STIX]{x2202}y}\right|_{y=0}\,\text{d}x=0.\end{eqnarray}$$
This relation may be interpreted as an integral force balance (per unit length in the
$z$
-direction) in the
$x$
-direction, where the first and second terms on the left-hand side represent the viscous forces which respectively act on the solid and free-surface portions of the compound boundary, and the nil right-hand side represents the absence of a net hydrodynamic force on the unit cell – a consequence of the absence of external forces. (Recall that the Marangoni forces originate in surface-tension gradients and should accordingly be considered as internal forces.)
Use of (2.15) together with (2.4) and (2.7) thus reveals that
$$\begin{eqnarray}\int _{\unicode[STIX]{x1D719}\unicode[STIX]{x1D6EC}}^{\unicode[STIX]{x1D6EC}}\left.\frac{\unicode[STIX]{x2202}u}{\unicode[STIX]{x2202}y}\right|_{y=0}\,\text{d}x=-1.\end{eqnarray}$$
Substitution into (2.21) then furnishes the integral relation
$$\begin{eqnarray}\int _{-\unicode[STIX]{x1D719}\unicode[STIX]{x1D6EC}}^{\unicode[STIX]{x1D719}\unicode[STIX]{x1D6EC}}\left.\frac{\unicode[STIX]{x2202}u}{\unicode[STIX]{x2202}y}\right|_{y=0}\,\text{d}x=2.\end{eqnarray}$$
Since this relation has been derived from the governing differential equations, it does not provide any independent information. Nonetheless, it comes in handy in resolving the small solid-fraction limit, addressed in § 6, where it is used for both the prediction of asymptotic scaling and the subsequent analysis.
3 General observations
In this section we make two general observations which follow from the problem formulation. We start with the thermal problem, where we identify a surprising analogy with a complementary problem of longitudinal shear-driven flow. We then consider the flow problem, where we obtain an integral representation of
$\bar{u}$
using Lorentz’s reciprocity.
3.1 An analogy with longitudinal shear-driven flow
We begin by embedding the harmonic field
$t(x,y)$
in a complex potential, say
$$\begin{eqnarray}t(x,y)+\text{i}\unicode[STIX]{x1D714}(x,y),\end{eqnarray}$$
wherein
$\unicode[STIX]{x1D714}$
, the harmonic conjugate of
$t$
, is related to
$t$
via the Cauchy–Riemann conditions,
$$\begin{eqnarray}\frac{\unicode[STIX]{x2202}t}{\unicode[STIX]{x2202}x}=\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D714}}{\unicode[STIX]{x2202}y},\quad \frac{\unicode[STIX]{x2202}t}{\unicode[STIX]{x2202}y}=-\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D714}}{\unicode[STIX]{x2202}x}.\end{eqnarray}$$
Making use of these conditions and the boundary conditions (2.4)–(2.7) satisfied by
$t$
we note that the harmonic function
$\unicode[STIX]{x1D714}$
satisfies: (i) the mixed conditions at
$y=0$
,
$$\begin{eqnarray}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D714}}{\unicode[STIX]{x2202}y}=0\quad \text{for }|x|<\unicode[STIX]{x1D719}\unicode[STIX]{x1D6EC},\quad \unicode[STIX]{x1D714}=0\quad \text{for }\unicode[STIX]{x1D719}\unicode[STIX]{x1D6EC}<|x|<\unicode[STIX]{x1D6EC};\end{eqnarray}$$
(ii) the homogeneous Neumann conditions at the periodic boundaries,
$$\begin{eqnarray}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D714}}{\unicode[STIX]{x2202}x}=0\quad \text{at }x=\pm \unicode[STIX]{x1D6EC};\end{eqnarray}$$
and (iii) the Dirichlet condition,
$$\begin{eqnarray}\unicode[STIX]{x1D714}=\text{const.}\quad \text{at }y=1.\end{eqnarray}$$
While
$\unicode[STIX]{x1D714}$
is defined to within an arbitrary additive constant, that freedom has already been exploited in setting the constant to zero in the Dirichlet condition (3.3b
). It follows that the value of the constant appearing in (3.5) cannot be set arbitrarily, implying in turn that an additional constraint is required. To obtain it we note that conditions (3.4), while reflecting the uniform temperature values at
$x=\pm \unicode[STIX]{x1D6EC}$
, do not express the corresponding temperature-jump magnitude, as implied by (2.7). Rewriting (2.7) as
$$\begin{eqnarray}\int _{-\unicode[STIX]{x1D6EC}}^{\unicode[STIX]{x1D6EC}}\frac{\unicode[STIX]{x2202}t}{\unicode[STIX]{x2202}x}\,\text{d}x=-2\unicode[STIX]{x1D6EC},\end{eqnarray}$$
where the integration may be carried out at any value of
$y\in (0,1)$
, and making use of (3.2a
), we obtain the requisite constraint
$$\begin{eqnarray}\int _{-\unicode[STIX]{x1D6EC}}^{\unicode[STIX]{x1D6EC}}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D714}}{\unicode[STIX]{x2202}y}\,\text{d}x=-2\unicode[STIX]{x1D6EC}.\end{eqnarray}$$
It is now readily observed that conditions (3.3)–(3.5) are identical to the boundary conditions governing the unidirectional longitudinal velocity between an ‘interchanged’ boundary, on which the liquid–air interface is at
$|x|<\unicode[STIX]{x1D719}\unicode[STIX]{x1D6EC}$
and the solid slats are at
$\unicode[STIX]{x1D719}\unicode[STIX]{x1D6EC}<x<\unicode[STIX]{x1D6EC}$
, and a solid boundary which moves rigidly in the
$z$
-direction. Constraint (3.7), which represents a force per unit area of unit magnitude which acts on the latter boundary in the negative
$z$
-direction, uniquely determines that problem. Since that unidirectional field is also governed by Laplace’s equation, we have a perfect analogy. (The spirit of this analogy is reminiscent of a similar observation due to Hasimoto (Reference Hasimoto1958).)
The solution to the problem governing
$\unicode[STIX]{x1D714}$
is derived in § 8 of Philip (Reference Philip1972a
), where the complex potential is provided in terms of the Jacobian elliptic functions. The associated force per unit area is provided in § 3.5 of Philip (Reference Philip1972b
).
3.2 An integral representation of
$\bar{u}$
Consider now the flow problem, as specified by (2.11)–(2.17) and (2.19). The only inhomogeneous equation in that problem is the Marangoni condition (2.15), which is conveniently written
$$\begin{eqnarray}\frac{\unicode[STIX]{x2202}u}{\unicode[STIX]{x2202}y}=\unicode[STIX]{x1D6EC}^{-1}\frac{\text{d}t(x,0)}{\text{d}x}\quad \text{for }\unicode[STIX]{x1D719}\unicode[STIX]{x1D6EC}<|x|<\unicode[STIX]{x1D6EC}.\end{eqnarray}$$
The problem linearity then implies that the flow variables are linear functionals of (the
$x$
-derivative of)
$t(x,0)$
, as evaluated for
$\unicode[STIX]{x1D719}\unicode[STIX]{x1D6EC}<|x|<\unicode[STIX]{x1D6EC}$
. It then follows from (2.20) that the same is true for the flux
$\bar{u}$
, which is the quantity of interest.
Making use of Lorentz reciprocity (Happel & Brenner Reference Happel and Brenner1965), the requisite functional representation may be obtained without the need to solve the flow problem. To this end, we employ two velocity fields, namely the present field
$\boldsymbol{u}=\hat{\boldsymbol{e}}_{x}u+\hat{\boldsymbol{e}}_{y}v$
and an auxiliary field
$\tilde{\boldsymbol{u}}=\hat{\boldsymbol{e}}_{x}\tilde{u} +\hat{\boldsymbol{e}}_{y}\tilde{v}$
. Denoting the respective stress fields by
$\unicode[STIX]{x1D748}$
and
$\tilde{\unicode[STIX]{x1D748}}$
, the Lorentz reciprocal theorem reads
$$\begin{eqnarray}\oint \text{d}a\,\hat{\boldsymbol{n}}\boldsymbol{\cdot }\unicode[STIX]{x1D748}\boldsymbol{\cdot }\tilde{\boldsymbol{u}}=\oint \text{d}a\,\hat{\boldsymbol{n}}\boldsymbol{\cdot }\tilde{\unicode[STIX]{x1D748}}\boldsymbol{\cdot }\boldsymbol{u},\end{eqnarray}$$
wherein
$\text{d}a$
is a differential area element, normalised by
$h^{2}$
,
$\hat{\boldsymbol{n}}$
is an outward-pointing unit vector, and the integration is carried over a rectangular box, constructed by translating the semi-cell (
$-\unicode[STIX]{x1D6EC}<x<\unicode[STIX]{x1D6EC}$
,
$0<y<1$
) by a unit length in the
$z$
-direction.
We take
$\tilde{\boldsymbol{u}}$
as a pressure-driven flow which would exist in a channel which is bounded by two superhydrophobic walls, one at
$y=0$
and one at
$y=2$
. It is governed by a problem of the form (2.11)–(2.18), with the Marangoni condition (2.15) being replaced by the shear-free condition
$$\begin{eqnarray}\frac{\unicode[STIX]{x2202}\tilde{u} }{\unicode[STIX]{x2202}y}=0\quad \text{for }\unicode[STIX]{x1D719}\unicode[STIX]{x1D6EC}<|x|<\unicode[STIX]{x1D6EC}\end{eqnarray}$$
and condition (2.18) replaced by
$$\begin{eqnarray}\tilde{p}(x=-\unicode[STIX]{x1D6EC},y)-\tilde{p}(x=\unicode[STIX]{x1D6EC},y)=2\unicode[STIX]{x1D6EC}\quad \text{for }0<y<1.\end{eqnarray}$$
With the fields
$\boldsymbol{u}$
and
$\tilde{\boldsymbol{u}}$
depending only upon
$x$
and
$y$
, the contributions to (3.9) from the ‘front’ and ‘back’ sides, parallel to the
$xy$
-plane, trivially vanish. Given the periodicity conditions, the contributions from the ‘side walls’
$x=\pm \unicode[STIX]{x1D6EC}$
to the left-hand side of (3.9) also vanish. On the other hand, the pressure-jump condition (3.11) implies that the side walls make a non-zero contribution to the right-hand side of (3.9); making use of definition (2.20), that contribution is readily seen to be given by
$2\unicode[STIX]{x1D6EC}\bar{u}$
.
All that remain are the contributions from the ‘bottom’ (
$y=0$
) and ‘top’ (
$y=1$
) sides. Making use of the boundary conditions at
$y=0$
and
$y=1$
it is readily seen that these sides do not contribute to the right-hand side of (3.9). When considering the left-hand side of (3.9) we similarly find that the top side does not contribute, but that the bottom side does contribute. Making use of (3.8) and noting the vanishing of
$\tilde{u}$
at the solid edge, the latter contribution is
$$\begin{eqnarray}-2\unicode[STIX]{x1D6EC}^{-1}\int _{\unicode[STIX]{x1D719}\unicode[STIX]{x1D6EC}}^{\unicode[STIX]{x1D6EC}}\frac{\text{d}t(x,0)}{\text{d}x}\tilde{u} (x,0)\,\text{d}x.\end{eqnarray}$$
We conclude that
$$\begin{eqnarray}\bar{u}=-\unicode[STIX]{x1D6EC}^{-2}\int _{\unicode[STIX]{x1D719}\unicode[STIX]{x1D6EC}}^{\unicode[STIX]{x1D6EC}}\frac{\text{d}t(x,0)}{\text{d}x}\tilde{u} (x,0)\,\text{d}x.\end{eqnarray}$$
To evaluate
$\bar{u}$
using representation (3.13) it is required to have both
$t(x,0)$
and
$\tilde{u} (x,0)$
available. As explained in § 3.1, the field
$t$
may be obtained using the complex potential obtained in § 8 of Philip (Reference Philip1972a
). We are not aware of any closed-form representation of the field
$\tilde{\boldsymbol{u}}$
, but semi-numerical solutions have been obtained using Fourier-series expansions (Teo & Khoo Reference Teo and Khoo2009). In principle, one may substitute these solutions into (3.13) to evaluate
$\bar{u}$
for any numerical values of
$\unicode[STIX]{x1D6EC}$
and
$\unicode[STIX]{x1D719}$
.
In what follows, we supplement (3.13) with asymptotic approximations for
$\bar{u}$
, obtained in three different geometric limits.
4 Deep channels
We consider first the deep-channel limit,
$\unicode[STIX]{x1D6EC}\ll 1$
. It is clear that the spatial variations of the excess temperature and flow are confined to a region of
$O(\unicode[STIX]{x1D6EC})$
depth about the boundary
$y=0$
(with a mirror-image region about
$y=2$
). The periodicity conditions (2.10) imply that the excess temperature must decay to zero outside these regions. As is evident from the symmetry conditions (2.16), so does the velocity component
$v$
. On the other hand, the latter conditions allow there for a non-zero uniform value of
$u$
, say
$u_{\infty }$
:
$$\begin{eqnarray}u\sim u_{\infty }+\cdots \quad \text{for }y\gg \unicode[STIX]{x1D6EC}.\end{eqnarray}$$
To obtain the ‘slip’ velocity
$u_{\infty }$
we consider in detail the near-boundary region about
$y=0$
. Towards this end, we employ the stretched coordinates,
$$\begin{eqnarray}X=\frac{x}{\unicode[STIX]{x1D6EC}},\quad Y=\frac{y}{\unicode[STIX]{x1D6EC}},\end{eqnarray}$$
representing non-dimensionalisation by
$l$
. In terms of these coordinates, the near-boundary region appears at leading order as the semi-strip
${\mathcal{D}}=\{(X,Y)|-1<X<1,Y>0\}$
. The problem has accordingly been reduced to heat transport and flow about a single compound surface. Of course, it follows from definition (2.20) that
$u_{\infty }$
provides a leading-order approximation for the mean velocity,
$$\begin{eqnarray}\lim _{\unicode[STIX]{x1D6EC}\rightarrow 0}\bar{u}=u_{\infty }.\end{eqnarray}$$
4.1 Thermal problem
Consider first the thermal problem in the near-boundary region. Since
$t$
varies by an
$O(\unicode[STIX]{x1D6EC})$
amount between
$X=\pm 1$
, we postulate the asymptotic expansion
$$\begin{eqnarray}t=\unicode[STIX]{x1D6EC}T(X,Y)+\cdots \,.\end{eqnarray}$$
Note that
$T$
represents non-dimensionalisation by
$Gl$
. This rescaled temperature satisfies Laplace’s equation in liquid domain,
$$\begin{eqnarray}\frac{\unicode[STIX]{x2202}^{2}T}{\unicode[STIX]{x2202}X^{2}}+\frac{\unicode[STIX]{x2202}^{2}T}{\unicode[STIX]{x2202}Y^{2}}=0\quad \text{in }{\mathcal{D}}.\end{eqnarray}$$
At
$Y=0$
it satisfies the homogeneous Dirichlet condition at the solid–liquid interface,
$$\begin{eqnarray}T=0\quad \text{for }|X|<\unicode[STIX]{x1D719},\end{eqnarray}$$
together with the no-flux condition at the liquid–gas interfaces,
$$\begin{eqnarray}\frac{\unicode[STIX]{x2202}T}{\unicode[STIX]{x2202}Y}=0\quad \text{for }\unicode[STIX]{x1D719}<|X|<1.\end{eqnarray}$$
As
$Y\rightarrow \infty$
it satisfies
$$\begin{eqnarray}T\rightarrow -X\quad \text{as }Y\rightarrow \infty ,\end{eqnarray}$$
while at
$X=\pm 1$
is satisfies the jump conditions
$$\begin{eqnarray}T=\mp 1\quad \text{at }X=\pm 1.\end{eqnarray}$$
4.2 Flow problem
It follows from (2.15) and (4.4) that
$u$
is
$O(1)$
in the near-boundary region. The continuity equation (2.11) then implies that so must be
$v$
, while the Stokes equations (2.12) suggest
$O(\unicode[STIX]{x1D6EC}^{-1})$
pressure variations. We accordingly employ the expansions,
$$\begin{eqnarray}u=U(X,Y)+\cdots \,,\quad v=V(X,Y)+\cdots \,,\quad p=\unicode[STIX]{x1D6EC}^{-1}P(X,Y)+\cdots \,.\end{eqnarray}$$
The leading-order flow is governed by the continuity and Stokes equations,
$$\begin{eqnarray}\frac{\unicode[STIX]{x2202}U}{\unicode[STIX]{x2202}X}+\frac{\unicode[STIX]{x2202}V}{\unicode[STIX]{x2202}Y}=0,\quad \frac{\unicode[STIX]{x2202}P}{\unicode[STIX]{x2202}X}=\frac{\unicode[STIX]{x2202}^{2}U}{\unicode[STIX]{x2202}X^{2}}+\frac{\unicode[STIX]{x2202}^{2}U}{\unicode[STIX]{x2202}Y^{2}},\quad \frac{\unicode[STIX]{x2202}P}{\unicode[STIX]{x2202}Y}=\frac{\unicode[STIX]{x2202}^{2}V}{\unicode[STIX]{x2202}X^{2}}+\frac{\unicode[STIX]{x2202}^{2}V}{\unicode[STIX]{x2202}Y^{2}}.\end{eqnarray}$$
At
$Y=0$
it satisfies the impermeability condition,
$$\begin{eqnarray}V=0\quad \text{at }Y=0;\end{eqnarray}$$
in addition, it satisfies a no-slip condition at the edge of the solid slats,
$$\begin{eqnarray}U=0\quad \text{for }|X|<\unicode[STIX]{x1D719},\end{eqnarray}$$
as well as the Marangoni condition at the liquid–air interfaces,
$$\begin{eqnarray}\frac{\unicode[STIX]{x2202}U}{\unicode[STIX]{x2202}Y}=\frac{\unicode[STIX]{x2202}T}{\unicode[STIX]{x2202}X}\quad \text{for }\unicode[STIX]{x1D719}<|X|<1.\end{eqnarray}$$
At
$X=\pm 1$
it satisfies the periodicity conditions,
$$\begin{eqnarray}V=\frac{\unicode[STIX]{x2202}U}{\unicode[STIX]{x2202}X}=0\quad \text{at }X=\pm 1.\end{eqnarray}$$
Finally, it satisfies the pressure-periodicity conditions,
$$\begin{eqnarray}P(X=1)=P(X=-1)\quad \text{for }Y>0,\end{eqnarray}$$
and the condition
$$\begin{eqnarray}\lim _{Y\rightarrow \infty }\frac{\unicode[STIX]{x2202}U}{\unicode[STIX]{x2202}Y}=0,\end{eqnarray}$$
reflecting the necessary matching with a uniform flow.
Since
$v$
vanishes outside the near-boundary region, the following decay condition applies,
$$\begin{eqnarray}\lim _{Y\rightarrow \infty }V=0.\end{eqnarray}$$
On the other hand, (4.1) implies
$$\begin{eqnarray}\lim _{Y\rightarrow \infty }U=u_{\infty }.\end{eqnarray}$$
Finally, note that in terms of the near-boundary variables, the integral balance (2.23) reads
$$\begin{eqnarray}\int _{-\unicode[STIX]{x1D719}}^{\unicode[STIX]{x1D719}}\left.\frac{\unicode[STIX]{x2202}U}{\unicode[STIX]{x2202}Y}\right|_{Y=0}\,\text{d}X=2.\end{eqnarray}$$
4.3 Lorentz’s reciprocity
The only inhomogeneous equation in the problem (4.11)–(4.17) governing the near-boundary flow is the Marangoni condition (4.14), which is conveniently written
$$\begin{eqnarray}\frac{\unicode[STIX]{x2202}U}{\unicode[STIX]{x2202}Y}=\frac{\text{d}T(X,0)}{\text{d}X}\quad \text{for }\unicode[STIX]{x1D719}<|X|<1.\end{eqnarray}$$
The problem linearity then implies that the flow variables are linear functionals of (the
$X$
-derivative of)
$T(X,0)$
. It then follows from (4.19) that the same is true for
$u_{\infty }$
, which is the quantity of interest.
In principle, one may obtain the functional representation of
$u_{\infty }$
by degenerating representation (3.13), obtained using Lorentz’s reciprocity, in the deep-channel limit. However, since we do not have available a closed-form expression for
$\tilde{\boldsymbol{u}}$
in the above representation, we prefer to employ Lorentz’s reciprocity directly in the near-boundary problem.
As in the derivation of the general representation (3.13), we employ two velocity fields, namely the present field
$\boldsymbol{U}=\hat{\boldsymbol{e}}_{x}U+\hat{\boldsymbol{e}}_{y}V$
and an auxiliary field
$\tilde{\boldsymbol{U}}=\hat{\boldsymbol{e}}_{x}\tilde{U} +\hat{\boldsymbol{e}}_{y}\tilde{V}$
. Denoting the respective stress fields by
$\unicode[STIX]{x1D72E}$
and
$\tilde{\unicode[STIX]{x1D72E}}$
, the Lorentz reciprocal theorem reads
$$\begin{eqnarray}\oint \text{d}A\,\hat{\boldsymbol{n}}\boldsymbol{\cdot }\unicode[STIX]{x1D72E}\boldsymbol{\cdot }\tilde{\boldsymbol{U}}=\oint \text{d}A\,\hat{\boldsymbol{n}}\boldsymbol{\cdot }\tilde{\unicode[STIX]{x1D72E}}\boldsymbol{\cdot }\boldsymbol{U},\end{eqnarray}$$
wherein
$\text{d}A$
is a differential area element, normalised by
$l^{2}$
, the integration is carried over a closed surface whose interior lies entirely in the liquid domain, and
$\hat{\boldsymbol{n}}$
is an outward-pointing unit vector. We choose the integration surface as the boundary of a rectangular box, constructed by translating the rectangle
$\{(X,Y)|-1<X<1,0<Y<Y_{\infty }\}$
a unit length in the
$z$
-direction. In the above,
$Y_{\infty }>0$
is arbitrary.
We take
$\tilde{\boldsymbol{U}}$
as the velocity field due to applied shear, in the absence of any thermocapillary effects. It is governed by a problem of the form (4.11)–(4.17), with the Marangoni condition (4.14) being replaced by the shear-free condition
$$\begin{eqnarray}\frac{\unicode[STIX]{x2202}\tilde{U} }{\unicode[STIX]{x2202}Y}=0\quad \text{for }\unicode[STIX]{x1D719}<|X|<1\end{eqnarray}$$
and the matching condition (4.17) being replaced by the imposed-shear condition
$$\begin{eqnarray}\tilde{U} \sim Y\quad \text{as }Y\rightarrow \infty .\end{eqnarray}$$
This large-
$Y$
linear variation represents the leading-order term in a large-
$Y$
asymptotic expansion. In particular, this term is followed by a constant term, namely the ‘slip length’
$\unicode[STIX]{x1D6FD}$
:
$$\begin{eqnarray}\lim _{Y\rightarrow \infty }\{\tilde{U} -Y\}=\unicode[STIX]{x1D6FD}.\end{eqnarray}$$
With the chosen fields
$\boldsymbol{U}$
and
$\tilde{\boldsymbol{U}}$
, which depend only upon
$X$
and
$Y$
, the contribution from the ‘front’ and ‘back’ sides, parallel to the
$XY$
-plane, trivially vanishes. Given the periodicity conditions, the contributions from the ‘side walls’
$X=\pm 1$
also vanish. All that remain are the contributions from the ‘bottom’ (
$Y=0$
) and ‘top’ (
$Y=Y_{\infty }$
) sides. Forming the limit
$Y_{\infty }\rightarrow \infty$
we consider first the left-hand side of (4.22). Making use of (4.17) and (4.24) we find that the top side does not contribute. The only remaining contribution is from the bottom side, which, given the vanishing of
$\tilde{U}$
at the solid edge, is
$$\begin{eqnarray}-2\int _{\unicode[STIX]{x1D719}}^{1}\frac{\text{d}T(X,0)}{\text{d}X}\tilde{U} (X,0)\,\text{d}X.\end{eqnarray}$$
Similarly, considering the right-hand side of (4.22) in the same limit we find from (4.13) and (4.23) that the bottom side does not contribute. The only remaining contribution is from the top side; upon making use of (4.19) and (4.24), we find that contribution to be
$2u_{\infty }$
. We conclude that
$$\begin{eqnarray}u_{\infty }=-\int _{\unicode[STIX]{x1D719}}^{1}\frac{\text{d}T(X,0)}{\text{d}X}\tilde{U} (X,0)\,\text{d}X.\end{eqnarray}$$
4.4 Complex potential
Representation (4.27) constitutes the transverse counterpart of the original representation of Baier et al. (Reference Baier, Steffes and Hardt2010), derived in the longitudinal problem. In that problem the longitudinal temperature gradient is uniform, so the associated quadrature may be readily evaluated. This is not the case in the present problem, where evaluation of the quadrature appearing in (4.27) requires detailed knowledge of
$T(X,0)$
. This obstacle has led Baier et al. (Reference Baier, Steffes and Hardt2010) to solve the transverse problem using numerical simulations.
In § 3.1 we have identified an analogy between the harmonic conjugate of the temperature field and a complementary pressure-driven problem. In principle, one may obtain
$T$
by using that analogy and degenerating it to the deep-channel limit. Given the complexity of the expression provided by Philip (Reference Philip1972a
), however, we elect here to identify a direct analogy in context of the near-boundary problem. That analogy makes use of a complementary shear-driven problem.
We begin by embedding the harmonic field
$T(X,Y)$
in a complex potential, say
$$\begin{eqnarray}G(Z)=T(X,Y)+\text{i}\unicode[STIX]{x1D6FA}(X,Y),\end{eqnarray}$$
wherein
$Z=X+\text{i}Y$
and
$\unicode[STIX]{x1D6FA}$
is the harmonic conjugate of
$T$
(cf. (3.1)). Making use of the Cauchy–Riemann conditions and the boundary conditions (4.6)–(4.9) satisfied by
$T$
we note that the harmonic function
$\unicode[STIX]{x1D6FA}$
satisfies: (i) the mixed conditions at
$Y=0$
,
$$\begin{eqnarray}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}}{\unicode[STIX]{x2202}Y}=0\quad \text{for }|X|<\unicode[STIX]{x1D719},\quad \unicode[STIX]{x1D6FA}=D\quad \text{for }\unicode[STIX]{x1D719}<|X|<1,\end{eqnarray}$$
wherein
$D$
is a constant; (ii) the homogeneous Neumann conditions at the periodic boundaries,
$$\begin{eqnarray}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FA}}{\unicode[STIX]{x2202}X}=0\quad \text{at }X=\pm 1;\end{eqnarray}$$
and (iii) the far-field condition,
$$\begin{eqnarray}\unicode[STIX]{x1D6FA}\sim -Y\quad \text{as }Y\rightarrow \infty .\end{eqnarray}$$
Since
$\unicode[STIX]{x1D6FA}$
is defined to within an arbitrary additive constant, we may set
$D=0$
; this does not affect the remaining conditions. It is now readily observed that the above problem, governing the temperature field due to transverse gradient, is analogous to the problem of shear-driven longitudinal velocity over an ‘interchanged’ boundary on which the liquid–air interface is at
$|X|<\unicode[STIX]{x1D719}$
while the solid slats are at
$\unicode[STIX]{x1D719}<|X|<1$
.
The solution to that problem is provided in § 5 of Philip (Reference Philip1972a ), where the velocity is represented as the imaginary part of a complex potential; in the present notation, this potential is
$$\begin{eqnarray}-\frac{2}{\unicode[STIX]{x03C0}}\cos ^{-1}\frac{\cos (\unicode[STIX]{x03C0}Z/2)}{\cos (\unicode[STIX]{x03C0}\unicode[STIX]{x1D719}/2)},\end{eqnarray}$$
for which the inverse cosine is defined such that
$X$
and the real part of the potential increase together from
$-1$
to
$1$
. (Note that the problem was also solved by Crowdy Reference Crowdy2011 using a method which avoids the branch points associated with Philip’s solution.) Expression (4.32) accordingly provides
$G(Z)$
, up to a possible addition of a real constant. Inspection reveals that no such addition is necessary. Considering (4.27), we actually need the temperature at the free-surface portions of
$Y=0$
. Forming the real part of (4.32) we obtain
$$\begin{eqnarray}T(X,0)=-\frac{2\operatorname{sgn}\{X\}}{\unicode[STIX]{x03C0}}\cos ^{-1}\frac{\cos (\unicode[STIX]{x03C0}X/2)}{\cos (\unicode[STIX]{x03C0}\unicode[STIX]{x1D719}/2)}\quad \text{for }\unicode[STIX]{x1D719}<|X|<1.\end{eqnarray}$$
This expression varies from
$0$
at
$|X|=\unicode[STIX]{x1D719}$
to
$\pm 1$
at
$X=\pm 1$
, as required.
4.5 Calculation of
$u_{\infty }$
: approximate and exact solutions
With
$T(X,0)$
determined, all that is required for the calculation of
$u_{\infty }$
using (4.27) is
$\tilde{U} (X,0)$
. The field
$\tilde{\boldsymbol{U}}$
, as specified after (4.22), was calculated in § 11 of Philip (Reference Philip1972a
). In particular, Philip (Reference Philip1972a
) provides the velocity at the liquid–air interfaces,
$$\begin{eqnarray}\tilde{U} (X,0)=\frac{1}{\unicode[STIX]{x03C0}}\cosh ^{-1}\frac{\sin (\unicode[STIX]{x03C0}X/2)}{\sin (\unicode[STIX]{x03C0}\unicode[STIX]{x1D719}/2)}\quad \text{for }\unicode[STIX]{x1D719}<|X|<1.\end{eqnarray}$$
(Note the error in (11.2) of Philip (Reference Philip1972a
), where
$a$
should be replaced by
$a^{2}$
.) Substitution of (4.33)–(4.34) into (4.27) yields the requisite integral representation of
$u_{\infty }$
,
$$\begin{eqnarray}u_{\infty }=\frac{1}{\unicode[STIX]{x03C0}}\int _{\unicode[STIX]{x1D719}}^{1}\frac{\sin (\unicode[STIX]{x03C0}X/2)}{\sqrt{\cos ^{2}(\unicode[STIX]{x03C0}\unicode[STIX]{x1D719}/2)-\cos ^{2}(\unicode[STIX]{x03C0}X/2)}}\cosh ^{-1}\frac{\sin (\unicode[STIX]{x03C0}X/2)}{\sin (\unicode[STIX]{x03C0}\unicode[STIX]{x1D719}/2)}\,\text{d}X.\end{eqnarray}$$
The quadrature (4.35) may be evaluated numerically for any value of
$\unicode[STIX]{x1D719}$
. The resulting variation of
$u_{\infty }$
with
$\unicode[STIX]{x1D719}$
is portrayed in figure 2.
The preceding calculation of
$u_{\infty }$
may be supplemented by approximate evaluations of the quadrature (4.27). Consider first the limit of small gas fraction,
$\unicode[STIX]{x1D6E5}=1-\unicode[STIX]{x1D719}\ll 1$
. Defining the scaled coordinate
$$\begin{eqnarray}\hat{x}=\frac{1-X}{\unicode[STIX]{x1D6E5}}\end{eqnarray}$$
the representation (4.27) becomes
$$\begin{eqnarray}u_{\infty }=\int _{0}^{1}\tilde{U} (1-\hat{x}\unicode[STIX]{x1D6E5},0)\frac{\text{d}}{\text{d}\hat{x}}T(1-\hat{x}\unicode[STIX]{x1D6E5},0)\,\text{d}\hat{x}.\end{eqnarray}$$
For
$\unicode[STIX]{x1D6E5}\ll 1$
and
$\hat{x}=O(1)$
we readily obtain from (4.33) and (4.34)
$$\begin{eqnarray}T(1-\hat{x}\unicode[STIX]{x1D6E5},0)\sim -\frac{2}{\unicode[STIX]{x03C0}}\cos ^{-1}\hat{x},\quad \tilde{U} (1-\hat{x}\unicode[STIX]{x1D6E5},0)\sim \unicode[STIX]{x1D6E5}\frac{(1-\hat{x}^{2})^{1/2}}{2}.\end{eqnarray}$$
Substitution into (4.43) yields
$$\begin{eqnarray}u_{\infty }\sim \frac{\unicode[STIX]{x1D6E5}}{\unicode[STIX]{x03C0}}\quad \text{for }\unicode[STIX]{x1D6E5}\ll 1.\end{eqnarray}$$
The second limit we consider is that of small solid fractions,
$\unicode[STIX]{x1D719}\ll 1$
, for which (4.33) gives
$T(X,0)\rightarrow -X$
. Substitution into (4.27) implies that
$u_{\infty }$
is given by the asymptotic limit of
$$\begin{eqnarray}\int _{\unicode[STIX]{x1D719}}^{1}\tilde{U} (X,0)\,\text{d}X\end{eqnarray}$$
as
$\unicode[STIX]{x1D719}\rightarrow 0$
. The representation (4.40) is reminiscent to that encountered in the longitudinal problem, where the temperature variation is linear. Following Baier et al. (Reference Baier, Steffes and Hardt2010), the integral (4.40) may be evaluated using, again, Lorentz reciprocity, with the first flow field being
$\tilde{\boldsymbol{U}}-Y\hat{\boldsymbol{e}}_{x}$
and the second one being the simple Couette flow
$Y\hat{\boldsymbol{e}}_{x}$
. Noting from (4.25) that the first field approaches the uniform velocity
$\unicode[STIX]{x1D6FD}\hat{\boldsymbol{e}}_{x}$
at large
$Y$
, with the accompanying stress field decaying there, we find that
$$\begin{eqnarray}\int _{\unicode[STIX]{x1D719}}^{1}\tilde{U} (X,0)\,\text{d}X=\unicode[STIX]{x1D6FD}.\end{eqnarray}$$
(Note that this relation holds for all
$\unicode[STIX]{x1D719}$
-values.) The value of
$\unicode[STIX]{x1D6FD}$
for the transverse flow problem calculated by Philip (Reference Philip1972a
) was determined by Lauga & Stone (Reference Lauga and Stone2003) as
$$\begin{eqnarray}\unicode[STIX]{x1D6FD}=-\frac{1}{\unicode[STIX]{x03C0}}\ln \sin \frac{\unicode[STIX]{x03C0}\unicode[STIX]{x1D719}}{2};\end{eqnarray}$$
Substitution into (4.40) of (4.41)–(4.42) gives
$$\begin{eqnarray}u_{\infty }\sim \frac{1}{\unicode[STIX]{x03C0}}\ln \frac{2}{\unicode[STIX]{x03C0}\unicode[STIX]{x1D719}}+o(1)\quad \text{for }\unicode[STIX]{x1D719}\ll 1.\end{eqnarray}$$
Approximations (4.39) are (4.43) are portrayed in figure 2. The agreement with the exact solution is evident.
5 Shallow channels
Consider the opposite limit of shallow channels,
$\unicode[STIX]{x1D6EC}\gg 1$
. Since variations of
$x$
in the unit cell are
$O(\unicode[STIX]{x1D6EC})$
, it is natural to handle this limit using the stretched coordinate
$\grave{x}=x/\unicode[STIX]{x1D6EC}$
. This coordinate is appropriate to describe the temperature profile in the ‘solid-boundary region’, where
$|x|<\unicode[STIX]{x1D719}\unicode[STIX]{x1D6EC}$
, and the ‘free-boundary region’, where
$\unicode[STIX]{x1D719}\unicode[STIX]{x1D6EC}<|x|<\unicode[STIX]{x1D6EC}$
. It is inadequate in two transition regions about
$x=\pm \unicode[STIX]{x1D719}\unicode[STIX]{x1D6EC}$
. However, since the extent of these regions in the
$x$
-direction is
$\ll \unicode[STIX]{x1D6EC}$
, they do not affect the leading-order results. In addition, it is convenient to employ here shifted coordinate
$\grave{y} =y-1$
, whereby the symmetry plane becomes
$\grave{y} =0$
. (Note the difference between
$(\grave{x},\grave{y} )$
and the scaled coordinates (4.2).)
Considering first the thermal problem, it follows from (2.9) that
$\unicode[STIX]{x1D703}$
is
$O(\unicode[STIX]{x1D6EC})$
large. We accordingly postulate the asymptotic expansion
$$\begin{eqnarray}\unicode[STIX]{x1D703}=\unicode[STIX]{x1D6EC}[\grave{\unicode[STIX]{x1D703}}_{0}(\grave{x},\grave{y} )+\unicode[STIX]{x1D6EC}^{-1}\grave{\unicode[STIX]{x1D703}}_{1}(\grave{x},\grave{y} )+\unicode[STIX]{x1D6EC}^{-2}\grave{\unicode[STIX]{x1D703}}_{2}(\grave{x},\grave{y} )+\cdots ]\end{eqnarray}$$
in both the solid-boundary region
$|\grave{x}|<\unicode[STIX]{x1D719}$
and the free-boundary region
$\unicode[STIX]{x1D719}<|\grave{x}|<1$
.
In the solid-boundary region, Laplace’s equation (2.3) gives at leading order
$$\begin{eqnarray}\frac{\unicode[STIX]{x2202}^{2}\grave{\unicode[STIX]{x1D703}}_{0}}{\unicode[STIX]{x2202}\grave{y} ^{2}}=0,\end{eqnarray}$$
implying that
$$\begin{eqnarray}\grave{\unicode[STIX]{x1D703}}_{0}=A(\grave{x})\grave{y} +B(\grave{x}).\end{eqnarray}$$
With the symmetry condition (2.6) giving
$A=0$
, it follows from the Dirichlet condition (2.9) that
$$\begin{eqnarray}\grave{\unicode[STIX]{x1D703}}_{0}=\grave{x}.\end{eqnarray}$$
Repeating the same process in the free-boundary region, we find there that both
$\grave{\unicode[STIX]{x1D703}}_{0}$
and
$\grave{\unicode[STIX]{x1D703}}_{1}$
are functions of
$\grave{x}$
alone, say
$\grave{\unicode[STIX]{x1D703}}_{0}(\grave{x})$
and
$\grave{\unicode[STIX]{x1D703}}_{1}(\grave{x})$
. These functions are not determined by the Neumann condition (2.5). Consider now Laplace’s equation (2.3) at
$O(\unicode[STIX]{x1D6EC}^{3})$
,
$$\begin{eqnarray}\frac{\text{d}^{2}\grave{\unicode[STIX]{x1D703}}_{0}}{\text{d}\grave{x}^{2}}+\frac{\unicode[STIX]{x2202}^{2}\grave{\unicode[STIX]{x1D703}}_{2}}{\unicode[STIX]{x2202}\grave{y} ^{2}}=0.\end{eqnarray}$$
Integration from
$\grave{y} =-1$
to
$\grave{y} =0$
in conjunction with the homogeneous conditions (2.5)–(2.6) gives
$$\begin{eqnarray}\frac{\text{d}^{2}\grave{\unicode[STIX]{x1D703}}_{0}}{\text{d}\grave{x}^{2}}=0,\end{eqnarray}$$
implying a variation of the form
$M\grave{x}+N$
. Making use of the periodicity conditions (2.10) in conjunction with the requisite continuity at
$\grave{x}=\pm \unicode[STIX]{x1D719}$
readily provides
$M$
and
$N$
. Summarising, aside from the narrow transition region about
$\grave{x}=\unicode[STIX]{x1D719}$
we have, for
$\grave{x}>0$
, the piecewise linear distribution,
$$\begin{eqnarray}\grave{\unicode[STIX]{x1D703}}_{0}=\left\{\begin{array}{@{}ll@{}}\grave{x}, & 0<\grave{x}<\unicode[STIX]{x1D719},\\ \displaystyle \unicode[STIX]{x1D719}\frac{1-\grave{x}}{1-\unicode[STIX]{x1D719}}, & \unicode[STIX]{x1D719}<\grave{x}<1.\end{array}\right.\end{eqnarray}$$
Since
$\unicode[STIX]{x1D703}$
is an odd function of
$x$
, the corresponding distribution at negative
$\grave{x}$
readily follows.
Consider now the flow problem. With the
$O(\unicode[STIX]{x1D6EC})$
scaling of
$x$
and
$\unicode[STIX]{x1D703}$
, the Marangoni condition (2.15) implies that
$u$
is
$O(\unicode[STIX]{x1D6EC}^{-1})$
small, thus suggesting the expansion
$$\begin{eqnarray}u=\unicode[STIX]{x1D6EC}^{-1}\grave{u} (\grave{x},\grave{y} )+\cdots\end{eqnarray}$$
in both the solid- and free-boundary regions. The scaling (5.8) corresponds to non-dimensionalisation of the velocity field by
$-G\unicode[STIX]{x1D70E}_{T}h/\unicode[STIX]{x1D707}$
, which is indeed the relevant scale for shallow channels.
With
$y$
-derivatives being much larger than
$x$
-derivatives, the Stokes equations lead to the familiar lubrication structure, with an
$O(1)$
pressure that is independent of
$\grave{y}$
,
$$\begin{eqnarray}p=\grave{p}(\grave{x})+\cdots \,.\end{eqnarray}$$
The Stokes equation in the
$x$
-direction in conjunction with the symmetry condition (2.16) then gives
$$\begin{eqnarray}\grave{u} =\frac{1}{2}\frac{\text{d}\grave{p}}{\text{d}\grave{x}}(\grave{y} ^{2}-1)+C(\grave{x}).\end{eqnarray}$$
The boundary conditions (2.14)–(2.15) necessitate that both
$\text{d}\grave{p}/\text{d}\grave{x}$
and
$C$
are piecewise uniform. We accordingly obtain the discontinuous Poiseuille profile
$$\begin{eqnarray}\grave{u} =\left\{\begin{array}{@{}ll@{}}\frac{1}{2}G_{s}(1-\grave{y} ^{2})+C_{s}, & |\grave{x}|<\unicode[STIX]{x1D719},\\[4.0pt] \frac{1}{2}G_{f}(1-\grave{y} ^{2})+C_{f}, & \unicode[STIX]{x1D719}<|\grave{x}|<1,\end{array}\right.\end{eqnarray}$$
where the no-slip condition (2.14) implies that
$C_{s}=0$
and the Marangoni condition (2.15) gives
$$\begin{eqnarray}G_{f}=-\frac{1}{1-\unicode[STIX]{x1D719}}.\end{eqnarray}$$
The absence (2.18) of macroscopic pressure reads at leading order,
$$\begin{eqnarray}\unicode[STIX]{x1D719}G_{s}+(1-\unicode[STIX]{x1D719})G_{f}=0,\end{eqnarray}$$
from which we conclude that
$$\begin{eqnarray}G_{s}=1/\unicode[STIX]{x1D719}.\end{eqnarray}$$
The flux through the (semi-)channel, which is independent of
$\grave{x}$
, is obtained from the solid-boundary region as
$(3\unicode[STIX]{x1D719})^{-1}$
. Mass conservation necessitates the same flux in the free-boundary region, giving in turn
$$\begin{eqnarray}C_{f}=\frac{1}{3\unicode[STIX]{x1D719}(1-\unicode[STIX]{x1D719})}.\end{eqnarray}$$
While this plug-flow component is always positive, flow reversal is possible in the free-boundary region. Indeed, with the centreline velocity being there
$$\begin{eqnarray}\grave{u} |_{y=0}=\frac{2-3\unicode[STIX]{x1D719}}{6\unicode[STIX]{x1D719}(1-\unicode[STIX]{x1D719})};\end{eqnarray}$$
it follows that, for
$\unicode[STIX]{x1D719}>2/3$
, the flow in the centred streamlines is antiparallel to the flux.
The main outcome of the present analysis is the following approximation for the mean velocity (2.20),
$$\begin{eqnarray}\bar{u}=\frac{1}{3\unicode[STIX]{x1D6EC}\unicode[STIX]{x1D719}}+\cdots \quad \text{for }\unicode[STIX]{x1D6EC}\gg 1.\end{eqnarray}$$
Note that the present type of Hele-Shaw approximation is inapplicable to the longitudinal problem, where the longitudinal velocity satisfies Laplace’s equation. The singularity of the longitudinal limit is closely related to that appearing in the associated pressure-driven problem (Schnitzer & Yariv Reference Schnitzer and Yariv2017).
6 Small solid fractions
We now address the small solid-fraction limit
$\unicode[STIX]{x1D719}\ll 1$
. In the context of pressure-driven channel flows it is known as a singular one (Lauga & Stone Reference Lauga and Stone2003; Choi & Kim Reference Choi and Kim2006; Lee, Choi & Kim Reference Lee, Choi and Kim2008); it has been recently analysed in that context by Yariv (Reference Yariv2017) using matched asymptotic expansions. The following calculation is closely related to that analysis.
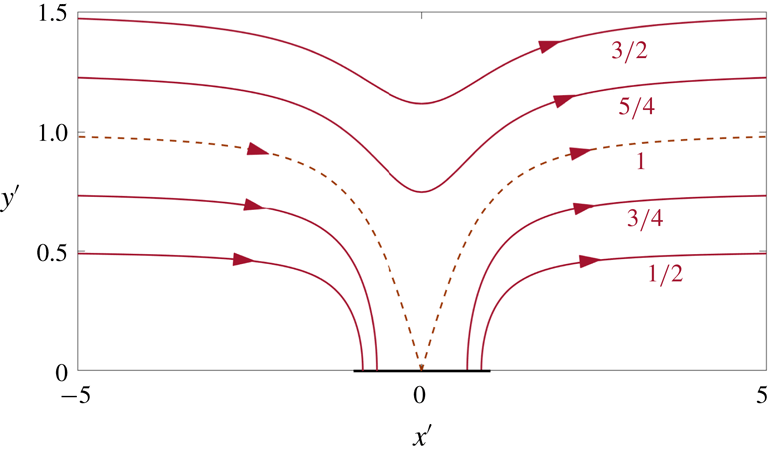
As in Yariv (Reference Yariv2017), we employ inner–outer asymptotic expansions, with an inner region of
$O(\unicode[STIX]{x1D719})$
extent about the solid slat and an outer region of
$O(1)$
extent in the remaining liquid domain. Defining the stretched coordinates,
$$\begin{eqnarray}x^{\prime }=\frac{x}{\unicode[STIX]{x1D719}\unicode[STIX]{x1D6EC}},\quad y^{\prime }=\frac{y}{\unicode[STIX]{x1D719}\unicode[STIX]{x1D6EC}},\end{eqnarray}$$
the inner region becomes the upper half-plane
$y^{\prime }>0$
. In that region, the excess temperature is animated by the continuity condition (2.9) on the solid edge. It therefore suggests an
$O(\unicode[STIX]{x1D719})$
inner scaling, leading to the expansion
$$\begin{eqnarray}\unicode[STIX]{x1D703}=\unicode[STIX]{x1D719}\unicode[STIX]{x1D6EC}\,\unicode[STIX]{x1D703}^{\prime }(x^{\prime },y^{\prime })+\cdots \,,\end{eqnarray}$$
where
$\unicode[STIX]{x1D6EC}$
is introduced for convenience. The anticipated decay of the excess temperature
$\unicode[STIX]{x1D703}^{\prime }$
, which is governed by a linear problem, suggests that
$\unicode[STIX]{x1D703}$
is asymptotically smaller in the outer region.
Since the integral balance (2.23) suggests
$O(1)$
inner velocities, we postulate the inner expansions
$$\begin{eqnarray}u=u^{\prime }(x^{\prime },y^{\prime })+\cdots \,,\quad v=v^{\prime }(x^{\prime },y^{\prime })+\cdots \,.\end{eqnarray}$$
Anticipating the familiar logarithmic behaviour in two-dimensional Stokes flows, we expect that the outer velocity is of order
$\ln \unicode[STIX]{x1D719}$
. We accordingly postulate the outer expansions,
$$\begin{eqnarray}u(x,y;\unicode[STIX]{x1D719})=u^{\ast }(x,y)\ln \frac{1}{\unicode[STIX]{x1D719}}+\cdots \,,\quad v(x,y;\unicode[STIX]{x1D719})=v^{\ast }(x,y)\ln \frac{1}{\unicode[STIX]{x1D719}}+\cdots \,.\end{eqnarray}$$
6.1 Leading-order flow problems
The leading-order outer flow is governed by the continuity and Stokes equations. Since at leading order the solid edge appears as a singular point, the shear-stress condition (2.15) applies at the entire
$y=0$
boundary (sans one point), namely for
$0<|x|<\unicode[STIX]{x1D6EC}$
. With the excess temperature being
$\ll \unicode[STIX]{x1D719}$
in the outer region, the Marangoni term in that condition does not affect the leading-order balance, which is accordingly homogeneous,
$$\begin{eqnarray}\frac{\unicode[STIX]{x2202}u^{\ast }}{\unicode[STIX]{x2202}y}=0\quad \text{for }0<|x|<\unicode[STIX]{x1D6EC}.\end{eqnarray}$$
In addition,
$u^{\ast }$
also satisfies the appropriate counterparts of (2.17)–(2.18). Since all these homogeneous conditions involve the velocity derivatives, it follows that
$u^{\ast }$
possesses a uniform solution. Considering the problem governing
$v^{\ast }$
and noticing the homogeneous symmetry condition (2.13) and the comparable Dirichlet condition implied by the impermeability condition (2.16), we conclude that
$v^{\ast }\equiv 0$
.
To determine the value of
$u^{\ast }$
we consider the inner problem. The leading-order flow in the half-space
$y^{\prime }>0$
is governed by the continuity and Stokes equations. In addition, at
$y^{\prime }=0$
it satisfies impermeability (cf. (2.13)),
$$\begin{eqnarray}v^{\prime }=0,\end{eqnarray}$$
together with the mixed conditions (cf. (2.14)–(2.15))
$$\begin{eqnarray}u^{\prime }=0\quad \text{for }|x^{\prime }|<1,\quad \frac{\unicode[STIX]{x2202}u^{\prime }}{\unicode[STIX]{x2202}y^{\prime }}=0\quad \text{for }|x^{\prime }|>1.\end{eqnarray}$$
Note that the preceding problem is entirely homogeneous and accordingly does not possess a unique solution. The homogeneity is a consequence of the small asymptotic magnitude of the Marangoni term in (2.15).
In principle, one can proceed to the next asymptotic order, where the Marangoni term appears explicitly. The alternative approach adopted here makes use instead of the integral condition (2.23). This condition, which applies here at the inner region, introduces the inhomogeneous dependence upon the thermal forcing. At leading order, it reads
$$\begin{eqnarray}\int _{-1}^{1}\left.\frac{\unicode[STIX]{x2202}u^{\prime }}{\unicode[STIX]{x2202}y^{\prime }}\right|_{y^{\prime }=0}\,\text{d}x^{\prime }=2.\end{eqnarray}$$
6.2 Analogy with the flow about a finite line segment
The structure of the continuity and Stokes equations in conjunction with the homogeneous conditions (6.6)–(6.7) allow for the forming of a symmetric extension of the flow problem about
$y^{\prime }=0$
, with
$$\begin{eqnarray}u^{\prime }(-y^{\prime })=u^{\prime }(y^{\prime }),\quad v^{\prime }(-y^{\prime })=-v(y^{\prime }).\end{eqnarray}$$
In the extended region the boundary conditions applying above and below the line segment
$\{-1<x^{\prime }<1,y^{\prime }=0\}$
are the same as those applying over a stationary solid segment; with that interpretation, the integral constraint (6.8) represents a hydrodynamic force of magnitude
$4$
which acts on that segment in the
$x$
-direction.
Considering now large distances away from the segment,
${x^{\prime }}^{2}+{y^{\prime }}^{2}\gg 1$
, we retrieve the problem of a two-dimensional point force. In the present dimensionless notation, a concentrated force
$\boldsymbol{F}$
(per unit length in the
$z$
-direction) which acts on the fluid at the origin results in the velocity field (Pozrikidis Reference Pozrikidis1992)
$$\begin{eqnarray}\frac{\boldsymbol{F}}{8\unicode[STIX]{x03C0}}\boldsymbol{\cdot }\left\{-\unicode[STIX]{x1D644}\ln ({x^{\prime }}^{2}+{y^{\prime }}^{2})+2\frac{\boldsymbol{x}^{\prime }\boldsymbol{x}^{\prime }}{|\boldsymbol{x}^{\prime }|^{2}}\right\}\end{eqnarray}$$
wherein
$\boldsymbol{x}^{\prime }=x^{\prime }\hat{\boldsymbol{e}}_{x}+y^{\prime }\hat{\boldsymbol{e}}_{y}$
and
$\unicode[STIX]{x1D644}$
is the idemfactor. With
$\boldsymbol{F}$
being here
$-4\hat{\boldsymbol{e}}_{x}$
we obtain, as
${x^{\prime }}^{2}+{y^{\prime }}^{2}\rightarrow \infty$
$$\begin{eqnarray}u^{\prime }\sim \frac{1}{2\unicode[STIX]{x03C0}}\ln ({x^{\prime }}^{2}+{y^{\prime }}^{2})-\frac{{x^{\prime }}^{2}}{\unicode[STIX]{x03C0}({x^{\prime }}^{2}+{y^{\prime }}^{2})}+o(1),\quad v^{\prime }\sim -\frac{x^{\prime }y^{\prime }}{\unicode[STIX]{x03C0}({x^{\prime }}^{2}+{y^{\prime }}^{2})}+o(1).\end{eqnarray}$$
In terms of the outer coordinates, the
$x$
-component (6.11a
) becomes
$$\begin{eqnarray}\frac{1}{\unicode[STIX]{x03C0}}\left\{\ln \frac{1}{\unicode[STIX]{x1D719}}+\ln \sqrt{x^{2}+y^{2}}-\frac{x^{2}}{\unicode[STIX]{x03C0}(x^{2}+y^{2})}+o(1)\right\}.\end{eqnarray}$$
The need for asymptotic matching implies that the corresponding leading-order outer velocity component should approach (6.12) as
$(x,y)\rightarrow (0,0)$
. Given expansion (6.4a
) and recalling that
$u^{\ast }$
is uniform we readily conclude that
$$\begin{eqnarray}u^{\ast }\equiv 1/\unicode[STIX]{x03C0}.\end{eqnarray}$$
Comparing with definition (2.20) it follows that the mean velocity is
$$\begin{eqnarray}\bar{u}\sim \frac{1}{\unicode[STIX]{x03C0}}\ln \frac{1}{\unicode[STIX]{x1D719}}+\cdots \quad \text{for }\unicode[STIX]{x1D719}\ll 1.\end{eqnarray}$$
Note that this is just half of the corresponding result in the longitudinal case: see indeed (3.7) of Yariv (Reference Yariv2018). At leading order, approximation (6.14) agrees with (4.43). On the other hand, it does not agree with (5.17). We conclude that the respective limits of small solid fraction and shallow channels do not commute. This is hardly surprising.
While the calculation of the excess temperature in the inner region is not required for deriving (6.13), its distribution is still of some interest. It is presented in appendix A.
7 Concluding remarks
The present contribution is concerned with transverse thermocapillary flows between a grooved superhydrophobic channel; it complements the longitudinal analysis of Yariv (Reference Yariv2018). Making use of the model proposed by Baier et al. (Reference Baier, Steffes and Hardt2010), we have considered a highly conducting solid substrate, assuming that the superhydrophobic microstructure is formed by long solid slats. Neglecting heat advection, the mathematical problem amounts to the analysis of two successive linear sub-problems, the first governing the temperature field and the second governing the engendered flow. Once these are solved, the volumetric flux through the channel is obtained. We have identified an analogy between the harmonic conjugate of the temperature field and a longitudinal shear-driven flow field which is defined in a complementary domain. Making use of Lorentz reciprocity in conjunction with an auxiliary pressure-driven flow field, we have obtained an integral representation for the volumetric flux which may serve for its evaluation. (It is worth remarking that one of the authors has made use of similar reciprocal-theorem arguments to study the effect of meniscus curvature and the presence of a subphase fluid (Crowdy Reference Crowdy2017b ) as well as shear-thinning fluid effects (Crowdy Reference Crowdy2017a ) in the associated shear-driven problem.)
This general representation has been supplemented by useful approximations, obtained via asymptotic analysis of separate geometric limits. Our principal interest is in the limit of deep channels, which leads to the consideration of the flow about a single superhydrophobic surface, in the spirit of Baier et al. (Reference Baier, Steffes and Hardt2010). Upon making use of the analogy between the harmonic conjugate of the temperature field and a shear-driven unidirectional velocity field we have obtained the effective slip about the surface as a simple quadrature, thus providing the analogue to the elegant result obtained by Baier et al. (Reference Baier, Steffes and Hardt2010) in the longitudinal problem. The quadrature, which depends upon the solid fraction
$\unicode[STIX]{x1D719}$
, is easily evaluated numerically. In addition, it is readily approximated in the diametric limits
$\unicode[STIX]{x1D719}\rightarrow 0^{+}$
and
$\unicode[STIX]{x1D719}\rightarrow 1^{-}$
. Thus, for small solid fractions it exhibits a logarithmic scaling with
$\unicode[STIX]{x1D719}$
, while at small gas fractions it scales as
$1-\unicode[STIX]{x1D719}$
. The other geometric limits considered in the present paper are those of shallow channels and small solid fractions. The former has been handled using a Hele-Shaw approximation scheme, while the latter has been analysed using matched asymptotic expansions. Comparison of the resulting fluxes reveals that these two limits do not commute.
In contrast to the longitudinal analysis of Yariv (Reference Yariv2018), the present work is limited by the neglect of heat advection. It is desirable to assess that approximation in realistic configurations. The ratio of advection to conduction is generally quantified by the Péclet number. In thermocapillary flows, where the velocity scale is set indirectly, this number is termed the Marangoni number. With the length and velocity scales being respectively given by
$h$
and
$-G\unicode[STIX]{x1D70E}_{T}l/\unicode[STIX]{x1D707}$
, the Marangoni number is
$-G\unicode[STIX]{x1D70E}_{T}lh/\unicode[STIX]{x1D707}\unicode[STIX]{x1D6FC}$
, wherein
$\unicode[STIX]{x1D6FC}$
is the thermal diffusivity of the liquid. Considering the common water–air system,
$\unicode[STIX]{x1D70E}_{T}\approx -0.155~\text{mN}~\text{m}^{-1}~\text{K}^{-1}$
,
$\unicode[STIX]{x1D707}\approx 10^{-3}~\text{kg}~\text{m}^{-1}~\text{s}^{-1}$
and
$\unicode[STIX]{x1D6FC}\approx 1.4\times 10^{-7}~\text{m}^{2}~\text{s}^{-1}$
. Taking both
$h$
and
$l$
as
$10~\unicode[STIX]{x03BC}\text{m}$
and using the characteristic value
$G=10~\text{K}~\text{cm}^{-1}$
, the Marangoni number is approximately
$0.1$
. For these values, it is reasonable to neglect advection. It is worth noting, however, that the direct dependence of the Marangoni number upon the product
$lh$
implies a sensitivity to a change of scale. Thus, enlarging the geometry by a factor of 2 would result in a Marangoni number of approximately
$0.4$
.
This sensitivity suggests the desirability of a general analysis at arbitrary Marangoni number. The associated problem may be represented as a sequence of two linear subproblems: one governing the flow, where the temperature enters linearly through the boundary conditions, and one governing the temperature, where the flow appears as a coefficient in the energy equation. While the latter appearance renders the entire problem nonlinear, the above sequence naturally suggests an iterative scheme where at each step one needs to confront linear subproblems. The above technical route may be supplemented by asymptotic analyses in the limits of both small (but finite) and large Marangoni numbers. In particular, following the classical analyses of thermo-capillary motion (Balasubramaniam & Subramaniam Reference Balasubramaniam and Subramaniam1996; Balasubramaniam & Subramanian Reference Balasubramaniam and Subramanian2000), we anticipate a non-intuitive singular behaviour in the limit of large Marangoni numbers.
Another desirable extension of the present work involves relaxing the approximation of long solid slats. When that approximation is avoided, the temperature profile has to be determined in the solid substrate even if one retains the assumption that it is highly conducting. The problem is still linear, but is more technically involved.
Acknowledgements
E.Y. was supported by the Israel Science Foundation (grant no. 1081/16).
Appendix A. Excess temperature in the limit of small solid fractions
The leading-order excess temperature is governed by (i) Laplace’s equation,
$$\begin{eqnarray}\frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D703}^{\prime }}{\unicode[STIX]{x2202}{x^{\prime }}^{2}}+\frac{\unicode[STIX]{x2202}^{2}\unicode[STIX]{x1D703}^{\prime }}{\unicode[STIX]{x2202}{y^{\prime }}^{2}}=0\quad \text{for }y^{\prime }>0;\end{eqnarray}$$
(ii) the mixed conditions at
$y^{\prime }=0$
,
$$\begin{eqnarray}\unicode[STIX]{x1D703}^{\prime }=x^{\prime }\quad \text{for }|x^{\prime }|<1,\quad \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}^{\prime }}{\unicode[STIX]{x2202}y^{\prime }}=0\quad \text{for }|x^{\prime }|>1;\end{eqnarray}$$
and (iii) far-field decay,
$$\begin{eqnarray}\unicode[STIX]{x1D703}^{\prime }\rightarrow 0\quad \text{as }y^{\prime }\rightarrow \infty .\end{eqnarray}$$
This problem is solved using conformal maps (Brown & Churchill Reference Brown and Churchill2003). Thus, we regard the harmonic function
$\unicode[STIX]{x1D703}^{\prime }(x^{\prime },y^{\prime })$
as the real part of an analytic potential
$\unicode[STIX]{x1D6E9}(z^{\prime })$
, wherein
$z^{\prime }=x^{\prime }+\text{i}y^{\prime }$
. We employ the mapping
$$\begin{eqnarray}z^{\prime }=f(\unicode[STIX]{x1D701}),\end{eqnarray}$$
wherein
$\unicode[STIX]{x1D701}=\unicode[STIX]{x1D709}+\text{i}\unicode[STIX]{x1D702}$
, which transforms a convenient domain in the
$\unicode[STIX]{x1D701}$
-plane onto the upper half-
$z^{\prime }$
-plane. We therefore need to find the complex potential in the
$\unicode[STIX]{x1D701}$
-plane,
$\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D701})=\unicode[STIX]{x1D6E9}[f(\unicode[STIX]{x1D701})]$
. Its real part, say
$\unicode[STIX]{x1D711}(\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})$
, satisfies Laplace’s equation as well as appropriate boundary conditions which follow from (A 2)–(A 3).
In what follows, we take the preimage of the upper half-
$z^{\prime }$
-plane as the semi-strip
$-\unicode[STIX]{x03C0}/2<\unicode[STIX]{x1D709}<\unicode[STIX]{x03C0}/2$
, with
$\unicode[STIX]{x1D702}>0$
and choose the mapping
$$\begin{eqnarray}f(\unicode[STIX]{x1D701})=\sin \unicode[STIX]{x1D701},\end{eqnarray}$$
or, equivalently,
$$\begin{eqnarray}x^{\prime }(\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})=\sin \unicode[STIX]{x1D709}\cosh \unicode[STIX]{x1D702},\quad y^{\prime }(\unicode[STIX]{x1D709},\unicode[STIX]{x1D702})=\cos \unicode[STIX]{x1D709}\sinh \unicode[STIX]{x1D702}.\end{eqnarray}$$
The real part
$\unicode[STIX]{x1D711}$
of
$\unicode[STIX]{x1D6F7}$
accordingly satisfies (i) Laplace’s equation in the Cartesian coordinates
$\unicode[STIX]{x1D709}$
and
$\unicode[STIX]{x1D702}$
; (ii) the Dirichlet condition
$$\begin{eqnarray}\unicode[STIX]{x1D711}=\sin \unicode[STIX]{x1D709}\quad \text{at }\unicode[STIX]{x1D702}=0;\end{eqnarray}$$
(iii) the homogeneous Neumann
$$\begin{eqnarray}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D711}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D709}}=0\quad \text{at }\unicode[STIX]{x1D709}=\pm \unicode[STIX]{x03C0}/2;\end{eqnarray}$$
and (iv) the decay condition
$$\begin{eqnarray}\unicode[STIX]{x1D711}\rightarrow 0\quad \text{as }\unicode[STIX]{x1D702}\rightarrow \infty .\end{eqnarray}$$
It is readily verified that the requisite complex potential is simply
$$\begin{eqnarray}\unicode[STIX]{x1D6F7}(\unicode[STIX]{x1D701})=-\text{i}\text{e}^{\text{i}\unicode[STIX]{x1D701}}\end{eqnarray}$$
whose real part is
$$\begin{eqnarray}\unicode[STIX]{x1D711}=\text{e}^{-\unicode[STIX]{x1D702}}\sin \unicode[STIX]{x1D709}.\end{eqnarray}$$
The excess temperature
$\unicode[STIX]{x1D703}^{\prime }(x^{\prime },y^{\prime })$
is provided by (A 11), in which
$\unicode[STIX]{x1D709}$
and
$\unicode[STIX]{x1D702}$
are replaced by the respective transformations
$\unicode[STIX]{x1D709}(x^{\prime },y^{\prime })$
and
$\unicode[STIX]{x1D702}(x^{\prime },y^{\prime })$
, namely the inverses of (A 6a,b
). For example, on the liquid–air interface to the right of the solid segment, where
$y^{\prime }=0$
and
$x^{\prime }>1$
(whence
$\unicode[STIX]{x1D709}=\unicode[STIX]{x03C0}/2$
),
$$\begin{eqnarray}\unicode[STIX]{x1D703}^{\prime }=\exp (-\cosh ^{-1}x^{\prime }),\end{eqnarray}$$
giving the large-
$x^{\prime }$
algebraic decay
$\unicode[STIX]{x1D703}^{\prime }\sim (2x^{\prime })^{-1}$
.
Making use of (2.8) and (6.1)–(6.2) we note that the inner-region temperature field possesses the asymptotic expansion
$$\begin{eqnarray}t=\unicode[STIX]{x1D719}\unicode[STIX]{x1D6EC}\,T+\cdots\end{eqnarray}$$
in which
$T=-x^{\prime }+\unicode[STIX]{x1D703}^{\prime }$
. Equivalently,
$T=\operatorname{Re}\{\unicode[STIX]{x1D6EF}\}$
in which
$$\begin{eqnarray}\unicode[STIX]{x1D6EF}=-z^{\prime }-\text{i}\text{e}^{\text{i}\unicode[STIX]{x1D701}}.\end{eqnarray}$$
Note that the lines of heat flux associated with the leading-order inner temperature are the isolines of
$\operatorname{Im}\{\unicode[STIX]{x1D6EF}\}$
, namely
$$\begin{eqnarray}y^{\prime }+\text{e}^{-\unicode[STIX]{x1D702}}\cos \unicode[STIX]{x1D709}=C,\end{eqnarray}$$
or, upon making use of (A 5),
$$\begin{eqnarray}\cos \unicode[STIX]{x1D709}\cosh \unicode[STIX]{x1D702}=C.\end{eqnarray}$$
Clearly,
$C\geqslant 0$
, with large
$C$
corresponding to straight lines which represent the far-field uniform gradient.
To understand the geometry of the flux lines it is expedient to consider large
$x^{\prime }$
, where
$y^{\prime }$
approaches a finite limit, say
$y_{\infty }^{\prime }$
. It follows from (A 6a
) that
$\unicode[STIX]{x1D702}$
must be large, whereby (A 6b
) necessitates that
$\unicode[STIX]{x1D709}$
is close to
$\unicode[STIX]{x03C0}/2$
hence
$$\begin{eqnarray}\unicode[STIX]{x03C0}/2-\unicode[STIX]{x1D709}\sim 2y_{\infty }^{\prime }\text{e}^{-\unicode[STIX]{x1D702}}\quad \text{as }\unicode[STIX]{x1D702}\rightarrow \infty .\end{eqnarray}$$
Substitution into (A 16) thus gives
$$\begin{eqnarray}y_{\infty }^{\prime }=C.\end{eqnarray}$$
The approach of the flux lines to straight lines for large
$C$
implies the existence of a critical value of
$C(=y_{\infty }^{\prime })$
, above which the flux lines do not reach the solid slat. To determine this value we make use of the symmetry about
$x^{\prime }=0$
(and hence also about
$\unicode[STIX]{x1D709}=0$
). Considering (A 16) at
$\unicode[STIX]{x1D709}=0$
we see that smallest value of
$C$
that is consistent with a flux line there (
$\unicode[STIX]{x1D702}\geqslant 0$
) is
$C=1$
. The flux lines meet the slat only for
$C<1$
. (Since the slat is isothermal, they must meet it at a
$90^{\circ }$
-angle.)
Figure 3. Lines of heat flux in the inner region for the indicated values of
$C$
. The dashed line is the separatrix.
The lines of flux, obtained numerically from (A 16), are shown in figure 3 for the indicated values of
$C$
. As predicted, the separatrix is realised at
$C=1$
. The asymptotic limit (A 18) is clearly observed.
