3.1. A new dilatation/contraction framework

To describe the dilatation/contraction process of both quasi-static and rapid flowing granular materials, a new dilatation/contraction framework is proposed. It suggests that the dilatancy effects in sheared granular flows consist of a frictional portion, which results from the rearrangement of enduring-contact force chains among the particles, and a collisional portion, which arises from inter-grain collisions. These portions correspond to the two components of solid pressure. The collisional dilatancy effect has been well studied (Forterre & Pouliquen Reference Forterre and Pouliquen2008), while a formulation of the frictional dilatation/contraction remains unavailable and is the focus of this paper.

Figure 1 presents a schematic representation of the frictional dilatation/contraction. It is postulated that the frictional dilatation and contraction of granular materials arise respectively from the sharp increase and decrease of the frictional solid pressure $p_s^e$ as a result of the rearrangement of contact force chains among the particles. As shown in figure 1(a), when the initially densely packed granular medium is sheared to a strain of $\gamma $, there is an intensification of the microscopic contact force chains leading to an increase in the macroscopic solid pressure $p_s^e$. The increased inter-grain pressure pushes the particles up, which leads to an expansion of the granular medium and an increase in the porosity. In immersed granular media, the enlargement of the void volume between grains results in a decrease of the pore pressure. Conversely, in figure 1(b), the contact force chains in the loosely packed granular assembly break down, which results in the decrease of frictional solid pressure, contraction of the particle assembly and a decrease in the porosity. In immersed granular media, the shrinkage of the inter-grain void volume leads to an increase in the pore pressure. A formulation of the changes in $p_s^e$ arising from the rearrangement of contact force chains is proposed in § 3.2.

Figure 1. Schematic illustrations of the frictional (a) dilatation and (b) contraction. The red solid lines linking the grains roughly represent the enduring-contact force chains among granular particles, and the red upward arrows below the symbol $p_s^e$ represent the macroscopic frictional solid pressure. The thickness of the red lines roughly indicates the magnitude of contact forces and the length of the red arrows denotes that of $p_s^e$.

3.2. Frictional dilatation/contraction

To quantify the frictional dilatation/contraction effect in granular flows, here, a formulation of the changes in $p_s^e$ arising from the rearrangement of contact force chains is proposed. We consider a granular assembly with a packing fraction of ${\phi _s}$ sheared at a finite rate. According to the introduced framework in figure 1, the change in the packing fraction arising from frictional dilatation/contraction against an increment of shear strain $\partial \gamma $ results from the variation of $p_s^e$, expressed as

(3.1)\begin{equation}\frac{{\partial {\phi _s}}}{{\partial \gamma }} ={-} \left|{\frac{{\partial {\phi_s}}}{{\partial p_s^e}}} \right|\frac{{\partial p_s^e}}{{\partial \gamma }}.\end{equation}

The negative sign in (3.1) indicates that an increase or decrease of $p_s^e$ respectively leads to a decrease or increase in ${\phi _s}$, as illustrated in figure 1. A similar expression was adopted by Lu, Brodsky & Kavehpour (Reference Lu, Brodsky and Kavehpour2007) to describe the shear-weakening behaviour of granular materials. Through multiplying (3.1) by $- |{\partial p_s^e/\partial {\phi_s}} |$, the changes in $p_s^e$, when $p_s^e \gt 0$ and ${\phi _s} \gt 0$, can be estimated by

(3.2)\begin{equation}\frac{{\partial p_s^e}}{{\partial \gamma }} ={-} \left|{\frac{{{\phi_s}}}{{p_s^e}}\frac{{\partial p_s^e}}{{\partial {\phi_s}}}} \right|\frac{{p_s^e}}{{{\phi _s}}}\frac{{\partial {\phi _s}}}{{\partial \gamma }}.\end{equation}

As in Rowe (Reference Rowe1962), a dilatancy angle $\psi $ is defined as:

(3.3)\begin{equation}\textrm{tan}\,\psi = \frac{1}{V}\frac{{\partial V}}{{\partial \gamma }} ={-} \frac{1}{{{\phi _s}}}\frac{{\partial {\phi _s}}}{{\partial \gamma }},\end{equation}

where V is the volume of the granular assembly and $\partial V$ is the volumetric change arising from frictional dilatation/contraction. Equation (3.3) implies that the mass of the granular assembly remains constant during frictional dilatation/contraction. By defining $\Re \equiv |{({\phi_s}/p_s^e)\partial p_s^e/\partial {\phi_s}} |$ and combining (3.2) and (3.3), we have

(3.4)\begin{equation}\frac{{\partial p_s^e}}{{\partial \gamma }} = \Re p_s^e\,\textrm{tan}\,\psi .\end{equation}

Note that (3.4) is applicable for any time instant. As the rearrangement of contact force chains takes place at the particle scale, the corresponding changes in the pressure occur in a very short duration of $O({d_s}/\sqrt {p_s^e/{\rho _s}} )$ (see Forterre & Pouliquen Reference Forterre and Pouliquen2008, where ${d_s}$ is the particle diameter), during which there is an exceedingly small shear strain increment of ${\gamma _ \ast }$ in the granular assembly. In this strain change, we replace the $p_s^e$ in the definition of $\Re $ by $p_{s0}^e$ as a first approximation and obtain

(3.5)\begin{equation}\Re \approx \left|{\frac{{{\phi_s}}}{{p_{s0}^e}}\frac{{\partial p_{s0}^e}}{{\partial {\phi_s}}}} \right|,\end{equation}

in which $p_{s0}^e$ is the frictional solid pressure excluding the frictional dilatation/contraction effect and is a function of ${\phi _s}$. Hence, both $\Re $ and $\textrm{tan}\,\psi $ are macroscopic properties of the granular assembly varying with the volume fraction ${\phi _s}$ on a timescale of $O(1/2||{{\boldsymbol{S}_s}} ||)$. In granular media, whose behaviour is dominated by inter-grain frictional contacts, the ratio of the timescale for the microscopic contact-force chain rearrangement to that for changes in macroscopic properties, i.e. $O(2{d_s}||{{\boldsymbol{S}_s}} ||/\sqrt {p_s^e/{\rho _s}} )$, has a value of $O({10^{ - 6}}) \sim O({10^{ - 1}})$ (Lu et al. Reference Lu, Brodsky and Kavehpour2007; Chialvo, Sun & Sundaresan Reference Chialvo, Sun and Sundaresan2012). Therefore, it is reasonable to regard the microscopic rearrangement of contact-force chains and adjustment of the solid pressure as a transient process in a continuum description of granular flows and, during this period, the macroscopic properties of the granular assembly $\Re $ and $\textrm{tan}\,\psi $ stay unchanged. We can then rearrange (3.4) to $\partial p_s^e/p_s^e = (\Re \,\textrm{tan}\,\psi )\partial \gamma$ and integrate it over $[0,{\gamma _ \ast }]$, which gives

(3.6)\begin{equation}p_s^e = p_{s0}^e\,{\textrm{e}^{\Re {\gamma _ \ast }\,\textrm{tan}\,\psi }}.\end{equation}

In general, the frictional solid pressure excluding the dilatation/contraction effect $p_{s0}^e$ is a function of the solid volume fraction and can be computed using a few existing formulae (Johnson & Jackson Reference Johnson and Jackson1987; van Wachem et al. Reference van Wachem, Schouten, van den Bleek, Krishna and Sinclair2001; Hsu, Jenkins & Liu Reference Hsu, Jenkins and Liu2004). Without loss of generality, $p_{s0}^e$ can be determined by

(3.7)\begin{equation}p_{s0}^e = \left\{ {\begin{array}{@{}ll} {G{{({\phi_s} - {\phi_ \ast })}^\chi }}&{{\phi_s} \gt {\phi_ \ast }}\\ 0&{{\phi_s} \le {\phi_ \ast }} \end{array}} \right.,\end{equation}

where ${\phi _ \ast }$ is the random loosely packed volume fraction; G is a compressibility coefficient of the grains, which is related to the Young's modulus and the Poisson's ratio of the solid material; and $\chi $ is a parameter to characterize the arrangement of contact force chains, which generally varies from 1.50 to 5.50 (Hsu et al. Reference Hsu, Jenkins and Liu2004; Lee & Huang Reference Lee and Huang2018). Rewriting (3.6) in terms of the packing fraction $0 \lt {\phi _s} - {\phi _ \ast } \lt 1$ as

(3.8)\begin{equation}p_s^e = p_{s0}^e{({\phi _s} - {\phi _ \ast })^{(\Re {\gamma _ \ast }\,\textrm{tan}\,\psi )/\ln ({\phi _s} - {\phi _ \ast })}},\end{equation}

and combining (3.7) and (3.8), we obtain

(3.9)\begin{equation}p_s^e = G{({\phi _s} - {\phi _ \ast })^{\chi + \varDelta \chi }} = G{({\phi _s} - {\phi _ \ast })^{\chi + (\Re {\gamma _ \ast }\,\textrm{tan}\,\psi )/\textrm{ln}({\phi _s} - {\phi _ \ast })}},\end{equation}

for ${\phi _s} \gt {\phi _ \ast }$. Equation (3.9) indicates that the change of $p_s^e$ results from the adjustment of the parameter $\chi $ for the arrangement of contact force chains, consistent with the proposed framework in figure 1.

By applying (3.7) to obtain $\partial p_{s0}^e/\partial {\phi _s}$ and $p_{s0}^e$ in (3.5) for the case of ${\phi _s} \gt {\phi _ \ast }$, we have

(3.10)\begin{equation}\Re \approx \frac{{\chi {\phi _s}}}{{{\phi _s} - {\phi _ \ast }}}.\end{equation}

With regards to the dilatancy angle, the critical state theory in Roux & Radjai (Reference Roux and Radjai1998) is employed, i.e.

(3.11)\begin{equation}\textrm{tan}\,\psi = K({\phi _s} - {\phi _c}),\end{equation}

in which K is a material parameter of granular assembly varying in the range of 1.0–25.0 and can be determined through simple shear tests (Pailha & Pouliquen Reference Pailha and Pouliquen2009; Bonnet, Richard & Philippe Reference Bonnet, Richard and Philippe2010; Gravish & Goldman Reference Gravish and Goldman2014); and ${\phi _c}$ is the critical volume fraction of dilatancy, at which there is no frictional dilatation/contraction effect. Here ${\phi _c}$ may vary with the imposed force and the shear rate (Bouchut et al. Reference Bouchut, Fernández-Nieto, Mangeney and Narbona-Reina2016) and, in this paper, is related to the flow dimensionless number ${I_m}$ following Iverson & George (Reference Iverson and George2014), written as

(3.12)\begin{equation}{\phi _c} = \frac{{{\phi _{c0}}}}{{1 + \sqrt {{I_m}} }},\end{equation}

where the dimensionless number ${I_m}$ is a combination of the inertia number and the viscous number of granular flows, defined by (3.18); and ${\phi _{c0}}$ is the critical volume fraction of dilatancy for static granular materials when ${I_m} = 0$.

The shear strain ${\gamma _ \ast }$ increases with the temporal duration of the microscopic rearrangement of inter-grain contact force chains, the scale of which is ${d_s}/\sqrt {p_{s0}^e/{\rho _s}} $ (for simplification, here we use $p_{s0}^e$ rather than $p_s^e$), and with the rate of the macroscopic mean deformation of the granular assembly, $2||{{\boldsymbol{S}_s}} ||$. A non-dimensional shear rate ${I_d}$ can thus be defined as

(3.13)\begin{equation}{I_d} \equiv \frac{{2{d_s}||{{\boldsymbol{S}_s}} ||}}{{\sqrt {p_{s0}^e/{\rho _s}} }},\end{equation}

and ${\gamma _ \ast }$ increases with ${I_d}$. It is noted that ${I_d}$ is used to quantify the shear strain of granular media in the process of frictional dilatation/contraction and is different from the inertia number ${I_i} \equiv 2{d_s}||{{\boldsymbol{S}_s}} ||/\sqrt {{p_s}/{\rho _s}}$. A preliminary analysis on the magnitude of ${\gamma _ \ast }$ in appendix A suggests that ${\gamma _ \ast }$ has a small order of $O({10^{ - 2}})$–$O({10^{ - 1}})$ and

(3.14)\begin{equation}{\gamma _ \ast } = {c_1}I_d^{{c_2}},\end{equation}

where ${c_1}$ and ${c_2}$ are coefficients. The analysis gives ${c_1} = 0\sim O(10)$ and ${c_2} = 0\sim 1$.

Combining (3.6), (3.10) and (3.11), we have the frictional solid pressure including the frictional dilatation/contraction effect expressed as

(3.15)\begin{equation}p_s^e = p_{s0}^e\,\textrm{exp}\left[ {K\frac{{\chi {\phi_s}}}{{{\phi_s} - {\phi_ \ast }}}({\phi_s} - {\phi_c}){\gamma_ \ast }} \right].\end{equation}

In (3.15), the frictional solid pressure is related to the shear strain ${\gamma _ \ast }$. Further, combining (3.15) and (3.14), we can relate the frictional solid pressure to the shear rate of granular flows as

(3.16)\begin{equation}p_s^e = p_{s0}^e\,\textrm{exp}\left[ {{c_1}K\frac{{\chi {\phi_s}}}{{{\phi_s} - {\phi_ \ast }}}({\phi_s} - {\phi_c})I_d^{{c_2}}} \right].\end{equation}

Equation (3.16) is valid when ${\phi _s} \gt {\phi _ \ast }$ and $p_s^e = p_{s0}^e = 0$ when ${\phi _s} \le {\phi _ \ast }$.

3.3. Collisional dilatancy

The rheological law proposed in Trulsson, Andreotti & Claudin (Reference Trulsson, Andreotti and Claudin2012) was adopted for the collisional dilatancy effect. The shear-rate-dependent collisional solid pressure $p_s^c$ is determined by

(3.17)\begin{equation}p_s^c = 2{\left( {\frac{{{c_3}{\phi_s}}}{{{\phi_0} - {\phi_s}}}} \right)^2}({\rho _f}{\nu _f} + 2{c_4}{\rho _s}d_s^2||{{\boldsymbol{S}_s}} ||)||{{\boldsymbol{S}_s}} ||,\end{equation}

in which ${\phi _0}$ is the jamming volume fraction, the maximum packing fraction of sheared granular materials in a steady state; ${\rho _f}$ is the density of interstitial fluid and ${\nu _f}$ is its kinematic viscosity; ${d_s}$ is the diameter of granular particles; and ${c_3}$ and ${c_4}$ are coefficients. In general, ${c_3} = 0.75\sim 3.00$ and ${c_4} = 0\sim 1.00$ (Chauchat Reference Chauchat2018; Lee & Huang Reference Lee and Huang2018). The effect of interstitial fluid viscosity is included in (3.17) but can be neglected when considering subaerial granular flows.

The rheological law relates the friction coefficient $\mu $ in (2.5) to a dimensionless number ${I_m}$ of granular flows, which is a combination of the inertia number ${I_i}$ and the viscous number ${I_\nu } \equiv 2||{{\boldsymbol{S}_s}} ||{\rho _f}{\nu _f}/{p_s}$. It is defined as

(3.18)\begin{equation}{I_m} \equiv {I_\nu } + {c_4}I_i^2 = \frac{{2||{{\boldsymbol{S}_s}} ||({\rho _f}{\nu _f} + 2{c_4}{\rho _s}d_s^2||{{\boldsymbol{S}_s}} ||)}}{{{p_s}}},\end{equation}

in which ${c_4}$ is the same coefficient as that in (3.17). A small value of ${I_m}$ indicates that the granular flow moves at a low speed and is in the quasi-static regime, while a large value of ${I_m}$ corresponds to a rapid granular flow in the inertia regime (Forterre & Pouliquen Reference Forterre and Pouliquen2008). According to Trulsson et al. (Reference Trulsson, Andreotti and Claudin2012), the friction coefficient depends on ${I_m}$ as

(3.19)\begin{equation}\mu = {\mu _1} + \frac{{{\mu _2} - {\mu _1}}}{{1 + \sqrt {{I_0}/{I_m}} }},\end{equation}

where ${\mu _1} = \textrm{tan}\,\varphi $ is the friction coefficient when ${I_m} = 0$ and the granular assembly is static; $\varphi $ is the internal friction angle of the grains; ${\mu _2} = \textrm{tan}\,\varphi \sim 1.0$ is the friction coefficient when ${I_m}$ is infinite and the granular assembly flows fairly rapidly; and ${I_0}$ is a model parameter and is set to be a value close to the characteristic ${I_m}$ of the flow (Boyer, Guazzelli & Pouliquen Reference Boyer, Guazzelli and Pouliquen2011).

4.1. Shear-weakening behaviour of granular samples

The experimental data of sheared granular samples within a torsional shear cell in Lu et al. (Reference Lu, Brodsky and Kavehpour2007) were used to verify the proposed theoretical formulation of dilatation/contraction. In the experiment, a granular sample composed of sifted beach sand, which had a mean diameter of ${d_s} = 438\;\mathrm{\mu m}$, a density of ${\rho _s} = 2.65\textrm{ g c}{\textrm{m}^{\textrm{ - 3}}}$ and an internal frictional angle of $\varphi = 37.5^\circ $, was sheared in a top-rotating torsional shear rheometer. The rheometer was a highly sensitive feedback-controlled instrument with the normal force, top-plate height and angular velocity monitored simultaneously, which hence can directly provide the values of inter-grain pressure, packing fraction and shear rate in the granular sample for the validation of the theory. The granular sample was initially loaded up to a height of 6 mm with a packing fraction of ${\phi _s} = 0.61$ when static. It was then sheared by rotating the top plate at a finite angular velocity with the column height staying fixed and the volume fraction of the medium remaining constant. The normal stress on the top plate was recorded. The shear angular velocity $\omega $ varied from 0.001 to 100 rad s⁻¹ in different experimental cases and the shear rate of the granular sample was correspondingly between 0.001 and 2800 s⁻¹. The results showed that the normal stress on the top plate varied little when the angular shearing velocity $\omega $ was lower than 0.01 rad s⁻¹ but became negatively correlated with $\omega $ when $\omega $ was increased up to 25 rad s⁻¹. This observation demonstrated a shear-weakening rheology with a dip of the normal stress. As $\omega $ increased further, the normal stress increased almost quadratically with the shear rate when the grains were in the inertia regime.

At the steady state when the sample is sheared at a rate of $\dot{\gamma }$, the normal stress on the top plate $\sigma $ is balanced by the inter-grain pressure ${p_s}$ as

(4.1)\begin{equation}\sigma = {p_s} = p_s^e + p_s^c.\end{equation}

Excluding the effect of interstitial fluid viscosity in (3.17) for subaerial granular samples and combining (3.12), (3.16), (3.17) and (4.1), the normal stress varies with the shear rate $\dot{\gamma } = 2||{{\boldsymbol{S}_s}} ||$ as

(4.2)\begin{equation}\sigma = p_{s0}^e\,\textrm{exp}\left[ {{c_1}K\frac{{\chi {\phi_s}}}{{{\phi_s} - {\phi_ \ast }}}({\phi_s} - {\phi_c})I_d^{{c_2}}} \right] + {c_4}{\left( {\frac{{{c_3}{\phi_s}}}{{{\phi_0} - {\phi_s}}}} \right)^2}{\rho _s}d_s^2{\dot{\gamma }^2}.\end{equation}

The frictional solid pressure without the dilatation/contraction effect $p_{s0}^e$, determined by (3.7), balances the initially imposed normal stress ${\sigma _0}$ to the static granular sample at the start of each experimental case, i.e.

(4.3)\begin{equation}{\sigma _0} = p_{s0}^e = G{({\phi _s} - {\phi _ \ast })^\chi }.\end{equation}

Dividing both sides of (4.2) by ${\sigma _0}$, we have the dimensionless normal stress varying with shear rate as

(4.4)\begin{equation}\frac{\sigma }{{{\sigma _0}}} = \exp \left[ {{c_1}K\frac{{\chi {\phi_s}}}{{{\phi_s} - {\phi_ \ast }}}({\phi_s} - {\phi_c})I_d^{{c_2}}} \right] + {c_4}{\left( {\frac{{{c_3}{\phi_s}}}{{{\phi_0} - {\phi_s}}}} \right)^2}\frac{{{\rho _s}d_s^2{{\dot{\gamma }}^2}}}{{{\sigma _0}}},\end{equation}

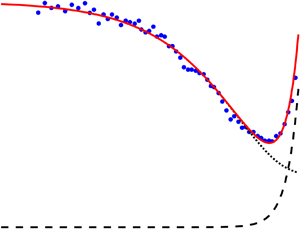
in which the non-dimensional shear rate ${I_d} = {d_s}\dot{\gamma }/\sqrt {{\sigma _0}/{\rho _s}} $. Figure 2 shows the comparisons between the results of (4.4) and the measured data. In the experiment, ${\sigma _0} = 1.25 \times {10^4}\;\textrm{Pa}$, ${\phi _ \ast } = 0.590$ and a random close-packing fraction ${\phi ^ \ast } = 0.640$. A jamming volume fraction ${\phi _0} = 0.630$ is set which is in a reasonable range of ${\phi _s}\sim {\phi ^ \ast }$. The compressibility coefficient of the natural sand G is ${10^9}\;\textrm{Pa}$ and, according to (4.3), the coefficient $\chi = \textrm{ln}({\sigma _0}/G)/\textrm{ln}({\phi _s} - {\phi _ \ast })$ is 2.89. A critical volume fraction of dilatancy ${\phi _{{c_0}}} = 0.630$ is estimated in the experiment. The parameter K was not measured and we take ${c_1}K$ as a single coefficient. Here, ${c_1}K = 1.50$ and ${c_2} = 0.42$ are set by fitting the computed results with the data in both quasi-static and transitional regimes, while ${c_3} = 1.80$ and ${c_4} = 0.0005$ are determined according to the fitness in the inertia regime. The values of the parameters are summarized in table 1.

Figure 2. Variation of normal stress on the rheometer top-plate with non-dimensional shear rate in the volume-constant experiments of Lu et al. (Reference Lu, Brodsky and Kavehpour2007). The non-dimensional frictional solid pressure $p_s^e/{\sigma _0}$ and collisional pressure $p_s^c/{\sigma _0}$ are computed by the first and the second terms on the right-hand side of (4.4), respectively.

Table 1. Parameters in the model. The third column shows whether a parameter is a material parameter, whose value is determined depending on the physical properties of solid grains and according to related experimental observations. In §§ 4.1 and 5, the material parameter K was not measured and we take ${c_1}K$ as a single adjustable parameter. In § 4.2, when concerning the critical incipient state of granular slopes, the frictional solid pressure is related to the shear strain ${\gamma _ \ast }$ and ${\gamma _ \ast } = {c_1}I_d^{{c_2}}$ is taken as an adjustable parameter. In specific analytical cases, if its value is not set, the parameter is not involved in the solutions.

As shown in figure 2, the predicted variation of the normal stress against shear rate agrees well with the measured data, which demonstrates that the proposed formulation of frictional solid pressure is capable of describing the shear-weakening behaviour of the granular sample. When the sample is in the quasi-static and the transitional regimes, the frictional solid pressure $p_s^e$ predominates and the decrease in $p_s^e$, owing to the frictional contraction, is the reason for the dip in the normal stress. When the sample is in the inertia regime, the collisional inter-grain pressure $p_s^c$ increases quadratically with the shear rate and becomes dominant in the balance with the normal stress on the top-plate. Equation (4.4), which is a direct result of the proposed dilatation/contraction theory, can map the variation of the normal stress imposed to the sheared sample smoothly between the quasi-static and the inertia regimes.

4.2. Incipient failure of granular slopes

In this section, the proposed theoretical formulation is assessed through predicting the incipient failure of dry and immersed granular slopes.

Gravish & Goldman (Reference Gravish and Goldman2014) experimentally studied the effects of initial packing fraction on the failure of dry granular slopes. An initially horizontal layer of grains with ${d_s} = 256\;\mathrm{\mu m}$, ${\rho _s} = 2.5\,\textrm{g}\;\textrm{c}{\textrm{m}^{ - 3}}$ and volume fraction ${\phi _s}$ ranging between 0.58 and 0.63 was prepared on a fluidized bed. The bed was then rotated to a 45° angle at a constant rate. The granular motion in the bed was recorded by cameras and the instant when incipient motion of grains on the surface occurred was detected. The angle of the slope at the instant ${\theta _0}$, referred to as the incipient angle, was then obtained according to the rotation rate of the bed. In different experimental cases, the initial packing fraction was varied and different failure behaviours of the granular slopes were observed. It was found that the bed with a packing fraction smaller than the critical value ${\phi _{{c_0}}} = 0.595 \pm 0.003$ experienced a rapid failure and a compaction, while the bed with a fraction larger than the critical value underwent a slow failure and a dilatation. Specifically, the bed with initial ${\phi _s} = 0.58$ had an incipient angle of ${\theta _0} = 7.7 \pm {1.4^ \circ }$, whereas the ${\theta _0}$ of the bed with ${\phi _s} = 0.63$ was $32.1 \pm 1.5^\circ $. Overall, the incipient angle of the slopes increased significantly with the initial packing fraction.

For comparison, the classical saw model of dilatancy (Rowe Reference Rowe1962; Pailha & Pouliquen Reference Pailha and Pouliquen2009) was applied to estimate the incipient angle of granular slopes. In the theory, forces are in equilibrium both along and normal to the slope and the dilatation/contraction affects the slope failure by leading to a change in the angle of shearing. At the critical incipient state, the grains on the bed surface are controlled by

(4.5)\begin{gather}{\phi _s}{p_s}\,\textrm{tan}\,\delta = {\phi _s}{\rho _s}gh\,\textrm{sin}\,{\theta _0},\end{gather}

(4.6)\begin{gather}{\phi _s}{p_s} = {\phi _s}{\rho _s}gh\,\textrm{cos}\,{\theta _0}\end{gather}

and

(4.7)\begin{equation}\textrm{tan}\,\delta = \textrm{tan}(\varphi + \psi ),\end{equation}

where $\delta $ is the angle of shearing; $\varphi $ is the internal friction angle of the grains and $\textrm{tan}\,\varphi $ is the friction coefficient when there is no dilatancy effect; and h is a characteristic depth of the grains to move. Recall that $\psi $ is the dilatancy angle. Equations (4.5) and (4.6) are respectively for the balance of forces in the directions along and normal to the slope. Combining (4.5)–(4.7) as well as (3.11), we have

(4.8)\begin{equation}{\theta _0} = \varphi + \psi = \varphi + \textrm{arctan}[K({\phi _s} - {\phi _c})].\end{equation}

Here, ${\phi _c} = {\phi _{{c_0}}}$ holds during the incipient failure of the slopes.

We then applied the proposed formulation to predict the incipient angle of granular slopes. It should be noted that the collisional solid pressure $p_s^c$ vanishes at the incipient failure stage and thus ${p_s} = p_s^e$. When the granular bed is static, in the direction normal to the slope, the inter-particle pressure without the frictional dilatation/contraction effect $p_{s0}^e$ balances the gravity as

(4.9)\begin{equation}{\phi _s}{p_s} = {\phi _s}{\rho _s}gh\,\cos \,{\theta _0},\end{equation}

where

(4.10)\begin{equation}{p_s} = p_{s0}^e = G{({\phi _s} - {\phi _ \ast })^\chi }.\end{equation}

Hence, $p_{s0}^e = G{({\phi _s} - {\phi _ \ast })^\chi } = {\rho _s}gh\,\textrm{cos}\,{\theta _0}$. As the granular slope approaches to the critical incipient state, before the incipient motion is detected, the grains on the slope surface undergo a small shear strain ${\gamma _ \ast }$ during the failure. Owing to the rearrangement of contact force chains along with the strain, the solid pressure changes from ${p_s} = p_{s0}^e$ to ${p_s} = p_{s0}^e\,{\textrm{e}^{\Re {\gamma _ \ast }\,\textrm{tan}\,\psi }}$ in the frictional dilatation/contraction and the forces in the direction normal to the slope cease to be in equilibrium. In the densely packed granular slope, the solid pressure increases and the resultant force in the normal direction becomes upward, which leads to a dilatation of the assembly. Conversely, in the loosely packed granular bed, the solid pressure decreases and the resultant force directs downward, which induces a contraction in the bed. In the direction along the slope, the equilibrium condition is still valid. Hence,

(4.11)\begin{equation}{\phi _s}{p_s}\,\textrm{tan}\,\varphi = {\phi _s}{\rho _s}gh\,\textrm{sin}\,{\theta _0},\end{equation}

where

(4.12)\begin{equation}{p_s} = p_{s0}^e\,{\textrm{e}^{\Re {\gamma _ \ast }\,\textrm{tan}\,\psi }} = {\rho _s}gh\,\textrm{cos}\,{\theta _0}\,{\textrm{e}^{\Re {\gamma _ \ast }\,\textrm{tan}\,\psi }}.\end{equation}

The effect of the dilatation/contraction on the friction coefficient during the incipient period is neglected. Combining (4.11) and (4.12) gives

(4.13)\begin{equation}\textrm{tan}\,{\theta _0} = {\textrm{e}^{\Re {\gamma _ \ast }\,\textrm{tan}\,\psi }}\,\textrm{tan}\,\varphi ,\end{equation}

which can be written explicitly as

(4.14)\begin{equation}{\theta _0} = \varphi + \arctan \left[ {\frac{{{\textrm{e}^{\Re {\gamma_ \ast }\,\textrm{tan}\,\psi }} - 1}}{{1/\textrm{tan}\,\varphi + {\textrm{e}^{\Re {\gamma_ \ast }\,\textrm{tan}\,\psi }}\,\textrm{tan}\,\varphi }}} \right].\end{equation}

Substituting $\chi {\phi _s}/({\phi _s} - {\phi _ \ast })$ for $\Re $ and $K({\phi _s} - {\phi _c})$ for $\textrm{tan}\,\psi $ as in § 3, we finally obtain

(4.15)\begin{equation}{\theta _0} = \varphi + \arctan \left[ {\frac{{{\textrm{e}^{c{\phi_s}({\phi_s} - {\phi_c})/({\phi_s} - {\phi_ \ast })}} - 1}}{{1/\textrm{tan}\,\varphi + {\textrm{e}^{c{\phi_s}({\phi_s} - {\phi_c})/({\phi_s} - {\phi_ \ast })}}\,\textrm{tan}\,\varphi }}} \right],\end{equation}

where $c = \chi {\gamma _ \ast }K$. It is noted that in this case we do not apply (3.14) to replace ${\gamma _ \ast }$ with ${c_1}I_d^{{c_2}}$ but keep ${\gamma _ \ast }$ in the equation as a parameter because the shear rate of the slope during the incipient motion is not measurable. Moreover, it is more reasonable to relate the incipient dynamics of granular slopes at the critical state to the shear strain than to the shear rate. In Gravish & Goldman (Reference Gravish and Goldman2014), the measured critical volume fraction of dilatancy ${\phi _c}$ was 0.595, the material parameter for dilatancy K was 22.4 and the internal friction angle of grains in the air $\varphi $ was $17.0^\circ $. A random loosely packed volume fraction of ${\phi _ \ast } = 0.570$ was determined according to the experimental setup. Here $\chi \textrm{ = 3}\textrm{.50}$ was set, which was the median value of its range (see § 3.2 and table 1). A shear strain of ${\gamma _ \ast } = 0.026$, consistent with the analysis in appendix A, was obtained by fitting the results to the experimental data.

Figure 3 compares the computed incipient angles of the granular slope using (4.8) and (4.15) with the measured data. The results given by the present formulation agreed with the data much better than those by the classical saw model, especially when the initial packing fraction of the granular slope was larger than the critical value of dilatancy and the bed dilates.

Figure 3. Variation of the incipient angle of dry granular slope with the initial packing fraction in the experiment of Gravish & Goldman (Reference Gravish and Goldman2014). The measured critical volume fraction ${\phi _c} = 0.595$ with the grey bar indicating the measurement uncertainty.

Bonnet et al. (Reference Bonnet, Richard and Philippe2010) conducted a similar experiment to study the failure of immersed granular slopes in static water $({\rho _f} = 1.0\;\textrm{g}\;\textrm{c}{\textrm{m}^{ - 3}})$. The grains had a diameter of ${d_s} = 600\;\mathrm{\mu m}$ and a density of ${\rho _s} = 2.65\;\textrm{g}\;\textrm{c}{\textrm{m}^{ - 3}}$. The initial packing fraction of the granular particles in the bed ${\phi _s}$ varied from 0.52 to 0.59 and the corresponding measured incipient angle of the slopes varied significantly with a notably high ratio of 2.5 between the maximal and the minimal values. It should be noted that the shear strain and the deformation of the free granular slope during the incipient stage are expected to be exceedingly small and, accordingly, the variation of pore pressure is not appreciable and neglected here. Therefore, the buoyancy of the grains was accounted for by substituting ${\rho _s} - {\rho _f}$ for ${\rho _s}$ in (4.5)–(4.6) and (4.9)–(4.12). Consequently, both (4.8) of the saw model and (4.15) of the present frictional dilatation/contraction theory can also be applied to determine the incipient angle of immersed granular slopes.

Figure 4 shows the comparisons between the computed results and the measured data. According to the experimental results of Bonnet et al. (Reference Bonnet, Richard and Philippe2010), the parameter $K = 20.8$, the critical volume fraction of dilatancy ${\phi _c} = 0.545$ and the internal friction angle of gains in the water $\varphi = 38.6^\circ $. A random loosely packed volume fraction of ${\phi _ \ast } = 0.510$ was roughly determined, as the minimal value of the packing fraction prepared in the experiment was between 0.51 and 0.52. Same as that in the dry slope case, a value of $\chi = 3.50$ was also set. According to the verification against the measured data, a shear strain of ${\gamma _ \ast } = 0.019$ was adopted, which had the same order as that in the dry slope case. Values of the parameters are summarized in table 1. Figure 4 shows that the computed incipient angle by the present formulation agreed generally well with the measured data and the fitness was better than that between the results of the classical saw model and the data. The present formulation performs well in the dilatation situation and only slightly overestimates the incipient angle when the bed experiences a contraction. For the cases of ${\phi _s} - {\phi _c} \le - 0.02$, where the incipient angle seems to vary little with the packing fraction, both the present theory and the classical saw model have an underestimation, which may arise from the lack of effect from the fluid viscosity on slope failures. In immersed granular media, solid particles have an additional cohesion owing to the viscosity of interstitial fluid, noted as $c^{\prime}$. At the critical state, there is a balance along the slope among the additional particle cohesion, the inter-particle shear stress and the gravity as ${\phi _s}(c^{\prime} + {p_s}\,\textrm{tan}\,\varphi ) = {\phi _s}({\rho _s} - {\rho _f})gh\,\textrm{sin}\,{\theta _0}$. In the cases of ${\phi _s} - {\phi _c} \le - 0.02$, owing to frictional contraction, the inter-particle pressure and shear stress decrease significantly and could have a smaller value than $c^{\prime}$. As a result, the additional particle cohesion predominates in resisting the incipient motion of the slope, which yields ${\theta _0} = \arcsin [c^{\prime}/({\rho _s} - {\rho _f})gh]$. Assuming a same value of $c^{\prime}$ for the cases with different packing fractions, we can find that the slope incipient angle varies little with the packing fraction. For an accurate quantification of the phenomenon, more measured data are required in further investigations.

Figure 4. Variation of the incipient angle of immersed granular slopes in water with the initial packing fraction in the experiment of Bonnet et al. (Reference Bonnet, Richard and Philippe2010). The measured critical volume fraction is ${\phi _c} = 0.545$ and the grey bar represents the uncertainty in the measurement.

5.1. Two-phase continuum model based on the smoothed particle hydrodynamics method

The present dilatation/contraction theory is integrated into the model of Shi et al. (Reference Shi, Si, Dong and Yu2019), which is a two-phase continuum model based on the weakly compressible smoothed particle hydrodynamics (WCSPH) method. The controlling equations, i.e. conservation equations of mass and momentum of the two phases, are obtained by first averaging the physical variables of each phase in a control volume following Drew (Reference Drew1983) for a continuum description of both phases, and then spatially filtering through Favre averaging for the turbulence. The equations are then written into Lagrangian form for numerical implementation using the SPH method. Here, for brevity, we only give a minimum description of the model. Detailed derivation of the equations and numerical implementations of the model can be found in Shi, Yu & Dalrymple (Reference Shi, Yu and Dalrymple2017) and Shi et al. (Reference Shi, Si, Dong and Yu2019).

The governing equations of the solid phase are

(5.1)\begin{gather}\frac{{\textrm{d}{\phi _s}}}{{\textrm{d}t}} ={-} {\phi _s}\boldsymbol{\nabla }\boldsymbol{\cdot }{\boldsymbol{u}_f} - \boldsymbol{\nabla }\boldsymbol{\cdot }[{\phi _s}({\boldsymbol{u}_s} - {\boldsymbol{u}_f})],\end{gather}

(5.2)\begin{gather}\begin{array}{ccccc} \dfrac{{\textrm{d}{\boldsymbol{u}_s}}}{{\textrm{d}t}} & ={-} [({\boldsymbol{u}_s} - {\boldsymbol{u}_f})\boldsymbol{\cdot }\boldsymbol{\nabla }]{\boldsymbol{u}_s} + \dfrac{1}{{{\phi _s}{\rho _s}}}\boldsymbol{\nabla }\boldsymbol{\cdot }({\phi _s}{\boldsymbol{\sigma }_s}) + \boldsymbol{g} + \dfrac{1}{{{\phi _s}{\rho _s}}}\boldsymbol{\nabla }\boldsymbol{\cdot }({\phi _s}\boldsymbol{\sigma }_s^t)\\ & \quad - \dfrac{1}{{{\rho _s}}}\boldsymbol{\nabla }{p_f} + \dfrac{\boldsymbol{F}}{{{\phi _s}{\rho _s}}}, \end{array}\end{gather}

and those of the interstitial fluid phase are

(5.3)\begin{gather}\frac{{\textrm{d}({\phi _f}{\rho _f})}}{{\textrm{d}t}} ={-} ({\phi _f}{\rho _f})\boldsymbol{\nabla }\boldsymbol{\cdot }{\boldsymbol{u}_f},\end{gather}

(5.4)\begin{gather}\frac{{\textrm{d}{\boldsymbol{u}_f}}}{{\textrm{d}t}} = \frac{1}{{{\phi _f}{\rho _f}}}\boldsymbol{\nabla }\boldsymbol{\cdot }({\phi _f}{\boldsymbol{\tau }_f}) + \boldsymbol{g} + \frac{1}{{{\phi _f}{\rho _f}}}\boldsymbol{\nabla }\boldsymbol{\cdot }{\bf (}{\phi _f}\boldsymbol{\tau }_f^t{\bf )} - \frac{1}{{{\rho _f}}}\boldsymbol{\nabla }{p_f} - \frac{\boldsymbol{F}}{{{\phi _f}{\rho _f}}}.\end{gather}

In the equations, ${\rho _f}$, ${\boldsymbol{u}_f}$ and ${\phi _f}$ are respectively the density, velocity and volumetric fraction of the fluid phase; and ${\boldsymbol{\tau}_f}$ and $\boldsymbol{\tau }_f^t$ are the kinetic and the turbulent shear stresses of the fluid phase, respectively. The other notations have the same meaning as in § 2. For any physical variable X, $\textrm{d}X/\textrm{d}t = \partial X/\partial t + ({\boldsymbol{u}_f}\boldsymbol{\cdot }\boldsymbol{\nabla })X$. This indicates that the velocity of a SPH particle is set to be the same as the fluid velocity it carries. When concerning saturated granular flows, we have ${\phi _s} + {\phi _f} = 1$.

The constitutive law integrating the present dilatation/contraction formulation is used to determine the inter-grain stress of the solid phase as

(5.5)\begin{align}{\boldsymbol{\sigma }_s} & = 2{\rho _s}{\nu _s}{\boldsymbol{S}_s} - {p_s}\boldsymbol{I} = 2{\rho _s}{\nu _s}{\boldsymbol{S}_s}\nonumber\\ & \quad - \left\{ {p_{s0}^e\,\textrm{exp}\left[ {{c_1}K\dfrac{{\chi {\phi_s}}}{{{\phi_s} - {\phi_ \ast }}}({\phi_s} - {\phi_c})I_d^{{c_2}}} \right] + 2{{\left( {\dfrac{{{c_3}{\phi_s}}}{{{\phi_0} - {\phi_s}}}} \right)}^2}({{\rho_f}{\nu_f} + 2{c_4}{\rho_s}d_s^2||{{\boldsymbol{S}_s}} ||} )||{{\boldsymbol{S}_s}} ||} \right\}\boldsymbol{I}, \end{align}

(5.6)\begin{align}{\nu _s} &= \frac{{\mu {p_s}}}{{2{\rho _s}||{{\boldsymbol{S}_s}} ||}},\end{align}

and

(5.7)\begin{equation}\mu = {\mu _1} + \frac{{{\mu _2} - {\mu _1}}}{{1 + \sqrt {{I_0}/{I_m}} }}.\end{equation}

The combined dimensionless number for immersed granular flows, ${I_m}$, is calculated by (3.18), which is recalled here as

(5.8)\begin{equation}{I_m} = \frac{{2||{{\boldsymbol{S}_s}} ||({\rho _f}{\nu _f} + 2{c_4}{\rho _s}d_s^2||{{\boldsymbol{S}_s}} ||)}}{{{p_s}}}.\end{equation}

Here ${\boldsymbol{S}_s}$ is defined as in (2.4) and $||{{\boldsymbol{S}_s}} ||= \sqrt {{\boldsymbol{S}_s}:{\boldsymbol{S}_s}/2}$. The notations have the same meaning as in §§ 2 and 3. The frictional solid pressure without the dilatation/contraction effect $p_{s0}^e$ can be determined by (3.7), which is a general form of the existing formulae for $p_{s0}^e$. However, for comparison with the model of Shi et al. (Reference Shi, Si, Dong and Yu2019) excluding the frictional dilatation/contraction effect, the formula of $p_{s0}^e$ adopted in Shi et al. (Reference Shi, Si, Dong and Yu2019) is also used in this section. It is shown as

(5.9)\begin{equation}p_{s0}^e = \left\{ {\begin{array}{@{}ll} {G{{({\phi_s} - {\phi_ \ast })}^\chi }\left[ {1 + \sin \left( {\dfrac{{{\phi_s} - {\phi_ \ast }}}{{{\phi^ \ast } - {\phi_ \ast }}}\pi - \dfrac{\pi }{2}} \right)} \right]}&{{\phi_s} \gt {\phi_ \ast }}\\ 0&{{\phi_s} \le {\phi_ \ast }} \end{array}} \right.,\end{equation}

where ${\phi ^ \ast }$ is the random close-packing volume fraction of the granular assembly. The difference between (5.9) and (3.7) is simply the inclusion of the volume fraction ${\phi _s}$ for the compressibility of grains. This inclusion only leads to a minor difference in the values of $\chi $ and has no notable effect on the results.

The stress of the solid phase induced by interstitial fluid turbulence $\boldsymbol{\sigma }_s^t$ is usually neglected in subaerial granular flows. In submerged cases, it is expressed as

(5.10)\begin{equation}\boldsymbol{\sigma }_s^t = 2{\rho _s}\nu _s^t{\boldsymbol{S}_s} - p_s^t\boldsymbol{I},\end{equation}

in which $\nu _s^t$ and $p_s^t$ are respectively the turbulent viscosity and pressure of the solid phase, which indicate the effects of interstitial fluid turbulence on grains. In dense granular flows, $p_s^t$ is generally much smaller than ${p_s}$ and can therefore be neglected (Bouchut et al. Reference Bouchut, Fernández-Nieto, Mangeney and Narbona-Reina2016; Baumgarten & Kamrin Reference Baumgarten and Kamrin2019). The turbulent viscosity $\nu _s^t$ is estimated by the Smagorinsky turbulence model in (5.13).

The kinetic and the turbulent shear stresses of the fluid phase are formulated as

(5.11)\begin{equation}{\boldsymbol{\tau }_f} = 2{\rho _f}{\nu _f}{\boldsymbol{S}_f},\end{equation}

and

(5.12)\begin{equation}\boldsymbol{\tau }_f^t = 2{\rho _f}\nu _f^t{\boldsymbol{S}_f},\end{equation}

where ${\nu _f}$ is the fluid kinematic viscosity and $\nu _f^t$ is the turbulent viscosity of the fluid phase. Here $\nu _f^t$, together with the turbulent solid viscosity $\nu _s^t$, is estimated by the Smagorinsky model proposed in Dalrymple & Rogers (Reference Dalrymple and Rogers2006) but integrated with a modification for the turbulence damping by solid particles. It is shown as

(5.13)\begin{equation}\nu _k^t = 2{({C_{S,k}}\mathrm{\Delta })^2}||{{S_k}} ||{\left( {1 - \frac{{{\phi_s}}}{{{\phi^ \ast }}}} \right)^n},\end{equation}

in which the subscript $k = f,\,s$; $\mathrm{\Delta }$ is the size of the SPH particles; ${C_{S,k}}$ is the Smagorinsky coefficient and, in this paper, we set ${C_{S,f}} = {C_{S,s}} = 0.1$; and the index n is for the effects of turbulence damping by solid particles and $n = 5$ is adopted according to Chen et al. (Reference Chen, Li, Niu, Chen and Yu2011) and Shi et al. (Reference Shi, Si, Dong and Yu2019).

In submerged dense granular flows, the inter-phase force $\boldsymbol{F}$ can be simplified to include only the drag force that is predominant. The formula proposed by Gidaspow (Reference Gidaspow1994) is adopted to estimate the drag force as

(5.14)\begin{equation}\boldsymbol{F} = {\phi _s}\beta ({\boldsymbol{u}_f} - {\boldsymbol{u}_s}),\end{equation}

where

(5.15)\begin{equation}\beta = \left\{ {\begin{array}{@{}ll} {\dfrac{3}{4}{C_D}\dfrac{{{\rho_f}|{{\boldsymbol{u}_f} - {\boldsymbol{u}_s}} |}}{{{d_s}}}\phi_f^{ - 1.65}}&{{\phi_s} \le 0.2}\\ {150\dfrac{{{\phi_s}{\rho_f}{\nu_f}}}{{{\phi_f}d_s^2}} + 1.75\dfrac{{{\rho_f}|{{\boldsymbol{u}_f} - {\boldsymbol{u}_s}} |}}{{{d_s}}}}&{{\phi_s} \gt 0.2} \end{array}} \right.\end{equation}

and

(5.16)\begin{equation}{C_D} = \left\{ {\begin{array}{@{}ll} {\dfrac{{24}}{{R{e_s}}}(1.0 + 0.15Re_s^{0.687})}&{R{e_s} \lt 1000}\\ {0.44}&{R{e_s} \ge 1000} \end{array}} \right..\end{equation}

Here ${C_D}$ is the drag coefficient and $R{e_s}$ is the particle Reynolds number, defined by $R{e_s} \equiv {\phi _f}|{\boldsymbol{u}_f} - {\boldsymbol{u}_s}|{d_s}/{\nu _f}$. The term $|{\boldsymbol{u}_f} - {\boldsymbol{u}_s}|$ is the norm of the relative velocity between the two phases.

In the WCSPH method, the fluid is assumed to be weakly compressible and thus ${\rho _f}$ is not a constant. Hence, one more equation is required to complete the model. The equation of state proposed by Shi et al. (Reference Shi, Yu and Dalrymple2017) is used to relate the fluid pressure ${p_f}$ in the solid–liquid mixture to the variable fluid density, shown as

(5.17)\begin{equation}{p_f} = \frac{{{\rho _{f0}}c_0^2}}{\xi }\frac{{{\phi _f}{\rho _f} + {\phi _s}{\rho _{f0}}}}{{{\phi _f}{\rho _f}}}\left[ {{{\left( {\frac{{{\phi_f}{\rho_f} + {\phi_s}{\rho_{f0}}}}{{{\rho_{f0}}}}} \right)}^\xi } - 1} \right],\end{equation}

where ${\rho _{f0}}$ is the reference density of the fluid when ${p_f} = 0$; $\xi $ is a material parameter; and ${c_0}$ is the speed of sound in the fluid at the reference density. Usually, for numerical stability, a value of ten times the maximum flow velocity in the problem is adopted. In the present simulations of submerged granular column collapse, $\xi = 7$ and ${c_0} = 25\;\textrm{m}\;{\textrm{s}^{ - 1}}$ are set for the viscous liquid used in the experiments.

5.2. Model parameter characterizing the frictional dilatation/contraction

Rondon et al. (Reference Rondon, Pouliquen and Aussillous2011) conducted a well-known experiment of submerged granular column collapse in a viscous fluid using an experimental set-up as illustrated in figure 5. The experimental flume had a length of 70 cm, a width of 15 cm and a height of 15 cm, and was filled with liquid having a density of ${\rho _f} = 1.0\;\textrm{g}\;\textrm{c}{\textrm{m}^{ - 3}}$ and a kinematic viscosity of ${\nu _f} = 1.2 \times {10^{ - 5}}\;{\textrm{m}^2}\;{\textrm{s}^{ - \textrm{1}}}$ to a depth of $H = 15\;\textrm{cm}$. Initially, the granular column was confined by a removable gate at the left end of the flume. The column was composed of glass beads of density ${\rho _s} = 2.5\;\textrm{g}\;\textrm{c}{\textrm{m}^{ - 3}}$, mean diameter ${d_s} = 225\;\mathrm{\mu m}$ and internal friction angle $\varphi = 20.0^\circ $. The horizontal and the vertical directions were respectively defined as x and z. The columns were well prepared to a finite packing fraction, being in either loosely packed or densely packed states. In the cases studied in this paper, the columns had a fixed width of 6 cm in the x direction and the initial depth of the columns h varied. In the loosely packed case, $h = 4.8\;\textrm{cm}$ and the initial mean volume fraction of the column was ${\bar{\phi }_s} = 0.55$. In the densely packed case, $h = 4.2\;\textrm{cm}$ and ${\bar{\phi }_s} = 0.60$. A slight variation of the volume fraction over the depth, owing to gravity, existed in the columns but only the depth-averaged value was measured. A critical volume fraction of dilatancy ${\phi _{{c_0}}} = 0.58$ was observed in the measured data, around which there was a transition in the behaviours between the loosely and the densely packed columns (Rondon et al. Reference Rondon, Pouliquen and Aussillous2011). Once the gate was suddenly removed (in less than 0.1 s), the column collapsed.

Figure 5. Schematic representation of the experimental set-up of Rondon et al. (Reference Rondon, Pouliquen and Aussillous2011), also showing the profiles of the initial solid volume fraction in the loosely and densely packed columns, the linear profile of inter-grain pressure ${p_s} = p_s^e = p_{s0}^e$ in the initially static columns, and the hydrostatic profile of fluid pressure ${p_f}$.

To simulate a problem such as submerged granular column collapse, especially its time evolution process, it is essential to determine the initial conditions of all necessary variables as closely as possible. As the initial inter-grain pressure in the static columns ${p_s} = p_s^e = p_{s0}^e$ is to resist the immersed weight of grains, initial values of $p_{s0}^e$ must satisfy the static condition and have an almost linear distribution over the depth. Once the collapse starts, the frictional inter-grain pressure may increase or decrease owing to the rearrangement of contact force chains, which leads to the frictional dilatation or contraction of the granular assembly and distinct collapsing behaviours. However, in previous work on this problem (Lee & Huang Reference Lee and Huang2018; Si, Shi & Yu Reference Si, Shi and Yu2018), the static condition for initial inter-grain pressure was not met and the model parameters in the formulae of $p_{s0}^e$ were determined through only matching the computed and measured collapsing behaviours of the columns. The change in frictional inter-grain pressure arising from the rearrangement of contact force chains that leads to the dilatation/contraction of the granular assembly was not considered in previous models. As a result, in their models, the initial values of inter-grain pressure in the stationary loosely packed column were smaller while those in the stationary densely packed column were much greater than the static immersed weight of the grains. Indeed, the initial inter-grain pressure to balance the immersed weight of the static loosely packed and densely packed columns is close as the original heights of the two columns are similar with $h = 4.8\;\textrm{cm}$ in the loosely packed case and $h = 4.2\;\textrm{cm}$ in the densely packed case. The reason for the similar initial inter-grain pressure in the two columns with essentially different porosities is the difference in the arrangement of contact-force chains among the solid grains. Therefore, the parameter $\chi $ in the formula of $p_{s0}^e$ that characterizes the effect of the arrangement of contact-force chains on the frictional solid pressure has different values in the two cases. Once the column collapses, $\chi $ adjusts according to the proposed $\varDelta \chi $ in (3.9), which leads to a change in the frictional solid pressure and the frictional dilatation/contraction of granular columns.

The parameters ${\phi _ \ast } = 0.540$ and ${\phi ^ \ast } = 0.625$ are chosen so that all the values of the prepared packing fraction in the experiment are in the range of ${\phi _ \ast }\sim {\phi ^ \ast }$. The compressibility coefficient G for glass beads is ${10^9}\;\textrm{Pa}$. To achieve a linear profile of initial inter-grain pressure in the static columns, i.e. ${ {{p_s}(z)} |_{t = 0}} = p_{s0}^e(z) = ({\rho _s} - {\rho _f})g(h - z)$, the initial volume fraction is set to slightly vary vertically but have the same mean value with the experimental setup. The value of $\chi $ is determined carefully so that the initial ${\phi _s}$ varies in a narrow range. For the loosely packed case, $\chi $ is set to be $\chi = 2.64$ and the initial volume fraction increases from ${\phi _s} = 0.546$ on the surface to ${\phi _s} = 0.552$ at the bottom with a vertical average value of ${\bar{\phi }_s} = 0.550$. For the densely packed case, $\chi = 5.50$ is set and the initial ${\phi _s}$ increases from ${\phi _s} = 0.579$ downwards to ${\phi _s} = 0.607$ with an average value of ${\bar{\phi }_s} = 0.599$. The profiles of the initial volume fraction and the initial solid pressure are shown in figure 5.

The coefficients in (5.5) for the frictional solid pressure are set to be ${c_1}K = 2.5$ and ${c_2} = 0.10$ according to the model calibrations. The parameter K of the used granular material was not measured in the experiment. In the simulations, ${c_1}K$ is taken as a single parameter. The other coefficients in the model are determined following a sensitivity study given in appendix C with ${c_3} = 2.50$, ${c_4} = 0.10$ and ${\phi _0} = 0.610$ for the collisional solid pressure in (5.5); and ${\mu _2} = 0.8$ and $\sqrt {{I_0}} = 0.005$ for the friction coefficient in (5.7). Values of all the material and the adjustable parameters are summarized in table 1.

The proposed model was numerically implemented on the basis of the open-source weakly compressible SPH-package GPUSPH (Hérault, Bilotta & Dalrymple Reference Hérault, Bilotta and Dalrymple2010). The computational domain was represented by 111 192 SPH particles, which had an initial size of $\mathrm{\Delta } = 0.002\;\textrm{m}$. The fixed time step of the simulations was $\varDelta t = {10^{ - 5}}\;\textrm{s}$. The parallel computations were conducted on a Nvidia Tesla K40c CUDA-enabled graphics processing units card, which had 2880 processor cores and a compute capability of 3.5. It took approximately 4.2 h of computational time to simulate 4 s of the column collapse.

5.3. Column profiles and pore-pressure feedback

Figures 6 and 7 show the comparisons between the computed column profiles and the measured data in the loosely packed and the densely packed cases, respectively. Results computed by the present model, which includes both the frictional and the collisional dilatation/contraction effects, and by the model of Shi et al. (Reference Shi, Si, Dong and Yu2019), which does not account for the frictional dilatation/contraction effect, are presented together for comparison. The coefficients in the two models were the same. In both cases, there was a general agreement between the column profiles computed by the present model with the experimental data, especially a good agreement in the final depositions. For the loosely packed case, once the gate was removed, the whole upper part of the column crashed down immediately. The flow front moved rapidly and then stopped in 4 s at $x = 22.1\;\textrm{cm}$, which resulted in a long runout distance. The final deposition of the column was triangular. For the densely packed case, only grains at the right edge of the column fell freely after the gate was removed, while most of the column remained static. The collapse went inward with time and the flow front moved forward smoothly. The flow front stopped at $x = 12.0\;\textrm{cm}$ and the collapse process was complete in 33 s with a trapezium-shaped final deposition. The present model clearly captured the distinct behaviours of the initially loosely and densely packed columns, while the model of Shi et al. (Reference Shi, Si, Dong and Yu2019), without accounting for the frictional dilatation/contraction effect, failed. The model of Shi et al. (Reference Shi, Si, Dong and Yu2019) produced similar results for the two cases, in which the collapse of the loosely packed column was much slower, while that of the densely packed column was slightly quicker than the corresponding results from the present model. The comparisons between the results of the two models demonstrate the importance of the frictional dilatation/contraction effect and the predicative capability of the present model integrating the proposed dilatation/contraction formulation.

Figure 6. Comparisons between the computed and the measured column profiles in the loosely packed case. The black dotted lines represent the initial profile of the column. The present model considers the frictional dilatation/contraction effect while the model of Shi et al. (Reference Shi, Si, Dong and Yu2019) does not. The magenta short-dotted curves are the column profiles computed by the model of Baumgarten & Kamrin (Reference Baumgarten and Kamrin2019), abbreviated as ‘B & K (2019)’ in the figure for brevity, which also takes the dilatation/contraction into account.

Figure 7. Comparisons between the computed and the measured column profiles in the densely packed case. The black dotted lines represent the initial profile of the column. The present model considers the frictional dilatation/contraction effect while the model of Shi et al. (Reference Shi, Si, Dong and Yu2019) does not. The magenta short-dotted curves are the column profiles computed by the model of Baumgarten & Kamrin (Reference Baumgarten and Kamrin2019), abbreviated as ‘B & K (2019)’ in the figure for brevity, which also takes the dilatation/contraction into account.

Another notable phenomenon resulting from the dilatation/contraction of submerged granular collapse is the change of pore pressure in the column. Rondon et al. (Reference Rondon, Pouliquen and Aussillous2011) reported that the pore pressure at the bottom of the granular column increased and decreased quickly in the loosely and the densely packed cases, respectively, once the collapse began. In the present two-phase model, the pore-pressure feedback in dilatation/contraction is implicitly taken into account by coupling the controlling equations of the two phases through the drag force and the constant total volumetric fraction. In the collapse of immersed granular columns, the rearrangement of contact-force chains induces a variation of inter-grain frictional stress, which further leads to an expansion/contraction of the solid phase and hence a relative motion between the solid and the liquid phases. In the case of dilatation, the expansion of the solid phase results in an increase in the column porosity and the liquid phase is pulled by the inter-phase drag force to expand, both of which induce a decrease in the pore pressure. Conversely, in the case of contraction, the pore pressure increases, owing to a decrease in the column porosity and a squeeze on the liquid phase by the drag force. Figure 8 shows the computed excess fluid pressure in the experimental domain at the early stage of the collapse. Figures 8(a) and 8(c) show that the pore pressure in the granular column computed by the present model increases in the loosely packed case but decreases in the densely packed case, which is consistent with the experimental observations. In figures 8(b) and 8(d), values of the excess pore pressure computed by the model without the frictional dilatation/contraction effect are negative in both the loosely and the densely packed cases, which differs markedly from the measurements. Hence, it is verified in figure 8 that the pore-pressure feedback can be reasonably captured by the present two-phase model integrating the proposed frictional dilatation/contraction formulation.

Figure 8. Computed excess fluid pressure by the present model (with the frictional dilatation/contraction) and the model of Shi et al. (Reference Shi, Si, Dong and Yu2019) (without the frictional dilatation/contraction). The black solid curves in the liquid represent the computed column profiles.

The computed variations of excess pore pressure and solid volume fraction at Point A (shown in figure 5) by the present model are given in figure 9. In the loosely packed case, the pore pressure increases rapidly once the column collapses and the maximum value of the computed excess pore pressure is approximately 210 Pa, which is slightly larger than the available measured data. In the densely-packed case, the pore pressure initially decreases significantly and then the excess pore pressure relaxes to zero. In both cases, the computed relaxation time by the present model is shorter than that observerd from the experimental results, especially in the loosely packed case. It should be noted that the fluctuations in the pressure are caused by the WCSPH numerical method itself. Figure 9 also shows that the solid volume fraction at Point A in the loosely packed case increases slightly and the fraction in the densely packed case decreases, which correspond respectively to the contraction and the dilatation of the columns.

Figure 9. Variations of excess pore pressure and solid volume fraction at Point A. The position of Point A is shown in figure 5. The magenta dotted curves are for the results computed by the model of Baumgarten & Kamrin (Reference Baumgarten and Kamrin2019), abbreviated as ‘B & K (2019)’ in the figures for brevity.

For further investigations on the performance of the proposed dilatation/contraction formulation, figures 6, 7 and 9 also compare the computed results by the present model with those by the model of Baumgarten & Kamrin (Reference Baumgarten and Kamrin2019). In their plastic constitutive law of granular materials, Baumgarten & Kamrin (Reference Baumgarten and Kamrin2019) integrated the dilatancy effect by adding a term of solid volumetric change to the plastic strain rate, which had a more complicated form than the present formulation. Figures 6 and 7 show that in the early stage of collapse, the computed column height by the present model agrees better with the measured data while the computed front position by Baumgarten & Kamrin (Reference Baumgarten and Kamrin2019) fits the data better. In both figures, the final deposition of the columns computed by the present model compares much better with the experimental observations. Figure 9, together with figure 14(a) of Baumgarten & Kamrin (Reference Baumgarten and Kamrin2019), shows that their model performs better in describing the variation of pore pressure even though there was a violent fluctuation in their results.