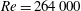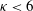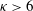1 Introduction
It is known that, for three-dimensional bodies, the first bifurcation in the flow solution as the Reynolds number is increased leads to steady symmetry-breaking modes. This has been demonstrated for axisymmetric bodies (Fabre, Auguste & Magnaudet Reference Fabre, Auguste and Magnaudet2008; Pier Reference Pier2008; Bohorquez et al. Reference Bohorquez, Sanmiguel-Rojas, Sevilla, Jiménez-González and Martínez-Bazán2011) and for bodies having a rectangular blunt base (Grandemange, Gohlke & Cadot Reference Grandemange, Gohlke and Cadot2012; Marquet & Larsson Reference Marquet and Larsson2014). At low Reynolds number, these steady modes play an important role in problems of fluid structure interaction – such as, for instance, the dynamics of falling bodies (Ern et al. Reference Ern, Risso, Fabre and Magnaudet2012). Recently, steady symmetry-breaking modes have been evidenced at large Reynolds numbers, leading to random multistable dynamics. For bodies having a reflectional symmetry, such as the Ahmed body, Grandemange, Gohlke & Cadot (Reference Grandemange, Gohlke and Cadot2013) have shown that the wake is bistable with a long time dynamics of random switching between two mirror-symmetry-breaking modes. These observations have been generalized to axisymmetric geometries by Grandemange, Gohlke & Cadot (Reference Grandemange, Gohlke and Cadot2014) and Rigas et al. (Reference Rigas, Oxlade, Morgans and Morrison2014), where the only two asymmetric states are replaced by an infinite number of asymmetric states due to the multiplicity of reflectional symmetries of the axisymmetric geometry.
As shown by Marquet & Larsson (Reference Marquet and Larsson2014), simple rectangular plates are subjected to these steady symmetry-breaking modes in the laminar regime, and one may wonder how they can interfere in the case of fluid structure interaction at large Reynolds numbers. The purpose of this work is to study the consequence of the dynamics of such static symmetry-breaking modes on a very simple fluid structure interaction experiment involving a three-dimensional turbulent wake.
The paper is organized as follows. Section 2 describes the flat plate geometry and the measurements. Results in § 3 are presented in three parts. Section 3.1 investigates the presence of the static symmetry-breaking modes for a fixed plate. The fluid structure interaction mechanism is then investigated in § 3.2. The effect of the plate aspect ratio on the plate dynamics is studied in § 3.3. Results are discussed with concluding remarks and perspectives in § 4.
2 Experimental set-up
The mechanical system is a simple plate that rotates freely around its short reflectional symmetry axis, as depicted in figure 1. The plate is made of Plexiglass, with a thickness
$L$
of 6 mm and a height
$H$
of 48 mm. The dimensional accuracy of the plate is approximately 0.05 mm. Aspect ratios
${\it\kappa}=H/W$
ranging from 1 to 8 are investigated with plates of different width
$W$
. The plates are pierced with a hole of 4.2 mm in diameter at the position
$H/2$
. The position of the hole is accurate only to 0.2 mm because it required a change of the machine tool. A brass rod (the axis of rotation) with a diameter of 4 mm, lubricated with silicone oil, is passed through the hole. The plate is then free to rotate around a fixed axis. Two Teflon annuli prevent the plate from sliding along the rod. We denote
${\it\theta}$
as the angle between the plate and the vertical unit vector
$\boldsymbol{e}_{y}$
, taken as positive in the clockwise direction.
Figure 1. Experimental set-up. Cross-section (a) and side view (b) of the hydrodynamic tunnel with a flat plate of aspect ratio
${\it\kappa}=H/W$
. In (a), the blocks T and R indicate the optical device that measures the position
${\it\delta}$
of the plate. The dashed frame in (b) represents the area for visualizations and PIV measurements. Angular velocity (c) during the free decay in air of the plate having
${\it\kappa}=2.4$
, and solid friction torque
${\it\gamma}_{S}$
(inlet) estimated from the linear decay displayed by the straight line.
The value of
${\it\gamma}_{S}$
, the friction torque per unit length (such that the total friction torque is
${\it\Gamma}_{S}={\it\gamma}_{S}W$
), is estimated for all the plates in air. The angular velocity decay
${\it\Omega}(t)$
of the free rotating plate is measured as shown in figure 1(c). In that case,
$I(\text{d}{\it\Omega}/\text{d}t)={\it\gamma}_{S}W$
, where the plate inertia is
$I={\it\rho}_{p}(H^{3}/12)WL$
and the plate density
${\it\rho}_{p}=1080~\text{kg}~\text{m}^{-3}$
. For all the plates, the velocity decrease becomes linear for
${\it\Omega}<100~\text{rad}~\text{s}^{-1}$
(the typical angular velocity never exceeds
$20~\text{rad}~\text{s}^{-1}$
in the following experiments). We find (see figure 1
c, inset) that
${\it\gamma}_{S}\simeq -4\times 10^{-3}~\text{N}$
for all plates.
The dynamical system is placed in a hydrodynamic tunnel of cross-section
$150~\text{mm}\times 80~\text{mm}$
. The test section is 800 mm long and completely transparent. The fluid is water (
${\it\rho}=1000~\text{kg}~\text{m}^{-3}$
). The main flow velocity is set to
$U_{0}=5.5~\text{m}~\text{s}^{-1}$
, such that the Reynolds number is defined as
$Re=(U_{0}H/{\it\nu})=264\,000$
, where
${\it\nu}$
is the kinematic viscosity of water. There is no cavitation in the flow except during visualizations for which the pressure in the tunnel is reduced to produce enough bubbles to seed the wake.
To determine the importance of the friction on the plate dynamics in the uniform water flow, it is convenient to estimate the hydrodynamic torque
${\it\gamma}$
from that of an oblique two-dimensional flat plate using the inviscid wake model (Wu Reference Wu1956). The theory gives
${\it\gamma}=-\ell ({\it\theta})F_{N}({\it\theta})$
, where
$\ell ({\it\theta})\simeq (1.8/7{\rm\pi})H{\it\theta}$
is the distance from the axis of rotation to the point of application of the normal force
$F_{N}({\it\theta})={\it\rho}U_{0}^{2}H({\rm\pi}\cos {\it\theta})(1+{\it\sigma})/(4+{\rm\pi}\cos {\it\theta})$
, as sketched in figure 2(a). For small angular deviations
$$\begin{eqnarray}{\it\gamma}({\it\theta})\simeq -\frac{{\rm\pi}}{4+{\rm\pi}}{\it\rho}U_{0}^{2}H(1+{\it\sigma})\ell ({\it\theta})=-C(1+{\it\sigma}){\it\theta},\end{eqnarray}$$
thus defining a hydrodynamic stiffness
$C=88\times 10^{-3}~\text{N}~\text{deg.}^{-1}$
, taking the cavity number (i.e. base suction)
${\it\sigma}=0$
, which corresponds to the Helmholtz wake that minimizes the normal force. At an inclination of
$1^{\circ }$
, the hydrodynamic torque
${\it\gamma}$
is one order of magnitude larger than the friction torque
${\it\gamma}_{S}$
, and friction is then negligible for angular positions
${\it\theta}>1^{\circ }$
.
Figure 2. Illustration (a) of the restoring torque due to the potential flow with cavity. Sketch of the low-pressure recirculation for the fixed plate (b) and steady state of the free plate with no net torque (c).
A Pegasus dual pulse 8 mJ Nd : YLF laser and a Photron APX RS camera with a resolution of
$1024\times 1024$
pixels are employed for particle image velocimetry (PIV) measurements using the Lavision software. The set-up acquires image pairs at a rate of
$f_{acq}=60~\text{Hz}$
, corresponding to the dimensionless frequency
$f_{acq}^{\ast }=f_{acq}(H/U_{0})=0.52$
. Conventional notations for the velocity components will be used, say
$(u,v,w)$
in the coordinate system
$(\boldsymbol{e}_{x},\boldsymbol{e}_{y},\boldsymbol{e}_{z})$
. The measurement area of the velocity field (plane
$z=0$
that gives access to
$u$
and
$v$
) is shown in figure 1(b). The thickness of the laser light sheet is approximately 3 mm. The interrogation window size is
$32\times 32$
pixels, with an overlap of 50 %. The window corresponds to a physical size of
$3.6~\text{mm}\times 3.6~\text{mm}$
. For simultaneous measurements with the plate angle,
${\it\theta}$
is deduced from the acquired frames. The resolution is then limited by the pixel density of the camera to
${\rm\Delta}{\it\theta}=\pm 0.15^{\circ }$
, and the sampling frequency of the angle is also 60 Hz. For the flow visualizations, the shutter of the camera is set to
$f_{acq}=60~$
Hz and the repetition rate of the laser to 2 kHz. As a result, bubble trajectories reveal the flow structure over a non-dimensional duration of
$\text{d}t^{\ast }=1/f_{acq}^{\ast }=1.91$
.
For accurate measurements of the angle, a high-speed, high-precision optical Keyence micrometer (LS-7070M), consisting of a transmission unit which emits light and a receiving unit which detects the position of the shadow of the targeting object, is used (see figure 1
a). The micrometer has an accuracy of
$\pm 3~{\rm\mu}\text{m}$
and a sampling frequency of 2000 Hz. In our case, it detects the horizontal position of the upper edge of the plate facing the flow, as indicated by the
${\it\delta}$
position in figure 1(b). The estimated accuracy for the angle measurements is
${\rm\Delta}{\it\theta}=\pm 0.01^{\circ }$
.
3 Results
For the remainder of the paper,
$a^{\ast }$
denotes the non-dimensional value of any quantity
$a(x,y,z,t)$
made dimensionless by a combination of the height
$H$
of the plate and the inlet velocity
$U_{0}$
. Time in non-dimensional units is thus defined as
$t^{\ast }=tU_{0}/H$
.
3.1 Fixed plate of aspect ratio
${\it\kappa}=3/2$
We first study the flow dynamics of the fixed plate using flow visualization. The striking result is the observation for a plate angle
${\it\theta}=0$
of an intermittency between two quasipermanent asymmetric recirculations, as shown in figure 3(a,b). Their lifetime is random and can be as long as a few seconds – say a few hundreds in terms of
$H/U_{0}$
units. In figure 3(a), a circular anticlockwise recirculation is clearly visible on the upper part of the plate base; we will call this flow structure the N state of the wake. Figure 3(b) is mirror symmetric with respect to figure 3(a), with a circular clockwise recirculation on the lower part of the base plate; it will be called the P state. The letter P for positive or N for negative refers to the sign of the vertical pressure gradient at the plate base, following the same terminology as in Grandemange et al. (Reference Grandemange, Gohlke and Cadot2013). The sign can be guessed from the visualization because the circular recirculation is a source of low pressure – as will be confirmed later in the paper, when the free plate is investigated.
Figure 3. Visualizations of N (a,c) and P (b,d) states of the wake with a fixed plate. (a,b)
${\it\theta}=0$
, (c)
${\it\theta}>0$
, (d)
${\it\theta}<0$
.
These two coherent wake states can be quasipermanently forced by breaking the top–bottom symmetry with a small inclination angle
${\it\theta}\neq 0$
. In figure 3(c) the state N is forced by a small positive angle, while in figure 3(d) the state P is forced with a small negative angle. It is worth mentioning that, for both cases, the base pressure gradient introduces a torque having the same sign as that of the torque in (2.1) resulting from the front pressure distribution. Hence, both front and base pressure distributions contribute constructively to a positive stiffness, as illustrated by the scheme in figure 2(b).
The long time dynamics is better quantified using the velocity field measurements, especially looking at the time series of the base velocity shown in figure 4(a) for three fixed angles defined as:
$$\begin{eqnarray}v_{b}^{\ast }=\int _{-1/2}^{+1/2}\,\text{d}y^{\ast }\int _{1/10}^{1/3}\,\text{d}x^{\ast }v^{\ast }.\end{eqnarray}$$
The bounding box size at the base is displayed on the instantaneous PIV field in figure 4(b1). For the vertical plate (
${\it\theta}=0$
), the base velocity in figure 4(a) explores both positive and negative values, but strikingly it is able to maintain the same sign during long time durations (approximately 100 non-dimensional units), thus confirming the previous visualizations. As expected, the positive base velocity event labelled (b1) in figure 4(a) is associated with an instantaneous N state in figure 4(b1) and the negative base velocity event (b2) is associated with an instantaneous P state in figure 4(b2). For both cases of a small inclination angle, the base velocity retains the same sign most of the time, corresponding instantaneously to either the N state for the positive angle and positive base velocity (figure 4
b3) or to the P state for the negative angle and negative base velocity (figure 4
b4).
Figure 4. Time series (a) of the base vertical velocity
$v_{b}^{\ast }$
of the fixed plate for, from top to bottom
${\it\theta}>0;=0;<0$
. The letters b1–b4 correspond respectively to the instantaneous PIV fields in (a) labelled (b1)–(b4). Velocity fields are displayed with streamlines (black lines) and the velocity modulus
$U_{xy}$
(colour map) in the
$(x,y)$
plane. The dashed rectangle in (a) is the integration area for the base velocity computation
$v_{b}^{\ast }$
in (3.1).
3.2 Free plate of aspect ratio
${\it\kappa}=3/2$
When the plate is free to rotate, it orientates itself almost perpendicularly to the flow direction (the horizontal position has a negative stiffness and is consequently unstable). The base velocity and the angle are simultaneously measured using the PIV set-up. Both time series are shown in figure 5 over a non-dimensional time duration of 350.
Figure 5. Angular position
${\it\theta}$
(crossed line) and base velocity (smooth line) versus time extracted from the PIV acquisition. Each label refers to an instantaneous velocity field in figure 6.
Figure 6. Instantaneous velocity field of the free plate. Each label refers to a time stamp denoted in figure 5.
The plate dynamics appears to be very singular, with discontinuities corresponding to high angular velocities. We can see that each of the large angular velocities
$\text{d}{\it\theta}/\text{d}t$
is correlated with an extreme base velocity
$v_{b}^{\ast }$
. Some of the large-deviation events move the system towards large
$|{\it\theta}|$
, such as during the periods [
$o1,o2$
] or [
$o3,o4$
], while others move the system back to small
$|{\it\theta}|$
, such as during the periods [
$b1,b2$
] or [
$b3,b4$
].
The wake is first investigated during deviations departing from
${\it\theta}=0$
at the instants o1–o4 in figure 6. In these figures, the plate picture is extracted from the PIV acquisition during which the velocity field is computed. It can be seen that the P state is present during the clockwise motion of the plate in the phase [
$o1,o2$
] with a strong negative base velocity (see figure 5). The clockwise motion indicates that the P state applies a positive torque on the plate. Similarly, the N state is present during the anticlockwise motion in the phase [
$o3,o4$
] with a strong positive base velocity (see figure 5). The anticlockwise motion indicates that the N state applies a negative torque on the plate. During the phase [
$o2,b1$
], the base velocity in figure 5 changes sign from an extreme negative value to an extreme positive value. At the instant b1, the wake has effectively changed to state N, as can be seen from figure 6, and again a negative torque is applied due to the presence of the N state during the phase [
$b1,b2$
]. An identical scenario is observed during the phase [
$o4,b4$
], where the base velocity changes sign again from an extreme positive value to an extreme negative value. At the instant
$o4$
the N state is present, whereas at the instant
$b3$
the definition of the state is not clear; however, at the instant
$b4$
the P state is clearly present, indicating a positive torque, producing a clockwise motion of the plate.
On the basis of these observations, the stochastic dynamics can be summarized as follows. Each state applies a torque on the plate that is able to produce an inclination angle which causes switching to the mirror state. For instance, the N state causes an inclination towards large negative angles
${\it\theta}<0$
, as during the phase [
$o3,o4$
], but from the fixed plate experiment, figure 4(d) indicates that
${\it\theta}<0$
is the condition for the observation of the P state, not the N state. Thus, the probability at
$o4$
to change state from N to P is very high. Indeed, the following switching revealed by the change in sign of the base velocity is clearly observable during the phase [
$o4,b3$
]. Finally, it is important to mention that, for the cases
$o2$
,
$o4$
and
$b4$
, the base pressure gradient of the wake mode introduces a torque with an opposite sign to that of the torque in (2.1) resulting from the front pressure distribution. These states, depicted in figure 2(c), can then correspond to stable equilibrium positions with an inclined plate. The lifetime of these equilibrium positions depends on the probability of the wake to change state for a given inclination angle
${\it\theta}$
.
3.3 Statistics and dynamics of free plates having different aspect ratio
Plates of 12 different widths
$W$
with free rotation are successively tested to study effect of the aspect ratio
${\it\kappa}$
on the fluid structure mechanism evidenced above. Time series are shown first over a non-dimensional duration of 1000 in figure 7.
Figure 7. Time series of the angular position
${\it\theta}(t^{\ast })$
for
${\it\kappa}=1$
to 8, in descending order from top to bottom.
At first glance, there is a huge variety of angle dynamics, depending on the value of the aspect ratio. Discontinuities, such as those evidenced in figure 5, are observable for
${\it\kappa}<6$
, with maximal amplitude deviations at approximately
${\it\kappa}=2.4$
. In this range, the dynamical system is able to maintain a constant non-zero angle for long non-dimensional periods of 100, and sometimes even longer. The power spectra in figure 8(a) are computed from time series acquired during a total non-dimensional time of 50 000, and are averaged over 500 time units, leading to a frequency resolution
$\text{d}f^{\ast }=0.002$
. All the spectra obtained with aspect ratio
${\it\kappa}<3.43$
exhibit a high energetic power law at low frequencies for
$f^{\ast }<0.2$
. The exponent, which varies from
$-2$
at
${\it\kappa}=1$
to
$-3$
at
${\it\kappa}=3.43$
, is associated with the random appearance of discontinuities (Grandemange et al.
Reference Grandemange, Gohlke and Cadot2013). Weak periodic oscillations of
${\it\theta}$
are observable in the spectra, as shown by the peak at Strouhal number
$St=0.235$
for
${\it\kappa}=1$
. Their frequencies are reduced to
$St=0.195$
as the aspect ratio is increased to
${\it\kappa}=2$
, with the periodic mode vanishing completely for even higher aspect ratios.
Figure 8. Power spectra (a) and probability density function (b) of the angular position
${\it\theta}(t^{\ast })$
for
${\it\kappa}=1$
to 8 in descending order from top to bottom. In (a), frequencies in non-dimensional units are defined as
$f^{\ast }=fH/U_{0}$
, dashed lines are
$-2$
and
$-3$
power laws.
The probability density functions (PDFs) of the angle
${\it\theta}$
are presented in figure 8(b). Wider distributions of angles are observed in the range
${\it\kappa}\simeq [2{-}4]$
. For these cases, the distributions are rather uniform, but sometimes (as for
${\it\kappa}=2,3$
) we can observe three weak, but significant, bumps. The central bump at
${\it\theta}=0$
is larger than the two symmetric ones located on both sides.
The mean angle is generally not zero, and some unexpected asymmetry of the distributions is observable. This emphasizes the sensitivity to symmetrical imperfection on the lever arm responsible for the plate dynamics, and is mainly due the accuracy in the axis position at
$H/2$
(see figure 1
b and § 2). We made new plates to improve this accuracy. However, the small clearance of 0.2 mm between the hole diameter and the axis diameter required for low-friction rotation creates a small permanent downward displacement of 0.1 mm of the plate from the origin
$O$
due to gravity, thus producing a plate angle equilibrium with uniform flow at a slightly positive value of
${\it\theta}$
.
At an aspect ratio
${\it\kappa}=6$
, the fluctuations of the angular position are minimum, and a clear transition to a very different regime occurs. For
${\it\kappa}>6$
, the spectra of the angular position look like the response of a linear oscillator to a random excitation with an eigenfrequency of
$St=0.14$
.
The high-frequency peaks in the spectrum obtained for
${\it\kappa}=8$
are suspected to originate from the vortex shedding of the plate, which is comparable to a square cylinder with
$W=6~$
mm sides. The highest-frequency peak at
$St=1.4$
provides a Strouhal number based on
$W$
,
$St_{W}=0.175$
, that is reasonable for this assumption. The motion can be caused by a rotation around the long axis of symmetry of the plate due to the small gap clearance around the cylindrical support, as well as a sliding motion in the
$z$
direction.
4 Discussion and concluding remarks
For aspect ratio
${\it\kappa}<6$
, the long time dynamics of the angular position (for frequencies
$f^{\ast }<0.2$
) is fully stochastic (i.e. no periodicity) with random appearances of high angular velocities. It is shown that static symmetry-breaking modes of the wake are responsible for the plate dynamics. Using a global stability analysis of the flow past rectangular plates, Marquet & Larsson (Reference Marquet and Larsson2014) predicted the presence of steady symmetry-breaking modes as soon as
${\it\kappa}<2.5$
and Reynolds number
$Re>150$
. There is then an agreement about the presence of the modes at low aspect ratios leading to a transition when the aspect ratio is increased. The larger critical aspect ratio obtained in the experiment can be ascribed to many effects – such as the large Reynolds number, the plate motion, the large blockage in the hydrodynamic tunnel and the presence of the cylinder axis.
The PDFs in figure 8(b) are almost uniform, meaning that the dynamics here is multistable (see the succession of steady angles in the dynamics shown in figure 7). From the low-Reynolds-number study of Marquet & Larsson (Reference Marquet and Larsson2014), we would actually expect four modes – a pair of static modes for each axis symmetry breaking. For the sake of simplicity, they can be roughly reduced to one asymmetric spatial mode, but with a variable azimuthal phase that can take four values. The static modes in a pair are then just shifted by
${\rm\pi}$
from each other (mirror modes, denoted P and N). From a more practical point of view, the azimuthal phase of the mode indicates the orientation of the torque exerted on the body. For our experiment, only both the mode P and N of the short-symmetry-axis breaking lead to a change of the angular positions of the plate, while the two modes of the long-symmetry-axis breaking do not have any effect on
${\it\theta}$
. If the four corresponding azimuthal phases are also explored during the turbulent dynamics, one would then expect a symmetric three-modal angle distribution with the probability for
${\it\theta}=0$
twice that of the probability at either
${\it\theta}>0$
or
${\it\theta}<0$
. It is clearly not the case; however, the distributions obtained for
${\it\kappa}=2,3$
in figure 8(b), with their three weak bumps, may present some similarity to this expectation. Since the distributions are almost uniform, it is likely that the wake dynamics is more similar to that of an axisymmetric body, as recently evidenced by Rigas et al. (Reference Rigas, Morgans, Brackston and Morrison2015). In that case, the dynamics is a combination of random noise of the azimuthal phase of the static mode, together with
${\rm\pi}$
phase jumps towards the mirror static mode. The appearance of the modulation in the angular distribution is perhaps due to a small preference towards azimuthal phase selections compatible with the two reflectional symmetries of the plate.
It is speculated that the projection of the resulting fluid force of the wake dynamics on the only degree of freedom (
${\it\theta}$
) of our simple mechanical system can produce the observed dynamics. A low-order model, based on the Langevin equation presented by Rigas et al. (Reference Rigas, Morgans, Brackston and Morrison2015), will be the next step in investigating the modelling of this stochastic fluid structure interaction.
Finally, it is noteworthy that, for low aspect ratios (
${\it\kappa}<6$
), the classical periodic vortex shedding (observed here at Strouhal numbers
$St\simeq 0.235{-}0.195$
), reminiscent of the Hopf bifurcation at low Reynolds number, is relegated as a second-order contribution to the dynamics, emphasizing the dominant strength of the asymmetric static modes and their related stochastic dynamics for large Reynolds numbers.
Acknowledgements
The work was motivated by a fruitful discussion with F. Gallaire and O. Marquet during the 6th International Symposium on Bifurcation and Instabilities in Fluid Dynamics. The author wish to thank O. Doaré for critical reading of the manuscript and for drawing attention to a characterization of the solid friction.
