1. Introduction
Natural convection is the buoyancy-driven flow resulting from unstable density variations, typically due to thermal or compositional inhomogeneities, in the presence of a gravitational field. It remains the focus of experimental, computational and theoretical research worldwide, in large part because buoyancy-driven flows are central to engineering heat transport, atmosphere and ocean dynamics, climate science, geodynamics and stellar physics. Rayleigh–Bénard convection, in which a layer of fluid is confined between isothermal horizontal boundaries with the higher temperature on the underside (Lord Rayleigh Reference Rayleigh1916), is studied extensively as a relatively simple system displaying the essential phenomena. Beyond the importance of buoyancy-driven flow in applications, Rayleigh's model has served for more than a century as a primary paradigm of nonlinear physics (Malkus & Veronis Reference Malkus and Veronis1958), complex dynamics (Lorenz Reference Lorenz1963), pattern formation (Newell & Whitehead Reference Newell and Whitehead1969) and turbulence (Kadanoff Reference Kadanoff2001).
A central feature of Rayleigh–Bénard convection is the Nusselt number 
$Nu$, the factor by which convection enhances heat transport relative to conduction alone. A fundamental challenge for the field is to understand how 
$Nu$ depends on the dimensionless control parameters: the Rayleigh number 
$Ra$, which is proportional to the imposed temperature difference across the layer, the fluid's Prandtl number 
$Pr$ and geometric parameters such as the domain's width-to-height aspect ratio 
$\varGamma$. Lord Rayleigh (Reference Rayleigh1916) studied the bifurcation from the static conduction state (where 
$Nu =1$) to convection (where 
$Nu >1$) when 
$Ra$ exceeds a 
$Pr$-independent finite value. In the strongly nonlinear large-
$Ra$ regime relevant to many applications, convective turbulence is characterized by chaotic plumes that emerge from thin thermal boundary layers and stir a statistically well-mixed bulk. Power-law behaviour, where 
$Nu$ scales like 
$Pr^\beta Ra^\gamma$, is often presumed for heat transport in the turbulent regime, but heuristic theories – i.e. physical arguments relying on uncontrolled approximations – yield various predictions for the scaling exponents. Rigorous upper bounds on 
$Nu$ derived from the equations of motion place restrictions on possible asymptotic exponents but do not imply unique values. Meanwhile, direct numerical simulations (DNS) and laboratory experiments designed to respect the approximations employed in Rayleigh's model have produced extensive data on 
$Nu$ over wide ranges of 
$Ra$, 
$Pr$ and 
$\varGamma$. Even so, consensus regarding the asymptotic large-
$Ra$ behaviour of 
$Nu$ remains to be achieved (Chillà & Schumacher Reference Chillà and Schumacher2012; Doering Reference Doering2020).
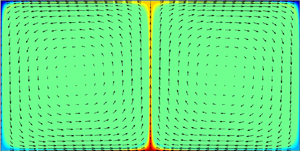
In addition to the turbulent convection generally observed at large 
${\textit {Ra}}$, there are much simpler steady solutions to the equations of motion, such as the pair of steady counter-rotating rolls shown in figure 1. Steady coherent flows are not typically seen in large-
${\textit {Ra}}$ simulations or experiments because they are dynamically unstable. Nonetheless, they are part of the global attractor for the infinite-dimensional dynamical system defined by Rayleigh's model, and recent results suggest that steady rolls may be one of the key coherent states comprising the ‘backbone’ of turbulent convection. In the case of no-slip top and bottom boundaries, Waleffe, Boonkasame & Smith (Reference Waleffe, Boonkasame and Smith2015) and Sondak, Smith & Waleffe (Reference Sondak, Smith and Waleffe2015) found that, over the range of Rayleigh numbers they explored, two-dimensional (2-D) steady rolls display 
${\textit {Nu}}$ values very close to those of three-dimensional (3-D) convective turbulence, provided that the horizontal period of the rolls is tuned to maximize 
${\textit {Nu}}$ at each value of 
${\textit {Ra}}$.
Figure 1. Steady convective rolls between stress-free boundaries for (a) 
$Ra=10^6$ and (b) 
$Ra=10^{8}$, with 
$Pr=1$ and a horizontal period that is twice the layer height. Colour represents dimensionless temperature and arrows indicate the velocity vector field. As 
$Ra\to \infty$, the temperature field develops an isothermal core while the thermal boundary layers and plumes become thinner and the velocity field converges to a 
$Ra$-independent pattern that lacks boundary layers.
Here we report computations of steady 2-D convective rolls in the case of stress-free top and bottom boundaries. We have carried out computations using spectral methods over eight orders of magnitude in 
${\textit {Ra}}$, four orders of magnitude in 
${\textit {Pr}}$ and more than an order of magnitude in the aspect ratio 
$\varGamma$, defined as the width-to-height ratio of a pair of rolls. As in the no-slip case, our steady states share many features with time-dependent simulations between stress-free boundaries (Paul et al. Reference Paul, Verma, Wahi, Reddy and Kumar2012; Wang et al. Reference Wang, Chong, Stevens, Verzicco and Lohse2020). Moreover, the results verify predictions about the 
$Ra\rightarrow \infty$ limit made by Chini & Cox (Reference Chini and Cox2009) who extended an approach initiated by Robinson (Reference Robinson1967) to construct matched asymptotic approximations of steady rolls between stress-free boundaries. In particular, our computations agree quantitatively with the asymptotic prediction that 
${\textit {Nu}} =\mathcal {O}({\textit {Ra}}^{1/3})$ uniformly in 
${\textit {Pr}}$ with a 
$\varGamma$-dependent prefactor that assumes its maximum value at 
$\varGamma \approx 1.9$, and with corresponding asymptotic predictions about the Reynolds number that are derived in appendix A. The rest of this paper is organized as follows. The equations governing Rayleigh–Bénard convection and our numerical scheme for computing steady solutions are outlined in § 2. The computational results are presented in § 3, followed by further discussion in § 4.
2. Governing equations and computational methods
The Boussinesq approximation to the Navier–Stokes equations used by Lord Rayleigh (Reference Rayleigh1916) to model convection in a 2-D fluid layer are, in dimensionless variables,
\begin{gather} \partial_t\boldsymbol{u} + \boldsymbol{u} \boldsymbol{\cdot} \boldsymbol{\nabla} \boldsymbol{u} = -\boldsymbol{\nabla} p + {\textit{Pr}} \nabla^2 \boldsymbol{u} + {\textit{Pr}} {\textit{Ra}}\,T \hat{\boldsymbol{z}}, \end{gather}
\begin{gather}\boldsymbol{\nabla} \boldsymbol{\cdot} \boldsymbol{u} = 0, \end{gather}
\begin{gather}\partial_t T + \boldsymbol{u} \boldsymbol{\cdot} \boldsymbol{\nabla} T = \nabla^2 T, \end{gather}
where 
$\boldsymbol {u} = u\hat {\boldsymbol {x}} + w\hat {\boldsymbol {z}}$ is the velocity, 
$p$ is the pressure and 
$T$ is the temperature. The system has been non-dimensionalized using the layer thickness 
$h$, the thermal diffusion time 
$h^2/\kappa$, where 
$\kappa$ is the thermal diffusivity, and the temperature drop 
$\varDelta$ from the bottom boundary to the top one.
The dimensionless spatial domain is 
$(x,z)\in [0,\varGamma ]\times [0,1]$, and all dependent variables are taken to be 
$\varGamma$-periodic in 
$x$. At the lower (
$z=0$) and upper (
$z=1$) boundaries, the temperature satisfies isothermal conditions while the velocity field satisfies no-penetration and stress-free boundary conditions:
\begin{equation} T|_{z=0}=1 \quad \text{and} \quad T|_{z=1} = 0, \quad w|_{z=0,1}=0, \quad \partial_z u|_{z=0,1}=0. \end{equation}
The three dimensionless parameters of the problem are the aspect ratio 
$\varGamma$, the Prandtl number 
${\textit {Pr}}=\nu /\kappa$, where 
$\nu$ is the kinematic viscosity, and the Rayleigh number 
$Ra=g\alpha {\rm \Delta} h^3/\nu \kappa$, where 
$-g\hat {\boldsymbol {z}}$ is the gravitational acceleration vector and 
$\alpha$ is the thermal expansion coefficient. A single pair of the steady rolls computed here fits in the domain, meaning the aspect ratio of the pair is 
$\varGamma$ while that of each individual roll is 
$\varGamma /2$.
The static conduction state, for which 
$\boldsymbol {u}=\mathbf 0$ and 
$T=1-z$, solves (2.1) and (2.2a–c) at all parameter values. Lord Rayleigh (Reference Rayleigh1916) showed that rolls vertically spanning the layer with aspect ratio 
$\varGamma$ bifurcate supercritically from the conduction state as 
${\textit {Ra}}$ increases past
\begin{equation} Ra_c(k) = \frac{(k^2+{\rm \pi}^2)^3}{k^2}, \end{equation}
where 
$k=2{\rm \pi} /\varGamma$ is the wavenumber of the fundamental period of the domain. The conduction state is absolutely stable if 
${\textit {Ra}}<{\textit {Ra}}_c(k)$ for all 
$k$ admitted by the domain (see e.g. Goluskin (Reference Goluskin2015)).
The Nusselt number is defined as the ratio of total mean heat flux in the vertical direction to the flux from conduction alone:
\begin{equation} {\textit{Nu}} = 1+ \langle wT\rangle, \end{equation}
where 
$w$ and 
$T$ are dimensionless solutions of (2.1) and 
$\langle \cdot \rangle$ indicates an average over space and infinite time. (For steady states, the time average is not needed.) The governing equations imply the equivalent expressions
\begin{equation} {\textit{Nu}} = \langle |\boldsymbol{\nabla} T|^2\rangle = 1+ \frac{1}{Ra} \langle |\boldsymbol{\nabla} u|^2 + |\boldsymbol{\nabla} w|^2 \rangle, \end{equation}
the latter of which self-evidently ensures 
${\textit {Nu}} > 1$ for all sustained convection. Another emergent measure of the intensity of convection is the bulk Reynolds number defined using the dimensional root-mean-squared velocity 
$U_{rms}$, which in terms of dimensional quantities is 
${\textit {Re}} ={U_{rms} h}/{\nu }$. We choose our reference frame such that 
$\left \langle u\right \rangle =0$, so in dimensionless terms
\begin{equation} {\textit{Re}} = \frac{1}{{\textit{Pr}}}\langle u^2+w^2\rangle^{1/2}. \end{equation} We compute steady (
$\partial _t = 0$) solutions of (2.1) using a vorticity–stream function formulation,
\begin{gather} \partial_z\psi\partial_x\omega - \partial_x\psi\partial_z\omega = {\textit{Pr}} \nabla^2 \omega + {\textit{Pr}} {\textit{Ra}}\partial_x \theta, \end{gather}
\begin{gather}\nabla^2 \psi = -\omega, \end{gather}
\begin{gather}\partial_z\psi\partial_x\theta - \partial_x\psi\partial_z\theta = -\partial_x\psi + \nabla^2 \theta, \end{gather}
where the stream function 
$\psi$ is defined by 
$\boldsymbol {u} = \hat {\boldsymbol {x}} \partial _z \psi - \hat {\boldsymbol {z}} \partial _x \psi$, the (negative) scalar vorticity is 
$\omega =\partial _x w- \partial _z u = -\nabla ^2 \psi$ and 
$\theta$ is the deviation of the temperature field 
$T$ from the conduction profile 
$1-z$. The boundary conditions used in our computations are that 
$\psi$, 
$\nabla ^2\psi$ and 
$\theta$ vanish on both boundaries. The latter two conditions follow from the stress-free and fixed-temperature conditions, respectively. Impenetrability of the boundaries implies that 
$\psi$ is constant on each boundary, and choosing the reference frame where 
$\left \langle u \right \rangle =0$ requires these constants to be identical. Their value can be fixed to zero since translating 
$\psi$ by a constant does not affect the dynamics.
We solve the time-independent (2.7) numerically using a Newton–GMRES (generalised minimal residual) iterative scheme. Starting with an initial iterate 
$(\omega ^0,\psi ^0,\theta ^0)$ that does not exactly solve (2.7), each iteration of the Newton's method applies a correction until the resulting iterates have converged to a solution of (2.7). Following Wen, Corson & Chini (Reference Wen, Corson and Chini2015b) and Wen & Chini (Reference Wen and Chini2018), the linear partial differential equations for the corrections are
\begin{gather} ({\textit{Pr}}\nabla^2 - \psi_z\partial_x + \psi_x\partial_z)^i\triangle^{\omega} + (-\omega_x\partial_z + \omega_z\partial_x)^i\triangle^{\psi} + {\textit{Ra}}{\textit{Pr}}\partial_x\triangle^{\theta} = -{F^\omega_{res}}^i, \end{gather}
\begin{gather}\triangle^{\omega} + \nabla^2\triangle^{\psi} = -{F^\psi_{res}}^i, \end{gather}
\begin{gather}(-\partial_x + \theta_z\partial_x - \theta_x\partial_z)^i\triangle^{\psi} + (\nabla^2 - \psi_z\partial_x + \psi_x\partial_z)^i\triangle^{\theta} = -{F^\theta_{res}}^i, \end{gather}
where the superscript 
$i$ denotes the 
$i\textrm {th}$ Newton iterate, the corrections are defined as
\begin{equation} \triangle^{\omega} = \omega^{i+1} - \omega^{i}, \quad \triangle^{\psi} = \psi^{i+1} - \psi^{i}, \quad \triangle^{\theta} = \theta^{i+1} - \theta^{i} \end{equation}and vanish on the boundaries, and
\begin{gather} F^\omega_{res} = {\textit{Pr}}\nabla^2\omega + {\textit{Ra}}{\textit{Pr}}\theta_x - \psi_z\omega_x + \psi_x\omega_z, \end{gather}
\begin{gather}F^\psi_{res} = \nabla^2\psi + \omega, \end{gather}
\begin{gather}F^\theta_{res} = \nabla^2 \theta - (\psi_z \theta_x - \psi_x \theta_z + \psi_x) \end{gather}
are the residuals of the nonlinear steady (2.7). We simplify the implementation by setting 
$F^\psi _{res}=0$, in which case 
$\triangle ^{\psi }$ can be obtained by solving 
$\nabla ^2\triangle ^{\psi } = -\triangle ^{\omega }$ for a given 
$\triangle ^{\omega }$. After this simplification, the pair (2.8a) and (2.8c) can be solved simultaneously for 
$\triangle ^{\omega }$ and 
$\triangle ^{\theta }$.
For each iteration of Newton's method, we solve (2.8a) and (2.8c) iteratively using the GMRES method (Trefethen & Bau III Reference Trefethen and Bau III1997). The spatial discretization is spectral, using a Fourier series in 
$x$ and a Chebyshev collocation method in 
$z$ (Trefethen Reference Trefethen2000). The 
$\nabla ^2$ operator is used as a preconditioner to accelerate convergence of the GMRES iterations. The roll states of interest have centro-reflection symmetries (cf. figure 1),
\begin{equation} [\omega, \psi, \theta](x, z) \!=\! [\omega, \psi, -\theta](\varGamma/2 - x, 1- z), \quad [\omega, \psi, \theta](x, z) = [-\omega, -\psi, \theta](\varGamma -\! x, z), \end{equation}
which allow the full fields to be recovered from their values on one quarter of the domain, so we encode these symmetries to reduce the number of unknowns. The GMRES iterations are stopped once the 
$L^2$-norm of the relative residual of (2.8a,c) is less than 
$10^{-2}$, and the Newton iterations are stopped once the 
$L^2$-norm of the relative residual of (2.7a,c) is less than 
$10^{-10}$. For 
${\textit {Ra}}$ not far above the critical value 
${\textit {Ra}}_c(k)$, convergence to rolls of period 
$\varGamma =2{\rm \pi} /k$ is accomplished by choosing the initial iterate with 
$\omega ^0 = -\sqrt {{\textit {Ra}}{\textit {Pr}}}\sin ({\rm \pi} z)\sin (k x)$ and 
$\theta ^0 = -0.1[\sin (2{\rm \pi} z) +\sin ({\rm \pi} z)\cos (k x)]$. For each 
$Pr$, results from smaller 
${\textit {Ra}}$ (or 
$\varGamma$) are used as the initial iterate for larger 
${\textit {Ra}}$ (or 
$\varGamma$).
3. Results
We computed steady rolls over a wide range of 
${\textit {Ra}}$ starting just above the value 
${\textit {Ra}}_c(k)$ at which the rolls bifurcate from the conduction state and ranging up to 
$10^9$ or higher depending on the other parameters. Computations were carried out for 
${\textit {Pr}}=10^{-2}, 10^{-1},1,10,10^2$ and a range of values of 
$\varGamma$ such that the fundamental wavenumber 
$k=2{\rm \pi} /\varGamma$ lies in 
$1/2\leqslant k\leqslant 10$. Data for all the 
$\varGamma =2$ cases are tabulated in the supplementary material available at https://doi.org/10.1017/jfm.2020.812.
Our computations reach sufficiently large 
${\textit {Ra}}$ to show clear asymptotic scalings of bulk quantities:
\begin{equation} {\textit{Nu}}\sim c_n(k){\textit{Ra}}^{1/3} \quad \mbox{and} \quad {\textit{Re}}\sim c_r(k){\textit{Pr}}^{-1}{\textit{Ra}}^{2/3} \quad \mbox{as} \quad {\textit{Ra}} \rightarrow \infty. \end{equation}
Both of these scalings are predicted by the asymptotic analysis of Chini & Cox (Reference Chini and Cox2009), although only the 
${\textit {Nu}}$ scaling was stated explicitly there. Chini & Cox (Reference Chini and Cox2009) gave an asymptotic prediction for the prefactor 
$c_n(k)$ but not for 
$c_r(k)$. Using their asymptotic approximations for the stream function and vorticity within each convection roll, we derived an expression for 
$c_r(k)$ in terms of 
$c_n(k)$ that is presented in appendix A.
Figure 2 shows the 
${\textit {Ra}}$-dependence of the compensated quantities 
${\textit {Nu}}/{\textit {Ra}}^{1/3}$ and 
${\textit {Re}}{\textit {Pr}}/{\textit {Ra}}^{2/3}$ for rolls of aspect ratio 
$\varGamma =2$ (
$k={\rm \pi}$) at various 
${\textit {Pr}}$. Rolls of this aspect ratio bifurcate from the conduction state at the Rayleigh number 
${\textit {Ra}}_c({\rm \pi} )=8{\rm \pi} ^4 \approx 779$. It is clear from figure 2 that both 
${\textit {Nu}}$ and the Péclet number 
${\textit {Re}}{\textit {Pr}}$ become independent of 
${\textit {Pr}}$ as 
${\textit {Ra}} \to \infty$, as predicted by the asymptotics of Chini & Cox (Reference Chini and Cox2009), and also as 
${\textit {Ra}}$ decreases towards the 
${\textit {Pr}}$-independent value 
${\textit {Ra}}_c$. Convergence to the large-
${\textit {Ra}}$ asymptotic scaling is slower when 
${\textit {Pr}}$ is larger, at least over the four decades of 
${\textit {Pr}}$ considered here. Numerical values of 
${\textit {Nu}}$ and 
${\textit {Re}}$ at large 
${\textit {Ra}}$ suggest scaling prefactors that are indistinguishable from the values 
$c_n({\rm \pi} )\approx 0.2723$ and 
$c_r({\rm \pi} ) \approx 0.0978$ predicted by asymptotic analysis.
Figure 2. The 
${\textit {Ra}}$-dependence of (a) 
${\textit {Nu}}$ and (b) 
${\textit {Re}}$, compensated by the asymptotic scalings (3.1), for steady convective rolls with 
$\varGamma =2$ (
$k={\rm \pi}$) at various 
${\textit {Pr}}$. Dashed lines in panels (a) and (b) denote, respectively, the asymptotic prefactor 
$c_n({\rm \pi} )\approx 0.2723$ from Chini & Cox (Reference Chini and Cox2009) and our asymptotic prediction 
$c_r({\rm \pi} ) \approx 0.0978$. Figure 6 shows the same 
${\textit {Nu}}$ values not compensated by 
${\textit {Ra}}^{1/3}$.
Nusselt and Reynolds numbers of steady rolls converge to the asymptotic scalings (3.1) over the full range 
$1/2\leqslant k\leqslant 10$ for which we have computed steady rolls. This is evident in figure 3 where the 
$k$-dependence of the compensated quantities 
${\textit {Nu}}/{\textit {Ra}}^{1/3}$ and 
${\textit {Re}} {\textit {Pr}} / {\textit {Ra}}^{2/3}$ is shown for various 
${\textit {Ra}}$ in the 
${\textit {Pr}}=1$ case. As 
${\textit {Ra}}$ increases, these quantities converge to asymptotic curves that we have called 
$c_n(k)$ and 
$c_r(k)$. It is clear from the figure that this convergence is slower when 
$k$ is larger, and that 
${\textit {Re}}$ reaches its asymptotic scaling sooner than 
${\textit {Nu}}$ does. Since rolls with 
$k={\rm \pi} /\sqrt 2$ are the first to bifurcate from the conduction state, at 
${\textit {Ra}}_c({\rm \pi} /\sqrt 2)=27{\rm \pi} ^4/4$, this is the 
$k$ that initially maximizes both 
${\textit {Nu}}$ and 
${\textit {Re}}$. As 
${\textit {Ra}}\to \infty$, the 
$k$ values that maximize 
${\textit {Nu}}$ and 
${\textit {Re}}$ approach the asymptotic values 
$k\approx 3.31$ (
$\varGamma \approx 1.9$) and 
$k\approx 1.4$ (
$\varGamma \approx 4.5$), respectively, where the corresponding maximal prefactors are 
$c_n\approx 0.273$ and 
$c_r\approx 0.117$.
Figure 3. The 
$k$-dependence of (a) 
${\textit {Nu}}$ and (b) 
${\textit {Re}}$, compensated by the asymptotic scalings (3.1), for steady convective rolls with 
${\textit {Pr}}=1$ at various 
${\textit {Ra}}$. The dashed lines in panels (a) and (b) are, respectively, the asymptotic prefactor 
$c_n(k)$ predicted by Chini & Cox (Reference Chini and Cox2009) and the corresponding prefactor 
$c_r(k)$ we derived using their results.
Both 
${\textit {Nu}}$ and the Péclet number 
${\textit {Re}} {\textit {Pr}}$ of steady rolls become nearly independent of 
${\textit {Pr}}$ as 
${\textit {Ra}}$ grows large. The large-
${\textit {Ra}}$ coalescence of data for different 
${\textit {Pr}}$ is evident for the 
$k={\rm \pi}$ case in figure 2, as is the fact that 
${\textit {Pr}}$ can have a substantial effect in the preasymptotic regime. To show that 
${\textit {Pr}}$-independence at large 
${\textit {Ra}}$ occurs over the full range 
$1/2\leqslant k\leqslant 10$ of our computations, figure 4 depicts the 
$k$-dependence of compensated 
${\textit {Nu}}$ and 
${\textit {Re}}$ at large 
${\textit {Ra}}$ for various 
${\textit {Pr}}$. All 
${\textit {Nu}}/{\textit {Ra}}^{1/3}$ and 
${\textit {Re}}{\textit {Pr}}/{\textit {Ra}}^{2/3}$ values plotted in figure 4 fall close to the asymptotic predictions for 
$c_n(k)$ and 
$c_r(k)$ that, at leading order in the asymptotic small parameter 
${\textit {Ra}}^{-1/3}$, are independent of 
${\textit {Pr}}$.
Figure 4. Dependence of compensated (a) 
${\textit {Nu}}$ and (b) 
${\textit {Re}}$ on 
$k$ for various 
${\textit {Pr}}$ in the large-
${\textit {Ra}}$ asymptotic regime. Reaching this regime requires larger 
${\textit {Ra}}$ when 
${\textit {Pr}}$ is larger. Asymptotic predictions (- - -) of 
$c_n(k)$ and 
$c_r(k)$ are as in figure 3.
The asymptotic scaling of steady rolls at large 
${\textit {Ra}}$ is reflected not only in the collapse of rescaled bulk quantities such as 
${\textit {Nu}}/{\textit {Ra}}^{1/3}$ and 
${\textit {Re}} {\textit {Pr}} / {\textit {Ra}}^{2/3}$ but also in the collapse of the boundary and internal layer profiles when the appropriate spatial variable is stretched by 
${\textit {Ra}}^{1/3}$. Figure 5 shows this collapse of the temperature and vorticity profiles at the bottom boundary and at the left edge of the periodic domain for the case where 
${\textit {Pr}}=1$ and 
$\varGamma =2$ (
$k={\rm \pi}$). Coincidence of these scaled profiles at large 
${\textit {Ra}}$ confirms that the thickness of both the thermal and vorticity layers scale as 
${\textit {Ra}}^{-1/3}$ on all four edges of a single convection roll, while both fields are strongly homogenized in the interior with 
$T\sim 1/2$ and 
$\omega \sim 0.522 {\textit {Ra}}^{2/3}$. Profiles at other 
${\textit {Pr}}$ are not shown but collapse similarly. These findings confirm the deduction of a homogenized interior by Chini & Cox (Reference Chini and Cox2009), as well as their prediction that the core vorticity magnitude is asymptotic to 
$\sqrt {c_n({\rm \pi} )}{\textit {Ra}}^{2/3}\approx 0.5218{\textit {Ra}}^{2/3}$ uniformly in 
${\textit {Pr}}$.
Figure 5. Scaled spatial structure of temperature 
$T$ and compensated vorticity 
$\omega$ near the (a) bottom and (b) left side of a convection roll where 
${\textit {Pr}}=1$ and 
$\varGamma =2$. Solid curves are spectral interpolants of 
$Ra=10^{10}$ values.
Another quantity of interest is the kinetic energy dissipation rate per unit mass,
\begin{equation} \varepsilon(\boldsymbol{x}^*,t^*) = \frac{\nu}{2} \sum_{i,j=1}^2(\partial_{x_i^*}u_j^* + \partial_{x_j^*}u_i^*)^2, \end{equation}
where 
$^*$ denotes dimensional variables. The corresponding bulk viscous dissipation coefficient 
$C = \langle \varepsilon \rangle h / U^{3}_{rms}$ can be expressed in dimensionless variables as
\begin{equation} C = {\textit{Re}}^{-3}{\textit{Pr}}^{-2}\left\langle \frac{1}{2} \sum_{i,j=1}^2(\partial_{i}u_j + \partial_{j}u_i)^2 \right\rangle. \end{equation}
Identity (2.5) gives 
$C = {\textit {Re}}^{-3}{\textit {Pr}}^{-2}{\textit {Ra}}({\textit {Nu}}-1)$, so the asymptotic scalings (3.1) imply
\begin{equation} C \sim c_n(k){c_r(k)}^{-3}{\textit{Pr}}{\textit{Ra}}^{-2/3} \sim c_n(k){c_r(k)}^{-2}{\textit{Re}}^{-1}. \end{equation}
That is, 
$C$ depends asymptotically on 
${\textit {Ra}}$ and 
${\textit {Pr}}$ via the distinguished combination 
${\textit {Pr}}{\textit {Ra}}^{-2/3}$ that is asymptotic to 
${\textit {Re}}^{-1}$. This scaling of the dissipation coefficient is characteristic of flows without viscous boundary layers, such as laminar Couette or Poiseuille flow, consistent with the steady velocity fields computed here (cf. figure 1). Indeed, for stress-free steady convection, viscous dissipation is dominated by that in the homogenized core since the vorticity is of the same asymptotic magnitude in the core as in the thin vorticity layers.
The average of dissipation over time and horizontal directions, denoted 
$\bar {\varepsilon }(z)$, has been used to compare convection between the cases of stress-free and no-slip boundaries. In 3-D simulations of the stress-free case at 
${\textit {Ra}}=5\times 10^6$, Petschel et al. (Reference Petschel, Stellmach, Wilczek, Lülff and Hansen2013) found that the normalized profile 
$\bar {\varepsilon }(z)/\langle \varepsilon \rangle$ exhibits ‘dissipation layers’ near the boundaries that depend strongly on 
${\textit {Pr}}$. In steady rolls, on the other hand, we find that 
$\bar {\varepsilon }(z)/\langle \varepsilon \rangle$ is independent of 
${\textit {Pr}}$ at asymptotically large 
${\textit {Ra}}$, as shown in figure S1 of the supplementary material.
4. Discussion
The steady rolls we have computed share many features with unsteady flows from DNS of Rayleigh–Bénard convection with isothermal stress-free boundary conditions. In recent simulations, Wang et al. (Reference Wang, Chong, Stevens, Verzicco and Lohse2020) found multistability between unsteady states exhibiting various numbers of roll pairs in wide 2-D domains. Each of the coexisting states suggested scalings approaching the 
${\textit {Nu}}=\mathcal {O}(Ra^{1/3})$ and 
${\textit {Re}}=\mathcal {O}({\textit {Ra}}^{2/3})$ asymptotic behaviour of steady rolls. As in the steady case, the prefactors of these scalings depended on the mean aspect ratios of the unsteady rolls. The highest Nusselt numbers among Wang et al.'s data occur in five-roll-pair states in a 
$\varGamma =16$ domain – meaning each roll pair has 
$\varGamma \approx 3.2$ on average – but steady 
$\varGamma = 3.2$ rolls have still larger 
${\textit {Nu}}$. At 
${\textit {Ra}} = 10^9$ and 
${\textit {Pr}}=10$, for example, the DNS exhibit 
${\textit {Nu}} = 198.01$ and 
${\textit {Re}} = 10\,135$ while steady 
$\varGamma = 3.2$ rolls at the same parameters yield the larger values of 
${\textit {Nu}} = 253.61$ and 
${\textit {Re}} = 11\,333$, and comparisons at other 
${\textit {Ra}}$ are similar (cf. table S4 of the supplementary material). Figure 6 shows the 
${\textit {Nu}}$ of these five-roll-pair DNS states along with the larger 
${\textit {Nu}}$ of the steady rolls computed here for various 
${\textit {Pr}}$ and 
$\varGamma =2$. The steady rolls also achieve larger 
${\textit {Nu}}$ values than have been attained in other unsteady simulations with stress-free boundaries in two dimensions (Goluskin et al. Reference Goluskin, Johnston, Flierl and Spiegel2014; van der Poel et al. Reference van der Poel, Ostilla-Mónico, Verzicco and Lohse2014) and in three dimensions (Petschel et al. Reference Petschel, Stellmach, Wilczek, Lülff and Hansen2013; Pandey, Verma & Mishra Reference Pandey, Verma and Mishra2014; Pandey & Verma Reference Pandey and Verma2016; Pandey et al. Reference Pandey, Verma, Chatterjee and Dutta2016).
Figure 6. Dependence of 
${\textit {Nu}}$ on 
${\textit {Ra}}$ for: steady rolls with 
$\varGamma =2$ and various 
${\textit {Pr}}$, time-dependent 2-D simulations with mean aspect ratio 
$\varGamma =3.2$ and 
${\textit {Pr}}=10$ (Wang et al. Reference Wang, Chong, Stevens, Verzicco and Lohse2020, see text), and upper bounds applying to all flows with 
$\varGamma =2\sqrt 2$ and any 
${\textit {Pr}}$ (Wen et al. Reference Wen, Chini, Kerswell and Doering2015a, see text). The dashed line is the asymptotic prediction 
${\textit {Nu}} \sim 0.2723 \,{\textit {Ra}}^{1/3}$ of Chini & Cox (Reference Chini and Cox2009) for 
$\varGamma =2$. The same 
${\textit {Nu}}$ values of steady rolls are shown compensated by 
${\textit {Ra}}^{1/3}$ in figure 1.
Comparing steady rolls in the stress-free case with those previously computed in the no-slip case, there are significant differences in their dependence on the aspect ratio 
$\varGamma$. With stress-free boundaries, 
${\textit {Nu}} =\mathcal {O}(Ra^{1/3})$ for each 
$\varGamma$ as 
${\textit {Ra}}\to \infty$, with maximal asymptotic heat transport attained by rolls of optimal aspect ratio 
$\varGamma \approx 1.9$. In the no-slip computations of Waleffe et al. (Reference Waleffe, Boonkasame and Smith2015) and Sondak et al. (Reference Sondak, Smith and Waleffe2015), on the other hand, the 
$\varGamma$ values that maximize 
${\textit {Nu}}$ decrease towards zero proportionally to 
${\textit {Ra}}^{-0.22}$ at large 
${\textit {Ra}}$. (A similar phenomenon occurs in porous medium Rayleigh–Bénard convection (see Wen et al. (Reference Wen, Corson and Chini2015b)).) The no-slip steady rolls display 
${\textit {Nu}}$ scaling like 
${\textit {Ra}}^{0.28}$ when 
$\varGamma$ is fixed but scaling like 
${\textit {Ra}}^{0.31}$ when the optimal 
$\varGamma$ is chosen to maximize 
${\textit {Nu}}$ at each 
${\textit {Ra}}$. The measured exponent 0.31 is unlikely to be exact, so it remains possible that the asymptotic scaling of optimal-
$\varGamma$ steady rolls is 
${\textit {Nu}}=\mathcal {O}({\textit {Ra}}^{1/3})$ in the no-slip case, as in the stress-free case.
Steady rolls in the stress-free and no-slip cases differ also in their dependence on the Prandtl number. Only with stress-free boundaries do the Nusselt number 
${\textit {Nu}}$ and Péclet number 
${\textit {Re}}{\textit {Pr}}$ apparently become uniform in 
${\textit {Pr}}$ as 
${\textit {Ra}}\to \infty$. To see how this 
$Pr$-independence emerges in the stress-free scenario, first note that area-integrated work by the buoyancy forces must balance area-integrated viscous dissipation – i.e. 
${\textit {Ra}} \left \langle wT\right \rangle =\left \langle |\boldsymbol {\nabla } u|^2 + |\boldsymbol {\nabla } w|^2 \right \rangle$ in the dimensionless formulation of (2.4) and (2.5). The former integral is dominated by plumes since the roll's core is isothermal, so it scales proportionally to the dimensional quantity 
$\alpha {\rm \Delta} g \delta hU_{rms}$, where 
$\delta$ is the dimensional plume thickness. The latter integral is dominated by the core since the vorticity is 
$\mathcal {O}(U_{rms}/h)$ everywhere in the stress-free case, so this integral scales proportionally to the dimensional quantity 
$\nu (U_{rms}/h)^2 h^2$. Balancing advection with diffusion of temperature anomalies in the thermal boundary layers, which also have thickness 
$\delta$, requires that 
$U_{rms}$ scales in proportion to 
$\kappa h/\delta ^2$. Combining this scaling relationship with that from the integral balance gives the dimensionless thermal boundary-layer thickness as 
$\delta /h = \mathcal {O}({\textit {Ra}}^{-1/3})$ – and so 
${\textit {Nu}} = \mathcal {O}(Ra^{-1/3})$ – uniformly in 
${\textit {Pr}}$. These relationships also imply that 
$U_{rms}$ is proportional to 
$(\kappa /h) {\textit {Ra}}^{2/3}$, and so the Péclet number 
${\textit {Re}}{\textit {Pr}}=U_{rms}h/\kappa$ scales as 
${\textit {Ra}}^{2/3}$ uniformly in 
${\textit {Pr}}$. Ultimately, it is the passivity of the vorticity boundary layers that results in the 
$Pr$-independence of these emergent bulk quantities. The vorticity layers not only make no contribution to the total dissipation at leading order but also have no leading-order effect on the stream function that is responsible for the convective flux 
$\langle wT\rangle$.
The 
${\textit {Re}}=\mathcal {O}({\textit {Ra}}^{2/3})$ scaling found at large 
${\textit {Ra}}$ for steady rolls and approximately evidenced in the DNS of Wang et al. (Reference Wang, Chong, Stevens, Verzicco and Lohse2020) means that buoyancy forces can sustain substantially faster-than-free-fall velocities. Indeed, if flow speeds were limited by the maximum buoyancy acceleration acting across the layer height then dimensional characteristic velocities could not be of larger order than 
$\sqrt {g \alpha {\rm \Delta} h}$, and 
${\textit {Re}}$ could not be larger than 
$\mathcal {O}({\textit {Ra}}^{1/2})$. Such 
${\textit {Re}}$ may be expected if the bulk flow was dominated by effectively independent rising and falling plumes. Significantly higher speeds apparently persist within coherent convection rolls, whether steady or unsteady.
Although steady rolls cannot give heat transport larger than 
${\textit {Nu}}=\mathcal {O}({\textit {Ra}}^{1/3})$ as 
${\textit {Ra}}\to \infty$ in the stress-free case (Chini & Cox Reference Chini and Cox2009), it is an open question whether larger 
${\textit {Nu}}$ can result from time-dependent flows or other types of steady states in either two dimensions or three dimensions. Rigorous upper bounds on 
${\textit {Nu}}$ derived from the governing equations – bounds depending on 
${\textit {Ra}}$ that apply to all flows regardless of whether they are steady or unsteady and stable or unstable – do not rule out 
${\textit {Nu}}$ growing faster than 
${\textit {Ra}}^{1/3}$. Specifically, for the 2-D stress-free case Whitehead & Doering (Reference Whitehead and Doering2011) proved analytically that 
${\textit {Nu}} \leqslant 0.289 \, {\textit {Ra}}^{5/12}$ uniformly in both 
${\textit {Pr}}$ and domain aspect ratio. Wen et al. (Reference Wen, Chini, Kerswell and Doering2015a) improved the prefactor of this bound by solving the relevant variational problem numerically, computing bounds up to large finite 
${\textit {Ra}}$ with a prefactor depending weakly on 
$\varGamma$. The numerical upper bound they computed for 
$\varGamma =2\sqrt 2$ is shown in figure 6; its scaling at large 
${\textit {Ra}}$ is 
${\textit {Nu}} \leqslant 0.106\, {\textit {Ra}}^{5/12}$. For 3-D flows in the stress-free case, only the larger upper bound 
${\textit {Nu}}\leqslant \mathcal {O}({\textit {Ra}}^{1/2})$ has been proved (Doering & Constantin Reference Doering and Constantin1996). It remains to be seen whether upper bounds smaller than 
$\mathcal {O}({\textit {Ra}}^{5/12})$ or 
$\mathcal {O}({\textit {Ra}}^{1/2})$ can be proved for 2-D or 3-D flows, respectively, and whether there exists any sequence of solutions for which 
${\textit {Nu}}$ grows faster than 
$\mathcal {O}{({\textit {Ra}}^{1/3})}$. In view of available evidence, it is possible that, at each 
${\textit {Ra}}$ and 
${\textit {Pr}}$, the steady 2-D roll with the largest value of 
${\textit {Nu}}$ – i.e. with 
${\textit {Nu}}$ maximized over 
$\varGamma$ – transports more heat than any other 2-D or 3-D solution. We are aware of no counterexamples to this possibility, either in the stress-free case studied here or in the no-slip case.
Acknowledgements
We thank L. M. Smith, D. Sondak and F. Waleffe for helpful discussions. This research was supported in part by US National Science Foundation awards DMS-1515161 and DMS-1813003, Canadian NSERC Discovery Grants Program awards RGPIN-2018-04263, RGPAS-2018-522657 and DGECR-2018-00371, and computational resources and services provided by Advanced Research Computing at the University of Michigan.
Declaration of interests
The authors report no conflict of interest.
Supplementary material
Supplementary material is available at https://doi.org/10.1017/jfm.2020.812.
Appendix A. Asymptotic calculation of 
$RePr/Ra^{2/3}$
In this appendix, we derive the asymptotic scaling relation for 
${\textit {Re}}$ that follows from the asymptotic analysis of Chini & Cox (Reference Chini and Cox2009) but is not reported there. In the large-
${\textit {Ra}}$ limit, a steady roll's velocity field is properly scaled by 
$(\kappa /h)Ra^{2/3}$ rather than by the thermal diffusion velocity 
$\kappa /h$. Accordingly, we introduce the rescaled dimensionless velocity 
$(u_\infty ,w_\infty )$, which is related to the dimensionless velocity in (2.1) by 
$(u,w) = Ra^{2/3}(u_\infty ,w_\infty )$. With this rescaling, the expression (2.6) for 
${\textit {Re}}$ becomes
\begin{equation} Re=\frac{1}{Pr}\left\langle u_\infty^2 + w_\infty^2 \right\rangle^{1/2} Ra^{2/3} = \frac{1}{Pr}\left\langle |\boldsymbol{\nabla} \psi_\infty|^2 \right\rangle^{1/2} Ra^{2/3},\end{equation}
where 
$\psi _\infty$ is the correspondingly rescaled stream function. Consequently, the prefactor in the asymptotic relation (3.1) for 
${\textit {Re}}$ satisfies
\begin{equation} c_r= \left\langle |\boldsymbol{\nabla} \psi_\infty|^2 \right\rangle^{1/2}. \end{equation}
To evaluate the right-hand side of (A 2) in 
$Ra\to \infty$ limit we first integrate by parts to find
\begin{equation} \int_0^1\int_0^{{\rm \pi}/k} |\boldsymbol{\nabla}\psi_\infty|^2\,\mathrm{d}\kern0.7pt x\,\mathrm{d}z=\left|\int_0^1\int_0^{{\rm \pi}/k} \psi_\infty \omega_\infty \,\mathrm{d}\kern0.7pt x\,\mathrm{d}z\right|\sim\varOmega_c(k)\left|\int_0^1\int_0^{{\rm \pi}/k} \psi_\infty(x,z) \,\mathrm{d}\kern0.7pt x\,\mathrm{d}z\right|_{\vphantom{\frac{2}/{3}}}, \end{equation}
where 
$\nabla ^2\psi _\infty =-\omega _\infty$. The asymptotic approximation in (A 3) follows from two asymptotic estimates. First, the vorticity 
$\omega _\infty (x,z)$ in a steady roll's core is homogenized to a spatially uniform value 
$\varOmega _c$ as 
$Ra\to \infty$, and, according to the analysis of Chini & Cox (Reference Chini and Cox2009), this value is related the prefactor in the 
$Nu$–
$Ra$ asymptotic relation via 
$\varOmega _c\sim \sqrt {c_n(k)}$. Second, owing to the stress-free conditions and symmetries on a steady roll's periphery, the vorticity field is of the same asymptotic order in both the vorticity boundary layers and the core, so the contribution of these boundary layers to the middle integral in (A 3) is negligible relative to that from the 
${O}(1)$ core where 
$\omega _\infty \sim \varOmega _c$.
Unlike the temperature and vorticity fields, the stream function 
$\psi _\infty$ at leading order in 
$Ra$ is a smooth function over the entire spatial domain. The leading-order expression for 
$\psi _\infty$ given by (22)–(23) of Chini & Cox (Reference Chini and Cox2009) is, in our notation,
\begin{equation} \psi_\infty(x,z)\sim\sum_{n=1,{odd}}^{\infty}\psi_n(z)\sin{(nkx)}= \sum_{n=1,odd}^{\infty}\frac{4\varOmega_c}{{\rm \pi} k^2 n^3}\left[1- \frac{\cosh{(nk(z-1/2))}}{\cosh{(nk/2)}}\right]\sin{(nkx)}. \end{equation}
Substituting (A 4) into the right-hand side of (A 3), integrating term-by-term, dividing by the cell width 
${\rm \pi} /k$ to obtain the spatial average, and taking the square root of the resulting expression gives the asymptotic prediction
\begin{equation} c_r(k)\sim\left(\frac{8c_n(k)}{{\rm \pi}^2k^2}\,\sum_{n=1,odd}^{\infty} \frac{1}{n^4}\left[1-\frac{2\tanh{(nk/2)}}{nk}\right]\right)^{1/2}. \end{equation}
Values of 
$c_n(k)$ and corresponding values of 
$c_r(k)$ for various 
$k\in [1/4,10]$ are given in table S1 of the supplementary material.
