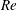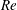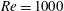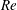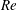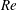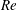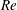1 Introduction
Swimming organisms span seven orders of magnitude in length (Gray Reference Gray1968): a motile bacterium may be only a few microns across whereas a large marine animal may be several metres in length. Completely different fluid flow regimes are observed at either end of this scale (Childress Reference Childress1981). The underlying flow physics are dictated by the relative strength of inertial to viscous forces within the fluid. The Reynolds number,
![]() $Re={\it\varrho}VL/{\it\mu}$
, represents the ratio of these forces, where
$Re={\it\varrho}VL/{\it\mu}$
, represents the ratio of these forces, where
![]() ${\it\varrho}$
is the fluid density,
${\it\varrho}$
is the fluid density,
![]() ${\it\mu}$
is the viscosity,
${\it\mu}$
is the viscosity,
![]() $V$
is a characteristic speed, and
$V$
is a characteristic speed, and
![]() $L$
is a characteristic length.
$L$
is a characteristic length.
Locomotion at macroscopic length scales is associated with large
![]() $Re$
flows dominated by inertial forces. Roughly all swimmers between the size of a small fish (
$Re$
flows dominated by inertial forces. Roughly all swimmers between the size of a small fish (
![]() $Re\sim 10^{3}$
) and a blue whale (
$Re\sim 10^{3}$
) and a blue whale (
![]() $Re\sim 10^{8}$
) fall into this Eulerian realm. Self-propulsion is primarily generated by reactionary forces arising from the acceleration of fluid opposite the swimming direction (Childress Reference Childress1981). This is accomplished, for instance, by the motion of a fish’s tail fin. The effects of viscosity are confined to thin boundary layers so long as the swimmer is streamlined in shape (Vogel Reference Vogel1996). Thus, fluid-mechanical analysis may be carried out using inviscid flow theory (Lighthill Reference Lighthill1975).
$Re\sim 10^{8}$
) fall into this Eulerian realm. Self-propulsion is primarily generated by reactionary forces arising from the acceleration of fluid opposite the swimming direction (Childress Reference Childress1981). This is accomplished, for instance, by the motion of a fish’s tail fin. The effects of viscosity are confined to thin boundary layers so long as the swimmer is streamlined in shape (Vogel Reference Vogel1996). Thus, fluid-mechanical analysis may be carried out using inviscid flow theory (Lighthill Reference Lighthill1975).
In contrast, microscopic organisms fall into the Stokesian realm, where viscous forces dominate and
![]() $Re$
is small, ranging from
$Re$
is small, ranging from
![]() $10^{-4}$
for bacteria to
$10^{-4}$
for bacteria to
![]() $10^{-2}$
for mammalian spermatozoa (Brennen & Winnet Reference Brennen and Winnet1977). Here, inertial mechanisms of thrust generation are unavailable; the swimming mechanics of these organisms are governed by resistive forces, where viscous thrust is balanced by viscous drag (Lauga & Powers Reference Lauga and Powers2009).
$10^{-2}$
for mammalian spermatozoa (Brennen & Winnet Reference Brennen and Winnet1977). Here, inertial mechanisms of thrust generation are unavailable; the swimming mechanics of these organisms are governed by resistive forces, where viscous thrust is balanced by viscous drag (Lauga & Powers Reference Lauga and Powers2009).
Lighthill (Reference Lighthill1952) and Blake (Reference Blake1971) introduced the spherical squirmer as a simple model for self-propulsion at small
![]() $Re$
, intended to mimic the locomotion of organisms possessing dense arrays of motile cilia. A squirmer of radius
$Re$
, intended to mimic the locomotion of organisms possessing dense arrays of motile cilia. A squirmer of radius
![]() $a$
achieves locomotion through small, axisymmetric deformations of its surface, such that the radial and tangential velocity components on its surface in a co-moving frame are
$a$
achieves locomotion through small, axisymmetric deformations of its surface, such that the radial and tangential velocity components on its surface in a co-moving frame are
respectively. Here,
![]() $r$
is the distance from the origin, located at the centre of the squirmer’s body,
$r$
is the distance from the origin, located at the centre of the squirmer’s body,
![]() ${\it\theta}$
is the polar coordinate measured from the direction of locomotion,
${\it\theta}$
is the polar coordinate measured from the direction of locomotion,
![]() $A_{n}$
and
$A_{n}$
and
![]() $B_{n}$
are time-dependent amplitudes (with units of velocity) and
$B_{n}$
are time-dependent amplitudes (with units of velocity) and
![]() $P_{n}$
(
$P_{n}$
(
![]() $P_{n}^{1}$
) are (associated) Legendre polynomials of order
$P_{n}^{1}$
) are (associated) Legendre polynomials of order
![]() $n$
. The direction of locomotion remains constant (at small
$n$
. The direction of locomotion remains constant (at small
![]() $Re$
) due to the axisymmetry of the swimming ‘stroke’ represented by (1.1a,b
), and thus the swimming velocity is
$Re$
) due to the axisymmetry of the swimming ‘stroke’ represented by (1.1a,b
), and thus the swimming velocity is
![]() $\boldsymbol{U}=U\boldsymbol{e}_{z}$
, where
$\boldsymbol{U}=U\boldsymbol{e}_{z}$
, where
![]() $\boldsymbol{e}_{z}$
is the unit vector along the swimming direction. From the requirement that the net hydrodynamic force must vanish on a steadily translating, neutrally buoyant body, the swimming speed of a squirmer in Stokes flow is
$\boldsymbol{e}_{z}$
is the unit vector along the swimming direction. From the requirement that the net hydrodynamic force must vanish on a steadily translating, neutrally buoyant body, the swimming speed of a squirmer in Stokes flow is
![]() $U=(2B_{1}-A_{1})/3$
(Lighthill Reference Lighthill1952). This depends only upon the first mode of each surface velocity component in (1.1a,b
) and is independent of viscosity, since thrust and drag scale linearly with viscosity at
$U=(2B_{1}-A_{1})/3$
(Lighthill Reference Lighthill1952). This depends only upon the first mode of each surface velocity component in (1.1a,b
) and is independent of viscosity, since thrust and drag scale linearly with viscosity at
![]() $Re=0$
.
$Re=0$
.
A reduced-order squirmer may be conceived by assuming that the surface deforms steadily and only in the tangential direction (
![]() $A_{n}=0$
and
$A_{n}=0$
and
![]() $B_{n}$
= constant). Furthermore, one may retain only the first two
$B_{n}$
= constant). Furthermore, one may retain only the first two
![]() $B_{n}$
coefficients, so that
$B_{n}$
coefficients, so that
Equation (1.2) is a slip flow along the squirmer surface that vanishes at the poles (
![]() ${\it\theta}=0$
and
${\it\theta}=0$
and
![]() ${\it\theta}={\rm\pi}$
). The first term in (1.2) is solely responsible for propulsion,
${\it\theta}={\rm\pi}$
). The first term in (1.2) is solely responsible for propulsion,
![]() $U|_{Re=0}=2B_{1}/3$
, and generates an irrotational velocity field decaying as
$U|_{Re=0}=2B_{1}/3$
, and generates an irrotational velocity field decaying as
![]() $1/r^{3}$
, characteristic of a potential dipole. The second term is associated with the stresslet exerted by the squirmer,
$1/r^{3}$
, characteristic of a potential dipole. The second term is associated with the stresslet exerted by the squirmer,
![]() $\unicode[STIX]{x1D64E}|_{Re=0}=4{\rm\pi}{\it\mu}a^{2}B_{2}(3\boldsymbol{e}_{z}\boldsymbol{e}_{z}-\unicode[STIX]{x1D644})/3$
, where
$\unicode[STIX]{x1D64E}|_{Re=0}=4{\rm\pi}{\it\mu}a^{2}B_{2}(3\boldsymbol{e}_{z}\boldsymbol{e}_{z}-\unicode[STIX]{x1D644})/3$
, where
![]() $\unicode[STIX]{x1D644}$
is the identity tensor (Batchelor Reference Batchelor1970; Ishikawa, Simmonds & Pedley Reference Ishikawa, Simmonds and Pedley2006). The flow field due to this term decays as
$\unicode[STIX]{x1D644}$
is the identity tensor (Batchelor Reference Batchelor1970; Ishikawa, Simmonds & Pedley Reference Ishikawa, Simmonds and Pedley2006). The flow field due to this term decays as
![]() $1/r^{2}$
in Stokes flow. There is no Stokeslet contribution to the velocity field because the squirmer is force-free: there is no net hydrodynamic force; drag balances thrust. Defining
$1/r^{2}$
in Stokes flow. There is no Stokeslet contribution to the velocity field because the squirmer is force-free: there is no net hydrodynamic force; drag balances thrust. Defining
![]() ${\it\beta}=B_{2}/B_{1}$
and with
${\it\beta}=B_{2}/B_{1}$
and with
![]() $B_{1}>0$
, squirmers are divided into pullers having
$B_{1}>0$
, squirmers are divided into pullers having
![]() ${\it\beta}>0$
and pushers having
${\it\beta}>0$
and pushers having
![]() ${\it\beta}<0$
(Ishikawa, Simmonds & Pedley Reference Ishikawa, Simmonds and Pedley2007) (figure 1). If
${\it\beta}<0$
(Ishikawa, Simmonds & Pedley Reference Ishikawa, Simmonds and Pedley2007) (figure 1). If
![]() $|{\it\beta}|>1$
, there exists an intermediate point within
$|{\it\beta}|>1$
, there exists an intermediate point within
![]() $0<{\it\theta}<{\rm\pi}$
at which
$0<{\it\theta}<{\rm\pi}$
at which
![]() $v_{s}({\it\theta})$
vanishes, leading to recirculating flow behind (in front of) a puller (pusher) (Magar, Goto & Pedley Reference Magar, Goto and Pedley2003). The magnitude of
$v_{s}({\it\theta})$
vanishes, leading to recirculating flow behind (in front of) a puller (pusher) (Magar, Goto & Pedley Reference Magar, Goto and Pedley2003). The magnitude of
![]() ${\it\beta}$
determines the amount of vorticity generation. If
${\it\beta}$
determines the amount of vorticity generation. If
![]() ${\it\beta}=0$
, the squirmer is ‘neutral’ and generates a potential flow, which, in fact, is a solution to the Navier–Stokes equations (NSEs) at any
${\it\beta}=0$
, the squirmer is ‘neutral’ and generates a potential flow, which, in fact, is a solution to the Navier–Stokes equations (NSEs) at any
![]() $Re$
. In this sense,
$Re$
. In this sense,
![]() ${\it\beta}$
quantifies the amount of fluid mixing by a squirmer. Importantly, the swimming speed is independent of
${\it\beta}$
quantifies the amount of fluid mixing by a squirmer. Importantly, the swimming speed is independent of
![]() ${\it\beta}$
at
${\it\beta}$
at
![]() $Re=0$
; there is no coupling between vorticity generation and propulsion in Stokes flow.
$Re=0$
; there is no coupling between vorticity generation and propulsion in Stokes flow.
Clearly, this reduced-order squirmer is a simplistic model for the locomotion of actual organisms. Nevertheless, it has been employed to examine various facets of self-propulsion in Stokes flow, including swimming in non-Newtonian fluids (Zhu et al. Reference Zhu, Do-Quang, Lauga and Brandt2011; Zhu, Lauga & Brandt Reference Zhu, Lauga and Brandt2012), mixing by swimmers (Thiffeault & Childress Reference Thiffeault and Childress2010; Lin, Thiffeault & Childress Reference Lin, Thiffeault and Childress2011; Pushkin, Shum & Yeomans Reference Pushkin, Shum and Yeomans2013), feeding and nutrient transport (Magar et al. Reference Magar, Goto and Pedley2003; Magar & Pedley Reference Magar and Pedley2005; Michelin & Lauga Reference Michelin and Lauga2011) and hydrodynamic interactions of swimmers (Ishikawa et al. Reference Ishikawa, Simmonds and Pedley2006; Drescher et al. Reference Drescher, Leptos, Tuval and Ishikawa2009; Llopis & Pagonabarraga Reference Llopis and Pagonabarraga2010). A detailed summary is provided by Pak & Lauga (Reference Pak, Lauga, Duprat and Stone2016).

Figure 1. (a) Illustration of the flow pattern around a pusher and puller squirmer in a co-moving frame. (b) Typical examples of pusher and puller squirmers. Arrows represent the force exerted by the fluid on the swimmer body. Pullers generate thrust from the front, e.g. by using a breast-stroke-like motion such as that performed by Chlamydamonas (a green algae). Pushers generate thrust from the rear, e.g. by propelling themselves by rearward facing flagella as in the case of Escherichia coli.
Recently, the locomotion of a squirmer with stroke (1.2) was studied at non-zero
![]() $Re$
. In particular, matched asymptotic expansions were used to compute
$Re$
. In particular, matched asymptotic expansions were used to compute
![]() $U$
to
$U$
to
![]() $O(Re)$
by Wang & Ardekani (Reference Wang and Ardekani2012) and to
$O(Re)$
by Wang & Ardekani (Reference Wang and Ardekani2012) and to
![]() $O(Re^{2})$
by Khair & Chisholm (Reference Khair and Chisholm2014). It was found that
$O(Re^{2})$
by Khair & Chisholm (Reference Khair and Chisholm2014). It was found that
![]() $U$
depends on
$U$
depends on
![]() ${\it\beta}$
at non-zero
${\it\beta}$
at non-zero
![]() $Re$
: pushers (
$Re$
: pushers (
![]() ${\it\beta}<0$
) swim faster than pullers (
${\it\beta}<0$
) swim faster than pullers (
![]() ${\it\beta}>0$
). Here, the Reynolds number is
${\it\beta}>0$
). Here, the Reynolds number is
![]() $Re\equiv 2{\it\varrho}B_{1}a/(3{\it\mu})$
. This is a result of vorticity generation, or mixing, being coupled to propulsion at finite
$Re\equiv 2{\it\varrho}B_{1}a/(3{\it\mu})$
. This is a result of vorticity generation, or mixing, being coupled to propulsion at finite
![]() $Re$
. Note that the vorticity distribution around a Stokesian squirmer evolves purely via diffusion and is thus fore–aft antisymmetric. This antisymmetry precludes the generation of a net force and hence propulsion. The antisymmetry is broken at finite
$Re$
. Note that the vorticity distribution around a Stokesian squirmer evolves purely via diffusion and is thus fore–aft antisymmetric. This antisymmetry precludes the generation of a net force and hence propulsion. The antisymmetry is broken at finite
![]() $Re$
as vorticity is advected past the squirmer into a far-field inertial wake. Khair & Chisholm (Reference Khair and Chisholm2014) demonstrate that the wake structure around a squirmer is consistent with previous work on steady self-propelled bodies at non-zero
$Re$
as vorticity is advected past the squirmer into a far-field inertial wake. Khair & Chisholm (Reference Khair and Chisholm2014) demonstrate that the wake structure around a squirmer is consistent with previous work on steady self-propelled bodies at non-zero
![]() $Re$
(Afanasyev Reference Afanasyev2004; Subramanian Reference Subramanian2010), underscoring the squirmer as a suitable reduced-order model for inertial locomotion. Additionally, Khair & Chisholm (Reference Khair and Chisholm2014) and Li & Ardekani (Reference Li and Ardekani2014) report numerical results for the swimming speed of a squirmer for
$Re$
(Afanasyev Reference Afanasyev2004; Subramanian Reference Subramanian2010), underscoring the squirmer as a suitable reduced-order model for inertial locomotion. Additionally, Khair & Chisholm (Reference Khair and Chisholm2014) and Li & Ardekani (Reference Li and Ardekani2014) report numerical results for the swimming speed of a squirmer for
![]() $Re\leqslant 1$
, which show that the asymptotic results are of practical value in the rather limited range of
$Re\leqslant 1$
, which show that the asymptotic results are of practical value in the rather limited range of
![]() $Re\lesssim 0.2$
.
$Re\lesssim 0.2$
.
The goal of the present article is to quantify the locomotion of a spherical squirmer in the transition from viscously to inertially dominated flow. Self-propulsion in this regime has not been fully explored, especially in comparison to the Stokesian and Eulerian limits. Here, viscous and inertial forces may be simultaneously responsible for thrust and drag on a swimmer, making analysis more difficult. Specifically, we focus on intermediate values of
![]() $Re$
that lie between 0.1 and 1000, thus bridging the gap between viscous and inertial swimming. A multitude of aquatic organisms, such as zooplankton that are on the millimetre to centimetre length scale, fall into this range and utilize a wide variety of swimming motions. The majority of past work has focused on the swimming of particular species of organisms (Jordan Reference Jordan1992; McHenry, Azizi & Strother Reference McHenry, Azizi and Strother2003; Kern & Koumoutsakos Reference Kern and Koumoutsakos2006; Tytell et al.
Reference Tytell, Hsu, Williams, Cohen and Fauci2010; Gazzola, Van Rees & Koumoutsakos Reference Gazzola, Van Rees and Koumoutsakos2012). Such work undoubtedly provides valuable information on the specific locomotive strategies of these organisms. However, in contrast to past work, our objective is to quantify finite
$Re$
that lie between 0.1 and 1000, thus bridging the gap between viscous and inertial swimming. A multitude of aquatic organisms, such as zooplankton that are on the millimetre to centimetre length scale, fall into this range and utilize a wide variety of swimming motions. The majority of past work has focused on the swimming of particular species of organisms (Jordan Reference Jordan1992; McHenry, Azizi & Strother Reference McHenry, Azizi and Strother2003; Kern & Koumoutsakos Reference Kern and Koumoutsakos2006; Tytell et al.
Reference Tytell, Hsu, Williams, Cohen and Fauci2010; Gazzola, Van Rees & Koumoutsakos Reference Gazzola, Van Rees and Koumoutsakos2012). Such work undoubtedly provides valuable information on the specific locomotive strategies of these organisms. However, in contrast to past work, our objective is to quantify finite
![]() $Re$
locomotion from a broad perspective using the simple (reduced-order) squirmer model. Specifically, through the numerical solution of the NSEs, we will determine the flow fields around pusher and puller squirmers for
$Re$
locomotion from a broad perspective using the simple (reduced-order) squirmer model. Specifically, through the numerical solution of the NSEs, we will determine the flow fields around pusher and puller squirmers for
![]() $0.01<Re<1000$
and
$0.01<Re<1000$
and
![]() $-5\leqslant {\it\beta}\leqslant 5$
, along with their swimming speeds, power expenditure and hydrodynamic efficiency. Furthermore, we will determine the stability of the steady axisymmetric flow about a squirmer and compute the critical values of
$-5\leqslant {\it\beta}\leqslant 5$
, along with their swimming speeds, power expenditure and hydrodynamic efficiency. Furthermore, we will determine the stability of the steady axisymmetric flow about a squirmer and compute the critical values of
![]() $Re$
at which transitions to three-dimensional (3-D) and transient flow occur. A prime outcome of our work is to demonstrate that the fluid mechanics of pusher and puller squirmers are dramatically distinct at intermediate
$Re$
at which transitions to three-dimensional (3-D) and transient flow occur. A prime outcome of our work is to demonstrate that the fluid mechanics of pusher and puller squirmers are dramatically distinct at intermediate
![]() $Re$
, in contrast to their similar locomotions at small
$Re$
, in contrast to their similar locomotions at small
![]() $Re$
.
$Re$
.
It must be noted that the squirmer model is indeed simple in that it only considers propulsion via generation of a surface velocity, and it may not well capture the detailed flows arising from the complex geometries and locomotions of many biological swimmers. Nonetheless, its simple geometry allows examination of the essential fluid mechanics of a self-propelling body. Moreover, our results are easily compared to the classic problems of flow past a no-slip sphere and flow past an inviscid spherical bubble, which are well studied at all
![]() $Re$
. Nonetheless, there also exist certain biological swimmers that provide reasonably close realizations of a finite
$Re$
. Nonetheless, there also exist certain biological swimmers that provide reasonably close realizations of a finite
![]() $Re$
squirmer. Paramecium, a ciliate 0.2 mm in size, can reach speeds of
$Re$
squirmer. Paramecium, a ciliate 0.2 mm in size, can reach speeds of
![]() $10~\text{mm}~\text{s}^{-1}$
while evading threats, corresponding to
$10~\text{mm}~\text{s}^{-1}$
while evading threats, corresponding to
![]() $Re\approx 2$
(Hamel et al.
Reference Hamel, Fisch, Combettes, Dupuis-Williams and Baroud2011). Ctenophores, the largest organisms known to use ciliary propulsion, are a few millimetres to a few centimetres in size and swim approximately one body-length per second when foraging (and faster when evading threats). Thus, the
$Re\approx 2$
(Hamel et al.
Reference Hamel, Fisch, Combettes, Dupuis-Williams and Baroud2011). Ctenophores, the largest organisms known to use ciliary propulsion, are a few millimetres to a few centimetres in size and swim approximately one body-length per second when foraging (and faster when evading threats). Thus, the
![]() $Re$
of the flow ranges from roughly 100 to 6000 (Matsumoto Reference Matsumoto1991). Moreover, some species of Ctenophores, such as Pleurobrachia bachei, have bodies that exhibit strong axial symmetry and are approximately spherical in shape (Tamm Reference Tamm2014). Such examples provide additional biological motivation for studying the squirmer model outside the small
$Re$
of the flow ranges from roughly 100 to 6000 (Matsumoto Reference Matsumoto1991). Moreover, some species of Ctenophores, such as Pleurobrachia bachei, have bodies that exhibit strong axial symmetry and are approximately spherical in shape (Tamm Reference Tamm2014). Such examples provide additional biological motivation for studying the squirmer model outside the small
![]() $Re$
limit.
$Re$
limit.
The remainder of this article is organized as follows. In § 2, we present the governing equations for a self-propelled squirmer. In § 3 we detail two numerical methods used for performing steady, axisymmetric and transient, 3-D simulation of flows about a squirmer, respectively. The subsequent results are presented and discussed in § 4. Finally, we conclude and suggest directions for future work in § 5.
2 Governing equations
Consider a single squirmer with a steady swimming stroke (1.2) in an unbounded incompressible Newtonian fluid (figure 1
a). We normalize length by the squirmer radius
![]() $a$
, velocity by the speed of a neutral squirmer in potential flow (
$a$
, velocity by the speed of a neutral squirmer in potential flow (
![]() $2B_{1}/3$
), time by
$2B_{1}/3$
), time by
![]() $3a/(2B_{1})$
, and pressure and viscous stresses by
$3a/(2B_{1})$
, and pressure and viscous stresses by
![]() $2B_{1}{\it\mu}/(3a)$
. Thus, the Reynolds number is defined as
$2B_{1}{\it\mu}/(3a)$
. Thus, the Reynolds number is defined as
![]() $Re\equiv 2{\it\varrho}B_{1}a/(3{\it\mu})$
. Henceforth, all quantities are dimensionless unless indicated otherwise. The fluid motion is governed by the NSEs,
$Re\equiv 2{\it\varrho}B_{1}a/(3{\it\mu})$
. Henceforth, all quantities are dimensionless unless indicated otherwise. The fluid motion is governed by the NSEs,
where
![]() $\boldsymbol{v}$
is the velocity vector,
$\boldsymbol{v}$
is the velocity vector,
![]() $p$
is the pressure,
$p$
is the pressure,
![]() $t$
is time and
$t$
is time and
![]() $\text{D}/\text{D}t$
represents the material derivative.
$\text{D}/\text{D}t$
represents the material derivative.
We assume that the squirmer body has a constant mass density
![]() ${\it\varrho}_{b}$
, equal to
${\it\varrho}_{b}$
, equal to
![]() ${\it\varrho}$
, and is thus neutrally buoyant. If the flow about the squirmer is axisymmetric, the net hydrodynamic force perpendicular to the squirmer’s axis (taken as the
${\it\varrho}$
, and is thus neutrally buoyant. If the flow about the squirmer is axisymmetric, the net hydrodynamic force perpendicular to the squirmer’s axis (taken as the
![]() $z$
-axis of an attached Cartesian frame) and the net hydrodynamic torque vanish. Thus, the squirmer does not rotate and maintains a straight-line path. The remaining
$z$
-axis of an attached Cartesian frame) and the net hydrodynamic torque vanish. Thus, the squirmer does not rotate and maintains a straight-line path. The remaining
![]() $z$
-component of the hydrodynamic force
$z$
-component of the hydrodynamic force
![]() $F_{z}$
is equal to the mass times acceleration of the squirmer body in the
$F_{z}$
is equal to the mass times acceleration of the squirmer body in the
![]() $z$
-direction,
$z$
-direction,
where
![]() $U$
is the swimming speed,
$U$
is the swimming speed,
![]() $S$
represents the spherical squirmer surface with outer unit normal
$S$
represents the spherical squirmer surface with outer unit normal
![]() $\boldsymbol{n}$
and
$\boldsymbol{n}$
and
![]() ${\bf\sigma}=-p\unicode[STIX]{x1D644}+\boldsymbol{{\rm\nabla}}\boldsymbol{v}+(\boldsymbol{{\rm\nabla}}\boldsymbol{v})^{\text{T}}$
is the stress tensor. The Stokes number,
${\bf\sigma}=-p\unicode[STIX]{x1D644}+\boldsymbol{{\rm\nabla}}\boldsymbol{v}+(\boldsymbol{{\rm\nabla}}\boldsymbol{v})^{\text{T}}$
is the stress tensor. The Stokes number,
![]() $Stk=Re{\it\varrho}_{b}/{\it\varrho}$
, is equal to
$Stk=Re{\it\varrho}_{b}/{\it\varrho}$
, is equal to
![]() $Re$
because
$Re$
because
![]() ${\it\varrho}={\it\varrho}_{b}$
. This force will vanish when the flow is at steady state and the squirmer translates with a steady velocity. Therefore, a steady squirmer in steady axisymmetric flow is force-free and torque-free.
${\it\varrho}={\it\varrho}_{b}$
. This force will vanish when the flow is at steady state and the squirmer translates with a steady velocity. Therefore, a steady squirmer in steady axisymmetric flow is force-free and torque-free.
However, the spherical squirmer is a bluff object; the steady axisymmetric flow around it may become unstable beyond a critical value of
![]() $Re$
, yielding to 3-D and/or unsteady flow. This leads to the production of instantaneous lift forces perpendicular to the squirmer’s axis and instantaneous hydrodynamic torques that result in lateral motion and rotation of the squirmer’s body, respectively. Here, for simplicity, forces and torques are externally applied to the squirmer to keep its direction and orientation constant and along the
$Re$
, yielding to 3-D and/or unsteady flow. This leads to the production of instantaneous lift forces perpendicular to the squirmer’s axis and instantaneous hydrodynamic torques that result in lateral motion and rotation of the squirmer’s body, respectively. Here, for simplicity, forces and torques are externally applied to the squirmer to keep its direction and orientation constant and along the
![]() $z$
-axis during our computations, although the speed is allowed to vary according to (2.2). Thus, the squirmer is not fully free-swimming but rather constrained to follow a straight-line path. This is a logical first step before considering the more complicated paths of motion that would arise if the squirmer trajectory were to be unconstrained. For instance, the transitions in flow that occur for a freely rising or sinking body, and the values of
$z$
-axis during our computations, although the speed is allowed to vary according to (2.2). Thus, the squirmer is not fully free-swimming but rather constrained to follow a straight-line path. This is a logical first step before considering the more complicated paths of motion that would arise if the squirmer trajectory were to be unconstrained. For instance, the transitions in flow that occur for a freely rising or sinking body, and the values of
![]() $Re$
at which they occur, are closely related to those that take place in the flow past an analogous fixed body (Horowitz & Williamson Reference Horowitz and Williamson2010; Ern et al.
Reference Ern, Risso, Fabre and Magnaudet2012). Thus, we expect that our study of a squirmer constrained to a single direction of swimming will be relevant to a fully free-swimming squirmer. Indeed, the two problems are identical in the regime of axisymmetric flow and only differ when such flow destabilizes. Although it is not considered here, note that the path of motion of a fully free squirmer could be computed via a force balance (in all directions) and an angular momentum balance on the squirmer body, similar to the computation of the paths of freely rising or falling bodies (Ern et al.
Reference Ern, Risso, Fabre and Magnaudet2012).
$Re$
at which they occur, are closely related to those that take place in the flow past an analogous fixed body (Horowitz & Williamson Reference Horowitz and Williamson2010; Ern et al.
Reference Ern, Risso, Fabre and Magnaudet2012). Thus, we expect that our study of a squirmer constrained to a single direction of swimming will be relevant to a fully free-swimming squirmer. Indeed, the two problems are identical in the regime of axisymmetric flow and only differ when such flow destabilizes. Although it is not considered here, note that the path of motion of a fully free squirmer could be computed via a force balance (in all directions) and an angular momentum balance on the squirmer body, similar to the computation of the paths of freely rising or falling bodies (Ern et al.
Reference Ern, Risso, Fabre and Magnaudet2012).
3 Numerical methods
Two numerical schemes were employed to compute the flow field around a squirmer for
![]() $-5\leqslant {\it\beta}\leqslant 5$
and
$-5\leqslant {\it\beta}\leqslant 5$
and
![]() $0.01\leqslant Re\leqslant 1000$
. The first assumes steady axisymmetric flow where the steady-state swimming speed
$0.01\leqslant Re\leqslant 1000$
. The first assumes steady axisymmetric flow where the steady-state swimming speed
![]() $U$
is that at which
$U$
is that at which
![]() $F_{z}$
in (2.2) vanishes. The second considers fully 3-D, transient flow, in which case
$F_{z}$
in (2.2) vanishes. The second considers fully 3-D, transient flow, in which case
![]() $U=U(t)$
is given by integrating (2.2) via a time-stepping procedure.
$U=U(t)$
is given by integrating (2.2) via a time-stepping procedure.
3.1 Computation of steady axisymmetric flow
We convert the NSEs into stream function–vorticity form. From (2.1a,b ), the steady vorticity transport equation is
where
![]() ${\bf\omega}=\boldsymbol{{\rm\nabla}}\times \boldsymbol{v}$
is the vorticity vector. A stream function
${\bf\omega}=\boldsymbol{{\rm\nabla}}\times \boldsymbol{v}$
is the vorticity vector. A stream function
![]() ${\it\psi}$
is defined in cylindrical coordinates, such that
${\it\psi}$
is defined in cylindrical coordinates, such that
where
![]() ${\it\rho}$
is the distance from the
${\it\rho}$
is the distance from the
![]() $z$
-axis and
$z$
-axis and
![]() $v_{{\it\rho}}$
and
$v_{{\it\rho}}$
and
![]() $v_{z}$
represent the fluid velocity components.
$v_{z}$
represent the fluid velocity components.
Combining (3.2a,b ) with (3.1) gives
where
![]() ${\it\omega}$
is the component of
${\it\omega}$
is the component of
![]() ${\bf\omega}$
in the azimuthal direction
${\bf\omega}$
in the azimuthal direction
![]() ${\it\varphi}$
about the
${\it\varphi}$
about the
![]() $z$
-axis; the other (
$z$
-axis; the other (
![]() ${\it\rho}$
and
${\it\rho}$
and
![]() $z$
) components of
$z$
) components of
![]() ${\bf\omega}$
vanish by symmetry. Expressing
${\bf\omega}$
vanish by symmetry. Expressing
![]() ${\it\omega}$
in terms of
${\it\omega}$
in terms of
![]() ${\it\psi}$
gives
${\it\psi}$
gives
Equations (3.3) and (3.4) are coupled partial differential equations, with the former being nonlinear. These may be simultaneously solved for the scalar quantities
![]() ${\it\psi}$
and
${\it\psi}$
and
![]() ${\it\omega}$
to give the flow field given appropriate boundary conditions.
${\it\omega}$
to give the flow field given appropriate boundary conditions.
In a co-moving frame, the squirmer surface (
![]() $r=1$
) is a streamline with tangential velocity given by (1.2). Thus,
$r=1$
) is a streamline with tangential velocity given by (1.2). Thus,
![]() ${\it\psi}|_{r=1}=0$
and
${\it\psi}|_{r=1}=0$
and
![]() $[\boldsymbol{{\rm\nabla}}{\it\psi}\boldsymbol{\cdot }\boldsymbol{n}]_{r=1}=v_{s}\sin {\it\theta}=3\sin ^{2}{\it\theta}(1+{\it\beta}\cos {\it\theta})/2$
. The values of
$[\boldsymbol{{\rm\nabla}}{\it\psi}\boldsymbol{\cdot }\boldsymbol{n}]_{r=1}=v_{s}\sin {\it\theta}=3\sin ^{2}{\it\theta}(1+{\it\beta}\cos {\it\theta})/2$
. The values of
![]() ${\it\beta}$
and
${\it\beta}$
and
![]() $Re$
are specified constants, so the swimming stroke is represented as a fixed boundary condition. By axisymmetry,
$Re$
are specified constants, so the swimming stroke is represented as a fixed boundary condition. By axisymmetry,
![]() ${\it\psi}|_{{\it\rho}=0}=0$
and
${\it\psi}|_{{\it\rho}=0}=0$
and
![]() ${\it\omega}|_{{\it\rho}=0}=0$
on the
${\it\omega}|_{{\it\rho}=0}=0$
on the
![]() $z$
-axis. Finally, the flow is uniform in the far-field, so
$z$
-axis. Finally, the flow is uniform in the far-field, so
![]() ${\it\psi}|_{r\rightarrow \infty }=-U{\it\rho}^{2}/2$
and
${\it\psi}|_{r\rightarrow \infty }=-U{\it\rho}^{2}/2$
and
![]() ${\it\omega}|_{r\rightarrow \infty }=0$
.
${\it\omega}|_{r\rightarrow \infty }=0$
.
A spectral element method (Karniadakis & Sherwin Reference Karniadakis and Sherwin2005) was used to spatially discretize (3.3), (3.4) and the boundary conditions. The shape functions were defined as a tensor product of
![]() $N$
th order Lagrange polynomials supported at the
$N$
th order Lagrange polynomials supported at the
![]() $N+1$
Gauss–Lobatto integration points over the square
$N+1$
Gauss–Lobatto integration points over the square
![]() $[-1,1]^{2}$
parametric space of each quadrilateral element. Integration over each element was carried out using the corresponding Gauss–Lobatto quadrature rule to produce a system of nonlinear algebraic equations. This system was solved iteratively using Newton–Raphson iteration. Iteration was terminated when the
$[-1,1]^{2}$
parametric space of each quadrilateral element. Integration over each element was carried out using the corresponding Gauss–Lobatto quadrature rule to produce a system of nonlinear algebraic equations. This system was solved iteratively using Newton–Raphson iteration. Iteration was terminated when the
![]() $L^{2}$
-norm of the relative errors in
$L^{2}$
-norm of the relative errors in
![]() ${\it\psi}$
and
${\it\psi}$
and
![]() ${\it\omega}$
over all discretization points was reduced below
${\it\omega}$
over all discretization points was reduced below
![]() $10^{-6}$
.
$10^{-6}$
.

Figure 2. Structured polar grids (a) were used for both axisymmetric and 3-D (by revolving them azimuthally) computations of the flow. For axisymmetric computations with
![]() $Re>10$
, a different mesh (b) was used with greater resolution in the wake of the squirmer to more accurately resolve the details of the flow in this region.
$Re>10$
, a different mesh (b) was used with greater resolution in the wake of the squirmer to more accurately resolve the details of the flow in this region.
The spatial domain was discretized into high-order computational grids using the software package ‘Gmsh’ (Geuzaine & Remacle Reference Geuzaine and Remacle2009). Three different grids were used depending on the value of
![]() $Re$
. For
$Re$
. For
![]() $Re\leqslant 0.1$
, a polar grid extending to
$Re\leqslant 0.1$
, a polar grid extending to
![]() $R_{\infty }=1000$
and consisting of
$R_{\infty }=1000$
and consisting of
![]() $9\times 9$
node quadrilateral elements was used. The elements were distributed evenly in the
$9\times 9$
node quadrilateral elements was used. The elements were distributed evenly in the
![]() ${\it\theta}$
-direction (
${\it\theta}$
-direction (
![]() $N_{{\it\theta}}=10$
) and progressed geometrically outward in the
$N_{{\it\theta}}=10$
) and progressed geometrically outward in the
![]() $r$
-direction (
$r$
-direction (
![]() $N_{r}=20$
). A similar grid was used for
$N_{r}=20$
). A similar grid was used for
![]() $0.1\leqslant Re\leqslant 10$
, with
$0.1\leqslant Re\leqslant 10$
, with
![]() $R_{\infty }=100$
(figure 2
a). For
$R_{\infty }=100$
(figure 2
a). For
![]() $Re>10$
, a different mesh was used to provide better resolution in the squirmer wake. Here, a boundary layer grid was used along the squirmer surface, with
$Re>10$
, a different mesh was used to provide better resolution in the squirmer wake. Here, a boundary layer grid was used along the squirmer surface, with
![]() $N_{r}=10$
and
$N_{r}=10$
and
![]() $N_{{\it\theta}}=51$
, extending
$N_{{\it\theta}}=51$
, extending
![]() $R_{BL}=0.25$
radii from the squirmer surface (here the subscript
$R_{BL}=0.25$
radii from the squirmer surface (here the subscript
![]() $BL$
stands for boundary layer). The radial grid size grew geometrically with
$BL$
stands for boundary layer). The radial grid size grew geometrically with
![]() $r$
, and was initially
$r$
, and was initially
![]() ${\it\Delta}_{r0}=0.01$
at the squirmer surface. The remainder of the grid was unstructured, with upstream boundaries extending to
${\it\Delta}_{r0}=0.01$
at the squirmer surface. The remainder of the grid was unstructured, with upstream boundaries extending to
![]() $R_{\infty }=32$
, and a rectangular wake region extending a distance of
$R_{\infty }=32$
, and a rectangular wake region extending a distance of
![]() $100$
radii behind the squirmer (figure 2
b). The far-field boundary conditions were enforced at the exterior boundary of the mesh. We refer the reader to the Appendix for details on grid convergence.
$100$
radii behind the squirmer (figure 2
b). The far-field boundary conditions were enforced at the exterior boundary of the mesh. We refer the reader to the Appendix for details on grid convergence.
The far-field boundary condition of uniform, oncoming flow cannot be directly applied because the steady-state swimming speed
![]() $U$
is unknown a priori. Since the flow is assumed to be steady and axisymmetric, we instead enforce that
$U$
is unknown a priori. Since the flow is assumed to be steady and axisymmetric, we instead enforce that
![]() $F_{z}$
is equal to zero. Expressing (2.2) in terms of
$F_{z}$
is equal to zero. Expressing (2.2) in terms of
![]() ${\it\omega}$
for an axisymmetric flow field gives (Khair & Chisholm Reference Khair and Chisholm2014)
${\it\omega}$
for an axisymmetric flow field gives (Khair & Chisholm Reference Khair and Chisholm2014)
A secant method was used to iteratively compute the value of
![]() $U$
at which (3.5) vanishes. At each iteration, the flow is solved with
$U$
at which (3.5) vanishes. At each iteration, the flow is solved with
![]() $U=U^{\langle n\rangle }$
, where
$U=U^{\langle n\rangle }$
, where
![]() $n$
is the iteration number, and (3.5) is evaluated to give
$n$
is the iteration number, and (3.5) is evaluated to give
![]() $F_{z}^{\langle n\rangle }$
. An improved estimate for
$F_{z}^{\langle n\rangle }$
. An improved estimate for
![]() $U$
is given by linear interpolation:
$U$
is given by linear interpolation:
![]() $U^{\langle n+1\rangle }=(U^{\langle n\rangle }F_{z}^{\langle n-1\rangle }-U^{\langle n-1\rangle }F_{z}^{\langle n\rangle })/(F_{z}^{\langle n-1\rangle }-F_{z}^{\langle n\rangle })$
. Iteration was terminated when
$U^{\langle n+1\rangle }=(U^{\langle n\rangle }F_{z}^{\langle n-1\rangle }-U^{\langle n-1\rangle }F_{z}^{\langle n\rangle })/(F_{z}^{\langle n-1\rangle }-F_{z}^{\langle n\rangle })$
. Iteration was terminated when
![]() $|U^{\langle n\rangle }-U^{\langle n-1\rangle }|$
was reduced below
$|U^{\langle n\rangle }-U^{\langle n-1\rangle }|$
was reduced below
![]() $10^{-5}$
.
$10^{-5}$
.
Computations for each value of
![]() ${\it\beta}$
were started initially with
${\it\beta}$
were started initially with
![]() $Re=0.01$
. Two initial guesses of the swimming speed are required, which were made as
$Re=0.01$
. Two initial guesses of the swimming speed are required, which were made as
![]() $U^{\langle 0\rangle }=0.99$
and
$U^{\langle 0\rangle }=0.99$
and
![]() $U^{\langle 1\rangle }=1.01$
, since
$U^{\langle 1\rangle }=1.01$
, since
![]() $U$
is close to unity at small
$U$
is close to unity at small
![]() $Re$
. An initial guess for the stream function and vorticity fields of uniformly zero was sufficient for convergence of the computed flow in this case. A simple continuation strategy was employed by incrementally increasing
$Re$
. An initial guess for the stream function and vorticity fields of uniformly zero was sufficient for convergence of the computed flow in this case. A simple continuation strategy was employed by incrementally increasing
![]() $Re$
. Initial guesses for
$Re$
. Initial guesses for
![]() $U$
and the flow field at a given
$U$
and the flow field at a given
![]() $Re$
were supplied by using the values computed at the last largest values of
$Re$
were supplied by using the values computed at the last largest values of
![]() $Re$
for which a converged solution was successfully reached.
$Re$
for which a converged solution was successfully reached.
3.2 Computation of unsteady 3-D flows
Unsteady 3-D flows were explored using the JADIM code described in detail in Magnaudet, Rivero & Fabre (Reference Magnaudet, Rivero and Fabre1995) and Legendre & Magnaudet (Reference Legendre and Magnaudet1998). The JADIM code has been extensively used and validated in previous studies concerning the 3-D flow dynamics of spheroidal and disk-shaped bodies with no-slip (solid) or slip (bubble) surfaces in uniform, shear or turbulent flows (see e.g. Legendre & Magnaudet Reference Legendre and Magnaudet1998; Merle, Legendre & Magnaudet Reference Merle, Legendre and Magnaudet2005; Legendre, Merle & Magnaudet Reference Legendre, Merle and Magnaudet2006; Hallez & Legendre Reference Hallez and Legendre2011). In particular, the wake transition from axisymmetric to 3-D flow for a fixed body has been considered in Mougin & Magnaudet (Reference Mougin and Magnaudet2001), Magnaudet & Mougin (Reference Magnaudet and Mougin2007) and Fabre, Auguste & Magnaudet (Reference Fabre, Auguste and Magnaudet2008). In the case of a sphere, a first bifurcation resulting in loss of axial symmetry in the flow is detected at a critical Reynolds number (based on the sphere radius and speed of translation
![]() $U$
) of
$U$
) of
![]() $Re_{U}^{(c1)}=105$
, in agreement with linear stability analysis (Natarajan & Acrivos Reference Natarajan and Acrivos1993) and previous numerical studies (Johnson & Patel Reference Johnson and Patel1999; Tomboulides & Orszag Reference Tomboulides and Orszag2000). A second (Hopf) bifurcation is observed at
$Re_{U}^{(c1)}=105$
, in agreement with linear stability analysis (Natarajan & Acrivos Reference Natarajan and Acrivos1993) and previous numerical studies (Johnson & Patel Reference Johnson and Patel1999; Tomboulides & Orszag Reference Tomboulides and Orszag2000). A second (Hopf) bifurcation is observed at
![]() $Re_{U}^{(c2)}=135$
, leading to time-dependent flow, which is also in good agreement with previous numerical findings (Johnson & Patel Reference Johnson and Patel1999; Tomboulides & Orszag Reference Tomboulides and Orszag2000), according to which the Hopf bifurcation lies in within the range
$Re_{U}^{(c2)}=135$
, leading to time-dependent flow, which is also in good agreement with previous numerical findings (Johnson & Patel Reference Johnson and Patel1999; Tomboulides & Orszag Reference Tomboulides and Orszag2000), according to which the Hopf bifurcation lies in within the range
![]() $135<Re_{U}^{(c2)}<137$
. In Magnaudet & Mougin (Reference Magnaudet and Mougin2007), the vortex shedding process for a sphere at
$135<Re_{U}^{(c2)}<137$
. In Magnaudet & Mougin (Reference Magnaudet and Mougin2007), the vortex shedding process for a sphere at
![]() $Re_{U}=150$
corresponds to a Strouhal number of
$Re_{U}=150$
corresponds to a Strouhal number of
![]() $St_{U}=fa/U=0.0665$
, where
$St_{U}=fa/U=0.0665$
, where
![]() $f$
is the dimensional frequency of vortex shedding. This falls within 2–3 % of that reported by Johnson & Patel (Reference Johnson and Patel1999) and Tomboulides & Orszag (Reference Tomboulides and Orszag2000) for the same
$f$
is the dimensional frequency of vortex shedding. This falls within 2–3 % of that reported by Johnson & Patel (Reference Johnson and Patel1999) and Tomboulides & Orszag (Reference Tomboulides and Orszag2000) for the same
![]() $Re$
.
$Re$
.
Briefly, the JADIM code solves the incompressible NSEs (2.1a,b
) in terms of velocity and pressure variables. The spatial discretization employs a staggered grid on which the equations are integrated using a second-order accurate finite-volume method. Fluid incompressibility is satisfied after each time step by solving a Poisson equation for an auxiliary potential. Time advancement is achieved through a second-order accurate Runge–Kutta/Crank–Nicholson algorithm. At each time step, the swimming speed
![]() $U$
is updated by integrating (2.2). For each simulation, the squirmer was started from rest with swimming stroke (1.2) and allowed to accelerate. Simulations were terminated after a steady time-averaged value of the swimming speed was reached.
$U$
is updated by integrating (2.2). For each simulation, the squirmer was started from rest with swimming stroke (1.2) and allowed to accelerate. Simulations were terminated after a steady time-averaged value of the swimming speed was reached.
A polar grid extending to
![]() $R_{\infty }=150$
and rotated around the
$R_{\infty }=150$
and rotated around the
![]() $z$
-axis was used for computation (figure 2
a). Nodes were distributed uniformly in the
$z$
-axis was used for computation (figure 2
a). Nodes were distributed uniformly in the
![]() ${\it\theta}$
-direction and in a geometric progression in the
${\it\theta}$
-direction and in a geometric progression in the
![]() $r$
-direction. The effect of the number of nodes (
$r$
-direction. The effect of the number of nodes (
![]() $N_{r}=150$
along the radial direction,
$N_{r}=150$
along the radial direction,
![]() $N_{{\it\theta}}=250$
along the polar direction and
$N_{{\it\theta}}=250$
along the polar direction and
![]() $N_{{\it\varphi}}=64$
along the azimuthal direction), as well as
$N_{{\it\varphi}}=64$
along the azimuthal direction), as well as
![]() $R_{\infty }$
and the radial grid size
$R_{\infty }$
and the radial grid size
![]() ${\it\Delta}_{r0}=0.001$
at the body surface, were checked in order to ensure grid independence of the results (see the Appendix).
${\it\Delta}_{r0}=0.001$
at the body surface, were checked in order to ensure grid independence of the results (see the Appendix).
The transition from steady axisymmetric to unsteady 3-D flow was investigated by running the simulation for a given period of time while allowing numerical error to perturb the initially axisymmetric flow profile. If the flow is unstable for a given
![]() ${\it\beta}$
and
${\it\beta}$
and
![]() $Re$
, such perturbations are expected to grow over time, resulting in a flow field that is potentially 3-D and/or unsteady. Such is the case for a no-slip sphere in uniform flow, where distinct axisymmetric, steady 3-D and unsteady 3-D flow regimes are respectively encountered as
$Re$
, such perturbations are expected to grow over time, resulting in a flow field that is potentially 3-D and/or unsteady. Such is the case for a no-slip sphere in uniform flow, where distinct axisymmetric, steady 3-D and unsteady 3-D flow regimes are respectively encountered as
![]() $Re$
is increased (Natarajan & Acrivos Reference Natarajan and Acrivos1993; Tomboulides & Orszag Reference Tomboulides and Orszag2000). Specifically, simulations were performed with
$Re$
is increased (Natarajan & Acrivos Reference Natarajan and Acrivos1993; Tomboulides & Orszag Reference Tomboulides and Orszag2000). Specifically, simulations were performed with
![]() $Re$
increased in coarse increments until a transition, if one occurred, was identified. Then,
$Re$
increased in coarse increments until a transition, if one occurred, was identified. Then,
![]() $Re$
was increased in finer increments within the interval in which the transition occurred. This process was repeated until a satisfactory estimate of the critical transition
$Re$
was increased in finer increments within the interval in which the transition occurred. This process was repeated until a satisfactory estimate of the critical transition
![]() $Re$
was procured. The simulation time was increased as the critical
$Re$
was procured. The simulation time was increased as the critical
![]() $Re$
of transition was approached, as it generally required longer times for perturbations to grow and hence for the flow to reach a final transitioned state.
$Re$
of transition was approached, as it generally required longer times for perturbations to grow and hence for the flow to reach a final transitioned state.
4 Results and discussion
4.1 Swimming speed of a squirmer
The calculated swimming speed
![]() $U$
versus
$U$
versus
![]() $Re$
of a squirmer with
$Re$
of a squirmer with
![]() ${\it\beta}=\pm 0.5$
and
${\it\beta}=\pm 0.5$
and
![]() $\pm 5$
is shown in figure 3. There,
$\pm 5$
is shown in figure 3. There,
![]() $U$
is normalized by
$U$
is normalized by
![]() $2B_{1}/3$
, which is the swimming speed at
$2B_{1}/3$
, which is the swimming speed at
![]() $Re=0$
for all
$Re=0$
for all
![]() ${\it\beta}$
, or the swimming speed of a neutral squirmer at arbitrary
${\it\beta}$
, or the swimming speed of a neutral squirmer at arbitrary
![]() $Re$
. At
$Re$
. At
![]() $Re=0$
,
$Re=0$
,
![]() $U$
is independent of
$U$
is independent of
![]() ${\it\beta}$
because the equations governing the flow are linear. Thus, the two terms in the swimming stroke (1.2) contribute to the flow field independently; only the first (treading) term generates propulsion, while the second only produces vorticity. This is not the case as
${\it\beta}$
because the equations governing the flow are linear. Thus, the two terms in the swimming stroke (1.2) contribute to the flow field independently; only the first (treading) term generates propulsion, while the second only produces vorticity. This is not the case as
![]() $Re$
is increased from zero: pushers (pullers) monotonically increase (decrease) in speed if
$Re$
is increased from zero: pushers (pullers) monotonically increase (decrease) in speed if
![]() $Re\lesssim O(1)$
, in agreement with results from asymptotic analyses (Wang & Ardekani Reference Wang and Ardekani2012; Khair & Chisholm Reference Khair and Chisholm2014). The increase or decrease in swimming speed is amplified as
$Re\lesssim O(1)$
, in agreement with results from asymptotic analyses (Wang & Ardekani Reference Wang and Ardekani2012; Khair & Chisholm Reference Khair and Chisholm2014). The increase or decrease in swimming speed is amplified as
![]() $|{\it\beta}|$
increases. However, as
$|{\it\beta}|$
increases. However, as
![]() $Re$
is increased beyond an
$Re$
is increased beyond an
![]() $O(1)$
value, significantly different behaviour of pushers versus pullers is observed. For all pushers and pullers with
$O(1)$
value, significantly different behaviour of pushers versus pullers is observed. For all pushers and pullers with
![]() ${\it\beta}<1$
,
${\it\beta}<1$
,
![]() $U$
continues to vary monotonically with increasing
$U$
continues to vary monotonically with increasing
![]() $Re$
, eventually reaching a terminal value. The computed swimming speed is nearly identical for axisymmetric and 3-D computations, suggesting that there is no departure from steady axisymmetric flow. In contrast, a non-monotonic trend is observed for pullers with
$Re$
, eventually reaching a terminal value. The computed swimming speed is nearly identical for axisymmetric and 3-D computations, suggesting that there is no departure from steady axisymmetric flow. In contrast, a non-monotonic trend is observed for pullers with
![]() ${\it\beta}>1$
, and no limiting value for
${\it\beta}>1$
, and no limiting value for
![]() $U$
is apparent up to
$U$
is apparent up to
![]() $Re=1000$
. Moreover, the axisymmetric and 3-D computations give drastically different results, suggesting the destabilization of the axisymmetric steady flow (see § 4.3 for more detail). We remind the reader that
$Re=1000$
. Moreover, the axisymmetric and 3-D computations give drastically different results, suggesting the destabilization of the axisymmetric steady flow (see § 4.3 for more detail). We remind the reader that
![]() $Re$
for a squirmer is defined as
$Re$
for a squirmer is defined as
![]() $2{\it\varrho}B_{1}a/(3{\it\mu})$
, in contrast to the Reynolds number based on the translational speed
$2{\it\varrho}B_{1}a/(3{\it\mu})$
, in contrast to the Reynolds number based on the translational speed
![]() $U$
, which we denote
$U$
, which we denote
![]() $Re_{U}={\it\varrho}Ua/{\it\mu}$
. Note that
$Re_{U}={\it\varrho}Ua/{\it\mu}$
. Note that
![]() $Re$
and
$Re$
and
![]() $Re_{U}$
are the same order of magnitude since
$Re_{U}$
are the same order of magnitude since
![]() $U\sim O(1)$
.
$U\sim O(1)$
.

Figure 3. Swimming speed,
![]() $U$
, normalized by
$U$
, normalized by
![]() $2B_{1}/3$
, for
$2B_{1}/3$
, for
![]() ${\it\beta}=\pm 0.5$
(a) and
${\it\beta}=\pm 0.5$
(a) and
![]() $\pm 5$
(b). The ‘▿’ markers represent pushers and the ‘▵’ markers represent pullers. Hollow markers represent steady axisymmetric solutions, and filled markers represent unsteady 3-D solutions. We follow these conventions for the remainder of the article. The dashed line represents the speed of a neutral (
$\pm 5$
(b). The ‘▿’ markers represent pushers and the ‘▵’ markers represent pullers. Hollow markers represent steady axisymmetric solutions, and filled markers represent unsteady 3-D solutions. We follow these conventions for the remainder of the article. The dashed line represents the speed of a neutral (
![]() ${\it\beta}=0$
) squirmer. For a
${\it\beta}=0$
) squirmer. For a
![]() ${\it\beta}=+5$
puller, the steady axisymmetric flow destabilizes at
${\it\beta}=+5$
puller, the steady axisymmetric flow destabilizes at
![]() $Re\approx 20$
, and hence the steady axisymmetric and unsteady 3-D solutions diverge. Time averages of
$Re\approx 20$
, and hence the steady axisymmetric and unsteady 3-D solutions diverge. Time averages of
![]() $U$
are taken in the case of unsteady flow. Dotted lines show the asymptotic result of Khair & Chisholm (Reference Khair and Chisholm2014) for
$U$
are taken in the case of unsteady flow. Dotted lines show the asymptotic result of Khair & Chisholm (Reference Khair and Chisholm2014) for
![]() $U$
to
$U$
to
![]() $O(Re^{2})$
.
$O(Re^{2})$
.

Figure 4. Streamlines of axisymmetric flow past a squirmer with
![]() ${\it\beta}=\pm 5$
; (a,c,e,g) pusher:
${\it\beta}=\pm 5$
; (a,c,e,g) pusher:
![]() ${\it\beta}=-5$
, (b,d,f,h) puller:
${\it\beta}=-5$
, (b,d,f,h) puller:
![]() ${\it\beta}=5$
;
${\it\beta}=5$
;
![]() $Re=0.1$
(a,b), 10 (c,d), 100 (e,f), 1000 (g,h). Dashed streamlines represent negative values of the stream function. The tick marks in (g) at
$Re=0.1$
(a,b), 10 (c,d), 100 (e,f), 1000 (g,h). Dashed streamlines represent negative values of the stream function. The tick marks in (g) at
![]() $Re=1000$
follow along streamlines of irrotational flow past a sphere.
$Re=1000$
follow along streamlines of irrotational flow past a sphere.
Distinct contributions to the thrust and drag on a squirmer are provided by the two terms on the right-hand side of (3.5). The first term, which equals
![]() $8{\rm\pi}Re{\it\beta}/15$
after integration, depends solely on the swimming stroke and vanishes when
$8{\rm\pi}Re{\it\beta}/15$
after integration, depends solely on the swimming stroke and vanishes when
![]() $Re=0$
. The second term also vanishes if
$Re=0$
. The second term also vanishes if
![]() $Re=0$
due to the antisymmetric, purely diffusive, distribution of the vorticity, and it is hence associated with forces arising from the flow asymmetry produced by inertia at finite
$Re=0$
due to the antisymmetric, purely diffusive, distribution of the vorticity, and it is hence associated with forces arising from the flow asymmetry produced by inertia at finite
![]() $Re$
. Thus, (3.5) is satisfied identically in Stokes flow, and a squirmer propels itself at the same speed regardless of
$Re$
. Thus, (3.5) is satisfied identically in Stokes flow, and a squirmer propels itself at the same speed regardless of
![]() ${\it\beta}$
. However, pushers increase in speed with
${\it\beta}$
. However, pushers increase in speed with
![]() $Re$
while pullers decrease at finite
$Re$
while pullers decrease at finite
![]() $Re\lesssim O(1)$
. In the former case, the first term represents a drag force because it is negative when
$Re\lesssim O(1)$
. In the former case, the first term represents a drag force because it is negative when
![]() ${\it\beta}<0$
. Thus, the redistribution of vorticity caused by inertia is responsible for the extra thrust that increases the swimming speed with
${\it\beta}<0$
. Thus, the redistribution of vorticity caused by inertia is responsible for the extra thrust that increases the swimming speed with
![]() $Re$
. The opposite occurs for a puller, where
$Re$
. The opposite occurs for a puller, where
![]() ${\it\beta}>0$
: the contribution of the first term is a thrust, but it is outweighed by drag produced by the inertial redistribution of vorticity. As
${\it\beta}>0$
: the contribution of the first term is a thrust, but it is outweighed by drag produced by the inertial redistribution of vorticity. As
![]() $Re$
is increased beyond an
$Re$
is increased beyond an
![]() $O(1)$
value, the monotonic trend continues for a pusher until a limiting speed is reached. In contrast, the swimming speed of a puller becomes non-monotonic. A fuller explanation of these trends, especially when
$O(1)$
value, the monotonic trend continues for a pusher until a limiting speed is reached. In contrast, the swimming speed of a puller becomes non-monotonic. A fuller explanation of these trends, especially when
![]() $Re$
is large, requires a closer examination of the flow fields generated by squirmers and how they differ for pushers versus pullers.
$Re$
is large, requires a closer examination of the flow fields generated by squirmers and how they differ for pushers versus pullers.
4.2 Flows generated by pushers and pullers
Streamlines illustrating the steady axisymmetric flow around pushers and pullers are shown in figures 4 and 5, and contours of constant vorticity are shown in figures 6 and 7. At
![]() $Re=0.1$
, symmetries in the near-field flow are apparent due to the dominance of viscous forces over inertial forces: reversing the sign of
$Re=0.1$
, symmetries in the near-field flow are apparent due to the dominance of viscous forces over inertial forces: reversing the sign of
![]() ${\it\beta}$
causes the streamlines to be mirrored along the
${\it\beta}$
causes the streamlines to be mirrored along the
![]() ${\it\rho}$
-axis. Also, the vorticity is fore–aft antisymmetric. Pushers generate positive vorticity ahead of their direction of travel and negative vorticity behind, while pullers do the opposite. Closed-streamline recirculatory regions appear in front of pushers and behind pullers if
${\it\rho}$
-axis. Also, the vorticity is fore–aft antisymmetric. Pushers generate positive vorticity ahead of their direction of travel and negative vorticity behind, while pullers do the opposite. Closed-streamline recirculatory regions appear in front of pushers and behind pullers if
![]() $|{\it\beta}|>1$
. Streamlines separate from the squirmer surface at the point where the stroke
$|{\it\beta}|>1$
. Streamlines separate from the squirmer surface at the point where the stroke
![]() $v_{s}({\it\theta})$
changes sign (Magar et al.
Reference Magar, Goto and Pedley2003).
$v_{s}({\it\theta})$
changes sign (Magar et al.
Reference Magar, Goto and Pedley2003).

Figure 5. Similar to figure 4 except with
![]() ${\it\beta}=\pm 0.5$
; (a) pusher:
${\it\beta}=\pm 0.5$
; (a) pusher:
![]() ${\it\beta}=-0.5$
;
${\it\beta}=-0.5$
;
![]() $Re=1000$
, (b) puller:
$Re=1000$
, (b) puller:
![]() ${\it\beta}=0.5$
;
${\it\beta}=0.5$
;
![]() $Re=1000$
.
$Re=1000$
.

Figure 6. Vorticity contours for axisymmetric flow with
![]() ${\it\omega}=\pm \{0.1,0.2,0.5,1,2,5,\ldots ,200\}$
. Dashed lines represent negative values. The dotted line in (h) at
${\it\omega}=\pm \{0.1,0.2,0.5,1,2,5,\ldots ,200\}$
. Dashed lines represent negative values. The dotted line in (h) at
![]() $Re=1000$
encircles the region where there is an approximately constant value of
$Re=1000$
encircles the region where there is an approximately constant value of
![]() ${\it\omega}/{\it\rho}=2.9\pm 0.05$
, indicating that the wake bubble behind a
${\it\omega}/{\it\rho}=2.9\pm 0.05$
, indicating that the wake bubble behind a
![]() ${\it\beta}=5$
puller has a structure resembling a Hill’s vortex; (a,c,e,g) pusher:
${\it\beta}=5$
puller has a structure resembling a Hill’s vortex; (a,c,e,g) pusher:
![]() ${\it\beta}=-5$
, (b,d,f,h) puller:
${\it\beta}=-5$
, (b,d,f,h) puller:
![]() ${\it\beta}=5$
;
${\it\beta}=5$
;
![]() $Re=0.1$
(a,b), 10 (c,d), 100 (e,f), 1000 (g,h).
$Re=0.1$
(a,b), 10 (c,d), 100 (e,f), 1000 (g,h).

Figure 7. Similar to figure 6 except with
![]() ${\it\beta}=\pm 0.5$
; (a) pusher:
${\it\beta}=\pm 0.5$
; (a) pusher:
![]() ${\it\beta}=-0.5$
;
${\it\beta}=-0.5$
;
![]() $Re=1000$
, (b) puller:
$Re=1000$
, (b) puller:
![]() ${\it\beta}=0.5$
;
${\it\beta}=0.5$
;
![]() $Re=1000$
.
$Re=1000$
.

Figure 8. The maximum value of
![]() $|{\it\omega}|$
, normalized by
$|{\it\omega}|$
, normalized by
![]() $|{\it\beta}|$
, from axisymmetric computations at
$|{\it\beta}|$
, from axisymmetric computations at
![]() ${\it\beta}=\pm 0.5$
and
${\it\beta}=\pm 0.5$
and
![]() $\pm 5$
and from 3-D computations for
$\pm 5$
and from 3-D computations for
![]() ${\it\beta}=+5$
. In Stokes flow,
${\it\beta}=+5$
. In Stokes flow,
![]() $\max |{\it\omega}/{\it\beta}|=9|{\it\beta}|/4$
, as indicated by the dashed line to which the data collapses as
$\max |{\it\omega}/{\it\beta}|=9|{\it\beta}|/4$
, as indicated by the dashed line to which the data collapses as
![]() $Re\rightarrow 0$
. The dotted line indicates a slope of one-half, revealing that
$Re\rightarrow 0$
. The dotted line indicates a slope of one-half, revealing that
![]() ${\it\omega}\sim \sqrt{Re}$
at large
${\it\omega}\sim \sqrt{Re}$
at large
![]() $Re$
.
$Re$
.
The flow patterns and swimming speed observed as
![]() $Re$
is increased depend critically on
$Re$
is increased depend critically on
![]() ${\it\beta}$
. For pushers at
${\it\beta}$
. For pushers at
![]() $Re\gg 1$
, the majority of the vorticity, along with the upstream closed-streamline region that is present if
$Re\gg 1$
, the majority of the vorticity, along with the upstream closed-streamline region that is present if
![]() ${\it\beta}<-1$
, is concentrated into a laminar boundary layer of thickness
${\it\beta}<-1$
, is concentrated into a laminar boundary layer of thickness
![]() $O(1/\sqrt{Re})$
. This vorticity is then transported into a narrow downstream wake due to the motion of the swimming stroke (figures 6
a,c,e,g and 7
a). The streamlines outside the boundary layer and wake tend toward a potential flow profile, and no standing wake eddy is present (figures 4
a,c,e,g and 5
a). Thus, the flow around a pusher apparently resembles that past an inviscid spherical bubble at large
$O(1/\sqrt{Re})$
. This vorticity is then transported into a narrow downstream wake due to the motion of the swimming stroke (figures 6
a,c,e,g and 7
a). The streamlines outside the boundary layer and wake tend toward a potential flow profile, and no standing wake eddy is present (figures 4
a,c,e,g and 5
a). Thus, the flow around a pusher apparently resembles that past an inviscid spherical bubble at large
![]() $Re_{U}$
, which exhibits the same characteristics (Moore Reference Moore1963; Leal Reference Leal1989). The key similarity is that the mobile surfaces of a bubble and a pusher squirmer cause advection of vorticity downstream, thus preventing it from accumulating into a recirculating wake. However, for a bubble, the shear-free surface produces
$Re_{U}$
, which exhibits the same characteristics (Moore Reference Moore1963; Leal Reference Leal1989). The key similarity is that the mobile surfaces of a bubble and a pusher squirmer cause advection of vorticity downstream, thus preventing it from accumulating into a recirculating wake. However, for a bubble, the shear-free surface produces
![]() ${\it\omega}\sim O(1)$
, whereas for a squirmer,
${\it\omega}\sim O(1)$
, whereas for a squirmer,
![]() ${\it\omega}\sim O(\sqrt{Re})$
in the boundary layer (figure 8) due to the fixed nature of the surface velocity profile (swimming stroke). This is akin to a towed, rigid sphere with a no-slip surface, where the greater amount of boundary layer vorticity results in flow separation and the appearance of a wake eddy if
${\it\omega}\sim O(\sqrt{Re})$
in the boundary layer (figure 8) due to the fixed nature of the surface velocity profile (swimming stroke). This is akin to a towed, rigid sphere with a no-slip surface, where the greater amount of boundary layer vorticity results in flow separation and the appearance of a wake eddy if
![]() $Re_{U}\gtrsim 10$
, which grows with
$Re_{U}\gtrsim 10$
, which grows with
![]() $Re_{U}$
(Dennis & Walker Reference Dennis and Walker1971; Fornberg Reference Fornberg1988). These phenomena are avoided by a streamlined no-slip body, but for a pusher, the strong vorticity advection due to the propulsive surface motion interestingly achieves a similar effect. Despite the bluff body shape and
$Re_{U}$
(Dennis & Walker Reference Dennis and Walker1971; Fornberg Reference Fornberg1988). These phenomena are avoided by a streamlined no-slip body, but for a pusher, the strong vorticity advection due to the propulsive surface motion interestingly achieves a similar effect. Despite the bluff body shape and
![]() $O(\sqrt{Re})$
surface vorticity of a pusher, no wake eddy is produced.
$O(\sqrt{Re})$
surface vorticity of a pusher, no wake eddy is produced.
The flow around pullers with
![]() $0<{\it\beta}<1$
may be described likewise. As
$0<{\it\beta}<1$
may be described likewise. As
![]() $Re$
is increased, the boundary layer and wake become smaller in extent, and the majority of the flow domain becomes irrotational (figures 5
b and 7
b). Again, vorticity is efficiently swept downstream by the mobile surface with a (monotonic) swimming stroke
$Re$
is increased, the boundary layer and wake become smaller in extent, and the majority of the flow domain becomes irrotational (figures 5
b and 7
b). Again, vorticity is efficiently swept downstream by the mobile surface with a (monotonic) swimming stroke
![]() $v_{s}({\it\theta})$
that is directed along the path of the flow. Consequently, pushers and pullers with
$v_{s}({\it\theta})$
that is directed along the path of the flow. Consequently, pushers and pullers with
![]() ${\it\beta}<1$
reach a terminal (dimensionless) swimming speed (i.e. a dimensional swimming speed that is proportional to
${\it\beta}<1$
reach a terminal (dimensionless) swimming speed (i.e. a dimensional swimming speed that is proportional to
![]() $B_{1}$
).
$B_{1}$
).
The axisymmetric flow that is observed around pullers with
![]() ${\it\beta}>1$
as
${\it\beta}>1$
as
![]() $Re$
increases is very different. A trailing vortical wake bubble is indeed present and grows with
$Re$
increases is very different. A trailing vortical wake bubble is indeed present and grows with
![]() $Re$
(figure 4
b,d,f,h). Thus, for pullers with
$Re$
(figure 4
b,d,f,h). Thus, for pullers with
![]() ${\it\beta}>1$
, the flow does not become irrotational within the majority of the flow domain as
${\it\beta}>1$
, the flow does not become irrotational within the majority of the flow domain as
![]() $Re$
becomes large. As a result, the swimming speed of a
$Re$
becomes large. As a result, the swimming speed of a
![]() ${\it\beta}>1$
squirmer does not attain a terminal value. The wake eddy is caused by the reversal of
${\it\beta}>1$
squirmer does not attain a terminal value. The wake eddy is caused by the reversal of
![]() $v_{s}$
along the rear half of the squirmer surface, which hinders the advection of vorticity downstream, and causes its accumulation behind the squirmer. This resembles flow past a rigid bluff body towed by an external force, where fluid deceleration along the no-slip surface has the same effect. Indeed, if the flow is restricted to be axisymmetric, the wake bubble resembles a Hill’s spherical vortex at
$v_{s}$
along the rear half of the squirmer surface, which hinders the advection of vorticity downstream, and causes its accumulation behind the squirmer. This resembles flow past a rigid bluff body towed by an external force, where fluid deceleration along the no-slip surface has the same effect. Indeed, if the flow is restricted to be axisymmetric, the wake bubble resembles a Hill’s spherical vortex at
![]() $Re=1000$
, where
$Re=1000$
, where
![]() ${\it\omega}/{\it\rho}$
is constant in the region of closed streamlines and
${\it\omega}/{\it\rho}$
is constant in the region of closed streamlines and
![]() ${\it\omega}=0$
elsewhere (figure 6
h). Batchelor (Reference Batchelor1956) proposed that such flow structures exist in the wake of bluff bodies in steady axisymmetric flow at large
${\it\omega}=0$
elsewhere (figure 6
h). Batchelor (Reference Batchelor1956) proposed that such flow structures exist in the wake of bluff bodies in steady axisymmetric flow at large
![]() $Re$
. The computations of Fornberg (Reference Fornberg1988) show the presence of a Hill’s vortex-like wake structure behind a sphere held fixed in a uniform flow, within which
$Re$
. The computations of Fornberg (Reference Fornberg1988) show the presence of a Hill’s vortex-like wake structure behind a sphere held fixed in a uniform flow, within which
![]() ${\it\omega}/{\it\rho}$
is nearly constant once
${\it\omega}/{\it\rho}$
is nearly constant once
![]() $Re_{U}$
is sufficiently large. Moreover, it is shown that such large
$Re_{U}$
is sufficiently large. Moreover, it is shown that such large
![]() $Re$
axisymmetric flows result in very low drag forces relative to that observed in 3-D flows beyond the onset of flow instabilities. The observation that
$Re$
axisymmetric flows result in very low drag forces relative to that observed in 3-D flows beyond the onset of flow instabilities. The observation that
![]() $U$
increases with
$U$
increases with
![]() $Re$
for an axisymmetric
$Re$
for an axisymmetric
![]() ${\it\beta}=5$
pusher when
${\it\beta}=5$
pusher when
![]() $Re\gtrsim O(1)$
(figure 3) indicates that the trailing vortex behind a
$Re\gtrsim O(1)$
(figure 3) indicates that the trailing vortex behind a
![]() ${\it\beta}>1$
puller is analogous to that behind a towed sphere; the wake eddy acts to decrease the overall drag. Note that the point of flow separation along the surface of a squirmer always occurs where
${\it\beta}>1$
puller is analogous to that behind a towed sphere; the wake eddy acts to decrease the overall drag. Note that the point of flow separation along the surface of a squirmer always occurs where
![]() $v_{s}({\it\theta})$
changes sign regardless of
$v_{s}({\it\theta})$
changes sign regardless of
![]() $Re$
(figure 4), whereas it depends on
$Re$
(figure 4), whereas it depends on
![]() $Re_{U}$
for a no-slip sphere.
$Re_{U}$
for a no-slip sphere.

Figure 9. Flow state as a function of
![]() ${\it\beta}$
and
${\it\beta}$
and
![]() $Re$
. The points of transition, marked with an ‘
$Re$
. The points of transition, marked with an ‘
![]() $\times$
’ and interpolated by the solid lines, were obtained numerically (see also table 1).
$\times$
’ and interpolated by the solid lines, were obtained numerically (see also table 1).
4.3 Transition to 3-D and unsteady flow
Figure 9 and table 1 detail the transition of the flow around a squirmer from steady and axisymmetric to unsteady and 3-D and are derived from unsteady 3-D flow simulations. The critical values of
![]() $Re$
at which the axisymmetry breaks (
$Re$
at which the axisymmetry breaks (
![]() $Re^{(c1)}$
) and at which the flow becomes unsteady (
$Re^{(c1)}$
) and at which the flow becomes unsteady (
![]() $Re^{(c2)}$
) are shown. For
$Re^{(c2)}$
) are shown. For
![]() ${\it\beta}>1$
pullers,
${\it\beta}>1$
pullers,
![]() $Re^{(c1)}<Re^{(c2)}$
, and a monotonic decrease of
$Re^{(c1)}<Re^{(c2)}$
, and a monotonic decrease of
![]() $Re^{(c1)}$
and
$Re^{(c1)}$
and
![]() $Re^{(c2)}$
with
$Re^{(c2)}$
with
![]() ${\it\beta}$
is observed. Moreover,
${\it\beta}$
is observed. Moreover,
![]() $Re^{(c1)}$
and
$Re^{(c1)}$
and
![]() $Re^{(c2)}$
both increase rapidly as
$Re^{(c2)}$
both increase rapidly as
![]() ${\it\beta}$
is decreased toward unity such that
${\it\beta}$
is decreased toward unity such that
![]() ${\it\beta}=1$
appears to be an asymptote; pushers and pullers with
${\it\beta}=1$
appears to be an asymptote; pushers and pullers with
![]() ${\it\beta}<1$
produce steady axisymmetric flows that remain stable up to at least
${\it\beta}<1$
produce steady axisymmetric flows that remain stable up to at least
![]() $Re=1000$
.
$Re=1000$
.
This highlights another apparent similarity between the flow past a
![]() ${\it\beta}<1$
squirmer and an inviscid spherical bubble. For the latter, the asymptotic analysis of Moore (Reference Moore1963) suggested that a potential flow is recovered as
${\it\beta}<1$
squirmer and an inviscid spherical bubble. For the latter, the asymptotic analysis of Moore (Reference Moore1963) suggested that a potential flow is recovered as
![]() $Re_{U}\rightarrow \infty$
. Specific studies have also been carried out to determine how the wake structure and flow stability vary with aspect ratio for oblate spheroidal bubbles (Dandy & Leal Reference Dandy and Leal1986; Blanco & Magnaudet Reference Blanco and Magnaudet1995; Magnaudet & Mougin Reference Magnaudet and Mougin2007). It was revealed that only bubbles with an aspect ratio larger than 1.65 or 2.21 exhibit a standing wake eddy or an unstable wake, respectively. The reason is that a sufficient amount of vorticity (produced at the bubble surface in an amount proportional to the surface curvature) must accumulate in its wake for these transitions to occur. For a squirmer, a comparatively large
$Re_{U}\rightarrow \infty$
. Specific studies have also been carried out to determine how the wake structure and flow stability vary with aspect ratio for oblate spheroidal bubbles (Dandy & Leal Reference Dandy and Leal1986; Blanco & Magnaudet Reference Blanco and Magnaudet1995; Magnaudet & Mougin Reference Magnaudet and Mougin2007). It was revealed that only bubbles with an aspect ratio larger than 1.65 or 2.21 exhibit a standing wake eddy or an unstable wake, respectively. The reason is that a sufficient amount of vorticity (produced at the bubble surface in an amount proportional to the surface curvature) must accumulate in its wake for these transitions to occur. For a squirmer, a comparatively large
![]() $O(\sqrt{Re})$
amount of boundary layer vorticity is generated, whereas it is
$O(\sqrt{Re})$
amount of boundary layer vorticity is generated, whereas it is
![]() $O(1)$
for a spherical bubble, so the stability of the flow past pushers and
$O(1)$
for a spherical bubble, so the stability of the flow past pushers and
![]() ${\it\beta}<1$
pullers despite this fact is an intriguing result. Again, vorticity is strongly advected downstream by the propulsive surface velocity, preventing its accumulation in the wake, and the stability of the steady axisymmetric flow is preserved.
${\it\beta}<1$
pullers despite this fact is an intriguing result. Again, vorticity is strongly advected downstream by the propulsive surface velocity, preventing its accumulation in the wake, and the stability of the steady axisymmetric flow is preserved.
However, this does not imply stability at all
![]() $Re$
. For no-slip objects where the vorticity is similarly
$Re$
. For no-slip objects where the vorticity is similarly
![]() $O(\sqrt{Re})$
, turbulent boundary layers develop when
$O(\sqrt{Re})$
, turbulent boundary layers develop when
![]() $Re$
is very large, even for streamlined objects such as airfoils or flat plates where there is no instability caused by a wake eddy. For example, the boundary layer of a no-slip sphere becomes turbulent at
$Re$
is very large, even for streamlined objects such as airfoils or flat plates where there is no instability caused by a wake eddy. For example, the boundary layer of a no-slip sphere becomes turbulent at
![]() $Re_{U}\approx 10^{5}$
(Deen Reference Deen1998, p. 512). For this reason, it is very possible that the laminar boundary layer of a squirmer will also become turbulent at sufficiently large
$Re_{U}\approx 10^{5}$
(Deen Reference Deen1998, p. 512). For this reason, it is very possible that the laminar boundary layer of a squirmer will also become turbulent at sufficiently large
![]() $Re$
, except, perhaps, in the singular
$Re$
, except, perhaps, in the singular
![]() ${\it\beta}=0$
case where potential flow results identically. Such a phenomenon likely occurs well above the maximum
${\it\beta}=0$
case where potential flow results identically. Such a phenomenon likely occurs well above the maximum
![]() $Re=1000$
considered in this work, and hence is not further discussed here.
$Re=1000$
considered in this work, and hence is not further discussed here.
Table 1. Numerically obtained critical values of
![]() $Re$
where the flow becomes 3-D (
$Re$
where the flow becomes 3-D (
![]() $Re^{(c1)}$
) and unsteady (
$Re^{(c1)}$
) and unsteady (
![]() $Re^{(c2)}$
) (see also figure 9).
$Re^{(c2)}$
) (see also figure 9).

Given the previously noted similarities of the steady axisymmetric flow around a
![]() ${\it\beta}>1$
puller to that past a no-slip sphere, one might expect that the transitions to 3-D and unsteady flows that occur will also be analogous. This indeed appears to be the case. For a no-slip sphere, the flow first bifurcates at
${\it\beta}>1$
puller to that past a no-slip sphere, one might expect that the transitions to 3-D and unsteady flows that occur will also be analogous. This indeed appears to be the case. For a no-slip sphere, the flow first bifurcates at
![]() $Re_{U}^{(c1)}\approx 105$
(Natarajan & Acrivos Reference Natarajan and Acrivos1993; Tomboulides & Orszag Reference Tomboulides and Orszag2000), resulting in a steady 3-D flow that exhibits planar symmetry and two counter-rotating vortices in the wake. The symmetry plane passes through the axis of translation, but its orientation is arbitrary due to the initial axisymmetry of the flow. The scenario is the same for
$Re_{U}^{(c1)}\approx 105$
(Natarajan & Acrivos Reference Natarajan and Acrivos1993; Tomboulides & Orszag Reference Tomboulides and Orszag2000), resulting in a steady 3-D flow that exhibits planar symmetry and two counter-rotating vortices in the wake. The symmetry plane passes through the axis of translation, but its orientation is arbitrary due to the initial axisymmetry of the flow. The scenario is the same for
![]() ${\it\beta}>1$
pullers, and planar flow symmetry is apparent in figure 10(a). The only difference is that
${\it\beta}>1$
pullers, and planar flow symmetry is apparent in figure 10(a). The only difference is that
![]() $Re^{(c1)}$
depends on
$Re^{(c1)}$
depends on
![]() ${\it\beta}$
in the latter case. A second transition from steady to unsteady flow takes place at
${\it\beta}$
in the latter case. A second transition from steady to unsteady flow takes place at
![]() $Re_{U}^{(c2)}\approx 140$
in the case of a no-slip sphere (Natarajan & Acrivos Reference Natarajan and Acrivos1993; Tomboulides & Orszag Reference Tomboulides and Orszag2000), and the same happens for a
$Re_{U}^{(c2)}\approx 140$
in the case of a no-slip sphere (Natarajan & Acrivos Reference Natarajan and Acrivos1993; Tomboulides & Orszag Reference Tomboulides and Orszag2000), and the same happens for a
![]() ${\it\beta}>1$
puller at
${\it\beta}>1$
puller at
![]() $Re^{(c2)}=Re^{(c2)}({\it\beta})$
. In both cases, the planar flow symmetry persists, and as
$Re^{(c2)}=Re^{(c2)}({\it\beta})$
. In both cases, the planar flow symmetry persists, and as
![]() $Re$
(or
$Re$
(or
![]() $Re_{U}$
) is further increased, shedding of the wake vortices begins to occur (figure 10
b). Table 1 reveals that the quantity
$Re_{U}$
) is further increased, shedding of the wake vortices begins to occur (figure 10
b). Table 1 reveals that the quantity
![]() $Re^{(c2)}-Re^{(c1)}$
decreases significantly as
$Re^{(c2)}-Re^{(c1)}$
decreases significantly as
![]() ${\it\beta}$
is increased; the difference is approximately 40 at
${\it\beta}$
is increased; the difference is approximately 40 at
![]() ${\it\beta}=1.5$
and decreases to only
${\it\beta}=1.5$
and decreases to only
![]() $3.2$
at
$3.2$
at
![]() ${\it\beta}=5$
. The flow is more quickly destabilized when the value of
${\it\beta}=5$
. The flow is more quickly destabilized when the value of
![]() ${\it\beta}$
is larger, and hence there is only a narrow range of
${\it\beta}$
is larger, and hence there is only a narrow range of
![]() $Re$
where it exhibits a steady 3-D state.
$Re$
where it exhibits a steady 3-D state.

Figure 10. The streamwise component of the vorticity for a
![]() ${\it\beta}=5$
puller at an isocontour of
${\it\beta}=5$
puller at an isocontour of
![]() ${\it\omega}_{z}=\pm 1.05$
. In (a),
${\it\omega}_{z}=\pm 1.05$
. In (a),
![]() $Re=22.6$
; the flow is planar symmetric and steady (
$Re=22.6$
; the flow is planar symmetric and steady (
![]() $Re^{(c1)}<Re<Re^{(c2)}$
). Two counter-rotating vortices are present in the wake. In (b),
$Re^{(c1)}<Re<Re^{(c2)}$
). Two counter-rotating vortices are present in the wake. In (b),
![]() $Re=100$
; the flow is also planar symmetric but unsteady (
$Re=100$
; the flow is also planar symmetric but unsteady (
![]() $Re>Re^{(c2)}$
), and the wake structure is more complicated; a pair of vortices is being shed downstream from the wake. Finally in (c),
$Re>Re^{(c2)}$
), and the wake structure is more complicated; a pair of vortices is being shed downstream from the wake. Finally in (c),
![]() $Re=158$
; the planar symmetry is broken and the flow appears to be almost chaotic in nature.
$Re=158$
; the planar symmetry is broken and the flow appears to be almost chaotic in nature.

Figure 11. Magnitude of the lift force
![]() $F_{\bot }$
normalized by
$F_{\bot }$
normalized by
![]() $2B_{1}a{\it\mu}/3$
(solid) and the azimuthal angle
$2B_{1}a{\it\mu}/3$
(solid) and the azimuthal angle
![]() ${\it\varphi}_{F}-{\it\varphi}_{F0}$
at which it acts (dashed) for a
${\it\varphi}_{F}-{\it\varphi}_{F0}$
at which it acts (dashed) for a
![]() ${\it\beta}=5$
squirmer accelerating from rest at time
${\it\beta}=5$
squirmer accelerating from rest at time
![]() $t=0$
. Time is normalized by
$t=0$
. Time is normalized by
![]() $3a/(2B_{1})$
. Here,
$3a/(2B_{1})$
. Here,
![]() ${\it\varphi}_{F0}$
represents the (arbitrary) initial angle of the lift when it first becomes non-zero. In (a)
${\it\varphi}_{F0}$
represents the (arbitrary) initial angle of the lift when it first becomes non-zero. In (a)
![]() $Re=21.7$
and (b)
$Re=21.7$
and (b)
![]() $Re=24.0$
,
$Re=24.0$
,
![]() $Re^{(c1)}<Re<Re^{(c2)}$
, and a constant steady-state lift force is observed. In (c)
$Re^{(c1)}<Re<Re^{(c2)}$
, and a constant steady-state lift force is observed. In (c)
![]() $Re=25.3$
and (d)
$Re=25.3$
and (d)
![]() $Re=26.7$
,
$Re=26.7$
,
![]() $Re>Re^{(c2)}$
, and the lift force is oscillatory. In (c), the direction of the lift remains constant, while in (d) it periodically reverses direction.
$Re>Re^{(c2)}$
, and the lift force is oscillatory. In (c), the direction of the lift remains constant, while in (d) it periodically reverses direction.
Once the flow enters an unsteady and/or 3-D state, the squirmer will no longer be force-free or torque-free in general. Examining the hydrodynamic forces and torques which arise in the vicinity of
![]() $Re^{(c1)}$
and
$Re^{(c1)}$
and
![]() $Re^{(c2)}$
yields some interesting observations. Figure 11 shows the lift, defined as the force perpendicular to the direction of translation, for a
$Re^{(c2)}$
yields some interesting observations. Figure 11 shows the lift, defined as the force perpendicular to the direction of translation, for a
![]() ${\it\beta}=5$
puller started from rest, in which case
${\it\beta}=5$
puller started from rest, in which case
![]() $Re^{(c1)}=21.0$
and
$Re^{(c1)}=21.0$
and
![]() $Re^{(c2)}=24.2$
. If
$Re^{(c2)}=24.2$
. If
![]() $Re^{(c1)}<Re<Re^{(c2)}$
, as in (a,b), a constant lift force is generated once the flow reaches a steady state. Some small oscillations that eventually die out are observed at
$Re^{(c1)}<Re<Re^{(c2)}$
, as in (a,b), a constant lift force is generated once the flow reaches a steady state. Some small oscillations that eventually die out are observed at
![]() $Re=24.0$
but not at
$Re=24.0$
but not at
![]() $Re=21.7$
. If
$Re=21.7$
. If
![]() $Re>Re^{(c2)}$
, the flow is unsteady and hence the lift does not reach a constant value in figure 11(c,d). At
$Re>Re^{(c2)}$
, the flow is unsteady and hence the lift does not reach a constant value in figure 11(c,d). At
![]() $Re=25.3$
, the lift is oscillatory but always acts along the same direction, while at
$Re=25.3$
, the lift is oscillatory but always acts along the same direction, while at
![]() $Re=26.7$
, the lift periodically reverses direction. The torque generated on the squirmer, plotted in figure 12, clearly follows the same pattern as the lift, although it is offset by
$Re=26.7$
, the lift periodically reverses direction. The torque generated on the squirmer, plotted in figure 12, clearly follows the same pattern as the lift, although it is offset by
![]() $90^{\circ }$
. The lift and torque are perpendicular due to the planar flow symmetry; the lift is in the symmetry plane, while the torque is normal to it (the symmetry can be seen visually in figures 10
a and10
b).
$90^{\circ }$
. The lift and torque are perpendicular due to the planar flow symmetry; the lift is in the symmetry plane, while the torque is normal to it (the symmetry can be seen visually in figures 10
a and10
b).

Figure 12. Analogous to figure 11 above, but now the magnitude of the hydrodynamic torque
![]() $T$
(normalized by
$T$
(normalized by
![]() $2B_{1}a^{2}{\it\mu}/3$
) is plotted along with the angle
$2B_{1}a^{2}{\it\mu}/3$
) is plotted along with the angle
![]() ${\it\varphi}_{T}-{\it\varphi}_{F0}$
that the torque forms with the initial lift force;
${\it\varphi}_{T}-{\it\varphi}_{F0}$
that the torque forms with the initial lift force;
![]() $Re=21.7$
(a), 24.0 (b), 25.3 (c), 26.7 (d). For all
$Re=21.7$
(a), 24.0 (b), 25.3 (c), 26.7 (d). For all
![]() $Re$
shown, the torque is perpendicular to both the direction of translation and the lift.
$Re$
shown, the torque is perpendicular to both the direction of translation and the lift.

Figure 13. (a) Swimming speed,
![]() $U/U_{0}$
versus time,
$U/U_{0}$
versus time,
![]() $t$
, for a
$t$
, for a
![]() ${\it\beta}=5$
puller accelerating from rest (3-D simulation). Time is normalized by
${\it\beta}=5$
puller accelerating from rest (3-D simulation). Time is normalized by
![]() $3a/(2B_{1})$
. (b) The Strouhal number
$3a/(2B_{1})$
. (b) The Strouhal number
![]() $St$
versus
$St$
versus
![]() $Re$
for a
$Re$
for a
![]() ${\it\beta}=5$
puller.
${\it\beta}=5$
puller.
Hydrodynamic forces acting parallel to the direction of swimming also cause oscillations in the swimming speed when
![]() $Re>Re^{(c2)}$
. The time-dependent speed of a
$Re>Re^{(c2)}$
. The time-dependent speed of a
![]() ${\it\beta}=5$
puller accelerating from rest is shown in figure 13(a). Note that these oscillations have double the frequency of that in the lift and torque. It is also apparent that the average normalized swimming speed decreases significantly with increasing
${\it\beta}=5$
puller accelerating from rest is shown in figure 13(a). Note that these oscillations have double the frequency of that in the lift and torque. It is also apparent that the average normalized swimming speed decreases significantly with increasing
![]() $Re$
. This can be ascribed to vortex shedding; the drag-reducing effect of the vorticity-trapping wake bubble observed in (unstable) axisymmetric flows is lost as the vorticity is instead shed downstream. This explains the deviation of the unsteady 3-D simulations from the axisymmetric ones seen in figure 3 at approximately the same point at which the flow becomes unsteady.
$Re$
. This can be ascribed to vortex shedding; the drag-reducing effect of the vorticity-trapping wake bubble observed in (unstable) axisymmetric flows is lost as the vorticity is instead shed downstream. This explains the deviation of the unsteady 3-D simulations from the axisymmetric ones seen in figure 3 at approximately the same point at which the flow becomes unsteady.
From the dominant dimensional frequency
![]() $f$
of the oscillations in the lift force, we define the Strouhal number as
$f$
of the oscillations in the lift force, we define the Strouhal number as
![]() $St=3fa/(2B_{1})$
, which is plotted for a
$St=3fa/(2B_{1})$
, which is plotted for a
![]() ${\it\beta}=5$
puller in figure 13(b). A rapid initial decrease of
${\it\beta}=5$
puller in figure 13(b). A rapid initial decrease of
![]() $St$
occurs just as
$St$
occurs just as
![]() $Re$
exceeds
$Re$
exceeds
![]() $Re^{(c2)}$
and unsteady flow is established. At slightly higher
$Re^{(c2)}$
and unsteady flow is established. At slightly higher
![]() $Re$
,
$Re$
,
![]() $St$
rebounds and maintains a value between 0.024 and 0.029 between
$St$
rebounds and maintains a value between 0.024 and 0.029 between
![]() $Re=60$
and
$Re=60$
and
![]() $Re=160$
. This can be roughly compared to flow past a no-slip sphere where
$Re=160$
. This can be roughly compared to flow past a no-slip sphere where
![]() $St_{U}=fa/U=0.067$
at
$St_{U}=fa/U=0.067$
at
![]() $Re_{U}=150$
(Natarajan & Acrivos Reference Natarajan and Acrivos1993; Tomboulides & Orszag Reference Tomboulides and Orszag2000).
$Re_{U}=150$
(Natarajan & Acrivos Reference Natarajan and Acrivos1993; Tomboulides & Orszag Reference Tomboulides and Orszag2000).
It is also apparent from figure 13(a) that the flow at
![]() ${\it\beta}=5$
transitions from having just a single frequency at
${\it\beta}=5$
transitions from having just a single frequency at
![]() $Re=63$
to appearing nearly chaotic at
$Re=63$
to appearing nearly chaotic at
![]() $Re=158$
. Also, the planar symmetry observed at
$Re=158$
. Also, the planar symmetry observed at
![]() $Re=100$
(figure 10
b) is clearly broken at
$Re=100$
(figure 10
b) is clearly broken at
![]() $Re=158$
(figure 10
c). Similar transitions occur for flow past a no-slip sphere in the range
$Re=158$
(figure 10
c). Similar transitions occur for flow past a no-slip sphere in the range
![]() $300<Re_{U}<500$
, and the fluctuations in the flow become increasingly irregular as
$300<Re_{U}<500$
, and the fluctuations in the flow become increasingly irregular as
![]() $Re$
is further increased, signifying the beginnings of turbulence (Tomboulides & Orszag Reference Tomboulides and Orszag2000). This is also observed for a
$Re$
is further increased, signifying the beginnings of turbulence (Tomboulides & Orszag Reference Tomboulides and Orszag2000). This is also observed for a
![]() ${\it\beta}=5$
puller at
${\it\beta}=5$
puller at
![]() $Re=1000$
, as the increasingly chaotic nature of the flow causes increasingly broadband fluctuations in the swimming speed.
$Re=1000$
, as the increasingly chaotic nature of the flow causes increasingly broadband fluctuations in the swimming speed.
4.4 Power expenditure and hydrodynamic efficiency
The dimensionless power
![]() $\mathscr{P}$
expended by a squirmer versus
$\mathscr{P}$
expended by a squirmer versus
![]() $Re$
for
$Re$
for
![]() ${\it\beta}=0$
,
${\it\beta}=0$
,
![]() $\pm 0.5$
and
$\pm 0.5$
and
![]() $\pm 5$
is shown in figure 14(a). This is calculated as the rate of work done on the fluid by the tangential motion of the squirmer surface,
$\pm 5$
is shown in figure 14(a). This is calculated as the rate of work done on the fluid by the tangential motion of the squirmer surface,
where
![]() $\mathscr{P}$
is normalized by
$\mathscr{P}$
is normalized by
![]() $4B_{1}^{2}a{\it\mu}/9$
. In axisymmetric flow, (4.1) simplifies to
$4B_{1}^{2}a{\it\mu}/9$
. In axisymmetric flow, (4.1) simplifies to
Additionally, power expended by the squirmer is dissipated viscously by the fluid. The dimensionless rate of viscous dissipation
![]() ${\it\Phi}$
in the flow around a tangentially deforming spherical body can be given in terms of the vorticity and surface velocity (Stone Reference Stone1993; Stone & Samuel Reference Stone and Samuel1996),
${\it\Phi}$
in the flow around a tangentially deforming spherical body can be given in terms of the vorticity and surface velocity (Stone Reference Stone1993; Stone & Samuel Reference Stone and Samuel1996),
and at steady state,
![]() ${\it\Phi}=\mathscr{P}$
. This implies that a squirmer that minimizes the amount of vorticity that it generates in the fluid will also minimize its power expenditure.
${\it\Phi}=\mathscr{P}$
. This implies that a squirmer that minimizes the amount of vorticity that it generates in the fluid will also minimize its power expenditure.
In fact, a neutral (
![]() ${\it\beta}=0$
) squirmer expends the least amount of energy at all
${\it\beta}=0$
) squirmer expends the least amount of energy at all
![]() $Re$
since it generates no vorticity. In this case, integrating (4.2) gives
$Re$
since it generates no vorticity. In this case, integrating (4.2) gives
![]() $\mathscr{P}|_{{\it\beta}=0}=12{\rm\pi}$
for all
$\mathscr{P}|_{{\it\beta}=0}=12{\rm\pi}$
for all
![]() $Re$
. We may also integrate (4.2) to give the power expenditure in Stokes flow,
$Re$
. We may also integrate (4.2) to give the power expenditure in Stokes flow,
![]() $\mathscr{P}|_{Re=0}=12{\rm\pi}(2+{\it\beta}^{2})/2$
(Wang & Ardekani Reference Wang and Ardekani2012), which gives the limits approached by the data in figure 14(a) as
$\mathscr{P}|_{Re=0}=12{\rm\pi}(2+{\it\beta}^{2})/2$
(Wang & Ardekani Reference Wang and Ardekani2012), which gives the limits approached by the data in figure 14(a) as
![]() $Re\rightarrow 0$
. As
$Re\rightarrow 0$
. As
![]() $Re$
is increased,
$Re$
is increased,
![]() $\mathscr{P}$
increases (if
$\mathscr{P}$
increases (if
![]() ${\it\beta}\neq 0$
) due to increased vorticity generation. As shown in figure 8,
${\it\beta}\neq 0$
) due to increased vorticity generation. As shown in figure 8,
![]() $|{\it\omega}|_{max}$
increases monotonically, scaling with
$|{\it\omega}|_{max}$
increases monotonically, scaling with
![]() $\sqrt{Re}$
within the boundary layer at large
$\sqrt{Re}$
within the boundary layer at large
![]() $Re$
. From (4.2) and (4.3), we expect the same scaling for
$Re$
. From (4.2) and (4.3), we expect the same scaling for
![]() $\mathscr{P}$
, which is indeed observed in figure 14(a). We also observe that
$\mathscr{P}$
, which is indeed observed in figure 14(a). We also observe that
![]() $\mathscr{P}({\it\beta},Re)>\mathscr{P}({\it\beta},0)$
for all
$\mathscr{P}({\it\beta},Re)>\mathscr{P}({\it\beta},0)$
for all
![]() $Re>0$
. One might conjecture that this behaviour is predicted by the Helmholtz minimum dissipation theorem (Batchelor Reference Batchelor1967), which guarantees that a Stokes flow field dissipates less energy than any other incompressible flow field with the same boundary velocities. However, the far-field boundary velocity for a squirmer is given by its swimming speed
$Re>0$
. One might conjecture that this behaviour is predicted by the Helmholtz minimum dissipation theorem (Batchelor Reference Batchelor1967), which guarantees that a Stokes flow field dissipates less energy than any other incompressible flow field with the same boundary velocities. However, the far-field boundary velocity for a squirmer is given by its swimming speed
![]() $U$
, which generally depends on
$U$
, which generally depends on
![]() $Re$
, so the theorem does not apply. Nonetheless, the observation that
$Re$
, so the theorem does not apply. Nonetheless, the observation that
![]() $\mathscr{P}$
is minimized at
$\mathscr{P}$
is minimized at
![]() $Re=0$
for a given value of
$Re=0$
for a given value of
![]() ${\it\beta}$
is intriguing. Moreover, we observe that
${\it\beta}$
is intriguing. Moreover, we observe that
![]() $\mathscr{P}$
increases monotonically with
$\mathscr{P}$
increases monotonically with
![]() $Re$
. This finding may be compared to the monotonic increase of the extensional viscosity of a dilute suspension of rigid spheres with
$Re$
. This finding may be compared to the monotonic increase of the extensional viscosity of a dilute suspension of rigid spheres with
![]() $Re$
in uniaxial extensional flow. Specifically, the extensional viscosity also increases monotonically and scales with
$Re$
in uniaxial extensional flow. Specifically, the extensional viscosity also increases monotonically and scales with
![]() $\sqrt{Re}$
at large
$\sqrt{Re}$
at large
![]() $Re$
due to intense
$Re$
due to intense
![]() $O(\sqrt{Re})$
boundary layer vorticity (Ryskin Reference Ryskin1980). The extensional viscosity is proportional to the viscous dissipation rate in the flow. Thus, it is an interesting observation that the power expended by a squirmer, which is viscously dissipated, behaves similarly to the extensional viscosity of a dilute suspension of spheres as a function of the Reynolds number.
$O(\sqrt{Re})$
boundary layer vorticity (Ryskin Reference Ryskin1980). The extensional viscosity is proportional to the viscous dissipation rate in the flow. Thus, it is an interesting observation that the power expended by a squirmer, which is viscously dissipated, behaves similarly to the extensional viscosity of a dilute suspension of spheres as a function of the Reynolds number.

Figure 14. Power
![]() $\mathscr{P}$
expended by a squirmer versus
$\mathscr{P}$
expended by a squirmer versus
![]() $Re$
(a), and the Lighthill efficiency
$Re$
(a), and the Lighthill efficiency
![]() ${\it\eta}_{L}$
versus the translational Reynolds number
${\it\eta}_{L}$
versus the translational Reynolds number
![]() $Re_{U}={\it\varrho}Ua/{\it\mu}$
(b). Here,
$Re_{U}={\it\varrho}Ua/{\it\mu}$
(b). Here,
![]() $\mathscr{P}^{\ast }$
is the power necessary to tow a sphere in steady axisymmetric flow. A neutral (
$\mathscr{P}^{\ast }$
is the power necessary to tow a sphere in steady axisymmetric flow. A neutral (
![]() ${\it\beta}=0$
) squirmer is indicated by the solid line (with no markers) and has
${\it\beta}=0$
) squirmer is indicated by the solid line (with no markers) and has
![]() $\mathscr{P}=12{\rm\pi}$
at all
$\mathscr{P}=12{\rm\pi}$
at all
![]() $Re$
.
$Re$
.
The Lighthill (Reference Lighthill1952) efficiency
![]() ${\it\eta}_{L}$
of a squirmer is defined as the ratio of the power
${\it\eta}_{L}$
of a squirmer is defined as the ratio of the power
![]() $\mathscr{P}^{\ast }$
required to tow a no-slip sphere at a speed
$\mathscr{P}^{\ast }$
required to tow a no-slip sphere at a speed
![]() $U$
to the power
$U$
to the power
![]() $\mathscr{P}$
expended by a squirmer to swim at that same speed. This quantity is plotted in figure 14(b). Here, the horizontal axis is the Reynolds number based on the translational swimming speed,
$\mathscr{P}$
expended by a squirmer to swim at that same speed. This quantity is plotted in figure 14(b). Here, the horizontal axis is the Reynolds number based on the translational swimming speed,
![]() $Re_{U}=ReU={\it\varrho}Ua/{\it\mu}$
. Note that we take
$Re_{U}=ReU={\it\varrho}Ua/{\it\mu}$
. Note that we take
![]() $\mathscr{P}^{\ast }$
as the power required to tow a sphere in steady axisymmetric flow at the same
$\mathscr{P}^{\ast }$
as the power required to tow a sphere in steady axisymmetric flow at the same
![]() $Re_{U}$
. At
$Re_{U}$
. At
![]() $Re=0$
,
$Re=0$
,
![]() ${\it\eta}_{L}=1/(2+{\it\beta}^{2})$
, pushers and pullers have the same efficiency. At small
${\it\eta}_{L}=1/(2+{\it\beta}^{2})$
, pushers and pullers have the same efficiency. At small
![]() $Re$
, asymptotic theory shows that pushers are slightly more efficient than pullers (Wang & Ardekani Reference Wang and Ardekani2012). Thus, it would be reasonable to expect that larger differences in efficiency might be observed at larger
$Re$
, asymptotic theory shows that pushers are slightly more efficient than pullers (Wang & Ardekani Reference Wang and Ardekani2012). Thus, it would be reasonable to expect that larger differences in efficiency might be observed at larger
![]() $Re$
. Interestingly, our results reveal that the difference in efficiency between a
$Re$
. Interestingly, our results reveal that the difference in efficiency between a
![]() ${\it\beta}=\pm 0.5$
pusher and puller is very slight, even up to
${\it\beta}=\pm 0.5$
pusher and puller is very slight, even up to
![]() $Re=1000$
. This is somewhat surprising considering that a
$Re=1000$
. This is somewhat surprising considering that a
![]() ${\it\beta}=-0.5$
pusher moves nearly 10 % faster than a
${\it\beta}=-0.5$
pusher moves nearly 10 % faster than a
![]() ${\it\beta}=0.5$
puller at
${\it\beta}=0.5$
puller at
![]() $Re=1000$
. Thus, in this case, a puller and pusher exert approximately the same amount of power once differences in speed are taken into account. Similarly, a
$Re=1000$
. Thus, in this case, a puller and pusher exert approximately the same amount of power once differences in speed are taken into account. Similarly, a
![]() ${\it\beta}=\pm 5$
puller and pusher have nearly the same efficiency up to the point where the steady axisymmetric flow destabilizes at
${\it\beta}=\pm 5$
puller and pusher have nearly the same efficiency up to the point where the steady axisymmetric flow destabilizes at
![]() $Re_{U}\approx 20$
, with that of a pusher being only slightly greater. If one considers the unstable axisymmetric flow that arises beyond
$Re_{U}\approx 20$
, with that of a pusher being only slightly greater. If one considers the unstable axisymmetric flow that arises beyond
![]() $Re_{U}\approx 20$
, pullers interestingly become more efficient than pushers. The drag reducing effect of the Hill’s vortex-like wake is responsible. However, if the flow is allowed to be unsteady and 3-D, pushers continue to be more efficient by a margin that increases with
$Re_{U}\approx 20$
, pullers interestingly become more efficient than pushers. The drag reducing effect of the Hill’s vortex-like wake is responsible. However, if the flow is allowed to be unsteady and 3-D, pushers continue to be more efficient by a margin that increases with
![]() $Re_{U}$
. The vortex shedding that takes place in the wake of a high
$Re_{U}$
. The vortex shedding that takes place in the wake of a high
![]() $Re$
puller reduces the amount of swimming work that goes into forward propulsion and causes a subsequent loss of efficiency. This suggests that ‘pushing’ may be more efficient than ‘pulling’ at larger
$Re$
puller reduces the amount of swimming work that goes into forward propulsion and causes a subsequent loss of efficiency. This suggests that ‘pushing’ may be more efficient than ‘pulling’ at larger
![]() $Re$
due to the increased flow stability.
$Re$
due to the increased flow stability.
One may notice that
![]() ${\it\eta}_{L}$
increases above unity in some cases, indicating that the power required to tow a sphere exceeds that expended by a squirmer swimming at the same speed. In Stokes flow,
${\it\eta}_{L}$
increases above unity in some cases, indicating that the power required to tow a sphere exceeds that expended by a squirmer swimming at the same speed. In Stokes flow,
![]() ${\it\eta}_{L}\leqslant 3/4$
for any spherical swimmer moving only by tangential surface deformations (Stone & Samuel Reference Stone and Samuel1996). For a neutral squirmer at
${\it\eta}_{L}\leqslant 3/4$
for any spherical swimmer moving only by tangential surface deformations (Stone & Samuel Reference Stone and Samuel1996). For a neutral squirmer at
![]() $Re=0$
,
$Re=0$
,
![]() ${\it\eta}_{L}=1/2$
. However, this bound does not apply when
${\it\eta}_{L}=1/2$
. However, this bound does not apply when
![]() $Re>0$
. Indeed,
$Re>0$
. Indeed,
![]() ${\it\eta}_{L}|_{{\it\beta}=0}$
increases above unity at
${\it\eta}_{L}|_{{\it\beta}=0}$
increases above unity at
![]() $Re_{U}\approx 7$
, and the same is true for
$Re_{U}\approx 7$
, and the same is true for
![]() ${\it\beta}=\pm 0.5$
squirmers at
${\it\beta}=\pm 0.5$
squirmers at
![]() $Re_{U}\approx 10$
. This highlights the difficulty of swimming against wholly resistive viscous forces (Purcell Reference Purcell1977). For a squirmer, swimming is always less efficient than being towed by an external force in the absence of fluid inertia, but may be more efficient when inertia is present.
$Re_{U}\approx 10$
. This highlights the difficulty of swimming against wholly resistive viscous forces (Purcell Reference Purcell1977). For a squirmer, swimming is always less efficient than being towed by an external force in the absence of fluid inertia, but may be more efficient when inertia is present.
Finally, we note that the propulsion of a squirmer via tangential surface motion is drag-based. This is in contrast to the flapping and undulatory mechanisms of propulsion employed by some (usually large
![]() $Re$
) swimmers such as fishes, which are lift-based. The efficiency of lift-based propulsion can be very high in inertial flows where
$Re$
) swimmers such as fishes, which are lift-based. The efficiency of lift-based propulsion can be very high in inertial flows where
![]() $Re$
is large. However, this efficiency decreases drastically with
$Re$
is large. However, this efficiency decreases drastically with
![]() $Re$
, and drag-based propulsion has superior efficiency when fluid viscosity is a strong factor (Walker Reference Walker2002). Thus, without rigorous calculation, we surmise that the efficiency of a squirmer improves compared to lift-based propulsion as
$Re$
, and drag-based propulsion has superior efficiency when fluid viscosity is a strong factor (Walker Reference Walker2002). Thus, without rigorous calculation, we surmise that the efficiency of a squirmer improves compared to lift-based propulsion as
![]() $Re$
is decreased, likely being comparable at moderate
$Re$
is decreased, likely being comparable at moderate
![]() $Re$
. This clearly makes sense from a biological perspective; the ciliated organisms most closely described by the squirmer model are often microorganisms that swim at small
$Re$
. This clearly makes sense from a biological perspective; the ciliated organisms most closely described by the squirmer model are often microorganisms that swim at small
![]() $Re$
, although ctenophores provide an interesting example of moderate to large
$Re$
, although ctenophores provide an interesting example of moderate to large
![]() $Re$
squirmers.
$Re$
squirmers.
5 Conclusion
We have demonstrated fundamental differences between the locomotions of pusher and puller squirmers with a fixed swimming stroke when inertia is important to the flow. Specifically, it is shown that a pusher, as well as a
![]() ${\it\beta}<1$
puller, does not generate a standing wake eddy, and also that it produces steady axisymmetric flow that remains stable to at least
${\it\beta}<1$
puller, does not generate a standing wake eddy, and also that it produces steady axisymmetric flow that remains stable to at least
![]() $Re=1000$
. The vorticity is confined to a laminar boundary layer of thickness
$Re=1000$
. The vorticity is confined to a laminar boundary layer of thickness
![]() $O(\sqrt{Re})$
, and the flow becomes largely irrotational as
$O(\sqrt{Re})$
, and the flow becomes largely irrotational as
![]() $Re$
increases. This is due to the strong downstream advection of vorticity by the propulsive surface velocity profile. Before, such behaviour had only been demonstrated for bubbles, which produce
$Re$
increases. This is due to the strong downstream advection of vorticity by the propulsive surface velocity profile. Before, such behaviour had only been demonstrated for bubbles, which produce
![]() $O(1)$
vorticity. That this also holds for a
$O(1)$
vorticity. That this also holds for a
![]() ${\it\beta}<1$
squirmer is a key result, as squirmers produce a much larger
${\it\beta}<1$
squirmer is a key result, as squirmers produce a much larger
![]() $O(\sqrt{Re})$
vorticity (similar to a no-slip body).
$O(\sqrt{Re})$
vorticity (similar to a no-slip body).
In contrast, a
![]() ${\it\beta}>1$
puller is ineffective at transporting vorticity from its wake, similar to a towed, rigid sphere. Thus, it exhibits a recirculating wake region that triggers a transition to unsteady 3-D flow at a critical
${\it\beta}>1$
puller is ineffective at transporting vorticity from its wake, similar to a towed, rigid sphere. Thus, it exhibits a recirculating wake region that triggers a transition to unsteady 3-D flow at a critical
![]() $Re$
. A progression of flow patterns is observed as
$Re$
. A progression of flow patterns is observed as
![]() $Re$
is further increased, which strongly resemble those that occur for a rigid sphere, until weakly turbulent flow develops when
$Re$
is further increased, which strongly resemble those that occur for a rigid sphere, until weakly turbulent flow develops when
![]() $Re\sim O(1000)$
.
$Re\sim O(1000)$
.
Finally, we show that squirmers that minimize vorticity generation generally maximize their efficiency. In the range of
![]() $Re$
where steady axisymmetric flow is stable, the swimming efficiency of pushers and pullers is surprisingly similar. However, the vortex shedding that occurs for
$Re$
where steady axisymmetric flow is stable, the swimming efficiency of pushers and pullers is surprisingly similar. However, the vortex shedding that occurs for
![]() ${\it\beta}>1$
pullers in unsteady 3-D flow at larger
${\it\beta}>1$
pullers in unsteady 3-D flow at larger
![]() $Re$
reduces their overall efficiency below that of a pusher where the axisymmetric flow remains stable.
$Re$
reduces their overall efficiency below that of a pusher where the axisymmetric flow remains stable.
Future work will entail further quantification of squirmers in unsteady 3-D flows; at sufficiently large
![]() $Re$
, the flow around
$Re$
, the flow around
![]() ${\it\beta}>1$
pullers is expected to become fully turbulent, similar to flow around a no-slip body. Furthermore, it would be worthwhile to consider the motion of squirmers that are not bound to move along a single axis of translation. In this case, the motion of the squirmer would be fully coupled to the flow, and different swimming paths would be observed depending upon the values of
${\it\beta}>1$
pullers is expected to become fully turbulent, similar to flow around a no-slip body. Furthermore, it would be worthwhile to consider the motion of squirmers that are not bound to move along a single axis of translation. In this case, the motion of the squirmer would be fully coupled to the flow, and different swimming paths would be observed depending upon the values of
![]() $Re$
and
$Re$
and
![]() ${\it\beta}$
. The present results will be useful in quantifying fluid mixing, production of feeding currents and hydrodynamic signalling by the abundance of aquatic swimmers living at
${\it\beta}$
. The present results will be useful in quantifying fluid mixing, production of feeding currents and hydrodynamic signalling by the abundance of aquatic swimmers living at
![]() $Re$
up to 1000.
$Re$
up to 1000.
Acknowledgements
This work was funded in part by the European Union through a CIG grant to E.L. N.G.C. acknowledges partial support from the John and Claire Bertucci Fellowship in Engineering. The freely licensed software libraries NumPy, SciPy (Jones, Oliphant & Peterson Reference Jones, Oliphant and Peterson2015) and Matplotlib (Hunter Reference Hunter2007) were used in producing many of the results and figures presented in this article.
Appendix. Validation of numerical solutions
Convergence of the flow computations with respect to the grid parameters was tested empirically. First, it was ensured that the distance
![]() $R_{\infty }$
from the squirmer at which uniform flow was imposed was large enough to not affect the computed swimming speed
$R_{\infty }$
from the squirmer at which uniform flow was imposed was large enough to not affect the computed swimming speed
![]() $U$
. Computations were relatively insensitive to this parameter due to the fast velocity decay from the squirmer surface (
$U$
. Computations were relatively insensitive to this parameter due to the fast velocity decay from the squirmer surface (
![]() ${\sim}1/r^{2}$
at
${\sim}1/r^{2}$
at
![]() $Re=0$
and
$Re=0$
and
![]() ${\sim}1/r^{3}$
at large
${\sim}1/r^{3}$
at large
![]() $Re$
, outside the wake) (Subramanian Reference Subramanian2010), provided that the domain was not so small as to restrict flow near the squirmer body. For the axisymmetric computations, the polynomial order
$Re$
, outside the wake) (Subramanian Reference Subramanian2010), provided that the domain was not so small as to restrict flow near the squirmer body. For the axisymmetric computations, the polynomial order
![]() $N$
of the shape functions within each element was incrementally increased to convergence (figure 15). In order to fully resolve the boundary layer, it was ensured that the condition
$N$
of the shape functions within each element was incrementally increased to convergence (figure 15). In order to fully resolve the boundary layer, it was ensured that the condition
![]() ${\it\Delta}_{r0}/{\it\delta}\lesssim N^{2}/9$
(Gottlieb & Orszag Reference Gottlieb and Orszag1977) was satisfied, where
${\it\Delta}_{r0}/{\it\delta}\lesssim N^{2}/9$
(Gottlieb & Orszag Reference Gottlieb and Orszag1977) was satisfied, where
![]() ${\it\Delta}_{r0}$
is the element size (perpendicular to the boundary layer) and
${\it\Delta}_{r0}$
is the element size (perpendicular to the boundary layer) and
![]() ${\it\delta}$
is the boundary layer thickness. The thickness of the boundary layer was estimated as
${\it\delta}$
is the boundary layer thickness. The thickness of the boundary layer was estimated as
![]() ${\it\delta}=O(1/\sqrt{Re})$
since the boundary layer is expected to be laminar. For the second-order accurate finite-volume method used for 3-D computations, a higher mesh resolution is required due to the lower order approximation, and satisfactorily converged solutions were reached with
${\it\delta}=O(1/\sqrt{Re})$
since the boundary layer is expected to be laminar. For the second-order accurate finite-volume method used for 3-D computations, a higher mesh resolution is required due to the lower order approximation, and satisfactorily converged solutions were reached with
![]() ${\it\Delta}_{r0}=0.001$
(figure 16).
${\it\Delta}_{r0}=0.001$
(figure 16).

Figure 15. Convergence of the swimming speed
![]() $U$
(a) and
$U$
(a) and
![]() $\max |{\it\omega}|$
(b) for a
$\max |{\it\omega}|$
(b) for a
![]() ${\it\beta}=5$
puller at
${\it\beta}=5$
puller at
![]() $Re=1000$
computed via a spectral element method for steady axisymmetric flow. The horizontal axis represents the degree of the shape functions within each element. The element thickness in the boundary layer was
$Re=1000$
computed via a spectral element method for steady axisymmetric flow. The horizontal axis represents the degree of the shape functions within each element. The element thickness in the boundary layer was
![]() ${\it\Delta}_{r0}=0.01$
.
${\it\Delta}_{r0}=0.01$
.

Figure 16. Convergence of the swimming speed
![]() $U$
(a) and
$U$
(a) and
![]() $\max |{\it\omega}|$
(b) with respect to the grid resolution at the squirmer surface for 3-D unsteady flow computed via a second-order accurate finite-volume method. Here,
$\max |{\it\omega}|$
(b) with respect to the grid resolution at the squirmer surface for 3-D unsteady flow computed via a second-order accurate finite-volume method. Here,
![]() ${\it\beta}=-0.5$
and
${\it\beta}=-0.5$
and
![]() $Re=1$
.
$Re=1$
.
Additional validation of our computational methods was carried out by computing the drag coefficient of a no-slip sphere in uniform flow and comparing to previously known results (figure 17). The drag coefficient is defined as
![]() $C_{D}=2F_{D}/({\rm\pi}{\it\varrho}a^{2}U^{2})$
, where
$C_{D}=2F_{D}/({\rm\pi}{\it\varrho}a^{2}U^{2})$
, where
![]() $F_{D}$
is the drag force and
$F_{D}$
is the drag force and
![]() $U$
is the far-field velocity of the oncoming flow. Known values are provided by the correlation
$U$
is the far-field velocity of the oncoming flow. Known values are provided by the correlation
![]() $C_{D}=(\sqrt{12/Re_{U}}+0.5407)^{2}$
(Abraham Reference Abraham1970). Additionally, values in (potentially unstable) steady axisymmetric flow up to
$C_{D}=(\sqrt{12/Re_{U}}+0.5407)^{2}$
(Abraham Reference Abraham1970). Additionally, values in (potentially unstable) steady axisymmetric flow up to
![]() $Re_{U}=2500$
are provided by Fornberg (Reference Fornberg1988). The computational meshes used for our computations were the same as those used for the squirmer computations at
$Re_{U}=2500$
are provided by Fornberg (Reference Fornberg1988). The computational meshes used for our computations were the same as those used for the squirmer computations at
![]() $Re=1000$
. The results of the comparison show good agreement. Note that when
$Re=1000$
. The results of the comparison show good agreement. Note that when
![]() $Re_{U}\gtrsim 500$
,
$Re_{U}\gtrsim 500$
,
![]() $C_{D}$
becomes nearly constant, and the reported computations reproduce this feature.
$C_{D}$
becomes nearly constant, and the reported computations reproduce this feature.

Figure 17. The drag coefficient
![]() $C_{D}$
of a no-slip sphere in uniform flow computed using the numerical methods described in § 3. Comparison is made to the results of Fornberg (Reference Fornberg1988) (for steady axisymmetric flow) and the correlation given by Abraham (Reference Abraham1970).
$C_{D}$
of a no-slip sphere in uniform flow computed using the numerical methods described in § 3. Comparison is made to the results of Fornberg (Reference Fornberg1988) (for steady axisymmetric flow) and the correlation given by Abraham (Reference Abraham1970).