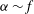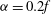1. Introduction
Density fronts are ubiquitous and important features of the upper ocean over a vast range of scales. Large-scale balanced fronts such as the Gulf Stream are vital components of the global circulation. However, the upper ocean, particularly in strongly eddying regions, also exhibits a vast web of smaller-scale fronts and filaments (e.g. Shcherbina et al.
Reference Shcherbina, D’Asaro, Lee, Klymak, Molemaker and McWilliams2013). These fronts have been shown to be sources of inertia–gravity waves, thereby providing a potential pathway for energy dissipation in the ocean (Alford, Shcherbina & Gregg Reference Alford, Shcherbina and Gregg2013). Recently, field observations and numerical simulations have shown that submesoscale (
${\sim}1{-}10~\text{km}$
) fronts and eddies, in particular, are associated with enhanced vertical velocities (e.g. Mahadevan & Tandon Reference Mahadevan and Tandon2006; Thomas, Tandon & Mahadevan Reference Thomas, Tandon and Mahadevan2008; Levy et al.
Reference Levy, Ferrari, Franks, Martin and Riviere2012).
Submesoscale dynamics presents significant theoretical challenges, not least in the study of ocean fronts. Classical theories of front formation, or frontogenesis, in eddy fields – such as that of Hoskins & Bretherton (Reference Hoskins and Bretherton1972, hereafter HB) – assume that the background strain flow associated with the eddies is characterised by a small Rossby number, defined as
$\mathit{Ro}_{L}=|\,f^{-1}\partial _{x}\bar{U}|$
, where
$\bar{U}$
is the cross-front strain flow and
$f$
is the inertial frequency. We emphasise that
$\partial _{x}\bar{U}$
in this definition is the strain associated with a background flow field, and is not associated with the ‘self-strain’ of the frontal circulation,
$\partial _{x}u$
, which can be large even for a small background strain (small
$\mathit{Ro}_{L}$
) if the front is sharp. In the oceanic context,
$\mathit{Ro}_{L}\ll 1$
is a reasonable approximation for a strain field associated with mesoscale eddies. Although it is difficult to disentangle the self-strain from the background flow, given the velocity and length scales associated with submesoscale eddies, the assumption that
$\mathit{Ro}_{L}\ll 1$
is unlikely to hold. A dynamical description of frontogenesis forced by strain associated with submesoscale eddies therefore requires an extension of HB frontogenesis theory.
Shakespeare & Taylor (Reference Shakespeare and Taylor2013, hereafter ST13) formulated a generalised model of frontogenesis that encompasses arbitrary initial conditions and order-one Rossby numbers (
$\mathit{Ro}_{L}$
). The basic configuration of the problem is similar to HB theory, consisting of a fluid with uniform potential vorticity (PV) trapped between rigid lids on which is imposed a buoyancy gradient (a front). The front is assumed to be straight and infinitely long, such that variations in the along-front direction may be neglected. A convergent strain field,
$\bar{U}=-{\it\alpha}x$
, is introduced, which squeezes the frontal gradient, and drives a secondary circulation around the front. Whereas the HB model requires that
$\mathit{Ro}_{L}={\it\alpha}/f\ll 1$
, the ST13 ‘generalised model’ permits
$\mathit{Ro}_{L}\sim 1$
and can be used to describe the frontogenetic response to strong strain flows such as those associated with submesoscale eddies.
Shakespeare & Taylor (Reference Shakespeare and Taylor2014, hereafter ST14) derived the forced solution for the generalised model introduced in ST13, defined as the solution that eliminates propagating waves associated with initial conditions. This allowed a direct comparison of predictions of the ST and HB models for the response of the flow to strain forcing. In both models, the strain field sharpens the front and drives a large-scale thermally direct secondary circulation. However, the generalised model of ST14 includes two important dynamical effects not described by the HB model: confinement and spontaneous wave generation. These effects arise due to the presence of the strain field modifying the propagation of waves in the system. Waves can only spread energy away from the front in the region where the maximum outward group speed exceeds the incoming strain flow speed, thus limiting the horizontal extent of the secondary circulation. This confinement leads to a secondary circulation that is more localised about the front, and consequently exhibits larger vertical velocities than predicted by the HB model. The confinement effect thus provides a possible explanation for enhanced vertical velocities observed near submesoscale eddies, where the stronger strain (larger
$\mathit{Ro}_{L}$
) leads to a more confined secondary circulation, as compared with the mesoscale. The trapping effect of the strain field also leads to the accumulation of wave energy at a certain distance from the front, resulting in the spontaneous generation of distinct ‘frontogenesis wave’ packets.
ST14 also extended the theory of ST13 to include a time-dependent strain flow, similar to the original HB theory. This extension makes the model more relevant to ocean fronts, which are often characterised by strongly temporally and spatially varying strain fields (e.g. Chavanne, Flament & Gurgel Reference Chavanne, Flament and Gurgel2010; Alford et al. Reference Alford, Shcherbina and Gregg2013). ST14 showed that the weakening of a strain field with time leads to trapped frontogenesis waves being released, and propagating freely away from the front. The time variation in the strain was also shown to generate additional ‘transience waves’ via an adjustment mechanism. Here we will test the validity of the generalised analytical model of ST14 by direct comparison with fully nonlinear numerical simulations for both constant and time-varying strain flows.
A large and growing literature examines the ‘spontaneous’ generation of inertia–gravity waves from balanced flows in various idealised and geophysical situations (see Vanneste (Reference Vanneste2013) and Plougonven & Zhang (Reference Plougonven and Zhang2014) for recent reviews on the topic). Previous work includes studies of inertia–gravity waves generated from Couette flow (Vanneste & Yavneh Reference Vanneste and Yavneh2004), stratified vortex dipoles (Viudez Reference Viudez2007) and baroclinic life cycles (Viudez & Dritschel Reference Viudez and Dritschel2006; Plougonven & Zhang Reference Plougonven and Zhang2007). Collectively, these studies demonstrate the ubiquity of wave generation in geophysical settings, and that, while spontaneous generation is exponentially weak at small Rossby numbers (near-balanced flows), it can be significant at large Rossby numbers. The ST14 model is a natural extension of this work: it provides a description of the inevitable breakdown of classical frontal semigeostrophic balance (e.g. Hoskins Reference Hoskins1982), and the associated spontaneous wave generation, when the background strain (or Rossby number,
$\mathit{Ro}_{L}$
) is large. Consistent with the aforementioned studies, ST14 show that the amplitude of the waves is exponentially small for weak strain fields,
$\mathit{Ro}_{L}<0.2$
, but substantial for larger strains.
Both the HB and ST14 analytical models of frontogenesis predict the collapse of the front to a discontinuity in finite time – known as the ‘critical time’. In real flows, frontal collapse will be arrested by either small-scale mixing or instabilities of the front. Previous studies have employed two-dimensional numerical simulations to test HB theory (e.g. Gall, Williams & Clark Reference Gall, Williams and Clark1987; Garner Reference Garner1989; Snyder, Skamarock & Rotunno Reference Snyder, Skamarock and Rotunno1993). In these simulations, the front collapses to the grid scale close to the critical time – regardless of resolution – and the numerical solution breaks down. Iterating the numerical solution beyond the point of frontal collapse requires the addition of an explicit diffusion.
The numerical studies noted above (Gall et al.
Reference Gall, Williams and Clark1987; Garner Reference Garner1989; Snyder et al.
Reference Snyder, Skamarock and Rotunno1993) focused mostly on the case of very weak strain,
$\mathit{Ro}_{L}=0.1$
, although some studied
$\mathit{Ro}_{L}=0.2$
. Snyder et al. (Reference Snyder, Skamarock and Rotunno1993) found that differences from the HB solution take the form of (a) higher-order corrections to the secondary circulation, and (b) waves that appear at late time, often following frontal collapse. Here we show, using numerical simulations, that the generalised model of ST14 is able to at least partially capture both of these features.
In order to arrive at analytical solutions, a number of simplifying approximations were made in formulating the ST14 model. The set-up of the problem follows the original HB model in considering the flow between two rigid horizontal surfaces, neglecting along-front variations, and assuming that the PV and background strain are both uniform in space. These assumptions restrict the direct applicability of the model results to fronts in the ocean and atmosphere, but we anticipate that the dynamics described by the ST14 model will be present in a more realistic setting. The scaling analysis discussed in ST14 also shows that the model solutions will break down when the Rossby number associated with the background strain and the Rossby number associated with the frontal circulation are both of order one. One of the main objectives of this paper is to use numerical simulations to test the validity of the ST14 model when applied to high-Rossby-number flows. Unlike the HB and ST analytical models, the numerical simulations retain all nonlinear terms and include non-hydrostatic effects. In § 3.2 we show that the nonlinear terms become important as frontogenesis proceeds and are responsible for the formation of intensified vertical jets near surface fronts.
A major challenge arising in previous numerical studies is the presence of so-called ‘spurious’ propagating waves in the solutions. These are due to the initial condition derived from the HB model not being precisely ‘balanced’ (Gall et al. Reference Gall, Williams and Clark1987). Here we are able to resolve this issue by initialising our numerical model in the state predicted from ST14 theory – rather than HB theory – greatly reducing the spurious wavefield. In other words, the initial condition implied by the generalised model of ST14 is more ‘balanced’ than that from the HB model, in the sense that it reduces the generation of propagating waves associated with adjustment to the initial condition. In § 3 we demonstrate this fact by comparison of numerical solutions initialised from the two analytical models.
The layout of the paper is as follows. In § 1 we introduce the governing equations for the system and identify the approximations made in the analytical model, as compared to the exact equations employed in the numerics. In § 3 we directly compare the predictions of the analytical model with the numerical solution for weak (
$\mathit{Ro}_{L}=0.2$
; § 3.1) and strong (
$\mathit{Ro}_{L}=0.9$
; § 3.2) strains. Similar to Snyder et al. (Reference Snyder, Skamarock and Rotunno1993), in § 4 we add horizontal diffusion to the numerical model to counteract frontogenesis and allow the front to attain steady state. The structure of this steady state agrees with ST14 analytical predictions for the long-time behaviour of the system. Lastly, in § 5 we summarise the results and discuss the usefulness of the ST14 model in understanding frontogenesis and wave generation in more complex flows.
2. Model equations
Here, we consider the incompressible non-hydrostatic Boussinesq equations for a rotating fluid in Cartesian coordinates. We will use
$(U,V,W)$
to denote the velocity components in the
$(x,y,z)$
directions, respectively,
$P$
the pressure,
${\it\rho}_{0}$
the reference density,
$b$
the buoyancy and
$f$
the (constant) Coriolis parameter. The front is assumed to be infinitely long and oriented along the
$y$
axis. Following ST14, an explicit background non-divergent deformation field of
$\bar{U}=-{\it\alpha}x$
and
$\bar{V}={\it\alpha}y$
is introduced, where
${\it\alpha}$
is a function of time only. The net velocity and pressure fields may be written as
$$\begin{eqnarray}\displaystyle U & = & \displaystyle \bar{U}+u(x,z,t),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle V & = & \displaystyle \bar{V}+v(x,z,t),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle W & = & \displaystyle w(x,z,t),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle P & = & \displaystyle \bar{P}+p(x,z,t),\end{eqnarray}$$
$y$
). Upon substitution of (2.1), the governing equations for the two-dimensional perturbation fields become 
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{D}u}{\text{D}t}-fv={\it\alpha}u-\frac{1}{{\it\rho}_{0}}\frac{\partial p}{\partial x}+{\it\kappa}_{h}\frac{\partial ^{n}u}{\partial x^{n}}+{\it\kappa}_{v}\frac{\partial ^{n}u}{\partial z^{n}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{D}v}{\text{D}t}+fu=-{\it\alpha}v+{\it\kappa}_{h}\frac{\partial ^{n}v}{\partial x^{n}}+{\it\kappa}_{v}\frac{\partial ^{n}v}{\partial z^{n}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{D}w}{\text{D}t}=b-\frac{1}{{\it\rho}_{0}}\frac{\partial p}{\partial z}+{\it\kappa}_{h}\frac{\partial ^{n}w}{\partial x^{n}}+{\it\kappa}_{v}\frac{\partial ^{n}w}{\partial z^{n}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{D}b}{\text{D}t}={\it\kappa}_{h}\frac{\partial ^{n}b}{\partial x^{n}}+{\it\kappa}_{v}\frac{\partial ^{n}b}{\partial z^{n}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\partial u}{\partial x}+\frac{\partial w}{\partial z}=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\frac{\text{D}}{\text{D}t}\equiv \frac{\partial }{\partial t}+(u+\bar{U})\frac{\partial }{\partial x}+w\frac{\partial }{\partial z}.\end{eqnarray}$$
Variables
${\it\kappa}_{h}$
and
${\it\kappa}_{v}$
are horizontal and vertical diffusivities/viscosities (the Prandtl number is assumed to be unity), respectively for
$n=2$
(or hyperdiffusion for
$n=4$
, 6, 8, …; note that
${\it\kappa}_{h},{\it\kappa}_{v}<0$
for
$n=4,8,\dots$
).
We are primarily interested in frontogenesis in the ocean surface layer. We therefore consider the idealised problem of a flow trapped between rigid lids at the ocean surface,
$z=0$
, and at depth (e.g. the thermocline),
$z=-H$
. An initial horizontal buoyancy gradient is imposed at the surface, and is then amplified by the convergent strain, thus driving frontogenesis. Within this context, (2.2) may be non-dimensionalised using the same scales as in ST13/14, which are also listed in table 1 for reference. The physical scales are the initial width of the frontal zone
$L$
, layer height
$H$
, buoyancy transition across the front
${\rm\Delta}B$
, background stratification
$N^{2}$
, inertial frequency
$f$
, strain
${\it\alpha}$
and horizontal diffusivity
${\it\kappa}$
. The time evolution of the system is thus entirely controlled by the six independent non-dimensional parameters: frontal Rossby number
$\mathit{Ro}=\sqrt{{\rm\Delta}BH}/(\,fL)$
, non-dimensional strain
${\it\delta}={\it\alpha}/f$
, Burger number
$\mathit{Bu}=(NH)/(\,fL)$
, aspect ratio
$A=L/H$
, horizontal Reynolds number
$\mathit{Re}_{h}=\sqrt{{\rm\Delta}BH}\,L^{(n-1)}/{\it\kappa}_{h}$
and vertical Reynolds number
$\mathit{Re}_{v}=\mathit{Re}_{h}({\it\kappa}_{h}/{\it\kappa}_{v})(H/L)^{n}$
. The non-dimensional strain is equal to the large-scale Rossby number characterising the background eddy-induced strain field,
${\it\delta}=\mathit{Ro}_{L}=|\,f^{-1}\partial _{x}\bar{U}|$
. With these scales, the governing equations (2.2) take the non-dimensional form
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{D}u}{\text{D}t}-v={\it\delta}u-\mathit{Ro}\,\frac{\partial p}{\partial x}+\frac{\mathit{Ro}}{\mathit{Re}_{h}}\,\frac{\partial ^{n}u}{\partial x^{n}}+\frac{\mathit{Ro}}{\mathit{Re }_{v}}\,\frac{\partial ^{n}u}{\partial z^{n}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{D}v}{\text{D}t}+u=-{\it\delta}v+\frac{\mathit{Ro}}{\mathit{Re }_{h}}\,\frac{\partial ^{n}v}{\partial x^{n}}+\frac{\mathit{Ro}}{\mathit{Re }_{v}}\,\frac{\partial ^{n}v}{\partial z^{n}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle A^{-2}\,\frac{\text{D}w}{\text{D}t}=\mathit{Ro}\,b-\mathit{Ro}\,\frac{\partial p}{\partial z}+\frac{A^{-2}Ro}{\mathit{Re}_{h}}\,\frac{\partial ^{n}w}{\partial x^{n}}+\frac{A^{-2}\mathit{Ro}}{\mathit{Re}_{v}}\,\frac{\partial ^{n}w}{\partial z^{n}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\text{D}b}{\text{D}t}=\frac{\mathit{Ro}}{\mathit{Re }_{h}}\,\frac{\partial ^{n}b}{\partial x^{n}}+\frac{\mathit{Ro}}{\mathit{Re }_{v}}\,\frac{\partial ^{n}b}{\partial z^{n}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \frac{\partial u}{\partial x}+\frac{\partial w}{\partial z}=0, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\frac{\text{D}}{\text{D}t}\equiv \frac{\partial }{\partial t}+\mathit{Ro}\left(u-\frac{{\it\delta}}{\mathit{Ro}}x\right)\frac{\partial }{\partial x}+\mathit{Ro}\,w\frac{\partial }{\partial z}.\end{eqnarray}$$
All variables are henceforth assumed to be non-dimensional, unless otherwise stated.
Table 1. Non-dimensional parameters and variable scales employed herein, consistent with ST13/14. The fundamental physical scales are the inertial frequency
$f$
, horizontal buoyancy step across the front
${\rm\Delta}B$
, buoyancy frequency
$N$
, strain
${\it\alpha}$
, initial horizontal width
$L$
, height
$H$
, horizontal diffusivity
${\it\kappa}_{h}$
and vertical diffusivity
${\it\kappa}_{v}$
. The strain ratio is equivalent to the large-scale Rossby number introduced in § 1:
${\it\delta}\equiv \mathit{Ro}_{L}$
.
ST14 formulated an analytical solution to (2.4) in the inviscid (
${\it\kappa}_{h}={\it\kappa}_{v}=0$
), hydrostatic (
$A\rightarrow \infty$
), uniform PV limit, for appropriately balanced initial conditions. The analytical solution proceeds through the introduction of a coordinate transformation,
$$\begin{eqnarray}X=\text{e}^{{\it\beta}(t)}(x+\mathit{Ro}\,v),\quad Z=z,\quad T=t,\end{eqnarray}$$
where
${\it\beta}$
is the time-integrated strain,
$$\begin{eqnarray}{\it\beta}(t)=\int _{0}^{t}{\it\delta}(t^{\prime })\,\text{d}t^{\prime }.\end{eqnarray}$$
The coordinate
$X$
in (2.6) is conserved in inviscid flow for any strain
${\it\delta}$
. It is called the generalised momentum coordinate (ST13), since it is a generalisation of the momentum coordinate,
$\mathscr{X}=x+\mathit{Ro}\,v$
, used by Blumen (Reference Blumen2000) (among others), which is conserved in the absence of a strain field. Frontogenesis, and ultimately the formation of a discontinuity in the inviscid buoyancy and velocity fields, emerges as a breakdown of the coordinate transformation (2.6). Specifically, a discontinuity forms when the inverse Jacobian of the transformation,
$$\begin{eqnarray}J^{-1}=\frac{\partial x}{\partial X}=\text{e}^{-{\it\beta}(T)}\left(1+\mathit{Ro}\frac{\partial v}{\partial x}\right)^{-1}=\text{e}^{-{\it\beta}(T)}-\mathit{Ro}\frac{\partial v}{\partial X},\end{eqnarray}$$
vanishes. The derivative transforms employed in (2.8) and other relevant quantities are listed in table 2 of ST13. The vanishing Jacobian implies a breakdown of inviscid dynamics since two fluid parcels of differing
$X$
(a materially conserved quantity for inviscid flow) will be brought into contact. The minimum value of the inverse Jacobian at a given time,
$d=\min J^{-1}$
, provides a scale for the non-dimensional frontal width. Here, we will refer to
$d$
as simply the ‘frontal width’.
As shown in ST13/14, the PV,
$q$
, in momentum coordinates has a very simple form,
$$\begin{eqnarray}q=\frac{\partial b}{\partial Z}\left(1-\text{e}^{{\it\beta}(T)}\mathit{Ro}\frac{\partial v}{\partial X}\right)^{-1}.\end{eqnarray}$$
Since PV is conserved in inviscid flow, the assumption of uniform PV,
$q=\mathit{Fr}^{-2}$
(where
$\mathit{Fr}$
is the Froude number, see table 1), implies a uniform background stratification. As shown in ST13, conservation of buoyancy (2.4d
) on the upper rigid-lid boundary (
$Z=0$
), where
$w=0$
, requires that the buoyancy is a function only of the momentum coordinate
$X$
; that is,
$b(Z=0)=b_{0}(X)$
. Since the background stratification is uniform, the lower lid must have a buoyancy of
$b(Z=-1)=b_{0}(X)-\mathit{Fr}^{-2}$
. It is therefore sufficient to prescribe the buoyancy along one boundary. Here, the function
$b_{0}(X)$
provides the initial buoyancy gradient that is amplified by the strain, giving rise to frontogenesis on both boundaries simultaneously.
ST14 showed that the general solution to (2.4) with
${\it\kappa}_{h}={\it\kappa}_{v}=0$
(inviscid) and
$A\rightarrow \infty$
(hydrostatic) can be reduced to the following partial differential equation in
${\it\phi}(X,Z,T)$
:
$$\begin{eqnarray}\left[\left(\frac{\partial ^{2}}{\partial T^{2}}+1-{\it\delta}(T)^{2}+{\it\delta}^{\prime }(T)\right)\frac{\partial ^{2}}{\partial Z^{2}}+\mathit{Bu}^{2}\text{e}^{2{\it\beta}(T)}\frac{\partial ^{2}}{\partial X^{2}}\right]{\it\phi}(X,Z,T)=\mathit{Ro}\,b_{0}^{\prime }(X)\,\text{e}^{{\it\beta}(T)}+\mathscr{N},\end{eqnarray}$$
where
${\it\phi}$
is the integral of the along-front velocity
$v$
,
$$\begin{eqnarray}{\it\phi}(X,Z,T)=\int _{-1}^{Z}v(X,Z^{\prime },T)\,\text{d}Z^{\prime }.\end{eqnarray}$$
The function
$\mathscr{N}$
on the right-hand side of (2.10) is the sum of the nonlinear terms,
$$\begin{eqnarray}\mathscr{N}=\mathit{Ro}\,\frac{\partial }{\partial Z}\left[w\,\frac{\partial u}{\partial Z}+\left({\it\delta}-\frac{\partial }{\partial T}\right)\left(w\frac{\partial v}{\partial Z}\right)\right]-\mathit{Ro}\,\text{e}^{{\it\beta}(T)}\left[\frac{\partial v}{\partial X}\frac{\partial v_{a}}{\partial Z}-\frac{\partial v}{\partial Z}\frac{\partial v_{a}}{\partial X}\right],\end{eqnarray}$$
where
$v_{a}\equiv v-\mathit{Ro}\,\partial _{x}p$
is the ageostrophic velocity. The dynamical fields may be determined from
${\it\phi}$
via
$$\begin{eqnarray}\displaystyle & \displaystyle v(X,Z,T)=\frac{\partial }{\partial Z}{\it\phi}(X,Z,T), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle b(X,Z,T)=b_{0}(X)+\mathit{Fr}^{-2}\,Z-\mathit{Ro}\,\mathit{Fr}^{-2}\text{e}^{{\it\beta}(T)}\frac{\partial }{\partial X}{\it\phi}(X,Z,T), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle {\it\psi}(X,Z,T)=\left(-{\it\delta}(T)-\frac{\partial }{\partial T}\right){\it\phi}(X,Z,T), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}u=\frac{\partial {\it\psi}}{\partial z}\quad \text{and}\quad w=-\frac{\partial {\it\psi}}{\partial x}.\end{eqnarray}$$
A key feature of the solution to (2.10) is that it permits inertia–gravity waves, owing to the double time derivative on the left-hand side. These waves can arise from unbalanced initial conditions (ST13), or, as discussed in ST14, emerge spontaneously from balanced initial conditions. The analytical solutions presented in ST14 involved the neglect of the nonlinear terms
$\mathscr{N}$
in (2.10). ST14 showed that the overall error in the solution due to the neglect of these terms scales with
$\mathit{Ro}^{2}{\it\delta}^{2}$
, implying that the neglect of the nonlinear terms is valid for sufficiently small
$\mathit{Ro}\,{\it\delta}$
. The error in the wave part of the flow was estimated to scale with
$\mathit{Ro}^{2}$
, implying that the analytical prediction of the wavefield (which for
${\it\delta}\ll 1$
is at least an order of magnitude smaller than the mean flow) is only accurate for sufficiently small Rossby number. In the present work, we will use a numerical solution to (2.4) first to validate the accuracy of the analytical model in the above limits, and then to investigate the behaviour of the system in regimes where the analytical model is no longer valid (e.g. order-one
$\mathit{Ro}$
and
${\it\delta}$
).
ST14 showed that for constant strain a ‘quasi-balanced’ solution may be obtained to (2.10) (with
$\mathscr{N}=0$
) that eliminates propagating waves associated with initial conditions. The only time dependence in the solution arises from the strain-driven contraction of the horizontal momentum coordinate,
$$\begin{eqnarray}{\it\phi}(X,Z,T)=\int _{-\infty }^{\infty }{\it\phi}_{I}((X-X_{0})\,\text{e}^{-{\it\delta}T},Z)\,b_{0}^{\prime }(X_{0})\;\text{d}X_{0},\end{eqnarray}$$
where
${\it\phi}_{I}(X,Z)$
is the Green’s function for the problem (see equation (4.12) of ST14). Equation (2.15) may be written more intuitively in the regular momentum coordinate as
$$\begin{eqnarray}{\it\phi}(\mathscr{X},Z,T)=\int _{-\infty }^{\infty }{\it\phi}_{I}(\mathscr{X}-\mathscr{X}_{0},Z)\,\frac{\partial }{\partial \mathscr{X}_{0}}\,b_{0}(\mathscr{X}_{0}\,\text{e}^{{\it\delta}T})\;\text{d}\mathscr{X}_{0}.\end{eqnarray}$$
Since the boundary buoyancy gradient function in (2.16) approaches the delta function at large time, the solution
${\it\phi}$
approaches the Green’s function
${\it\phi}_{I}$
. Hence, the Green’s function may be interpreted as the late-time limit of the solution (see § 5). The Green’s function can be separated into two components: a stationary non-propagating wave part, and a thermally direct secondary circulation (see equation (4.15) of ST14). ST14 demonstrated that the wave part is exponentially small at small strain, approximately
${\it\delta}<0.2$
, but of order one at larger strains. The secondary circulation component – which ST14 called the ‘generalised secondary circulation’ – has differences at
$O({\it\delta}^{2})$
compared with the HB model. An equivalent statement is that the HB model is the first term in a Taylor expansion in
${\it\delta}$
of the generalised model solution (2.16). Thus, (2.16) more accurately represents the secondary circulation about the front, and thus is more ‘balanced’ than the HB model. Given its higher degree of balance, the generalised model solution will be used to generate the initial condition (
$T=0$
) for the constant-strain numerical simulations considered below. The fact that the generalised model solution is more ‘balanced’ than the HB ‘semigeostrophic balance’ solution is demonstrated numerically in § 3.
Note that the analytic solution computed from (2.16) is always smooth and well defined in momentum (
$\mathscr{X}$
) coordinates. In both the HB and ST14 models, frontal collapse and singularities only emerge through the coordinate transformation from momentum to Eulerian coordinates,
$x=\mathscr{X}-\mathit{Ro}\,v$
. Convolutions like (2.16) are computed using a Fourier transform method.
2.1. Numerical set-up
The numerical model to be employed is DIABLO (Taylor Reference Taylor2008), which solves the incompressible, non-hydrostatic Navier–Stokes equations. Here it will be used to solve the non-dimensionalised system of (2.4) in a two-dimensional box. The numerical method is pseudospectral in the horizontal (
$x$
) direction, and periodic boundary conditions are applied in this direction, while finite differences are used in the vertical (
$z$
) direction. The boundary conditions applied in the numerical model on the rigid lids (
$z=-1,0$
) are no vertical flow,
$w=0$
, free-slip horizontal flow,
$$\begin{eqnarray}\frac{\partial u}{\partial z}=\frac{\partial v}{\partial z}=0,\end{eqnarray}$$
and a vertical buoyancy gradient fixed to the value of the background stratification,
$$\begin{eqnarray}\frac{\partial b}{\partial z}=\mathit{Fr}^{-2}.\end{eqnarray}$$
These numerical boundary conditions differ from the analytical ones in that they are inconsistent with conservation of PV on the boundary. The analytical model boundary conditions are determined implicitly from the uniform-PV relations (2.13) – and therefore must satisfy conservation of PV – and the constraint that
$w$
and therefore
${\it\phi}$
vanish on the rigid-lid boundaries. While it is theoretically possible to apply numerical boundary conditions that agree precisely with the analytical ones, these would be time dependent and rather complicated, and hard to relate to physical boundary conditions typically used in more sophisticated numerical models. Instead, we have chosen to use simple free-slip and constant-flux numerical boundary conditions (2.17) and (2.18), which, while minimising the PV boundary layers appearing in the numerical solution, also show that the ST14 analytic results are relatively insensitive to a change in the boundary conditions and therefore more robust.
Here, we will describe model runs without explicit diffusion (
${\it\kappa}_{h}={\it\kappa}_{v}=0$
in (2.2)) as ‘inviscid numerical solutions’, although there will inevitably be some small amount of numerical diffusion. For these inviscid model runs, the numerical solution will break down once the frontal width becomes smaller than the numerical resolution,
$d\sim {\rm\Delta}x$
, where
${\rm\Delta}x$
is the horizontal resolution. The numerical simulations are ended upon reaching this threshold. The horizontal resolution is set to
${\rm\Delta}x=0.005$
, or
$1/200$
th of the initial frontal width, allowing a contraction in the front of over two orders of magnitude before the numerical model breaks down. The vertical resolution is set to
${\rm\Delta}z=0.01$
or smaller. For the diffusive simulations in § 4, we employ a horizontal hyperdiffusion to prevent the collapse of the front to the grid scale. The explicit vertical diffusion is set to zero,
${\it\kappa}_{v}=0$
or
$\mathit{Re}_{v}\rightarrow \infty$
, as the addition of explicit vertical diffusion leads to boundary layers that complicate the comparison of the numerical and analytical solutions.
Given the pseudospectral numerical method, care must be taken to ensure that equations (2.4) are periodic in the horizontal direction. In particular, the material derivative contains a non-periodic operator,
$-{\it\alpha}x\partial _{x}$
, corresponding to the horizontal advection of the perturbation fields by the background strain flow. However, the perturbation fields are guaranteed to vanish sufficiently far from the front, owing to the trapping effect of the strain field studied in ST14. Thus, selecting a numerical domain of width
$L_{N}\gg 2\,\mathit{Bu}/{\it\delta}$
(see ST14), with the front located in the centre, ensures that the solution vanishes at the edge of the domain, and hence
$-{\it\alpha}x\partial _{x}=0$
there.
3. Comparison of numerical and analytical solutions
Here we compare the solution from the generalised analytical model (2.10) with that arising from the fully nonlinear numerical solution to the inviscid governing equations (2.4). As noted above, the numerical model is initialised with the constant-strain generalised model solution (i.e. (2.15) with
$T=0$
), since this is the most ‘balanced’ state available and will minimise any generation of waves associated with adjustment to the initial condition.
As an explicit demonstration of this fact, figure 1 compares the numerical model solution when initialised from the generalised (GM) and semigeostrophic (HB) models for parameter values of
$\mathit{Ro}=0.6$
,
$\mathit{Bu}=1.5$
, and
${\it\delta}=0.2$
. The initial streamfunctions from the GM and HB models are shown in figure 1(a) and (b), respectively. The difference between the initial conditions is
$O({\it\delta}^{2})$
and is shown in figure 1(e). The initial GM streamfunction is narrower than the HB streamfunction, with increased amplitude in the centre but reduced amplitude on the periphery (owing to the confinement effect discussed in ST14, and below). The numerical model is allowed to evolve freely from these initial conditions, and around
$t=14.5$
approaches a discontinuity on the boundaries. The streamfunctions just prior to this critical time are shown in 1(b) and (d), and the difference in ( f). The large-scale secondary circulation is similar for both model runs, but the HB-initialised run displays an order
${\it\delta}^{2}\sim 0.04$
transient wave signal that is not present in the GM-initialised run. These are the ‘spurious’ waves reported in previous numerical frontogenesis studies (e.g. Snyder et al.
Reference Snyder, Skamarock and Rotunno1993, see their figure 3). The presence of these waves implies that the HB initial condition is less balanced than the GM initial condition, owing to the neglect of effects at
$O({\it\delta}^{2})$
in the semigeostrophic model that are included in the generalised model (see ST14). In other words, the constant-strain generalised model solution (2.15) represents a higher-order balance than semigeostrophy. As seen in the Hovmöller plot in figure 1(g), the
$O({\it\delta}^{2})$
imbalance in the HB initial condition gives rise to an adjustment process, and wave emission and trapping by the same mechanism as studied in ST13 (e.g. compare figure 1(g) here to figure 15(a) of ST13). Given the above analysis, the numerical simulations presented below will be initialised from the generalised model to minimise wave generation associated with the initial condition.
Figure 1. (a,c) A comparison of the streamfunctions from the numerical model when initialised in the state predicted by the generalised model (GM) and semigeostrophic balance (HB), for parameter values
$\mathit{Ro}=0.6$
,
$\mathit{Bu}=1.5$
,
${\it\delta}=0.2$
and
$A=100$
: (a)
$\text{GM}_{I}$
and (c)
$\text{HB}_{I}$
. Buoyancy contours are overlaid in grey. (e) The difference between the initial states,
$\text{HB}_{I}-\text{GM}_{I}$
. (b,d) The streamfunctions just prior to the critical time (
$t=14.5$
) for the GM- and HB-initialised runs: (b)
$\text{GM}_{F}$
and (d)
$\text{HB}_{F}$
. ( f) The difference between the final states,
$\text{HB}_{F}-\text{GM}_{F}$
. (g) The time evolution of the difference at mid-depth (
$z=-0.5$
),
$\text{HB}-\text{GM}$
. Positive (anticlockwise) values are represented by black contours, and negative by grey. The contour interval in (e–g) is 10 % of that in (a–d).
In figure 2, the analytical and numerical solutions are compared for five sets of parameter values with a Burger number
$\mathit{Bu}=1.5$
, a range of Rossby numbers
$\mathit{Ro}$
, and either weak strain (characterised by
${\it\delta}=0.2$
) or strong strain (characterised by
${\it\delta}=0.9$
). Figure 2 displays time series of (a) frontal width
$d$
and (b) maximum vertical velocity for each of the five cases as derived from the generalised (long-dashed line), HB (short-dashed line) and numerical (solid line) models. Each case is colour-coded according to the legend in figure 2(a). The smaller-Rossby-number cases (
$\mathit{Ro}=0.6$
; green and black) have relatively weak broad fronts at time zero (i.e.
$d\simeq 1$
) and only form a discontinuity for time
$t\gg {\it\delta}^{-1}$
. By contrast, larger Rossby numbers correspond to a sharper initial front (smaller
$d$
) and thus more rapid formation of a discontinuity on times
$t\sim {\it\delta}^{-1}$
. As expected, the frontal width and maximum vertical velocity derived from the generalised, HB and numerical models are essentially indistinguishable for the small strain cases (black, magenta). The generalised and numerical models also agree for small Rossby number, but strong strain (green). The vertical velocity in this case increases exponentially during the course of frontogenesis, unlike the weak strain cases, and is an order of magnitude larger than the HB prediction. Such behaviour indicates that strong strain is a different dynamical regime to weak strain and that these dynamics are well captured by the generalised model. By contrast, for a given Rossby number (e.g.
$\mathit{Ro}=0.6$
, green/black, or
$\mathit{Ro}=1.5$
, magenta/red), the time evolution of the frontal width,
$d({\it\delta}t)$
, predicted by the HB model is the same for all strains, and the HB maximum vertical velocity differs only via scaling by a constant.
Figure 2. Time series of the (a) frontal width
$d=\min J^{-1}$
and (b) maximum vertical velocity
$w$
, from the generalised model (long-dashed), HB model (short-dashed) and numerical model (solid). The colours correspond to different values of Rossby number
$\mathit{Ro}$
and uniform strain
${\it\delta}$
as indicated in panel (a). The Burger number is
$\mathit{Bu}=1.5$
in each case. The time axis is in units of
${\it\delta}t$
; that is, time is normalised by the strain rate rather than the inertial frequency. The evolution of the frontal width,
$d({\it\delta}t)$
, from the HB model is independent of strain, meaning that the red/magenta lines and green/black lines in panel (a) are overlaid.
The numerical results in figure 2 depart from the generalised model prediction at late times, for cases with both order-one Rossby numbers and order-one strains (red, blue), indicating that neglected nonlinear effects are becoming important. The most notable difference in the numerical model is the super-exponential increase in the peak vertical velocity as the front collapses (the GM prediction only increases exponentially, not super-exponentially). The critical time – that is, the time taken for frontal collapse – is also increased relative to the analytical prediction, particularly for
$\mathit{Ro}=1.5$
(red).
In the next sections (§§ 3.1 and 3.2) we will examine each of the cases shown in figure 2 in more detail, beginning with the two weak-strain (
${\it\delta}=0.2$
) examples. The five cases are also summarised in table 2 for reference, along with the estimated and observed errors in the HB and generalised model predictions.
Table 2. Parameter values for cases (i)–(v) shown in figure 2 and discussed in § 3. The strain is constant in time, and
$\mathit{Bu}=1.5$
for each case. The structure of the generalised, HB and numerical model solutions for each case are shown in the figure listed in the ‘Fig.’ column. The table lists the fractional error expected from scaling arguments for the HB model,
$(\mathit{Ro}^{2}+1){\it\delta}^{2}$
, and the GM model,
$\mathit{Ro}^{2}{\it\delta}^{2}$
, in addition to the root-mean-square (RMS) error (in the vertical velocity field) computed from comparison of the analytic solutions at their critical times with the numerical solutions at their critical times, as shown in each of the figures.
3.1. Weak strain
Traditionally, the HB model has been employed for weakly strained fronts,
${\it\delta}^{2}\ll 1$
, and has been found to be accurate at first order (e.g. Snyder et al.
Reference Snyder, Skamarock and Rotunno1993). However, the HB model does not include a description of inertia–gravity waves. In contrast, ST14 argued that, where the Rossby number is small, the generalised model will be able to accurately describe the wavefield associated with frontogenesis. ST14 also proposed that, even at order-one Rossby numbers, while not able to accurately describe the wavefield, the generalised model is more accurate than the HB model, owing to the inclusion of additional
$O({\it\delta}^{2})$
terms from the governing equations. Here we test these predictions.
Case (i)
Consider a front with parameter values of
$\mathit{Ro}=0.6$
,
${\it\delta}=0.2$
and
$\mathit{Bu}=1.5$
– the same parameter values as used in figures 4 and 5 of ST14. Figure 3 shows the vertical velocity fields just prior to the critical time arising from the (a) generalised analytical (GM) and (b) numerical models. The fields arising from the two models are remarkably similar. Both are dominated by a large-scale thermally direct circulation, similar to that predicted by the HB model (shown in figure 3
c). However, the generalised and numerical models also include wave structures – most notably the bands of intensified vertical flow on the periphery of the front. These wavepackets form during the course of frontogenesis as the strain shrinks horizontal scales – or increases horizontal wavenumbers
$k=k_{0}\text{e}^{{\it\delta}t}$
– meaning that all wavenumbers with a given vertical mode number
$n$
approach a constant phase speed,
$c=\mathit{Bu}/(n{\rm\pi})$
, which equals the maximum group speed
$(c_{g})$
of hydrostatic inertia–gravity waves of vertical mode
$n$
. Waves of all horizontal scales therefore accumulate at the same location where the maximum outward group speed equals the incoming strain flow speed, or
$c_{g}={\it\delta}x$
. We call these locations the ‘stagnation points’. The wave signals in figure 3(a,b) appear at the first vertical mode stagnation points,
$x=\pm \mathit{Bu}/({\rm\pi}{\it\delta})=\pm 2.4$
.
Figure 3. Case (i). The vertical velocity field from the (a) generalised (GM), (b) numerical (NUM) and (c) semigeostrophic (HB) models, just prior to the time of discontinuity formation in each model, for parameter values of
$\mathit{Ro}=0.6$
,
$\mathit{Bu}=1.5$
and constant strain
${\it\delta}=0.2$
. Contours of buoyancy from each model are overlaid in grey.
Figure 4. Case (ii). The vertical velocity field from the (a) generalised (GM), (b) numerical (NUM) and (c) semigeostrophic (HB) models, just prior to the time of discontinuity formation in each model, for parameter values of
$\mathit{Ro}=1.5$
,
$\mathit{Bu}=1.5$
and constant strain
${\it\delta}=0.2$
. Contours of buoyancy from each model are overlaid in grey.
Case (ii)
Now consider a case with large Rossby number,
$\mathit{Ro}=1.5$
, but the same Burger number and strain as employed above (i.e.
$\mathit{Bu}=1.5$
,
${\it\delta}=0.2$
). This choice of Rossby and Burger numbers is similar to those employed by Snyder et al. (Reference Snyder, Skamarock and Rotunno1993) to compare the HB model with numerical solutions. Figure 4 shows the vertical velocity fields just prior to the critical time arising from the (a) generalised, (b) numerical and (c) HB models. The large-scale thermally direct secondary circulation is similar in all three models, although the GM and numerical circulations are narrower compared with the HB prediction (similar to figure 1
a,c,e). The narrower GM/numerical circulation is due to the convergent strain flow confining the spread of energy associated with an element of boundary gradient to the region where the maximum group speed of inertia–gravity waves exceeds the strain flow speed. By contrast, the HB model permits the spread of energy far from the front, giving rise to a broader circulation. While the confinement of the circulation by the convergent strain is an
$O({\it\delta}^{2})$
effect and is relatively weak in this example, the correction associated with the GM solution is important in preventing the generation of spurious waves in the numerical solution, as demonstrated in figure 1. In § 3.2 we will see that confinement becomes of leading-order importance for strong strain.
The numerical solution in figure 4(b) displays some notable differences from both the HB and GM predictions. For example, there is a distinct double jet over the surface fronts
$x\sim \pm 1$
(also noted by Snyder et al.
Reference Snyder, Skamarock and Rotunno1993), not present in either analytical solution, which appears to be associated with a vertical mode-2 wave. This mode-2 wave becomes particularly prominent if the numerical model is iterated past the critical time through the introduction of explicit diffusion (see § 4). Figure 4(b) also displays some additional vertical mode-1 wave structures, for example, near
$x\sim \pm 1.75$
. These waves are generated in part due to the adjustment of a slight imbalance in the initial conditions, since the nonlinear terms
$\mathscr{N}$
in (2.10), which are neglected in the generalised model, are not exactly zero at time zero and increase with Rossby number. The behaviour and propagation of such ‘imbalance waves’ in a strain field was examined in ST13.
3.2. Strong strain
Here we consider order-one values of strain (
${\it\delta}\sim 1$
), where the wavefield becomes of similar order to the secondary circulation. For strong strains, the HB model, which omits waves and assumes that the cross-front acceleration is small, is not valid even at first order. By contrast, for sufficiently small Rossby number,
$\mathit{Ro}^{2}\ll {\it\delta}^{-2}$
, the generalised model of ST14 is valid. We first examine this small-Rossby-number limit, before considering order-one Rossby numbers, for which the generalised model is expected to break down.
Case (iii)
Consider a front with Rossby number
$\mathit{Ro}=0.6$
, strain
${\it\delta}=0.9$
and Burger number
$\mathit{Bu}=1.5$
– the same parameter values as employed in figure 6 of ST14, which displayed the analytical prediction for the time evolution of the streamfunction. In figure 5 we show the vertical velocity field just prior to the critical time (
$t=2.7$
) from the (a) generalised and (b) numerical models. The vertical velocity is dominated by two wavepackets located at the first vertical mode stagnation points,
$x=\pm \mathit{Bu}/({\rm\pi}{\it\delta})=\pm 0.53$
. These stagnant waves form by the same mechanism discussed in the weak strain example (i.e. case (i); figure 3), although in that case the waves are a small second-order correction to the flow. The strain shrinks the horizontal scale of the wavepackets indefinitely, giving rise to the exponential increase in the maximum vertical velocity seen in figure 2(b).
Figure 5. Case (iii). The vertical velocity field from the (a) generalised (GM), (b) numerical (NUM) and (c) semigeostrophic (HB) models, just prior to the time of discontinuity formation in each model, for parameter values of
$\mathit{Ro}=0.6$
,
$\mathit{Bu}=1.5$
and constant strain
${\it\delta}=0.9$
. Contours of buoyancy from each model are overlaid in grey.
The structure of the solution in this strong-strain case is qualitatively different from the previous weak-strain cases (figures 3 and 4), where the vertical velocity was dominated by a thermally direct large-scale overturning, and waves appeared as second-order features. To emphasise this distinction, in figure 5(c) we display the vertical velocity from the HB model for the parameter values under consideration, just prior to the critical time predicted by that model,
$t=3.3$
. Even at this later time, the HB vertical velocity is an order of magnitude weaker than the numerical/generalised models, and displays the broad, thermally direct overturning characteristic of the small-strain limit.
Case (iv)
Now consider a front with larger Rossby number,
$\mathit{Ro}=1$
, but the same Burger number and strain as considered previously (
${\it\delta}=0.9$
,
$\mathit{Bu}=1.5$
). Since the product
$\mathit{Ro}\,{\it\delta}$
is now of order one, the scaling arguments of ST14 suggest that the generalised model will not be valid, even at first order. Figure 6 displays the vertical velocity from the (a) generalised and (b) numerical models, just prior to the critical time. Both models predict a thermally direct circulation, strongly confined about the surface front. For comparison, the relatively weak broad circulation predicted by the HB model is shown in figure 6(c). The numerical model exhibits intensified vertical jets directly over the surface fronts that are not present in the generalised analytical model. These jets emerge at late time, close to frontal collapse, and are associated with the super-exponential growth in the maximum vertical velocities shown in figure 2(b). It is difficult to distinguish between the secondary circulation and waves in this case. The absence of distinct waves is a result of the larger Rossby number driving more rapid frontal collapse. The front is not strained for a sufficiently long period before frontal collapse to permit the accumulation of energy and the formation of the stagnant wavepackets seen previously in figure 5.
Figure 6. Case (iv). The vertical velocity field from the (a) generalised (GM), (b) numerical (NUM) and (c) semigeostrophic (HB) models, just prior to the time of discontinuity formation in each model, for parameter values of
$\mathit{Ro}=1.0$
,
$\mathit{Bu}=1.5$
and constant strain
${\it\delta}=0.9$
. Contours of buoyancy from each model are overlaid in grey.
Case (v)
As noted above, the generalised model breaks down at late times for order-one strain and Rossby number, as strong vertical jets form over the surface fronts. Here we examine this behaviour at an even larger Rossby number, using parameter values of
$\mathit{Ro}=1.5$
,
${\it\delta}=0.9$
and
$\mathit{Bu}=1.5$
. Figure 7 displays three snapshots of the streamfunction from the numerical model at (a) time zero, (b) 50 % of the critical time and (c) just prior to the critical time. The net cross-front velocity vectors,
$(u-{\it\delta}x/\mathit{Ro},w)$
, are displayed as black arrows. The locations of the surface fronts, defined as the maximum of
$\partial _{x}b$
on the boundary, are denoted by red circles. Three momentum coordinate contours,
$\mathscr{X}=x+\mathit{Ro}\,v=0$
,
$\pm \mathit{Bu}/({\rm\pi}{\it\delta})$
, are also displayed on each plot. The outer contours are the so-called ‘stagnation lines’ (predicted from the ST14 analytical model) along which the maximum outward wave group speed in momentum coordinates equals the strain-forced contraction of the coordinate, or
$$\begin{eqnarray}\frac{\text{D}\mathscr{X}}{\text{D}t}=-{\it\delta}\mathscr{X}=\pm \max c_{g}=\pm \frac{\mathit{Bu}}{{\rm\pi}}.\end{eqnarray}$$
The use of momentum coordinates accounts for the effect of the perturbation horizontal flow
$(u,v)$
on the propagation of the wave. As can be seen from figure 7(c), the circulation is largely confined within the outward limits of these contours (
$x\sim \pm 1$
) by the critical time. Thus, despite the ST14 generalised model breaking down, the confinement effect predicted by that model still operates for order-one strain and Rossby numbers. For these larger Rossby numbers, the greater buoyancy difference across the front drives a larger along-front velocity
$v$
, and thus significant slumping of the
$\mathscr{X}=x+\mathit{Ro}\,v$
contours, such that a balance is established between buoyancy-driven flow and rotation. Consequently, the circulation is broader for larger Rossby numbers (but the same Burger number and strain), as may be confirmed by comparison of figures 5–7.
Figure 7. Case (v). The streamfunction, buoyancy field and net velocity vectors from the numerical model at times (a) 0, (b) 0.5 and (c) 1.0 (critical time), for parameter values of
$\mathit{Ro}=1.5$
,
$\mathit{Bu}=1.5$
and constant strain
${\it\delta}=0.9$
. The net cross-front velocity vectors,
$(u-{\it\delta}x/\mathit{Ro},w)$
, are displayed as black arrows.
Figure 7(a) shows the numerical model streamfunction at time zero, initialised from the generalised analytical model. The overturning circulation is relatively broad and smooth. As time progresses (
$t=0.5$
; figure 7
b), the surface front (red circle) slumps outwards, buoyancy gradients increase, and the circulation becomes narrower and more intense as it is squeezed inwards by the strain flow. However, the interior flow and buoyancy contours remain relatively smooth. The time series in figure 2 (red curve) indicates good agreement with the generalised model up to this time. Between
$t=0.5$
and
$t=1$
(the critical time; figure 7
c), sharp ‘kinks’ develop in the interior buoyancy field, directly over the surface fronts, associated with intense vertical jets. The vertical velocity and interior buoyancy gradient grow super-exponentially over this period.
The super-exponential growth in the vertical velocity and interior buoyancy gradient results from a combination of two effects discussed above: the slumping of the front for large Rossby number, and the strong confinement of the circulation for large strain. These two effects lead to the surface front (red circle), associated with large surface and near-surface gradients, becoming coincident with the stagnation lines, associated with large vertical velocities, at late time, as shown in figure 7(b,c). Consequently, there is strong vertical advection of the near-surface buoyancy gradient into the interior of the flow (associated with the nonlinear terms that are neglected in the analytical model,
$\mathscr{N}$
in (2.10)), thereby steepening isopycnal slopes directly above/below the surface fronts. The horizontal strain flow converging across the steepened isopycnals then drives an increased vertical flow at these locations. This result is readily derived from buoyancy conservation,
$$\begin{eqnarray}\frac{\text{D}b}{\text{D}t}=0\quad \Longrightarrow \quad w=\frac{\displaystyle -\frac{\partial b}{\partial t}-\mathit{Ro}\left(u-\frac{{\it\delta}}{\mathit{Ro}}x\right)\frac{\partial b}{\partial x}}{\displaystyle \frac{\partial b}{\partial z}}\simeq \mathit{Fr}^{2}{\it\delta}x\,\frac{\partial b}{\partial x},\end{eqnarray}$$
where we have, at first approximation, neglected perturbations from the background. Thus, for the upper boundary front at
$x\sim -1$
, the advection of a positive buoyancy gradient into the interior of the flow will drive an increased downward velocity (and vice versa for lower boundary front). The larger vertical velocity will then lead to even greater advection of the near-surface frontal gradient into the flow interior, giving rise to sharper interior buoyancy gradients, and thus even larger vertical velocities as per (3.2). This positive feedback mechanism drives the formation of the sharp ‘kinks’ in the buoyancy fields in figure 7(c) and the associated vertical jets. The result is the super-exponential growth (exponential on a log scale) in the vertical velocity seen in figure 2(b). The feedback effect also delays frontogenesis by advecting buoyancy gradient away from the boundary, thereby increasing the interior buoyancy gradient, but reducing the boundary gradient. This behaviour is shown in figure 2(a) (red curve), where the frontal width in the numerical model is increased relative the generalised model prediction at late time,
${\it\delta}t>0.45$
.
3.3. Time-varying strain
Ocean fronts typically exist within strain fields with significant temporal and spatial variation. The ST14 analytical model only directly incorporates temporal variations in strain,
${\it\delta}(t)$
. However, we can approximate spatial variations by considering how the strain experienced by a patch of fluid will vary as it is advected in a strain field. For example, a patch of fluid in the ocean mixed layer initially in a region of convergence between two eddies will ultimately be advected out of that region, implying an effective decrease of the strain with time. As discussed in ST14, this decrease in strain allows waves generated spontaneously by the front and trapped by the strain flow to be released and propagate freely. ST14 also showed that time variation in the strain field drives additional wave generation by continually forcing imbalances in the flow. Below we will examine how these analytical predictions compare with the results of the numerical model for a case with strong strain and moderate Rossby number. The comparison provides insight into the dynamics that are captured by the GM solution, and those features that are missed.
Consider a front subject to large strain (
${\it\delta}=0.9$
) with initial Rossby number
$\mathit{Ro}=0.6$
and Burger number
$\mathit{Bu}=1.5$
, as in figure 5. These parameters are representative of, for example, frontogenesis between submesoscale eddies in the ocean mixed layer. In the previous example (figure 5), the constant strain drove the spontaneous generation of stagnant wavepackets, and ultimately the collapse of the surface front to a discontinuity on the boundary. Here, we will consider an initially constant strain, leading to the generation of frontogenesis waves as in figure 5. We will then decrease the strain smoothly to zero prior to the formation of a discontinuity, permitting the release and propagation of these waves; that is,
$$\begin{eqnarray}{\it\delta}(T)=\left\{\begin{array}{@{}ll@{}}{\it\delta}_{0}\quad & T<{\it\tau}_{1},\\ \displaystyle {\it\delta}_{0}\cos ^{2}\left(\frac{T-{\it\tau}_{1}}{{\it\tau}_{2}-{\it\tau}_{1}}\,\frac{{\rm\pi}}{2}\right)\quad & {\it\tau}_{1}\leqslant T\leqslant {\it\tau}_{2},\\ 0\quad & T>{\it\tau}_{2},\end{array}\right.\end{eqnarray}$$
with
${\it\delta}_{0}=0.9$
,
${\it\tau}_{1}=1.5$
and
${\it\tau}_{2}=3$
. Figure 8 displays Hovmöller plots of the vertical velocity just below the surface (
$z=-0.25$
) from the (a) generalised and (b) numerical models. The analytical and numerical solutions are very similar; we will first describe the common features before examining the differences. Contours of surface (
$z=0$
) buoyancy are overlaid in black on each plot, showing the collapse of the initially broad surface front into a relatively sharp front by time
${\it\tau}_{2}=3$
. Associated with the surface front collapse, the vertical velocity (and buoyancy gradient) just below the surface is concentrated into two distinct bands on the periphery of the front (
$x\sim \pm 0.5$
); these are the same frontogenesis wavepackets from the constant-strain case (figure 5). As the strain is decreased to zero, these waves are released and propagate outwards as free inertia–gravity waves. The waves propagate parallel to the characteristics (see equation (5.3) of ST14) for the first vertical mode predicted from the analytical model (overlaid in grey; characteristics for modes 2 and 3 also shown). The maximum vertical velocity (the time series of which is overlaid in black) is located at the leading edge of these outward-propagating waves. The velocity gradually decreases with time as the horizontal scales in the mode-1 wavepackets disperse. The propagation of the wavepacket in figure 8(a) is indicated by the arrow labelled ‘FG1’. A relatively weak third vertical mode frontogenesis wavepacket is also visible propagating outwards in each model, following the mode-3 characteristic (labelled ‘FG3’). This wave was visible in the constant-strain velocity fields (figure 5) at the critical time.
Figure 8. Hovmöller plot of the vertical velocity just below the surface, at
$z=-0.25$
, from the (a) generalised (GM) and (b) numerical (NUM) models for the time-dependent strain defined by (3.3), and parameter values of
$\mathit{Ro}=0.6$
,
$\mathit{Bu}=1.5$
,
${\it\delta}_{0}=0.9$
and
$A=100$
. Contours of surface (
$z=0$
) buoyancy are overlaid in black, showing the collapse of the front with time. The strain field
${\it\delta}(T)$
is overlaid at
$x=-4$
, and time series of the maximum of the velocities
$u$
,
$v$
and
$w$
near
$x=4$
. The characteristics predicted from the analytical model (see equation (5.3) of ST14) for vertical modes
$n=1$
to 3 are overlaid in grey.
Apart from the frontogenesis wavepackets, generated spontaneously during the collapse of the front, there are many other waves visible in figure 8 that are generated due to the time variation in the strain (3.3); we call these ‘transience waves’. Specifically, as shown in ST14, these waves arise due to a change in the strain magnitude altering the secondary circulation that can be supported at the front, thus causing a ‘momentum imbalance’ and driving a continuous adjustment process in response. This adjustment process is analogous to the mass imbalance problem discussed in ST13, and leads to a decaying oscillation in the frontal zone and the continual emission of inertia–gravity waves as the front adjusts back towards geostrophic balance. Slowly decaying near-inertial oscillations are clearly visible in figure 8, both in the surface buoyancy contours and in the time series of maximum horizontal velocities overlaid on figure 8. With each period of surface front oscillation, figure 8 shows the production of a near-inertial wavepacket, which slowly propagates away from the front. The propagation of these wavepackets is indicated by the arrow labelled ‘T1’.
Let us now consider the differences between the numerical and analytical solutions. First, as in the constant-strain example (figure 5), the numerical mode-1 frontogenesis wavepackets are intensified compared with the analytical ones, corresponding to a greater vertical velocity. There are also mode-2 wave signals in the numerical model generated both during frontogenesis (arrow labelled ‘FG2’ in figure 8 b) and associated with the frontal oscillations once the strain field is turned off (arrow labelled ‘T2’) – by contrast, the generalised model solution has no even modes. The mode-2 wavepacket generated during frontogenesis can be seen in the vertical velocity field from the constant-strain case (figure 5), in between the primary mode-1 wavepacket and the mode-3 wavepacket. This wavepacket propagates outwards along the mode-2 characteristic in figure 8(b), once the strain is turned off. Interestingly, subsequent oscillations of the surface front, as shown in figure 8(b), generate additional high-horizontal-wavenumber mode-2 wavepackets, propagating parallel to the mode-2 characteristic. These generation events are indicated by four black arrows in figure 8(b). The horizontal scale of these waves is much smaller than the other transience waves seen in the solution. Indeed, the waves appear to be generated from a ‘pinching’ of the surface frontal gradient (indicated by the black ellipse in figure 8 b) that occurs during each oscillation in the numerical model – but is not seen in the analytical model. The generation of additional transience waves in the numerical solution leads to more rapid loss of energy from the oscillating front, and hence a more rapid decay in the oscillation amplitude. Despite these differences, the error in the analytical solution remains less than approximately 20 % over the time period shown.
4. Equilibrated fronts
As seen in earlier sections, larger Rossby numbers lead to greater slumping of the surface front and more rapid frontal collapse. One consequence of such rapid frontogenesis is that wave energy has insufficient time to accumulate at the wave stagnation points prior to frontal collapse, and thus distinct wave features are not readily observed in the flow fields at the critical time for large Rossby numbers (e.g.
$\mathit{Ro}=1.5$
, figure 4) – in contrast to smaller Rossby numbers (e.g.
$\mathit{Ro}=0.6$
, figure 3). Since many fronts in the ocean mixed layer may be characterised by
$\mathit{Ro}=O(1)$
, an important question is whether waves will develop after the formation of a sharp front, and whether the generalised analytical model can be of use in predicting the structure of these waves.
We can address this question by adding explicit horizontal diffusion to the numerical model to arrest frontogenesis before the front collapses to the grid scale. For this purpose, we use horizontal hyperdiffusion (
$n=4$
in (2.4)) to localise the smoothing to regions of large horizontal gradient (i.e. the front), without substantially affecting the larger-scale flow. In this context, the hyperdiffusion is intended as a crude representation of the small-scale processes that are not captured by the numerical model but may arrest frontogenesis. The addition of hyperdiffusion will be unable to realistically represent the often fully three-dimensional process of frontal equilibration. However, it is sufficient for the present investigation, since our focus is on the wavefield and not on the surface front itself, and, in particular, determining whether the wavefield is substantially modified by the local dynamics at the surface front.
With horizontal diffusion and a steady, uniform strain, the numerical model eventually achieves a steady state where strain-driven advection (and sharpening of the front) is balanced by diffusion. Figure 9(a) displays the steady-state vertical velocity field for a front with parameter values of
$\mathit{Ro}=1.5$
,
$\mathit{Bu}=1.5$
,
${\it\delta}=0.2$
,
$A=100$
and
$|\mathit{Re}_{h}|=10^{7}$
. These are the same parameter values as for the inviscid solution shown in figure 4(b); we note that waves are not clearly identifiable in that case. The steady state has a large-scale thermally direct circulation as would be expected from both the generalised and HB models. It also possesses intense wavepackets at the first vertical-mode stagnation points (
$x=\pm \mathit{Bu}/({\rm\pi}{\it\delta})=\pm 2.4$
), similar to those observed for smaller Rossby numbers in the inviscid simulations (e.g.
$\mathit{Ro}=0.6$
, figure 3). However, the largest-amplitude features are the pair of mode-2 wavepackets at the second vertical-mode stagnation points (
$x=\pm 1.2$
). These wavepackets were also visible in the inviscid solution prior to frontal collapse (near
$x\sim \pm 1$
in figure 4
b).
Figure 9. Numerical solution for parameter values of
$\mathit{Ro}=1.5$
,
$\mathit{Bu}=1.5$
,
${\it\delta}=0.2$
and
$A=100$
, as in figure 4, but with horizontal hyperdiffusion of
$|\mathit{Re}_{h}|=10^{7}$
. (a) The steady-state vertical velocity field with buoyancy contours overlaid (thin grey lines). The presence of diffusion modifies the PV from the background value of
$q=\mathit{Fr}^{-2}$
; the PV contours for 90 % and 110 % of the background value are displayed (thick grey lines). PV is reduced along the boundary between the fronts and increased in the interior along the frontal axis. (b) Hovmöller plot of the vertical velocity at mid-depth. (c) The diffusive analytical prediction from (4.3) for the vertical velocity at mid-depth. (d) The difference between panels (b) and (c).
Figure 9(b) displays the time evolution of the vertical velocity at mid-depth towards the steady state. The mode-1 wavepackets near
$\pm 2.4$
noted above develop in the solution around
$t=15$
. There are also propagating waves that appear to be generated around the analytical critical time (
$t\sim 5.3$
), near the location of the surface fronts (
$x\sim \pm 1$
). This time and location of generation suggest that the waves are associated with the action of diffusion in counteracting frontal collapse and developing a steady state. The generation of these propagating waves may also be associated with the formation of PV anomalies in the numerical solution, since the numerical boundary conditions (2.17) and (2.18) and hyperdiffusion are inconsistent with PV conservation. As shown by the thick grey PV contours in figure 9(a), the PV anomalies in the numerical solution are largest near the surface fronts, where the propagating waves appear to originate.
In order to better understand the dynamics of the waves in figure 9(b), it is useful to consider how the ST14 solution would be modified in the presence of diffusion. As described in § 2, the constant-strain GM solution is determined from the convolution of a Green’s function with the boundary buoyancy gradient in momentum coordinates as per (2.16). The presence of diffusion will modify the buoyancy on the rigid boundary as per (2.4d
) with
$w=0$
,
$$\begin{eqnarray}\frac{\partial b}{\partial T}-{\it\delta}\mathscr{X}\frac{\partial b}{\partial \mathscr{X}}=\frac{\mathit{Ro}(-1)^{n/2+1}}{|\mathit{Re}_{h}|}\frac{\partial ^{n}b}{\partial x^{n}},\end{eqnarray}$$
where the left hand-side is written in regular momentum coordinates
$(\mathscr{X},Z,T)$
and the right-hand side in Eulerian coordinates
$(x,z,t)$
. The inviscid (
$|\mathit{Re}_{h}|\rightarrow \infty$
) solution to (4.1) is simply
$b=b_{0}(\mathscr{X}\text{e}^{{\it\delta}T})$
for an arbitrary function
$b_{0}$
, giving rise to the boundary gradient in the GM solution (2.16). We can derive an approximate solution for a finite
$\mathit{Re}_{h}$
by replacing the buoyancy gradient in (2.16) by an approximation to the solution of (4.1) for finite
$\mathit{Re}_{h}$
. To solve (4.1) we assume that the Eulerian derivative on the right-hand side of (4.1) is equivalent to the momentum coordinate derivative,
$\partial _{x}\sim \partial _{\mathscr{X}}$
, which is true except near the location of the surface front. With this approximation, the solution to (4.1) for the buoyancy gradient
$\partial _{\mathscr{X}}b$
, written in terms of its Fourier transform (denoted by a hat), is
$$\begin{eqnarray}\widehat{\partial _{\mathscr{X}}b}=\widehat{\partial _{\mathscr{X}}b_{0}}(k\,\text{e}^{-{\it\delta}T})\,\exp \left(-k^{n}\frac{\mathit{Ro}}{n{\it\delta}|\mathit{Re}_{h}|}(1-\text{e}^{-n{\it\delta}T})\right),\end{eqnarray}$$
where
$k$
is the horizontal wavenumber. The solution (4.2) satisfies the initial condition
$b=b_{0}$
, and boundary conditions
$\partial _{\mathscr{X}}b(\mathscr{X}\rightarrow \pm \infty )=0$
. Taking the Fourier transform of the generalised model solution (2.16), and replacing the inviscid boundary buoyancy gradient with our diffusive approximation (4.2), we have an estimate for the diffusive solution of
$$\begin{eqnarray}\widehat{{\it\phi}}(k,Z,T)=\widehat{{\it\phi}_{I}}(k,Z)\,\widehat{\partial _{\mathscr{X}}b_{0}}(k\,\text{e}^{-{\it\delta}T})\,\exp \left(-k^{n}\frac{\mathit{Ro}}{n{\it\delta}|\mathit{Re}_{h}|}(1-\text{e}^{-n{\it\delta}T})\right).\end{eqnarray}$$
Equation (4.3) is well defined in momentum coordinates at all times, and collapses to a steady state at late time. The steady state is defined by
$$\begin{eqnarray}\widehat{{\it\phi}_{SS}}(k,Z)=\widehat{{\it\phi}_{I}}(k,Z)\,\exp \left(-k^{n}\frac{\mathit{Ro}}{n{\it\delta}|\mathit{Re}_{h}|}\right),\end{eqnarray}$$
assuming an appropriately normalised
$b_{0}$
. The corresponding (approximate) velocity and buoyancy fields at a given time can be generated from
${\it\phi}$
through the relations (2.13), assuming that the interior flow is essentially inviscid and uniform PV. The solution given by (4.3) will still become multivalued in Eulerian coordinates (
$x=\mathscr{X}-\mathit{Ro}\,v$
) near the locations of the surface fronts, but will be well defined for all time at mid-depth (
$z=-0.5$
) where
$v=0$
and hence
$x=\mathscr{X}$
.
The time evolution of the vertical velocity at mid-depth predicted from (4.3) is shown in figure 9(c). The prediction is remarkably similar to the numerical result shown above (figure 9
c). The prediction captures the overall confinement of the circulation within the first vertical mode stagnation points,
$|x|<2.4$
. It also predicts the formation of stagnant wavepackets near
$x=\pm 2.4$
with the same amplitude and structure as those seen in the numerical solution. The origin of these wavepackets is the same accumulation mechanism as discussed in the inviscid case that gave rise to the wavepackets seen in the inviscid generalised model and numerical solutions at smaller Rossby numbers (e.g. figure 3). As noted above, larger Rossby numbers – as in the present example – lead to more rapid frontal collapse, and hence these wavepackets are not visible in the inviscid solution (e.g. figure 4) since there is insufficient time for energy to accumulate. Here, with frontal collapse arrested by the introduction of diffusion, energy continues to accumulate beyond the inviscid critical time and the wavepackets ultimately develop as seen in figure 9. However, the structure of these wavepackets is modified by the presence of the diffusion. In the inviscid case, the scale of the wavepackets shrinks continually with time, and the amplitude increases. With the addition of diffusion, the wavepacket shrinks to the diffusive length scale, at which point a steady state is reached. The structure of the steady-state wavepacket is controlled by the balance between the strain-driven sharpening and the diffusive smoothing, as described by the steady-state solution (4.4). Since the Green’s function
${\it\phi}_{I}$
is a delta function at the location of the wavepackets (see ST14), we have
$\widehat{{\it\phi}_{I}}\rightarrow 1$
, and thus the steady wavepacket structure is defined by the second factor in (4.4) and depends on the type of diffusion (i.e.
$n=2,4,\dots$
). For Laplacian diffusion (
$n=2$
), the structure is a simple Gaussian profile. For the hyperdiffusion used in the present example (
$n=4$
), the structure has a dominant central maximum, and decaying oscillations to either side – exactly as seen in figure 9.
The difference between the numerical vertical velocity at mid-depth and the diffusive approximation (4.3) is shown in figure 9(d). The apparently diffusively generated waves are clearly visible propagating outwards from the locations of the surface fronts (
$x\sim \pm 1$
). There is a weak near-inertial oscillation in the region
$|x|<1$
at early times, possibly associated with the initial conditions being slightly out of balance. The stagnant wavepackets discussed above also contribute to the difference field in figure 9(d), owing to the fact that they are slightly shifted between the numerical solution (centred on the dashed grey line at
$x=\pm 2.37$
) and the analytical prediction (centred at
$x=\pm 2.4$
, outside of the dashed grey line). The shift is due to the analytical prediction (4.3) not including the reduction in group speed of the wavepacket associated with the fact that it has a diffusion-limited maximum wavenumber (minimum scale), and hence a maximum group speed less than the inviscid maximum of
$\mathit{Bu}/{\rm\pi}$
that occurs as
$k\rightarrow \infty$
. The lower group speed results in the wavepacket stagnating at a slightly smaller value of
$|x|$
.
5. Discussion
Here we have used fully nonlinear numerical simulations to test the generalised model of strain-forced frontogenesis developed in ST14, which extends the model of Hoskins & Bretherton (Reference Hoskins and Bretherton1972, HB) to larger values of strain. Consistent with the scaling analysis of ST14, the examples considered in § 3 show that the generalised model is accurate at first order for both small (
${\it\alpha}=0.2f$
) and large (
${\it\alpha}=0.9f$
) values of strain so long as
$\mathit{Ro}^{2}{\it\delta}^{2}\ll 1$
. Even for small strain, the generalised model represents an improvement on the HB model by correctly describing the confinement of the frontal circulation by the strain field (e.g. figure 3). Further, for sufficiently small Rossby number, the examples in § 3 (particularly figures 3 and 5) show that the generalised model is capable of accurately describing the spontaneous generation of waves at a strained front. In the case of constant strain, these waves take the form of stationary bands of vertical flow a fixed distance ahead of the surface front.
The generalised model also accurately describes frontogenesis, and the generation and propagation of waves, in a time-varying strain flow. As shown in § 3.2, the waves generated at constant strain and trapped by the strain field are released when the strain weakens and propagate away from the front. As predicted by the generalised model, the presence of a weakening strain field also drives additional wave generation and oscillations by way of a geostrophic adjustment process (see figure 8). These wave dynamics are likely to be relevant to ocean fronts, which often exist within strongly time-varying strain fields (e.g. Alford et al. Reference Alford, Shcherbina and Gregg2013).
Furthermore, the dynamics described by the generalised model – including confinement and wave generation – remain relevant beyond the point of discontinuity formation in the inviscid model if some diffusive process is introduced to counteract frontogenesis. In § 5 we added a horizontal hyperdiffusion to the numerical model in order to allow the front to attain a steady state; the hyperdiffusion can be interpreted as a parametrisation of missing frontolytic processes. We introduced a simple method to expand the generalised analytical model of ST14 to (approximately) incorporate the effects of diffusion (i.e. (4.3)). As seen in figure 9, this approximate solution provides a good estimate of both the secondary circulation and spontaneously generated waves observed in the numerical model, even though these waves are generated beyond the time of discontinuity formation in the generalised model (when it is formally invalid). Thus, the spontaneous generation of wavepackets on the periphery of the front appears to be a generic feature of any sharp front that has been subject to a convergent strain for a sufficiently long period of time,
$t\gg {\it\alpha}^{-1}$
, such that wave energy has time to accumulate.
In § 3.2 we used the numerical model to explore the dynamics of two-dimensional fronts in the limit of large Rossby numbers and large strains (
$\mathit{Ro}\,{\it\delta}\sim 1$
), where the generalised analytical model is no longer expected to be valid. Even in this parameter regime, numerical simulations produce a frontal circulation that is horizontally confined within the region of possible wave propagation at large time, dimensionally
$x+v/f<NH/({\it\alpha}{\rm\pi})$
, as would be predicted by the generalised model. Hence, the confinement effect appears to be a fundamental constraint on the system that is independent of approximations made in the generalised model. One important consequence of confinement is increased vertical velocity on the edges of the confinement region. The breakdown of the analytical model for order-one
$\mathit{Ro}$
and
${\it\delta}$
is due to the combination of strong confinement (due to large
${\it\delta}$
), and hence large vertical velocities, and significant outward slumping of the surface front (due to large
$\mathit{Ro}$
). As a consequence, the surface front is coincident with the large velocities (e.g. see figure 7), and the vertical advection terms neglected in the ST14 analytical model (2.10) become important in the numerical solution. The vertical velocities advect the near-surface frontal gradient into the interior of the flow, leading to large interior gradients, whereupon convergence of the strain field across these gradients further amplifies the vertical flow. The positive feedback results in super-exponential growth of the vertical velocity at sharp fronts. This feedback mechanism may provide a dynamical explanation for the exceptionally large vertical velocities directly below submesoscale fronts in the ocean mixed layer, where
$\mathit{Ro}$
and
${\it\delta}$
may both be order-one quantities (Mahadevan & Tandon Reference Mahadevan and Tandon2006).
The generalised model of frontogenesis developed in ST14 provides an accurate description of frontal sharpening and spontaneous wave generation in a simple idealised theoretical framework. In particular, the validity of the ST14 model for order-one values of strain,
${\it\alpha}\sim f$
, makes it applicable to regimes such as the ocean submesoscale. Further, the ST14 model includes important dynamical differences – which we have shown here to be robust – compared with the classical Hoskins & Bretherton (Reference Hoskins and Bretherton1972) model even for relatively small values of strain,
${\it\alpha}\sim 0.2f$
. However, neglected factors such as frontal curvature, spatial variation in the background strain, vertical variations in shear and stratification, and many other features of more realistic frontal systems, will modify the dynamics of frontogenesis and wave generation predicted by the model.
Acknowledgements
C.J.S. was supported by a Gates Cambridge Scholarship, and J.R.T. was supported by the Natural Environment Research Council award NE/J010472/1. The authors would like to thank P. Haynes, J. Methven, M. McIntyre, R. Plougonven and L. Thomas for helpful comments and discussion.
