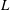1 Introduction
If a wave approaching the coast is long and the variation of the coastal slope is gradual, spilling breakers usually appear. They are characterized by the presence of a finite turbulent zone riding down the forward slope of the wave (Longuet-Higgins & Turner Reference Longuet-Higgins and Turner1974; Duncan Reference Duncan2001). At the toe of this turbulent zone, the wave slope changes sharply, resulting in flow separation and vorticity creation. The breaking waves entrain air into the water by forming ‘whitecaps’ where an intensive dissipation occurs. Such a turbulent zone has a strong influence on the wave evolution.
As mentioned in Duncan (Reference Duncan2001), theoretical models of spilling breakers are rare. Indeed, beyond the multiphase aspects, the modelling depends crucially on a precise description of the flow structure. One actually uses an interesting approach (cf. Tissier et al. Reference Tissier, Bonneton, Marche, Chazel and Lannes2011) based on coupling between the dispersive equations describing long waves far from the coast (Serre Reference Serre1953; Su & Gardner Reference Su and Gardner1969; Green & Naghdi Reference Green and Naghdi1976) and the hyperbolic Saint-Venant equations describing wave breaking near the coast. The difficulty is to understand when we replace one model by another. The search for such a ‘switching criterion’ is not a well-defined problem even if several empirical criteria have been proposed in the literature (wave phase velocity becomes larger than the flow velocity, or the wave slope attains the critical value, for example). A unified model that is capable of describing both dispersion and breaking, as well as the transition between different flow regimes, is thus needed.
To understand the formation of spilling breakers, consider for illustrative purposes solitary wave breaking. The full Euler equations for potential flows of a finite layer of incompressible fluid under gravity admit solitary waves whose maximum amplitude is limited. Physically, the waves of larger amplitude break, but the exact potential theory does not allow us to describe the breaking process. The wave breaking is accompanied by a strong vorticity generation, dissipation and eventually air entrainment. The vorticity generation mechanism can easily be understood by using the following mechanical analogy. Consider fluid particles at the free surface as ‘material particles’ whose kinetic energy does not allow them to reach the wave crest. The particles then attain a maximum admissible height at the forward face of the wave, and then spread downslope, thus creating a surface shear layer. The vortices of the upper shear layer then ‘contaminate’ the potential fluid core by developing a mixing layer. Such a two-layer approach can be considered as a simplified version of spilling breaker formation (Misra, Brocchini & Kirby Reference Misra, Brocchini and Kirby2006).
Svendsen & Madsen (Reference Svendsen and Madsen1984) constructed a four-equation ‘equilibrium’ hydrostatic hyperbolic model of a turbulent bore. ‘Equilibrium’ means that the turbulent upper layer is already formed. The shear velocity profile in the turbulent region was approximated by a cubic polynomial of the vertical coordinate. Misra et al. (Reference Misra, Brocchini and Kirby2006) proposed a non-hydrostatic approach for spilling breakers. The presence of the turbulent shear layer was regarded as turbulent free-surface boundary conditions for the irrotational flow below.
A two-layer framework has also been used in Liapidevskii & Xu (Reference Liapidevskii and Xu2006) to establish a criterion of solitary wave breaking over an obstacle.
It is clear that a three-layer mathematical model is needed to describe the interaction between the underlying potential layer, the intermediate single-phase turbulent layer and the surface two-phase layer (Brocchini & Peregrine Reference Brocchini and Peregrine2001a ,Reference Brocchini and Peregrine b ; Brocchini Reference Brocchini2002). However, as mentioned in Brocchini & Peregrine (Reference Brocchini and Peregrine2001b ) in connection with the closure relations for the two-phase region, ‘our knowledge of the properties of strong turbulence at a (water–air) free surface is insufficient to make such closures’.
In this paper we will neglect air entrainment and thus will restrict ourselves to two-layer modelling. The upper layer is turbulent and described within the framework of shear shallow water flows (cf. Teshukov Reference Teshukov2007, Richard & Gavrilyuk Reference Richard and Gavrilyuk2012, Reference Richard and Gavrilyuk2013, Castro & Lannes Reference Castro and Lannes2014). The lower layer is potential and can approximately be described by the Serre–Su–Gardner–Green–Naghdi type model. The interaction between the layers is taken into account through a natural mixing process, where the mixing velocity is proportional to the intensity of large eddies of the upper layer. Experimental data on the structure of the turbulent flow field under breaking waves shows that the frontiers between the turbulent and potential regions are clearly visible (Nadaoka, Hino & Koyano Reference Nadaoka, Hino and Koyano1989; Lin & Rockwell Reference Lin and Rockwell1994; Misra et al. Reference Misra, Brocchini and Kirby2006, Reference Misra, Kirby, Brocchini, Veron, Thomas and Kambhamettu2008). This justifies a two-layer scheme for the modelling of breaking waves. The model is more general than that of Liapidevskii & Chesnokov (Reference Liapidevskii and Chesnokov2014), where the hydrostatic approximation in both layers was used, and that of Richard & Gavrilyuk (Reference Richard and Gavrilyuk2015), where such a two-layer approach was used in the limit of vanishing thickness of the upper shear layer.
The new mathematical model thus aims to describe the formation and interaction of such a two-layer flow without taking air entrainment into account. It contains several mathematical mechanisms for vorticity generation. The first mechanism is the same as that proposed in Teshukov (Reference Teshukov2007) and Richard & Gavrilyuk (Reference Richard and Gavrilyuk2012, Reference Richard and Gavrilyuk2013). The pressure distribution being hydrostatic in the upper turbulent mixing layer, the corresponding submodel is hyperbolic. Thus the upper layer submodel generates the vorticity through the shock relations (Rankine–Hugoniot relations) in the same way as the entropy production in shocks for the Euler equations of compressible fluids.
Such a shock formation is very natural when the upper layer is already developed (has a non-vanishing thickness). However, even if the upper layer was initially absent, it may develop through at least two bifurcation mechanisms. The first one is a classical supercritical bifurcation from a uniform flow (for Froude number larger than one): together with the formation of the solitary wave, the upper shear layer is forming. When the solitary wave is already formed, a second type of bifurcation may happen: an abrupt transition to subcritical from supercritical flow occurs followed by a continuous transition again to a supercritical flow. The second type of bifurcation produces a finite turbulent subcritical region.
When a stationary wave train is propagating, the criticality condition can be attained not necessarily at the first wave but, for example, at the second one. Physically, this corresponds to roller formation at the top of the second wave. This fact was observed, in particular, in the experiments by Ryabenko (Reference Ryabenko1990) in a wide (1 m), deep (1 m) and long (39 m) channel.
This non-stationary mathematical model having both hyperbolic and dispersive properties was numerically solved by combining finite volume methods with the inversion of an elliptic operator for the dispersive part of the model, as proposed in Le Metayer, Gavrilyuk & Hank (Reference Le Metayer, Gavrilyuk and Hank2010) and Bonneton et al. (Reference Bonneton, Chazel, Lannes, Marche and Tissier2011).
In § 2 we derive the two-layer depth-averaged equations. In § 3, stationary solutions are studied. Favre waves and the shoaling and breaking of solitary waves are studied in § 4. Technical details are presented in appendices A and B.
2 Two-layer flow over a flat bottom
The simplest model for spilling breakers, without taking into account air bubble trapping, should be able to describe the interaction between an upper turbulent layer and a lower almost potential layer (see figure 1). First, we will derive such a two-layer model for flows over a flat bottom. We neglect the influence of the bottom and sidewall boundary layers, which is a reasonable approximation for waves propagating in a large-scale flume. We will derive first the Euler depth-averaged equations. Two dissipation source terms will then be added compatible with the total energy decrease. The first one is related to the expansion of the upper turbulent layer due to ‘contamination’ of the potential layer by vertical vortices. The second one is a classical bulk turbulent dissipation source term. Even if these two dissipation source terms could be insufficient to describe breaking waves in the general case, it appears that they are able to model with a good accuracy at least two interesting experiments presented below. For narrow and shallow channels, the bottom and wall friction can naturally be taken into account by adding a standard drag force that is quadratic in velocity.

Figure 1. Two-layer flow over topography.
Consider the Euler equations for two-dimensional flows. In the horizontal direction
![]() $Ox$
the component of the velocity is
$Ox$
the component of the velocity is
![]() $u$
, and in the vertical direction
$u$
, and in the vertical direction
![]() $Oz$
the velocity component is
$Oz$
the velocity component is
![]() $w$
. With
$w$
. With
![]() $\unicode[STIX]{x1D70C}$
being the fluid density and
$\unicode[STIX]{x1D70C}$
being the fluid density and
![]() $p$
being the fluid pressure, the Euler equations can be written as
$p$
being the fluid pressure, the Euler equations can be written as
Here
![]() $g$
is the gravitational acceleration in the vertical direction. The kinematic boundary condition at
$g$
is the gravitational acceleration in the vertical direction. The kinematic boundary condition at
![]() $z=0$
is
$z=0$
is
At the internal boundary
![]() $z=h(t,x)$
separating the lower layer where the flow is potential and the upper turbulent layer, the kinematic condition is
$z=h(t,x)$
separating the lower layer where the flow is potential and the upper turbulent layer, the kinematic condition is
Here the right-hand side
![]() $M$
is responsible for the mixing between layers (a formula for
$M$
is responsible for the mixing between layers (a formula for
![]() $M$
will be proposed later). At the free boundary
$M$
will be proposed later). At the free boundary
![]() $z=h(t,x)+\unicode[STIX]{x1D702}(t,x)$
we assume that
$z=h(t,x)+\unicode[STIX]{x1D702}(t,x)$
we assume that
We introduce a classical scaling of the shallow water theory:
 $$\begin{eqnarray}\left.\begin{array}{@{}l@{}}\displaystyle x=Lx^{\star },\quad z=Hz^{\star },\quad t=\frac{L}{\sqrt{gH}}\,t^{\star },\quad u=\sqrt{gH}u^{\star },\\ \displaystyle w=\frac{H}{L}\sqrt{gH}w^{\star },\quad p=\unicode[STIX]{x1D70C}gHp^{\star },\quad h=Hh^{\star }.\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}l@{}}\displaystyle x=Lx^{\star },\quad z=Hz^{\star },\quad t=\frac{L}{\sqrt{gH}}\,t^{\star },\quad u=\sqrt{gH}u^{\star },\\ \displaystyle w=\frac{H}{L}\sqrt{gH}w^{\star },\quad p=\unicode[STIX]{x1D70C}gHp^{\star },\quad h=Hh^{\star }.\end{array}\right\}\end{eqnarray}$$
Here
![]() $H$
is the characteristic vertical scale,
$H$
is the characteristic vertical scale,
![]() $L$
is the characteristic horizontal scale, and the dimensionless variables are denoted with the ‘star’. We suppose that the waves are long, so the dimensionless parameter
$L$
is the characteristic horizontal scale, and the dimensionless variables are denoted with the ‘star’. We suppose that the waves are long, so the dimensionless parameter
![]() $\unicode[STIX]{x1D700}=H/L$
is small. Equations (2.1)–(2.3) are transformed into dimensionless form where, to simplify the writing of equations, we drop the stars on the dimensionless variables:
$\unicode[STIX]{x1D700}=H/L$
is small. Equations (2.1)–(2.3) are transformed into dimensionless form where, to simplify the writing of equations, we drop the stars on the dimensionless variables:
Equations (2.8)–(2.10) admit the conservation of energy,
where
is the dimensionless specific energy.
2.1 Depth-averaged equations for the lower potential layer
Integrating the incompressibility, horizontal momentum and energy equations with respect to
![]() $z$
over the fluid depth and using the boundary conditions (2.4) and (2.5), we obtain the following exact integral relations for the lower layer:
$z$
over the fluid depth and using the boundary conditions (2.4) and (2.5), we obtain the following exact integral relations for the lower layer:
 $$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}\left(\int _{0}^{h}\left(\frac{u^{2}}{2}+\unicode[STIX]{x1D700}^{2}\frac{w^{2}}{2}+z\right)\,\text{d}z\right)+\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x}\left(\int _{0}^{h}u\left(\frac{u^{2}}{2}+\unicode[STIX]{x1D700}^{2}\frac{w^{2}}{2}+z\right)\,\text{d}z+\int _{0}^{h}pu\,\text{d}z\right)\nonumber\\ \displaystyle & & \displaystyle \qquad =-p|_{z=h}(h_{t}+M)-M\left.\left(\frac{u^{2}}{2}+\unicode[STIX]{x1D700}^{2}\frac{w^{2}}{2}+h\right)\right|_{z=h}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}\left(\int _{0}^{h}\left(\frac{u^{2}}{2}+\unicode[STIX]{x1D700}^{2}\frac{w^{2}}{2}+z\right)\,\text{d}z\right)+\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x}\left(\int _{0}^{h}u\left(\frac{u^{2}}{2}+\unicode[STIX]{x1D700}^{2}\frac{w^{2}}{2}+z\right)\,\text{d}z+\int _{0}^{h}pu\,\text{d}z\right)\nonumber\\ \displaystyle & & \displaystyle \qquad =-p|_{z=h}(h_{t}+M)-M\left.\left(\frac{u^{2}}{2}+\unicode[STIX]{x1D700}^{2}\frac{w^{2}}{2}+h\right)\right|_{z=h}.\end{eqnarray}$$
Introducing the average velocity in the lower layer,
we can rewrite the mass conservation law in the following form:
To obtain a closed system of governing equations, we need to know the pressure distribution in the layer. Integrating equation (2.1) from
![]() $0$
to
$0$
to
![]() $z$
,
$z$
,
![]() $0<z<h(t,x)$
, we obtain
$0<z<h(t,x)$
, we obtain
In zero order with respect to
![]() $\unicode[STIX]{x1D700}$
, the vertical velocity is
$\unicode[STIX]{x1D700}$
, the vertical velocity is
A second-order approximation for the pressure comes from (2.10) where we have to replace
![]() $w$
by (2.19):
$w$
by (2.19):
Integrating this from
![]() $h$
to
$h$
to
![]() $z$
(
$z$
(
![]() $0<z<h$
) we obtain
$0<z<h$
) we obtain
The integral of the pressure can thus be evaluated as
One can also prove that, if the flow is weakly sheared, i.e. the dimensionless flow vorticity
![]() $\unicode[STIX]{x1D714}=u_{z}-\unicode[STIX]{x1D700}^{2}w_{x}=O(\unicode[STIX]{x1D700}^{\unicode[STIX]{x1D6FD}})$
with
$\unicode[STIX]{x1D714}=u_{z}-\unicode[STIX]{x1D700}^{2}w_{x}=O(\unicode[STIX]{x1D700}^{\unicode[STIX]{x1D6FD}})$
with
![]() $1<\unicode[STIX]{x1D6FD}\leqslant 2$
, then
$1<\unicode[STIX]{x1D6FD}\leqslant 2$
, then
(for the proof, see Barros, Gavrilyuk & Teshukov (Reference Barros, Gavrilyuk and Teshukov2007) or Gavrilyuk, Kalisch & Khorsand (Reference Gavrilyuk, Kalisch and Khorsand2015)). In particular, in the potential case,
![]() $\unicode[STIX]{x1D6FD}=2$
. Analogous estimation of integrals can be given for the energy equation. Keeping only terms of order one and
$\unicode[STIX]{x1D6FD}=2$
. Analogous estimation of integrals can be given for the energy equation. Keeping only terms of order one and
![]() $\unicode[STIX]{x1D700}^{2}$
, we obtain the final system for a lower potential layer with mixing at the interface
$\unicode[STIX]{x1D700}^{2}$
, we obtain the final system for a lower potential layer with mixing at the interface
![]() $z=h(t,x)$
:
$z=h(t,x)$
:
 $$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}\left(h\left(\frac{U^{2}}{2}+\unicode[STIX]{x1D700}^{2}\frac{U_{x}^{2}}{6}h^{2}+\frac{h}{2}\right)\right)+\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x}\left(hU\left(\frac{U^{2}}{2}+\unicode[STIX]{x1D700}^{2}\frac{U_{x}^{2}}{6}h^{2}+\frac{h}{2}\right)+U\int _{0}^{h}p\,\text{d}z\right)\nonumber\\ \displaystyle & & \displaystyle \qquad =-p|_{z=h}(h_{t}+M)-M\left.\left(\frac{u^{2}}{2}+\unicode[STIX]{x1D700}^{2}\frac{U_{x}^{2}h^{2}}{2}+h\right)\right|_{z=h},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}\left(h\left(\frac{U^{2}}{2}+\unicode[STIX]{x1D700}^{2}\frac{U_{x}^{2}}{6}h^{2}+\frac{h}{2}\right)\right)+\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x}\left(hU\left(\frac{U^{2}}{2}+\unicode[STIX]{x1D700}^{2}\frac{U_{x}^{2}}{6}h^{2}+\frac{h}{2}\right)+U\int _{0}^{h}p\,\text{d}z\right)\nonumber\\ \displaystyle & & \displaystyle \qquad =-p|_{z=h}(h_{t}+M)-M\left.\left(\frac{u^{2}}{2}+\unicode[STIX]{x1D700}^{2}\frac{U_{x}^{2}h^{2}}{2}+h\right)\right|_{z=h},\end{eqnarray}$$
where
The value of the velocity
![]() $u|_{z=h}$
is not yet determined. Let us remark that we have formally three governing equations for only two unknowns
$u|_{z=h}$
is not yet determined. Let us remark that we have formally three governing equations for only two unknowns
![]() $h$
and
$h$
and
![]() $U$
. The compatibility condition between the energy, momentum and mass equations gives us only one possibility (for proof, see appendix A):
$U$
. The compatibility condition between the energy, momentum and mass equations gives us only one possibility (for proof, see appendix A):
2.2 Depth-averaged equations for the upper turbulent layer
Consider the following hydrostatic equations in the upper layer having the same density as the lower layer. In dimensionless variables, the equations are
The hydrostatic distribution of the pressure already takes into account the dynamic condition at the free surface. They admit the energy conservation law:
The corresponding kinematic boundary conditions at the free surface and at the internal surface are
Averaging the incompressibility equation, we obtain
with
Averaging of the horizontal momentum equation gives us
or
with the specific turbulent energy
![]() $e$
defined as
$e$
defined as
The quantity
![]() $e$
actually measures the flow dispersiveness. In Antuono & Brocchini (Reference Antuono and Brocchini2013) the evaluation of this term has been given for different flow regimes. Instead, we will obtain the evolution equation for
$e$
actually measures the flow dispersiveness. In Antuono & Brocchini (Reference Antuono and Brocchini2013) the evaluation of this term has been given for different flow regimes. Instead, we will obtain the evolution equation for
![]() $e$
. The averaged energy equation is
$e$
. The averaged energy equation is
 $$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}\left(\int _{h}^{h+\unicode[STIX]{x1D702}}\left(\frac{u^{2}}{2}+z\right)\,\text{d}z\right)+\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x}\left(\int _{h}^{h+\unicode[STIX]{x1D702}}\left(u\left(\frac{u^{2}}{2}+z\right)+pu\right)\,\text{d}z\right)\nonumber\\ \displaystyle & & \displaystyle \qquad =M\left(\left.\frac{u^{2}}{2}\right|_{z=h}+h\right)+p|_{z=h}(h_{t}+M).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}\left(\int _{h}^{h+\unicode[STIX]{x1D702}}\left(\frac{u^{2}}{2}+z\right)\,\text{d}z\right)+\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x}\left(\int _{h}^{h+\unicode[STIX]{x1D702}}\left(u\left(\frac{u^{2}}{2}+z\right)+pu\right)\,\text{d}z\right)\nonumber\\ \displaystyle & & \displaystyle \qquad =M\left(\left.\frac{u^{2}}{2}\right|_{z=h}+h\right)+p|_{z=h}(h_{t}+M).\end{eqnarray}$$
We suppose that the shear effects in the upper layer are now more important. More exactly, the dimensionless flow vorticity is
![]() $\unicode[STIX]{x1D714}=u_{z}-\unicode[STIX]{x1D700}^{2}w_{x}\approx u_{z}$
. Let us assume that initially
$\unicode[STIX]{x1D714}=u_{z}-\unicode[STIX]{x1D700}^{2}w_{x}\approx u_{z}$
. Let us assume that initially
![]() $u_{z}=O(\unicode[STIX]{x1D700}^{\unicode[STIX]{x1D6FD}})$
with
$u_{z}=O(\unicode[STIX]{x1D700}^{\unicode[STIX]{x1D6FD}})$
with
![]() $0<\unicode[STIX]{x1D6FD}<1$
. One can prove that this property is then valid for any time. It also implies that
$0<\unicode[STIX]{x1D6FD}<1$
. One can prove that this property is then valid for any time. It also implies that
This term is now more important than the dispersion, which is of order
![]() $\unicode[STIX]{x1D700}^{2}$
, and should be kept in the momentum equation. The vorticity is ‘weak’ in the sense that it is not of order one, but it could be quite ‘large’ (‘almost’ of order one) when
$\unicode[STIX]{x1D700}^{2}$
, and should be kept in the momentum equation. The vorticity is ‘weak’ in the sense that it is not of order one, but it could be quite ‘large’ (‘almost’ of order one) when
![]() $\unicode[STIX]{x1D6FD}$
is small. Analogous estimation of integrals can be given for the energy equation (for details, see Teshukov Reference Teshukov2007; Richard & Gavrilyuk Reference Richard and Gavrilyuk2012, Reference Richard and Gavrilyuk2013). Keeping only terms of order one and
$\unicode[STIX]{x1D6FD}$
is small. Analogous estimation of integrals can be given for the energy equation (for details, see Teshukov Reference Teshukov2007; Richard & Gavrilyuk Reference Richard and Gavrilyuk2012, Reference Richard and Gavrilyuk2013). Keeping only terms of order one and
![]() $\unicode[STIX]{x1D700}^{2\unicode[STIX]{x1D6FD}}$
, we obtain the energy equation for the upper turbulent layer in the form
$\unicode[STIX]{x1D700}^{2\unicode[STIX]{x1D6FD}}$
, we obtain the energy equation for the upper turbulent layer in the form
 $$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}\left(\unicode[STIX]{x1D702}\left(\frac{\bar{u}^{2}}{2}+\frac{e}{2}+\frac{\unicode[STIX]{x1D702}+2h}{2}\right)\right)+\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x}\left(\unicode[STIX]{x1D702}\bar{u}\left(\frac{\bar{u}^{2}}{2}+e+\frac{\unicode[STIX]{x1D702}+2h}{2}\right)+\frac{\unicode[STIX]{x1D702}^{2}}{2}\bar{u}\right)\nonumber\\ \displaystyle & & \displaystyle \qquad =M\left(\left.\frac{u^{2}}{2}\right|_{z=h}+h\right)+p|_{z=h}(h_{t}+M).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}\left(\unicode[STIX]{x1D702}\left(\frac{\bar{u}^{2}}{2}+\frac{e}{2}+\frac{\unicode[STIX]{x1D702}+2h}{2}\right)\right)+\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x}\left(\unicode[STIX]{x1D702}\bar{u}\left(\frac{\bar{u}^{2}}{2}+e+\frac{\unicode[STIX]{x1D702}+2h}{2}\right)+\frac{\unicode[STIX]{x1D702}^{2}}{2}\bar{u}\right)\nonumber\\ \displaystyle & & \displaystyle \qquad =M\left(\left.\frac{u^{2}}{2}\right|_{z=h}+h\right)+p|_{z=h}(h_{t}+M).\end{eqnarray}$$
Since the pressure distribution in the upper layer is linear with
![]() $z$
(the pressure is hydrostatic), one obviously has
$z$
(the pressure is hydrostatic), one obviously has
Remark 1. The rate at which the potential layer is ‘contaminated’ by the vorticity (the term
![]() $M$
) should be specified. We take it in the form
$M$
) should be specified. We take it in the form
The justification for (2.42) can be done in the following way. Consider two co-flowing horizontal fluid layers having the same velocity. The upper layer is turbulent, and the lower one is potential. We denote the classical Reynolds averaging of the dimensionless Euler equations (with
![]() $\unicode[STIX]{x1D700}=1$
) by angle brackets
$\unicode[STIX]{x1D700}=1$
) by angle brackets
![]() $\langle \cdots \rangle$
, with a classical representation for any
$\langle \cdots \rangle$
, with a classical representation for any
![]() $f$
in the form
$f$
in the form
![]() $f=\langle f\rangle +\tilde{f}$
, where
$f=\langle f\rangle +\tilde{f}$
, where
![]() $\langle \tilde{f}\rangle =0$
. The corresponding dimensionless Reynolds equations are
$\langle \tilde{f}\rangle =0$
. The corresponding dimensionless Reynolds equations are
 $$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\langle u\rangle _{x}+\langle w\rangle _{z}=0,\quad \langle u\rangle _{t}+(\langle u\rangle ^{2}+\langle \tilde{u} ^{2}\rangle +\langle p\rangle )_{x}+(\langle u\rangle \langle w\rangle +\langle \tilde{u} \tilde{w}\rangle )_{z}=0,\\ \langle w\rangle _{t}+(\langle u\rangle \langle w\rangle +\langle \tilde{u} \tilde{w}\rangle )_{x}+(\langle w\rangle ^{2}+\langle \tilde{w}^{2}\rangle +\langle p\rangle )_{z}=-1,\\ \langle E\rangle _{t}+(\langle u\rangle \langle E\rangle +\langle \tilde{u} \tilde{E}\rangle +\langle p\rangle \langle u\rangle +\langle \tilde{p}\tilde{u} \rangle )_{x}\qquad \;\\ \qquad +(\langle w\rangle \langle E\rangle +\langle \tilde{w}\tilde{E}\rangle +\langle p\rangle \langle w\rangle +\langle \tilde{p}\tilde{w}\rangle )_{z}=-\langle w\rangle .\end{array}\right\} & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\langle u\rangle _{x}+\langle w\rangle _{z}=0,\quad \langle u\rangle _{t}+(\langle u\rangle ^{2}+\langle \tilde{u} ^{2}\rangle +\langle p\rangle )_{x}+(\langle u\rangle \langle w\rangle +\langle \tilde{u} \tilde{w}\rangle )_{z}=0,\\ \langle w\rangle _{t}+(\langle u\rangle \langle w\rangle +\langle \tilde{u} \tilde{w}\rangle )_{x}+(\langle w\rangle ^{2}+\langle \tilde{w}^{2}\rangle +\langle p\rangle )_{z}=-1,\\ \langle E\rangle _{t}+(\langle u\rangle \langle E\rangle +\langle \tilde{u} \tilde{E}\rangle +\langle p\rangle \langle u\rangle +\langle \tilde{p}\tilde{u} \rangle )_{x}\qquad \;\\ \qquad +(\langle w\rangle \langle E\rangle +\langle \tilde{w}\tilde{E}\rangle +\langle p\rangle \langle w\rangle +\langle \tilde{p}\tilde{w}\rangle )_{z}=-\langle w\rangle .\end{array}\right\} & & \displaystyle\end{eqnarray}$$
Here
 $$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\displaystyle E=\frac{u^{2}+w^{2}}{2},\quad \langle E\rangle =\frac{\langle u\rangle ^{2}+\langle w\rangle ^{2}}{2}+\frac{k}{2},\quad k=\langle \tilde{u} ^{2}\rangle +\langle \tilde{w}^{2}\rangle ,\\ \displaystyle \tilde{E}=\langle u\rangle \tilde{u} +\langle w\rangle \tilde{w}+\frac{\tilde{u} ^{2}+\tilde{w}^{2}}{2}-\frac{k}{2},\end{array}\right\} & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\displaystyle E=\frac{u^{2}+w^{2}}{2},\quad \langle E\rangle =\frac{\langle u\rangle ^{2}+\langle w\rangle ^{2}}{2}+\frac{k}{2},\quad k=\langle \tilde{u} ^{2}\rangle +\langle \tilde{w}^{2}\rangle ,\\ \displaystyle \tilde{E}=\langle u\rangle \tilde{u} +\langle w\rangle \tilde{w}+\frac{\tilde{u} ^{2}+\tilde{w}^{2}}{2}-\frac{k}{2},\end{array}\right\} & & \displaystyle\end{eqnarray}$$
the subscripts
![]() $t$
,
$t$
,
![]() $x$
and
$x$
and
![]() $z$
mean differentiation with respect to
$z$
mean differentiation with respect to
![]() $t$
,
$t$
,
![]() $x$
and
$x$
and
![]() $z$
, respectively, and
$z$
, respectively, and
![]() $k$
equals twice the kinetic turbulent energy. Consider now particular solutions of (2.43) where all the variables depend only on
$k$
equals twice the kinetic turbulent energy. Consider now particular solutions of (2.43) where all the variables depend only on
![]() $(t,z)$
, and the term
$(t,z)$
, and the term
![]() $\langle u\rangle \langle w\rangle$
is negligible with respect to the Reynolds shear stress. Also, we will assume that the third-order correlations and the correlation
$\langle u\rangle \langle w\rangle$
is negligible with respect to the Reynolds shear stress. Also, we will assume that the third-order correlations and the correlation
![]() $\langle \tilde{p}\tilde{w}\rangle$
are negligible. Such a solution is suitable for the description of a horizontal mixing layer. Equations (2.43) imply that
$\langle \tilde{p}\tilde{w}\rangle$
are negligible. Such a solution is suitable for the description of a horizontal mixing layer. Equations (2.43) imply that
System (2.45) simplifying (2.43) with the closure
![]() $-\langle \tilde{u} \tilde{w}\rangle =\unicode[STIX]{x1D70E}k$
, where
$-\langle \tilde{u} \tilde{w}\rangle =\unicode[STIX]{x1D70E}k$
, where
![]() $\unicode[STIX]{x1D70E}=\text{const}.$
is the shear coefficient, is hyperbolic, with the characteristic slopes
$\unicode[STIX]{x1D70E}=\text{const}.$
is the shear coefficient, is hyperbolic, with the characteristic slopes
![]() $\pm \unicode[STIX]{x1D70E}\sqrt{2k}$
. In a vertically sheared flow, the sign of
$\pm \unicode[STIX]{x1D70E}\sqrt{2k}$
. In a vertically sheared flow, the sign of
![]() $\unicode[STIX]{x1D70E}$
coincides with the sign of the vertical mean velocity gradient. The value of
$\unicode[STIX]{x1D70E}$
coincides with the sign of the vertical mean velocity gradient. The value of
![]() $\unicode[STIX]{x1D70E}$
is approximately
$\unicode[STIX]{x1D70E}$
is approximately
![]() $0.15$
(Townsend Reference Townsend1956; Bradshaw, Ferriss & Atwell Reference Bradshaw, Ferriss and Atwell1967). The mixing front between the turbulent layer and the potential layer can be seen as a shock separating the two regions. Applying the Rankine–Hugoniot relations coming from (2.45) we obtain
$0.15$
(Townsend Reference Townsend1956; Bradshaw, Ferriss & Atwell Reference Bradshaw, Ferriss and Atwell1967). The mixing front between the turbulent layer and the potential layer can be seen as a shock separating the two regions. Applying the Rankine–Hugoniot relations coming from (2.45) we obtain
Here the square brackets mean the jump of variables, and
![]() $D$
is the front velocity. Let
$D$
is the front velocity. Let
![]() $u^{-},k^{-}$
and
$u^{-},k^{-}$
and
![]() $u^{+},k^{+}=0$
be the values of the unknowns in the turbulent and potential regions, respectively, with
$u^{+},k^{+}=0$
be the values of the unknowns in the turbulent and potential regions, respectively, with
![]() $u^{-}>u^{+}$
. Then we have
$u^{-}>u^{+}$
. Then we have
This is exactly the empirical relation (2.42) for
![]() $M$
, if we identify the turbulent energy
$M$
, if we identify the turbulent energy
![]() $k$
with the energy
$k$
with the energy
![]() $e$
measuring the flow dispersiveness, and the shock front velocity
$e$
measuring the flow dispersiveness, and the shock front velocity
![]() $D$
with
$D$
with
![]() $M$
. The ‘minus’ sign corresponds to the fact that
$M$
. The ‘minus’ sign corresponds to the fact that
![]() $\unicode[STIX]{x1D702}$
is growing at the same time as
$\unicode[STIX]{x1D702}$
is growing at the same time as
![]() $z$
is decreasing. Such a shock is stable in the sense of Lax (the characteristics overlap at the shock). A detailed discussion can also be found in Liapidevskii & Teshukov (Reference Liapidevskii and Teshukov2000).
$z$
is decreasing. Such a shock is stable in the sense of Lax (the characteristics overlap at the shock). A detailed discussion can also be found in Liapidevskii & Teshukov (Reference Liapidevskii and Teshukov2000).
Remark 2. Besides the dissipation term coming from the mixing at the boundary between the layers, it is necessary to add the bulk dissipation term in the turbulent layer, describing the turbulent energy dissipation toward smaller scales (smaller than the scale of large vortices defined by
![]() $\unicode[STIX]{x1D702}$
). The most simple and classical expression for the energy dissipation rate
$\unicode[STIX]{x1D702}$
). The most simple and classical expression for the energy dissipation rate
![]() $d$
can be taken in the form (Townsend Reference Townsend1956)
$d$
can be taken in the form (Townsend Reference Townsend1956)
Here the coefficient
![]() $\unicode[STIX]{x1D705}/2$
is of order one (it is a ‘calibration’ coefficient to the model); the factor
$\unicode[STIX]{x1D705}/2$
is of order one (it is a ‘calibration’ coefficient to the model); the factor
![]() $1/2$
is added for convenience. The shear coefficient
$1/2$
is added for convenience. The shear coefficient
![]() $\unicode[STIX]{x1D70E}$
has an effect on the length of surface waves, while the dissipation coefficient
$\unicode[STIX]{x1D70E}$
has an effect on the length of surface waves, while the dissipation coefficient
![]() $\unicode[STIX]{x1D705}$
is responsible for the rate of turbulent layer thickness development. The variation of
$\unicode[STIX]{x1D705}$
is responsible for the rate of turbulent layer thickness development. The variation of
![]() $\unicode[STIX]{x1D705}$
between
$\unicode[STIX]{x1D705}$
between
![]() $2$
and
$2$
and
![]() $6$
did not show a qualitative and quantitative modification of solution properties. The value
$6$
did not show a qualitative and quantitative modification of solution properties. The value
![]() $\unicode[STIX]{x1D705}=3$
was chosen for comparison of the model predictions to experimental data. As before, the energy
$\unicode[STIX]{x1D705}=3$
was chosen for comparison of the model predictions to experimental data. As before, the energy
![]() $e$
is given by (2.37).
$e$
is given by (2.37).
Remark 3. The model derived is the ‘dispersive generalization’ of the two-layer hydrostatic model with shear (turbulence) effects in the upper layer proposed in Liapidevskii & Chesnokov (Reference Liapidevskii and Chesnokov2014). The dispersive effects are more important in the lower layer, while the shear (turbulence) effects are more important in the upper layer. The model is more general than that proposed in Richard & Gavrilyuk (Reference Richard and Gavrilyuk2015), where a dispersive model for shear flows was derived. In that paper, a small-thickness upper shear layer was also introduced, but its dynamical development was assumed to be negligible. The approach by Antuono & Brocchini (Reference Antuono and Brocchini2013), where Reynolds averaging and depth averaging were combined for the derivation of an integro-differential system for wave propagation has some similarity with our approach because it also enables a better modelling of the turbulent energy evolution. A close model combining both shear and dispersive effects, but containing also third-order correlations of the velocity, was recently proposed by Castro & Lannes (Reference Castro and Lannes2014). It supposes a regularity of the velocity field in the vertical direction, while in our model the velocity field is singular (a two-layer system is considered).
2.3 Final two-layer system
The final dimensionless system for the thickness of the upper turbulent layer
![]() $\unicode[STIX]{x1D702}$
, its average velocity
$\unicode[STIX]{x1D702}$
, its average velocity
![]() $\bar{u}$
, energy
$\bar{u}$
, energy
![]() $e$
, thickness of the low potential layer
$e$
, thickness of the low potential layer
![]() $h$
and its average velocity
$h$
and its average velocity
![]() $U$
can be written as
$U$
can be written as
 $$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}\left(\unicode[STIX]{x1D702}\left(\frac{\bar{u}^{2}}{2}+\frac{e}{2}+\frac{\unicode[STIX]{x1D702}+2h}{2}\right)\right)+\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x}\left(\unicode[STIX]{x1D702}\bar{u}\left(\frac{\bar{u}^{2}}{2}+\frac{e}{2}+\frac{\unicode[STIX]{x1D702}+2h}{2}\right)+\left(\unicode[STIX]{x1D702}e+\frac{\unicode[STIX]{x1D702}^{2}}{2}\right)\bar{u}\right)\nonumber\\ \displaystyle & & \displaystyle \qquad =M\left(\frac{U^{2}}{2}+h\right)+\unicode[STIX]{x1D702}(h_{t}+M)-d,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}\left(\unicode[STIX]{x1D702}\left(\frac{\bar{u}^{2}}{2}+\frac{e}{2}+\frac{\unicode[STIX]{x1D702}+2h}{2}\right)\right)+\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x}\left(\unicode[STIX]{x1D702}\bar{u}\left(\frac{\bar{u}^{2}}{2}+\frac{e}{2}+\frac{\unicode[STIX]{x1D702}+2h}{2}\right)+\left(\unicode[STIX]{x1D702}e+\frac{\unicode[STIX]{x1D702}^{2}}{2}\right)\bar{u}\right)\nonumber\\ \displaystyle & & \displaystyle \qquad =M\left(\frac{U^{2}}{2}+h\right)+\unicode[STIX]{x1D702}(h_{t}+M)-d,\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}\left(h\left(\frac{U^{2}}{2}+\unicode[STIX]{x1D700}^{2}\frac{U_{x}^{2}}{6}h^{2}+\frac{h}{2}\right)\right)+\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x}\left(hU\left(\frac{U^{2}}{2}+\unicode[STIX]{x1D700}^{2}\frac{U_{x}^{2}}{6}h^{2}+\frac{h}{2}\right)+U\int _{0}^{h}p\,\text{d}z\right)\nonumber\\ \displaystyle & & \displaystyle \qquad =-\unicode[STIX]{x1D702}(h_{t}+M)-M\left(\frac{U^{2}}{2}+\unicode[STIX]{x1D700}^{2}\frac{U_{x}^{2}h^{2}}{2}+h\right),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}\left(h\left(\frac{U^{2}}{2}+\unicode[STIX]{x1D700}^{2}\frac{U_{x}^{2}}{6}h^{2}+\frac{h}{2}\right)\right)+\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x}\left(hU\left(\frac{U^{2}}{2}+\unicode[STIX]{x1D700}^{2}\frac{U_{x}^{2}}{6}h^{2}+\frac{h}{2}\right)+U\int _{0}^{h}p\,\text{d}z\right)\nonumber\\ \displaystyle & & \displaystyle \qquad =-\unicode[STIX]{x1D702}(h_{t}+M)-M\left(\frac{U^{2}}{2}+\unicode[STIX]{x1D700}^{2}\frac{U_{x}^{2}h^{2}}{2}+h\right),\end{eqnarray}$$
with
It is shown in appendix A that equation (2.54) (the energy balance for the lower layer) is not independent – it is a consequence of (2.52) and (2.53). It is added just to have a ‘symmetric’ presentation of the governing equations. Summing the momentum equations for each layer (2.50) and (2.53), and the energy balances (2.51) and (2.54), one immediately obtains the total momentum conservation law,
and the total energy balance equation,
 $$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}\left(\unicode[STIX]{x1D702}\left(\frac{\bar{u}^{2}}{2}+\frac{e}{2}+\frac{\unicode[STIX]{x1D702}+2h}{2}\right)+h\left(\frac{U^{2}}{2}+\unicode[STIX]{x1D700}^{2}\frac{U_{x}^{2}}{6}h^{2}+\frac{h}{2}\right)\right)\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x}\left(\unicode[STIX]{x1D702}\bar{u}\left(\frac{\bar{u}^{2}}{2}+\frac{e}{2}+\frac{\unicode[STIX]{x1D702}+2h}{2}\right)+\left(\unicode[STIX]{x1D702}e+\frac{\unicode[STIX]{x1D702}^{2}}{2}\right)\bar{u}\right.\nonumber\\ \displaystyle & & \displaystyle \left.\qquad +\,hU\left(\frac{U^{2}}{2}+\unicode[STIX]{x1D700}^{2}\frac{U_{x}^{2}}{6}h^{2}+\frac{h}{2}\right)+U\int _{0}^{h}p\,\text{d}z\right)\nonumber\\ \displaystyle & & \displaystyle \quad =-M\unicode[STIX]{x1D700}^{2}\frac{U_{x}^{2}h^{2}}{2}-d.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}\left(\unicode[STIX]{x1D702}\left(\frac{\bar{u}^{2}}{2}+\frac{e}{2}+\frac{\unicode[STIX]{x1D702}+2h}{2}\right)+h\left(\frac{U^{2}}{2}+\unicode[STIX]{x1D700}^{2}\frac{U_{x}^{2}}{6}h^{2}+\frac{h}{2}\right)\right)\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x}\left(\unicode[STIX]{x1D702}\bar{u}\left(\frac{\bar{u}^{2}}{2}+\frac{e}{2}+\frac{\unicode[STIX]{x1D702}+2h}{2}\right)+\left(\unicode[STIX]{x1D702}e+\frac{\unicode[STIX]{x1D702}^{2}}{2}\right)\bar{u}\right.\nonumber\\ \displaystyle & & \displaystyle \left.\qquad +\,hU\left(\frac{U^{2}}{2}+\unicode[STIX]{x1D700}^{2}\frac{U_{x}^{2}}{6}h^{2}+\frac{h}{2}\right)+U\int _{0}^{h}p\,\text{d}z\right)\nonumber\\ \displaystyle & & \displaystyle \quad =-M\unicode[STIX]{x1D700}^{2}\frac{U_{x}^{2}h^{2}}{2}-d.\end{eqnarray}$$
Since
![]() $M>0$
(the thickness of the upper layer is increasing because of the mixing) and
$M>0$
(the thickness of the upper layer is increasing because of the mixing) and
![]() $d>0$
, the total energy is decreasing.
$d>0$
, the total energy is decreasing.
2.4 An equivalent form of the momentum equation for the lower layer
The flux in the momentum equation (2.53) for the lower layer contains the higher-order derivatives of the velocity
![]() $U$
. It appears that for numerical purposes the following new variable
$U$
. It appears that for numerical purposes the following new variable
is more convenient for the model formulation. The variable
![]() $K$
is nothing but the tangential velocity along the free surface (cf. Gavrilyuk & Teshukov Reference Gavrilyuk and Teshukov2001; Bardos & Lannes Reference Bardos and Lannes2012; Gavrilyuk et al.
Reference Gavrilyuk, Kalisch and Khorsand2015). For this, we replace the momentum equation by an equivalent equation (for proof see appendix B):
$K$
is nothing but the tangential velocity along the free surface (cf. Gavrilyuk & Teshukov Reference Gavrilyuk and Teshukov2001; Bardos & Lannes Reference Bardos and Lannes2012; Gavrilyuk et al.
Reference Gavrilyuk, Kalisch and Khorsand2015). For this, we replace the momentum equation by an equivalent equation (for proof see appendix B):
In the case where the mixing is absent (
![]() $M=0$
), this equation is reduced to the conservative one:
$M=0$
), this equation is reduced to the conservative one:
2.5 Production of the turbulent energy
An evolution equation for the turbulent energy
![]() $e$
in the upper layer can also be obtained. Consider the subsystem for the upper layer (2.49)–(2.51). Using the equations of mass (2.49) and momentum (2.50), one can obtain from (2.51):
$e$
in the upper layer can also be obtained. Consider the subsystem for the upper layer (2.49)–(2.51). Using the equations of mass (2.49) and momentum (2.50), one can obtain from (2.51):
This is equivalent to
which implies that
For numerics, a conservative equation for
![]() $q$
will be used. Replacing
$q$
will be used. Replacing
![]() $e$
by
$e$
by
![]() $q^{2}$
and using the equation for
$q^{2}$
and using the equation for
![]() $\unicode[STIX]{x1D702}$
, one can derive a conservative equation for
$\unicode[STIX]{x1D702}$
, one can derive a conservative equation for
![]() $q=\sqrt{e}$
:
$q=\sqrt{e}$
:
2.6 Flow over topography
The derivation of the governing equations for the flow over topography is analogous. However, the final system contains second-order material derivatives of
![]() $b$
along the mean velocity of the lower layer. The equations can be simplified considerably under the following assumption. Let the dimensionless bottom variation be weak:
$b$
along the mean velocity of the lower layer. The equations can be simplified considerably under the following assumption. Let the dimensionless bottom variation be weak:
![]() $z=b(\unicode[STIX]{x1D700}^{\unicode[STIX]{x1D6FC}}x),\unicode[STIX]{x1D6FC}>0$
. Then one can obviously neglect the terms containing second-order material derivatives of
$z=b(\unicode[STIX]{x1D700}^{\unicode[STIX]{x1D6FC}}x),\unicode[STIX]{x1D6FC}>0$
. Then one can obviously neglect the terms containing second-order material derivatives of
![]() $b$
and keep in the right-hand side of the dimensionless momentum equation for the upper layer only the term
$b$
and keep in the right-hand side of the dimensionless momentum equation for the upper layer only the term
![]() $-\unicode[STIX]{x1D702}b_{x}$
, and in the dimensionless equation for
$-\unicode[STIX]{x1D702}b_{x}$
, and in the dimensionless equation for
![]() $K$
the term
$K$
the term
![]() $-b_{x}$
. Such a mild slope approximation was used, for example, in Serre (Reference Serre1953) and Liapidevskii and Gavrilova (Reference Liapidevskii and Gavrilova2008).
$-b_{x}$
. Such a mild slope approximation was used, for example, in Serre (Reference Serre1953) and Liapidevskii and Gavrilova (Reference Liapidevskii and Gavrilova2008).
3 Stationary solutions for a flat bottom
The governing equations (2.49)–(2.53) are Galilean invariant. The study of travelling wave solutions is thus equivalent to the study of stationary solutions. We denote by ‘prime’ the derivative with respect to
![]() $x$
. Continuous stationary solutions written in dimensional form satisfy the equations:
$x$
. Continuous stationary solutions written in dimensional form satisfy the equations:
with
The normal form of (3.1)–(3.3) is
 $$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\displaystyle \unicode[STIX]{x1D702}^{\prime }=\frac{1}{\unicode[STIX]{x1D6E5}}\left(\unicode[STIX]{x1D70E}q\left(2\bar{u}-U+\frac{1}{\bar{u}}((U-\bar{u})^{2}-(3+\unicode[STIX]{x1D705})q^{2})\right)+g\unicode[STIX]{x1D702}h^{\prime }\right),\\ \displaystyle \bar{u}^{\prime }=\frac{\unicode[STIX]{x1D70E}q-\bar{u}\unicode[STIX]{x1D702}^{\prime }}{\unicode[STIX]{x1D702}},\quad U^{\prime }=W,\quad W^{\prime }=Z,\end{array}\right\} & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\displaystyle \unicode[STIX]{x1D702}^{\prime }=\frac{1}{\unicode[STIX]{x1D6E5}}\left(\unicode[STIX]{x1D70E}q\left(2\bar{u}-U+\frac{1}{\bar{u}}((U-\bar{u})^{2}-(3+\unicode[STIX]{x1D705})q^{2})\right)+g\unicode[STIX]{x1D702}h^{\prime }\right),\\ \displaystyle \bar{u}^{\prime }=\frac{\unicode[STIX]{x1D70E}q-\bar{u}\unicode[STIX]{x1D702}^{\prime }}{\unicode[STIX]{x1D702}},\quad U^{\prime }=W,\quad W^{\prime }=Z,\end{array}\right\} & & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\displaystyle Z^{\prime }=\frac{3}{Uh^{2}}\left(UW+g(h^{\prime }+\unicode[STIX]{x1D702}^{\prime })+\frac{h^{2}}{3}WZ-h(UZ-W^{2})h^{\prime }\right),\\ \displaystyle q^{\prime }=\frac{1}{2\unicode[STIX]{x1D702}\bar{u}}\{\unicode[STIX]{x1D70E}((U-\bar{u})^{2}-(3+\unicode[STIX]{x1D705})q^{2})+2q\bar{u}\unicode[STIX]{x1D702}^{\prime }\}.\end{array}\right\} & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\displaystyle Z^{\prime }=\frac{3}{Uh^{2}}\left(UW+g(h^{\prime }+\unicode[STIX]{x1D702}^{\prime })+\frac{h^{2}}{3}WZ-h(UZ-W^{2})h^{\prime }\right),\\ \displaystyle q^{\prime }=\frac{1}{2\unicode[STIX]{x1D702}\bar{u}}\{\unicode[STIX]{x1D70E}((U-\bar{u})^{2}-(3+\unicode[STIX]{x1D705})q^{2})+2q\bar{u}\unicode[STIX]{x1D702}^{\prime }\}.\end{array}\right\} & & \displaystyle\end{eqnarray}$$
Here
The ‘true’ normal form is obtained by replacing the derivatives
![]() $\unicode[STIX]{x1D702}^{\prime }$
and
$\unicode[STIX]{x1D702}^{\prime }$
and
![]() $h^{\prime }$
by the corresponding algebraic relations. To avoid cumbersome expressions, we will present only a reduced form (3.5)–(3.7). The variables describing the lower dispersive layer (
$h^{\prime }$
by the corresponding algebraic relations. To avoid cumbersome expressions, we will present only a reduced form (3.5)–(3.7). The variables describing the lower dispersive layer (
![]() $U$
and
$U$
and
![]() $h$
) are always continuous in the flow. However, the variables describing the upper turbulent layer may be discontinuous when the supercritical–subcritical transition occurs. If the stationary solution is discontinuous, the following Rankine–Hugoniot relations for the upper layer are satisfied:
$h$
) are always continuous in the flow. However, the variables describing the upper turbulent layer may be discontinuous when the supercritical–subcritical transition occurs. If the stationary solution is discontinuous, the following Rankine–Hugoniot relations for the upper layer are satisfied:
Here the square brackets mean the jump of the corresponding quantities. Relations (3.9) represent conservation of mass, momentum and energy in the upper layer. Also, the momentum equation for the lower layer implies that
Here we used the continuity of
![]() $h$
,
$h$
,
![]() $U$
and
$U$
and
![]() $U^{\prime }$
at the shock. Formula (3.10) gives us the jump of the second derivative
$U^{\prime }$
at the shock. Formula (3.10) gives us the jump of the second derivative
![]() $U^{\prime \prime }$
at the shock. The jump is not zero because the jump of
$U^{\prime \prime }$
at the shock. The jump is not zero because the jump of
![]() $\unicode[STIX]{x1D702}$
is non-vanishing.
$\unicode[STIX]{x1D702}$
is non-vanishing.
We are looking for stationary solutions of (3.5)–(3.7) having supercritical constant potential flow as
![]() $x\rightarrow -\infty$
:
$x\rightarrow -\infty$
:
The flow is potential at negative infinity, so the upper turbulent layer and the corresponding turbulent energy are vanishing. To construct such a solution, it is necessary first to understand the asymptotic behaviour of the supercritical solution at negative infinity. Linearizing the equations for the total mass and momentum of the lower layer, we obtain
Eliminating
![]() $\tilde{h}^{\prime }+\tilde{\unicode[STIX]{x1D702}}^{\prime }$
we get the equation for
$\tilde{h}^{\prime }+\tilde{\unicode[STIX]{x1D702}}^{\prime }$
we get the equation for
![]() $\tilde{U}$
:
$\tilde{U}$
:
Here and below, the ‘tilde’ symbol stands for perturbations:
This implies that, as
![]() $x\rightarrow -\infty$
, the solution in the lower layer behaves asymptotically as the solution of the Green–Naghdi equations:
$x\rightarrow -\infty$
, the solution in the lower layer behaves asymptotically as the solution of the Green–Naghdi equations:
where
![]() $\hat{U}$
is a constant amplitude. Perturbations (nonlinear) for the upper-layer variables satisfy the following equations:
$\hat{U}$
is a constant amplitude. Perturbations (nonlinear) for the upper-layer variables satisfy the following equations:
Looking for the solutions that vanish at negative infinity in the form
we obtain the following expressions for the unknown amplitudes (denoted with the ‘hat’ symbol):
The minus sign in the expression for
![]() $\hat{q}$
occurs because
$\hat{q}$
occurs because
![]() $\hat{U} <0$
. Also, it is interesting to note that, in this case,
$\hat{U} <0$
. Also, it is interesting to note that, in this case,
because
![]() $F^{2}>1$
. This means that at the beginning of mixing the velocity in the upper layer is larger than the velocity in the lower layer. Asymptotic expressions (3.19) were used when the conditions at negative infinity are imposed in the numerical treatment of the stationary system. We used MATHEMATICA (edition 10.1) to solve system (3.5)–(3.7).
$F^{2}>1$
. This means that at the beginning of mixing the velocity in the upper layer is larger than the velocity in the lower layer. Asymptotic expressions (3.19) were used when the conditions at negative infinity are imposed in the numerical treatment of the stationary system. We used MATHEMATICA (edition 10.1) to solve system (3.5)–(3.7).
3.1 The structure of stationary solutions
The mixing process is dissipative, so the stationary solution is rather an undular bore, and not a sequence of solitary (or periodic) waves. The upper layer develops quite slowly if the flow is supercritical everywhere (the determinant (3.8) is positive). A typical flow picture is shown in figure 2.

Figure 2. A typical supercritical stationary flow for Froude number
![]() $F=1.2$
. The lower boundary separates potential and turbulent layers. The mixing region of thickness
$F=1.2$
. The lower boundary separates potential and turbulent layers. The mixing region of thickness
![]() $\unicode[STIX]{x1D702}$
is gradually increasing. The parameters are as follows:
$\unicode[STIX]{x1D702}$
is gradually increasing. The parameters are as follows:
![]() $H_{0}=0.1~\text{m}$
,
$H_{0}=0.1~\text{m}$
,
![]() $U_{0}=1.19~\text{m}~\text{s}^{-1}$
,
$U_{0}=1.19~\text{m}~\text{s}^{-1}$
,
![]() $g=9.81~\text{m}~\text{s}^{-2}$
,
$g=9.81~\text{m}~\text{s}^{-2}$
,
![]() $\unicode[STIX]{x1D70E}=0.15$
and
$\unicode[STIX]{x1D70E}=0.15$
and
![]() $\unicode[STIX]{x1D705}=0$
.
$\unicode[STIX]{x1D705}=0$
.
There exists a critical Froude number
![]() $F_{\star }$
such that the flow becomes critical (the determinant (3.8) vanishes) at the crest of the leading wave. This value can easily be determined numerically. For example,
$F_{\star }$
such that the flow becomes critical (the determinant (3.8) vanishes) at the crest of the leading wave. This value can easily be determined numerically. For example,
![]() $F_{\star }\approx 1.338$
for
$F_{\star }\approx 1.338$
for
![]() $\unicode[STIX]{x1D705}=0$
.
$\unicode[STIX]{x1D705}=0$
.
One can also find another critical value
![]() $F_{\star \star }$
for which the determinant vanishes at the crest of the second wave. For example,
$F_{\star \star }$
for which the determinant vanishes at the crest of the second wave. For example,
![]() $F_{\star \star }\approx 1.283$
for
$F_{\star \star }\approx 1.283$
for
![]() $\unicode[STIX]{x1D705}=0$
. A sequence of the corresponding critical values can thus be constructed. The smaller the Froude number (but always larger than one), the larger is the domain where the solution is supercritical. The critical Froude numbers increase with increasing
$\unicode[STIX]{x1D705}=0$
. A sequence of the corresponding critical values can thus be constructed. The smaller the Froude number (but always larger than one), the larger is the domain where the solution is supercritical. The critical Froude numbers increase with increasing
![]() $\unicode[STIX]{x1D705}$
. For example, for
$\unicode[STIX]{x1D705}$
. For example, for
![]() $\unicode[STIX]{x1D705}=3$
, one has
$\unicode[STIX]{x1D705}=3$
, one has
![]() $F_{\star }\approx 1.3832$
and
$F_{\star }\approx 1.3832$
and
![]() $F_{\star \star }\approx 1.3201$
.
$F_{\star \star }\approx 1.3201$
.
When the supercritical–subcritical transition happens, i.e. the determinant (3.8) changes sign from positive to negative, the solution may contain a jump of the variables of the upper turbulent layer. The thickness of the upper layer in the subcritical local zone will rapidly increase with increasing distance downstream because of the mixing process. The pressure distribution approaches the hydrostatic one because the turbulent layer will expand. The transition can occur not necessarily at the leading wave, but, for example, at the second wave. Physically, this corresponds to a possibility of the roller appearance at the second wave of the wave train, and not at the first one. This fact was observed, in particular, in the experiments by Ryabenko (Reference Ryabenko1990) performed in a wide channel. The wide channel experiments correspond better to our modelling because the sidewall effects can be neglected. For narrow channels, the sidewall effects are dominant, and the roller appears first always at the leading wave (see the classification of the flow patterns for undular hydraulic jumps in Chanson & Montes (Reference Chanson and Montes1995)).
Now we will show how to construct another solution containing a jump riding down the forward slope of the leading wave even for
![]() $F<F_{\star }$
. The construction of such a solution can be done as follows. Take any Froude number
$F<F_{\star }$
. The construction of such a solution can be done as follows. Take any Froude number
![]() $F<F_{\star }$
. We put the jump at a point
$F<F_{\star }$
. We put the jump at a point
![]() $x=x_{0}$
, which should be properly chosen. For given values
$x=x_{0}$
, which should be properly chosen. For given values
![]() $\unicode[STIX]{x1D702}_{0}=\unicode[STIX]{x1D702}(x_{0})$
,
$\unicode[STIX]{x1D702}_{0}=\unicode[STIX]{x1D702}(x_{0})$
,
![]() $\bar{u}_{0}=\bar{u}(x_{0})$
and
$\bar{u}_{0}=\bar{u}(x_{0})$
and
![]() $q_{0}=q(x_{0})$
, one can use the Rankine–Hugoniot relations (3.9):
$q_{0}=q(x_{0})$
, one can use the Rankine–Hugoniot relations (3.9):
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle \unicode[STIX]{x1D702}\bar{u}=\unicode[STIX]{x1D702}_{0}\bar{u}_{0}=Q,\quad \unicode[STIX]{x1D702}\bar{u}^{2}+\unicode[STIX]{x1D702}q^{2}+\frac{g}{2}\unicode[STIX]{x1D702}^{2}=\unicode[STIX]{x1D702}_{0}{\bar{u}_{0}}^{2}+\unicode[STIX]{x1D702}_{0}q_{0}^{2}+\frac{g}{2}\unicode[STIX]{x1D702}_{0}^{2},\\ \displaystyle \frac{\bar{u}^{2}}{2}+\frac{3}{2}q^{2}+g\unicode[STIX]{x1D702}=\frac{\bar{u}_{0}^{2}}{2}+\frac{3}{2}q_{0}^{2}+g\unicode[STIX]{x1D702}_{0}.\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle \unicode[STIX]{x1D702}\bar{u}=\unicode[STIX]{x1D702}_{0}\bar{u}_{0}=Q,\quad \unicode[STIX]{x1D702}\bar{u}^{2}+\unicode[STIX]{x1D702}q^{2}+\frac{g}{2}\unicode[STIX]{x1D702}^{2}=\unicode[STIX]{x1D702}_{0}{\bar{u}_{0}}^{2}+\unicode[STIX]{x1D702}_{0}q_{0}^{2}+\frac{g}{2}\unicode[STIX]{x1D702}_{0}^{2},\\ \displaystyle \frac{\bar{u}^{2}}{2}+\frac{3}{2}q^{2}+g\unicode[STIX]{x1D702}=\frac{\bar{u}_{0}^{2}}{2}+\frac{3}{2}q_{0}^{2}+g\unicode[STIX]{x1D702}_{0}.\end{array}\right\}\end{eqnarray}$$
Eliminating the velocities, one can obtain a quadratic equation for the layer thickness after the jump:
The equation has two positive roots. Only one of them (the minimal one), having the property
![]() $\unicode[STIX]{x1D702}<2\unicode[STIX]{x1D702}_{0}$
, must be chosen (see the discussion in Richard & Gavrilyuk (Reference Richard and Gavrilyuk2012)). Since the value of
$\unicode[STIX]{x1D702}<2\unicode[STIX]{x1D702}_{0}$
, must be chosen (see the discussion in Richard & Gavrilyuk (Reference Richard and Gavrilyuk2012)). Since the value of
![]() $\unicode[STIX]{x1D702}_{0}$
is almost negligible, the jump of
$\unicode[STIX]{x1D702}_{0}$
is almost negligible, the jump of
![]() $\unicode[STIX]{x1D702}$
is almost invisible. However, the corresponding turbulent energy considerably increases. The flow in the turbulent region becomes subcritical. The thickness of the turbulent layer increases, the flow in this layer decelerates and the determinant (3.8) in the equation for
$\unicode[STIX]{x1D702}$
is almost invisible. However, the corresponding turbulent energy considerably increases. The flow in the turbulent region becomes subcritical. The thickness of the turbulent layer increases, the flow in this layer decelerates and the determinant (3.8) in the equation for
![]() $\unicode[STIX]{x1D702}$
vanishes at some point
$\unicode[STIX]{x1D702}$
vanishes at some point
![]() $x=x_{1}$
. If at the same point the numerator vanishes, the solution can be extended again to the supercritical regime for
$x=x_{1}$
. If at the same point the numerator vanishes, the solution can be extended again to the supercritical regime for
![]() $x>x_{1}$
. The value of
$x>x_{1}$
. The value of
![]() $x=x_{0}$
can always be chosen, and thus a new solution containing a local subcritical zone between
$x=x_{0}$
can always be chosen, and thus a new solution containing a local subcritical zone between
![]() $x_{0}$
and
$x_{0}$
and
![]() $x_{1}$
can be constructed. Such a new solution is shown in figure 3 for the Froude number
$x_{1}$
can be constructed. Such a new solution is shown in figure 3 for the Froude number
![]() $F=1.2$
. The local subcritical zone can be associated with wave breaking.
$F=1.2$
. The local subcritical zone can be associated with wave breaking.
It is interesting to note that the local wavelength of the stationary wave train strongly decreases with increasing distance downstream. This is in accordance with the experimental observations of Lemoine (Reference Lemoine1948, p. 185). In particular, he commented on this fact: que l’on voit
![]() $\unicode[STIX]{x1D706}$
décroître en s’éloignant du front d’onde [we see that
$\unicode[STIX]{x1D706}$
décroître en s’éloignant du front d’onde [we see that
![]() $\unicode[STIX]{x1D706}$
decreases away from the wavefront]. Here
$\unicode[STIX]{x1D706}$
decreases away from the wavefront]. Here
![]() $\unicode[STIX]{x1D706}$
denotes the wavelength. A physical explanation of this fact is the following. The appearance of a localized subcritical turbulent region is a highly dissipative phenomenon. It intensifies the mixing process and thus leads to a drastic decrease of the amplitude and wavelength.
$\unicode[STIX]{x1D706}$
denotes the wavelength. A physical explanation of this fact is the following. The appearance of a localized subcritical turbulent region is a highly dissipative phenomenon. It intensifies the mixing process and thus leads to a drastic decrease of the amplitude and wavelength.

Figure 3. A new supercritical–subcritical stationary solution for Froude number
![]() $F=1.2$
. The subcritical turbulent region rapidly increases after the jump. The flow continuously passes to the supercritical regime. The flow parameters are as follows:
$F=1.2$
. The subcritical turbulent region rapidly increases after the jump. The flow continuously passes to the supercritical regime. The flow parameters are as follows:
![]() $H_{0}=0.1~\text{m}$
,
$H_{0}=0.1~\text{m}$
,
![]() $U_{0}=1.19~\text{m}~\text{s}^{-1}$
,
$U_{0}=1.19~\text{m}~\text{s}^{-1}$
,
![]() $g=9.81~\text{m}~\text{s}^{-2}$
,
$g=9.81~\text{m}~\text{s}^{-2}$
,
![]() $\unicode[STIX]{x1D70E}=0.15$
and
$\unicode[STIX]{x1D70E}=0.15$
and
![]() $\unicode[STIX]{x1D705}=0$
. The supercritical–subcritical transition is at the point
$\unicode[STIX]{x1D705}=0$
. The supercritical–subcritical transition is at the point
![]() $x_{0}\approx -0.124$
; the subcritical–supercritical transition is at the point
$x_{0}\approx -0.124$
; the subcritical–supercritical transition is at the point
![]() $x_{1}\approx 0.025$
.
$x_{1}\approx 0.025$
.
These two solutions have completely different properties. The first one, without the jump, has long modulations and quite narrow mixing region (figure 2). The second one, with the jump, has shorter modulations at the same space interval, smaller amplitude and thicker mixing zone (see figure 3). The same boundary conditions at negative infinity can thus produce completely different stationary solutions. Such a non-uniqueness of the stationary solutions is often associated with the hysteresis phenomenon, where one or another solution can appear through non-stationary scenarios.
The model also contains a criterion of wave breaking, which is characterized by the Froude number between
![]() $1.3$
and
$1.3$
and
![]() $1.4$
depending on the energy dissipation parameter
$1.4$
depending on the energy dissipation parameter
![]() $\unicode[STIX]{x1D705}$
. An interesting feature of this model is the possibility of existence of a local subcritical zone
$\unicode[STIX]{x1D705}$
. An interesting feature of this model is the possibility of existence of a local subcritical zone
![]() $[x_{0},x_{1}]$
, which can be associated with wave breaking. The non-stationary wave breaking will be studied in the next sections.
$[x_{0},x_{1}]$
, which can be associated with wave breaking. The non-stationary wave breaking will be studied in the next sections.
4 Applications to non-stationary problems
4.1 Numerical method
For numerical treatment, the following dimensional form of the governing equations is used:
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}{\unicode[STIX]{x2202}t}+\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x}(\unicode[STIX]{x1D702}\bar{u})=\unicode[STIX]{x1D70E}q,\quad \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}(h+\unicode[STIX]{x1D702})+\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x}(hU+\unicode[STIX]{x1D702}\bar{u})=0,\\ \displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}(\unicode[STIX]{x1D702}\bar{u})+\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x}\left((\bar{u}^{2}+q^{2})\unicode[STIX]{x1D702}+\frac{g\unicode[STIX]{x1D702}^{2}}{2}\right)=\unicode[STIX]{x1D70E}qU+\unicode[STIX]{x1D6FC}_{1},\\ \displaystyle \frac{\unicode[STIX]{x2202}q}{\unicode[STIX]{x2202}t}+\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x}(q\bar{u})=\frac{\unicode[STIX]{x1D70E}}{2\unicode[STIX]{x1D702}}((U-\bar{u})^{2}-(1+\unicode[STIX]{x1D705})q^{2}),\\ \displaystyle \frac{\unicode[STIX]{x2202}K}{\unicode[STIX]{x2202}t}+\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x}\left(KU+g(h+\unicode[STIX]{x1D702})-\frac{U^{2}}{2}+\unicode[STIX]{x1D6FC}_{2}\right)=\unicode[STIX]{x1D70E}q\left(\frac{K-U}{h}+\unicode[STIX]{x1D6FC}_{3}\right)-gb_{x},\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D702}}{\unicode[STIX]{x2202}t}+\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x}(\unicode[STIX]{x1D702}\bar{u})=\unicode[STIX]{x1D70E}q,\quad \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}(h+\unicode[STIX]{x1D702})+\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x}(hU+\unicode[STIX]{x1D702}\bar{u})=0,\\ \displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}(\unicode[STIX]{x1D702}\bar{u})+\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x}\left((\bar{u}^{2}+q^{2})\unicode[STIX]{x1D702}+\frac{g\unicode[STIX]{x1D702}^{2}}{2}\right)=\unicode[STIX]{x1D70E}qU+\unicode[STIX]{x1D6FC}_{1},\\ \displaystyle \frac{\unicode[STIX]{x2202}q}{\unicode[STIX]{x2202}t}+\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x}(q\bar{u})=\frac{\unicode[STIX]{x1D70E}}{2\unicode[STIX]{x1D702}}((U-\bar{u})^{2}-(1+\unicode[STIX]{x1D705})q^{2}),\\ \displaystyle \frac{\unicode[STIX]{x2202}K}{\unicode[STIX]{x2202}t}+\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x}\left(KU+g(h+\unicode[STIX]{x1D702})-\frac{U^{2}}{2}+\unicode[STIX]{x1D6FC}_{2}\right)=\unicode[STIX]{x1D70E}q\left(\frac{K-U}{h}+\unicode[STIX]{x1D6FC}_{3}\right)-gb_{x},\end{array}\right\}\end{eqnarray}$$
where
and the velocity
![]() $U$
is determined by the equation
$U$
is determined by the equation
For a given
![]() $K$
, equation (4.3) is an ordinary differential equation for
$K$
, equation (4.3) is an ordinary differential equation for
![]() $U$
. The function
$U$
. The function
![]() $z=b(x)$
defines the bottom variation;
$z=b(x)$
defines the bottom variation;
![]() $\unicode[STIX]{x1D70E}$
and
$\unicode[STIX]{x1D70E}$
and
![]() $\unicode[STIX]{x1D705}$
are constants. The preceding system (4.1) can be written in conservative form as
$\unicode[STIX]{x1D705}$
are constants. The preceding system (4.1) can be written in conservative form as
where
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle \boldsymbol{u}=(\unicode[STIX]{x1D702},\,h+\unicode[STIX]{x1D702},\,\unicode[STIX]{x1D702}\bar{u},\,q,\,K)^{\text{T}},\\ \displaystyle \boldsymbol{f}=\left(\unicode[STIX]{x1D702}\bar{u},\,hU+\unicode[STIX]{x1D702}\bar{u},\,(\bar{u}^{2}+q^{2})\unicode[STIX]{x1D702}+\frac{g\unicode[STIX]{x1D702}^{2}}{2},q\bar{u},KU+g(h+\unicode[STIX]{x1D702})-\frac{U^{2}}{2}+\unicode[STIX]{x1D6FC}_{2}\right)^{\text{T}},\\ \displaystyle \boldsymbol{g}=\left(\unicode[STIX]{x1D70E}q,\,0,\,\unicode[STIX]{x1D70E}qU+\unicode[STIX]{x1D6FC}_{1},\,\frac{\unicode[STIX]{x1D70E}}{2\unicode[STIX]{x1D702}}((U-\bar{u})^{2}-(1+\unicode[STIX]{x1D705})q^{2}),\,\unicode[STIX]{x1D70E}q\left(\frac{K-U}{h}+\unicode[STIX]{x1D6FC}_{3}\right)-gb_{x}\right)^{\text{T}}.\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle \boldsymbol{u}=(\unicode[STIX]{x1D702},\,h+\unicode[STIX]{x1D702},\,\unicode[STIX]{x1D702}\bar{u},\,q,\,K)^{\text{T}},\\ \displaystyle \boldsymbol{f}=\left(\unicode[STIX]{x1D702}\bar{u},\,hU+\unicode[STIX]{x1D702}\bar{u},\,(\bar{u}^{2}+q^{2})\unicode[STIX]{x1D702}+\frac{g\unicode[STIX]{x1D702}^{2}}{2},q\bar{u},KU+g(h+\unicode[STIX]{x1D702})-\frac{U^{2}}{2}+\unicode[STIX]{x1D6FC}_{2}\right)^{\text{T}},\\ \displaystyle \boldsymbol{g}=\left(\unicode[STIX]{x1D70E}q,\,0,\,\unicode[STIX]{x1D70E}qU+\unicode[STIX]{x1D6FC}_{1},\,\frac{\unicode[STIX]{x1D70E}}{2\unicode[STIX]{x1D702}}((U-\bar{u})^{2}-(1+\unicode[STIX]{x1D705})q^{2}),\,\unicode[STIX]{x1D70E}q\left(\frac{K-U}{h}+\unicode[STIX]{x1D6FC}_{3}\right)-gb_{x}\right)^{\text{T}}.\end{array}\right\}\end{eqnarray}$$
Following Le Metayer et al. (Reference Le Metayer, Gavrilyuk and Hank2010), we divide the numerical resolution of system (4.1) into three successive steps:
-
(1) the numerical approximations of the terms
 $\unicode[STIX]{x1D6FC}_{i},\;i=1,2,3$
, containing spatial derivatives (see relations (4.2));
$\unicode[STIX]{x1D6FC}_{i},\;i=1,2,3$
, containing spatial derivatives (see relations (4.2)); -
(2) the time evolution of the conservative variables
 $\boldsymbol{u}$
using the method based on modification of Godunov’s scheme; and
$\boldsymbol{u}$
using the method based on modification of Godunov’s scheme; and -
(3) the resolution of the ordinary differential equation (4.3) to obtain the values of velocity
 $U$
from variables
$U$
from variables
 $h$
and
$h$
and
 $K$
.
$K$
.
To solve the differential balance laws (4.4) numerically, we implement here the Nessyahu & Tadmor (Reference Nessyahu and Tadmor1990) second-order central scheme (see also Russo Reference Russo, Rionero and Romano2005):
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\begin{array}{@{}c@{}}\displaystyle \boldsymbol{u}_{j}^{n+1/2}=\boldsymbol{u}_{j}^{n}-\unicode[STIX]{x1D6EC}\boldsymbol{f}_{j}^{\prime }/2+\boldsymbol{g}(\boldsymbol{u}_{j}^{n})\unicode[STIX]{x0394}t/2\quad (\unicode[STIX]{x1D6EC}=\unicode[STIX]{x0394}t/\unicode[STIX]{x0394}x),\end{array}\\ \begin{array}{@{}rcl@{}}\displaystyle \boldsymbol{u}_{j+1/2}^{n+1}\, & =\, & (\boldsymbol{u}_{j}^{n}+\boldsymbol{u}_{j+1}^{n})/2+(\boldsymbol{u}_{j}^{\prime }-\boldsymbol{u}_{j+1}^{\prime })/8-\unicode[STIX]{x1D6EC}(\boldsymbol{f}(\boldsymbol{u}_{j+1}^{n+1/2})-\boldsymbol{f}(\boldsymbol{u}_{j}^{n+1/2}))\\ \displaystyle \, & \, & +\,(\boldsymbol{g}(\boldsymbol{u}_{j}^{n})+\boldsymbol{g}(\boldsymbol{u}_{j+1}^{n}))\unicode[STIX]{x0394}t/2.\end{array}\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\begin{array}{@{}c@{}}\displaystyle \boldsymbol{u}_{j}^{n+1/2}=\boldsymbol{u}_{j}^{n}-\unicode[STIX]{x1D6EC}\boldsymbol{f}_{j}^{\prime }/2+\boldsymbol{g}(\boldsymbol{u}_{j}^{n})\unicode[STIX]{x0394}t/2\quad (\unicode[STIX]{x1D6EC}=\unicode[STIX]{x0394}t/\unicode[STIX]{x0394}x),\end{array}\\ \begin{array}{@{}rcl@{}}\displaystyle \boldsymbol{u}_{j+1/2}^{n+1}\, & =\, & (\boldsymbol{u}_{j}^{n}+\boldsymbol{u}_{j+1}^{n})/2+(\boldsymbol{u}_{j}^{\prime }-\boldsymbol{u}_{j+1}^{\prime })/8-\unicode[STIX]{x1D6EC}(\boldsymbol{f}(\boldsymbol{u}_{j+1}^{n+1/2})-\boldsymbol{f}(\boldsymbol{u}_{j}^{n+1/2}))\\ \displaystyle \, & \, & +\,(\boldsymbol{g}(\boldsymbol{u}_{j}^{n})+\boldsymbol{g}(\boldsymbol{u}_{j+1}^{n}))\unicode[STIX]{x0394}t/2.\end{array}\end{array}\right\}\end{eqnarray}$$
Here
![]() $\boldsymbol{u}_{j}^{n}=\boldsymbol{u}(t^{n},x_{j})$
,
$\boldsymbol{u}_{j}^{n}=\boldsymbol{u}(t^{n},x_{j})$
,
![]() $\unicode[STIX]{x0394}x$
is the spatial grid spacing and
$\unicode[STIX]{x0394}x$
is the spatial grid spacing and
![]() $\unicode[STIX]{x0394}t$
is the time step satisfying the Courant condition, defined by the velocity of characteristics of the dispersionless part of the model. The computational domain on the
$\unicode[STIX]{x0394}t$
is the time step satisfying the Courant condition, defined by the velocity of characteristics of the dispersionless part of the model. The computational domain on the
![]() $x$
axis is divided into
$x$
axis is divided into
![]() $N$
cells, the cell centres being denoted by
$N$
cells, the cell centres being denoted by
![]() $x_{j}$
. Values
$x_{j}$
. Values
![]() $\boldsymbol{u}_{j}^{\prime }/\unicode[STIX]{x0394}x$
and
$\boldsymbol{u}_{j}^{\prime }/\unicode[STIX]{x0394}x$
and
![]() $\boldsymbol{f}_{j}^{\prime }/\unicode[STIX]{x0394}x$
are approximations of the first-order derivatives with respect to
$\boldsymbol{f}_{j}^{\prime }/\unicode[STIX]{x0394}x$
are approximations of the first-order derivatives with respect to
![]() $x$
, calculated according to the ‘MinMod’ procedure. At
$x$
, calculated according to the ‘MinMod’ procedure. At
![]() $t=0$
the initial data
$t=0$
the initial data
![]() $\boldsymbol{u}_{j}^{0}$
are specified. The boundary conditions
$\boldsymbol{u}_{j}^{0}$
are specified. The boundary conditions
![]() $\boldsymbol{u}_{1-k}^{n}$
and
$\boldsymbol{u}_{1-k}^{n}$
and
![]() $\boldsymbol{u}_{N+k}^{n}$
(
$\boldsymbol{u}_{N+k}^{n}$
(
![]() $k=1,2$
) should also be prescribed. Since the state
$k=1,2$
) should also be prescribed. Since the state
![]() $\boldsymbol{u}_{j}^{n}$
is known using formulae (4.6), one can obtain the conservative variable
$\boldsymbol{u}_{j}^{n}$
is known using formulae (4.6), one can obtain the conservative variable
![]() $\boldsymbol{u}$
at time
$\boldsymbol{u}$
at time
![]() $t^{n+1}$
. Scheme (4.6) does not require an exact or approximate solution of the Riemann problem, which is very convenient in our case, since system (4.1) includes five equations. It should be noted that other schemes (in particular, on non-staggered grids) based on the local Lax–Friedrichs flux are also appropriate here.
$t^{n+1}$
. Scheme (4.6) does not require an exact or approximate solution of the Riemann problem, which is very convenient in our case, since system (4.1) includes five equations. It should be noted that other schemes (in particular, on non-staggered grids) based on the local Lax–Friedrichs flux are also appropriate here.
The numerical estimation of the first-order derivatives of any function
![]() $\unicode[STIX]{x1D711}$
at
$\unicode[STIX]{x1D711}$
at
![]() $x=x_{j}$
is given by the following relation:
$x=x_{j}$
is given by the following relation:
This discretization is used to determine the terms
![]() $\unicode[STIX]{x1D6FC}_{i}$
in (4.2). As a result, we obtain the flux
$\unicode[STIX]{x1D6FC}_{i}$
in (4.2). As a result, we obtain the flux
![]() $\boldsymbol{f}_{j}^{n}$
at time
$\boldsymbol{f}_{j}^{n}$
at time
![]() $t^{n}$
.
$t^{n}$
.
The last ingredient concerns the determination of the velocity
![]() $U_{j}$
at the next time step when the vector of conservative variables
$U_{j}$
at the next time step when the vector of conservative variables
![]() $\boldsymbol{u}_{j}^{n+1}$
is known. Applying finite difference discretization (4.7), one can rewrite equation (4.3) in the following form:
$\boldsymbol{u}_{j}^{n+1}$
is known. Applying finite difference discretization (4.7), one can rewrite equation (4.3) in the following form:
where
All the variables in the preceding relation are those at time
![]() $t^{n+1}$
. As a consequence, the variables
$t^{n+1}$
. As a consequence, the variables
![]() $h_{j}$
and
$h_{j}$
and
![]() $K_{j}$
are known and come from the time evolution of conservative variables with the help of the numerical scheme presented above. The only unknowns are the terms
$K_{j}$
are known and come from the time evolution of conservative variables with the help of the numerical scheme presented above. The only unknowns are the terms
![]() $U_{j}$
at each node. Relations represent a tridiagonal system of linear equations that can be solved by a direct (Gauss) method. We apply here a simplified form of Gaussian elimination, which is known as the Thomas algorithm.
$U_{j}$
at each node. Relations represent a tridiagonal system of linear equations that can be solved by a direct (Gauss) method. We apply here a simplified form of Gaussian elimination, which is known as the Thomas algorithm.
The next section is devoted to numerical results obtained with the present method for different applications.
4.2 Water hammer problem with a free surface (Favre waves)
Pioneering experimental work concerning the development of undular bores was performed by Favre (Reference Favre1935), who studied their formation in long open channels due to a rapid opening or closing of a gate. Similar experiments with a detailed investigation of the formation of surge waves in open channels were performed by Treske (Reference Treske1994) and by Soares-Frazão & Zech (Reference Soares-Frazão and Zech2002). The analytical approach to the study of undular bores was developed in El, Grimshaw & Kamchatnov (Reference El, Grimshaw and Kamchatnov2005) and El, Grimshaw & Smyth (Reference El, Grimshaw and Smyth2006) within a framework of the Serre–Su–Gardner–Green–Naghdi equations (Serre Reference Serre1953; Su & Gardner Reference Su and Gardner1969; Green & Naghdi Reference Green and Naghdi1976). This problem was studied numerically in Soares-Frazão & Guinot (Reference Soares-Frazão and Guinot2008) and Tissier et al. (Reference Tissier, Bonneton, Marche, Chazel and Lannes2011). Laboratory experiments (Treske Reference Treske1994; Chanson Reference Chanson2009) showed that the wave Froude number
![]() $F$
, which is defined as
$F$
, which is defined as
controls the bore shape. In the supercritical regime (
![]() $F>1$
), undulations start developing at the bore front in the near-critical state (
$F>1$
), undulations start developing at the bore front in the near-critical state (
![]() $F\approx 1$
). However, when the Froude number is approximately between 1.3 and 1.4, the transition from an undular bore to a bore consisting of a steep front (breaking bore) occurs. Figure 4 shows a definition sketch for the Favre waves in the undular regime. Constants
$F\approx 1$
). However, when the Froude number is approximately between 1.3 and 1.4, the transition from an undular bore to a bore consisting of a steep front (breaking bore) occurs. Figure 4 shows a definition sketch for the Favre waves in the undular regime. Constants
![]() $U_{0}$
and
$U_{0}$
and
![]() $H_{0}$
are the upstream flow velocity and depth. In the following,
$H_{0}$
are the upstream flow velocity and depth. In the following,
![]() $D$
denotes the propagation speed of the wavefront;
$D$
denotes the propagation speed of the wavefront;
![]() $a_{m}$
represents the jump height; and
$a_{m}$
represents the jump height; and
![]() $a_{max}$
and
$a_{max}$
and
![]() $a_{min}$
are the maximum and minimum amplitude of the first wave. Below, we present some results related to the numerical modelling of Favre waves on the basis of (4.1)–(4.3) in the domain of Froude number between
$a_{min}$
are the maximum and minimum amplitude of the first wave. Below, we present some results related to the numerical modelling of Favre waves on the basis of (4.1)–(4.3) in the domain of Froude number between
![]() $1$
and
$1$
and
![]() $1.3$
corresponding to the domain of existence of the undular bore. We also demonstrate the transition from undular to purely breaking bores with increasing Froude number, and, in particular, compare numerical results for the first wave amplitude with experimental data (Treske Reference Treske1994).
$1.3$
corresponding to the domain of existence of the undular bore. We also demonstrate the transition from undular to purely breaking bores with increasing Froude number, and, in particular, compare numerical results for the first wave amplitude with experimental data (Treske Reference Treske1994).

Figure 4. Definition sketch for the Favre waves.
We perform calculations in dimensionless variables in the domain
![]() $x\in [0,100]$
for
$x\in [0,100]$
for
![]() $N=1000$
. We take here
$N=1000$
. We take here
![]() $g=1$
,
$g=1$
,
![]() $\unicode[STIX]{x1D70E}=0.15$
and
$\unicode[STIX]{x1D70E}=0.15$
and
![]() $\unicode[STIX]{x1D705}=3$
. To start the calculations, we specify the unknown variables
$\unicode[STIX]{x1D705}=3$
. To start the calculations, we specify the unknown variables
![]() $\boldsymbol{u}$
in the node points
$\boldsymbol{u}$
in the node points
![]() $x=x_{j}$
at
$x=x_{j}$
at
![]() $t=0$
as follows:
$t=0$
as follows:
![]() $\unicode[STIX]{x1D702}=0.01$
,
$\unicode[STIX]{x1D702}=0.01$
,
![]() $h+\unicode[STIX]{x1D702}=1$
,
$h+\unicode[STIX]{x1D702}=1$
,
![]() $\bar{u}=K=U_{0}$
and
$\bar{u}=K=U_{0}$
and
![]() $q=0$
. On the left boundary we assume that
$q=0$
. On the left boundary we assume that
![]() $\boldsymbol{u}_{1-k}^{n}=\boldsymbol{u}_{1}^{n}$
. These conditions allow us to calculate until the perturbations reach the boundary of the computational domain. To satisfy the impermeability condition (
$\boldsymbol{u}_{1-k}^{n}=\boldsymbol{u}_{1}^{n}$
. These conditions allow us to calculate until the perturbations reach the boundary of the computational domain. To satisfy the impermeability condition (
![]() $\bar{u}=U=0$
) on the right wall
$\bar{u}=U=0$
) on the right wall
![]() $x=100$
, we use the reflecting boundary conditions:
$x=100$
, we use the reflecting boundary conditions:
![]() $\boldsymbol{u}_{N+k}^{n}=\boldsymbol{u}_{N-k}^{n}$
except for variables
$\boldsymbol{u}_{N+k}^{n}=\boldsymbol{u}_{N-k}^{n}$
except for variables
![]() $\unicode[STIX]{x1D702}\bar{u}$
and
$\unicode[STIX]{x1D702}\bar{u}$
and
![]() $K$
which are treated as
$K$
which are treated as
![]() $(\unicode[STIX]{x1D702}\bar{u})_{N+k}^{n}=-(\unicode[STIX]{x1D702}\bar{u})_{N-k}^{n}$
and
$(\unicode[STIX]{x1D702}\bar{u})_{N+k}^{n}=-(\unicode[STIX]{x1D702}\bar{u})_{N-k}^{n}$
and
![]() $K_{N+k}^{n}=-K_{N-k}^{n}$
.
$K_{N+k}^{n}=-K_{N-k}^{n}$
.
It should be noted that, instead of the upstream velocity
![]() $U_{0}$
, it is more convenient to prescribe the upstream Froude number
$U_{0}$
, it is more convenient to prescribe the upstream Froude number
![]() $F$
. A simple relation between them can be obtained. Indeed, according to conservation of mass and momentum, we have the following relations (in dimensional variables):
$F$
. A simple relation between them can be obtained. Indeed, according to conservation of mass and momentum, we have the following relations (in dimensional variables):
 $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle (U_{0}-D)H_{0}=(U_{1}-D)H_{1},\\ \displaystyle (U_{0}-D)^{2}H_{0}+\frac{gH_{0}^{2}}{2}=(U_{1}-D)^{2}H_{1}+\frac{gH_{1}^{2}}{2},\end{array}\right\}\end{eqnarray}$$
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\displaystyle (U_{0}-D)H_{0}=(U_{1}-D)H_{1},\\ \displaystyle (U_{0}-D)^{2}H_{0}+\frac{gH_{0}^{2}}{2}=(U_{1}-D)^{2}H_{1}+\frac{gH_{1}^{2}}{2},\end{array}\right\}\end{eqnarray}$$
where
![]() $U_{0}$
and
$U_{0}$
and
![]() $U_{1}$
are the upstream and downstream velocities, respectively, and
$U_{1}$
are the upstream and downstream velocities, respectively, and
![]() $H_{0}$
and
$H_{0}$
and
![]() $H_{1}=H_{0}+a_{m}$
are the corresponding water depths. In our case,
$H_{1}=H_{0}+a_{m}$
are the corresponding water depths. In our case,
![]() $U_{1}=0$
. The Bélanger formula
$U_{1}=0$
. The Bélanger formula
is the consequence of (4.10) and (4.11). Taking into account (4.12), one can express
![]() $U_{0}$
from (4.11) in terms of the Froude number:
$U_{0}$
from (4.11) in terms of the Froude number:
Figure 5 shows the results of computations at dimensionless time instant
![]() $t_{\ast }=90$
for
$t_{\ast }=90$
for
![]() $F=1.28$
(undular bore) and
$F=1.28$
(undular bore) and
![]() $F=1.40$
(breaking bore) which correspond to the following upstream velocities:
$F=1.40$
(breaking bore) which correspond to the following upstream velocities:
![]() $U_{0}=0.3511$
and
$U_{0}=0.3511$
and
![]() $U_{0}=0.4921$
. Thus, the proposed model (4.1)–(4.3) allows one to describe both undular and breaking bores without any ‘switching’ criteria. In both cases, the surface turbulent layer is formed and shear velocity
$U_{0}=0.4921$
. Thus, the proposed model (4.1)–(4.3) allows one to describe both undular and breaking bores without any ‘switching’ criteria. In both cases, the surface turbulent layer is formed and shear velocity
![]() $q$
is generated. The thickness of the layer grows with increasing jump amplitude
$q$
is generated. The thickness of the layer grows with increasing jump amplitude
![]() $a_{m}$
(or Froude number
$a_{m}$
(or Froude number
![]() $F$
). Also, it is interesting to note that the region of high turbulence (lower curve in the figure corresponding to the scaled variable
$F$
). Also, it is interesting to note that the region of high turbulence (lower curve in the figure corresponding to the scaled variable
![]() $q^{\ast }=q/U_{0}$
) is situated at the crests of the waves (figure 5
a for undular bores), or immediately at the wavefront (figure 5
b for breaking bores). In the latter case the dispersion effects are clearly negligible and the hydrostatic approximation can be used. Such an intensive region of turbulence can be associated with the roller appearance.
$q^{\ast }=q/U_{0}$
) is situated at the crests of the waves (figure 5
a for undular bores), or immediately at the wavefront (figure 5
b for breaking bores). In the latter case the dispersion effects are clearly negligible and the hydrostatic approximation can be used. Such an intensive region of turbulence can be associated with the roller appearance.
Further we compare the amplitudes of undular bores obtained by model (4.1)–(4.3) with experimental data of Treske (Reference Treske1994, p. 365, figure 21). In this case we perform calculations in the domain
![]() $x\in [0,200]$
with
$x\in [0,200]$
with
![]() $N=4000$
for different Froude numbers from the interval
$N=4000$
for different Froude numbers from the interval
![]() $F\in [1.10,1.30]$
. For larger Froude numbers, the amplitude of the leading wave rapidly decreases and transition to a breaking bore occurs. As in the previous case, we choose
$F\in [1.10,1.30]$
. For larger Froude numbers, the amplitude of the leading wave rapidly decreases and transition to a breaking bore occurs. As in the previous case, we choose
![]() $g=1$
,
$g=1$
,
![]() $H_{0}=1$
,
$H_{0}=1$
,
![]() $\unicode[STIX]{x1D70E}=0.15$
and
$\unicode[STIX]{x1D70E}=0.15$
and
![]() $\unicode[STIX]{x1D705}=3$
. The maximum and minimum amplitudes of the leading wave are taken at
$\unicode[STIX]{x1D705}=3$
. The maximum and minimum amplitudes of the leading wave are taken at
![]() $t_{\ast }=190$
. Figure 6 shows that the results obtained by the model (4.1)–(4.3) are in good agreement with the experimental data.
$t_{\ast }=190$
. Figure 6 shows that the results obtained by the model (4.1)–(4.3) are in good agreement with the experimental data.

Figure 5. Favre waves: the free surface
![]() $h+\unicode[STIX]{x1D702}$
, the thickness of the lower potential layer
$h+\unicode[STIX]{x1D702}$
, the thickness of the lower potential layer
![]() $h$
, and the scaled shear velocity
$h$
, and the scaled shear velocity
![]() $q^{\ast }=q/U_{0}$
at
$q^{\ast }=q/U_{0}$
at
![]() $t_{\ast }=90$
,
$t_{\ast }=90$
,
![]() $t_{\ast }=t\sqrt{g/H_{0}}$
for
$t_{\ast }=t\sqrt{g/H_{0}}$
for
![]() $F=1.28$
(a) and
$F=1.28$
(a) and
![]() $F=1.40$
(b). The parameters are as follows:
$F=1.40$
(b). The parameters are as follows:
![]() $g=1$
,
$g=1$
,
![]() $\unicode[STIX]{x1D70E}=0.15$
and
$\unicode[STIX]{x1D70E}=0.15$
and
![]() $\unicode[STIX]{x1D705}=3$
.
$\unicode[STIX]{x1D705}=3$
.

Figure 6. Amplitude of undular bores for different Froude numbers.
4.3 The shoaling and breaking of a solitary wave
Here we consider the evolution of breaking solitary waves on a mildly sloping beach and compare numerical results with the experiments of Hsiao et al. (Reference Hsiao, Hsu, Lin and Chang2008). We perform calculations of the model (4.1)–(4.3) in the interval
![]() $x\in [0,200]$
. The bottom topography is specified as follows:
$x\in [0,200]$
. The bottom topography is specified as follows:
![]() $b(x)=0$
for
$b(x)=0$
for
![]() $x\in [0,50]$
;
$x\in [0,50]$
;
![]() $b(x)=(x-50)/60$
for
$b(x)=(x-50)/60$
for
![]() $x\in (50,175)$
; and
$x\in (50,175)$
; and
![]() $b(x)=25/12$
for
$b(x)=25/12$
for
![]() $x\in [175,200]$
. To avoid modelling of the wave propagation over dry bottom (run-up), we introduce a shelf zone near the right boundary. On both (left and right) walls we assume reflecting boundary conditions. Initial data represent a solitary wave having amplitude
$x\in [175,200]$
. To avoid modelling of the wave propagation over dry bottom (run-up), we introduce a shelf zone near the right boundary. On both (left and right) walls we assume reflecting boundary conditions. Initial data represent a solitary wave having amplitude
![]() $a_{0}=0.3344~\text{m}$
that propagates with velocity
$a_{0}=0.3344~\text{m}$
that propagates with velocity
![]() $C_{0}=\sqrt{g(a_{0}+H_{0})}$
, where
$C_{0}=\sqrt{g(a_{0}+H_{0})}$
, where
![]() $H_{0}=2.2~\text{m}$
is the undisturbed water depth and
$H_{0}=2.2~\text{m}$
is the undisturbed water depth and
![]() $g=9.8~\text{m}~\text{s}^{-2}$
. These data correspond to trial 43 in the experiments by Hsiao et al. (Reference Hsiao, Hsu, Lin and Chang2008). The initial thickness of the upper turbulent layer
$g=9.8~\text{m}~\text{s}^{-2}$
. These data correspond to trial 43 in the experiments by Hsiao et al. (Reference Hsiao, Hsu, Lin and Chang2008). The initial thickness of the upper turbulent layer
![]() $\unicode[STIX]{x1D702}_{0}$
is equal to
$\unicode[STIX]{x1D702}_{0}$
is equal to
![]() $0.01~\text{m}$
. The parameter values are the same as those in the case of Favre waves:
$0.01~\text{m}$
. The parameter values are the same as those in the case of Favre waves:
![]() $\unicode[STIX]{x1D70E}=0.15$
and
$\unicode[STIX]{x1D70E}=0.15$
and
![]() $\unicode[STIX]{x1D705}=3$
. We take
$\unicode[STIX]{x1D705}=3$
. We take
![]() $N=2000$
nodes for space resolution. Here we use dimensional variables.
$N=2000$
nodes for space resolution. Here we use dimensional variables.
Figure 7 shows the results of numerical calculations of the free surface at different time moments. As we can see from figure 7, when the wave breaks, the turbulent layer near the free surface is formed (
![]() $\unicode[STIX]{x1D702}$
is increasing).
$\unicode[STIX]{x1D702}$
is increasing).

Figure 7. The evolution of a solitary wave on a mildly sloping beach: 1, bottom topography; 2, 3 and 4, free surface at
![]() $t_{\ast }=0$
,
$t_{\ast }=0$
,
![]() $50$
and
$50$
and
![]() $75$
, respectively; and 5, the boundary of the lower potential layer at
$75$
, respectively; and 5, the boundary of the lower potential layer at
![]() $t_{\ast }=75$
, where the dimensionless time
$t_{\ast }=75$
, where the dimensionless time
![]() $t_{\ast }$
is given by
$t_{\ast }$
is given by
![]() $t_{\ast }=t\sqrt{g/H_{0}}$
.
$t_{\ast }=t\sqrt{g/H_{0}}$
.
The temporal evolution of the free-surface displacements at different positions along the channel is shown in figure 8. The numerical results were compared with the experimental data corresponding to trial 43 of the experiments by Hsiao et al. (Reference Hsiao, Hsu, Lin and Chang2008) (see figure 4(a) on p. 979 therein). Excellent agreement with the experimental data is observed everywhere except in the region near the right boundary corresponding to
![]() $x=172~\text{m}$
(the last graphic in figure 8). This is due to the fact that we have introduced the shelf zone for
$x=172~\text{m}$
(the last graphic in figure 8). This is due to the fact that we have introduced the shelf zone for
![]() $x>175~\text{m}$
, while experimentally the wave continues running up the slope.
$x>175~\text{m}$
, while experimentally the wave continues running up the slope.

Figure 8. Time history of free-surface displacement: solid curves, experimental data (Hsiao et al. Reference Hsiao, Hsu, Lin and Chang2008); dashed curves, numerical results.
5 Conclusion
We constructed depth-averaged governing equations for a two-layer long-wave approximation of the homogeneous Euler equations with a free surface evolving over a mild slope. The upper layer is turbulent and is described by system (2.49)–(2.51). The lower layer is almost potential and can be described by Serre–Su–Gardner–Green–Naghdi equations (2.52)–(2.53). The interface separating the two layers is considered as a discontinuity surface through which turbulent mixing occurs. The constructed model reveals the main mechanism of the spilling breaker development. For waves of moderate amplitude, the upper thin layer is dynamically passive and the flow is principally governed by the dispersive model. However, for waves of larger amplitude, the upper turbulent layer dynamics becomes crucial. The larger the wave amplitude, the greater is the difference in the average flow velocities of the layers. It finally results in an intensive growing of the upper turbulent layer (spilling breaker formation).
In particular, the model predicts quite well the transition from undular bores to breaking bores. This point is very important. Indeed, the undular bore can be described by the dispersive Serre–Su–Gardner–Green– Naghdi model where a viscosity is added, but not the breaking bore. The breaking bore can be described by a hyperbolic model of the Saint-Venant type (see also a recent model proposed in Richard & Gavrilyuk (Reference Richard and Gavrilyuk2012, Reference Richard and Gavrilyuk2013)), but not the undular bore. A combination of these simple model ‘bricks’ (dispersive and hyperbolic ones) allows us to obtain a natural transition between the two types of bores. Also, a classical problem of the shoaling and breaking of a solitary wave on a mildly sloping beach is well predicted by the new model.
Future work will consist in the modelling of air bubble entrainment by the breaking waves and a natural multi-dimensional extension of the model.
Acknowledgements
The authors thank S.-C. Hsiao and T.-C. Lin for providing us with the experimental data, and anonymous reviewers for their constructive comments. The work was supported by the Russian Science Foundation (grant no. 15-11-20013). S.L.G. has been partially supported by the ANR project BoND (ANR-13-BS01-0009-01).
Appendix A
The system describing the lower layer is
 $$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}\left(h\left(\frac{U^{2}}{2}+\unicode[STIX]{x1D700}^{2}\frac{U_{x}^{2}}{6}h^{2}+\frac{h}{2}\right)\right)+\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x}\left(hU\left(\frac{U^{2}}{2}+\unicode[STIX]{x1D700}^{2}\frac{U_{x}^{2}}{6}h^{2}+\frac{h}{2}\right)+UP\right)\nonumber\\ \displaystyle & & \displaystyle \qquad =-p|_{z=h}(h_{t}+M)-M\left.\left(\frac{u^{2}}{2}+\unicode[STIX]{x1D700}^{2}\frac{U_{x}^{2}h^{2}}{2}+h\right)\right|_{z=h},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}\left(h\left(\frac{U^{2}}{2}+\unicode[STIX]{x1D700}^{2}\frac{U_{x}^{2}}{6}h^{2}+\frac{h}{2}\right)\right)+\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x}\left(hU\left(\frac{U^{2}}{2}+\unicode[STIX]{x1D700}^{2}\frac{U_{x}^{2}}{6}h^{2}+\frac{h}{2}\right)+UP\right)\nonumber\\ \displaystyle & & \displaystyle \qquad =-p|_{z=h}(h_{t}+M)-M\left.\left(\frac{u^{2}}{2}+\unicode[STIX]{x1D700}^{2}\frac{U_{x}^{2}h^{2}}{2}+h\right)\right|_{z=h},\end{eqnarray}$$
where
The momentum equation is equivalent to
Developing the energy equation, we have
 $$\begin{eqnarray}\displaystyle & & \displaystyle h\frac{\text{D}}{\text{D }t}\left(\frac{U^{2}}{2}+\unicode[STIX]{x1D700}^{2}\frac{U_{x}^{2}}{6}h^{2}+\frac{h}{2}\right)-M\left(\frac{U^{2}}{2}+\unicode[STIX]{x1D700}^{2}\frac{U_{x}^{2}h^{2}}{6}+\frac{h}{2}\right)+U_{x}P+P_{x}U\nonumber\\ \displaystyle & & \displaystyle \qquad =-p|_{z=h}\,(h_{t}+M)-M\left.\left(\frac{u^{2}}{2}+\unicode[STIX]{x1D700}^{2}\frac{U_{x}^{2}h^{2}}{2}+h\right)\right|_{z=h}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle h\frac{\text{D}}{\text{D }t}\left(\frac{U^{2}}{2}+\unicode[STIX]{x1D700}^{2}\frac{U_{x}^{2}}{6}h^{2}+\frac{h}{2}\right)-M\left(\frac{U^{2}}{2}+\unicode[STIX]{x1D700}^{2}\frac{U_{x}^{2}h^{2}}{6}+\frac{h}{2}\right)+U_{x}P+P_{x}U\nonumber\\ \displaystyle & & \displaystyle \qquad =-p|_{z=h}\,(h_{t}+M)-M\left.\left(\frac{u^{2}}{2}+\unicode[STIX]{x1D700}^{2}\frac{U_{x}^{2}h^{2}}{2}+h\right)\right|_{z=h}.\end{eqnarray}$$
Using the momentum equation, we can simplify the energy equation to
 $$\begin{eqnarray}\displaystyle & & \displaystyle h\frac{\text{D}}{\text{D }t}\left(\unicode[STIX]{x1D700}^{2}\frac{U_{x}^{2}}{6}h^{2}\right)+M\left(\frac{1}{2}(U-u|_{z=h})^{2}+\unicode[STIX]{x1D700}^{2}\frac{U_{x}^{2}h^{2}}{3}\right)\nonumber\\ \displaystyle & & \displaystyle \qquad -\,U_{x}\left(\unicode[STIX]{x1D700}^{2}\frac{h^{3}}{3}(U_{xt}+UU_{xx}-U_{x}^{2})\right)=0\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle h\frac{\text{D}}{\text{D }t}\left(\unicode[STIX]{x1D700}^{2}\frac{U_{x}^{2}}{6}h^{2}\right)+M\left(\frac{1}{2}(U-u|_{z=h})^{2}+\unicode[STIX]{x1D700}^{2}\frac{U_{x}^{2}h^{2}}{3}\right)\nonumber\\ \displaystyle & & \displaystyle \qquad -\,U_{x}\left(\unicode[STIX]{x1D700}^{2}\frac{h^{3}}{3}(U_{xt}+UU_{xx}-U_{x}^{2})\right)=0\end{eqnarray}$$
or
This implies that
or, since the formula is valid for any
![]() $M$
, one obtains
$M$
, one obtains
Appendix B
We replace the momentum equation for the lower layer by an equivalent one:
This can be transformed to
 $$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle U_{t}+\left(\frac{U^{2}}{2}+h+\unicode[STIX]{x1D702}\right)_{x}\nonumber\\ \displaystyle & & \displaystyle \displaystyle \quad -\,\unicode[STIX]{x1D700}^{2}\left(hh_{x}(U_{xt}+UU_{xx}-U_{x}^{2})+\frac{h^{2}}{3}\left(U_{xxt}+UU_{xxx}-U_{x}U_{xx}\right)\right)=0,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle U_{t}+\left(\frac{U^{2}}{2}+h+\unicode[STIX]{x1D702}\right)_{x}\nonumber\\ \displaystyle & & \displaystyle \displaystyle \quad -\,\unicode[STIX]{x1D700}^{2}\left(hh_{x}(U_{xt}+UU_{xx}-U_{x}^{2})+\frac{h^{2}}{3}\left(U_{xxt}+UU_{xxx}-U_{x}U_{xx}\right)\right)=0,\end{eqnarray}$$
which is equivalent to
 $$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle U_{t}+\left(\frac{U^{2}}{2}+h+\unicode[STIX]{x1D702}\right)_{x}\nonumber\\ \displaystyle & & \displaystyle \displaystyle \quad -\,\unicode[STIX]{x1D700}^{2}\left(hh_{x}U_{xt}+\frac{h^{2}}{3}U_{xxt}+hh_{x}\left(UU_{xx}-U_{x}^{2}\right)+\frac{h^{2}}{3}\left(UU_{xxx}-U_{x}U_{xx}\right)\right)=0.\qquad\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle U_{t}+\left(\frac{U^{2}}{2}+h+\unicode[STIX]{x1D702}\right)_{x}\nonumber\\ \displaystyle & & \displaystyle \displaystyle \quad -\,\unicode[STIX]{x1D700}^{2}\left(hh_{x}U_{xt}+\frac{h^{2}}{3}U_{xxt}+hh_{x}\left(UU_{xx}-U_{x}^{2}\right)+\frac{h^{2}}{3}\left(UU_{xxx}-U_{x}U_{xx}\right)\right)=0.\qquad\end{eqnarray}$$
This implies that
 $$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle K_{t}+\left(\frac{U^{2}}{2}+h+\unicode[STIX]{x1D702}\right)_{x}\nonumber\\ \displaystyle & & \displaystyle \displaystyle \quad -\,\unicode[STIX]{x1D700}^{2}\left(hh_{x}(UU_{xx}-U_{x}^{2})+\frac{h^{2}}{3}(UU_{xxx}-U_{x}U_{xx})-U_{x}h_{t}h_{x}-U_{x}hh_{tx}-\frac{2}{3}hh_{t}U_{xx}\right)=0.\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle K_{t}+\left(\frac{U^{2}}{2}+h+\unicode[STIX]{x1D702}\right)_{x}\nonumber\\ \displaystyle & & \displaystyle \displaystyle \quad -\,\unicode[STIX]{x1D700}^{2}\left(hh_{x}(UU_{xx}-U_{x}^{2})+\frac{h^{2}}{3}(UU_{xxx}-U_{x}U_{xx})-U_{x}h_{t}h_{x}-U_{x}hh_{tx}-\frac{2}{3}hh_{t}U_{xx}\right)=0.\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
Replacing
![]() $h_{t}$
by
$h_{t}$
by
we obtain
 $$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle K_{t}+\left(\frac{U^{2}}{2}+h+\unicode[STIX]{x1D702}\right)_{x}\nonumber\\ \displaystyle & & \displaystyle \displaystyle \quad -\unicode[STIX]{x1D700}^{2}\left(U_{x}h_{x}(M+(hU)_{x})+U_{x}h(M+(hU)_{x})_{x}+\frac{2}{3}h(M+(hU)_{x})U_{xx}\right.\nonumber\\ \displaystyle & & \displaystyle \displaystyle \quad \left.+\,hh_{x}(UU_{xx}-U_{x}^{2})+\frac{h^{2}}{3}(UU_{xxx}-U_{x}U_{xx})\right)=0.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle K_{t}+\left(\frac{U^{2}}{2}+h+\unicode[STIX]{x1D702}\right)_{x}\nonumber\\ \displaystyle & & \displaystyle \displaystyle \quad -\unicode[STIX]{x1D700}^{2}\left(U_{x}h_{x}(M+(hU)_{x})+U_{x}h(M+(hU)_{x})_{x}+\frac{2}{3}h(M+(hU)_{x})U_{xx}\right.\nonumber\\ \displaystyle & & \displaystyle \displaystyle \quad \left.+\,hh_{x}(UU_{xx}-U_{x}^{2})+\frac{h^{2}}{3}(UU_{xxx}-U_{x}U_{xx})\right)=0.\end{eqnarray}$$
This yields
 $$\begin{eqnarray}\displaystyle & & \displaystyle K_{t}+\left(\frac{U^{2}}{2}+h+\unicode[STIX]{x1D702}\right)_{x}-\unicode[STIX]{x1D700}^{2}\left(U_{x}h_{x}(hU)_{x}\vphantom{\frac{h^{2}}{3}}\right.\nonumber\\ \displaystyle & & \displaystyle \left.\quad +\,U_{x}h(hU)_{xx}+\frac{2}{3}h(hU)_{x}U_{xx}+hh_{x}(UU_{xx}-U_{x}^{2})+\frac{h^{2}}{3}(UU_{xxx}-U_{x}U_{xx})\right)\nonumber\\ \displaystyle & & \displaystyle \quad -\,\unicode[STIX]{x1D700}^{2}\left(\frac{2}{3}(U_{x}hM)_{x}+\frac{1}{3}U_{x}(hM)_{x}\right)=0,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle K_{t}+\left(\frac{U^{2}}{2}+h+\unicode[STIX]{x1D702}\right)_{x}-\unicode[STIX]{x1D700}^{2}\left(U_{x}h_{x}(hU)_{x}\vphantom{\frac{h^{2}}{3}}\right.\nonumber\\ \displaystyle & & \displaystyle \left.\quad +\,U_{x}h(hU)_{xx}+\frac{2}{3}h(hU)_{x}U_{xx}+hh_{x}(UU_{xx}-U_{x}^{2})+\frac{h^{2}}{3}(UU_{xxx}-U_{x}U_{xx})\right)\nonumber\\ \displaystyle & & \displaystyle \quad -\,\unicode[STIX]{x1D700}^{2}\left(\frac{2}{3}(U_{x}hM)_{x}+\frac{1}{3}U_{x}(hM)_{x}\right)=0,\end{eqnarray}$$
or
 $$\begin{eqnarray}\displaystyle & & \displaystyle K_{t}+\left(\frac{U^{2}}{2}+h+\unicode[STIX]{x1D702}-\unicode[STIX]{x1D700}^{2}\frac{2}{3}hMU_{x}\right)_{x}-\unicode[STIX]{x1D700}^{2}\left(U_{x}h_{x}(hU)_{x}+U_{x}h(hU)_{xx}\vphantom{\frac{h^{2}}{3}}\right.\nonumber\\ \displaystyle & & \displaystyle \left.\quad +\,\frac{2}{3}h(hU)_{x}U_{xx}+hh_{x}(UU_{xx}-U_{x}^{2})+\frac{h^{2}}{3}(UU_{xxx}-U_{x}U_{xx})\right)=\frac{\unicode[STIX]{x1D700}^{2}}{3}U_{x}(hM)_{x}.\qquad \quad\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle K_{t}+\left(\frac{U^{2}}{2}+h+\unicode[STIX]{x1D702}-\unicode[STIX]{x1D700}^{2}\frac{2}{3}hMU_{x}\right)_{x}-\unicode[STIX]{x1D700}^{2}\left(U_{x}h_{x}(hU)_{x}+U_{x}h(hU)_{xx}\vphantom{\frac{h^{2}}{3}}\right.\nonumber\\ \displaystyle & & \displaystyle \left.\quad +\,\frac{2}{3}h(hU)_{x}U_{xx}+hh_{x}(UU_{xx}-U_{x}^{2})+\frac{h^{2}}{3}(UU_{xxx}-U_{x}U_{xx})\right)=\frac{\unicode[STIX]{x1D700}^{2}}{3}U_{x}(hM)_{x}.\qquad \quad\end{eqnarray}$$
This can be simplified as
One can transform the flux to obtain
an equivalent form of which is
From the definition of
![]() $K$
we obtain
$K$
we obtain
This allows us to eliminate
![]() $U_{xx}$
as a function of
$U_{xx}$
as a function of
![]() $K$
and
$K$
and
![]() $U_{x}$
:
$U_{x}$
:
The derivative
![]() $U_{x}$
is continuous at the jump, so the right-hand side of the equation for
$U_{x}$
is continuous at the jump, so the right-hand side of the equation for
![]() $K$
is now well defined. An equivalent form is
$K$
is now well defined. An equivalent form is