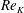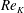1 Introduction
Wall surfaces of real materials are usually not perfectly smooth but have roughness and sometimes permeability. Flow characteristics over permeable porous surfaces such as foamed metals, woven or non-woven fabrics and vegetative canopies are different from those over impermeable surfaces. Since it has never been fully understood how different they are, many studies have been performed to discuss flow physics over porous media so far.
The study of Beavers & Joseph (Reference Beavers and Joseph1967) was one of the most classic experimental reports on the friction over porous walls. They reported that the friction factor reduced due to the porosity when the flow was laminar. However, in turbulent flows it turned out to be larger than that over impermeable rough walls (e.g. Lovera & Kennedy Reference Lovera and Kennedy1969; Ruff & Gelhar Reference Ruff and Gelhar1972; Ho & Gelhar Reference Ho and Gelhar1973; Zagni & Smith Reference Zagni and Smith1976). For open channel flows, Zagni & Smith (Reference Zagni and Smith1976) systematically measured flow rates and velocities over 20 different porous beds made of spherical particles and attributed the increase in the friction factor to additional energy dissipation caused by exchange of momentum across the porous interface. The experiments of Kong & Schetz (Reference Kong and Schetz1982), Zippe & Graf (Reference Zippe and Graf1983) also indicated that the velocity profiles over the porous layers became more turbulent than those over impermeable rough walls. Using modern particle image velocimetry (PIV), Pokrajac & Manes (Reference Pokrajac and Manes2009) measured the detailed flow field over a porous bed composed of glass spheres and concluded that, near the porous interface, turbulent fluctuations of the normal velocity were affected by the permeability.
The above-mentioned experimental reports suggested that the wall permeability affected the flow structure over porous walls, enhancing momentum exchange. Due to the wall permeability, the blocking effect on the wall normal fluctuation velocity is significantly weakened, resulting in stronger near-wall turbulent shear stress. The direct numerical simulation (DNS) studies by Breugem, Boersma & Uittenbogaard (Reference Breugem, Boersma and Uittenbogaard2006), Chandesris et al. (Reference Chandesris, D’Hueppe, Mathieu, Jamet and Goyeau2013), Rosti, Cortelezzi & Quadrio (Reference Rosti, Cortelezzi and Quadrio2015) of turbulent porous-walled channel flows also indicated that the effect of the permeability was dominant on turbulence over porous media. To find a turbulence scaling law of flows over permeable walls, systematic studies have been conducted (Breugem et al.
Reference Breugem, Boersma and Uittenbogaard2006; Suga et al.
Reference Suga, Matsumura, Ashitaka, Tominaga and Kaneda2010; Manes, Poggi & Ridol Reference Manes, Poggi and Ridol2011; Suga, Mori & Kaneda Reference Suga, Mori and Kaneda2011). The numerical study by Breugem et al. (Reference Breugem, Boersma and Uittenbogaard2006) and the PIV experiments by the present authors’ group (Suga et al.
Reference Suga, Matsumura, Ashitaka, Tominaga and Kaneda2010, Reference Suga, Mori and Kaneda2011; Suga Reference Suga2016) of turbulent porous-walled channel flows indicated that a permeability Reynolds number was one of the candidates to correlate inner layer phenomena. Suga et al. (Reference Suga, Matsumura, Ashitaka, Tominaga and Kaneda2010) indicated that the von Kármán coefficient, the zero-plane displacement and the roughness length scale of the semi-logarithmic mean velocity profiles were well correlated with the permeability Reynolds number, defined as
![]() $Re_{K}=u_{\unicode[STIX]{x1D70F}}^{p}\sqrt{K}/\unicode[STIX]{x1D708}$
, with the friction velocity
$Re_{K}=u_{\unicode[STIX]{x1D70F}}^{p}\sqrt{K}/\unicode[STIX]{x1D708}$
, with the friction velocity
![]() $u_{\unicode[STIX]{x1D70F}}^{p}$
, the wall permeability
$u_{\unicode[STIX]{x1D70F}}^{p}$
, the wall permeability
![]() $K$
and the fluid kinematic viscosity
$K$
and the fluid kinematic viscosity
![]() $\unicode[STIX]{x1D708}$
. For turbulent boundary layers over polyurethane foam arranged in a laboratory flume, Manes et al. (Reference Manes, Poggi and Ridol2011) performed laser Doppler anemometer (LDA) measurements. After the discussion on the shear penetration depth and the boundary layer thickness, it was concluded that they could be used respectively for the inner and outer length scales of boundary layers.
$\unicode[STIX]{x1D708}$
. For turbulent boundary layers over polyurethane foam arranged in a laboratory flume, Manes et al. (Reference Manes, Poggi and Ridol2011) performed laser Doppler anemometer (LDA) measurements. After the discussion on the shear penetration depth and the boundary layer thickness, it was concluded that they could be used respectively for the inner and outer length scales of boundary layers.
Furthermore, due to the wall permeability, the near-wall streaky structure appeared to be destroyed in the DNS studies (Breugem et al. Reference Breugem, Boersma and Uittenbogaard2006; Chandesris et al. Reference Chandesris, D’Hueppe, Mathieu, Jamet and Goyeau2013; Rosti et al. Reference Rosti, Cortelezzi and Quadrio2015; Kuwata & Suga Reference Kuwata and Suga2016a ,Reference Kuwata and Suga b ) of turbulent porous-walled channel flows. Breugem et al. (Reference Breugem, Boersma and Uittenbogaard2006) reported that above a highly permeable wall, there were no low- and high-speed streaks and the associated quasi-streamwise vortices. They concluded that turbulent transport across the permeable wall interface prevented the development of elongated streaks. Comparing their simulation results of permeable porous and impermeable rough wall cases, Kuwata & Suga (Reference Kuwata and Suga2016a ) concluded that over the porous layer, the vortex structure became shredded and the streamwise coherent structure became shorter due to the wall roughness, whereas the pitch of the streaks over the porous layer became approximately twice as wide as that over the impermeable (rough or smooth) walls. Moreover, the presence of the streaks over the porous wall tended to be less visible than those over the impermeable walls.
From the experimental view point, by analysing the PIV data in streamwise-wall-normal (
![]() $x$
–
$x$
–
![]() $y$
) planes, Suga et al. (Reference Suga, Mori and Kaneda2011) investigated the near-wall structure and discussed the mechanism behind the destruction of the streaky structure. Their discussions aided by the quadrant analysis confirmed that sweeps became most dominant very near the permeable wall whilst ejections became dominant in the buffer region. Through conditional quadrant-hole analysis of the Reynolds shear stress, it was concluded that due to the increase of the wall permeability, stronger sweeps tended to move towards the wall. However, ejections tended to lose their strength since the fluid pushed out from the porous wall by the strong inward penetrating motions had already lost its energy inside the porous wall. These effects were generally enhanced by an increase in the permeability Reynolds number. Thus, at least, at a moderate permeability Reynolds number these phenomena resulted in shortening the longitudinal leg vortices of a hairpin vortex since vortex motions could not be maintained with the weakened ejections over highly permeable walls.
$y$
) planes, Suga et al. (Reference Suga, Mori and Kaneda2011) investigated the near-wall structure and discussed the mechanism behind the destruction of the streaky structure. Their discussions aided by the quadrant analysis confirmed that sweeps became most dominant very near the permeable wall whilst ejections became dominant in the buffer region. Through conditional quadrant-hole analysis of the Reynolds shear stress, it was concluded that due to the increase of the wall permeability, stronger sweeps tended to move towards the wall. However, ejections tended to lose their strength since the fluid pushed out from the porous wall by the strong inward penetrating motions had already lost its energy inside the porous wall. These effects were generally enhanced by an increase in the permeability Reynolds number. Thus, at least, at a moderate permeability Reynolds number these phenomena resulted in shortening the longitudinal leg vortices of a hairpin vortex since vortex motions could not be maintained with the weakened ejections over highly permeable walls.
However, it is still unknown how the structure of the streaks changes in size and shape due to the wall permeability. Therefore, the present study investigates turbulent vortex structure over permeable walls, focusing on the spanwise flow structure using instantaneous and statistical data by PIV experiments of streamwise–spanwise (
![]() $x$
–
$x$
–
![]() $z$
) planes. In our previous studies (Suga et al.
Reference Suga, Matsumura, Ashitaka, Tominaga and Kaneda2010, Reference Suga, Mori and Kaneda2011; Suga Reference Suga2016), turbulence characteristics were well characterized by the permeability Reynolds number, and there seemed to be a transition to full porous wall turbulence in the range under
$z$
) planes. In our previous studies (Suga et al.
Reference Suga, Matsumura, Ashitaka, Tominaga and Kaneda2010, Reference Suga, Mori and Kaneda2011; Suga Reference Suga2016), turbulence characteristics were well characterized by the permeability Reynolds number, and there seemed to be a transition to full porous wall turbulence in the range under
![]() $Re_{K}\simeq 3$
. Accordingly, the present study attempts to explain the change of the spatial structure when the permeability Reynolds number increases.
$Re_{K}\simeq 3$
. Accordingly, the present study attempts to explain the change of the spatial structure when the permeability Reynolds number increases.
2 Experimental method
Figure 1 illustrates the experimental set-up and the coordinate system in the test section of the present study. As shown in figure 1(a), tap water is pumped up from a water tank equipped with a cooler (TRL-117GS2, THOMAS KAGAKU) to maintain a constant water temperature of 285
![]() $\pm 1$
K, and its total flow rate is measured by a digital flow meter (FD-MH200A/500A, KEYENCE). The water flow is conditioned by a honeycomb-bundled nozzle, where its temperature is recorded by a digital thermometer (FD-T1, KEYENCE). Then the flow is fully developed in a driver section whose length is 3.0 m and enters the test section of length 1.0 m. Both the sections consist of solid smooth acrylic walls with a porous bottom layer. The sectional width
$\pm 1$
K, and its total flow rate is measured by a digital flow meter (FD-MH200A/500A, KEYENCE). The water flow is conditioned by a honeycomb-bundled nozzle, where its temperature is recorded by a digital thermometer (FD-T1, KEYENCE). Then the flow is fully developed in a driver section whose length is 3.0 m and enters the test section of length 1.0 m. Both the sections consist of solid smooth acrylic walls with a porous bottom layer. The sectional width
![]() $W$
and total height are, respectively, 0.305 m and 0.093 m, two-thirds of which are filled by a porous layer. For the porous layer, as in the previous reports (Suga et al.
Reference Suga, Matsumura, Ashitaka, Tominaga and Kaneda2010, Reference Suga, Mori and Kaneda2011; Suga Reference Suga2016), three kinds of foamed ceramics (shown in figure 2) are used. They are named No. 20, No. 13 and No. 06, and correspond to low-, medium- and high-permeability porous media, respectively. All of them have an isotopic open-cell foam structure with the same porosity of
$W$
and total height are, respectively, 0.305 m and 0.093 m, two-thirds of which are filled by a porous layer. For the porous layer, as in the previous reports (Suga et al.
Reference Suga, Matsumura, Ashitaka, Tominaga and Kaneda2010, Reference Suga, Mori and Kaneda2011; Suga Reference Suga2016), three kinds of foamed ceramics (shown in figure 2) are used. They are named No. 20, No. 13 and No. 06, and correspond to low-, medium- and high-permeability porous media, respectively. All of them have an isotopic open-cell foam structure with the same porosity of
![]() $\unicode[STIX]{x1D711}=0.8$
, but the mean pore diameter, the permeability and the Forchheimer coefficient vary as
$\unicode[STIX]{x1D711}=0.8$
, but the mean pore diameter, the permeability and the Forchheimer coefficient vary as
![]() $D_{p}=1.7{-}3.8~\text{mm}$
and
$D_{p}=1.7{-}3.8~\text{mm}$
and
![]() $K=0.020{-}0.087~\text{mm}^{2}$
and
$K=0.020{-}0.087~\text{mm}^{2}$
and
![]() $c_{F}=0.17{-}0.095$
, respectively, as listed in table 1. Here, in the measurement of Suga et al. (Reference Suga, Matsumura, Ashitaka, Tominaga and Kaneda2010) to obtain the permeability and the Forchheimer coefficient, the following Darcy–Forchheimer equation was applied between the pressure drop
$c_{F}=0.17{-}0.095$
, respectively, as listed in table 1. Here, in the measurement of Suga et al. (Reference Suga, Matsumura, Ashitaka, Tominaga and Kaneda2010) to obtain the permeability and the Forchheimer coefficient, the following Darcy–Forchheimer equation was applied between the pressure drop
![]() $\unicode[STIX]{x0394}P/\unicode[STIX]{x0394}x$
and the Darcy velocity
$\unicode[STIX]{x0394}P/\unicode[STIX]{x0394}x$
and the Darcy velocity
![]() $U_{d}$
:
$U_{d}$
:
where
![]() $\unicode[STIX]{x1D707}$
and
$\unicode[STIX]{x1D707}$
and
![]() $\unicode[STIX]{x1D70C}$
are the fluid viscosity and density, respectively. Since the height of the clear fluid region is set to
$\unicode[STIX]{x1D70C}$
are the fluid viscosity and density, respectively. Since the height of the clear fluid region is set to
![]() $H=0.03~\text{m}$
, the aspect ratio of the cross-section of the clear fluid region is approximately 10. To compare the results with those of solid smooth-walled channel flows, a different set of ducts (of height 0.03 m) are also used. By controlling the output of the pump with the power converter, inlet flow rates are adjusted. The measured range of the bulk Reynolds number
$H=0.03~\text{m}$
, the aspect ratio of the cross-section of the clear fluid region is approximately 10. To compare the results with those of solid smooth-walled channel flows, a different set of ducts (of height 0.03 m) are also used. By controlling the output of the pump with the power converter, inlet flow rates are adjusted. The measured range of the bulk Reynolds number
![]() $Re_{b}$
(
$Re_{b}$
(
![]() $U_{b}H/\unicode[STIX]{x1D708}$
) is 1500–15 900, where
$U_{b}H/\unicode[STIX]{x1D708}$
) is 1500–15 900, where
![]() $\unicode[STIX]{x1D708}$
is determined by the measured water temperature. To obtain the bulk mean velocity
$\unicode[STIX]{x1D708}$
is determined by the measured water temperature. To obtain the bulk mean velocity
![]() $U_{b}$
in the clear fluid region, the wall shear stress and the other parameters related to the mean velocity profile, additional corresponding measurements of
$U_{b}$
in the clear fluid region, the wall shear stress and the other parameters related to the mean velocity profile, additional corresponding measurements of
![]() $x$
–
$x$
–
![]() $y$
planes at the symmetry of the test section are also performed by the same method as reported in the previous study (Suga et al.
Reference Suga, Matsumura, Ashitaka, Tominaga and Kaneda2010).
$y$
planes at the symmetry of the test section are also performed by the same method as reported in the previous study (Suga et al.
Reference Suga, Matsumura, Ashitaka, Tominaga and Kaneda2010).

Figure 1. Experimental set-up: (a) channel flow facility; (b) schematic view of the test section.

Figure 2. Surface photographs of the foamed ceramics: (a) No. 20: low permeability, (b) No. 13: medium permeability, (c) No. 06: high permeability.
Table 1. Characteristics of the foamed ceramics;
![]() $\unicode[STIX]{x1D711},D_{p},K$
and
$\unicode[STIX]{x1D711},D_{p},K$
and
![]() $c_{F}$
are porosity, mean pore diameter, permeability and Forchheimer coefficient, respectively.
$c_{F}$
are porosity, mean pore diameter, permeability and Forchheimer coefficient, respectively.

The employed planar PIV system consists of a double-pulse Nd-YAG laser (Dual Power 200-15, Litron) with
![]() $200~\text{mJ}~\text{pulse}^{-1}$
at a wavelength of 532 nm. The laser beam is formed into a sheet approximately 1.0 mm in thickness by several cylindrical lenses and illuminates
$200~\text{mJ}~\text{pulse}^{-1}$
at a wavelength of 532 nm. The laser beam is formed into a sheet approximately 1.0 mm in thickness by several cylindrical lenses and illuminates
![]() $x$
–
$x$
–
![]() $z$
planes as shown in figure 1(b). Two CCD cameras (Flowsense 4M Mk2, DANTEC DYNAMICS) operating at 30 f.p.s with 85 mm
$z$
planes as shown in figure 1(b). Two CCD cameras (Flowsense 4M Mk2, DANTEC DYNAMICS) operating at 30 f.p.s with 85 mm
![]() $f/1.8$
lenses (AF Nikkor, Nikon) and extension tubes (Kenko Tokina 12 mm) are arranged in tandem. The recorded frame of each CCD camera covers a zone of
$f/1.8$
lenses (AF Nikkor, Nikon) and extension tubes (Kenko Tokina 12 mm) are arranged in tandem. The recorded frame of each CCD camera covers a zone of
![]() $80(x)\times 80(z)~\text{mm}^{2}$
located in the middle of the test section with
$80(x)\times 80(z)~\text{mm}^{2}$
located in the middle of the test section with
![]() $2048\times 2048$
pixels, for which 20 % of the area overlaps with another camera’s frame.
$2048\times 2048$
pixels, for which 20 % of the area overlaps with another camera’s frame.
For the tracer particles, polymer fluorescent particles containing Rhodamine B, whose mean diameter and specific gravity are respectively
![]() $10~\unicode[STIX]{x03BC}\text{m}$
and 1.50, are used. (By Stokes’ law, the settling velocity of the particles can be estimated as
$10~\unicode[STIX]{x03BC}\text{m}$
and 1.50, are used. (By Stokes’ law, the settling velocity of the particles can be estimated as
![]() $2.2\times 10^{-5}~\text{m}~\text{s}^{-1}$
, which is negligibly small compared with the bulk mean velocity of
$2.2\times 10^{-5}~\text{m}~\text{s}^{-1}$
, which is negligibly small compared with the bulk mean velocity of
![]() $6.2\times 10^{-2}$
for the lowest Reynolds number case at
$6.2\times 10^{-2}$
for the lowest Reynolds number case at
![]() $Re_{b}=1500$
.) Correspondingly, a long-pass filter with cutoff wavelength 560 nm is located in front of each camera lens. The seeding density is adjusted to obtain 10–15 particle-image pairs as in Adrian, Meinhart & Tomkins (Reference Adrian, Meinhart and Tomkins2000) in each interrogation window of size
$Re_{b}=1500$
.) Correspondingly, a long-pass filter with cutoff wavelength 560 nm is located in front of each camera lens. The seeding density is adjusted to obtain 10–15 particle-image pairs as in Adrian, Meinhart & Tomkins (Reference Adrian, Meinhart and Tomkins2000) in each interrogation window of size
![]() $32\times 32$
pixels. Thus the measurement sampling volume is
$32\times 32$
pixels. Thus the measurement sampling volume is
![]() $1.25(x)\times 1.0(y)\times 1.25(z)~\text{mm}^{3}$
. The image sampling rate is 4 Hz. The timing of the laser pulse interval is adjusted depending on the average particle displacement during the interval. In the present experiments, the average particle displacement is set to be approximately 25 % of the length (3–6 pixels) of the interrogation cell. To obtain the statistical data, in each zone, 4000 image pairs are processed in this study. The recorded data are processed by Dynamics Studio 3.1 (DANTEC DYNAMICS) software with the fast Fourier transform cross-correlation technique (Willert & Gharib Reference Willert and Gharib1991). Each image is processed to produce
$1.25(x)\times 1.0(y)\times 1.25(z)~\text{mm}^{3}$
. The image sampling rate is 4 Hz. The timing of the laser pulse interval is adjusted depending on the average particle displacement during the interval. In the present experiments, the average particle displacement is set to be approximately 25 % of the length (3–6 pixels) of the interrogation cell. To obtain the statistical data, in each zone, 4000 image pairs are processed in this study. The recorded data are processed by Dynamics Studio 3.1 (DANTEC DYNAMICS) software with the fast Fourier transform cross-correlation technique (Willert & Gharib Reference Willert and Gharib1991). Each image is processed to produce
![]() $127\times 127$
vectors from interrogation windows with a 50 % overlap in each direction. When the ratio of the first and the second correlation peaks in an interrogation window is smaller than 1.3, it is removed from the process as an error vector. Furthermore, the moving-average validation (Host-Madsen & McCluskey Reference Host-Madsen and McCluskey1994) is applied with an acceptance factor of 0.1. In the present study, the removed error vectors amount to less than 3 % of the total data processed.
$127\times 127$
vectors from interrogation windows with a 50 % overlap in each direction. When the ratio of the first and the second correlation peaks in an interrogation window is smaller than 1.3, it is removed from the process as an error vector. Furthermore, the moving-average validation (Host-Madsen & McCluskey Reference Host-Madsen and McCluskey1994) is applied with an acceptance factor of 0.1. In the present study, the removed error vectors amount to less than 3 % of the total data processed.
By using image processing software, the average number of pixels for a particle image captured by the CCD camera in the present study is counted to be approximately 3–4 pixels. According to the discussions of Prasad et al. (Reference Prasad, Adrian, Landreth and Offutt1992), when particle images are well resolved so that the ratio of particle-image diameter to the size of a CCD pixel on the photograph is greater than 3–4, the uncertainty of the measurements is approximately
![]() $1/10$
–
$1/10$
–
![]() $1/20$
of the particle-image diameter. This indicates that the particle images are well resolved in the present experiments, and the uncertainty in the measured displacement can be expected to be approximately less than
$1/20$
of the particle-image diameter. This indicates that the particle images are well resolved in the present experiments, and the uncertainty in the measured displacement can be expected to be approximately less than
![]() $1/10$
of the diameter of the particle image. Normalizing this uncertainty by the mean displacement length of particles indicates that the estimated error of the magnitude of the instantaneous velocity is less than 4 % of the maximum velocity near the channel centreline.
$1/10$
of the diameter of the particle image. Normalizing this uncertainty by the mean displacement length of particles indicates that the estimated error of the magnitude of the instantaneous velocity is less than 4 % of the maximum velocity near the channel centreline.
3 Results and discussions
Figure 3 shows examples indicating the two-dimensionality of the flow field and the reproducibility of the data between the
![]() $x$
–
$x$
–
![]() $y$
and
$y$
and
![]() $x$
–
$x$
–
![]() $z$
plane measurements. From figure 3(a), two-dimensionality can be reasonably attained in
$z$
plane measurements. From figure 3(a), two-dimensionality can be reasonably attained in
![]() $z/W=0.1{-}0.9$
and the measured flow fields of
$z/W=0.1{-}0.9$
and the measured flow fields of
![]() $x$
–
$x$
–
![]() $z$
planes for
$z$
planes for
![]() $z/W=0.37{-}0.63$
are well assured to be two-dimensional. It is seen that the measured velocities for the
$z/W=0.37{-}0.63$
are well assured to be two-dimensional. It is seen that the measured velocities for the
![]() $x$
–
$x$
–
![]() $z$
planes agree well with the data of the
$z$
planes agree well with the data of the
![]() $x$
–
$x$
–
![]() $y$
plane measurement in figure 3(b). In the plots of the
$y$
plane measurement in figure 3(b). In the plots of the
![]() $x$
–
$x$
–
![]() $z$
planes, there is a small gap around
$z$
planes, there is a small gap around
![]() $y/H=0.3$
. It suggests that the setting error for the
$y/H=0.3$
. It suggests that the setting error for the
![]() $x$
–
$x$
–
![]() $z$
plane measurements was of such an order.
$z$
plane measurements was of such an order.
The
![]() $x$
–
$x$
–
![]() $z$
plane measurements are performed for solid smooth wall, No. 20, No. 13 and No. 06 porous wall cases, changing
$z$
plane measurements are performed for solid smooth wall, No. 20, No. 13 and No. 06 porous wall cases, changing
![]() $Re_{b}$
from 1500 to 15 900 to achieve the conditions of
$Re_{b}$
from 1500 to 15 900 to achieve the conditions of
![]() $Re_{K}$
approximately at 1.0, 2.0, 3.0, 6.0 and 10.0. There are altogether 15 cases, as shown in table 2. For each case, several measurement planes in the wall normal direction are measured. In table 2, measured sections 5, 5
$Re_{K}$
approximately at 1.0, 2.0, 3.0, 6.0 and 10.0. There are altogether 15 cases, as shown in table 2. For each case, several measurement planes in the wall normal direction are measured. In table 2, measured sections 5, 5
![]() $^{\ast }$
, 14, 14
$^{\ast }$
, 14, 14
![]() $^{\ast }$
, 15 and 18 correspond to sections of (1.0, 2.0, 3.0, 4.0, 5.0 mm), (0.5, 1.0, 1.5, 2.0, 2.5 mm),
$^{\ast }$
, 15 and 18 correspond to sections of (1.0, 2.0, 3.0, 4.0, 5.0 mm), (0.5, 1.0, 1.5, 2.0, 2.5 mm),
![]() $(1.0,2.0,3.0,\ldots ,14.0,15.0~\text{mm})$
,
$(1.0,2.0,3.0,\ldots ,14.0,15.0~\text{mm})$
,
![]() $(1.0,2.0,3.0,\ldots ,13.0,14.0~\text{mm})$
,
$(1.0,2.0,3.0,\ldots ,13.0,14.0~\text{mm})$
,
![]() $(0.5,1.0,1.5,2.0,2.5,3.0,4.0,\ldots ,10.0,11.0~\text{mm})$
and
$(0.5,1.0,1.5,2.0,2.5,3.0,4.0,\ldots ,10.0,11.0~\text{mm})$
and
![]() $(0.5,1.0,1.5,2.0,2.5,3.0,4.0,\ldots ,14.0,15.0~\text{mm})$
from the bottom surface, respectively.
$(0.5,1.0,1.5,2.0,2.5,3.0,4.0,\ldots ,14.0,15.0~\text{mm})$
from the bottom surface, respectively.

Figure 3. Two-dimensionality and reproducibility in the flow field measurements: (a) streamwise mean velocity distribution in the spanwise direction at
![]() $y/H=0.5$
and
$y/H=0.5$
and
![]() $Re_{b}=6200$
for No. 06 porous wall, (b) comparison of the streamwise mean velocity distribution between
$Re_{b}=6200$
for No. 06 porous wall, (b) comparison of the streamwise mean velocity distribution between
![]() $x$
–
$x$
–
![]() $y$
and
$y$
and
![]() $x$
–
$x$
–
![]() $z$
plane measurements at
$z$
plane measurements at
![]() $Re_{b}=3100$
for No. 13 porous wall.
$Re_{b}=3100$
for No. 13 porous wall.
Table 2. Experimental conditions and measured parameters of the mean velocity fields;
![]() $u_{\unicode[STIX]{x1D70F}}^{t}$
and
$u_{\unicode[STIX]{x1D70F}}^{t}$
and
![]() $u_{\unicode[STIX]{x1D70F}}^{p}$
are the friction velocities on the top solid and bottom porous walls;
$u_{\unicode[STIX]{x1D70F}}^{p}$
are the friction velocities on the top solid and bottom porous walls;
![]() $\unicode[STIX]{x1D705},d$
and
$\unicode[STIX]{x1D705},d$
and
![]() $h$
are the von Kármán coefficient, the zero-plane displacement and the roughness length scale, respectively;
$h$
are the von Kármán coefficient, the zero-plane displacement and the roughness length scale, respectively;
![]() $(\cdot )^{p+}$
corresponds to a value normalized by using
$(\cdot )^{p+}$
corresponds to a value normalized by using
![]() $u_{\unicode[STIX]{x1D70F}}^{p}$
.
$u_{\unicode[STIX]{x1D70F}}^{p}$
.

3.1 Snapshots of streaks
Figure 4 shows snapshots of the instantaneous streamwise velocity fluctuation
![]() $u^{\prime }$
indicating low- and high-speed streaks and corresponding vorticity maps over porous walls at
$u^{\prime }$
indicating low- and high-speed streaks and corresponding vorticity maps over porous walls at
![]() $y^{p+}\simeq 20$
, where
$y^{p+}\simeq 20$
, where
![]() $(\cdot )^{p+}$
is a value normalized by the friction velocity
$(\cdot )^{p+}$
is a value normalized by the friction velocity
![]() $u_{\unicode[STIX]{x1D70F}}^{p}$
on the porous wall which is estimated by extrapolating the Reynolds shear stress distribution obtained by the corresponding
$u_{\unicode[STIX]{x1D70F}}^{p}$
on the porous wall which is estimated by extrapolating the Reynolds shear stress distribution obtained by the corresponding
![]() $x$
–
$x$
–
![]() $y$
plane measurement. Since in the previous study (Suga et al.
Reference Suga, Matsumura, Ashitaka, Tominaga and Kaneda2010) all the data for No. 20, No. 13 and No. 06 porous media were well correlated with
$y$
plane measurement. Since in the previous study (Suga et al.
Reference Suga, Matsumura, Ashitaka, Tominaga and Kaneda2010) all the data for No. 20, No. 13 and No. 06 porous media were well correlated with
![]() $Re_{K}$
, figure 4 arranges the snapshots in the order of
$Re_{K}$
, figure 4 arranges the snapshots in the order of
![]() $Re_{K}$
irrespective of the porous media. (Indeed, the patterns of different porous medium cases are very similar to each other at similar
$Re_{K}$
irrespective of the porous media. (Indeed, the patterns of different porous medium cases are very similar to each other at similar
![]() $Re_{K}$
conditions.) Note that
$Re_{K}$
conditions.) Note that
![]() $y=0$
corresponds to the porous wall surface and all area sizes of the sub-figures are set to
$y=0$
corresponds to the porous wall surface and all area sizes of the sub-figures are set to
![]() $L_{x}^{p+}\times L_{z}^{p+}=990\times 550$
to compare the scales of structural elements. The existence of the streaky structure is obvious in figure 4(a–d) at
$L_{x}^{p+}\times L_{z}^{p+}=990\times 550$
to compare the scales of structural elements. The existence of the streaky structure is obvious in figure 4(a–d) at
![]() $Re_{K}=0.93{-}1.79$
although they are twisted. It is obvious that the patterns in the vorticity
$Re_{K}=0.93{-}1.79$
although they are twisted. It is obvious that the patterns in the vorticity
![]() $\unicode[STIX]{x1D714}_{y}^{p+}$
maps are consistent with those in the maps of the high- and low-speed streaks. In figure 4(e,f) at
$\unicode[STIX]{x1D714}_{y}^{p+}$
maps are consistent with those in the maps of the high- and low-speed streaks. In figure 4(e,f) at
![]() $Re_{K}=2.94$
, the twisting degree significantly increases and the streaks tend to be torn into fragments. Such a tendency is obvious in the vorticity map of figure 4(f), and longitudinally elongated streaks can no longer be observed. Accordingly, it is confirmed that the quasi-streak-like structure is maintained near a wall at a lower
$Re_{K}=2.94$
, the twisting degree significantly increases and the streaks tend to be torn into fragments. Such a tendency is obvious in the vorticity map of figure 4(f), and longitudinally elongated streaks can no longer be observed. Accordingly, it is confirmed that the quasi-streak-like structure is maintained near a wall at a lower
![]() $Re_{K}$
, while it tends to be destroyed as
$Re_{K}$
, while it tends to be destroyed as
![]() $Re_{K}$
increases.
$Re_{K}$
increases.

Figure 4. Snapshots of streamwise velocity fluctuation indicating low- and high-speed streaks and instantaneous wall normal vorticity
![]() $\unicode[STIX]{x1D714}_{y}^{p+}=(\unicode[STIX]{x2202}u/\unicode[STIX]{x2202}z-\unicode[STIX]{x2202}w/\unicode[STIX]{x2202}x)\unicode[STIX]{x1D708}/(u_{\unicode[STIX]{x1D70F}}^{p+})^{2}$
in the window of
$\unicode[STIX]{x1D714}_{y}^{p+}=(\unicode[STIX]{x2202}u/\unicode[STIX]{x2202}z-\unicode[STIX]{x2202}w/\unicode[STIX]{x2202}x)\unicode[STIX]{x1D708}/(u_{\unicode[STIX]{x1D70F}}^{p+})^{2}$
in the window of
![]() $L_{x}^{p+}\times L_{z}^{p+}=990\times 550$
at
$L_{x}^{p+}\times L_{z}^{p+}=990\times 550$
at
![]() $y^{p+}\simeq 20$
: (a,c,e,g,i) are fluctuation velocity contours and (b,d,f,h,j) are vorticity contours. (a,b) No. 20 porous wall at
$y^{p+}\simeq 20$
: (a,c,e,g,i) are fluctuation velocity contours and (b,d,f,h,j) are vorticity contours. (a,b) No. 20 porous wall at
![]() $Re_{K}=0.93$
and
$Re_{K}=0.93$
and
![]() $Re_{b}=2500$
, (c,d) No. 13 porous wall at
$Re_{b}=2500$
, (c,d) No. 13 porous wall at
![]() $Re_{K}=1.79$
and
$Re_{K}=1.79$
and
![]() $Re_{b}=3100$
, (e,f) No. 06 porous wall at
$Re_{b}=3100$
, (e,f) No. 06 porous wall at
![]() $Re_{K}=2.94$
and
$Re_{K}=2.94$
and
![]() $Re_{b}=2700$
, (g,h) No. 20 porous wall at
$Re_{b}=2700$
, (g,h) No. 20 porous wall at
![]() $Re_{K}=6.23$
and
$Re_{K}=6.23$
and
![]() $Re_{b}=14800$
, (i,j) No. 06 porous wall at
$Re_{b}=14800$
, (i,j) No. 06 porous wall at
![]() $Re_{K}=11.12$
and
$Re_{K}=11.12$
and
![]() $Re_{b}=9900$
. The flow direction is left to right.
$Re_{b}=9900$
. The flow direction is left to right.

Figure 5. Snapshots of low- and high-speed fluid lumps in the measurement areas of
![]() $L_{x}/H\times L_{z}/H=4.8\times 2.7$
at
$L_{x}/H\times L_{z}/H=4.8\times 2.7$
at
![]() $y^{p+}\simeq 20$
: (a) No. 20 porous wall at
$y^{p+}\simeq 20$
: (a) No. 20 porous wall at
![]() $Re_{K}=6.23$
and
$Re_{K}=6.23$
and
![]() $Re_{b}=14800$
(corresponding to figure 4
g), (b) No. 06 porous wall at
$Re_{b}=14800$
(corresponding to figure 4
g), (b) No. 06 porous wall at
![]() $Re_{K}=11.12$
and
$Re_{K}=11.12$
and
![]() $Re_{b}=9900$
(corresponding to figure 4
i).
$Re_{b}=9900$
(corresponding to figure 4
i).

Figure 6. Two-point correlation of the streamwise velocity versus spanwise spacing: (a) solid wall at
![]() $Re_{b}=5600$
, (b) porous wall No. 20 at
$Re_{b}=5600$
, (b) porous wall No. 20 at
![]() $Re_{K}=0.93$
and
$Re_{K}=0.93$
and
![]() $Re_{b}=2500$
, (c) porous wall No. 13 at
$Re_{b}=2500$
, (c) porous wall No. 13 at
![]() $Re_{K}=1.79$
and
$Re_{K}=1.79$
and
![]() $Re_{b}=3100$
, (d) porous wall No. 06 at
$Re_{b}=3100$
, (d) porous wall No. 06 at
![]() $Re_{K}=2.94$
and
$Re_{K}=2.94$
and
![]() $Re_{b}=2700$
, (e) porous wall No. 20 at
$Re_{b}=2700$
, (e) porous wall No. 20 at
![]() $Re_{K}=6.23$
and
$Re_{K}=6.23$
and
![]() $Re_{b}=14\,800$
, (f) porous wall No. 06 at
$Re_{b}=14\,800$
, (f) porous wall No. 06 at
![]() $Re_{K}=11.12$
and
$Re_{K}=11.12$
and
![]() $Re_{b}=9900$
.
$Re_{b}=9900$
.
At the higher-
![]() $Re_{K}$
cases of
$Re_{K}$
cases of
![]() $Re_{K}=6.23$
and 11.12, in figure 4(g–j), although low- and high-speed fluid lumps exist, obvious streak-like vorticity patterns cannot be observed in the windows of
$Re_{K}=6.23$
and 11.12, in figure 4(g–j), although low- and high-speed fluid lumps exist, obvious streak-like vorticity patterns cannot be observed in the windows of
![]() $L_{x}^{p+}\times L_{z}^{p+}=990\times 550$
. To see those fluid lumps on a wider scale, figure 5 shows patterns of low- and high-speed fluid lumps for the cases of figure 4(g,i). The window size of these sub-figures is
$L_{x}^{p+}\times L_{z}^{p+}=990\times 550$
. To see those fluid lumps on a wider scale, figure 5 shows patterns of low- and high-speed fluid lumps for the cases of figure 4(g,i). The window size of these sub-figures is
![]() $L_{x}/H\times L_{z}/H=4.8\times 2.7$
, which corresponds to
$L_{x}/H\times L_{z}/H=4.8\times 2.7$
, which corresponds to
![]() $L_{x}^{p+}\times L_{z}^{p+}=6670\times 3670$
and
$L_{x}^{p+}\times L_{z}^{p+}=6670\times 3670$
and
![]() $5660\times 3100$
for figures 5(a) and 5(b), respectively. Obviously, the pattens shown in figure 5 are very different from the longitudinally elongated streak structure, and large-scale spanwise patterns seem to be developing as in figure 5(b). Indeed, in the streamwise direction, black and white block areas can be seen in turn. This is considered to be footprints of the spanwise transverse rolls induced by the Kelvin–Helmholtz (K–H) instability as reported numerically by Jiménez et al. (Reference Jiménez, Uhlmann, Pinelli and Kawahara2001) and Kuwata & Suga (Reference Kuwata and Suga2016a
).
$5660\times 3100$
for figures 5(a) and 5(b), respectively. Obviously, the pattens shown in figure 5 are very different from the longitudinally elongated streak structure, and large-scale spanwise patterns seem to be developing as in figure 5(b). Indeed, in the streamwise direction, black and white block areas can be seen in turn. This is considered to be footprints of the spanwise transverse rolls induced by the Kelvin–Helmholtz (K–H) instability as reported numerically by Jiménez et al. (Reference Jiménez, Uhlmann, Pinelli and Kawahara2001) and Kuwata & Suga (Reference Kuwata and Suga2016a
).

Figure 7. Distribution of spanwise spacing of streaks in the wall normal direction: (a) solid wall, (b) porous wall No. 20, (c) porous wall No. 13, (d) porous wall No. 06; hatching zone is the zone where the plots start to deviate largely from the broken line; broken line indicates the fitting line of the solid-wall cases.
3.2 Scales of spanwise structure
To discuss scales of the coherent structure, the normalized two-point correlation function:
in the spanwise direction is discussed. Figure 6 shows
![]() $\widehat{R_{11}}(\unicode[STIX]{x0394}z)$
distributions which correspond to the solid-wall case: figure 6(a), and the five
$\widehat{R_{11}}(\unicode[STIX]{x0394}z)$
distributions which correspond to the solid-wall case: figure 6(a), and the five
![]() $Re_{K}$
cases shown in figure 4. For all the cases local minima can be seen, while their depths (magnitudes) and positions change depending on the wall normal distance. This trend is consistent with the results of Breugem et al. (Reference Breugem, Boersma and Uittenbogaard2006). Moreover, generally the depth tends to decrease, and the oscillations observed after the local minima vanish as
$Re_{K}$
cases shown in figure 4. For all the cases local minima can be seen, while their depths (magnitudes) and positions change depending on the wall normal distance. This trend is consistent with the results of Breugem et al. (Reference Breugem, Boersma and Uittenbogaard2006). Moreover, generally the depth tends to decrease, and the oscillations observed after the local minima vanish as
![]() $Re_{K}$
increases. Since the local minimum corresponds to the average spanwise distance between low-speed and neighbouring high-speed regions, the decrease of its magnitude and vanishing oscillations indicate that the streak structure tends to vanish as
$Re_{K}$
increases. Since the local minimum corresponds to the average spanwise distance between low-speed and neighbouring high-speed regions, the decrease of its magnitude and vanishing oscillations indicate that the streak structure tends to vanish as
![]() $Re_{K}$
increases.
$Re_{K}$
increases.
From the locations of the local minima, the distributions of the spanwise spacing of streaks
![]() $\unicode[STIX]{x1D706}_{z}^{p+}$
(or
$\unicode[STIX]{x1D706}_{z}^{p+}$
(or
![]() $\unicode[STIX]{x1D706}_{z}^{+}$
for solid walls) against the wall normal distance (plus the zero-plane displacement) are obtained as in figure 7. Figure 7(a) compares the solid smooth wall results and published data in the literature (Smith & Metzler Reference Smith and Metzler1983; Iritani, Kasagi & Hirata Reference Iritani, Kasagi and Hirata1985; Kim, Moin & Moser Reference Kim, Moin and Moser1987; Tomkins & Adrian Reference Tomkins and Adrian2003). It is seen that all the data align well on a single curve, indicating that the streaks over the solid smooth walls are well organized and their spacing is approximately 100 wall units under
$\unicode[STIX]{x1D706}_{z}^{+}$
for solid walls) against the wall normal distance (plus the zero-plane displacement) are obtained as in figure 7. Figure 7(a) compares the solid smooth wall results and published data in the literature (Smith & Metzler Reference Smith and Metzler1983; Iritani, Kasagi & Hirata Reference Iritani, Kasagi and Hirata1985; Kim, Moin & Moser Reference Kim, Moin and Moser1987; Tomkins & Adrian Reference Tomkins and Adrian2003). It is seen that all the data align well on a single curve, indicating that the streaks over the solid smooth walls are well organized and their spacing is approximately 100 wall units under
![]() $y^{+}=20$
, while it gradually increases as the wall normal distance increases.
$y^{+}=20$
, while it gradually increases as the wall normal distance increases.
In figure 7(b–d), it is found that the points of
![]() $\unicode[STIX]{x1D706}_{z}^{p+}$
collapse around the curve under
$\unicode[STIX]{x1D706}_{z}^{p+}$
collapse around the curve under
![]() $(y+d)^{p+}\simeq 100$
reasonably well when the zero-plane displacement
$(y+d)^{p+}\simeq 100$
reasonably well when the zero-plane displacement
![]() $d$
is combined with the wall normal distance. The zero-plane displacement is a parameter in the log-law form for the mean velocity over porous walls. (See appendix A for comments on the parameters of log-law velocities listed in table 2.) Indeed, in figure 7(b–d) plots for No. 20, No. 13 and No. 06 cases are in reasonable agreement with the line representing the correlation of the solid-wall case under
$d$
is combined with the wall normal distance. The zero-plane displacement is a parameter in the log-law form for the mean velocity over porous walls. (See appendix A for comments on the parameters of log-law velocities listed in table 2.) Indeed, in figure 7(b–d) plots for No. 20, No. 13 and No. 06 cases are in reasonable agreement with the line representing the correlation of the solid-wall case under
![]() $(y+d)^{p+}\simeq 70$
, 90 and 80, respectively. It is considered that quasi-coherent streaks over a porous wall generated by the wall shear are pushed into the porous wall by downward motions of the K–H waves. Since the zero-plane displacement is considered to be a length scale associated with the penetration, the agreement between the plots and lines in figure 7(b–d) suggests that the structure retains the characteristics of streaks even if their bottom parts penetrate into the porous walls. Hence,
$(y+d)^{p+}\simeq 70$
, 90 and 80, respectively. It is considered that quasi-coherent streaks over a porous wall generated by the wall shear are pushed into the porous wall by downward motions of the K–H waves. Since the zero-plane displacement is considered to be a length scale associated with the penetration, the agreement between the plots and lines in figure 7(b–d) suggests that the structure retains the characteristics of streaks even if their bottom parts penetrate into the porous walls. Hence,
![]() $\unicode[STIX]{x1D706}_{z}^{p+}$
shows the correlation with
$\unicode[STIX]{x1D706}_{z}^{p+}$
shows the correlation with
![]() $(y+d)^{p+}$
. However, at positions of certain distances from the wall surfaces, in the regions which are marked by hatching zones, the plotted values start to deviate largely from the correlation line. Although the ranges of the hatching zones are different in the porous layer cases, their locations are around
$(y+d)^{p+}$
. However, at positions of certain distances from the wall surfaces, in the regions which are marked by hatching zones, the plotted values start to deviate largely from the correlation line. Although the ranges of the hatching zones are different in the porous layer cases, their locations are around
![]() $(y+d)^{p+}\simeq 100$
. This region where the trend changes is considered to be a structural transition region. It is considered that the quasi-streaky structure is smeared or may no longer exist over such regions. Indeed, the snapshots shown in figure 5 are the cases inside and over the hatching zones.
$(y+d)^{p+}\simeq 100$
. This region where the trend changes is considered to be a structural transition region. It is considered that the quasi-streaky structure is smeared or may no longer exist over such regions. Indeed, the snapshots shown in figure 5 are the cases inside and over the hatching zones.
Suga et al. (Reference Suga, Mori and Kaneda2011) observed another transitional change in the distributions of turbulence fluctuation velocities over porous walls. The shape of the joint probability density function
![]() $p(u^{\prime },v^{\prime })$
of the fluctuation velocity at
$p(u^{\prime },v^{\prime })$
of the fluctuation velocity at
![]() $y^{p+}\simeq 15$
changed in the condition under
$y^{p+}\simeq 15$
changed in the condition under
![]() $Re_{K}\simeq 3$
. (The turbulence anisotropy tended to rapidly weaken as
$Re_{K}\simeq 3$
. (The turbulence anisotropy tended to rapidly weaken as
![]() $Re_{K}$
increased up to
$Re_{K}$
increased up to
![]() $Re_{K}\simeq 3$
.) The location at
$Re_{K}\simeq 3$
.) The location at
![]() $y^{p+}\simeq 15$
under
$y^{p+}\simeq 15$
under
![]() $Re_{K}\simeq 3$
corresponds to the region under
$Re_{K}\simeq 3$
corresponds to the region under
![]() $(y+d)^{p+}\simeq 47$
if the correlation
$(y+d)^{p+}\simeq 47$
if the correlation
![]() $d^{p+}\simeq 15.1Re_{K}-13.5$
, which was seen in Suga et al. (Reference Suga, Matsumura, Ashitaka, Tominaga and Kaneda2010), is valid. (In the present cases of
$d^{p+}\simeq 15.1Re_{K}-13.5$
, which was seen in Suga et al. (Reference Suga, Matsumura, Ashitaka, Tominaga and Kaneda2010), is valid. (In the present cases of
![]() $Re_{K}=2.90{-}3.00$
,
$Re_{K}=2.90{-}3.00$
,
![]() $y^{p+}=15$
corresponds to
$y^{p+}=15$
corresponds to
![]() $(y+d)^{p+}=36-60$
.) This indicates that the transitional change of the spanwise turbulence scale occurs after the transitional change of the near-wall turbulence anisotropy.
$(y+d)^{p+}=36-60$
.) This indicates that the transitional change of the spanwise turbulence scale occurs after the transitional change of the near-wall turbulence anisotropy.
To see the vortex length scales, figure 8 shows the distribution of the spanwise integral length
![]() $\unicode[STIX]{x1D6EC}_{11}$
, which is defined as
$\unicode[STIX]{x1D6EC}_{11}$
, which is defined as
It is seen that a cluster involving the solid-wall case extends up to
![]() $(y+d)^{p+}\simeq 300$
and the length scale size ranges as
$(y+d)^{p+}\simeq 300$
and the length scale size ranges as
![]() $\unicode[STIX]{x1D6EC}_{11}^{p+}=5{-}25$
. However, it is indicated that at
$\unicode[STIX]{x1D6EC}_{11}^{p+}=5{-}25$
. However, it is indicated that at
![]() $(y+d)^{p+}>100$
, flow motions with much larger scales coexist and start to be dominant. This suggests that fragments of the torn longitudinal vortex tubes are entrained by the large-scale fluid lumps moving with travelling transverse waves.
$(y+d)^{p+}>100$
, flow motions with much larger scales coexist and start to be dominant. This suggests that fragments of the torn longitudinal vortex tubes are entrained by the large-scale fluid lumps moving with travelling transverse waves.

Figure 8. Integral length variations in the wall normal direction.
4 Concluding summary
At a lower
![]() $Re_{K}$
, low- and high-speed streaks, which are similar to those of solid-wall turbulence, are observed near the permeable walls. In case of a large
$Re_{K}$
, low- and high-speed streaks, which are similar to those of solid-wall turbulence, are observed near the permeable walls. In case of a large
![]() $Re_{K}$
, although some large-scale patterns are observed in the velocity field, they are confirmed to be very different from those of the solid-wall turbulence structure. It is found that the spanwise spacing of the streaks
$Re_{K}$
, although some large-scale patterns are observed in the velocity field, they are confirmed to be very different from those of the solid-wall turbulence structure. It is found that the spanwise spacing of the streaks
![]() $\unicode[STIX]{x1D706}_{z}$
and the spanwise integral length
$\unicode[STIX]{x1D706}_{z}$
and the spanwise integral length
![]() $\unicode[STIX]{x1D6EC}_{11}$
can be reasonably correlated with the wall normal distance including the zero-plane displacement
$\unicode[STIX]{x1D6EC}_{11}$
can be reasonably correlated with the wall normal distance including the zero-plane displacement
![]() $d$
of the log-law mean velocity profile. Since there is a correlation between
$d$
of the log-law mean velocity profile. Since there is a correlation between
![]() $d^{p+}$
and
$d^{p+}$
and
![]() $Re_{K}$
(Suga et al.
Reference Suga, Matsumura, Ashitaka, Tominaga and Kaneda2010), these phenomena have a correlation with
$Re_{K}$
(Suga et al.
Reference Suga, Matsumura, Ashitaka, Tominaga and Kaneda2010), these phenomena have a correlation with
![]() $Re_{K}$
via
$Re_{K}$
via
![]() $d^{p+}$
. It is considered that quasi-coherent streaks over permeable walls generated by the wall shear are pushed into the porous walls by the downward motions of the K–H waves. Since the zero-plane displacement
$d^{p+}$
. It is considered that quasi-coherent streaks over permeable walls generated by the wall shear are pushed into the porous walls by the downward motions of the K–H waves. Since the zero-plane displacement
![]() $d$
is considered to be a length scale associated with the penetration, the distribution profiles of those scales (
$d$
is considered to be a length scale associated with the penetration, the distribution profiles of those scales (
![]() $\unicode[STIX]{x1D706}_{z}$
and
$\unicode[STIX]{x1D706}_{z}$
and
![]() $\unicode[STIX]{x1D6EC}_{11}$
) indicate that the structure keeps the characteristics of streaks even if their bottom parts penetrate into the porous walls. Accordingly, the surviving elements of the streaks exist and their scales maintain correlations with the wall normal distance under the transitional range starting from
$\unicode[STIX]{x1D6EC}_{11}$
) indicate that the structure keeps the characteristics of streaks even if their bottom parts penetrate into the porous walls. Accordingly, the surviving elements of the streaks exist and their scales maintain correlations with the wall normal distance under the transitional range starting from
![]() $(y+d)^{p+}\simeq 100$
, while those elements tend to be disturbed by the K–H instability as the wall normal distance increases. From the region at
$(y+d)^{p+}\simeq 100$
, while those elements tend to be disturbed by the K–H instability as the wall normal distance increases. From the region at
![]() $(y+d)^{p+}>100$
, flow motions with much larger spanwise length scales start to be dominant. Such flow motions are considered to be transverse roll cells which are generated by the K–H instability and destroy the longitudinal vortex trails. It is considered that fragments of the torn longitudinal vortex tubes surf over the transverse travelling waves. When
$(y+d)^{p+}>100$
, flow motions with much larger spanwise length scales start to be dominant. Such flow motions are considered to be transverse roll cells which are generated by the K–H instability and destroy the longitudinal vortex trails. It is considered that fragments of the torn longitudinal vortex tubes surf over the transverse travelling waves. When
![]() $Re_{K}$
is large enough,
$Re_{K}$
is large enough,
![]() $d^{p+}$
becomes close to or even surpasses 100, resulting in the loss of the quasi-streak structure near the surfaces.
$d^{p+}$
becomes close to or even surpasses 100, resulting in the loss of the quasi-streak structure near the surfaces.
Acknowledgements
The authors thank their colleague A. Taneo for processing the experimental data. A part of this study was financially supported by a research grant (no. 24360073) of the JSPS Japan.
Appendix A. Parameters of log-law velocity profile
For turbulent flows above rough beds or submerged canopies, following Best (Reference Best1935), the log-law form:
is usually applied (e.g. Nikora et al.
Reference Nikora, Koll, McLean, Dittrich and Aberle2002; Nepf & Ghisalberti Reference Nepf and Ghisalberti2008; Suga et al.
Reference Suga, Matsumura, Ashitaka, Tominaga and Kaneda2010; Manes et al.
Reference Manes, Poggi and Ridol2011), where
![]() $\unicode[STIX]{x1D705}$
is the von Kármán coefficient,
$\unicode[STIX]{x1D705}$
is the von Kármán coefficient,
![]() $h$
is the roughness length scale and
$h$
is the roughness length scale and
![]() $d$
is the depth of the zero-plane from the surface in the present geometrical definition. Figure 9(a) illustrates those parameters. Note that the correlation by Nikuradse (Reference Nikuradse1933) for rough wall boundary layers is essentially the same as (A 1) if the origin of
$d$
is the depth of the zero-plane from the surface in the present geometrical definition. Figure 9(a) illustrates those parameters. Note that the correlation by Nikuradse (Reference Nikuradse1933) for rough wall boundary layers is essentially the same as (A 1) if the origin of
![]() $y$
-axis is set to the zero-plane illustrated in figure 9(a). Table 2 lists the values of
$y$
-axis is set to the zero-plane illustrated in figure 9(a). Table 2 lists the values of
![]() $\unicode[STIX]{x1D705}$
,
$\unicode[STIX]{x1D705}$
,
![]() $d$
and
$d$
and
![]() $h$
obtained by the fitting method for velocity profiles described below. (At
$h$
obtained by the fitting method for velocity profiles described below. (At
![]() $Re_{b}<2000$
, the values are not listed in table 2 since the logarithmic layers cannot be obviously recognized.) Although the listed values of
$Re_{b}<2000$
, the values are not listed in table 2 since the logarithmic layers cannot be obviously recognized.) Although the listed values of
![]() $d$
and
$d$
and
![]() $h$
are non-dimensionalized, they can be easily dimensionalized by taking ratios by
$h$
are non-dimensionalized, they can be easily dimensionalized by taking ratios by
![]() $Re_{K}$
. For example, since
$Re_{K}$
. For example, since
![]() $d^{p+}/Re_{K}=(u_{\unicode[STIX]{x1D70F}}^{p}d/\unicode[STIX]{x1D708})/(u_{\unicode[STIX]{x1D70F}}^{p}K^{1/2}/\unicode[STIX]{x1D708})=d/K^{1/2}$
, with the value of the permeability listed in table 1 one can calculate the dimensional value of
$d^{p+}/Re_{K}=(u_{\unicode[STIX]{x1D70F}}^{p}d/\unicode[STIX]{x1D708})/(u_{\unicode[STIX]{x1D70F}}^{p}K^{1/2}/\unicode[STIX]{x1D708})=d/K^{1/2}$
, with the value of the permeability listed in table 1 one can calculate the dimensional value of
![]() $d$
.
$d$
.

Figure 9. Parameters of mean velocity: (a) zero-plane displacement
![]() $d$
and roughness length scale
$d$
and roughness length scale
![]() $h$
, (b) logarithmic layer indicated by
$h$
, (b) logarithmic layer indicated by
![]() $(y+d)\,\text{d}U^{p+}/\text{d}y$
.
$(y+d)\,\text{d}U^{p+}/\text{d}y$
.

Figure 10. Distribution of parameters of mean velocity profiles against the permeability Reynolds number: (a) von Kármán coefficient, (b) zero-plane displacement, (c) roughness length scale; ○, ●,
![]() $\times$
and * are the present data, the data of Suga et al. (Reference Suga, Matsumura, Ashitaka, Tominaga and Kaneda2010), Breugem et al. (Reference Breugem, Boersma and Uittenbogaard2006) and Manes et al. (Reference Manes, Poggi and Ridol2011), respectively.
$\times$
and * are the present data, the data of Suga et al. (Reference Suga, Matsumura, Ashitaka, Tominaga and Kaneda2010), Breugem et al. (Reference Breugem, Boersma and Uittenbogaard2006) and Manes et al. (Reference Manes, Poggi and Ridol2011), respectively.
The extent of the logarithmic layer can be determined from plots of
![]() $(y+d)\,\text{d}U^{+}/\text{d}y$
as a function of
$(y+d)\,\text{d}U^{+}/\text{d}y$
as a function of
![]() $y^{+}$
, changing the values of
$y^{+}$
, changing the values of
![]() $d$
(Breugem et al.
Reference Breugem, Boersma and Uittenbogaard2006). Since
$d$
(Breugem et al.
Reference Breugem, Boersma and Uittenbogaard2006). Since
![]() $(y+d)\,\text{d}U^{+}/\text{d}y$
must be a constant equal to
$(y+d)\,\text{d}U^{+}/\text{d}y$
must be a constant equal to
![]() $1/\unicode[STIX]{x1D705}$
inside the logarithmic layer, a value of
$1/\unicode[STIX]{x1D705}$
inside the logarithmic layer, a value of
![]() $d$
giving a flat plateau in the profile must be the best fitted value. For example, in figure 9(b), a flat plateau can be obtained with
$d$
giving a flat plateau in the profile must be the best fitted value. For example, in figure 9(b), a flat plateau can be obtained with
![]() $d^{p+}=51.5$
and the value of the plateau becomes
$d^{p+}=51.5$
and the value of the plateau becomes
![]() $(y+d)\,\text{d}U^{+}/\text{d}y=3.5$
, which corresponds to
$(y+d)\,\text{d}U^{+}/\text{d}y=3.5$
, which corresponds to
![]() $1/\unicode[STIX]{x1D705}$
to be obtained. Then, with these
$1/\unicode[STIX]{x1D705}$
to be obtained. Then, with these
![]() $d$
and
$d$
and
![]() $\unicode[STIX]{x1D705}$
, equation (A 1) is best fitted to the velocity profile to obtain the roughness length scale
$\unicode[STIX]{x1D705}$
, equation (A 1) is best fitted to the velocity profile to obtain the roughness length scale
![]() $h$
.
$h$
.
Suga et al. (Reference Suga, Matsumura, Ashitaka, Tominaga and Kaneda2010) found that
![]() $\unicode[STIX]{x1D705}$
,
$\unicode[STIX]{x1D705}$
,
![]() $d^{p+}$
and
$d^{p+}$
and
![]() $h^{p+}$
had close relationships with the permeability Reynolds number. As seen in figure 10, the data of Suga et al. (Reference Suga, Matsumura, Ashitaka, Tominaga and Kaneda2010) and the present study suggest relationships between
$h^{p+}$
had close relationships with the permeability Reynolds number. As seen in figure 10, the data of Suga et al. (Reference Suga, Matsumura, Ashitaka, Tominaga and Kaneda2010) and the present study suggest relationships between
![]() $Re_{K}$
and the parameters. It is noticeable that, as
$Re_{K}$
and the parameters. It is noticeable that, as
![]() $Re_{K}$
increases,
$Re_{K}$
increases,
![]() $\unicode[STIX]{x1D705}$
becomes smaller than 0.4 while generally
$\unicode[STIX]{x1D705}$
becomes smaller than 0.4 while generally
![]() $d^{p+}$
and
$d^{p+}$
and
![]() $h^{p+}$
monotonically increase. Breugem et al. (Reference Breugem, Boersma and Uittenbogaard2006) also reported that
$h^{p+}$
monotonically increase. Breugem et al. (Reference Breugem, Boersma and Uittenbogaard2006) also reported that
![]() $\unicode[STIX]{x1D705}$
decreased to 0.23 and 0.31, respectively, in the cases of
$\unicode[STIX]{x1D705}$
decreased to 0.23 and 0.31, respectively, in the cases of
![]() $\unicode[STIX]{x1D711}=0.95$
and 0.8 of turbulent porous-walled channel flows at
$\unicode[STIX]{x1D711}=0.95$
and 0.8 of turbulent porous-walled channel flows at
![]() $Re_{b}=5500$
. Their permeability Reynolds numbers correspond to
$Re_{b}=5500$
. Their permeability Reynolds numbers correspond to
![]() $Re_{K}=1.06$
and 9.35, respectively. In the turbulent open channel flows over polyurethane foam beds whose porosities were 96.4
$Re_{K}=1.06$
and 9.35, respectively. In the turbulent open channel flows over polyurethane foam beds whose porosities were 96.4
![]() $-$
98.0 by Manes et al. (Reference Manes, Poggi and Ridol2011),
$-$
98.0 by Manes et al. (Reference Manes, Poggi and Ridol2011),
![]() $\unicode[STIX]{x1D705}$
ranged between 0.31 and 0.33, depending on the permeability Reynolds number at
$\unicode[STIX]{x1D705}$
ranged between 0.31 and 0.33, depending on the permeability Reynolds number at
![]() $Re_{K}=1.9{-}17.2$
. Those results shown in figure 10(a) support that
$Re_{K}=1.9{-}17.2$
. Those results shown in figure 10(a) support that
![]() $\unicode[STIX]{x1D705}$
becomes smaller than 0.4 in flows over highly porous walls. Such low values of
$\unicode[STIX]{x1D705}$
becomes smaller than 0.4 in flows over highly porous walls. Such low values of
![]() $\unicode[STIX]{x1D705}$
are mainly related to the wall permeability, as Breugem et al. (Reference Breugem, Boersma and Uittenbogaard2006) concluded, since
$\unicode[STIX]{x1D705}$
are mainly related to the wall permeability, as Breugem et al. (Reference Breugem, Boersma and Uittenbogaard2006) concluded, since
![]() $\unicode[STIX]{x1D705}$
is usually approximately 0.4 even for rough walls as in Raupach, Antonia & Rajagopalan (Reference Raupach, Antonia and Rajagopalan1991). The data points in figure 10(a) indicate that there is a relationship between
$\unicode[STIX]{x1D705}$
is usually approximately 0.4 even for rough walls as in Raupach, Antonia & Rajagopalan (Reference Raupach, Antonia and Rajagopalan1991). The data points in figure 10(a) indicate that there is a relationship between
![]() $\unicode[STIX]{x1D705}$
and
$\unicode[STIX]{x1D705}$
and
![]() $Re_{K}$
, though with a certain amount of scattering. As seen in figure 10(b,c),
$Re_{K}$
, though with a certain amount of scattering. As seen in figure 10(b,c),
![]() $d^{p+}$
and
$d^{p+}$
and
![]() $h^{p+}$
increase as
$h^{p+}$
increase as
![]() $Re_{K}$
increases. These trends are also consistent with the results of Breugem et al. (Reference Breugem, Boersma and Uittenbogaard2006) and Manes et al. (Reference Manes, Poggi and Ridol2011).
$Re_{K}$
increases. These trends are also consistent with the results of Breugem et al. (Reference Breugem, Boersma and Uittenbogaard2006) and Manes et al. (Reference Manes, Poggi and Ridol2011).