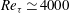1 Introduction
The reduction of skin friction in wall-bounded turbulent shear flows is an important goal to decrease energy expenditure in many industrial sectors. It has a wide range of engineering applications ranging from massive pipelines for oil and gas transport to almost all types of vehicles, ground, air or sea based. Many of these applications typically take place at high Reynolds numbers, and a wealth of systems and techniques to reduce turbulent skin-friction drag have been proposed over many years. In practice, only very few of these systems and techniques have been implemented with any success, and many of them appear to be subject to a performance loss as the Reynolds number increases, as well as suffering from other technical constraints (Bushnell Reference Bushnell2002; García-mayoral & Jiménez Reference García-mayoral and Jiménez2011; Quadrio Reference Quadrio2011; Kornilov Reference Kornilov2015). At low Reynolds numbers, the origin of turbulent skin friction has been inextricably linked to the near-wall region. In this region, the interaction between two predominant coherent structures, streaks (Kline et al.
Reference Kline, Reynolds, Schraub and Rundstatler1967) and quasi-streamwise vortices (Kim, Moin & Moser Reference Kim, Moin and Moser1987; Jeong & Hussain Reference Jeong and Hussain1997), with a mean spanwise spacing of
$\unicode[STIX]{x1D706}_{z}^{+}\approx 100$
, plays a central role in turbulent production (Jiménez & Moin Reference Jiménez and Moin1991; Hamilton, Kim & Waleffe Reference Hamilton, Kim and Waleffe1995; Schoppa & Hussain Reference Schoppa and Hussain2002). The interactive process is essentially independent of the motions in the logarithmic and outer regions, as it survives even when the motions in the logarithmic and outer regions are either poorly resolved (Jiménez & Moin Reference Jiménez and Moin1991) or artificially damped out (Jiménez & Pinelli Reference Jiménez and Pinelli1999; Hwang Reference Hwang2013). The generation of turbulent skin friction (or wall shear stress) has been understood to be directly linked to this near-wall process, and, in particular, the streamwise vortices have been found to be strongly correlated to the near-wall turbulent skin friction (Kravchenko, Choi & Moin Reference Kravchenko, Choi and Moin1993; Choi, Moin & Kim Reference Choi, Moin and Kim1994; Orlandi & Jimenez Reference Orlandi and Jimenez1994). This observation led to the design of flow control strategies aimed at direct disruption of the near-wall streamwise vortices: for example, spanwise oscillations (Stadsted & Moin Reference Stadsted and Moin1991; Jung, Mangiavacchi & Akhavan Reference Jung, Mangiavacchi and Akhavan1992) and opposition control (Choi et al.
Reference Choi, Moin and Kim1994). All these control strategies perform very well at low Reynolds numbers with a considerable amount of turbulent drag reduction. However, it has recently been reported that their effectiveness deteriorates with increasing Reynolds number (Chang, Collis & Ramakrishnan Reference Chang, Collis and Ramakrishnan2002; Gatti & Quadrio Reference Gatti and Quadrio2013), even though the direct effect of these controls on the near-wall region appears to remain unchanged (Agostini, Touber & Leschziner Reference Agostini, Touber and Leschziner2014).
Over the past decade, there has been a substantial amount of evidence that the logarithmic and outer regions of wall-bounded turbulence are organised with remarkable coherence. The most well-known coherent structures in these regions are probably large-scale motions (LSMs) (Kovasznay Reference Kovasznay1970) and very-large-scale motions (VLSMs) (Kim & Adrian Reference Kim and Adrian1999; del Alamo & Jiménez Reference del Alamo and Jiménez2003; Hutchins & Marusic Reference Hutchins and Marusic2007a
). In particular, the latter structures were found to prevail over the entire wall-normal location (del Alamo et al.
Reference del Alamo, Jiménez, Zandonade and Moser2004; Tomkins & Adrian Reference Tomkins and Adrian2005), strongly influencing the near-wall region through direct penetration (del Alamo & Jiménez Reference del Alamo and Jiménez2003; Hutchins & Marusic Reference Hutchins and Marusic2007b
) and/or modulation of the near-wall processes (Mathis, Hutchins & Marusic Reference Mathis, Hutchins and Marusic2009; Marusic, Mathis & Hutchins Reference Marusic, Mathis and Hutchins2010; Agostini & Leschziner Reference Agostini and Leschziner2016). Wall shear stress was also reported to be affected by these large-scale structures (Abe, Kawamura & Choi Reference Abe, Kawamura and Choi2004; Schlatter et al.
Reference Schlatter, Örlü, Li, Brethouwer, Fransson, Johansson, Alfredsson and Henningson2009). Recently, Hwang (Reference Hwang2013) showed that removal of the structures, the spanwise sizes of which are larger than
$\unicode[STIX]{x1D706}_{z}^{+}\simeq 100$
, leads to a substantial amount of reduction of skin-friction drag in turbulent channel flow. Importantly, the contribution of the isolated near-wall structures to wall shear stress was found to rapidly decay on increasing the Reynolds number, suggesting that a significant amount of turbulent skin friction originates from the logarithmic and outer regions. The large contribution of the structures above the near-wall region was also confirmed in a turbulent boundary layer more recently by Deck et al. (Reference Deck, Renard, Laraufie and Weiss2014), who calculated contribution of large-scale outer structures to turbulent skin friction. In this work, the FIK identity (Fukagata, Iwamoto & Kasagi Reference Fukagata, Iwamoto and Kasagi2002), which calculates turbulent skin friction with the wall-normal distribution of the Reynolds shear stress, was used with the spectral contribution of the large-scale outer structures to the Reynolds shear stress.
Despite this important progress, it has only been in very recent years that the general organisation of coherent structures above the near-wall region has begun to be unveiled. A growing body of novel evidence has suggested that the logarithmic and outer regions are likely to be composed of statistically self-similar coherent structures, as originally hypothesized by Townsend (Reference Townsend1961, Reference Townsend1976) and Perry & Chong (Reference Perry and Chong1982) who called each of these structures the ‘attached eddy’. For example, recent numerical and laboratory experiments have confirmed the existence of the logarithmic wall-normal dependence of the streamwise and spanwise turbulence intensities (Jiménez & Hoyas Reference Jiménez and Hoyas2008; Marusic et al.
Reference Marusic, Monty, Hultmark and Smits2013; Lee & Moser Reference Lee and Moser2015), as originally predicted by Townsend (Reference Townsend1976). Very recently, Hwang (Reference Hwang2015) directly computed the statistical structure of each of the hypothetical attached eddies using their self-sustaining nature (Hwang & Cossu Reference Hwang and Cossu2010b
, Reference Hwang and Cossu2011). Based on the linearly growing feature of the spanwise length scale with the distance from the wall (Tomkins & Adrian Reference Tomkins and Adrian2003; del Alamo et al.
Reference del Alamo, Jiménez, Zandonade and Moser2004), he found that, in a turbulent channel, the energy-containing motions at each of the spanwise length scales between
$\unicode[STIX]{x1D706}_{z}^{+}\simeq 100$
and
$\unicode[STIX]{x1D706}_{z}\simeq 1.5h$
(
$h$
is half height of the channel) are statistically self-similar to one another, demonstrating the existence of the hypothetical attached eddies. It was shown that the smallest attached eddies are characterized by
$\unicode[STIX]{x1D706}_{z}^{+}\simeq 100$
and are composed of the well-known near-wall streaks and the quasi-streamwise vortices (see also Hwang Reference Hwang2013). On the other hand, the largest ones, characterized by
$\unicode[STIX]{x1D706}_{z}\simeq 1.5h$
, consist of the VLSMs (outer streaks) and the LSMs (outer streamwise vortical structures) (for a detailed discussion, see Hwang Reference Hwang2015). The motions at the intermediate spanwise length scale between
$\unicode[STIX]{x1D706}_{z}^{+}\simeq 100$
and
$\unicode[STIX]{x1D706}_{z}\simeq 1.5h$
were also given in the form of streaks and quasi-streamwise vortical structures, and their size is proportional to the distance from the wall. It was further shown that each of these attached eddies in the logarithmic and outer regions has the self-sustaining process almost identical to that in the near-wall region (Hamilton et al.
Reference Hamilton, Kim and Waleffe1995; Jiménez & Pinelli Reference Jiménez and Pinelli1999; Schoppa & Hussain Reference Schoppa and Hussain2002): the self-sustaining process of each of the attached eddies is composed of streak amplification by streamwise vortical structures via the lift-up effect, breakdown of the amplified streak with secondary instability or transient growth and the following nonlinear regeneration of the streamwise vortical structures (see Bengana & Hwang Reference Bengana and Hwang2015; Hwang & Bengana Reference Hwang and Bengana2016).
Given the remarkable self-similarities of the energy-containing motions existing from the near-wall to the outer region (i.e. attached eddies), it would not be unreasonable to hypothesize that all of these energy-containing motions in the logarithmic and outer regions would involve turbulent skin-friction generation to some extent as the near-wall motions do. Townsend (Reference Townsend1976) originally speculated on the possible influence of the attached eddies on skin-friction fluctuation through their ‘inactive’ component. The numerical experiments of Hwang (Reference Hwang2013) at low Reynolds numbers (up to
$Re_{\unicode[STIX]{x1D70F}}\approx 660$
where
$Re_{\unicode[STIX]{x1D70F}}$
is the friction Reynolds number) also hinted that such an idea would be relevant, even to mean skin friction. Interestingly, very recent work by Renard & Deck (Reference Renard and Deck2016) revealed that the logarithmic region is mainly responsible for turbulent skin-friction generation by applying a theoretical formula based on the production of turbulent kinetic energy to an existing simulation database of a turbulent boundary layer.
The goal of the present study is to explore this issue from a structural viewpoint, by quantifying turbulent skin-friction generation using the self-similar coherent structures in the form of Townsend’s attached eddies at moderately high Reynolds numbers (up to
$Re_{\unicode[STIX]{x1D70F}}\simeq 4000$
). To this end, we introduce three different numerical simulation-based approaches, each of which independently quantifies the contribution of the energy-containing motions at each of the spanwise length scales to turbulent skin friction: (i) the FIK-identity-based method with the spanwise wavenumber spectra from existing direct numerical simulation (DNS) data by modifying the approach of Deck et al. (Reference Deck, Renard, Laraufie and Weiss2014); (ii) exclusion of the motions by confining the spanwise computational domain (Flores & Jiménez Reference Flores and Jiménez2010; Hwang & Cossu Reference Hwang and Cossu2011); (iii) artificial damping of the motions at certain spanwise length scales in a sufficiently large computational box through a body forcing. Particular emphasis of the present study is given to answering the questions of potential importance in the design of novel flow control strategies: what are the contributions of the largest attached eddies given by VLSMs and LSMs to turbulent skin-friction drag? Does their removal yield any appreciable skin-friction reduction? If so, is the amount of the drag reduction potentially interesting for flow control? How large is the contribution of the self-similar attached eddies in the logarithmic region? What is the role of the interaction between the attached eddies at different length scales in turbulent skin-friction generation?
This paper is organised as follows. In § 2, we introduce the three approaches quantifying turbulent skin-friction generation by the attached eddies at each spanwise length scale with validation of the numerical tools we use. The results of the three independent quantifications are given in § 3, and we will see that dominant turbulent skin-friction generation occurs in the logarithmic region where most of the self-similar energy-containing motions reside. A detailed discussion on the skin-friction generation by these motions is given in § 4 in relation to their self-sustaining process, scale interaction and flow control. This paper concludes with some remarks in § 5.
2 Numerical experiment
2.1 Numerical methods
The numerical experiments in the present study are performed with near-wall-resolved large-eddy simulations in a turbulent channel with half-height
$h$
. The streamwise, wall-normal and spanwise directions are denoted by
$x$
,
$y$
and
$z$
, respectively, and the corresponding velocities are denoted by
$u$
,
$v$
and
$w$
. A numerical solver, which has been previously validated with DNS (Hwang Reference Hwang2013) and large-eddy simulations (LES) (Hwang & Cossu Reference Hwang and Cossu2010b
, Reference Hwang and Cossu2011), is used in the present study. In this solver, the streamwise and spanwise directions are discretized using Fourier series with
$2/3$
dealiasing rule, whereas the wall-normal direction is discretised using a second-order central difference. The time steps are semi-implicitly advanced with a fractional step method: a Crank–Nicholson method is used for terms with wall-normal derivatives, and a third-order Runge–Kutta method is used for all the remaining terms. Constant mass flux is imposed across the channel.
The residual stress of the present LES is approximated with an eddy viscosity based on the model proposed by Vreman (Reference Vreman2004). The Vreman model was developed to closely match the theoretically predicted algebraic properties of subgrid-scale dissipation for an extensive database of flows. An important feature of this model is that dissipation by the eddy viscosity becomes relatively small in transitional and near-wall regions, not requiring any special treatment for the near-wall region. The model shows performance comparable to the standard dynamic Smagorinsky model (e.g. Germano et al. Reference Germano, Piomelli, Moin and Cabot1991), and its dynamic variant has recently demonstrated a range of applicability to several canonical flows (Park et al. Reference Park, Lee, Lee and Choi2006). For further details, the reader may refer to Vreman (Reference Vreman2004) and Park et al. (Reference Park, Lee, Lee and Choi2006).
2.2 Assessment of skin-friction generation by self-similar attached eddies
2.2.1 FIK identity with spanwise wavenumber spectra
Figure 1. Premultiplied spanwise wavenumber spectra of the Reynolds shear stress at
$Re_{\unicode[STIX]{x1D70F}}=2003$
in a turbulent channel flow (Hoyas & Jiménez Reference Hoyas and Jiménez2006). The contour labels indicate 0.2, 0.4, 0.6, and 0.8 of the maximum, respectively.
The first approach is designed to follow the one recently proposed by Deck et al. (Reference Deck, Renard, Laraufie and Weiss2014) who combined the streamwise wavenumber spectra of the Reynolds shear stress with the FIK identity (Fukagata et al.
Reference Fukagata, Iwamoto and Kasagi2002) to calculate the contribution of large-scale outer structures to turbulent skin friction. In the present study, we use the spanwise wavenumber spectra, unlike the approach of Deck et al. (Reference Deck, Renard, Laraufie and Weiss2014), as they are more instructive than the streamwise ones to identify the length scale of the energy-containing motions (Hwang Reference Hwang2015). Figure 1 shows the spanwise wavenumber spectra of the Reynolds shear stress in a turbulent channel flow at
$Re_{\unicode[STIX]{x1D70F}}=2003$
(Hoyas & Jiménez Reference Hoyas and Jiménez2006). The spectra are well aligned along the ridge given by
$y\simeq 0.27\unicode[STIX]{x1D706}_{z}$
, indicating the linear spanwise scale growth with the distance from the wall. This feature enables us to clearly identify three different length scales of the energy-containing motions in wall-bounded shear flows: the inner (
$\unicode[STIX]{x1D706}_{z}^{+}\simeq 100$
), log-layer (
$\unicode[STIX]{x1D706}_{z}\sim y$
) and outer (
$\unicode[STIX]{x1D706}_{z}\simeq 1.5h$
) length scales. The motions at
$\unicode[STIX]{x1D706}_{z}^{+}\simeq 100$
are composed of the near-wall streaks and the quasi-streamwise vortices (Hwang Reference Hwang2013), whereas the motions at
$\unicode[STIX]{x1D706}_{z}\simeq 1.5h$
are represented by the VLSMs (outer streaky structures) and the LSMs (outer streamwise vortical structures) (Hwang & Cossu Reference Hwang and Cossu2010b
; Hwang Reference Hwang2015). At the intermediate length scale between
$\unicode[STIX]{x1D706}_{z}^{+}\simeq 100$
and
$\unicode[STIX]{x1D706}_{z}\simeq 1.5h$
, the motions at each
$\unicode[STIX]{x1D706}_{z}$
also consist of streamwise vortical structures and streaks, and they are self-similar to one another, forming the behaviour hypothesized by Townsend (Reference Townsend1976) (i.e. attached eddy hypothesis). For further details, the reader may refer to Hwang (Reference Hwang2015).
For a statistically stationary turbulent channel flow, the FIK identity gives the following relation between the skin-friction coefficient and the Reynolds shear stress:
$$\begin{eqnarray}\displaystyle C_{f}=\frac{12}{Re_{m}}+12\int _{0}^{h}2\left(1-\frac{y}{h}\right)\left(-\frac{\overline{u^{\prime }v^{\prime }}}{4U_{m}^{2}}\right)\,\text{d}y, & & \displaystyle\end{eqnarray}$$
where
$U_{m}$
is the bulk velocity. Here, the first term represents the contribution of the laminar part and the second term gives the contribution from turbulence. Using one-dimensional spanwise power spectral density
$\unicode[STIX]{x1D6F7}_{uv}(y;k_{z})$
, the Reynolds shear stress is written as
$$\begin{eqnarray}\displaystyle -\overline{u^{\prime }v^{\prime }}(y)=2\int _{0}^{\infty }\unicode[STIX]{x1D6F7}_{uv}(y;k_{z})\,\text{d}k_{z}, & & \displaystyle\end{eqnarray}$$
where
$k_{z}(=2\unicode[STIX]{x03C0}/\unicode[STIX]{x1D706}_{z})$
is the spanwise wavenumber and the overbar denotes average in time and two homogenous directions. Here, the factor 2 in (2.2) is given to take the contribution of
$\unicode[STIX]{x1D6F7}_{uv}(y;k_{z})$
for
$k_{z}<0$
into account. Equation (2.2) then enables us to calculate the Reynolds shear stress contribution of the motions, the spanwise size
$\unicode[STIX]{x1D706}_{z}$
of which is smaller than a given cutoff wavelength
$\unicode[STIX]{x1D706}_{z,t}$
, such that:
$$\begin{eqnarray}\displaystyle -(\overline{u^{\prime }v^{\prime }})_{t}(y;\unicode[STIX]{x1D706}_{z,t})=2\int _{2\unicode[STIX]{x03C0}/\unicode[STIX]{x1D706}_{z,t}}^{\infty }\unicode[STIX]{x1D6F7}_{uv}(y;k_{z})\,\text{d}k_{z}, & & \displaystyle\end{eqnarray}$$
where
$(\overline{u^{\prime }v^{\prime }})_{t}$
is the Reynolds shear stress obtained with the spanwise wavenumber spectra for
$\unicode[STIX]{x1D706}_{z}<\unicode[STIX]{x1D706}_{z,t}$
. Substituting
$(\overline{u^{\prime }v^{\prime }})_{t}$
into
$\overline{u^{\prime }v^{\prime }}$
in (2.1) then leads to
$$\begin{eqnarray}\displaystyle C_{f,t}(\unicode[STIX]{x1D706}_{z,t})=\frac{12}{Re_{m}}+12\int _{0}^{h}2\left(1-\frac{y}{h}\right)\left(-\frac{(\overline{u^{\prime }v^{\prime }})_{t}(y;\unicode[STIX]{x1D706}_{z,t})}{4U_{m}^{2}}\right)\,\text{d}y, & & \displaystyle\end{eqnarray}$$
yielding the skin-friction coefficient generated by the motions at
$\unicode[STIX]{x1D706}_{z}\leqslant \unicode[STIX]{x1D706}_{z,t}$
and the laminar flow component: if
$\unicode[STIX]{x1D706}_{z,t}\rightarrow 0$
, (2.4) yields the skin-friction coefficient given by the corresponding laminar flow. This approach is designed to apply to the existing data obtained by a full-scale simulation (DNS by Hoyas & Jiménez Reference Hoyas and Jiménez2006), and quantifies the skin-friction generation by the motions at
$\unicode[STIX]{x1D706}_{z}\leqslant \unicode[STIX]{x1D706}_{z,t}$
in the ‘presence of all the motions’. It is also worth being noted that the last term on the right-hand side of (2.4), the key part of this approach, basically evaluates the amount of Reynolds shear stress at
$\unicode[STIX]{x1D706}_{z}\leqslant \unicode[STIX]{x1D706}_{z,t}$
with a weight
$1-y/h$
. This weight, which decreases linearly with
$y$
, gives more importance to the Reynolds shear stress carried by smaller structures in the region closer to the wall, and less importance to that of larger structures located further from the wall. Finally, it should be mentioned that this approach is solely based on a post processing of the computed data (i.e. the spanwise wavenumber spectra of Reynolds shear stress). Therefore, the approach does not affect other flow parameters and statistical quantities. We shall refer to this method as the ‘FIK-identity-based approach’.
2.2.2 Confining computational domain
The second approach is based on the minimal box technique proposed by Hwang & Cossu (Reference Hwang and Cossu2010b
, Reference Hwang and Cossu2011) and Flores & Jiménez (Reference Flores and Jiménez2010) for the structures in the logarithmic and outer regions. The key parameter of this approach is the spanwise size of the computational domain
$L_{z}$
, as setting
$$\begin{eqnarray}\displaystyle L_{z}=\unicode[STIX]{x1D706}_{z,t}, & & \displaystyle\end{eqnarray}$$
allows one to simulate only the motions at
$\unicode[STIX]{x1D706}_{z}\leqslant \unicode[STIX]{x1D706}_{z,t}$
. This approach clearly differs from the FIK-identity-based approach as it quantifies skin-friction generation by the motions at
$\unicode[STIX]{x1D706}_{z}\leqslant \unicode[STIX]{x1D706}_{z,t}$
in the absence of those at
$\unicode[STIX]{x1D706}_{z}>\unicode[STIX]{x1D706}_{z,t}$
. This approach was used by Hwang (Reference Hwang2013) for the near-wall motions, and revealed that the contribution of the near-wall motions to turbulent skin friction decays rapidly with the Reynolds number. In the present study, we further extend this approach by considering an order of magnitude higher Reynolds number (up to
$Re_{\unicode[STIX]{x1D70F}}\simeq 4000$
). The spanwise computational domain is also varied up to the largest spanwise length scale of the motions,
$L_{z}=1.5h$
(i.e. the spanwise length scale of the LSM and the VLSM).
In this approach, the constraint imposed on the spanwise domain size (2.5) provides the upper limit for the maximum finite value of
$\unicode[STIX]{x1D706}_{z}$
. Nonetheless, the computational domain retains some motions at
$\unicode[STIX]{x1D706}_{z}>\unicode[STIX]{x1D706}_{z,t}$
in the form of the spanwise uniform eddy: i.e. the motions at
$\unicode[STIX]{x1D706}_{z}\rightarrow \infty$
(
$k_{z}=0$
). The eddy corresponding to this wavelength could still influence the remaining structures of the flow. In order to assess the influence of this uniform mode, the filter used in Hwang (Reference Hwang2013) is also introduced to remove the
$k_{z}=0$
component of the streamwise and wall-normal velocities. This approach modifies the right-hand side of the momentum equation at each Runge–Kutta substep, such that:
$$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\widehat{\text{RHS}}_{x}(y,k_{x}\neq 0,k_{z}=0)=0,\\ \widehat{\text{RHS}}_{y}(y,k_{x}\neq 0,k_{z}=0)=0,\end{array}\right\} & & \displaystyle\end{eqnarray}$$
where
$\widehat{\cdot }$
denotes the Fourier coefficient in the
$x$
and
$z$
directions,
$k_{x}$
is the streamwise wavenumber and
$\text{RHS}_{x}$
and
$\text{RHS}_{y}$
are respectively the right-hand sides of the streamwise and wall-normal components of the discretised momentum equation. More details of this technique, along with a broader discussion on its effects at low Reynolds numbers, can be found in Hwang (Reference Hwang2013, Reference Hwang2015). With this technique, we will show that the effect of the spanwise uniform mode on the skin friction is very limited (see § 3.1 and appendix B).
It should be noted that, in applying this approach, considering a very long streamwise domain has been found not to be very critical (see also appendices A and B). This appears to be because the long streaky structures in the logarithmic and outer regions are well resolved with the streamwise uniform Fourier component. Indeed, the mean-velocity profile and skin-friction coefficient at a given Reynolds number have been found to be well recovered even with
$L_{x}=3.0h$
and
$L_{z}=1.5h$
, consistent with previous studies (Flores & Jiménez Reference Flores and Jiménez2010; Hwang & Cossu Reference Hwang and Cossu2011; Lozano-Durán & Jiménez Reference Lozano-Durán and Jiménez2014). A careful examination has further revealed that the change of the streamwise domain yields a variation of the skin-friction coefficient only within
$2\,\%$
if
$L_{x}>2L_{z}$
(appendix A). This amount of deviation is small enough for the given scope of the present study, as the skin friction has been found to vary up to 85 % with the designed numerical experiment (e.g. figure 6). This feature also allows us to explore a relatively wide range of the parameter space of
$Re_{m}$
and
$\unicode[STIX]{x1D706}_{z,t}$
without very long streamwise domain sizes. All the computations with this approach are therefore carried out with
$L_{x}=2L_{z}$
. We note that this aspect ratio is equivalent to the smallest box size allowing for the self-sustaining process of the motions at each spanwise length scale
$L_{z}$
(Hwang & Cossu Reference Hwang and Cossu2010b
, Reference Hwang and Cossu2011), and also corresponds well to the size of the self-similar vortex clusters (del Alamo et al.
Reference del Alamo, Jiménez, Zandonade and Moser2006). Simulation parameters for the biggest computational domain at four different Reynolds numbers are summarized in table 1. This method shall be referred to as the ‘box-confinement approach’.
Table 1. Simulation parameters of the largest computational domain for the box-confinement approach (before dealiasing).
2.2.3 Artificial damping of the motions
The last approach employed is to compute skin-friction drag after eliminating the structures at
$\unicode[STIX]{x1D706}_{z}>\unicode[STIX]{x1D706}_{z,t}$
in a sufficiently large computational domain. In this case, the removal of the motions at
$\unicode[STIX]{x1D706}_{z}>\unicode[STIX]{x1D706}_{z,t}$
is implemented by introducing an artificial damping in the form of a body forcing to the right-hand side of the Navier–Stokes equation, such that:
$$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x2202}\boldsymbol{u}}{\unicode[STIX]{x2202}t}+(\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{u})\boldsymbol{u}=-\frac{1}{\unicode[STIX]{x1D70C}}\unicode[STIX]{x1D735}p+\unicode[STIX]{x1D708}\unicode[STIX]{x1D6FB}^{2}\boldsymbol{u}+\boldsymbol{f}, & & \displaystyle\end{eqnarray}$$
where
$\boldsymbol{u}=(u,v,w)$
,
$t$
is time,
$\unicode[STIX]{x1D70C}$
the density of fluid,
$p$
the pressure,
$\unicode[STIX]{x1D708}$
the kinematic viscosity and
$\boldsymbol{f}$
the introduced body forcing, respectively. To damp the motions at
$\unicode[STIX]{x1D706}_{z}>\unicode[STIX]{x1D706}_{z,t}$
,
$\boldsymbol{f}$
is set for its Fourier component to satisfy
$$\begin{eqnarray}\displaystyle \hat{\boldsymbol{f}}(y,t;\unicode[STIX]{x1D706}_{x},\unicode[STIX]{x1D706}_{z})=-\unicode[STIX]{x1D707}(\unicode[STIX]{x1D706}_{z})\hat{\boldsymbol{u}}(y,t;\unicode[STIX]{x1D706}_{x},\unicode[STIX]{x1D706}_{z}), & & \displaystyle\end{eqnarray}$$
with
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D707}(\unicode[STIX]{x1D706}_{z})=\left\{\begin{array}{@{}ll@{}}0 & \text{for }\unicode[STIX]{x1D706}_{z}\leqslant \unicode[STIX]{x1D706}_{z,t},\\ \unicode[STIX]{x1D707}_{0} & \text{for }\unicode[STIX]{x1D706}_{z}>\unicode[STIX]{x1D706}_{z,t},\end{array}\right. & & \displaystyle\end{eqnarray}$$
where
$\hat{\cdot }$
denotes the Fourier coefficient in the
$x$
and
$z$
directions and
$\unicode[STIX]{x1D706}_{x}$
is the streamwise wavelength. We note that the damping is also applied to
$\unicode[STIX]{x1D706}_{z}<0$
, but is not applied to zero spanwise wavenumber (
$k_{z}=0$
) to make direct comparison with the result of the box-confinement approach without (2.6). A set of small different values of
$\unicode[STIX]{x1D707}_{0}$
, ranging from
$5.3\times 10^{-4}$
to
$4.2\times 10^{-3}$
, have been chosen to minimize the effect of damping to other scales. These values have also been examined to check the robustness of this approach to the choice of
$\unicode[STIX]{x1D707}_{0}$
. The statistics and skin-friction drag are found not to be appreciably dependent on the value of
$\unicode[STIX]{x1D707}_{0}$
considered and
$\unicode[STIX]{x1D707}_{0}=1.4\times 10^{-3}$
is used throughout the present study. The simulation parameters for this numerical experiment are summarized in table 2. Two computational domains are considered: one is with a sufficiently long streamwise domain (
$F2000$
) and the other is the minimal one for the largest structures (
$W2000$
). Most of the computations are performed with
$W2000$
, and a few cases are also verified with
$F2000$
. We shall call this method ‘artificial damping’.
Figure 2. (a) Mean-velocity profile
$U^{+}(y^{+})$
and (b) turbulent velocity fluctuations at
$Re_{\unicode[STIX]{x1D70F}}\approx 2000$
: ——, DNS by Bernardini, Pirozzoli & Orlandi (Reference Bernardini, Pirozzoli and Orlandi2014); ○, present LES (
$F2000$
).
Table 2. Parameters of reference simulation for artificial damping (before dealiasing).
It should finally be noted that the approach damping the spanwise Fourier components for
$\unicode[STIX]{x1D706}_{z}>\unicode[STIX]{x1D706}_{z,t}$
has an important difference from the box-confinement approach described in § 2.2.2. The box-confinement approach basically excludes the motions at
$\unicode[STIX]{x1D706}_{z}>\unicode[STIX]{x1D706}_{z,t}$
by not resolving them except through zero spanwise wavenumber (i.e.
$k_{z}=0$
). This implies that the motions at
$\unicode[STIX]{x1D706}_{z}\leqslant \unicode[STIX]{x1D706}_{z,t}$
in a confined computational domain have no way to transfer energy to the motions at
$\unicode[STIX]{x1D706}_{z}>\unicode[STIX]{x1D706}_{z,t}$
, except through zero spanwise wavenumber
$(k_{z}=0)$
. On the contrary, the damping approach allows for such energy transfer, and the transferred energy is damped in the range of the spanwise wavelengths at
$\unicode[STIX]{x1D706}_{z}>\unicode[STIX]{x1D706}_{z,t}$
. The two methods therefore do not necessary yield the same result.
2.3 Validation
The numerical experiment has been validated with several tests carried out at different values of
$Re_{\unicode[STIX]{x1D70F}}$
to appraise the performance of the Vreman model. Figure 2 compares the mean-velocity profile and turbulent velocity fluctuations of the present LES at
$Re_{\unicode[STIX]{x1D70F}}\simeq 2000$
(
$F2000$
) with those from DNS by Bernardini et al. (Reference Bernardini, Pirozzoli and Orlandi2014). Very good agreement is observed in the mean-velocity profile, and the velocity fluctuations also show acceptable agreement as well. The peak for the streamwise velocity fluctuation is slightly over-predicted, as it is commonly seen in LES. The spanwise and wall-normal components show somewhat smaller intensities than those of DNS, especially in the region closer to the wall, and this behaviour has been reported previously (Dukowicz & Dvinsky Reference Dukowicz and Dvinsky1992; Kravchenko & Moin Reference Kravchenko and Moin1997; Sarghini, Piomelli & Balaras Reference Sarghini, Piomelli and Balaras1999; Gullbrand Reference Gullbrand2000).
Figure 3. Variation of skin-friction coefficient with
$Re_{m}$
: ——, empirical fit of turbulent skin friction (
$C_{f}=0.073Re_{m}^{-0.25}$
, Dean Reference Dean1978); – – – –, laminar skin friction (
$C_{f}=12/Re_{m}$
); ▿, DNS (Hoyas & Jiménez Reference Hoyas and Jiménez2006; Lozano-Durán & Jiménez Reference Lozano-Durán and Jiménez2014); ♢, DNS (Bernardini et al.
Reference Bernardini, Pirozzoli and Orlandi2014); ▫, DNS (Lee & Moser Reference Lee and Moser2015); *, experiment (Schultz & Flack Reference Schultz and Flack2013); ●, present LES (
$L_{x}=3.0h$
and
$L_{z}=1.5h$
).
In order to assess the suitability of the use of the box-confinement approach, the skin-friction coefficients with the largest computational domain in this case (i.e.
$L_{x}=3.0h$
and
$L_{z}=1.5h$
) are compared with those obtained by experiment (Schultz & Flack Reference Schultz and Flack2013) and previous DNS (Hoyas & Jiménez Reference Hoyas and Jiménez2006; Bernardini et al.
Reference Bernardini, Pirozzoli and Orlandi2014; Lozano-Durán & Jiménez Reference Lozano-Durán and Jiménez2014; Lee & Moser Reference Lee and Moser2015) in figure 3. The present LES shows good agreement with both of the existing data and the empirical fit of Dean (Reference Dean1978) over the range of
$Re_{m}$
considered. The small difference at large Reynolds numbers (
$Re_{m}>10^{5}$
) appears to be due to a slight imprecision in Dean’s original formula, and the issue has been recently addressed by Zanoun, Nagib & Durst (Reference Zanoun, Nagib and Durst2009).
3 Results
3.1 Skin-friction generation at
$Re_{\unicode[STIX]{x1D70F}}\simeq 2000$
Figure 4. Variation of
$C_{f}$
with the cutoff spanwise wavelength
$\unicode[STIX]{x1D706}_{z,t}$
at
$Re_{\unicode[STIX]{x1D70F}}\simeq 2000$
: ♢, FIK-identity-based approach; *, box-confinement approach (with spanwise uniform mode); ▵, box-confinement approach (without spanwise uniform mode) ○, artificial damping with
$W2000$
; ▫, artificial damping with
$F2000$
. Here, the upper and lower horizontal lines indicate turbulent (from DNS by Hoyas & Jiménez Reference Hoyas and Jiménez2006) and laminar skin-friction coefficient (
$C_{f}=12/Re_{m}$
), respectively.
The skin-friction generation by the motions at
$\unicode[STIX]{x1D706}_{z}\leqslant \unicode[STIX]{x1D706}_{z,t}$
is assessed by the three methods in § 2 at
$Re_{\unicode[STIX]{x1D70F}}\simeq 2000$
and is reported in figure 4. We note that the spanwise length of the largest energy-containing structures (VLSMs and LSMs) is
$\unicode[STIX]{x1D706}_{z}=1.5h$
, and that of the smallest ones (near-wall streaks and quasi-streamwise vortices) is
$\unicode[STIX]{x1D706}_{z}\simeq 0.05h$
(from
$\unicode[STIX]{x1D706}_{z}/h=\unicode[STIX]{x1D706}_{z}^{+}/Re_{\unicode[STIX]{x1D70F}}$
with
$\unicode[STIX]{x1D706}_{z}^{+}=100$
) at this Reynolds number. The most immediate and evident conclusion in figure 4 is that, no matter which approach we take, the spanwise scales in the range of
$0.2h\leqslant \unicode[STIX]{x1D706}_{z}\leqslant 1h$
are responsible for the largest portion of the skin friction and their removal leads to significant reduction of wall shear stress. The FIK-identity-based approach shows that this range of the spanwise scales is responsible for
$41\,\%$
of total skin friction, while the box-confinement approach and the artificial damping reveal that around
$60\,\%$
of skin-friction reduction is achieved by removing the motions at
$\unicode[STIX]{x1D706}_{z}>0.2h$
. This striking result implies that the largest amount of the skin friction at sufficiently high Reynolds numbers is generated by the self-similar energy-containing motions, most of which belong to the logarithmic region in the sense that their spanwise length scale is proportional to the distance from the wall.
An important difference is, however, observed between the skin frictions obtained with the FIK-identity-based approach and with the other two approaches. The FIK-identity-based method shows that the largest motions at
$\unicode[STIX]{x1D706}_{z}\geqslant 1.5h$
are responsible for a considerable amount of skin friction, i.e. 25–30 % of the total skin friction. This amount is not very far from that obtained by Deck et al. (Reference Deck, Renard, Laraufie and Weiss2014), who computed the skin-friction generation by large-scale structures using the streamwise spectra for
$\unicode[STIX]{x1D706}_{x}>1{-}2\unicode[STIX]{x1D6FF}$
in a turbulent boundary layer (
$\unicode[STIX]{x1D6FF}$
is the boundary-layer thickness). This approach also shows that skin-friction generation by the spanwise length scales of
$\unicode[STIX]{x1D706}_{z}>1.5h$
is not negligible, despite the fact that the spanwise length of both the VLSMs and the LSMs is
$\unicode[STIX]{x1D706}_{z}\simeq 1.5h$
. This is because the spanwise wavenumber spectra from the DNS with a large spanwise computational domain (
$L_{z}=3\unicode[STIX]{x03C0}$
) contain a non-negligible amount of energy for
$\unicode[STIX]{x1D706}_{z}>1.5h$
(see also figure 1). However, the box-confinement approach and the artificial damping, both of which show very similar behaviour to each other, yield very different trend of
$C_{f}$
with
$\unicode[STIX]{x1D706}_{z,t}$
from the FIK-based approach. In particular, both of the box-confinement approach and the artificial damping do not yield any significant change in
$C_{f}$
until the cutoff spanwise wavelength is reduced to
$\unicode[STIX]{x1D706}_{z,t}=1{-}1.5h$
. A sensible amount of skin-friction reduction (4–8 %) is observed only when
$\unicode[STIX]{x1D706}_{z,t}\simeq 0.75{-}1.0h$
, by which the largest structures at
$\unicode[STIX]{x1D706}_{z}\simeq 1.5h$
are removed. Both of the box-confinement approach and the artificial damping consistently show larger skin friction than that obtained with the FIK-identity-based approach, indicating that removal of relatively large motions does not yield reduction of the skin friction for which they are responsible. It is difficult to explain this feature if we exclude the role of scale interaction in the skin-friction generation process. A detailed discussion on this issue will be given in § 4.1.
Finally, it is worth mentioning that the uniform spanwise mode in the box-confinement approach is found to have little influence on the skin friction, as also shown in figure 4. Indeed, the removal of the spanwise uniform mode with (2.6) slightly reduces the skin friction only for relatively small
$\unicode[STIX]{x1D706}_{z,t}~(=0.2{-}0.3h)$
by the removal of the spanwise uniform mode (▵ in figure 4). This implies that the direct interaction between the spanwise uniform mode and the motions at
$\unicode[STIX]{x1D706}_{z}\leqslant \unicode[STIX]{x1D706}_{z,t}~(=L_{z})$
is probably very minor. Further detailed evaluation of the differences between simulations with and without the uniform spanwise mode is presented in appendix B.
3.2 Different Reynolds numbers
Figure 5. Variation of
$C_{f}$
with
$Re_{m}$
for the box-confinement approach (i.e.
$L_{z}=\unicode[STIX]{x1D706}_{z,t}$
): (a) constant
$L_{z}(=0.2,0.4,0.75,1.5h)$
; (b) constant
$L_{z}^{+}(\simeq 400,1000,3000)$
. The filled square symbols (▪) represent the artificial damping approach. Here, ——,
$C_{f}$
suggested by Dean (Reference Dean1978) (
$C_{f}=0.073Re_{m}^{-0.25}$
).
Since the box-confinement approach and the artificial damping do not yield very different skin friction (see also discussion in § 4.1), the assessment of the skin-friction generation by the motions at
$\unicode[STIX]{x1D706}_{z}\leqslant \unicode[STIX]{x1D706}_{z,t}$
is further explored only with the box-confinement approach up to
$Re_{\unicode[STIX]{x1D70F}}\simeq 4000$
. Figure 5 shows the skin-friction generation with respect to
$\unicode[STIX]{x1D706}_{z,t}(=L_{z})$
at four different
$Re_{m}$
. When
$L_{z}$
is chosen to scale with the outer unit, the reduced skin friction is found to follow a similar curvature with that of the full skin friction obtained with
$L_{z}=1.5h$
without any further deviation on increasing
$Re_{m}$
(figure 5
a). In contrast, when
$L_{z}$
is set to scale with the inner unit, the deviation between
$C_{f}$
for
$L_{z}^{+}<3000$
and that for
$L_{z}^{+}=3000$
gradually increases with the Reynolds number. This implies that the contribution of the motions, the spanwise size of which is smaller than the given inner-scaled one, to total skin friction continuously decreases on increasing
$Re_{m}$
. This is consistent with the low Reynolds number result in Hwang (Reference Hwang2013), who observed that the structures smaller than a fixed value of
$L_{z}^{+}(\simeq 100,~200)$
yield decreasing portions of skin friction on increasing
$Re_{m}$
. The behaviour in figure 5 clearly suggests that, at very high Reynolds numbers, most of skin friction would be generated by the motions, the spanwise size of which lies between
$\unicode[STIX]{x1D706}_{z}^{+}\approx 100$
and
$\unicode[STIX]{x1D706}_{z}\simeq 1.5h$
. Given the size of these motions is proportional to the distance from the wall (i.e.
$\unicode[STIX]{x1D706}_{z}\sim y$
), this indicates that the dominant skin-friction generation takes place essentially in the logarithmic region.
Figure 6. Variation of normalized skin-friction coefficient with
$L_{z}(=\unicode[STIX]{x1D706}_{z,t})$
: ○,
$Re_{m}=38\,100$
; *,
$Re_{m}=89\,100$
; ♢,
$Re_{m}=89\,100$
, artificial damping; ▫,
$Re_{m}=137\,500$
; ▵,
$Re_{m}=193\,200$
.
Finally, the reduced amount of skin friction by setting
$L_{z}<1.5h$
is found to approximately scale with the outer unit if the Reynolds number is sufficiently high. In figure 6, the skin-friction coefficients normalized by the reference one with
$L_{z}=1.5h$
are plotted with respect to
$L_{z}/h$
for all the Reynolds numbers considered. All the data, obtained at four different
$Re_{m}$
, appear to collapse approximately well into a single curve. For instance, a reduction in skin friction in the region of 7–8 % is obtained by halving the spanwise width (i.e.
$L_{z}=0.75h$
). Another 10 % of the original friction is lost by reducing the box width to
$L_{z}=0.5h$
. At
$L_{z}=0.2h$
, the amount of skin friction generated is very close to 40 % of the initial value for all three of the larger Reynolds number.
3.3 Probability density function of turbulent skin friction
To further investigate how the statistical behaviour of turbulent skin-friction generation is changed by the removal of the structures at
$\unicode[STIX]{x1D706}_{z}>\unicode[STIX]{x1D706}_{z,t}$
, probability density functions (PDFs) of skin friction are computed with the box-confinement approach (
$\unicode[STIX]{x1D706}_{z,t}=L_{z}$
) at
$Re_{\unicode[STIX]{x1D70F}}\simeq 2000$
. It has been found that the PDFs of instantaneous skin friction are positively skewed in a wide range of the Reynolds numbers (Keirsbulck, Labraga & Gad-El-Hak Reference Keirsbulck, Labraga and Gad-El-Hak2012; de Silva et al.
Reference de Silva, Gnanamanickam, Atkinson, Buchmann, Hutchins, Soria and Marusic2014). This feature has often been interpreted to appear because the large-scale positive excursion of wall shear stress accompanies energetic small-scale wall shear stress fluctuations (Chernyshenko, Marusic & Mathis Reference Chernyshenko, Marusic and Mathis2012; Mathis et al.
Reference Mathis, Marusic, Chernyshenko and Hutchins2013; Baars et al.
Reference Baars, Talluru, Hutchins and Marusic2015). The positive skewness of the PDFs also implies that if a high pass filter is applied to the instantaneous wall shear stress signal, its mean would be reduced, consistent with the observations in §§ 3.1 and 3.2.
Figure 7(a) shows the PDFs of the skin-friction coefficient
$C_{f}$
for several
$L_{z}$
. As
$L_{z}$
decreases, the peak location of the PDF moves towards smaller
$C_{f}$
, indicating reduction of mean skin friction. Also, the width of the PDFs is found to be decreased on decreasing
$L_{z}$
, suggesting that the variance of wall shear stress is also reduced by the decrease of
$L_{z}$
. Interestingly, the normalized PDFs, shown in figure 7(b), do not appear to be so different from one another, indicating that the skin-friction generation process in each confined computational domain is statistically self-similar. We note that, given the findings in §§ 3.1 and 3.2, the skin-friction generation process for all of the sufficiently large
$L_{z}$
would involve to some extent the hierarchical organization of self-similar energy-containing motions, the largest one of which is determined by the spanwise computational domain
$L_{z}$
. This implies that the only difference among the processes in different computational domains would stem from the largest energy-containing motions and the resulting extent of the hierarchical organization. Except for these, the processes in different computational domains are supposed to be similar to one another. This is clearly indicated by figure 7(b), also consistent with the notion that all the self-similar energy-containing motions throughout the entire wall-normal directions involve turbulent skin-friction generation.
Figure 7. Probability density functions of instantaneous skin friction
$C_{f}$
from the box-confinement approach (i.e.
$\unicode[STIX]{x1D706}_{z,t}=L_{z}$
) with (a) the original variable
$C_{f}$
and (b) normalized variable,
$(C_{f}-\overline{C}_{f})/C_{f,rms}$
where
$C_{f,rms}$
is the root mean square of
$C_{f}$
: ——,
$L_{z}=1.5h$
; – – – –,
$L_{z}=1h$
;
$\cdots \cdots$
,
$L_{z}=0.75h$
; – ⋅ – ⋅ –,
$L_{z}=0.5h$
; *
$L_{z}=0.3h$
; ○
$L_{z}=0.2h$
.
4 Discussion
All the three independent approaches introduced in the present study consistently show that all the energy-containing motions ranging from the inner to the outer units are actively involved in turbulent skin-friction generation. In particular, the self-similar energy-containing motions at the spanwise length scale
$\unicode[STIX]{x1D706}_{z}$
between
$\unicode[STIX]{x1D706}_{z}^{+}\simeq 100$
and
$\unicode[STIX]{x1D706}_{z}\simeq 1.5h$
have been shown to be mainly responsible for turbulent skin-friction generation at sufficiently high Reynolds numbers. It is evident that the near-wall region gradually loses its dominant role in the friction generation on increasing the Reynolds number (figure 5
a), consistent with previous findings (Chang et al.
Reference Chang, Collis and Ramakrishnan2002; Gatti & Quadrio Reference Gatti and Quadrio2013; Hwang Reference Hwang2013). A little surprisingly, the contribution from the largest scales in the flow also appears to be limited. This is particularly true, as their removal does not result in reduction of the skin friction for which they are responsible (figure 4; see also a further discussion in § 4.3).
This finding is also consistent with the well-documented logarithmic growth of the near-wall streamwise turbulence intensity with the Reynolds number (Marusic & Kunkel Reference Marusic and Kunkel2003), i.e. the feature reflecting the increasing influence of the energy-containing motions in the logarithmic and outer regions to the near-wall region. The wall-attached part of each of the attached eddies is mainly composed of the streamwise and spanwise velocity components due to impermeability condition at the wall (Townsend Reference Townsend1976; Perry & Chong Reference Perry and Chong1982; Hwang Reference Hwang2015). This therefore implies that the collective skin-friction generation by the self-similar energy-containing motions is probably a consequence of their near-wall influence, establishing a tight physical link with the logarithmic growth of the near-wall streamwise turbulence intensity with the Reynolds number. In this respect, it is also worth mentioning that this finding is consistent with very recent observation by Renard & Deck (Reference Renard and Deck2016), who identified the dominant contribution of the logarithmic region to skin-friction generation using a theoretical formula based on the mean streamwise kinetic-energy budget. Lastly, it is worth pointing out that DNS data for channel flow at
$Re_{\unicode[STIX]{x1D70F}}\approx 5200$
(Lee & Moser Reference Lee and Moser2015) have shown an increase in the energy carried by the outer structures (the VLSM in particular) with a consequent impact on the velocity spectra as well. While this may potentially signify a more pronounced contribution of the largest scales to turbulent skin friction, it is difficult to disregard the observation made with figure 5(b) even at higher Reynolds numbers.
Finally, it should be pointed out that the wall-attached part of each of the attached eddies is ‘inactive’ in the sense that they carry very little Reynolds shear stress, since there is little wall-normal velocity in the vicinity to the wall (Townsend Reference Townsend1976; Hwang Reference Hwang2015). However, this does not necessarily imply that the inactive wall-attached part is not related to turbulent skin-friction generation, as the skin friction is nothing more than the streamwise velocity in the very vicinity to the wall, given its mathematical definition (i.e.
$\unicode[STIX]{x1D708}\unicode[STIX]{x2202}u/\unicode[STIX]{x2202}y$
at the wall). This rather indicates that the energy-containing motions, which essentially reside in the logarithmic and outer regions, transport the streamwise momentum to the near-wall region through their inactive part, while generating Reynolds shear stress with their wall-detached wall-normal velocity component in the region much further from the wall. This transport process of the streamwise momentum by the wall-normal velocity described here is likely to be the so-called ‘lift-up’ effect (Cossu, Pujals & Depardon Reference Cossu, Pujals and Depardon2009; Hwang & Cossu Reference Hwang and Cossu2010a
), a part of the self-sustaining process extensively discussed in Hwang & Bengana (Reference Hwang and Bengana2016). The following discussion addresses this issue.
4.1 Skin-friction generation and the self-sustaining process
The concept of the self-sustaining process was originally proposed by Hamilton et al. (Reference Hamilton, Kim and Waleffe1995) for the near-wall motions, which were recently shown to be the smallest attached eddies (Hwang Reference Hwang2015; Hwang & Bengana Reference Hwang and Bengana2016). The self-sustaining process is a cyclic dynamical process composed of three substeps: (i) the streaks are amplified by streamwise vortices via the lift-up effect, the process by which the streamwise vortices transfer the energy of the mean shear to the streaks (Landahl Reference Landahl1990; Kim & Lim Reference Kim and Lim2000; Chernyshenko & Baig Reference Chernyshenko and Baig2005; Cossu et al.
Reference Cossu, Pujals and Depardon2009; Pujals et al.
Reference Pujals, García-Villalba, Cossu and Depardon2009; Hwang & Cossu Reference Hwang and Cossu2010a
); (ii) the amplified streaks break down with a sinuous-mode secondary instability and/or transient growth (Hamilton et al.
Reference Hamilton, Kim and Waleffe1995; Schoppa & Hussain Reference Schoppa and Hussain2002; Park, Hwang & Cossu Reference Park, Hwang and Cossu2011); (iii) the streamwise vortices are regenerated by nonlinear mechanisms (Hamilton et al.
Reference Hamilton, Kim and Waleffe1995; Schoppa & Hussain Reference Schoppa and Hussain2002; Hwang & Bengana Reference Hwang and Bengana2016). It has recently been shown that the energy-containing motions in the logarithmic and outer regions bear the same self-sustaining process with a single turnover time period given by
$Tu_{\unicode[STIX]{x1D70F}}/\unicode[STIX]{x1D706}_{z}\simeq 2$
(Hwang & Bengana Reference Hwang and Bengana2016).
In the box-confinement approach, the size of the largest energy-containing motions is determined by the spanwise computational box size. The temporal evolution of these largest motions would therefore be reasonably well resolved by the flow quantities obtained by averaging over the computational domain, as also shown in Hwang & Bengana (Reference Hwang and Bengana2016). Using this approach, here we investigate the temporal evolution of each element in the self-sustaining process, and relate it with the generation of turbulent skin-friction drag by the largest scale in the given computational domain. For this purpose, we first introduce the following four integral quantities of interest:
$$\begin{eqnarray}\displaystyle & \displaystyle E_{u}=\frac{1}{2L_{x}L_{z}}\int _{0}^{L_{z}}\int _{0}^{2/3L_{z}}\int _{0}^{L_{x}}{u^{\prime }}^{2}\,\text{d}x\,\text{d}y\,\text{d}z, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle E_{v}=\frac{1}{2L_{x}L_{z}}\int _{0}^{L_{z}}\int _{0}^{2/3L_{z}}\int _{0}^{L_{x}}{v^{\prime }}^{2}\,\text{d}x\,\text{d}y\,\text{d}z, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle E_{1}=\int _{0}^{2/3L_{z}}|\hat{u} (y,k_{x},k_{z})|^{2}+|\hat{v}(y,k_{x},k_{z})|^{2}+|{\hat{w}}(y,k_{x},k_{z})|^{2}\,\text{d}y, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle E_{d}=\frac{1}{L_{x}L_{z}}\int _{0}^{L_{z}}\int _{0}^{L_{x}}\unicode[STIX]{x1D70F}_{w}\,\text{d}x\,\text{d}z, & \displaystyle\end{eqnarray}$$
$k_{x}=2\unicode[STIX]{x03C0}/L_{z}$
and
$k_{z}=2\unicode[STIX]{x03C0}/L_{z}$
and
$\unicode[STIX]{x1D70F}_{w}$
is the instantaneous wall shear stress. Here, we note that the wall-normal domain for the integrations in (4.1) is defined to be
$y\in [0,2/3L_{z}]$
to include the most energetic part of the self-similar self-sustaining motions in each computational domain (see also Hwang & Bengana Reference Hwang and Bengana2016, for further details). We also note that
$E_{u}$
represents the streaks,
$E_{v}$
the quasi-streamwise vortices and
$E_{1}$
the streamwise meandering motions caused by streak instability, respectively, and their definitions exactly follow Hwang & Bengana (Reference Hwang and Bengana2016) where their physical relevance is extensively discussed. In the present study, we also introduce
$E_{d}$
, which would represent the instantaneous wall shear stress of the largest scale permitted by the given computational domain. However, one should bear in mind that
$E_{d}$
is not a full representation of the skin-friction generation by the largest structures in the domain, as it would not completely exclude the effect of smaller-scale structures on large-scale turbulent skin-friction generation.
To find exactly at which point in the self-sustaining process the skin-friction drag becomes maximized, we then compute temporal cross-correlation among these quantities in (4.1), such that:
$$\begin{eqnarray}\displaystyle C_{ij}(\unicode[STIX]{x1D70F})=\frac{\overline{E_{i}(t+\unicode[STIX]{x1D70F})E_{j}(t)}}{\sqrt{\overline{E_{i}^{2}}(t)}\sqrt{\overline{E_{j}^{2}}(t)}}, & & \displaystyle\end{eqnarray}$$
with
$i,j=u,v,1,d$
from (4.1). Since an extensive discussion on the correlations among
$E_{u}$
,
$E_{v}$
and
$E_{1}$
was given in Hwang & Bengana (Reference Hwang and Bengana2016), the focus in the present study will be mainly given to understanding of the cross-correlations involving the spatially averaged wall shear stress, i.e
$E_{d}$
.
Figure 8. Cross-correlation functions obtained with the box-confinement approach (
$\unicode[STIX]{x1D706}_{z,t}=L_{z}$
): (a)
$C_{ud}$
; (b)
$C_{1d}$
; (c)
$C_{vd}$
; (d)
$C_{1v}$
. Here, – – – –,
$L_{z}=1h$
;
$\cdots \cdots$
,
$L_{z}=0.75h$
; – ⋅ – ⋅ –,
$L_{z}=0.5h$
; *
$L_{z}=0.3h$
; ○
$L_{z}=0.2h$
.
The computed correlations,
$C_{ud}$
,
$C_{1d}$
,
$C_{vd}$
and
$C_{uv}$
, are shown in figure 8 for several different spanwise domains
$L_{z}$
. The cross-correlations with
$E_{d}$
reveal that at least their peak locations scale well with respect to the self-similar time scale
$\unicode[STIX]{x1D70F}u_{\unicode[STIX]{x1D70F}}/L_{z}$
. The correlations are also quite large: the peak values of
$C_{ud}$
and
$C_{vd}$
are greater than 0.6. In the cross-correlations, the peak location of
$C_{ud}$
is found to be at
$\unicode[STIX]{x1D70F}\approx -0.6$
(figure 8
a), while those of
$C_{1d}$
and
$C_{vd}$
are at
$\unicode[STIX]{x1D70F}\approx -0.3\sim -0.1$
(figure 8
b,c). Unfortunately, it is difficult to find a clear difference between the peak locations of
$C_{1d}$
and
$C_{vd}$
. This is presumably because the streak instability, represented by
$E_{1}$
, is a fast dynamical process, as shown in Hwang & Bengana (Reference Hwang and Bengana2016). Further to this, it should be noted that all the flow quantities in (4.1) contain some effect of smaller-scale motions. In other words, these quantities do not precisely represent the structure of interest, yielding another complication. Nonetheless, the correlation
$C_{1v}$
in figure 8(d) clearly shows that the amplification of
$E_{1}$
emerges before
$E_{v}$
reaches a large amplitude, consistent with Hwang & Bengana (Reference Hwang and Bengana2016). The cross-correlations in figure 8 therefore suggest that the sequence of the excursion of
$E_{u}$
(streak),
$E_{1}$
(streak instability),
$E_{v}$
(streamwise vortical structure) and
$E_{d}$
(skin-friction generation) would be cyclically given as:
$$\begin{eqnarray}\displaystyle E_{u}\rightarrow E_{1}\rightarrow E_{v}\rightarrow E_{d}. & & \displaystyle\end{eqnarray}$$
The self-sustaining process is essentially a cyclic process represented by
$E_{u}\rightarrow E_{1}\rightarrow E_{v}$
with the single turnover time scale of
$Tu_{\unicode[STIX]{x1D70F}}/L_{z}\simeq 2$
(Hwang & Bengana Reference Hwang and Bengana2016), and the process of
$E_{v}\rightarrow E_{u}$
should follow with occurrence of the next cycle. Given the small time scale of the physical process of
$E_{v}\rightarrow E_{d}$
at
$\unicode[STIX]{x0394}\unicode[STIX]{x1D70F}/L_{z}\approx 0.1{-}0.3$
(figure 8
c), the only conclusion we can reach here would therefore be that the large amplification of
$E_{d}$
appears in the process of
$E_{v}\rightarrow E_{u}$
: i.e. the skin-friction generation by the largest structure (
$E_{d}$
) takes place when the streamwise vortices
$(E_{v})$
are converted to the streak
$(E_{u})$
. This conversion of vortices to streaks is exactly the lift-up process, and the small time scale of the process of
$E_{v}\rightarrow E_{d}$
suggests that the skin-friction generation is dominant at the early stage of the lift-up process. This observation is also consistent with the numerical experiment in Hwang & Bengana (Reference Hwang and Bengana2016) where the artificial suppression of the lift-up effect of the energy-containing motions in the logarithmic and outer regions was found to yield significant amounts of skin-friction reduction. Finally, it is important to highlight that the lift-up effect is a linear process, which is well described by the Navier–Stokes equation linearized around the mean flow (e.g. Cossu et al.
Reference Cossu, Pujals and Depardon2009; Hwang & Cossu Reference Hwang and Cossu2010a
). Therefore, performing a linear analysis to understand skin-friction generation would provide a useful physical insight, as already demonstrated by a number of previous studies (e.g. Lim & Kim Reference Lim and Kim2004; Moarref & Jovanović Reference Moarref and Jovanović2012; Blesbois et al.
Reference Blesbois, Chernyshenko, Touber and Leschziner2013; Luhar, Sharma & McKeon Reference Luhar, Sharma and Mckeon2014).
4.2 Scale interaction and skin-friction generation
Although the three independent assessment methods in the present study consistently suggest that turbulent skin friction at sufficiently high Reynolds numbers is dominantly generated by self-similar motions in the logarithmic region, an important difference between the FIK-identity-based approach and the other two approaches has also been observed (figure 4). This difference originates from the fact that the FIK-identity-based approach computes contribution of the motions at
$\unicode[STIX]{x1D706}_{z}\leqslant \unicode[STIX]{x1D706}_{z,t}$
in the presence of all the structures, whereas the other two approaches actually remove the motions at
$\unicode[STIX]{x1D706}_{z}>\unicode[STIX]{x1D706}_{z,t}$
during the simulation and calculate the skin friction with the remaining motions. It is evident that this large difference would not have been observed if there was no interaction among the energy-containing motions at different length scales.
Figure 9. Premultiplied one-dimensional spanwise wavenumber spectra of (a) streamwise, (b) wall-normal, (c) spanwise velocities and (d) Reynolds shear stress. Here, the shaded, solid and dashed contours indicate the full domain simulation (
$F2000$
), the box-confinement approach and the artificial damping applied to
$F2000$
, respectively. For the box-confinement approach and the artificial damping, the cutoff spanwise wavelength is
$\unicode[STIX]{x1D706}_{z,t}=0.5h$
. The contour labels are chosen to be 0.2, 0.4, 0.6, 0.8 times each of the maximum for comparison.
To further understand the related scale interaction, one-dimensional spanwise wavenumber spectra from the LES with a sufficiently large spanwise domain (
$F2000$
), a confined box with
$L_{z}=0.5h$
and an artificial damping applied to
$F2000$
with
$\unicode[STIX]{x1D706}_{z,t}=0.5h$
are compared in figure 9. The spectra with the confined box and the artificial damping are quite different from those of the full simulation, particularly near
$\unicode[STIX]{x1D706}_{z}\simeq \unicode[STIX]{x1D706}_{z,t}$
. However, the two approaches, both of which physically remove the motions at
$\unicode[STIX]{x1D706}_{z}>\unicode[STIX]{x1D706}_{z,t}$
from the simulations, do not yield very significant difference from each other in their spectra (see also figure 4). Overall, the spectral density of all the flow variables with the box-confinement approach and the artificial damping is found to be elevated compared to that of the full simulation particularly at the wall-normal location where the removed motions originally reside. Furthermore, this influence persists over a fairly wide range of the spanwise wavelength: the wall-normal velocity and the spanwise velocity spectra show non-negligibly large distortions even at
$\unicode[STIX]{x1D706}_{z}^{+}\simeq 100{-}200$
(figure 9
b,c). This indicates that the scale interaction is not localized only near the cutoff wavelength,
$\unicode[STIX]{x1D706}_{z}\simeq \unicode[STIX]{x1D706}_{z,t}$
.
The generation of such a ‘tall’ turbulent fluctuation both in the simulations with the box confinement and the artificial damping is reminiscent of the feature commonly observed in the minimal channel simulations using a small spanwise domain (e.g. Jiménez & Pinelli Reference Jiménez and Pinelli1999; Hwang Reference Hwang2013, Reference Hwang2015). In the minimal channel, such a fluctuation has been understood to be induced by the remaining self-sustaining motions, as its removal does not significantly affect the statistics and dynamics of the remaining motions. Here, the appearance of such a fluctuation also with the artificial damping suggests that this is not a specific behaviour observed only in the confined spanwise domain, but may be an important general physical feature associated with a scale interaction occurring in the remaining motions. The spectra show that this fluctuation is responsible for generation of a considerable amount of Reynolds shear stress over a range of spanwise wavelength (figure 9 d), explaining why the skin friction obtained by the box-confinement approach and the artificial damping is elevated than what is expected by the FIK identity.
Although the generation mechanism of the tall fluctuation is not entirely clear at the moment, a dimensional analysis, similar to the one given by Jiménez & Pinelli (Reference Jiménez and Pinelli1999), provides a physical insight into a possible origin of this behaviour. In a full domain simulation, the production in the logarithmic region would be
${\mathcal{P}}\sim u_{\unicode[STIX]{x1D70F}}^{3}/y$
, while dissipation is
${\mathcal{E}}\sim \unicode[STIX]{x1D708}\unicode[STIX]{x1D74E}^{2}$
where
$\unicode[STIX]{x1D74E}$
is denoted as the total vorticity fluctuation. If the production and the dissipation are assumed to be locally balanced at each wall-normal location, this yields
$\unicode[STIX]{x1D74E}\sim 1/y^{1/2}$
, indicating that the vorticity fluctuation would decay with
$y$
. However, in the simulations with a narrow spanwise domain width
$L_{z}$
where the motions at
$\unicode[STIX]{x1D706}_{z}>L_{z}$
are not resolved, the production of the largest energy-containing motions resolved would be
${\mathcal{P}}\sim u_{\unicode[STIX]{x1D70F}}^{3}/L_{z}$
due to
$\unicode[STIX]{x1D706}_{z}\sim y$
. Therefore, the resulting
$\unicode[STIX]{x1D74E}$
would become
$\unicode[STIX]{x1D714}\sim 1/L_{z}^{1/2}$
, indicating that the vorticity fluctuation in a confined spanwise domain would not significantly decay along the wall-normal direction, at least to some extent. Furthermore, the dimensional analysis indicates that the vorticity fluctuation would ‘increase’ as
$L_{z}$
is decreased.
Figure 10. Vorticity fluctuations for different
$L_{z}$
with the box-confinement approach (
$\unicode[STIX]{x1D706}_{z,t}=L_{z}$
): (a)
$\unicode[STIX]{x1D714}_{x,rms}^{+}$
; (b)
$\unicode[STIX]{x1D714}_{y,rms}^{+}$
; (c)
$\unicode[STIX]{x1D714}_{z,rms}^{+}$
. Here, ——,
$L_{z}=1.5h$
; – – – –,
$L_{z}=1h$
;
$\cdots \cdots$
,
$L_{z}=0.75h$
; – ⋅ – ⋅ –,
$L_{z}=0.5h$
; *
$L_{z}=0.3h$
; ○
$L_{z}=0.2h$
.
Figure 10 reports the vorticity fluctuations for several
$L_{z}$
in the box-confinement approach (i.e.
$\unicode[STIX]{x1D706}_{z,t}=L_{z}$
). Despite the fact that the present numerical experiments are based on a set of large-eddy simulations, all the vorticity fluctuations indeed appear to increase on decreasing
$L_{z}$
, consistent with the dimensional analysis above. This behaviour is particularly prominent in the wall-normal vorticity statistics, and the wall-normal distribution also appears to be roughly constant for
$10^{2}<y^{+}<10^{3}$
. This observation indicates that the dimensional analysis provides at least a partial explanation for the origin of the tall fluctuation. Given the dimensional analysis simply relying on the balance between production and dissipation, it is also important to mention that the mechanism of generation of the tall fluctuation would be associated with the energy cascade rather than the energy extraction of the large eddies from mean shear. In this respect, it is worth mentioning the recent work by Cimarelli et al. (Reference Cimarelli, De Angelis, Jiménez and Casciola2016), who showed the presence of the wall-normal energy flux progressing from smaller to larger attached eddies located further from the wall. This process might be related to the generation of the tall fluctuation, although other possible origins of the tall fluctuation should not be excluded.
Finally, it should be pointed out that all the spectra in figure 9 exhibit fairly good inner scaling for
$y^{+}<100{-}200$
and
$\unicode[STIX]{x1D706}_{z}^{+}<100{-}200$
. However, this does not necessarily mean that the original near-wall motions in the full simulation are not affected by the removal of the motions at
$\unicode[STIX]{x1D706}_{z}\simeq \unicode[STIX]{x1D706}_{z,t}$
. It should be stressed that the removal of large-scale motions either by the box-confinement approach or by the artificial damping reduces the skin friction, resulting in a reduced friction velocity. In other words, the good inner scaling nature of the spectra near
$\unicode[STIX]{x1D706}_{z}^{+}\simeq 100$
in all the three simulations precisely implies that the removal of the motions at
$\unicode[STIX]{x1D706}_{z}\simeq \unicode[STIX]{x1D706}_{z,t}$
makes the near-wall motions resettled such that they scale well with the ‘new’ inner units given by the reduced friction velocity.
Figure 11. Comparison of the Reynolds shear stress: ——, DNS (Hoyas & Jiménez Reference Hoyas and Jiménez2006); – – – –, FIK-identity-based approach; ♢, box-confinement approach; ▫, artificial damping of
$F2000$
. Here, the cutoff spanwise wavelength applied is
$\unicode[STIX]{x1D706}_{z,t}=0.5h$
.
The scale interaction process discussed above is also directly supported by the Reynolds shear stress distribution, as shown in figure 11. Here, we note that both of the box-confinement approach and the artificial damping are designed not to change the FIK identity itself. Therefore, the Reynolds shear stress profiles, normalized by
$2U_{m}$
, are supposed to be directly related to their contribution to turbulent skin friction through the FIK identity in (2.4). Not surprisingly, all the Reynolds shear stress profiles obtained by applying the three approaches are overall smaller than that of full DNS. The profile obtained with the FIK-identity-based approach is almost identical to that of full DNS for
$y/h\lesssim 0.01$
, but is very different from those with the box-confinement approach and the artificial damping. In the region close to the wall (
$y/h\lesssim 0.06$
), the application of the FIK-identity-based approach to the full DNS data yield larger Reynolds shear stress than those with the other two approaches. This suggests that removing the motions larger than a given length scale indeed affects the near-wall motions such that they are adjusted to the reduced friction velocity. On the other hand, in the region relatively further from the wall (
$y/h\gtrsim 0.06$
), both of the box-confinement approach and the artificial damping exhibit larger Reynolds shear stress than that obtained with the FIK-identity-based approach. This indicates that the remaining motions in the absence of the motions at
$\unicode[STIX]{x1D706}_{z}>\unicode[STIX]{x1D706}_{z,t}$
indeed generate additional Reynolds shear stress in this region, resulting in an elevated skin friction compared to what is expected from the FIK identity.
4.3 Implications for flow control
It has been consistently reported that the effectiveness of flow control strategies targeting the near-wall structures, such as opposition control (Chang et al. Reference Chang, Collis and Ramakrishnan2002) and spanwise wall oscillations (Quadrio Reference Quadrio2011; Agostini et al. Reference Agostini, Touber and Leschziner2014), is reduced on increasing the Reynolds number. It has often been speculated that the undesirable performance degradation with the Reynolds number would possibly be due to the energetic large-scale structures such as large-scale and very-large scale motions (Touber & Leschziner Reference Touber and Leschziner2012). However, the present finding suggests that this behaviour is rather due to a large number of self-similar energy-containing structures in the form of Townsend’s attached eddies, most of which populate in the logarithmic region. In this respect, the trends shown by Hwang (Reference Hwang2013) have been successfully extended to much higher Reynolds numbers (figure 5 b).
It is also important to remember that the inhibition of the largest structures at scales
$\unicode[STIX]{x1D706}_{z}\geqslant 1.5h$
(i.e. VLSMs and LSMs) does not yield sufficiently large amounts of drag reduction, possibly due to the scale interaction discussed, even though they are expected to be responsible for 25–30 % of total skin friction at
$Re_{\unicode[STIX]{x1D70F}}=2000$
according to the FIK-identity-based approach (figure 4): the removal of the motions at
$\unicode[STIX]{x1D706}_{z}\geqslant 0.75h$
by both of the box-confinement and the artificial damping approaches have reduced only 7–8 % of total skin friction. These levels of performance are a little discouraging, especially given the fact that the spanwise grooved surface (riblet), which does not require any external energy input to the system, has been shown to potentially give similar amounts of drag reduction, at least in optimal conditions (Walsh Reference Walsh1982; Squire & Savill Reference Squire and Savill1989; Choi, Moin & Kim Reference Choi, Moin and Kim1993; Viswanath Reference Viswanath2002; Spalart & McLean Reference Spalart and Mclean2011). It is also worth noting that the amount of skin-friction reduction with the removal of the largest structures does not appear to be highly dependent upon the way of removing and/or disturbing these motions. For example, destruction of the self-sustaining process of these motions through inhibition of the lift-up effect also yielded 8 % of skin-friction reduction at
$Re_{\unicode[STIX]{x1D70F}}\simeq 950$
(Hwang & Bengana Reference Hwang and Bengana2016), a value not very different from that obtained here. Of course, it is still too early to conclude that this value would be the largest amount of drag reduction possible by inhibiting the largest structures.
Despite this discouraging postulation, it is still hopeful to observe the outer scaling behaviour of the normalized skin friction with gradual removal of the motions from the largest scale (see figure 6). This observation suggests that a drag reduction of 20–30 % may be achievable with an array of actuators and/or sensors, the size of which is only an order of magnitude smaller than the outer length scale. Since the boundary-layer thickness over wing or surface of a commercial aircraft is
$O(1~\text{cm})$
(Kasagi, Suzuki & Fukagata Reference Kasagi, Suzuki and Fukagata2009), the expected size of the actuators and sensors would be
$O(1~\text{mm})$
, significantly relieving the micro-scale design restriction posed by targeting the near-wall structures (Kasagi et al.
Reference Kasagi, Suzuki and Fukagata2009).
5 Concluding remarks
Thus far, we have assessed the contribution of the energy-containing motions in the form of Townsend’s attached eddies to turbulent skin friction at sufficiently high Reynolds numbers. In particular, skin-friction generation by the motions, the spanwise size of which is smaller than a given cutoff wavelength (i.e.
$\unicode[STIX]{x1D706}_{z}\leqslant \unicode[STIX]{x1D706}_{z,t}$
), has been quantified by employing three different approaches: (i) the FIK-identity-based approach; (ii) the box-confinement approach; (iii) artificial damping. The near-wall motions have been found to continuously lose their importance on increasing the Reynolds number, consistent with the previous finding at low Reynolds numbers (Hwang Reference Hwang2013). However, interestingly, the largest structures (i.e. very-large-scale and large-scale motions) at
$\unicode[STIX]{x1D706}_{z}=1.5h$
have also been found to be of limited importance: although the FIK-identity-based approach shows that the largest motions at
$\unicode[STIX]{x1D706}_{z}=1.5h$
(i.e. large-scale and very-large-scale motions) are responsible for 20–30 % of total skin friction at
$Re_{\unicode[STIX]{x1D70F}}\simeq 2000$
, their actual removal by the box-confinement and the artificial damping approaches yields only 5–8 % of skin-friction reduction, possibly due to a non-trivial scale interaction. All the three methods have consistently revealed that the largest amount of skin friction is generated by the self-similar energy-containing motions, the spanwise size of which lie between
$\unicode[STIX]{x1D706}_{z}^{+}\simeq 100$
and
$\unicode[STIX]{x1D706}_{z}\simeq 1.5h$
at sufficiently high Reynolds numbers. These motions essentially belong to the logarithmic region in the sense that their size is proportional to the distance from the wall (Hwang Reference Hwang2015), and their contribution has been found to gradually increase with the value of
$Re_{\unicode[STIX]{x1D70F}}$
, eventually being responsible for most of turbulent skin-friction generation. The significance of attached eddies to drag is also shown by the probability density function of wall-shear stress, which retains its fundamental characteristics of positive skewness even with the removal of the largest eddies. Finally, it has been shown that the normalized skin-friction reduction with respect to the cutoff spanwise wavelength
$\unicode[STIX]{x1D706}_{z,t}$
scales in the outer unit (figure 6), at least in the range of Reynolds number investigated in the present study.
The next step of the present study would be naturally to control the self-similar energy-containing motions for an appreciable amount of drag reduction. However, the multi-scale skin-friction generation involving little understood scale interactions suggests that designing a practically realizable flow controller would be highly challenging. Simple trial and error approaches would be unlikely to work for this problem, and much more innovative and systematic approaches need to be taken with very careful inspection of the given system.
Acknowledgements
Y.H. was supported by the Engineering and Physical Sciences Research Council (EPSRC) in the UK (EP/N019342/1). H.C. was supported by the NRF program (No. NRF-2014M3C1B1033848) of MSIP, Korea.
Appendix A. Comparison of box streamwise domain
Table 3. Effect of the streamwise computational domain on the friction coefficient with
$L_{z}=0.5h$
and
$L_{z}=1.5h$
. Here,
$\unicode[STIX]{x0394}C_{f}=|C_{f}-C_{f,0}|/C_{f,0}$
where
$C_{f,0}$
is the friction coefficient of each of the reference cases (i.e.
$VL2000a$
for
$L_{z}=0.5h$
and
$VL2000$
for
$L_{z}=1.5h$
). Note that, for each
$L_{z}$
, the case with the longest streamwise domain is chosen as the reference case.
The effect of the streamwise domain size on the skin-friction coefficient is examined here for
$L_{z}=0.5h$
and
$L_{z}=1.5h$
, and is reported in table 3. For
$L_{z}=1.5h$
, three different streamwise domains are tested with
$L_{x}=3,6,9h$
. The skin friction changes little with
$\unicode[STIX]{x0394}C_{f}<2\,\%$
even for
$L_{x}=2L_{z}$
, as one would have expected from the existing literature (e.g. Lozano-Durán & Jiménez Reference Lozano-Durán and Jiménez2014). In the case of
$L_{z}=0.5h$
, this behaviour remains essentially the same, justifying the use of a short streamwise domains for the box-confinement approach.
Appendix B. Influence of uniform spanwise mode on small and large streamwise computational domains
With the box-confinement approach applied to DNS at low Reynolds numbers, it was previously shown that the role of the spanwise uniform mode (
$k_{z}=0$
) in turbulent skin friction is very limited (Hwang Reference Hwang2013). Here, the related discussion is further extended for larger
$L_{z}(=\unicode[STIX]{x1D706}_{z,t})$
, and, in particular, here we show that the effect of the uniform spanwise mode in a short streamwise computational domain is even smaller than that in a long streamwise computational domain. This is presumably because the short streamwise computational domain does not allow for the streamwise space required for the spanwise uniform motion, which was found to be energetic at
$\unicode[STIX]{x1D706}_{x}\simeq 2{-}4h$
(Hwang Reference Hwang2013). Figure 12 shows the spanwise wavenumber spectra of following three tested cases for
$L_{z}=0.5h$
: (i) the short domain (
$L_{x}=1.0h$
) with the spanwise uniform mode (solid;
$M2000a$
in table 3); (ii) the short domain (
$L_{x}=1.0h$
) without the spanwise uniform mode (dashed); (iii) the long domain at least for this case (
$L_{x}=4h$
) without the spanwise uniform mode (shaded). Overall, the spectra of the three tested cases do not show significant differences from one another, except for the streamwise velocity spectra. However, this may have been expected, given the streamwise elongated nature of the streamwise velocity fluctuation. The overall deviation of the spectra (especially for the Reynolds shear stress) appear to be reasonably small, suggesting the relatively minor roles of the spanwise uniform mode and the streamwise box size. The role of the spanwise uniform mode in the first- and second-order statistics is also examined for
$L_{z}=0.5h$
, as reported in figure 13. The change in the mean velocity appears to be small, consistent with the very small change in
$C_{f}$
in figure 4. Non-negligible effects were observed in the velocity fluctuations, but these also appear to be small and insignificant, explaining the minor role of the spanwise uniform mode in skin-friction generation.
Figure 12. Premultiplied one-dimensional spanwise wavenumber spectra of (a) streamwise, (b) wall-normal, (c) spanwise velocities and (d) Reynolds shear stress for
$L_{z}=0.5h$
. Here, the solid, dashed and shaded contours indicate
$L_{x}=1h$
with the spanwise uniform mode (
$M2000a$
),
$L_{x}=1h$
without the spanwise uniform mode and
$L_{x}=4h$
without the spanwise uniform mode, respectively. The contour labels are chosen to be 0.2, 0.4, 0.6, 0.8 times each of the maximum for comparison.
Figure 13. (a) Mean-velocity profile and (b) turbulent velocity fluctuations at
$Re_{\unicode[STIX]{x1D70F}}\approx 2000$
(
$L_{x}=1h$
): ——,
$L_{z}=0.5h$
with uniform mode; ○,
$L_{z}=0.5h$
without uniform mode.
