Hostname: page-component-6dbcb7884d-fw45b Total loading time: 0 Render date: 2025-02-13T18:17:43.014Z Has data issue: false hasContentIssue false
  • English
  • Français

Revisiting ignited–quenched transition and the non-Newtonian rheology of a sheared dilute gas–solid suspension

Published online by Cambridge University Press:  03 November 2017

Saikat Saha  and
Meheboob Alam Open the ORCID record for Meheboob Alam [Opens in a new window]
Saikat Saha
Affiliation:
Engineering Mechanics Unit, Jawaharlal Nehru Centre for Advanced Scientific Research, Jakkur P.O., Bangalore 560064, India
Meheboob Alam
Affiliation:
Engineering Mechanics Unit, Jawaharlal Nehru Centre for Advanced Scientific Research, Jakkur P.O., Bangalore 560064, India
Get access Rights & Permissions [Opens in a new window]

Abstract

The hydrodynamics and rheology of a sheared dilute gas–solid suspension, consisting of inelastic hard spheres suspended in a gas, are analysed using an anisotropic Maxwellian as the single particle distribution function. For the simple shear flow, the closed-form solutions for granular temperature and three invariants of the second-moment tensor are obtained as functions of the Stokes number (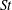$St$), the mean density ($\unicode[STIX]{x1D708}$) and the restitution coefficient ($e$). Multiple states of high and low temperatures are found when the Stokes number is small, thus recovering the ‘ignited’ and ‘quenched’ states, respectively, of Tsao & Koch (J. Fluid Mech., vol. 296, 1995, pp. 211–246). The phase diagram is constructed in the three-dimensional (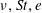$\unicode[STIX]{x1D708},St,e$)-space that delineates the regions of ignited and quenched states and their coexistence. The particle-phase shear viscosity and the normal-stress differences are analysed, along with related scaling relations on the quenched and ignited states. At any $e$, the shear viscosity undergoes a discontinuous jump with increasing shear rate at the ‘quenched–ignited’ transition. The first (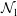${\mathcal{N}}_{1}$) and second (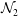${\mathcal{N}}_{2}$) normal-stress differences also undergo similar first-order transitions: (i) 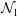${\mathcal{N}}_{1}$ jumps from large to small positive values and (ii) 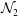${\mathcal{N}}_{2}$ from positive to negative values with increasing 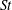$St$, with the sign change of 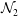${\mathcal{N}}_{2}$ identified with the system making a transition from the quenched to ignited states. The superior prediction of the present theory over the standard Grad’s method and the Burnett-order Chapman–Enskog solution is demonstrated via comparisons of transport coefficients with simulation data for a range of Stokes number and restitution coefficient.

JFM classification

Rarefied Gas Flow: Kinetic theory Non-Newtonian Flows: Rheology Complex Fluids: Suspensions
Type
Papers
Information
Journal of Fluid Mechanics , Volume 833 , 25 December 2017 , pp. 206 - 246
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alam, M. & Luding, S. 2005 Non-Newtonian granular fluid: simulation and theory. In Powders & Grains (ed. Garcia-Rojo, R., Herrmann, H. J. & McNamara, S.), pp. 1141–1144. A. A. Balkema.Google Scholar
Alam, M. & Nott, P. R. 1997 Influence of friction on the stability of unbounded granular shear flow. J. Fluid Mech. 343, 267–301.Google Scholar
Alam, M. & Saha, S. 2017 Normal stress differences and beyond-Navier–Stokes hydrodynamics. EPJ Conf. Proc. 140, 11014.Google Scholar
Anderson, T. B. & Jackson, R. 1968 A fluid mechanical description of fluidized beds: equations of motion. Ind. Engng Chem. Fundam. 6, 527–539.CrossRefGoogle Scholar
Araki, S. 1988 The dynamics of particle disks: II. Effects of spin degrees of freedom. Icarus 76, 182–198.CrossRefGoogle Scholar
Araki, S. & Tremaine, S. 1986 The dynamics of dense particle disks. Icarus 65, 83–109.Google Scholar
Boyer, F., Pouliquen, O. & Guazzelli, E. 2011 Dense suspensions in rotating-rod flows: normal stresses and particle migration. J. Fluid Mech. 686, 5–25.Google Scholar
Brady, J. F. & Bossis, G. 1988 Stokesian dynamics. Annu. Rev. Fluid Mech. 20, 111–157.Google Scholar
Brey, J. J., Dufty, J. W., Kim, C. S. & Santos, A. 1998 Hydrodynamics for granular flow at low density. Phys. Rev. E 58, 4638–4653.Google Scholar
Brilliantov, N. V. & Pöschel, T. 2004 Kinetic Theory of Granular Gases. Oxford University Press.Google Scholar
Brown, E. & Jaeger, H. M. 2014 Shear thickening in concentrated suspensions. Rep. Prog. Phys. 77, 046602.Google Scholar
Buyevich, Y. A. 1971 Statistical hydrodynamics of disperse systems. Part 1. Physical background and general equations. J. Fluid Mech. 49, 489–507.Google Scholar
Callen, H. B. 1985 Thermodynamics and an Introduction to Thermostatics. Wiley.Google Scholar
Campbell, C. S. 1990 Rapid granular flows. Annu. Rev. Fluid Mech. 22, 57–90.CrossRefGoogle Scholar
Chamorro, M. G., Reyes, F. V. & Garzo, V. 2015 Non-newtonian hydrodynamics for a dilute granular suspension under uniform shear flow. Phys. Rev. E 92, 052205.Google ScholarPubMed
Chapman, S. & Cowling, T. G. 1970 The Mathematical Theory for Non-uniform Gases. Cambridge University Press.Google Scholar
Chou, C. S. & Richman, M. W. 1998 Constitutive theory for homogeneous granular shear flows of highly inelastic spheres. Physica A 259, 430–448.Google Scholar
Davidson, J. F. & Harrison, D. 1963 Fluidized Particles. Cambridge University Press.Google Scholar
Forterre, Y. & Pouliquen, O. 2008 Flows of dense granular media. Annu. Rev. Fluid Mech. 40, 1–24.CrossRefGoogle Scholar
Garzo, V., Tenneti, S., Subramaniam, S. & Hrenya, C. 2012 Enskog kinetic theory for monodisperse gas–solid flows. J. Fluid Mech. 712, 129–168.CrossRefGoogle Scholar
Gayen, B. & Alam, M. 2006 Algebraic and exponential instabilities in a sheared micropolar granular fluid. J. Fluid Mech. 567, 195.Google Scholar
Gayen, B. & Alam, M. 2008 Orientation correlation and velocity distributions in uniform shear flow of a dilute granular gas. Phys. Rev. Lett. 100, 068002.Google Scholar
Gidaspow, D. 1994 Multiphase Flow and Fluidization. Academic.Google Scholar
Goddard, J. D. & Alam, M. 1999 Shear-flow and material instabilities in particulate suspensions and granular media. Part. Sci. Technol. 17, 69.CrossRefGoogle Scholar
Goldhirsch, I. 2003 Rapid granular flows. Annu. Rev. Fluid Mech. 35, 267–293.CrossRefGoogle Scholar
Goldreich, P. & Tremaine, S. 1978 The velocity dispersion in Saturn’s rings. Icarus 34, 227–239.CrossRefGoogle Scholar
Grad, H. 1949 On the kinetic theory of rarefied gases. Commun. Pure Appl. Maths 2, 331–407.Google Scholar
Guazzelli, E. & Morris, J. F. 2011 A Physical Introduction to Suspension Dynamics. Cambridge University Press.CrossRefGoogle Scholar
Gupta, R. & Alam, M. 2017 Hydrodynamics, wall-slip, and normal-stress differences in rarefied granular Poiseuille flow. Phys. Rev. E 95, 022903.Google ScholarPubMed
Hayakawa, H., Takada, S. & Garzo, V. 2017 Kinetic theory of shear-thickening for a moderately dense gas–solid suspension. Phys. Rev. E 96, 042903.Google ScholarPubMed
Herdegen, N. & Hess, S. 1982 Nonlinear flow behavior of the Boltzmann gas. Physica A 115, 281–299.Google Scholar
Hoffman, R. L. 1972 Discontinuous and dilatant viscosity behaviour in concentrated suspensions. Trans. Soc. Rheol. 16, 155.Google Scholar
Holway, L. H. 1966 New statistical models for kinetic theory: methods of construction. Phys. Fluids 9, 1658–1673.CrossRefGoogle Scholar
Jackson, R. 2000 Dynamics of Fluidized Particles. Cambridge University Press.Google Scholar
Jaynes, E. T. 1957 Information theory and statistical mechanics. Phys. Rev. 106, 620–630.Google Scholar
Jenkins, J. T. & Richman, M. W. 1985 Grad’s 13-moment system for a dense gas of inelastic spheres. Arch. Rat. Mech. Anal. 87, 355–377.CrossRefGoogle Scholar
Jenkins, J. T. & Richman, M. W. 1988 Plane simple shear of smooth inelastic circular disks. J. Fluid Mech. 192, 313–328.Google Scholar
Koch, D. L. 1990 Kinetic theory for a monodisperse gas–solid suspension. Phys. Fluids A 2, 1711–1723.CrossRefGoogle Scholar
Koch, D. L. & Hill, R. J. 2001 Inertial effects in gas–solid suspension and porous-media flows. Annu. Rev. Fluid Mech. 33, 619–647.Google Scholar
Kremer, G. M. 2010 Introduction to Boltzmann Equation. Springer.Google Scholar
Kremer, G. M. & Marques, W. 2011 Fourteen moment theory for granular gases. Kinet. Relat. Models 4, 317–331.Google Scholar
Kumaran, V., Tsao, H.-K. & Koch, D. L. 1993 Velocity distribution functions for a bidisperse sedimenting particle-gas suspension. Intl J. Multiphase Flow 19, 665–681.Google Scholar
Lees, A. W. & Edwards, S. 1972 The computer study of transport processes under extreme conditions. J. Phys. C 5, 1921–1929.Google Scholar
Louge, M., Mastorakos, E. & Jenkins, J. T. 1991 The role of particle collisions in pneumatic transport. J. Fluid Mech. 231, 345–359.CrossRefGoogle Scholar
Lun, C. K. K. & Savage, S. B. 2003 Kinetic theory for inertia flows of dilute turbulent gas–solids mixtures. In Granular Gas Dynamics (ed. Pöschel, T. & Brilliantov, N. V.), p. 263. Springer.Google Scholar
Lun, C. K. K., Savage, S. B., Jeffrey, D. J. & Chepurniy, N. 1984 Kinetic theories for granular flow: inelastic particles in Couette flow and slightly inelastic particles in a general flow field. J. Fluid Mech. 140, 223–256.Google Scholar
Lutsko, J. F. 2004 Rheology of dense polydisperse granular fluids under shear. Phys. Rev. E 70, 061101.Google Scholar
Parmentier, J.-F. & Simonin, O. 2012 Transition models from the quenched to ignited states for flows of inertial particles suspended in a simple sheared viscous fluid. J. Fluid Mech. 711, 147–160.Google Scholar
Rao, K. K. & Nott, P. R. 2008 An Introduction to Granular Flow. Cambridge University Press.Google Scholar
Richman, M. W. 1989 The source of second moment in dilute granular flows of highly inelastic spheres. J. Rheol. 33, 1293–1306.Google Scholar
Rongali, R. & Alam, M. 2014 Higher-order effects on orientational correlation and relaxation dynamics in homogeneous cooling of a rough granular gas. Phys. Rev. E 89, 062201.Google Scholar
Saha, S. & Alam, M. 2014 Non-Newtonian stress, collisional dissipation and heat flux in the shear flow of inelastic disks: a reduction via Grad’s moment method. J. Fluid Mech. 757, 251–296.Google Scholar
Saha, S. & Alam, M. 2016a Normal stress differences, their origin and constitutive relations for a sheared granular fluid. J. Fluid Mech. 795, 549–580.Google Scholar
Saha, S. & Alam, M.2016b Normal stress differences in a sheared gas–solid suspension. In Bulletin of American Physical Society (69th Annual Meeting of APS Division of Fluid Dynamics, 20–22 November, Portland, USA), vol. 61, no. 20, L26.00010.Google Scholar
Sangani, A. S., Mo, G., Tsao, H-K. & Koch, D. L. 1996 Simple shear flows of dense gas–solid suspensions at finite stokes numbers. J. Fluid Mech. 313, 309–341.Google Scholar
Savage, S. B. & Jeffrey, D. J. 1981 The stress tensor in a granular flow at high shear rates. J. Fluid Mech. 110, 255–272.Google Scholar
Sela, N. & Goldhirsch, I. 1998 Hydrodynamic equations for rapid flows of smooth inelastic spheres, to Burnett order. J. Fluid Mech. 361, 41–74.Google Scholar
Shukhman, G. 1984 Collisional dynamics of particles in Saturn’s rings. Sov. Astron. 28, 547–584.Google Scholar
Tsao, H.-K. & Koch, D. L. 1995 Simple shear flows of dilute gas–solid suspensions. J. Fluid Mech. 296, 211–246.Google Scholar
Supplementary material: File

Saha and Alam supplementary material

Saha and Alam supplementary material 1

Download Saha and Alam supplementary material(File)
File 497.4 KB