2 Hydrodynamics around an oscillating stick–slip Janus particle

Consider the motion of a spherical SSJP of radius $a$ in an incompressible viscous fluid of density $\unicode[STIX]{x1D70C}$ and viscosity $\unicode[STIX]{x1D707}$ . As depicted in figure 2, the slip part of the particle has polar angle $\unicode[STIX]{x1D703}_{0}$ in division with the remaining stick part. The particle undergoes an oscillatory translation at speed ${\mathcal{U}}_{p}\text{e}^{-\text{i}\unicode[STIX]{x1D714}t}$ with the peak velocity ${\mathcal{U}}_{p}$ and frequency $\unicode[STIX]{x1D714}$ . It is more convenient to solve the problem in the translating coordinate system with the origin at the instantaneous centre of the particle. Having length, time, velocity and pressure scaled by $a$ , $\unicode[STIX]{x1D714}^{-1}$ , ${\mathcal{U}}_{p}$ and $\unicode[STIX]{x1D707}{\mathcal{U}}_{p}/a$ , respectively, the velocity field $\boldsymbol{v}^{\prime }$ and pressure $p^{\prime }$ around the particle are governed by the continuity equation and the unsteady Stokes flow equation,

(2.1) $$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{v}^{\prime }=0, & \displaystyle\end{eqnarray}$$

(2.2) $$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D6FA}\boldsymbol{v}_{t^{\prime }}^{\prime }=-\unicode[STIX]{x1D735}p^{\prime }+\unicode[STIX]{x1D6FB}^{2}\boldsymbol{v}^{\prime }, & \displaystyle\end{eqnarray}$$

where $\unicode[STIX]{x1D6FA}=\unicode[STIX]{x1D714}a^{2}/\unicode[STIX]{x1D708}$ is the dimensionless frequency (with $\unicode[STIX]{x1D708}=\unicode[STIX]{x1D707}/\unicode[STIX]{x1D70C}$ being the kinematic viscosity). For simplicity, we assume that the particle is moving along its bipolar direction so that the flow field $\boldsymbol{v}^{\prime }=(u^{\prime },v^{\prime })$ can be expressed in terms of the meridional $(\unicode[STIX]{x1D703})$ component $u^{\prime }$ and the radial $(r)$ component $v^{\prime }$ . This axisymmetric fluid motion is likely to be the case in steady oscillation because any misalignment of the particle movement from the bipolar direction will cause the particle to rotate until an alignment is achieved.

Figure 2. Sketch of a spherical stick–slip Janus particle and the coordinate system.

Because the fluid motion is oscillatory, it is more convenient to solve the problem in the frequency domain by letting $(u^{\prime },v^{\prime },p^{\prime })=(u,v,p)\text{e}^{-\text{i}t^{\prime }}$ . Taking curl for (2.2) to eliminate pressure with $\unicode[STIX]{x1D735}\times \unicode[STIX]{x1D735}p=0$ and writing the velocity components in terms of the stream function $\unicode[STIX]{x1D713}$ for satisfying (2.1),

(2.3a,b ) $$\begin{eqnarray}u=-\frac{1}{r\sin \unicode[STIX]{x1D703}}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}}{\unicode[STIX]{x2202}r},\quad v=\frac{1}{r^{2}\sin \unicode[STIX]{x1D703}}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}},\end{eqnarray}$$

we can transform (2.2) into

(2.4) $$\begin{eqnarray}\text{E}^{2}(\text{E}^{2}-\unicode[STIX]{x1D6FC}^{2})\unicode[STIX]{x1D713}=0,\end{eqnarray}$$

where $\text{E}^{2}=\unicode[STIX]{x2202}_{rr}+r^{-2}(1-\unicode[STIX]{x1D702}^{2})\unicode[STIX]{x2202}_{\unicode[STIX]{x1D702}\unicode[STIX]{x1D702}}$ with $\unicode[STIX]{x1D702}=\cos \unicode[STIX]{x1D703}$ and $\unicode[STIX]{x1D6FC}=(-\text{i}\unicode[STIX]{x1D6FA})^{1/2}$ is the complex Womersley number with $Re\{\unicode[STIX]{x1D6FC}\}>0$ .

Boundary conditions are the mixed stick–slip condition at $r=1$ , the impenetrability condition at $r=1$ , and the vanishing velocity condition as $r\rightarrow \infty$ ,

(2.5) $$\begin{eqnarray}\displaystyle & \displaystyle u+\sin \unicode[STIX]{x1D703}=\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D703})\left[r\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}r}\left(\frac{u}{r}\right)+\frac{1}{r}\frac{\unicode[STIX]{x2202}v}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}}\right]\quad \text{at}~r=1, & \displaystyle\end{eqnarray}$$

(2.6) $$\begin{eqnarray}\displaystyle & \displaystyle v=\cos \unicode[STIX]{x1D703}\quad \text{at}~r=1, & \displaystyle\end{eqnarray}$$

(2.7) $$\begin{eqnarray}\displaystyle & \displaystyle u,v\rightarrow 0\quad \text{as}~r\rightarrow \infty . & \displaystyle\end{eqnarray}$$

In (2.5), $\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D703})=\hat{\unicode[STIX]{x1D706}}$ for the slip face and $0$ otherwise, where $\hat{\unicode[STIX]{x1D706}}=\unicode[STIX]{x1D706}/a$ is the dimensionless slip length.

As in Lawrence & Weinbaum (Reference Lawrence and Weinbaum1986), the solution of (2.4) that satisfies (2.7) takes the form

(2.8) $$\begin{eqnarray}\unicode[STIX]{x1D713}=\mathop{\sum }_{n=2}^{\infty }[A_{n}H_{n}(r)+B_{n}R_{n}(r)]G_{n}(\unicode[STIX]{x1D702}),\end{eqnarray}$$

where $H_{n}(r)=r^{-n+1}$ , $R_{n}(r)=r^{1/2}\text{K}_{n-1/2}(\unicode[STIX]{x1D6FC}r)$ with $\text{K}_{n-1/2}$ being modified Bessel functions of second kind, and $G_{n}$ the Gegenbauer functions of degree $-1/2$ . The coefficients $A_{n}$ and $B_{n}$ are determined by substituting (2.8) into (2.5) and (2.6) and applying the orthogonality $\int _{-1}^{1}G_{m}(\unicode[STIX]{x1D702})G_{n}(\unicode[STIX]{x1D702})/(1-\unicode[STIX]{x1D702}^{2})\,\text{d}\unicode[STIX]{x1D702}=\unicode[STIX]{x1D6FF}_{mn}C_{n}$ over these two boundary conditions, where $\unicode[STIX]{x1D6FF}_{mn}$ is the Kronecker delta and $C_{n}=2/n(n-1)(2n-1)$ . From (2.6), we can express $B_{n}$ in terms of $A_{n}$ as $B_{n}=\unicode[STIX]{x1D6FF}_{2n}-A_{n}H_{n}(1)/R_{n}(1)$ . Applying (2.5) and eliminating $B_{n}$ , we arrive at the following infinite system of linear equations (via $m$ ) for $A_{n}$ :

(2.9) $$\begin{eqnarray}\mathop{\sum }_{n=2}^{\infty }\left\{\unicode[STIX]{x1D6FF}_{mn}C_{n}{\mathcal{G}}_{n}+{\mathcal{L}}_{mn}d_{n}\right\}A_{n}=2\left\{C_{2}\unicode[STIX]{x1D6FF}_{2m}+{\mathcal{L}}_{m2}\right\}-C_{m}j_{m}\unicode[STIX]{x1D6FF}_{2m}-\mathop{\sum }_{n=2}^{\infty }{\mathcal{L}}_{mn}e_{n}\unicode[STIX]{x1D6FF}_{2n},\end{eqnarray}$$

where

(2.10) $$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}c@{}}\displaystyle {\mathcal{G}}_{n}={H_{n}}^{\prime }(1)-\frac{H_{n}(1)}{R_{n}(1)}{R_{n}}^{\prime }(1),\quad d_{n}=2{H_{n}}^{\prime }(1)-{H_{n}}^{\prime \prime }(1)-\frac{H_{n}(1)}{R_{n}(1)}\{2{R_{n}}^{\prime }(1)-{R_{n}}^{\prime \prime }(1)\},\\ \displaystyle {\mathcal{L}}_{mn}=\int _{-1}^{1}\frac{G_{m}(\unicode[STIX]{x1D702})G_{n}(\unicode[STIX]{x1D702})\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D702})}{1-\unicode[STIX]{x1D702}^{2}}\,\text{d}\unicode[STIX]{x1D702},\quad e_{n}=\frac{1}{R_{n}(1)}\{2{R_{n}}^{\prime }(1)-{R_{n}}^{\prime \prime }(1)\},\quad j_{n}=\frac{{R_{n}}^{\prime }(1)}{R_{n}(1)}.\end{array}\right\} & & \displaystyle \nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$

After solving (2.9), the force on the particle can be readily determined as $F=\hat{F}\text{e}^{-\text{i}\unicode[STIX]{x1D714}t}$ with

(2.11) $$\begin{eqnarray}\hat{F}=\unicode[STIX]{x1D707}{\mathcal{U}}_{p}a(-2\unicode[STIX]{x03C0}A_{2}+V_{p})\unicode[STIX]{x1D6FC}^{2},\end{eqnarray}$$

where $V_{p}=4\unicode[STIX]{x03C0}/3$ is the dimensionless particle volume. In this work we are mainly concerned with the viscous part of $\hat{F}$ after subtracting the added mass contribution $-6\unicode[STIX]{x03C0}\unicode[STIX]{x1D707}{\mathcal{U}}_{p}a\times (\unicode[STIX]{x1D6FC}^{2}/9)$ ,

(2.12) $$\begin{eqnarray}\hat{F}^{vis}=6\unicode[STIX]{x03C0}\unicode[STIX]{x1D707}{\mathcal{U}}_{p}a(-A_{2}+1)\times (\unicode[STIX]{x1D6FC}^{2}/3).\end{eqnarray}$$

We have verified analytically that when $\unicode[STIX]{x1D6FD}$ is constant, (2.12) is reduced to the viscous part of (1.3). For given $\unicode[STIX]{x1D6FC}$ , $\unicode[STIX]{x1D703}_{0}$ and $\hat{\unicode[STIX]{x1D706}}$ , equation (2.9) can be solved by truncation and matrix inversion. In the present work, convergent results can be obtained by retaining 100 terms in the solution (2.8).

Figure 3. (a) Plot of the calculated viscous force amplitude $|\hat{F}^{vis}|/(6\unicode[STIX]{x03C0}\unicode[STIX]{x1D707}{\mathcal{U}}_{p}a)$ (using (2.12)) against $\hat{\unicode[STIX]{x1D6FF}}$ for an SSJP with a slip hemisphere $(\unicode[STIX]{x1D703}_{0}=90^{\circ })$ , showing that all the curves with different values of $\hat{\unicode[STIX]{x1D706}}$ approach towards the same re-entry Basset $1/\hat{\unicode[STIX]{x1D6FF}}$ asymptote (3.27) as $\hat{\unicode[STIX]{x1D6FF}}\rightarrow 0$ (see the inset). (b) Plot of the corresponding phase $\unicode[STIX]{x1D719}^{vis}$ as a function of $\hat{\unicode[STIX]{x1D6FF}}$ , showing that $\unicode[STIX]{x1D719}^{vis}$ also approaches $-\unicode[STIX]{x03C0}/4$ as $\hat{\unicode[STIX]{x1D6FF}}\rightarrow 0$ .

Figure 3(a) plots the viscous force amplitude $|\hat{F}^{vis}|$ against $\hat{\unicode[STIX]{x1D6FF}}=(2/\unicode[STIX]{x1D6FA})^{1/2}$ for an SSJP with a slip hemisphere $(\unicode[STIX]{x1D703}_{0}=90^{\circ })$ . Several features can be immediately observed. First, for a given value of $\hat{\unicode[STIX]{x1D706}}$ the high frequency force plateau seen for the uniform slip case disappears. Instead, a Basset $1/\hat{\unicode[STIX]{x1D6FF}}$ decay emerges and dominates the force response in the small $\hat{\unicode[STIX]{x1D6FF}}$ regime. This is the re-entry Basset force after a slippery particle is partially covered by a stick cap. Second, all the curves with different values of $\hat{\unicode[STIX]{x1D706}}$ approach towards the same re-entry Basset asymptote as $\hat{\unicode[STIX]{x1D6FF}}\rightarrow 0$ (see the inset). Third, the amplitude of such an asymptote is slightly smaller than that of the no-slip Basset force. The corresponding phase $\unicode[STIX]{x1D719}^{vis}=\tan ^{-1}(\text{Im}(\hat{F}^{vis})/\text{Re}(\hat{F}^{vis}))$ also approaches the Basset value $-\unicode[STIX]{x03C0}/4$ as $\hat{\unicode[STIX]{x1D6FF}}\rightarrow 0$ , as indicated by figure 3(b). Note that there is a phase jump between the no-slip case ( $\unicode[STIX]{x1D719}_{vis}=-\unicode[STIX]{x03C0}/4$ ) and the uniform slip case ( $\unicode[STIX]{x1D719}_{vis}=0$ ). So returning from $\unicode[STIX]{x1D719}_{vis}=0$ for a completely slip sphere to $\unicode[STIX]{x1D719}_{vis}=-\unicode[STIX]{x03C0}/4$ for an SSJP is also an indication of the re-entry Basset force seen in the latter.

The appearance of the re-entry Basset decay between the no-slip Basset decay and the uniform slip force plateau seen in figure 3(a) implies that there must be a competition between no-slip and slip memory effects, depending on the stick–slip partition measured by $\unicode[STIX]{x1D703}_{0}$ . Figure 4(a) plots the viscous force responses when the stick portion is gradually reduced by increasing $\unicode[STIX]{x1D703}_{0}$ . We find that when the stick portion is shrunk, not only will the re-entry Basset $1/\hat{\unicode[STIX]{x1D6FF}}$ decay reduce its amplitude, but also a slip plateau will start to re-appear on the tail of the re-entry Basset decay. When the stick portion becomes tiny such as that of the $\unicode[STIX]{x1D703}_{0}=150^{\circ }$ case, in particular, the force response shows the coexistence of a re-entry Basset decay and a slip plateau. This clearly signifies an RHFT, featured with two transition points: (i) the RHFT point when the re-entry Basset decay starts to level off towards the slip plateau, and (ii) the SST point $\hat{\unicode[STIX]{x1D6FF}}\sim \hat{\unicode[STIX]{x1D706}}$ around which the slip plateau starts to decrease towards the usual Basset decay. We should clarify that either transition represents a gradual change from one force response to another, so the corresponding point should be understood as a ‘crossover’ between two different force responses. Interestingly, if a Janus particle is made of two slip surfaces, the re-entry Basset decay will disappear and the slip force plateau will return to dominate the viscous force response in the small $\hat{\unicode[STIX]{x1D6FF}}$ regime, as also revealed by figure 4(a). The disappearance of the re-entry Basset force in the small $\hat{\unicode[STIX]{x1D6FF}}$ regime is accompanied by a jump of the phase $\unicode[STIX]{x1D719}^{vis}(\hat{\unicode[STIX]{x1D6FF}}\rightarrow 0)$ from $-\unicode[STIX]{x03C0}/4$ to zero when the stick–slip case changes to the slip–slip case, as shown in figure 4(b).

Figure 4. (a) History force transition between the re-entry Basset decay and the slip plateau can be more clearly revealed from the viscous force response when the stick portion of an SSJP is gradually reduced. When the stick portion becomes tiny such as that of $\unicode[STIX]{x1D703}_{0}=150^{\circ }$ case, the prevailing re-entry Basset decay can exhibit a slip plateau on its tail in the small $\hat{\unicode[STIX]{x1D6FF}}$ regime (see pink solid line), showing two transition points: RHFT and SST points given by (3.30) and (3.28), respectively. For a slip–slip Janus particle, however, the re-entry Basset decay will disappear and a constant force plateau will return to dominate the force response again (see green dashed line). (b) A jump of the phase $\unicode[STIX]{x1D719}^{vis}(\hat{\unicode[STIX]{x1D6FF}}\rightarrow 0)$ from $-\unicode[STIX]{x03C0}/4$ to zero when the stick–slip case changes to the slip–slip case.

3 Matched asymptotic boundary layer theory

To explain the results shown in figures 3 and 4 as well as to see how RHFT occurs, we develop a matched asymptotic boundary layer theory for capturing the force response in the small $\unicode[STIX]{x1D6FF}$ regime when $\unicode[STIX]{x1D6FA}$ is large. Similar to previous studies by Wang (Reference Wang1965) and Riley (Reference Riley1966), we let $\unicode[STIX]{x1D716}=1/\unicode[STIX]{x1D6FA}^{1/2}=\hat{\unicode[STIX]{x1D6FF}}/\sqrt{2}$ be the small parameter to expand the flow fields outside and inside the boundary layer as follows.

3.1 Outer inviscid core region

In the outer core regime, we let $\boldsymbol{{\mathcal{V}}}=(U,V)$ and $P$ stand for the velocity field and pressure, respectively, and expand them as

(3.1) $$\begin{eqnarray}\displaystyle & \displaystyle \boldsymbol{{\mathcal{V}}}=\boldsymbol{{\mathcal{V}}}_{0}+\unicode[STIX]{x1D716}\boldsymbol{{\mathcal{V}}}_{1}+O(\unicode[STIX]{x1D716}^{2}), & \displaystyle\end{eqnarray}$$

(3.2) $$\begin{eqnarray}\displaystyle & \displaystyle P=\unicode[STIX]{x1D716}^{-2}P_{0}+\unicode[STIX]{x1D716}^{-1}P_{1}+O(\unicode[STIX]{x1D716}^{0}). & \displaystyle\end{eqnarray}$$

Substituting the above into (2.1) and (2.2), we find that at both $O(\unicode[STIX]{x1D716}^{0})$ and $O(\unicode[STIX]{x1D716}^{1})$ the flows are inviscid and irrotational, governed by $\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{{\mathcal{V}}}_{n}=0$ and $-\text{i}\boldsymbol{{\mathcal{V}}}_{n}=-\unicode[STIX]{x1D735}P_{n}$ . So the flows can be solved using $\unicode[STIX]{x1D6FB}^{2}\unicode[STIX]{x1D719}_{n}=0$ with $\boldsymbol{{\mathcal{V}}}_{n}=\unicode[STIX]{x1D735}\unicode[STIX]{x1D719}_{n}$ , giving the velocity and pressure distributions at each order as follows.

$O(\unicode[STIX]{x1D716}^{0})$ :

(3.3) $$\begin{eqnarray}\displaystyle & \displaystyle U_{0}=-({\mathcal{A}}/r^{3})\sin \unicode[STIX]{x1D703}, & \displaystyle\end{eqnarray}$$

(3.4) $$\begin{eqnarray}\displaystyle & \displaystyle V_{0}=-2({\mathcal{A}}/r^{3})\cos \unicode[STIX]{x1D703}, & \displaystyle\end{eqnarray}$$

(3.5) $$\begin{eqnarray}\displaystyle & \displaystyle P_{0}=\text{i}({\mathcal{A}}/r^{2})\cos \unicode[STIX]{x1D703}. & \displaystyle\end{eqnarray}$$

$O(\unicode[STIX]{x1D716})$ :

(3.6) $$\begin{eqnarray}\displaystyle & \displaystyle U_{1}=({\mathcal{A}}_{1}/r^{3})\sin \unicode[STIX]{x1D703}, & \displaystyle\end{eqnarray}$$

(3.7) $$\begin{eqnarray}\displaystyle & \displaystyle V_{1}=-2({\mathcal{A}}_{1}/r^{3})\cos \unicode[STIX]{x1D703}, & \displaystyle\end{eqnarray}$$

(3.8) $$\begin{eqnarray}\displaystyle & \displaystyle P_{1}=\text{i}({\mathcal{A}}_{1}/r^{2})\cos \unicode[STIX]{x1D703}. & \displaystyle\end{eqnarray}$$

Here the coefficients ${\mathcal{A}}$ and ${\mathcal{A}}_{1}$ will be determined through matching to the solution in the inner boundary layer region.

3.2 Inner boundary layer region

For the inner boundary layer region where viscous effects are important, we stretch the radial coordinate as $r=1+\unicode[STIX]{x1D716}y$ and expand the flow variables as

(3.9) $$\begin{eqnarray}\displaystyle & \displaystyle u=u_{0}+\unicode[STIX]{x1D716}u_{1}+O(\unicode[STIX]{x1D716}^{2}), & \displaystyle\end{eqnarray}$$

(3.10) $$\begin{eqnarray}\displaystyle & \displaystyle v=\cos \unicode[STIX]{x1D703}+\unicode[STIX]{x1D716}v_{0}+O(\unicode[STIX]{x1D716}^{2}), & \displaystyle\end{eqnarray}$$

(3.11) $$\begin{eqnarray}\displaystyle & \displaystyle p=\unicode[STIX]{x1D716}^{-2}p_{0}+\unicode[STIX]{x1D716}^{-1}p_{1}+O(\unicode[STIX]{x1D716}^{0}). & \displaystyle\end{eqnarray}$$

Substituting the above into (2.1) and (2.2), at leading order the equations are

(3.12) $$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x2202}_{y}v_{0}+\frac{1}{\sin \unicode[STIX]{x1D703}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}}(u_{0}\sin \unicode[STIX]{x1D703})=0, & \displaystyle\end{eqnarray}$$

(3.13) $$\begin{eqnarray}\displaystyle & \displaystyle -\text{i}u_{0}=-\unicode[STIX]{x2202}_{\unicode[STIX]{x1D703}}p_{0}+\unicode[STIX]{x2202}_{yy}u_{0}, & \displaystyle\end{eqnarray}$$

(3.14) $$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x2202}_{y}p_{0}=0. & \displaystyle\end{eqnarray}$$

Because of (3.14), $p_{0}$ remains constant across the boundary layer. Matching $\unicode[STIX]{x1D716}^{-2}p_{0}$ to the outer pressure $\unicode[STIX]{x1D716}^{-2}P_{0}(r\rightarrow 1^{+})$ with (3.5), we can determine $p_{0}$ as

(3.15) $$\begin{eqnarray}p_{0}=\text{i}{\mathcal{A}}\cos \unicode[STIX]{x1D703}.\end{eqnarray}$$

Next, we substitute (3.15) into (3.13) to determine $u_{0}$ using the mixed stick-slip boundary condition at $y=0$ ,

(3.16) $$\begin{eqnarray}u_{0}+\sin \unicode[STIX]{x1D703}=(\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D703})/\unicode[STIX]{x1D716})\unicode[STIX]{x2202}_{y}u_{0}.\end{eqnarray}$$

In (3.16) we retain both the no-slip part (on the left-hand side) and the slip part (on the right-hand side) in the present analysis, just like those in the Stokes 1st problem (Fujioka & Wei Reference Fujioka and Wei2018). The reasons are twofold. First, because the fluid is dragging along with the particle through the driving velocity $\sin \unicode[STIX]{x1D703}$ along the particle surface, impacts of slip can only be brought by having the slip term at least balanced to the $\sin \unicode[STIX]{x1D703}$ term in the no-slip part, especially when the amount of slip $\hat{\unicode[STIX]{x1D706}}=\unicode[STIX]{x1D706}/a$ varies. Second, to capture the non-trivial transition from the no-slip response to the slip response, it is more convenient to retain both parts in (3.16). Specifically, since the effective slip coefficient $\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D703})/\unicode[STIX]{x1D716}$ can be either small or large depending on the polar angle $\unicode[STIX]{x1D703}_{0}$ that divides the stick and the slip faces for an SSJP, it is necessary to keep the no-slip part in (3.16) so that one can see how its effects compete with the slip part’s as $\unicode[STIX]{x1D703}_{0}$ varies.

With (3.15) and (3.16), we solve (3.13) to determine $u_{0}$ as

(3.17) $$\begin{eqnarray}u_{0}=({\mathcal{A}}-1)\sin \unicode[STIX]{x1D703}[\text{e}^{-ky}g(\unicode[STIX]{x1D703})-1]-\sin \unicode[STIX]{x1D703},\end{eqnarray}$$

where $k=\text{e}^{-\text{i}\unicode[STIX]{x03C0}/4}$ and $g(\unicode[STIX]{x1D703})=(1+k\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D703})/\unicode[STIX]{x1D716})^{-1}$ is a piecewise continuous function because of $\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D703})$ in (2.5). Strictly speaking, the present boundary layer analysis is valid only if $|\text{d}\unicode[STIX]{x1D6FD}/\text{d}\unicode[STIX]{x1D703}|\ll \unicode[STIX]{x1D716}^{-1}$ . As will be shown later in the force expression (3.25), since we will be only concerned with the first two harmonic contributions from $g(\unicode[STIX]{x1D703})$ , effects of the piecewise continuity, which contribute to higher harmonics, will not matter. Substituting (3.17) into (3.12), we can solve for $v_{0}$ with $v_{0}(y=0)=0$ ,

(3.18) $$\begin{eqnarray}v_{0}=k^{-1}({\mathcal{A}}-1)(\text{e}^{-ky}-1)\frac{1}{\sin \unicode[STIX]{x1D703}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}}(g(\unicode[STIX]{x1D703})\sin ^{2}\unicode[STIX]{x1D703})+2{\mathcal{A}}y\cos \unicode[STIX]{x1D703}.\end{eqnarray}$$

At the next order, we only need to determine the pressure which again is a function of $\unicode[STIX]{x1D703}$ only because $\unicode[STIX]{x2202}_{y}p_{1}=0$ . Similar to (3.15), matching $\unicode[STIX]{x1D716}^{-1}p_{1}$ to the outer pressure $\unicode[STIX]{x1D716}^{-2}P_{1}(r\rightarrow 1^{+})$ with (3.8) gives

(3.19) $$\begin{eqnarray}p_{1}=\text{i}{\mathcal{A}}_{1}\cos \unicode[STIX]{x1D703}.\end{eqnarray}$$

3.3 Matching

To determine the coefficients ${\mathcal{A}}$ and ${\mathcal{A}}_{1}$ we match the radial velocities of the outer and the inner regions,

(3.20) $$\begin{eqnarray}\lim _{r\rightarrow 1}(V_{0}+\unicode[STIX]{x1D716}V_{1}+\cdots \,)\;\Longleftrightarrow \;\lim _{y\rightarrow \infty }(\cos \unicode[STIX]{x1D703}+\unicode[STIX]{x1D716}v_{0}+\cdots \,)\quad \text{as }\unicode[STIX]{x1D716}\rightarrow 0.\end{eqnarray}$$

This is equivalent to the matching between the outer and the inner stream functions (Riley Reference Riley1966). Substituting (3.4) and (3.7) into the left-hand side of (3.20) and taking an expansion in $\unicode[STIX]{x1D716}$ , we arrive at

(3.21) $$\begin{eqnarray}(V_{0}+\unicode[STIX]{x1D716}V_{1}+\cdots \,)_{r\rightarrow 1}=[-2{\mathcal{A}}+\unicode[STIX]{x1D716}(-2{\mathcal{A}}_{1}+6{\mathcal{A}}y)+\cdots \,]\cos \unicode[STIX]{x1D703}+\cdots \,.\end{eqnarray}$$

As for the right-hand side of (3.20), substituting (3.18) into it gives

(3.22) $$\begin{eqnarray}(\cos \unicode[STIX]{x1D703}+\unicode[STIX]{x1D716}v_{0}+\cdots \,)_{y\rightarrow \infty }=\cos \unicode[STIX]{x1D703}-\unicode[STIX]{x1D716}k^{-1}({\mathcal{A}}-1)\frac{1}{\sin \unicode[STIX]{x1D703}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}}(g(\unicode[STIX]{x1D703})\sin ^{2}\unicode[STIX]{x1D703})+2{\mathcal{A}}\unicode[STIX]{x1D716}y\cos \unicode[STIX]{x1D703}.\end{eqnarray}$$

Expanding $g(\unicode[STIX]{x1D703})\sin ^{2}\unicode[STIX]{x1D703}$ in terms of the Gegenbauer functions $G_{n}(\cos \unicode[STIX]{x1D703})$ of degree $-1/2$ and matching the terms in (3.21) to those in (3.22), we find

(3.23) $$\begin{eqnarray}\displaystyle {\mathcal{A}}=-1/2,\quad {\mathcal{A}}_{1}=(3/2k)({\mathcal{A}}-1)\int _{-1}^{1}g(\unicode[STIX]{x1D702})G_{2}(\unicode[STIX]{x1D702})\,\text{d}\unicode[STIX]{x1D702}. & & \displaystyle\end{eqnarray}$$

3.4 Hydrodynamic force

The amplitude of the hydrodynamic force on the particle can be evaluated according to

(3.24) $$\begin{eqnarray}\frac{\hat{F}}{\unicode[STIX]{x1D707}{\mathcal{U}}_{p}a}=2\unicode[STIX]{x03C0}\int _{0}^{\unicode[STIX]{x03C0}}(\unicode[STIX]{x1D70E}_{rr}\cos \unicode[STIX]{x1D703}-\unicode[STIX]{x1D70E}_{r\unicode[STIX]{x1D703}}\sin \unicode[STIX]{x1D703})_{y=0}\sin \unicode[STIX]{x1D703}\,\text{d}\unicode[STIX]{x1D703}.\end{eqnarray}$$

The normal stress $\unicode[STIX]{x1D70E}_{rr}(y=0)=-p(y=0)+2(\unicode[STIX]{x2202}v/\unicode[STIX]{x2202}r)_{y=0}$ is dominated by the pressure term until $O(\unicode[STIX]{x1D716}^{-1})$ because of (3.11) and $(\unicode[STIX]{x2202}v/\unicode[STIX]{x2202}r)_{y=0}\sim O(\unicode[STIX]{x1D716}^{0})$ . With (3.15) and (3.19), it can be evaluated as $\unicode[STIX]{x1D70E}_{rr}(y=0)=\text{i}{\mathcal{A}}\cos \unicode[STIX]{x1D703}\unicode[STIX]{x1D716}^{-2}+\text{i}{\mathcal{A}}_{1}\cos \unicode[STIX]{x1D703}\unicode[STIX]{x1D716}^{-1}+O(\unicode[STIX]{x1D716}^{0})$ . With (3.17), the tangential stress can be evaluated as $\unicode[STIX]{x1D70E}_{r\unicode[STIX]{x1D703}}(y=0)=\unicode[STIX]{x1D716}^{-1}(\unicode[STIX]{x2202}u_{0}/\unicode[STIX]{x2202}y)_{y=0}+O(\unicode[STIX]{x1D716}^{0})=-\unicode[STIX]{x1D716}^{-1}k\sin \unicode[STIX]{x1D703}g(\unicode[STIX]{x1D703})({\mathcal{A}}-1)+O(\unicode[STIX]{x1D716}^{0})$ . Combining the above stresses into (3.24) together with (3.23), we obtain the force amplitude as

(3.25) $$\begin{eqnarray}\frac{\hat{F}}{-6\unicode[STIX]{x03C0}\unicode[STIX]{x1D707}{\mathcal{U}}_{p}a}=\frac{1}{9\unicode[STIX]{x1D716}^{2}}\text{e}^{-\text{i}\unicode[STIX]{x1D70B}/2}+\frac{1}{\unicode[STIX]{x1D716}}\text{e}^{-\text{i}\unicode[STIX]{x1D70B}/4}\left(g_{0}-\frac{1}{5}g_{2}\right)+O(\unicode[STIX]{x1D716}^{0}).\end{eqnarray}$$

Here the $\unicode[STIX]{x1D716}^{-2}$ term is the added mass, and the $\unicode[STIX]{x1D716}^{-1}$ term is the viscous force with $g_{0}=(1/2)\int _{-1}^{1}g(\unicode[STIX]{x1D702}){\mathcal{P}}_{0}(\unicode[STIX]{x1D702})\,\text{d}\unicode[STIX]{x1D702}$ and $g_{2}=(5/2)\int _{-1}^{1}g(\unicode[STIX]{x1D702}){\mathcal{P}}_{2}(\unicode[STIX]{x1D702})\,\text{d}\unicode[STIX]{x1D702}$ representing the monopole and the quadrupole contributions, respectively, where ${\mathcal{P}}_{n}$ are the Legendre functions.

For the slip–slip case with $\unicode[STIX]{x1D6FD}(\unicode[STIX]{x1D702})=\hat{\unicode[STIX]{x1D706}}_{1}+{\mathcal{H}}(\unicode[STIX]{x1D702}-\unicode[STIX]{x1D702}_{0})(\hat{\unicode[STIX]{x1D706}}_{2}-\hat{\unicode[STIX]{x1D706}}_{1})$ where ${\mathcal{H}}$ is the Heaviside step function, the viscous part of (3.25) becomes

(3.26) $$\begin{eqnarray}\displaystyle \frac{\hat{F}^{vis}}{-6\unicode[STIX]{x03C0}\unicode[STIX]{x1D707}{\mathcal{U}}_{p}a} & = & \displaystyle \frac{\text{e}^{-\text{i}\unicode[STIX]{x03C0}/4}}{\unicode[STIX]{x1D716}\unicode[STIX]{x1D6E5}}\left[1+\frac{k}{2\unicode[STIX]{x1D716}}\left\{(\hat{\unicode[STIX]{x1D706}}_{1}+\hat{\unicode[STIX]{x1D706}}_{2})+\unicode[STIX]{x1D702}_{0}\left(1-\frac{1}{2}(\unicode[STIX]{x1D702}_{0}-1)(\unicode[STIX]{x1D702}_{0}+1)\right)(\hat{\unicode[STIX]{x1D706}}_{2}-\hat{\unicode[STIX]{x1D706}}_{1})\right\}\right]\nonumber\\ \displaystyle & & \displaystyle +\,O(\unicode[STIX]{x1D716}^{0}),\end{eqnarray}$$

where $\unicode[STIX]{x1D6E5}=(1+k\hat{\unicode[STIX]{x1D706}}_{1}/\unicode[STIX]{x1D716})(1+k\hat{\unicode[STIX]{x1D706}}_{2}/\unicode[STIX]{x1D716})$ . As $\unicode[STIX]{x1D716}\rightarrow 0$ , equation (3.26) gives a constant force plateau having zero phase shift. In the case of $\unicode[STIX]{x1D702}_{0}=0$ (hemisphere), the plateau value is $1/\hat{\unicode[STIX]{x1D706}}_{eff}$ where the effective slip length $\hat{\unicode[STIX]{x1D706}}_{eff}=2/(\hat{\unicode[STIX]{x1D706}}_{1}^{-1}+\hat{\unicode[STIX]{x1D706}}_{2}^{-1})$ is exactly the harmonic mean of $\hat{\unicode[STIX]{x1D706}}_{1}$ and $\hat{\unicode[STIX]{x1D706}}_{2}$ .

For the stick–slip case with $\hat{\unicode[STIX]{x1D706}}_{1}=0$ , equation (3.26) is reduced to

(3.27) $$\begin{eqnarray}\displaystyle \frac{\hat{F}^{vis}}{-6\unicode[STIX]{x03C0}\unicode[STIX]{x1D707}{\mathcal{U}}_{p}a}=\frac{1}{\unicode[STIX]{x1D716}}\text{e}^{-\text{i}\unicode[STIX]{x03C0}/4}\frac{1}{(1+k\hat{\unicode[STIX]{x1D706}}_{2}/\unicode[STIX]{x1D716})}\left[1+\frac{k\hat{\unicode[STIX]{x1D706}}_{2}}{\unicode[STIX]{x1D716}}(\unicode[STIX]{x1D702}_{0}+1)^{2}{\mathcal{C}}\right]+O(\unicode[STIX]{x1D716}^{0}), & & \displaystyle\end{eqnarray}$$

where ${\mathcal{C}}=(2-\unicode[STIX]{x1D702}_{0})/4$ . The small $\hat{\unicode[STIX]{x1D6FF}}$ force responses seen in figures 3 and 4 can be excellently captured by the asymptotic result (3.27). On the right-hand side of (3.27), the first term is the reduced force due to slip, which yields a constant force plateau $1/\hat{\unicode[STIX]{x1D706}}_{2}$ at $\unicode[STIX]{x1D716}$ below the SST point at $|k|\hat{\unicode[STIX]{x1D706}}_{2}/\unicode[STIX]{x1D716}\approx 1$ ,

(3.28) $$\begin{eqnarray}\unicode[STIX]{x1D716}_{{\rm \small{sst}}}\approx \hat{\unicode[STIX]{x1D706}}_{2}.\end{eqnarray}$$

The second term arises from the stick part. This term outweighs the first as $\unicode[STIX]{x1D716}\rightarrow 0$ , giving the re-entry Basset force,

(3.29) $$\begin{eqnarray}\frac{\hat{F}_{{\rm \small{rb}}}}{-6\unicode[STIX]{x03C0}\unicode[STIX]{x1D707}{\mathcal{U}}_{p}a}=\unicode[STIX]{x1D716}^{-1}\text{e}^{-\text{i}\unicode[STIX]{x03C0}/4}(\unicode[STIX]{x1D702}_{0}+1)^{2}{\mathcal{C}},\end{eqnarray}$$

which depends solely on the coverage of the stick face but not on the slip length $\hat{\unicode[STIX]{x1D706}}_{2}$ . This re-entry Basset force will start to decrease towards the slip plateau when $\unicode[STIX]{x1D716}$ is increased to the RHFT point at $|k|\hat{\unicode[STIX]{x1D706}}_{2}(\unicode[STIX]{x1D702}_{0}+1)^{2}C/\unicode[STIX]{x1D716}\approx 1$ in (3.27),

(3.30) $$\begin{eqnarray}\unicode[STIX]{x1D716}_{{\rm \small{rhft}}}\approx \hat{\unicode[STIX]{x1D706}}_{2}(\unicode[STIX]{x1D702}_{0}+1)^{2}{\mathcal{C}}\approx (\unicode[STIX]{x1D702}_{0}+1)^{2}{\mathcal{C}}\unicode[STIX]{x1D716}_{{\rm \small{sst}}}.\end{eqnarray}$$

As indicated by (3.30), if the stick face is small (i.e. $\unicode[STIX]{x1D702}_{0}$ is close to $-1$ ), $\unicode[STIX]{x1D716}_{{\rm \small{rhft}}}$ will become well separated from $\unicode[STIX]{x1D716}_{{\rm \small{sst}}}$ given by (3.28), as can be clearly seen from the $\unicode[STIX]{x1D703}_{0}=150^{\circ }$ curve in figure 4(a). But if changing this small stick face to be slippery, no matter how small $\hat{\unicode[STIX]{x1D706}}_{1}$ is, RHFT will disappear and the constant force plateau will return to dominate the force response again, as indicated by (3.26).

Re-entrant history force transition can be best revealed from (3.27) in the memory integral form if the particle undergoes a transient movement. In this case, we can express the particle velocity as a Fourier integral, convert (3.27) in terms of the Laplace variable $s$ with $-\text{i}\unicode[STIX]{x1D714}\rightarrow s$ , and then carry out an inverse Laplace transform. If the particle starts from rest, i.e. ${\mathcal{U}}_{p}=0$ for $t\leqslant 0$ , and moves at ${\mathcal{U}}_{p}={\mathcal{U}}_{p}(t)$ for $t>0$ , equation (3.27) can be written as the following memory integral:

(3.31) $$\begin{eqnarray}\frac{F^{vis}(t)}{-6\unicode[STIX]{x03C0}\unicode[STIX]{x1D707}a}=\int _{0}^{t}\frac{\text{d}{\mathcal{U}}_{p}(\unicode[STIX]{x1D70F})}{\text{d}\unicode[STIX]{x1D70F}}M(t-\unicode[STIX]{x1D70F})\,\text{d}\unicode[STIX]{x1D70F},\end{eqnarray}$$

with the memory kernel

(3.32) $$\begin{eqnarray}M(t)=\frac{1}{\hat{\unicode[STIX]{x1D706}}_{2}}\text{exp}\left(\frac{t}{t_{{\rm \small{sst}}}}\right)\text{erfc}\left(\left(\frac{t}{t_{{\rm \small{sst}}}}\right)^{1/2}\right)(1-(\unicode[STIX]{x1D702}_{0}+1)^{2}{\mathcal{C}})+\frac{(\unicode[STIX]{x1D702}_{0}+1)^{2}{\mathcal{C}}}{\sqrt{\unicode[STIX]{x03C0}}}\left(\frac{t}{t_{\unicode[STIX]{x1D708}}}\right)^{-1/2}+\cdots \,.\end{eqnarray}$$

Here $t_{\unicode[STIX]{x1D708}}=a^{2}/\unicode[STIX]{x1D708}$ is the viscous diffusion time. The slip–stick transition time, $t_{{\rm \small{sst}}}$ , is

(3.33) $$\begin{eqnarray}t_{{\rm \small{sst}}}=\hat{\unicode[STIX]{x1D706}}_{2}^{2}t_{\unicode[STIX]{x1D708}}=\unicode[STIX]{x1D706}_{2}^{2}/\unicode[STIX]{x1D708},\end{eqnarray}$$

which is shorter than $t_{\unicode[STIX]{x1D708}}$ for $\hat{\unicode[STIX]{x1D706}}_{2}<1$ . As clearly revealed by (3.32), $M(t)$ consists of two contributions: the slip kernel and the Basset kernel, characterized by $t_{{\rm \small{sst}}}$ and $t_{\unicode[STIX]{x1D708}}$ , respectively. For $\unicode[STIX]{x1D702}_{0}=-1$ , it recovers the uniform slip result (Premlata & Wei Reference Premlata and Wei2019). If ${\mathcal{U}}_{p}(t)={\mathcal{U}}_{0}$ (const.), equation (3.31) with $\hat{\unicode[STIX]{x1D706}}_{2}<1$ has the following short-term response for $t/t_{\unicode[STIX]{x1D708}}\ll 1$ ,

(3.34) $$\begin{eqnarray}\frac{F^{vis}(t)}{-6\unicode[STIX]{x03C0}\unicode[STIX]{x1D707}{\mathcal{U}}_{0}a}=\frac{{\mathcal{C}}(\unicode[STIX]{x1D702}_{0}+1)^{2}}{\sqrt{\unicode[STIX]{x03C0}}}\left(\frac{t}{t_{\unicode[STIX]{x1D708}}}\right)^{-1/2}+\frac{1-{\mathcal{C}}(\unicode[STIX]{x1D702}_{0}+1)^{2}}{\hat{\unicode[STIX]{x1D706}}_{2}}\left(1-\frac{2}{\sqrt{\unicode[STIX]{x03C0}}}\left(\frac{t}{t_{{\rm \small{sst}}}}\right)^{1/2}\right)+O(t/t_{\unicode[STIX]{x1D708}}).\end{eqnarray}$$

The leading contribution is the re-entry Basset $t^{-1/2}$ decay. The next is the $O(t^{0})$ slip plateau with a $t^{1/2}$ tail due to SST. Re-entrant history force transition occurs when the former is decreased to the latter when the boundary layer of thickness $\unicode[STIX]{x1D6FF}\sim (\unicode[STIX]{x1D708}t)^{1/2}$ grows to the size at time

(3.35) $$\begin{eqnarray}t_{{\rm \small{rhft}}}\approx \left(\frac{{\mathcal{C}}(\unicode[STIX]{x1D702}_{0}+1)^{2}}{\sqrt{\unicode[STIX]{x03C0}}(1-{\mathcal{C}}(\unicode[STIX]{x1D702}_{0}+1)^{2})}\right)^{2}t_{{\rm \small{ sst}}}.\end{eqnarray}$$

So $t_{{\rm \small{rhft}}}$ becomes quite sensitive to the coverage of the stick face, $(\unicode[STIX]{x1D702}_{0}+1)$ . If the stick portion is small, RHFT will occur at time ${\sim}(\unicode[STIX]{x1D702}_{0}+1)^{4}t_{{\rm \small{sst}}}$ much earlier than SST upon the start of the particle movement. If such a particle undergoes an oscillatory motion, the RHFT frequency corresponding to (3.35) is $\unicode[STIX]{x1D714}_{{\rm \small{rhft}}}\sim (\unicode[STIX]{x1D702}_{0}+1)^{-4}\unicode[STIX]{x1D714}_{{\rm \small{sst}}}$ much higher than the SST frequency $\unicode[STIX]{x1D714}_{{\rm \small{sst}}}\sim \unicode[STIX]{x1D708}/\unicode[STIX]{x1D706}_{2}^{2}$ corresponding to (3.33).

4 Concluding remarks

We have demonstrated that an SSJP can display unusual history force responses that are of neither the no-slip nor the purely slip type but mixed with both. We find that the stick portion of an SSJP, no matter how small it is, will always render a Basset force to exhibit $1/\hat{\unicode[STIX]{x1D6FF}}$ or $t^{-1/2}$ decay in the high frequency or short time regime but of amplitude smaller than that of a no-slip particle. This is the re-entry Basset force because it not only replaces the constant force plateau seen for a slippery particle (Premlata & Wei Reference Premlata and Wei2019) but also re-emerges when a slippery particle is patched with a no-slip face. In the case where the stick portion is small, in particular, the re-entry Basset decay will be further accompanied by a slip plateau at a lower frequency or longer time, displaying an RHFT prior to the SST. These unusual force responses only occur to stick–slip Janus particles and are very distinct from those for drops and bubbles (Galindo & Gerbeth Reference Galindo and Gerbeth1993; Magnaudet & Legendre Reference Magnaudet and Legendre1998). As these force responses are very sensitive to the frequency of the prescribed oscillatory motion, one may be able to utilize them to characterize heterogeneous particles or to perform hydrodynamic sorting of these particles. Alternatively, because how much the stick face covers an SSJP and the amount of slip on the slip face can strongly influence the behaviour of the re-entry Basset force in competition with the slip force plateau, this may offer an advantage for controlling the motion of an SSJP via selecting a proper stick–slip partition. This may be in particular useful to the design of an SSJP if one would like to employ it as a self-propelled swimmer.

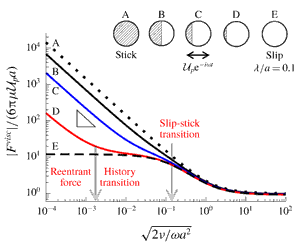
Experimentally, the mixed history force responses may be realized by having an SSJP propelled by an acoustic force at frequency $\unicode[STIX]{x1D714}$ typically ranging from 100 kHz to 10 MHz (Laurell, Petersson & Nilsson Reference Laurell, Petersson and Nilsson2007). Consider an SSJP of radius $a\sim 10~\unicode[STIX]{x03BC}\text{m}$ and let it undergo an oscillatory translation at the peak velocity ${\mathcal{U}}_{p}\sim 10~\unicode[STIX]{x03BC}\text{m}~\text{s}^{-1}$ in water (of $\unicode[STIX]{x1D70C}=1~\text{g}~\text{cm}^{-3}$ and $\unicode[STIX]{x1D707}=10^{-2}~\text{g}~\text{cm}^{-1}~\text{s}^{-1}$ ). At frequencies lower than the viscous damping frequency $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D708}}=\unicode[STIX]{x1D708}/2\unicode[STIX]{x03C0}a^{2}\sim 10^{3}~\text{Hz}$ (with $\unicode[STIX]{x1D708}=\unicode[STIX]{x1D707}/\unicode[STIX]{x1D70C}$ being the kinematic viscosity), the particle can experience a steady Stokes drag $F_{Stokes}=6\unicode[STIX]{x03C0}\unicode[STIX]{x1D707}{\mathcal{U}}_{p}a\approx 2~\text{pN}$ . Suppose the slip length is $\unicode[STIX]{x1D706}\sim 1~\unicode[STIX]{x03BC}\text{m}$ , taken as 10 % of the particle radius. The force plateau $F_{plateau}=F_{Stokes}(a/\unicode[STIX]{x1D706})\approx 20~\text{pN}$ may appear at $\unicode[STIX]{x1D714}$ higher than the SST frequency $\unicode[STIX]{x1D714}_{{\rm \small{ssf}}}\sim \unicode[STIX]{x1D708}/2\unicode[STIX]{x03C0}\unicode[STIX]{x1D706}^{2}\sim 10^{5}~\text{Hz}$ according to (3.28). The re-entry Basset force $F_{RB}\sim F_{Stokes}(\unicode[STIX]{x1D714}/\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D708}})^{1/2}(\unicode[STIX]{x1D702}_{0}+1)^{2}$ according to (3.29). For an SSJP with a slip hemisphere (of $2\unicode[STIX]{x1D703}_{0}=180^{\circ }$ or $\unicode[STIX]{x1D702}_{0}=0$ ), there is no plateau in the force response (see figure 3 a). The $F_{{\rm \small{rb}}}$ for this case will be at least $10F_{Stokes}\approx 20~\text{pN}$ at $\unicode[STIX]{x1D714}$ higher than $\unicode[STIX]{x1D714}_{{\rm \small{ssf}}}$ . But if $F_{{\rm \small{rb}}}$ starts to show a tail with a slower decay rate as occurring to an SSJP having a small stick cap of angle $2\times (180-\unicode[STIX]{x1D703}_{0})=120^{\circ }$ or $\unicode[STIX]{x1D702}_{0}=-1/2$ (see figure 4 a), $F_{{\rm \small{rb}}}$ can only be seen if $\unicode[STIX]{x1D714}$ is raised to the RHFT frequency $\unicode[STIX]{x1D714}_{{\rm \small{rhft}}}\sim (\unicode[STIX]{x1D702}_{0}+1)^{-4}\unicode[STIX]{x1D714}_{{\rm \small{ssf}}}\sim 10^{6}~\text{Hz}$ or higher. The above estimates can also be used to design an acoustically powered microswimmer made by an SSJP for controlling its motion according to $a$ , $\unicode[STIX]{x1D706}$ , $\unicode[STIX]{x1D714}$ and $\unicode[STIX]{x1D702}_{0}$ .