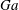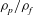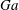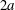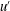1 Introduction
The gravity-driven motion of solid particles in a viscous fluid is a relevant process in a wide number of environmental and engineering applications. Among these we recall volcanic eruptions, fluidized beds, soot particle dispersion, rain droplets, snow and settling of micro-organisms such as plankton.
The settling process may occur in quiescent fluids or in already-turbulent flows. In the latter case the settling dynamics, which depends on the solid-to-fluid density ratio
$\unicode[STIX]{x1D70C}_{p}/\unicode[STIX]{x1D70C}_{f}$
, the solid volume fraction
$\unicode[STIX]{x1D719}$
and on the Galileo number
$Ga$
(i.e. the ratio between buoyancy and viscous forces), is further complicated by the interaction among the particles and the turbulent eddies.
The vast majority of previous investigations focused on the settling of particles smaller or at least comparable in size to the Kolmogorov lengthscale,
$\unicode[STIX]{x1D702}$
. In these conditions, turbulence can either enhance, reduce or inhibit the settling. As shown by Squires & Eaton (Reference Squires and Eaton1991), small inertial particles tend to be expelled from the vortex core and accumulate in regions of low vorticity and high strain rate. Owing to this and to gravitational settling, particles are often swept into regions of downdrafts (the so-called preferential sweeping or fast-tracking). Thus, the particle mean settling velocity increases, as first observed in simulations in random flows (Maxey Reference Maxey1987) and in turbulence (Wang & Maxey Reference Wang and Maxey1993), and later confirmed by experiments (Nielsen Reference Nielsen1993; Aliseda et al.
Reference Aliseda, Cartellier, Hainaux and Lasheras2002; Yang & Shy Reference Yang and Shy2003, Reference Yang and Shy2005).
A reduction in mean settling velocity, on the other hand, has also been observed both in experiments (Murray Reference Murray1970; Nielsen Reference Nielsen1993; Yang & Shy Reference Yang and Shy2003; Kawanisi & Shiozaki Reference Kawanisi and Shiozaki2008) and numerical simulations (Wang & Maxey Reference Wang and Maxey1993; Good et al.
Reference Good, Ireland, Bewley, Bodenschatz, Collins and Warhaft2014). Note, however, that reduction of the mean settling velocity can only be observed in direct numerical simulations (DNS) of sub-Kolmogorov particles if nonlinear drag corrections are employed (i.e. for a finite particle Reynolds number,
$Re_{p}$
, as shown by Good et al.
Reference Good, Ireland, Bewley, Bodenschatz, Collins and Warhaft2014). Reduced settling speeds are observed when particles oversample upward flow and not downward motions as in the case of preferential sweeping. Nielsen (Reference Nielsen1993) suggested that fast-falling particles need longer times to cross regions of upward flow (a phenomenology usually referred to as loitering), the more so if the particle settling speed is of the order of the turbulent velocity fluctuations,
$u^{\prime }$
. Good et al. (Reference Good, Ireland, Bewley, Bodenschatz, Collins and Warhaft2014) performed a series of experiments and numerical simulations and found that reduction of the mean settling velocity occurs when the ratio
$\unicode[STIX]{x1D70F}_{p}g/u^{\prime }$
(where
$\unicode[STIX]{x1D70F}_{p}=2(\unicode[STIX]{x1D70C}_{p}/\unicode[STIX]{x1D70C}_{f}-1)a^{2}/(9\unicode[STIX]{x1D708})$
is the particle relaxation time with
$a$
the particle radius and
$\unicode[STIX]{x1D708}$
the fluid viscosity) is greater than one (i.e. when the particle terminal velocity is larger than the turbulent velocity fluctuations). Heuristically it can be said that when
$\unicode[STIX]{x1D70F}_{p}g$
(the Stokes settling velocity) is sufficiently high, the particles fall along almost straight vertical paths, their horizontal velocity fluctuations are weak and hence they are unable to side step the turbulent eddies: fast-tracking is suppressed and the mean settling velocity reduces due to a drag increase related to finite Reynolds number.
Thus far, just few studies consider the settling of finite-size particles in turbulent environments. The experiments by Byron (Reference Byron2015) investigate the settling of Taylor-scale particles using refractive-index-matched hydrogel particles and particle image velocimetry (PIV) and show that particles with quiescent settling velocities of the same order of the turbulence root-mean-square (r.m.s.) velocity fall on average 40 %–60 % more slowly in turbulence (depending on their density and shape). Previous numerical studies had focused mostly on settling in quiescent environments (see, for example, Yin & Koch Reference Yin and Koch2007; Uhlmann & Doychev Reference Uhlmann and Doychev2014; Zaidi, Tsuji & Tanaka Reference Zaidi, Tsuji and Tanaka2014), or on the dynamics of neutrally buoyant particles in homogeneous isotropic turbulence (HIT) (Homann & Bec Reference Homann and Bec2010). Recently, Fornari, Picano & Brandt (Reference Fornari, Picano and Brandt2016b
) compared the settling of spheres in quiescent and sustained HIT. In this study, the sphere radius was chosen to be about six Kolmogorov lengthscales, the density ratio
$\unicode[STIX]{x1D70C}_{p}/\unicode[STIX]{x1D70C}_{f}=1.02$
and the ratio between the quiescent settling velocity and the turbulence r.m.s. velocity
$u^{\prime }$
was chosen to be about
$3.3$
. In dilute conditions, the particle mean settling velocity reduces by about
$4\,\%$
in still fluid and by about
$12\,\%$
in turbulence when compared with the terminal velocity
$V_{t}$
of an isolated particle. This reduction is attributed to unsteady phenomena such as vortex shedding (absent in the quiescent cases), and to the modification of the particle wakes by the turbulence (see also Bagchi & Balachandar Reference Bagchi and Balachandar2003; Homann, Bec & Grauer Reference Homann, Bec and Grauer2013).
In the present study, we investigate the effect of the Galileo number,
$Ga$
, on the settling in a turbulent environment. The background sustained homogeneous isotropic turbulent flow has a nominal Reynolds number based on the Taylor microscale
$Re_{\unicode[STIX]{x1D706}}$
of about
$90$
. By varying the Galileo number, via the density ratio
$\unicode[STIX]{x1D70C}_{p}/\unicode[STIX]{x1D70C}_{f}$
, we control the ratio between the terminal velocity
$V_{t}$
and the turbulent velocity fluctuations
$u^{\prime }$
. We show that the reduction in mean settling velocity increases from about
$10\,\%$
to
$55\,\%$
as the Galileo number
$Ga$
(i.e.
$V_{t}/u^{\prime }$
) is reduced. Analysing the mean forces acting on the particles, we attribute the significant reduction in mean settling velocity observed at the lower
$Ga$
to the increase of the vertical component of the drag originating from the horizontal components of the particle relative velocity.
2 Set-up and methodology
Sedimentation of a dilute suspension is considered in a computational domain with periodic boundary conditions in the
$x$
,
$y$
and
$z$
directions, with gravity acting in the positive
$z$
direction. The computational box has size
$32a\times 32a\times 320a$
and the volume fraction
$\unicode[STIX]{x1D719}=0.5\,\%$
, corresponding to
$391$
particles; these are initially randomly distributed in the computational volume with zero velocity and rotation. We consider non-Brownian rigid spherical particles, slightly heavier than the suspending fluid with density ratios
$\unicode[STIX]{x1D70C}_{p}/\unicode[STIX]{x1D70C}_{f}=1.00035$
,
$1.0034$
,
$1.020$
and
$1.038$
. The parameter governing the settling is the Galileo number
$Ga=\sqrt{(\unicode[STIX]{x1D70C}_{p}/\unicode[STIX]{x1D70C}_{f}-1)g(2a)^{3}}/\unicode[STIX]{x1D708}$
, the non-dimensional number that quantifies the importance of the gravitational forces acting on the particle with respect to viscous forces. For the different density ratios
$\unicode[STIX]{x1D70C}_{p}/\unicode[STIX]{x1D70C}_{f}$
considered here we have
$Ga=19$
,
$60$
,
$145$
and
$200$
.
To generate and sustain an isotropic and homogeneous turbulent flow field, a random forcing is applied to the first wavenumber in the directions perpendicular to gravity, and to the tenth wavenumber in the settling direction. Since in the settling direction the box length is
$10$
times that in the other directions, forcing the tenth wavenumber is equivalent to forcing the first wavenumber in a cube of size
$32a\times 32a\times 32a$
. The forcing is
$\unicode[STIX]{x1D6FF}$
-correlated in time and of fixed amplitude (Vincent & Meneguzzi Reference Vincent and Meneguzzi1991). This forcing induces a turbulent flow with Reynolds number based on the Taylor microscale,
$Re_{\unicode[STIX]{x1D706}}=\unicode[STIX]{x1D706}u^{\prime }/\unicode[STIX]{x1D708}=90$
(where
$u^{\prime }$
is the fluctuating velocity r.m.s.,
$\unicode[STIX]{x1D706}=\sqrt{15\unicode[STIX]{x1D708}u^{\prime 2}/\unicode[STIX]{x1D716}}$
the transverse Taylor length scale and
$\unicode[STIX]{x1D716}$
the dissipation). The ratio between the Kolmogorov lengthscale
$\unicode[STIX]{x1D702}=(\unicode[STIX]{x1D708}^{3}/\unicode[STIX]{x1D716})^{1/4}$
and the grid spacing (
$\unicode[STIX]{x1D702}/\unicode[STIX]{x0394}x$
) is approximately
$1.3$
while the particle diameter is approximately
$12\unicode[STIX]{x1D702}$
. The parameters of the turbulent flow field are summarized in table 1.
Table 1. Turbulent flow parameters pertaining to the present direct numerical simulation, where
$L_{\unicode[STIX]{x1D716}}$
is the integral lengthscale and
$u_{\unicode[STIX]{x1D702}}$
is the Kolmogorov velocity scale. The box size in the directions perpendicular and parallel to gravity is denoted by
$L_{x}$
and
$L_{z}$
.
Each Galileo number
$Ga$
also defines a different value of the ratio between the terminal velocity
$V_{t}$
(i.e. the settling velocity of a single particle in quiescent fluid) and the turbulent velocity fluctuations. This parameter directly influences the average settling as noted by Nielsen (Reference Nielsen1993) and Byron (Reference Byron2015) among others. For the four cases considered here this ratio attains the values
$V_{t}/u^{\prime }=0.19$
,
$0.99$
,
$3.38$
and
$4.81$
.
The simulations have been performed using the immersed boundary method originally developed by Breugem (Reference Breugem2012); this fully models the coupling between the solid and fluid phases. The flow is evolved according to the incompressible Navier–Stokes equations, whereas the particle motion is governed by the Newton–Euler Lagrangian equations for the particle centroid linear and angular velocities. Using the immersed boundary method, the boundary condition at the moving fluid/solid interfaces is modelled by an additional force on the right-hand side of the Navier–Stokes equations, making it possible to discretize the computational domain with a fixed staggered mesh on which the fluid phase is evolved using a second-order finite-difference scheme. Time integration is performed by a third-order Runge–Kutta scheme combined with pressure correction at each sub-step. When the distance between two particles becomes smaller than twice the mesh size, lubrication models based on Brenner’s asymptotic solution (Brenner Reference Brenner1961) are used to correctly reproduce the interaction between the particles. A soft-sphere collision model is used to account for collisions between particles. An almost elastic rebound is ensured with a restitution coefficient set at
$0.97$
. A cubic mesh with eight points per particle radius is used for the results presented, which corresponds to
$256\times 256\times 2560$
grid points. This resolution is a good compromise in terms of accuracy and computational cost as shown in previous publications (Breugem Reference Breugem2012; Lambert et al.
Reference Lambert, Picano, Breugem and Brandt2013; Picano, Breugem & Brandt Reference Picano, Breugem and Brandt2015; Lashgari et al.
Reference Lashgari, Picano, Breugem and Brandt2016; Fornari et al.
Reference Fornari, Formenti, Picano and Brandt2016a
,Reference Fornari, Picano and Brandt
b
), wherein more details and validations of the numerical code are provided. Note finally that zero total volume flux is imposed in the simulations.
When studying settling in a turbulent flow, the fluid phase is evolved for approximately six eddy turnover times before adding the solid phase. Statistics are collected after an initial transient phase so that the difference between the statistics presented here and those computed from half the samples is below
$1\,\%$
for the first and second moments. The transient is approximately nine integral time scales (
$T_{\unicode[STIX]{x1D716}}=L_{\unicode[STIX]{x1D716}}/u^{\prime }$
) in HIT and at least
$100\unicode[STIX]{x1D70F}_{p}$
in the quiescent cases. After these transient periods, velocities and accelerations oscillate on average with a constant amplitude around the mean. In the following we will use
$\boldsymbol{U}$
and
$\boldsymbol{V}$
for the fluid and particle velocities.
3 Results
3.1 Particle statistics
The most striking result of our study is that in a turbulent flow, as the Galileo number is reduced, the mean settling speed
$\langle V_{z}\rangle _{p,t}$
becomes significantly smaller than the terminal velocity of a single particle in still fluid,
$V_{t}$
. The notation
$\langle \cdot \rangle _{p,t}$
denotes averaging over the total number of particles and time.
The mean settling speed
$\langle V_{z}\rangle _{p,t}$
normalized by
$V_{t}$
, is shown as a function of
$Ga$
in figure 1(a) for both quiescent and turbulent cases. In quiescent fluid,
$\langle V_{z}\rangle _{p,t}$
is smaller than the terminal velocity
$V_{t}$
of an isolated particle due to the hindering effect (Yin & Koch Reference Yin and Koch2007; Guazzelli & Morris Reference Guazzelli and Morris2011) for the three smallest Galileo numbers. The ratio
$\langle V_{z}\rangle _{p,t}/V_{t}\approx 0.92$
for
$Ga=19$
and
$60$
, increases to
$0.96$
for
$Ga=145$
and becomes larger than unity,
$1.05$
, for
$Ga=200$
. This is associated with the formation of particle clusters that settle faster than isolated particles, as documented in Uhlmann & Doychev (Reference Uhlmann and Doychev2014). Indeed, the probability density function (p.d.f.), of
$\langle V_{z}\rangle _{p,t}/V_{t}$
for
$Ga=200$
is highly skewed toward settling speeds greater than the modal value (not shown).
The mean settling speed
$\langle V_{z}\rangle _{p,t}$
is always lower in sustained HIT than in quiescent fluid and, for the Galileo numbers investigated here, smaller than the terminal velocity
$V_{t}$
. The reduction of
$\langle V_{z}\rangle _{p,t}$
with respect to the quiescent cases is
$55\,\%$
,
$23\,\%$
,
$9\,\%$
and
$10\,\%$
for
$Ga=19,$
$60$
,
$145$
and
$200$
. As
$V_{t}/u^{\prime }$
is reduced, the reduction in average settling speed drastically increases. Interestingly, the settling speed of heavy sub-Kolmogorov particles reduces instead when increasing the ratio
$V_{t}/u^{\prime }$
. The two different mechanisms will be discussed below.
Figure 1. (a) Mean settling velocity
$\langle V_{z}\rangle _{p,t}$
as a function of
$Ga$
for both quiescent and turbulent cases. The green triangle shows the result obtained via two additional simulations with
$Ga=19$
and
$\unicode[STIX]{x1D70C}_{p}/\unicode[STIX]{x1D70C}_{f}=1.02$
(same
$\unicode[STIX]{x1D70C}_{p}/\unicode[STIX]{x1D70C}_{f}$
as for
$Ga=145$
but with smaller
$g$
). (b) Evolution in time of
$\langle V_{z}\rangle _{p}/u^{\prime }$
for
$Ga=19$
,
$60$
and
$145$
. The shaded zones represent at each time the range of variation of
$\langle V_{z}\rangle _{p}/u^{\prime }$
.
It is worth noting that we could have changed the Galileo number
$Ga$
via the gravity
$g$
while keeping
$\unicode[STIX]{x1D70C}_{p}/\unicode[STIX]{x1D70C}_{f}$
constant. To check the effect of varying
$Ga$
via
$g$
, we have performed additional simulations at
$Ga=19$
and
$\unicode[STIX]{x1D70C}_{p}/\unicode[STIX]{x1D70C}_{f}=1.02$
(the density ratio used for
$Ga=145$
). We consider a single sphere settling in quiescent fluid as well as a suspension settling in a turbulent flow (
$\unicode[STIX]{x1D719}=0.5\,\%$
) and find that the mean settling speed
$\langle V_{z}\rangle _{p,t}$
is about
$43\,\%V_{t}$
while
$\langle V_{z}\rangle _{p,t}\sim 42\,\%V_{t}$
when the same
$Ga$
is obtained with
$\unicode[STIX]{x1D70C}_{p}/\unicode[STIX]{x1D70C}_{f}=1.00035$
. Hence, the results discussed here can be extended to suspensions of slightly buoyant settling spheres with different
$Ga$
but constant
$\unicode[STIX]{x1D70C}_{p}/\unicode[STIX]{x1D70C}_{f}$
. The normalized mean settling speed
$\langle V_{z}\rangle _{p,t}/V_{t}$
obtained from this last set of simulations is also reported in figure 1(a) (green triangle).
The time evolution of
$\langle V_{z}\rangle _{p}/u^{\prime }$
, the velocity component in the direction of gravity averaged over the total number of spheres, is reported after the initial transients in figure 1(b) for the three lowest
$Ga$
considered. The shaded zones around each curve represent the instantaneous range of variation of
$\langle V_{z}\rangle _{p}/u^{\prime }$
, which is larger in the cases at lower
$Ga$
. At
$Ga=19$
, when the ratio
$\langle V_{z}\rangle _{p}/u^{\prime }$
is closest to zero (
${\sim}0.07$
), the turbulence intensity is sufficiently high for particles to move in the direction opposite to gravity. Since the turbulent velocity fluctuations are considerably larger than the mean settling speed, particles are also subject to strong lateral motions. To understand the significant reduction in
$\langle V_{z}\rangle _{p,t}$
we consider the balance of the mean forces acting on the particles.
3.2 Force analysis
The equation of motion for a spherical particle settling due to gravity reads
$$\begin{eqnarray}\frac{4}{3}\unicode[STIX]{x03C0}a^{3}\unicode[STIX]{x1D70C}_{p}\frac{\text{d}\boldsymbol{V}}{\text{d}t}=\frac{4}{3}\unicode[STIX]{x03C0}a^{3}(\unicode[STIX]{x1D70C}_{p}-\unicode[STIX]{x1D70C}_{f})\boldsymbol{g}+\mathop{\oint }_{\unicode[STIX]{x2202}{\mathcal{V}}_{p}}^{}\unicode[STIX]{x1D749}\boldsymbol{\cdot }\boldsymbol{n}\,\text{d}S,\end{eqnarray}$$
where the integral is over the surface of the sphere
$\unicode[STIX]{x2202}{\mathcal{V}}_{p}$
,
$\boldsymbol{n}$
is the outward normal and
$\unicode[STIX]{x1D749}$
is the fluid stress. As usually done in aerodynamics, equation (3.1) can be rewritten as
$$\begin{eqnarray}\frac{4}{3}\unicode[STIX]{x03C0}a^{3}\unicode[STIX]{x1D70C}_{p}\frac{\text{d}\boldsymbol{V}}{\text{d}t}=\frac{4}{3}\unicode[STIX]{x03C0}a^{3}(\unicode[STIX]{x1D70C}_{p}-\unicode[STIX]{x1D70C}_{f})\boldsymbol{g}-\boldsymbol{D},\end{eqnarray}$$
where
$\boldsymbol{D}$
is the drag acting on the particle (see also Fornari et al.
Reference Fornari, Picano and Brandt2016b
). This drag term can be further expressed as the sum of two contributions: the first depends only on the particle Reynolds number,
$Re_{p}$
, while the second accounts for various non-stationary effects (such as history effects and hindering). For sub-Kolmogorov particles with Reynolds numbers
$Re_{p}<1$
in unsteady non-uniform flows, the correct form of
$\boldsymbol{D}$
was derived by Maxey & Riley (Reference Maxey and Riley1983) as the sum of Stokes drag, pressure gradient, added mass and Basset history forces.
Ensemble averaging (3.2) over time and the number of particles we can isolate single contributions to the overall drag. The steady-state average equation projected along the direction of gravity reads
$$\begin{eqnarray}0={\textstyle \frac{4}{3}}\unicode[STIX]{x03C0}a^{3}(\unicode[STIX]{x1D70C}_{p}-\unicode[STIX]{x1D70C}_{f})g-F_{D}^{S}-F_{D}^{U},\end{eqnarray}$$
where
$F_{D}^{S}$
and
$F_{D}^{U}$
are the mean contributions to the overall drag due to steady nonlinear effects and to unsteady effects (such as those due to the history force and hindering).
The particle Reynolds number is defined as
$Re_{p}=2a|\boldsymbol{U}_{r}|/\unicode[STIX]{x1D708}$
, where
$\boldsymbol{U}_{r}$
is the relative velocity between particles and fluid. The term
$F_{D}^{S}$
depends only on
$Re_{p}$
and can be written as
$$\begin{eqnarray}F_{D}^{S}={\textstyle \frac{1}{2}}\unicode[STIX]{x1D70C}_{f}\unicode[STIX]{x03C0}a^{2}\langle |\boldsymbol{U}_{r}|U_{r,z}C_{D_{0}}(Re_{p})\rangle ,\end{eqnarray}$$
where
$\unicode[STIX]{x03C0}a^{2}$
is the particle reference area and
$C_{D_{0}}(Re_{p})$
the steady drag coefficient. The first term on the right-hand side of (3.3) is known, while
$F_{D}^{S}$
can be calculated from the relative velocity
$\boldsymbol{U}_{r}$
and the steady drag coefficient
$C_{D_{0}}$
.
To evaluate
$\boldsymbol{U}_{r}$
from the present simulations, we consider spherical shells surrounding each particle, inspired by the works of Bellani & Variano (Reference Bellani and Variano2012), Cisse, Homann & Bec (Reference Cisse, Homann and Bec2013), Kidanemariam et al. (Reference Kidanemariam, Chan-Braun, Doychev and Uhlmann2013). The relative velocity is calculated as the difference between the particle velocity and the fluid velocity averaged over the volume of the shell of inner radius
$\unicode[STIX]{x1D6E5}$
. The thickness of the shell is
$\unicode[STIX]{x1D6FF}=(2a)/8$
while
$\unicode[STIX]{x1D6E5}$
is
$3.5a$
for all
$Ga$
. Here
$\unicode[STIX]{x1D6E5}$
is chosen large enough so that the shell is well outside the boundary layer at particle surface (due to no-slip and no-penetration conditions) and small enough for the fluid motion to be still correlated to that of the particle (see the discussion in Fornari et al.
Reference Fornari, Picano and Brandt2016b
). Once the relative velocity
$\boldsymbol{U}_{r}$
is known, the steady drag coefficient
$C_{D_{0}}$
can be found by means of empirical formulae. Among the different expressions for the nonlinear correction to the Stokes drag that can be found in the literature (Schiller & Naumann Reference Schiller and Naumann1935; Di Felice Reference Di Felice1999; Yin & Koch Reference Yin and Koch2007), we follow Yin & Koch (Reference Yin and Koch2007):
$$\begin{eqnarray}C_{D_{0}}=(24/Re_{p})\left(1+\unicode[STIX]{x1D6FC}Re_{p}^{\unicode[STIX]{x1D6FD}}\right)\end{eqnarray}$$
with
$\unicode[STIX]{x1D6FC}=0.1315$
,
$\unicode[STIX]{x1D6FD}=0.82-0.05\log _{10}Re_{p}$
when
$Re_{p}<20$
, and
$\unicode[STIX]{x1D6FC}=0.1935$
,
$\unicode[STIX]{x1D6FD}=0.6305$
for
$Re_{p}\geqslant 20$
. Using the definitions of
$F_{D}^{S}$
and
$C_{D_{0}}$
in (3.3) we obtain
$$\begin{eqnarray}\frac{4}{3}\unicode[STIX]{x03C0}a^{3}(\unicode[STIX]{x1D70C}_{p}-\unicode[STIX]{x1D70C}_{f})g=\frac{1}{2}\unicode[STIX]{x1D70C}_{f}\unicode[STIX]{x03C0}a^{2}\langle |\boldsymbol{U}_{r}|U_{r,z}\frac{24}{Re_{p}}\left(1+\unicode[STIX]{x1D6FC}Re_{p}^{\unicode[STIX]{x1D6FD}}\right)\rangle +F_{D}^{U}.\end{eqnarray}$$
Next, we define the new variable
$K=\unicode[STIX]{x1D6FC}Re_{p}^{\unicode[STIX]{x1D6FD}}$
and divide (3.6) by the buoyancy term to find
$$\begin{eqnarray}1=\frac{\langle U_{r,z}(1+K)\rangle }{V_{s}}+f_{D}^{U},\end{eqnarray}$$
where
$V_{s}=2(\unicode[STIX]{x1D70C}_{p}-\unicode[STIX]{x1D70C}_{f})ga^{2}/(9\unicode[STIX]{x1D70C}_{f}\unicode[STIX]{x1D708})$
is the Stokes settling velocity and
$f_{D}^{U}=F_{D}^{U}/(4\unicode[STIX]{x03C0}a^{3}(\unicode[STIX]{x1D70C}_{p}-\unicode[STIX]{x1D70C}_{f})g/3)$
.
The steady nonlinear term, the first on the right-hand side above, can be split into two components by writing the relative velocity along gravity and
$K$
as the sum of their mean values and fluctuations:
$U_{r,z}=\overline{U}_{r,z}+U_{r,z}^{\prime }$
and
$K=\overline{K}+K^{\prime }$
(where
$\overline{K}=\langle \unicode[STIX]{x1D6FC}Re_{p}^{\unicode[STIX]{x1D6FD}}\rangle$
and
$K^{\prime }$
are the fluctuations about the mean value
$\overline{K}$
). Equation (3.7) hence becomes
$$\begin{eqnarray}1=\frac{\overline{U}_{r,z}(1+\overline{K})}{V_{s}}+\frac{\langle U_{r,z}^{\prime }K^{\prime }\rangle }{V_{s}}+f_{D}^{U}.\end{eqnarray}$$
The term corresponding to the contribution from mean settling in (3.8) can be further decomposed by defining
$\widehat{K}=\unicode[STIX]{x1D6FC}(2a\overline{U}_{r,z}/\unicode[STIX]{x1D708})^{\unicode[STIX]{x1D6FD}}$
, such that
$\overline{K}=\widehat{K}+K^{\prime \prime }$
. Note that
$\overline{K}$
is calculated with the particle Reynolds number defined with
$|\boldsymbol{U}_{r}|$
, and if the particle lateral motions vanish,
$\widehat{K}$
coincides with
$\overline{K}$
(i.e.
$K^{\prime \prime }\approx 0$
). In contrast, when particles are horizontally swept by turbulent eddies the term
$K^{\prime \prime }$
becomes greater than zero. Thus, we finally get
$$\begin{eqnarray}1=\frac{\overline{U}_{r,z}(1+\widehat{K})}{V_{s}}+\frac{\overline{U}_{r,z}K^{\prime \prime }}{V_{s}}+\frac{\langle U_{r,z}^{\prime }\,K^{\prime }\rangle }{V_{s}}+f_{D}^{U},\end{eqnarray}$$
where
$\overline{U}_{r,z}(1+\widehat{K})$
is the drag of the mean settling and is the only term in the case of a single sphere settling in still fluid.
$\overline{U}_{r,z}\,K^{\prime \prime }$
is the cross-flow-induced drag, i.e. the vertical component of the drag due to a non-zero horizontal relative motion. We name the term
$\langle U_{r,z}^{\prime }\,K^{\prime }\rangle$
as nonlinear-induced drag. This term becomes relevant in a turbulent flow when the variance of the particle velocity is larger than in still fluid. Finally, the term
$f_{D}^{U}$
accounts for unsteady effects, particle–particle and wake interactions and increases with the volume fraction (Fornari et al.
Reference Fornari, Picano and Brandt2016b
).
Figure 2. Relative contributions to the overall mean drag: (a) turbulent flow; (b) quiescent environment. The dashed line separates the contributions from the nonlinear-induced drag and the cross-flow-induced drag.
The relative importance of the 4 terms on the right-hand side of (3.9) is shown as percentage of the total drag in figure 2(a,b) for settling in turbulent and quiescent flow. In turbulence, the contributions due to the nonlinear-induced drag and the cross-flow-induced drag increase while reducing
$Ga$
. These increase from
$1\,\%$
and
$2\,\%$
at
$Ga=145$
to
$9\,\%$
and
$38\,\%$
at
$Ga=19$
and are the main responsible for the reduction in settling speed shown above. For
$Ga=19$
the mean nonlinear drag is
$44\,\%$
of the overall steady drag when settling occurs in quiescent fluid, while it increases to
$72\,\%$
of the overall mean steady drag in a turbulent flow. Thus, at small
$Ga$
, the nonlinear part of the overall mean steady drag increases drastically in turbulence. When
$Ga$
is large, in contrast, the nonlinear contribution to the overall mean steady drag is of the same order in the quiescent and turbulent cases (e.g. for
$Ga=145$
it amounts to
$84\,\%$
of the mean steady drag in both cases).
Unsteady effects also increase the overall drag in turbulent flows, see figure 2(a). The increase of the unsteady contribution in turbulent flow amounts to about
$10\,\%$
for
$Ga=145$
and
$6\,\%$
for
$Ga=19$
and
$60$
, which alone is not enough to explain the large reduction in
$\langle V_{z}\rangle _{p,t}$
at the lower
$Ga$
. These values are an estimate obtained by subtracting the percentage obtained in the quiescent cases to the percentage for the turbulent cases and show the additional increase in drag due to new unsteady effects, clearly weaker for particles settling in a quiescent fluid.
Further, we investigate the contribution of added mass to the overall mean drag. The added mass force is expressed as
$\unicode[STIX]{x1D712}(4\unicode[STIX]{x03C0}\unicode[STIX]{x1D70C}_{f}a^{3}/3)((\text{D}U_{z}/\text{D}t)-(\text{d}V_{z}/\text{d}t))$
, where
$\text{D}U_{z}/\text{D}t$
is the material derivative of the fluid velocity seen by the particle, and
$\unicode[STIX]{x1D712}=0.5$
the added mass coefficient (Chang & Maxey Reference Chang and Maxey1995; Merle, Legendre & Magnaudet Reference Merle, Legendre and Magnaudet2005). For each particle, we calculate the added mass force as an average over the volume of the spherical shells used to estimate the relative velocities. Finally, we compute an ensemble average for each particle and all time steps and normalize by the buoyancy term. The average values indicate that for the larger Galileo numbers the added mass contribution is negligible. For the lower
$Ga$
values, we find instead that the added mass contributes about
$1.5\,\%$
of the overall mean drag and
$25\,\%$
of the unsteady term.
Hence, our main finding is that when the turbulent velocity fluctuations
$u^{\prime }$
are larger than the characteristic reference velocity of the settling process (i.e. the terminal velocity of an isolated particle
$V_{t}$
) the overall drag significantly increases. This is due to the increased intensity of the particle relative motions and to the increase of the variance of the particle velocity.
In quiescent fluid, the major contribution to the overall drag comes from the term
$\overline{U}_{r,z}(1+\widehat{K})$
, see figure 2(b). The remaining part is due to the hindering effect (
$1\,\%$
for
$Ga=145$
and approximately
$10\,\%$
at lower
$Ga$
). These values are in agreement with the reduction of the mean settling velocity
$\langle V_{z}\rangle _{p,t}$
reported above. Note that we checked that for an isolated particle in quiescent fluid
$F_{D}^{S}=4\unicode[STIX]{x03C0}a^{3}(\unicode[STIX]{x1D70C}_{p}-\unicode[STIX]{x1D70C}_{f})\boldsymbol{g}/3$
(within
$\pm 3.5\,\%$
error for all
$Ga$
). Indeed, for single particles at these
$Ga$
there are no unsteady contributions to the overall drag and
$F_{D}^{U}=0$
. Possible reasons for this inaccuracy are the use of empirical formulae, and the thickness of the shell used in the definition of
$\boldsymbol{U}_{r}$
.
Given the finding above, we quantify the importance of the cross-flow induced motions by examining the p.d.f.s of
$|\boldsymbol{U}_{r}|$
and
$U_{r,z}$
, shown in figure 3(a). First, we consider the origin of possible differences between the absolute relative velocity and the mean settling speed. To this aim, we express each velocity component in
$|\boldsymbol{U}_{r}|$
as the sum of mean and fluctuations,
$$\begin{eqnarray}|\boldsymbol{U}_{r}|=\sqrt{U_{r,x}^{\prime 2}+U_{r,y}^{\prime 2}+(\overline{U}_{r,z}+U_{r,z}^{\prime })^{2}}=\overline{U}_{r,z}\sqrt{\frac{U_{r,x}^{\prime 2}}{\overline{U}_{r,z}^{2}}+\frac{U_{r,y}^{\prime 2}}{\overline{U}_{r,z}^{2}}+\left(1+\frac{2U_{r,z}^{\prime }}{\overline{U}_{r,z}}+\frac{U_{r,z}^{\prime 2}}{\overline{U}_{r,z}^{2}}\right)}\end{eqnarray}$$
(with
$\overline{U}_{r,x}\simeq \overline{U}_{r,y}\simeq 0$
by symmetry). In the quiescent cases
$U_{r,i}^{\prime }\ll \overline{U}_{r,z}$
and
$|\boldsymbol{U}_{r}|\simeq \overline{U}_{r,z}$
. In a turbulent flow, if
$V_{t}/u^{\prime }$
is large the quadratic terms are negligible and
$|\boldsymbol{U}_{r}|\simeq \overline{U}_{r,z}\sqrt{1+2U_{r,z}^{\prime }/\overline{U}_{r,z}}$
(i.e. only fluctuations in the direction of gravity are important). If
$V_{t}/u^{\prime }<1$
, instead, the quadratic terms are dominant and
$|\boldsymbol{U}_{r}|$
can be substantially larger than
$\overline{U}_{r,z}$
.
Figure 3. (a) Probability density functions of
$|\boldsymbol{U}_{r}|$
and
$U_{r,z}$
. The shaded zones show the difference between the mean values of
$|\boldsymbol{U}_{r}|$
and
$U_{r,z}$
. The inset shows the ratio between
$\overline{|\boldsymbol{U}_{r}|}$
and
$\overline{U}_{r,z}$
. (b) Anisotropy in the particle velocity fluctuations
$\unicode[STIX]{x1D70E}_{n}/\unicode[STIX]{x1D70E}_{z}$
(blue circles) and standard deviation of the settling angle
$\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D703}^{\circ }}$
(orange squares) as a function of
$Ga$
.
We see indeed in figure 3(a) that the difference
$\overline{|\boldsymbol{U}_{r}|}-\overline{U}_{r,z}$
(given by the shaded zones) increases by reducing
$Ga$
. Roughly assuming that
$U_{r,i}^{\prime }/\overline{U}_{r,z}\approx u^{\prime }/V_{t}$
, one can obtain estimates of the relative velocity
$|\boldsymbol{U}_{r}|$
in agreement with the DNS data: for
$Ga=19$
, we obtain
$\overline{|\boldsymbol{U}_{r}|}\sim 9.3\overline{U}_{r,z}$
instead of the actual value
$9.4$
, for
$Ga=60$
,
$\overline{|\boldsymbol{U}_{r}|}\sim 2.4\overline{U}_{r,z}$
instead of
$1.5$
, for
$Ga=145$
,
$\overline{|\boldsymbol{U}_{r}|}\sim 1.3\overline{U}_{r,z}$
instead of
$1$
, see the inset of figure 3(a). Hence, the cross-flow-induced drag may be estimated a priori. It is important to note that at low
$Ga$
, the relative velocity fluctuations in the direction of gravity also contribute to
$|\boldsymbol{U}_{r}|$
and therefore to the increase in drag. However, the contribution from transverse fluctuations is twice that in the direction of gravity. Hence, the name cross-flow-induced drag.
Here
$\langle |\boldsymbol{U}_{r}|\rangle$
can be used to estimate the particle Reynolds number
$Re_{p}=(2a)\langle |\boldsymbol{U}_{r}|\rangle /\unicode[STIX]{x1D708}$
for each case studied. For
$Ga=19$
,
$60$
,
$145$
and
$200$
we find
$Re_{p}=45.6$
,
$61.9$
,
$176.7$
and
$263.6$
in turbulence and
$Re_{p}=9.3$
,
$52.1$
,
$185.5$
and
$272.4$
in quiescent fluid. This confirms that the relative velocities drastically increase at low
$Ga$
in the turbulent cases.
In figure 3(b) we show the ratio between the particle fluctuating velocities in the directions perpendicular and parallel to gravity,
$\unicode[STIX]{x1D70E}_{n}/\unicode[STIX]{x1D70E}_{z}$
. We note that
$\unicode[STIX]{x1D70E}_{n}/\unicode[STIX]{x1D70E}_{z}$
grows with
$Ga$
. At the lowest
$Ga$
, the particle velocity fluctuations are approximately the same in all directions. At high
$Ga$
the anisotropy increases (
$\unicode[STIX]{x1D70E}_{n}/\unicode[STIX]{x1D70E}_{z}$
increases), as particles fall faster and the fluctuations in the vertical direction are relatively less important. As
$\unicode[STIX]{x1D70E}_{n}/u^{\prime }$
is approximately constant for all cases, particles are seen to undergo less-intense lateral motions at high
$Ga$
when the dynamics is dominated by buoyancy. Interestingly, the opposite behaviour is observed for heavy point particles (Good et al.
Reference Good, Ireland, Bewley, Bodenschatz, Collins and Warhaft2014) showing the importance of particle size. In the same figure, we also display the standard deviation
$\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D703}^{\circ }}$
of the angle between the mean particle velocity and the vertical axis,
$\unicode[STIX]{x1D703}=\text{arctg}(V_{n}/V_{z})$
. In agreement with the previous observations,
$\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D703}^{\circ }}$
is
$4$
times larger for
$Ga=19$
than for
$Ga=200$
. Heavy finite-size particles fall along almost straight vertical paths, whereas lighter particles are strongly swept laterally by intense eddies and, hence, the larger
$\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D703}^{\circ }}$
.
As discussed above, the particle mean settling speed
$\langle V_{z}\rangle$
is mostly governed by buoyancy at high
$Ga$
, while it is affected strongly by turbulence at low
$Ga$
. It is, however, interesting to observe that the variance of the particle settling speeds is similar for each
$Ga$
. To show this we report in figure 4(a) the p.d.f.s of particle settling speeds
$V_{z}$
and of
$V_{z}-\langle V_{z}\rangle _{p,t}$
(inset) in turbulence, normalized by
$u^{\prime }$
. these indicate that the variance is similar in all cases and that the different curves almost overlap. Hence, although the effect of the turbulence on the mean settling speed depends on
$V_{t}/u^{\prime }$
, fluctuations of the settling speed depend mostly on the properties of the turbulent flow (i.e. on
$u^{\prime }$
).
Figure 4. (a) Probability density functions of
$V_{z}/u^{\prime }$
and
$(V_{z}-\langle V_{z}\rangle _{p,t})/u^{\prime }$
(inset) in turbulence. (b) Probability density functions of particle accelerations in turbulence (
$\text{d}V_{x}/\text{d}t$
and
$\text{d}V_{z}/\text{d}t$
, scaled by
$(2a)/u^{\prime 2}$
), for
$Ga=19$
and
$145$
. (c) Particle mean-square displacement in the settling direction
$S_{2}^{Z}$
in turbulence. In the inset we show the mean-square displacements along the settling direction for
$Ga=19$
and
$200$
, for both quiescent and turbulent cases.
Next we examine particle accelerations in turbulence. We therefore depict in figure 4(b) the p.d.f.s of
$\text{d}V_{x}/\text{d}t$
and
$\text{d}V_{z}/\text{d}t$
scaled by
$u^{\prime 2}/(2a)$
, for
$Ga=19$
and
$145$
(since the configuration is axialsymmetric,
$\text{d}V_{y}/\text{d}t$
is not reported). We note, surprisingly, that the p.d.f.s of particle accelerations collapse onto one curve (the p.d.f.s are not shown for
$Ga=60$
and
$200$
for the sake of clarity); only the p.d.f.s of
$\text{d}V_{x}/\text{d}t$
for
$Ga=145$
and
$200$
are slightly different. Hence, particle accelerations are also almost completely governed by turbulence and all curves are almost perfectly symmetric. Note also that similar shapes for the p.d.f.s of accelerations have been found experimentally for negatively buoyant spheres (Mathai et al.
Reference Mathai, Prakash, Brons, Sun and Lohse2015).
The particle mean-square displacement in the settling direction
$S_{2}^{Z}=\langle (\unicode[STIX]{x0394}z-\langle V_{z}\rangle t)^{2}\rangle$
is also mainly determined by the properties of the turbulent flow. As shown in figure 4(c), the mean-square displacements pertaining to all
$Ga$
almost collapse when scaling time with
$(2a)/u^{\prime }$
. In the inset of the same figure, we compare
$S_{2}^{Z}$
for quiescent and turbulent cases at
$Ga=19$
and
$200$
, where times are scaled by
$(2a)/V_{t}$
. For particles falling relatively fast,
$Ga=200$
,
$S_{2}^{Z}$
is similar in quiescent and turbulent flow. In contrast,
$S_{2}^{Z}$
increases significantly in the turbulent case for the smallest
$Ga$
under investigation.
To conclude, we would like to note that our results are qualitatively consistent with the findings of Homann et al. (Reference Homann, Bec and Grauer2013) and Chouippe & Uhlmann (Reference Chouippe and Uhlmann2015). These authors suggest that the nonlinear drag acting on particles in a turbulent flow is higher than in laminar or quiescent fluid. They suggest that the relative increase in drag is proportional to
$C(Re_{p})I^{2}$
, where
$C(Re_{p})$
is a nonlinear function of the particle Reynolds number
$Re_{p}$
, while
$I\sim u^{\prime }/U_{r,z}$
is the relative turbulence intensity (similar to our definition). This scaling confirms that drag nonlinearity increases as the relative turbulence intensity
$I$
increases, in agreement with our results.
3.3 Comparison with sub-Kolmogorov particles
Finally, we wish compare the reduction observed for finite-size slightly buoyant particles to the behaviour of heavy sub-Kolmogorov particles. Their settling speed,
$\langle V_{z}\rangle /V_{t}$
, is found to reduce when increasing particle inertia (i.e. increasing
$V_{t}/u^{\prime }$
and
$\unicode[STIX]{x1D70F}_{p}$
), the opposite of what reported here for finite-size particles. We therefore performed simulations of heavy (
$\unicode[STIX]{x1D70C}_{p}/\unicode[STIX]{x1D70C}_{f}\sim 1000$
) point particles in HIT (see Olivieri et al.
Reference Olivieri, Picano, Sardina, Iudicone and Brandt2014, for details on the method). At high
$\unicode[STIX]{x1D70C}_{p}/\unicode[STIX]{x1D70C}_{f}$
, the particle acceleration is determined only by gravity and drag
$$\begin{eqnarray}\frac{\text{d}\boldsymbol{V}}{\text{d}t}=-\frac{\boldsymbol{U}_{r}}{\unicode[STIX]{x1D70F}_{p}}\unicode[STIX]{x1D701}+\boldsymbol{g},\end{eqnarray}$$
where
$\unicode[STIX]{x1D701}=1+0.15Re_{p}^{0.687}$
is the nonlinear drag correction also used by Good et al. (Reference Good, Ireland, Bewley, Bodenschatz, Collins and Warhaft2014). We study three different cases, characterized by particle relaxation times
$\unicode[STIX]{x1D70F}_{p}=0.389,1.296$
and
$12.96$
and ratio between settling speed and turbulence intensity
$V_{s}/u^{\prime }=0.1,0.3$
and
$3$
. The turbulent flow field has
$Re_{\unicode[STIX]{x1D706}}=90$
and a ratio
$u^{\prime }/u_{\unicode[STIX]{x1D702}}=4.77$
.
In figure 5(a) we report the mean settling speed,
$\langle V_{z}\rangle /V_{t}$
where the reference settling speed is
$V_{t}=V_{s}/\unicode[STIX]{x1D701}$
, the mean fluid velocity sampled by the particles
$\langle U_{z}\rangle$
and the relative velocity
$\langle U_{r,z}\rangle /V_{t}$
. In agreement with the previous studies mentioned above, the mean settling speed decreases with
$V_{t}/u^{\prime }$
and becomes smaller than unity for the largest
$V_{t}/u^{\prime }$
(
$\unicode[STIX]{x1D70F}_{p}=12.96$
). The fluid velocity at the particle position is positive at small
$V_{t}/u^{\prime }$
(small
$\unicode[STIX]{x1D70F}_{p}$
) and tends to zero when increasing the particle inertia. In other words, at small
$V_{t}/u^{\prime }$
, preferential sweeping occurs and sub-Kolmogorov particles settle with
$\langle V_{z}\rangle >V_{t}$
. The reduction of the mean settling velocity at large
$V_{t}/u^{\prime }$
is thus due to the absence of sampling of downdrafts.
It can be proven that using nonlinear drag corrections is necessary to find
$\langle V_{z}\rangle /V_{t}<1$
, as observed at large
$V_{t}/u^{\prime }$
. To this end, we express
$U_{r,z}$
and
$V_{z}$
in terms of a power series of the modified Reynolds number
$\widehat{R}e=0.15Re_{p}^{0.687}$
:
$$\begin{eqnarray}\displaystyle & U_{r,z}=u_{0}+u_{1}\widehat{R}e+u_{2}\widehat{Re}^{2}+\text{h.o.t.}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & V_{z}=v_{0}+v_{1}\widehat{R}e+v_{2}\widehat{Re}^{2}+\text{h.o.t.}, & \displaystyle\end{eqnarray}$$
where ‘h.o.t.’ denotes higher order terms. Substituting in the particle equation (3.11), projecting along gravity and time averaging, we obtain at first order
$$\begin{eqnarray}\langle V_{z}\rangle =\langle U_{z}\rangle +V_{t}(1-\widehat{Re}^{2}).\end{eqnarray}$$
It appears therefore clearly that drag nonlinearity is responsible for the reduction of settling speed in the absence of preferential sampling.
The effect of drag nonlinearity is however modest and the nonlinear contribution to the overall drag increases slowly with
$V_{t}/u^{\prime }$
. To show this, we perform the same force analysis done for finite-size particles. We average (3.11) and express velocity and drag coefficient as the sum of mean values (
$\overline{\cdot }$
) and fluctuating components (
$\cdot ^{\prime }$
). As above, we finally obtain
$$\begin{eqnarray}g\unicode[STIX]{x1D70F}_{p}=\overline{U}_{r,z}(1+\widehat{K})+\overline{U}_{r,z}K^{\prime \prime }+\langle U_{r,z}^{\prime }\,K^{\prime }\rangle\end{eqnarray}$$
with
$\overline{K}=\widehat{K}+K^{\prime \prime }$
(where
$\widehat{K}=0.15(2a\overline{U}_{r,z}/\unicode[STIX]{x1D708})^{0.687}$
). The results in figure 5(b) show that increasing
$V_{t}/u^{\prime }$
, the nonlinear-induced drag and the cross-flow-induced drag only slightly increase.
We finally consider the role of loitering (Nielsen Reference Nielsen1993). As in Good et al. (Reference Good, Ireland, Bewley, Bodenschatz, Collins and Warhaft2014) we perform simulations in which the particles are constrained to settle along vertical paths. In such artificial case, the settling speed,
$\langle V_{p,z}\rangle /V_{t}$
, is always less than one and the fluid velocity at the particle position,
$\langle U_{z}\rangle /V_{t}$
, is negative (opposite to the direction to gravity). In other words, particles preferentially sample updrafts. According to Nielsen (Reference Nielsen1993), loitering should become effective when
$V_{s}/u^{\prime }\geqslant 0.3$
. However, simulations of particles free to move horizontally show that the preferential sampling occurs always in downdrafts and tends to zero as
$V_{t}/u^{\prime }$
(or equivalently
$\unicode[STIX]{x1D70F}_{p}$
) increases. Loitering seems therefore absent in HIT.
Figure 5. (a) Plots of
$\langle V_{z}\rangle /V_{t}$
,
$\langle U_{z}\rangle /V_{t}$
and
$\langle U_{r,z}\rangle /V_{t}$
and (b) drag map for the point-particle cases as a function of
$V_{t}/u^{\prime }$
. Here
$V_{s}/u^{\prime }=0.1$
,
$0.3$
and
$3$
correspond to
$V_{t}/u^{\prime }=0.095$
,
$0.268$
and
$1.9$
.
4 Final remarks
We have examined how the settling of finite-size particles in HIT is affected by the relative turbulence intensity,
$V_{t}/u^{\prime }$
. In particular, we have considered particles that are slightly heavier than the carrier fluid. We find that as
$Ga$
or
$V_{t}/u^{\prime }$
decrease the mean settling speed reduces. This reduction is stronger when
$V_{t}/u^{\prime }<1$
(about
$60\,\%$
for
$Ga=19$
and
$V_{t}/u^{\prime }=0.19$
). We attribute this reduction at small
$V_{t}/u^{\prime }$
to unsteady effects and, prominently, to drag nonlinearity. The component of the drag acting in the direction of gravity increases due to the increase of the fluid–particle relative velocity in comparison to the quiescent cases. This is associated with the strong lateral/cross-flow motions induced by the turbulent eddies on the settling particles. When
$Ga$
(or
$V_{t}/u^{\prime }$
) is large, particles fall along vertical paths with weak relative lateral velocities. Lighter particles, instead, are subjected to velocity fluctuations one order of magnitude larger than their mean settling velocities. These particles have therefore significant lateral relative velocities and this, in turn, determines an increase of the drag acting on them. Indeed at small
$Ga$
, the particle Reynolds number
$Re_{p}$
(defined via the magnitude of the slip velocity
$|\boldsymbol{U}_{r}|$
) is substantially larger in a turbulent flow than in quiescent fluid, for which it is of the order of the average settling speed
$\langle |\boldsymbol{U}_{r}|\rangle \sim \langle V_{z}\rangle$
.
Although the reduction of the mean settling speed,
$\langle V_{z}\rangle$
, depends on the relative turbulence intensity (i.e.
$V_{t}/u^{\prime }$
), other quantities depend exclusively on the turbulent velocity fluctuations,
$u^{\prime }$
. Indeed, we report that the particle velocity fluctuations are very similar in all directions for all
$Ga$
. These are just slightly smaller in the direction perpendicular to gravity at the higher
$Ga$
. Moreover, the p.d.f.s of particle accelerations and the mean-square displacements almost perfectly collapse on a single curve when scaling appropriately the different quantities with the turbulence intensity,
$u^{\prime }$
.
Finally, we have compared the behaviour of finite-size and sub-Kolmogorov particles. As already discussed, the mean settling speed of large particles decreases as their inertia is reduced (i.e. lower
$Ga$
and
$\unicode[STIX]{x1D70F}_{p}$
). The reduced settling speed of finite-size particles is related to the large fluctuations of the relative velocity and, hence, to the increase of the nonlinear drag. In contrast, the variation of settling speed of point-like particles can be mainly explained by preferential sampling of downdrafts. Indeed, for this type of particles the mean settling speed is reduced as their inertia increases and eventually reaches a plateau around
$\langle V_{z}\rangle \simeq V_{t}$
at very large
$\unicode[STIX]{x1D70F}_{p}$
, since preferential sampling progressively disappears. For the range of parameters here studied, we also find that loitering plays a negligible role in reducing the mean settling speed of point-like particles.
Acknowledgements
This work was supported by the European Research Council grant no. ERC-2013-CoG-616186, TRITOS and by the Swedish Research Council (VR). Computer time was provided by SNIC (Swedish National Infrastructure for Computing). The support from the COST Action MP1305: Flowing matter is also acknowledged.
